Abstract
We introduce the multivariable connected sum which is a generalization of Seki–Yamamoto’s connected sum and prove the fundamental identity for these sums by series manipulation. This identity yields explicit procedures for evaluating multivariable connected sums and for giving relations among special values of multiple polylogarithms. In particular, our class of relations contains Ohno’s relations for multiple polylogarithms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In [13], a symmetrical double series expression of\(\zeta (2)\) due to B. Cloitre is exhibited:
The right-hand side of (1.1) is a special case of the connected sum introduced by the third author and Yamamoto [12]. We provide a brief review of this theory here. We call a tuple of positive integers \(\varvec{k}=(k_1,\dots ,k_r)\) an index. If \(k_r\ge 2\), then we call \(\varvec{k}\) an admissible index. We call r (resp. \(k_1+\cdots +k_r\)) the depth (resp. weight) of \(\varvec{k}\) and denote it by \(\mathrm {dep}(\varvec{k})\) (resp. \(\mathrm {wt}(\varvec{k})\)). We regard the empty tuple \(\varnothing \) as an admissible index and call it the empty index. We set \(\mathrm {dep}(\varnothing ){:}{=}0\) and \(\mathrm {wt}(\varnothing ){:}{=}0\). For two indices \(\varvec{k}=(k_1,\dots ,k_r)\) and \(\varvec{l}=(l_1,\dots , l_s)\), the connected sum \(Z(\varvec{k};\varvec{l})\) is defined by

Throughout, we understand that the empty product (resp. sum) is 1 (resp. 0). It is straightforward to see that the symmetry \(Z(\varvec{k};\varvec{l})=Z(\varvec{l};\varvec{k})\) and the boundary condition \(Z(\varvec{k};\varnothing )=\zeta (\varvec{k})\) hold. Here, \(\zeta (\varvec{k})\) is the multiple zeta value (MZV)
and this series is convergent if \(\varvec{k}\) is admissible. The most important properties for the connected sum are the transport relations. To state them, we introduce arrow notation for indices. For a non-empty index \(\varvec{k}=(k_1,\dots ,k_r)\), we define \(\varvec{k}_{\rightarrow }\) (resp. \(\varvec{k}_{\uparrow }\)) to be \((k_1,\dots ,k_r,1)\) (resp. \((k_1,\dots ,k_{r-1},k_r+1)\)). We set \(\varnothing _{\rightarrow }{:}{=}(1)\) and \(\varnothing _{\uparrow }{:}{=}\varnothing \). Then, the transport relations for \(Z(\varvec{k};\varvec{l})\) are as follows (the \(q\rightarrow 1\), \(x\rightarrow 0\) case of [12, Theorem 2.2]):
By using these properties of the connected sum, we can prove the duality relation for MZVs “\(\zeta (\varvec{k})=\zeta (\varvec{k}^{\dagger })\).” Here, we explain the definition of the dual index \(\varvec{k}^{\dagger }\). For a non-negative integer m and a complex number z, the symbol \(\{z\}^m\) denotes m repetitions of z. Any admissible index \(\varvec{k}\ne \varnothing \) is uniquely expressed as \(\varvec{k}=(\{1\}^{a_1-1},b_1+1,\dots ,\{1\}^{a_h-1},b_h+1)\), where \(h,a_1,\dots ,a_h,b_1,\dots ,b_h\) are positive integers. Then, the dual index is defined as \(\varvec{k}^{\dagger }{:}{=}(\{1\}^{b_h-1},a_h+1,\dots ,\{1\}^{b_1-1},a_1+1)\). For the empty index, we use \(\varnothing ^{\dagger }{:}{=}\varnothing \). The duality relation is immediately proved by the change of variables in the iterated integral representation of the MZV (a special case of (1.6) below). We emphasize that Seki–Yamamoto’s proof is executed using only series manipulation and no iterated integral is required.
Since the single index \(\varvec{k}=(2)\) is self-dual, the duality for this \(\varvec{k}\) is a tautology “\(\zeta (2)=\zeta (2)\).” However, the transportation process includes a non-trivial component as follows:
We see that the identity \(\zeta (2)=Z(1;1)\) is nothing but Cloitre’s identity (1.1). Note that parentheses will often be omitted, such as \(Z((2);\varnothing )=Z(2;\varnothing )\) and \(Z((1);(1))=Z(1;1)\).
In [14], an elegant series expression of Apéry’s constant \(\zeta (3)\) owing to O. Oloa is exhibited:
Identities (1.1) and (1.4) are also discussed on the website “les-mathematiques.net” in a forum post entitled “Accélération pour zeta(2)” [1]. In a post entitled “Série triple” [10] on the same website, the following series identity is given:
Furthermore, a user named Amtagpa showed

for a general positive integer n by using the iterated integral representation. Here, the multiple polylogarithm (MPL)  is of the so-called shuffle-type:
is of the so-called shuffle-type:

where \(\varvec{k}=(k_1,\dots , k_r)\) is an index and \(z_1,\dots , z_r\) are complex numbers satisfying \(|z_1|,\dots ,|z_r|\le 1\). If \((k_r,|z_r|)\ne (1,1)\), then this series is absolutely convergent. The shuffle-type MPL has the iterated integral representation

in the notation of [5]. The shuffle-type MPLs inherit the shuffle product property of iterated integrals directly in the \(z_i\) variables, and this fact is the reason why we call these series “shuffle-type.” There is another type of MPL, the harmonic-type MPL used and defined in Sect. 4, but we principally focus on the shuffle-type MPL in this paper. We can check that  holds. For example, by the duality for MPLs (the \(n=2\) case of (5.1)), we see that
holds. For example, by the duality for MPLs (the \(n=2\) case of (5.1)), we see that  ; see Sect. 3.2 for the notation for the alternating multiple zeta values. Then, the evaluation \(-2\zeta (\overline{1},\overline{2})=\frac{13}{4}\zeta (3)-\frac{\pi ^2}{2}\log 2\) is confirmed by [16, Proposition 14.2.7].
; see Sect. 3.2 for the notation for the alternating multiple zeta values. Then, the evaluation \(-2\zeta (\overline{1},\overline{2})=\frac{13}{4}\zeta (3)-\frac{\pi ^2}{2}\log 2\) is confirmed by [16, Proposition 14.2.7].
Our focus in this paper is on interpreting identities (1.4) and (1.5) by transporting indices in the same way as in Cloitre’s identity (1.1). For this purpose, we extend Seki–Yamamoto’s connected sum to the multiple connected sum as follows. We set \(S_r{:}{=}\{\varvec{m}=(m_0,m_1,\dots ,m_r)\in \mathbb {Z}^{r+1}\mid m_0=0<m_1<\cdots <m_r\}\) and \(S^{\star }_s(m){:}{=}\{\varvec{q}=(q_0,q_1,\dots ,q_s)\in \mathbb {Z}^{s+1}\mid q_0=0<q_1\le \cdots \le q_s=m\}\) for non-negative integers r, s and m. Furthermore, we set
for a positive integer n and non-negative integers \(a_1,\dots , a_n\). This value \(C(a_1,a_2,\dots ,a_n)\) is just the inverse of a multinomial coefficient, but in the context of multiple connected sums, we call it the connector because of its role. Using these notation, for a positive integer n and indices \(\varvec{k}_1=(k_1^{(1)},\dots ,k_{r_1}^{(1)}),\dots , \varvec{k}_n=(k_1^{(n)},\dots ,k_{r_n}^{(n)})\) and \(\varvec{l}=(l_1,\dots ,l_s)\), we define the multiple connected sum \(Z_n(\varvec{k}_1;\dots ;\varvec{k}_n\mid \varvec{l})\) as
where \(\varvec{m}^{(1)}=(m_1^{(1)},\dots ,m_{r_1}^{(1)}),\dots , \varvec{m}^{(n)}=(m_1^{(n)},\dots , m_{r_n}^{(n)})\) and \(\varvec{q}=(q_1,\dots , q_s)\). Set \(Z_n(\varvec{k}_1;\dots ;\varvec{k}_n\mid \varnothing ){:}{=}0\) and \(Z_n(\varvec{k}_1;\dots ;\varvec{k}_n){:}{=}Z_n(\varvec{k}_1;\dots ;\varvec{k}_n\mid 1)\).
The original Seki–Yamamoto’s connected sum \(Z(\varvec{k};\varvec{l})\) coincides with our \(Z_2(\varvec{k};\varvec{l})=Z_2(\varvec{k};\varvec{l}\mid 1)\), not \(Z_1(\varvec{k}\mid \varvec{l})\). The series appearing in identities (1.4) and (1.5) are \(Z_2(1;1\mid 1,1)\) and \(Z_{n+1}(1;\dots ;1)\), respectively. The presence of the \(\varvec{l}\)-component in the definition is advantageous for obtaining relations among MZVs or MPLs, and the \(n=1\) case of our connected sum has been explored in previous studies; \(Z_1(\varvec{k}\mid \varvec{l}_{\uparrow })\) (\(\varvec{k}, \varvec{l}\ne \varnothing \)) is the multiple zeta value of Kaneko–Yamamoto type introduced in [6], and \(Z_1(\varvec{k}\mid \varvec{l}_{\rightarrow })\) (\(\varvec{k}\) is admissible) is the Schur multiple zeta value of anti-hook type introduced in [7]. Note that these two kinds of series are the same object by definition or by the \(n=1\) case of Proposition 2.2 below.
In what follows, we provide an explicit procedure for calculating \(Z_n(\varvec{k}_1;\dots ;\varvec{k}_n\mid \varvec{l})\) via transportations of indices and prove the transport relations by series manipulation. In addition to identities (1.4) and (1.5), our method leads to a formula for \(\zeta (4)\) (see Example 5.4):
More generally, we prove the following.
Theorem 1.1
Let n be an integer at least 2 and \(\varvec{k}_1,\ldots ,\varvec{k}_n,\varvec{l}\) non-empty indices. We set \(k{:}{=}\mathrm {wt}(\varvec{k}_1)+\cdots +\mathrm {wt}(\varvec{k}_n)+\mathrm {wt}(\varvec{l})\) and define \(\mathrm {MPL}(n,k)\) by

Then, the multiple connected sum \(Z_n(\varvec{k}_1;\dots ;\varvec{k}_n\mid \varvec{l})\) can be written explicitly as a \(\mathbb {Z}\)-linear combination of elements of \(\mathrm {MPL}(n,k)\).
The proof of this theorem by transporting indices requires the use of more general connected sums; see Example 3.3 for instance. In view of this phenomenon, it is natural to define the following generalization of the multiple connected sum. Let n be a positive integer and \(\varvec{k}_1=(k_1^{(1)},\dots ,k_{r_1}^{(1)}),\dots , \varvec{k}_n=(k_1^{(n)},\dots ,k_{r_n}^{(n)})\) and \(\varvec{l}=(l_1,\dots ,l_s)\) indices. Let \(\varvec{z}_1=(z_1^{(1)},\dots ,z_{r_1}^{(1)}),\dots , \varvec{z}_n=(z_1^{(n)},\dots ,z_{r_n}^{(n)})\) and \(\varvec{w}=(w_1,\dots , w_s)\) be elements of \(\mathbb {D}^{r_1},\dots ,\mathbb {D}^{r_n}\) and \(\mathbb {D}^{s}\), respectively. Here, the symbol \(\mathbb {D}\) denotes the unit disk \(\{z\in \mathbb {C}\mid |z|\le 1\}\) and the unique element of \(\mathbb {D}^0\) is denoted by \(\varnothing \). Then, the multivariable connected sum is defined by

where \(\varvec{m}^{(1)}=(m_1^{(1)},\dots ,m_{r_1}^{(1)}),\dots , \varvec{m}^{(n)}=(m_1^{(n)},\dots , m_{r_n}^{(n)})\) and \(\varvec{q}=(q_1,\dots , q_s)\). Set  and
and  . We establish the fundamental identity for multivariable connected sums. To do so, we generalize the arrow notation appropriately. Let \(\varvec{k}\) be an index and \(\varvec{z}\in \mathbb {D}^{\mathrm {dep}(\varvec{k})}\). Let v be an element of \(\mathbb {D}\setminus \{0\}\). Then, we use the following notation:
. We establish the fundamental identity for multivariable connected sums. To do so, we generalize the arrow notation appropriately. Let \(\varvec{k}\) be an index and \(\varvec{z}\in \mathbb {D}^{\mathrm {dep}(\varvec{k})}\). Let v be an element of \(\mathbb {D}\setminus \{0\}\). Then, we use the following notation:
In relation to the last symbol, we use the following definition:

for \(\epsilon _1,\dots , \epsilon _n\in \{1,-1\}\).
The following identity is key to this paper.
Theorem 1.2
(Fundamental identity) Let n be an integer greater than 1 and \(\varvec{k}_1,\dots , \varvec{k}_{n+1}\) indices. Take tuples of complex numbers \(\varvec{z}_i\in \mathbb {D}^{\mathrm {dep}(\varvec{k}_i)}\) for all \(1\le i \le n+1\). Furthermore, take \(v_1,\dots , v_n\in (\mathbb {D}\setminus \{0\})\cup \{\infty \}\) and \(v_{n+1}\in \mathbb {D}\) satisfying
and the assumption that
-
(1)
if \(\varvec{k}_i=\varnothing \) \((1\le i\le n)\), then \(v_i\ne \infty \), and
-
(2)
if \(n=2\) and \(\varvec{k}_i=\varnothing \) for \(1\le i\le 2\), then \(|v_{3-i}|\ne 1\) or \(|v_3|<1\).
Here, we understand \(1/\infty =0\) and \(|\infty |=\infty \). Then, we have

Here, the symbol  means that only the ith component is not equipped with the arrow notation.
means that only the ith component is not equipped with the arrow notation.
For example, the \(n=3\) case for the fundamental identity is

The fundamental identity supplies all needed transport relations for the multivariable connected sums in this paper. By transporting indices and variables algorithmically, in accordance with the method presented in [11], a given multivariable connected sum satisfying a suitable condition is written as a \(\mathbb {Z}\)-linear combination of \(Z_1\)-values. We regard the boundary conditions for multivariable connected sums as the fact that \(Z_1\)-values are written as \(\mathbb {Z}\)-linear combinations of MPLs; if \(\varvec{w}=\varvec{l}=(1)\), then the boundary conditions are trivial.
Thus, main theorems of the present paper are Theorem 1.1, Theorem 1.2 and the following two theorems:
Theorem 1.3
(see Theorem 5.2 for the precise statement) Every multivariable connected sum with transportable variables can be expressed explicitly as a \(\mathbb {Z}\)-linear combination of absolutely convergent multiple polylogarithms.
Theorem 1.4
(see Sect. 6.1 for the precise recipe) Transport relations and boundary conditions for multivariable connected sums give a family of functional relations among multiple polylogarithms. As a special case, Ohno’s relation for multiple polylogarithms is obtained.
For simplicity, conditional convergent series and analytic continuations are disregarded herein.
The remainder of the paper is organized as follows. In Sect. 2, we prove the fundamental identity. In Sect. 3, we explain transport relations derived from the fundamental identity and reprove the duality relation for MPLs. In Sect. 4, we describe the boundary conditions. In Sect. 5, we give the recipe for obtaining evaluations of multivariable connected sums and prove Theorem 1.1 and Theorem 1.3. Finally, in Sect. 6, we give the recipe for obtaining relations among MPLs and prove Theorem 1.4. Ohno’s relation for MPLs is also proved here. Some examples are exhibited in Sects. 3–6.
2 The fundamental identity
First, we prepare basic properties of the multivariable connected sum.
Proposition 2.1
Let n be a positive integer and \(\varvec{k}_1,\dots , \varvec{k}_n, \varvec{l}\) indices. Take tuples of complex numbers \(\varvec{z}_i\in \mathbb {D}^{\mathrm {dep}(\varvec{k}_i)}\) for all \(1\le i\le n\) and \(\varvec{w}\in \mathbb {D}^{\mathrm {dep}(\varvec{l})}\). Then, the following statements hold:
-
(i)
For \(\varvec{z}_1=(z_1,\dots , z_r), \varvec{w}=(w_1,\dots , w_s)\) \((r=\mathrm {dep}(\varvec{k}_1), s=\mathrm {dep}(\varvec{l}))\), we assume that \(|z_r|<1\) or \(|w_s|<1\) holds if both \(\varvec{k}_1\) and \(\varvec{l}\) are non-admissible. Then,
 converges absolutely, and for the case of \(\varvec{l}=(1)\), \(\varvec{w}=(1)\), we have
converges absolutely, and for the case of \(\varvec{l}=(1)\), \(\varvec{w}=(1)\), we have  .
. -
(ii)
If \(n>1\) and all \(\varvec{k}_i\) are non-empty, then the multivariable connected sum

converges absolutely.
-
(iii)
For any permutation \(\sigma \) of degree n,

holds.
-
(iv)
Let \(n>1\). For all \(1\le i\le n\), we have

where
 denotes the skipped entry.
denotes the skipped entry.
Proof
We prove only (ii) because the others are obvious by definition. It is sufficient to show that \(Z_n(\varvec{k}_1;\dots ;\varvec{k}_n\mid \varvec{l})\) converges. Since \(n>1\), the inequality
holds for positive integers \(m_1,\dots , m_n\); the case \(n=2\) is proved from the estimate
and then the general case follows from induction on n. Take any \(\varepsilon >0\) and set \(s=\mathrm {dep}(\varvec{l})\) and \(\varvec{l}=(l_1,\dots ,l_s)\). Then, there exists some positive constant \(c_{\varepsilon ,s,n}\) depending on \(\varepsilon , s, n\) such that
By these elementary facts, we see that \(Z_n(\varvec{k}_1;\dots ;\varvec{k}_n\mid \varvec{l})\) is bounded above by a constant multiple of a product of n convergent special values of the multiple zeta function. \(\square \)
By virtue of Proposition 2.1 (iii), Theorem 1.2 is a consequence of Proposition 2.2 and Theorem 2.4 below.
Proposition 2.2
Let n be a positive integer. Let \(\varvec{k}_1,\dots , \varvec{k}_n, \varvec{l}\) be non-empty indices. Take tuples of complex numbers \(\varvec{z}_i\in \mathbb {D}^{\mathrm {dep}(\varvec{k}_i)}\) for all \(1\le i \le n\) and \(\varvec{w}\in \mathbb {D}^{\mathrm {dep}(\varvec{l})}\). Then, we have

Proof
This follows from the identity
for positive integers \(m_1,\dots , m_n\). \(\square \)
For a convergence argument, we need the following lemma.
Lemma 2.3
Let n and N be integers satisfying \(N\ge n\ge 2\). Then, we have

Proof
By estimates \(\frac{1}{ab}\le \frac{2}{a+b}=\frac{2}{N}\) and
the statement for \(n=2\) is true. Next, we assume that \(n\ge 3\) and the desired estimate for \(n-1\) holds. Then, there exists some positive constant c such that we have
Since \(\frac{8}{n-1}\le 1\) for \(n\ge 9\), we can take a constant in the big-O notation to be independent of n. This proves the lemma. \(\square \)
Theorem 2.4
Let n and d be integers satisfying \(n\ge 2\) and \(1\le d\le n\). Let \(\varvec{k}_1,\dots , \varvec{k}_d, \varvec{l}\) be indices and \(\varvec{k}_{d+1},\dots , \varvec{k}_n\) non-empty indices. Take tuples of complex numbers \(\varvec{z}_i\in \mathbb {D}^{\mathrm {dep}(\varvec{k}_i)}\) for all \(1\le i \le n\), \(\varvec{w}\in \mathbb {D}^{\mathrm {dep}(\varvec{l})}\) and complex numbers \(v_1,\ldots ,v_d\in \mathbb {D}\setminus \{0\}\), \(t\in \mathbb {D}\) satisfying
and the assumption that if \(n=d=2\) and \(\varvec{k}_i=\varnothing \) \((1\le i\le 2)\), then \(|v_{3-i}|<1\) or \(|t|<1\). Then, we have

Proof
For vectors \(\varvec{x}=(x_1,\dots ,x_d)\) and \(\varvec{y}=(y_1,\dots ,y_d)\), we use the following notation in this proof:
Then, it is sufficient to show that an identity
holds for non-negative integers \(m_1,\ldots ,m_d, q\) and positive integers \(m_{d+1},\dots , m_n\). Here, we abbreviated \((m_1,\dots ,m_d)\) (resp. \((m_{d+1},\dots ,m_n)\)) to \(\varvec{m}^-\) (resp. \(\varvec{m}^+\)). We also abbreviated \((a_1,\dots , a_d)\) to \(\varvec{a}\) for variables. The symbol \(|\varvec{a}|+|\varvec{m}^+|\) denotes \(a_1+\cdots +a_d+m_{d+1}+\cdots +m_n\). Note that \(C(a_1,\dots ,a_d,\varvec{m}^+)\) means \(C(a_1,\dots ,a_d,m_{d+1},\dots ,m_n)\), not \(C(a_1,\dots ,a_d, (m_{d+1},\dots ,m_n))\). We see that each series above converges absolutely from the estimate (2.1) or the assumption for the case where \(n=d=2\). Note that we cover the case where \(t=0\) by considering \(0^0\) as 1. For the \(d=n\) case, we understand that \(\varvec{m}^+=\varnothing \) and \(m_{d+1}\cdots m_n=1\). For the \(d=1\) case, we understand the first term of the left-hand side of the above identity as
when \(q\le m_1+\cdots +m_n\) and 0 otherwise.
Take a sufficiently large integer N. For each \(1\le i\le d\),
For the first term of the right-hand side, by replacing \(a_i\) with \(a_i-1\),
By summing from \(i=1\) to d and using (2.2), we have
On the remaining terms,
By combining these calculations, we have
The last term tends to 0 as N tends to infinity by Lemma 2.3. This completes the proof. \(\square \)
3 Transport relations
Let m be a positive integer. For \(t\in \mathbb {D}\), we define \(\mathbb {B}_m(t)\) by

For example, \(\mathbb {B}_1(1)=\{z\in \mathbb {D}\setminus \{0\} \mid \mathrm {Re}(z)\le \frac{1}{2}\}\cup \{1,\infty \}\), where \(\mathrm {Re}(z)\) denotes the real part of z.
Let n be an integer greater than 1. Let \(\varvec{k}_1,\dots ,\varvec{k}_n, \varvec{l}\) be indices and \(\varvec{z}_1\in \mathbb {D}^{\mathrm {dep}(\varvec{k}_1)},\dots ,\varvec{z}_n\in \mathbb {D}^{\mathrm {dep}(\varvec{k}_n)},\varvec{w}\in \mathbb {D}^{\mathrm {dep}(\varvec{l})}\). Let \(t\in \mathbb {D}\) and \((v_1,\dots ,v_{n-1})\in \mathbb {B}_{n-1}(t)\). We assume that
-
if \(\varvec{k}_i=\varnothing \) (\(1\le i \le n-1\)), then \(v_i\ne \infty \),
-
if \(\varvec{k}_n=\varnothing \), then \(\sum _{i=1}^{n-1}\frac{1}{v_i}\ne t\),
-
if \(n=2\), \(\varvec{k}_1=\varnothing \) and \(|t|=1\), then \(\left| t-\frac{1}{v_1}\right| \ne 1\) and
-
if \(n=2\), \(\varvec{k}_2=\varnothing \) and \(|t|=1\), then \(|v_1|\ne 1\).
In this setting, by the fundamental identity, we have

where \(v_n\in (\mathbb {D}\setminus \{0\})\cup \{\infty \}\) is defined by \(\frac{1}{v_n}=t-\sum _{i=1}^{n-1}\frac{1}{v_i}\). In this equality, the total weight of indices (including the arrow parts) except for the nth index of each multivariable connected sum appearing in the right-hand side is 1 less than the total weight of indices except for the nth index of the multivariable connected sum in the left-hand side. Equality (3.1) is the same as the fundamental identity, but when it is used for the purpose of transforming the left-hand side into the right-hand side, we also call it a transport relation. If we classify transport relations for \(Z_n\) according to whether the actual direction of each of \(\overset{v_1}{\rightarrow }\), \(\dots ,\overset{v_{n-1}}{\rightarrow }\) and \(\overset{t}{\rightarrow }\) is vertical or horizontal, that is, whether each of \(v_1,\dots ,v_{n-1}\) (resp. t) is the infinity (resp. 0) or not, there are \(2^n\) different patterns of transport relations; see Example 3.1 for instance.
3.1 Examples
The settings of \(\varvec{k}_1,\varvec{k}_2,\varvec{l},\varvec{z}_1,\varvec{z}_2\) and \(\varvec{w}\) are as per those at the beginning of this section (the case of \(n=2\)).
Example 3.1
(Transport relations for \(Z_2\)) Let \(t\in \mathbb {D}\) and \(v_1\in \mathbb {B}_1(t)\). Assume that if \(\varvec{k}_2=\varnothing \), then \(t\ne \frac{1}{v_1}\), and if \(\varvec{k}_1=\varnothing \) (resp. \(\varvec{k}_2=\varnothing \)) and \(|t|=1\), then \(\left| t-\frac{1}{v_1}\right| \ne 1\) (resp. \(|v_1|\ne 1\)). We define \(v_2\in (\mathbb {D}\setminus \{0\})\cup \{\infty \}\) by \(\frac{1}{v_2}=t-\frac{1}{v_1}\).
-
(1)
The case of \(v_1\ne \infty \), \(t\ne 0\):

-
(2)
The case of \(v_1=\infty \), \(t\ne 0\), \(\varvec{k}_1\ne \varnothing \) (\(v_2=1/t\)):

-
(3)
The case of \(v_1\ne \infty \), \(t=0\) (\(v_2=-v_1\)):

-
(4)
The case of \(v_1=\infty \), \(t=0\), \(\varvec{k}_1\ne \varnothing \) (\(v_2=\infty \)):

Example 3.2
(Transport relations for duality) We consider a special case of Example 3.1: the case where \(\varvec{l}=\varnothing \), \(t=1\). In the case of Example 3.1 (1), we further classify it by whether the actual direction of \(\overset{v_2}{\longrightarrow }\) is vertical or horizontal. Let \(v\in \mathbb {D}\setminus \{0\}\) satisfying \(\mathrm {Re}(v)\le \frac{1}{2}\). Assume that if \(\varvec{k}_1=\varnothing \), then \(\mathrm {Re}(v)\ne \frac{1}{2}\) and if \(\varvec{k}_2=\varnothing \), then \(|v|\ne 1\). Then, we have
These transport relations will be used to reprove the duality relation for MPLs in the next subsection and recover those of Seki–Yamamoto (1.2) by considering the case \(\varvec{z}_1=(\{1\}^{\mathrm {dep}(\varvec{k}_1)})\) and \(\varvec{z}_2=(\{1\}^{\mathrm {dep}(\varvec{k}_2)})\).
Example 3.3
(Transport relations for special cases of \(Z_3\)) In the general case of \(Z_3\), there are 8 patterns of transport relations, considered in the same way as in Example 3.1. Here, we focus on transport relations restricted to the case where it is necessary to calculate the multiple connected sum \(Z_3(\varvec{k}_1;\varvec{k}_2;\varvec{k}_3)\). Let \(\varvec{k}_3\) be an index and \(\varvec{\epsilon }\) an element of \(\{1,-1\}^{\mathrm {dep}(\varvec{k}_3)}\). If the tuple of complex variables to be written onto an index has the form \((1,\dots ,1)\), then we omit the tuple from our notation. In this setting, we have
-
(1)
The case of \((v_1,v_2,v_3)=(1,1,-1)\):
$$\begin{aligned} Z_3\left( (\varvec{k}_1)_{\rightarrow };(\varvec{k}_2)_{\rightarrow };{\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) =-Z_3\left( \varvec{k}_1;(\varvec{k}_2)_{\rightarrow };\left( {\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) _{\overset{-1}{\longrightarrow }}\right) -Z_3\left( (\varvec{k}_1)_{\rightarrow };\varvec{k}_2;\left( {\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) _{\overset{-1}{\longrightarrow }}\right) . \end{aligned}$$ -
(2)
The case of \((v_1,v_2,v_3)=(1,\infty ,\infty )\), \(\varvec{k}_2,\varvec{k}_3\ne \varnothing \):
$$\begin{aligned} Z_3\left( (\varvec{k}_1)_{\rightarrow };(\varvec{k}_2)_{\uparrow };{\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) =Z_3\left( \varvec{k}_1;(\varvec{k}_2)_{\uparrow };\left( {\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) _{\uparrow }\right) -Z_3\left( (\varvec{k}_1)_{\rightarrow };\varvec{k}_2;\left( {\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) _{\uparrow }\right) . \end{aligned}$$ -
(3)
The case of \((v_1,v_2,v_3)=(\infty ,1,\infty )\), \(\varvec{k}_1,\varvec{k}_3\ne \varnothing \):
$$\begin{aligned} Z_3\left( (\varvec{k}_1)_{\uparrow };(\varvec{k}_2)_{\rightarrow };{\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) =-Z_3\left( \varvec{k}_1;(\varvec{k}_2)_{\rightarrow };\left( {\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) _{\uparrow }\right) +Z_3\left( (\varvec{k}_1)_{\uparrow };\varvec{k}_2;\left( {\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) _{\uparrow }\right) . \end{aligned}$$ -
(4)
The case of \((v_1,v_2,v_3)=(\infty ,\infty ,1)\), \(\varvec{k}_1,\varvec{k}_2\ne \varnothing \):
$$\begin{aligned} Z_3\left( (\varvec{k}_1)_{\uparrow };(\varvec{k}_2)_{\uparrow };{\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) =Z_3\left( \varvec{k}_1;(\varvec{k}_2)_{\uparrow };\left( {\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) _{\overset{1}{\longrightarrow }}\right) +Z_3\left( (\varvec{k}_1)_{\uparrow };\varvec{k}_2;\left( {\begin{array}{c} \varvec{\epsilon }\\ \varvec{k}_3 \end{array}}\right) _{\overset{1}{\longrightarrow }}\right) . \end{aligned}$$
In particular, if all \(\varvec{k}_1, \varvec{k}_2\) and \(\varvec{k}_3\) are not empty, then we see that \(Z_3(\varvec{k}_1;\varvec{k}_2;\varvec{k}_3)\) belongs to the space of alternating multiple zeta values, which will be defined below, by the recipe explained later in Sect. 5.1.
3.2 Duality for multiple polylogarithms
Prior to Sect. 6, we prove the duality for MPLs by using transport relations in Example 3.2, because of its simplicity.
Let \(\varvec{k}\) be an index and \(\varvec{z}=(z_1,\dots ,z_r)\in \mathbb {D}^r\), where \(r{:}{=}\mathrm {dep}(\varvec{k})\). Further, we assume that all of the following are true:
-
\(z_1,\dots ,z_r\in \mathbb {B}_1(1)\),
-
\(\mathrm {Re}(z_1)\ne \frac{1}{2}\),
-
if \(\varvec{k}\) is non-admissible, then \(|z_r|\ne 1\).
We refer this condition as the dual condition. For such a pair \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \), by using transport relations in Example 3.2, we can transport \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \) from left to right in the absolutely convergent multivariable connected sum \(Z_2\) as

where \(\iota (\varvec{z})=r-\)(the number of 1’s in \(\varvec{z}\)). Here, we define a pair \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) ^{\dagger }\) satisfying the dual condition by this transportation. We also write an explicit definition. Recall the definition of the dual index of an admissible index in Sect. 1. Any pair \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \) with the dual condition is uniquely expressed as
where d is a non-negative integer, \(a_1,\dots , a_d\), \(b_1,\dots , b_d\) are positive integers, all \(w_1,\dots , w_d\) are not 1, \(\varvec{l}_1,\dots ,\varvec{l}_{d+1}\) are admissible indices, and \(r_1{:}{=}\mathrm {dep}(\varvec{l}_1),\dots , r_{d+1}{:}{=}\mathrm {dep}(\varvec{l}_{d+1})\). Then, \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) ^{\dagger }\) is defined by
where \(s_1{:}{=}\mathrm {dep}((\varvec{l}_1)^{\dagger }),\dots , s_{d+1}{:}{=}\mathrm {dep}((\varvec{l}_{d+1})^{\dagger })\). In particular, we have \(\left( {\begin{array}{c} \{1\}^r \\ \varvec{k} \end{array}}\right) ^{\dagger }= \left( {\begin{array}{c} \{1\}^{s}\\ \varvec{k}^{\dagger } \end{array}}\right) \), where \(\varvec{k}\) is an admissible index and \(r{:}{=}\mathrm {dep}(\varvec{k})\), \(s{:}{=}\mathrm {dep}(\varvec{k}^{\dagger })\). The transportation (3.2) with Proposition 2.1 (i) and (iv) gives the following duality relation which was proved by Borwein–Bradley–Broadhurst–Lisoněk in [3, §6.1] using a change of variables for iterated integrals; here, we state only the case for absolutely convergent MPLs.
Theorem 3.4
Let \(\varvec{k}\) be an index and \(\varvec{z}\in \mathbb {D}^{\mathrm {dep}(\varvec{k})}\). We assume that the pair \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \) satisfies the dual condition and write \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) ^{{\dagger }}\) as \(\bigl ({\begin{array}{c} \varvec{z}'\\ \varvec{k}' \end{array}}\bigr )\). Then, we have

Here, we recall the definition of the alternating multiple zeta value. For a non-empty index \(\varvec{k}=(k_1,\dots ,k_r)\) and \(\varvec{\epsilon }=(\epsilon _1,\dots ,\epsilon _r)\in \{1,-1\}^r\) satisfying \((k_r,\epsilon _r)\ne (1,1)\), we define \(\zeta (\varvec{k};\varvec{\epsilon })\) by
We use bar notation for indicating signs; e.g., \(\zeta (\overline{1},2,\overline{3},4)=\zeta (1,2,3,4;-1,1,-1,1)\).
Example 3.5
The identity

is deduced from
Borwein, Bradley, Broadhurst and Lisoněk remarked that this is “a result that would doubtless be difficult to prove by naïve series manipulations alone” in [3, Example 6.1]. However, our proof is contrary to their prediction; if we state the proof of Theorem 2.4 in this case, then it is quite simple.
Example 3.6
Let r be a positive integer. Take \((z_1,\dots ,z_r)\in \left( \mathbb {B}_1(1)\setminus \{\infty \}\right) ^r\) satisfying \(\mathrm {Re}(z_1)\ne \frac{1}{2}\) and \(|z_r|\ne 1\). Then, the identity

is deduced from
4 Boundary condition
We call the following fact the boundary condition for multivariable connected sums: every absolutely convergent \(Z_1\)-value is written explicitly as a \(\mathbb {Z}\)-linear combination of absolutely convergent shuffle-type MPLs. We explain this fact in detail.
Let r be a positive integer, \(\varvec{k}=(k_1,\dots ,k_r)\) an index and \(\xi _1,\dots , \xi _r\) complex numbers satisfying \(\left| \prod _{i=j}^r\xi _i\right| \le 1\) for all \(1\le j\le r\) and that if \(k_r=1\), then \(|\xi _r|<1\). Then, the harmonic-type multiple polylogarithm \(\mathrm {Li}^*_{\varvec{k}}(\xi _1,\dots ,\xi _r)\) is defined by
Let \(\varvec{z}=(z_1,\dots ,z_r)\in (\mathbb {D}\setminus \{0\})^r\) satisfying that if \(\varvec{k}\) is non-admissible, then \(|z_r|<1\). By definition, there are the following relationships between \(\mathrm {Li}^*_{\varvec{k}}\) and  :
:


Furthermore, let s be a positive integer, \(\varvec{l}=(l_1,\dots ,l_s)\) an index and \(\varvec{w}=(w_1,\dots , w_s)\in (\mathbb {D}\setminus \{0\})^s\). We replace the assumption about \(z_r\) with the following: if \(k_r=l_s=1\), then \(|z_r|<1\) or \(|w_s|<1\). By definition, we have

Since the product of truncated sums for a fixed n obeys the harmonic product rule,  is written as a \(\mathbb {Z}\)-linear combination of harmonic-type MPLs, and hence of shuffle-type by (4.2). For example, we have
is written as a \(\mathbb {Z}\)-linear combination of harmonic-type MPLs, and hence of shuffle-type by (4.2). For example, we have

Remark 4.1
If \(z_1=\cdots =z_r=w_1=\cdots =w_s=1\), then another decomposition approach using 2-posets and associated integrals is attributable to Kaneko and Yamamoto; see [6, §4].
5 Evaluations of the multivariable connected sum
5.1 Recipe for evaluations
First, we introduce the notion of transportable variables. This is just a condition to complete all transportation process while maintaining absolute convergence of multivariable connected sums. We use the notation \([n]{:}{=}\{1,\dots ,n\}\) for a positive integer n.
Definition 5.1
Let \(r_1,\dots , r_n\) and s be positive integers, where n is an integer at least 2. Let \(\varvec{z}_1=(z_1^{(1)},\dots ,z_{r_1}^{(1)}),\dots ,\varvec{z}_n=(z_1^{(n)},\dots ,z_{r_n}^{(n)})\) and \(\varvec{w}=(w_1,\dots , w_s)\) be elements of \(\mathbb {D}^{r_1}, \dots , \mathbb {D}^{r_n}\) and \(\mathbb {D}^{s}\), respectively. We declare that \((\varvec{z}_1,\dots ,\varvec{z}_n;\varvec{w})\) is transportable if there exists \(j\in [n]\) such that for any non-empty subset \(J\subset [n]\setminus \{j\}\), the following holds true:
-
For every \((a_i)_{i\in J}\) (\(a_i\in [r_i]\)) and every component \(w_k\) of \(\varvec{w}\),
$$\begin{aligned} (z_{a_i}^{(i)})_{i\in J}\in \mathbb {B}_{\#J}(w_k). \end{aligned}$$ -
For every component \(w_k\) of \(\varvec{w}\) with \(|w_k|=1\),
$$\begin{aligned} \left| w_k-\frac{1}{z_1^{(i)}}\right| \ne 1\quad \text {for all } i\in [n]\setminus \{j\}. \end{aligned}$$
If every \(\varvec{z}_i\) is an element of \(\{1,-1\}^{r_i}\) and \(\varvec{w}\in \{0,1,-1\}^s\), then \((\varvec{z}_1,\dots ,\varvec{z}_n;\varvec{w})\) is transportable by definition.
Given the above, we can provide an explicit decomposition of the multivariable connected sum according to the following recipe:
Theorem 5.2
Let \(r_1,\dots , r_n\) and s be positive integers, where n is an integer at least 2. Let \(\varvec{k}_1,\dots ,\varvec{k}_n\) and \(\varvec{l}\) be indices satisfying \(\mathrm {dep}(\varvec{k}_1)=r_1,\dots ,\mathrm {dep}(\varvec{k}_n)=r_n\), \(\mathrm {dep}(\varvec{l})=s\). Let \(\varvec{z}_1,\dots ,\varvec{z}_n\) and \(\varvec{w}\) be elements of \(\mathbb {D}^{r_1}, \dots , \mathbb {D}^{r_n}\) and \(\mathbb {D}^{s}\), respectively. We assume that if \(\varvec{l}=\{1\}^s\) (resp. \(\varvec{l}\ne \{1\}^s )\), then \((\varvec{z}_1,\dots ,\varvec{z}_n;\varvec{w})\) (resp. \((\varvec{z}_1,\dots ,\varvec{z}_n;(\varvec{w},0)) )\) is transportable. Then, the multivariable connected sum  is expressed as a \(\mathbb {Z}\)-linear combination of absolutely convergent multiple polylogarithms. Explicitly, we obtain such an expression by the following procedures:
is expressed as a \(\mathbb {Z}\)-linear combination of absolutely convergent multiple polylogarithms. Explicitly, we obtain such an expression by the following procedures:
-
(i)
Take an integer \(j\in [n]\) in Definition 5.1 and replace the jth component with the nth component by Proposition 2.1 (iii).
-
(ii)
Apply the transport relation (3.1) repeatedly until
 is expressed as a \(\mathbb {Z}\)-linear combination of \(Z_{n-1}\)-values by Proposition 2.1 (iv).
is expressed as a \(\mathbb {Z}\)-linear combination of \(Z_{n-1}\)-values by Proposition 2.1 (iv). -
(iii)
If \(n\ge 3\), then apply the transport relation (3.1) (replace n with \(n-1\) \()\) to each \(Z_{n-1}\)-value repeatedly until it is expressed as a \(\mathbb {Z}\)-linear combination of \(Z_{n-2}\)-values.
-
(iv)
Repeat the same procedure as in (iii) to express
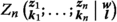 as a \(\mathbb {Z}\)-linear combination of \(Z_{1}\)-values.
as a \(\mathbb {Z}\)-linear combination of \(Z_{1}\)-values. -
(v)
Apply the boundary condition in Sect. 4 to each \(Z_1\)-value obtained in (iv); then, we have the desired \(\mathbb {Z}\)-linear combination of absolutely convergent multiple polylogarithms.
Proof
All that needs to be checked is that sufficient conditions for applying the transport relation in (ii)–(iv) are satisfied, which is accomplished by the assumption and Definition 5.1. \(\square \)
Proof of Theorem 1.1
Let k be a positive integer and \(\varvec{k}_1,\dots ,\varvec{k}_n,\varvec{l}\) indices as in the statement. We decompose \(Z_n(\varvec{k}_1;\dots ;\varvec{k}_n\mid \varvec{l})\) as a \(\mathbb {Z}\)-linear combination of \(Z_1\)-values according to the recipe (ii)–(iv) in Theorem 5.2; the transportable condition is satisfied for all \(j\in [n]\) in this case, and thus, we may assume that \(j=n\). Then, we see that each of the \(Z_1\)-value belongs to

where \(I_r\) (resp. \(I_s\)) denotes the set of indices whose depth is r (resp. s). By the boundary condition in Sect. 4, it is straightforward to see that every \(Z_1\)-value belonging to the above set is expressed as a \(\mathbb {Z}\)-linear combination of elements of

Finally, every element of this set coincides with an element of \(\mathrm {MPL}(n,k)\) up to sign by the duality (Theorem 3.4). \(\square \)
5.2 Examples
Example 5.3
(= Equality (1.4))
Proof
By the transport relation, we have

Boundary conditions for this case are \(Z_1(2\mid 1,1)=\zeta (1,2)+\zeta (3)=2\zeta (3)\) and \(Z_1(3)=\zeta (3)\). \(\square \)
Example 5.4
(= Equality (1.7))
Proof
By the transport relation, we have

Boundary conditions for this case are

Hence, we have
The facts that \(\zeta (2,2)=\frac{3}{4}\zeta (4)\) and \(\zeta (\overline{2},\overline{2})=-\frac{3}{16}\zeta (4)\) are well-known. \(\square \)
Example 5.5
(= Equality (1.5)) For a positive integer n, we have

Proof
By the transport relation (3.1) and Proposition 2.1 (iv),
holds for an integer \(r\ge 2\), a non-empty index \(\varvec{k}\) and \(\varvec{z}\in \mathbb {D}^{\mathrm {dep}(\varvec{k})}\). Applying this repeatedly and then applying the transport relation for the duality, we have

Since

holds as a consequence of the duality (Theorem 3.4), the proof is completed. \(\square \)
Example 5.6
(Equality (1.1) with variables) Let \(z_1\) and \(z_2\) be complex numbers whose absolute values are less than 1. Assume that \(\mathrm {Re}(z_i)<\frac{1}{2}\) holds for \(i=1\) or 2. Then, we have
Here, \(\mathrm {Li}_2(z)\) is the dilogarithm.
Proof
We may assume that \(z_1\ne 0\) and \(\mathrm {Re}(z_1)<\frac{1}{2}\). By the transport relation and Proposition 2.1 (iv), (i), we have

By substituting \(z_2(z_1-1)/z_1\) (resp. \(z_1/(z_1-1)\)) into x (resp. y) in Zagier’s formula [15, Proposition 1]
we have the desired formula. \(\square \)
6 Relations among special values of multiple polylogarithms
6.1 Recipe for relations
We have already derived the duality for MPLs by using our transport relations in Sect. 3.2. In this subsection, we describe a general recipe for obtaining relations among MPLs based on transport relations and evaluations of multivariable connected sums (Theorem 5.2).
We consider data
-
n: an integer at least 2,
-
\(\varvec{k}_1,\dots ,\varvec{k}_{n-1}\) and \(\varvec{l}\): non-empty indices,
-
\(\varvec{z}_1=(z_1^{(1)},\dots , z_{r_1}^{(1)})\in \mathbb {D}^{r_1},\dots , \varvec{z}_{n-1}=(z_1^{(n-1)},\dots ,z_{r_{n-1}}^{(n-1)})\in \mathbb {D}^{r_{n-1}}\) and \(\varvec{w}=(w_1,\dots ,w_s)\in \mathbb {D}^s\), where \(r_1=\mathrm {dep}(\varvec{k}_1),\dots ,r_{n-1}=\mathrm {dep}(\varvec{k}_{n-1})\) and \(s=\mathrm {dep}(\varvec{l})\)
satisfying the following assumptions:
-
If \(\varvec{l}\) is non-admissible, then
$$\begin{aligned} \sum _{\begin{array}{c} 1\le i\le n-1 \\ \varvec{k}_i \ \text {is non-admissible} \end{array}}\frac{1}{z_{r_i}^{(i)}}\ne w_s, \end{aligned}$$and if \(\varvec{l}\) is admissible, then
$$\begin{aligned} \sum _{\begin{array}{c} 1\le i\le n-1 \\ \varvec{k}_i \ \text {is non-admissible} \end{array}}\frac{1}{z_{r_i}^{(i)}}\ne 0. \end{aligned}$$ -
For every non-empty subset \(J\subset [n-1]\), every \((a_i)_{i\in J}\) (\(a_i\in [r_i]\)) and every component \(w_k\) of \(\varvec{w}\),
$$\begin{aligned} (z_{a_i}^{(i)})_{i\in J}\in \mathbb {B}_{\#J}(w_k). \end{aligned}$$ -
If \(\varvec{l}\ne \{1\}^s\), then the second assumption with \(\varvec{w}\) replaced by \((\varvec{w},0)\) is valid.
-
For every component \(w_k\) of \(\varvec{w}\) with \(|w_k|=1\),
$$\begin{aligned} \left| w_k-\frac{1}{z_1^{(i)}}\right| \ne 1\quad \text {for all } i\in [n-1]. \end{aligned}$$ -
If \(n=2\) and both \(\varvec{k}_1\) and \(\varvec{l}\) are non-admissible, then \(|z_{r_1}^{(1)}|<1\) or \(|w_s|<1\) holds.
For such given data, we can obtain a relation among MPLs by the following procedure:
-
(i)
By Proposition 2.1 (iv), we have
 (6.1)
(6.1)and then we can decompose the right-hand side as a \(\mathbb {Z}\)-linear combination of MPLs by Theorem 5.2 or the boundary condition.
-
(ii)
On the other hand, by using the transport relation (3.1) and Propositions 2.1 (iv) as needed, we can decompose the left-hand side of (6.1) as a \(\mathbb {Z}\)-linear combination of \(Z_n\)-values and \(Z_{n-1}\)-values. Then, we decompose all these \(Z_n\)-values and \(Z_{n-1}\)-values as \(\mathbb {Z}\)-linear combinations of MPLs by Theorem 5.2 or the boundary condition.
-
(iii)
By comparing the output results of (i) and (ii), we obtain a relation among MPLs.
Using assumptions regarding the data and contents in Sects. 3–5, it is true that the above procedure yields a relation among MPLs; note that the relation can be tautological as in (1.3). The family of relations obtained by executing the above procedure on data satisfying \(n=2\), \(\varvec{l}=(\{1\}^s)\) and \(\varvec{w}=(\{1\}^s)\) is actually a natural extension of the family of Ohno’s relations for MZVs to the MPLs case. We prove Ohno’s relation for MPLs in the next subsection; see Theorem 6.10.
The above description is the concrete content of Theorem 1.4.
6.2 Ohno’s relation for multiple polylogarithms
For a non-negative integer h, we use the following shorthand notation for multivariable connected sums:

Let \(\varvec{k}_1, \varvec{k}_2\) be indices, \(\varvec{z}_1\in \mathbb {D}^{\mathrm {dep}(\varvec{k}_1)}\), \(\varvec{z}_2\in \mathbb {D}^{\mathrm {dep}(\varvec{k}_2)}\) and \(v\in \mathbb {B}{:}{=}\mathbb {B}_1(1)\setminus \{\infty \}\). We assume that if \(\varvec{k}_1=\varnothing \) (resp. \(\varvec{k}_2=\varnothing \)), then \(\mathrm {Re}(v)\ne \frac{1}{2}\) (resp. \(|v|\ne 1\)). Then, by transport relations for \(Z_2\) (Example 3.1 (1), (2)), the following relations hold:
Here, set \(Z^{(-1)}(*;*){:}{=}0\); the case where \(h=0\) in the above relations gives the transport relations for the duality (Example 3.2).
It can be proved by direct calculation that the space of relations obtained by restricting to the use of transport relations for \(\{Z^{(h)}\}_{h\ge 0}\) coincides with the space of Ohno’s relations for MPLs. However, in this subsection, we derive Ohno’s relations for MPLs more clearly in terms of a formal power series ring over a Hoffman-type algebra. This also gives a new proof of Ohno’s relation for MZVs; compare this with another proof using connected sums by the third author and Yamamoto [12].
First, we prepare some terminology of the Hoffman-type algebra appropriately.
Definition 6.1
Prepare letters x and \(e_z\) for all \(z\in \mathbb {B}\). Let \(\mathcal {A}\) be a non-commutative polynomial algebra \(\mathcal {A}{:}{=}\mathbb {Q}\langle x, e_z \ (z\in \mathbb {B})\rangle \). Furthermore, we define its subalgebras \(\mathcal {A}^1\) and \(\mathcal {A}^0\) by
We say that a word \(w\in \mathcal {A}^1\) is associated with \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \) when \(w=e_{z_1}x^{k_1-1}\cdots e_{z_r}x^{k_r-1}\), where \(\varvec{z}=(z_1,\dots ,z_r)\) (\(z_i\in \mathbb {B}\)) and \(\varvec{k}=(k_1,\dots ,k_r)\) (\(k_i\in \mathbb {Z}_{>0}\)). In addition, \(1\in \mathcal {A}^1\) is associated with \(\left( {\begin{array}{c} \varnothing \\ \varnothing \end{array}}\right) \). Note that a word of \(\mathcal {A}^0\) is associated with a pair satisfying the dual condition in Sect. 3.2.
We define a \(\mathbb {Q}\)-linear map \(L:\mathcal {A}^0[\![t]\!]\rightarrow \mathbb {C}[\![t]\!]\) by
and a \(\mathbb {Q}\)-linear map \(\mathfrak {L}:\mathcal {A}^0[\![t]\!]\rightarrow \mathbb {C}[\![t]\!]\) by
Here,

for each word \(w\in \mathcal {A}^0\) associated with \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \).
Definition 6.2
Let \(\mathcal {A}[\![t]\!]\) be the formal power series ring over \(\mathcal {A}\). We define two automorphisms \(\sigma , \rho \) and two anti-automorphisms \(\tau ,\tau '\) on \(\mathcal {A}[\![t]\!]\) by
and \(\sigma (t)=\rho (t)=\tau (t)=\tau '(t)=t\). Images of the generators under \(\sigma ^{-1}\) and \(\rho ^{-1}\) are given by
with \(\sigma ^{-1}(t)=\rho ^{-1}(t)=t\). Furthermore, \(\tau ^{-1}=\tau \) and \(\tau '^{-1}=\tau '\) hold.
Lemma 6.3
\(\rho \circ \tau '=\tau \circ \rho \).
Proof
It is sufficient to check that \((\rho \circ \tau ')(u)=(\tau \circ \rho )(u)\) holds for \(u\in \{x\}\cup \{e_z \mid z\in \mathbb {B}\}\). \(\square \)
Proposition 6.4
(Boundary condition) For every \(w\in \mathcal {A}^0[\![t]\!]\), we have
Proof
It is sufficient to show the case \(w=e_{z_1}x^{k_1-1}\cdots e_{z_r}x^{k_r-1}\in \mathcal {A}^0\). By definition, we have
Since
holds, we have \(L\left( (\sigma \circ \rho )(w)\right) =\mathfrak {L}(w)\) by definition. \(\square \)
Definition 6.5
For a non-negative integer h, we define a \(\mathbb {Q}\)-bilinear map \(\mathfrak {Z}^{(h)}:\mathcal {A}'\times \mathcal {A}'\rightarrow \mathbb {C}\) by
where \(\mathcal {A}'{:}{=}\bigoplus _{z\in \mathbb {B}}e_z\mathcal {A}\) (non-unital) and \(w_1\) and \(w_2\) are associated with \(\bigl ({\begin{array}{c} \varvec{z}_1\\ \varvec{k}_1 \end{array}}\bigr )\) and \(\bigl ({\begin{array}{c} \varvec{z}_2\\ \varvec{k}_2 \end{array}}\bigr )\), respectively. Furthermore, we define a \(\mathbb {Q}\)-bilinear map \(\mathfrak {Z}:\mathcal {A}'[\![t]\!]\times \mathcal {A}'[\![t]\!]\rightarrow \mathbb {C}[\![t]\!]\) by
and
Proposition 6.6
(Transport relation) We have the following:
-
(i)
For \(w_1, w_2 \in \mathcal {A}'[\![t]\!]\) and \(u\in \mathcal {A}[\![t]\!]\),
$$\begin{aligned} \mathfrak {Z}(w_1u;w_2)=\mathfrak {Z}(w_1;w_2\tau '(u)). \end{aligned}$$ -
(ii)
For \(w\in \mathcal {A}'[\![t]\!]\) and \(u\in \{x\}\cup \{e_z\mid z\in \mathbb {B}, |z|\ne 1\}\),
$$\begin{aligned} \mathfrak {L}(wu)=\mathfrak {Z}(w;\tau '(u)). \end{aligned}$$ -
(iii)
For \(w\in \mathcal {A}'[\![t]\!]\) and \(u\in \{e_z\mid z\in \mathbb {B}, \mathrm {Re}(z)\ne \frac{1}{2}\}\),
$$\begin{aligned} \mathfrak {Z}(u;w)=\mathfrak {L}(w\tau '(u)). \end{aligned}$$ -
(iv)
For \(z\in \mathbb {B}\) with \(\mathrm {Re}(z)\ne \frac{1}{2}\) and \(|z|\ne 1\),
$$\begin{aligned} \mathfrak {L}(e_z)=\mathfrak {L}(\tau '(e_z)). \end{aligned}$$
Proof
It is sufficient to show the case where \(w_1,w_2,w\) are words and u is a letter. In this case, it follows immediately from the transport relations for \(\{Z^{(h)}\}_{h\ge 0}\). \(\square \)
Theorem 6.7
For \(w\in \mathcal {A}^0[\![t]\!]\), we have
Proof
By Proposition 6.6, we have
Therefore, by Proposition 6.4 and Lemma 6.3, we have
Since \(\rho \) is invertible and \(\rho ^{-1}(\mathcal {A}^0[\![t]\!])\subset \mathcal {A}^0[\![t]\!]\), we have \(L(\sigma (w))=L(\sigma (\tau (w)))\) for all \(w\in \mathcal {A}^0[\![t]\!]\). \(\square \)
To restate Theorem 6.7 without terminology of the Hoffman-type algebra, we define some new notation. Recall the notion of the dual condition, \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) ^{\dagger }\) and \(\iota (\varvec{z})\) from Sect. 3.2.
Definition 6.8
Let r be a positive integer, \(\varvec{k}=(k_1,\dots , k_r)\) an index and \(\varvec{z}=(z_1,\dots ,z_r)\in \mathbb {D}^r\) satisfying that if \(k_r=1\), then \(|z_r|\ne 1\). For a non-negative integer h, we define \(O_h\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \) by

Definition 6.9
Let \(\varvec{k}\) be a non-empty index and \(\varvec{z}\in \mathbb {D}^{\mathrm {dep}(\varvec{k})}\). Set \(d=\iota (\varvec{z})\). When \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \) is written as
where \(a_1,\dots , a_{d+1}\) are non-negative integers, \(z_1,\dots , z_d\in \mathbb {D}\setminus \{1\}\), \(\varvec{k}_1,\dots , \varvec{k}_{d+1}\) are indices with \(\mathrm {dep}(\varvec{k}_1)=a_1,\dots , \mathrm {dep}(\varvec{k}_{d+1})=a_{d+1}\) and \(l_1,\dots ,l_d\) are positive integers. Let \(b_1,\dots , b_d\) be non-negative integers. Then, we define \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) _{b_1,\dots , b_d}\) by

Theorem 6.10
(Ohn o’s relation for multiple polylogarithms) Let \(\varvec{k}\) be a non-empty index and \(\varvec{z}\in \mathbb {D}^{\mathrm {dep}(\varvec{k})}\). We assume that the pair \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) \) satisfies the dual condition and write \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) ^{{\dagger }}\) as \(\bigl ({\begin{array}{c} \varvec{z}' \\ \varvec{k}' \end{array}}\bigr )\). Set \(d=\iota (\varvec{z})\). Then, for any non-negative integer h, we have
In particular, when \(d=0\) (then \(\varvec{k}\) is admissible), this means
which is the well-known Ohno’s relation for multiple zeta values [8].
Proof
In Theorem 6.7, we compare the coefficients of \(t^h\) for the case where \(w\in \mathcal {A}^0\) is a word. Then, we have the desired formula from various definitions of notation. \(\square \)
In the following corollary, we use the symbol  for the 1-variable multiple polylogarithm.
for the 1-variable multiple polylogarithm.
Corollary 6.11
(The depth 1 case of the Landen connection formula,[9]) For a positive integer k and a complex number z satisfying \(|z|<1\) and \(\mathrm {Re}(z)<\frac{1}{2}\), we have
where \(\varvec{k}\) runs over all indices whose weight equal k.
Proof
This is the case where \(\left( {\begin{array}{c} \varvec{z}\\ \varvec{k} \end{array}}\right) = \left( {\begin{array}{c} z\\ 1 \end{array}}\right) \) and \(h=k-1\) in Theorem 6.10.\(\square \)
6.3 Other relations
Example 6.12
For \(k\ge 2\), we have
Proof
Consider the data \(n=2\), \(\varvec{k}_1=(\{1\}^{k-1})\), \(\varvec{z}_1=(\{1\}^{k-1})\), \(\varvec{l}=(2)\) and \(\varvec{w}=(1)\) in the recipe in Sect. 6.1. First, with the duality for MZVs, we have

On the other hand, by Example 3.1 (3),

holds, and by the transport relation for the duality (Example 3.2),

holds for each j. Furthermore,

holds and thus, we have the desired formula. \(\square \)
Remark 6.13
By using \(\zeta (\overline{k})=-(1-2^{1-k})\zeta (k)\), equality (6.2) is rewritten as
which was recently proved by Dilcher–Vignat [4, Theorem 4.1]; their proof is different from ours. The case where \(k=3\) is the famous formula \(\zeta (3)=8\zeta (1,\overline{2})\); see [2].
Example 6.14
Let \(z_1,z_2,z_3\) be elements of \(\{z\in \mathbb {C}\mid 0<|z|<1, \mathrm {Re}(z)<\frac{1}{2}\}\) satisfying \(\frac{1}{z_1}+\frac{1}{z_2}+\frac{1}{z_3}=1\). Then, we have

Proof
By the fundamental identity, we have
and by Propositions 2.1 (iv), this is
Then, we have the desired formula by a similar calculation as in equality (5.2). \(\square \)
Remark 6.15
By applying Example 5.6 to (6.3), we have the six-term relation for dilogarithms (\(z_1,z_2,z_3\) as in Example 6.14)
attributable to Kummer and Newman; see [15, p.9].
Example 6.16
Let \(z_1,z_2,z_3,z_4\) be elements of \(\{z\in \mathbb {C}\mid 0<|z|<1, \mathrm {Re}(z)<\frac{1}{2}\}\) satisfying \(\frac{1}{z_1}+\frac{1}{z_2}+\frac{1}{z_3}+\frac{1}{z_4}=1\) and \(|g(a,b)|\le 1\) for \((a,b)=(z_1,z_2), (z_2,z_3), (z_3,z_4), (z_4,z_1)\), where \(g(a,b){:}{=}\frac{ab}{ab-a-b}\). Then, we have an eight-term relation for  ,
,
where

Proof
By the fundamental identity, we have
and by Proposition 2.1 (iv), this is
According to the recipe for evaluations (Theorem 5.2), we have

The remaining three \(Z_3\)-values can be calculated in the same way. \(\square \)
References
Accélération pour zeta\((2)\), forum post on Les-Mathematiques.net. http://www.les-mathematiques.net/phorum/read.php?4,837804,843195
Borwein, J.M., Bradley, D.M.: Thirty-two Goldbach variations. Int. J. Number Theory 2, 65–103 (2006)
Borwein, J.M., Bradley, D.M., Broadhurst, D.K., Lisoněk, P.: Special values of multiple polylogarithms. Trans. Am. Math. Soc. 353, 907–941 (2001)
Dilcher, K., Vignat, C.: On a result of Koecher concerning Markov–Apéry type formulas for the Riemann zeta function, preprint available at arXiv:2010.15424
Goncharov, A.B.: Multiple polylogarithms and mixed Tate motives, preprint available at arXiv:math/0103059v4
Kaneko, M., Yamamoto, S.: A new integral-series identity of multiple zeta values and regularizations. Sel. Math. 24, 2499–2521 (2018)
Nakasuji, M., Phuksuwan, O., Yamasaki, Y.: On Schur multiple zeta functions: a combinatoric generalization of multiple zeta functions. Adv. Math. 333, 570–619 (2018)
Ohno, Y.: A generalization of the duality and sum formulas on the multiple zeta values. J. Number Theory 74, 39–43 (1999)
Okuda, J., Ueno, K.: Relations for multiple zeta values and Mellin transforms of multiple polylogarithms. Publ. Res. Inst. Math. Sci. 40, 537–564 (2004)
Série triple, forum post on Les-Mathematiques.net. http://www.les-mathematiques.net/phorum/read.php?4,839111,839178
Seki, S.: Connectors. RIMS Kôkyûroku 2160, 15–27 (2020)
Seki, S., Yamamoto, S.: A new proof of the duality of multiple zeta values and its generalizations. Int. J. Numb. Theory 15, 1261–1265 (2019)
Weisstein, E.W.: Riemann Zeta Function zeta\((2)\), from MathWorld—A Wolfram Web Resource.https://mathworld.wolfram.com/RiemannZetaFunctionZeta2.html
Weisstein, E.W.: Apéry’s Constant, from MathWorld—A Wolfram Web Resource. https://mathworld.wolfram.com/AperysConstant.html
Zagier, D.: The dilogarithm function, Frontiers in Number Theory, Physics, and Geometry. II, 3–65, Springer, Berlin (2007)
Zhao, J.: Multiple zeta functions, multiple polylogarithms and their special values, Series on Number Theory and Its Applications, vol. 12. World Scientific, Hackensack (2016)
Acknowledgements
The authors would like to express their sincere gratitude to Professor Masanobu Kaneko and Professor Tetsushi Ito for their helpful comments. The first author would like to thank Dr. Junpei Tsuji for guiding him through the program code for experiments on our proof of Ohno’s relation. The authors are grateful to the anonymous referee for valuable comments and useful suggestions to improve the manuscript.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was supported in part by JST Global Science Campus ROOT program and by JSPS KAKENHI Grant Numbers 18J00151, 21K13762.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kawamura, H., Maesaka, T. & Seki, Si. Multivariable connected sums and multiple polylogarithms. Res Math Sci 9, 4 (2022). https://doi.org/10.1007/s40687-021-00297-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40687-021-00297-w




 converges absolutely, and for the case of
converges absolutely, and for the case of  .
.


 denotes the skipped entry.
denotes the skipped entry.



 is expressed as a
is expressed as a 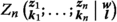 as a
as a 