Abstract
The u-plane integral is the contribution of the Coulomb branch to correlation functions of \({\mathcal {N}}=2\) gauge theory on a compact four-manifold. We consider the u-plane integral for correlators of point and surface observables of topologically twisted theories with gauge group \(\mathrm{SU}(2)\), for an arbitrary four-manifold with \((b_1,b_2^+)=(0,1)\). The u-plane contribution equals the full correlator in the absence of Seiberg–Witten contributions at strong coupling, and coincides with the mathematically defined Donaldson invariants in such cases. We demonstrate that the u-plane correlators are efficiently determined using mock modular forms for point observables, and Appell–Lerch sums for surface observables. We use these results to discuss the asymptotic behavior of correlators as function of the number of observables. Our findings suggest that the vev of exponentiated point and surface observables is an entire function of the fugacities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A powerful approach to understand the dynamics of supersymmetric field theories is to consider such theories on a compact four-manifold without boundary [1,2,3,4,5,6,7]. We consider in this paper the topologically twisted counterpart of \({\mathcal {N}}=2\) supersymmetric Yang–Mills theory with gauge group \(\mathrm{SU}(2)\) and in the presence of arbitrary ’t Hooft flux [8]. The gauge group is broken to \(\mathrm{U}(1)\) on the Coulomb branch \({\mathcal {B}}\), which is parametrized by the vacuum expectation value \(u=\frac{1}{16\pi ^2}\left\langle \mathrm {Tr}[\phi ^2]\right\rangle _{{\mathbb {R}}^4}\), where the subscript indicates that this is a vev in a vacuum state of the theory on flat \({\mathbb {R}}^4\). The Coulomb branch, also known as the “u-plane,” can be considered as a three-punctured sphere, where the punctures correspond to the weak coupling limit, \(u\rightarrow \infty \), and the two strong coupling singularities for \(u=\pm \Lambda ^2\).
The contribution of the u-plane to a correlation function \(\left\langle {\mathcal {O}}_1{\mathcal {O}}_2\dots \right\rangle \) is non-vanishing if the four-manifold M satisfies the topological condition \(b_2^+(M)\le 1\), where \(b_2^+\) is the number of positive definite eigenvalues of the intersection form of two-cycles of M. For an observable \({\mathcal {O}}={\mathcal {O}}_1{\mathcal {O}}_2\dots \), the vev \(\left\langle {\mathcal {O}}\right\rangle \) can be expressed as a sum of two contributions: the Seiberg–Witten contribution \(\left\langle {\mathcal {O}}\right\rangle _{\mathrm{SW}}\) from the strong coupling singularities \(u=\pm \Lambda ^2\), and the contribution from the u-plane \(\Phi [{\mathcal {O}}]\),
This paper considers the u-plane contribution \(\Phi [{\mathcal {O}}]\) for compact four-manifolds with \(b_2^+=1\) known as the u-plane integral [3].Footnote 1 The integrand of \(\Phi [{\mathcal {O}}]\) for \(b_2^+=1\) does not receive perturbative corrections, such that the path integral reduces to a finite dimensional integral over the zero modes of the fields. After including the non-perturbative corrections to the integrand using the Seiberg–Witten solution [9], the u-plane integral has been evaluated for some four-manifolds with \(b_2=1\) or 2, namely for four-manifolds which are rational or ruled complex surfaces [3, 10,11,12,13,14]. The final expressions appeared to be in terms of mock modular forms [15, 16], which could be traced to simplifying features, such as a vanishing chamber, wall-crossing, or birational transformations. For generic four-manifolds with \(b_2^+=1\), these simplifying features are not available. Nevertheless, we will demonstrate that u-plane integrals of arbitrary four-manifolds with \(b_2^+=1\) can be readily evaluated by integration by parts leading to expressions in terms of mock modular forms and Appell–Lerch sums. For simplicity, we will restrict to four-manifolds with \((b_1,b_2^+)=(0,1)\), but not necessarily simply connected.
To achieve the evaluation of these u-plane integrals, we change variables from u to the effective coupling constant \(\tau \), such that \(\Phi \) becomes an integral over the modular fundamental domain \({\mathbb {H}}/\Gamma ^0(4)\), where \(\Gamma ^0(4)\) is the duality group of the theory. We are able to express the integrand as a total derivative \({\mathrm{d}}\tau \wedge {\mathrm{d}}{\bar{\tau }}\,\partial _{{{\bar{\tau }}}} (\frac{{\mathrm{d}}u}{{\mathrm{d}}\tau } H_{\mathcal {O}})\), for some \(H_{\mathcal {O}}\) which depends on the observable \({\mathcal {O}}\). Reversing the change of variables, this demonstrates that the integrand takes the form \({\mathrm{d}}u\wedge {\mathrm{d}}\bar{u}\,\partial _{{\bar{u}}} H_{\mathcal {O}}\), and the integral is thus reduced to integrals over the boundaries \(\partial _j {\mathcal {B}}\), \(j=1,2,3\) in the vicinity of each singularity \(\{-1, +1, \infty \}\) by Stokes’ theorem. See Fig. 1. More explicitly, we have
In order for this expression to be useful, it is necessary that \(H_{\mathcal {O}}(u,{\bar{u}})\), when expressed in terms of \(\tau , {{\bar{\tau }}}\), has good modular properties allowing one to make the required duality transformation near strong coupling singularities. We will find, for a special choice of metric, that \(H_{\mathcal {O}}(\tau , {{\bar{\tau }}})\) can be expressed in terms of mock modular forms. Then, given the expression for the wall-crossing formula using indefinite theta functions [17, 18] the same result follows for general metric.
Schematic representation of the u-plane, with the singularities \(\{\infty , -1, +1 \}\). The black circles indicate the boundaries \(\partial _j{\mathcal {B}}\) of the u-plane after removing neighborhoods of the singularities, while the dashed circle denotes the wall of marginal stability between the strong and weak coupling regions of the u-plane
The expression for the u-plane integral as a modular integral over \({\mathbb {H}}/\Gamma ^0(4)\) paves the way for its evaluation. Earlier work has demonstrated that such modular integrals evaluate to the constant term of a q-series, or more specifically, the \(q^0\) term of a mock modular form [19, 20]. We thus establish a close connection between u-plane correlation functions and mock modular forms. Said more mathematically, we have established a connection between Donaldson invariants for general manifolds with \(b_2^+=1\) and mock modular forms. The explicit expressions are (5.44) for manifolds with odd intersection form and just point observables inserted, (5.65) for manifolds with odd intersection form and just surface observables inserted, and (5.84) for manifolds with even intersection form and just surface observables inserted. These expressions hold for a particularly nice choice of metric. The metric dependence only enters through the choice of period point, i.e., the unique self-dual degree two cohomology class in the forward light-cone in \(H^2(M;{\mathbb {R}})\). Using the expression for the wall-crossing formula in terms of indefinite theta functions [17, 18], one can produce analogous mock modular forms relevant to other chambers. Expressions (5.44), (5.65) and (5.84) (or close cousins thereof) have appeared before in [10]. The derivations in [10] relied on the existence of a vanishing chamber and applied wall-crossing formulae. By contrast, in this paper we evaluate the u-plane integral directly and do not rely on the existence of a vanishing chamber. Consequently, our formulae are justified for a larger class of manifolds.
Using the expression for \(\Phi [{\mathcal {O}}]\) in terms of mock modular forms (see, for example, Eq. 5.44), we can address analytic properties of the correlators for \(b_2^+=1\), analogously to the structural results for manifolds with \(b_2^+>1\) [21]. We study the asymptotic behavior of \(\Phi [u^\ell ]\) for large \(\ell \) and find experimental evidence that \(\Phi [u^\ell ]\sim 1/ (\ell \,\log (\ell ))\) for any four-manifold with \((b_1,b_2^+)=(0,1)\). Remarkably, the asymptotic behavior of \(\Phi [u^\ell ]\) suggests that \(\Phi [e^{2p\,u}]=\sum _{\ell \ge 0} (2p)^\ell \,\Phi [u^\ell ]/\ell !\) is an entire function of p rather than a formal expansion. We find similar experimental evidence that the u-plane contribution to the exponentiated surface observable \(\Phi [e^{I_-({{\varvec{x}}})}]\) is an entire function of \({{\varvec{x}}}\in H_2(M,{\mathbb {C}})\). We leave a more rigorous analysis of these aspects for future work. The questions we address here would seem to be related to the analysis of correlation functions of large charge that have recently been studied in [22] and again we leave the investigation of this potential connection for future work.
One can change variables from q to the complex electric mass a in \(\Phi [{\mathcal {O}}]\) and express the u-plane integral as a residue of a around \(\infty \) and 0. One may in this way connect to other techniques for the evaluation of Donaldson invariants, for examples those using toric localization [23, 24]. Our results may also be useful for the evaluation of Coulomb branch integrals of different theories, such as those including matter and superconformal theories [18], and for four-manifolds with \(b_1\ne 0\).
The outline of the paper is as follows. Section 2 reviews Seiberg–Witten theory and its topological twist. Section 3 gives a lightning overview of compact four-manifolds with \(b_2^+=1\). Section 4 continues with introducing the path integral and correlation functions of the theory on these manifolds, which are evaluated in Section 5. We close in Sect. 6 with an analysis on the asymptotic behavior of correlation functions with a large number of fields inserted.
2 Seiberg–Witten theory and Donaldson–Witten theory
We give a brief review of pure Seiberg–Witten theory [9, 25], and its topologically twisted counterpart aka Donaldson–Witten theory [8]. See [26, 27] for a detailed introduction to both of these theories.
2.1 Seiberg–Witten theory
Seiberg–Witten theory is the low-energy effective theory of \({\mathcal {N}}= 2\) supersymmetric Yang–Mills theory with gauge group \(G = \mathrm{SU}(2)\) or \(\mathrm{SO}(3)\) and Lie algebra \(\mathfrak {su}(2)\). The building blocks of the theory contain a \({\mathcal {N}}=2\) vector multiplet which consists of a gauge field A, a pair of (chiral, anti-chiral) spinors \(\psi \) and \({{\bar{\psi }}}\), a complex scalar Higgs field \(\phi \) (valued in \(\mathfrak {su}(2)\otimes {\mathbb {C}}\)), and an auxiliary scalar field \(D_{ij}\) (symmetric in \(\mathrm{SU}(2)_R\) indices i and j, which run from 1 to 2). \({\mathcal {N}}=2\) hypermultiplets can be included in general. Here we will consider pure Seiberg–Witten theory with gauge group as above, so we assume no hypermultiplets. The gauge group is spontaneously broken to \(\mathrm {U}(1)\) on the Coulomb branch \({\mathcal {B}}\). The pair \((a,a_D)\in {\mathbb {C}}^2\) are the central charges for a unit electric and magnetic charge. The parameters a and \(a_D\) are expressed in terms of the holomorphic prepotential \({\mathcal {F}}\) of the theory
Its second derivative equals the effective coupling constant
where \(\theta \) is the instanton angle with periodicity \(4\pi \), g is the Yang–Mills coupling and \({\mathbb {H}}\) is the complex upper half-plane. The Coulomb branch \({\mathcal {B}}\) is parametrized by the order parameter,
where the trace is in the 2-dimensional representation of \(\mathrm {SU}(2)\). The renormalization group flow relates the Coulomb branch parameter u and the effective coupling constant \(\tau \). Using the Seiberg–Witten geometry [9], the order parameter u can be exactly expressed as a function of \(\tau \) in terms of modular forms,
where \(\Lambda \) is a dynamically generated scale, \(q=e^{2\pi i \tau }\), and \(\vartheta _i(\tau )\) are the Jacobi theta functions, which are explicitly given in “Appendix A.” The function \(u(\tau )\) is invariant under transformations \(\tau \mapsto \frac{a\tau +b}{c\tau +d}\) given by elements of the congruence subgroup \(\Gamma ^{0}(4) \subset \mathrm {SL}(2,{\mathbb {Z}})\).Footnote 2 See Eq. (A.2) in “Appendix A” for the definition of this group. A change of variables from u to \(\tau \) maps the u-plane to a fundamental domain of \(\Gamma ^0(4)\) in the upper-half plane \({\mathbb {H}}\). We choose the fundamental domain as the union of the images of the familiar key-hole fundamental domain of \(\mathrm {SL}(2,{\mathbb {Z}})\) under \(\tau \mapsto \tau +1\), \(\tau + 2\), \(\tau +3\), \(-1/\tau \) and \(2-1/\tau \), which is displayed in Fig. 2. Let \(u_D\) be the vector-multiplet scalar for the dual photon vector multiplet with coupling constant \(\tau _D=-1/\tau \). Then
At the cusp \(\tau \rightarrow 0\) (respectively, \(\tau \rightarrow 2\)) a monopole (respectively, a dyon) becomes massless, and the effective theory breaks down since new additional degrees of freedom need to be taken into account. Another quantity which we will frequently encounter is the derivative \(\frac{{\mathrm{d}}a}{{\mathrm{d}}u}\). It is expressed as function of \(\tau \) as
and transforms under a standard pair of generators of \(\Gamma ^0(4)\) as
Let us also give the expression of the dual of this quantity \((\frac{{\mathrm{d}}a}{{\mathrm{d}}u})_D\)
2.2 Donaldson–Witten theory
Donaldson–Witten theory is the topologically twisted version of Seiberg–Witten theory with gauge group \(\mathrm {SU}(2)\) or \(\mathrm {SO}(3)\) and contains a class of observables in its \({\mathcal {Q}}\)-cohomology, which famously provide a physical realization of the mathematically defined Donaldson invariants [28, 29].
Topological twisting preserves a scalar fermionic symmetry \({\mathcal {Q}}\) of \({\mathcal {N}}=2\) Yang–Mills on an arbitrary four-manifoldFootnote 3 [8]. The twisting involves a choice of an isomorphism of an associated bundle to the SU(2) R-symmetry bundle with an associated bundle to the frame bundle. Namely, we choose an isomorphism of the adjoint bundle of the \(\mathrm{SU}(2)_{R}\) R-symmetry bundle with the bundle of anti-self-dual 2-forms, and we choose a connection on the R-symmetry bundle, which under this isomorphism becomes the Levi–Civita connection on the bundle of anti-self-dual 2-forms. In practice, this allows us to replace the quantum numbers of fields under the \(\mathrm {SU(2)}_{-}\times \mathrm {SU}(2)_{+}\) factor of the \({\mathcal {N}}=2\) supergroup by the quantum numbers of a diagonally embedded SU(2) group.
The original supersymmetry generators transform as the \((\mathbf { 1,2,2})\oplus (2,1,2)\) representation of \(\mathrm {SU}(2)_{+} \times \mathrm {SU}(2)_{-} \times \mathrm {SU}(2)_R\) group. Their representation under the twisted rotation group \(\mathrm {SU}(2)'_{+} \times \mathrm {SU}(2)_{-} \times \mathrm {U}(1)_{\mathrm{R}}\) is \(({\mathbf { 1,1}})^{+1} \oplus ({\mathbf { 2,2}})^{-1} \oplus ({\mathbf { 1,3}})^{+1} \). The first term \(({\mathbf { 1,1}})^{+1}\) corresponds to the BRST-type operator \({{\mathcal {Q}}}\), whose cohomology provides operators in the topological field theory. The second term \(({\mathbf { 2,2}})^{-1}\) corresponds to the one-form operator K, which provides a canonical solution to the descent equations
by setting \({\mathcal {O}}^{(i)} = K^i {\mathcal {O}}^{(0)}\) [3, 4, 30]. Integration of the operators \({\mathcal {O}}^{(i)}\) over i-cycles gives topological observables since \(\{ {\mathcal {Q}}, K \} = d\).
The field content of the topologically twisted theory is a one-form gauge potential A, a complex scalar a, together with anti-commuting (Grassmann valued) self-dual two-form \(\chi \), one-form \(\psi \) and zero-form \(\eta \). The auxiliary fields of the non-twisted theory combine to a self-dual two-form D. The action of the BRST operator \({\mathcal {Q}}\) on these fields is given by
The low-energy Lagrangian of the Donaldson–Witten theory is given by [3]
where \(y=\mathrm {Im}(\tau )>0\).
3 A survey of four-manifolds with \(b_2^+=1\)
We aim to evaluate and analyze the u-plane integral for compact four-manifolds with \((b_1,b_2^+)=(0,1)\) (and without boundary).Footnote 4 This is a large class of manifolds which includes among others complex rational surfaces and examples of symplectic manifolds. The u-plane integral is well defined and can be evaluated for all these four-manifolds. This section gives a brief review of the standard geometric aspects of these four-manifolds.
3.1 Four-manifolds and lattices
Let M be a compact four-manifold, and let \(b_j=\dim (H^j(M,{\mathbb {R}}))\) be the Betti numbers of M. For simplicity, we restrict to manifolds with \(b_1=0\), and we do not require them to be simply connected. The torsion subgroups of \(H_1(M,{\mathbb {Z}})\) and \(H^2(M,{\mathbb {Z}})\) are naturally dual by Poincaré duality. They will not play an important role here, since they simply lead to an overall factor (the order) from the addition of flat connections.
We denote by L the image of the Abelian group \(H^2(M,{\mathbb {Z}})\in H^2(M,{\mathbb {R}})\), which effectively mods out the torsion in \(H^2(M,{\mathbb {Z}})\). As a result, L is a lattice in a real vector space, and we can divide elements of L without ambiguity. If the context allows, we will occasionally use \(H^2(M,{\mathbb {Z}})\) and L interchangeably. The intersection form on \(H^2(M,{\mathbb {Z}})\) provides a natural non-degenerate bilinear form \(B: (L\otimes {\mathbb {R}})\times (L\otimes {\mathbb {R}}) \rightarrow {\mathbb {R}}\) that pairs degree two co-cycles,
and whose restriction to \(L \times L\) is an integral bilinear form. The bilinear form provides the quadratic form \(Q({{\varvec{k}}}) := B({{\varvec{k}}}, {{\varvec{k}}})\equiv {{\varvec{k}}}^2\), which is uni-modular and possibly indefinite. For later use, recall that a characteristic element of L is an element \({{\varvec{c}}}\in L\), such that
We let furthermore \(H^2(M,{\mathbb {R}})^{\pm }\) be the positive definite and negative definite subspaces of \(H^2(M,{\mathbb {R}})\), and set \(b_2^{\pm }= \mathrm{dim}(H^2(M,{\mathbb {R}})^\pm )\). Van der Blij’s lemma states that a characteristic element \({{\varvec{c}}}\) of a lattice L satisfies \(Q({{\varvec{c}}})=\sigma _L \mod 8\), where \(\sigma _L=b_2^+-b_2^-\) is the signature of L.
The second Stiefel–Whitney class \(w_2(T_M)\) is a class in \(H^2(M,{\mathbb {Z}}_2)\), which distinguishes spinnable from non-spinnable manifolds. A smooth, spinnable manifold has \(w_2(T_M)=0\), while \(w_2(T_M)\ne 0\) for non-spinnable manifolds. The class \(w_2(T_M)\) has implications for the intersection form of the lattice L. In four (but not in higher) dimensions, the Stiefel–Whitney class always has an integral lift. Any integral lift of the Stiefel–Whitney class defines a characteristic vector in L. Therefore, \(w_2(T_M)=0\) implies that L is an even lattice. The converse is however only true if M is simply connected due to the possibility that \(w_2(T_M)\) is represented by a torsion class in \(H^2(M,{\mathbb {Z}})\). An even stronger statement for the intersection form of smooth, spinnable four-manifolds is Rokhlin’s theorem, which states that the signature of such manifolds satisfies \(\sigma _L=0\mod 16\). Note that the Enriques surface is smooth while it has intersection form \({\mathbb {I}}^{1,1}\oplus L_{E_8}\), where \({\mathbb {I}}^{1,1}\) is the two-dimensional lattice with quadratic form \(\textstyle {\left( {\begin{matrix} 0 &{} 1 \\ 1 &{} 0 \end{matrix}}\right) }\), and \(L_{E_8}\) is minus the \(E_8\) root lattice. This does not contradict Rokhlin’s theorem since the Enriques surface is not spinnable; \(w_2(T_M)\) is represented by a torsion element. It is also worth noting that for complex manifolds the canonical class K is an integral lift of the Stiefel–Whitney class and therefore any other integral lift differs by twice a lattice vector in L.
Any closed, orientable four-manifold admits a Spin\(^{\mathbb {C}}\) structure. To a Spin\(^{\mathbb {C}}\) structure, one attaches a first Chern class of a certain line bundle, which we refer to as the first Chern class of the Spin\(^{\mathbb {C}}\) structure. The first Chern class of a Spin\(^{\mathbb {C}}\) structure is an integral lift of \(w_2(T_M)\) and is therefore a characteristic vector \({{\varvec{c}}}\in L\). Interestingly, the existence of an almost complex structure for a smooth four-manifold M is related to the existence of a characteristic vector \({{\varvec{c}}}\) with fixed norm. Note that an almost complex structure ensures that the tangent bundle \(T_M\) is complex, such that its Chern class \(c_1(T_M)\in H^2(M,{\mathbb {Z}})\) and canonical class \(K=-c_1(T_M)\) are well defined. The Riemann–Roch theorem for four-manifolds with an almost complex structure demonstrates that its canonical class K is a characteristic element of L. Moreover:
-
The modulo 2 reduction of K satisfies
$$\begin{aligned} w_2(T_M)=K \mod 2. \end{aligned}$$(3.3) -
By the Hirzebruch signature theorem
$$\begin{aligned} Q(K)=2\chi +3\sigma , \end{aligned}$$(3.4)where \(\chi =2-2\,b_1+b_2\) is the Euler number of M, and \(\sigma =b_2^+-b_2^-\) is the signature of M.
In fact the converse holds as well: any characteristic vector \({{\varvec{c}}}\in L\), which satisfies (3.3) and (3.4), gives rise to an almost complex structure [31, 32]. Combination of this statement with Van der Blij’s lemma demonstrates that if M admits an almost complex structure, then \(b_2^++b_1\) must be odd.
3.2 Four-manifolds with \(b_2^+=1\)
We will specialize in the following to \(b_2^+=1\). In this case, the quadratic form Q can be brought to a simple standard form [29, Section 1.1.3], which will be instrumental to evaluate the u-plane integral in Sect. 5. The standard form depends on whether the lattice is even or odd:
-
If Q is odd, an integral change of basis can bring the quadratic form to the diagonal form
$$\begin{aligned} \left\langle 1 \right\rangle \oplus m \left\langle -1\right\rangle , \end{aligned}$$(3.5)with \(m=b_2-1\). This has an important consequence for characteristic elements of such lattices. If K is a characteristic element, \({{\varvec{k}}}^2+B(K,{{\varvec{k}}})\in 2{\mathbb {Z}}\) for any \({{\varvec{k}}}\in L\). In the diagonal basis (3.5) this equivalent to \(\sum _{j=1}^{b_2} k_j^2 +K_j k_j\in 2{\mathbb {Z}}\) with \(K=(K_1,K_2,\dots , K_{b_2})\). This can only be true for all \({{\varvec{k}}}\in L\) if \(K_j\) is odd for all \(j=1,\dots , b_2\).
-
If Q is even, the quadratic form Q can be brought to the form
$$\begin{aligned} {\mathbb {I}}^{1,1} \oplus n\, L_{E_8}, \end{aligned}$$(3.6)where \({\mathbb {I}}^{1,1}\) and \(L_{E_8}\) as defined above and \(n=(b_2-2)/8\). The components \(K_{j}\), \(j=1,2\) must therefore be even in this basis.
Another important aspect of M is its period point \(J\in H^2(M,{\mathbb {R}})\), which is the generator of \(H^2(M,{\mathbb {R}})^+\), normalized such that \(Q(J)=1\). The period point depends on the metric due to the self-duality condition. In fact, the metric dependence in the expressions below only enters through a choice of J. Using J, we can project \({{\varvec{k}}}\in L\) to the positive and negative definite subspaces \(H^2(M,{\mathbb {R}})^\pm \): \({{\varvec{k}}}_+=B({{\varvec{k}}},{J})\,{J}\) is the projection of \({{\varvec{k}}}\) to \(H^2(M,{\mathbb {R}})^+\), and \({{\varvec{k}}}_-={{\varvec{k}}}-{{\varvec{k}}}_+\) is the projection to \(H^2(M,{\mathbb {R}})^-\). Note that these projections are also the self-dual and anti-self-dual parts of \({{\varvec{k}}}\) with respect to the Hodge \(*\)-operation.
3.2.1 Complex four-manifolds with \(b_2^+=1\)
Complex four-manifolds with \(b_2^+=1\) are well-studied and classified by the Enriques–Kodaira classification. This classification starts with the notion of a minimal complex surface. This is a non-singular surface which can not be obtained from another non-singular surface by blowing up a point. This is equivalent to the statement that the surface does not contain rational curves with self-intersection \(-1\) (or \((-1)\)-curves). The Enriques–Kodaira classification classifies minimal surfaces using the so-called Kodaira dimension.
The relevant surfaces for us are those with \((b_1,b_2^+)=(0,1)\), whose Kodaira dimension is either \(-\infty \), 0, 1 or 2:
-
Surfaces with Kodaira dimension \(-\infty \) are surfaces whose canonical bundle does not admit holomorphic sections. These surfaces are birational to more than one minimal surface. The simply connected surfaces with \(b_2^+=1\) in this family are the rational surfaces, i.e., the complex projective plane \({\mathbb {P}}^2\), Hirzebruch surfaces and blow-ups of these surfaces. A special property of these surfaces are vanishing chambers where the moduli spaces of instantons are empty. This has been useful for the explicit determination of partition functions on these geometries, including the u-plane integral [3, 10, 33, 34].
-
Surfaces with Kodaira dimension 0 are surfaces for which the canonical class K satisfies \(Q(K)=0\) and \(B(K,C)=0\) for any curve C. If they satisfy in addition \((b_1,b_2^+)=(0,1)\), they are known as Enriques surfaces. Their intersection form is \({\mathbb {I}}^{1,1}\oplus L_{E_8}\). Note that this four-manifold is not simply connected and that \(w_2(T_M)\) is represented by a torsion class in \(H^2(M,{\mathbb {Z}})\).
-
Surfaces with Kodaira dimension 1 are surfaces for which the canonical class K satisfies \(Q(K)=0\), and \(B(K,C)>0\) for any curve C. Such surfaces are elliptic (but the converse is not always true). The Dolgachev surfaces are a family of simply connected surfaces with Kodaira dimension 1.
-
Surfaces with Kodaira dimension 2 are surfaces of general type. If a surface in this class is simply connected with \(b_2^+=1\), its holomorphic Euler character \(\chi _{h}\) equals 1. Their Euler numbers lie between 3 and 11, and there are examples for each integer in this set such as the Godeaux and Barlow surfaces which both have Euler number 11. See, for example, [35] for a more comprehensive list and details.
3.2.2 Beyond complex four-manifolds
Although many four-manifolds with \(b_2^+=1\) admit an almost complex structure, most four-manifolds are not complex and their classification is an important open problem. A distinguished class of four-manifolds with \(b_2^+=1\) are symplectic ones, which partially overlap with the complex four-manifolds. For a four-manifold to be symplectic, its period point J must provide a symplectic structure.Footnote 5 Reference [36] provides a survey of such manifolds. Examples of symplectic four-manifolds which are not complex are four-manifolds denoted by \(E(1)_N\), that is, four-manifolds which are homotopy equivalent to a rational elliptic surface and whose construction relies on a fibered knot N in \(S^3\) [37, 38]. The manifolds in this class have \(b_1=0\). For recent progress on symplectic, non-complex manifolds with Kodaira dimension 1 (\(Q(K)=0\) and \(B(K,C)>0\)) with \(b_1\ne 0\), see [39].
3.3 Donaldson invariants
Donaldson invariants have been of crucial importance for the classification of four-manifolds, since they can distinguish among smooth structures on four-manifolds [21, 29]. These invariants are based on ASD equations and via the Donaldson–Uhlenbeck–Yau theorem to semi-stable vector bundles. We briefly recall the definition of the Donaldson invariants in the formalism of topological field theory. Let \({\mathcal {M}}_{\gamma }\) be the moduli space of solutions to the ASD equations for gauge group \(\mathrm{SU}(2)\) or \(\mathrm{SO}(3)\), where \(\gamma =(c_1,k)\) represents the topological numbers of the solution, that is to say \(c_1=\frac{i}{2\pi }\mathrm {Tr}(F)\in H^2(M,{\mathbb {Z}})\) and \(k=\frac{1}{8\pi ^2}\int _M \mathrm {Tr}[F^2]\). The map \(\mu ^\gamma _D: H_i(M,{\mathbb {Q}})\rightarrow H^{4-i}({\mathcal {M}}_\gamma ,{\mathbb {Q}})\) maps an i-cycle on M to a \((4-i)\)-form on \({\mathcal {M}}_{\gamma }\).
This map is constructed using the universal curvature \({\mathcal {F}}\) of the universal bundle \({\mathcal {U}}\) over \(M\times {\mathcal {M}}_\gamma \) if it exists, which can be expressed as a formal sum of the fields of the topological theory \({\mathcal {F}}=F+\psi +\phi \) [40]. The class \(\mu _D\) is defined in terms of the first Pontryagin class of the universal bundle,
where the trace is in the two-dimensional representation of the gauge group, i.e., the fundamental representation for SU(2) and the spinor representation for SO(3).
We will only consider the image of \(\mu _D\) for 0- and 2-cycles of M. Let \(\{r_j\}\) be a finite set of points of M and \({{\varvec{p}}}= [r_1] + [r_2] + \dots \in H_0(M,{\mathbb {Z}})\) the corresponding 0-cycle. Then \(\mu _D({{\varvec{p}}})\) evaluates to
where \({\hat{u}}\) is the UV operator,
Given (3.7), we also interpret \(\mu _D({{\varvec{p}}})\) as a four-form on the moduli space \({\mathcal {M}}_\gamma \). Since its cohomology class is independent of position, we can express \(\mu _D({{\varvec{p}}})\) equivalently as
where \(p:H_0(M,{\mathbb {Z}})\rightarrow {\mathbb {R}}\) the unique linear map satisfying \(p({{\varvec{e}}})=1\), where \({{\varvec{e}}}\) is a generator of \(H_0(M,{\mathbb {Z}})\). For \({{\varvec{x}}}\in H_2(M,{\mathbb {Z}})\), \(\mu _D({{\varvec{x}}})\) provides similarly a two-form on \({\mathcal {M}}_\gamma \). See Eq. (4.14) for the precise expression in terms of the physical fields. Using the linearity of the map \(\mu _D\), we extend the definition of \(\mu _D\) from \(H_*(M,{\mathbb {Z}})\) to \(H_*(M,{\mathbb {C}})\).
Using the map \(\mu _D\), we can define the Donaldson invariant \(D^\gamma _{\ell ,s}({{\varvec{p}}},{{\varvec{x}}})\in {\mathbb {Q}} \) as the intersection number
The number \(D^{\gamma }_{\ell ,s}\) is only non-vanishing if \(4\ell +2s=\mathrm {dim}_{\mathbb {R}}({\mathcal {M}}_\gamma )\). For smooth four-manifolds, the virtual dimension of the moduli space is
and in general this is in fact the dimension. For complex surfaces, we can write \(2\ell +s =4k-c_1^2-3\chi _h\) with \(k\in {\mathbb {Z}}\) and \(\chi _h\) the holomorphic Euler characteristic, \(\chi _h=(\chi +\sigma )/4\).
4 Path integral and correlation functions
This section reviews general properties the u-plane integral. We will treat the partition function in Sect. 4.1 and correlation functions in Sect. 4.2.
4.1 Path integral
We consider Donaldson–Witten theory on a four-manifold M with \(b_2^+=1\) as discussed in the previous section. For the case of pure SYM with no hypermultiplets, we are always free to consider the case where the principal SO(3) gauge bundle has a nontrivial ’t Hooft flux \(w_2(P) \in H^2(M;{\mathbb {Z}}_2)\). We choose an integral lift \(\overline{w_2(P)}\) (and we assume such a lift exists) and embed it in \(H^2(M;{\mathbb {R}})\), and we denote \({\varvec{\mu }}:= \frac{1}{2} \overline{w_2(P)} \in L\otimes {\mathbb {R}}\). The dependence on the choice of lift will only enter through an overall sign. The path integral over the Coulomb branch of Donaldson–Witten theory, denoted by \(\Phi _{{\varvec{\mu }}}^J\), is an integral over the infinite dimensional field space, which reduces to a finite dimensional integral over the zero modes [3]. We restrict for simplicity to four-manifolds with \(b_1=0\), such that there are no zero modes for the one-form fields \(\psi \). The path integral of the effective theory on the Coulomb branch then becomes
where \({\mathcal {L}}_0\) is the Lagrangian (2.11) specialized to the zero modes including the ones of the gauge field. The functions A(u) and B(u) are curvature couplings; they are holomorphic functions of u, given by [3, 41]
The coefficients \(\alpha \) and \(\beta \) are numerical factors, which we choose to match with results on Donaldson invariants from the mathematical literature. Note that \(A(u)^{\chi }\,B(u)^{\sigma }\) has dimension \(\Lambda ^2\) since \(\chi +\sigma =4\). Moreover, \(da\wedge {\mathrm{d}}{\bar{a}}\wedge {\mathrm{d}}D\wedge {\mathrm{d}}\eta \wedge {\mathrm{d}}\chi \) has dimension \(\Lambda \), such that \(\Phi _{{\varvec{\mu }}}^J\) (4.1) is dimensionless.Footnote 6 We denote the contribution of the Coulomb branch to a correlation function \(\left\langle {\mathcal {O}}_1 {\mathcal {O}}_2\dots \right\rangle _{\varvec{\mu }}^J\) by \(\Phi _{\varvec{\mu }}^J[{\mathcal {O}}_1 {\mathcal {O}}_2\dots ]\). This corresponds to an insertion of \({\mathcal {O}}_1{\mathcal {O}}_2\dots \) in the rhs of (4.1) plus possible contact terms depending on the \({\mathcal {O}}_j\).
We proceed by reviewing the evaluation of \(\Phi _{\varvec{\mu }}^J\). Integration over D, and the fermions \(\eta \) and \(\chi \) gives
where the vector \({{\varvec{k}}}\) equals \([F]/4\pi \) and represents a class in \(L+{\varvec{\mu }}\) with \({\varvec{\mu }}\in L/2\). The factor \(\frac{{\mathrm{d}}{{\bar{\tau }}}}{{\mathrm{d}}{\bar{a}}}\) suggests that it is natural to change variables from a to the effective coupling constant \(\tau \in {\mathbb {H}}/\Gamma ^0(4)\) in (4.1). To this end, we define the holomorphic “measure factor"
so that Eq. (4.12) below will hold. Using Matone’s relation [42]
and (2.4) and (2.6), we can express \({{\tilde{\nu }}}\) in terms of modular functions
where we fixed the constants \(\alpha \) and \(\beta \),Footnote 7
The modular transformations of \({{\tilde{\nu }}}\) for the two generators \(ST^{-1}S: \tau \mapsto \frac{\tau }{\tau +1}\) and \(T^4: \tau \mapsto \tau +4\) of \(\Gamma ^0(4)\) are:
The measure \({\tilde{\nu }}(\tau )\) behaves near the weak coupling cusp \(\tau \rightarrow i\infty \) as \(\sim q^{-\frac{3}{8}}\). Near the monopole cusp, we have \({{\tilde{\nu }}}(-1/\tau _D)=(-i\tau _D)^{2-b_2/2}\,\tilde{\nu }_D(\tau _D)\) with
whose \(q_D\)-series starts at \(q_D^{1+\frac{\sigma }{8}}\).
The photon path integral takes the form of a Siegel–Narain theta function with kernel \({\mathcal {K}}\)
where K is a characteristic vector for L corresponding to an almost complex structure or Spin\(^{\mathbb {C}}\) structure.Footnote 8 If one considers correlation functions rather than the partition function, the sum over \(\mathrm {U}(1)\) fluxes can be expressed as \(\Psi ^J_{\varvec{\mu }}\left[ {\mathcal {K}}\right] \), with the kernel \({\mathcal {K}}\) dependent on the fields in the correlation function [19]. For the partition function, the factor (4.3) leads to \(\Psi ^J_{\varvec{\mu }}\left[ {\mathcal {K}}_0 \right] \) with
where we have left out the factor \(\frac{{\mathrm{d}}{{\bar{\tau }}}}{{\mathrm{d}}{\bar{a}}}\), which provides the change of variables from the Coulomb branch parameters to a fundamental domain of \(\Gamma ^0(4)\) in \({\mathbb {H}}\). Combining all ingredients, we arrive at the following expression for \(\Phi _{\varvec{\mu }}^J\),
An important requirement for (4.12) is the modular invariance of the integrand under \(\Gamma ^0(4)\) transformations. We can easily determine the modular transformations of \(\Psi _{{\varvec{\mu }}}^J[{\mathcal {K}}_0]=:\Psi _{{\varvec{\mu }}}^J\) from those of \(\Psi _{{\varvec{\mu }}}^J[1]\) (B.5). The effect of replacing 1 by \({\mathcal {K}}_0\) in \(\Psi _{{\varvec{\mu }}}^J[1]\) is to increase the weight by \((\frac{1}{2},\frac{3}{2})\). (The factor \(1/\sqrt{y}\) contributes \((\frac{1}{2},\frac{1}{2})\) and \(B({{\varvec{k}}}, J)\) contributes (0, 1) to the total weight.) We then arrive at
where we used that \(Q(K)=\sigma \mod 8\). Combining (4.8) and (4.13), we deduce that the integrand of (4.12) is invariant under the \(\tau \mapsto \frac{\tau }{\tau +1}\) transformation. Moreover, the integrand is invariant under \(\tau \mapsto \tau +4\) if \(B({\varvec{\mu }}, K)=\frac{1}{2} \mod \mathbb {Z}\). However, if \(B({\varvec{\mu }}, K)=0 \mod \mathbb {Z}\), the integrand is multiplied by \(-1\) for \(\tau \mapsto \tau +4\). Since \(\Psi _{{\varvec{\mu }}}^J\) vanishes identically in the latter case case, there is no violation of the duality.
We conclude therefore that the Coulomb branch integral (4.12) is well defined since the measure \({\mathrm{d}}\tau \wedge {\mathrm{d}}{\bar{\tau }}\) transforms as a mixed modular form of weight \((-2,-2)\) while the product \({\tilde{\nu }}\, \Psi _{{\varvec{\mu }}}^J\) is a mixed modular form of weight (2,2) for the group \(\Gamma ^0(4)\) making the integrand modular invariant. We close this subsection with Table 1 that collects the weights of the various modular forms that appear in the context of u-plane integrals. Evaluation of the integral is postponed to Sect. 5.
4.2 Correlators of point and surface observables
Much more information about the theory is obtained if we include observables in the path integral [3, 8], which contain integrals over positive degree homology cycles of the four-manifold M. Since we restrict to four-manifolds with \(b_1=b_3=0\), we will focus in this article on surface observables involving integrals over elements of \(H_0(M,{\mathbb {Q}})\) and \(H_2(M,{\mathbb {Q}})\).
The Donaldson invariants are correlation functions of observables in Donaldson–Witten theory. The canonical UV surface observable of Donaldson–Witten theory is defined using the descent operator K mentioned below Eq. (2.9),
with \({{\varvec{x}}}\in H_2(M,{\mathbb {Q}})\). The Donaldson invariant \(D^{\gamma }_{\ell ,s}\) (3.11) can be expressed as a correlation function of the twisted Yang–Mills theory,
where on the rhs, \(\gamma =(2{\varvec{\mu }},k)\) with \(k\in {\mathbb {Z}}-2{\varvec{\mu }}^2\). The map \(p:H_0(M,{\mathbb {Z}})\rightarrow {\mathbb {R}}\) was introduced below (3.8).
Note that \(D^{\gamma }_{\ell ,s}({{\varvec{p}}},{{\varvec{x}}})\in {\mathbb {Z}}\) if \({{\varvec{p}}}/4\in H_0(M,{\mathbb {Z}})\) and \({{\varvec{x}}}/2\in H_2(M,{\mathbb {Z}})\), since the coefficients of \(u(\tau )\) are in \({\mathbb {Z}}/8\) and the flux \([F]/2\pi \in H^2(M,{\mathbb {Z}})\). It is natural to form a generating function of correlation functions by including exponentiated observables in the path integral
We will often suppress the argument of p and consider it simply as a fugacity in which we can make a (formal) series expansion.
In terms of the zero modes of the fields in the effective infrared theory, the operator \(I_-({{\varvec{x}}})\) is represented by
where u is the zero mode of \({\hat{u}}\), or equivalently the vev of \({\hat{u}}\) as in (2.3). Inclusion of this operator in the path integral gives rise to a contact term in the IR, \(e^{{{\varvec{x}}}^2\,T(u)}\) [3, 4], with
where \(\vartheta _4\) is the fourth classical Jacobi theta function. The dual contact term reads
We include moreover the \({\mathcal {Q}}\)-exact operator \(I_+({{\varvec{x}}})\) [17],
which can aid the analysis in the context of mock modular forms. As explained in [19], addition of this observable to \(I_-({{\varvec{x}}})\) does not change the answer, once the integrals over the u-plane are suitably defined. And more generally, if we add \(\alpha \,I_{+}({{\varvec{x}}})\), the integral is independent of \(\alpha \). Nevertheless, the integrand depends in an interesting way on \(\alpha \). We will discuss this in more detail in Sect. 6.2. Here we will continue with \(\alpha =1\). In the effective infrared theory, \(I_{+}({{\varvec{x}}})\) becomes
With (4.17) and (4.21), we find that the contribution of the Coulomb branch to \(\left\langle e^{I_-({{\varvec{x}}})+I_+({{\varvec{x}}})}\right\rangle ^J_{\varvec{\mu }}\) reads
As a first step towards evaluating this integral, we carry out the integral over D. If we just consider the terms in (4.22) that depend on D, this gives
where we have defined \({{\varvec{b}}}\in L\otimes {\mathbb {R}}\) through
The variable \({\varvec{\rho }}\) transforms with weight \(-1\). With this normalization, it will appear as a natural elliptic variable in the sum over fluxes. The dual variable is
where \(\left( \frac{{\mathrm{d}}u}{{\mathrm{d}}a}\right) _{\!\!D}\) is given in (2.8).
Substitution of (4.23) in the path integral and integration over the \(\eta \) and \(\chi \) zero modes modifies the sum over the \(\mathrm{U}(1)\) fluxes to \(\Psi ^J_{\varvec{\mu }}[{\mathcal {K}}_{\mathrm{s}}]\) (4.10) where the kernel \({\mathcal {K}}_{\mathrm{s}}\) given by [3, 17]
This gives the standard generalization of \(\Psi _{\varvec{\mu }}^J(\tau ,\bar{\tau })\) to a theta series with an elliptic variable \({\varvec{\rho }}\). The holomorphic part couples to \({{\varvec{k}}}_-\) and the anti-holomorphic part to \({{\varvec{k}}}_+\) We will therefore also denote \(\Psi ^J_{\varvec{\mu }}[{\mathcal {K}}_{\mathrm{s}}]\) as
Note that \(\Psi _{\varvec{\mu }}^J(\tau ,{{\bar{\tau }}},0,0)=\Psi _{\varvec{\mu }}^J [{\mathcal {K}}_0](\tau ,{{\bar{\tau }}})\) (4.10). We postpone the remaining steps of the evaluation to Sect. 5.5.
After describing the u-plane integrand, we can also give the Seiberg–Witten contribution of the strong coupling singularities \(u=\pm \Lambda ^2\) to \(\left\langle e^{2p\,{\hat{u}}+I_-({{\varvec{x}}})} \right\rangle ^J_{\varvec{\mu }}\). Setting \(\Lambda =1\), the contribution for \(u=1\) from a Spin\(^{{\mathbb {C}}}\) structure \({{\varvec{k}}}\) is [3]
with \(n=-(2\chi +3\sigma )/8+{{\varvec{k}}}^2/2\) and the functions C(u), P(u), L(u) given by
For four-manifolds of SW-simple type, the only \({{\varvec{k}}}\) for which the (4.28) is non-vanishing have \(n=0\). The expression then simplifies considerably [2, 3]. For the contribution from \(u=1\),Footnote 9
and for the contribution from \(u=-1\),
The full correlation function for manifolds of simple type therefore reads
Manifolds with \(b_2^+=1\) are however rarely of SW-simple type [36]. These manifolds may give rise to SW moduli spaces of arbitrarily high dimension. The SW contributions will then be more involved, but are entire functions of p and \({{\varvec{x}}}\) as is the case for (4.30) and (4.31).
4.3 Summary
For compact four-manifolds with \((b_1,b_2^+)=(0,1)\), the contribution of the u-plane to the vev of an observable \({\mathcal {O}}\) is given by
Besides the choice of \({\mathcal {O}}\), it depends on the following data of the four-manifolds
-
the lattice L with signature \((1,b_2-1)\),
-
a period point \(J \in L \otimes {\mathbb {R}}\), normalized to \(Q(J)=1\),
-
An integral lift \(K\in L\) of \(w_2(T_M)\),
-
An integral lift \(\overline{w_2(P)}\) of the ’t Hooft flux so that \({\varvec{\mu }}= \frac{1}{2}\overline{w_2(P)}\in H^2(M,{\mathbb {R}})\).
5 Evaluation of u-plane integrals
This section discusses the evaluation of u-plane integrals using mock modular forms. Section 5.1 reviews the evaluation and renormalization of integrals over a modular fundamental domain [3, 19, 20]. Section 5.2 explains the strategy for arbitrary correlation functions. Section 5.3 factors the sum over fluxes into holomorphic and non-holomorphic terms for a specific choice of J. We apply this result to the evaluation of the partition function and topological correlators in Sects. 5.4 and 5.5.
5.1 Integrating over \({\mathbb {H}}/ \mathrm{SL}(2,{\mathbb {Z}})\)
In the previous section, we arrived at the general form (4.33) for the contribution of the u-plane to the correlators. Order by order in \({{\varvec{x}}}\) we encounter modular integrals of the form
where f is a non-holomorphic modular form of weight \((2-s,2-s)\), and \({\mathcal {F}}_\infty \) is the standard keyhole fundamental domain for the modular group, \({\mathcal {F}}_\infty = {\mathbb {H}}/\mathrm {SL}(2,{\mathbb {Z}})\). The integral is naturally independent of the choice of fundamental domain due to the modular properties of f. We assume that f has a convergent Fourier series expansion
where the exponents m, n are bounded below. They may be real and negative, but \(m-n \in {\mathbb {Z}}\) by the requirement that f is a modular form. Since m and n can be both negative, the integral \({\mathcal {I}}_f\) is in general divergent and needs to be properly defined [19, 20, 43, 44]. While the definition of the regularized and renormalized integral \({\mathcal {I}}^{\mathrm{r}}_f\) is quite involved, the final result is quite elegant and compact, at least if f can be expressed as a total anti-holomorphic derivative,
where \({\widehat{h}}\) transforms as a modular form of weight (2, 0). In this case, the integrand of (5.1) is exact and equal to \(-d({\mathrm{d}}\tau \,{\widehat{h}})\). If only terms with \(n>0\) contribute to the sum in (5.2), \({\widehat{h}}\) is a mock modular form and can be expressed as
where h is a (weakly) holomorphic function with Fourier expansion
Note that the two terms on the rhs of (5.4) are separately invariant under \(\tau \rightarrow \tau +1\), while the transformation of the integral under \(\tau \rightarrow -1/\tau \) implies for \(h(\tau )\),
Reference [19] gives a definition of the integral \({\mathcal {I}}^{\mathrm{r}}_f\) such that the value turns out to be
As a result, the only contribution to the integral arises from the constant term of \(h(\tau )\). The definition in [19] reduces to the older definition for \({\mathcal {I}}_f\) if either m or n is non-negative [3, 44] but is new if both n, m are negative. It is shown in [19] that, at least for Donaldson–Witten theory, the new definition is physically sensible in the sense that \({{\mathcal {Q}}}\)-exact operators decouple.
Note that the absence of holomorphic modular forms of weight two for \(\mathrm {SL}(2,{\mathbb {Z}})\) implies that \(h(\tau )\) is uniquely determined by the polar coefficients, that is to say those d(m) with \(m<0\). The ambiguity in polar coefficients gives thus rise to an ambiguity in the anti-derivative \(h(\tau )\). Different choices for \(h(\tau )\) differ by a weakly holomorphic modular form of weight 2. However, this ambiguity does not lead to an ambiguity in the final result, d(0), since the constant term of such weakly holomorphic modular forms vanishes. This can be understood from the cohomology of \({\mathcal {F}}_\infty \). Since the first cohomology of \({\mathcal {F}}_\infty \) is trivial, any closed one-form \(\xi \) is necessarily exact. Such a one-form \(\xi \) can be expressed as \(C(\tau )\,{\mathrm{d}}\tau \), with \(C(\tau )\) a (weakly holomorphic) modular form of weight two. Since \(\xi \) is exact, the period \(\int ^{Y+1}_{Y}C(\tau )\,{\mathrm{d}}\tau \) vanishes, which implies that the constant term of \(C(\tau )\) vanishes. Indeed, a basis of weakly holomorphic modular forms of weight 2 is given by derivatives of powers of the modular invariant J-function, \(\partial _{\tau }\! \left( J(\tau )^\ell \right) \), \(\ell \in {\mathbb {N}}\), which all have vanishing constant terms.
5.2 General strategy
Recall that in Sect. 4 we analyzed the partition function of Donaldson–Witten theory, which led to an integrand of the form \({{\tilde{\nu }}}(\tau )\,\Psi _{\varvec{\mu }}^J[{\mathcal {K}}_0](\tau ,{\bar{\tau }})\), with a specific kernel \({\mathcal {K}}_0\) (4.11). For more general correlation functions, the integrand takes a similar form,
where the kernel \({\mathcal {K}}_{\mathcal {O}}\) depends on the insertion \({\mathcal {O}}={\mathcal {O}}_1{\mathcal {O}}_2\dots \). This can be expressed as an integral of the form (5.1), whose integrand could consist of several terms \(\sum _{j} y^{-s_j} f_j \). Moreover, one can express the integral over \(\Gamma ^0(4)\) as the sum of six integrals over \({\mathcal {F}}_\infty \) using modular transformations. As explained in the previous subsection, an efficient technique to evaluate these integrals is to express the integrand as a total derivative with respect to \({{\bar{\tau }}}\), which has indeed been used in a few special cases to evaluate the u-plane integral [3, 12,13,14]. We express the integrand of the generic integral (5.8) as
which by a change of variables is equivalent to an anti-holomorphic derivative in u as discussed in the Introduction. The inverse map \(u^{-1}: {\mathcal {B}}\rightarrow {\mathbb {H}}/\Gamma ^0(4)\) maps each of the boundaries \(\partial _j {\mathcal {B}}\) to arcs in \({\mathbb {H}}/\Gamma ^0(4)\) in the vicinity of the cusps \(\{i\infty , 0 ,2\}\) displayed in Fig. 2.
The function \({\widehat{{\mathcal {H}}}}_{\varvec{\mu }}^J[{\mathcal {O}}](\tau , {\bar{\tau }})\) is required to transform as a modular form of weight (2, 0) with trivial multiplier system, which one may hope to determine explicitly using methods from analytic number theory, especially the theory of mock modular forms [15, 16]. To derive a suitable \({\widehat{{\mathcal {H}}}}^J_{\varvec{\mu }}[{\mathcal {O}}]\), we will choose a convenient period point J. Once \({\widehat{{\mathcal {H}}}}^J_{\varvec{\mu }}[{\mathcal {O}}]\) is known it is straightforward to apply the discussion of Sect. 5.1. To relate the integral over \({\mathbb {H}}/\Gamma ^0(4)\) to an integral over \({\mathcal {F}}_\infty \), we use coset representatives of \(\mathrm {SL}(2,{\mathbb {Z}})/\Gamma ^0(4)\) to map the six different images of \({\mathcal {F}}_\infty \) within \({\mathbb {H}}/\Gamma ^0(4)\), displayed in Fig. 2, back to \({\mathcal {F}}_\infty \). After this inverse mapping, we use the modular properties of the integrand to express each of the six integrands as a series in q and \({\bar{q}}\), after which the techniques of Sect. 5.1 can be applied. To this end, one can use the relations (B.4) for \(\Psi _{\varvec{\mu }}^J\), while the q-series for \({{\tilde{\nu }}}(\tau )\) follows from the standard relations for Jacobi theta functions.
Since the maps \(\tau \mapsto \tau - n\), \(n=1,2,3\) do not change the constant part of the integrand, we find that \(\Phi _{{\varvec{\mu }}}^J[{\mathcal {O}}]\) evaluates to
where for the second and third brackets on the rhs, one makes the indicated modular transformation for \(\tau \), S and \(T^2S\) and then determines the \(q^0\) coefficient of the resulting Fourier expansion.
An important point is the possibility to add to \({\widehat{{\mathcal {H}}}}^J_{\varvec{\mu }}[{\mathcal {O}}]\) a holomorphic integration “constant” \(s_{\mathcal {O}}\), which is required to be a weight 2 modular form for \(\Gamma ^0(4)\). Of course, \(\Phi ^J_{\varvec{\mu }}[{\mathcal {O}}]\) should be independent of \(s_{\mathcal {O}}\), since definite integrals do not depend on the integration constant. To see the independence of \(\Phi ^J_{\varvec{\mu }}[{\mathcal {O}}]\) on \(s_{\mathcal {O}}\), note that \(s_{\mathcal {O}}\) will be mapped to a weight 2 form for \(\mathrm {SL}(2,{\mathbb {Z}})\) by the inverse mapping. As discussed in Sect. 5.1, there are no holomorphic \(\mathrm {SL}(2,{\mathbb {Z}})\) modular forms with weight 2, and the weakly holomorphic ones have a vanishing constant term. There is therefore no ambiguity arising from the holomorphic integration constant.
On the other hand, the integration constant \(s_{\mathcal {O}}\) can modify the contribution from each cusp, since a non-vanishing holomorphic modular form of weight 2 for \(\Gamma ^0(4)\) exists. It is explicitly given by \(\vartheta _2(\tau )^4+\vartheta _3(\tau )^4\), and while it contributes 4 at the cusp at infinity, the contributions of the three cusps together add up to 0. We can make a natural choice of the integration constant by requiring that the exponential behavior of \({\mathcal {H}}^J_{{\varvec{\mu }}}\) for \(\tau \rightarrow i\infty \) matches the behavior of \({{\tilde{\nu }}}\,\Psi ^J_{\varvec{\mu }}\) in this limit.
Once we have determined \(\Phi _{{\varvec{\mu }}}^J[{\mathcal {O}}]\) for a specific period point J, one can change to an arbitrary J quite easily using indefinite theta functions as discussed in [10, 17, 18]. The integrand can thus be expressed as a total derivative (5.8) for any J.
5.3 Factoring \(\Psi ^J_{\varvec{\mu }}\)
To evaluate the partition function \(\Phi _{\varvec{\mu }}^J\), we will choose a convenient period point J so that \(\Psi ^J_{\varvec{\mu }}\), as a function of \(\tau \), has a simple factorization as a holomorphic times an anti-holomorphic function. In this way, we can easily determine an anti-derivative using the theory of mock modular forms. Using the classification of the uni-modular lattices, Eqs. (3.5) and (3.6), a convenient factorization is possible for any intersection form.
5.3.1 Odd intersection form
Let us first assume that the intersection lattice L is odd, such that its quadratic form can be brought to the standard form in Eq. (3.5). Since the wall-crossing formula for Donaldson invariants is known [3], it suffices to determine \(\Phi ^J_{\varvec{\mu }}\) for a convenient choice of J. To this end, we choose the polarization
where \({\mathbf {0}}\) is the \((b_2-1)\)-dimensional 0-vector. For this choice of J, the orthogonal decomposition of the lattice, \(L=L_+\oplus L_-\) into a 1-dimensional positive definite lattice \(L_+\) and \((b_2-1)\)-dimensional negative definite sublattice \(L_-\), implies that the sum over the \(\mathrm{U}(1)\) fluxes \(\Psi _{{\varvec{\mu }}}^{J}(\tau , {\bar{\tau }})\) factors. To see this explicitly, we let \({{\varvec{k}}}= (k_1, {{\varvec{k}}}_{-})\in L\), and \(k_1 \in {\mathbb {Z}}+ \mu _1\), \({{\varvec{k}}}_{-} \in L_{-} +{\varvec{\mu }}_{-}\) and \({\varvec{\mu }}=(\mu _1,{\varvec{\mu }}_-)\). The Siegel–Narain theta function \(\Psi _{{\varvec{\mu }}}^{J}=\Psi _{{\varvec{\mu }}}^{J}[{\mathcal {K}}_0]\) (4.10) now factors as
with
We used also that \(K_{1}\) is odd since K is a characteristic vector, as discussed in Eq. (3.5). Using
we can express \(f_\mu \) in terms of the Dedekind eta function \(\eta \),
We can similarly evaluate \(\Theta _{L_-,{\varvec{\mu }}_-}\). Since all \(K_j\) are odd, \(\Theta _{L_-,{\varvec{\mu }}_-}(\tau )\) vanishes, except if \({\varvec{\mu }}_-={\mathbf {0}} \mod \mathbb {Z}^{b_2-1}\). In that case, \(\Theta _{L_-,{\varvec{\mu }}_-}\) is a power of the Jacobi theta function \(\vartheta _4\),
After substitution of \({{\tilde{\nu }}}\) (4.6), we find for the integrand
Note that the dependence of the integrand on \(b_2\) has disappeared and that the integrand diverges for \(\tau \rightarrow \infty \).
5.3.2 Even intersection form
We continue with the even lattices, whose quadratic form can be brought to the form given in Eq. (3.6), \(L={\mathbb {I}}^{1,1}\oplus n\,L_{E_8}\). We choose for the period point
where the first two components correspond to \({\mathbb {I}}^{1,1}\subset L\), and \({\mathbf {0}}\) is now the \((b_2-2)\)-dimensional 0-vector. We have then for the positive and negative definite components of \({{\varvec{k}}}\in L\),
where \({{\varvec{k}}}_n\in nL_{E_8}\). Note \({{\varvec{k}}}_n^2\le 0\), since \(L_{E_8}\) is the negative \(E_8\) lattice.
The sum over fluxes \(\Psi _{\varvec{\mu }}^J\) factors for this choice of J,
where the subscript is \({\varvec{\mu }}=(\mu _+,\mu _-,{\varvec{\mu }}_n)\), and \(\Psi _{{\mathbb {I}},(\mu _+,\mu _-)}(\tau ,{\bar{\tau }})\) is given by
Moreover, the theta series \(\Theta _{nE_8,{\varvec{\mu }}}\) for the negative definite lattice equals
As before, the \(K_{j}\) are components of the characteristic element \(K\in L\), this time in the basis (3.6). Recall \(K_1\) and \(K_2\in 2{\mathbb {Z}}\) since they are components of a characteristic vector of \({\mathbb {I}}^{1,1}\). Changing the sign of \(k_1\) and \(k_2\) in the summand gives \(\Psi _{{\mathbb {I}},(\mu _+,\mu _-)}=-\Psi _{{\mathbb {I}},(\mu _+,\mu _-)}\), hence \(\Psi _{{\mathbb {I}},(\mu _+,\mu _-)}\) vanishes identically. Nevertheless, it is instructive to evaluate the integral using the approach of Sect. 5.2, to set up notation for working with the closely analogous function in Eq. (5.69), which is definitely nonzero.
To express \(\Psi _{{\mathbb {I}},(\mu _+,\mu _-)}\) as an anti-holomorphic derivative, we split the lattice into a positive and negative definite one, by changing summation variables to
and similarly for the ’t Hooft flux and the canonical class,
where \(\mu _j\in {\mathbb {Z}}/2\) as before. Given \(\mu _\pm \), the summation over \(n_\pm \) runs over two sets, namely \(n_\pm \in 2{\mathbb {Z}} +\mu _\pm +j\) with \(j=0,1\). We can now express the sum over fluxes as
where \({\varvec{\mu }}=(\mu _+,\mu _-)\) and
with \(\nu \in {\mathbb {Z}}/2 \mod 2{\mathbb {Z}}\). For the four conjugacy classes of \(\nu \), we find that \(h_{\nu }\) equals
We have similarly for \(t_{\nu }\)
Substitution of the expressions (5.26), (5.27) in (5.24) confirms the vanishing of \(\Psi _{{\mathbb {I}},{\varvec{\mu }}}\).
5.4 u-Plane integrands and mock modular forms
Our next aim is to express the integrand as an anti-holomorphic derivative of a non-holomorphic modular form. We will determine functions \({\widehat{F}}_\mu \) (respectively, \({\widehat{H}}_\mu \)), which transform as weight \(\frac{1}{2}\) modular forms, and such that
for odd and even lattices, respectively. The holomorphic parts of \({\widehat{F}}_\mu \) and \({\widehat{H}}_\nu \) are known as mock modular forms and contain interesting arithmetic information [15, 16].
We consider first the case that the lattice L is odd. We deduce from Eq. (5.16) that for \(\mu _1\in {\mathbb {Z}}\), we can take \({\widehat{F}}_{\mu _1}=0\). We thus only need to be concerned with finding an anti-derivative \({\widehat{F}}_\frac{1}{2}\) of \(-\frac{i}{2\sqrt{2y}}\,{{\overline{\eta }}}^3\). Let us reduce notation by setting \({\widehat{F}}={\widehat{F}}_\frac{1}{2}\), then \({\widehat{F}}\) takes the general form
and is required to transform as a \(\Gamma ^0(4)\) modular form with (holomorphic) weight \(\frac{1}{2}\). The first term on the rhs is holomorphic and is a mock modular form [15, 16], while the second term on the right-hand side is known as a period integral and transforms with a shift under transformations of \(\mathrm{SL}(2,{\mathbb {Z}})\). The function \(\eta ^3\) is known as the shadow of the mock modular form F. Similarly to the discussion above Eq. (5.6), we deduce that the holomorphic part \(F(\tau )\) must be non-vanishing to cancel the shift.
The derivation of such a function is in general non-trivial. The theory of indefinite theta functions provides a constructive approach to derive a suitable \(F(\tau )\). “Appendix C” provides a brief introduction to these functions and derives an explicit expression for F:
To evaluate \(\Phi _{\varvec{\mu }}^J\) following (5.10), we need to determine the q-expansion of F at the other cusps. We introduce to this end \(F_D\) and \({\widehat{F}}_D\),
where \(\tau \) is now the local coordinate which goes to \(i\infty \) near the strong coupling cusp \(u \rightarrow \Lambda ^2\). “Appendix C” discusses how to derive the q-expansion of \(F_D\) using the transformations of the indefinite theta function (C.5). One finds
For the cusp \(\tau \rightarrow 2\), the q-expansion is \(-i\,F_D(\tau )\).
We leave the precise evaluation for later in this subsection and continue with the even lattices, which can be treated more briefly. We see from (5.26) that \(h_{\mu }(\tau , {\bar{\tau }})=\frac{1}{4}\, f_{\mu }(\tau /2,{{\bar{\tau }}}/2)\), with \(f_\mu \) as in (5.14). We can thus easily determine a suitable anti-derivative for \(h_\mu \), namely
with \({\widehat{F}}\) as in (5.29). We similarly define \(H(\tau /2)=\frac{1}{2}F(\tau /2)\) with F as in (5.30).
Remark
Malmendier and Ono have emphasized the connection between q-series appearing in the context of Mathieu moonshine and the u-plane integral for the complex projective plane \({\mathbb {P}}^2\) [45]. See [46,47,48,49,50] for overviews of the moonshine phenomenon. Our discussion above demonstrates that the appearance of these q-series is quite generic for four-manifolds with \(b_2^+=1\). In particular, the function F (5.30) equals 1/8 times the function \(H_{1A,2}^{(4)}\), which appears in the context of umbral moonshine on page 107 of [51]. Similarly, \(F_D\) (5.32) equals 1/8 times the function \(H_{2A,1}^{(2)}\) on page 103 of [51].
Moreover, F and \(F_D\) can be expressed in terms of the famous q-series \(H^{(2)}(\tau )\) of Mathieu moonshine [52], whose coefficients are sums of dimensions of irreducible representations of the finite sporadic group \(M_{24}\), and which appeared in the elliptic genus of the K3 sigma model with (4, 4) supersymmetry. We have for F,
where [53],
Whereas F is a mock modular form for the subgroup \(\Gamma ^0(4)\subset \mathrm{SL}(2,{\mathbb {Z}})\), \(H^{(2)}\) is a mock modular form for the full \(\mathrm{SL}(2,{\mathbb {Z}})\). The completion
transforms under the two generators of \(\mathrm{SL}(2,{\mathbb {Z}})\) as
The holomorphic part \(H^{(2)}\) therefore transforms as
We can express \(F_D\) in terms of \(H^{(2)}\) as
As a last example of a mock modular form with shadow \(\eta ^3\), we mention the function \(Q^+\), which was introduced by Malmendier and Ono in the context of the u-plane integral [12, 45]
Since F, \(H^{(2)}\) and \(Q^+\) are all weight \(\frac{1}{2}\) mock modular forms for \(\Gamma ^0(4)\) and have shadows proportional to \(\eta ^3\), each of them can be used for the evaluation of the u-plane integral. Note that among these functions, only F vanishes in the limit \(\tau \rightarrow i\infty \). Thus it behaves similarly to its derivative \(f_{\frac{1}{2}}\) in this limit.
5.5 Evaluation
We continue by evaluating the u-plane integral for an arbitrary four-manifold with \((b_1,b_2^+)=(0,1)\). As mentioned in Sect. 5.3, the partition function \(\Phi _{\varvec{\mu }}^J\) is only non-vanishing for odd lattices, and with ’t Hooft flux \({\varvec{\mu }}\) with \(\mu _1=\frac{1}{2}\) in the standard basis. We have then using (5.16) and (5.28),
where the first term in the straight brackets is due to the contribution at \(i\infty \) and the second term due to the two strong coupling singularities, which contribute equally. The strong coupling singularities do not contribute to the \(q^0\) term. We finally arrive at
This is in agreement with the results for \({\mathbb {P}}^2\) for which \(K_1=3\) [54].
It is straightforward to include the exponentiated point observable \(e^{2p\,u}\) in the path integral.Footnote 10 One then arrives at
with \(u_D\) given in (2.5). We deduce from the expansion of \(F_D\) (5.32) and \(u_D(\tau )=1+O(q)\) that the monopole cusps do not contribute to the \(q^0\)-term for any power of p. The result is therefore completely due to the weak coupling cusp,
Only even powers of p contribute to the constant term, which is in agreement with the interpretation of the point observable as a four-form on the moduli space of instantons. Except for the mild dependence of (5.43) on \(K_1\), this equation demonstrates that the contribution from the u-plane to \(\left\langle e^{2p\,u} \right\rangle _{\varvec{\mu }}^J\) is universal for any four-manifold with odd intersection form and period point J (5.11).
We list \(\Phi _{\varvec{\mu }}^J[u^\ell ]\) for small \(\ell \) in Table 2. See [54] for a more extensive list. Section 6 will discuss these numbers and the convergence of \(\Phi _{\varvec{\mu }}^J[e^{2p\,u}]=\sum _{\ell \ge 0} \Phi _{\varvec{\mu }}^J[u^\ell ]\,(2\,p)^\ell /\ell !\) in more detail.
5.6 Evaluation of surface observables
This subsection continues with the evaluation of the contribution of the u-plane to vevs of surface observables.
5.6.1 Odd intersection form
We proceed as in Sect. 5.3 choosing \(J=(1, {\mathbf {0}})\) and set \(\rho _+=B({\varvec{\rho }},J)\) and \({\varvec{\rho }}_-={\varvec{\rho }}-\rho _+\,J\). Specializing (4.27) gives
with
where \(b=\mathrm {Im}(\rho )/y\), and we removed the subscript of \(\mu _1\) as before in Sect. 5. Moreover, \(\Theta _{L_-,{\varvec{\mu }}_-}(\tau ,{\varvec{\rho }}_-)\) is given by
The functions \(f_{\mu }(\tau ,{{\bar{\tau }}},\rho _+,{{\bar{\rho }}}_+)\) and \(\Theta _{L_-,{\varvec{\mu }}_-}(\tau ,{\varvec{\rho }}_-)\) specialize to \(f_{\mu }(\tau ,{\bar{\tau }})\) and \(\Theta _{L_-,{\varvec{\mu }}_-}(\tau )\) (5.13) for \({\varvec{\rho }}=0\). The theta series \(\Theta _{L_-,{\varvec{\mu }}_-}(\tau ,{\varvec{\rho }}_-)\) can be expressed as a product of \(\vartheta _1\) and \(\vartheta _4\) (A.8) depending on the precise value of \({\varvec{\mu }}_-\). We define the dual theta series \(\Theta _{D,L_-,{\varvec{\mu }}_-}\) as
We aim to write this as a total anti-holomorphic derivative of a real-analytic function \({\widehat{F}}_\mu (\tau ,{{\bar{\tau }}},\rho ,{{\bar{\rho }}})\) of \(\tau \) and \(\rho \). We can achieve this using the Appell–Lerch sum \(M(\tau ,u,v)\), with \(u,v\in {\mathbb {C}}\backslash \{{\mathbb {Z}}\tau +{\mathbb {Z}}\}\), which has appeared at many places in mathematics and mathematical physics. See, for examples, [53, 55, 56]. The function \(M(\tau ,u,v)\) is meromorphic in u and v, and weakly holomorphic in \(\tau \). More properties are reviewed in “Appendix D.” Equation (D.10) is the main property for us. It states that \({\widehat{M}}(\tau ,{{\bar{\tau }}},u,\bar{u},v,{\bar{v}})=M(\tau ,u,v)+\frac{i}{2}R(\tau ,{{\bar{\tau }}},u-v,{\bar{u}}-{\bar{v}})\) transforms as a multi-variable Jacobi form of weight \(\frac{1}{2}\), where \(R(\tau ,{{\bar{\tau }}},u,{\bar{u}})\) is real analytic in both \(\tau \) and u. To determine \({\widehat{F}}_\mu (\tau ,{{\bar{\tau }}},\rho ,{{\bar{\rho }}})\), we express \(f_\mu (\tau ,{\bar{\tau }},\rho ,{{\bar{\rho }}})\) in terms of \(\partial _{{{\bar{\tau }}}} R(\tau ,{\bar{\tau }},u,{\bar{u}})\) (D.8). With \(w=e^{2\pi i \rho }\), we find
We can thus determine the anti-derivative of \(f_\mu \) in terms of the completion \({\widehat{M}}\) (D.9) in “Appendix D” by choosing u and v such that \(u-v=\rho +\nu \tau \) while avoiding the poles in u and v. We will find below that the choice \(u=\rho + \mu \tau \) and \(v=\frac{1}{2}\tau \) is particularly convenient. From “Appendix D”, we find that a candidate for the completed function is
We will find that for this choice of u and v, the holomorphic part \(F_{\frac{1}{2}}(\tau ,\rho )\) reduces to \(F_\frac{1}{2}(\tau )=F(\tau )\) (5.30) for \(\rho =0\). Indeed, substitution of this choice in \(M(\tau ,u,v)\) gives for \(F_{\frac{1}{2}}(\tau ,\rho )\)
which satisfies \(F_{\frac{1}{2}}(\tau ,0)=F_{\frac{1}{2}}(\tau )\).
Let us move on to \(\mu \in {\mathbb {Z}}\), or \(\mu =0\) to be specific. The function \({\widehat{F}}_0(\tau ,{{\bar{\tau }}},\rho ,{{\bar{\rho }}})\) (5.50) evaluates then to
where we used \(\vartheta _1(\tau ,\frac{1}{2}\tau )=-i\,q^{-\frac{1}{8}}\vartheta _4(\tau )\). Note that (5.52) contains a pole for \(\rho =0\), since \(n=0\) is included in the sum. We will discuss this in more detail later. Let us mention first that we have to be careful with singling out the holomorphic part of (5.52), i.e., the part which does not vanish in the limit \(y\rightarrow \infty \), \(b\rightarrow 0\), keeping \(\rho \) and \(\tau \) fixed. Since the elliptic argument of R is shifted by \(-\frac{1}{2}\tau \), we have \(\lim _{y\rightarrow \infty } q^{-\frac{1}{8}}\,w^{\frac{1}{2}} R(\tau ,{{\bar{\tau }}},-\frac{1}{2}\tau ,-\frac{1}{2}{{\bar{\tau }}})=1\). The holomorphic part of (5.52) is thus
To write the non-holomorphic part, we define for \(\mu \in \{0,\frac{1}{2}\} \mod \mathbb {Z}\),
Note that \(R_\mu \) vanishes in the limit \(y\rightarrow \infty \) with \(b=0\) for any \(\mu \). Using these expressions, we can write the completed functions \({\widehat{F}}_\mu \) as
We mentioned in the previous subsection the connection to dimensions of representations of sporadic groups. Other arithmetic information that has appeared in the context of the u-plane integral are the Hurwitz class numbers [3], which count binary integral quadratic forms with fixed determinant. Using relations for the Appell–Lerch sum (D.3), we can make this connection more manifest for the \(F_\mu \). To this end, let us consider the functions
These functions appear in the refined partition function of SU(2) and SO(3) Vafa-Witten theory on \({\mathbb {P}}^2\) [57,58,59]. They vanish for \(z\rightarrow 0\), while their first derivative give generating functions of Hurwitz class numbers H(n) [59]:
Using (D.3), we can express the functions \(g_j\) in terms of \(F_\mu \) as
which demonstrates the connection of the integrand to the class numbers.
It might come as a surprise that the expressions we have defined give well defined power series in \({{\varvec{x}}}\) after integration, since the integrand involves expressions with poles in \({{\varvec{x}}}\). This could be avoided by the addition of a meromorphic Jacobi form of weight 2 and index 0, with a pole at \(\rho =0\) with opposite residue. The reason is that the addition of such a meromorphic Jacobi form does not alter the value of the integral. To see this, note that a meromorphic Jacobi form \(\phi \) of weight 2 and index 0 has a Laurent expansion in \({{\varvec{x}}}\) of the form
where \({\varvec{\ell }}=(\ell _1,\dots , \ell _{b_2})\in {\mathbb {N}}^{b_2}\) and \({{\varvec{x}}}^{\varvec{\ell }}=x_1^{\ell _1}\cdots x_{b_2}^{\ell _{b_2}}\). The \(\phi _{\varvec{\ell }}\) are weakly holomorphic modular forms for \(\Gamma ^0(4)\) of weight 2, since \({{\varvec{x}}}\) is invariant under \(\Gamma ^0(4)\). Mapping the six images of \({\mathcal {F}}_\infty \) in \({\mathbb {H}}/\Gamma ^0(4)\) to \({\mathcal {F}}_\infty \) gives us a meromorphic Jacobi form \({{\widetilde{\phi }}}\) for \({\text {SL}}(2,{\mathbb {Z}})\) with expansion
where the \({{\widetilde{\phi }}}\) are modular forms for \({\text {SL}}(2,{\mathbb {Z}})\) of weight 2. These have a vanishing constant term as discussed before and thus do not contribute to \(\Phi ^J_{\varvec{\mu }}\).
To illustrate this, we present an alternative for \(F_0(\tau ,\rho )\) (5.53),
This series is analytic for \(\rho \rightarrow 0\) and can be expressed as
This is the series in terms of which Göttsche expressed the Donaldson invariants of \({\mathbb {P}}^2\) [60, Theorem 3.5].
Let us return to the evaluation of \(\Phi _{\varvec{\mu }}^J[e^{I_-({{\varvec{x}}})}]\). To this end, we also need to determine the magnetic dual versions \(F_{D,\mu }\). We let \(w_D=e^{2\pi i \rho _D}\), and define \({\widehat{F}}_{D,\mu }\) by
We evaluate the RHS using the transformation of \({\widehat{M}}\) (D.10). Subtracting the subleading non-holomorphic part gives for \(F_{D,\mu }(\tau ,\rho _D)\)
which indeed reduces for \(\mu =\frac{1}{2}\) and \(\rho _D\rightarrow 0\) to \(F_D\) (5.32).
Having determined \(F_{D,\mu }(\tau ,\rho _D)\), we can write down our final expression for \(\Phi ^J_{\varvec{\mu }}[ e^{I_-({{\varvec{x}}})}]\) for four-manifolds with an odd intersection form. Similarly to Sect. 5.4, we express \(\Phi ^J_{\varvec{\mu }}[ e^{I_-({{\varvec{x}}})}]\), as a sum of three terms, one from each cusp,
with
Note that for this choice of J, \(\Phi ^J_{\varvec{\mu }}[e^{I_-({{\varvec{x}}})}]\) only depends on \({\varvec{\mu }}\), K and \(b_2\) (assuming \(b_1=0\)). We list \(\Phi ^J_{\varvec{\mu }}[I^s_-({{\varvec{x}}})]\) for the first few non-vanishing s in Table 3. If we specialize to the four-manifold \({\mathbb {P}}^2\), these results are in agreement with the results in Reference [54, Theorem 4.2 and Theorem 4.4].
5.6.2 Even intersection form
We proceed similarly for the case that the lattice L is even. As in the discussion of Sect. 5.3, we choose for the period point \(J=\frac{1}{\sqrt{2}}\,(1,1,{\mathbf {0}})\in L \otimes {\mathbb {R}}\). To factor the sum over fluxes \(\Psi _{\varvec{\mu }}^J\) in the presence of the surface observable, we introduce the vector \(C=\frac{1}{\sqrt{2}}\,(1,-1,{\mathbf {0}})\in L \otimes {\mathbb {R}}\). The vectors J and C form an orthonormal basis of \({\mathbb {I}}^{1,1}\otimes {\mathbb {R}} \subset L \otimes {\mathbb {R}}\). We denote by \(\rho _+\) and \(\rho _-\) the projections of the elliptic variable \({\varvec{\rho }}\in L \otimes {\mathbb {C}}\) to J and C,
With respect to the basis (3.6), \({\varvec{\rho }}\) reads
with \({\varvec{\rho }}_n\in nL_{E_8}\otimes {\mathbb {C}}\). As in the case of the partition function (5.19), the sum over fluxes \(\Psi _{\varvec{\mu }}^J(\tau ,{{\bar{\tau }}},{\varvec{\rho }},{{\bar{{\varvec{\rho }}}}})\) (4.27) factors,
with
where \(b_+=\mathrm {Im}(\rho _+)/y\), and
The modular transformations are easily determined if we express \(\Theta _{nE_8,{\varvec{\mu }}_n}(\tau ,{\varvec{\rho }}_n)\) in terms of Jacobi theta series. We define the dual theta series \(\Theta _{D,nE_8,{\varvec{\mu }}_n}\) as
Unlike Eqs. (5.20), (5.69) is definitely nonzero. The series can be decomposed further as
with
where \(b=\mathrm {Im}(\rho )/y\). These functions reduce to those in (5.25) in the limit \({\varvec{\rho }}\rightarrow 0\).
While \(\Psi _{{\mathbb {I}},(\mu _+,\mu _-)}\) is a modular form for \(\Gamma ^0(4)\), the functions \(h_\nu \) and \(t_\nu \) are not. To continue working with modular forms for \(\Gamma ^0(4)\), we rewrite \(\Psi _{{\mathbb {I}},(\mu _+,\mu _-)}\) (5.72) as
with
These functions are modular forms for \(\Gamma ^0(4)\), which becomes manifest when we express them in terms of functions we encountered before. We can express the \(g^\pm _\nu \) in terms of \(f_\nu \),
The \(\theta ^\pm _\nu \) can be expressed in terms of the Jacobi theta functions \(\vartheta _j\) as
We define the dual functions as
These are explicitly given by
Since the \(g^\pm _\nu \) can be expressed in terms of the \(f_\nu \), we can determine anti-derivatives \({\widehat{G}}^\pm _\nu \) in terms of \({\widehat{F}}_\mu \). Namely,
The holomorphic parts of these completed functions are
with the \(F_\nu \) given by (5.51) and (5.53). We define the dual \({\widehat{G}}^\pm _{D,\nu }\) as
These evaluate to
With these expressions, we can present our final expression \(\Phi _{\varvec{\mu }}^J[e^{I_-({{\varvec{x}}})}]\) for four-manifolds with even intersection form,
with
The overall factor 2 for the strong coupling contributions is due to the factors of \(\sqrt{2}\) in (5.78) and (5.82).
Table 4 lists the contribution from the u-plane to Donaldson polynomials for small instanton number. The expressions confirm that \(I_-({{\varvec{x}}})\) is an integral class for gauge group SU(2) \({\varvec{\mu }}={\mathbf {0}} \mod \mathbb {Z}\), and half-integral for \({\varvec{\mu }}\ne {\mathbf {0}} \mod \mathbb {Z}\).
6 Asymptology of the u-plane integral
Up to this point, we have treated the u-plane integral \(\Phi _{\varvec{\mu }}^J[e^{2pu +I_-({{\varvec{x}}})}]\) as a formal generating series in the homology elements p and \({{\varvec{x}}}\). However, one might ask if the integral actually expresses a well-defined function on the homology of the four-manifold M. In other words, one might ask if the formal series is in fact convergent. The contribution of the Seiberg–Witten invariants is a finite sum and hence in fact defines an entire function on \(H_*(M,{\mathbb {C}})\). Therefore the Donaldson–Witten partition function is a well-defined function on the homology if and only if the u-plane is a well-defined function. If that were the case, then one could explore interesting questions such as the analytic structure of the resulting partition function, which, in turn, might signal interesting physical effects, such as the realization of the fugacities as background fields. In this Section we will explore that question, starting with the point observable in Sect. 6.1. We will find strong evidence that in fact the u-plane integral is indeed an entire function of p.
The situation for \({{\varvec{x}}}\) is less clear, since the numerical results are more limited. We discuss in Sect. 6.1 that the results do suggest that \(\Phi _{\varvec{\mu }}^J[e^{2pu +I_-({{\varvec{x}}})}]\) is also an entire function \({{\varvec{x}}}\). As a step towards understanding the analytic structure in \({{\varvec{x}}}\), we will consider in Sect. 6.2 the magnitude of the integrand in the weak-coupling limit. Although the integral is independent of \(\alpha \), we will see that the integrand behaves best when \(\alpha =1\).
6.1 Asymptotic growth of point and surface observables
We will analyze the dependence of the contribution from the u-plane \(\Phi ^J_{\varvec{\mu }}[e^{2p\,u}]\) to the correlation function \(\left\langle e^{2p\,u}\right\rangle ^J_{\varvec{\mu }}\). Due to the exponential divergence of u (2.4) for \(\tau \rightarrow i\infty \), the divergence of \(e^{2p\,u}\) is doubly exponential. The u-plane integral thus formally diverges. The discussion of Sect. 5.1 does not provide an immediate definition of such divergent expressions. On the other hand, the vev of the exponentiated point observable \(e^{2p\,u}\) should be understood as a generating function of correlation functions, and we can define \(\Phi _{\varvec{\mu }}^J[e^{2p\,u}]\) as
As discussed in Sect. 5.4, there is no problem evaluating \(\Phi _{\varvec{\mu }}^J[u^\ell ]\) using the definition of Sect. 5.1.
We consider the case of odd lattices, and the period point J (5.11). Modifying (5.43), we express \(\Phi _{\varvec{\mu }}^J[u^\ell ]\) as
We have replaced here F by \(\frac{1}{24}H^{(2)}\), since its completion is an equally good choice of anti-derivative. It is straightforward to determine \(\Phi _{\varvec{\mu }}^J[u^\ell ]\) using this expression. We list in Table 5 values of \(\Phi _{\varvec{\mu }}^J[u^\ell ]\) for various large values of \(\ell \).
Before giving evidence that the \(\Phi _{\varvec{\mu }}^J[e^{2p\,u}]\) is an entire function of p, let us discuss the integrand in more detail. We first write \(\Phi _{\varvec{\mu }}^J[u^\ell ]\) as an integral from 0 to 1:
We can express the integrand in a \(\mathrm{SL}(2,{\mathbb {Z}})\) invariant form. To this end, note
For \(\ell \) even, we find thus that \(\Phi _{\varvec{\mu }}^J\) can be expressed as
where \(Q_\ell \) is the weight \(6+3\ell \) modular form defined by
The first few terms are
The most straightforward way of trying to establish the large \(\ell \) asymptotics is by a saddle point analysis. Expressing \(u^\ell \) as \(u_D(-1/\tau )^\ell \sim e^{32\,\ell \,e^{-\frac{2\pi i}{\tau }}}\), we find that, to first approximation, the saddle point is at \(\tau _*=\frac{2\pi i}{\log (-32\,\ell )}\) for large \(\ell \). We find that the contribution of this saddle point to \(\left| \Phi ^J_{\varvec{\mu }}[u^\ell ] \right| \) behaves as \(C/\ell \) for some constant C. We leave an investigation into the difference between the saddle point contribution and Table 5 for another occasion.
Let us explore the consequences of the large \(\ell \) asymptotics for \(\Phi _{\varvec{\mu }}^J[e^{2pu}]\). We deduce from Table 5 that \(\Phi _{\varvec{\mu }}^J[u^\ell ]\) also decreases faster than \(C\,(\ell +1)^{-1}\). This estimate strongly suggests that radius of convergence for \(\sum _{\ell \ge 0}p^\ell \,\Phi _{\varvec{\mu }}^J[u^\ell ]/\ell !\) is infinite and thus that \(\Phi _{\varvec{\mu }}^J[e^{2pu}]\) is an entire function of p. Moreover, we can easily bound \(|\Phi _{\varvec{\mu }}^J[e^{2pu}]|\) for real p by
The exponentials in \(\sinh (2p)\) resemble the SW contribution at \(u=\pm \Lambda ^2\). Comparing with the SW-simple type expression (4.30), we see that the SW contribution to \(\left\langle u^\ell \right\rangle \) is O(1), while the u-plane contribution is subleading.
While we have focused in this subsection on the point observables, the behavior of \(\Phi _{\varvec{\mu }}^J[I^s_-({{\varvec{x}}})]\) for large s is equally if not more interesting. We list in Table 6 some numerical data for \(\log (\Phi _{\varvec{\mu }}[I_-({{\varvec{x}}})^s])/s\). These data, while admittedly limited, do give the impression that the asymptotic growth of \(\Phi ^J_{\varvec{\mu }}[I_-({{\varvec{x}}})^s]\) is bounded by \(e^{\alpha s\,\log (s)}\) for some positive constant \(\alpha \), and that \(\alpha <1\). Assuming that this is the correct behavior for large s, the radius of convergence for x of \(\Phi ^J_{\varvec{\mu }}[e^{I_-({{\varvec{x}}})}]=\sum _{s\ge 0} \Phi ^J_{\varvec{\mu }}[I_-({{\varvec{x}}})^s]/s!\) is infinite, implying that \(\Phi ^J_{\varvec{\mu }}[e^{I_-({{\varvec{x}}})}]\) is entire in \({{\varvec{x}}}\). We hope to get back to the asymptotics of these correlators in future work.
6.2 Weak coupling limit of the integrand
As a first step towards understanding the asymptotic behavior of the series in \({{\varvec{x}}}\), we investigate here the growth of the integrand of the u-plane integral in the weak coupling region. In order to do this, it is useful to recall that one can add to the surface observable the operator \(I_+({{\varvec{x}}})\) discussed in Sect. 4.2 with an arbitrary coefficient \(\alpha \). Since \(I_+({{\varvec{x}}})\) is \({{\mathcal {Q}}}\) exact such an addition does not modify the resulting integral. (Because the integral is subtle and formally divergent this statement requires careful justification, but it turns out to be correct [19].) In this way, we can interpolate between \(\alpha =0\) [3] and \(\alpha =1\) [17]. While the result is independent of \(\alpha \), the dependence of the integrand is worth exploring in more detail, in particular the behavior in the weak coupling limit. In this limit, \(\frac{{\mathrm{d}}u}{{\mathrm{d}}a}\) diverges as \(q^{-\frac{1}{8}}=e^{-i\frac{\theta }{8}+\frac{\pi y}{4}}\). As a result, the elliptic variable \({\varvec{\rho }}=\frac{{{\varvec{x}}}}{2\pi } \frac{{\mathrm{d}}u}{{\mathrm{d}}a}\) diverges. This subsection studies this divergence as function of \(\alpha \).
The u-plane integral with observable \(e^{I_-+\alpha \,I_+}\) results in a modified sum over fluxes \(\Psi ^J_{{\varvec{\mu }},\alpha }\). This sum is defined as in (4.27), but with \({{\bar{{\varvec{\rho }}}}}\) replaced by \(\alpha {\bar{{\varvec{\rho }}}}\), and reads
By completing the squares in the exponent, we can write this as
where \({{\varvec{b}}}=\mathrm{Im}({\varvec{\rho }})/y\) as before. The sum over \({{\varvec{k}}}\in L+{\varvec{\mu }}\) is dominated by the \({{\varvec{k}}}\) for which \(-({{\varvec{k}}}+{{\varvec{b}}})_-^2+({{\varvec{k}}}+{{\varvec{b}}})_+^2\) is minimized. For a generic choice of period point J, there is only one \({{\varvec{k}}}\in L+{\varvec{\mu }}\) which minimizes this quantity. The leading asymptotic behavior is given by the exponential multiplying the sum. This evaluates to
Thus we see that \(\alpha = 1\) is special, since for this choice the exponent is negative definite for \({{\varvec{x}}}^2>0\). Moreover, for large y, \(\Psi ^J_{{\varvec{\mu }},\alpha }\) will only remain finite in the domain \(\varphi =\mathrm {Re}(\tau )\in [0,4]\) for this choice of parameters. The double exponential divergence of the exponentiated surface observable is therefore mitigated at \(\alpha =1\).
Let us make a rough estimate for the magnitude of the u-plane integral using (6.11),
where we only consider terms which are non-vanishing in the limit for \(y\rightarrow \infty \). The integral over \(\varphi \) is a Bessel function \(I_0(z)\) with \(z=\frac{\pi {{\varvec{x}}}^2}{2y} e^{\frac{1}{2}\pi y}\), which behaves for large z as \(e^z/\sqrt{2\pi z}\). This leads to a single exponential divergence, \(\int {\mathrm{d}}y\, e^{\frac{1}{4}\pi y}\), which can be treated as discussed before. We leave a more detailed analysis including the dependence on \({\varvec{\mu }}\) and possible cancellations in the integral along the interval \(\varphi \in [0,4]\) for future work.
Notes
The u-plane integral also contributes for manifolds with \(b_2^+=0\). The integrand is one-loop exact in this case [3], but the one-loop determinants have never been worked out with great care.
One way to understand this duality group is that the Seiberg–Witten family of curves is the universal family of family of elliptic curves with a distinguished order 4 point [9].
We will only consider four-manifolds without boundary in this paper.
A symplectic structure of a four-manifold is given by a two-form \(\omega \), which satisfies \(d\omega =0\) and \(\omega \wedge \omega >0\) for every point on M. In other words, \(\omega \) is closed and non-degenerate.
The dimensions of a, \(A_\mu \), \(D_{\mu \nu }\), \(\eta \), \(\psi _\mu \) and \(\chi _{\mu \nu }\) are, respectively, 1, 1, 2, \(\frac{3}{2}\), \(\frac{3}{2}\) and \(\frac{3}{2}\) in powers of \(\Lambda \). The dimension of differential form fields is reduced by their form degree. For example, the dimension of \(F=dA\) is 0. The dimensions of the differentials \({\mathrm{d}}a\), \({\mathrm{d}}D\), \({\mathrm{d}}\eta \) and \({\mathrm{d}}\chi \) are, respectively, 1, 0, \(-\frac{3}{2}\) and \(\frac{1}{2}\).
Note \(\alpha \) and \(\beta \) are chosen dimensionless here. The values of \(\alpha \) and \(\beta \) are slightly different from those used in [17], since we have used a different normalization for the integral over D.
Note that, compared to equation (3.13) of [3] there is an overall phase difference. This phase difference can be written as \(\exp [ \frac{i \pi }{2} \left( {{\varvec{k}}}_0^2 - B({{\varvec{k}}}_0, K)\right) ]\), where \({{\varvec{k}}}_0\) is a lift of \(w_2(P)\) to \(H^2(M,{\mathbb {Z}})\). Because K is a characteristic vector this factor is a \({{\varvec{k}}}_0\)-dependent sign. The choice of sign is related to a choice of orientation of instanton moduli space.
Recall footnote 8 for different overall signs used in the literature.
For an unambiguous value of the square root, we define the phase of \(z\in {\mathbb {C}}^*\) by \(\log z:=\log |z|+i\,\mathrm {arg}(z)\) with \(-\pi <\arg (z)\le \pi \).
Indefinite theta functions can often be expressed as product of a mock modular form and modular form, in other words they are a mixed mock modular form. We therefore use the notion of “shadow” slightly differently from its definition for mock modular forms [16].
References
Witten, E.: Supersymmetric Yang–Mills theory on a four manifold. J. Math. Phys. 35, 5101–5135 (1994). arxiv: hep-th/9403195
Witten, E.: Monopoles and four manifolds. Math. Res. Lett. 1, 769–796 (1994). arxiv: hep-th/9411102
Moore, G.W., Witten, E.: Integration over the u plane in Donaldson theory. Adv. Theor. Math. Phys. 1, 298–387 (1997). arxiv: hep-th/9709193
Losev, A., Nekrasov, N., Shatashvili, S.L.: Issues in topological gauge theory. Nucl. Phys. B 534, 549–611 (1998). arxiv: hep-th/9711108
Marino, M., Moore, G.W.: The Donaldson–Witten function for gauge groups of rank larger than one. Commun. Math. Phys. 199, 25–69 (1998). arxiv: hep-th/9802185
Pestun, V.: Localization of gauge theory on a four-sphere and supersymmetric Wilson loops. Commun. Math. Phys. 313, 71–129 (2012). arxiv: 0712.2824
Shapere, A.D., Tachikawa, Y.: Central charges of \(N = 2\) superconformal field theories in four dimensions. JHEP 09, 109 (2008). arxiv: 0804.1957
Witten, E.: Topological quantum field theory. Commun. Math. Phys. 117, 353 (1988)
Seiberg, N., Witten, E.: Electric–magnetic duality, monopole condensation, and confinement in N = 2 supersymmetric Yang–Mills theory. Nucl. Phys. B 426, 19–52 (1994). arxiv: hep-th/9407087
Gottsche, L., Zagier, D.: Jacobi forms and the structure of Donaldson invariants for 4-manifolds with \(b_2^+=1\). arxiv: alg-geom/9612020
Marino, M., Moore, G.W.: Donaldson invariants for nonsimply connected manifolds. Commun. Math. Phys. 203, 249 (1999). arxiv: hep-th/9804104
Malmendier, A., Ono, K.: SO(3)-Donaldson invariants of \(\mathbb{P}^2\) and mock theta functions. Geom. Topol. 16, 1767–1833 (2012). arxiv: 0808.1442
Malmendier, A.: Donaldson invariants of \(\mathbb{P}^1 \times \mathbb{P}^1\) and mock theta functions. Commun. Numer. Theor. Phys. 5, 203–229 (2011). arxiv: 1008.0175
Griffin, M., Malmendier, A., Ono, K.: SU(2)-Donaldson invariants of the complex projective plane. Forum Math. 27, 2003–2023 (2015). arxiv: 1209.2743
Zwegers, S.P.: Mock theta functions. Ph.d thesis (2008)
Zagier, D.: Ramanujan’s mock theta functions and their applications (after Zwegers and Ono-Bringmann), Astérisque (2009) Exp. No. 986, vii–viii, 143–164 (2010)
Korpas, G., Manschot, J.: Donaldson–Witten theory and indefinite theta functions. JHEP 11, 083 (2017). arxiv: 1707.06235
Moore, G.W., Nidaiev, I.: The partition function of Argyres–Douglas theory on a four-manifold. arxiv: 1711.09257
Korpas, G., Manschot, J., Moore, G.W., Nidaiev, I.: Renormalization and BRST symmetry in Donaldson–Witten theory. Annales Henri Poincaré (2019). arxiv: 1901.03540
Bringmann, K., Diamantis, N., Ehlen, S.: Regularized inner products and errors of modularity. Int. Math. Res. Not. 2017, 7420–7458 (2017)
Kronheimer, P.B., Mrowka, T.S.: Embedded surfaces and the structure of Donaldson polynomial invariants. J. Differ. Geom. 41, 573–734 (1995)
Grassi, A., Komargodski, Z., Tizzano, L.: Extremal correlators and random matrix theory. JHEP 04, 214 (2021). arxiv: 1908.10306
Nekrasov, N.A.: Localizing gauge theories. In: Mathematical Physics. Proceedings, 14th International Congress, ICMP 2003, Lisbon, Portugal, July 28–August 2, 2003, pp. 645–654 (2003)
Bershtein, M., Bonelli, G., Ronzani, M., Tanzini, A.: Exact results for \({\cal{N} }\) = 2 supersymmetric gauge theories on compact toric manifolds and equivariant Donaldson invariants. JHEP 07, 023 (2016). arxiv: 1509.00267
Seiberg, N., Witten, E.: Monopoles, duality and chiral symmetry breaking in N = 2 supersymmetric QCD. Nucl. Phys. B 431, 484–550 (1994). arxiv: hep-th/9408099
Labastida, J., Marino, M.: Topological Quantum Field Theory and Four Manifolds, vol. 25. Springer, Dordrecht (2005). https://doi.org/10.1007/1-4020-3177-7
Moore, G.W.: Lectures on the Physical Approach to Donaldson and Seiberg–Witten Invariants, Item 78 at http://www.physics.rutgers.edu/~gmoore/ (2017)
Donaldson, S.: Polynomial invariants for smooth four-manifolds. Topology 29, 257–315 (1990)
Donaldson, S.K., Kronheimer, P.B. (eds.): The Geometry of Four-Manifolds. Clarendon Press, Oxford University Press, Oxford, New York (1990)
Labastida, J.M.F., Llatas, P.M.: Topological matter in two-dimensions. Nucl. Phys. B 379, 220–258 (1992). arxiv: hep-th/9112051
Wu, W.-T.: Sur les classes caractéristiques des structures fibrées sphériques. Actualités Schi. Ind. 1183 (1952)
Scorpan, A.: The Wild World of 4-Manifolds. American Mathematical Society, Wiley Classics Library, New York (2005)
Yoshioka, K.: The betti numbers of the moduli space of stable sheaves of rank2 on p2. Journal fur die reine und angewandte Mathematik 453, 193–220 (1994)
Manschot, J.: Sheaves on \(\mathbb{P}^2\) and generalized Appell functions. Adv. Theor. Math. Phys. 21, 655–681 (2017). arxiv: 1407.7785
Barth, W., Hulek, K., Peters, C., van de Ven, A.: Compact Complex Surfaces, 2nd edn. Springer, Berlin, Heidelberg (2004)
McDuff, D., Salamon, D.: A survey of symplectic manifolds with \(b^+=1\). Turl. J. Math. 20, 47–60 (1996)
Park, J.: Non-complex symplectic 4-manifolds with \({b}_{2}^+=1\). Bull. Lond. Math. Soc. 36, 231–240 (2004)
Park, J.: Simply connected symplectic 4-manifolds with b2+=1 and c12=2. Invent. Math. 159, 657–667 (2005)
Baldridge, S.: New symplectic 4-manifolds with \(b_+=1\). Math. Ann. 333, 633–643 (2005)
Baulieu, L., Singer, I.M.: The topological sigma model. Commun. Math. Phys. 125, 227–237 (1989)
Witten, E.: On S duality in Abelian gauge theory. Selecta Math. 1, 383 (1995). arxiv: hep-th/9505186
Matone, M.: Instantons and recursion relations in \(N = 2\) SUSY gauge theory. Phys. Lett. B 357, 342–348 (1995). arxiv: hep-th/9506102
Dixon, L.J., Kaplunovsky, V., Louis, J.: Moduli dependence of string loop corrections to gauge coupling constants. Nucl. Phys. B 355, 649–688 (1991)
Harvey, J.A., Moore, G.W.: Algebras, BPS states, and strings. Nucl. Phys. B 463, 315–368 (1996). arxiv: hep-th/9510182
Malmendier, A., Ono, K.: Moonshine and Donaldson invariants of \(\mathbb{P}^2\). Commun. Number Theory Phys. 6, 759–770 (2012). arxiv: 1207.5139
Harvey, J.A.: Permutation groups, Mock modular forms, K3 surfaces and Moonshine, Lectures at Isaac Newton Institute. https://www.newton.ac.uk/seminar/20120126140015001 (2012)
Harvey, J.A.: (Mock) Modular Forms and Applications to String Theory, Lectures at LACES, GGI. https://www.youtube.com/watch?v=CSmKdMc3a64 (2015)
Kachru, S.: Elementary introduction to Moonshine. (2016) arxiv: 1605.00697
Harvey, J.A.: Moonshine and String Theory, Lectures at ICTP Spring School on Superstring Theory and Related Topics. https://www.youtube.com/watch?v=NPI6bAI_Rdc (2016)
Anagiannis, V., Cheng, M.C.N.: TASI Lectures on moonshine. PoS TASI2017, 010 (2018). arxiv: 1807.00723
Cheng, M.C.N., Duncan, J.F.R., Harvey, J.A.: Umbral Moonshine and the Niemeier lattices. arxiv: 1307.5793
Eguchi, T., Ooguri, H., Tachikawa, Y.: Notes on the K3 surface and the Mathieu group \(M_{24}\). Exp. Math. 20, 91–96 (2011). arxiv: 1004.0956
Dabholkar, A., Murthy, S., Zagier, D.: Quantum Black Holes, Wall Crossing, and Mock Modular Forms. arxiv: 1208.4074
Ellingsrud, G., Göttsche, L.: Wall-crossing formulas, bott residue formula and the donaldson invariants of rational surfaces, Quart. J. Math. Oxford Ser. 49, 307–329 (1998). arxiv: alg-geom/9506019
Semikhatov, A.M., Taormina, A., Tipunin, IYu.: Higher level Appell functions, modular transformations, and characters. Commun. Math. Phys. 255, 469 (2005). arxiv: math/0311314
Manschot, J.: BPS invariants of \({\cal{N}}=4\) gauge theory on Hirzebruch surfaces. Commun. Number Theor. Phys. 6, 497–516 (2012). arxiv: 1103.0012
Vafa, C., Witten, E.: A strong coupling test of S duality. Nucl. Phys. B 431, 3–77 (1994). arxiv: hep-th/9408074
Yoshioka, K.: The Betti numbers of the moduli space of stable sheaves of rank 2 on \(\mathbb{P}^2\). J. Reine Angew. Math. 453, 193–220 (1994)
Bringmann, K., Manschot, J.: From sheaves on \(\mathbb{P}^2\) to a generalization of the Rademacher expansion. Am. J. Math. 135, 1039–1065 (2013). arxiv: 1006.0915
Göttsche, L.: Modular forms and Donaldson invariants for 4-manifolds with \(b_2^+= 1\). J. Am. Math. Soc. 9, 827–843 (1996). arxiv:alg-geom/9506.018
Serre, J.P.: A Course in Arithmetic. Graduate Texts in Mathematics, vol. 7. Springer, New York (1973)
Zagier, D.: Introduction to Modular Forms; From Number Theory to Physics, pp. 238–291. Springer, Berlin (1992)
Bruinier, G.H.J.H., van der Geer, G., Zagier, D.: The 1-2-3 of Modular Forms. Springer, Berlin, Heidelberg (2008). https://doi.org/10.1007/978-3-540-74119-0
Vignéras, M.-F.: Séries thêta des formes quadratiques indéfinies. Springer Lecture Notes 627, 227–239 (1977)
Acknowledgements
We thank Johannes Aspman, Aliakbar Daemi, Elias Furrer, Lothar Göttsche, Jeff Harvey, John Morgan, Tom Mrowka and Hiraku Nakajima for discussions. GK would like to thank the Institute Of Pure and Applied Mathematics of UCLA and the Physics Department of the National and Kapodistrian University of Athens for hospitality. JM would like to thank the NHETC, Rutgers University for hospitality. JM is supported by the Laureate Award 15175 “Modularity in Quantum Field Theory and Gravity” of the Irish Research Council. GM and IN are supported by the US Department of Energy under grant DE-SC0010008.
Funding
Open Access funding provided by the IReL Consortium
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Modular forms and theta functions
In this appendix we collect a few essential aspects of the theory of modular forms, Siegel–Narain theta functions and indefinite theta functions. For more comprehensive treatments we refer the reader to the available literature. See, for example, [61,62,63].
1.1 Modular groups
The modular group \({\text {SL}}(2,{\mathbb {Z}})\) is the group of integer matrices with unit determinant
We introduce moreover the congruence subgroup \(\Gamma ^0(n)\)
1.2 Eisenstein series
We let \(\tau \in {\mathbb {H}}\) and define \(q=e^{2\pi i \tau }\). Then the Eisenstein series \(E_k:{\mathbb {H}}\rightarrow {\mathbb {C}}\) for even \(k\ge 2\) are defined as the q-series
with \(\sigma _k(n)=\sum _{d|n} d^k\) the divisor sum. For \(k\ge 4\), \(E_{k}\) is a modular form of \({\text {SL}}(2,{\mathbb {Z}})\) of weight k. In other words, it transforms under \({\text {SL}}(2,{\mathbb {Z}})\) as
Note that the space of modular forms of \(\mathrm{SL}(2,{\mathbb {Z}})\) forms a ring that is generated precisely by \(E_4(\tau )\) and \(E_6(\tau )\). On the other hand, \(E_2\) is a quasi-modular form, which means that the \({\text {SL}}(2,{\mathbb {Z}})\) transformation of \(E_2\) includes a shift in addition to the weight,
1.3 Dedekind eta function
The Dedekind eta function \(\eta :{\mathbb {H}}\rightarrow {\mathbb {C}}\) is defined as
It is a modular form of weight \(\frac{1}{2}\) under SL\((2,{\mathbb {Z}})\) with a non-trivial multiplier system. It transforms under the generators of SL\((2,{\mathbb {Z}})\) asFootnote 11
1.4 Jacobi theta functions
The four Jacobi theta functions \(\vartheta _j:{\mathbb {H}}\times {\mathbb {C}}\rightarrow {\mathbb {C}}\), \(j=1,\dots ,4\), are defined as
We let \(\vartheta _j(\tau ,0)=\vartheta _j(\tau )\) for \(j=2,3,4\). These have the following transformations for modular inversion
and for the shift
Their transformations under the generators of \(\Gamma ^0(4)\) are
Two useful identities are
Siegel–Narain theta function
Siegel–Narain theta functions form a large class of theta functions of which the Jacobi theta functions are a special case. For our applications in the main text, it is sufficient to consider Siegel–Narain theta functions for which the associated lattice L is a uni-modular lattice with signature \((1,n-1)\) (or a Lorentzian lattice). We denote the bilinear form by \(B({{\varvec{x}}},{{\varvec{y}}})\) and the quadratic form by \(B({{\varvec{x}}},{{\varvec{x}}})\equiv Q({{\varvec{x}}})\equiv {{\varvec{x}}}^2 \). Let K be a characteristic vector of L, such that \( Q({{\varvec{k}}}) + B({{\varvec{k}}}, K) \in 2{\mathbb {Z}}\) for each \({{\varvec{k}}}\in L\).
Given an element \(J\in L\otimes {\mathbb {R}}\) with \(Q(J)=1\), we may decompose the space \(L\otimes {\mathbb {R}}\) in a positive definite subspace \(L_+\) spanned by J, and a negative definite subspace \(L_-\), orthogonal to \(L_+\). The projections of a vector \({{\varvec{k}}}\in L\) to \(L_+\) and \(L_-\) are then given by
Given this notation, we can introduce the Siegel–Narain theta function of our interest \(\Psi ^J_{\varvec{\mu }}[{\mathcal {K}}]:{\mathbb {H}}\rightarrow {\mathbb {C}}\), as
where \({\varvec{\mu }}\in L/2\) and \({\mathcal {K}}: L\otimes {\mathbb {R}} \rightarrow {\mathbb {C}}\) is a summation kernel. Let us be slightly more generic and include the elliptic variables which are relevant for the Donaldson observables. We define
with \({{\varvec{b}}}=\mathrm {Im}({{\varvec{z}}})/y\).
The modular properties of \(\Psi ^J_{\varvec{\mu }}[{\mathcal {K}}]\) depend on the kernel \({\mathcal {K}}\). The modular transformations under the \(\mathrm{SL}(2,{\mathbb {Z}})\) generators for \(\Psi ^J_{\varvec{\mu }}[1]\) are
For the case of the partition function, we set the elliptic variables \({{\varvec{z}}}, {{\bar{{{\varvec{z}}}}}}\) to zero. Using the above \(\mathrm{SL}(2,{\mathbb {Z}})\) transformations and Poisson resummation, one may verify that \(\Psi ^J_{\varvec{\mu }}[1]\) is a modular form for the congruence subgroup \(\Gamma ^0(4)\). The transformations under the generators of this group read
where we have set \({{\varvec{z}}}= {{\bar{{{\varvec{z}}}}}} = 0\). Transformations for other kernels appearing in the main text are easily determined from these expressions.
Indefinite theta functions for uni-modular lattices of signature \((1,n-1)\)
In this appendix, we discuss various aspects of the theory of indefinite theta functions and their modular completion. We assume that the corresponding lattice L is unimodular and of signature \((1,n-1)\), and use the notation introduced in “Appendix B.” To define the indefinite theta function \(\Theta _{\varvec{\mu }}^{JJ'}\), we let \({\varvec{\mu }}\in L/2\) and choose a vector \(J\in L\otimes {\mathbb {R}}\) and a vector \(J'\in L\), such that
-
(i)
J is positive definite, \(Q(J)=1\),
-
(ii)
\(J'\) is a null-vector, \(Q(J')=0\),
-
(iii)
\(B(J,J')>0\),
-
(iv)
\(B({{\varvec{k}}},J')\ne 0\) for all \({{\varvec{k}}}\in L +{\varvec{\mu }}\).
The indefinite theta function \(\Theta _{\varvec{\mu }}^{JJ'}(\tau ,{{\varvec{z}}})\) is then defined as
The kernel within the straight brackets ensures that the sum over the indefinite lattice is convergent, since it vanishes on positive definite vectors [15]. This is also the case if both J and \(J'\) are positive definite, without the need to impose condition (iv). One may start from this situation and obtain the conditions above by taking the limit that \(J'\) approaches a null vector. The indefinite theta series \(\Theta ^{JJ'}_{{\varvec{\mu }}}\) can also be defined, for \({\varvec{\mu }}\) which do not satisfy requirement (iv) above, but this requires more care.
We can express \(\Theta ^{JJ'}_{{\varvec{\mu }}}\) also as \(\Psi _{\varvec{\mu }}^J[{\mathcal {K}}]\) (B.2) with the kernel
where \({{\varvec{b}}}=\mathrm {Im}({{\varvec{z}}})/y\).
While the sum over L is convergent, \(\Theta ^{JJ'}_{{\varvec{\mu }}}\) only transforms as a modular form after addition of certain non-holomorphic terms. References [15, 16] explain that the modular completion \({\widehat{\Theta }}^{JJ'}_{\varvec{\mu }}\) of \(\Theta ^{JJ'}_{\varvec{\mu }}\) is obtained by substituting (rescaled) error function for the sgn-function in (C.1). We let \(E(u):{\mathbb {R}}\rightarrow (-1,1)\) be defined as
The completion \({\widehat{\Theta }}^{JJ'}_{\varvec{\mu }}\) then transforms as a modular form of weight n/2 and is explicitly given by
Note that in the limit \(y\rightarrow \infty \), \(E(\sqrt{2y}\,u)\) approaches the \(\mathrm {sgn}\)-function of (C.1),
The transformation properties under SL\((2,{\mathbb {Z}})\) follow from Chapter 2 of Zwegers’ thesis [15] or Vignéras [64]. One finds
The argument of E in (C.4) depends only on the imaginary part of \({{\varvec{z}}}\) in and is valued in \({\mathbb {R}}\). Reference [18] demonstrates that if one formally sets \({{\bar{{{\varvec{z}}}}}}=0\) such that the argument of E is complex-valued, the modular properties of \({\widehat{\Theta }}^{JJ'}_{{\varvec{\mu }}}\) remain unchanged.
When \({{\varvec{z}}}=0\), we set \({\widehat{\Theta }}^{JJ'}_{{\varvec{\mu }}}(\tau ,\bar{\tau },0,0)={\widehat{\Theta }}^{JJ'}_{{\varvec{\mu }}+K/2}(\tau ,{{\bar{\tau }}})\). One finds for the action of the generators on \(\widehat{\Theta }^{JJ'}_{{\varvec{\mu }}}(\tau ,{{\bar{\tau }}})\)
For our application, the \({{\bar{\tau }}}\)-derivative of \({\widehat{\Theta }}^{JJ'}_{\varvec{\mu }}\) is of particular interest. This gives the “shadow”Footnote 12 of \(\Theta ^{JJ'}_{\varvec{\mu }}\), whose modular properties are easier to determine than those of \(\Theta ^{JJ'}_{\varvec{\mu }}\). We obtain here
with \(\Psi ^J_{\varvec{\mu }}\) (B.2) the same function discussed in “Appendix B” and \({\mathcal {K}}_0\),
1.1 An example
Let us now specialize to an example which is useful in Sect. 5.4. We consider a two-dimensional lattice \(L \cong {\mathbb {Z}}^{1,1}\) with quadratic form \(-\big ( {\begin{matrix} 1 &{} 1\\ 1 &{} 0 \end{matrix}} \big )\). The positive and negative definite cones of this lattices are illustrated in Fig. 3. The upper-right component of the negative cone for this lattice is generated by the vectors (0, 1) and \((2,-1)\). Any linear combination of these vectors with positive definite coefficients will be negative definite. We choose the vectors J and \(J'\) as follows: \(J=(-1,1)\) and \(J'=(0,1)\). For \({{\varvec{k}}}= (n, \ell )\), the kernel in (C.1) becomes \((\mathrm{sgn}(\ell ) + \mathrm{sgn}(n))\). Then the only elements of L which contribute to the theta series are those in the two yellow areas in Fig. 3.
For the characteristic vector, we choose \(K=(0,-1)\), while we choose for \({\varvec{\mu }}=\frac{1}{2}(1,1)\). With these choices, \(\Theta ^{JJ'}_{\varvec{\mu }}\) becomes the following q-series,
where we performed the geometric sum over \(\ell \) on the second line. The first part of this Appendix discussed that \(\Theta ^{JJ'}_{\varvec{\mu }}\) can be completed by replacing \(\mathrm {sgn}(\ell )\) in (C.1) by \(E(\sqrt{2y}\,\ell )\), where E is the rescaled error function defined in (C.3). We can write \(E(\sqrt{2y}\,\ell )\) as \(\mathrm {sgn}(\ell )\) plus a non-holomorphic period integral,
The completion can then be written as
and transforms as a non-holomorphic modular form for \(\Gamma ^0(4)\) as discussed in “Appendix C.” We thus find that \(F=-i\,\Theta ^{JJ'}_{\varvec{\mu }}/\vartheta _4\) is the holomorphic part of \({\widehat{F}}\) in Sect. 5.4.
We conclude this appendix by deriving \(F_D\), which is the holomorphic part of \({\widehat{F}}_{D}(\tau ,{{\bar{\tau }}})=-(-i\tau )^{-\frac{1}{2}}{\widehat{F}}(-1/\tau ,-1/{{\bar{\tau }}})\). We are instructed by (C.5) to determine \({\widehat{\Theta }}^{JJ'}_{K/2}(\tau ,-{\varvec{\mu }}+K/2)\) with \({\varvec{\mu }}=\frac{1}{2}(1,1)\). Its holomorphic part reads
This gives for \(F_D\)
The Appell–Lerch sum
We recall the definition and properties of the Appell–Lerch sum. We will denote this function by \(M(\tau ,u,v)\) rather then the more common \(\mu (\tau ,u,v)\) to avoid a class of notation with the ’t Hooft fluxes. We will mostly follow the exposition of Zwegers [15].
For fixed \(\tau \), the Appell–Lerch function is a function of two complex variables \(M:({\mathbb {C}}\backslash \{{\mathbb {Z}}\tau +{\mathbb {Z}}\})^2 \rightarrow {\mathbb {C}}\), defined as
It has single-order poles at \({\mathbb {Z}}\tau +{\mathbb {Z}}\) for both u and v.
We list a number of useful properties, whose proofs can be found in [15]:
-
1.
Periodicity of u and v:
$$\begin{aligned} M(u+1,v)=M(u,v+1)=-M(u,v). \end{aligned}$$(D.2) -
2.
Quasi-periodicity of M under simultaneous translations of u and v. For \(u,v,u+z,v+z\ne {\mathbb {Z}}\tau +{\mathbb {Z}}\), M satisfies
$$\begin{aligned} M(u+z,v+z)-M(u,v)=\frac{i\,\eta ^3\,\vartheta _1(u+v+z)\,\vartheta _1(z)}{\vartheta _1(u)\,\vartheta _1(v)\,\vartheta _1(u+z)\,\vartheta _1(v+z)}. \end{aligned}$$(D.3)This relation can be demonstrated by showing that the periodicity, zeroes and poles of the variable z are identical on the left- and right-hand side.
-
3.
Inversion of the elliptic arguments leaves \(\mu \) invariant:
$$\begin{aligned} M(-u,-v)=M(u,v) \end{aligned}$$(D.4) -
4.
M is symmetric under exchange of u and v:
$$\begin{aligned} M(v,u)=M(u,v). \end{aligned}$$(D.5)Note that this relation follows from (D.3) and (D.4) using \(z=-u-v\).
A further property of M is that M transforms as a Jacobi form after the addition of a suitable non-holomorphic function R, which is analytic in its arguments. It is defined explicitly as
where \(a=\mathrm {Im}(u)/y\), and \(\mathrm {Erf}(t)\) is the error function
The anti-holomorphic derivative of \(R(\tau ,{{\bar{\tau }}}, u,{\bar{u}})\) is
Addition of this function to M provides a function \({\widehat{M}}\), which transforms as a weight \(\frac{1}{2}\) Jacobi form. This non-holomorphic completion \({\widehat{M}}\) of M is explicitly given by
This function transforms under \(\mathrm{SL}(2,{\mathbb {Z}})\) as
where \(\varepsilon (\gamma )\) is the multiplier system of the Dedekind \(\eta \) function. The anti-holomorphic derivative of \({\widehat{M}}\) is given by
where \(a=\mathrm {Im}(u)/y\) and \(b=\mathrm {Im}(v)/y\), and we hope there is no confusion with the a, b, c, d used in Eq. (D.10).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Korpas, G., Manschot, J., Moore, G.W. et al. Mocking the u-plane integral. Res Math Sci 8, 43 (2021). https://doi.org/10.1007/s40687-021-00280-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40687-021-00280-5


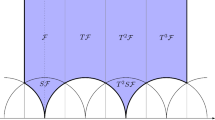




 . The negative definite set of this lattice is the union of the yellow and purple regions. For the given choices of J and
. The negative definite set of this lattice is the union of the yellow and purple regions. For the given choices of J and