Abstract
The present paper introduces a novel notion of ‘(effective) computability,’ called viability, of strategies in game semantics in an intrinsic (i.e., without recourse to the standard Church–Turing computability), non-inductive, non-axiomatic manner and shows, as a main technical achievement, that viable strategies are Turing complete. Consequently, we have given a mathematical foundation of computation in the same sense as Turing machines but beyond computation on natural numbers, e.g., higher-order computation, in a more abstract fashion. As immediate corollaries, some of the well-known theorems in computability theory such as the smn theorem and the first recursion theorem are generalized. Notably, our game-semantic framework distinguishes high-level computational processes that operate directly on mathematical objects such as natural numbers (not on their symbolic representations) and their symbolic implementations that define their ‘computability,’ which sheds new light on the very concept of computation. This work is intended to be a stepping stone toward a new mathematical foundation of computation, intuitionistic logic and constructive mathematics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The present work introduces an intrinsic, non-inductive, non-axiomatic formulation of ‘(effectively) computable’ strategies in game semantics and proves as a main theorem that they are Turing complete. This result leads to a novel mathematical foundation of computation beyond classical computation, e.g., higher-order computation, that distinguishes high-level and low-level computational processes, where the latter defines ‘effective computability’ of the former.
Convention
We shall informally use computational processes and algorithms almost as synonyms of computation, but they put more emphasis on ‘processes.’
1.1 Search for Turing machines beyond classical computation
Turing machines (TMs) introduced in the classic work [67] by Alan Turing have been widely accepted as giving a reasonable, highly convincing definition of ‘effectivity’ or ‘(effective) computability’ of (partial) functions on (finite sequences of) natural numbers, which let us call in this paper recursiveness, classical computability or Church–Turing computability, in a mathematically rigorous manner. This is because ‘computability’ of a function intuitively means the very existence of an algorithm that implements the function’s input/output behavior, and TMs are none other than a mathematical formulation of this informal concept.
In mathematics, however, there are various kinds of non-classical computation, where by classical computation we mean what merely implements a function on natural numbers, since there are a variety of mathematical objects other than natural numbers, for which TMs have certain limitations.
As an example of non-classical computation, consider higher-order computation [50], i.e., computation that takes (as an input) or produces (as an output) another computation, which abounds in mathematics, e.g., quantification in mathematical logic, differentiation in analysis or simply an application \((f, a) \mapsto f(a)\) of a function \(f : A \rightarrow B\) to an argument \(a \in A\). However, TMs cannot capture higher-order computation in a natural or systematic fashion. In fact, although TMs may compute on symbols that encode other TMs, e.g., consider universal TMs [35, 48, 64], they cannot compute on ‘external behavior’ of an input computation, which implies that the input is limited to a recursive one (to be encoded); however, it makes perfect sense to consider computation on non-recursive objects such as non-recursive real numbers. For this point, one may argue that oracle TMs [47, 64] may treat an input computation as an oracle, a black-box-like computation that does not have to be recursive; however, it is like a function (rather than a computational process) that computes just in a single step, which appears conceptually mysterious and technically ad hoc. (Another approach is to give an input computation as a potentially infinite sequence of symbols on the input tape [69], but it may be criticized in a similar manner.)
On the other hand, most of the other models of higher-order computation are, unlike TMs, either syntactic (such as \(\lambda \)-calculi and programming languages [9, 50]), inductive and/or axiomatic (such as Kleene’s schemata S1 - S9 [40, 41]) or extrinsic (i.e., reducing to classical computation by encoding whose ‘effectivity’ is usually left imprecise [16, 50]), thus lacking the semantic, direct, intrinsic nature of TMs. Also, unlike classical computability, a confluence between different notions of higher-order computability has been rarely established [50]. For this problem, it would be a key step to establish a TMs-like model of higher-order computation since it may tell us which notion of higher-order computability is a ‘correct’ one.
1.2 Search for mathematics of high-level computational processes
Perhaps more crucially than the limitation for non-classical computation mentioned above, one may argue that TMs are not appropriate as mathematics of computational processes since computational steps of TMs are often too low-level to see what they are supposed to compute. In other words, we need mathematics of high-level computational processes that gives a ‘birds-eye-view’ of low-level computational processes.Footnote 1 Also, what TMs formulate is essentially symbol manipulations; however, the content of computation on mathematical, semantic, non-symbolic objects seems completely independent of its symbolic representation, e.g., consider a process (not a function) to add numbers or to take the union of sets.
Therefore, it would be rather appropriate, at least from the conceptual and the mathematical points of view, to formulate such high-level computational processes in a more abstract, in particular syntax-independent, manner, in order to explain low-level computational processes, and then regard the latter as executable symbolic implementations of the former.
1.3 Our research problem: mathematics of computational processes
To summarize, it would be reasonable and meaningful from both of the conceptual and the mathematical viewpoints to develop mathematics of abstract (in particular syntax-independent), high-level computational processes as well as executable, low-level ones beyond classical computation such that the former is defined to be ‘effectively computable’ if it is implementable or representable by the latter.
In fact, this (or similar) perspective is nothing new and shared with various prominent researchers; for instance, Robin Milner stated:
... we should have achieved a mathematical model of computation, perhaps highly abstract in contrast with the concrete nature of paper and register machines, but such that programming languages are merely executable fragment of the theory ...[52]
We address this problem in the present paper. However, since there are so many kinds of computation, e.g., parallel, concurrent, probabilistic, non-deterministic and quantum, as the first step, this paper focuses on a certain kind of higher-order, sequential (i.e., at most one computational step may be performed at a time) computation, which is based on (sequential) game semantics Footnote 2 introduced below.
1.4 Game semantics
Game semantics (of computation) [3, 6, 37] is a particular kind of denotational semantics of programming languages [8, 32, 70], in which types and terms are modeled as games and strategies (whose definitions are given in Sect. 2), respectively. Historically, having its roots in ‘games-based’ approaches in mathematical logic to capture validity [19, 59], higher-order computability [21, 42,43,44,45,46] and proofs in linear logic [5, 11, 36], combined with ideas from sequential algorithms [10], process calculi [34, 53] and geometry of interaction [24,25,26, 28,29,30] in theoretical computer science, several variants of game semantics in its modern form were developed in the early 1990s to give the first syntax-independent characterization of the higher-order programming language PCF [7, 38, 55]; since then, a variety of games and strategies have been proposed to model various programming features [6].
An advantage of game semantics is this flexibility: It models a wide range of programming languages by simply varying constraints on strategies [6], which enables one to systematically compare and relate different languages ignoring syntactic details. Also, as full completeness and full abstraction results [15] in the literature have demonstrated, game semantics in general has an appropriate degree of abstraction (and thus it has a good potential to be mathematics of high-level computational processes). Finally, yet another strong point of game semantics is its conceptual naturality: It interprets syntax as ‘dynamic interactions’ between the participants of games, providing a computational, intensional explanation of syntax in a natural, intuitive (yet mathematically precise) manner. Informally, one can imagine that games provide a high-level description of interactive computation between a TM and an oracle, and therefore, they seem appropriate as an approach to the research problem defined in Sect. 1.3. Note that such an intensional nature stands in sharp contrast to the traditional domain-theoretic denotational semantics [8] which, e.g., cannot capture sequentiality of PCF (but the game models [7, 38, 55] can).
In the following, let us give a brief, informal introduction to games and strategies (as defined in [6]) in order to sketch the main idea of the present paper.
A game, roughly, is a certain kind of a rooted forest whose branches represent possible ‘developments’ or (valid) positions of a ‘game in the usual sense’ (such as chess, poker, etc.). Moves of a game are nodes of the game, where some moves are distinguished and called initial; only initial moves can be the first element (or occurrence) of a position of the game. Plays of a game are increasing sequences \(\varvec{\epsilon }, m_1, m_1 m_2, \ldots \) of positions of the game, where \(\varvec{\epsilon }\) is the empty sequence. For our purpose, it suffices to focus on rather standard sequential (as opposed to concurrent [2]) and unpolarized (as opposed to polarized [49]) games played by two participants, Player (P), who represents a ‘computational agent,’ and Opponent (O), who represents a ‘computational environment,’ in each of which O always starts a play (i.e., unpolarized), and then they alternately and separately (i.e., sequential) perform moves allowed by the rules of the game. Strictly speaking, a position of each game is not just a sequence of moves: Each occurrence m of O’s or O- (resp. P’s or P-) non-initial move in a position points to a previous occurrence \(m'\) of P- (resp. O-) move in the position, representing that m is performed specifically as a response to \(m'\). A strategy on a game, on the other hand, is what tells P which move (together with a pointer) she should make at each of her turns in the game. Hence, a game semantics \(\llbracket \_ \rrbracket _{\mathcal {G}}\) of a programming language \(\mathcal {L}\) interprets a type \(\mathsf {A}\) of \(\mathcal {L}\) as a game \(\llbracket \mathsf {A} \rrbracket _{\mathcal {G}}\) that specifies possible plays between P and O, and a term \(\mathsf {M : A}\) Footnote 3 of \(\mathcal {L}\) as a strategy \(\llbracket \mathsf {M} \rrbracket _{\mathcal {G}}\) that describes for P how to play on \(\llbracket \mathsf {A} \rrbracket _{\mathcal {G}}\); an execution of the term \(\mathsf {M}\) is then modeled as a play of \(\llbracket \mathsf {A} \rrbracket _{\mathcal {G}}\) in which P follows \(\llbracket \mathsf {M} \rrbracket _{\mathcal {G}}\).
Let us consider a simple example. The game N of natural numbers is the following rooted tree (which is infinite in width):

in which a play starts with O’s question q (‘What is your number?’) and ends with P’s answer \(n \in \mathbb {N}\) (‘My number is n!’), where \(\mathbb {N}\) is the set of all natural numbers, and n points to q (though this pointer is omitted in the diagram). A strategy \(\underline{10}\) on N, for instance, that corresponds to \(10 \in \mathbb {N}\) can be represented by the map \(q \mapsto 10\) equipped with a pointer from 10 to q (though it is the only choice). In the following, the pointers of most strategies are obvious, and thus, we often omit them.
There is a construction \(\otimes \) on games, called tensor (product). Conceptually, a position \(\varvec{s}\) of the tensor \(A \otimes B\) of games A and B is an interleaving mixture of a position \(\varvec{t}\) of A and a position \(\varvec{u}\) of B developed ‘in parallel without communication’; more specifically, \(\varvec{t}\) (resp. \(\varvec{u}\)) is the subsequence of \(\varvec{s}\) consisting of moves of A (resp. B) such that the change of AB-parity (i.e., the switch between \(\varvec{t}\) and \(\varvec{u}\)) in \(\varvec{s}\) must be made by O. The pointers in \(\varvec{s}\) are inherited from those in \(\varvec{t}\) and \(\varvec{u}\) in the obvious manner; this point holds also for other constructions on games and strategies in the rest of the introduction, and thus, we shall not mention it again. For instance, a maximal position of the tensor \(N \otimes N\) is either of the following formsFootnote 4:

where \(n, m \in \mathbb {N}\), and \((\_)^{[i]}\) (\(i = 0, 1\)) are (arbitrary, unspecified) ‘tags’ to distinguish the two copies of N (but we often omit them if it does not bring confusion), and the arrows represent pointers (n.b., they are distinct from edges of the game).
Next, a fundamental construction ! on games, called exponential, is basically the countably infinite iteration of \(\otimes \), i.e., \(!A {\mathop {=}\limits ^{\mathrm {df. }}} A \otimes A \otimes \dots \) for each game A, where the ‘tag’ for each copy of A is typically given as \((\_, i)\), where \(i \in \mathbb {N}\).
Another central construction \(\multimap \), called linear implication, captures the notion of linear functions, i.e., functions that consume exactly one input to produce an output. A position of the linear implication \(A \multimap B\) from A to B is almost like a position of the tensor \(A \otimes B\) except the following three points:
-
1.
The first occurrence of the position must be a move of B;
-
2.
A change of AB-parity in the position must be made by P;
-
3.
Each occurrence of an initial move (called an initial occurrence) of A points to an initial occurrence of B.
Thus, a typical position of the game \(N \multimap N\) is the following:

where \(n, m \in \mathbb {N}\), which can be read as follows:
-
1
O’s question \(q^{[1]}\) for an output (‘What is your output?’);
-
2
P’s question \(q^{[0]}\) for an input (‘Wait, what is your input?’);
-
3
O’s answer, say, \(n^{[0]}\), to \(q^{[0]}\) (‘OK, here is an input n.’);
-
4
P’s answer, say, \(m^{[1]}\), to \(q^{[1]}\) (‘Alright, the output is then m.’).
This play corresponds to any linear function that maps \(n \mapsto m\). The strategy \( succ \) (resp. \( double \)) on \(N \multimap N\) for the successor (resp. doubling) function is represented by the map \(q^{[1]} \mapsto q^{[0]}, q^{[1]}q^{[0]}n^{[0]} \mapsto n+1^{[1]}\) (resp. \(q^{[1]} \mapsto q^{[0]}, q^{[1]}q^{[0]}n^{[0]} \mapsto 2 \cdot n^{[1]}\)).
Let us remark here that the following play, which corresponds to a constant linear function that maps \(x \mapsto m\) for all \(x \in \mathbb {N}\), is also possible: \(\varvec{\epsilon }, q^{[1]}, q^{[1]}m^{[1]}\). Thus, strictly speaking, \(A \multimap B\) is the game of affine functions from A to B, but we follow the standard convention to call \(\multimap \) linear implication.
Another construction & on games, called product, is similar to yet simpler than tensor: A position \(\varvec{s}\) of the product \( A \& B\) of A and B is either a position \(\varvec{t}^{[0]}\) of \(A^{[0]}\) or a position \(\varvec{u}^{[1]}\) of \(B^{[1]}\). It is the product in the category \(\mathcal {G}\) of games and strategies, e.g., there is the pairing \( \langle \sigma , \tau \rangle : \ !C \multimap A \& B\) of given strategies \(\sigma : \ !C \multimap A\) and \(\tau : \ !C \multimap B\) that plays as \(\sigma \) (resp. \(\tau \)) if O initiates a play by a move of A (resp. B). Clearly, we may generalize product and pairing to n-ary ones for any \(n \in \mathbb {N}\).
These four constructions \(\otimes \), !, \(\multimap \) and & come from the corresponding ones in linear logic [5, 27]. Thus, in particular, the usual implication (or the function space) \(\Rightarrow \) is recovered by Girard translation [27]: \(A \Rightarrow B {\mathop {=}\limits ^{\mathrm {df. }}} \ !A \multimap B\).
Girard translation makes explicit the point that some functions need to refer to an input more than once to produce an output, i.e., there are nonlinear functions. For instance, consider the game \((N \Rightarrow N) \Rightarrow N\) of higher-order functions, in which the following position is possible:

where \(n, n', m, m', l, i, i', j, j' \in \mathbb {N}\) and \(j \ne j'\), which can be read as follows:
-
1.
O’s question q for an output (‘What is your output?’);
-
2.
P’s question (q, j) for an input function (‘Wait, your first output please!’);
-
3.
O’s question ((q, i), j) for an input (‘What is your first input then?’);
-
4.
P’s answer, say, ((n, i), j), to ((q, i), j) (‘Here is my first input n.’);
-
5.
O’s answer, say, (m, j), to (q, j) (‘OK, then here is my first output m.’);
-
6.
P’s question \((q, j')\) for an input function (‘Your second output please!’);
-
7.
O’s question \(((q, i'), j')\) for an input (‘What is your second input then?’);
-
8.
P’s answer, say, \(((n', i'), j')\), to \(((q, i'), j')\) (‘Here is my second input \(n'\).’);
-
9.
O’s answer, say, \((m', j')\), to \((q, j')\) (‘OK, then here is my second output \(m'\).’);
-
10.
P’s answer, say, l, to q (‘Alright, my output is then l.’).
In this play, P asks O twice about an input strategy \(N \Rightarrow N\). Clearly, such a play is not possible on the linear implication \((N \multimap N) \multimap N\) or \((N \Rightarrow N) \multimap N\). The strategy \( pazo : (N \Rightarrow N) \Rightarrow N\) that computes the sum \(f(0)+f(1)\) for a given function \(f : \mathbb {N} \Rightarrow \mathbb {N}\), for instance, plays as follows:

where \(j = 0\) and \(j' = 1\) are arbitrarily chosen, i.e., any \(j, j' \in \mathbb {N}\) with \(j \ne j'\) work.
Finally, let us point out that any strategy \(\phi \) on the implication \(!A \multimap B\) induces its promotion \(\phi ^{\dagger } : \ !A \multimap \ !B\) such that if \(\phi \) plays, for instance, as

then \(\phi ^{\dagger }\) plays as

where \(\langle \_, \_ \rangle : \mathbb {N} \times \mathbb {N} {\mathop {\rightarrow }\limits ^{\sim }} \mathbb {N}\) is an arbitrarily fixed bijection, i.e., \(\phi ^{\dagger }\) plays as \(\phi \) for each thread in a position of \(!A \multimap \ !B\) that corresponds to a position of \(!A \multimap B\).
1.5 Toward a game-semantic model of computation
As seen in the examples given above, games and strategies capture higher-order computation in an abstract, conceptually natural fashion, where O plays the role of an oracle as part of the formalization. Note also that P computes on ‘external behavior’ of O, and thus O’s computation does not have to be recursive at all. Thus, one may expect that games and strategies would be appropriate as mathematics of high-level computational processes, solving the research problem of Sect. 1.3.
However, conventional games and strategies have never been formulated as a mathematical model of computation (in the sense of TMs); rather, the primary focus of the field has been full abstraction [8, 15], i.e., to characterize observational equivalences in syntax. In other words, game semantics has not been concerned that much with step-by-step processes in computation or their ‘effective computability,’ and it has been identifying programs with the same value [32, 70].
For instance, strategies on the game \(N \Rightarrow N\) typically play by q. (q, i) . (n, i) .m, where \(n, m, i \in \mathbb {N}\), as described above, and so they are essentially functions that map \(n \mapsto m\); in particular, it is not formulated at all how they calculate the fourth move m from the third one (n, i).Footnote 5 As a consequence, ‘effective computability’ in game semantics has been extrinsic: A strategy has been defined to be ‘effective’ or recursive if it is representable by a partial recursive function [7, 20, 38].
This situation is in a sense frustrating since games and strategies seem to have a good potential to give a semantic, intrinsic (i.e., without recourse to an established model of computation), non-axiomatic, non-inductive formulation of higher-order computation, but they have not taken advantage of this potential.
For the potential, we have decided to employ games and strategies as our basic mathematical framework and extend them to give mathematics of computational processes in the sense described in Sect. 1.3. For this aim, we shall first refine the category \(\mathcal {G}\) of games and strategies in such a way that accommodates step-by-step processes in computation, and then define their ‘effectivity’ in terms of their atomic computational steps. Fortunately, there is already the bicategory \(\mathcal {DG}\) of dynamic games and strategies [71], which addresses the first point.
1.6 Dynamic games and strategies
In the literature, there are several game models [13, 18, 31, 56] that exhibit step-by-step processes in computation to serve as a tool for program verification and analysis (the work [17, 23] may be called ‘intensional game semantics,’ but they rather keep track of costs in computation, not computational steps themselves). However, these variants of games and strategies are just conventional ones, and consequently, such step-by-step processes have no official status in their categories.
The problem lies in the point that in conventional game semantics composition of strategies is executed as parallel composition plus hiding [3], where hiding is the matter. Let us illustrate this point by a simple, informal example as follows. Consider again strategies \( succ \) and \( double \), but this time they are adjusted to the game \(N \Rightarrow N\). Their computations can be described by the following diagrams:

where the ‘tag’ \((\_, 0)\) on moves of the domain !N has been arbitrarily chosen (i.e., any \(i \in \mathbb {N}\) instead of 0 works). The composition \( double \bullet succ {\mathop {=}\limits ^{\mathrm {df. }}} double \circ succ ^{\dagger } = succ ^{\dagger } ; double : N \Rightarrow N\) is calculated as follows. First, by internal communication, we mean that \( succ ^{\dagger }\) and \( double \) are ‘synchronized’ via the codomain \(!N^{[1]}\) of \( succ ^{\dagger }\) and the domain \(!N^{[2]}\) of \( double \) (n.b., we take the promotion of \( succ \) to match its codomain with the domain of \( double \)), for which P also plays the role of O in \(!N^{[1]}\) and \(!N^{[2]}\) by copying her last P-moves,Footnote 6 resulting in the following play:

where moves for internal communication are marked by square boxes just for clarity, and a pointer from \((q, 0)^{[1]}\) to \((q, 0)^{[2]}\) is added because the move \((q, 0)^{[1]}\) is no longer initial. Importantly, it is assumed that O plays on the ‘external game’ \(!N^{[0]} \multimap N^{[3]}\), ‘seeing’ only moves of \(!N^{[0]}\) or \(N^{[3]}\). The resulting play is to be read as follows:
-
1.
O’s question \(q^{[3]}\) for an output in \(!N^{[0]} \multimap N^{[3]}\) (‘What is your output?’);
-
2.
P’s question
 by \( double \) for an input in \(!N^{[2]} \multimap N^{[3]}\) (‘Wait, what is your input?’);
by \( double \) for an input in \(!N^{[2]} \multimap N^{[3]}\) (‘Wait, what is your input?’); -
3.
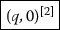 in turn triggers the question
in turn triggers the question
 for an output in \(!N^{[0]} \multimap \ !N^{[1]}\) (‘What is your output?’);
for an output in \(!N^{[0]} \multimap \ !N^{[1]}\) (‘What is your output?’); -
4.
P’s question \((q, \langle 0, 0 \rangle )^{[0]}\) by \( succ ^{\dagger }\) for an input in \(!N^{[0]} \multimap \ !N^{[1]}\) (‘Wait, what is your input?’);
-
5.
O’s answer, say, \((n, \langle 0, 0 \rangle )^{[0]}\), to the question \((q, \langle 0, 0 \rangle )^{[0]}\) in \(!N^{[0]} \multimap \ !N^{[3]}\) (‘Here is an input n.’);
-
6.
P’s answer
 to the question
to the question
 by \( succ ^{\dagger }\) in \(!N^{[0]} \multimap \ !N^{[1]}\) (‘The output is then \(n+1\).’);
by \( succ ^{\dagger }\) in \(!N^{[0]} \multimap \ !N^{[1]}\) (‘The output is then \(n+1\).’); -
7.
 in turn triggers the answer
in turn triggers the answer
 to the question
to the question
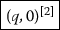 in \(!N^{[2]} \multimap N^{[3]}\) (‘Here is the input \(n+1\).’);
in \(!N^{[2]} \multimap N^{[3]}\) (‘Here is the input \(n+1\).’); -
8.
P’s answer \(2 \cdot (n+1)^{[3]}\) to the initial question \(q^{[3]}\) by \( double \) in \(!N^{[0]} \multimap N^{[3]}\) (‘The output is then \(2 \cdot (n+1)\)!’).
Next, hiding means to hide or delete all moves with the square boxes from the play, resulting in the strategy for the function \(n \mapsto 2 \cdot (n + 1)\) as expected:

By the hiding operation, the resulting play is a legal one of the game \(N \Rightarrow N\), but let us point out that the intermediate occurrences of moves (with the square boxes), representing step-by-step processes in computation, are deleted by the operation.
Nevertheless, the present author and Samson Abramsky have introduced a novel, dynamic variant of games and strategies that systematically model dynamics and intensionality of computation, and also studied their algebraic structures [71]. In contrast to the previous work mentioned above, dynamic strategies themselves embody step-by-step processes in computation by retaining intermediate occurrences of moves, and composition of them is parallel composition without hiding. In addition, the categorical structure of existing game semantics is not lost but rather refined by the cartesian closed bicategory [57] \(\mathcal {DG}\) of dynamic games and strategies, forming a categorical ‘universe’ of high-level computational processes.
1.7 Viable strategies
Now, the remaining problem is to define ‘effective’ dynamic strategies in an intrinsic (i.e., solely in terms of games and strategies), non-inductive, non-axiomatic manner. Of course, we need to provide a convincing argument that justifies their ‘effectivity’ (though such an argument can never be mathematically precise) as in the case of TMs. Moreover, to obtain a powerful model of computation, they should be at least Turing complete, i.e., they ought to subsume all classically computable partial functions. This sets up, in addition to the conceptual quest so far, an intriguing mathematical question in its own right:
Is there any intrinsic, non-inductive, non-axiomatic notion of ‘effectivity’ of dynamic strategies that is Turing complete?
Not surprisingly, perhaps, this problem has turned out to be challenging, and the main technical achievement of the present paper is to give a positive answer to it.
As already mentioned, our solution is to give low-level computational processes (which are clearly ‘executable’) in order to define ‘effectivity’ of dynamic strategies (or high-level computational processes). This is achieved roughly as follows.
Remark
The concepts introduced below make sense for conventional (i.e., non-dynamic) games and strategies too, but they do not give rise to a Turing complete model of computation for composition of conventional strategies does not preserve our notion of ‘effectivity’ or viability as we shall see.
First, we give, by a fixed alphabet, a concrete formalization of ‘tags’ for disjoint union of sets of moves for constructions on games in order to rigorously formulate ‘effectivity’ of strategies. As we see in Sect. 1.4, a finite number of ‘tags’ suffice for most constructions on games, but it is not the case for exponential !. Then, we formalize ‘tags’ for exponential by an unary representation \(\ell ^i {\mathop {=}\limits ^{\mathrm {df. }}} \underbrace{\ell \ell \dots \ell }_i\) of natural numbers \(i \in \mathbb {N}\) (extended by a symbolic implementation of a recursive bijection \(\mathbb {N}^*{\mathop {\rightarrow }\limits ^{\sim }} \mathbb {N}\) [16], but here we omit the extension for simplicity) and employ, instead of the game N, the lazy variant \(\mathcal {N}\) of natural number game whose maximal positions are either of the following forms:

where the number n of \( yes \) in the position ranges over all natural numbers, which represents the number intended by P. In this way, \(\mathcal {N}\) gives an unary representationFootnote 7 of natural numbers. Note that the initial question \(\hat{q}\) must be distinguished from the non-initial one q for a technical reason, which will be clarified in Sect. 2. This sets up a finitary representation of game-semantic computation on natural numbers.
Next, as we shall see, dynamic strategies modeling PCF only need to refer to at most three moves in the history of previous moves which may be ‘effectively’ identified by pointers (specifically the last three moves in the P-view [6, 38]; see Definition 16). Thus, it may seem at first glance that finitary dynamic strategies in the following sense suffice: A strategy is finitary if its representation by a partial function [38, 51] that assigns the next P-move to previous moves, called its table, is finite. However, it is not the case: Finitary strategies cannot handle unboundedly many manipulations of ‘tags’ for exponential (more precisely, manipulations such that the length of input or output ‘tags’ is unbounded), but such manipulations seem to be necessary for Turing completeness, e.g., a strategy that models primitive recursion or minimization has to interact with input strategies unboundedly many times, and thus, it must handle unboundedly many ‘tags.’
Then, the main idea of our solution is to define a strategy to be viable if its table is ‘describable’ by a finitary strategy. To state it more precisely, let us note that there is the terminal game T which has only the empty sequence \(\varvec{\epsilon }\) as a position, and each game G is identical up to ‘tags’ to the implication \(T \Rightarrow G\). Hence, we may regard strategies \(\sigma : G\) as the one on the implication \(T \Rightarrow G\) up to ‘tags,’ and vice versa; we shall not take the trouble of distinguishing the two. Also, we define for each move \(m = [m']_{\varvec{e}}\) of a game G, where \(\varvec{e} = e_1 . e_2 \dots e_{k}\) is a unary representation of the ‘tag’ for exponential on m, the strategy \(\underline{m}\) on a suitable game \(\mathcal {G}(M_G)\) that plays as \(\hat{q} . \mathsf {m'} . q . \mathsf {e_1} . q . \mathsf {e_2} \dots q . \mathsf {e_{k}} . q . \checkmark \), where each non-initial element points to the last element, and the font difference between the moves is just for clarity. In this manner, the strategy \(\underline{m} : \mathcal {G}(M_G)\) encodes the move m. Then, viability of strategies is given more precisely as follows: A strategy \(\sigma : G\) is defined to be viable if its partial function representation \((m_3, m_2, m_1) \mapsto m\), where \(m_1\), \(m_2\) and \(m_3\) are the last, the second last and the third last moves of the current P-view, respectively, is ‘implementable’ by a finitary strategy \( \mathcal {A}(\sigma )^\circledS : \mathcal {G}(M_{G}) \& \mathcal {G}(M_{G}) \& \mathcal {G}(M_{G}) \Rightarrow \mathcal {G}(M_{G})\), called an instruction strategy for \(\sigma \), in the sense that the composition \(\mathcal {A}(\sigma )^\circledS \circ \langle \underline{m_3}, \underline{m_2}, \underline{m_1} \rangle ^{\dagger } : \mathcal {G}(M_G)\) coincides with \(\underline{m} : \mathcal {G}(M_{G})\) for all quadruples \((m_3, m_2, m_1) \mapsto m\) in the table of \(\sigma \), where \( \langle \underline{m_3}, \underline{m_2}, \underline{m_1} \rangle : T \Rightarrow \mathcal {G}(M_G) \& \mathcal {G}(M_G) \& \mathcal {G}(M_G)\) is the ternary pairing of the strategies \(\underline{m_i} : T \Rightarrow \mathcal {G}(M_G)\) (i = 1, 2, 3).
For instance, consider the successor and the doubling strategies modified for the lazy natural number game \(\mathcal {N}\), whose plays (on a nonzero input) are as in Fig. 1. Roughly, \( succ \) copies a given input on \(!\mathcal {N}^{[0]}\) and repeats it as an output on \(\mathcal {N}^{[1]}\), but it adds one more \([ yes ^{[1]}]\) to \(\mathcal {N}^{[1]}\) before \([ no ^{[1]}]\); similarly, \( double \) copies an input and repeats it as an output, but it doubles the number of \([ yes ^{[1]}]\)’s in the output. It is easy to see that for computing the next P-move (with a pointer) at an odd-length position \(\varvec{s} = m_1 m_2 \ldots m_{2i+1}\) the strategies only need to refer to at most the last O-move \(m_{2i+1}\), the P-move \(m_{2j}\) pointed by \(m_{2i+1}\) and the O-move \(m_{2j-1}\) (they are the last three moves in the P-view of \(\varvec{s}\)), e.g., \( succ : (\square , \square , [\hat{q}^{[1]}]) \mapsto [\hat{q}^{[0]}]\), \(([\hat{q}^{[1]}], [\hat{q}^{[0]}], [ yes ^{[0]}]) \mapsto [ yes ^{[1]}]\), and so on, where \(\square \) denotes ‘no move.’ Note that these strategies do not need unboundedly many manipulations of ‘tags’; they are in fact finitary (it is easy to construct finite tables for them, each of which consists of a finite number of quadruples of moves of the form \((m_3, m_2, m_1) \mapsto m\)).
On the other hand, consider the strategy \( min : \mathcal {N} \Rightarrow \mathcal {N}\) that implements the minimization \((\mathbb {N} \rightharpoonup \mathbb {N}) \rightharpoonup \mathbb {N}\) that maps a given partial function \(f : \mathbb {N} \rightharpoonup \mathbb {N}\) to the least \(n \in \mathbb {N}\) such that \(f(n) = 0\) if it exists. For simplicity, the domain of \( min \) is \(!\mathcal {N}\), not \(\mathcal {N} \Rightarrow \mathcal {N}\); \( min \) informs an input computation of an input number \(n \in \mathbb {N}\) by the ‘tag’ \([\_]_{\ell ^n}\) for exponential. As described in Fig. 2, \( min \) simply investigates if the input computation gives back zero just by checking the first digit (\([ yes ^{[0]}]\) or \([ no ^{[0]}]\)) and adds \([ yes ^{[1]}]\) to the output if the input computation gives back nonzero (i.e., if the first digit is \([ yes ^{[0]}]\)). Note that \( min \) only needs to refer to at most the last three moves of each odd-length position (n.b., in this case, they are the last three moves of the P-view of the position as well). The point here is that the number of ‘tags’ for exponential that \( min \) has to manipulate is unbounded (though the manipulation is very simple), and therefore, the strategy is not finitary; however, it is easy to show that the strategy is viable as follows. First, its partial function representation can be given by the following infinitary table (n.b., n for \([\_]_{\ell ^n}\) given below ranges over all natural numbers):
This high-level computational process is ‘implementable’ by a strategy \( \mathcal {A}( min )^\circledS : \mathcal {G}(M_{\mathcal {N} \Rightarrow \mathcal {N}}) \& \mathcal {G}(M_{\mathcal {N} \Rightarrow \mathcal {N}}) \& \mathcal {G}(M_{\mathcal {N} \Rightarrow \mathcal {N}}) \Rightarrow \mathcal {G}(M_{\mathcal {N} \Rightarrow \mathcal {N}})\), which computes as in Fig. 3, where the rather trivial pointers and the ‘tags’ \((\_)^{[i]}\) in the underlying game are omitted for brevity. Then clearly, there is a finite table for \(\mathcal {A}( min )^\circledS \) that maps the last k-moves in the P-view of each odd-length position to the next P-move for some fixed \(k \in \mathbb {N}\) (though it is a bit too tedious to write down the table here), proving viability of \( min \). Observe in particular how the infinitary manipulation of ‘tags’ by \( min \) is reduced to a finitary computation by \(\mathcal {A}( min )^\circledS \).
This example illustrates why we need viable (not only finitary) dynamic strategies for Turing completeness, where recall that minimization (in the general form) or an equivalent construction is vital to construct all partial recursive functions [16]. Also, it should be intuitively clear now why we have to employ composition of strategies without hiding: An instruction strategy for the composition of strategies \(\phi : A \Rightarrow B\) and \(\psi : B \Rightarrow C\) without hiding can be obtained simply as the disjoint union of instruction strategies for \(\phi ^{\dagger }\) and \(\psi \) (see the proof of Theorem 76 for the details), but it is not possible for composition with hiding. (In fact, there is no obvious way to construct an instruction strategy for the composition of \(\phi \) and \(\psi \) with hiding.)
We advocate that viability of strategies gives a reasonable notion of ‘effective computability’ as finitary strategies are clearly ‘effective,’ and so their descriptions or instruction strategies can be ‘effectively read off’ by P. Note also that viability is defined solely in terms of games and strategies without any axiom or induction. Moreover, viability is at least as strong as Church–Turing computability: As the main results of the present work, we show that dynamic strategies definable by PCF are all viable (Theorem 81), and therefore, they are Turing complete in particular (Corollary 82).
Also, viable dynamic strategies solve the problem defined in Sect. 1.3 in the following sense. First, as we have seen via examples, games and strategies give an abstract, syntax-independent formulation of high-level computational processes, e.g., the lazy natural number game \(\mathcal {N}\) defines natural numbers (not their symbolic representation) as ‘counting processes’ in an abstract, syntax-independent fashion, beyond classical computation, e.g., higher-order computation. Moreover, an instruction strategy for a viable dynamic strategy describes a low-level computational process that implements the dynamic strategy. In this manner, we have obtained a single mathematical framework for both high-level and low-level computational processes as well as ‘effective computability’ of the former in terms of the latter.
1.8 Our contribution and related work
Our main technical achievement is to define an intrinsic, non-inductive, non-axiomatic notion of ‘effectivity’ of strategies in game semantics, namely viable dynamic strategies, and show that they are Turing complete (Corollary 82). We have also shown the converse (though it is not that surprising): The input/output behavior of each viable dynamic strategy computing on natural numbers coincides with a partial recursive function (Theorem 85). This result immediately implies a universality result [7, 15, 58] as well: Every viable dynamic strategy on a dynamic game interpreting a type of PCF is (up to intrinsic equivalence) the denotation of a term of PCF (Corollary 89). In addition, some of the well-known theorems in computability theory [16, 60] such as the smn theorem and the first recursion theorem are generalized to non-classical computation (Corollaries 83 and 84). We hope that these technical results would convince the reader that viability of dynamic strategies is a natural, reasonable generalization of Church–Turing computability.
Another, more conceptual contribution of the present work is to establish a single mathematical framework for both high-level and low-level computational processes, where the former defines what computation does, while the latter describes how to execute the former. In comparison with existing mathematical models of computation, our game-semantic approach has some novel features. First, in comparison with computation by TMs or programming languages, plays of games are a more abstract concept; in particular they are not necessarily symbol manipulations, which is why they are suitable for abstract, high-level computational processes. Next, computation in a game proceeds as an interaction between P and O, which may be seen as a generalization of computation by TMs in which just one interaction occurs (i.e., O gives an input on the infinite tape, and then P returns an output on the tape); this in particular means that O’s computation does not have to be recursive, and it is part of the formalization, which is why game semantics in general captures higher-order computation in a natural, systematic manner. The present work inherits this interactive nature of game semantics. Last but not least, games are a semantic counterpart of types, where note that types do not a priori exist in TMs, and types in programming languages are syntactic entities. Hence, our approach provides a deeper clarification of types in the context of theory of computation.
Moreover, by exploiting the flexibility of game semantics, our approach would be applicable to a wide range of computation though it is left as future work. Also, game semantics has interpreted various logics as well [1, 5, 37, 72], and so it would be possible to employ our framework for a realizability interpretation of constructive logic [65, 68], for which viable dynamic strategies would be more suitable as realizers than existing strategies such as [12] since the former contains more ‘computational contents’ and makes more sense as a model of computation than the latter. Furthermore, the game models [1, 72] interpret Martin-Löf type theory, one of the most prominent foundations of constructive mathematics, and thus our framework would provide a mathematical, syntax-independent formalization of constructive mathematics too.Footnote 8 Of course, we need to work out details for these developments, which is out of the scope of the present paper, but it is in principle clear how to apply our framework to existing game semantics. In this sense, the present work would serve as a stepping stone toward these extensions.
In the literature, there have been several attempts to provide a mathematical foundation of computation beyond classical or symbolic ones. We do not claim at all our game-semantic approach is best or canonical in comparison with the previous work; however, our approach certainly has some advantages. For instance, Robin Gandy proposed in the famous paper [22] a notion of ‘mechanical devices,’ now known as Gandy machines (GMs), which appear more general than TMs, but showed that TMs are actually as powerful as GMs. However, since GMs are an axiomatic approach to define a general class of ‘mechanical devices’ that are ‘effectively executable,’ they do not give a distinction between high-level and low-level computational processes, where GMs formulate the latter. More recent abstract state machines (ASMs) [33] introduced by Yuri Gurevich employ a similar idea to that of GMs for ‘effectivity,’ namely to require an upper bound of elements that may change in a single step of computation, utilizing structures in the sense of mathematical logic [63]. Notably, ASMs define a very general notion of computation, namely computation as structure transition. However, it seems that this framework is in some sense too general; for instance, it is possible that an ASM computes a real number in a single step, but then its ‘effectivity’ is questionable. In general, an appropriate notion of ‘effective computability’ of ASMs has been missing. Also, the way of computing a function by an ASM is to update input/output pairs of the function in the element-wise fashion, but it does not seem to be a common or natural processes in practice. In addition, Yiannis Moschovakis considered a mathematical foundation of algorithms [54] in which, similarly to us, he proposed that algorithms and their ‘implementations’ should be distinguished, where by algorithms he refers to what we call high-level computational processes. However, his framework, called recursors, is also based on structures, and his notion of algorithms is relative to atomic operations given in each structure; thus, it does not give a foundational analysis on the notion of ‘effective computability.’ Therefore, although the previous work captures broader notions of computation than the present work, our approach has the advantage of achieving both of the distinction between high-level and low-level computational processes, and the primitive, intrinsic notion of ‘effective computability.’ Also, the interactive, typed nature of game semantics stands in sharp contrast to the previous work as well.
At this point, we need to mention computability logic [39] developed by Giorgi Japaridze since his idea is similar to ours; he defines ‘effective computability’ via computing machines playing in games. Nevertheless, there are notable differences between computability logic and the present work. First, computing machines in computability logic are a variant of TMs, and thus they are less novel as a model of computation than our approach; in fact, the definition of ‘effective computability’ in computability logic can be seen more or less as a consequence of just spelling out the standard notion of recursive strategies [7, 20, 38]. Next, our framework inherits the categorical structure of existing game semantics (see [71] for this point), providing a compositional formulation of logic and computation, i.e., a compound proof or program is constructed from its components, while there has been no known categorical structure of computability logic. Nevertheless, it would be interesting to adopt his TMs-based approach in our framework and compare the resulting computational power with that of the present work.
Finally, let us mention some of the precursors of game semantics. To clarify the notion of higher-order computability, Stephen Cole Kleene considered a model of higher-order computation based on dialogues between computational oracles in a series of papers [42,43,44], which can be seen as the first attempt to define a mathematical notion of algorithms in a higher-order setting [50]. Moreover, Gandy and his student Giovanni Pani refined these works by Kleene to obtain a model of PCF that satisfies universality though this work was not published. These previous papers are direct ancestors of game semantics (in particular the so-called HO-games [38] by Martin Hyland and Luke Ong). As another line of research (motivated by the full abstraction problem for PCF [58]), Pierre-Louis Curien and Gerard Berry conceived of sequential algorithms [10] which was the first attempt to go beyond (extensional) functions to capture sequentiality of PCF. Sequential algorithms preceded and became highly influential to the development of game semantics; in fact, sequential algorithms are presented in the style of game semantics in [50], and it is shown in [14] that the oracle computation developed by Kleene can be represented by sequential algorithms (though the converse does not hold). Nevertheless, a point we would like to emphasize here is that neither of the previous attempts defines ‘effective computability’ in a similar manner to the present work; our approach has an advantage in its intrinsic, non-inductive, non-axiomatic nature.
1.9 Structure of the paper
The rest of the paper proceeds roughly as follows. This introduction ends with fixing some notation. Then, recalling dynamic games and strategies in Sect. 2, we define viability of strategies and establish, as the main theorem, the fact that viable dynamic strategies may interpret all terms of PCF in Sect. 3, proving their Turing completeness as a corollary. Finally, we draw a conclusion and propose future work in Sect. 4.
Notation
We use the following notation throughout the paper:
-
We use bold letters \(\varvec{s}, \varvec{t}, \varvec{u}, \varvec{v}\), etc. for sequences, in particular \(\varvec{\epsilon }\) for the empty sequence, and letters a, b, c, d, m, n, x, y, z, etc. for elements of sequences;
-
We often abbreviate a finite sequence \(\varvec{s} = (x_1, x_2, \dots , x_{|\varvec{s}|})\) as \(x_1 x_2 \dots x_{|\varvec{s}|}\), where \(|\varvec{s}|\) denotes the length (i.e., the number of elements) of \(\varvec{s}\), and write \(\varvec{s}(i)\), where \(i \in \{ 1, 2, \dots , |\varvec{s}| \}\), as another notation for \(x_i\);
-
A concatenation of sequences is represented by the juxtaposition of them, but we often write \(a \varvec{s}\), \(\varvec{t} b\), \(\varvec{u} c \varvec{v}\) for \((a) \varvec{s}\), \(\varvec{t} (b)\), \(\varvec{u} (c) \varvec{v}\), etc., and also write \(\varvec{s} . \varvec{t}\) for \(\varvec{s t}\);
-
We define \(\varvec{s}^n {\mathop {=}\limits ^{\mathrm {df. }}} \underbrace{\varvec{s} \varvec{s} \cdots \varvec{s}}_n\) for a sequence \(\varvec{s}\) and a natural number \(n \in \mathbb {N}\);
-
We write \(\mathsf {Even}(\varvec{s})\) (resp. \(\mathsf {Odd}(\varvec{s})\)) iff \(\varvec{s}\) is of even-length (resp. odd-length);
-
We define \(S^\mathsf {P} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in S \mid \mathsf {P}(\varvec{s}) \}\) for a set S of sequences and \(\mathsf {P} \in \{ \mathsf {Even}, \mathsf {Odd} \}\);
-
\(\varvec{s} \preceq \varvec{t}\) means \(\varvec{s}\) is a prefix of \(\varvec{t}\), i.e., \(\varvec{t} = \varvec{s} . \varvec{u}\) for some sequence \(\varvec{u}\), and given a set S of sequences, we define \(\mathsf {Pref}(S) {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \mid \exists \varvec{t} \in S . \ \! \varvec{s} \preceq \varvec{t} \ \! \}\);
-
For a poset P and a subset \(S \subseteq P\), \(\mathsf {Sup}(S)\) denotes the supremum of S;
-
\(X^* {\mathop {=}\limits ^{\mathrm {df. }}} \{ x_1 x_2 \ldots x_n \mid n \in \mathbb {N}, \forall i \in \{ 1, 2, \ldots , n \} . \ \! x_i \in X \ \! \}\) for each set X;
-
For a function \(f : A \rightarrow B\) and a subset \(S \subseteq A\), we define \(f \upharpoonright S : S \rightarrow B\) to be the restriction of f to S, and \(f^*: A^*\rightarrow B^*\) by \(f^*(a_1 a_2 \dots a_n) {\mathop {=}\limits ^{\mathrm {df. }}} f(a_1) f(a_2) \dots f(a_n) \in B^*\) for all \(a_1 a_2 \dots a_n \in A^*\);
-
Given sets \(X_1, X_2, \dots , X_n\), and an index \(i \in \{ 1, 2, \dots , n \}\), we write \(\pi _i\) (or \(\pi _i^{(n)}\)) for the ith projection function \(X_1 \times X_2 \times \dots \times X_n \rightarrow X_i\) that maps \((x_1, x_2, \dots , x_n) \mapsto x_i\) for all \(x_j \in X_j\) (\(j = 1, 2, \ldots , n\));
-
\(\simeq \) denote the Kleene equality, i.e., \(x \simeq y {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} (x \downarrow \wedge \ y \downarrow \wedge \ x = y) \vee (x \uparrow \wedge \ y \uparrow )\), where we write \(x \downarrow \) if an element x is defined, and \(x \uparrow \) otherwise.
2 Preliminary: games and strategies
Our games and strategies are essentially the ‘dynamic refinement’ of McCusker’s variant [6, 51],Footnote 9 which has been proposed under the name of dynamic games and strategies by the present author and Abramsky in [71] to capture dynamics (or rewriting) and intensionality (or algorithms) of computation by mathematical, particularly syntax-independent, concepts. As already explained, we have chosen this variant since, in contrast to conventional games and strategies, dynamic games and strategies capture step-by-step processes in computation, which is essential for a TMs-like model of computation.
However, we need some modifications of dynamic games and strategies. First, although disjoint union of sets of moves (for constructions on games) is usually treated informally for brevity, we need to adopt a particular formalization of ‘tags’ for the disjoint union because we are concerned with ‘effective computability’ of strategies, and thus, we must show that manipulations of ‘tags’ are all ‘effectively executable’ by strategies. In particular, we have to employ exponential ! in which different ‘rounds’ or threads are distinguished by such ‘effective tags.’
In addition, we slightly refine the original definition of dynamic games by requiring that an intermediate occurrence of an O-move in a position of a dynamic game must be a mere copy of the last occurrence of a P-move, which reflects the example of composition without hiding in the introduction. This modification is due to our computability-theoretic motivation: Intermediate occurrences of moves are ‘invisible’ to O (as in the example of composition without hiding), and therefore, P has to ‘effectively’ compute intermediate occurrences of O-moves too (though this point does not matter in [71]); note that it is clearly ‘effective’ to just copy and repeat a move. Also, it conceptually makes sense as well: Intermediate occurrences of O-moves are just copies or dummies of those of P-moves, and thus what happens in the intermediate part of each play is essentially P’s calculation only. Technically, this is achieved by introducing dummy internal O-moves (Definition 8) and strengthening the axiom DP2 (Definition 18). Let us remark, however, that this refinement is technically trivial, and it is not our main contribution.
This section presents the resulting variant of games and strategies. Fixing an implementation of ‘tags’ in Sect. 2.1 as a preparation, we recall (the slightly modified) dynamic games and strategies in Sects. 2.2 and 2.3, respectively. To make this paper essentially self-contained, we shall explain motivations and intuitions behind the definitions.
2.1 On ‘tags’ for disjoint union of sets
Let us begin with fixing ‘tags’ for disjoint union of sets that can be ‘effectively’ manipulated. We first define outer tags (Definition 3) for exponential (Definition 33), and then inner tags (Definition 5) for other constructions on games.
Definition 1
(Effective tags) An effective tag is a finite sequence over the two-element set \(\Sigma = \{ \ell , \hbar \}\), where \(\ell \) and \(\hbar \) are arbitrarily fixed elements such that \(\ell \ne \hbar \).
Definition 2
(Decoding and encoding) The decoding function \( de : \Sigma ^*\rightarrow \mathbb {N}^*\) and the encoding function \( en : \mathbb {N}^*\rightarrow \Sigma ^*\) are defined, respectively, by:
for all \(\varvec{\gamma } \in \Sigma ^*\) and \((j_1, j_2, \dots , j_l) \in \mathbb {N}^*\), where \(\varvec{\gamma } = \ell ^{i_1} \hbar \ \! \ell ^{i_2} \hbar \dots \ell ^{i_{k-1}} \hbar \ \! \ell ^{i_k}\).
Clearly, the functions \( de : \Sigma ^*\leftrightarrows \mathbb {N}^*: en \) are mutually inverses (n.b., they both map the empty sequence \(\varvec{\epsilon }\) to itself). In fact, each effective tag \(\varvec{\gamma } \in \Sigma ^*\) is intended to be a binary representation of the finite sequence \( de (\varvec{\gamma }) \in \mathbb {N}^*\) of natural numbers.
However, effective tags are not sufficient for our purpose: For nested exponentials occurring in promotion (Definition 57) and fixed-point strategies (Example 75), we need to ‘effectively’ associate a natural number to each pair of natural numbers in an ‘effectively’ invertible manner. Of course it is possible as there is a recursive bijection \(\mathbb {N} \times \mathbb {N} {\mathop {\rightarrow }\limits ^{\sim }} \mathbb {N}\) whose inverse is recursive too, which is an elementary fact in computability theory [16, 60], but we cannot rely on it for we are aiming at developing an autonomous foundation of ‘effective computability.’
On the other hand, such a bijection is necessary only for manipulating effective tags, and so we would like to avoid an involved mechanism to achieve it. Then, our solution for this problem is to simply introduce elements to denote the bijection:
Definition 3
(Outer tags) An outer tag or an extended effective tags is an expression  , where
, where  and
and  are arbitrarily fixed elements such that
are arbitrarily fixed elements such that  and
and  , generated by the grammar \(\varvec{e} {\mathop {\equiv }\limits ^{\mathrm {df. }}} \varvec{\gamma } \mid \varvec{e}_1 \hbar \ \! \varvec{e}_2 \mid \)
, generated by the grammar \(\varvec{e} {\mathop {\equiv }\limits ^{\mathrm {df. }}} \varvec{\gamma } \mid \varvec{e}_1 \hbar \ \! \varvec{e}_2 \mid \)
 , where \(\varvec{\gamma }\) ranges over effective tags.
, where \(\varvec{\gamma }\) ranges over effective tags.
Notation
Let \(\mathcal {T}\) denote the set of all outer tags.
Definition 4
(Extended decoding) The extended decoding function \( ede : \mathcal {T} \rightarrow \mathbb {N}^*\) is recursively defined by:

where \(\wp : \mathbb {N}^*{\mathop {\rightarrow }\limits ^{\sim }} \mathbb {N}\) is any recursive bijection fixed throughout the present paper such that \(\wp (i_1, i_2, \dots , i_k) \ne \wp ( j_1, j_2, \dots , j_l)\) whenever \(k \ne l\) (see, e.g., [16]).
Of course, we lose the bijectivity between \(\Sigma ^*\) and \(\mathbb {N}^*\) for outer tags (e.g., if  , then \( ede (\ell ^{i}) = (i)\), but
, then \( ede (\ell ^{i}) = (i)\), but  ), but in return, we may ‘effectively execute’ the bijection \(\wp : \mathbb {N}^*{\mathop {\rightarrow }\limits ^{\sim }} \mathbb {N}\) by just inserting the elements
), but in return, we may ‘effectively execute’ the bijection \(\wp : \mathbb {N}^*{\mathop {\rightarrow }\limits ^{\sim }} \mathbb {N}\) by just inserting the elements  and
and  .Footnote 10 We shall utilize outer tags for exponential !; see Definition 33.
.Footnote 10 We shall utilize outer tags for exponential !; see Definition 33.
On the other hand, for ‘tags’ on moves for other constructions on games, i.e., \((\_)^{[i]}\) in the introduction, let us employ just four distinguished elements:
Definition 5
(Inner tags) Let \(\mathscr {W}\), \(\mathscr {E}\), \(\mathscr {N}\) and \(\mathscr {S}\) be arbitrarily fixed, pairwise distinct elements. A finite sequence \(\varvec{s} \in \{ \mathscr {W}, \mathscr {E}, \mathscr {N}, \mathscr {S} \}^*\) is called an inner tag.
We shall focus on games whose moves are all tagged elements:
Definition 6
(Inner elements) An inner element is a finitely nested pair \(( \dots ((m, t_1), t_2), \dots , t_k)\), usually written \(m_{t_1 t_2 \dots t_k}\), such that m is a distinguished element, called the substance of \(m_{t_1 t_2 \dots t_k}\), and \(t_1 t_2 \dots t_k\) is an inner tag.
Definition 7
(Tagged elements) A tagged element is any pair \((m_{t_1 t_2 \dots t_k}, \varvec{e})\), usually written \([m_{t_1 t_2 \dots t_k}]_{\varvec{e}}\), of an inner element \(m_{t_1 t_2 \dots t_k}\) and an outer tag \(\varvec{e} \in \mathcal {T}\).
Convention
We often abbreviate an inner element \(m_{t_1 t_2 \dots t_k}\) as m if the inner tag \(t_1 t_2 \dots t_k\) is not very important.
2.2 Games
As already stated, our games are (slightly modified) dynamic games introduced in [71]. The main idea of dynamic games is to introduce, in McCusker’s games [6, 51], a distinction between internal and external moves, where internal moves constitute internal communication between strategies (i.e., moves with square boxes in the introduction), and they are to be a posteriori hidden by the hiding operation, in order to capture intensionality and dynamics of computation by internal moves and the hiding operation, respectively. Conceptually, internal moves are ‘invisible’ to O as they represent how P ‘internally’ calculates the next external P-move (i.e., step-by-step processes in computation). In addition, unlike [71], we restrict internal O-moves to dummies of internal P-moves (Definition 8) for the computability-theoretic motivation already mentioned at the beginning of Sect. 2.
We first review (the slightly modified) dynamic games in the present section; see [71] for the details, and [3, 6, 37] for a general introduction to game semantics.
Convention
To distinguish our ‘dynamic concepts’ from conventional ones [6, 51], we add the word static in front of the latter, e.g., static arenas, static games, etc.
2.2.1 Arenas and legal positions
Similarly to McCusker’s games, dynamic games are based on two preliminary concepts: (dynamic) arenas and legal positions. An arena defines the basic components of a game, which in turn induces its legal positions that specify the basic rules of the game. Let us begin with recalling these two concepts.
Definition 8
(Dynamic arenas [71]) A dynamic arena is a quadruple \(G = (M_G, \lambda _G, \vdash _G, \Delta _G)\), where:
-
\(M_G\) is a set of tagged elements, called moves, such that: (M) the set \(\pi _1(M_G)\) of all inner elements of G is finite;
-
\(\lambda _G\) is a function \(M_G \rightarrow \{ \mathsf {O}, \mathsf {P} \} \times \{ \mathsf {Q}, \mathsf {A} \} \times \mathbb {N}\), called the labeling function, where \(\mathsf {O}\), \(\mathsf {P}\), \(\mathsf {Q}\) and \(\mathsf {A}\) are arbitrarily fixed, pairwise distinct symbols, called the labels, that satisfies: (L) \(\mu (G) {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Sup}(\{ \lambda _G^{\mathbb {N}}(m) \mid m \in M_G \ \! \}) \in \mathbb {N}\);
-
\(\vdash _G\) is a subset of \((\{ \star \} \cup M_G) \times M_G\), where \(\star \) is an arbitrarily fixed symbol such that \(\star \not \in M_G\), called the enabling relation, that satisfies:
-
(E1) If \(\star \vdash _G m\), then \(\lambda _G(m) = (\mathsf {O}, \mathsf {Q}, 0)\), and \(n = \star \) whenever \(n \vdash _G m\);
-
(E2) If \(m \vdash _G n\) and \(\lambda _G^{\mathsf {QA}}(n) = \mathsf {A}\), then \(\lambda _G^{\mathsf {QA}}(m) = \mathsf {Q}\) and \(\lambda _G^{\mathbb {N}}(m) = \lambda _G^{\mathbb {N}}(n)\);
-
(E3) If \(m \vdash _G n\) and \(m \ne \star \), then \(\lambda _G^{\mathsf {OP}}(m) \ne \lambda _G^{\mathsf {OP}}(n)\);
-
(E4) If \(m \vdash _G n\), \(m \ne \star \) and \(\lambda _G^{\mathbb {N}}(m) \ne \lambda _G^{\mathbb {N}}(n)\), then \(\lambda _G^{\mathsf {OP}}(m) = \mathsf {O}\);
-
-
\(\Delta _G\) is a bijection \(M_G^{\mathsf {PInt}} {\mathop {\rightarrow }\limits ^{\sim }} M_G^{\mathsf {OInt}}\), called the dummy function, that satisfies: (D) there exists some finite partial function \(\delta _G\) on inner tags such that if \([m_{\varvec{t}}]_{\varvec{e}} \in M_G^{\mathsf {PInt}}\), \([n_{\varvec{u}}]_{\varvec{f}} \in M_G^{\mathsf {OInt}}\) and \(\Delta _G([m_{\varvec{t}}]_{\varvec{e}}) = [n_{\varvec{u}}]_{\varvec{f}}\), then \(m = n\), \(\varvec{e} = \varvec{f}\), \(\lambda _G^{\mathsf {QA}}([m_{\varvec{t}}]_{\varvec{e}}) = \lambda _G^{\mathsf {QA}}([n_{\varvec{u}}]_{\varvec{f}})\), \(\lambda _G^{\mathbb {N}}([m_{\varvec{t}}]_{\varvec{e}}) = \lambda _G^{\mathbb {N}}([n_{\varvec{u}}]_{\varvec{f}})\) and \(\varvec{u} = \delta _G(\varvec{t})\)
in which \(\lambda _G^{\mathsf {OP}} {\mathop {=}\limits ^{\mathrm {df. }}} \pi _1 \circ \lambda _G : M_G \rightarrow \{ \mathsf {O}, \mathsf {P} \}\), \(\lambda _G^{\mathsf {QA}} {\mathop {=}\limits ^{\mathrm {df. }}} \pi _2 \circ \lambda _G : M_G \rightarrow \{ \mathsf {Q}, \mathsf {A} \}\), \(\lambda _G^{\mathbb {N}} {\mathop {=}\limits ^{\mathrm {df. }}} \pi _3 \circ \lambda _G : M_G \rightarrow \mathbb {N}\), \(M_G^{\mathsf {PInt}} {\mathop {=}\limits ^{\mathrm {df. }}} \langle \lambda _G^{\mathsf {OP}}, \lambda _G^{\mathbb {N}} \rangle ^{-1}(\{ (\mathsf {P}, d) \mid d \geqslant 1 \ \! \})\) and \(M_G^{\mathsf {OInt}} {\mathop {=}\limits ^{\mathrm {df. }}} \langle \lambda _G^{\mathsf {OP}}, \lambda _G^{\mathbb {N}} \rangle ^{-1}(\{ (\mathsf {O}, d) \mid d \geqslant 1 \ \! \})\). A move \(m \in M_G\) is initial if \(\star \vdash _G m\), an O-move (resp. a P-move) if \(\lambda _G^{\mathsf {OP}}(m) = \mathsf {O}\) (resp. if \(\lambda _G^{\mathsf {OP}}(m) = \mathsf {P}\)), a question (resp. an answer) if \(\lambda _G^{\mathsf {QA}}(m) = \mathsf {Q}\) (resp. if \(\lambda _G^{\mathsf {QA}}(m) = \mathsf {A}\)), and internal or \(\varvec{\lambda _{{\varvec{G}}}^{\mathbb {N}}({{\varvec{m}}})}\)-internal (resp. external) if \(\lambda _G^{\mathbb {N}}(m) > 0\) (resp. if \(\lambda _G^{\mathbb {N}}(m) = 0\)). A finite sequence \(\varvec{s} \in M_G^*\) of moves is \({{{\varvec{d}}}}\)-complete if it ends with a move m such that \(\lambda _G^{\mathbb {N}}(m) = 0 \vee \lambda _G^{\mathbb {N}}(m) > d\), where \(d \in \mathbb {N} \cup \{ \omega \}\), and \(\omega \) is the least transfinite ordinal. For each \(m \in M_G^{\mathsf {PInt}}\), \(\Delta _G(m) \in M_G^{\mathsf {OInt}}\) is the dummy of m.
Notation
We write \(M_G^{\mathsf {Init}}\) (resp. \(M_G^{\mathsf {Int}}\), \(M_G^{\mathsf {Ext}}\)) for the set of all initial (resp. internal, external) moves of a dynamic arena G.
A dynamic arena is a static arena defined in [6], equipped with another labeling \(\lambda _G^{\mathbb {N}}\) on moves and dummies of internal P-moves, satisfying additional axioms about them. From the opposite angle, dynamic arenas are a generalization of static arenas: A static arena is equivalent to a dynamic arena whose moves are all external.
Recall that a static arena A determines possible moves of a game, each of which is O’s/P’s question/answer, and specifies which move n can be performed for each move m by the relation \(m \vdash _A n\) (and \(\star \vdash _A m\) means that m can initiate a play). Its axioms are E1, E2 and E3 (excluding the conditions on \(\lambda _A^{\mathbb {N}}\)):
-
E1 sets the convention that an initial move must be O’s question, and an initial move cannot be performed for a previous move;
-
E2 states that an answer must be performed for a question;
-
E3 mentions that an O-move must be performed for a P-move, and vice versa.
Then, as an additional structure for dynamic arenas G, the work [71] employs all natural numbers for \(\lambda _G^{\mathbb {N}}\), not only the internal/external (I/E)-parity, to define a step-by-step execution of the hiding operation \(\mathcal {H}\): The operation \(\mathcal {H}\) deletes all internal moves m such that \(\lambda _G^{\mathbb {N}}(m)\), called the priority order of m (since it indicates the priority order of m with respect to the execution of \(\mathcal {H}\)), is 1 and decreases the priority orders of the remaining internal moves by 1.Footnote 11
In addition, unlike [71], we have introduced the additional structure of dummy functions for the computability-theoretic motivation mentioned at the beginning of Sect. 2. The idea is that each internal O-move \(m \in M_G^{\mathsf {OInt}}\) of a dynamic game G must be the dummy of a unique internal P-move \(m' \in M_G^{\mathsf {PInt}}\), i.e., \(m = \Delta _G(m')\), and m may occur in a position only right after an occurrence of \(m'\), which axiomatizes the phenomenon of intermediate occurrences of moves in the composition of \( succ \) and \( double \) without hiding described in the introduction. We shall formalize this restriction on occurrences of internal O-moves by the axiom DP2 in Definition 18.
Note that the additional axioms for dynamic areas are intuitively natural:
-
M requires the set \(\pi _1 (M_G)\) to be finite so that each move is distinguishable, which is not required in [71] yet necessary to define ‘effectivity’ in the present work;
-
L requires the least upper bound \(\mu (G)\) to be finite as it is conceptually natural and technically necessary for concatenation \(\ddagger \) of games (Definition 36);
-
E1 adds \(\lambda _G^{\mathbb {N}}(m) = 0\) for all \(m \in M_G^{\mathsf {Init}}\) as O cannot ‘see’ internal moves, and thus, he cannot initiate a play with an internal move;
-
E2 additionally requires the priority orders between a ‘QA pair’ to be the same since otherwise an output of the hiding operation may not be well defined;
-
E4 states that only P can perform a move for a previous move if they have different priority orders because internal moves are ‘invisible’ to O (as we shall see, if \(\lambda _G^{\mathbb {N}}(m_1) = k_1 < k_2 = \lambda _G^{\mathbb {N}}(m_2)\), then after the \(k_1\)-many iteration of the hiding operation, \(m_1\) and \(m_2\) become external and internal, respectively, i.e., the I/E-parity of moves is relative, which is why E4 is not only concerned with I/E-parity but more fine-grained priority orders);
-
D requires that each internal P-move \(p \in M_G^{\mathsf {PInt}}\) and its dummy \(\Delta _G(p) \in M_G^{\mathsf {OInt}}\) may differ only in their inner tags since the latter is the dummy of the former (n.b., it reflects the informal example in the introduction), and \(\Delta _G(p)\) is ‘effectively’ obtainable from p by a finitary calculation \(\delta _G\) on inner tags.
Convention
From now on, arenas refer to dynamic arenas by default.
As explained previously, an interaction between P and O in a game is represented by a finite sequence of moves that satisfies certain axioms (under the name of (valid) positions; see Definition 18). Strictly speaking, however, we equip such sequences with an additional structure, called justifiers or pointers, to distinguish similar yet different computational processes (see, e.g., [6] for this point):
Definition 9
(Occurrences of moves) Given a finite sequence \(\varvec{s} \in M_G^*\) of moves of an arena G, an occurrence (of a move) in \(\varvec{s}\) is a pair \((\varvec{s}(i), i)\) such that \(i \in \{ 1, 2, \dots , |\varvec{s}| \}\). More specifically, we call the pair \((\varvec{s}(i), i)\) an initial occurrence (resp. a non-initial occurrence) in \(\varvec{s}\) if \(\star \vdash _G \varvec{s}(i)\) (resp. otherwise).
Remark
We have been so far casual about the distinction between moves and occurrences, but we shall be more precise from now on.
Definition 10
(J-sequences [6, 38]) A justified (j-) sequence of an arena G is a pair \(\varvec{s} = (\varvec{s}, \mathcal {J}_{\varvec{s}})\) of a finite sequence \(\varvec{s} \in M_G^*\) and a map \(\mathcal {J}_{\varvec{s}} : \{ 1, 2, \dots , |\varvec{s}| \} \rightarrow \{ 0, 1, 2, \dots , |\varvec{s}| \}\) such that for all \(i \in \{ 1, 2, \dots , |\varvec{s}| \}\) \(\mathcal {J}_{\varvec{s}}(i) = 0\) if \(\star \vdash _G \varvec{s}(i)\), and \(0< \mathcal {J}_{\varvec{s}}(i) < i \wedge \varvec{s}({\mathcal {J}_{\varvec{s}}(i)}) \vdash _G \varvec{s}(i)\) otherwise. The justifier of each non-initial occurrence \((\varvec{s}(i), i)\) in \(\varvec{s}\) is the occurrence \((\varvec{s}({\mathcal {J}_{\varvec{s}}(i)}), \mathcal {J}_{\varvec{s}}(i))\) in \(\varvec{s}\). We say that \((\varvec{s}(i), i)\) is justified by \((\varvec{s}({\mathcal {J}_{\varvec{s}}(i)}), \mathcal {J}_{\varvec{s}}(i))\), or there is a (necessarily unique) pointer from the former to the latter.
Notation
We write \(\mathscr {J}_G\) for the set of all j-sequences of an arena G.
Convention
By abuse of notation, we usually keep the pointer structure \(\mathcal {J}_{\varvec{s}}\) of each j-sequence \(\varvec{s} = (\varvec{s}, \mathcal {J}_{\varvec{s}})\) implicit and often abbreviate occurrences \((\varvec{s}(i), i)\) in \(\varvec{s}\) as \(\varvec{s}(i)\). Thus, \(\varvec{s} = \varvec{t} \in \mathscr {J}_G\) means \(\varvec{s} = \varvec{t}\) and \(\mathcal {J}_{\varvec{s}} = \mathcal {J}_{\varvec{t}}\). Moreover, we usually write \(\mathcal {J}_{\varvec{s}}(\varvec{s}(i)) = \varvec{s}(j)\) for \(\mathcal {J}_{\varvec{s}}(i) = j\). This convention is mathematically imprecise, but it is very convenient in practice, and it does not bring any serious confusion (in fact, it has been standard in the literature of game semantics).
The idea is that each non-initial occurrence in a j-sequence must be performed for a specific previous occurrence, viz. its justifier. Since the present paper is not concerned with a faithful interpretation of programs, one may wonder if justifiers would play any important role in the rest of the paper; however, they do in a novel manner: They allow P to ‘effectively’ collect, from the history of previous occurrences, a bounded number of necessary ones, as we shall see in Sect. 3.1.
Note that the first element m of each non-empty j-sequence \(m \varvec{s} \in \mathscr {J}_G\) must be initial; we particularly call m the opening occurrence of \(m \varvec{s}\). Clearly, an opening occurrence must be an initial occurrence, but not necessarily vice versa.
Let us now consider justifiers, j-sequences and arenas from the ‘external viewpoint’ (Definitions 12, 13 and 14):
Definition 11
(J-subsequences [71]) Given an arena G and a j-sequence \(\varvec{s} \in \mathscr {J}_G\), a j-subsequence of \(\varvec{s}\) is a j-sequence \(\varvec{t} \in \mathscr {J}_G\) such that \(\varvec{t}\) is a subsequence of \(\varvec{s}\), and \(\mathcal {J}_{\varvec{t}}(n) = m\) iff there are occurrences \(m_1, m_2, \dots , m_k\) (\(k \in \mathbb {N}\)) in \(\varvec{s}\) eliminated in \(\varvec{t}\) such that \(\mathcal {J}_{\varvec{s}}(n) = m_1 \wedge \mathcal {J}_{\varvec{s}}(m_1) = m_2 \dots \wedge \mathcal {J}_{\varvec{s}}(m_{k-1}) = m_k \wedge \mathcal {J}_{\varvec{s}}(m_{k}) = m\).
Definition 12
(External justifiers [71]) Let G be an arena, \(\varvec{s} \in \mathscr {J}_G\) and \(d \in \mathbb {N} \cup \{ \omega \}\). Each non-initial occurrence n in \(\varvec{s}\) has a unique sequence of justifiers \(m m_k \dots m_2 m_1 n\) \((k \in \mathbb {N})\) such that \(\mathcal {J}_{\varvec{s}}(n) = m_1\), \(\mathcal {J}_{\varvec{s}}(m_1) = m_{2}\), ..., \(\mathcal {J}_{\varvec{s}}(m_{k-1}) = m_k\), \(\mathcal {J}_{\varvec{s}}(m_k) = m\), \(\lambda _G^{\mathbb {N}}(m) = 0 \vee \lambda _G^{\mathbb {N}}(m) > d\) and \(0 < \lambda _G^{\mathbb {N}}(m_i) \leqslant d\) for \(i = 1, 2, \dots , k\). The occurrence m is called the \({{{\varvec{d}}}}\)-external justifier of n in \(\varvec{s}\), and written \(\mathcal {J}_{\varvec{s}}^{\circleddash d}(n)\).
Note that d-external justifiers are a simple generalization of justifiers: 0-external justifiers coincide with justifiers. d-external justifiers are intended to be justifiers after the d-times iteration of the hiding operation \(\mathcal {H}\), as we shall see shortly.
Definition 13
(External j-subsequences [71]) Given an arena G, \(\varvec{s} \in \mathscr {J}_G\) and \(d \in \mathbb {N} \cup \{ \omega \}\), the \({{{\varvec{d}}}}\)-external justified (j-) subsequence \(\mathcal {H}^d_G(\varvec{s})\) of \(\varvec{s}\) is obtained from \(\varvec{s}\) by deleting occurrences of internal moves m such that \(0 < \lambda _G^{\mathbb {N}}(m) \leqslant d\) and equipping the resulting subsequence of \(\varvec{s}\) with pointers \(\mathscr {J}_{\mathcal {H}_G^d(\varvec{s})} : n \mapsto \mathscr {J}_{\varvec{s}}^{\circleddash d}(n)\).
Remark
It should be clear how to reformulate Definitions 11, 12 and 13 more formally, following Definitions 9 and 10.
Definition 14
(External arenas [71]) Let G be an arena, and assume \(d \in \mathbb {N} \cup \{ \omega \}\). The \({{{\varvec{d}}}}\)-external arena \(\mathcal {H}^d(G)\) of G is defined by:
-
\(M_{\mathcal {H}^d(G)} {\mathop {=}\limits ^{\mathrm {df. }}} \{ m \in M_G \mid \lambda _G^{\mathbb {N}}(m) = 0 \vee \lambda _G^{\mathbb {N}}(m) > d \ \! \}\);
-
\(\lambda _{\mathcal {H}^d(G)} {\mathop {=}\limits ^{\mathrm {df. }}} \lambda _G^{\circleddash d} \upharpoonright M_{\mathcal {H}^d(G)}\), where \(\lambda _G^{\circleddash d} {\mathop {=}\limits ^{\mathrm {df. }}} \langle \lambda _G^{\mathsf {OP}}, \lambda _G^{\mathsf {QA}}, m \mapsto \lambda _G^{\mathbb {N}} (m) \circleddash d \rangle \) and \(n \circleddash d {\mathop {=}\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} n - d &{}\text {if }n \geqslant d; \\ 0 &{}\text {otherwise} \end{array}\right. }\) for all \(n \in \mathbb {N}\);
-
\(m \vdash _{\mathcal {H}^d(G)} \! n {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} \exists k \in \mathbb {N}, m_1, m_2, \dots , m_{2k-1}, m_{2k} \in M_G {\setminus } M_{\mathcal {H}^d(G)} . \ \! m \vdash _G m_1 \wedge m_1 \vdash _G m_2 \dots \wedge m_{2k-1} \vdash _G m_{2k} \wedge m_{2k} \vdash _G n\) (\(\Leftrightarrow m \vdash _G n\) if \(k = 0\));
-
\(\Delta _{\mathcal {H}^d(G)} {\mathop {=}\limits ^{\mathrm {df. }}} \Delta _G \upharpoonright M_{\mathcal {H}^d(G)}\).
That is, \(\mathcal {H}^d(G)\) is obtained from G by deleting internal moves m such that \(0 < \lambda _G^{\mathbb {N}}(m) \leqslant d\), decreasing by d the priority orders of the remaining internal moves, ‘concatenating’ the enabling relation to form the ‘d-external’ one and taking the obvious restrictions of the labeling and the dummy functions.
Convention
Given \(d \in \mathbb {N} \cup \{ \omega \}\), we regard \(\mathcal {H}^d\) as an operation on arenas G, called the \({{{\varvec{d}}}}\)-hiding operation (on arenas), and \(\mathcal {H}_G^d\) as an operation on j-sequences of G, called the \({{{\varvec{d}}}}\)-hiding operation (on j-sequences).
Lemma 15
(Closure of arenas and j-sequences under hiding [71]) If G is an arena, then, for all \(d \in \mathbb {N} \cup \{ \omega \}\), so is \(\mathcal {H}^d(G)\), and \(\mathcal {H}_G^d(\varvec{s}) \in \mathscr {J}_{\mathcal {H}^d(G)}\) for all \(\varvec{s} \in \mathscr {J}_G\). Also, \(\underbrace{\mathcal {H}^1 \circ \mathcal {H}^1 \cdots \circ \mathcal {H}^1}_i(G) = \mathcal {H}^i (G)\) and \(\mathcal {H}^1_{\mathcal {H}^{i-1}(G)} \circ \mathcal {H}^1_{\mathcal {H}^{i-2}(G)} \cdots \circ \mathcal {H}^1_{\mathcal {H}^{1}(G)} \circ \mathcal {H}^1_{G}(\varvec{s}) = \mathcal {H}_G^i(\varvec{s})\) for any \(i \in \mathbb {N}\) (it means \(G = G\) and \(\varvec{s} = \varvec{s}\) if \(i = 0\)), arena G and \(\varvec{s} \in \mathscr {J}_G\).
Proof
We need to consider the additional structure of dummy functions; everything else has been proved in [71]. Let G be an arena, and \(d \in \mathbb {N} \cup \{ \omega \}\). For each \(p \in M_G^{\mathsf {PInt}}\), we clearly have \(p \in M_{\mathcal {H}^d(G)} \Leftrightarrow \Delta _G(p) \in M_{\mathcal {H}^d(G)}\) by the axiom D on \(\Delta _G\); thus, \(\Delta _{\mathcal {H}^d(G)}\) is a well-defined bijection \(M_{\mathcal {H}^d(G)}^{\mathsf {PInt}} {\mathop {\rightarrow }\limits ^{\sim }} M_{\mathcal {H}^d(G)}^{\mathsf {OInt}}\). Finally, the axiom D on \(\Delta _{\mathcal {H}^d(G)}\) clearly follows from that on \(\Delta _G\), completing the proof. \(\square \)
Convention
Thanks to Lemma 15, we henceforth regard the i-hiding operations \(\mathcal {H}^i\) and \(\mathcal {H}^i_G\) as the i-times iteration of the 1-hiding operations \(\mathcal {H}^1\) and \(\mathcal {H}^1_G\), respectively, for all \(i \in \mathbb {N}\). For this reason, we write \(\mathcal {H}\) and \(\mathcal {H}_G\) for \(\mathcal {H}^1\) and \(\mathcal {H}^1_G\), respectively, and call them the hiding operations (on arenas and j-sequences, respectively).
Next, let us recall the notion of ‘relevant part’ of previous moves, called views:
Definition 16
(Views [6, 38]) Given a j-sequence \(\varvec{s}\) of an arena G, the Player (P-) view \(\lceil \varvec{s} \rceil _G\) and the Opponent (O-) view \(\lfloor \varvec{s} \rfloor _G\) (we often omit the subscript G) are given by the following induction on \(|\varvec{s}|\):
-
\(\lceil \varvec{\epsilon } \rceil _G {\mathop {=}\limits ^{\mathrm {df. }}} \varvec{\epsilon }\);
-
\(\lceil \varvec{s} m \rceil _G {\mathop {=}\limits ^{\mathrm {df. }}} \lceil \varvec{s} \rceil _G . m\) if m is a P-move;
-
\(\lceil \varvec{s} m \rceil _G {\mathop {=}\limits ^{\mathrm {df. }}} m\) if m is initial;
-
\(\lceil \varvec{s} m \varvec{t} n \rceil _G {\mathop {=}\limits ^{\mathrm {df. }}} \lceil \varvec{s} \rceil _G . m n\) if n is an O-move with \(\mathcal {J}_{\varvec{s} m \varvec{t} n}(n) = m\);
-
\(\lfloor \varvec{\epsilon } \rfloor _G {\mathop {=}\limits ^{\mathrm {df. }}} \varvec{\epsilon }\);
-
\(\lfloor \varvec{s} m \rfloor _G {\mathop {=}\limits ^{\mathrm {df. }}} \lfloor \varvec{s} \rfloor _G . m\) if m is an O-move;
-
\(\lfloor \varvec{s} m \varvec{t} n \rfloor _G {\mathop {=}\limits ^{\mathrm {df. }}} \lfloor \varvec{s} \rfloor _G . m n\) if n is a P-move with \(\mathcal {J}_{\varvec{s} m \varvec{t} n}(n) = m\)
where the justifiers of the remaining non-initial occurrences in \(\lceil \varvec{s} \rceil \) (resp. \(\lfloor \varvec{s} \rfloor \)) are unchanged if they occur in \(\lceil \varvec{s} \rceil \) (resp. \(\lfloor \varvec{s} \rfloor \)), and undefined otherwise. A view is a P- or O-view.
The idea behind Definition 16 is as follows. For a j-sequence \(\varvec{t}m\) of an arena G such that m is a P-move (resp. an O-move), the P-view \(\lceil \varvec{t} \rceil \) (resp. the O-view \(\lfloor \varvec{t} \rfloor \)) is intended to be the currently ‘relevant part’ of \(\varvec{t}\) for P (resp. O). That is, P (resp. O) is concerned only with the last O-move (resp. P-move), its justifier and that justifier’s P-view (resp. O-view), which then recursively proceeds.
As explained in [6], strategies (Definition 42) that model computation without state refer only to P-views, not entire histories of previous occurrences, as inputs; they are called innocent strategies (Definition 46). In this sense, innocence captures state-freeness of strategies. In this paper, however, P-views play a different yet fundamental role for our notion of ‘effective computability’ in Sect. 3.1.
We are now ready to define:
Definition 17
(Dynamic legal positions [71]) A dynamic legal position of an arena G is a j-sequence \(\varvec{s} \in \mathscr {J}_G\) that satisfies:
-
(Alternation) If \(\varvec{s} = \varvec{t} m n \varvec{u}\), then \(\lambda _G^\mathsf {OP} (m) \ne \lambda _G^\mathsf {OP} (n)\);
-
(Generalized visibility) If \(\varvec{s} = \varvec{v} m \varvec{w}\) with m non-initial, and \(d \in \mathbb {N} \cup \{ \omega \}\) satisfy \(\lambda _G^{\mathbb {N}}(m) = 0 \vee \lambda _G^{\mathbb {N}}(m) > d\), then \(\mathcal {J}^{\circleddash d}_{\varvec{s}}(m)\) occurs in \(\lceil \mathcal {H}_G^d(\varvec{v}) \rceil _{\mathcal {H}^d(G)}\) if m is a P-move, and it occurs in \(\lfloor \mathcal {H}_G^d(\varvec{v}) \rfloor _{\mathcal {H}^d(G)}\) if m is an O-move;
-
(IE-switch) If \(\varvec{s} = \varvec{t} m n \varvec{u}\) with \(\lambda _G^{\mathbb {N}}(m) \ne \lambda _G^{\mathbb {N}}(n)\), then m is an O-move.
Notation
We write \(\mathscr {L}_G\) for the set of all dynamic legal positions of an arena G.
Recall that a static legal position defined in [6] is a j-sequence that satisfies alternation and visibility, i.e., generalized visibility only for \(d = 0\) [6, 38, 51], which is technically to guarantee that the P- and the O-views of a j-sequence are again j-sequences and conceptually to ensure that the justifier of each non-initial occurrence belongs to the ‘relevant part’ of the history of previous occurrences.
Static legal positions specify the basic rules of a static game: Every (valid) position of the game must be a static legal position of the underlying arena [6]:
-
In a position of the game, O always performs the first move by a question, and then P and O alternately play (by alternation), in which every non-initial occurrence is performed for a specific previous occurrence (by justification);
-
The justifier of each non-initial occurrence in a position belongs to the ‘relevant part’ of the previous occurrences in the position (by visibility).
Similarly, dynamic legal positions are to specify the basic rules of a dynamic game (Definition 18). They are static legal positions that satisfy additional axioms:
-
Generalized visibility is a generalization of visibility; it requires that visibility holds after any iteration of the hiding operations on arenas and j-sequences;
-
IE-switch states that only P can change a priority order during a play because internal moves are ‘invisible’ to O, where the same remark as in E4 is applied for its finer distinction of priority orders than the I/E-parity.
Note that a dynamic legal position in which no internal move occurs is equivalent to a static legal position.
Convention
Legal positions henceforth mean dynamic legal positions.
2.2.2 Games
We are now ready to recall dynamic games:
Definition 18
(Dynamic games [71]) A dynamic game is a quintuple \(G = (M_G, \lambda _G, \vdash _G, \Delta _G, P_G)\) such that the quadruple \((M_G, \lambda _G, \vdash _G, \Delta _G)\) is an arena, and \(P_G\) is a subset of \(\mathscr {L}_G\) whose elements are called (valid) positions of G that satisfies:
-
(P1) \(P_G\) is non-empty and prefix-closed (i.e., \(\varvec{s}m \in P_G \Rightarrow \varvec{s} \in P_G\));
-
(DP2) If \(\varvec{s} = \varvec{t} . p . o' . \varvec{u} . p' . o\) (resp. \(\varvec{s} = \varvec{t} . o' . \varvec{u} . p' . o\)), where o is an internal O-move, and \(o'\) is an internal (resp. external) O-move such that \(o' = \mathcal {J}_{\varvec{s}}(p')\), then \(o = \Delta _G(p')\) and \(\mathcal {J}_{\varvec{s}}(o) = p\) (resp. \(\mathcal {J}_{\varvec{s}}(o) = p'\)).
A play of G is a (finitely or infinitely) increasing (with respect to \(\preceq \)) sequence \((\varvec{\epsilon }, m_1, m_1m_2, \dots )\) of positions of G.
Remark
In [71], each dynamic game G is equipped with an equivalence relation \(\simeq _G\) on its positions in order to ignore permutations of ‘tags’ for exponential ! as in [7] and Section 3.6 of [51]. Naturally, dynamic strategies \(\sigma : G\) are identified up to \(\simeq _G\), i.e., the equivalence class \([\sigma ]\) of \(\sigma \) with respect to \(\simeq _G\) is a morphism in the bicategory of dynamic games and strategies [71], which matches the syntactic equality on terms. However, our notion of ‘effective computability’ or viability (Definition 70) is defined on dynamic strategies, not their equivalence classes, and our focus is not a fully complete interpretation of a programming language; thus, we do not have to take such equivalence classes at all. Hence, for simplicity, we exclude such equivalence relations on positions from the structure of dynamic games in the present paper.
Of course, we may easily adopt the full definition of dynamic games G (i.e., with \(\simeq _G\)) and equivalence classes \([\sigma ]\) of dynamic strategies \(\sigma : G\) as in [71]: We may simply define \([\sigma ]\) to be viable if there is some viable representative \(\tau \in [\sigma ]\).
Thus, dynamic games are static games defined in [6, 51] except that their arenas are dynamic ones and they additionally satisfy the axiom DP2. The axiom P1 talks about the natural phenomenon that each non-empty position or ‘moment’ of a play must have the previous ‘moment.’ In addition, by the axiom DP2 for dynamic games, internal O-moves must be performed as dummies of the last internal P-moves, where the pointers specified by the axiom would make sense if one considers the example of composition of \( succ \) and \( double \) without hiding in the introduction. Conceptually, we impose the axiom for O cannot ‘see’ internal moves, and thus the internal part of each play must be essentially P’s calculation only; technically, it is to ensure external consistency of dynamic strategies: Dynamic strategies act always in the same way from the viewpoint of O, i.e., the external part of each play by a dynamic strategy does not depend on the internal part (see [71] for the details).
Remark
The axiom DP2 defined in [71] just requires determinacy of internal O-moves in each play (it is similar to determinacy of P-moves for strategies), which works for the purpose of the work. However, in the present paper, we are concerned with ‘effective computability’ of strategies, and thus in particular computation of internal O-moves by P must be ‘effective’ (since O cannot compute them). For this point, we have strengthened the axiom DP2 as above so that computation of internal O-moves becomes trivial.
Convention
Henceforth, games refer to dynamic games by default.
Definition 19
(Subgames [71]) A subgame of a game G is a game H that satisfies \(M_H \subseteq M_G\), \(\lambda _H = \lambda _G \upharpoonright M_H\), \(\vdash _H \ \subseteq \ \vdash _G \cap \ (\{ \star \} \cup M_H) \times M_H\), \(\Delta _H = \Delta _G \upharpoonright M_H\), \(P_H \subseteq P_G\) and \(\mu (H) = \mu (G)\). In this case, we write  .
.
Example 20
The terminal game T is defined by \(T {\mathop {=}\limits ^{\mathrm {df. }}} (\emptyset , \emptyset , \emptyset , \emptyset , \{ \varvec{\epsilon } \})\). Note that T is the simplest game as its position is only the empty sequence \(\varvec{\epsilon }\).
Example 21
The boolean game \(\varvec{2}\) is defined by:
-
\(M_{\varvec{2}} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [\hat{q}], [ tt ], [ ff ] \}\);
-
\(\lambda _{\varvec{2}} : [\hat{q}] \mapsto (\mathsf {O}, \mathsf {Q}, 0), [ tt ] \mapsto (\mathsf {P}, \mathsf {A}, 0), [ ff ] \mapsto (\mathsf {P}, \mathsf {A}, 0)\);
-
\(\vdash _{\varvec{2}} {\mathop {=}\limits ^{\mathrm {df. }}} \{ (\star , [\hat{q}]), ([\hat{q}], [ tt ]), ([\hat{q}], [ ff ]) \}\);
-
\(\Delta _{\varvec{2}} {\mathop {=}\limits ^{\mathrm {df. }}} \emptyset \);
-
\(P_{\varvec{2}} {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Pref}(\{ [\hat{q}] [ tt ], [\hat{q}] [ ff ] \})\), where \([ tt ]\) and \([ ff ]\) are both justified by \([\hat{q}]\).
There are just two maximal positions of \(\varvec{2}\): \([\hat{q}] [ tt ]\) and \([\hat{q}] [ ff ]\), where each answer (i.e., \([ tt ]\) or \([ ff ]\)) is performed for the initial question \([\hat{q}]\). The former (resp. the latter) is to represent the truth value true (resp. false).
Example 22
The natural number game N is defined by:
-
\(M_{N} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [\hat{q}] \} \cup \{ [n] \mid n \in \mathbb {N} \ \! \}\);
-
\(\lambda _{N} : [\hat{q}] \mapsto (\mathsf {O}, \mathsf {Q}, 0), [n] \mapsto (\mathsf {P}, \mathsf {A}, 0)\);
-
\(\vdash _{N} {\mathop {=}\limits ^{\mathrm {df. }}} \{ (\star , [\hat{q}]) \} \cup \{ ([\hat{q}], [n]) \mid n \in \mathbb {N} \ \! \}\);
-
\(\Delta _{N} {\mathop {=}\limits ^{\mathrm {df. }}} \emptyset \);
-
\(P_{N} {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Pref}(\{ [\hat{q}] [n] \mid n \in \mathbb {N} \ \! \})\), where [n] is justified by \([\hat{q}]\).
The position \([\hat{q}] [n]\) is to represent the natural number \(n \in \mathbb {N}\), where the answer [n] is performed for the question \([\hat{q}]\). This is the formal definition of N sketched in the introduction though we have slightly changed the notation for the moves.
However, although the game N is standard in the literature, the ‘content’ of N is almost the same as that of the set \(\mathbb {N}\) of all natural numbers except the trivial one-round communication between the participants. This point is unsatisfactory because:
-
1.
It is difficult to define an intrinsic, non-inductive, non-axiomatic notion of ‘effective computability’ of strategies on games generated from N via the construction \(\Rightarrow \) of function space (which will be given shortly) since there is no intensional or low-level structure in N (see, e.g., [4] for this point);
-
2.
The game N contributes almost nothing new to foundations of mathematics.
Motivated by these points, we adopt the following ‘lazy’ variant:
Example 23
The lazy natural number game \(\mathcal {N}\) is defined by:
-
\(M_{\mathcal {N}} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [\hat{q}], [q], [ yes ], [ no ] \}\);
-
\(\lambda _{\mathcal {N}} : [\hat{q}] \mapsto (\mathsf {O}, \mathsf {Q}, 0), [q] \mapsto (\mathsf {O}, \mathsf {Q}, 0), [ yes ] \mapsto (\mathsf {P}, \mathsf {A}, 0), [ no ] \mapsto (\mathsf {P}, \mathsf {A}, 0)\);
-
\(\vdash _{\mathcal {N}} {\mathop {=}\limits ^{\mathrm {df. }}} \{ (\star , [\hat{q}]), ([\hat{q}], [ no ]), ([\hat{q}], [ yes ]), ([q], [ no ]), ([q], [ yes ]), ([ yes ], [q]) \}\);
-
\(\Delta _{\mathcal {N}} {\mathop {=}\limits ^{\mathrm {df. }}} \emptyset \);
-
\(P_{\mathcal {N}} {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Pref}(\{ [\hat{q}] . ([ yes ] . [q])^n . [ no ] \mid n \in \mathbb {N} \ \! \})\), where each non-initial occurrence is justified by the last occurrence.
We need two questions \([\hat{q}]\) and [q], the initial and non-initial ones, respectively, for the axiom E1. Intuitively, a play of \(\mathcal {N}\) proceeds by repeating the following: O asks by a question \([\hat{q}]\) or [q] if P would like to ‘count one more,’ and P replies it by \([ yes ]\) if she would like to, and by \([ no ]\) otherwise. Thus, for each \(n \in \mathbb {N}\), the position \([\hat{q}] . ([ yes ] . [q])^n . [ no ]\) is to represent the number n, where each occurrence of an answer (i.e., \([ yes ]\) or \([ no ]\)) is performed for the last occurrence of a question (i.e., \([\hat{q}]\) or [q]).
The game \(\mathcal {N}\) defines natural numbers in an intuitively natural manner, namely as ‘counting processes,’ where our choice of notation for moves is inessential, i.e., \(\mathcal {N}\) is syntax-independent. Moreover, we may actually define it intrinsically, i.e., without recourse to the set \(\mathbb {N}\), by specifying its positions inductively: \([\hat{q}] [ no ] \in P_{\mathcal {N}} \wedge ([\hat{q}] . \varvec{s} . [ no ] \in P_{\mathcal {N}} \Rightarrow [\hat{q}] . \varvec{s} . [ yes ] [q] [ no ] \in P_{\mathcal {N}})\). Thus, we may define (rather than represent) natural numbers to be positions of \(\mathcal {N}\) though we will not investigate foundational consequences of this definition in the present paper.
As we shall see, such step-by-step processes underlying natural numbers allow us to define ‘effective computability’ of strategies on natural numbers in an intrinsic, non-inductive, non-axiomatic manner in Sect. 3.1.
Now, let us recall the hiding operation on games:
Definition 24
(Hiding on games [71]) Let \(d \in \mathbb {N} \cup \{ \omega \}\); the \({{{\varvec{d}}}}\)-hiding operation \(\mathcal {H}^{{\varvec{d}}}\) on games is defined as follows. Given a game G, the \({{{\varvec{d}}}}\)-external game \(\mathcal {H}^d(G)\) of G consists of the d-external arena \((M_{\mathcal {H}^d(G)}, \lambda _{\mathcal {H}^d(G)}, \vdash _{\mathcal {H}^d(G)}, \Delta _{\mathcal {H}^d(G)})\) of the arena G, and the set \(P_{\mathcal {H}^d(G)} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \mathcal {H}^d_G(\varvec{s}) \mid \varvec{s} \in P_G \ \! \}\) of positions. A game H is normalized if \(\mathcal {H}^\omega (H) = H\), i.e., if \(M_H\) does not contain any internal moves.
Theorem 25
(Closure of games under hiding [71]) For any game G, \(\mathcal {H}^d(G)\) forms a well-defined game for all \(d \in \mathbb {N} \cup \{ \omega \}\). Moreover, if  , then
, then  for all \(d \in \mathbb {N} \cup \{ \omega \}\). Furthermore, \(\underbrace{\mathcal {H}^1 \circ \mathcal {H}^1 \cdots \circ \mathcal {H}^1}_i(G) = \mathcal {H}^i(G)\) for all \(i \in \mathbb {N}\).
for all \(d \in \mathbb {N} \cup \{ \omega \}\). Furthermore, \(\underbrace{\mathcal {H}^1 \circ \mathcal {H}^1 \cdots \circ \mathcal {H}^1}_i(G) = \mathcal {H}^i(G)\) for all \(i \in \mathbb {N}\).
Proof
Based on Lemma 15; see [71]. \(\square \)
Convention
Thanks to Theorem 25, the i-hiding operation \(\mathcal {H}^i\) on games for each \(i \in \mathbb {N}\) can be thought of as the i-times iteration of the 1-hiding operation \(\mathcal {H}^1\), which we call the hiding operation (on games) and write \(\mathcal {H}\) for it.
2.2.3 Constructions on games
Now, let us recall the constructions on games given in [71] with ‘tags’ formalized by outer and inner tags defined in Sect. 2.1. A tag refers to an outer or inner tag.
On the other hand, for readers who are not familiar with game semantics, we first give a rather standard presentation of each construction, which keeps ‘tags’ informal and unspecified, before its formal definition. For this aim, we employ:
Notation
Let S and T be sets, and we write \(S + T\) for their disjoint union. Then, we write \(x \in S + T\) if \(x \in S\) or \(x \in T\), where we cannot have both \(x \in S\) and \(x \in T\) by the implicit ‘tag’ for the disjoint union \(S+T\). Also, given functions \(f : S \rightarrow U\) and \(g : T \rightarrow U\), we write [f, g] for the function \(S + T \rightarrow U\) that maps \(x \in S + T\) to \(f(x) \in U\) if \(x \in S\), and to \(g(x) \in U\) otherwise (n.b., it is generalized to more than two functions in the obvious manner). Moreover, given relations \(R_S \subseteq S \times S\) and \(R_T \subseteq T \times T\), we write \(R_S + R_T\) for the relation on \(S + T\) such that \((x, y) \in R_S + R_T {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} (x, y) \in R_S \vee (x, y) \in R_T\).
Let us begin with tensor (product) \(\otimes \). As mentioned in the introduction, a position of the tensor \(A \otimes B\) of given games A and B consists of a position of A and a position of B played ‘in parallel without communication.’ More precisely, the tensor \(A \otimes B\) is given by:
-
\(M_{A \otimes B} {\mathop {=}\limits ^{\mathrm {df. }}} M_A + M_B\);
-
\(\lambda _{A \otimes B} {\mathop {=}\limits ^{\mathrm {df. }}} [\lambda _A, \lambda _B]\);
-
\(\vdash _{A \otimes B} \ {\mathop {=}\limits ^{\mathrm {df. }}} \ \vdash _A + \ \! \vdash _B\);
-
\(\Delta _{A \otimes B} {\mathop {=}\limits ^{\mathrm {df. }}} [\Delta _A, \Delta _B]\);
-
\(P_{A \otimes B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{A \otimes B} \mid \varvec{s} \upharpoonright A \in P_A, \varvec{s} \upharpoonright B \in P_B \ \! \},\) where \(\varvec{s} \upharpoonright A\) (resp. \(\varvec{s} \upharpoonright B\)) denotes the j-subsequence of \(\varvec{s}\) that consists of moves of A (resp. B). As an illustration, recall the example \(N \otimes N\) in the introduction, in which the ‘tags’ are informally written as \((\_)^{[i]}\) (\(i = 0, 1\)).
As explained in [3], it is easy to see that during a play of the tensor \(A \otimes B\) only O can switch between the component games A and B (by alternation).
Let us now give the formal definition of tensor, for which the ‘tags’ \((\_)^{[0]}\) and \((\_)^{[1]}\) are formalized by inner tags \((\_, \mathscr {W})\) and \((\_, \mathscr {E})\), respectively:
Definition 26
(Tensor of games [6]) The tensor (product) \(A \otimes B\) of games A and B is defined by:
-
\(M_{A \otimes B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [(a, \mathscr {W})]_{\varvec{e}} \mid [a]_{\varvec{e}} \in M_A \ \! \} \cup \{ [(b, \mathscr {E})]_{\varvec{f}} \mid [b]_{\varvec{f}} \in M_B \ \! \}\);
-
\(\lambda _{A \otimes B} ([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} \lambda _A([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {W}; \\ \lambda _B([m]_{\varvec{e}}) &{}\text {otherwise;} \end{array}\right. }\)
-
\(\star \vdash _{A \otimes B} [(m, X)]_{\varvec{e}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} (X = \mathscr {W} \wedge \star \vdash _A [m]_{\varvec{e}}) \vee (X = \mathscr {E} \wedge \star \vdash _B [m]_{\varvec{e}})\);
-
\([(m, X)]_{\varvec{e}} \vdash _{A \otimes B} [(n, Y)]_{\varvec{f}} {\mathop {\Leftrightarrow }\limits ^{{\mathrm {df. }}}} (X = \mathscr {W} = Y \wedge [m]_{\varvec{e}} \vdash _A [n]_{\varvec{f}}) \vee (X = \mathscr {E} = Y \wedge [m]_{\varvec{e}} \vdash _B [n]_{\varvec{f}})\);
-
\(\Delta _{A \otimes B} ([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{{\mathrm {df. }}}} \left\{ \begin{array}{lll} {[}(m', \mathscr {W})]_{\varvec{e}} &{}\text {if }X = \mathscr {W},\text { where } \Delta _A([m]_{\varvec{e}}) = [m']_{\varvec{e}}; \\ {[}(m'', \mathscr {E})]_{\varvec{e}} &{}\text {otherwise, where } \Delta _B([m]_{\varvec{e}}) = [m'']_{\varvec{e}}; \end{array}\right. \)
-
\(P_{A \otimes B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{A \otimes B} \mid \varvec{s} \upharpoonright \mathscr {W} \in P_A, \varvec{s} \upharpoonright \mathscr {E} \in P_B \ \! \}\), where \(\varvec{s} \upharpoonright X\) is the j-subsequence of \(\varvec{s}\) that consists of moves of the form \([(m, X)]_{\varvec{e}}\) yet changed into \([m]_{\varvec{e}}\) (\(X \in \{ \mathscr {W}, \mathscr {E} \}\)).
Example 27
Some typical plays of the tensor \(\mathcal {N} \otimes \mathcal {N}\) are as follows:

Next, the linear implication \(A \multimap B\) is the space of linear functions from A to B in the sense of linear logic [27], i.e., they consume exactly one input in A to produce an output in B (n.b., strictly speaking, it is an affine implication as explained in the introduction). Usually, the linear implication \(A \multimap B\) is given by:
-
\(M_{A \multimap B} {\mathop {=}\limits ^{\mathrm {df. }}} M_{\mathcal {H}^\omega (A)} + M_B\);
-
\(\lambda _{A \multimap B} {\mathop {=}\limits ^{\mathrm {df. }}} [\overline{\lambda _{\mathcal {H}^\omega (A)}}, \lambda _B]\), where \(\overline{\lambda _{\mathcal {H}^\omega (A)}} {\mathop {=}\limits ^{\mathrm {df. }}} \langle \overline{\lambda _{\mathcal {H}^\omega (A)}^\textsf {OP}}, \lambda _{\mathcal {H}^\omega (A)}^\textsf {QA}, \lambda _{\mathcal {H}^\omega (A)}^\mathbb {N} \rangle \), and \(\overline{\lambda _{G}^\textsf {OP}} (m) {\mathop {=}\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} \mathsf {P} \ &{} \text {if }\lambda _{G}^\textsf {OP} (m) = \textsf {O}; \\ \textsf {O} \ &{}\text {otherwise} \end{array}\right. }\) for any game G;
-
\(\star \vdash _{A \multimap B} m {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} \star \vdash _B m\);
-
\(m \vdash _{A \multimap B} n \ (m \ne \star ) {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} (m \vdash _{\mathcal {H}^\omega (A)} n) \vee (m \vdash _B n) \vee (\star \vdash _B m \wedge \star \vdash _{\mathcal {H}^\omega (A)} n)\);
-
\(\Delta _{A \multimap B} {\mathop {=}\limits ^{\mathrm {df. }}} [\emptyset , \Delta _B]\) (n.b., note that \(\Delta _{\mathcal {H}^\omega (A)} = \emptyset \));
-
\(P_{A \multimap B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{\mathcal {H}^\omega (A) \multimap B} \mid \varvec{s} \upharpoonright \mathcal {H}^\omega (A) \in P_{\mathcal {H}^\omega (A)}, \varvec{s} \upharpoonright B \in P_B \ \! \}\).
As an illustration, recall the example of \(N \multimap N\) in the introduction.
Note that the domain A must be normalized into \(\mathcal {H}^\omega (A)\) since otherwise the linear implication \(A \multimap B\) may not satisfy the axiom DP2. It conceptually makes sense too for the roles of P and O in A are exchanged, and thus P should not be able to ‘see’ internal moves of A. Note also that \(A \multimap B\) is almost \(A \otimes B\) if A is normalized except the switch of the roles in A; dually to \(A \otimes B\), only P can switch between A and B during a play of \(A \multimap B\) (see [3] for the proof). Surprisingly, this simple point changes \(A \otimes B\) into \(A \multimap B\).
Similarly to tensor, the formal definition of linear implication is as follows:
Definition 28
(Linear implication between games [6]) The linear implication \(A \multimap B\) between games A and B is defined by:
-
\(M_{A \multimap B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [(a, \mathscr {W})]_{\varvec{e}} \mid [a]_{\varvec{e}} \in M_{\mathcal {H}^\omega (A)} \ \! \} \cup \{ [(b, \mathscr {E})]_{\varvec{f}} \mid [b]_{\varvec{f}} \in M_B \ \! \}\);
-
\(\lambda _{A \multimap B} ([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} \overline{\lambda _{\mathcal {H}^\omega (A)}}([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {W}, \text { where } \overline{\lambda _{\mathcal {H}^\omega (A)}}\text { is defined above;} \\ \lambda _B([m]_{\varvec{e}}) &{}\text {otherwise;} \end{array}\right. }\)
-
\(\star \vdash _{A \multimap B} [(m, X)]_{\varvec{e}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} X = \mathscr {E} \wedge \star \vdash _B [m]_{\varvec{e}}\);
-
\([(m, X)]_{\varvec{e}} \vdash _{A \multimap B} [(n, Y)]_{\varvec{f}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} \begin{aligned} &{}(X = \mathscr {W} = Y \wedge [m]_{\varvec{e}} \vdash _{\mathcal {H}^\omega (A)} [n]_{\varvec{f}}) \\ &{}\vee (X = \mathscr {E} = Y \wedge [m]_{\varvec{e}} \vdash _B [n]_{\varvec{f}}) \\ &{}\vee (X = \mathscr {E} \wedge Y = \mathscr {W} \wedge \star \vdash _B [m]_{\varvec{e}} \wedge \star \vdash _{\mathcal {H}^\omega (A)} [n]_{\varvec{f}}); \end{aligned} \end{array}\right. }\)
-
\(\Delta _{A \multimap B}([(b, \mathscr {E})]_{\varvec{f}}) {\mathop {=}\limits ^{\mathrm {df. }}} [(b', \mathscr {E})]_{\varvec{f}}\), where \(\Delta _B([b]_{\varvec{f}}) = [b']_{\varvec{f}}\);
-
\(P_{A \multimap B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{\mathcal {H}^\omega (A) \multimap B} \mid \varvec{s} \upharpoonright \mathscr {W} \in P_{\mathcal {H}^\omega (A)}, \varvec{s} \upharpoonright \mathscr {E} \in P_B \ \! \}\), where pointers in \(\varvec{s}\) from initial occurrences of A to those of B are deleted in \(\varvec{s} \upharpoonright \mathscr {W}\) and \(\varvec{s} \upharpoonright \mathscr {E}\).
Example 29
Any game B and the linear implication \(T \multimap B\) coincide up to tags. Also, some typical plays of the linear implication \(\varvec{2} \multimap \varvec{2}\) are as follows:

Note that the left diagram describes a strict linear function, i.e., a one that asks an input before producing an output, while the right diagram does a non-strict one.
Next, let us recall product & of games. As stated in the introduction, a position of the product \( A \& B\) is essentially a position of A or B; it is given by:
-
\( M_{A \& B} {\mathop {=}\limits ^{\mathrm {df. }}} M_A + M_B\);
-
\( \lambda _{A \& B} {\mathop {=}\limits ^{\mathrm {df. }}} [\lambda _A, \lambda _B]\);
-
\( \vdash _{A \& B} \ {\mathop {=}\limits ^{\mathrm {df. }}} \ \vdash _A + \ \! \vdash _B\);
-
\( \Delta _{A \& B} {\mathop {=}\limits ^{\mathrm {df. }}} [\Delta _A, \Delta _B]\);
-
\( P_{A \& B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{A \& B} \mid (\varvec{s} \upharpoonright A \in P_A \wedge \varvec{s} \upharpoonright B = \varvec{\epsilon }) \vee (\varvec{s} \upharpoonright A = \varvec{\epsilon } \wedge \varvec{s} \upharpoonright B \in P_B) \ \! \}\).
Similarly to the case of tensor, we formalize product as follows:
Definition 30
(Product of games [6]) The product \( A \& B\) of games A and B is given by:
-
\( M_{A \& B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [(a, \mathscr {W})]_{\varvec{e}} \mid [a]_{\varvec{e}} \in M_A \ \! \} \cup \{ [(b, \mathscr {E})]_{\varvec{f}} \mid [b]_{\varvec{f}} \in M_B \ \! \}\);
-
\( \lambda _{A \& B} ([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} \lambda _A([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {W}; \\ \lambda _B([m]_{\varvec{e}}) &{}\text {otherwise;} \end{array}\right. }\)
-
\( \star \vdash _{A \& B} [(m, X)]_{\varvec{e}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} (X = \mathscr {W} \wedge \star \vdash _A [m]_{\varvec{e}}) \vee (X = \mathscr {E} \wedge \star \vdash _B [m]_{\varvec{e}})\);
-
\( [(m, X)]_{\varvec{e}} \vdash _{A \& B} [(n, Y)]_{\varvec{f}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} (X = \mathscr {W} = Y \wedge [m]_{\varvec{e}} \vdash _A [n]_{\varvec{f}}) \vee (X = \mathscr {E} = Y \wedge [m]_{\varvec{e}} \vdash _B [n]_{\varvec{f}})\);
-
\( \Delta _{A \& B} ([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{\mathrm {df. }}} \left\{ \begin{array}{ll} {[}(m',\mathscr {W})]_{\varvec{e}} &{}\text {if }X = \mathscr {W},\text { where } \Delta _A([m]_{\varvec{e}}) = [m']_{\varvec{e}}; \\ {[}(m'', \mathscr {E})]_{\varvec{e}} &{}\text {otherwise, where } \Delta _B([m]_{\varvec{e}}) = [m'']_{\varvec{e}}; \end{array}\right. \)
-
\( P_{A \& B} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{A \& B} \mid (\varvec{s} \upharpoonright \mathscr {W} \in P_A \wedge \varvec{s} \upharpoonright \mathscr {E} = \varvec{\epsilon }) \vee (\varvec{s} \upharpoonright \mathscr {W} = \varvec{\epsilon } \wedge \varvec{s} \upharpoonright \mathscr {E} \in P_B) \ \! \}\).
For the cartesian closed bicategory
\(\mathcal {DG}\) of dynamic games and strategies defined in [71], however, we have to generalize the construction \( C \multimap A \& B\) on normalized games A, B and C, where & precedes \(\multimap \), because we need to pair strategies \(\sigma : L\) and \(\tau : R\) such that  and
and  , and the ambient game of the pairing \(\langle \sigma , \tau \rangle \) would be such a generalization of \( C \multimap A \& B\).
, and the ambient game of the pairing \(\langle \sigma , \tau \rangle \) would be such a generalization of \( C \multimap A \& B\).
For this point, [71] defines the pairing \(\langle L, R \rangle \) of such games L and R by:
-
\(M_{\langle L, R \rangle } {\mathop {=}\limits ^{\mathrm {df. }}} M_C + (M_L {\setminus } M_C) + (M_R {\setminus } M_C)\);
-
\(\lambda _{\langle L, R \rangle } {\mathop {=}\limits ^{\mathrm {df. }}} [\overline{\lambda _C}, \lambda _L \downharpoonright M_C, \lambda _R \downharpoonright M_C]\);
-
\(m \vdash _{\langle L, R \rangle } n {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} m \vdash _L n \vee m \vdash _R n\);
-
\(\Delta _{\langle L, R \rangle } {\mathop {=}\limits ^{\mathrm {df. }}} [\Delta _L, \Delta _R]\);
-
\( P_{\langle L, R \rangle } {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{L \& R} \mid (\varvec{s} \upharpoonright L \in P_L \wedge \varvec{s} \upharpoonright B = \varvec{\epsilon }) \vee (\varvec{s} \upharpoonright A = \varvec{\epsilon } \wedge \varvec{s} \upharpoonright R \in P_R) \ \! \}\)
where given a function \(f : X \rightarrow Y\) and a subset \(Z \subseteq X\) we write \(f \downharpoonright Z : X {\setminus } Z \rightarrow Y\) for the restrictions of f to the subset \(X {\setminus } Z \subseteq X\).
Note that the pairing \(\langle L, R \rangle \) does not depend on the choice of the normalized games A, B and C such that  and
and  . Also, we have \( \langle C \multimap A, C \multimap B \rangle = C \multimap A \& B\); in particular, \(\langle T \multimap A, T \multimap B\rangle \) and \( A \& B\) coincide up to tags; pairing of games generalizes this phenomenon in the sense that
. Also, we have \( \langle C \multimap A, C \multimap B \rangle = C \multimap A \& B\); in particular, \(\langle T \multimap A, T \multimap B\rangle \) and \( A \& B\) coincide up to tags; pairing of games generalizes this phenomenon in the sense that  holds (see [71] for the proof), where the ‘tags’ for the disjoint union \(M_{\langle L, R \rangle } = M_C + (M_L {\setminus } M_C) + (M_R {\setminus } M_C)\) must be formulated in such a way that establishes the subgame relation
holds (see [71] for the proof), where the ‘tags’ for the disjoint union \(M_{\langle L, R \rangle } = M_C + (M_L {\setminus } M_C) + (M_R {\setminus } M_C)\) must be formulated in such a way that establishes the subgame relation 
Let us now formalize ‘tags’ for the disjoint union \(M_{\langle L, R \rangle }\) by:
-
Adding no tags on external moves of the form \([(c, \mathscr {W})]_{\varvec{e}}\) of L or R, where \([c]_{\varvec{e}}\) must be a move of C by the definition of \(\multimap \) (Definition 28);
-
Changing external moves of the form \([(a, \mathscr {E})]_{\varvec{f}}\) of L, where \([a]_{\varvec{f}}\) must be a move of A by the definition of \(\multimap \), into \([((a, \mathscr {W}), \mathscr {E})]_{\varvec{f}}\);
-
Changing external moves of the form \([(b, \mathscr {E})]_{\varvec{g}}\) of R, where \([b]_{\varvec{g}}\) must be a move of B by the definition of \(\multimap \), into \([((b, \mathscr {E}), \mathscr {E})]_{\varvec{g}}\);
-
Changing internal moves \([l]_{\varvec{h}}\) of L into \([(l, \mathscr {S})]_{\varvec{h}}\);
-
Changing internal moves \([r]_{\varvec{k}}\) of R into \([(r, \mathscr {N})]_{\varvec{k}}\).
These tags are of course not canonical at all, but they would certainly achieve the required subgame relation 
Then, we formalize the labeling function, the enabling relation and the dummy function of \(\langle L, R \rangle \) by the obvious pattern matching on inner tags; positions of \(\langle L, R \rangle \) are formalized in the obvious manner. However, the enabling relation is rather involved; thus, for convenience, we define the peeling \( peel _{\langle L, R \rangle }(m) \in M_L \cup M_R\) of each move \(m \in M_{\langle L, R \rangle }\) such that changing the inner tag of \( peel _{\langle L, R \rangle }(m)\) as defined above results in m, and also the attribute \( att _{\langle L, R \rangle }(m) \in \{ L, R, C \}\) of m by:
The enabling relation \(m \vdash _{\langle L, R \rangle } n\) is then easily defined as the conjunction of:
-
\( att _{\langle L, R \rangle }(m) = att _{\langle L, R \rangle }(n) \vee att _{\langle L, R \rangle }(m) = C \vee att _{\langle L, R \rangle }(n) = C\);
-
\( peel _{\langle L, R \rangle }(m) \vdash _L peel _{\langle L, R \rangle }(n) \vee peel _{\langle L, R \rangle }(m) \vdash _R peel _{\langle L, R \rangle }(n)\).
Formally, we define pairing of games as follows:
Definition 31
(Pairing of games [71]) The pairing
\(\langle L, R \rangle \) of games L and R such that  and
and  for any normalized games A, B and C is given by:
for any normalized games A, B and C is given by:
-
\(\centerdot M_{\langle L, R \rangle } {\mathop {=}\limits ^{\mathrm {df. }}} \{ [(c, \mathscr {W})]_{\varvec{e}} \mid [(c, \mathscr {W})]_{\varvec{e}} \in M_L^{\mathsf {Ext}} \cup M_R^{\mathsf {Ext}}, [c]_{\varvec{e}} \in M_C \ \! \}\) \( \cup \{ [((a, \mathscr {W}), \mathscr {E})]_{\varvec{f}} \mid [(a, \mathscr {E})]_{\varvec{f}} \in M_L^{\mathsf {Ext}}, [a]_{\varvec{f}} \in M_A \ \! \}\) \(\cup \{ [((b, \mathscr {E}), \mathscr {E})]_{\varvec{g}} \mid [(b, \mathscr {E})]_{\varvec{g}} \in M_R^{\mathsf {Ext}}, [b]_{\varvec{g}} \in M_B \ \! \}\) \(\cup \{ [(l, \mathscr {S})]_{\varvec{h}} \mid [l]_{\varvec{h}} \in M_L^{\mathsf {Int}} \} \cup \{ [(r, \mathscr {N})]_{\varvec{k}} \mid [r]_{\varvec{k}} \in M_R^{\mathsf {Int}} \ \! \};\)
-
\(\lambda _{\langle L, R \rangle } ([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} \overline{\lambda _C} ([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {W}; \\ \lambda _A([a]_{\varvec{e}}) &{}\text {if }X = \mathscr {E},\text { and }m \text { is of the form } (a, \mathscr {W}); \\ \lambda _B([b]_{\varvec{e}}) &{}\text {if }X = \mathscr {E}, \text { and } m \text { is of the form }(b, \mathscr {E}); \\ \lambda _L([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {S}; \\ \lambda _R([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {N}; \end{array}\right. }\)
-
\(\star \vdash _{\langle L, R \rangle } [(m, X)]_{\varvec{e}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} X = \mathscr {E} \wedge (\exists [a]_{\varvec{e}} \in M_A^{\mathsf {Init}} . \ \! m = (a, \mathscr {W}) \vee \exists [b]_{\varvec{e}} \in M_B^{\mathsf {Init}} . \ \! m = (b, \mathscr {E}))\);
-
\([(m, X)]_{\varvec{e}} \vdash _{\langle L, R \rangle } [(n, Y)]_{\varvec{f}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} ( att _{\langle L, R \rangle }([(m, X)]_{\varvec{e}}) = att _{\langle L, R \rangle }([(n, Y)]_{\varvec{f}}) \vee att _{\langle L, R \rangle }([(m, X)]_{\varvec{e}}) = C \vee att _{\langle L, R \rangle }([(n, Y)]_{\varvec{f}}) = C) \wedge ( peel _{\langle L, R \rangle }([(m, X)]_{\varvec{e}}) \vdash _L peel _{\langle L, R \rangle }([(n, Y)]_{\varvec{f}}) \vee peel _{\langle L, R \rangle }([(m, X)]_{\varvec{e}}) \vdash _R peel _{\langle L, R \rangle }([(n, Y)]_{\varvec{f}}))\), where the map \( peel _{\langle L, R \rangle } : M_{\langle L, R \rangle } \rightarrow M_L \cup M_R\) is given by \([(c, \mathscr {W})]_{\varvec{e}} \mapsto [(c, \mathscr {W})]_{\varvec{e}}\), \([((a, \mathscr {W}), \mathscr {E})]_{\varvec{f}} \mapsto [(a, \mathscr {E})]_{\varvec{f}}\), \([((b, \mathscr {E}), \mathscr {E})]_{\varvec{g}} \mapsto [(b, \mathscr {E})]_{\varvec{g}}\), \([(l, \mathscr {S})]_{\varvec{h}} \mapsto [l]_{\varvec{h}}\), \([(r, \mathscr {N})]_{\varvec{k}} \mapsto [r]_{\varvec{k}}\), and the map \( att _{\langle L, R \rangle } : M_{\langle L, R \rangle } \rightarrow \{ L, R, C \}\) by \([(c, \mathscr {W})]_{\varvec{e}} \mapsto C\), \([((a, \mathscr {W}), \mathscr {E})]_{\varvec{f}} \mapsto L\), \([((b, \mathscr {E}), \mathscr {E})]_{\varvec{g}} \mapsto R\), \([(l, \mathscr {S})]_{\varvec{h}} \mapsto L\), \([(r, \mathscr {N})]_{\varvec{k}} \mapsto R\);
-
\(\Delta _{\langle L, R \rangle } ([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{\mathrm {df. }}} \left\{ \begin{array}{ll} {[}(l', \mathscr {S})]_{\varvec{e}} &{}\text {if }X = \mathscr {S}, \text { where } \Delta _L([l]_{\varvec{e}}) = [l']_{\varvec{e}}; \\ {[}(r', \mathscr {N})]_{\varvec{e}} &{}\text {if }X = \mathscr {N}, \text { where } \Delta _R([r]_{\varvec{e}}) = [r']_{\varvec{e}}; \end{array}\right. \)
-
\(P_{\langle L, R \rangle } {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{\langle L, R \rangle } \mid (\varvec{s} \upharpoonright L \in P_L \wedge \varvec{s} \upharpoonright B = \varvec{\epsilon }) \vee (\varvec{s} \upharpoonright R \in P_R \wedge \varvec{s} \upharpoonright A = \varvec{\epsilon }) \ \! \}\), where \(\varvec{s} \upharpoonright L\) (resp. \(\varvec{s} \upharpoonright R\)) is the j-subsequence of \(\varvec{s}\) that consists of moves x such that \( peel _{\langle L, R \rangle }(x) \in M_L\) (resp. \( peel _{\langle L, R \rangle }(x) \in M_R\)) yet changed into \( peel _{\langle L, R \rangle }(x)\), and \(\varvec{s} \upharpoonright B\) (resp. \(\varvec{s} \upharpoonright A\)) is the j-subsequence of \(\varvec{s}\) that consists of moves \([((b, \mathscr {E}), \mathscr {E})]_{\varvec{g}}\) with \([b]_{\varvec{g}} \in M_B\) (resp. \([((a, \mathscr {W}), \mathscr {E})]_{\varvec{f}}\) with \([a]_{\varvec{f}} \in M_A\)) yet changed into \([b]_{\varvec{g}}\) (resp. \([a]_{\varvec{f}}\)).
Example 32
Some typical plays of the pairing \(\langle \varvec{2} \multimap \varvec{2}, \varvec{2} \multimap \varvec{2} \rangle \) are as follows:

Next, let us recall exponential ! in the sense of linear logic, i.e., \(!A {\mathop {=}\limits ^{\mathrm {df. }}} A \otimes A \otimes \dots \) The exponential !A is usually given by:
-
\(M_{!A} {\mathop {=}\limits ^{\mathrm {df. }}} M_A \times \mathbb {N}\);
-
\(\lambda _{!A} : (a, i) \mapsto \lambda _A(a)\);
-
\(\star \vdash _{!A} (a, i) {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} \star \vdash _A a\);
-
\((a, i) \vdash _{!A} (a', j) {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} i = j \wedge a \vdash _A a'\);
-
\(\Delta _{!A} : (a, i) \mapsto (\Delta _A(a), i)\);
-
\(P_{!A} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{!A} \mid \forall i \in \mathbb {N} . \ \! \varvec{s} \upharpoonright i \in P_A \ \! \}\), where \(\varvec{s} \upharpoonright i\) is the j-subsequence of \(\varvec{s}\) that consists of moves (a, i) yet changed into a.
A naive idea is then to formalize each ‘tag’ \((\_, i)\) for exponential by an effective tag \([\_]_{\ell ^{i}}\) (Definition 1), but as mentioned before, we need to generalize it to an extended effective tag \([\_]_{\varvec{f}}\) (Definition 3). Thus, we formalize exponential as follows:
Definition 33
(Exponential of games [6, 51]) The exponential !A of a game A is defined by:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 , where \(\Delta _A([m]_{\varvec{e}}) = [m']_{\varvec{e}}\);
, where \(\Delta _A([m]_{\varvec{e}}) = [m']_{\varvec{e}}\); -
\(P_{!A} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{!A} \mid \forall \varvec{f} \in \mathcal {T} . \ \! \varvec{s} \upharpoonright \varvec{f} \in P_A \wedge (\varvec{s} \upharpoonright \varvec{f} \ne \varvec{\epsilon } \Rightarrow \forall \varvec{g} \in \mathcal {T} . \ \! \varvec{s} \upharpoonright \varvec{g} \ne \varvec{\epsilon } \Rightarrow ede (\varvec{f}) \ne ede (\varvec{g})) \ \! \}\), where \(\varvec{s} \upharpoonright \varvec{f}\) is the j-subsequence of \(\varvec{s}\) that consists of moves of the form
 yet changed into \([m]_{\varvec{e}}\).
yet changed into \([m]_{\varvec{e}}\).
Thus, our exponential !A is essentially a slight modification of the one in [37, 51] which generalizes moves \([m]_{\ell ^{i} \hbar \varvec{e}}\) to  , where \([m]_{\varvec{e}} \in M_A\), \(i \in \mathbb {N}\) and \(\varvec{f} \in \mathcal {T}\). By the condition on positions of !A, an element \(\varvec{f}\) in an outer tag
, where \([m]_{\varvec{e}} \in M_A\), \(i \in \mathbb {N}\) and \(\varvec{f} \in \mathcal {T}\). By the condition on positions of !A, an element \(\varvec{f}\) in an outer tag  that represents a natural number \(i \in \mathbb {N}\), i.e., \( ede (\varvec{f}) = (i)\), is unique in each \(\varvec{s} \in P_{!A}\).
that represents a natural number \(i \in \mathbb {N}\), i.e., \( ede (\varvec{f}) = (i)\), is unique in each \(\varvec{s} \in P_{!A}\).
Notation
We often write \(A \Rightarrow B\) for the linear implication \(!A \multimap B\) for any games A and B, which we call the implication or function space from A to B. The constructions \(\multimap \) and \(\Rightarrow \) are both right associative.
Example 34
Any game B and the implication \(T \Rightarrow B\) coincide up to tags. Also, some typical plays of the exponential \(! \varvec{2}\) are as follows:

Similarly to the case of pairing, exponential is generalized in [71]: Given a game G such that  for some normalized games A and B, there is the promotion
\(G^{\dagger }\) of G such that
for some normalized games A and B, there is the promotion
\(G^{\dagger }\) of G such that  In fact, promotion is a generalization of exponential because \((!T \multimap B)^{\dagger }\) and !B coincide up to tags for any normalized game B; see [71] for the proof. Promotion of games is defined in [71] because a morphism \(A \rightarrow B\) in the bicategory \(\mathcal {DG}\) is a strategy \(\phi : G\) such that
In fact, promotion is a generalization of exponential because \((!T \multimap B)^{\dagger }\) and !B coincide up to tags for any normalized game B; see [71] for the proof. Promotion of games is defined in [71] because a morphism \(A \rightarrow B\) in the bicategory \(\mathcal {DG}\) is a strategy \(\phi : G\) such that  and therefore, it is necessary to take a generalized promotion \(\phi ^{\dagger }\) (Definition 57) for composition of strategies in \(\mathcal {DG}\), whose ambient game is \(G^{\dagger }\).
and therefore, it is necessary to take a generalized promotion \(\phi ^{\dagger }\) (Definition 57) for composition of strategies in \(\mathcal {DG}\), whose ambient game is \(G^{\dagger }\).
The promotion \(G^{\dagger }\) is simply given by:
-
\(M_{G^{\dagger }} {\mathop {=}\limits ^{\mathrm {df. }}} ((M_G {\setminus }M_{!A})\times \mathbb {N})+ \{ (a, \langle i, k \rangle ) \mid (a, k) \in M_{!A}, i \in \mathbb {N} \}\);
-
\(\lambda _{G^{\dagger }} : ((m, i) \in (M_G {\setminus } M_{!A}) \times \mathbb {N}) \mapsto \lambda _G(m), (a, \langle i, k \rangle ) \mapsto \lambda _G(a, k)\);
-
\(\star \vdash _{G^{\dagger }} (m, i) {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} \star \vdash _G m\) for all \(i \in \mathbb {N}\);
-
$$\begin{aligned}&(m, i) \vdash _{G^{\dagger }} (n, j) {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} (i = j \wedge m, n \in M_G {\setminus } M_{!A} \wedge m \vdash _G n) \\&\quad \vee (i = j \wedge m \vdash _A n) \vee (m \in M_G {\setminus } M_{!A} \wedge (n, j) \in M_{!A} \wedge m \vdash _G (n, j) \wedge \exists k \in \mathbb {N} . \ \! j = \langle i, k \rangle ; \end{aligned}$$
-
\(\Delta _{G^{\dagger }} : (m, i) \mapsto (\Delta _G(m), i)\);
-
\(P_{G^{\dagger }} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{G^{\dagger }} \mid \forall i \in \mathbb {N} . \ \! \varvec{s} \upharpoonright i \in P_G \ \! \}\), where \(\varvec{s} \upharpoonright i\) is the j-subsequence of \(\varvec{s}\) that consists of moves of the form (m, i) with \(m \in M_G {\setminus } M_{!A}\) or \((a, \langle i, k \rangle )\) with \(a \in M_A \wedge k \in \mathbb {N}\) yet changed into m and (a, k), respectively.
Note that the promotion \(G^{\dagger }\) does not depend on the choice of normalized games A and B such that  Also, we in fact get
Also, we in fact get 
Then, let us formalize ‘tags’ on moves of \(G^{\dagger }\) as follows:
-
We duplicate moves of G coming from !A, i.e., ones of the form
 for each \(\varvec{g} \in \mathcal {T}\);
for each \(\varvec{g} \in \mathcal {T}\); -
We duplicate moves of G coming from B, i.e., ones of the form \([(b, \mathscr {E})]_{\varvec{e}}\), as
 for each \(\varvec{g} \in \mathcal {T}\);
for each \(\varvec{g} \in \mathcal {T}\); -
We duplicate internal moves \([m]_{\varvec{e}}\) of G as
 for each \(\varvec{g} \in \mathcal {T}\)
for each \(\varvec{g} \in \mathcal {T}\)
where note again that this way of formalizing ‘tags’ is far from canonical, but it certainly achieves the required subgame relation 
Then, the labeling function, the enabling relation and the dummy function of \(G^{\dagger }\) are again defined by pattern matching on inner tags in the obvious manner, for which like the case of pairing we use peeling and attributes just for convenience. Also, positions of \(G^{\dagger }\) are given by a straightforward generalization of those of exponential defined in Definition 33. Formally, we define promotion of games as follows:
Definition 35
(Promotion of games [71]) Given a game G with  for some normalized games A and B, the promotion
\(G^{\dagger }\) of G is given by:
for some normalized games A and B, the promotion
\(G^{\dagger }\) of G is given by:
-

-
\(\lambda _{G^{\dagger }} {\mathop {=}\limits ^{\mathrm {df. }}} \lambda _G \circ peel _{G^{\dagger }}\), where \( peel _{G^{\dagger }}\) is the function \(M_{G^{\dagger }} \rightarrow M_G\) that maps
 ,
,  ,
,  ;
; -
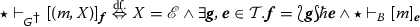 ;
; -
\(x \vdash _{G^{\dagger }} y {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} att _{G^{\dagger }}(x) = att _{G^{\dagger }}(y) \wedge peel _{G^{\dagger }}(x) \vdash _G peel _{G^{\dagger }}(y)\), where \( att _{G^{\dagger }}\) is the function \(M_{G^{\dagger }} \rightarrow \mathcal {T}\) that maps
 ,
,  ,
, 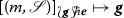 ;
; -
 , where \(\Delta _G([m]_{\varvec{e}}) = [m']_{\varvec{e}}\);
, where \(\Delta _G([m]_{\varvec{e}}) = [m']_{\varvec{e}}\); -
\(P_{G^{\dagger }} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{G^{\dagger }} \mid \forall \varvec{g} \in \mathcal {T} . \ \! \varvec{s} \upharpoonright \varvec{g} \in P_G \wedge (\varvec{s} \upharpoonright \varvec{g} \ne \varvec{\epsilon } \Rightarrow \forall \varvec{h} \in \mathcal {T} . \ \! \varvec{s} \upharpoonright \varvec{h} \ne \varvec{\epsilon } \Rightarrow ede (\varvec{g}) \ne ede (\varvec{h})) \ \! \}\), where \(\varvec{s} \upharpoonright \varvec{g}\) is the j-subsequence of \(\varvec{s}\) that consists of moves x such that \( att _{G^{\dagger }}(x) = \varvec{g}\) yet changed into \( peel _{G^{\dagger }}(x)\).
Now, let us recall concatenation of games, which was first introduced in [71]: Given games J and K such that  and
and  for some normalized games A, B and C, the concatenation \(J \ddagger K\) of J and K is given by:
for some normalized games A, B and C, the concatenation \(J \ddagger K\) of J and K is given by:
-
\(M_{J \ddagger K} {\mathop {=}\limits ^{\mathrm {df. }}} M_J + M_K\), where let \((\_)^{[0]}\) (resp. \((\_)^{[1]}\)) be the ‘tag’ on B in J (resp. K);
-
\(\lambda _{J \ddagger K} {\mathop {=}\limits ^{\mathrm {df. }}} [\lambda _J \downharpoonright M_{B^{[0]}}, \lambda ^{+\mu }_J \upharpoonright M_{B^{[0]}}, \lambda ^{+\mu }_K \upharpoonright M_{B^{[1]}}, \lambda _K \downharpoonright M_{B^{[1]}}]\), where \(\lambda _G^{+ \mu } {\mathop {=}\limits ^{\mathrm {df. }}} \langle \lambda _G^{\mathsf {OP}}, \lambda _G^{\mathsf {QA}}, n \mapsto \lambda _G^{\mathbb {N}} (n) + \mu \rangle \) (G is J or K), and \(\mu {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Max}(\mu (J), \mu (K)) + 1\);
-
\(\star \vdash _{J \ddagger K} m {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} \star \vdash _K m\);
-
\(m \vdash _{J \ddagger K} n \ (m \ne \star ) {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} m \vdash _J n \vee m \vdash _K n \vee (\star \vdash _{B^{[1]}} m \wedge \star \vdash _{B^{[0]}} n)\);
-
\(\Delta _{J \ddagger K} {\mathop {=}\limits ^{\mathrm {df. }}} [\Delta _J, \Delta _K] \upharpoonright M_{J \ddagger K}\);
-
\(P_{J \ddagger K} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {J}_{J \ddagger K} \mid \varvec{s} \upharpoonright J \in P_J, \varvec{s} \upharpoonright K \in P_K, \varvec{s} \upharpoonright B^{[0]}, B^{[1]} \in pr _B \ \! \}\), where \( pr _B {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in P_{B^{[0]} \multimap B^{[1]}} \mid \forall \varvec{t} \preceq {\varvec{s}}. \ \mathsf {Even}(\varvec{t}) \Rightarrow \varvec{t} \upharpoonright B^{[0]} = \varvec{t} \upharpoonright B^{[1]} \ \! \}\).
Note that moves of B (in J or K) become internal in \(J \ddagger K\), and therefore, they would be deleted by the hiding operation \(\mathcal {H}\) on games. Note also that the concatenation \(J \ddagger K\) does not depend on the choice of normalized games A, B and C such that  and
and 
Concatenation corresponds to composition without hiding in the introduction, and it plays a central role in [71]. We shall see later that concatenation
\(\sigma \ddagger \tau \)
of strategies
\(\sigma : J\) and \(\tau : K\) (Definition 60), where  and
and  for some normalized games A, B and C, forms a well-defined strategy on the game \(J \ddagger K\), and also \(\mathcal {H}^\omega (\sigma ) : A \multimap B\), \(\mathcal {H}^\omega (\tau ) : B \multimap C\) and
for some normalized games A, B and C, forms a well-defined strategy on the game \(J \ddagger K\), and also \(\mathcal {H}^\omega (\sigma ) : A \multimap B\), \(\mathcal {H}^\omega (\tau ) : B \multimap C\) and  whence the composition (with hiding) \(\mathcal {H}^\omega (\sigma ) ; \mathcal {H}^\omega (\tau )\) of \(\mathcal {H}^\omega (\sigma )\) and \(\mathcal {H}^\omega (\tau )\) (Definition 60) satisfies \(\mathcal {H}^\omega (\sigma ) ; \mathcal {H}^\omega (\tau ) : A \multimap C\) (for
whence the composition (with hiding) \(\mathcal {H}^\omega (\sigma ) ; \mathcal {H}^\omega (\tau )\) of \(\mathcal {H}^\omega (\sigma )\) and \(\mathcal {H}^\omega (\tau )\) (Definition 60) satisfies \(\mathcal {H}^\omega (\sigma ) ; \mathcal {H}^\omega (\tau ) : A \multimap C\) (for  implies \(\phi : H\) for any strategy \(\phi \) and games G and H; see [71] for the proof).
implies \(\phi : H\) for any strategy \(\phi \) and games G and H; see [71] for the proof).
Note that  is just the familiar relation \(\sigma ; \tau : A \multimap C\) when \(\sigma : J = A \multimap B\) and \(\tau : K = B \multimap C\); concatenation is to capture a generalization of this phenomenon.
is just the familiar relation \(\sigma ; \tau : A \multimap C\) when \(\sigma : J = A \multimap B\) and \(\tau : K = B \multimap C\); concatenation is to capture a generalization of this phenomenon.
Let us formalize ‘tags’ for concatenation as follows:
-
We do not change moves of A or C, i.e., ones of the form \([(a, \mathscr {W})]_{\varvec{e}} \in M_J^{\mathsf {Ext}}\) or \([(c, \mathscr {E})]_{\varvec{f}} \in M_K^{\mathsf {Ext}}\);
-
We change moves of \(B^{[0]}\) in J, i.e., external ones of the form \([(b, \mathscr {E})]_{\varvec{g}}\), into \([((b, \mathscr {E}), \mathscr {S})]_{\varvec{g}}\);
-
We change moves of \(B^{[1]}\) in K, i.e., external ones of the form \([(b, \mathscr {W})]_{\varvec{g}}\), into \([((b, \mathscr {W}), \mathscr {N})]_{\varvec{g}}\);
-
We change internal moves \([m]_{\varvec{l}}\) of J into \([(m, \mathscr {S})]_{\varvec{l}}\);
-
We change internal moves \([n]_{\varvec{r}}\) of K into \([(n, \mathscr {N})]_{\varvec{r}}\).
Again, this implementation of ‘tags’ is not canonical at all, but the point is that it achieves the required subgame relation 
Then, the labeling function, the enabling relation and the dummy function of \(J \ddagger K\) are defined by the obvious pattern matching on inner tags, and positions of \(J \ddagger K\) are defined as usual. Formally, concatenation of games is defined as follows, where it should be clear how the peeling \( peel _{J \ddagger K}\) and the attributes \( att _{J \ddagger K}\) work:
Definition 36
(Concatenation of games [71]) Given games J and K, and normalized games A, B and C such that  and
and  , the concatenation
\(J \ddagger K\) of J and K is defined by:
, the concatenation
\(J \ddagger K\) of J and K is defined by:
-
$$\begin{aligned}&M_{J \ddagger K} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [(a, \mathscr {W})]_{\varvec{e}} \mid [(a, \mathscr {W})]_{\varvec{e}} \in M_J^{\mathsf {Ext}}, [a]_{\varvec{e}} \in M_A \ \! \} \\&\quad \cup \{ [(c, \mathscr {E})]_{\varvec{f}} \mid [(c, \mathscr {E})]_{\varvec{f}} \in M_K^{\mathsf {Ext}}, [c]_{\varvec{f}} \in M_C \ \! \} \\&\quad \cup \{ [((b, \mathscr {E}), \mathscr {S})]_{\varvec{g}} \mid [(b, \mathscr {E})]_{\varvec{g}} \in M_J^{\mathsf {Ext}}, [b]_{\varvec{g}} \in M_B \ \! \} \\&\quad \cup \{ [((b, \mathscr {W}), \mathscr {N})]_{\varvec{g}} \mid [(b, \mathscr {W})]_{\varvec{g}} \in M_K^{\mathsf {Ext}}, [b]_{\varvec{g}} \in M_B \ \! \} \\&\quad \cup \{ [(m, \mathscr {S})]_{\varvec{l}} \mid [m]_{\varvec{l}} \in M_J^{\mathsf {Int}} \ \! \} \cup \{ [(n, \mathscr {N})]_{\varvec{r}} \mid [n]_{\varvec{r}} \in M_K^{\mathsf {Int}} \ \! \}; \end{aligned}$$
-
\(\lambda _{J \ddagger K}([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} \lambda _J^{+\mu }([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {S} \wedge \exists [b]_{\varvec{e}} \in M_B . \ \! [m]_{\varvec{e}} = [(b, \mathscr {E})]_{\varvec{e}} \in M_J^{\mathsf {Ext}}; \\ \lambda _J([m]_{\varvec{e}}) &{}\text {if } X = \mathscr {W} \vee (X = \mathscr {S} \wedge [m]_{\varvec{e}} \in M_J^{\mathsf {Int}}); \\ \lambda _K^{+\mu }([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {N} \wedge \exists [b]_{\varvec{e}} \in M_B . \ \! [m]_{\varvec{e}} = [(b, \mathscr {W})]_{\varvec{e}} \in M_K^{\mathsf {Ext}}; \\ \lambda _K([m]_{\varvec{e}}) &{}\text {if }X = \mathscr {E} \vee (X = \mathscr {N} \wedge [m]_{\varvec{e}} \in M_K^{\mathsf {Int}}) \end{array}\right. }\) where \(\lambda _J^{+ \mu }\) and \(\lambda _K^{+ \mu }\) are as defined above;
-
\(\star \vdash _{J \ddagger K} [(m, X)]_{\varvec{e}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} X = \mathscr {E} \wedge \star \vdash _C [m]_{\varvec{e}}\);
-
\([(m, X)]_{\varvec{e}} \vdash _{J \ddagger K} [(n, Y)]_{\varvec{f}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} {\left\{ \begin{array}{ll} \begin{aligned} &{} ( att _{J \ddagger K}([(m, X)]_{\varvec{e}}) = J = att _{J \ddagger K}([(n, Y)]_{\varvec{f}}) \\ &{} \ \wedge peel _{J \ddagger K}([(m, X)]_{\varvec{e}}) \vdash _J peel _{J \ddagger K}([(n, Y)]_{\varvec{f}})) \\ &{}\vee ( att _{J \ddagger K}([(m, X)]_{\varvec{e}}) = K = att _{J \ddagger K}([(n, Y)]_{\varvec{f}}) \\ &{} \ \ \ \ \wedge peel _{J \ddagger K}([(m, X)]_{\varvec{e}}) \vdash _K peel _{J \ddagger K}([(n, Y)]_{\varvec{f}})) \\ &{}\vee (X = \mathscr {N} \wedge Y = \mathscr {S} \wedge \exists [b]_{\varvec{e}}, [b']_{\varvec{f}} \in M_B^{\mathsf {Init}} . \\ &{} \ \ \ \ \ m = (b, \mathscr {W}) \wedge n = (b, \mathscr {E})) \end{aligned} \end{array}\right. }\) where the function \( att _{J \ddagger K} : M_{J \ddagger K} \rightarrow \{ J, K \}\) is defined by \([(a, \mathscr {W})]_{\varvec{e}} \mapsto J\), \([(m, \mathscr {S})]_{\varvec{l}} \mapsto J\), \([((b, \mathscr {E}), \mathscr {S})]_{\varvec{g}} \mapsto J\), \([(c, \mathscr {E})]_{\varvec{f}} \mapsto K\), \([(n, \mathscr {N})]_{\varvec{r}} \mapsto K\), \([((b, \mathscr {W}), \mathscr {N})]_{\varvec{g}} \mapsto K\), and the function \( peel _{J \ddagger K} : M_{J \ddagger K} \rightarrow M_J \cup M_K\) by \([(a, \mathscr {W})]_{\varvec{e}} \mapsto [(a, \mathscr {W})]_{\varvec{e}}\), \([(c, \mathscr {E})]_{\varvec{f}} \mapsto [(c, \mathscr {E})]_{\varvec{f}}\), \([((b, \mathscr {E}), \mathscr {S})]_{\varvec{g}} \mapsto [(b, \mathscr {E})]_{\varvec{g}}\), \([((b, \mathscr {W}), \mathscr {N})]_{\varvec{g}} \mapsto [(b, \mathscr {W})]_{\varvec{g}}\), \([(m, \mathscr {S})]_{\varvec{l}} \mapsto [m]_{\varvec{l}}\), \([(n, \mathscr {N})]_{\varvec{r}} \mapsto [n]_{\varvec{r}}\);
-
\(\Delta _{J \ddagger K} ([(m, X)]_{\varvec{e}}) {\mathop {=}\limits ^{\mathrm {df. }}} \left\{ \begin{array}{ll} { [}(m', \mathscr {S})]_{\varvec{e}} &{}\text {if }X = \mathscr {S} \text { and } \Delta _J([m]_{\varvec{e}}) = [m']_{\varvec{e}}; \\ {[}(m'', \mathscr {N})]_{\varvec{e}} &{}\text {if }X = \mathscr {N}\text { and } \Delta _K([m]_{\varvec{e}}) = [m'']_{\varvec{e}}; \\ {[}((b, \mathscr {W}), \mathscr {N})]_{\varvec{e}} &{}\text {if }X = \mathscr {S}, \Delta _J([m]_{\varvec{e}}) \uparrow \text { and }m = (b, \mathscr {E}); \\ {[}((b, \mathscr {E}), \mathscr {S})]_{\varvec{e}} &{}\text {if }X = \mathscr {N}, \Delta _K([m]_{\varvec{e}}) \uparrow \text { and }m = (b, \mathscr {W}); \end{array}\right. \)
-
\(P_{J \ddagger K} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {J}_{J \ddagger K} \mid \varvec{s} \upharpoonright J \in P_J, \varvec{s} \upharpoonright K \in P_K, \varvec{s} \upharpoonright B^{[0]}, B^{[1]} \in pr _B \ \! \}\), where \(\varvec{s} \upharpoonright J\) (resp. \(\varvec{s} \upharpoonright K\)) is the j-subsequence of \(\varvec{s}\) that consists of moves m such that \( att _{J \ddagger K}(m) = J\) (resp. \( att _{J \ddagger K}(m) = K\)) yet changed into \( peel _{J \ddagger K}(m)\), \(\varvec{s} \upharpoonright B^{[0]}, B^{[1]}\) is the j-subsequence of \(\varvec{s}\) that consists of moves of \(B^{[0]}\) or \(B^{[1]}\), i.e., moves \([((b, X), Y)]_{\varvec{e}}\) such that \([b]_{\varvec{e}} \in M_B \wedge ((X = \mathscr {E} \wedge Y = \mathscr {S}) \vee (X = \mathscr {W} \wedge Y = \mathscr {N}))\) yet changed into \([(b, \overline{X})]_{\varvec{e}}\), for which \(\overline{\mathscr {E}} {\mathop {=}\limits ^{\mathrm {df. }}} \mathscr {W}\) and \(\overline{\mathscr {W}} {\mathop {=}\limits ^{\mathrm {df. }}} \mathscr {E}\), and \( pr _B {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{t} \in P_{B \multimap B} \mid \forall \varvec{u} \preceq {\varvec{t}}. \ \mathsf {Even}(\varvec{u}) \Rightarrow \varvec{u} \upharpoonright \mathscr {W} = \varvec{u} \upharpoonright \mathscr {E} \ \! \}\).
Example 37
A typical plays of the concatenation \((\mathcal {N} \multimap \mathcal {N}) \ddagger (\mathcal {N} \multimap \mathcal {N})\) is:

Finally, let us recall the rather trivial currying \(\Lambda \) and uncurrying \(\Lambda ^{\circleddash }\) [6] of games. Roughly, currying \(\Lambda \) generalizes the map \(A \otimes B \multimap C \mapsto A \multimap (B \multimap C)\), and uncurrying \(\Lambda ^\circleddash \) does the inverse \(A \multimap (B \multimap C) \mapsto A \otimes B \multimap C\), where A, B and C are arbitrary normalized games. Note that the games \(A \otimes B \multimap C\) and \(A \multimap (B \multimap C)\) coincide up to ‘tags,’ and therefore, the currying and the uncurrying operations boil down to the trivial manipulations on ‘tags.’
Nevertheless, we formalize such manipulations of ‘tags’ here. For their simplicity, let us skip their informal definitions and just present the formal ones:
Definition 38
(Currying of games [71]) If a game G satisfies  for some normalized games A, B and C, then the currying
\(\Lambda (G)\) of G is given by:
for some normalized games A, B and C, then the currying
\(\Lambda (G)\) of G is given by:
-
$$\begin{aligned}&M_{\Lambda (G)} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [(a, \mathscr {W})]_{\varvec{e}} \mid [((a, \mathscr {W}), \mathscr {W})]_{\varvec{e}} \in M_G^{\mathsf {Ext}}, [a]_{\varvec{e}} \in M_A \ \! \} \\&\cup \{ [((b, \mathscr {W}), \mathscr {E})]_{\varvec{f}} \mid [((b, \mathscr {E}), \mathscr {W})]_{\varvec{f}} \in M_G^{\mathsf {Ext}}, [b]_{\varvec{f}} \in M_B \ \! \} \\&\cup \{ [((c, \mathscr {E}), \mathscr {E})]_{\varvec{g}} \mid [(c, \mathscr {E})]_{\varvec{g}} \in M_G^{\mathsf {Ext}}, [c]_{\varvec{g}} \in M_C \ \! \} \cup \{ [(m, \mathscr {N})]_{\varvec{h}} \mid [m]_{\varvec{h}} \in M_G^{\mathsf {Int}} \ \! \}; \end{aligned}$$
-
\(\lambda _{\Lambda (G)}(x) {\mathop {=}\limits ^{\mathrm {df. }}} \lambda _G( peel _{\Lambda (G)}(x))\) for all \(x \in M_{\Lambda (G)}\), where the map \( peel _{\Lambda (G)} : M_{\Lambda (G)} \rightarrow M_G\) is given by \([(a, \mathscr {W})]_{\varvec{e}} \mapsto [((a, \mathscr {W}), \mathscr {W})]_{\varvec{e}}\), \([((b, \mathscr {W}), \mathscr {E})]_{\varvec{f}} \mapsto [((b, \mathscr {E}), \mathscr {W})]_{\varvec{f}}\), \([((c, \mathscr {E}), \mathscr {E})]_{\varvec{g}} \mapsto [(c, \mathscr {E})]_{\varvec{g}}\), \([(m, \mathscr {N})]_{\varvec{h}} \mapsto [m]_{\varvec{h}}\);
-
\(\star \vdash _{\Lambda (G)} [m]_{\varvec{e}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} \exists [c]_{\varvec{e}} \in M_C^{\mathsf {Init}} . \ \! m = ((c, \mathscr {E}), \mathscr {E})\);
-
\([m]_{\varvec{e}} \vdash _{\Lambda (G)} [n]_{\varvec{f}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} peel _{\Lambda (G)}([m]_{\varvec{e}}) \vdash _{G} peel _{\Lambda (G)}([n]_{\varvec{f}})\);
-
\(\Delta _{\Lambda (G)} : [(m, \mathscr {N})]_{\varvec{e}} \mapsto [(m', \mathscr {N})]_{\varvec{e}}\), where \(\Delta _G : [m]_{\varvec{e}} \mapsto [m']_{\varvec{e}}\);
-
\(P_{\Lambda (G)} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{\Lambda (G)} \mid peel _{\Lambda (G)}^*(\varvec{s}) \in P_G \ \! \}\), where pointers in \( peel _{\Lambda (G)}^*(\varvec{s})\) are inherited from the ones in \(\varvec{s}\) in the obvious sense.
It is easy to see that  if
if  which is a generalization of the equation \(\Lambda (A \otimes B \multimap C) = A \multimap (B \multimap C)\).
which is a generalization of the equation \(\Lambda (A \otimes B \multimap C) = A \multimap (B \multimap C)\).
Definition 39
(Uncurrying of games [71]) If a game H, and normalized games A, B and C satisfy  then the uncurrying
\(\Lambda ^{\circleddash }(H)\) of H is defined by:
then the uncurrying
\(\Lambda ^{\circleddash }(H)\) of H is defined by:
-
$$\begin{aligned}&M_{\Lambda ^\circleddash (H)} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [((a, \mathscr {W}), \mathscr {W})]_{\varvec{e}} \mid [(a, \mathscr {W})]_{\varvec{e}} \in M_H^{\mathsf {Ext}}, [a]_{\varvec{e}} \in M_A \ \! \} \\&\quad \cup \{ [((b, \mathscr {E}), \mathscr {W})]_{\varvec{f}} \mid [((b, \mathscr {W}), \mathscr {E})]_{\varvec{f}} \in M_H^{\mathsf {Ext}}, [b]_{\varvec{f}} \in M_B \ \! \} \\&\quad \cup \{ [(c, \mathscr {E})]_{\varvec{g}} \mid [((c, \mathscr {E}), \mathscr {E})]_{\varvec{g}} \in M_H^{\mathsf {Ext}}, [c]_{\varvec{g}} \in M_C \ \! \} \cup \{ [(m, \mathscr {S})]_{\varvec{h}} \mid [m]_{\varvec{h}} \in M_H^{\mathsf {Int}} \ \! \}; \end{aligned}$$
-
\(\lambda _{\Lambda ^\circleddash (H)}(x) {\mathop {=}\limits ^{\mathrm {df. }}} \lambda _H( peel _{\Lambda ^\circleddash (H)}(x))\) for all \(x \in M_{\Lambda ^\circleddash (H)}\), where the map \( peel _{\Lambda ^\circleddash (H)} : M_{\Lambda ^\circleddash (H)} \rightarrow M_H\) is defined by \([((a, \mathscr {W}), \mathscr {W})]_{\varvec{e}} \mapsto [(a, \mathscr {W})]_{\varvec{e}}\), \([((b, \mathscr {E}), \mathscr {W})]_{\varvec{f}} \mapsto [((b, \mathscr {W}), \mathscr {E})]_{\varvec{f}}\), \([(c, \mathscr {E})]_{\varvec{g}} \mapsto [((c, \mathscr {E}), \mathscr {E})]_{\varvec{g}}\), \([(m, \mathscr {S})]_{\varvec{h}} \mapsto [m]_{\varvec{h}}\);
-
\(\star \vdash _{\Lambda ^\circleddash (H)} [m]_{\varvec{e}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} \exists [c]_{\varvec{e}} \in M_C^{\mathsf {Init}} . \ \! m = (c, \mathscr {E})\);
-
\([m]_{\varvec{e}} \vdash _{\Lambda ^\circleddash (H)} [n]_{\varvec{f}} {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} peel _{\Lambda ^\circleddash (H)}([m]_{\varvec{e}}) \vdash _{H} peel _{\Lambda ^\circleddash (H)}([n]_{\varvec{f}})\);
-
\(\Delta _{\Lambda ^\circleddash (H)} : [(m, \mathscr {S})]_{\varvec{h}} \mapsto [(m', \mathscr {S})]_{\varvec{h}}\), where \(\Delta _H : [m]_{\varvec{h}} \mapsto [m']_{\varvec{h}}\);
-
\(P_{\Lambda ^\circleddash (H)} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \varvec{s} \in \mathscr {L}_{\Lambda ^\circleddash (H)} \mid peel _{\Lambda ^\circleddash (H)}^*(\varvec{s}) \in P_H \ \! \}\), where pointers in \( peel _{\Lambda ^\circleddash (H)}^*(\varvec{s})\) are inherited from the ones in \(\varvec{s}\).
Dually to currying,  holds if
holds if  which generalizes the equation \(\Lambda ^\circleddash (A \multimap (B \multimap C)) = A \otimes B \multimap C\). It is also easy to see that \(\Lambda \) and \(\Lambda ^\circleddash \) are inverses to each other on normalized games, i.e., \(\Lambda \circ \Lambda ^\circleddash (A \multimap (B \multimap C)) = A \multimap (B \multimap C)\) and \(\Lambda ^\circleddash \circ \Lambda (A \otimes B \multimap C) = A \otimes B \multimap C\) for any normalized games A, B and C. Note also that currying \(\Lambda (G)\) and the uncurrying \(\Lambda ^\circleddash (H)\) both do not depend on the choice of the normalized games A, B and C such that
which generalizes the equation \(\Lambda ^\circleddash (A \multimap (B \multimap C)) = A \otimes B \multimap C\). It is also easy to see that \(\Lambda \) and \(\Lambda ^\circleddash \) are inverses to each other on normalized games, i.e., \(\Lambda \circ \Lambda ^\circleddash (A \multimap (B \multimap C)) = A \multimap (B \multimap C)\) and \(\Lambda ^\circleddash \circ \Lambda (A \otimes B \multimap C) = A \otimes B \multimap C\) for any normalized games A, B and C. Note also that currying \(\Lambda (G)\) and the uncurrying \(\Lambda ^\circleddash (H)\) both do not depend on the choice of the normalized games A, B and C such that  and
and 
The following are two of the technical highlights of [71], where it is straightforward to see that the additional structure of dummy functions and the strengthened axiom DP2 are preserved under the constructions on games introduced so far (and therefore the two results still hold).
Theorem 40
(Constructions on games [71]) Games are closed under \(\otimes \), \(\multimap \),&, \(\langle \_, \_ \rangle \), !, \((\_)^{\dagger }\), \(\ddagger \), \(\Lambda \) and \(\Lambda ^{\circleddash }\). Moreover, the subgame relation is preserved under these constructions, i.e.,  if
if  for all \(i \in I\), where \(\clubsuit _{i \in I}\) is either \(\otimes \), \(\multimap \),&, \(\langle \_, \_ \rangle \), !, \((\_)^{\dagger }\), \(\ddagger \), \(\Lambda \) or \(\Lambda ^{\circleddash }\) (and thus, I is either \(\{ 1 \}\) or \(\{ 1, 2 \}\)).
for all \(i \in I\), where \(\clubsuit _{i \in I}\) is either \(\otimes \), \(\multimap \),&, \(\langle \_, \_ \rangle \), !, \((\_)^{\dagger }\), \(\ddagger \), \(\Lambda \) or \(\Lambda ^{\circleddash }\) (and thus, I is either \(\{ 1 \}\) or \(\{ 1, 2 \}\)).
Lemma 41
(Hiding lemma on games [71]) Let \(\clubsuit _{i \in I}\) be either \(\otimes \), \(\multimap \),&, \(\langle \_, \_ \rangle \), !, \((\_)^{\dagger }\), \(\ddagger \), \(\Lambda \) or \(\Lambda ^\circleddash \), and \(d \in \mathbb {N} \cup \{ \omega \}\). Then, for any family \((G_i)_{i \in I}\) of games,
-
1
 if \(\clubsuit _{i \in I}\) is not \(\ddagger \);
if \(\clubsuit _{i \in I}\) is not \(\ddagger \); -
2
\(\mathcal {H}^d (G_1 \ddagger G_2) = \mathcal {H}^d(G_1) \ddagger \mathcal {H}^d(G_2)\) if \(\mathcal {H}^d(G_1 \ddagger G_2)\) is not yet normalized, and
 otherwise, where
otherwise, where  and
and  for some normalized game B.
for some normalized game B.
2.3 Strategies
Next, let us recall another central notion of strategies.
2.3.1 Strategies
Our strategies are the dynamic variant introduced in [71]. However, there is nothing special in the definition: A dynamic strategy on a (dynamic) game is a strategy on the game in the conventional sense [6, 51], i.e.,
Definition 42
(Dynamic strategies [6, 51, 71]) A dynamic strategy \(\sigma \) on a (dynamic) game G, written \(\sigma : G\), is a subset \(\sigma \subseteq P_G^{\mathsf {Even}}\) that satisfies:
-
(S1) It is non-empty and even-prefix-closed (i.e., \(\varvec{s}mn \in \sigma \Rightarrow \varvec{s} \in \sigma )\);
-
(S2) It is deterministic (i.e., \(\varvec{s}mn, \varvec{s'}m'n' \in \sigma \wedge \varvec{s}m = \varvec{s'}m' \Rightarrow \varvec{s}mn = \varvec{s'}m'n'\)).
Convention
Henceforth, strategies refer to dynamic strategies by default.
Notation
Henceforth, we often indicate the form of tags of moves \([m_{X_1 X_2 \dots X_k}]_{\varvec{e}}\) of a game G informally by \([G_{X_1 X_2 \dots X_k}]_{\varvec{e}}\).
Example 43
Given a natural number \(n \in \mathbb {N}\), the \({{{\varvec{n}}}}{{{{\varvec{th}}}}}\)
numeral strategy is the strategy  defined by:
defined by:
Example 44
The successor strategy
 is defined by:
is defined by:

where \( y \) and \( n \) abbreviate \( yes \) and \( no \), respectively. Note that it is a formalization of the successor strategy in the introduction.
Example 45
The predecessor strategy
 is defined by:
is defined by:

It is easy to see that \( pred \) implements the predecessor function \(0 \mapsto 0\), \(n+1 \mapsto n\).
Next, let us recall two constraints on strategies: innocence and well bracketing. One of the highlights of HO-games [38] is to establish a one-to-one correspondence between terms of PCF in a certain \(\eta \)-long normal form, known as PCF Böhm trees [8], and innocent, well-bracketed strategies (on games modeling types of PCF). That is, the two conditions limit the codomain of the interpretation of PCF, i.e., the category of HO-games, in such a way that the interpretation becomes full.
Roughly, a strategy is innocent if its computation depends only on the P-view of each odd-length position (rather than the entire position), and well bracketed if every ‘question-answering’ by the strategy is done in the ‘last-question-first-answered’ fashion. Formally:
Definition 46
(Innocence of strategies [6, 38, 51]) A strategy \(\sigma : G\) is innocent if \(\varvec{s}mn, \varvec{t} \in \sigma \wedge \varvec{t} m \in P_G \wedge \lceil \varvec{t} m \rceil _G = \lceil \varvec{s} m \rceil _G \Rightarrow \varvec{t}mn \in \sigma \wedge \lceil \varvec{t}mn \rceil _G = \lceil \varvec{s}mn \rceil _G\).
Definition 47
(Well bracketing of strategies [6, 38, 51]) A strategy \(\sigma : G\) is well bracketed if, whenever \(\varvec{s} q \varvec{t} a \in \sigma \), where q is a question that justifies an answer a, every question in \(\varvec{t'}\) defined by \(\lceil \varvec{s} q \varvec{t} \rceil _G = \lceil \varvec{s} q \rceil _G . \varvec{t'}\) Footnote 12 justifies an answer in \(\varvec{t'}\).
The bijective correspondence holds also for the game model [6], on which our games and strategies are based. Moreover, it corresponds to modeling states and control operators to relaxing innocence and well bracketing in the model; in this sense, the two conditions characterize ‘purely functional’ languages [6].
Note that innocence and well bracketing have been imposed on strategies in order to establish full abstraction and/or definability [15], but neither is our main concern in the present paper. However, we would like P to be able to collect a bounded number of ‘relevant’ moves from each odd-length position in an ‘effective’ fashion; for this point, it is convenient to focus on innocent strategies since it then suffices for P to trace back the chain of justifiers. In fact, we shall define our notion of ‘effective computability’ only on innocent strategies in Sect. 3.
On the other hand, we do not impose well bracketing on strategies (thus, control operators are ‘effective’ in our sense); nevertheless, we shall consider only strategies modeling terms of PCF in the present work, which are all well bracketed.
Remark
We conjecture that it is possible to define ‘effectivity’ of non-innocent strategies in a fashion similar to the case of innocent ones defined in Sect. 3.1. For this, however, we need to modify the procedure for P to collect a bounded number of moves from each odd-length position (defined in Sect. 3.1) so that she may refer to moves outside of P-views, which is left as future work.
Convention
From now on, a strategy refers to an innocent strategy by default. We may clearly regard innocent strategies \(\sigma : G\) as (partial) view functions \(f_\sigma : \lceil P_G^{\mathsf {Odd}} \rceil _G \rightharpoonup M_G\) with the pointer structure implicit (see [51] for the details); we shall freely exchange the tree-representation \(\sigma \) and the function representation \(f_\sigma \), and often write \(\sigma \) for \(f_\sigma \).
As in the case of games, we now define the hiding operation on strategies. Note that an even-length position is not necessarily preserved under the hiding operation on j-sequences. For instance, let \(\varvec{s} m n \varvec{t}\) be an even-length position of a game G such that \(\varvec{s} m\) (resp. \(\varvec{t} n\)) consists of external (resp. internal) moves only. By IE-switch on G, m is an O-move, and so \(\mathcal {H}^\omega (\varvec{s} m n \varvec{t}) = \varvec{s} m\) is of odd-length. Thus, we define:
Definition 48
(Hiding on strategies [71]) Given a game G, a position \(\varvec{s} \in P_G\) and a number \(d \in \mathbb {N} \cup \{ \omega \}\), let
The \({{{\varvec{d}}}}\)-hiding operation \(\mathcal {H}^{{\varvec{d}}}\) on strategies is given by \(\mathcal {H}^d : (\sigma : G) \mapsto \{ \varvec{s} \natural \mathcal {H}_G^d \mid \varvec{s} \in \sigma \ \! \}\). A strategy \(\sigma : G\) is normalized if \(\mathcal {H}^\omega (\sigma ) = \sigma \).
The following beautiful theorem in a sense implies that the above definition is a reasonable one. Also, it induces the hiding functor \(\mathcal {H}^\omega \) from the bicategory \(\mathcal {DG}\) of dynamic games and strategies to the category \(\mathcal {G}\) of static games and strategies [71].
Theorem 49
(Hiding theorem [71]) If \(\sigma : G\), then \(\mathcal {H}^d(\sigma ) : \mathcal {H}^d(G)\) for all \(d \in \mathbb {N} \cup \{ \omega \}\), and \(\underbrace{\mathcal {H}^1 \circ \mathcal {H}^1 \cdots \circ \mathcal {H}^1}_i (\sigma ) = \mathcal {H}^i(\sigma ) : \mathcal {H}^i(G)\) for all \(i \in \mathbb {N}\).
Convention
Thanks to Theorem 49, the i-hiding operation \(\mathcal {H}^i\) on strategies for each \(i \in \mathbb {N}\) can be thought of as the i-times iteration of the 1-hiding operation \(\mathcal {H}^1\), which we call the hiding operation (on strategies) and write \(\mathcal {H}\) for it.
It is straightforward to see that normalized games (resp. strategies) are equivalent to static games (resp. strategies) given in [6]; see [71] for the details.
2.3.2 Constructions on strategies
Next, let us review standard constructions on strategies [6, 51], for which we need to adopt our tags. Having introduced our formalization of ‘tags’ for constructions on games in Sect. 2.2.3, let us just present formalized constructions on strategies (without standard, informal versions) as it should be clear enough.
First, the following derelictions just ‘copy-cat’ the last occurrence of an O-move:
Definition 50
(Derelictions [6, 7, 51]) The dereliction \( der _A : A \Rightarrow A\) on a normalized game A is defined by:

where  (resp. \(\varvec{t} \upharpoonright (\mathscr {E})_{\_}\)) is the j-subsequence of \(\varvec{t}\) that consists of moves of the form
(resp. \(\varvec{t} \upharpoonright (\mathscr {E})_{\_}\)) is the j-subsequence of \(\varvec{t}\) that consists of moves of the form  (resp. \([(a', \mathscr {E})]_{\varvec{e'}}\)) yet changed into \([a]_{\varvec{e}}\) (resp. \([a']_{\varvec{e'}}\)).
(resp. \([(a', \mathscr {E})]_{\varvec{e'}}\)) yet changed into \([a]_{\varvec{e}}\) (resp. \([a']_{\varvec{e'}}\)).
Example 51
The computation of the dereliction \( der _A\) may be depicted as follows:

where \([a^{(1)}]_{\varvec{e^{(1)}}} [a^{(2)}]_{\varvec{e^{(2)}}} [a^{(3)}]_{\varvec{e^{(3)}}} [a^{(4)}]_{\varvec{e^{(4)}}} \dots \in P_A\).
Next, as in the case of tensor of games, we have:
Definition 52
(Tensor of strategies [5, 6, 51]) Given normalized games A, B, C and D, and normalized strategies \(\sigma : A \multimap C\) and \(\tau : B \multimap D\), the tensor (product) \(\sigma \! \otimes \! \tau : A \otimes B \multimap C \otimes D\) of \(\sigma \) and \(\tau \) is defined by:
where \(\varvec{s} \upharpoonright (\mathscr {W}, \_)\) (resp. \(\varvec{s} \upharpoonright (\mathscr {E}, \_)\)) is the j-subsequence of \(\varvec{s}\) that consists of moves of the form \([((m, \mathscr {W}), X)]_{\varvec{e}}\) (resp. \([((m', \mathscr {E}), Y)]_{\varvec{e'}}\)) yet changed into \([(m, X)]_{\varvec{e}}\) (resp. \([(m', Y)]_{\varvec{e'}}\)).
Intuitively, the tensor \(\sigma \! \otimes \! \tau : A \otimes B \multimap C \otimes D\) plays by \(\sigma \) if the last occurrence of an O-move belongs to \(A \multimap C\), and by \(\tau \) otherwise.
Example 53
Consider the tensor  . A typical play by \( succ \otimes pred \) is as follows:
. A typical play by \( succ \otimes pred \) is as follows:

The next one is the pairing in the category \(\mathcal {G}\) of static games and strategies [6]:
Definition 54
(Pairing of strategies [6, 7, 38]) Given normalized games A, B and C, and normalized strategies \(\sigma : C \multimap A\) and \(\tau : C \multimap B\), the pairing \( \langle \sigma , \tau \rangle : C \multimap A \& B\) of \(\sigma \) and \(\tau \) is defined by:
where \(\varvec{s} \upharpoonright (\mathscr {W} \multimap \mathscr {W} \mathscr {E})\) (resp. \(\varvec{s} \upharpoonright (\mathscr {W} \multimap \mathscr {E} \mathscr {E})\)) is the j-subsequence of \(\varvec{s}\) that consists of moves of the form \([(c, \mathscr {W})]_{\varvec{e}}\) or \([((a, \mathscr {W}), \mathscr {E})]_{\varvec{f}}\) with \([a] \in M_A\) (resp. or \([((b, \mathscr {E}), \mathscr {E})]_{\varvec{g}}\) with \([b] \in M_B\)) yet the latter changed into \([(a, \mathscr {E})]_{\varvec{f}}\) (resp. \([(b, \mathscr {E})]_{\varvec{g}}\)).
However, for the bicategory \(\mathcal {DG}\) of dynamic games and strategies [71], we need the following generalization (for the reason explained right before Definition 31):
Definition 55
(Generalized pairing of strategies [71]) Given strategies \(\sigma : L\) and \(\tau : R\) such that 
 for some normalized games A, B and C, the generalized pairing
\(\langle \sigma , \tau \rangle : \langle L, R \rangle \) of \(\sigma \) and \(\tau \) is defined by:
for some normalized games A, B and C, the generalized pairing
\(\langle \sigma , \tau \rangle : \langle L, R \rangle \) of \(\sigma \) and \(\tau \) is defined by:
It is clearly a generalization of static pairing; consider the case where \(L = C \multimap A\) and \(R = C \multimap B\).
Convention
Henceforth, pairing of strategies refers to the generalized one.
Example 56
Consider the pairing  . Its typical plays are as follows:
. Its typical plays are as follows:

Next, let us recall promotion of strategies:
Definition 57
(Promotion of strategies [6, 7, 51]) Given normalized games A and B, and a normalized strategy \(\phi : \ !A \multimap B\), the promotion \(\phi ^{\dagger } : \ !A \multimap \ !B\) of \(\phi \) is given by:
where \(\varvec{s} \upharpoonright \varvec{e}\) is the j-subsequence of \(\varvec{s}\) that consists of moves of the form  with
with  with \([a]_{\varvec{f'}} \in M_A\), which are, respectively, changed into \([(b, \mathscr {E})]_{\varvec{e'}}\) and
with \([a]_{\varvec{f'}} \in M_A\), which are, respectively, changed into \([(b, \mathscr {E})]_{\varvec{e'}}\) and  .
.
As stated before, [71] generalizes promotion of strategies (for the reason explained before Definition 35) as follows:
Definition 58
(Generalized promotion of strategies [71]) Given a strategy \(\phi : G\) such that  for some normalized games A and B, the generalized promotion
\(\phi ^{\dagger } : G^{\dagger }\) of \(\phi \) is defined by:
for some normalized games A and B, the generalized promotion
\(\phi ^{\dagger } : G^{\dagger }\) of \(\phi \) is defined by:
where \(\varvec{s} \upharpoonright \varvec{e}\) is the j-subsequence of \(\varvec{s}\) that consists of moves of the form  with \([b]_{\varvec{e'}} \in M_B\),
with \([b]_{\varvec{e'}} \in M_B\),  with \([a]_{\varvec{f'}} \in M_A\), or
with \([a]_{\varvec{f'}} \in M_A\), or  with \([m]_{\varvec{e'}} \in M_G^{\mathsf {Int}}\), which are respectively changed into \([(b, \mathscr {E})]_{\varvec{e'}}\),
with \([m]_{\varvec{e'}} \in M_G^{\mathsf {Int}}\), which are respectively changed into \([(b, \mathscr {E})]_{\varvec{e'}}\),  .
.
It is clearly a generalization of static promotion; consider the case \(G = \ !A \multimap B\).
Convention
Henceforth, promotion of strategies refers to the generalized one.
Example 59
Consider the promotion  . Its typical play is as depicted in the following diagram:
. Its typical play is as depicted in the following diagram:

Note that there are two threads Footnote 13 in the above play, and the strategy \( succ ^{\dagger }\) behaves as \( succ \) in both of the threads.
Now, let us recall a central construction of strategies in [71], which reformulates composition (with hiding) of strategies as follows:
Definition 60
(Concatenation and composition of strategies [71]) Let \(\sigma : J\) and \(\tau : K\) such that  and
and  for some normalized games A, B and C. The concatenation
\(\sigma \ddagger \tau : J \ddagger K\) of \(\sigma \) and \(\tau \) is defined by:
for some normalized games A, B and C. The concatenation
\(\sigma \ddagger \tau : J \ddagger K\) of \(\sigma \) and \(\tau \) is defined by:
and their composition \(\sigma ; \tau : \mathcal {H}^\omega (J \ddagger K)\) by \(\sigma ; \tau {\mathop {=}\limits ^{\mathrm {df. }}} \mathcal {H}^\omega (\sigma \ddagger \tau )\) (see Theorem 49).
We also write \(\tau \circ \sigma \) for \(\sigma ; \tau \). If \(J = A \multimap B\), \(K = B \multimap C\), then our composition  coincides with the standard one [6, 38, 51]; see [71] for the details. In this sense, our composition generalizes the standard one, and moreover it is decomposed into concatenation plus hiding.
coincides with the standard one [6, 38, 51]; see [71] for the details. In this sense, our composition generalizes the standard one, and moreover it is decomposed into concatenation plus hiding.
Example 61
Consider the concatenation  . Its typical play is as follows:
. Its typical play is as follows:

Finally, we recall the currying and the uncurrying of strategies:
Definition 62
(Currying and uncurrying of strategies [6]) If \(\phi : G\) (resp. \(\psi : H\)) and  (resp.
(resp.  ) for some normalized games A, B and C, then the currying
\(\Lambda (\phi ) : \Lambda (G)\) of \(\phi \) (resp. the uncurrying
\(\Lambda ^\circleddash (\psi ) : \Lambda ^\circleddash (H)\) of \(\psi \)) is defined, respectively, by:
) for some normalized games A, B and C, then the currying
\(\Lambda (\phi ) : \Lambda (G)\) of \(\phi \) (resp. the uncurrying
\(\Lambda ^\circleddash (\psi ) : \Lambda ^\circleddash (H)\) of \(\psi \)) is defined, respectively, by:
Theorem 63
(Constructions on strategies [71]) Derelictions are well-defined strategies, and strategies are closed under \(\otimes \), \(\langle \_, \_ \rangle \), \((\_)^{\dagger }\), \(\ddagger \), \(\Lambda \) and \(\Lambda ^\circleddash \).
Lemma 64
(Hiding lemma on strategies [71]) Let \(\spadesuit _{i \in I}\) be either \(\otimes \), \(\langle \_, \_ \rangle \), \((\_)^{\dagger }\), \(\ddagger \), \(\Lambda \) or \(\Lambda ^\circleddash \), and \(d \in \mathbb {N} \cup \{ \omega \}\). Then, for any family \((\sigma _i)_{i \in I}\) of strategies, we have:
-
1
\(\mathcal {H}^d(\spadesuit _{i \in I}\sigma _i) = \spadesuit _{i \in I} \mathcal {H}^d(\sigma _i)\) if \(\spadesuit _{i \in I}\) is not \(\ddagger \);
-
2
\(\mathcal {H}^d (\sigma _1 \ddagger \sigma _2) = \mathcal {H}^d(\sigma _1) \ddagger \mathcal {H}^d(\sigma _2)\) if \(\mathcal {H}^d(\sigma _1 \ddagger \sigma _2)\) is not yet normalized, and \(\mathcal {H}^d(\sigma _1 \ddagger \sigma _2) = \mathcal {H}^d(\sigma _1) ; \mathcal {H}^d(\sigma _2)\) otherwise.
3 Viable strategies
We have defined our games and strategies in the previous section. In this main section of the present paper, we introduce a novel notion of ‘effective’ or viable strategies, and show that viable (dynamic)Footnote 14 strategies subsume all computations of the programming language PCF [58, 61], and thus they are Turing complete in particular.
In Sect. 3.1, we define viability of strategies and show that it is preserved under all the constructions on strategies defined in Sect. 2.3.2. We then describe various examples of viable strategies in Sect. 3.2, based on which we finally prove in Sect. 3.3 that viable (dynamic) strategies may interpret all terms of PCF.
3.1 Viable strategies
The idea of viable strategies is as follows. First, it seems necessary to restrict the number of previous occurrences which P is allowed to look at (to calculate the next P-move) to a bounded one since the number of odd-length positions of a game can be infinite, e.g., consider the game \(\mathcal {N}\) (Example 23).Footnote 15 Fortunately, to model the language PCF, it turns out that strategies only need to read off at most the last three occurrences of each P-view (and possibly a few initial or internal moves, which are easily identified as well) as we shall see, which is clearly ‘effective’ in an informal sense. Thus, it remains to formulate how strategies ‘effectively’ compute the next P-move from such a bounded number of previous occurrences. Note that (as already mentioned) computation of internal O-moves should be done by P, but it is rather trivial by the axiom DP2 (Definition 18), and therefore, we shall omit it for brevity. Note also that we shall focus on innocent strategies as a means to narrow down previous occurrences to be concerned with.Footnote 16
As the set \(\pi _1(M_G)\) is finite for any game G (Definition 8), innocent strategies that are finitary in the sense that their view functions are finite seem sufficient at first glance. However, to model fixed-point combinators in PCF, strategies need to initiate new threads unboundedly many times [7, 38] (Example 75); also, ‘effective’ strategies have to be closed under promotion (Definition 57) for modeling PCF, in which possible outer tags are infinitely many. Thus, finitary strategies are not strong enough.
Then, how can we give a stronger notion of ‘effectivity’ of the next P-move from (a bounded number of) previous occurrences solely in terms of games and strategies? Our solution, which is the main achievement of the present work, is to define a strategy \(\sigma : G\) to be ‘effective’ or viable (Definition 70) if it is ‘describable’ by a finitary strategy, called an instruction strategy for \(\sigma \) (Definition 68), on the instruction game for G (Definition 65); see Sect. 1.7 for an illustration of the idea.
Having explained the idea of viable strategies, let us proceed in the present section to make it mathematically precise.
Notation
Given a game G, we assign a symbol \(\mathsf {m}\) to each \(m \in \pi _1(M_G)\), for which we may assume that these symbols are pairwise distinct for the set \(\pi _1 (M_G)\) is finite, and define \(\mathsf {Sym}(\pi _1 (M_G)) {\mathop {=}\limits ^{\mathrm {df. }}} \{ \mathsf {m} \mid m \in \pi _1(M_G) \}\). Also, we assign symbols to elements of outer tags by the map \(\mathscr {C} : \ell \mapsto \prime \), \(\hbar \mapsto \sharp \),  ,
,  , and define \(\mathsf {T} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \prime , \sharp , \langle , \rangle \}\). (N.b., these symbols are technically not necessary at all; they are just for conceptual clarity.)
, and define \(\mathsf {T} {\mathop {=}\limits ^{\mathrm {df. }}} \{ \prime , \sharp , \langle , \rangle \}\). (N.b., these symbols are technically not necessary at all; they are just for conceptual clarity.)
Definition 65
(Instruction games) The instruction game on a game G is the game \(\mathcal {G}(M_G)\) given by:
-
\(M_{\mathcal {G}(M_G)} {\mathop {=}\limits ^{\mathrm {df. }}} \{ [\hat{q}], [q], [\square ], [\checkmark ] \} \cup \{ [\mathsf {m}] \mid \mathsf {m} \in \mathsf {Sym}(\pi _1(M_G)) \} \cup \{ [\mathsf {e}] \mid \mathsf {e} \in \mathsf {T} \ \! \}\), where the elements of \(M_{\mathcal {G}(M_G)}\) are assumed to be pairwise distinct;
-
\(\lambda _{\mathcal {G}(M_G)} : [\hat{q}] \mapsto (\mathsf {O}, \mathsf {Q}, 0)\), \([q] \mapsto (\mathsf {O}, \mathsf {Q}, 0)\), \([\square ] \mapsto (\mathsf {P}, \mathsf {A}, 0)\), \([\checkmark ] \mapsto (\mathsf {P}, \mathsf {A}, 0)\), \([\mathsf {m}] \mapsto (\mathsf {P}, \mathsf {A}, 0)\), \([\mathsf {e}] \mapsto (\mathsf {P}, \mathsf {A}, 0)\);
-
\(\vdash _{\mathcal {G}(M_G)} {\mathop {=}\limits ^{\mathrm {df. }}} \{ (\star , [\hat{q}]), ([\hat{q}], [\square ]), ([q], [\checkmark ]) \} \cup \{ ([\hat{q}], [\mathsf {m}]) \mid \mathsf {m} \in \mathsf {Sym}(\pi _1(M_G)) \} \cup \{ ([\mathsf {m}], [q]) \mid \mathsf {m} \in \mathsf {Sym}(\pi _1(M_G)) \} \cup \{ ([q], [\mathsf {e}]) \mid \mathsf {e} \in \mathsf {T} \ \! \} \cup \{ ([\mathsf {e}], [q]) \mid \mathsf {e} \in \mathsf {T} \ \! \}\);
-
\(\Delta _{\mathcal {G}(M_G)} {\mathop {=}\limits ^{\mathrm {df. }}} \emptyset \);
-
\(P_{\mathcal {G}(M_G)} {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Pref} (\{ [\hat{q}] [\square ] \} \cup \{ [\hat{q}] [\mathsf {m}] [q] [\mathscr {C}(e_1)] [q] [\mathscr {C}(e_2)] \dots [q] [\mathscr {C}(e_k)] [q] [\checkmark ] \mid \mathsf {m} \in \mathsf {Sym}(\pi _1(M_G)), e_1 e_2 \dots e_k \in \mathcal {T} \ \! \})\), where each non-initial occurrence is justified by the last occurrence.
Convention
We loosely call games of the form \( \mathcal {G}(M_G) \& \mathcal {G}(M_G) \& \mathcal {G}(M_G) \Rightarrow \mathcal {G}(M_G)\), where G is some game, instruction games as well. For brevity, we write ‘tags’ for instruction games \( \mathcal {G}(M_G) \& \mathcal {G}(M_G) \& \mathcal {G}(M_G) \Rightarrow \mathcal {G}(M_G)\) informally, i.e., \( \mathcal {G}(M_G)^{[0]} \& \mathcal {G}(M_G)^{[1]} \& \mathcal {G}(M_G)^{[2]} \Rightarrow \mathcal {G}(M_G)^{[3]}\), \(\hat{q}^{[0]}\), \(q^{[1]}\), \(\sharp ^{[2]}\), \(\checkmark ^{[3]}\), etc.
The positions \([\hat{q}] [\mathsf {m}] [q] [\mathscr {C}(e_1)] [q] [\mathscr {C}(e_2)] \dots [q] [\mathscr {C}(e_k)] [q] [\checkmark ]\) and \([\hat{q}_G] [\square ]\) of \(\mathcal {G}(M_G)\) are to represent the move \([m]_{e_1 e_2 \dots e_k} \in M_G\) (if it exists) and ‘no move,’ respectively. Note that pointers in these positions are all trivial, and thus, we usually omit them.
Notation
Let G be a game, and \([m]_{\varvec{e}} \in M_G\) with \(\varvec{e} = e_1 e_2 \dots e_k\). We write \(\underline{[m]_{\varvec{e}}}\) for the strategy on \(\mathcal {G}(M_G)\) given by:
and similarly \(\underline{[\square ]} {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Pref}(\{ [\hat{q}] [\square ] \})^{\mathsf {Even}} : \mathcal {G}(M_G)\). Given a finite sequence \(\varvec{s} = [m_l]_{\varvec{e^{(l)}}} [m_{l-1}]_{\varvec{e^{(l-1)}}} \dots [m_1]_{\varvec{e^{(1)}}} \in M_G^*\) and a natural number \(n \geqslant l\), we define \( \underline{\varvec{s}}_n {\mathop {=}\limits ^{\mathrm {df. }}} \langle \underbrace{\underline{[\square ]}, \dots , \underline{[\square ]}}_{n-l}, \underline{[m_l]_{\varvec{e^{(l)}}}}, \underline{[m_{l-1}]_{\varvec{e^{(l-1)}}}}, \dots , \underline{[m_1]_{\varvec{e^{(1)}}}} \rangle : \mathcal {G}(M_G)^n {\mathop {=}\limits ^{\mathrm {df. }}} \underbrace{\mathcal {G}(M_G) \& \mathcal {G}(M_G) \dots \& \mathcal {G}(M_G)}_{n}\), where the n-ary pairing and product are abbreviations of the \((n-1)\)-times iteration of the binary ones from the left.Footnote 17 Given a strategy \(\sigma : \mathcal {G}(M_G)\), we define \(\mathcal {M}(\sigma )\) to be the unique move in \(M_G\) such that \(\underline{\mathcal {M}(\sigma )} = \sigma \) if it exists, and undefined otherwise.
Once again, the idea is to ‘describe’ or realize an ‘effective’ strategy \(\sigma : G\) by a finitary strategy \(\mathcal {A}(\sigma )^\circledS \) on the instruction game \(\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)\) in the sense illustrated in Sect. 1.7. For instance, recall the successor strategy \( succ : \mathcal {N} \Rightarrow \mathcal {N}\) in Example 44, which computes as in Fig. 4. It is then easy to see that this computation is representable by a finite partial function \((m_3, m_2, m_1) \mapsto m\), where \(m_1\), \(m_2\), \(m_3\) are the last, the second last and the third last occurrences of the P-view of each odd-length position of \(\mathcal {N} \Rightarrow \mathcal {N}\), respectively, and m is the next P-move (n.b., thus, \( succ \) is actually \( finitary \)). Concretely, the finite partial function is given by the following table:

Clearly, \( succ \) is realizable by a finitary strategy \(\mathcal {A}( succ )^\circledS : \mathcal {G}(M_{\mathcal {N} \Rightarrow \mathcal {N}})^3 \Rightarrow \mathcal {G}(M_{\mathcal {N} \Rightarrow \mathcal {N}})\) in the sense that \(\mathcal {A}( succ )^\circledS \circ \langle \underline{m_3}, \underline{m_2}, \underline{m_1} \rangle ^{\dagger } = \underline{m}\) holds for all pairs \((m_3, m_2, m_1) \mapsto m\) in the table. Diagrammatically, \(\mathcal {A}( succ )^\circledS \) computes as follows:




where \(\mathsf {x}\) is either \(\mathsf {yes}\) or \(\mathsf {no}\). Obviously, \(\mathcal {A}( succ )^\circledS \) is finitary,Footnote 18 and it realizes the computation of \( succ \). In Definition 67, we shall define generally finite tables \(\mathcal {A}(\sigma )\) for such strategies \(\mathcal {A}(\sigma )^\circledS : \mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)\) as st-algorithms for a given viable strategy \(\sigma : G\).
However, there remain two problems. The first one is the pairing \(\langle \sigma , \tau \rangle : \langle L, R \rangle \) of strategies \(\sigma : L\) and \(\tau : R\) such that  and
and  for some normalized games A, B and C: Because moves of C are common to \(\sigma \) and \(\tau \), the last three occurrences of each P-view may not suffice; the pairing \(\langle \sigma , \tau \rangle \) needs to know whether A or B the first occurrence of each position of \(\langle L, R \rangle \) belongs to. Also, the occurrence becomes no longer initial as soon as the pairing is post-concatenated; thus, it does not suffice to trace the first occurrence of each position. We shall overcome this point by collecting necessary information as states (Definition 67).
for some normalized games A, B and C: Because moves of C are common to \(\sigma \) and \(\tau \), the last three occurrences of each P-view may not suffice; the pairing \(\langle \sigma , \tau \rangle \) needs to know whether A or B the first occurrence of each position of \(\langle L, R \rangle \) belongs to. Also, the occurrence becomes no longer initial as soon as the pairing is post-concatenated; thus, it does not suffice to trace the first occurrence of each position. We shall overcome this point by collecting necessary information as states (Definition 67).
The second one is how to ‘effectively’ calculate the ‘relevant’ (and finite) part of outer tags represented by moves occurring in an instruction game (for the number of all outer tags is infinite). For this point, we introduce the notion of m-views:
Definition 66
(M-views) Let G be a game, and assume \(\varvec{s} \in P_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)}\), where we omit tags in \(\varvec{s}\) in the present definition for brevity. Pairing each occurrence of \(\langle \) in \(\varvec{s}\) with the most recent yet unpaired occurrence of \(\rangle \) in \(\varvec{s}\), one component of such a pair is called the mate of the other. The depth of an occurrence of \(\langle \) in \(\varvec{s}\) is the number of previous occurrences of \(\langle \) in the same component game \(\mathcal {G}(M_G)\) whose mate does not occur before that occurrence; the depth of an occurrence of \(\rangle \) in \(\varvec{s}\) is the depth of its mate in \(\varvec{s}\). The matching view (m-view) \(\llbracket \varvec{s} \rrbracket _G^d\) of \(\varvec{s}\) up to depth \(d \in \mathbb {N}\) is the subsequence of \(\varvec{s}\) that consists of occurrences of \(\langle \) or \(\rangle \) of depth \(\leqslant d\).
It is clearly ‘effective’ to calculate the m-view of a given position of an instruction game in an informal sense. For instance, deterministic pushdown automata [35, 48, 64] may compute m-views into the stack, where we assume that positions of games are written on the input tape, in the obvious manner. We may even dispense with a stack by embedding the depth d of each occurrence of \(\langle \) or \(\rangle \) by the d-times iteration of \(q . \prime \) right after the occurrence in positions of instruction games (for which we need to slightly modify the notion of instruction games accordingly). Nevertheless, for simplicity, we shall not specify a method for the calculation of m-views.
Notation
Given a finite sequence \(\varvec{s} = x_k x_{k-1} \dots x_1\) and a number \(l \in \mathbb {N}\), we define:
A function \(f : \pi _1(M_G) \rightarrow \{ \top , \bot \}\), where G is a game, and \(\top \) and \(\bot \) are arbitrarily fixed, distinct symbols, induces another function \(f^\star : M_G^*\rightarrow \pi _1(M_G)^*\) defined by \(f^\star ([m_k]_{\varvec{e^{(k)}}} [m_{k-1}]_{\varvec{e^{(k-1)}}} \dots [m_1]_{\varvec{e^{(1)}}}) {\mathop {=}\limits ^{\mathrm {df. }}} m_{i_l} m_{i_{l-1}} \dots m_{i_1}\), where \(l \leqslant k\), and \(m_{i_l} m_{i_{l-1}} \dots m_{i_1}\) is the subsequence of \(m_k m_{k-1} \dots m_1\) that consists of \(m_{i_j}\) such that \(f(m_{i_j}) = \top \) for \(j = 1, 2, \dots , l\).
We are now ready to make the notion of ‘describable by a finitary strategy’ precise:
Definition 67
(St-algorithms) An st-algorithm \(\mathcal {A}\) on a game G, written \(\mathcal {A} {:}{:} G\), is a family \(\mathcal {A} = (\mathcal {A}_{\varvec{m}}, |\mathcal {A}_{\varvec{m}}|, \Vert \mathcal {A}_{\varvec{m}} \Vert )_{\varvec{m} \in \mathcal {S}_{\mathcal {A}}}\) of triples of a finite partial function \( \mathcal {A}_{\varvec{m}} : \partial _{\varvec{m}} (P_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G) \& \varvec{2}}^{\mathsf {Odd}}) \rightharpoonup M_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G) \& \varvec{2}}\) and natural numbers \(|\mathcal {A}_{\varvec{m}}|, \Vert \mathcal {A}_{\varvec{m}} \Vert \in \mathbb {N}\), called the view-scope and the mate-scope of \(\mathcal {A}_{\varvec{m}}\), respectively, where:
-
\(\mathcal {S}_{\mathcal {A}} \subseteq \pi _1(M_G)^*\) is a finite set, whose elements are called states;
-
\(\partial _{\varvec{m}} (\varvec{t}x) {\mathop {=}\limits ^{\mathrm {df. }}} (\varvec{t}x \! \downharpoonright |\mathcal {A}_{\varvec{m}}|, \llbracket \varvec{t}x \rrbracket _G^{\Vert \mathcal {A}_{\varvec{m}}\Vert })\) for all \( \varvec{t}x \in P_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G) \& \varvec{2}}^{\mathsf {Odd}}\)
equipped with the query (function) \(\mathcal {Q}_{\mathcal {A}} : \pi _1(M_G) \rightarrow \{ \top , \bot \}\) that satisfies:
-
(Q) \([m]_{\varvec{e}} \in M_G^{\mathsf {Init}} \Rightarrow \mathcal {Q}_{\mathcal {A}}(m) = \top \).
Remark
Note that it does not make a difference if each st-algorithm \(\mathcal {A} {:}{:} G\) focuses on the P-views of each \( \varvec{t}x \in P_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G) \& \varvec{2}}^{\mathsf {Odd}}\) for \(\lceil \varvec{t} x \rceil = \varvec{t} x\) by the trivial pointers.
Definition 68
(Instruction strategies) Given a game G, an st-algorithm \(\mathcal {A} {:}{:} G\) and a state \(\varvec{m} \in \mathcal {S}_{\mathcal {A}}\), the instruction strategy \(\mathcal {A}_{\varvec{m}}^\circledS \) of \(\mathcal {A}\) at \(\varvec{m}\) is the strategy on the game \( \mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G) \& \varvec{2}\) defined by:
where the justifier of y in \(\varvec{t} x y\) is the obvious, canonical one.
Convention
Given an st-algorithm \(\mathcal {A} {:}{:} G\), each instruction strategy \(\mathcal {A}_{\varvec{m}}^\circledS \) has to specify pointers in \(P_G\), which in the present work are always either the last or the third last occurrence, or the justifier of the second occurrence of the P-view of each odd-length position of G (as we shall see); it is why \(\mathcal {A}_{\varvec{m}}^\circledS \) is on the game \( \mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G) \& \varvec{2}\), not the instruction game \(\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)\), so that it may specify the ternary choice on the justifiers in the component game \(\varvec{2}\) (by \( tt \), \( ff \) or ‘no answer’). However, since justifiers in \(P_G\) occurring in this paper are all obvious ones, we henceforth regard \(\mathcal {A}_{\varvec{m}}\) and \(\mathcal {A}_{\varvec{m}}^\circledS \) as \(\mathcal {A}_{\varvec{m}} : \partial _{\varvec{m}} (P_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)}^{\mathsf {Odd}}) \rightharpoonup M_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)}\) and \(\mathcal {A}_{\varvec{m}}^\circledS : \mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)\), respectively, keeping the justifiers implicit.
Remark
Since an st-algorithm \(\mathcal {A} {:}{:} G\) refers to m-views only occasionally, we regard each \(\mathcal {A}_{\varvec{m}}\) as a partial function \(\{ \varvec{t}x \! \downharpoonright |\mathcal {A}_{\varvec{m}}| \mid \varvec{t}x \in P_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)}^{\mathsf {Odd}} \} \rightharpoonup M_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)}\) in most cases. Accordingly, \(\mathcal {A}_{\varvec{m}}^\circledS \) is mostly a strategy on the game \(\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)\) whose partial function representation \(\mathcal {A}_{\varvec{m}}\) is finite.
Thus, an instruction strategy is a strategy on the game \(\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)\), where G is a game, that is finitary in the sense that it is representable by a finite partial function, and so it is clearly ‘effective’ in an informal sense. We shall see that the number 3 on \(\mathcal {G}(M_G)^3\) is the least number to achieve Turing completeness in Sect. 3.3. As already mentioned, our idea is to utilize such an instruction strategy as a ‘description’ of a strategy on G, which may be ‘effectively’ read off:
Definition 69
(Realizability) The strategy \(\mathsf {st}(\mathcal {A}) : G\) realized by an st-algorithm \(\mathcal {A} {:}{:} G\) is defined by:
where \(\mathcal {A}^\circledS (\lceil \varvec{s}a \rceil \! \downharpoonright 3) {\mathop {\simeq }\limits ^{\mathrm {df. }}} \mathcal {M}(\mathcal {A}^\circledS _{\mathcal {Q}_{\mathcal {A}}^\star (\lceil \varvec{s}a \rceil )} \circ (\underline{\lceil \varvec{s}a \rceil \! \downharpoonright 3}_3)^{\dagger })\),Footnote 19 \(\mathcal {A}^\circledS (\lceil \varvec{s}a \rceil \! \downharpoonright 3) \downarrow \) presupposes \(\mathcal {Q}_{\mathcal {A}}^\star (\lceil \varvec{s}a \rceil ) \in \mathcal {S}_{\mathcal {A}}\), and the justifier of b in \(\varvec{s} a b\) is the occurrence specified by \(\mathcal {A}^\circledS _{\mathcal {Q}_{\mathcal {A}}^\star (\lceil \varvec{s}a \rceil )}\) (see the convention below Definition 68).
Clearly, \(\mathcal {A} {:}{:} G \Rightarrow \mathsf {st}(\mathcal {A}) : G\) holds. We are now ready to define the central notion of the present work, namely ‘effective computability’ of strategies:
Definition 70
(Viability of strategies) A strategy \(\sigma : G\) is viable if there exists an st-algorithm \(\mathcal {A} {:}{:} G\) that realizes \(\sigma \), i.e., \(\mathsf {st}(\mathcal {A}) = \sigma \).
That is, a strategy \(\sigma : G\) is viable if there is a finitary strategy on \(\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)\) that ‘describes’ the computation of \(\sigma \). The terms realize and realizability come from mathematical logic, in which a realizer refers to some computational information that ‘realizes’ the constructive truth of a mathematical statement [65].
Given an st-algorithm \(\mathcal {A} {:}{:} G\) that realizes a strategy \(\sigma : G\), P may ‘effectively’ execute \(\mathcal {A}\) to compute \(\sigma \) roughly as follows:
-
1
Given \(\varvec{s}a \in P_G^{\mathsf {Odd}}\), P calculates the current state \(\varvec{m} {\mathop {=}\limits ^{\mathrm {df. }}} \mathcal {Q}_{\mathcal {A}}^\star (\lceil \varvec{s}a \rceil )\) and the last (up to) three moves \(\lceil \varvec{s}a \rceil \! \downharpoonright 3\) of the P-view; if \(\varvec{m} \not \in \mathcal {S}_{\mathcal {A}}\), then she stops, i.e., the next move is undefined;
-
2
Otherwise, she composes \((\underline{\lceil \varvec{s}a \rceil \! \downharpoonright 3}_3)^{\dagger }\) with \(\mathcal {A}_{\varvec{m}}^\circledS \), calculating \(\mathcal {A}_{\varvec{m}}^\circledS \circ (\underline{\lceil \varvec{s}a \rceil \! \downharpoonright 3}_3)^{\dagger }\);
-
3
Finally, she reads off the next move \(\mathcal {M}(\mathcal {A}_{\varvec{m}}^\circledS \circ (\underline{\lceil \varvec{s}a \rceil \! \downharpoonright 3}_3)^{\dagger })\) (and its justifier) and performs that move (with the pointer).
For conceptual clarity, here we assume that P may write down moves \([m]_{\varvec{e}}\) in P-views as \([\mathsf {m}]_{\mathscr {C}^*(\varvec{e})}\) and execute strategies on instruction games symbolically on her ‘scratch pad,’ and also she may read off strategies \(\sigma : \mathcal {G}(M_G)\) on the ‘scratch pad’ and reproduce them as moves \(\mathcal {M}(\sigma ) \in M_G\). This procedure is clearly ‘effective’ in an informal sense, which is our justification of the notion of viable strategies.
Note that there are two kinds of processes in viable strategies \(\sigma : G\). The first one is the process of \(\sigma \) per se whose atomic steps are \((\varvec{s} a \in P_G^{\mathsf {Odd}}) \mapsto \varvec{s}a . \sigma (\lceil \varvec{s}a \rceil )\), and the second one is the process of an st-algorithm \(\mathcal {A}\) realizing \(\sigma \) whose atomic steps are \(\varvec{t} x \in P_{\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)}^{\mathsf {Odd}} \mapsto \varvec{t} x . \mathcal {A}_{\varvec{m}} \circ \partial _{\varvec{m}}(\varvec{t} x)\), where \(\varvec{m}\) is the current state. The former is abstract and high-level, while the latter is symbolic and low-level. In this manner, we have achieved a mathematical formulation of high-level and low-level computational processes and ‘effective computability’ of the former in terms of the latter (as promised in the introduction).
Henceforth, in order to establish Theorem 76, which is a key result for the main theorem (Theorem 81), we shall focus on the following st-algorithms:
Definition 71
(Standard st-algorithms) An st-algorithm \(\mathcal {A} {:}{:} G\) is standard if:
-
1.
The symbol \(\square \) does not occur in \(\mathcal {A}_{\varvec{m}}\) for any \(\varvec{m} \in \mathcal {S}_{\mathcal {A}}\);
-
2.
It does not refer to any input outer tag when it computes an inner element, i.e., if \( \hat{q}^{[3]} . \varvec{s} . \mathsf {n}^{[3]} \in \mathcal {A}^\circledS _{\varvec{m}} : \mathcal {G}(M_G)^{[0]} \& \mathcal {G}(M_G)^{[1]} \& \mathcal {G}(M_G)^{[2]} \Rightarrow \mathcal {G}(M_G)^{[3]}\), where \(\varvec{m} \in \mathcal {S}_{\mathcal {A}}\) and \(n \in \pi _1(M_G)\), then \(q^{[0]}\), \(q^{[1]}\) and \(q^{[2]}\) do not occur in \(\varvec{s}\);
-
3.
If it refers to an input outer tag, then it must belongs to the last move of the current P-view of G, i.e., if q occurs as a P-move in some \(\varvec{s} \in \mathcal {A}^\circledS _{\varvec{m}}\), where \(\varvec{m} \in \mathcal {S}_{\mathcal {A}}\), then the ‘tag’ on the move is \((\_)^{[2]}\).
Convention
Henceforth, st-algorithms refer to standard ones by default. Of course, standardness is closed under all constructions on st-algorithms (see the proof of Theorem 76), and st-algorithms given below are all standard.
Example 72
The zero strategy
 on any normalized game A is viable since we may give an st-algorithm \(\mathcal {A}( zero _A)\) by
on any normalized game A is viable since we may give an st-algorithm \(\mathcal {A}( zero _A)\) by
and \(\mathcal {A}( zero _A)_{\hat{q}_\mathscr {E} } : \hat{q}^{[3]} \mapsto \mathsf {\mathsf {no}_E}^{[3]} \mid \hat{q}^{[3]} \mathsf {no_E}^{[3]} q^{[3]} \mapsto \mathsf {\checkmark }^{[3]}\). Then, the instruction strategy \(\mathcal {A}( zero _A)_{\hat{q}_{\mathscr {E}}}^\circledS \) computes as in the following diagram:

Clearly, \(\mathcal {A}( zero _A)\) is standard, and \(\mathsf {st}(\mathcal {A}( zero _A)) = zero _A\).
Example 73
Let us complete the example of successor strategy  (Example 44 and Fig. 4). We give an st-algorithm \(\mathcal {A}( succ )\) for \( succ \) by
(Example 44 and Fig. 4). We give an st-algorithm \(\mathcal {A}( succ )\) for \( succ \) by
and the table is given in “Appendix A.” Clearly, we have \(\mathsf {st}(\mathcal {A}( succ )) = succ \), which establishes viability of \( succ \). Also, it is easy to see that \(\mathcal {A}( succ )\) is standard.
Example 74
Similarly to \( zero \) and \( succ \), we may give an st-algorithm \(\mathcal {A}( pred )\) for the predecessor strategy  (Example 45) as follows. We define the states, the view- and the mate-scopes, and the query of \(\mathcal {A}( pred )\) to be the same as those of \(\mathcal {A}( succ )\). At this point, it should suffice to show diagrams for \(\mathcal {A}( pred )_{\hat{q}_\mathscr {E}}^\circledS \) since it is clear that there is a finite table \(\mathcal {A}( pred )_{\hat{q}_\mathscr {E}}\) for \(\mathcal {A}( pred )_{\hat{q}_\mathscr {E}}^\circledS \):
(Example 45) as follows. We define the states, the view- and the mate-scopes, and the query of \(\mathcal {A}( pred )\) to be the same as those of \(\mathcal {A}( succ )\). At this point, it should suffice to show diagrams for \(\mathcal {A}( pred )_{\hat{q}_\mathscr {E}}^\circledS \) since it is clear that there is a finite table \(\mathcal {A}( pred )_{\hat{q}_\mathscr {E}}\) for \(\mathcal {A}( pred )_{\hat{q}_\mathscr {E}}^\circledS \):




Clearly \(\mathsf {st}(\mathcal {A}( pred )) = pred \), establishing viability of \( pred \). Also, it is easy to see that \(\mathcal {A}( pred )\) is standard.
Example 75
Consider the fixed-point strategy
 for each normalized game A, interpreting the fixed-point combinator
\(\mathsf {fix_A}\) in PCF [7, 38, 51], where A is the interpretation of a type \(\mathsf {A}\) of PCF. Roughly, \( fix _A\) computes as follows (for its detailed description, see [37, 38]):
for each normalized game A, interpreting the fixed-point combinator
\(\mathsf {fix_A}\) in PCF [7, 38, 51], where A is the interpretation of a type \(\mathsf {A}\) of PCF. Roughly, \( fix _A\) computes as follows (for its detailed description, see [37, 38]):
-
After an opening occurrence \([a_\mathscr {E}]_{\varvec{g}}\), \( fix _A\) copies it and performs the move
 with the pointer toward the initial occurrence \([a_\mathscr {E}]_{\varvec{g}}\);
with the pointer toward the initial occurrence \([a_\mathscr {E}]_{\varvec{g}}\); -
If O initiates a new thread in the inner implication by a move
 , then \( fix _A\) copies it and launches a new thread in the outer implication by performing the move
, then \( fix _A\) copies it and launches a new thread in the outer implication by performing the move  with the pointer toward the justifier of the second last occurrence of the current P-view;
with the pointer toward the justifier of the second last occurrence of the current P-view; -
If O performs a move
 (resp.
(resp.  ,
,  , \([a''_{\mathscr {E}}]_{\varvec{f}}\)) in an existing thread, then \( fix _A\) copies it and performs the move
, \([a''_{\mathscr {E}}]_{\varvec{f}}\)) in an existing thread, then \( fix _A\) copies it and performs the move  (resp. \([a''_{\mathscr {E}}]_{\varvec{f}}\),
(resp. \([a''_{\mathscr {E}}]_{\varvec{f}}\),  ,
, 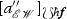 ) in the dual thread, i.e., the thread to which the third last occurrence of the current P-view belongs, with the pointer toward the third last occurrence.
) in the dual thread, i.e., the thread to which the third last occurrence of the current P-view belongs, with the pointer toward the third last occurrence.
A typical play by \( fix _A\) is depicted in Fig. 5. Clearly, \( fix _A\) is not finitary for the calculation of outer tags. It is, however, viable for any normalized game A, which is perhaps surprising to many readers. Here, let us just informally describe an st-algorithm \(\mathcal {A}( fix _A)\) that realizes \( fix _A\) as a preparation for Sect. 3.2. Let \(\mathcal {Q}_{\mathcal {A}( fix _A)}(m) = \top {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} m \in \pi _1(M_{(A \Rightarrow A) \Rightarrow A}^{\mathsf {Init}})\) and \(\mathcal {S}_{\mathcal {A}( fix _A)} {\mathop {=}\limits ^{\mathrm {df. }}} \pi _1(M_{(A \Rightarrow A) \Rightarrow A}^{\mathsf {Init}})\). Since \(\mathcal {A}( fix _A)_{m}\) does not depend on m, fix an arbitrary state \(m \in \mathcal {S}_{\mathcal {A}( fix _A)}\). We proceed by a case analysis on the rightmost component of input strategies on \(\mathcal {G}(M_{(A \Rightarrow A) \Rightarrow A})^3\) for \(\mathcal {A}( fix _A)_{m}^\circledS \) (which corresponds to the last occurrence of the P-view of each odd-length position of the game \((A \Rightarrow A) \Rightarrow A\)):
-
If the rightmost component is of the form \((\underline{[a_\mathscr {E}]_{\varvec{f}}})^{\dagger }\), then \(\mathcal {A}( fix _A)_{m}^\circledS \) recognizes it by the inner tag \(\mathscr {E}\), and calculates the next move
 once and for all for the inner element \(a_{\mathscr {EW}}\) and ‘digit-by-digit’ for the outer tag
once and for all for the inner element \(a_{\mathscr {EW}}\) and ‘digit-by-digit’ for the outer tag  (by giving
(by giving 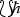 and copying \(\varvec{f}\));
and copying \(\varvec{f}\)); -
If the rightmost component is of the form
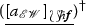 , then the leftmost component (which corresponds to the third last occurrence of the current P-view of the game \((A \Rightarrow A) \Rightarrow A\)) is of the form \((\underline{[a'_\mathscr {E}]_{\varvec{f}}})^{\dagger }\), and thus \(\mathcal {A}( fix _A)_{m}^\circledS \) recognizes it by the inner tags \(\mathscr {EW}\) and \(\mathscr {E}\), and calculates the next move \([a_\mathscr {E}]_{\varvec{f}}\) once and for all for the inner element \(a_\mathscr {E}\) and ‘digit-by-digit’ for the outer tag \(\varvec{f}\) (by ignoring
, then the leftmost component (which corresponds to the third last occurrence of the current P-view of the game \((A \Rightarrow A) \Rightarrow A\)) is of the form \((\underline{[a'_\mathscr {E}]_{\varvec{f}}})^{\dagger }\), and thus \(\mathcal {A}( fix _A)_{m}^\circledS \) recognizes it by the inner tags \(\mathscr {EW}\) and \(\mathscr {E}\), and calculates the next move \([a_\mathscr {E}]_{\varvec{f}}\) once and for all for the inner element \(a_\mathscr {E}\) and ‘digit-by-digit’ for the outer tag \(\varvec{f}\) (by ignoring  and copying \(\varvec{f}\));
and copying \(\varvec{f}\)); -
If the rightmost component is of the form
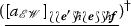 , then \(\mathcal {A}( fix _A)_{m}^\circledS \) calculates the next move
, then \(\mathcal {A}( fix _A)_{m}^\circledS \) calculates the next move  similarly to the above case yet with the help of m-views for the outer tag (see Sect. 3.2 for the details);
similarly to the above case yet with the help of m-views for the outer tag (see Sect. 3.2 for the details); -
If the rightmost component is of the form
 , then \(\mathcal {A}( fix _A)_{m}^\circledS \) calculates the next move
, then \(\mathcal {A}( fix _A)_{m}^\circledS \) calculates the next move 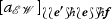 in a similar manner to the above case with the help of m-views for the outer tag (see Sect. 3.2 for the details);
in a similar manner to the above case with the help of m-views for the outer tag (see Sect. 3.2 for the details);
We now turn to establishing a key theorem, which states that viability of strategies is preserved under all the constructions on strategies defined in Sect. 2.3.2:
Theorem 76
(Preservation of viability) Viable strategies are closed under tensor \(\otimes \), pairing \(\langle \_, \_ \rangle \), promotion \((\_)^{\dagger }\), concatenation \(\ddagger \), currying \(\Lambda \) and uncurrying \(\Lambda ^\circleddash \) if the underlying st-algorithms are standard, where the standardness is also preserved.
Proof
Let us first show that tensor \(\otimes \) preserves viability of normalized strategies. Let \(\sigma : [A_\mathscr {W}]_{\varvec{e}} \multimap [C_\mathscr {E}]_{\varvec{e'}}\) and \(\tau : [B_\mathscr {W}]_{\varvec{f}} \multimap [D_\mathscr {E}]_{\varvec{f'}}\) be viable strategies with st-algorithms \(\mathcal {A}(\sigma )\) and \(\mathcal {A}(\tau )\) realizing \(\sigma \) and \(\tau \), respectively. We have to construct an st-algorithm \(\mathcal {A}(\sigma \otimes \tau )\) such that \(\mathsf {st}(\mathcal {A}(\sigma \otimes \tau )) = \sigma \otimes \tau : [A_{\mathscr {WW}}]_{\varvec{e}} \otimes [B_{\mathscr {EW}}]_{\varvec{f}} \multimap [C_{\mathscr {WE}}]_{\varvec{e'}} \otimes [D_{\mathscr {EE}}]_{\varvec{f'}}\). Let us define the finite set \(\mathcal {S}_{\mathcal {A}(\sigma \otimes \tau )}\) of states and the query \(\mathcal {Q}_{\mathcal {A}(\sigma \otimes \tau )}\) by:
where \(X_k, X_{k-1}, \dots , X_1, Y_l, Y_{l-1}, \dots , Y_1 \in \{ \mathscr {W}, \mathscr {E} \}\). Clearly, \(\mathcal {Q}_{\mathcal {A}(\sigma \otimes \tau )}\) satisfies the axiom Q (Definition 67). Given \(m^{(k)}_{X_k} m^{(k-1)}_{X_{k-1}} \dots m^{(1)}_{X_1} \in \mathcal {S}_{\mathcal {A}(\sigma )}\) and \(n^{(l)}_{Y_l} n^{(l-1)}_{Y_{l-1}} \dots n^{(1)}_{Y_1} \in \mathcal {S}_{\mathcal {A}(\tau )}\), we construct finite partial functions \(\mathcal {A}(\sigma \otimes \tau )_{m^{(k)}_{\mathscr {W}X_k} m^{(k-1)}_{\mathscr {W}X_{k-1}} \dots m^{(1)}_{\mathscr {W}X_1}}\) and \(\mathcal {A}(\sigma \otimes \tau )_{n^{(l)}_{\mathscr {E}Y_l} n^{(l-1)}_{\mathscr {E}Y_{l-1}} \dots n^{(1)}_{\mathscr {E}Y_1}}\) from \(\mathcal {A}(\sigma )_{m^{(k)}_{X_k} m^{(k-1)}_{X_{k-1}} \dots m^{(1)}_{X_1}}\) and \(\mathcal {A}(\tau )_{n^{(l)}_{Y_l} n^{(l-1)}_{Y_{l-1}} \dots n^{(1)}_{Y_1}}\) simply by changing symbols \(\mathsf {m_{X}} \in \mathsf {Sym}(\pi _1(M_{A \multimap C}))\) and \(\mathsf {n_{Y}} \in \mathsf {Sym}(\pi _1(M_{B \multimap D}))\) into \(\mathsf {m_{W X}}\) and \(\mathsf {n_{E Y}}\), respectively, in their finite tables, where the view-scopes are defined by:
and the mate-scopes are defined similarly. Then, because a P-view of \(\sigma \otimes \tau \) is either a P-view of \(\sigma \) or \(\tau \) (which is shown by induction on the length of positions of \(\sigma \otimes \tau \)), it is straightforward to see that \(\mathsf {st}(\mathcal {A}(\sigma \otimes \tau )) = \sigma \otimes \tau \) holds. Also, it is clear that \(\mathcal {A}(\sigma \otimes \tau )\) is standard if so are \(\mathcal {A}(\sigma )\) and \(\mathcal {A}(\tau )\). Intuitively, \(\mathcal {A}(\sigma \otimes \tau )\) sees the new digit (\(\mathscr {W}\) or \(\mathscr {E}\)) of the current state \(\varvec{s} \in \mathcal {S}_{\mathcal {A}(\sigma \otimes \tau )}\) and decides \(\mathcal {A}(\sigma )\) or \(\mathcal {A}(\tau )\) to apply (n.b., since \(\mathcal {Q}_{\mathcal {A}(\sigma \otimes \tau )}\) tracks every initial move by the axiom Q, the state must be non-empty).
It is clear that pairing of strategies may be handled in a completely similar manner; currying and uncurrying are even simpler. Thus, we skip the proof for them.
Now, consider the concatenation \(\iota \ddagger \kappa : J \ddagger K\) of viable strategies \(\iota : J\) and \(\kappa : K\) such that  and
and  for some normalized games A, B and C. Let \(\mathcal {A}(\iota )\) and \(\mathcal {A}(\kappa )\) be standard st-algorithms such that \(\mathsf {st}(\mathcal {A}(\iota )) = \iota \) and \(\mathsf {st}(\mathcal {A}(\kappa )) = \kappa \). We define the set \(\mathcal {S}_{\mathcal {A}(\iota \ddagger \kappa )}\) of states and the query \(\mathcal {Q}_{\mathcal {A}(\iota \ddagger \kappa )}\) by:
for some normalized games A, B and C. Let \(\mathcal {A}(\iota )\) and \(\mathcal {A}(\kappa )\) be standard st-algorithms such that \(\mathsf {st}(\mathcal {A}(\iota )) = \iota \) and \(\mathsf {st}(\mathcal {A}(\kappa )) = \kappa \). We define the set \(\mathcal {S}_{\mathcal {A}(\iota \ddagger \kappa )}\) of states and the query \(\mathcal {Q}_{\mathcal {A}(\iota \ddagger \kappa )}\) by:
where
and
We construct the finite partial function \(\mathcal {A}(\iota \ddagger \kappa )_{n^{(k)}_{G(Y_k)} n^{(k-1)}_{G(Y_{k-1})} \dots n^{(1)}_{G(Y_1)} m^{(l)}_{F(X_l)} m^{(l-1)}_{F(X_{l-1})} \dots m^{(1)}_{F(X_1)}}\) (as well as the view- and the mate-scopes) from \(\mathcal {A}(\kappa )_{n^{(k)}_{Y_k} n^{(k-1)}_{Y_{k-1}} \dots n^{(1)}_{Y_1}}\) if \(l = 0\), and from \(\mathcal {A}(\iota )_{m^{(l)}_{X_l} m^{(l-1)}_{X_{l-1}} \dots m^{(1)}_{X_1}}\) otherwise, by modifying the symbols in the table similarly to the case of tensor (where the view- and the mate-scopes are just inherited). Again, \(\mathcal {Q}_{\mathcal {A}(\iota \ddagger \kappa )}\) clearly satisfies the axiom Q. Because a P-view of \(\iota \ddagger \kappa \) is a one of \(\kappa \) or a one of \(\iota \) followed by a one of \(\kappa \) (it is crucial here that \(\mathcal {Q}_{\mathcal {A}(\iota )}\) tracks initial moves by the axiom Q, and \(\square \) does not occur in \(\mathcal {A}(\iota )\) for it is standard), we may conclude that \(\mathsf {st}(\mathcal {A}(\iota \ddagger \kappa )) = \iota \ddagger \kappa \). Moreover, \(\mathcal {A}(\iota \ddagger \kappa )\) is clearly standard as so are \(\mathcal {A}(\iota )\) and \(\mathcal {A}(\kappa )\).
Finally, assume that  is the promotion of a viable strategy
is the promotion of a viable strategy  with an st-algorithm \(\mathcal {A}(\varphi )\) that realizes \(\varphi \). As the more general case \(\varphi : G\), where
with an st-algorithm \(\mathcal {A}(\varphi )\) that realizes \(\varphi \). As the more general case \(\varphi : G\), where  is similar (as internal moves of \(G^{\dagger }\) retain new digits of outer tags on moves of !B), we focus on the case \(\varphi : A \Rightarrow B\) for simplicity. We define \(\mathcal {S}_{\mathcal {A}(\varphi ^{\dagger })} {\mathop {=}\limits ^{\mathrm {df. }}} \mathcal {S}_{\mathcal {A}(\varphi )}\) and \(\mathcal {Q}_{\mathcal {A}(\varphi ^{\dagger })} {\mathop {=}\limits ^{\mathrm {df. }}} \mathcal {Q}_{\mathcal {A}(\varphi )}\). Then, roughly, the idea is that if \(\varphi \) makes the next P-move
is similar (as internal moves of \(G^{\dagger }\) retain new digits of outer tags on moves of !B), we focus on the case \(\varphi : A \Rightarrow B\) for simplicity. We define \(\mathcal {S}_{\mathcal {A}(\varphi ^{\dagger })} {\mathop {=}\limits ^{\mathrm {df. }}} \mathcal {S}_{\mathcal {A}(\varphi )}\) and \(\mathcal {Q}_{\mathcal {A}(\varphi ^{\dagger })} {\mathop {=}\limits ^{\mathrm {df. }}} \mathcal {Q}_{\mathcal {A}(\varphi )}\). Then, roughly, the idea is that if \(\varphi \) makes the next P-move  (resp. \([b_\mathscr {E}]_{\varvec{f'}}\)) at an odd-length position \(\varvec{t}x\) of
(resp. \([b_\mathscr {E}]_{\varvec{f'}}\)) at an odd-length position \(\varvec{t}x\) of  , then \(\varphi ^{\dagger }\) at an odd-length position \(\varvec{t'} x'\) of
, then \(\varphi ^{\dagger }\) at an odd-length position \(\varvec{t'} x'\) of  that begins with an initial move
that begins with an initial move  and satisfies \(\varvec{t'} x' \upharpoonright \varvec{\hat{e}} = \varvec{t} x\) makes the corresponding next P-move
and satisfies \(\varvec{t'} x' \upharpoonright \varvec{\hat{e}} = \varvec{t} x\) makes the corresponding next P-move  (resp.
(resp.  ). As opposed to other constructions, however, the table of each \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{m}}\), where \(\varvec{m} \in \mathcal {S}_{\mathcal {A}(\varphi ^{\dagger })}\), is rather involved; thus, we just informally describe how to obtain the table of \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{m}}\) from that of \(\mathcal {A}(\varphi )_{\varvec{m}}\), which should suffice for the reader to see how to construct the tables if he or she wishes to. Fix any \(\varvec{s} \in \mathcal {S}_{\mathcal {A}(\varphi ^{\dagger })} = \mathcal {S}_{\mathcal {A}(\varphi )}\).
). As opposed to other constructions, however, the table of each \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{m}}\), where \(\varvec{m} \in \mathcal {S}_{\mathcal {A}(\varphi ^{\dagger })}\), is rather involved; thus, we just informally describe how to obtain the table of \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{m}}\) from that of \(\mathcal {A}(\varphi )_{\varvec{m}}\), which should suffice for the reader to see how to construct the tables if he or she wishes to. Fix any \(\varvec{s} \in \mathcal {S}_{\mathcal {A}(\varphi ^{\dagger })} = \mathcal {S}_{\mathcal {A}(\varphi )}\).
-
1.
Let \(\varvec{t} [m]_{\varvec{\tilde{e}}} [n]_{\varvec{e}} \in \varphi \) and \(\varvec{t'} [m]_{\varvec{\tilde{e}'}} [n]_{\varvec{e'}} \in \varphi ^{\dagger }\) such that \(\mathcal {Q}_{\mathcal {A}(\varphi ^{\dagger })}^\star (\lceil \varvec{t'}[m]_{\varvec{\tilde{e}}} \rceil ) = \varvec{s}\) and \(\varvec{t'} [m]_{\varvec{\tilde{e}'}} [n]_{\varvec{e'}} \upharpoonright \varvec{\hat{e}} = \varvec{t} [m]_{\varvec{\tilde{e}}} [n]_{\varvec{e}}\), where the initial move that hereditarily justifies \([n]_{\varvec{e'}}\) in \(\varphi ^{\dagger }\) is of the form
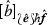 . Let us describe how \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) calculates the representation \(\mathsf {n} . \mathscr {C}^*(\varvec{e'})\) of the next move \([n]_{\varvec{e'}}\) by a case analysis on m and n:
. Let us describe how \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) calculates the representation \(\mathsf {n} . \mathscr {C}^*(\varvec{e'})\) of the next move \([n]_{\varvec{e'}}\) by a case analysis on m and n:-
If m and n both belong to A, which \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) may recognize by the method described below, then \(\varvec{\tilde{e}}\), \(\varvec{e}\), \(\varvec{\tilde{e}'}\) and \(\varvec{e'}\) are, respectively, of the form
 ,
,  ,
,  and
and 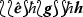 .Footnote 20 Then, with the help of m-views, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) calculates the first half \(\mathsf {n} . \langle \langle \mathscr {C}^*(\varvec{\hat{e}}) \rangle \sharp \) of \(\mathsf {n} . \mathscr {C}^*(\varvec{e'})\) by simulating the computation of \(\mathsf {n}\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\) and referring to \(\mathscr {C}^*(\varvec{\tilde{e}'})\), and computes the remaining half \(\langle \mathscr {C}^*(\varvec{g}) \rangle \rangle \sharp \mathscr {C}^*(\varvec{h})\) by simulating the computation of \(\mathscr {C}^*(\varvec{e})\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\) (inserting \(\rangle \) before \(\sharp \)). Clearly, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) is standard.
.Footnote 20 Then, with the help of m-views, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) calculates the first half \(\mathsf {n} . \langle \langle \mathscr {C}^*(\varvec{\hat{e}}) \rangle \sharp \) of \(\mathsf {n} . \mathscr {C}^*(\varvec{e'})\) by simulating the computation of \(\mathsf {n}\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\) and referring to \(\mathscr {C}^*(\varvec{\tilde{e}'})\), and computes the remaining half \(\langle \mathscr {C}^*(\varvec{g}) \rangle \rangle \sharp \mathscr {C}^*(\varvec{h})\) by simulating the computation of \(\mathscr {C}^*(\varvec{e})\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\) (inserting \(\rangle \) before \(\sharp \)). Clearly, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) is standard. -
If m and n belong to A and B, respectively, then \(\varvec{\tilde{e}}\), \(\varvec{e}\), \(\varvec{\tilde{e}'}\) and \(\varvec{e'}\) are of the form
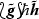 ,
,  and
and  , respectively. Again, with the help of m-views, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) calculates the first half \(\mathsf {n} . \langle \mathscr {C}^*(\varvec{\hat{e}}) \rangle \sharp \) of \(\mathsf {n} . \mathscr {C}^*(\varvec{e'})\) by simulating the computation of \(\mathsf {n}\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\) and referring to \(\mathscr {C}^*(\varvec{\tilde{e}'})\), and then computes the remaining half \(\mathscr {C}^*(\varvec{h})\) by simulating the computation of \(\mathscr {C}^*(\varvec{e})\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\). Again, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) is clearly standard.
, respectively. Again, with the help of m-views, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) calculates the first half \(\mathsf {n} . \langle \mathscr {C}^*(\varvec{\hat{e}}) \rangle \sharp \) of \(\mathsf {n} . \mathscr {C}^*(\varvec{e'})\) by simulating the computation of \(\mathsf {n}\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\) and referring to \(\mathscr {C}^*(\varvec{\tilde{e}'})\), and then computes the remaining half \(\mathscr {C}^*(\varvec{h})\) by simulating the computation of \(\mathscr {C}^*(\varvec{e})\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\). Again, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) is clearly standard. -
The remaining two cases are completely analogous to the above cases.
-
-
2.
It remains to stipulate how \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) distinguishes the above four cases. Assume \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} \in \mathcal {A}(\varphi )_{\varvec{s}}\) when \(\mathcal {A}(\varphi )_{\varvec{s}}\) has computed the inner element n. Note that \(\varvec{v}\) has enough information to identify \(\mathsf {n}\), and every move occurring in \(\varvec{v}\) has a ‘tag’ \((\_)^{[0]}\), \((\_)^{[1]}\) or \((\_)^{[2]}\) (but not \((\_)^{[3]}\)). Thus, by simulating this computation of \(\mathsf {n}\) by \(\mathcal {A}(\varphi )_{\varvec{s}}\) but replacing \(\mathsf {n}^{[3]}\) with \(\hat{q}^{[2]}\) to learn about \(\mathsf {m}\), \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) may recognize the current case out of the four described above. Specifically, if \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} \mapsto x\) is the first step for \(\mathcal {A}(\varphi )_{\varvec{s}}\) to compute \(\varvec{e}\), then correspondingly \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) computes as \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} \mapsto v_1\), \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} v_1 v_2 \mapsto v_3\), ..., \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} \varvec{v} \mapsto \hat{q}^{[2]}\), \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} \varvec{v} \hat{q}^{[2]} \mathsf {m}^{[2]} \mapsto x'\), where \(x'\) is the first step for \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) to compute \(\varvec{e'}\); and if \(\mathcal {A}(\varphi )_{\varvec{s}}\) next computes \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} x y \mapsto z\), then correspondingly \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) computes as \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} \varvec{v} \hat{q}^{[2]} \mathsf {m}^{[2]} x' y' \mapsto v_1\), \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} \varvec{v} \hat{q}^{[2]} \mathsf {m}^{[2]} x' y' v_1 v_2 \mapsto v_3\), ..., \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} \varvec{v} \hat{q}^{[2]} \mathsf {m}^{[2]} x' y' \varvec{v} \mapsto \hat{q}^{[2]}\), \(\hat{q}^{[3]} \varvec{v} \mathsf {n}^{[3]} q^{[3]} \varvec{v} \hat{q}^{[2]} \mathsf {m}^{[2]} x' y' \varvec{v} \hat{q}^{[2]} \mathsf {m}^{[2]} \mapsto z'\), where \(y', z'\) are the second and the third steps for \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) to compute \(\varvec{e'}\), and so on. That is, \(\mathcal {A}(\varphi ^{\dagger })_{\varvec{s}}\) remembers the current case by inserting the sequence \(\varvec{v} \hat{q}^{[2]} \mathsf {m}^{[2]}\) (of length \(\leqslant 8\) for \(\mathcal {A}(\varphi )\) is standard) between each computational step. Note that \(\mathcal {A}(\varphi ^{\dagger })\) remains to be standard.
It should be clear from the above description how to construct \(\mathcal {A}(\varphi ^{\dagger })\) from \(\mathcal {A}(\varphi )\), completing the proof. \(\square \)
3.2 Examples of viable strategies
This section presents various examples of a viable strategy realized by a standard st-algorithm. These strategies except fixed-point strategies \( fix _A\) are actually finitary; thus, we need the notion of viable strategies only for promotion \((\_)^{\dagger }\) and \( fix _A\), both of which are necessary for the proof of Turing completeness in Sect. 3.3.
Example 77
Given a normalized game A, we define an st-algorithm \(\mathcal {A}( der _A)\) that realizes the dereliction  (Definition 50) by
(Definition 50) by
for all \(m \in \mathcal {S}_{ der _A}\); given \(m \in \mathcal {S}_{ der _A}\), \(\mathcal {A}( der _A)_m^\circledS \) computes as in the following diagrams (n.b., we skip describing the table of \(\mathcal {A}( der _A)_m\)):


It is straightforward to see that \(\mathsf {st}(\mathcal {A}( der _A)) = der _A\) holds, showing viability of \( der _A\). Also, \(\mathcal {A}( der _A)\) is clearly standard.
Example 78
The case strategy
 for each normalized game A is defined by:
for each normalized game A is defined by:

where  are the same as the dereliction
are the same as the dereliction  up to inner tags. As the name suggests, it implements the case distinction on A: Given input strategies \(\sigma _1, \sigma _2 : T \Rightarrow A\) and \(\beta : T \Rightarrow \varvec{2}\), the composition \( case _A \circ \langle \langle \sigma _1, \sigma _2 \rangle , \beta \rangle ^{\dagger }\) is \(\sigma _1\) (resp. \(\sigma _2\)) if \(\beta \) is \(\{ \varvec{\epsilon }, [\hat{q}_{\mathscr {E}}] [ tt _{\mathscr {E}}] \}\) (resp. \(\{ \varvec{\epsilon }, [\hat{q}_{\mathscr {E}}] [ ff _{\mathscr {E}}] \}\)).
up to inner tags. As the name suggests, it implements the case distinction on A: Given input strategies \(\sigma _1, \sigma _2 : T \Rightarrow A\) and \(\beta : T \Rightarrow \varvec{2}\), the composition \( case _A \circ \langle \langle \sigma _1, \sigma _2 \rangle , \beta \rangle ^{\dagger }\) is \(\sigma _1\) (resp. \(\sigma _2\)) if \(\beta \) is \(\{ \varvec{\epsilon }, [\hat{q}_{\mathscr {E}}] [ tt _{\mathscr {E}}] \}\) (resp. \(\{ \varvec{\epsilon }, [\hat{q}_{\mathscr {E}}] [ ff _{\mathscr {E}}] \}\)).
We give an st-algorithm \(\mathcal {A}( case _A)\) that realizes \( case _A\) as follows. The states, the query, the view- and the mate-scopes of \(\mathcal {A}( case _A)\) are similar to those of \(\mathcal {A}( der _A)\), and the instruction strategy \(\mathcal {A}( case _A)_m^\circledS \) for each \(m \in \mathcal {S}_{\mathcal {A}( case _A)}\) plays as follows (again, we skip writing the table of \(\mathcal {A}( case _A)_m\)), where \( A^{A \& A \& \varvec{2}} {\mathop {=}\limits ^{\mathrm {df. }}} A \& A \& \varvec{2} \Rightarrow A\):

where \( \hat{a}_{\mathscr {E}} \in \pi _1(M_{A^{A \& A \& \varvec{2}}}^{\mathsf {Init}})\), which can be recognized as the set \( \pi _1(M_{A^{A \& A \& \varvec{2}}})\) is finite. The iteration of \(\hat{q}^{[2]} . \mathsf {\hat{a}_{E}}^{[2]}\) in the diagram is to distinguish the case from other cases; this remark is applied to the remaining diagrams below.



where \( a_{\mathscr {E}} \not \in \pi _1(M_{A^{A \& A \& \varvec{2}}}^{\mathsf {Init}})\). Clearly, \(\mathsf {st}(\mathcal {A}( case _A)) = case _A\), and therefore, \( case _A\) is viable. Also, it is easy to see that \(\mathcal {A}( case _A)\) is standard.
Example 79
Consider the ifzero strategy
 defined by
defined by  . Roughly, it outputs \( tt \) (resp. \( ff \)) if the input is \(\underline{0}\) (resp. \(\underline{n+1}\) for some \(n \in \mathbb {N}\)). We give an st-algorithm \(\mathcal {A}( zero? )\) that realizes \( zero? \) as follows. Let
. Roughly, it outputs \( tt \) (resp. \( ff \)) if the input is \(\underline{0}\) (resp. \(\underline{n+1}\) for some \(n \in \mathbb {N}\)). We give an st-algorithm \(\mathcal {A}( zero? )\) that realizes \( zero? \) as follows. Let
and the instruction strategy \(\mathcal {A}( zero? )_{\hat{q}_\mathscr {E}}^\circledS \) computes as in the following diagrams (again, we omit the formal description of \(\mathcal {A}( zero? )_{\hat{q}_\mathscr {E}}\) because it should be clear at this point):


Clearly, \(\mathsf {st}(\mathcal {A}( zero? )) = zero? \), and \(\mathcal {A}( zero? )\) is standard.
Example 80
Now, let us give an st-algorithm \(\mathcal {A}( fix _A)\) that realizes the fixed-point strategy  for each normalized game A [7, 38, 51]. We have already described \(\mathcal {A}( fix _A)\) informally in Example 75; here let us give a more detailed account, but now, it should suffice to give diagrams for \(\mathcal {A}( fix _A)_m^\circledS \) (where \(m \in \mathcal {S}_{ fix _A}\) is arbitrary). In the following diagrams, just for clarity, we write \(\langle @ d\) (resp. \(\rangle @ d\)) to indicate that the corresponding occurrence
for each normalized game A [7, 38, 51]. We have already described \(\mathcal {A}( fix _A)\) informally in Example 75; here let us give a more detailed account, but now, it should suffice to give diagrams for \(\mathcal {A}( fix _A)_m^\circledS \) (where \(m \in \mathcal {S}_{ fix _A}\) is arbitrary). In the following diagrams, just for clarity, we write \(\langle @ d\) (resp. \(\rangle @ d\)) to indicate that the corresponding occurrence  (resp.
(resp.  ) in the outer tag is of depth d (Definition 66).
) in the outer tag is of depth d (Definition 66).


where we have omitted the iteration of \(\hat{q}^{[2]} . \mathsf {a_{WW}}^{[2]}\) for the lack of space.


where we have omitted the iteration of \(\hat{q}^{[2]} . \mathsf {a_{EW}}^{[2]} . \hat{q}^{[0]} . \mathsf {a'_{WW}}^{[0]}\) for the lack of space.
With the help of m-views, there is clearly a finite table \(\mathcal {A}( fix _A)_m\) that implements \(\mathcal {A}( fix _A)^\circledS _m\). It is then not hard to see that \(\mathsf {st}(\mathcal {A}( fix _A)) = fix _A\) holds, showing that \( fix _A\) is viable. Also, it is easy to see that \(\mathcal {A}( fix _A)\) is standard.
3.3 Turing completeness
In the last two sections, we have seen through examples that each ‘atomic’ strategy definable by PCF [6, 71] is viable, and it is realized by a standard st-algorithm. In addition, Theorem 76 shows that constructions on strategies preserve this property. From these two facts, our main theorem immediately follows:
Theorem 81
(Main theorem) Every normalized strategy \(\sigma : S_\sigma \) definable by PCF has a viable strategy \(\phi _\sigma : D_\sigma \) that satisfies 
Proof
First, see [6] for normalized strategies definable by PCF. We enumerate these strategies \(\sigma : S_\sigma \) by the following construction of a set \(\mathcal {PCF}\) of normalized strategies (which also contains strategies not definable by PCF):
-
1.
\((\sigma : S_\sigma ) \in \mathcal {PCF}\) if \(\sigma : S_\sigma \) is PCF-atomic, i.e., \( der _A : A \Rightarrow A\), \( zero _A : A \Rightarrow \mathcal {N}\), \( succ : \mathcal {N} \Rightarrow \mathcal {N}\), \( pred : \mathcal {N} \Rightarrow \mathcal {N}\), \( zero ? : \mathcal {N} \Rightarrow \varvec{2}\), \( case _{A} : A \& A \& \varvec{2} \Rightarrow A\) or \( fix _A : (A \Rightarrow A) \Rightarrow A\), where A is generated from \(\mathcal {N}\), \(\varvec{2}\) and/or T, by & and/or \(\Rightarrow \) (n.b., the construction of A is ‘orthogonal’ to that of \(\sigma : S_\sigma \));
-
2.
\((\Lambda (\sigma ) : A \Rightarrow (B \Rightarrow C)) \in \mathcal {PCF}\) if \( (\sigma : A \& B \Rightarrow C) \in \mathcal {PCF}\) for some normalized games A, B and C, where note that
 ;
; -
3.
\( (\langle \varphi , \psi \rangle : C \Rightarrow A \& B) \in \mathcal {PCF}\) if \((\varphi : C \Rightarrow A), (\psi : C \Rightarrow B) \in \mathcal {PCF}\) for some normalized games A, B and C;
-
4.
\((\iota ^{\dagger } ; \kappa : A \Rightarrow C) \in \mathcal {PCF}\) if \((\iota : A \Rightarrow B), (\kappa : B \Rightarrow C) \in \mathcal {PCF}\) for some normalized games A, B and C
where since projections and evaluations are derelictions up to inner tags, we count them as PCF-atomic ones as well. Note that the nth numeral strategy \(\underline{n} : T \Rightarrow \mathcal {N}\) (Example 43) may be obtained by \( zero ^{\dagger }_{T}; \underbrace{ succ ^{\dagger }; succ ^{\dagger } \dots ; succ ^{\dagger } ; succ }_{n}\) for each \(n \in \mathbb {N}\), interpreting numerals of PCF.
We then assign a strategy \(\phi _\sigma : D_\sigma \) to each \((\sigma : S_\sigma ) \in \mathcal {PCF}\) along with the above construction of \(\sigma : S_\sigma \) as follows: 1. \(D_\sigma {\mathop {=}\limits ^{\mathrm {df. }}} S_\sigma \) and \(\phi _\sigma {\mathop {=}\limits ^{\mathrm {df. }}} \sigma \) (where \(\sigma : S_\sigma \) is PCF-atomic); 2. \(D_{\Lambda (\sigma )} {\mathop {=}\limits ^{\mathrm {df. }}} \Lambda (D_\sigma )\) and \(\phi _{\Lambda (\sigma )} {\mathop {=}\limits ^{\mathrm {df. }}} \Lambda (\phi _\sigma )\); 3. \(D_{\langle \varphi , \psi \rangle } {\mathop {=}\limits ^{\mathrm {df. }}} \langle D_\varphi , D_\psi \rangle \) and \(\phi _{\langle \varphi , \psi \rangle } {\mathop {=}\limits ^{\mathrm {df. }}} \langle \phi _\varphi , \phi _\psi \rangle \); 4. \(D_{\iota ^{\dagger } ;\, \kappa } {\mathop {=}\limits ^{\mathrm {df. }}} D_\iota ^{\dagger } \ddagger D_\kappa \) and \(\phi _{\iota ^{\dagger } ;\, \kappa } {\mathop {=}\limits ^{\mathrm {df. }}} \phi _\iota ^{\dagger } \ddagger \phi _\kappa \).
We have shown in the previous sections that PCF-atomic strategies are all viable and realized by standard st-algorithms. Also, the constructions \(\Lambda \), \(\langle \_, \_ \rangle \) and \((\_)^{\dagger } \ddagger (\_)\) on strategies have been shown to preserve viability, more specifically, realizability by standard st-algorithms, of strategies in Theorem 76. Thus, we may conclude that \(\phi _\sigma : D_\sigma \) is viable (and realized by a standard st-algorithm) for each \((\sigma : S_\sigma ) \in \mathcal {PCF}\).
It remains to show \(\mathcal {H}^\omega (\phi _\sigma ) = \sigma \) and  for all \((\sigma : S_\sigma ) \in \mathcal {PCF}\); we show it by induction on the construction of \(\sigma : S_\sigma \) as follows:
for all \((\sigma : S_\sigma ) \in \mathcal {PCF}\); we show it by induction on the construction of \(\sigma : S_\sigma \) as follows:
-
1.
\(\mathcal {H}^\omega (\phi _\sigma ) = \mathcal {H}^\omega (\sigma ) = \sigma \) and \(\mathcal {H}^\omega (D_\sigma ) = \mathcal {H}^\omega (S_\sigma ) = S_\sigma \) if \(\sigma : S_\sigma \) is PCF-atomic since in this case \(\sigma \) and \(S_\sigma \) are both normalized;
-
2.
\(\mathcal {H}^\omega (\phi _{\Lambda (\sigma )}) = \mathcal {H}^\omega (\Lambda (\phi _\sigma )) = \Lambda (\mathcal {H}^\omega (\phi _\sigma )) = \Lambda (\sigma )\) and
 ;
; -
3.
\(\mathcal {H}^\omega (\phi _{\langle \varphi , \psi \rangle }) = \mathcal {H}^\omega (\langle \phi _\varphi , \phi _\psi \rangle ) = \langle \mathcal {H}^\omega (\phi _\varphi ), \mathcal {H}^\omega (\phi _\psi ) \rangle = \langle \varphi , \psi \rangle \) and
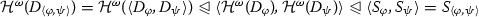 ;
; -
4.
\(\mathcal {H}^\omega (\phi _{\iota ^{\dagger } ;\, \kappa }) = \mathcal {H}^\omega (\phi _\iota ^{\dagger } \ddagger \phi _\kappa ) = \mathcal {H}^\omega (\phi _\iota )^{\dagger } ; \mathcal {H}^\omega (\phi _\kappa ) = \iota ^{\dagger } ; \kappa \) and

where the last three cases are by the induction hypothesis, Theorem 40 and Lemmata 41 and 64, which completes the proof. \(\square \)
Since PCF is Turing complete [32, 50], this result particularly implies:
Corollary 82
(Turing completeness) Every partial recursive function \(f : \mathbb {N}^k \rightharpoonup \mathbb {N}\), where \(k \in \mathbb {N}\) and \(\mathbb {N}^k {\mathop {=}\limits ^{\mathrm {df. }}} \underbrace{\mathbb {N} \times \mathbb {N} \dots \times \mathbb {N}}_{k}\), has a viable strategy \(\phi _f : D_f\) such that  , where \( \mathcal {N}^k {\mathop {=}\limits ^{\mathrm {df. }}} \underbrace{\mathcal {N} \& \mathcal {N} \dots \& \mathcal {N}}_k\), and \(\mathcal {H}^\omega (\langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle ^{\dagger } \ddagger \phi _f) \simeq \underline{f(n_1, n_2, \dots , n_k)}\) for all \((n_1, n_2, \dots , n_k) \in \mathbb {N}^k\).Footnote 21
, where \( \mathcal {N}^k {\mathop {=}\limits ^{\mathrm {df. }}} \underbrace{\mathcal {N} \& \mathcal {N} \dots \& \mathcal {N}}_k\), and \(\mathcal {H}^\omega (\langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle ^{\dagger } \ddagger \phi _f) \simeq \underline{f(n_1, n_2, \dots , n_k)}\) for all \((n_1, n_2, \dots , n_k) \in \mathbb {N}^k\).Footnote 21
Proof
Let \(\mathsf {x_1 : N, x_2 : N, \dots , x_k : N \vdash F : N}\) be a term of PCF that implements a given partial recursive function \(f : \mathbb {N}^k \rightharpoonup \mathbb {N}\), i.e., \(\mathsf {F [n_1/x_1, n_2/x_2, \dots , n_k/x_k]}\) evaluates to \(\mathsf {f(n_1, n_2, \dots , n_k)}\) if \(f(n_1, n_2, \dots , n_k)\) is defined, and diverges otherwise, for all \(n_i \in \mathbb {N}\) (\(i = 1, 2, \dots , k\)), where \(\mathsf {n_i : N}\) is the \(n_i\)th numeral, and \(\mathsf {F [n_1/x_1, n_2/x_2, \dots , n_k/x_k]}\) is the result of substituting \(\mathsf {n_i}\) for \(\mathsf {x_i}\) in \(\mathsf {F}\) for \(i = 1, 2, \dots , k\) (see, e.g., [32, 50] for Turing completeness of PCF). Then, there exists a normalized strategy \(\sigma _f : \mathcal {N}^k \Rightarrow \mathcal {N}\) in \(\mathcal {PCF}\) that interprets \(\mathsf {F}\) in the standard game semantics of PCF [6]. By Theorem 81, there exists a viable strategy \(\phi _f : D_f\) such that \(\mathcal {H}^\omega (\phi _f) = \sigma _f\) and  Hence, \(\mathcal {H}^\omega (\langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle ^{\dagger } \ddagger \phi _f) = \mathcal {H}^\omega (\langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle )^{\dagger } ; \mathcal {H}^\omega (\phi _f) = \langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle ^{\dagger } ; \sigma _f \simeq \underline{f(n_1, n_2, \dots , n_k)}\), where the last Kleene equality \(\simeq \) is by the adequacy [8] of the standard game semantics of PCF. \(\square \)
Hence, \(\mathcal {H}^\omega (\langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle ^{\dagger } \ddagger \phi _f) = \mathcal {H}^\omega (\langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle )^{\dagger } ; \mathcal {H}^\omega (\phi _f) = \langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle ^{\dagger } ; \sigma _f \simeq \underline{f(n_1, n_2, \dots , n_k)}\), where the last Kleene equality \(\simeq \) is by the adequacy [8] of the standard game semantics of PCF. \(\square \)
Remark
Crucially, there is clearly a partial recursive function \(f : \mathbb {N}^k \rightharpoonup \mathbb {N}\) such that \(\sigma _f\) is not viable (but \(\phi _f\) is) by the finitary nature of tables for st-algorithms.
As our game-semantic model of computation is Turing complete, some of the well-known theorems in computability theory [16, 60] are immediately generalized (in the sense that they are not restricted to computation on natural numbers):
Corollary 83
(Generalized smn theorem) If strategies \(\sigma _i : T \Rightarrow A_i\) for \(i = 1, 2, \dots , n\) and \(\phi : D\) such that  are realized by standard st-algorithms, then we may obtain a standard st-algorithm that realizes a viable strategy \(\phi _{\sigma _1, \sigma _2, \dots , \sigma _n} : D_{A_1, A_2, \dots , A_n}\) such that:
are realized by standard st-algorithms, then we may obtain a standard st-algorithm that realizes a viable strategy \(\phi _{\sigma _1, \sigma _2, \dots , \sigma _n} : D_{A_1, A_2, \dots , A_n}\) such that:
-
1
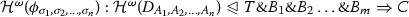 ;
; -
2
\(\langle \{ \varvec{\epsilon } \}, \tau _1, \tau _2, \dots , \tau _m \rangle ^{\dagger } \ddagger \phi _{\sigma _1, \sigma _2, \dots , \sigma _n} \simeq \langle \sigma _1, \sigma _2, \dots , \sigma _n, \tau _1, \tau _2, \dots , \tau _m \rangle ^{\dagger } \ddagger \phi \) for any strategies \(\tau _j : T \Rightarrow B_j\) (\(j = 1, 2, \dots , m\)).
Proof
We define \(\phi _{\sigma _1, \sigma _2, \dots , \sigma _n} {\mathop {=}\limits ^{\mathrm {df. }}} \underbrace{\Lambda ^\circleddash (\cdots \Lambda ^\circleddash }_m(\langle \sigma _1, \sigma _2, \dots , \sigma _n \rangle ^{\dagger } \ddagger \underbrace{\Lambda ( \cdots \Lambda }_m(\phi ) \cdots )) \cdots )\), where the proof of Theorem 76 describes how to ‘effectively’ obtain a standard st-algorithm that realizes \(\phi _{\sigma _1, \sigma _2, \dots , \sigma _n}\) in an informal sense.Footnote 22 Note that Corollary 82 implies that it is in fact a generalization of the conventional smn theorem [16]. \(\square \)
Corollary 84
(Generalized FRT) Given a viable strategy \(\varphi : D\) realized by a standard st-algorithm such that  for some normalized game A, there is another viable strategy \(\sigma _\varphi : D_\varphi \) realized by a standard st-algorithm such that
for some normalized game A, there is another viable strategy \(\sigma _\varphi : D_\varphi \) realized by a standard st-algorithm such that  and \(\mathcal {H}^\omega (\sigma _\varphi ^{\dagger } \ddagger \varphi ) = \mathcal {H}^\omega (\sigma _\varphi ) : T \Rightarrow A\).
and \(\mathcal {H}^\omega (\sigma _\varphi ^{\dagger } \ddagger \varphi ) = \mathcal {H}^\omega (\sigma _\varphi ) : T \Rightarrow A\).
Proof
Just define \(D_\varphi {\mathop {=}\limits ^{\mathrm {df. }}} (T \Rightarrow D)^{\dagger } \ddagger ((A \Rightarrow A) \Rightarrow A)\) and \(\sigma _\varphi {\mathop {=}\limits ^{\mathrm {df. }}} (\varphi _T)^{\dagger } \ddagger fix _A\), where \(\varphi _T : T \Rightarrow D\) is \(\varphi \) up to tags. Again, Corollary 82 implies that it is in fact a generalization of the conventional first recursion theorem (FRT) [16]. \(\square \)
Finally, let us show that the converse of the main theorem (i.e., Theorem 81) also holds for classical computation because it would then give further naturality and/or reasonability of our definition of ‘effectivity,’ viz. viability, of strategies:
Theorem 85
(Conservativeness) Any viable strategy \(\phi : G\) with  , where \(k \in \mathbb {N}\), can be simulated by a partial recursive function \(f_\phi : \mathbb {N}^k \rightharpoonup \mathbb {N}\) in the sense that \(\mathcal {H}^\omega (\langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle ^{\dagger } \ddagger \phi ) \simeq \underline{f_\phi (n_1, n_2, \dots , n_k)}\) for all \(n_1, n_2, \dots , n_k \in \mathbb {N}\).
, where \(k \in \mathbb {N}\), can be simulated by a partial recursive function \(f_\phi : \mathbb {N}^k \rightharpoonup \mathbb {N}\) in the sense that \(\mathcal {H}^\omega (\langle \underline{n_1}, \underline{n_2}, \dots , \underline{n_k} \rangle ^{\dagger } \ddagger \phi ) \simeq \underline{f_\phi (n_1, n_2, \dots , n_k)}\) for all \(n_1, n_2, \dots , n_k \in \mathbb {N}\).
Proof
(sketch) This theorem is not as surprising as Theorem 81 for one may just employ the Church–Turing thesis [16]. Nevertheless, let us give a proof sketch for the theorem, by which ardent readers may fill in the details if they wish to.
The idea is to simulate a given viable strategy \(\phi : G\) by a 6-tape TM \(\mathscr {M}\) by writing down an input on the first tape, the entire history of previous occurrences of moves, i.e., each position during a play, on the second tape, and the last three occurrences of each P-view as well as the next P-move on the third tape, where the fourth, the fifth and the sixth tapes are used for auxiliary computations (specified below).
Let us first specify the format of the first and the second tapes. On each of these tapes, moves are separated by an occurrence of a distinguished symbol \(\mathsf {\$}\), and each move \([m]_{e_1 e_2 \dots e_k}\) together with the identifier \(j \in \mathbb {N}\) of its justifier defined below is written as the sequence

where there are j-many \(\prime \)’s, representing the identifier j, between the left occurrence of \(\mathsf {\$}\) and the occurrence of \(\mathsf {m}\). We define the identifier of each occurrence of a move \([n]_{f_1 f_2 \dots f_l}\) on the tape to be the number \(i \in \mathbb {N}\) such that \(\mathsf {n}\) is written on the ith cell of the tape, where note that \(i \geqslant 1\). Then, the number j of \(\prime \)’s displayed above is defined to be the identifier of the justifier of \([m]_{e_1 e_2 \dots e_k}\) if it exists, and 0 otherwise (i.e., if \([m]_{e_1 e_2 \dots e_k}\) is initial). In this manner, we encode pointers on the tape. We also assume without loss of generality that the symbol \(\mathsf {m}\) contains information for the I/E-parity of each move \([m]_{e_1 e_2 \dots e_k}\); an obvious (though not canonical) way to achieve it is to use two different fonts for \(\mathsf {m}\).
On the other hand, the last three occurrences of the P-view of each odd-length position (in the format described above yet without identifiers), their identifiers and m-views (when the moves \([m]_{e_1 e_2 \dots e_k}\) are encoded as strategies \(\underline{[m]_{e_1 e_2 \dots e_k}}\)) are written, respectively, on the third, the fourth and the fifth tapes, where each occurrence of a move, an identifier or an m-view is separated again by \(\mathsf {\$}\).
Next, note that computation of the next move is trivial if it is an O-move because external O-moves of the output \(\mathcal {N}\) are all obvious questions, external O-moves of the input \(\mathcal {N}\) are already given as an input on the first tape, and internal O-moves are just dummies of internal P-moves by the axiom DP2 (Definition 18). Note also that \(\mathscr {M}\) may recognize the O/P-parity of the next move by its state (and the I/E-parity by the symbolic information on the tape assumed above). Hence, it suffices to focus on computation of the next P-move; \(\mathscr {M}\) computes it as follows:
-
1.
Copy the last occurrence \([m_1]_{\varvec{e^{(1)}}}\) of the current P-view on the second tape onto the initial cells of the third tape, calculate its identifier and m-view, possibly utilizing the sixth tape as a working tape, and write them down on the fourth and the fifth tapes, respectively, in the obvious manner, erasing all contents of the sixth tape after the calculation;
-
2.
Locate the second last occurrence \([m_2]_{\varvec{e^{(2)}}}\) of the current P-view on the second tape by the identifier associated with the occurrence \([m_1]_{\varvec{e^{(1)}}}\) and then execute the same computation as the one on \([m_1]_{\varvec{e^{(1)}}}\), where the new contents prefixed with \(\mathsf {\$}\) on the third, the fourth and the fifth tapes are concatenated to the existing contents;
-
3.
Similarly, locate the third last occurrence \([m_3]_{\varvec{e^{(3)}}}\) of the current P-view on the second tape (which is easy as it locates next to \([m_2]_{\varvec{e^{(2)}}}\)) and execute the same computation on it (so that the third, the fourth and the fifth tapes contain all information of the last three occurrences of the P-view);
-
4.
With the contents on the third, the fourth and the fifth tapes, compute the next P-move \([m]_{\varvec{e}}\) and the identifier of its justifier, write them down on the second tape and erase all contents on the third, the fourth and the fifth tapes.
Note that \(\mathscr {M}\) is clearly able to execute all the computational steps described above, in particular the last step \(([m_3]_{\varvec{e^{(3)}}}, [m_2]_{\varvec{e^{(2)}}}, [m_1]_{\varvec{e^{(1)}}}) \mapsto [m]_{\varvec{e}}\) by simulating the computation of an instruction strategy for \(\phi \), completing the proof. \(\square \)
Remark
Theorem 85 does not hold for higher-order computation because TMs cannot take additional inputs from O during the course of computation. Of course, one may consider generalized TMs that may interact with O, but then it is no longer TMs in the usual sense; in fact, this idea naturally leads to the game-semantic model of computation developed in the present paper.
Also, as an immediate corollary of Theorem 85, we obtain Corollary 89, for which we first need some auxiliary concepts:
Definition 86
(Standard strategies on PCF-games) A PCF-game is a normalized game constructed from \(\mathcal {N}\), \(\varvec{2}\) and/or T, via & and/or \(\Rightarrow \). A strategy \(\sigma \) on a PCF-game G is standard if the substance (Definition 6) of the last move of the j-subsequence \(\varvec{s} \upharpoonright \mathcal {N}^{[i]}\) of each maximal (with respect to \(\preceq \)) element \(\varvec{s} \in \sigma \) that consists of moves of the same component game \(\mathcal {N}^{[i]}\) (i.e., moves of \(\mathcal {N}\) with the same inner tag) is \( no \) if \(\varvec{s} \upharpoonright \mathcal {N}^{[i]}\) is non-empty and of even-length.
Next, let us introduce the translation \(\mathscr {T}\) that maps PCF-games and standard strategies on them to the corresponding conventional games and strategies on them, respectively, simply by replacing \(\mathcal {N}\) with N:
Definition 87
(Translation \(\mathscr {T}\)) Given a PCF-game G, the game \(\mathscr {T}(G)\) is defined inductively by:
-
\(\mathscr {T}(T) {\mathop {=}\limits ^{\mathrm {df. }}} T\), \(\mathscr {T}(\varvec{2}) {\mathop {=}\limits ^{\mathrm {df. }}} \varvec{2}\) and \(\mathscr {T}(\mathcal {N}) {\mathop {=}\limits ^{\mathrm {df. }}} N\);
-
\( \mathscr {T}(A \& B) {\mathop {=}\limits ^{\mathrm {df. }}} \mathscr {T}(A) \& \mathscr {T}(B)\);
-
\(\mathscr {T}(A \Rightarrow B) {\mathop {=}\limits ^{\mathrm {df. }}} \mathscr {T}(A) \Rightarrow \mathscr {T}(B)\).
Given a standard strategy \(\sigma : G\), the strategy \(\mathscr {T}(\sigma ) : \mathscr {T}(G)\) is obtained from \(\sigma \) by:
-
1
Replacing the j-subsequence \(\varvec{s} \upharpoonright \mathcal {N}^{[i]}\) of each maximal element \(\varvec{s} \in \sigma \) that consists of moves of the same component game \(\mathcal {N}^{[i]}\) with the j-sequence \([\hat{q}] [n]\) (1.a. by deleting all occurrences of [q] or \([ yes ]\), and replacing [no] with [n]) if \(\varvec{s} \upharpoonright \mathcal {N}^{[i]}\) is the maximal element of \(\underline{n}\) (Example 43), and with the j-sequence \([\hat{q}]\) (1.b. by deleting all non-initial occurrences) otherwise (i.e., if \(\varvec{s} \upharpoonright \mathcal {N}^{[i]}\) is of odd-length), where we omit tags for brevity; let us write \(\mathscr {T}(\varvec{s})\) for the resulting j-sequence obtained from \(\varvec{s}\);
-
2
Defining \(\mathscr {T}(\sigma ) {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Pref}(\{ \mathscr {T}(\varvec{s}) \mid \varvec{s} \in \sigma , \varvec{s} \text { is maximal in }\sigma \ \! \})^{\mathsf {Even}}\).
Remark
By the specific methods 1.a and 1.b in the step 1 of the translation \(\sigma \mapsto \mathscr {T}(\sigma )\), the relative order between occurrences in different component games of \(\mathscr {T}(G)\) is automatically determined (and thus \(\mathscr {T}(\sigma )\) is unambiguous). Note also that the strategy \(\sigma : G\) is required to be standard since otherwise some j-subsequence \(\varvec{s} \upharpoonright \mathcal {N}^{[i]}\) is \([\hat{q}] [ yes ] ([q] [ yes ])^n\) for some \(n \in \mathbb {N}\), and thus \(\mathscr {T}\) on \(\sigma \) would not be well defined (n.b., for instance, how to translate a nonstandard strategy \(\sigma : \mathcal {N}^{[0]} \Rightarrow \mathcal {N}^{[1]}\) that contains the maximal position \([\hat{q}]^{[1]} [\hat{q}]^{[0]} [ yes ]^{[0]} [ no ]^{[1]}\)?).
Definition 88
(Intrinsic equivalence [6, 7, 38]) The intrinsic equivalence \(\simeq _G\) on strategies on a game G is defined by \(\sigma \simeq _G \tilde{\sigma } {\mathop {\Leftrightarrow }\limits ^{\mathrm {df. }}} \forall \tau : G \Rightarrow \Sigma . \ \! \tau \circ \sigma _T^{\dagger } = \tau \circ \tilde{\sigma }_T^{\dagger }\) for all \(\sigma , \tilde{\sigma } : G\), where \(\sigma _T, \tilde{\sigma }_T : T \Rightarrow G\) are \(\sigma \) and \(\tilde{\sigma }\) up to tags, respectively, and \(\Sigma \) is the game given by \(M_\Sigma {\mathop {=}\limits ^{\mathrm {df. }}} \{ [\hat{q}], [a] \}\), where a is any element with \(a \ne \hat{q}\), \(\lambda _\Sigma : [\hat{q}] \mapsto (\mathsf {O}, \mathsf {Q}, 0), [a] \mapsto (\mathsf {P}, \mathsf {A}, 0)\), \(\vdash _\Sigma {\mathop {=}\limits ^{\mathrm {df. }}} \{ (\star , [\hat{q}]), ([\hat{q}], [a]) \}\), \(\Delta _\Sigma {\mathop {=}\limits ^{\mathrm {df. }}} \emptyset \) and \(P_\Sigma {\mathop {=}\limits ^{\mathrm {df. }}} \mathsf {Pref}(\{ [\hat{q}] [a] \})\).
See [7, 38, 51] for the proof that shows \(\simeq _G\) is in fact an equivalence relation on strategies on a given game G. We are finally ready to establish:
Corollary 89
(Universality) Let A be the dynamic game semantics of a type \(\mathsf {A}\) of PCF (following [71]). Given any viable strategy \(\alpha : A\) such that \(\mathcal {H}^\omega (\alpha ) : \mathcal {H}^\omega (A)\) is standard, \(\mathscr {T}(\mathcal {H}^\omega (\alpha )) : \mathscr {T}(\mathcal {H}^\omega (A))\) coincides with the conventional game semantics \(\tilde{\alpha } : \mathscr {T}(\mathcal {H}^\omega (A))\) of some term of PCF up to intrinsic equivalence [6].
Proof
(sketch) Applying the proof of Theorem 85, we may see that \(\mathscr {T}(\mathcal {H}^\omega (\alpha )) : \mathscr {T}(\mathcal {H}^\omega (A))\) is recursive, i.e., each move performed by \(\mathscr {T}(\mathcal {H}^\omega (\alpha ))\) is computable by a TM; thus, it is the conventional game semantics \(\tilde{\alpha } : \mathscr {T}(\mathcal {H}^\omega (A))\) of some term of PCF up to intrinsic equivalence by the universality theorem of [7, 38].
4 Conclusion and future work
The present work has given a novel notion of ‘computability,’ namely viability of strategies. Due to its intrinsic, non-inductive, non-axiomatic nature, it can be seen as a fundamental investigation of ‘effective’ computation beyond classical computation, where note that viability of strategies makes sense universally, i.e., regardless of the underlying games (e.g., games do not have to correspond to types of PCF).
Furthermore, our game-semantic model of computation formulates both high-level and low-level computational processes and defines ‘computability’ of the former in terms of the latter, which sheds new light on the very notion of computation. For instance, strategies \(\underline{n} : T \Rightarrow \mathcal {N}\) may be seen as the definition of natural numbers, and thus, a viable strategy of the form \(\phi : \mathcal {N}^k \Rightarrow \mathcal {N}\) can be regarded as high-level computation on natural numbers, not on their representations, and (the table of) an st-algorithm that realizes \(\phi \) can be seen as its symbolic implementation.
There are various directions for further work. First, we need to analyze the exact computational power of viable strategies, in comparison with other known notion of higher-order computability [50]. Also, as an application, the present framework may give an accurate measure for computational complexity [47], where note that the work on dynamic games and strategies [71] has already given such a measure via internal moves, but the present work may refine it further since two single steps in a game G may take different numbers of steps in the instruction game \(\mathcal {G}(M_G)^3 \Rightarrow \mathcal {G}(M_G)\). Moreover, it is of theoretical interest to see which theorems in computability theory can be generalized by the present framework in addition to the smn and the first recursion theorems. However, the most imminent future work is perhaps, by exploiting the flexibility of game semantics, to enlarge the scope of the present work (i.e., not only the language PCF) in order to establish a computational model of various logics and programming languages. We are particularly interested in how to apply our approach to non-innocent strategies.
Finally, let us propose two open questions. Since the definition of viable strategies is somewhat reflexive (as it is via strategies), we may naturally consider strategies that can be realized by a viable strategy. Let us define such strategies to be 2-viable. More generally, rephrasing viability as 1-viability, we define a strategy to be \((n+1)\)- viable if it can be realized by an n-viable strategy for each \(n \in \mathbb {N}\). Clearly, any n-viable strategy is ‘effective’ in an informal sense. Then, the first questions is:
Is the class of all \((n+1)\)-viable strategies strictly larger than that of all n-viable strategies for each \(n \in \mathbb {N}\)?
This question seems highly interesting from a theoretical perspective.Footnote 23
If the answer is positive for all \(n \in \mathbb {N}\), then there would be an infinite hierarchy of generalized viable strategies. It is then natural to ask the following second question:
Does the hierarchy, if it exists, correspond to any known hierarchy (perhaps in computability theory or proof theory)?
We shall aim to answer these questions as future work as well.
Acknowledgements
The author acknowledges the financial support from Funai Overseas Scholarship, and also he is grateful to Samson Abramsky and Robin Piedeleu for fruitful discussions.
Notes
This idea is similar to that of \( denotational \) \( semantics \) of programming languages [62], but there is an important difference: Denotational semantics interprets programs usually by (extensional) functions, but we are concerned with (intensional) \( processes \).
It is both technically and conceptually simpler to focus on \( sequential \) games, in which two participants \( alternately\,\, and\,\, separately \) take actions, than to consider more general \( concurrent \) games, in which both participants may be active \( simultaneously \) [2].
For simplicity, here we focus on \( closed \) terms, i.e., ones with the \( empty \) \( context \).
The diagrams are only to make it explicit which component game each move belongs to; the two positions are just finite sequences \(q^{[0]} n^{[0]} q^{[1]} m^{[1]}\) and \(q^{[1]} m^{[1]} q^{[0]} n^{[0]}\) equipped with the pointers \(q^{[0]} \leftarrow n^{[0]}\) and \(q^{[1]} \leftarrow m^{[1]}\).
But they exhibit simple communication between the participants as in the above examples, i.e., game semantics is intensional to some degree but not completely. It is roughly why game semantics has been highly successful in denotational semantics.
More precisely, they are the \( last \) \( occurrences \) \( of \) P-moves; however, for convenience we shall keep using this abuse of terminology in the rest of the introduction.
This choice is far from canonical; it should also work to employ another representation of natural numbers, e.g., the binary one. We have chosen the unary representation for its simplicity.
This would be seen, if achieved, as a mathematical formalization of Brouwer’s \( intuitionism \) [66], in which ‘(mental) constructions’ are made precise as game-semantic computational processes, viz. plays by viable dynamic strategies, and moreover extended to \( interactive \) ‘constructions.’
Strictly speaking, the variants [6, 51] are slightly different, and [71] chooses [6] as the basis, but [51] describes a lot of useful technical details. [6] is chosen in [71] because it combines good points of the two best-known variants, \(\textit{AJM}\)-games [7] and \(\textit{HO}\)-games [38] so that it may model linearity as in [5] and also characterize various programming features as in [6] though these points are left as future work in [71].
We have employed (a representation of) a bijection \(\mathbb {N}^*{\mathop {\rightarrow }\limits ^{\sim }} \mathbb {N}\), rather than \(\mathbb {N} \times \mathbb {N} {\mathop {\rightarrow }\limits ^{\sim }} \mathbb {N}\), for a simple definition of outer tags.
Although the main focus of the work [71] is to capture the small-step operational semantics of a programming language by such a step-by-step hiding operation \(\mathcal {H}\), such fine-grained steps do not play a main role in the present work. Nevertheless, we keep the structure \(\lambda _G^{\mathbb {N}}\) as it makes sense for a model of computation to be equipped with the step-by-step hiding operation, and it would be interesting as future work to consider ‘effective computability’ of the hiding operation.
\(\lceil \varvec{s} q \varvec{t} \rceil _G\) must be of the form \(\lceil \varvec{s} q \rceil _G . \varvec{t'}\) by \( (generalized) \) \( visibility \) on \(\varvec{s} q \varvec{t} a\) (Definition 17).
As already mentioned in the introduction, viability makes sense for conventional or static strategies as well, but viable static strategies are \( not \) Turing complete.
Note that this is analogous to the computation of a TM which looks at only one cell of an infinite tape at a time.
Of course, there might be another way to ‘effectively’ eliminate irrelevant occurrences from the history of previous occurrences; in fact, we need more than P-views to model languages with \( states \) [6], which is left as future work.
Strictly speaking, the pairing is up to ‘tags,’ as already explained in Sect. 1.7.
Note, however, that \( succ \) itself is already finitary; \(\mathcal {A}( succ )^\circledS \) is just for an illustration, and viability of strategies is necessary only for more complex strategies.
Again, the composition is up to ‘tags,’ as already explained in Sect. 1.7.
The outer tags which \(\mathcal {A}(\varphi )_{\varvec{s}}\) refers to for computing \(\varvec{e}\) are only \(\varvec{\tilde{e}}\) as \(\mathcal {A}(\varphi )\) is standard, and therefore, it is clearly possible to adjust the computation of \(\mathscr {C}^*(\varvec{e})\) by \(\mathcal {A}(\varphi )\) to the computation of the latter half \(\langle \mathscr {C}^*(\varvec{g}) \rangle \rangle \sharp \mathscr {C}^*(\varvec{h})\) of \(\mathscr {C}^*(\varvec{e'})\) by \(\mathcal {A}(\varphi ^{\dagger })\) given below.
Recall that \(\langle \_, \_ \rangle \), \((\_)^{\dagger }\) and \(\ddagger \) are \( pairing \), \( promotion \) and \( concatenation \) of strategies given in Sect. 2.3.2.
It is interesting future work to formalize this informal ‘effective computability’ by certain viable strategies.
Note that this question would not have arisen in the first place if we had not defined ‘effective computability’ \( solely \) \( in \) \( terms \) \( of \) \( games \) \( and \) \( strategies \).
References
Abramsky, S., Jagadeesan, R., Vákár, M.: Games for dependent types. In: Halldórsson, M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) Automata, Languages, and Programming, pp. 31–43. Springer, Berlin (2015)
Abramsky, S., Mellies, P.-A.: Concurrent games and full completeness. In: Proceedings of the 14th Symposium on Logic in Computer Science, pp. 431–442. IEEE (1999)
Abramsky, S.: Semantics of interaction: an introduction to game semantics. In: Dybjer, P., Pitts, A. (eds.) Semantics and Logics of Computation. Publications of the Newton Institute, pp. 1–31. Cambridge University Press, Cambridge (1997)
Abramsky, S.: Intensionality, definability and computation. In: Baltag, A., Smets, S. (eds.) Johan van Benthem on Logic and Information Dynamics, pp. 121–142. Springer, Cham (2014)
Abramsky, S., Jagadeesan, R.: Games and full completeness for multiplicative linear logic. J. Symb. Log. 59(02), 543–574 (1994)
Abramsky, S., McCusker, G.: Game semantics. In: Schwichtenberg, H., Berger, U. (eds.) Computational Logic, pp. 1–55. Springer, New York (1999)
Abramsky, S., Jagadeesan, R., Malacaria, P.: Full abstraction for PCF. Inf. Comput. 163(2), 409–470 (2000)
Amadio, R.M., Curien, P.-L.: Domains and Lambda-Calculi, vol. 46. Cambridge University Press, Cambridge (1998)
Barendregt, H.P., et al.: The Lambda Calculus, vol. 3. North-Holland, Amsterdam (1984)
Berry, G., Curien, P.-L.: Sequential algorithms on concrete data structures. Theor. Comput. Sci. 20(3), 265–321 (1982)
Blass, A.: A game semantics for linear logic. Ann. Pure Appl. Log. 56(1), 183–220 (1992)
Blot, V.: Realizability for Peano arithmetic with winning conditions in HON games. Ann. Pure Appl. Log. 168(2), 254–277 (2017)
Blum, W., Ong, C.: A Concrete Presentation of Game Semantics. Citeseer (2008)
Bucciarelli, A.: Another approach to sequentiality: Kleene’s unimonotone functions. In: Brookes, S., Main, M., Melton, A., Mislove, M., Schmidt, D. (eds.) Mathematical Foundations of Programming Semantics, pp. 333–358. Springer, New York (1994)
Curien, P.-L.: Definability and full abstraction. Electron. Not. Theor. Comput. Sci. 172, 301–310 (2007)
Cutland, N.: Computability: An Introduction to Recursive Function Theory. Cambridge University Press, Cambridge (1980)
Dal Lago, U., Laurent, O.: Quantitative game semantics for linear logic. In: International Workshop on Computer Science Logic, pp. 230–245. Springer (2008)
Dimovski, A., Ghica, D.R., Lazić, R.: Data-abstraction refinement: a game semantic approach. In: International Static Analysis Symposium, pp. 102–117. Springer (2005)
Felscher, W.: Dialogues as a foundation for intuitionistic logic. In: Gabbay, D., Guenthner, F. (eds.) Handbook of Philosophical Logic, pp. 341–372. Springer, Dordrecht (1986)
Férée, H.: Game semantics approach to higher-order complexity. J. Comput. Syst. Sci. 87, 1–15 (2017)
Gandy, R.: Dialogues, Blass games and sequentiality for objects of finite type. Unpublished manuscript (1993)
Gandy, R.: Church’s thesis and principles for mechanisms. Stud. Log. Found. Math. 101, 123–148 (1980)
Ghica, D.R.: Slot games: a quantitative model of computation. In: ACM SIGPLAN Notices, vol. 40, pp. 85–97. ACM (2005)
Girard, J.-Y.: Geometry of interaction II: deadlock-free algorithms. In: COLOG-88, pp. 76–93. Springer (1990)
Girard, J.-Y.: Geometry of interaction IV: the feedback equation. In: Stoltenberg-Hausen, V., Väänänen, J. (eds.) Logic Colloquium, vol. 3, pp. 76–117. Citeseer (2003)
Girard, J.-Y.: Geometry of interaction VI: a blueprint for transcendental syntax. Preprint (2013)
Girard, J.-Y.: Linear logic. Theor. Comput. Sci. 50(1), 1–101 (1987)
Girard, J.-Y.: Geometry of interaction I: interpretation of system F. Stud. Log. Found. Math. 127, 221–260 (1989)
Girard, J.-Y.: Geometry of Interaction III: Accommodating the Additives. London Mathematical Society Lecture Note Series, pp. 329–389. Cambridge University Press, Cambridge (1995)
Girard, J.-Y.: Geometry of interaction V: logic in the hyperfinite factor. Theor. Comput. Sci. 412(20), 1860–1883 (2011)
Greenland, W.E.: Game semantics for region analysis. Ph.D. thesis, University of Oxford (2005)
Gunter, C.A.: Semantics of Programming Languages: Structures and Techniques. MIT Press, Cambridge (1992)
Gurevich, Y.: Abstract state machines: an overview of the project. In: Seipel, D., Turull-Torres, J.M. (eds.) Foundations of Information and Knowledge Systems, pp. 6–13 (2004)
Hoare, C.A.R.: Communicating sequential processes. Commun. ACM 21(8), 666–677 (1978)
Hopcroft, J.E., Motwani, R., Ullman, J.D.: Introduction to Automata Theory, Languages, and Computation. Addison-Wesley, Reading (1979)
Hyland, J.M.E., Ong, C.-H.L.: Fair games and full completeness for multiplicative linear logic without the mix-rule. Preprint 190 (1993)
Hyland, M.: Game semantics. Semant. Log. Comput. 14, 131 (1997)
Hyland, J.M.E., Ong, C.-H.: On full abstraction for PCF: I, II, and III. Inf. Comput. 163(2), 285–408 (2000)
Japaridze, G.: Introduction to computability logic. Ann. Pure Appl. Log. 123(1–3), 1–99 (2003)
Kleene, S.C.: Recursive functionals and quantifiers of finite types I. Trans. Am. Math. Soc. 91(1), 1–52 (1959)
Kleene, S.C.: Recursive functionals and quantifiers of finite types II. Trans. Am. Math. Soc. 108(1), 106–142 (1963)
Kleene, S.C.: Recursive functionals and quantifiers of finite types revisited I. Stud. Log. Found. Math. 94, 185–222 (1978)
Kleene, S.C.: Recursive functionals and quantifiers of finite types revisited II. Stud. Log. Found. Math. 101, 1–29 (1980)
Kleene, S.C.: Recursive functionals and quantifiers of finite types revisited III. Stud. Log. Found. Math. 109, 1–40 (1982)
Kleene, S.: Unimonotone functions of finite types (recursive functionals and quantifiers of finite types revisited IV). Recur. Theory 42, 119–138 (1985)
Kleene, S.C.: Recursive functionals and quantifiers of finite types revisited, V. Trans. Am. Math. Soc. 325(2), 593–630 (1991)
Kozen, D.C.: Theory of Computation. Springer, London (2006)
Kozen, D.C.: Automata and Computability. Springer, New York (2012)
Laurent, O.: Polarized games. Ann. Pure Appl. Log. 130(1–3), 79–123 (2004)
Longley, J., Normann, D.: Higher-Order Computability. Springer, Heidelberg (2015)
McCusker, G.: Games and Full Abstraction for a Functional Metalanguage with Recursive Types. Springer, London (1998)
Milner, R.: Software science: from virtual to reality. Bull. EATCS 87, 12–16 (2005)
Milner, R.: A Calculus of Communicating Systems. Lecture Notes in Computer Science, vol. 92. Springer-Verlag Berlin Heidelberg, New York (1980)
Moschovakis, Y.N.: On founding the theory of algorithms. In: Dales, H.G., Oliveri, G. (eds.) Truth in Mathematics, pp. 71–104 (1998)
Nickau, H.: Hereditarily sequential functionals. In: Nerode, A., Matiyasevich, Y.V. (eds.) Logical Foundations of Computer Science, pp. 253–264. Oxford University Press, USA (1994)
Ong, C.-H.: On model-checking trees generated by higher-order recursion schemes. In: 21st Annual IEEE Symposium on Logic in Computer Science (LICS’06), pp. 81–90. IEEE (2006)
Ouaknine, J.: A Two-Dimensional Extension of Lambek’s Categorical Proof Theory. Ph.D. thesis, McGill University, Montréal (1997)
Plotkin, G.D.: LCF considered as a programming language. Theor. Comput. Sci. 5(3), 223–255 (1977)
Requena, E., Lorenzen, P., Lorenz, K.: Dialogische Logik. JSTOR (1980)
Rogers, H., Rogers, H.: Theory of Recursive Functions and Effective Computability, vol. 5. McGraw-Hill, New York (1967)
Scott, D.S.: A type-theoretical alternative to ISWIM, CUCH, OWHY. Theor. Comput. Sci. 121(1), 411–440 (1993)
Scott, D.S., Strachey, C.: Toward a Mathematical Semantics for Computer Languages, vol. 1. Oxford University Computing Laboratory, Programming Research Group, Oxford (1971)
Shoenfield, J.R.: Mathematical Logic, vol. 21. Addison-Wesley, Boston (1967). Reading
Sipser, M.: Introduction to the Theory of Computation, vol. 2. Thomson Course Technology, Boston (2006)
Troelstra, A.S.: Realizability. In: Buss, S.R. (ed.) Handbook of Proof Theory. North-Holland/Elsevier, Amsterdam (1998)
Troelstra, A.S., Van Dalen, D.: Constructivism in Mathematics, vol. 2. Elsevier, Amsterdam (2014)
Turing, A.M.: On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 2(1), 230–265 (1937)
Van Oosten, J.: Realizability: An Introduction to Its Categorical Side, vol. 152. Elsevier, Amsterdam (2008)
Weihrauch, K.: Computable Analysis: An Introduction. Springer, Berlin (2012)
Winskel, G.: The Formal Semantics of Programming Languages: An Introduction. MIT Press, Cambridge (1993)
Yamada, N., Abramsky, S.: Dynamic game semantics. arXiv preprint arXiv:1601.04147 (2016)
Yamada, N.: Game semantics for Martin–Löf type theory. arXiv preprint arXiv:1610.01669 (2016)
Author information
Authors and Affiliations
Corresponding author
Appendix A: A finite table for successor strategy
Appendix A: A finite table for successor strategy
The finite table for an st-algorithm \(\mathcal {A}( succ )\) for the successor strategy \( succ : \mathcal {N} \Rightarrow \mathcal {N}\) is as follows:
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yamada, N. A game-semantic model of computation. Res Math Sci 6, 3 (2019). https://doi.org/10.1007/s40687-018-0163-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40687-018-0163-z





 by
by 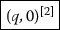 in turn triggers the question
in turn triggers the question
 for an output in
for an output in  to the question
to the question
 by
by  in turn triggers the answer
in turn triggers the answer
 to the question
to the question
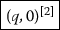 in
in 


 ;
; ;
; ;
; ;
; , where
, where  yet changed into
yet changed into  for each
for each  for each
for each  for each
for each 
 ,
,  ,
,  ;
;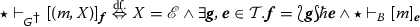 ;
; ,
,  ,
, 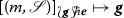 ;
; , where
, where  if
if  otherwise, where
otherwise, where  and
and  for some normalized game B.
for some normalized game B.

 with the pointer toward the initial occurrence
with the pointer toward the initial occurrence  , then
, then  with the pointer toward the justifier of the second last occurrence of the current P-view;
with the pointer toward the justifier of the second last occurrence of the current P-view; (resp.
(resp.  ,
,  ,
,  (resp.
(resp.  ,
, 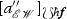 ) in the dual thread, i.e., the thread to which the third last occurrence of the current P-view belongs, with the pointer toward the third last occurrence.
) in the dual thread, i.e., the thread to which the third last occurrence of the current P-view belongs, with the pointer toward the third last occurrence. once and for all for the inner element
once and for all for the inner element  (by giving
(by giving 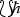 and copying
and copying 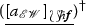 , then the leftmost component (which corresponds to the third last occurrence of the current P-view of the game
, then the leftmost component (which corresponds to the third last occurrence of the current P-view of the game  and copying
and copying 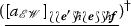 , then
, then  similarly to the above case yet with the help of m-views for the outer tag (see Sect.
similarly to the above case yet with the help of m-views for the outer tag (see Sect.  , then
, then 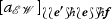 in a similar manner to the above case with the help of m-views for the outer tag (see Sect.
in a similar manner to the above case with the help of m-views for the outer tag (see Sect.  . Let us describe how
. Let us describe how  ,
,  ,
,  and
and 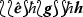 .
.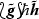 ,
,  and
and  , respectively. Again, with the help of m-views,
, respectively. Again, with the help of m-views,  ;
; ;
;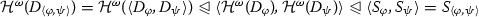 ;
;
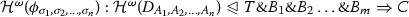 ;
;