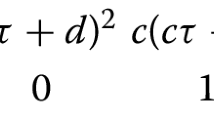Holomorphic modular forms and cocycles

Abstract

This is a slightly expanded version of my lecture at the conference Modular forms are everywhere at Bonn, May 2017, taking into account remarks by Don Zagier and Shaul Zemel, and suggestions of the referees.

1 Introduction

The relation between modular forms and cohomology may be studied in several contexts:

Classical :

For modular cusp forms of even weight the Eichler integral determines for a given modular cusp form of even positive weight a cohomology class with values in a module of polynomial functions. The names to mention are Eichler [5] and Shimura [10].

Real weight :

There are interesting holomorphic modular cusp forms of positive real weight. For instance the Dedekind eta function

$$\begin{aligned} \eta (\tau ) = \mathrm{e}^{\pi i \tau /12} \prod _{n\ge 1} \bigl (1-\mathrm{e}^{2\pi i n \tau }\bigr ), \end{aligned}$$

(1.1)

with weight $\frac{1}{2}$. One can assign cohomology classes to such cusp forms. The values are in a much larger module. The name to mention is Knopp [6].

Maass cusp forms :

Modular Maass wave forms are functions on the upper half-plane that are invariant under the transformation of the modular group. They are not holomorphic, but satisfy a second-order linear differential equation: There are infinitely many linearly independent Maass cusp forms, although none of them can be given explicitly for the full modular group.

There is a way to associate cohomology classes to Maass cusp form, with values in a large module of functions on the real projective line $\mathbb {P}^1_{{\mathbb {R}}}$. This can be generalized to cuspidal automorphic forms on larger Lie groups than ${\mathrm {SL}}_2({\mathbb {R}})$. I mention Bunke and Ohlbrich [3, 4].

Don Zagier, John Lewis and I looked at the relation between Maass forms and cohomology. We could associate cocycles to Maass forms with large growth at the cusps and established a quite satisfactory theory [1]. In the Eichler–Shimura theory the cohomology groups have finite dimension. So a linear map from infinite-dimensional spaces of modular forms (with unrestricted growth at the cusp) has a huge kernel. In the context of Maass forms we obtained an injective map to cohomology and could describe the image of various spaces of Maass forms.

Later YoungJu Choie, Nikos Diamantis and I tried to apply the ideas that worked for Maass forms to holomorphic modular forms. For classical modular forms this does not work well. However, in the case of holomorphic forms of real weight not in ${\mathbb {Z}}_{\ge 2}$ the ideas in [1] turned out to be applicable. We get an injective map to a cohomology group and characterize the image. The module for the cohomology has still infinite dimension, but is much smaller than the module in Knopp’s approach.

Many details in [2] differ from those in [1], but on the whole I would put holomorphic forms of real weight not in ${\mathbb {Z}}_{\ge 2}$ and Maass forms in one group, and the classical case in another group, as far as it concerns the relation between modular forms and cohomology. This in contrast with what one might think at first. Holomorphic modular forms of real weight look like a reasonable generalization of classical modular forms, and those strange Maass forms seem to form a quite different class.

Here I discuss results from [2] for the full modular group $\Gamma ={\mathrm {SL}}_2({\mathbb {Z}})$, to stay close to the theme of the conference. Figure 5 summarizes the results, which in fact are valid for general cofinite discrete groups with cusps.

2 Eichler cocycles

For a cusp form $f\in S_{\!k}(\Gamma )$ with $k\in 2{\mathbb {Z}}_{\ge 1}$ the Eichler cocycle $\gamma \mapsto \psi _\gamma$ is defined by

$$\begin{aligned} \psi _\gamma (z) = \int _{\gamma ^{-1}\infty }^\infty f(\tau )\, (\tau -z)^{k-2}\, \mathrm{d}\tau .\end{aligned}$$

(2.1)

The points $\infty$ and $\gamma ^{-1}\infty$ are on the boundary of the upper half-plane and are connected by a path in ${{\mathfrak {H}}}$. Near the end point the path should approach $\gamma ^{-1} \infty$ and $\infty$ along geodesic half-lines, for instance along vertical lines. The exponential decay of cusp forms at cusps ensures absolute convergence of the integral. The result is a polynomial in z of degree at most $k-2$.

The cocycle relation

$$\begin{aligned} \psi _{\gamma \delta } = \psi _\gamma |_{2-k}\delta +\psi _\delta \end{aligned}$$

(2.2)

holds for the action of ${\mathrm {SL}}_2({\mathbb {R}})$ given by

(2.3)

So $\psi \,{:}\,\gamma \mapsto \psi _\gamma$ in (2.1) is in the space of group cocycles $Z^1( \Gamma ;V_{k-2})$ with values in the module $V_{k-2}$ of polynomial functions of degree at most $k-2$ with the action in (2.3). It determines a cohomology class in the cohomology group

$$\begin{aligned} H^1(\Gamma ;V_{k-2}) = Z^1(\Gamma ;V_{k-2}) \bigm / B^1(\Gamma ;V_{k-2}). \end{aligned}$$

(2.4)

The space of cocycles $B^1(\Gamma ;V_{k-2})$ consists of the cocycles $\gamma \mapsto v|_{2-k}( \gamma - 1)$ with $v\in V_{k-2}$.

The conjugate Eichler cocycle associated with $f\in S_{\!k}(\Gamma )$ is

$$\begin{aligned} \psi ^c_\gamma (z) = \int _{\gamma ^{-1}\infty }^\infty \overline{ f(\tau )}\, (\bar{\tau }-z)^{k-2}\, \mathrm{d}{\bar{\tau }}. \end{aligned}$$

(2.5)

It is also in $Z^1(\Gamma ;V_{k-2})$. In fact we have the Eichler–Shimura theorem

$$\begin{aligned} S_{\!k}(\Gamma ) \oplus S_{\!k}(\Gamma ) {\mathop {\longrightarrow }\limits ^{\cong }}H^1_p(\Gamma ;V_{k-2}). \end{aligned}$$

The map is ${\mathbb {C}}$-linear on the first summand and antilinear on the second summand. The subscript p denotes the subgroup of parabolic classes, represented by parabolic cocycles for which . (For groups with more than one orbit of cusps the definition of parabolic cocycles is more complicated.)

3 Knopp cocycles

The powers of the Dedekind eta function are

$$\begin{aligned} \eta ^{2r}(\tau ) = \mathrm{e}^{ \pi i r \tau /6} \prod _{n\ge 1} \bigl ( 1-\mathrm{e}^{2\pi i n\tau }\bigr )^{2r}. \end{aligned}$$

(3.1)

It is holomorphic on the upper half-plane ${{\mathfrak {H}}}$ and has modular transformation behavior of weight $r\in {\mathbb {R}}$. For

$$\begin{aligned} \eta ^{2r}(\gamma \tau ) = v_r(\gamma ) \, (c\tau +d)^{-r}\, \eta ^{2r}(\tau ).\end{aligned}$$

(3.2)

For the factors $\left( c\tau +d\right) ^{-r}$ we need a choice of the argument; I use $\arg \left( c\tau +d\right) \in (-\pi ,\pi ]$. Without the factor $v_r(\gamma )$ the relation would not allow nonzero solutions. It is a multiplier system, which is a map $\Gamma \rightarrow {\mathbb {C}}^*$ with properties that ensure that there are nonzero functions with this transformation behavior. We need it for $r\not \in 2{\mathbb {Z}}$. For integral weight a multiplier system is a character of ${\mathrm {SL}}_2({\mathbb {Z}})$.

Functions with a transformation like that in (3.2) correspond to functions on the universal covering group ${\tilde{G}}$ of ${\mathrm {SL}}_2({\mathbb {R}})$ that transform on the left according to a character of a discrete subgroup of ${\tilde{G}}$. See, e.g., [2, Appendix], of for half-integral weight [11, Section 2]. Conceptually this approach has advantages. In this overview I prefer to use the classical point of view.

The formula in (2.1) for the Eichler cocycle causes problems if $r\not \in {\mathbb {Z}}$: The factor $(\tau -z)^{r-2}$ is multi-valued in $\tau$ and z, branching where $\tau =z$. This difficulty does not occur for the conjugate cocycle in (2.5). Now ${\bar{\tau }}$ is in the lower half-plane and z in the upper half-plane. We choose a branch of $({\bar{\tau }}-z)^{r-2}$ and get a cocycle $\psi ^c$ associated with a cusp form f of real weight.

So the conjugate Eichler cocycle has values in the holomorphic functions on the upper half-plane ${{\mathfrak {H}}}$, not in the polynomial functions. Knopp [6] showed that the Eichler integral produces functions that have polynomial growth near the boundary $\mathbb {P}^1_{{\mathbb {R}}}$ of ${{\mathfrak {H}}}$:

$$\begin{aligned} \psi ^c_\gamma (z) = \mathrm {O}\bigl ( |z|^A \bigr ) + \mathrm {O}\bigl ( ({\mathrm {Im}\,}z)^{-a} \bigr ). \end{aligned}$$

(3.3)

We denote by ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\infty }$ the space of holomorphic functions on ${{\mathfrak {H}}}$ with at most polynomial growth, provided with the action

(3.4)

where v is a multiplier system suitable for the real weight r. The presence of a multiplier system turns this into an action of $\Gamma$. This action does not extend to an action of the group ${\mathrm {SL}}_2({\mathbb {R}})$.

Knopp [6] defined the resulting map to cohomology and conjectured that it gave an antilinear isomorphism for all $r\in {\mathbb {R}}$

$$\begin{aligned} S_{\!r}(\Gamma ,v) \longrightarrow H^1_p\left( \Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{- \infty }\right) = H^1\left( \Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{- \infty }\right) .\end{aligned}$$

(3.5)

The space $S_{\!r}(\Gamma ,v)$ is the space of cusp forms of weight r and corresponding multiplier system v. For functions with polynomial growth the cuspidal condition on cocycles is always satisfied. The theorem is interesting for negative weights, for which the space of cusp forms is zero. Then the theorem gives the vanishing of the cohomology group. Knopp proved most of the statements in his 1974 paper and completed the proof with Mawi [7].

Knopp used a simpler notation for the module of functions with at most polynomial growth. Here I use a notation that comes from representation theory, and was useful in [1, 2].

The Eichler cocycle in (2.1) leads for real weights to holomorphic functions on the lower half-plane ${{\mathfrak {H}}}^-$ with at most polynomial growth at the boundary. That is what we did in [2]. The plus in the notation of the modules indicates that here we work with functions on the upper half-plane. Both approaches are equivalent. The operator $(\textit{JF})(z) = \overline{F({\bar{z}})}$ gives for real weights an ${\mathbb {R}}$-linear isomorphism ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\infty } \leftrightarrow {}{\mathcal {D}}_{v,2-r}^{-\infty }$.

The theorem of Knopp and Mawi is valid in the classical situation $r\in 2{\mathbb {Z}}_{\ge 1}$. The cocycles defined by the holomorphic Eichler integral become coboundaries when we enlarge the module from $V_{r-2}$ to ${}^+{\mathcal {D}}_{1,2-r}^{-\infty }$.

4 Smaller modules

The $\Gamma$-module ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\infty }$ fits into a sequence of modules

$$\begin{aligned} {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\omega } \,\supset \, {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\infty } \,\supset \, {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\infty }\,\supset \, {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega }, \end{aligned}$$

(4.1)

where the last module contains the submodule $V_{r-2}$ if $r\in {\mathbb {Z}}_{\ge 2}$. The largest module ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\omega }$ consists of all holomorphic functions on ${{\mathfrak {H}}}$. The superscript $-\infty$ indicates at most polynomial growth near the boundary $\mathbb {P}^1_{{\mathbb {R}}}= \partial {{\mathfrak {H}}}$. The functions in ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\infty }$ extend to functions in $C^\infty \left( {{\mathfrak {H}}}\cup {\mathbb {R}}\right)$, and the functions in ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega }$ extend holomorphically to a neighborhood of ${\mathbb {R}}$ in ${\mathbb {C}}$. The action in all these modules is $|_{{\bar{v}},2-r}$ in (3.4). We need a condition at $\infty$ as well. It may be formulated as the requirement that for a holomorphic function F on ${{\mathfrak {H}}}$ the function $F|_{{\bar{v}},2-r}S$, with , is smooth on ${{\mathfrak {H}}}\cup {\mathbb {R}}$ (for ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\infty }$), or has a holomorphic extension to a neighborhood of 0 in ${\mathbb {C}}$ (for ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega }$). These spaces are related to lowest weight subspaces of principal series representations of the universal covering group ${\tilde{G}}$. The modules in (4.1) correspond to the spaces of hyperfunction vectors, distribution vectors, smooth vectors and analytic vectors, respectively.

One associates with the cusp form $f\in S_{\!r}(\Gamma ,v)$ the cocycle $\psi ^c$ in (2.5). It is determined by its values $\psi ^c_T=0$ and $\psi _S^c$ on the generators and S of the modular group $\Gamma$. So it is determined by the period function

$$\begin{aligned} P(z) = \psi ^c_S(z) = \int _{\tau =0}^{\infty } \overline{f(\tau )}\,({\bar{\tau }}-z)^{r-2}\, \mathrm{d}{\bar{\tau }}.\end{aligned}$$

(4.2)

It satisfies the relations $P|_{{\bar{v}},r-2}S=-P$ and

$$\begin{aligned} P = P|_{{\bar{v}},r-2}T + P|_{{\bar{v}},r-2}{} \textit{TST}. \end{aligned}$$

(4.3)

In the integral in (4.2) the obvious choice of the path lets ${\bar{\tau }}$ run from 0 to $\infty$ downward along the negative imaginary axis. So P has a holomorphic extension to ${\mathbb {C}}{\setminus } -i[0,\infty )$. The function $x\mapsto P(x)$ is real-analytic on ${\mathbb {R}}{\setminus } \{0\}$. A further analysis based on the quick decay of cusps forms at the cusp 0 shows that $x\mapsto P(x)$ extends as a function in $C^\infty ({\mathbb {R}})$. Also $P|_{{\bar{v}},2-r}S$ has this property. So $P\in {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\infty }$. It is even an element of the intermediate module ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,\infty }$

$$\begin{aligned} {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\infty }\,\supset \, {}^+{\mathcal {D}}_{\bar{v},2-r}^{\omega ^0,\infty }\,\supset \, {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega },\end{aligned}$$

(4.4)

defined as the subspace of $F\in {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\infty }$ that extend holomorphically to a neighborhood of ${\mathbb {R}}{\setminus } E$ for a finite set E of cusps.

Fig. 1

Deformation of the path of integration and a region of holomorphic continuation of P. The period function associated with a cusp form has a holomorphic extension to ${\mathbb {C}}$ minus a path in the lower half-plane from 0 to $\infty$

As shown in Fig. 1 we can get other domains of continuation by deforming the path. Adapting the path of integration to the point z in the lower half-plane ${{\mathfrak {H}}}^-$ we can get a continuation $P_r$ of P to ${\mathbb {C}}{\setminus }(-\infty ,0]$ and another continuation $P_\ell$ to ${\mathbb {C}}{\setminus }[0,\infty )$. These continuations are equal on ${{\mathfrak {H}}}$. See Fig. 2. The period function P associated with a cusp form in $S_{\!r}(\Gamma ,v)$ has properties analogous to those of the period function described by John Lewis and Don Zagier [9].

Fig. 2

The holomorphic period function P on ${{\mathfrak {H}}}$ has extensions $P_r$ (left) and $P_\ell$ (right)

All values $\psi ^c_\gamma$ of the cocycle associated with a cusp form in $S_{\!r}(\Gamma ,v)$ can be expressed in the linear span of the functions $P|_{{\bar{v}},2-r}\gamma$ with $\gamma$ in $\Gamma$. So $\psi ^c\in Z^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,\infty })$. In [2, Theorems B and E] we established the isomorphism

$$\begin{aligned} S_{\!r}(\Gamma ,v) \cong H^1_p\left( \Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,\infty }\right) \quad (r\in {\mathbb {R}}{\setminus }{\mathbb {Z}}_{\ge 2}). \end{aligned}$$

(4.5)

Together with the theorem of Knopp and Mawi in Sect. 3 this implies all isomorphisms illustrated in Fig. 3, under the condition that $r\not \in {\mathbb {Z}}_{\ge 2}$.

Fig. 3

Spaces of cusp forms are ${\mathbb {R}}$-linearly isomorphic to various parabolic cohomology groups, for real weights r not in ${\mathbb {Z}}_{\ge 2}$

5 Base point in the upper half-plane

Let $z_0\in {{\mathfrak {H}}}$. The integral in (2.5) can be modified to give for $\gamma \in \Gamma$

$$\begin{aligned} \psi ^{z_0}_\gamma (z) = \int _{\gamma ^{-1}z_0}^{z_0} \overline{f(\tau )}\,({\bar{\tau }}-z)^{r-2}\, \mathrm{d}{\bar{\tau }}. \end{aligned}$$

(5.1)

For this integral to make sense we do not need information concerning the decay of f at cusps. So now we can now take f in the space $A_r(\Gamma ,v)$ of holomorphic functions on ${{\mathfrak {H}}}$ with automorphic transformation behavior (invariant under $|_{{\bar{v}},r}\gamma$ for all $\gamma \in \Gamma$). We may call functions in $A_r(\Gamma ,v)$ unrestricted modular forms. It contains the so-called weakly holomorphic modular forms, and many more. For instance $\mathrm{e}^J \in A_0(\Gamma ,1)$.

The integral in (5.1) associates cocycles in $Z^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega })$ to $f\in A_r(\Gamma ,v)$. The cohomology class of the cocycle does not depend on the choice of the base point. We obtain a commutative diagram:

(5.2)

If $r\not \in {\mathbb {Z}}_{\ge 2}$ the map from $A_r(\Gamma ,v)$ to the analytic cohomology group $H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega })$ is injective, but far from surjective.

The image of $A_r(\Gamma ,v)$ in $H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega })$ can be described as a mixed parabolic cohomology group. If $V\subset W$ is an inclusion of $\Gamma$-modules, the mixed parabolic cohomology group $H^1_p(\Gamma ;V,W)$ consists of those cohomology classes $[\psi ]$ in $H^1(\Gamma ;V)$ for which $\psi _T \in W|(T-1)$. (For groups with more than one cuspidal orbit the definition is slightly more complicated; one has to take into account all cuspidal orbits.) The image of $S_{\!r}(\Gamma ,v)$ is equal to the mixed parabolic cohomology group $H^1_p(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega }, {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,\infty })$.

To describe the image of $A_r(\Gamma )$ we need the module ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,{\mathrm {exc}}}$ containing ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega }$ and contained in ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\omega }$. It consists of the holomorphic functions F on ${{\mathfrak {H}}}$ that extend into the lower half-plane ${{\mathfrak {H}}}^-$ across ${\mathbb {R}}{\setminus } C$ where C is a finite set of cusps. Near each of the cusps $\xi \in C$ we require that the region where F is not holomorphic is contained in a Siegel domain in ${{\mathfrak {H}}}^-$, a translate by an element of ${\mathrm {SL}}_2({\mathbb {R}})$ of a set of the form $\{z\in {{\mathfrak {H}}}^-\;:\; x_1\le {\mathrm {Re}\,}z \le x_2,\; {\mathrm {Im}\,}z< -y_0\bigr \}$. See Fig. 4.

Fig. 4

Elements $F\in {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,{\mathrm {exc}}}$ extend holomorphically in the lower half-plane, except at a finite number of cusps. Near such a cusp the set where F is not holomorphic should be in the region between two geodesic half-lines with end point c. In the sketch we indicate with “nh” the region where F need not be holomorphic. On the left is an example of a Siegel domain near c, and on the right the region is not a Siegel domain

The image of $A_r(\Gamma ,v)$ in $H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega })$ is equal to the mixed parabolic cohomology group $H^1_p(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega }, {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,{\mathrm {exc}}})$ [2, Theorem A]. This description is our central result. The proof of the surjectivity takes a lot of work. We have to go over to other $\Gamma$-modules consisting of germs of nonholomorphic functions at the boundary $\partial {{\mathfrak {H}}}$.

Fig. 5

Summary of the results for weight $r\in {\mathbb {R}}{\setminus } {\mathbb {Z}}_{\ge 2}$. Definitions on the various modules can be found on the following pages: p4: ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\omega }$; p3: ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\infty }$; p4: ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\infty }$; p4: ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega }$; p5: ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,\infty }$; p7Doe: ${}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,{\mathrm {exc}}}$. See p6 for the space $A_r(\Gamma ,v)$ of unrestricted automorphic forms and p7 for the mixed parabolic cohomology group $H^1_p(\Gamma ;\cdot ,\cdot )$

Figure 5 summarizes the results we discussed. Following the arrows we get an ${\mathbb {R}}$-linear map $A_r(\Gamma ,v)\rightarrow H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\infty })$. This map has a huge kernel since this cohomology group is isomorphic to $S_{\!r}(\Gamma ,v)$. The kernel of the composition $H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega })\rightarrow H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\infty })$ on the right in Fig. 5 is even larger, since the mixed parabolic cohomology group $H^1_p(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega }, {}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega ^0,{\mathrm {exc}}})$ has infinite codimension in $H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{\omega })$. See Part i)c) of Theorem E in [2].

On top in Fig. 5 I have added the cohomology group $H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\omega })$. In the classical case $r\in {\mathbb {Z}}_{\ge 2}$ it is known to be zero [8, Theorem 5]. I do not know whether this cohomology group vanishes for general real weights r. Each element of $A_r(\Gamma ,v)$ has an image in $H^1(\Gamma ;{}^+{\mathcal {D}}_{{\bar{v}},2-r}^{-\omega })$ via the bottom and the right-hand side of the diagram in Fig. 5. Theorem C in [2] relates the vanishing of this image and the existence of harmonic lifts of f.

I end with the conclusion that for real weights $r\not \in {\mathbb {Z}}_{\ge 2}$ the theory of cocycles attached to modular form is more complicated than the classical theory. It is more similar to what is discussed in [1] for Maass forms.