Demand response through automated air conditioning in commercial buildings—a data-driven approach

Abstract

Building operation faces great challenges in electricity cost control as prices on electricity markets become increasingly volatile. Simultaneously, building operators could nowadays be empowered with information and communication technology that dynamically integrates relevant information sources, predicts future electricity prices and demand, and uses smart control to enable electricity cost savings. In particular, data-driven decision support systems would allow the utilization of temporal flexibilities in electricity consumption by shifting load to times of lower electricity prices. To contribute to this development, we propose a simple, general, and forward-looking demand response (DR) approach that can be part of future data-driven decision support systems in the domain of building electricity management. For the special use case of building air conditioning systems, our DR approach decides in periodic increments whether to exercise air conditioning in regard to future electricity prices and demand. The decision is made based on an ex-ante estimation by comparing the total expected electricity costs for all possible activation periods. For the prediction of future electricity prices, we draw on existing work and refine a prediction method for our purpose. To determine future electricity demand, we analyze historical data and derive data-driven dependencies. We embed the DR approach into a four-step framework and demonstrate its validity, utility and quality within an evaluation using real-world data from two public buildings in the US. Thereby, we address a real-world business case and find significant cost savings potential when using our DR approach.

Introduction

To date, the energy transition is mostly pushed forward in advanced European economies (e.g., Germany, Norway, Sweden, Switzerland), but there is also a world-wide political endeavor (e.g., South America, Japan) to stop global warming (World Economic Forum 2017). With an increasing number of countries aiming for an entirely sustainable energy production (especially from wind and solar), sustainable energy sources evolved to be the world’s (relatively) fastest-growing energy source (U.S. Energy Information Administration 2018). The adverse effect of sustainable energy sources is their lack of controllability (e.g., sun shining, wind blowing), which brings volatility to energy supply (Goebel 2013; Ludig, et al. 2011). As a result, the expansion of sustainable energy sources results in more volatile electricity prices (Smith et al. 2010; Ketterer 2014).

Additionally, the world’s energy consumption is projected to increase by 28% between 2015 and 2040, especially due to increased economic growth, access to marketed energy, and quickly growing populations in non-OECD countries (U.S. Energy Information Administration 2017), that outweigh increasingly energy-efficient technologies. Thereby, in 2017, domestic and commercial building sectors’ combined contribution to U.S. energy consumption has reached 27% (Pérez-Lombard, et al. 2008; U.S. Energy Information (Pérez-Lombard, et al. 2008; U.S. Energy Information Administration 2015) and is projected to increase by 32% between 2015 and 2040, an increasing proportion of which is electricity consumption with an annual increase of 2% (U.S. Energy Information Administration 2017). Thus, for building operation, which has the objective to manage buildings and their facilities (e.g., technical infrastructure, heating, ventilation and air conditioning), volatile electricity prices are a difficult challenge and electricity demand management is an important task.

Building operators can reduce their volatility-exacerbated electricity costs by utilizing flexibility in electricity consumption, which “bear[s] economic value” (Fridgen, et al. 2016, p.538). As electricity prices—depending on the market—are likely to be lower during some periods (e.g., night times), it is preferable to consume electricity in these periods rather than during periods, in which prices are regularly at their peak (e.g., noon). Following Rozali, et al. (2014, p.2464) load shifting (LS) defines the “process of reallocating the electricity demands from the peak periods when the electricity tariff is high, to off-peak periods when the electricity tariff is low”. While LS is usually not possible for the entire electricity demand, already minor LS flexibilities can yield substantial electricity cost savings. More precisely, certain appliances are interactive and usually lack flexibility potential (e.g., television, lighting, stove, office equipment) (Barker, et al. 2012), however, other appliances may contain flexibility potential that can be utilized by smarter control systems (e.g., air conditioning systems, water boiler, washing machine). The research domain for utilizing LS flexibility is called demand response (DR). DR is defined as “changes in electric usage by end-use customers from their normal consumption patterns in response to changes in the price of electricity over time […]” (Federal Energy Regulatory Commission 2008, C-2).

In U.S. building operation, a/c systems are an important influencing factor of electricity costs (U.S. Energy Information Administration 2016) and denote a sub-category of building automation systems, i.e., systems which are “widely employed in modern buildings to realize automatic monitoring and control of building services systems” (Liu, et al. 2009, p.1138). Nevertheless, to this day, there are many a/c systems that are manually controlled ((Ferreira, et al. 2012) and prone to run constantly throughout the day, even during disused hours on working days, weekends, and night times. These a/c systems possess LS flexibility potential by reducing a/c to the on-demand usage in advance to the occupancy of a room or building. Other a/c systems provide “automatic control of the indoor environment conditions” (Ducreux, et al. 2012, p.4847) and either preset a/c activation to a fixed time of day or trigger a/c activation by temperature measurements within the building’s sensor networks.

Opposite to these approaches, the present paper aims to contribute to the development of data-driven decision support systems (DSS) that make a/c additionally cost-sensitive. In general, DSSs are “computer technology solutions that can be used to support complex decision making and problem-solving” (Shim, et al. 2002, p.111). According to the “Expanded DSS Framework” of (Power 2008, p.127), the special type of data-driven DSS “emphasizes access to and manipulation of a time series of internal […] data and sometimes external and real-time data”. Data-driven DSSs can significantly improve electricity management for a/c systems by monitoring and processing decision-relevant information from different information sources. They can integrate both building-specific information (e.g., current and required inside temperature, occupancy schedules) and external information (e.g., historical and real-time electricity price information, weather information) to enable ex-ante optimal LS decision making. Compared to many existing approaches to building automation, these decisions are time-saving and cost-saving under consideration of human objectives and frame conditions. Hence, the present paper covers a relevant real-world problem:

“How can data-driven decision support for load shifting reduce electricity costs in real estate air conditioning systems?”

For the creation of data-driven DSSs, smart and machine supported information systems are of great value. An advanced metering infrastructure (AMI) as a subcategory of information and communication technology (ICT) records “customer consumption (and possibly other parameters) hourly or more frequently and provides for daily or more frequent transmittal of measurements over a [bidirectional] communication network to a central collection point” (Federal Energy Regulatory Commission 2008, p.5). Therefore, AMI enables rapid information exchange and remote control for activating and deactivating a/c systems.

A building operator’s LS decision on a/c depicts a dynamic and stochastic optimization problem. Therefore, this paper presents an artifact to address this real-world problem by following principles of the design science research (DSR) paradigm (Gregor and Hevner 2013; Hevner, et al. 2004; Peffers, et al. 2007). The artifact comprises a DR approach for data-driven DSSs, which enables building operators to perform real-time decision making on LS. The DR approach is embedded into a standardized four-step framework and decision making is realized by an algorithm that requires building operators to set a few input parameters. Thereby, the DR approach automatically searches for the expected optimal activation time of the a/c system within a specified temporal flexibility window. Three artifact requirements are postulate

d: It must be easy to understand and use, without requiring engineering expertise or thermal modeling (i.e., simple). It must be applicable for a broad range of applications scenarios (i.e., general), and it must integrate electricity price and demand prediction (i.e., forward-looking).

The paper is structured as follows: This section discusses the purpose and scope of the artifact and its relevance for the target audience (building operators). Section 2 specifies the problem context in detail and presents findings from prior research. Section 3 presents the artifact referred to as DR approach. Section 4 contains the artifact demonstration and a rigorous design evaluation that underpins the validity, utility, and quality of the artifact based on a real-world business case with historical data from two large public buildings. Section 5 summarizes results and discusses limitations and possible future research.

Related work

The development of an artifact, which enables building operators to reduce electricity costs using ICT-enabled decision support, is a contribution to energy informatics (EI). EI is concerned with “analyzing, designing, and implementing systems to increase the efficiency of energy demand and supply systems” (Watson, et al. 2010, p.24). An application domain of EI is demand-side management (DSM), which comprises “approaches such as the general increase in energy efficiency and time-based electricity pricing for end-consumers” (Feuerriegel and Neumann 2014, p.359). Strbac (2008) provides an overview of DSM, explaining both benefits and challenges. The author lists DSM as a means to reduce long-term electricity reserve, to reduce preventive measures for power system security, to improve operation efficiency, and to manage network constraints at the distribution level (Strbac 2008). DR is a subclass of DSM (Sui, et al. 2011), which is an umbrella term (Feuerriegel and Neumann 2014). DR is more customer-centric by promoting their interaction and responses to market signals (e.g., electricity prices) (Albadi and El-Saadany 2008; Siano 2014; Palensky and Dietrich 2011). Fridgen et al. (2016) propose a DR valuation method for LS flexibility from a utility’s perspective using real option analysis. They build on prior research applying real option analysis (Benaroch and Kauffman 1999; Ronn 2002; Sezgen et al. 2007; Ullrich 2013) and develop a model to dynamically optimize LS in discrete time increments. For households and small businesses, Conejo et al. (2010) develop a model to dynamically adjust the hourly load level in response to consumption constraints and electricity prices, which are forecasted within confidence intervals. Lujano-Rojas et al. (2012) present an optimal DR load management strategy, which considers electricity price prediction, user-defined preferences on energy demand, renewable power production, and electric vehicle utilization. In two case studies, they illustrate that users of the proposed model can reduce electricity bills between 8 and 22%. Presenting a tool to maximize social welfare, Su and Kirschen (2009) illustrate that electricity prices tend to decline by increasing usage of LS. In a case study, Albadi and El-Saadany (2008) demonstrate that DR reduces electricity price peaks and changes the consumption patterns of end-consumers. The authors list the benefits of DR and find that savings are not only possible for participating customers, but for all customers in the market. Further, they find positive effects of DR on electricity system reliability and electricity market performance. Mohsenian-Rad, et al. (2010, p.329) use a game-theoretic approach to illustrate that in the presence of a real-time electricity market, each user has the incentive to participate in a scheduling game. They propose an “optimal, autonomous, and distributed incentive-based energy consumption scheduling algorithm” that aims to minimize “the cost of energy and also to balance the total residential load” (Mohsenian-Rad, et al. 2010, p.329). Further, they focus on communication among users rather than interactions between a utility company and its customers. For residential customers, Gottwalt, et al. (2011) build different scenarios with flat and time-based electricity tariffs. Without uncertainty in a day-ahead hourly pricing regime, households can realize significant savings in electricity costs.

In the context of commercial building operation, Zhou, et al. (2011) build an agent-based simulation model and illustrate that DR actions by several building operators shave load profiles at peak hours (peak clipping), reduce the volatility of aggregated electricity demand, reduce electricity prices (and therefore electricity costs), and reduce electricity price volatility. Bahrami, et al. (2012) suggest a new load management strategy to reduce building operators’ electricity costs. Their DR approach models electricity prices as a convex function of electricity demand and supply, i.e., an individual building operator’s hourly market price is influenced by information about the total electricity consumption of all customers and the total generation capacity of the respective utility. However, since building operators usually lack such detailed market information, this approach is rather game theoretic and only applicable from a utility’s perspective. A model for electricity price prediction is developed by Mohsenian-Rad and Leon-Garcia (2010) who propose an automatic energy consumption scheduling framework. Similar to the present paper’s objectives, these authors intent to help building operators “to shape their response [to electricity prices] properly and in an automated fashion” (Mohsenian-Rad and Leon-Garcia 2010, p.121). While the present paper’s approach takes into account the dependence of electricity demand on temperature forecasts, Mohsenian-Rad and Leon-Garcia (2010) require building operators to manually announce their upcoming electricity demand using AMI. Henze (2005) presents a model-based approach for predictive control of active and passive thermal storage inventory. Their supervisory controller includes short-term weather prediction and therefore a/c electricity demand prediction, time-of-use differentiated electricity prices, and real-time control strategies with dynamically updated forecasts. However, since these authors assume electricity rate structures to be visible and exogenously predetermined by the utility, their model is not suited for situations in which a building operator must decide based on real-time electricity market price information with stochastic future development. The present paper grasps this situation by applying a prediction methodology for intraday electricity price development under consideration of historical price patterns. Another approach that integrates dynamic electricity tariffs and electricity storage management is presented by Oldewurtel, et al. (2011). Like the present paper’s approach, these authors model dynamic electricity prices with stochastic future development to achieve electricity cost savings by exploiting LS flexibilities. Instead of predicting electricity demand, however, these authors empirically collect and aggregate historical demand profiles, which makes their model insensitive for individual electricity consumption. While these articles focus on a macrogrid perspective, there is also a substantial research stream on decentral microgrid concepts (e.g., Guerrero, et al. 2012; Hatziargyriou, et al. 2007; Münsing, et al. 2017; Thiam 2010). Though this perspective is gaining increasing importance with the further distribution of decentralized (renewable) electricity generation (e.g., solar, wind), this manuscript focuses on the optimization of electricity costs in the presence of a macro electricity market (i.e., against public market prices).

Most of the mentioned studies rely on data-driven decision making and assume smart grids and respective ICT (especially AMI) as technological enablers. Concluding, researchers have already started to develop data-driven DR approaches by suggesting new control logics in building operation, which might be part of future DSSs. The present paper strives to contribute to this development by addressing especially one identified research gap: To the best of the authors knowledge, formal DR approaches which dynamically predict electricity prices and electricity demand for a/c systems based on weather information and occupancy schedules and that perform automated and real-time decision support on LS with the objective to reduce electricity costs do not exist so far.

Artifact description

In this section, the present paper continues to “create and evaluate(the appropriate) IT artifact intended to solve [the] identified problem” (Hevner, et al. 2004, p.77). In line with the EI framework introduced by Watson, et al. (2010), the artifact supports building operators using flow networks (AMI) and sensitized objects (a/c system) to smarter consume electricity. Hence, it addresses the problem of a “lack of information to enable and motivate economic and behaviorally driven solutions” (Watson, et al. 2010, p.24).

Scenario introduction

The present paper defines an “a/c system” as technology that building operators use to change temperature (i.e., heating, or cooling) inside a room or building. Although many authors use the term heating, ventilation and air conditioning systems, this paper applies a/c systems as a general term, which can comprise all these use cases. The a/c system is part of a greater information system that “ties together the various elements to provide a complete solution” (Watson, et al. 2010, p.27). In the following, the artifact’s application scenario is explained along with prerequisite assumptions and the four-step framework embedding the DR approach to reduce electricity costs.

The application scenario is characterized as follows: A building operator must prepare appropriate temperature according to an exogenously specified room or building (in the following referred to as object) occupancy schedule (Fig. 1). Occupancy time is the time when the considered object is not empty. The required inside temperature (${\mathrm{temp}}_{\mathrm{req}}$) needs to be achieved until occupancy starts ($\mathrm{T}$), whereas inside temperature prior to occupancy may deviate. For the DR approach, the present paper focuses on the time span between the first possible starting time for a/c (t₀) and the latest possible starting time for a/c (t_L). The latter is necessary to guarantee ${\mathrm{temp}}_{\mathrm{req}}$ until occupancy: ${\mathrm{t}}_{\mathrm{L}}$ is the latest point prior to $\mathrm{T}$ at which a/c activation ensures temp_req until T. By finding the expectedly optimal point in time between t₀ and t_L (i.e., the temporal flexibility window for LS) to activate the a/c system, building operators can minimize expected electricity costs. During each day, several subsequent, non-overlapping events can take place in one object.

• Assumption 1: Building operators can deduce ${t}_{0}$ and ${t}_{L}$ by analyzing the occupancy schedule and ${temp}_{req}$ is constant for different object occupancies.

  The DR approach uses the end of one occupancy as ${\mathrm{t}}_{0}$ to optimize a/c for subsequent occupancy (if an occupancy is the first on the day, ${\mathrm{t}}_{0}$ could be the previous day). Hence, due to the previous occupancy, the object’s inside temperature in ${\mathrm{t}}_{0}$ can be assumed to be ${\mathrm{temp}}_{\mathrm{req}}$. If a/c is deactivated in ${\mathrm{t}}_{0}$, the object’s inside temperature starts striving toward outside temperature due to thermal movement.

• Assumption 2: The object’s inside temperature in ${t}_{0}$ equals ${temp}_{req}$.

  Considering the first artifact requirement (“easy to understand and use”), the DR approach applies discrete-time optimization, which is less complex and demanding (for decision-makers and ICT) than continuous-time optimization. Moreover, the DR approach requires an appropriate a/c procedure, i.e., a sequence of a/c activations and deactivations with specific durations and intensities. A/c procedures are specified by their control levers: Cooling and heating can be activated unilaterally or alternately. Then, cooling and heating can be activated continuously or with interruptions. Finally, cooling and heating can be performed at different intensities within certain technical boundaries. These control levers can be applied either solely or jointly within one procedure. The common objective of all procedures is to achieve ${\mathrm{temp}}_{\mathrm{req}}$ until $\mathrm{T}$.

Fig. 1

Exemplary time scheme prior to occupancy time

Figure 2 illustrates three exemplarily procedures (for cooling): A procedure where a/c is activated dynamically over multiple periods (1). At each discrete time step, an algorithm decides to either activate or deactivate a/c and, for activation, a/c intensity. Although this is a very promising procedure to minimize electricity costs for a/c, it also entails the largest optimization complexity. Then, a less complex procedure in which ${\mathrm{temp}}_{\mathrm{req}}$ (until $\mathrm{T}$) is achieved by one-time activation and deactivation (2). To compensate for an object’s thermal movement, inside temperature during activation (before $\mathrm{T}$) is undercooled. However, this procedure has technical restrictions (e.g., the a/c system may cool below the freezing point of cooling water) wherefore additional optimization conditions are necessary. Finally, a procedure in which a/c runs constantly (without interruption) from ${\mathrm{t}}_{0}$ to ${\mathrm{t}}_{\mathrm{L}}$ (3). This procedure foregoes LS flexibility and is (in most cases) a waste of savings potential and energy.

Fig. 2

Objective and variants of a/c procedures

The present paper applies a procedure that is more simplistic than procedure (1) and a combination of procedure (2) and (3) with modifications to avoid technical restrictions resulting from undercooling or overheating and to reduce the waste of energy: After activation, a/c is performed continuously and not allowed to interrupt. After reaching ${\mathrm{temp}}_{\mathrm{req}}$, it is performed at a lower intensity to keep ${\mathrm{temp}}_{\mathrm{req}}$ until $\mathrm{T}$ (Fig. 3).

Fig. 3

The applied procedure

Thereby, $x\ge 1$ is the duration (number of discrete-time increments) after a/c activation until ${\mathrm{temp}}_{\mathrm{req}}$ is restored. The algorithm of the DR approach starts in ${\mathrm{t}}_{0}$ and examines whether immediate activation of a/c is expected to be optimal. The activation of a/c is expected to be optimal if the total expected electricity costs resulting from a/c activation in the current period until $\mathrm{T}$ are lower compared to later activation times. If a later activation is expected to be optimal, a/c is not activated and computation is repeated the next discrete time step (${\mathrm{t}}_{\mathrm{L}}$ at the latest).

Framework introduction

The data-driven DR approach is embedded within a standardized four-step framework (Fig. 4).

Fig. 4

Four-step framework of the DR approach

It consists of an inner cycle (decision algorithm for LS) and an outer cycle (feedback cycle). In step 1 (scheduling), the DR approach imports input information for data-driven decision making. In step 2, the DR approach predicts future electricity prices (a) and demand (b). This information is used in step 3, when the DR approach decides upon LS, i.e., activation of the a/c system. If activation is deferred, the DR approach reiterates step 2 and 3 in the next period. After the optimization is completed, the DR approach evaluates realized cost savings (step 4). In the following, this paper explains each step and the accompanying assumptions in more detail.

Step 1: scheduling

The first step is the collection of three human input parameters according to Assumption 1: ${\mathrm{t}}_{0}$, ${\mathrm{t}}_{\mathrm{L}}$, and ${\mathrm{temp}}_{\mathrm{req}}$. ${\mathrm{t}}_{0}$ and ${\mathrm{t}}_{\mathrm{L}}$ may be implicitly derived out of the object’s occupancy schedule. These parameters strongly influence further decision making and set the boundaries for optimization.

Step 2a: Price prediction

As the DR approach optimizes a/c activation under consideration of expected electricity costs, the algorithm must integrate currently observable and expected future electricity (market) prices. Therefore, the DR approach requires an electricity price prediction model, which is not only accurate but also able to keep comprehensiveness and simplicity. Although different price prediction models are conceivable, the present paper builds upon the work of Fridgen, et al. (2016), who develop a discrete-time price prediction model for the valuation of LS flexibility in an intraday electricity market. In the following, their model is referred to as “price prediction model”.

Within the price prediction model, the authors develop a stochastic process “which realistically replicates intraday electricity spot price development” (Fridgen, et al. 2016, p.537). Their stochastic process predicts electricity price movements and thereby certain reoccurring intraday patterns out of historical data. Since this paper does also focus on intraday flexibility in discrete-time increments, the price prediction model is appropriate for the present purpose.

The price prediction model uses geometric electricity spot price returns to set up a geometric Brownian motion consisting of two components: A component depicting expected price changes (drift) and a component depicting uncertain price changes (volatility). The computation of the drift integrates historical time (of day)-dependent mean electricity prices and expects that the process reverts to these patterns (mean-reversion). Since mean price and volatility patterns vary between different times (of day), the price prediction model ties a “chain of single-period stochastic processes” (Fridgen, et al. 2016, p.1001). However, the present paper makes some modifications to align the price prediction model: The original model values LS flexibility using a real options approach, since flexibility is purchased in these authors’ scenario. Real options and their value are dependent on price volatility. Whereas Fridgen et al. (2016) model only electricity prices as the underlying asset to their real option, this paper would have to model both electricity prices and demand, which would result in a far more complex real option analysis. Instead, a simple expectation maximization on already existing flexibility is applied. Assuming risk-neutral building operators, price volatility is no influencing factor for ex-ante decision making:

The decision-maker is risk-neutral in his decision making.

The resulting electricity price prediction model based on Fridgen, et al. (2016) is defined by the following term ($\mathrm{E}$ is the expectation value, $\mathrm{S}$ is the spot price for electricity, $\mathrm{t}$ is the time of day, $\theta \in [\mathrm{0,1}]$ is the speed of mean-reversion, $\stackrel{-}{\mathrm{S}}$ is the long-term mean electricity price, and $\alpha = \frac{{\mathop \sum \nolimits_{i = 0}^{i = n} S\left( {t - i} \right)}}{{\mathop \sum \nolimits_{i = 0}^{i = n} \overline{S}\left( {t - i} \right)}} \in \left[ {0,\infty } \right)$; a parameter for short-term adjustment of$\stackrel{-}{\mathrm{S}}$):

$$E\left( {S\left( {t + 1} \right)} \right) = E\left( {S\left( t \right)} \right) + \theta * \left( {\alpha * \overline{S}\left( {t + 1} \right)} \right) - E\left( {S\left( t \right)} \right)$$

(1)

The speed of mean-reversion $\uptheta$ determines how fast the electricity price is expected to return to its long-term price pattern during the next discrete time increment. If $\theta =1$, the electricity price in $\mathrm{t}+1$ is expected to equal the adjusted long-term mean price in $\mathrm{t}+1$. If $\theta =0$, the electricity price in $t+1$ is expected to equal the price in $\mathrm{t}$. The short-term adjustment $\mathrm{\alpha }$ determines the adjustment of $\stackrel{-}{\mathrm{S}}$ to represent recent price information. In particular, daily electricity prices usually deviate from their long-term mean price level because of temporary fluctuations in electricity demand and supply. The DR approach integrates current observable price information and applies the price prediction model whenever it must decide about a/c activation.

Step 2b: demand calculation

Besides electricity prices, building operator’s electricity costs depend on electricity demand. In step 2b, the DR approach calculates electricity demand ($\mathrm{D}\left({t}_{i},{t}_{\mathrm{L}},x\right)$) for a/c activation. $\mathrm{D}\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{L}},\mathrm{x}\right)$ is the total amount of electricity (in kwh) that is consumed between ${\mathrm{t}}_{\mathrm{i}}$ and ${\mathrm{t}}_{\mathrm{L}}$. It depends on the difference between outside temperature and ${\mathrm{temp}}_{\mathrm{req}}$, which is referred to as $\mathrm{\Delta temperature}(t)$. For further analysis, $\mathrm{D}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x\right)$ is separated into two components (Fig. 5):

Fig. 5

Electricity demand in the applied procedure

$\mathrm{ID}({t}_{\mathrm{i}},x)$ is the initial electricity demand or payback load (Illerhaus and Verstege 2000) for a/c deactivation in ${t}_{0}$ and subsequent thermal movement until a/c (re)activation. $\mathrm{ID}\left({t}_{\mathrm{i}},x\right)$ is the initial electricity demand per time increment

$$ID\left( {t_{i} ,x} \right) = \sum\nolimits_{{t = t_{i} }}^{{t = t_{i} + x - 1}} {ID\left( t \right)}$$

(2)

To estimate $\mathrm{ID}(t),$ building operators analyze the historical data-based dependence of $\mathrm{ID}(t)$ on previous periods’ development of $\Delta \mathrm{temperature}(t)$. They regress $\mathrm{ID}(t)$, for example, on mean temperature or use a weighted average with a higher weighting for more recent temperature developments (due to thermal movement). A multi-dimensional model that regresses $\mathrm{ID}(t)$ simultaneously on every previous periods’ $\Delta \mathrm{temperature}(t)$ is also conceivable but exposed to great complexity and data requirements. If historical data is absent, building operators could conduct experimental runs to collect the required information. Moreover, starting in ${t}_{\mathrm{i}}$, further electricity $\mathrm{PD}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x\right)$ is required to compensate for continuous thermal movement until $\mathrm{T}$. After achieving ${\mathrm{temp}}_{\mathrm{req}}$, $\mathrm{PD}(t)$ is the periodical amount of electricity (in kwh) that is required to keep ${\mathrm{temp}}_{\mathrm{req}}$ constant between $\mathrm{t}$ and $t+1$. In addition, until ${\mathrm{temp}}_{\mathrm{req}}$ is achieved (i.e., during the initial cooling process between ${t}_{i}$ and ${t}_{\mathrm{i}}+x$), there is already a fraction of $\mathrm{PD}(t)$ that is required (in addition to $\mathrm{ID}({\mathrm{t}}_{\mathrm{i}},\mathrm{x})$) as the a/c system starts to regulate the inside temperature toward ${\mathrm{temp}}_{\mathrm{req}}$, which also initializes energy loss due to thermal movement. For simplification, this amount of energy is estimated by $\frac{\mathrm{PD}(\mathrm{t})}{2}$ for $\mathrm{t}\in [{t}_{\mathrm{i}},{t}_{\mathrm{i}}+x-1]$. Hence, $\mathrm{PD}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x\right)$ can be computed as

$$PD\left( {t_{i} ,t_{L} ,x} \right) = \sum\nolimits_{{t = t_{i} }}^{{t_{i} + x - 1}} {\frac{PD\left( t \right)}{2}} + \sum\nolimits_{{t = t_{i} + x}}^{{t = t_{L} }} {PD\left( t \right)}$$

(3)

Like $\mathrm{ID}(t)$, building operators can measure the dependence of $\mathrm{PD}\left(t\right)$ on $\Delta \mathrm{temperature}(t)$. Figure 6 illustrates a schematic dependency structure for $\mathrm{PD}\left(t\right)$. Thus, the algorithm can compute the total electricity demand between ${t}_{\mathrm{i}}$ and ${t}_{\mathrm{L}}$:

$$D\left( {t_{i} ,t_{L} ,x} \right) = ID\left( {t_{i} ,x} \right) + PD\left( {t_{i} ,t_{L} ,x} \right)$$

(4)

Fig. 6

Schematic dependence of $PD(t)$ on $\Delta temperature(t)$

Step 3: decision-making

In this step, the DR approach decides either to activate the a/c system in the current period or to defer the activation decision to the next period. More precisely, for each possible (discrete) activation time ${t}_{\mathrm{i}}$ until ${t}_{\mathrm{L}}$, estimated in time ${t}_{\mathrm{m}}$ ($\mathrm{m}\le \mathrm{i}$, refers to the current point in time for decision making), the algorithm calculates expected total electricity costs for a/c activation. For $\mathrm{ID}({t}_{\mathrm{i}},\mathrm{x})$ and $\mathrm{PD}({t}_{\mathrm{i}},{t}_{\mathrm{L}},x)$, costs amount to:

$$E\left( {C\left( {ID(t_{i} ,x} \right))} \right) = \sum\nolimits_{{t = t_{i} }}^{{t = t_{i} + x - 1}} {\left( {E\left( {ID\left( t \right)} \right)*E\left( {S\left( t \right)} \right)} \right)}$$

(5)

$$E\left( {C\left( {PD(t_{i} ,t_{L} ,x} \right)} \right)) = \mathop \sum \limits_{{t = t_{i} }}^{{t = t_{i} + x - 1}} \left( {\frac{PD\left( t \right)}{2}*E\left( {S\left( t \right)} \right)} \right) + \mathop \sum \limits_{{t = t_{i} + x}}^{{t = t_{L} }} \left( {PD\left( t \right)*E\left( {S\left( t \right)} \right)} \right)$$

(6)

adding $\mathrm{E}\left(\mathrm{C}\left(\mathrm{ID}({t}_{\mathrm{i}},x\right))\right)$ and $\mathrm{E}(\mathrm{C}\left(\mathrm{PD}({t}_{\mathrm{i}},{t}_{\mathrm{L}},x\right)))$, building operators can calculate the expected total electricity costs $\mathrm{E}(\mathrm{C}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x\right))$. In particular, $\mathrm{E}(\mathrm{C}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x|{t}_{\mathrm{m}}\right))$ expresses these costs estimated in time ${\mathrm{t}}_{\mathrm{m}}$. The objective of the algorithm in time ${\mathrm{t}}_{\mathrm{m}}$ is therefore to identify the minimum $\mathrm{E}(\mathrm{C}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x|{\mathrm{t}}_{\mathrm{m}}\right))$ out of all possible activation times t_i, i.e., $\underset{\mathrm{i}}{\mathrm{min}}(\mathrm{E}(\mathrm{C}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x|{t}_{\mathrm{m}}\right)))$. If the algorithm expects $\underset{\mathrm{i}}{\mathrm{min}}(\mathrm{E}(\mathrm{C}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x|{t}_{\mathrm{m}}\right)))=\mathrm{E}(\mathrm{C}\left({t}_{\mathrm{i}},{t}_{\mathrm{L}},x|{\mathrm{t}}_{\mathrm{m}}\right))$, a/c is activated and ex-ante optimization is terminated. Otherwise, the algorithm defers the activation decision for one period to update information and to decide again. If ${{\mathrm{t}}_{\mathrm{m}}=\mathrm{t}}_{\mathrm{L}}$ is reached, a/c activation is obligatory.

Step 4: feedback

In the last step, the activation decision and resulting electricity costs are ex-post evaluated. The algorithm’s activation decision bases on electricity price and demand predictions and does not necessarily yield optimal results. Hence, there is a need to quantify electricity cost savings to evaluate the quality of the artifact (Goebel 2013; Strueker and Dinther 2012). Absolute and relative cost savings can be computed by comparing the results of the applied procedure (Fig. 3) and a procedure with no DR. As a reference for no DR (“default procedure”), procedure (3) from Fig. 2 can be applied in which a/c is activated continuously throughout the day. In addition, the feedback should contain a comparison between cost savings and cost savings potential. Cost savings potential is defined as the maximum of electricity costs that could have been saved within the applied procedure by optimally applying LS within the given flexibility window from an ex-post perspective. This is the benchmark for the DR approach. Finally, observable information can be recorded (e.g. time of day, electricity prices, outside temperature, and electricity demand) and processed into a continuously growing database that the DR approach can use to maintain or improve prediction quality.

Artifact demonstration and evaluation

Real-world scenario description

In this section, the artifact is evaluated as required within the DSR paradigm. Therefore, the artifact’s functionality is illustrated within an example, i.e., the decision algorithm of LS is applied to demonstrate that the DR approach “can be implemented in a working system” (Hevner, et al. 2004, p.79). Afterward, the DR approach is evaluated with multiple simulations of random scenarios to demonstrate that the “artifact (generally) works and does what it is meant to do” (validity) (Gregor and Hevner 2013, p.351). For both, real-world data is applied.

The object that serves for demonstration and evaluation is located in the southeastern part of the United States, in Georgia. Georgia is known for its subtropical climate, with humid summers and moderate winters. Especially during summer months (May to September), temperatures are comparatively high (between 15–31.7 °C on average). During winter months (November to March), temperatures are on average above freezing point (between 0.6 °C and 18.3 °C). For research purposes at the University of Georgia, a/c data were collected from two University buildings. The rooms within the buildings are used as offices and for large meetings. Both buildings are partly open to the public. Using measuring points, different parameters were collected during a period ranging from January 2010 to December 2014. Collected parameters comprise inside temperature on a room level, outside temperature, and electricity consumption (kWh) for a/c usage. Measuring points recorded instantaneous, i.e., not as averaged values within a certain time span. Main components of the a/c system are two chiller systems that jointly air-condition via chilled water loops. Together, both chiller systems have a maximum wattage of 1.2 MW and are responsible for 90% of the a/c system’s total electricity consumption. The remaining 10% are consumed by auxiliary equipment that scales up with the chillers’ current load level. By applying variable load control, the a/c system is designed to provide a constant supply water temperature (about 5 °C + /−0.2 °C). Electricity consumption of the a/c system depends on the temperature of return water (that, in turn, depends on outside and the buildings’ inside temperature). Warmer return water increases electricity consumption and vice versa. To date, no DR mechanism is in place and the (central) a/c system runs all day (not to be confused with a single room’s air supply, which can toggle on and off), even in times of low or no occupancy (e.g., on weekends and at night). Overall, the current system wastes energy and yields unnecessary electricity costs.

The University purchases electricity for the a/c system from a local utility company. The company charges real-time electricity prices rather than offering a flat plan. Thus, electricity prices are sometimes high and the University incurs significant electricity costs. The collected data of the a/c system and payed electricity prices make this example suitable for the DR approach’s demonstration and evaluation. Although a data-driven DSS that integrates the DR approach is not implemented yet, its theoretical cost savings potential is evaluated in this scenario.

For variable load control, the a/c system already possesses sensor systems that measure further parameters such as supply water temperature and current load level, a web server that collects all sensor information, and a remote controller that building operators can access using a web portal. Access to the utility’s real-time electricity prices is available using the customer portal. To establish cost-sensitive a/c control, there is a need for changes and enhancements in the monitoring and control system as it must dynamically import the utility’s price information (by accessing a respective application interface) and possess control software that applies the data-driven DR approach. Moreover, hardware for faster communication and computation would be useful in order that the system can react on changes in input information in near real-time (which is especially necessary to scale downtime increment length between two optimization iterations). Due to an expert’s opinion (an engineer at the university with a PhD who is specialized in a/c systems), the sum of all university-internal and -external costs for implementing such cost-sensitive control in the considered a/c system amounts to about $100.000. Further running costs are expected to be insignificantly low. Besides this application scenario, the expert expects the control software to be applicable in other university buildings as soon as they are also equipped with modern monitoring and control systems. To obtain a conservative estimate, the present paper limits the business case analyses to the described scenario.

Step 1 Scheduling (demonstration)

For artifact demonstration, ${\mathrm{temp}}_{\mathrm{req}}$ is set to 21 °C. This is the currently targeted inside temperature in the scenario’s buildings. As Georgia, USA, is known for its humid and hot summers, a typical day in September is chosen, when a/c is required to cool (keep) the inside temperature to (at) 21 °C. In particular, the DR approach is applied on September 04, 2014. The hypothetical event of interest (e.g., a major event of a university initiative) takes place at 2 pm (occupancy time) in both buildings. The earliest possible a/c activation is set to 7am. The University’s expert stated that every room within the two buildings (regardless of current inside and outside temperature) can be cooled down to ${\mathrm{temp}}_{\mathrm{req}}$ by a/c within one hour. Hence, ${\mathrm{t}}_{\mathrm{L}}$ is at 1 pm (i.e., $x=1$). As the dataset of historically payed electricity prices features hourly time increments, artifact demonstration and evaluation is also conducted with hourly time increments between ${t}_{0}$ and ${t}_{\mathrm{L}}$. Table 1 illustrates the schedule.

Table 1 Schedule for artifact demonstration

Step 2a: Price prediction (demonstration)

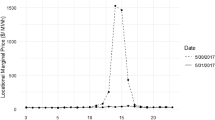
As described in Sect. 3, this paper modifies and applies the price prediction model developed by Fridgen, et al. (2016). This price prediction model draws upon the existence of historical time of day- and season-specific price patterns and updates price prediction at every time step by integrating new observable price information. Figure 7 illustrates historical time of day-specific price patterns of electricity prices. Further, Table 2 illustrates descriptive statistics on electricity price patterns of different months.

Fig. 7

Hourly mean electricity prices (June 2012–November 2014)

Table 2 Descriptive statistics for electricity prices per month [$/kWh]

For configuration purposes, building operators can adjust three endogenous (model) parameters within the DR approach’s price prediction model: $\theta$, $n$ (the adjustment reference interval to compute shot-term adjustment $\alpha$), and an estimation corridor to compute $\stackrel{-}{\mathrm{S}}(t)$. Fridgen, et al. (2016) vary $\theta$ within an interval between 0 and 1. For artifact demonstration, $\uptheta$ is arbitrarily set to 0.8 and further analysis of its influence is left to the subsequent evaluation. Similar, $\mathrm{n}$ is set to 0. To calculate $\stackrel{-}{\mathrm{S}}(t)$, Fridgen, et al. (2016) analyze seasonal price patterns. The authors differentiate between summer, winter, and intermediate season. However, this does not fully reflect the course of historical time-of-day-specific price patterns. For example, their intermediate seasons include March–May and September–November. Therefore, March and September share the same $\stackrel{-}{\mathrm{S}}(t)$, which is (in our case) not accurate as shown in Table 2. Hence, this paper calculates $\stackrel{-}{\mathrm{S}}(t)$ based on a historical corridor around the date of interest and time-of-day. For the presented example (September 04, 2014), $\stackrel{-}{\mathrm{S}}(t)$ at (e.g.) 12 noon is calculated by averaging previous-years’ historical electricity prices from (e.g.) 30 days prior to 30 days after the date of interest, i.e., from August 05, (2010–2013) to October 04, (2010–2013) each of which at 12 noon. Table 3 illustrates respective results (with $\mathrm{S}(t)$ being the actual observable electricity prices).

Table 3 Price prediction parameters

Example:

$E\left( {S\left( {9am{|}8am} \right)} \right) = E(S\left( {8am{|}8am} \right) + \theta {*}(\alpha \left( {8am} \right){*}\overline{S}\left( {9am} \right) - E\left( {S\left( {8am{|}8am} \right)} \right) = 0.0599 + 0.8{*}\left( {0.9552{*}0.0625 - 0.0599} \right) = 0.0597$

In the next step, the DR approach estimates $\mathrm{D}({t}_{i},1\mathrm{pm},1)$. As described in Sect. 3.5, $\mathrm{D}({\mathrm{t}}_{\mathrm{i}},1\mathrm{pm},1)$ is split into $\mathrm{ID}\left({\mathrm{t}}_{\mathrm{i}},1\right)$ and $\mathrm{PD}\left({\mathrm{t}}_{\mathrm{i}},1\mathrm{pm},1\right)$ (as $x=1$ is constant within the real-world scenario, this section continues with a reduced formal notation that neglects $x$). For the real-world scenario, Table 4 illustrates related $\mathrm{\Delta temperature}(t)$ and $\mathrm{PD}(t)$ observations and a respective linear regression.

Table 4 Empirical dependence of PD ${{\varvec{t}}}_{{\varvec{i}}}$ on ∆temperature

The real-world scenario’s a/c system is intended for cooling only. Cooling for $\mathrm{\Delta temperature}(t)<0$ implies that the two buildings were still heated up when outside temperature already fell below ${\mathrm{temp}}_{\mathrm{req}}$. Unfortunately, historical temperature forecasts that match the given historical data set were not obtainable. Hence, for artifact demonstration and evaluation, this paper requires an assumption to predict electricity demand:

Actual outside temperature equals previous weather forecasts

Generally, Assumption 4 depicts a great simplification of reality. However, since the DR approach focusses on short-term schedules for only a few hours, weather forecasts are close to reality (National Weather Service 2017). Moreover, subsequent evaluation integrates an artificial demand prediction error to analyze electricity cost savings’ sensitivity to demand forecasting quality. Hence, the algorithm can use historical outside temperature as previous weather forecasts to compute $\mathrm{PD}(t)$. Table 5 illustrates the respective results.

Table 5 Development of $\Delta temperature(t)$ and PD (t)

To date, historically collected parameters are only appropriate for the estimation of$\mathrm{PD}(\mathrm{t})$. To precisely estimate$\mathrm{ID}({t}_{\mathrm{i}})$, experimental runs would be necessary that analyze different a/c deactivation durations and different outside temperature developments. However, these experimental runs have not been conducted yet. As interim solution, threshold values are applied that logically contain the correct$\mathrm{ID}({t}_{\mathrm{i}})$. For the lower limit applies:$\underset{\_}{\mathrm{ID}}({t}_{\mathrm{i}})=0$, i.e., a situation in which no a/c is required to restore${\mathrm{temp}}_{\mathrm{req}}$. For the upper limit applies: $\overline{{{\text{ID}}}} \left( {{\text{t}}_{{\text{i}}} } \right) = \mathop \sum \limits_{{{\text{t}} = {\text{t}}_{0} }}^{{{\text{t}} = {\text{t}}_{{\text{i}}} - 1}} {\text{PD}}\left( {\text{t}} \right)$, which equals the sum of all electricity that would have been necessary to keep the inside temperature at ${\mathrm{temp}}_{\mathrm{req}}$ at any time since${\mathrm{t}}_{0}$. Until more accurate solutions or historical data are available, $\mathrm{ID}({\mathrm{t}}_{\mathrm{i}})\in [0,\sum_{{\mathrm{t}=\mathrm{t}}_{0}}^{{\mathrm{t}=\mathrm{t}}_{\mathrm{i}-1}}\mathrm{PD}(\mathrm{t})]$ is an appropriate interval to estimate$\mathrm{ID}({t}_{\mathrm{i}})$. For demonstration, we arbitrarily choose a parameter$\varepsilon =0.4$, which simulates a building that absorbs heat to a medium extent. Table 5 (vii) illustrates estimations for $\mathrm{ID}({t}_{i})$ and (viii) estimations for $\mathrm{D}\left({t}_{i},12\right).$

$$ID\left( {t_{i} } \right) = \varepsilon *\mathop \sum \limits_{{t = t_{0} }}^{{t = t_{i} - 1}} PD\left( t \right)$$

(7)

Example:

$PD\left( {8am{|}2pm} \right) = Intercept{*}\Delta temperature\left( t \right){*}Estimate = 428.5889 + 3.8{*}21.8235$

$PD\left( {8am{|}2pm} \right) = \frac{{PD\left( {8am} \right)}}{2} + \mathop \sum \limits_{{{\text{t}} = 9am}}^{2pm} PD\left( t \right) = \frac{511.52}{2} + 520.25 + \ldots + 697.02 + 550.80$

$ID\left( {1pm} \right) = \varepsilon {*}\mathop \sum \limits_{{t = t_{0} }}^{{t = t_{i} - 1}} PD\left( t \right) = 0.4{*}\left( {507.15 + 511.52 + \ldots } \right) = 1411.83$

$D\left( {1pm,2pm} \right) = ID\left( {1pm} \right) + \frac{{PD\left( {1pm} \right)}}{2} + \mathop \sum \limits_{t = 2pm}^{2pm} PD\left( t \right) = 1411.83 + \frac{697.02}{2} + 550.80 = 2311.14$

4.5 Step 3: Decision making (demonstration)

In the third step, the decision algorithm for LS determines if immediate a/c activation is ex-ante optimal (cost minimal). In particular, from the perspective of the current period, the algorithm predicts and compares expected total electricity costs for all possible activation periods. Table 6 illustrates computations from the perspectives of 7a.m., 8a.m., 1p.m., and 2p.m. In this example, the algorithm would wait until 1 pm to initialize a/c.

Table 6 Decision making within artifact demonstration

Example:

$E\left( {C\left( {1pm,2pm{|}1pm} \right)} \right) = ID\left( {1pm} \right){*}E(S\left( {1pm{|}2pm} \right) + \mathop \sum \limits_{t = 1pm}^{2pm} E\left( {S\left( {t{|}2pm} \right){*}PD\left( t \right)} \right) =$ $0.0708{*}1411.83 + 0.0708{*}\frac{697.02}{2} + .0925{*}550.80 = 175.58$

4.6 Step 4: Feedback (demonstration)

In the last step, the DR approach ex-post evaluates the ex-ante chosen activation time as described in Sect. 3.7. Therefore, the DR approach computes savings of its decision compared to the default procedure with no DR. By applying DR and activating a/c at 1 pm, total electricity costs would have been $174.53 (cf. Table 7ii). These are the lowest actual (not expected) total costs and can be computed by utilizing F-6 with the actual (not expected) electricity prices. The default procedure, however, would have yielded total electricity costs of $312.90 (cf. Table 7ii). This equals an electricity cost reduction of 44.22% due to the DR approach. Moreover, the theoretically optimal point in time for a/c activation (the benchmark) was also at 1 pm. In particular, the DR approach was able to utilize the entire cost savings potential. Table 7 summarizes the results for the presented example. ${C}_{ex-post}$ are calculated using the demand for each hour and according actual prices, not the expected prices. Since this example is biased in its validity because it was manually picked, the next section contains randomly chosen historical simulations and sensitivity analysis. Thereby, the general usefulness of the artifact is analyzed.

Table 7 Decision making within artifact demonstration

Evaluation

DSR methodology calls for an evaluation of a developed artifact to provide evidence “how well the artifact supports a solution to the problem “(Peffers, et al. 2007, p.56). A possible evaluation method within DSR are simulations (Hevner, et al. 2004). This paper’s evaluation is divided into three parts and presents historical simulations on the real-world scenario with 200,000 simulation runs each: The first part gives an impression on the DR approach’s effectiveness in terms of average electricity cost savings and sensitivity of the latter to endogenous model parameters ($\uptheta$,$\mathrm{n}$, and estimation corridor, c.f. Section 4.3). Subsequently, the triple of endogenous model parameters that yields the highest average electricity cost savings is fixed for the second part of the historical simulation. This calibration procedure for the prediction model is valid, as building operators can individually chose model parameters. The electricity cost savings of the second part are then analyzed on their sensitivity to exogenous scenario parameters (${t}_{0}$,${t}_{\mathrm{L}}$, flexibility window length${ t}_{\mathrm{L}}-{t}_{0}$, and dependency of ${\mathrm{ID}}_{{\mathrm{t}}_{\mathrm{i}}}$ on ${\mathrm{PD}}_{\mathrm{t}}$). To lift Assumption 4, a third simulation part integrates an artificial hourly demand prediction error). Therefore, the sensitivity of electricity cost savings to forecasting quality of electricity demand is measured. For all simulation parts, sensitivity of the results to the electricity market is analyzed by also repeating every simulation with electricity prices from the German-Austrian market area of EPEX SPOT. This market has a significantly growing capacity of renewable energy generation (EPEX SPOT 2017) that may evolve to a global trend. To isolate market influences on the results, the object and temperature conditions are assumed to equal the real-world scenario. In the following, this section refers to both markets as US market and EU market, respectively. Results of all simulation parts are discussed afterward.

Historical simulation – part 1

A multivariate sensitivity analysis identifies the triple of all three endogenous model parameters that yield (in combination) the highest average electricity cost savings: $\theta =1.0$, $n=6\mathrm{h}$, and estimation corridor length $=30$ days with average electricity cost savings of $99.76 (or 45.40%) for the US market and $\theta =1.0$, $n=0\mathrm{h}$, and estimation corridor length $=60$ days with average electricity cost savings of €51.28 (or 46.11%) for the EU market. As building operators can individually select endogenous model parameters, they should always conduct such pre-simulations on their individual historical data to maximize electricity cost savings. Thereby, as the present example illustrates, the best parameter combination can vary between different electricity markets. In the second part of the simulation, the respective best parameter combinations are fixed for both markets.

Historical simulation–part 2

Table 8 illustrates the evaluation parameters and their range. Simulation runs are conducted by sampling with replacement. Overall parameter combinations, the DR approach yields average electricity cost savings of $94.61 (or 44.52%) for the US market and €48.42 (or 44.07%) for the EU market compared to the default procedure with no DR. Standard deviation is $134.62 (142.29% of mean) for the US market and €52.30 (108.01% of mean) for the EU market. The cost savings potential (i.e., the benchmark) is $99.63 (or 46.88%) for the US market and €50.58 (or 46.03%) for the EU market. Therefore, the utilization of cost savings potential by applying the DR approach is 94.96% for the US market and 95.74% for the EU market. Table 9 presents the result’s sensitivity to endogenous model parameters:

Table 8 Range of evaluation parameters (Simulation—part 1)

Table 9 Sensitivity of absolute and relative savings to endogenous (model) parameters

For the second evaluation part with fixed (calibrated) endogenous model parameters (cf. Table 10), the DR approach yields average electricity cost savings of $95.49 (or 45.03%) for the US market and €49.47 (or 45.14%) for the EU market compared to the default procedure with no DR. Standard deviation is $132.81 (139.07% of mean) for the US market and €51.83 (104.75% of mean) for the EU market. The cost savings potential is $99.84 (or 47.08%) for the US market and €50.61 (or 46.18%) for the EU market. Therefore, the utilization of cost savings potential by applying the DR approach is 95.65% (first evaluation part, without calibration, 94.96%) for the US market and 97.75% (first evaluation part 95.74%) for the EU market. Figure 8 illustrates the histograms and Table 11 presents the result’s sensitivity to exogenous model parameters:

Table 10 Range of evaluation parameters (Simulation—Part 2)

Fig. 8

Histogram of absolute savings (0 excluded, bin width: 1 [$ or €])

Table 11 Sensitivity of absolute and relative savings to exogenous (scenario) parameters

Historical simulation—part 3

In the third evaluation part, Assumption 4 is lifted and an artificial hourly demand prediction error (DPE) is integrated. More precisely, for the first predicted discrete time step (i.e., hour), the DR approach estimates upcoming electricity demand by drawing from an equal distribution to the extent of the DPE around the historically measured value of that time. Predicting the subsequent discrete time step (i.e., the second hour in future), the algorithm reiterates this procedure but additionally adds the first hour’s prognosis error. This approach is applied for all remaining discrete time steps within the temporal flexibility window.

With fixed endogenous model parameters and DPE (cf. Table 12), the DR approach yields average electricity cost savings of $93.44 (or 44.10%) for the US market and €48.28 (or 44.01%) for the EU market compared to the default procedure with no DR. Standard deviation is $132.40 (141.69% of mean) for the US market and €52.28 108.28% of mean) for the EU market. The cost savings potential is $99.45 (or 46.94% compared to the default procedure) for the US market and €50.50 (or 46.04%) for the EU market. Therefore, the utilization of cost savings potential by applying the DR approach is 93.95% (second evaluation part 95.65%) for the US market and 95.60% (second evaluation part 97.75%) for the EU market. Table 13 presents the result’s sensitivity to the DPE:

Table 12 Range of evaluation parameters (Simulation—Part 3)

Table 13 Sensitivity of absolute and relative savings to hourly demand prediction error

Discussion of evaluation results:

Summarizing all evaluation results, the authors derive the following insights and interpretations: Within the real-world scenario, there is a huge savings potential in electricity costs by applying the DR approach. Thereby, the DR approach utilizes almost the entire cost savings potential, although it uses an algorithm with ex-ante (uncertain) electricity price prediction. The high exploitation of savings potentials is due to the following reasons:

Electricity cost savings potential does only refer to cost savings that can (theoretically) be obtained by applying the present paper’s applied a/c procedure (Fig. 3). It excludes further cost savings potential that would exist for more flexible but complex a/c procedures [e.g., “dynamic (de)activation” as illustrated in Fig. 2, (1)] or for managerial flexibility that differs from temporal flexibility (e.g., flexibility in temperature limits that this paper excluded by Assumption 1).

Furthermore, for the second simulation part, early a/c activation (before ${t}_{\mathrm{L}}$) was ex-post optimal in only 30.80% of all simulations for the US market and 25.63% for the EU market. More precisely, as this paper models hourly time increments within a real-world scenario that exhibits significant electricity demand to keep the inside temperature at ${\mathrm{temp}}_{\mathrm{req}}$, it is often disadvantageous to cool before ${t}_{\mathrm{L}}$. The DR approach correctly anticipated that fact and had only a few misjudgments. If this paper had modeled shorter time increments (e.g., quarter-hourly instead of hourly), more flexibility of action would (on the one hand) increase the DR approach’s cost savings potential and (on the other hand) stronger challenge decision making (with possibly more misjudgments of the algorithm and therefore less exploitation of the savings potential). However, as the present paper’s real-world example is restricted to hourly electricity market data (cf. Section 4.2), a sensitivity analysis for time increment length is subject to future research.

Besides, some electricity cost savings are due to Assumption 4, i.e., missing uncertainty in electricity demand forecasts. However, as the third simulation part and Table 13 illustrates, this effect is rather small and has only a significant impact for huge misjudgments of the prediction model.

Finally, the DR approach’s performance within the presented real-world scenario is significant, since today’s cost-insensitive a/c control wastes a huge amount of energy as a/c runs constantly throughout the day, even during disused hours on working days, weekends, and night times. Therefore, smart a/c control that considers occupation schedules, electricity price prediction, and weather forecasts can yield huge electricity cost savings, even for minor misjudgments that fail ex-post optimal decision making.

The results also indicate that relative electricity cost savings, relative cost savings potential and the utilization of cost savings potential by applying the DR approach differ only slightly between the US and the EU market. This implies that the DR approach is applicable to different electricity markets that offer volatile electricity spot market prices. However, standard deviations of electricity cost savings are comparatively high and larger on the US market than on the EU market. The former results from the fact that average electricity cost savings depend on the simulation’s (randomly chosen) model and scenario parameters (as illustrated within respective sensitivity analysis). As many parameter combinations are possible, electricity cost savings can vary significantly. In addition, the evaluation puts forth some implications of parameter sensitivity analysis:

Sensitivity of electricity cost savings to endogenous (model) parameters: Significant greater electricity cost savings due to greater $\theta$ confirm the value of modeling mean-reversion to time-of-day-specific price patterns for short-term electricity prediction. While such patterns do not exist in many other spot markets (such as stock prices on capital markets) due to the instability of arbitrage opportunities, they occur in electricity spot markets as electricity consumption depends on time-dependent customer preferences that lack flexibility potential and renewable electricity generation that lacks controllability (cf. Introduction). Significant greater electricity cost savings due to the existence of an adjustment factor $\alpha$ that is computed on current observable price information ($n=0$) indicates that instantaneous price developments are likely to deviate from long-term historical mean prices. Therefore, an appropriate prediction model should consider short-term effects on electricity market prices. As electricity cost savings did not significantly depend on estimation corridor length, historical time-of-day-specific price patterns on the two researched electricity markets are rather stationary, i.e., seasonal price patterns’ influence on results are low.

Sensitivity of electricity cost savings to exogenous (scenario) parameters: The observation that electricity cost savings for the US and the EU market significantly depend on ${t}_{0}$ and ${t}_{\mathrm{L}}$ is another indicator for the impact of both market’s (individual) time-of-day-specific price patterns that help building operators to identify lucrative opportunities to utilize flexibility in a/c. In addition, ${t}_{0}$ and ${t}_{\mathrm{L}}$ are critical influencing factors for available flexibility window length. The observation of longer flexibility window length significantly increasing electricity cost savings is intuitive, as a longer flexibility window (that is favored by low room or building occupancy) provides the DR approach with a greater economic scope of action. Similar, the dependency of electricity cost savings on ${\mathrm{ID}}_{{\mathrm{t}}_{\mathrm{i}}}$ is intuitive as buildings with less insulation are exposed stronger to (outside) temperature development and, therefore, thermal movement, which results in a higher payback load that shrinks electricity cost savings due to temporal a/c deactivation.

For the University of Georgia’s business case calculation, the expert estimated total costs for implementing and running cost-sensitive a/c control (using the DR approach) to about $100.000 (cf. Section 4.1). Evaluation results illustrate that the payback period for this investment depends especially on electricity cost savings per LS measure and therefore on exogenous scenario parameters (as endogenous model parameters can be calibrated by the building operator). For discounting electricity cost savings, building operators require an appropriate annual risk-free interest rate ${r}_{\mathrm{f}}$. Therefore, for example, they can calculate the mean of the 3-month U.S. Treasury Bill yields observed over the last 10 years, which would currently amount to ${r}_{\mathrm{f}}=0.7\%$ (Mukherji 2011; U.S. Department of Treasury 2017). Moreover, LS frequency is relevant, i.e., how often building operators can conduct LS measures. Applying a common net present value approach, Table 13 shows calculations for the payback period of the business case (without economies of scales, cf. Section 4.1) that authors use to support investment decision making within the described real-world scenario (Table 14).

Table 14 Business Case Payback Periods [Y]

Implications, limitations, and further research

Implications

The present research contributes to the development of data-driven DSSs that can significantly reduce building operators’ electricity costs. In particular, a DR approach is presented, which utilizes existing LS flexibility potential of a/c systems by performing real-time decision making. The latter requires rapid information exchange and remote control for activating and deactivating a/c, which is enabled using modern ICT (especially AMI).

The DR approach satisfies the requirements stated in the introduction: It is simple, general, and forward-looking. Computations are feasible without engineering expertise because they focus on data-driven decision making. Building operators can use the presented four-step framework to derive their individual DR approach for real-estate a/c systems. The development of the DR approach follows the principles of the DSR Paradigm. The artifact demonstration and evaluation propose that the DR approach is valid (“validity”) (Gregor and Hevner 2013). By applying real-world data from two university buildings and a respective business case, the present paper demonstrates the usability of the artifact in practice (“utility”) (Hevner, et al. 2004). Within the real-world scenario, the artifact would be able to yield remarkable electricity cost savings compared to current existing a/c procedure (“quality”) (Gregor and Hevner 2013). However, sensitivity analysis illustrate that the payback period of the real-world business case does strongly depend on endogenous model and exogenous scenario parameters.

Within similar frame conditions, the developed artifact provides considerable electricity cost savings between 42 and 45% across the German and a special US electricity market. The tested parameters illustrate that mean-reversion parameter, adjustment reference interval, and estimation corridor length tend to influence electricity cost savings. Moreover, this research paper suggests how to analyze the business case for implementing and running cost-sensitive a/c control (using the DR approach). Our results imply that the viability of such an investment depends critically on the frequency of LS measures and the extent of possible electricity cost savings.

Limitations and further research

There are also limitations to the DR approach. First, an assumption is made that actual outside temperature equals previous temperature forecasts (i.e., there is no uncertainty in electricity demand). Indeed, weather forecasts for only a few hours are close to reality (National Weather Service 2017), which is confirmed by this paper as it additionally applies an additional sensitivity analysis, which implements an artificial hourly demand prediction error that proves to have only little influences on results. However, future research should further develop the presented approach and waive this simplification. Second, this paper assumes a constant required room temperature ${\mathrm{temp}}_{\mathrm{req}}$ and, therefore, focuses on temporal flexibility of a/c systems. However, we neglect the possibility to generate further cost savings by considering flexibility in quality (i.e., flexibility of ${\mathrm{temp}}_{\mathrm{req}}$), which would be a promising extension for future research. Third, since authors have no data to estimate the dependence of initial a/c electricity demand on the previous hours’ outside temperature development, only an interim solution is applied that basis on interval estimation. Especially an application in practice or the cooperation with other fields of research would yield important insights to further specify the quantification of initial a/c electricity demand. Fourth, the DR approach is limited to only one procedure of performing a/c. In particular, for reasons of simplicity, it cannot account for scenarios in which a building operator dynamically activates and deactivates the a/c system. A procedure that allows at each discrete time step to either activate or deactivate a/c and (for a/c activation) to control a/c intensity should further increase the cost savings potential. Fifth, there is also a proportion of simulation runs, in which cost savings are negative. To strengthen confidence, trust, and attention into DR technologies, future research should try to develop DR approaches that reduce the occasions of negative results. As negative results are more formative (Rozin and Royzman 2001), this might deter building operators to apply DR (Venkatesh, et al. 2003). Nevertheless, the designed artifact is a robust data-driven method for building operators and can be used beyond the application domain. By its simplicity, generality, and forward-look, it depicts a suitable solution for many applicants. In line with Palensky and Dietrich (2011), this is also a further step to make DSM more customer-centric in the future. Sixth, besides presented approaches for electricity price and demand prediction, future research could apply and compare other common modeling approaches such as Holt-Winters seasonal models (Holt 2004; Winters 1960) for electricity price prediction or consumption-based asset pricing models (Breeden 1979) for electricity demand prediction. Finally, we consider macrogrids as the only source for electricity. In times of increasingly decentralized power generation, e.g., by local solar modules on building roofs, integrated approaches of “make-or-buy-electricity” should be worth consideration. Therefore, future research could grasp our approach, e.g., to build an algorithm that decides in discrete time increments to either sell self-generated electricity or use it for premature a/c before room occupation.