Abstract
Motivated by recent developments to deploy collaborative robots in industrial production systems, we investigate the assembly line balancing problem with collaborative robots. The problem is characterized by the possibility that human and robots can simultaneously execute tasks at the same workpiece either in parallel or in collaboration. For this novel problem type, we present a mixed-integer programming formulation for balancing and scheduling of assembly lines with collaborative robots. The model decides on both the assignment of collaborative robots to stations and the distribution of workload to workers and robotic partners, aiming to minimize the cycle time. Given the high problem complexity, a hybrid genetic algorithm is presented as a solution procedure. Based on extensive computational experiments, the algorithm reveals promising results in both computational time and solution quality. Moreover, the results indicate that substantial productivity gains can be utilized by deploying collaborative robots in manual assembly lines. This holds especially true for a high average number of robots and tasks to be assigned to every station as well as a high portion of tasks that can be executed by the robot and in collaboration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The role of automation in modern manufacturing companies has increased significantly over the past decades. Several types of automated equipment, such as industrial robots, are frequently included in production systems (Graves and Redfield 1988). In 2017, for instance, worldwide robot sales reached 374,000 units, an increase of 217% compared to 2010. This growth is mainly driven by the automotive and electronics industry (International Federation of Robotics 2018), where industrial robots are utilized in assembly lines to ensure the companies’ ability of high-volume production at low costs. Additionally, the use of highly automated assembly lines assures standardized product quality and process safety (Boysen et al. 2008). As a result of the evolving role of automation technology, enterprises predominantly focused on achieving economy of scale by standardization of processes and inclusion of industrial robots (Hu et al. 2011).
In the current state, however, manufacturers cannot efficiently automate many tasks as the established robot technology does not provide the required degree of flexibility. Consequently, economy of scope is achieved by manual assembly utilizing human advantages in manufacturing corporations and small- and medium-sized enterprises (SMEs) (Antonelli et al. 2016; Hu et al. 2011; Krüger et al. 2009; Michalos et al. 2014). Humans comprise characteristics like flexibility, adaptability, decision making skills, and creativity while strength, endurance, speed, and accuracy are attributes of robots (Helms et al. 2002; Michalos et al. 2014). To remain competitive, manufacturing enterprises have to introduce new production concepts to increase their performance.
Human–robot collaboration (HRC) is an emerging technology in the field of novel production systems. By introducing stations with collaborative task execution by workers and robots, the advantages of both automated and manual production lines can be realized in a combined production system. As a result, the production efficiency and quality can increase. Additionally, the introduction of HRC can be beneficial for the workers’ states of health if the robot executes ergonomically stressful and repetitive tasks. This is of particular importance against the background of demographic change (Schmidtler and Bengler 2015). Further advantages arise from the possibility of parallel work from either side of the station. The length of the assembly line may decrease, which results in higher space utilization. Also, the robot as an additional resource reduces the production lead time. In addition, material handling, workers’ movement, and set-up times may also be reduced (Bartholdi 1993; Lee et al. 2001).
Manufacturers name manifold application areas for collaborative robots (Kuka 2018; Universal Robots A/S 2018b) and they have been successfully implemented in both manufacturing corporations (BMW Group 2013; Daimler 2014; Volkswagen 2018) and SMEs (Fraunhofer IAO 2016; International Federation of Robotics 2015a, b, c). Despite its increasing distribution in real-world industry applications, the trend of human–robot collaboration has not yet been considered in the balancing of assembly lines, and many companies state the necessity of additional support for the planning process (Fraunhofer IAO 2016).
Aside from assigning tasks to the stations of the assembly line under the consideration of precedence relations (assembly line balancing), further challenges arise for the balancing of assembly lines with collaborative robots. Since robots are considered as additional resources, it has to be decided about the allocation of a limited number of collaborative robots to the manual stations of the assembly line (equipment selection). For stations with robots, tasks also have to be allocated to the resources (worker and/or robot) overtime. Consequently, the assembly line balancing problem with equipment selection is enriched by a collection of scheduling problems. In scheduling these stations, logical relations between the resources have to be considered. For instance, a task can only be performed collaboratively if neither the worker nor the robot is occupied by a different task (scheduling with logical relations). Additionally, these modes have different efficiency. Collaborative execution by a worker and a robot, for instance, is faster than execution only by the human worker (allocation-dependent task times), leading to a tradeoff between time and resource consumption.
From the challenges described above, a novel planning problem for assembly line balancing arises, which we strive to investigate in detail. Our contribution is fourfold. First, since there are a multitude of possible applications for collaborative robots in industrial manufacture, we discuss possible fields of application and limit the scope of our contribution toward the balancing of assembly lines with collaborative robots. Second, a mathematical optimization model of the considered assembly line balancing problem is presented. Third, we develop a hybrid genetic algorithm to solve larger problems. Fourth, by conducting an extensive computational experiment, the performance of the mathematical optimization model and the genetic algorithm is analyzed, and general recommendations for decision makers wavering with collaborative robots’ implementation are derived.
The remainder of this contribution is structured as follows: in the next section, we introduce the problem of balancing assembly lines with collaborative robots based on the classification of the problem setting and an illustrative example. Subsequently, we review the relevant literature in the field of assembly line balancing problems in Sect. 3. A mathematical formulation for the human–robot collaborative assembly line balancing and scheduling problem is introduced in Sect. 4. The hybrid genetic algorithm is presented in Sect. 5. In Sect. 6, we deliver insights into computational results. The paper closes with a conclusion and an outlook for future research in Sect. 7.
2 Balancing of assembly lines with collaborative robots
2.1 Problem setting
Collaborative robots (colloquially named cobots) are a novel type of lightweight robots that are able to collaborate with humans. According to their manufacturers, the technology is suitable for a wide range of applications faced in industrial manufacture, for instance, pick and place, screw driving, injection molding, measuring and inspection, and assembly operations (Kuka 2018; Universal Robots A/S 2018b). Besides this variety of applications, collaborative robots are additionally assumed to be fast set up and easily programmed (within half a day), yielding an agility advantageous in the production of small batches or processes with fast changeovers. Since collaborative robots are also designed mobile, a quick redeployment among the stations is possible (Robert Bosch Manufacturing Solutions GmbH 2018b; Universal Robots A/S 2018a).
While collaborative robots may be utilized to replace human workers, they are originally intended to support human workers in a common station (Bernhardt et al. 2007). As defined by the International Organization for Standardization (2011), human–robot collaboration is an operation between a person and a robot while both share a common workspace. Besides this definition, different authors tried to classify the characteristics of human–robot collaboration. Ogorodnikova (2007) characterizes cooperative assembly as human and robot working without physical separation, since the systems are safe by themselves. According to Chen et al. (2011), HRC is characterized by human and robot sharing the same working place and time without physical barriers. The closest type of cooperation between human and robot occurs, as described by Helms et al. (2002), if tasks at the same workpiece are processed jointly. The latter argumentation is supported by Krüger et al. (2009), who additionally refine that human and robot can either jointly perform the same task or different tasks in parallel. The decision on the processing mode, particularly the decision toward optional collaboration of the two resources, consequently requires the consideration of the temporal dependencies of tasks and resources within common stations (scheduling with logical relations).
While there may be promising applications of human–robot collaboration in any of the organizational forms of production, we focus on mass production using assembly lines. Due to the high degree of specialization and repetition of tasks, we consider this organizational form of production as particularly promising for the application of human–robot collaboration. The planning problem related to the design of assembly lines is known to be the assembly line balancing problem. The first mathematical formulation for assembly line balancing (ALB) was published by Salveson (1955) and is referred to as simple assembly line balancing problem (SALBP). Due to simplifying assumptions of SALBP, this planning approach is not applicable for real-world scenarios of industrial practice (Falkenauer 2005; Sternatz 2014). Therefore, a variety of extensions for more realistic balancing problems have been developed. Contributions have, among others, been devoted to assembly systems with different layouts (e.g., U-shaped or two-sided lines), different product mixes, varying processing times, or the necessity of resource allocation (Battaïa and Dolgui 2013; Boysen et al. 2007).
Contributions in the field of assembly line balancing can be classified by the objective they pursue. Common objectives are the minimization of the number of stations, minimization of cycle time, minimization of costs, or maximization of profit (Boysen et al. 2008). Collaborative robots may be suitable to support either of these objectives. The number of stations may be reduced due to a high extent of parallel work of robot and worker. Costs may be minimized (and profit maximized) by replacing a worker by a robot, if the robot is cheaper than the worker and able to perform each of the required tasks. The installation of collaborative robots, however, is usually considered within existing, manual assembly systems. An initial configuration of the assembly line is consequently given, i.e., stations and material flow technology are yet installed and tools are available. In addition, it is usually not possible to reduce the workforce in most industries within a short period of time. The minimization of the number of stations (and thus workers) consequently does not seem to be a prioritized objective. The consideration of cost- or profit-oriented approaches seems mainly beneficial in the initial design of assembly lines and, thus, does not suit the scenario we pursue. In this contribution, we therefore propose an approach to minimize cycle time of an existing manual system with the given number of stations (type-2 assembly line balancing problem). This is also in line with the survey conducted by Fraunhofer IAO (2016) concerned with use cases of collaborative robots in industrial practice.
Further assumptions concern the number of collaborative robots that can be deployed, their capabilities to perform certain tasks, and the resulting processing times. For the number of collaborative robots to be assigned, we define robot density (\({\text{RD}}\)) as the ratio of number of robots and number of stations. Consequently, with \({\text{RD}} = 1\), a robot is assigned to each station, while \({\text{RD}} = 0\) describes a scenario with manual production only (equipment selection). To equivalently describe the density of assembly tasks in stations, the West ratio is defined as the average number of tasks to be assigned to each station of a production system (Dar-El 1973). With regard to the performance of tasks by collaborative robots, we assume limited capabilities compared to the human workers. While the human is considered to be capable of performing each task, this is not necessarily true for robotic and collaborative performance. Similarly to the robot flexibility introduced by Rubinovitz et al. (1993), we define robot flexibility (\({\text{RF}}\)) and collaboration flexibility (\({\text{CF}}\)) as measures for the portion of tasks that can be executed by the robot and in collaboration, respectively. Consequently, \({\text{RF}} = 1\) (\({\text{CF}} = 1\)) indicates that each task can be executed by a robot (in collaboration). Vice versa, with \({\text{RF}} = 0\) and \({\text{CF}} = 0\), no task can be performed by the robot and in collaboration, respectively. To estimate the potential of robot deployment to single stations of an assembly line, Teiwes et al. (2016) develop a procedure to estimate the automation potential of a given line balance and apply their study to an automotive assembly line. Using their scoring system, they find that the majority of stations reach low (around 20%) or medium potential (around 40%) for deployment of collaborative robots. Their findings also correspond to logical reasoning, since higher automation potential would yet be utilized by complete automation of the respective assembly tasks.
For the determination of processing times, we assume the robot to complement the human worker. Thus, we compare motion speed of human and robot in their shared station to derive consistent times. The maximum human motion speed is considered to be 1.6 m/s when evaluating human–machine interaction (International Organization for Standardization 2010; Marvel and Norcross 2017). Collaborative robots’ velocity depends on the specific robot model and its safety modes. Motion speed of this robot class, however, is strongly reduced around the human workers. In realistic settings, maximum velocity is assumed between 0.5 and 1.0 m/s (Robert Bosch Manufacturing Solutions GmbH 2018a; Universal Robots A/S 2016). We therefore assume the robot to require significantly higher processing time than the human worker. The human worker, however, is vacant and can perform a different task in parallel. While collaboratively conducting the same task, a time reduction may be yielded due to the robot’s support on its common task (allocation-dependent task times).
A further important parameter to describe the assembly situation considered is the task flexibility ratio (F-ratio). It describes the characteristics of a product’s precedence relations, and thus the freedom within the assignment of tasks to stations (Dar-El 1973, 1975). Maximum flexibility is denoted by F-ratio = 1, i.e., no precedence relations among tasks exist. On the contrary, F-ratio = 0 refers to a case with no flexibility, i.e., the only feasible solution is serial assignment in a predetermined order.
2.2 Illustrative example
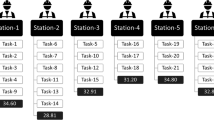
To exemplify the main ideas of our approach and also its effectiveness, an illustration of the problem that we consider is given in Fig. 1. The initially given assembly line comprises three stations (three workers). One product with ten tasks is to be assembled utilizing the stations of the line. The West ratio consequently is calculated as 3.33. The F-ratio of the example problem is 0.76 and thus provides rather high freedom in assignment of tasks to stations. Since one robot is available for three stations, robot density is 0.33. Out of the ten tasks, four (seven) tasks are compliant with execution by robot (in collaboration), resulting in robot flexibility of 0.4 and collaboration flexibility of 0.7. As can be seen from the processing times, execution by robot is assumed slower than execution by human, while collaborative execution is assumed faster.
For the given example problem, the optimal solution of the manual assembly line is calculated according to the formulation of SALBP-2 proposed by Scholl (1999, Chapter 2.2.3.3, Formulation 1), while the collaborative line is calculated utilizing our model introduced in Sect. 4. For the manual line, the model decides on the stations the tasks are assigned to, and its solution results to a cycle time of 21 time units. In the collaborative scenario, one robot is available and assigned to complement the human worker in the first station. In this example, both parallel work (on tasks 1 and 2) and collaborative execution by both resources (on tasks 4 and 7) are utilized. A cycle time of 17 time units is achieved and production output consequently increases by 23.5%.
3 Review of relevant research
In recent years, the concept of collaboration has received increasing attention in production (e.g., Leng and Jiang 2018; Salamati-Hormozi et al. 2018), logistics (e.g., Basso et al. 2019; Guajardo et al. 2018), and supply chain management (e.g., Herczeg et al. 2018; Ponte et al. 2018). In this context, collaboration is typically seen as a form of cooperation between two or more independent companies planning and executing jointly specific operations. The aim is to achieve mutual benefits, which can be related to cost reductions or the compliance with environmental regulations, for instance. Most commonly, cooperation can either take place between (competing) companies on the same stage of a supply chain (horizontal collaboration) or among partners that operate on different supply chain levels (vertical collaboration) (Basso et al. 2019; Simatupang and Sridharan 2002).
In this paper, in contrast, we are concerned with another form of collaboration, namely the cooperation of robots and human workers on the shop floor (Krüger et al. 2009; Tsarouchi et al. 2016a, b). In particular, we consider the balancing of manual assembly lines, in which collaborative robots either support manual task execution by human workers or perform tasks themselves as an additional resource. In this field, two relevant streams of literature can be distinguished. The first stream discusses the allocation of equipment (robots) with different capabilities to stations of a production system and is referred to as equipment selection problem. The second stream is concerned with scheduling problems within the context of assembly line balancing.
In the stream of equipment selection problems, automated assembly lines are examined. The first to explicitly consider industrial robots in line balancing were Rubinovitz et al. (1993). They stress the practical relevance of task times, which are dependent on the specific robot, and consider these in their algorithm to solve the robotic assembly line balancing problem (RALBP). In the recent literature, only few papers are devoted to RALBP with the objective of minimizing the cycle time. Levitin et al. (2006) develop a genetic algorithm (GA) for the RALBP to maximize the production rate and conduct experiments on randomly generated test sets. To improve results and reduce computational effort, Gao et al. (2009) propose a GA and combine it with heuristic local search procedures. They suggest an integer non-linear programming model and compare its optimal results with results from their GA and results from the aforementioned paper. Yoosefelahi et al. (2012) propose a mixed-integer programming (MIP) model with multiple objectives. They aim at minimizing the cycle time, robot investments, and robot setup costs and solve the problem with different evolution strategies. Results of the different strategies are compared among each other. Mukund Nilakantan and Ponnambalam (2015) consider a U-shaped robotic assembly system and propose a 0–1 integer programming model and particle swarm optimization approach. Müller et al. develop an approach for the redundant configuration of automated assembly lines to mitigate the effect of robot failures (Müller et al. 2016, 2017, 2018). Pereira et al. (2018) pursue a cost-oriented approach on the robotic assembly line balancing problem. Novel solution procedures for the RALBP are proposed by Borba et al. (2018).
Overall, the contributions in this stream of literature consider allocation-dependent task times, since the equipment types are associated with different levels of efficiency when performing the tasks. These assumptions are very similar to a literature stream on the assembly line worker assignment and balancing problem (ALWABP) for manual assembly lines based on the contribution of Miralles et al. (2007). In the ALWABP, a heterogeneous workforce has to be assigned to stations, where processing times depend on the actual worker. In neither RALBP nor ALWABP, however, decisions on collaboration of resources are taken into account.
In the second stream, assembly line balancing problems with consideration of scheduling components for (certain) stations are considered. These problems arise, if multiple resources are assigned among a common station and may consequently execute tasks at the same workpiece in parallel. In this field, assembly lines with multi-manned stations are of particular importance. In this problem, tasks and workers have to be allocated among the stations and tasks are explicitly (and exclusively) assigned to the workers. The minimization of the number of workers is pursued by Roshani et al. (2013) and Kellegöz and Toklu (2015). Fattahi et al. (2011) minimize the number of workers as a primary objective and the number of stations as a secondary objective. An improved mathematical formulation for the same problem is proposed by Kellegöz (2016). The minimization of cycle time with the secondary objective to minimize the number of workers is proposed by Roshani and Giglio (2017). An extension toward multiple sides within each station is presented by Naderi et al. (2018). Common tasks to be executed by more than one worker simultaneously are suggested by Yazgan et al. (2011) and Sikora et al. (2017). The collaboration of workers in their examples, however, is given as an external assignment restriction and does not allow deciding on optional collaboration. Moreover, all contributions in this stream assume resource-independent processing times, i.e., a homogeneous workforce is considered. ALB problems with multi-manned stations consequently pursue determination of an advantageous amount of workers rather than the decision on their exact entities. Please note that some contributions of two-sided assembly line balancing also consider collaboration of resources on a common task (Bartholdi 1993; Gansterer and Hartl 2018; Pinnoi and Wilhelm 1997). As in multi-manned ALBP, however, these approaches propose collaboration of resources for these tasks as obligatory and do not consider this as variable. Reviews on the two-sided ALB problem are given by Abdullah Make et al. (2017) and Li et al. (2017).
The literature review indicates that recent research comprises certain characteristics required for modeling human–robot collaboration in ALB. Allocation-dependent processing times are frequently considered in RALBP and ALWABP. In contrast, planning approaches for balancing lines with multiple resources consider scheduling of tasks between the resources while task times are assumed to be independent of the resource the respective task is assigned to. None of these approaches, however, takes into account the optional collaboration of multiple resources on one task (scheduling with logical relations). This characteristic, however, is of major importance for balancing lines with collaborative robots. For that reason, we develop a novel approach for the human–robot collaborative assembly line balancing and scheduling problem (HRCALBSP) in the following.
4 Model formulation
To provide a detailed description of the problem setting we consider, a mathematical model formulation is given in this section. The assembly line consists of a given set of stations \(K\), which is connected by a material handling system, and a set \(P\) of different process alternatives is available for each task. \(P\) contains the alternatives of human (\(p_{\text{H}}\)), robotic (\(p_{\text{R}}\)), and collaborative (\(p_{\text{C}}\)) execution. Process alternatives \(p_{\text{R}} , p_{{{\text{C}} }} \in P\) require the assignment of one of \(q\) equal collaborative robots to the respective station, which is captured by the binary decision variable \(r_{k}\). A set of tasks \(I\) have to be assigned to the stations and each task \(i \in I\) requires a deterministic processing time \(t_{ip}\) depending on its process alternative \(p \in P\). The station a task is assigned to is encoded in decision variable \(z_{i}\). Whether two tasks are subject to direct precedence relations, is modeled in the corresponding set \(E\). In practice, not each task can be processed with each process alternative. To model this, \(t_{ip}\) equals a sufficiently large number if a task \(i \in I\) is considered not to be processible with the specific alternative \(p \in P\) (Levitin et al. 2006). Whether a task is assigned to a station and process alternative is indicated by the binary decision variable \(x_{ikp}\). To allow for parallel and collaborative execution, tasks are scheduled within the stations. The decision variable \(s_{i}\) represents the start time of task \(i \in I\) relative to entry of the workpiece in the respective station. The auxiliary variables \(y_{ij}\) serve to indicate whether scheduling of tasks \(\left( {i,j} \right) \in I\) is required. The decision variable \(c\) denotes the cycle time of a system configuration. The parameter \(\bar{c}\) equals the upper bound on the cycle time and is utilized as a big-M parameter in our model formulation. The used notation is summarized in Table 1.
The modeling approach is further based on the following assumptions: (i) a homogeneous product is produced. (ii) Stations are arranged serially. (iii) The necessary equipment and tools are available at each station. (iv) Processing times are deterministic, known, and constant for any process alternative. (v) The robots have limited capabilities. For instance, robotic and collaborative execution may be infeasible for certain tasks. (vi) Each task and robot can be assigned to any station and (vii) each task has to be assigned to exactly one station and process alternative. (viii) The precedence relations are known, captured in a precedence graph, and have to be respected, while (ix) no other assignment restrictions apply to the considered product.
Based on the notation and assumptions, a model formulation is derived.
Subject to:
The objective (1) is to minimize the cycle time. Constraints (2) assure that each task \(i \in I\) is assigned to exactly one station \(k \in K\) and process alternative \(p \in P\) using the binary decision variables \(x_{ikp}\). Constraint set (3) serves to define the cycle time. Constraints (4) determine the station number each task is assigned to. Constraint set (5) ensures precedence relations of tasks \(\left( {i,j} \right) \in E\), where \(i\) is a direct predecessor of \(j\). Constraints (6) and (7) ensure that both human and robot are required to perform tasks collaboratively. If a task \(i \in I\) is executed collaboratively, both human and robot are occupied with this task. Consequently, a task \(j \in I\) cannot start until \(i\) is finished. Alternatively, if task \(j \in I\) is executed collaboratively, both human and robot have to be available. Thus, a preceding task \(i \in I\) has to be finished irrespective of its processing alternative. Constraints (8) ensure that manually processed tasks \(j \in I\) can only start after the manually processed tasks \(i < j\) have been completed at the same station. The same constraint set applies to the robotic execution of two tasks \(\left( {i,j} \right) \in I\). Collaborative and robotic process alternatives are available only if robots are assigned to the respective stations. This is assured by constraint set (9). The total number of robots in the system is limited to \(q\) by constraint (10). Constraints (11) serve to determine the order of tasks within the stations. The variables are defined by constraints (12)–(15).
Our scheduling constraints extend formulations from Kim et al. (2009) and Esmaeilbeigi et al. (2016). Kim et al. consider a two-sided assembly line. In contrast, Esmaeilbeigi et al. concentrate on the setup assembly line balancing and scheduling problem. From Kim et al., we adapt the general idea of modeling the scheduling problem utilizing big-M formulations. From Esmaeilbeigi et al., we adapt the idea to encode tasks’ stations in decision variables \(z_{i}\) and to denote entry time of a workpiece in a station rather than launch time in the first station.
Since neither of the approaches are suitable to model collaborative robots’ behavior within line balancing, we explicitly model the logic relations between resources and the equipment selection problem. With our formulation, implementing the upper bound on the cycle time as a big-M parameter results in a sufficiently large number. From this, we are able to relax the big-M parameter in the scheduling constraints. \(\bar{c}\) is calculated according to the definition provided by Scholl (1999, Formula 2.63). Due to nature and assignment of the decision variables, our formulation can be classified as a MIP model.
Since the NP-hard bin packing problem can be considered as a special case of SALBP without precedence relations, SALBP is NP-hard (Álvarez-Miranda and Pereira 2019). Therefore, our generalized problem is expected to be contained in the same class. Consequently, the problem characteristics are expected to strongly influence the computational time required to solve our model. The main complexity driver of problem instances is the number of tasks (Wee and Magazine 1982; Scholl 1999, Chapter 2.2.1.5). To provide support to decision makers wavering with large problems in reasonable computational time, we develop a heuristic solution procedure for the HRCALBSP. This solution procedure is described in the following section.
5 Hybrid genetic algorithm with MIP-based scheduling
5.1 Overview
In this section, we develop a solution procedure to solve large problem instances. For this purpose, a metaheuristic is used since these heuristics have proven to find good solutions for a wide range of ALB problems. Even though other metaheuristics such as simulated annealing or tabu search could be used to solve the problem at hand, we opted for a hybrid genetic algorithm as this is a simple but yet powerful metaheuristic that has successfully been applied to two closely related problem types. On the one hand, previous works in two-sided ALB demonstrate that GAs provide very good solutions for balancing problems with basic scheduling characteristics and are, therefore, the most frequently used solution procedure to solve this problem type (Abdullah Make et al. 2017). On the other hand, GAs have also proven to be highly effective to solve ALB problems that include the selection of equipment types with the objective of minimizing the overall cycle time (Gao et al. 2009; Levitin et al. 2006).
A GA is a stochastic procedure imitating the biological evolutionary process to achieve optimal or near-to-optimal solutions. The hybrid GA developed in this paper consists of seven main steps, which are shown in Algorithm 1 and described in the following. First, the initial population is generated (Step 1). We utilize a fitness estimation method and subsequently apply an improvement procedure on the solutions (Step 2). The fitness evaluation method decomposes the problem and solves the scheduling problem optimally for stations with robots (Step 3). Until the predetermined stop criterion is met, the population is evolved over several generations. Parents are selected randomly and offspring created by crossover. Thereby, offspring can be subjected to mutation (Step 4). Prior to the exact fitness evaluation of the offspring (Step 6), our heuristic fitness estimation and improvement method are carried out on the new solutions (Step 5). Finally, admission of the offspring to the population is decided (Step 7).
To efficiently search the solution space, we need to develop genetic components suitable for HRCALBSP. We therefore adapt the basic procedure and certain components from the GA proposed by Kim et al. (2009) to suit our problem. This particularly concerns the encoding, selection, crossover, and replacement schemes. The mutation procedure is adapted from Müller et al. (2018). Methods for the robot encoding, fitness estimation, improvement, fitness evaluation, and workload distribution among (initial) individuals as well as the stop criterion are developed by us. In the following, the components of the GA are briefly described.

5.2 Encoding
Generated solutions are encoded within lists representing the solution characteristics. For our problem, we introduce two lists. The first list includes the tasks to station allocation. This list is of length \(n\), each element of which is an integer between 1 and \(m\). Consequently, the \(i\)th element represents the station task \(i\) is assigned to. The second list of length \(m\) represents the assignment of robots to stations, each element of which is a binary representing whether a robot is assigned to the respective station. An example solution representation is shown in Fig. 2.
5.3 Initial population (Step 1)
To generate a pre-specified number of individuals in the initial population, a stochastic process is iterated. First, the available robots are randomly assigned to the stations of the system. Subsequently, tasks are assigned to stations. To this end, one random task among tasks having no (unassigned) predecessor is chosen until all tasks are assigned to stations. Thereby, it is ensured that the assignment satisfies precedence relations. Consequently, the generated solutions are feasible and do not require repair or reordering. Tasks are assigned to stations in ascending order. If the assigned workload of any station exceeds a predetermined workload limit, tasks are assigned to the next station.
The workload limit depends on whether a robot is assigned to a station or not. Since stations with robots are more efficient than manual stations, we allow for higher workload of such stations. We therefore define a workload distribution factor. In the range of zero and the predetermined workload distribution factor, we subsequently choose a random number for each individual by which its stations with robots are loaded higher than its manual stations. The procedure is precisely described in Appendix A.
5.4 Fitness estimation and improvement procedures (Steps 2 and 5)
We apply an improvement procedure on the individuals. During this procedure, station finish times repeatedly have to be evaluated. Since the actual fitness evaluation generates high computational effort (see Sect. 5.5 below), we apply a heuristic fitness estimation routine to calculate the individuals’ resulting cycle time. For stations without robots, finish time can be calculated as sum of human processing times of the tasks assigned to the respective station. For stations with robots, we estimate finish time by applying a priority rule-based heuristic scheduling approach we developed. Within this heuristic procedure, we evaluate the process alternatives for any task to be scheduled and, hence, assign it to the most advantageous alternative. The procedure is repeated until all tasks are scheduled. We describe the procedure precisely in Appendix B.
Based on the station finish times, the improvement procedure is conducted. We randomly select a task from the station with the highest finish time and, within the set of feasible stations with respect to precedence relations, finish times of these stations are estimated supposed the task was assigned to a specific station. The selected task finally is (re-)assigned to the station with the lowest estimated finish time, which may also be the original station. This procedure is repeated for a predetermined number of iterations. Since the heuristic fitness estimation procedure may both under- or overestimate a solution’s quality, we evaluate the actual fitness exactly.
5.5 Fitness evaluation (Steps 3 and 6)
The fitness estimation procedure described above returns exact solutions for stations without robots. For stations with robots, the scheduling problem arises. Therefore, we adapt the MIP proposed in Sect. 3 to suit the less complex problem of scheduling for single stations. Notation and model formulation are illustrated in Appendices C and D, respectively. We integrate the model in our GA and solve the single-station scheduling problems optimally.
5.6 Selection, crossover, and mutation procedures (Step 4)
Based on the individuals’ fitness, we choose two parents for the genetic replication. We utilize a fitness proportionate selection procedure (roulette wheel selection), i.e., individuals with lower cycle time have higher chance of selection for replication. The formula for the calculation of selection probabilities of the individuals is given in Appendix E.
To create offspring, a crossover method is applied on the selected parents. We adapt the structured one-point crossover approach suggested by Kim et al. (2009) as precedence relations of the produced offspring are satisfied utilizing their method. A crossover and mutation example is illustrated in Fig. 3. Offspring are generated according to the following procedure. Prior to actual crossover, a random cross point \(r \in \left\{ {1,m - 1} \right\}\) is selected. From parent 1, tasks are copied to the offspring, which are assigned to stations \(1\) to \(r\). If the respective element has not been copied from parent 1, tasks in stations \(r + 1\) to \(m\) are copied from parent 2. The robot allocation is handed to the offspring from parent 1.
Please note that some elements in the genome may remain blank after crossover (marked * in the figure). This case occurs if a task is neither assigned to stations \(1\) to \(r\) in parent 1 nor to stations \(r + 1\) to \(m\) in parent 2. This can particularly be well observed for the third element of the genome (i.e., the third task) in Fig. 3. In the example, this task is assigned to station 2 in parent 1 and station 1 in parent 2, respectively. Since the cross point is randomly determined to 1 in this example, tasks assigned to station 1 are copied to the child from parent 1, and tasks assigned to station 2 and 3 are copied from parent 2. Since task 3 is neither assigned to station 1 in parent 1 nor to stations 2 or 3 in parent 2, this element remains blank. We repair these elements utilizing the fitness estimation and improvement procedures described above, i.e., the unassigned tasks are allocated to feasible stations with the lowest resulting finish time (task 3 to station 2, task 5 to station 3 in the example).
To avoid premature convergence of the GA, each individual is mutated with a pre-specified probability after crossover (offspring mutation probability). This operator randomly selects two tasks in the offspring. If the station assignments of the tasks can be swapped without violating precedence relations, station assignments of the tasks are swapped (tasks 5 and 8 in the example). This operation may be repeated for a predetermined number of iterations (number of swaps). Furthermore, robot assignment is subjected to mutation with a different probability (robot mutation probability). This operator randomly chooses a station with robot and assigns its robot to a station without robot (station 1 to station 2). A second offspring is generated with the roles of the parents reversed, i.e., from parent 2, tasks are copied to the offspring, which are assigned to stations \(1\) to \(r\), while tasks in stations \(r + 1\) to \(m\) are copied from parent 1.
5.7 Replacement procedure (Step 7)
After fitness evaluation of the generated offspring, their admission to the population is decided. If the cycle time of any offspring is lower than the population’s highest cycle time, the latter individual is removed from population and is replaced by the offspring.
6 Computational experiments
Since we strive to provide a decision support system for decision makers wavering with collaborative robots’ implementation, we conduct computational experiments to examine the effectivity of our solution approaches (MIP and GA) for a variety of scenarios. Therefore, instances with realistic characteristics are constructed in Sect. 6.1. Utilizing the mathematical model, we evaluate the complexity of the introduced problem and illustrate the drivers of computational complexity in Sect. 6.2. The parametrization of the genetic algorithm and an illustration of its convergence are provided in Sect. 6.3. In Sect. 6.4, we provide a comparison of our solution approaches. Managerial insights are provided in Sect. 6.5.
6.1 Instance generation
While there is no benchmark data set available for HRCALBSP, literature contains several well-known test sets for SALBP. For our study, we use test instances from the SALBP dataset of Otto et al. (2013), which are available at http://www.assembly-line-balancing.de. The authors stress the systematic generation of the instances and the use of different task time distributions and precedence graph complexities, which can typically be found in real-world settings.
By deploying collaborative robots, decision makers aim to support human task execution where the object of consideration mainly is the supplementary automation of the existing facilities. In automotive manufacturing, for instance, collaborative robots may be implemented in small feeder lines in component manufacturing (Kuka 2017). In SMEs, manual assembly lines are generally of small size, too (International Federation of Robotics 2015a, b, c). From the data set from the literature, we consider small instances with 20 tasks, medium instances with 50 tasks, and large instances with 100 tasks to be of sufficient size to suit assembly lines of small- and medium-sized companies. This is also in line with Scholl (1999), who summarizes real-world data sets for ALBP.
With regard to the task flexibility ratio, the given test set comprises precedence graphs in the limits of \(0.147 \le F-{\text{ ratio}} \le 0.858\) for small instances, \(0.195 \le F-{\text{ ratio}} \le 0.904\) for medium instances, and \(0.098 \le F-{\text{ ratio}} \le 0.805\) for large instances. For our experiments, we consider two categories with high (\(F-{\text{ ratio}} = 0.8\)) and low (\(F-{\text{ ratio}} = 0.2\)) task flexibility ratio, respectively. For each instance size and from each category, we choose the 25 test instances with minimum deviation of F-ratio within the category, resulting in a total of 150 different precedence graphs.
For our experiments, we choose robot and collaboration flexibilities of \({\text{RF}},\,{\text{CF}} \in \left\{ {0.2, 0.4} \right\}\), which correspond to the findings of Teiwes et al. (2016) introduced in Sect. 2.1. We randomly decide about the tasks that are feasible with robotic and collaborative execution according to the given flexibilities. Thereby, the tasks are not forced to be exclusively feasible with either robotic or collaborative execution. That is, some tasks can be performed by human, robot, and in collaboration, while other tasks can only be conducted manually. Since each test instance is analyzed for multiple flexibilities, we ensure consistent settings by systematically extending the original instances. For each instance, a setting with higher robot flexibility contains the same task feasibilities as the same instance with lower robot flexibility. On that basis, the flexibility is increased by choosing additional tasks randomly to be feasible with robotic execution. The same approach is utilized deciding about tasks that are feasible with collaborative execution. Following the technical data introduced in Sect. 2.1, we consider the robotic process alternative to require twice the time a human worker needs on each identical task (\(t_{{i{\text{R}}}} = 2 \cdot t_{{i{\text{H}}}}\)). For collaborative execution of any task, we assume processing time to be reduced by 30% compared to the original effort (\(t_{{i{\text{C}}}} = 0.7 \cdot t_{{i{\text{H}}}}\)).
We strive to investigate the systems’ behavior for \({\text{West}}\,{\text{ratio}} \in \left\{ {2, 4} \right\}\), resulting in \(m \in \left\{ {5, 10} \right\}\) stations for small instances, \(m \in \left\{ {13, 25} \right\}\) stations for medium instances, and \(m \in \left\{ {25, 50} \right\}\) stations for large instances, respectively. Following the automation potential introduced in Sect. 2.1, we consider robot density \({\text{RD}} \in \left\{ {0, 0.2, 0.4} \right\}\). The resulting scenarios are presented in Table 2.
The model formulations of HRCALBSP and SALBP-2 are implemented in Java (8u151) and solved using the Gurobi 8.1 Java API. The solution procedure of the MIP terminates, if no optimal value can be confirmed within 7200 s for small and medium instances and 28,800 s for large instances, respectively. As the model formulation, the genetic algorithm is implemented in Java, and the single-station scheduling problems are solved using the Gurobi 8.1 Java API. No time limit is applied on computations utilizing the GA. For all calculations, standard computers with Intel Core i3-400M processor with two cores at 2.4 GHz and 4 GB RAM are used to solve the instances.
6.2 Analysis of MIP results
In this section, we will provide detailed analyses of the MIP results to evaluate drivers of the considered problems’ complexity. Thereby, we will report on four different measures that serve as complexity indicators: (i) the number of instances the MIP obtained a feasible solution within its runtime (named Feasible [# of 200] in the tables), (ii) the relative gap remaining after termination of the solution procedure (reporting on average relative gap and its standard deviation, named Gap \(\emptyset \left( \sigma \right)\) in the following tables), (iii) the computational time until the first feasible solution is found (CPU 1st \(\emptyset \left( \sigma \right)\), in seconds), and (iv) the overall computational time for the termination of the solution procedure (CPU \(\emptyset \left( \sigma \right)\), in seconds).
Generally, the computational complexity of ALB problems is known to increase with the number of feasible task sequences the considered precedence graph allows for. With \(n!/2^{\left| E \right|}\), the number of sequences of a given precedence graph can be estimated, where \(n\) corresponds to the number of tasks of the precedence graph and \(\left| E \right|\) describes the number of precedence relations between the tasks. The number of sequences and computational complexity thus increase with increasing number of tasks and increasing F-ratio (Boysen and Fliedner 2008; Hoffmann 1959). Results on this relation are reported in Table 3. Scenarios without robot were excluded from the results (Scenario 1 and 6 as described in Table 2). Following the results in Table 3 and the theoretical implications on the complexity given above, it is plausible for gap and computational time to increase with increasing instance size and F-ratio. Since higher F-ratio, however, provides for a higher number of feasible task sequences, feasible solutions can evidently be found within less computational time subject to high F-ratio.
Please note that the results on large instances only contain 106 (98) of 200 instances for low (high) F-ratio since we only included instances with at least one feasible solution found within the time limit. The instances excluded from analyses either terminated without feasible solution after the regular time limit or run out of memory during the solution procedure. If we assumed those instances (by definition, incorrectly) to comprise a gap of 1 and included them into the results of Table 3, instances of both F-ratio 0.2 and 0.8 were characterized by an average gap of 0.68.
While the problem we consider thus follows theoretical implications described in the literature, additional parameters may potentially account for an increase in complexity. A major effect on complexity can be identified for the West ratio (cf. Table 4). An increase in the number of stations (thus a decrease in West ratio) results in an increase in the number of decision variables \(x_{ikp}\) (cf. (12)) and constraints (6)–(9), which scale with the number of stations. Caused by the more restrictive solution space, the feasibility problem becomes particularly hard, which is well observed for large instances. For these, only 29 of 200 instances achieved a feasible solution within the given time limit.
Contrary to the described effects, the number of robots (robot density) and the flexibility of the robotic resources (robot and collaboration flexibility) cause minor impact on the computational complexity. Therefore, we do not report their results in detail, but refer the interested reader toward Appendices F and G.
These results promote our genetic algorithm as a promising solution procedure. Given scenarios with low West ratio or precedence graphs with low F-ratio, the number of feasible task sequences diminishes. For these settings, the MIP solver experiences difficulties determining a feasible (and thus first) solution (observe CPU 1st in the tables). Utilizing the method for initial population creation of our GA (Step 1 as described in Sect. 5.3), we are able to construct a variety of feasible solutions within low computational time.
However, the major proportion of computational effort is caused by the search for an optimal solution (observe difference of CPU 1st and CPU in the tables). To simplify this search, we apply problem-specific knowledge in our GA as follows: we do not compute the cycle time globally, but decompose the problem into simple parts (stations without robot result in makespan of cumulated human task time of the tasks allocated) and complex parts (stations with robot require actual scheduling for makespan evaluation). Only for the latter problems, we apply the simplified MIP as given in Appendices C and D. In the following section, we will provide details on the initial parametrization of our GA and proof of its adequate convergence.
6.3 Parameters and convergence of the hybrid genetic algorithm
Based on the preliminary studies, we choose parameters for our genetic algorithm such that good solutions are obtained in reasonable computational time. GAs terminate, if a predetermined stop criterion is met. Frequently, the total number of reproduced individuals is chosen as termination criterion. The solution space of ALB problems, however, depends on the size of the precedence graphs under consideration, i.e., larger instances require larger number of reproduced individuals to meet the desired solution quality. We develop a dynamic stop criterion. The algorithm terminates, if no solution is created for 1000 crossovers that has a lower cycle time than the best solution found so far. Utilizing this approach, we do not have to adapt the stop criterion to suit the different problem sizes under consideration. In our preliminary studies, we compared our stop criterion with termination by a predetermined, absolute number of reproduced individuals, and found results of both stop criteria to be equally good in solution quality. Each problem instance is solved ten times. The remainder of the parameters determined by our preliminary computation is reported in Table 5.
The main driver of computational effort within our GA is caused by the fitness evaluation of stations with robots, since the one-station scheduling model has to be solved using the Gurobi 8.1 Java API. To improve the performance of our GA, we limit fitness evaluation to promising offspring solutions. If any of an offspring’s stations without robot has a finish time higher than the population’s worst individual’s cycle time, fitness of the respective offspring will not be evaluated and the individual is rejected from the population. The same procedure is applied on offspring, where their fitness estimation (i.e., including estimation of stations with robots) exceeds the worst individual’s actual cycle time by at least 10%.
In evolutionary computation, the problem of premature convergence of the population toward one identical (suboptimal) solution may arise. To avoid this problem, we apply two diversity-generating techniques on the individuals, i.e., mutation of robot allocation and mutation of task allocation (as described in Sect. 5.6). In Fig. 4, we illustrate convergence of two exemplary, large instances with F-ratio of 0.2 (left diagram) and 0.8 (right diagram). In the former example, the MIP terminates after 28,800 s (with a lower bound of 269 time units corresponding to a gap of 43.5%) and a best integer solution (i.e., cycle time) of 476 time units. The GA found a lower objective value already after the creation of the initial population and henceforth converges (from 452) to 298 time units with an average computational time of 4358 s per run. By limiting fitness evaluation of the individuals to promising offspring solutions, eventually six out of eight individuals require computationally expensive solutions to the scheduling problem. For this example, however, it is uncertain whether the GA obtained an optimal solution, since the MIP procedure did not provide proof of optimality.
In the latter example with F-ratio of 0.8, the MIP terminates after 25,092 s with an optimal solution of 364 time units. The GA converges toward this solution within average computational time of 2853 s per run. Due to our limitation in fitness evaluation, five of eight individuals are eventually being evaluated by the MIP. For this reason, we conclude our algorithm to converge properly. In the following section, a comparison of the computational performance of MIP and GA is provided.
6.4 Computational results
Since we propose a novel planning problem yet unconsidered in the literature, no benchmark models or algorithms can be compared to our approach. Hence, we analyze performances of the MIP and the GA throughout all generated instances comprising robots.
Results on the computational comparison of our solution approaches are provided in Table 6. We report on the number of instances the GA achieved the better solution, GA and MIP tied, and the MIP obtained the better solution [referred to as # (of 400) in the table], the average computational time of one GA run of the related instances and its standard deviation (\(\emptyset \left( \sigma \right)\) CPU GA, in seconds), and the average computational time of the MIP and its standard deviation (\(\emptyset \left( \sigma \right)\) CPU MIP, in seconds).
Generally, an advantage of using the MIP model is to obtain solutions with proof of optimality. For our problem, the MIP could proof optimality for 251 of 400 small instances, 119 of 400 medium instances, and 15 of 400 large instances. Consequently, its advantage diminishes with an increase in instance size. Particularly for large instances, the GA obtains solutions with better or the same objective values as the MIP in 370 of 400 cases. For these instances, already the initially constructed solutions of the GA (prior actual optimization) frequently provide a better objective value than the MIP after its termination (as can for example be observed in the left diagram of Fig. 4). For some instances, the MIP achieved better results than the GA. However, the objective discrepancy is rather small in these cases. The average deviation of MIP and GA objective values is 1.6% in these cases across all instance sizes.
From the results, we deduce adequate performance and solution quality of our algorithm. Our GA is a suitable tool for fast construction of a large amount of possible assembly line configurations when considering collaborative robots in industrial practice. The effect of robot deployment on cycle time can quickly be estimated. Based on the results of the GA, we will therefore evaluate the potential of collaborative robot deployment in manual lines and derive managerial implications in the following section.
6.5 Managerial insights
To quantify the potential of deploying collaborative robots, we analyze their impact on the reduction of cycle time and the assignment of tasks to the different processing alternatives (manual, robot only, and collaboration between worker and robot). Thereby, we concentrate on the large problem instances. The results for the small and medium instances are structurally similar and can be found in Appendices H–M.
In Tables 7 and 8, the average relative improvement in cycle time and the corresponding standard deviation is presented for different values of the robot density and the robot flexibility, respectively. The results are broken down according to different levels for the West ratio and the F-ratio. Overall, it can be seen that a higher robot density and a higher robot flexibility allow to reduce cycle times substantially compared to a fully manual assembly line, i.e., \({\text{RD}} = 0\). In accordance with the law of decreasing marginal utility, the efficiency gains decrease with increasing deployment and flexibility of robots. With regard to the West ratio, the potential of robots to reduce cycle time is especially pronounced for a high average number of tasks to be assigned to every station. On the contrary, the F-ratio has almost no influence on the improvement of cycle time.
The results can be explained by analyzing the modes selected for conducting the tasks in the different instances. For that reason, the average number of tasks assigned to human (H), robotic (R), and collaborative (C) modes is illustrated in Fig. 5 for the large instances. Moreover, the proportion of tasks assigned to modes in stations with robots for large instances is presented in Fig. 6. The distribution of tasks among modes is sourced from the best found solution of the GA for each instance. Each average hereby considers the solutions to all 25 precedence graphs contained in the respective F-ratio group. Given the tradeoff between short execution times (i.e., collaborative mode) and smaller resource requirements (i.e., human and robotic mode, preferably utilized in parallel), all processing modes are utilized in relevant scale and no processing mode dominates another. Thereby, the deployment of the different modes is heavily influenced by the variation in robot density (i.e., number of robots by number of stations), West ratio (i.e., number of tasks by number of stations), and F-ratio (i.e., degree of freedom within the assignment of tasks to stations).
With an increase in West ratio and robot density (ceteris paribus), the average number of tasks assigned to both robotic and collaborative modes increases, leading to a reduction in cycle time. The same holds true for an increase in robot flexibility. Each additional robot and each additional unit of flexibility, however, utilize less automation and collaboration potential (law of decreasing marginal utility).
Since the F-ratio has almost no influence on the improvement of cycle time (as reported in Tables 7 and 8), its variation requires a more differentiated assessment. The average number of tasks assigned to the robotic and collaborative modes increases with a higher F-ratio for low levels of robot flexibility, while it decreases with a higher F-ratio for high levels of robot flexibility, respectively. This is mainly a consequence of the differences of the precedence graphs associated with a low and a high F-ratio and relates to the favorability between robot-based modes.
The favorability between robot-based modes is particularly based on differences in F-ratio and West ratio, respectively. A higher portion of automated processing is favored by a higher West ratio, which is due to higher combinatorial potential in task assignment. Consequently, with high West ratio, it is more likely to find a combination of tasks in which the high processing time of the robotic task can be complemented by manual tasks resulting in equal (and low) finish time. A lower West ratio, on the other hand, favors serial task assignment in collaborative mode, taking advantage of shorter processing times. An exception to these rules can be seen for the combination of a high West ratio and low F-ratio. Here, slightly more tasks are assigned to the collaborative mode than to the robotic mode if the robot flexibility is high. This can be explained by the fact that a low F-ratio comes along with less potential to parallelize task execution due to more distinct precedence relations between tasks. As a consequence, serial task assignment in the collaborative mode becomes necessary to utilize the full potential of automation. For the same reason, tasks are generally executed more often by the collaborative mode with a decreasing F-ratio. This evidence, therefore, explains why the improvement of cycle time (as provided in Tables 7 and 8) is almost unaffected by the level of F-ratio.
From the results, the following managerial implications can be derived: First, productivity of manual assembly lines can be substantially improved by deploying collaborative robots independent of the actual setting. The higher the robot flexibility and the higher the number of robots compared to the number of stations, the more pronounced this effect will be, yet with decreasing marginal utility. Second, all processing modes are of relevance when balancing assembly lines with collaborative robots. Industrial planners should particularly focus on enabling robots for autonomous performance in stations with a high number of tasks. For stations that only perform few tasks, they should create the preconditions for collaborative execution by worker and robot. Third, given the complexity of the decision situation under consideration and the tradeoffs between the different operating modes, a model-based planning approach as presented in this paper should be utilized to derive an optimal assembly line configuration for a specific setting. Especially the influence of the product structure, i.e., precedence relations between the assembly tasks, on the task assignment cannot be determined intuitively and needs to be analyzed in detail.
7 Conclusions and future research
The trend of increasing automation enhances the efficiency of modern manufacturing enterprises. However, certain tasks cannot efficiently be automated, for instance, due to product complexity in manufacturing corporations and small-batch production in small- and medium-sized enterprises. These challenges are predominantly faced by manual labor. In recent years, human–robot collaboration has established opportunities to increase efficiency of manual work.
Therefore, we consider the novel planning problem of configuring manual assembly lines with collaborative robots. In our balancing approach, robots can be assigned to stations to support human task execution, where both human and robotic advantages can be utilized. As robots are capable of working in collaboration with the human as well as performing tasks autonomously, the assembly line balancing problem is extended to a scheduling problem. We present a mathematical formulation to minimize assembly lines’ cycle times for a given number of stations and collaborative robots, and develop a hybrid genetic algorithm to solve the corresponding problem. In our approach, we decide about the stations the robots are assigned to and the distribution of workload among the workers and the robots. Due to the high problem complexity, only few system configurations can be determined optimally with a standard solver, which in particular holds true for large problem instances. On the contrary, the hybrid genetic algorithm allows proposing a variety of advantageous system configurations considering collaborative robots complementing workers in manual assembly lines with little computational effort.
Overall, the results indicate that substantial productivity gains can be utilized by deploying the collaborative robots. For products with 100 tasks being manufactured on an assembly line with 25 stations, deployment of 10 (5) collaborative robots may yield an average increase in productivity of 12% (7%) compared to the manual case. Due to the tradeoff between time and resource consumption of the different modes within collaborative assembly, all modes are of relevance and the actual task allocation depends heavily on the characteristics of the production system and the product structure. Therefore, line planners should carefully evaluate the production system and the product under consideration before deciding on the deployment of collaborative robots.
Further research is needed in this field. Industrial manufacturers also appreciate collaborative robots as they are able to release workers from physically stressful tasks. Consequently, aspects of ergonomics should be considered in the system configuration. Also, the determination of an economically optimal number of robots and their capabilities should be focused rather than to assume them to be given externally. Future approaches should, therefore, extend the scope of investigation and be based on multi-objective formulations considering the aspects mentioned above. Moreover, due to their object-oriented approach, the further development of genetic algorithms appears to be a promising field, particularly for multi-objective problem formulations.
References
Abdullah Make, M.R., M.F.F. Ab. Rashid, and M.M. Razali. 2017. A review of two-sided assembly line balancing problem. The International Journal of Advanced Manufacturing Technology 89: 1743–1763. https://doi.org/10.1007/s00170-016-9158-3.
Álvarez-Miranda, E., and J. Pereira. 2019. On the complexity of assembly line balancing problems. Computers & Operations Research 108: 182–186. https://doi.org/10.1016/j.cor.2019.04.005.
Antonelli, D., S. Astanin, and G. Bruno. 2016. Applicability of human–robot collaboration to small batch production. In Collaboration in a hyperconnected world, vol. 480, ed. H. Afsarmanesh, L.M. Camarinha-Matos, and A. Lucas Soares, 24–32. Cham: Springer International Publishing.
Bartholdi, J.J. 1993. Balancing two-sided assembly lines: a case study. International Journal of Production Research 31: 2447–2461. https://doi.org/10.1080/00207549308956868.
Basso, F., S. D’Amours, M. Rönnqvist, and A. Weintraub. 2019. A survey on obstacles and difficulties of practical implementation of horizontal collaboration in logistics. International Transactions in Operational Research 26: 775–793. https://doi.org/10.1111/itor.12577.
Battaïa, O., and A. Dolgui. 2013. A taxonomy of line balancing problems and their solution approaches. International Journal of Production Economics 142: 259–277. https://doi.org/10.1016/j.ijpe.2012.10.020.
Bernhardt, R., D. Surdilovic, V. Katschinski, and K. Schröer. 2007. Flexible assembly systems through workplace-sharing and time-sharing human–machine cooperation—PISA. IFAC Proceedings Volumes 40: 247–251. https://doi.org/10.3182/20070523-3-ES-4908.00041.
BMW Group (2013) Innovative human–robot cooperation in BMW Group Production. http://bit.ly/29NxTA7. Accessed 7 July 2019.
Borba, L., M. Ritt, and C. Miralles. 2018. Exact and heuristic methods for solving the robotic assembly line balancing problem. European Journal of Operational Research 270: 146–156. https://doi.org/10.1016/j.ejor.2018.03.011.
Boysen, N., and M. Fliedner. 2008. A versatile algorithm for assembly line balancing. European Journal of Operational Research 184: 39–56. https://doi.org/10.1016/j.ejor.2006.11.006.
Boysen, N., M. Fliedner, and A. Scholl. 2007. A classification of assembly line balancing problems. European Journal of Operational Research 183: 674–693. https://doi.org/10.1016/j.ejor.2006.10.010.
Boysen, N., M. Fliedner, and A. Scholl. 2008. Assembly line balancing: which model to use when? International Journal of Production Economics 111: 509–528. https://doi.org/10.1016/j.ijpe.2007.02.026.
Chen F, Sekiyama K, Sasaki H, Huang J, Sun B, Fukuda T (2011) Assembly strategy modeling and selection for human and robot coordinated cell assembly. In 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, 4670–4675. https://doi.org/10.1109/iros.2011.6048306.
Daimler AG (2014) Employees and robots working directly together in production: Mercedes-Benz Cars receives international award for groundbreaking “Robot Farming” production concept. http://bit.ly/2axmJCR. Accessed 7 July 2019.
Dar-El, E.M. 1973. MALB—a heuristic technique for balancing large single-model assembly lines. AIIE Transactions 5: 343–356. https://doi.org/10.1080/05695557308974922.
Dar-El, E.M. 1975. Solving large single-model assembly line balancing problems—a comparative study. AIIE Transactions 7: 302–310. https://doi.org/10.1080/05695557508975011.
Esmaeilbeigi, R., B. Naderi, and P. Charkhgard. 2016. New formulations for the setup assembly line balancing and scheduling problem. OR Spectrum 38: 493–518. https://doi.org/10.1007/s00291-016-0433-3.
Falkenauer E (2005) Line balancing in the real world. In Proceedings of the International Conference on Product Lifecycle Management PLM 05, Lumiere University Lyon, France, 360–370.
Fattahi, P., A. Roshani, and A. Roshani. 2011. A mathematical model and ant colony algorithm for multi-manned assembly line balancing problem. International Journal of Advanced Manufacturing Technology 53: 363–378. https://doi.org/10.1007/s00170-010-2832-y.
Fraunhofer IAO (2016) Lightweight robots in manual assembly: best to start simply!. Examining companies’ initial experiences with lightweight robots. https://bit.ly/2xsEHz2. Accessed 7 July 2019.
Gansterer, M., and R.F. Hartl. 2018. One- and two-sided assembly line balancing problems with real-world constraints. International Journal of Production Research 56: 3025–3042. https://doi.org/10.1080/00207543.2017.1394599.
Gao, J., L. Sun, L. Wang, and M. Gen. 2009. An efficient approach for type II robotic assembly line balancing problems. Computers & Industrial Engineering 56: 1065–1080. https://doi.org/10.1016/j.cie.2008.09.027.
Graves, S.C., and C.H. Redfield. 1988. Equipment selection and task assignment for multiproduct assembly system design. The International Journal of Flexible Manufacturing Systems 1: 31–50.
Guajardo, M., M. Rönnqvist, P. Flisberg, and M. Frisk. 2018. Collaborative transportation with overlapping coalitions. European Journal of Operational Research 271: 238–249. https://doi.org/10.1016/j.ejor.2018.05.001.
Helms E, Schraft RD, Hägele M (2002) rob@work: robot assistant in industrial environments. In Proceedings/IEEE ROMAN 2002, 11th IEEE International Workshop on Robot and Human Interactive Communication, Berlin, Germany, 399–404.
Herczeg, G., R. Akkerman, and M.Z. Hauschild. 2018. Supply chain collaboration in industrial symbiosis networks. Journal of Cleaner Production 171: 1058–1067. https://doi.org/10.1016/j.jclepro.2017.10.046.
Hoffmann TR (1959) Generation of permutations and combinations. Engineering Experiment Station Report Nr. 13, University of Wisconsin, Madision.
Hu, S.J., J. Ko, L. Weyand, H.A. ElMaraghy, T.K. Lien, Y. Koren, H. Bley, G. Chryssolouris, N. Nasr, and M. Shpitalni. 2011. Assembly system design and operations for product variety. CIRP Annals—Manufacturing Technology 60: 715–733. https://doi.org/10.1016/j.cirp.2011.05.004.
International Federation of Robotics (2015a) SHAD opts for UR robot arms to optimize its manufacturing processes. http://bit.ly/2CRXuDH. Accessed 7 July 2019.
International Federation of Robotics (2015b) The UR5 robot arm manufactures components for EGR valves. http://bit.ly/2BKXmqr. Accessed 7 July 2019.
International Federation of Robotics (2015c) Universal robots helps Betacom light up New Zealand. http://bit.ly/2Bu7XsT. Accessed 7 July 2019.
International Federation of Robotics (2018) Executive summary world robotics 2018 industrial robots. https://bit.ly/2r4FG4F. Accessed 7 July 2019.
International Organization for Standardization. 2010. ISO 13855:2010: Safety of machinery—positioning of safeguards with respect to the approach speeds of parts of the human body. Geneva: International Standards Organization.
International Organization for Standardization. 2011. ISO 10218-1:2011: Robots and robotic devices—safety requirements for industrial robots—Part 1: Robots. Geneva: International Standards Organization.
Kellegöz, T. 2016. Assembly line balancing problems with multi-manned stations: a new mathematical formulation and Gantt based heuristic method. Annals of Operations Research 2016: 1–18. https://doi.org/10.1007/s10479-016-2156-x.
Kellegöz, T., and B. Toklu. 2015. A priority rule-based constructive heuristic and an improvement method for balancing assembly lines with parallel multi-manned workstations. International Journal of Production Research 53: 736–756. https://doi.org/10.1080/00207543.2014.920548.
Kim, Y.K., W.S. Song, and J.H. Kim. 2009. A mathematical model and a genetic algorithm for two-sided assembly line balancing. Computers & Operations Research 36: 853–865. https://doi.org/10.1016/j.cor.2007.11.003.
Krüger, J., T.K. Lien, and A. Verl. 2009. Cooperation of human and machines in assembly lines. CIRP Annals—Manufacturing Technology 58: 628–646. https://doi.org/10.1016/j.cirp.2009.09.009.
Kuka AG (2017) HRC system in production at BMW Dingolfing. http://bit.ly/2BKHhkI. Accessed 7 July 2019.
Kuka AG (2018) LBR IIWA. http://bit.ly/2CiSHeV. Accessed 7 July 2019.
Lee, T.O., Y. Kim, and Y.K. Kim. 2001. Two-sided assembly line balancing to maximize work relatedness and slackness. Computers & Industrial Engineering 40: 273–292. https://doi.org/10.1016/S0360-8352(01)00029-8.
Leng, J., and P. Jiang. 2018. Evaluation across and within collaborative manufacturing networks: a comparison of manufacturers’ interactions and attributes. International Journal of Production Research 56: 5131–5146. https://doi.org/10.1080/00207543.2018.1430903.
Levitin, G., J. Rubinovitz, and B. Shnits. 2006. A genetic algorithm for robotic assembly line balancing. European Journal of Operational Research 168: 811–825. https://doi.org/10.1016/j.ejor.2004.07.030.
Li, Z., I. Kucukkoc, and J.M. Nilakantan. 2017. Comprehensive review and evaluation of heuristics and meta-heuristics for two-sided assembly line balancing problem. Computers & Operations Research 84: 146–161. https://doi.org/10.1016/j.cor.2017.03.002.
Marvel, J.A., and R. Norcross. 2017. Implementing speed and separation monitoring in collaborative robot workcells. Robot Comput Integr Manuf 44: 144–155. https://doi.org/10.1016/j.rcim.2016.08.001.
Michalos, G., S. Makris, J. Spiliotopoulos, I. Misios, P. Tsarouchi, and G. Chryssolouris. 2014. ROBO-PARTNER: seamless human–robot cooperation for intelligent, flexible and safe operations in the assembly factories of the future. Procedia CIRP 23: 71–76. https://doi.org/10.1016/j.procir.2014.10.079.
Miralles, C., J.P. García-Sabater, C. Andrés, and M. Cardos. 2007. Advantages of assembly lines in sheltered work centres for disabled. a case study. International Journal of Production Economics 110: 187–197. https://doi.org/10.1016/j.ijpe.2007.02.023.
Mukund Nilakantan, J., and S.G. Ponnambalam. 2015. Robotic U-shaped assembly line balancing using particle swarm optimization. Engineering Optimization 48: 231–252. https://doi.org/10.1080/0305215X.2014.998664.
Müller C, Weckenborg C, Grunewald M, Spengler TS (2016) Consideration of redundancies in the configuration of automated flow lines. In 2016—Logistics Management, ed. Mattfeld, Spengler et al., 173–185.
Müller, C., M. Grunewald, and T.S. Spengler. 2017. Redundant configuration of automated flow lines based on “Industry 4.0”-technologies. Journal of Business Economics 87: 877–898. https://doi.org/10.1007/s11573-016-0831-7.
Müller, C., M. Grunewald, and T.S. Spengler. 2018. Redundant configuration of robotic assembly lines with stochastic failures. International Journal of Production Research 56: 3662–3682. https://doi.org/10.1080/00207543.2017.1406672.
Naderi, B., A. Azab, and K. Borooshan. 2018. A realistic multi-manned five-sided mixed-model assembly line balancing and scheduling problem with moving workers and limited workspace. International Journal of Production Research 44: 1–19. https://doi.org/10.1080/00207543.2018.1476786.
Ogorodnikova O (2007) Robot introduction in human work environment. Developments, challenges and solutions. In 5th IEEE International Conference on Computational Cybernetics, 167–172.
Otto, A., C. Otto, and A. Scholl. 2013. Systematic data generation and test design for solution algorithms on the example of SALBPGen for assembly line balancing. European Journal of Operational Research 228: 33–45. https://doi.org/10.1016/j.ejor.2012.12.029.
Pereira, J., M. Ritt, and Ó.C. Vásquez. 2018. A memetic algorithm for the cost-oriented robotic assembly line balancing problem. Computers & Operations Research 99: 249–261. https://doi.org/10.1016/j.cor.2018.07.001.
Pinnoi, A., and W.E. Wilhelm. 1997. A family of hierarchical models for the design of deterministic assembly systems. International Journal of Production Research 35: 253–280. https://doi.org/10.1080/002075497196073.
Ponte, B., J. Costas, J. Puche, R. Pino, and D. La de Fuente. 2018. The value of lead time reduction and stabilization: a comparison between traditional and collaborative supply chains. Transportation Research Part E: Logistics and Transportation Review 111: 165–185. https://doi.org/10.1016/j.tre.2018.01.014.
Robert Bosch Manufacturing Solutions GmbH (2018a) APAS assistant: Product scope. http://bit.ly/2ByBAcy. Accessed 7 July 2019.
Robert Bosch Manufacturing Solutions GmbH (2018b) APAS assistant mobile. https://bit.ly/2RiSuj6. Accessed 7 July 2019.
Roshani, A., and D. Giglio. 2017. Simulated annealing algorithms for the multi-manned assembly line balancing problem: minimising cycle time. International Journal of Production Research 55: 2731–2751. https://doi.org/10.1080/00207543.2016.1181286.
Roshani, A., A. Roshani, A. Roshani, M. Salehi, and A. Esfandyari. 2013. A simulated annealing algorithm for multi-manned assembly line balancing problem. Journal of Manufacturing Systems 32: 238–247. https://doi.org/10.1016/j.jmsy.2012.11.003.
Rubinovitz, J., J. Bukchin, and E. Lenz. 1993. RALB—A heuristic algorithm for design and balancing of robotic assembly lines. CIRP Annals—Manufacturing Technology 42: 497–500. https://doi.org/10.1016/S0007-8506(07)62494-9.
Salamati-Hormozi, H., Z.-H. Zhang, O. Zarei, and R. Ramezanian. 2018. Trade-off between the costs and the fairness for a collaborative production planning problem in make-to-order manufacturing. Computers & Industrial Engineering 126: 421–434. https://doi.org/10.1016/j.cie.2018.09.044.
Salveson, M.E. 1955. The assembly line balancing problem. Journal of Industrial Engineering 6: 18–25.
Schmidtler, J., and K. Bengler. 2015. Fast or accurate?—Performance measurements for physical human–robot collaborations. Procedia Manufacturing 3: 1387–1394. https://doi.org/10.1016/j.promfg.2015.07.298.
Scholl A (1999) Balancing and sequencing of assembly lines: With 75 tables. Zugl.: Darmstadt, Techn. Hochsch., Diss., 1995, 2., rev. ed. Contributions to management science. Physica-Verl., Heidelberg.
Sikora, C.G.S., T.C. Lopes, and L. Magatão. 2017. Traveling worker assembly line (re)balancing problem: model, reduction techniques, and real case studies. European Journal of Operational Research 259: 949–971. https://doi.org/10.1016/j.ejor.2016.11.027.
Simatupang, T.M., and R. Sridharan. 2002. The collaborative supply chain. International Journal of Logistics Management 13: 15–30. https://doi.org/10.1108/09574090210806333.
Sternatz, J. 2014. Enhanced multi-Hoffmann heuristic for efficiently solving real-world assembly line balancing problems in automotive industry. European Journal of Operational Research 235: 740–754. https://doi.org/10.1016/j.ejor.2013.11.005.
Teiwes J, Bänziger T, Kunz A, Wegener K (2016) Identifying the potential of human–robot collaboration in automotive assembly lines using a standardised work description. In 22nd International Conference on Automation and Computing, ICAC 2016; University of EssexColchester; United Kingdom; 7 September 2016 through 8 September 2016, 78–83. https://doi.org/10.1109/iconac.2016.7604898.
Tsarouchi, P., J. Spiliotopoulos, G. Michalos, S. Koukas, A. Athanasatos, S. Makris, and G. Chryssolouris. 2016a. A decision making framework for human robot collaborative workplace generation. Procedia CIRP 44: 228–232. https://doi.org/10.1016/j.procir.2016.02.103.
Tsarouchi, P., S. Makris, and G. Chryssolouris. 2016b. Human–robot interaction review and challenges on task planning and programming. International Journal of Computer Integrated Manufacturing 29: 916–931. https://doi.org/10.1080/0951192X.2015.1130251.
Universal Robots A/S (2016) UR5 Technical specifications. http://bit.ly/2Dvf9SP. Accessed 7 July 2019.
Universal Robots A/S (2018a) Cobots offer game changing benefits. https://bit.ly/2vxAEQS. Accessed 7 July 2019.
Universal Robots A/S (2018b) Collaborative robot applications. https://bit.ly/2PYUNv4. Accessed 7 July 2019.
Volkswagen AG (2018) What exactly does a robotics expert do? https://bit.ly/2FcCgGJ. Accessed 7 July 2019.
Wee, T.S., and M.J. Magazine. 1982. Assembly line balancing as generalized bin packing. Operations Research Letters 1: 56–58. https://doi.org/10.1016/0167-6377(82)90046-3.
Yazgan, H.R., I. Beypinar, S. Boran, and C. Ocak. 2011. A new algorithm and multi-response Taguchi method to solve line balancing problem in an automotive industry. International Journal of Advanced Manufacturing Technology 57: 379–392. https://doi.org/10.1007/s00170-011-3291-9.
Yoosefelahi, A., M. Aminnayeri, H. Mosadegh, and H.D. Ardakani. 2012. Type II robotic assembly line balancing problem: an evolution strategies algorithm for a multi-objective model. Journal of Manufacturing Systems 31: 139–151. https://doi.org/10.1016/j.jmsy.2011.10.002.
Acknowledgements
The authors wish to thank the editor and the anonymous reviewers for their valuable comments and suggestions which significantly helped to improve a former version of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
1.1 Appendix A: Pseudocode—generation of initial individuals

1.2 Appendix B: Pseudocode—fitness estimation procedure

1.3 Appendix C: Notation of the single-station scheduling model
Sets and parameters | |
|---|---|
\(n\) | Number of tasks |
\(I_{k}\) | Subset of tasks assigned to station k (index \(i,j\)) |
\(P\) | Set of process alternatives (index \(p\)) |
\(p_{\text{H}} , p_{\text{R}} , p_{\text{C}}\) | Process alternatives, in which tasks are processed by human (H), robot (R) or in collaboration (C), respectively |
\(E\) | Set of direct precedence relations |
\(t_{ip}\) | Execution time of task \(i \in I_{k}\) with processing alternative \(p \in P\) |
\(\bar{c}\) | Upper bound on makespan (\(\mathop \sum \limits_{i \in I_{k}} t_{{ip_{\text{H}} }}\)) |
Decision and auxiliary variables | |
|---|---|
\(x_{ip}\) | Binary variable with value 1, if task \(i \in I_{k}\) is assigned to processing alternative \(p \in P\) |
\(s_{i}\) | Continuous variable for encoding the start time of task \(i \in I_{k}\) in the station it is assigned to |
\({\text{FinishTime}}\) | Non-negative variable for encoding the finish time of the considered station |
\(y_{ij}\) | Binary variable with value 1, if task \(i \in I_{k}\) starts before task \(j \in I_{k}\) (\(s_{i} \le s_{j} )\) |
1.4 Appendix D: Single-station scheduling model of station \(k\)
Subject to:
1.5 Appendix E: Calculation of selection probabilities
- \({\text{Prob}}_{a}\) :
-
Selection probability of individual \(a\)
- \({\text{CT}}_{\hbox{max} }\) :
-
Maximum cycle time among the individuals of the population
- \({\text{CT}}_{a}\) :
-
Cycle time of individual \(a\)
- ε :
-
Sufficiently small number to ensure probabilities to be larger zero, since \({\text{CT}}_{\hbox{max} } - {\text{CT}}_{a}\) results to zero in case of saturated population
- \(A\) :
-
Number of individuals in the population
1.6 Appendix F: Analysis of robot density on complexity indicators [with West ratio = 4, * solved with SALBP-2 model as in Scholl (1999)]
RD | Small instances (\(n = 20\,{\text{tasks}}\)) | Medium instances (\(n = 50\,{\text{tasks}}\)) | Large instances (\(n = 100\,{\text{tasks}}\)) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Feasible (optimal) (# of #) | Gap \(\emptyset \left( \sigma \right)\) | CPU 1st \(\emptyset \left( \sigma \right)\) (s) | CPU \(\emptyset \left( \sigma \right)\) (s) | Feasible (optimal) (# of #) | Gap \(\emptyset \left( \sigma \right)\) | CPU 1st \(\emptyset \left( \sigma \right)\) (s) | CPU \(\emptyset \left( \sigma \right)\) (s) | Feasible (optimal) (# of #) | Gap \(\emptyset \left( \sigma \right)\) | CPU 1st \(\emptyset \left( \sigma \right)\) (s) | CPU \(\emptyset \left( \sigma \right)\) (s) | |
0* | 50 (50) of 50 | 0 (0) | 0 (0) | 1 (1) | 50 (26) of 50 | 0 (0) | 0 (0) | 3479 (3577) | 49 (23) of 50 | 0 (0) | 0 (0) | 16,848 (13,558) |
0.2 | 100 (49) of 100 | 0.13 (0.16) | 2 (0) | 3617 (3583) | 100 (2) of 100 | 0.37 (0.14) | 135 (55) | 7132 (576) | 86 (0) of 100 | 0.41 (0.13) | 3565 (3539) | 28,800 (0) |
0.4 | 100 (50) of 100 | 0.11 (0.15) | 2 (0) | 3608 (3557) | 100 (1) of 100 | 0.32 (0.16) | 128 (54) | 7137 (627) | 89 (0) of 100 | 0.37 (0.13) | 3724 (3910) | 28,800 (0) |
1.7 Appendix G: Analysis of robot and collaboration flexibility on complexity indicators (with West ratio = 4)
RF, CF | Small instances (\(n = 20\,{\text{tasks}}\)) | Medium instances (\(n = 50\,{\text{tasks}}\)) | Large instances (\(n = 100\,{\text{tasks}}\)) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Feasible (optimal) (# of #) | Gap \(\emptyset \left( \sigma \right)\) | CPU 1st \(\emptyset \left( \sigma \right)\) (s) | CPU \(\emptyset \left( \sigma \right)\) (s) | Feasible (optimal) (# of #) | Gap \(\emptyset \left( \sigma \right)\) | CPU 1st \(\emptyset \left( \sigma \right)\) (s) | CPU \(\emptyset \left( \sigma \right)\) (s) | Feasible (optimal) (# of #) | Gap \(\emptyset \left( \sigma \right)\) | CPU 1st \(\emptyset \left( \sigma \right)\) (s) | CPU \(\emptyset \left( \sigma \right)\) (s) | |
0.2 | 100 (49) of 100 | 0.11 (0.15) | 2 (0) | 3587 (3576) | 100 (3) of 100 | 0.32 (0.16) | 113 (44) | 7069 (847) | 86 (0) of 100 | 0.37 (0.11) | 2797 (1689) | 28,800 (0) |
0.4 | 100 (50) of 100 | 0.14 (0.17) | 2 (0) | 3638 (3564) | 100 (0) of 100 | 0.37 (0.13) | 150 (58) | 7200 (0) | 89 (0) of 100 | 0.41 (0.14) | 4466 (4824) | 28,800 (0) |
1.8 Appendix H: Analysis of robot density on relative improvement of cycle time for small instances \(\emptyset \left(\varvec{\sigma}\right)\)
RD | West ratio | F-ratio | ||
|---|---|---|---|---|
2 | 4 | 0.2 | 0.8 | |
0.0 | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
0.2 | 0.05 (0.05) | 0.08 (0.02) | 0.07 (0.05) | 0.06 (0.03) |
0.4 | 0.07 (0.06) | 0.13 (0.03) | 0.10 (0.06) | 0.10 (0.05) |
1.9 Appendix I: Analysis of robot flexibility on relative improvement of cycle time for small instances \(\emptyset \left(\varvec{\sigma}\right)\)
RF, CF | West ratio | F-ratio | ||
|---|---|---|---|---|
2 | 4 | 0.2 | 0.8 | |
0.0 | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
0.2 | 0.04 (0.05) | 0.10 (0.04) | 0.06 (0.05) | 0.08 (0.05) |
0.4 | 0.08 (0.06) | 0.11 (0.04) | 0.10 (0.06) | 0.09 (0.05) |
1.10 Appendix J: Analysis of robot density on relative improvement of cycle time for medium instances \(\emptyset \left(\varvec{\sigma}\right)\)
RD | West ratio | F-ratio | ||
|---|---|---|---|---|
2 | 4 | 0.2 | 0.8 | |
0.0 | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
0.2 | 0.05 (0.05) | 0.08 (0.02) | 0.06 (0.04) | 0.06 (0.04) |
0.4 | 0.06 (0.06) | 0.12 (0.02) | 0.08 (0.05) | 0.09 (0.06) |
1.11 Appendix K: Analysis of robot flexibility on relative improvement of cycle time for medium instances \(\emptyset \left(\varvec{\sigma}\right)\)
RF, CF | West ratio | F-ratio | ||
|---|---|---|---|---|
2 | 4 | 0.2 | 0.8 | |
0.0 | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
0.2 | 0.04 (0.05) | 0.09 (0.03) | 0.06 (0.04) | 0.07 (0.05) |
0.4 | 0.06 (0.06) | 0.11 (0.03) | 0.08 (0.05) | 0.08 (0.05) |
1.12 Appendix L: Average number of tasks assigned to modes for small (top) and medium (bottom) instances

1.13 Appendix M: Proportion of tasks assigned to modes in stations with robots for small (top) and medium (bottom) instances

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Weckenborg, C., Kieckhäfer, K., Müller, C. et al. Balancing of assembly lines with collaborative robots. Bus Res 13, 93–132 (2020). https://doi.org/10.1007/s40685-019-0101-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40685-019-0101-y