Abstract
Shelf-space optimization models support retailers in making optimal shelf-space decisions. They determine the number of facings for each item included in an assortment. One common characteristic of these models is that they do not account for in-store replenishment processes. However, the two areas of shelf-space planning and in-store replenishment are strongly interrelated. Keeping more shelf stock of an item increases the demand for it due to higher visibility, permits decreased replenishment frequencies and increases inventory holding costs. However, because space is limited, it also requires the reduction of shelf space for other items, which then deplete faster and must be reordered and replenished more often. Furthermore, the possibility of keeping stock of certain items in the backroom instead of the showroom allows for more showroom shelf space for other items, but also generates additional replenishment costs for the items kept in the backroom. The joint optimization of both shelf-space decisions and replenishment processes has not been sufficiently addressed in the existing literature. To quantify the cost associated with the relevant in-store replenishment processes, we conducted a time and motion study for a German grocery retailer. Based on these insights, we propose an optimization model that addresses the mutual dependence of shelf-space decisions and replenishment processes. The model optimizes retail profits by determining the optimum number of facings, the optimum display orientation of items, and the optimum order frequencies, while accounting for space-elasticity effects as well as limited shelf and backroom space. Applying our model to the grocery retailer’s canned foods category, we found a profit potential of about 29%. We further apply our model to randomly generated data and show that it can be solved to optimality within very short run times, even for large-scale problem instances. Finally, we use the model to show the impact of backroom space availability and replenishment cost on retail profits and solution structures. Based on the insights gained from the application of our model, the grocery retailer has decided to change its current approach to shelf-space decisions and in-store replenishment planning.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Retailers use shelves to offer their products to customers. In doing so, they must decide how much shelf space to allocate to which item. Because shelf quantities assigned to retail shelves become depleted over time due to customer purchases, retailers need to regularly refill shelves and reorder items. Reordering directly impacts replenishment processes. As soon as reorders arrive at the store, the respective items are transported to the showroom, where shelves are replenished (i.e., direct replenishment). As a result, every order process triggers a direct replenishment process. Items that do not fit onto the showroom shelf space are stored in the backroom, from where shelves are later replenished (i.e., indirect replenishment from backroom).
Both decisions, i.e., shelf space and reordering, are interrelated, because, e.g., to meet customer demand, a retailer has the option of increasing the shelf quantity and decreasing the order frequency for a specific item, or vice versa. If space is limited, a higher shelf quantity for one item implies less frequent reorders and replenishments for this item, but also less space available for other items, which in turn must be reordered more frequently.
Shelf-space and reorder planning are of great importance to retailers for several reasons: The increasing number of products is in conflict with limited shelf space. Today, up to 30% more products than ten years ago compete for scare space (EHI Retail Institute 2014; Hübner et al. 2016). This puts retailers under pressure to manage profitability with narrow margins and to maintain space productivity (Gutgeld et al. 2009). In fact, shelf space has been referred to as a retailer’s scarcest resource (cf. e.g., Lim et al. 2004; Irion et al. 2012; Geismar et al. 2015; Bianchi-Aguiar et al. 2015a). Above all, changes in shelf space impact customer demand due to the higher visibility of items (Eisend 2014). In other words, the demand for an item grows, the more shelf space is allocated to it. This is referred to as “space-elastic demand”. Additionally, the costs associated with in-store replenishment are significant, because in-store logistics costs amount to up to 50% of total retail supply chain costs (Kotzab and Teller 2005; Broekmeulen et al. 2006; Reiner et al. 2013; Kuhn and Sternbeck 2013). However, the options for changing replenishment frequencies are subject to the availability of backroom inventory for intermediate storage (Eroglu et al. 2013; Pires et al. 2016) and the degree of freedom to choose different delivery frequencies (Sternbeck and Kuhn 2014). Besides product margins and demand effects, the shelf-space planner should therefore also consider options for arranging items on the shelf, in-store replenishment frequencies and costs, and the availability of a backroom for replenishment.
Current literature on shelf-space management mainly addresses the demand side by modeling the effect of space-elastic demand. In this case, a retailer’s profit is maximized under shelf-space constraints by defining the number of facings for each product (i.e., first visible unit of an item in the front row; Hübner and Kuhn 2012; Kök et al. 2015). Existing models do not account for replenishment frequencies and costs, or options for leveraging backroom inventory (Hübner and Kuhn 2012; Bianchi-Aguiar et al. 2016).
To investigate the above-mentioned relationships, we conducted a time and motion study for a German grocery retailer and identified both the relevant in-store replenishment processes and the associated costs. Building on these insights, we then develop an optimization model that simultaneously optimizes shelf-space and in-store replenishment decisions while also accounting for space-elastic demand as well as limited showroom and backroom space. The model accounts not only for product margins, but also for the costs of direct shelf replenishment upon delivery of orders to the store, and for replenishment from the backroom. Furthermore, we consider the cost of inventory kept in the showroom and the backroom. This extended model addresses the research question of how different replenishment procedures and the opportunity to use backroom space impact shelf-space planning. We apply the model to show why an integrated perspective on shelf-space and in-store replenishment optimization is worthwhile and demonstrate how retailers can apply the model to increase their profits.
We address the trade-offs between shelf-space allocation and in-store replenishment (e.g., more space, less frequent orders and replenishments). Because retailers use backrooms as a planned buffer or for excess inventory after shelf replenishment, we further investigate how the availability of a backroom impacts shelf-space decisions and order frequencies.
The remainder of this paper is organized as follows: Sect. 2 provides the conceptual background of our paper and presents the related literature on shelf-space optimization. The time and motion study, and the description of identified replenishment processes, are presented in Sect. 3. Section 4 explains the optimization model and presents a solution approach. Numerical results for testing our model and the impact of backroom space and replenishment cost on objective values and solution structures are presented in Sect. 5. Finally, Sect. 6 has the conclusion and outlook.
2 Conceptual background and related literature
2.1 Conceptual background and decision problem
In the following, we analyze the basic decisions retailers need to make in shelf-space and reorder planning, namely (1) how much shelf space to allocate to items, and (2) how often to reorder them.
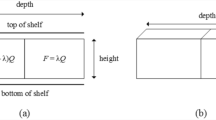
(1) Shelf-space decision Shelf-space planning is a mid-term task and typically executed every six months, requiring a retailer to assign shelf space and shelf quantities to listed products under the constraints of limited shelf size (Hübner and Kuhn 2012; Hübner et al. 2013; Bianchi-Aguiar et al. 2016). The results of these decisions are visualized in a planogram which displays the number of facings, display orientation and position on the shelf for every item (cf. Fig. 1). A facing is the first visible unit of an item in the front row of a shelf. Behind each facing, there is certain quantity of stock, i.e., additional units of the respective item. The number of facings and the stock per facing determine the total shelf quantity of an item. Furthermore, items can be displayed lengthwise or crosswise (cf. Drèze et al. 1994). Particularly when single units of an item are stored in cartons, the retailer must decide on the display orientation of the respective carton. Figure 1, left, shows the difference between facings and shelf quantities. For example, item a gets 2 facings with a stock of 4 units each, resulting in a total quantity of \(2 \cdot 4=8\) units. Item b gets 1 facing with a stock of 6 units and a total shelf quantity of 6. The right of Fig. 1 explains the difference between length- and crosswise display orientation.
Display orientation also impacts the stock per facing since more or fewer units of an item fit behind one facing depending on whether the item is positioned length- or crosswise. In Fig. 1, fewer units would fit behind one facing lengthwise and more units behind a facing with crosswise display orientation. The stock that can be placed behind one facing is determined by the depth of the shelf and the item dimensions. Since the space behind one facing is always filled completely after a replenishment (i.e., filled up until the shelf depth is fully occupied), the stock per facing is not itself a decision of the retailer, but is determined via shelf and item dimensions as well as the decision on the display orientation.
Finally, the position of an item on the shelf is described by its vertical (i.e., which shelf level) and horizontal position (i.e., which items are located next to each other). We focus on the core demand effect of space elasticity, and therefore do not account for these positioning effects in our model. For models accounting for item positioning, we refer the reader to e.g., Hwang et al. (2009), Hansen et al. (2010), Russell and Urban (2010) and Hübner and Schaal (2017).
Shelf-space decisions impact customer demand. Item demand depends on the visible quantity on the shelf and the display orientation. The higher the visibility of an item, the higher its demand. The visibility of an item increases with the number of facings assigned to that item and its display orientation, i.e., the visible item width the customer sees. Empirical studies examine these so-called “space-elasticity effects”, (cf. e.g., Cox 1964; Frank and Massy 1970; Curhan 1972; Drèze et al. 1994; Desmet and Renaudin 1998). Chandon et al. (2009) show that the number of facings is the most important in-store factor affecting customer demand. Using a meta-analysis across empirical studies, Eisend (2014) quantified the average space-elasticity factor as 17%, which implies a demand increase of 17% each time the number of facings is doubled. The discussion of the demand effect on other items (referred to as “cross-space elasticity”) is ambiguous in the pertinent literature. For example, Zufryden (1986) and Kök et al. (2015) state that there is no empirical evidence that product-level demand can be modeled with cross-space elasticity. In addition, the measured effects of cross-space elasticity appear to have only a limited influence on sales (Eisend 2014; Hübner and Schaal 2016). We therefore comply with these results in the literature and disregard cross-space elasticity effects in the remainder of our paper.
Furthermore, shelf-space decisions also depend on assortment planning. However, in retail practice assortment and shelf-space decisions are typically two sequential planning steps of the category planning process (Hübner et al. 2013; Kök et al. 2015; Bianchi-Aguiar et al. 2016). Assortment planning is usually executed in an overarching planning step by the marketing department, whereas shelf planning is a subordinate planning problem and generally owned by the sales department. However, if the shelf space planner can also make assortment decisions and delist items (due to shelf space constraints, for instance, or low profitability of items), one needs to take into account potential substitutions due to demand switches from delisted to listed items.
(2) Ordering decision Since ordering decisions impact store operations, thorough reorder planning is crucial for retailers (see e.g., Fisher 2009; Zelst et al. 2009; Donselaar et al. 2010; DeHoratius and Zeynep 2015). Kuhn and Sternbeck (2013) use qualitative interviews to identify that space management and in-store logistics are not yet well aligned, and that this constitutes a new area of research. Reiner et al. (2013) identify opportunities for improving in-store logistics and show that it is important to not only consider customer needs and the demand side when designing store layout and taking shelf-space decisions, but also logistics requirements. Their process analysis reveals that the efficient design of in-store logistics processes leads to substantial service performance improvements. Furthermore, Kotzab et al. (2005) and Kotzab et al. (2007) use qualitative interviews with store managers to identify the relevant in-store logistics and replenishment processes. Their findings and process descriptions form the starting point of our research.
Because shelves are depleted over time due to customer purchases, retailers need to reorder items and replenish shelves. Consequently, a retailer needs to decide how often to reorder an item. This order frequency impacts in-store logistic processes, because each order triggers a delivery from the warehouse to the store, which again results in a direct replenishment effort to transport the delivered items to the showroom shelves. Beyond this, the order frequency also impacts the number of replenishments from the backroom, because the less frequently items are ordered from warehouses, the higher the backroom quantity at the store that needs to be kept if shelf space is not sufficient to fulfill customer demand, and the higher the number of replenishments of showroom shelves from the backroom. We discuss the in-store logistics processes related to direct and backroom replenishment in more detail in Sect. 3.
2.2 Related literature on shelf-space optimization
Following Seuring et al. (2005) and Kotzab et al. (2005), we first defined the scope of our contribution (as in Sect. 2.1), and then identified the related literature. The identification step included the material collection/selection and category selection. Finally, we completed a content analysis. Because we focus on quantitative decision models, we excluded literature that strictly covers general management, marketing and service management issues, and does not discuss modeling aspects and decision support systems at all. Papers were assessed based on their decision modeling, demand models and their relation to space and reorder planning.
In the following we introduce the fundamental modeling papers and analyze only the shelf-space modeling papers that contain considerations of replenishment, inventory holding and store operations. Further modeling papers dealing with shelf-space problems that do not include any of these considerations or that are not related to our decision problem are not the focus and not further analyzed. Shelf-space models typically assume a given assortment with space-elastic demand, ignore substitution (because the assortment is predetermined), and account for limited shelf space. Our problem relates to the shelf-space literature, and we therefore focus on this area. For comprehensive overviews of shelf-space problems, we refer to Hübner and Kuhn (2012), Kök et al. (2015) and Bianchi-Aguiar et al. (2016).
The models reviewed here all optimize the number of facings for a given set of items and limited shelf space. The main demand effect considered is space elasticity. To account for the non-linearity arising from the polynomial demand function, various solution approaches are applied and space-elasticity effects either assumed to be linearly dependent on the number of facings, approximated by piecewise linearization, or non-linear models applied and solved with heuristics.
Basic shelf-space management literature uses deterministic demand models to factor in space-elasticity effects (cf. Kök et al. 2015). One of the first models is proposed by Hansen and Heinsbroek (1979), who formulate a non-linear model with various constraints, such as minimum and integer shelf quantities and space elasticities of polynomial form. To solve the problem, they apply a Lagrangian relaxation. Corstjens and Doyle (1981) propose a limited shelf-space model that considers space and cross-space elasticities of polynomial form. Geometric programming is applied to solve the model for up to five product groups. The model cannot be applied to large-scale problems on an item-level, and therefore, works with product groups rather than SKUs. Zufryden (1986) formulates a model with space-elastic demand of polynomial form, which is solved through dynamic programming for up to 40 products. Borin et al. (1994) propose a model that considers space- and cross-space elasticities of polynomial form. Substitution effects are integrated and the model is solved with a simulated annealing heuristic for six items. Yang and Chen (1999) assumes a linear space elasticity function and solves the model through a multi-knapsack heuristic. Urban (1998) provides the first enhancement with available inventory and replenishment systems. The polynomial demand model takes into account restrictions in backroom capacity, minimum order quantities and ensures that replenish quantities meet demand. The decision variables for facings and order quantities are continuous values, and thus violate integer requirements. They are only rounded afterwards. Furthermore, the proposed solution heuristic is only applied to a small data set and no efficiency analysis is conducted in terms of solution quality. Hwang et al. (2005) develop a shelf-space optimization model with inventory control aspects. Space elasticity is assumed to be polynomial and the model solved through a genetic algorithm and a gradient search heuristic. Tests are limited to instances of up to four items on six shelves. Hariga et al. (2007) propose a model that simultaneously optimizes assortments, shelf-space, store location and inventory replenishment frequencies. The model accounts for space- and cross-space elasticities of polynomial form, but does not differentiate between direct and backroom replenishment costs. The problem is tested with instances of four items and solved by a standard solver. Ramaseshan et al. (2008, 2009) determine shelf-space allocation and inventory quantities. Their decision model is implemented in Excel and generates an approximate solution for up to 14 items. Murray et al. (2010) present a model that considers pricing aspects and optimizes shelf-space allocations. Best to our knowledge, this is the only contribution so far additionally accounting for the display orientation of items. The problem is solved through a non-linear solver and tested on large-scale instances with up to 100 items. Hübner and Kuhn (2011) develop a MIP model to account for polynomial space-elasticity and replenishment cost. They show that demand effects have a significant impact on item profit. The model balances the trade-off between over- and undersupply situations where either store staff need to refill shelves in between two regular shelf refills or where overstocks result in capital cost. The order frequency decision is not explicitly taken. Direct and indirect replenishment is not distinguished and backroom capacity is not accounted for. Irion et al. (2012) develop a non-linear model for cross-space and space elasticities that is then solved by piecewise linear approximation, which makes it possible to handle data sets of a size relevant in practice. They include inventory holding costs in the model. Hariga and Al-Ahmari (2013) develop an integrated space allocation and inventory model for a single item with stock-dependent demand. They analyze different setups regarding the supplier-retailer relationship and optimize the order quantity, reorder point and number of facings. However, this paper is restricted to one single product, showroom and backroom replenishments are not distinguished, and facing-dependent space-elasticity effects not considered. Bianchi-Aguiar et al. (2015a) use a MIP approach to develop a model that considers product grouping and display orientation constraints, and therefore incorporates merchandising rules. Tests for instances with up to 256 items are conducted.
2.3 Summary and research contribution
When retail shelf space is limited, retailers need to thoroughly consider the trade-off between shelf-space and ordering decisions. The two decisions are interdependent and impact in-store logistics processes for shelf replenishment, since every order triggers direct replenishment of shelves and since items that do not fit onto the showroom shelf must be indirectly replenished from the backroom. Despite these interdependencies in in-store logistics and space assignment, an integrated optimization model is lacking in the existing literature. The contributions on shelf-space planning mentioned all focus on optimizing the number of facings. Demand is assumed to be facing-dependent (i.e., space-elastic). Non-linearities arising from this are dealt with either via linear approximations or solution heuristics that are limited in their capability to solve instances of practice-relevant size.
To close this research gap, our contribution is threefold: (1) Based on a detailed time and motion study for a retailer, we first quantify costs associated with direct and backroom replenishment processes; (2) Using the insights from the time and motion study, we propose an integrated model to optimize planograms (i.e., facings and display orientations) and order frequencies. Our model accounts for space-elastic demand, assumes limited showroom and backroom space, and differentiates between direct and indirect replenishment cost as well as showroom and backroom inventory holding cost. By means of our modeling approach, we obtain optimal solutions within very short runtimes, even for large-scale instances. (3) By applying our model to a real data set, we show how the retailer can increase profits with optimized shelf-space decisions and order frequencies. Furthermore, we use our model to show how backroom availability impacts profits and solution structures, and prove the advantage of our model over other approaches that do not account for the relevant costs.
3 Time and motion study for in-store replenishment processes
To accurately quantify the costs associated with the different replenishment processes, we conducted a time and motion study. Current literature serves as a starting point for defining the process steps for in-store logistics (e.g., Kotzab and Teller 2005; Zelst et al. 2009; Reiner et al. 2013), but does not sufficiently detail the costs affected by shelf-space planning and reordering. Curşeu et al. (2009) conduct a similar time and motion study on parts of the direct replenishment process. They measure process times for shelf refilling and waste disposal but ignore transport to the shelves from the receiving area. Moreover, backroom replenishment is not part of the investigation. Hence, our investigations serve to further specify replenishment processes and the interdependencies with shelf-space decisions.
3.1 Replenishment processes observed during time and motion study
Figure 2 provides an overview of the in-store logistics processes and the associated subprocesses for replenishment. It visualizes all shelf replenishment processes, from the unloading of a store delivery from the truck, to shelf restocking and waste disposal. The processes can be distinguished by the respective store locations where they are executed, namely the (1) receiving area, the (2) showroom, and the (3) backroom. The relevant processes are described below.
(1) Preparation processes in the receiving area Are the starting point of related in-store logistics. When store deliveries arrive at the receiving area, they are unloaded and brought to a presorting area, where they are sorted by category prior to actual shelf replenishment, and finally brought to the showroom to a central category location (cf. Kotzab and Teller 2005). From there, the actual shelf replenishment starts. This implies that a pallet, roll cage or other means of transport is placed at this central category location, from which stock clerks take individual items and transport them to the shelves.
Based on the process flow in Fig. 2, a distinction can basically be made between two types of replenishment: direct and backroom (i.e., indirect) replenishment.
(2) Direct replenishment Occurs for every order delivered from the warehouse and describes the processes after the items arrive in the showroom. Upon arrival at the central category location, items are individually picked, transported to the specific shelf location and then refilled. Finally, waste from the packaging of refilled items is disposed of. The fact that every order (and store delivery) induces a direct replenishment process implies that the number of orders equals the number of direct replenishments for an item.
(3) Backroom (i.e., indirect) replenishment Refers to the processes that occur when items that did not fit on the shelf are returned to the backroom, where they are stored for later replenishment. As soon as items are depleted on showroom shelves, employees restock them from the backroom. To do so, a stock clerk searches for the relevant items in the backroom, transports them through the store to the shelves and refills them. Because the backroom replenishment process includes both the returning of excess units from the showroom after a direct replenishment as well as the refilling of shelves from the backroom, indirect replenishment typically is at least twice as expensive as direct replenishment. Retailers do not have a dedicated ordering process for backroom inventory. Only surplus items from the showroom are temporarily stored in the backroom.
3.2 Identification of decision-relevant replenishment costs
Data collection through time and motion study To assign the cost to the in-store replenishment processes described in the previous section, we conducted a time and motion study for a German grocery retailer. Stock clerks were accompanied to identify the different steps involved in the in-store replenishment process. To do so, we made use of the methods-time measurement concept (Maynard et al. 1948). Following Barnes (1949) and Niebel (1988), we analyzed the replenishment process systematically by first identifying subprocesses and the most efficient way of executing them, then categorizing and standardizing the subprocesses identified, and ultimately determining the standard time required by a qualified stock clerk to execute each subprocess. To level the effects of potential outliers in observed process times due to factors such as time, staff capability or store location, we measured the process times across two stores on all weekdays and for various employees. Product groups were from the ambient assortment, including both fast- and slow-movers. The division into subprocesses was as granular as possible to accurately differentiate between constant and variable elements (Barnes 1949). Process mapping was used to detect potential process improvements, but also to calculate the standard time required for a task.
During the data collection period, the stores were asked to have their most qualified and properly trained personnel perform replenishment. Moreover, the observation days were selected such that they did not include any periods of major demand changes (e.g., holidays). Moreover, we observed replenishments of single units as well as whole packages (cartons) with different case pack sizes (cf. Zelst et al. 2009).
Decision-relevant replenishment cost Retailers make use of delivery patterns, which define specific days for store deliveries from the warehouse for each store and each product group (Hübner et al. 2013). These delivery patterns mainly depend on given network structures and product groups (e.g., fresh products are delivered more often than dry foods). These fixed, mid-term delivery patterns allow for higher stability in warehousing, transportation and in stores, especially in terms of capacity management and workforce planning, such that external stock clerks, for instance, can be scheduled for the day a specific category is delivered (Holzapfel et al. 2016). The costs associated with each delivery (i.e., cost of transportation to the store, unloading at the store, transport of a pallet to the receiving area) can only be avoided if no single product among all the categories is ordered for a certain delivery day. The same holds true for the costs associated with each replenishment of an entire category (i.e., presorting by category in the receiving area, transporting category-specific pallets to the category location in the showroom). Without compromising on the general applicability of our approach, we assume that these fixed delivery costs and fixed replenishment costs per category are not decision-relevant in shelf-space planning.
In contrast, costs arising from the replenishment of single items are decision-relevant for our problem context. Direct and backroom replenishment processes generate decision-relevant costs of this kind due to the subprocesses described above, e.g., from the transportation of items to shelves to replenishment from the backroom on depletion. The decision-relevant costs can be divided into variable costs, incurred for every unit refilled, and fixed costs, incurred for every replenishment procedure:
-
Fixed costs for each direct replenishment are incurred for every replenishment process of an item. This includes further sorting in the showroom (e.g., readjusting the placement of pallets for better accessibility, positioning roll cages or shopping carts), in-store transportation from the central category location to the shelf, the search time to find the shelf location of the items, rearranging existing stock, and finally waste disposal.
-
Variable costs for direct replenishment are incurred for every delivered unit of an item. These are quantity-dependent costs for actual shelf-stacking and shelf-refilling activities per unit (e.g., positioning the delivered units, unpacking).
-
Fixed costs for backroom replenishment are incurred for every replenishment of shelves with items from the backroom. These costs include the return transport of excess items from direct replenishment. These units did not fit on the shelf and are stored in the backroom. Furthermore, these costs include searching for the items in the backroom, in-store transport to showroom shelves, searching for the shelf locations, preparing the shelves for refilling and disposing of waste.
-
Variable costs for backroom replenishment are incurred per unit refilled from the backroom to the showroom. These are quantity-dependent costs for actual shelf-stacking and shelf-refilling activities per unit (e.g., positioning the delivered units, unpacking) during the replenishment process.
Finally, depending on the quantity kept on shelves and in the backroom, inventory holding costs are incurred. Typically, holding inventory in the showroom is slightly more costly, because shelves cannot be used as efficiently as a storage location like the backroom. One reason is that showroom shelves have to look appealing, which is not necessarily a requirement for backrooms.
In summary, the relevant costs for the problem considered here must include all in-store replenishment processes after an item has reached the showroom. The decision-relevant costs can be separated into fixed and variable replenishment costs for direct and backroom replenishment, as well as inventory holding costs for items in the showroom and backroom.
4 Model development
In this section, we develop the Capacitated Shelf-Space and Reorder Problem with Backroom Space, which addresses the decision problem described above. It is abbreviated by CSRPBS below. A retailer considers a category with a given set of items \({\mathbb {N}}\) where \(N = |{\mathbb {N}}\)| and with the item index i, \(i \in {\mathbb {N}}\). For this set of items, the retailer simultaneously needs to decide how much shelf space to allocate to the items (i.e., the number of facings), whether to display them on the shelf lengthwise or crosswise (i.e., the display orientation) and how often to order them (i.e., reorder frequency). We assume a limited showroom shelf space of S and a limited backroom space of B. Because we aim to investigate the interdependencies between shelf-space and reorder planning and its consequences on direct and indirect replenishment, we follow the majority of contributions and consider a single showroom shelf (cf. e.g., Zufryden 1986; Corstjens and Doyle 1981; Irion et al. 2012), i.e., we do not account for different shelf levels and assume the shelf consists of one level with a one-dimensional space S. Accordingly, we focus on space elasticity as the dominant demand effect (cf. Chandon et al. 2009).
Table 1 provides an overview of the notation used.
The model optimizes three types of decisions variables. The first type \(k_i\) determines the integer number of facings on the showroom shelf for each item i. The second type, the visible width of a facing of an item \(b_i\), defines whether an item i is displayed lengthwise or crosswise. This impacts whether the customer sees the item length (\(b_i=l_i\)) or width (\(b_i=w_i\)) when looking at the shelf from the front. Finally, the third type, order frequency \(f_i\), determines the integer number of orders per period, and consequently the number of direct store replenishments.
Three types of auxiliary variables, \(g_{ib_i}\) for the stock per facing, \(x_{ib_i}\) for the total shelf quantity and \(y_i\) for the backroom inventory, are used in addition: Behind each facing, a certain stock, \(g_{ib_i}\), can be put onto the shelf. This stock depends on the visible width of a facing determined through the display orientation. For each of the two possible widths \(b_i\), a fixed number of units can be placed behind the facing. How many units fit behind the facing depends on the item dimensions (\(l_i\) or \(w_i\), determined by the display orientation chosen), and on the shelf depth. The second auxiliary variable, the total shelf quantity \(x_{ib_i}\), depends on the number of facings \(k_i\) and the stock per facing \(g_{ib_i}\), and is computed by \(x_{ib_i}=k_i \cdot g_{ib_i}\). To derive the third auxiliary variable, the backroom quantity \(y_i\), we consider the fact that the order frequency \(f_i\) divides the considered period into equal \(f_i\) subperiods. A subperiod demand needs to be covered during each of these subperiods. This subperiod demand corresponds to the total item demand \(D_i\) divided by the number of subperiods: \(D_i/f_i\). The subperiod demand is fulfilled by the shelf quantity \(x_{ib_i}\) and the backroom inventory \(y_i\), which we calculate as the part of the subperiod demand not covered by the shelf quantity: \(y_i = {\text {max}} [\lceil \frac{D_i}{f_i} - x_{ib_i} \rceil ; 0]\). This ensures that customer demand is always fulfilled. Total demand \(D_i\) for an item is assumed to be deterministic, which implies that out-of-stock situations cannot arise. The demand is only dependent on the initial facing assignment and does not change between replenishments, when one of several facings are empty. We do not consider joint replenishment effects, which would allow the fixed direct or backroom replenishment cost to be spread across several items. Furthermore, we do not account for delivery patters with unequal intervals and assume that the time in between two replenishments is always the same, i.e., if \(f=2\), a delivery occurs in a six day period, e.g., on days 1 and 4, but not on days 1 and 5. We also do not model further cost savings via a joint vehicle routing and delivery frequency selection across stores.
The retailer pursues the objective of maximizing the total profit through selecting the optimal number of facings \(k_i\), visible width of a facing \(b_i\) and order frequencies \(f_i\) across all items, represented by the respective vectors \(\bar{k}, \bar{b}\) and \(\bar{f}\), with \(\bar{k} = \{k_1,k_2, \ldots , k_N\}\), \(\bar{b} = \{b_1,b_2, \ldots , b_N\}\) and \(\bar{f} = \{f_1,f_2, \ldots , f_N\}\) (cf. Eq. 1).
To obtain the item profit \(p_i\), we deduct the total cost of direct replenishment \({\text {C}}^\mathrm{{DIR}}_{i}\) and the total cost of backroom replenishment \({\text {C}}^\mathrm{{BR}}_{i}\) (cf. Eq. 2) from the total gross margin of an item. The gross margin of an item is calculated as the product of its total demand \(D_i\) and its unit margin \(m_i\). The item unit margin \(m_i\) corresponds to the difference between its sales price \(r_i\) and its purchase cost \(c_i\).
The total period demand \(D_i(k_i,b_i)\) of an item i is a composite function of the minimum demand \(d_i\) and the facing- and display orientation-dependent demand. The minimum demand rate \(d_i\) represents the retailer’s forecast for an item that is independent of the facing and visible facing width (cf. Hansen and Heinsbroek 1979; Hübner and Kuhn 2012; Bianchi-Aguiar et al. 2015a). The forecast may be based on historical sales, but may also incorporate further demand effects such as shelf location in the store or other marketing effects. The higher the visibility of an item, the higher is its demand. The visibility increases with the number of facings \(k_i\). Furthermore, it increases when the item dimension visible to the customer increases, which is either the item width or the item length. In accordance with prior research (cf. e.g., Hansen and Heinsbroek 1979; Irion et al. 2012), the facing- and display orientation-dependent demand rate is a polynomial function of the number of facings \(k_i\) allocated to an item, the visible facing width \(b_i\) and the space-elasticity \(\beta _i\) (with \(0 \le \beta _i \le 1\)). Most existing models assume that items have a fixed item width, as they can be displayed in one display orientation only. We use the demand model assumed by Irion et al. (2012) to factor in the visible facing width \(b_i\). Eq. 3 summarizes the demand calculation applied.
Total direct replenishment cost (\({\text {C}}^\mathrm{{DIR}}_i\)) comprises three parts, as shown in Eq. (4): fixed replenishment costs for each replenishment of an item (\(\mathrm{FC}_i^\mathrm{{DIR}}\)), variable replenishment costs for each unit replenished of an item (\(\mathrm{VC}_i^\mathrm{{DIR}}\)) and showroom inventory holding costs (\(h_i^\mathrm{{SR}}\)) per unit. Assuming continuous demand, the average showroom inventory used for calculating the related inventory costs is calculated as \(x_{i_i}/2\).
The total backroom replenishment costs (\({\text {C}}^\mathrm{{BR}}_i\)) consist of the same three elements (cf. Eq. 5), where we also need to consider the number of shelf refills from the backroom (\(\lceil \frac{y_i}{x_{ib_i}} \rceil\)) during a subperiod for the fixed replenishment costs, the backroom inventory \(y_i\) instead of the showroom shelf quantity, and the backroom’s inventory holdings costs per unit (\(h_i^\mathrm{{BR}}\)).
Solution approach Equations (3)–(5) contain several non-linear components relating to the decision variables (e.g., space-elastic demand with \((k_i \cdot b_i)^{\beta _i}\) or the division of two variables in the backroom replenishment costs \(\lceil \frac{y_i}{x_{ib_i}} \rceil\)). Therefore, it is a non-linear model. To handle the non-linearity, we precalculate the associated profit \(p_{i}(k_i,b_i,f_i)\) and space requirements in the show- and backroom (\(s^\mathrm{{SR}}_{i}(k_i,b_i,f_i)\), \(s^\mathrm{{BR}}_{i}(k_i,b_i,f_i)\)) for each item i and each possible combination of facings, visible facing width and order frequencies. The precalculated data is then used in a MIP to ultimately choose the optimal combination, and thus globally optimize profits. The usage of a MIP comes with various computational conveniences. We handle the non-linear model terms outside the optimization model using precalculation. Suboptimal heuristics are therefore not required. The MIP can be solved optimally in a time-efficient manner (see runtime tests in Sect. 5.2.1). Finally, the MIP offers the possibility of adding further model constraints in case these are required from a practical perspective. An example of this is the restriction that a certain item must be positioned with a predefined display orientation. This precalculation approach can be applied because in practice, all decision variables have upper limits. First, a retailer will only assign a certain number of facings to an item with \(k_i \in {\mathbb {K}}_i\), typically not more than 20–25 facings. Second, only two values are possible for the visible width of a facing of item i, i.e., \(b_i = l_i\) for lengthwise and \(b_i = w_i\) for crosswise display orientation. In the MIP model, we decode the visible width of a facing of item i by o, where \(o=1\) if \(b_i = l_i\), and by \(o=2\) if \(b_i = w_i\). Third, the frequency of direct replenishments (i.e., orders) cannot exceed the maximum number of warehouse deliveries with \(f_i \in {\mathbb {F}}_i\), e.g., not more than six times per week. This allows us to precalculate the profit (denoted as \(\pi _\mathrm{{ikof}}\) in the MIP) for every item i and every possible combination of the three decision variables for the predefined ranges \(k_i \in {\mathbb {K}}_i\), \(o \in {\mathbb {O}}\) and \(f_i \in {\mathbb {F}}_i\), \(i \in {\mathbb {N}}\). This means that \(\pi _\mathrm{{ikof}}\) is the profit for item i if it gets k facings, is given the display orientation o and is ordered f times a period. Similarly, we precalculate how much showroom (backroom) space item i consumes for every combination of k, o and f. The respective space consumption is denoted as \(s_\mathrm{{ikof}}^\mathrm{{SR}}\) for the showroom and \(s_\mathrm{{ikof}}^\mathrm{{BR}}\) for the backroom.
Using the precalculated profits as data input, the MIP model then selects the binary variable \(\gamma _\mathrm{{ikof}}\) to indicate how many facings item i should be given, how it is displayed and how often it should be ordered. The objective function and the constraints for the resulting model CSRPBS can be formulated as follows:
Subject to:
Equation (6) is the objective function and is the summation of all item-specific profits. Equations (7) and (8) ensure that showroom shelf S and backroom space B restrictions are met. Finally, Eq. (9) ensures that each item i gets exactly one combination of facings, item display orientations, and order frequencies. Equation (10) declares \(\gamma _\mathrm{{ikof}}\) as a binary variable. Note that the available showroom space S is the one-dimensional shelf length (front row) available for the placement of facings, e.g., measured in centimeters or meters. In contrast, the size of the backroom B is measured in space units, e.g., in m2, because in the backroom, items can theoretically be stored behind each other, whereas items need to be placed next to each other on showroom shelves for reasons of visibility. Analoguously to that, \(s_\mathrm{{ikof}}^\mathrm{{SR}}\) is a one-dimensional length and \(s_\mathrm{{ikof}}^\mathrm{{BR}}\) is a two-dimensional area.
Model complexity The MIP model developed belongs to the class of knapsack problems, which are known to be NP-hard (cf. Kellerer et al. 2004; Pisinger 2005). In our case, the model complexity is driven not only by the number of combinations for allocating N items to a shelf of size S, but also by the fact that each item can be ordered up to F times and get one of two different display orientations. The resulting model complexity can therefore be calculated by Eq. (11):
The binomial coefficient calculates the number of possible combinations for allocating N items to a showroom shelf of size S. The second term accounts for the fact that each item can be ordered up to F times, and finally, the third term accounts for the display orientation. For example, for \(N=50\), a showroom shelf of \(S=100\), up to daily deliveries (\(F=6\)) and one of two possible display orientations, the number of possible configurations is \(4.59\cdot 10^{82}\). Our modeling approach based on precalculated profits helps to significantly reduce this complexity, because instead of the Y combinations, we only need to precalculate \(N \cdot K \cdot F \cdot 2\) profits (assuming K is the number of elements in \({\mathbb {K}}_i\), with \(k_i=1, \ldots K\); similarly for F). These are then provided as input into the MIP choosing the optimal combination. For the example above, the number of required precalculations corresponds to \(N \cdot K \cdot F \cdot 2 = 50 \cdot 25 \cdot 6 \cdot 2 = 15,000\), if we assume an upper limit for the number of facings per item of \(K=25\). Note that our MIP is always solved to optimality within these assumed limits.
5 Numerical results
The numerical results are presented in this section. Our model is first applied to a case study in Sect. 5.1. To generalize the results, Sect. 5.2 uses randomly generated data to test the runtime performance and investigate the impact of backroom space and replenishment processes on objective values and solutions. Section 5.3 summarizes the findings from the numerical results. All numerical tests were conducted on a Windows 7 32-bit Intel Core i5-2520 with 2.5 GHz and 4 GB memory. The tests were implemented in VB.net (Visual Studio 2013) and GAMS 24.1 to use the CPLEX solver for the MIP.
5.1 Application to real data: case study
This section applies our model to the canned foods assortment of a German grocery retailer.
Data applied We consider the product category for which we also obtained the process descriptions and cost structures from our time and motion study. This category encompasses 70 different items. In this category, the retailer only puts the items onto the shelf in case packs (i.e., cartons) and not in single customer units (i.e., cans). We treat one carton as one facing and each carton contains a quantity of six or twelve units. The display orientation-dependent stock per facing \(g_{ib_i}\) is derived here as follows: As the shelf depth does not allow case packs to be put behind each other regardless of a crosswise or lengthwise positioning, the stock per facing is given by the quantity per carton. Please note that here the space-elasticity effect is reflected in Eq. (3) by the b-value for the crosswise/lengthwise display orientation of the facing, i.e., demand increases when the larger of the two carton dimensions is displayed.
We consider a sales period of one week. The average minimum demand \(d_i\) of the items \(i \in {\mathbb {N}}\) is between 1 and 110 units per week. For determining \(d_i\), we first measured the average total demand \(D_i\) across 10 months with the current number of facings \(k_i\), the current visible width of a facing \(b_i\), an assumed space elasticity of \(\beta _i\) and then recalculated the average minimum demand \(d_i\) using Eq. (3). We assume that space elasticity is equal for all items within the canned foods category. The items are sold for a price of 0.50 € \(\le r_i \le\) 2.49 €. For reasons of confidentiality, the corresponding values for unit, replenishment and inventory cost cannot be provided. Showroom shelf space is limited to \(S=5920\) cm and backroom utilization is currently very low, which is why we can consider backroom space capacity to be unlimited. At the time of data collection, the retailer assigned between 1 and 21 facings to the items, which all have a lengthwise display orientation. The number of facings was determined according to a sales-proportional allocation (SPA) rule, which assigns shelf space to items based on their share of category sales, but ignores replenishment cost (cf. Hübner and Kuhn 2012). The item length \(l_i\) is 14.8 cm \(\le l_i \le\) 40.0 cm and item width \(w_i\) is 22.4 cm \(\le w_i \le\) 41.7 cm. All items are currently ordered twice a week (\(f_i = 2\)).
Approaches analyzed To show the extent to which the retailer benefits from the model, we investigate the following modeling approaches: [1] “Status quo”—which represents the number of facings and display orientation as observed in the current shelf-space assignment and a given order frequency of \(f=2\) for all items. To ensure comparability, we evaluate the observed values of all decision variables using the objective function (cf. Eq. 6) of the CSRPBS-model. To compute margins and replenishment costs “a posteriori”, we apply the respective “a posteriori” model, denoted as CSRP*. Furthermore, we ensure that all constraints (7–10) are fulfilled. From here, we derive the profit potential in steps: Approaches [2] and [3] are partial optimizations, where either order frequencies (approach [2], model CSRPBS*\((\bar{f})\)) or facings and display orientations (approach [3], model CSRPBS*\((\bar{k}, \bar{b})\)) are optimized. In [2] we keep k and b as per current and in [3] we do so for f. All profit components are evaluated by applying the respective “a posteriori” calculation for the non-optimized variables. Finally, in approach [4] “Integrated optimization”, the CSRPBS\((\bar{k}, \bar{b}, \bar{f})\) model optimizes k, b and f simultaneously, and therefore, shows the full potential. This model corresponds to the CSRPBS introduced in Sect. 4. To highlight the differences to approaches [1]–[3], we add here the superscript for the decision variables. Table 2 summarizes the respective assumptions for each modeling approach:
Results Figure 3 illustrates the advantage of the fully integrated model (CSRPBS\((\bar{k}, \bar{b}, \bar{f})\)) over the partial optimization models and the status quo for different values of the space elasticity. The analysis reveals several insights: First, independent of space elasticity, a significant opportunity exists for the retailer to improve the status quo. If we assume a space elasticity of 15% (cf. Eisend 2014 who identified an average of 17%), the full potential of integrated optimization compared to the status quo (approach [4] vs. [1]) amounts to approximately 29%. Second, the retailer also profits from partial optimization, i.e., only optimizing order frequencies ([2] vs. [1]) or facings and display orientations ([3] vs. [1]). The higher potential clearly lies in the optimization of facings and display orientations. However, the results from [4] show that an integrated perspective is still better than partial optimization. Finally, we see that the advantage of the integrated model (CSRPBS\((\bar{k}, \bar{b}, \bar{f})\)) over pure shelf-space optimization (CSRPBS*\((\bar{k}, \bar{b})\)) diminishes with increasing space elasticity. This is due to the fact that the importance of assigning the right amount of space to high-margin items increases as space elasticity and the connected demand increase, which is achieved by both models. Simultaneously, the magnitude of replenishment cost decreases and so does the advantage of the fully integrated over the shelf-space optimization model.
To better understand the latter, Fig. 4 shows the absolute values for total profits (\(\sum _{i \in {\mathbb {N}}} p_i\)), total gross margins (\(\sum _{i \in {\mathbb {N}}} D_i\cdot m_i\)) and total replenishment cost (\(\sum _{i \in {\mathbb {N}}}\,{\text {C}}^\mathrm{{DIR}}_i\) and \(\sum _{i \in {\mathbb {N}}} {\text {C}}^\mathrm{{BR}}_i\)) for the four approaches. The profit increase is mainly driven by the increase in gross margins, while replenishment costs are much lower in magnitude. With increasing space elasticity, the impact of the gross margin effect rises even higher. Note that in CSRP* and CSRPBS*\((\bar{f})\), \(k_i\) and \(b_i\) are determined regardless of the space elasticity, and are therefore, identical across all \(\beta\)-values. However, the gross margin increases also for these two approaches, because the demand realized increases with an increase in the assumed space elasticity (see Eq. 2).
Table 3 shows the changes in solution structure, i.e., facings, visible facing width and order frequencies. The comparison of the partial and full optimization models with the status quo shows significant differences in all three optimization variables, e.g., 90% of all items get a different number of facings in the full optimization compared to the status quo. Furthermore, the comparison of the full optimization to the partial optimizations shows that there is still a significant share of items with differences in either order frequencies (21.4% with different order frequencies, [2] vs. [4]) or facings and display orientations (15.7% with different facings, 2.9% with different display orientation, [3] vs. [4]).
5.2 Generalization using randomly generated data
After having shown how the retailer can use our model to increase profits, we can now generalize these insights by conducting more extensive analyses with randomly generated data. Section 5.2.1 describes the data used and the test setting. Section 5.2.2 then provides runtime tests. Section 5.2.3 investigates the impact of backroom availability on profits and solution structures and Sect. 5.2.4 analyzes the profit advantages retailers can achieve when thoroughly accounting for replenishment processes. We compare our model to a sales-proportional allocation rule in Sect. 5.2.5 and develop an extension to account for assortment decisions in Sect. 5.2.6.
5.2.1 Data applied, models and test bed
The data generation process is based on the data obtained from the case study. If not stated otherwise, we use a uniform distribution to randomly generate the item-specific parameters which are within the following intervals: \(d_i \in [50,70]\); \(r_i \in [10,20]\); \(c_i \in [75\%\cdot r_i,80\%\cdot r_i]\); \(g_{ib_i} \in [3,5]\); \(\mathrm{VC}_i^\mathrm{{DIR}} = [0.02,0.06]\); \(\mathrm{VC}_i^\mathrm{{BR}} = [0.06,0.10]\); \(\mathrm{FC}_i^\mathrm{{DIR}}=[0.08,0.12]\); \(\mathrm{FC}_i^\mathrm{{BR}} =[0.16,0.24]\); \(h_i^\mathrm{{SR}} \in [2.5\% \cdot r_i, 3.5\% \cdot r_i]\) and \(h_i^\mathrm{{BR}} \in [1.5\% \cdot c_i, 2.0\% \cdot c_i]\). In other words, replenishment from the backroom is twice as expensive as direct replenishment on average, and inventory holding costs are lower in the showroom than in the backroom. Space elasticity of the single items \(\beta _i\) is assumed to vary between 0 and 35%. To focus on the core effects, we assume \(w_i=l_i=1\), if not stated otherwise. Furthermore, we set \(K=15\) and \(F=6\) for the precalculations, were K(F) corresponds to the number of elements in \({\mathbb {K}}_i\) with \(k_i = 1, \ldots , K\) (\({\mathbb {F}}_i\) with \(f_i = 1,\ldots ,F\)).
We use the model CSRPBS to optimize facings, visible facing width and order frequencies, and solve it using the MIP introduced in Sect. 4 (cf. Eqs. 6–10). The CSRP* model is used to evaluate the impact of ignoring specific effects (e.g., replenishment cost) “a posteriori”. The measured effects are averages across 100 randomly generated instances of N items.
5.2.2 Runtime test
Table 4 shows the average runtime for different problem instances and shows that our model can efficiently generate optimal results even for large-scale problem instances. While we assumed \(w_i=l_i=1\) for all instances up to \(N=400\) items, for the instance with \(N=2000\), \(S=60,000\) and \(B=30,000\) we randomly generated item dimensions with \(w_i \in [2,10]\) and \(l_i \in [5,15]\) to test runtime performance under more complex assumptions. The model still generates optimal results in a minimum amount of time in less than a minute runtime on average.
The CSRPBS is a knapsack problem. It becomes a hard knapsack problem when item weight (in our case the shelf space occupied by the item) and the item contribution (in our case the unit margin) are strongly correlated (cf. Pisinger 2005). To test the performance of our approach on hard knapsack problems, we run a further test on instances with \(N=2000\), \(S=60,000\) and \(B=30,000\), where unit margins and space occupied correlate with \(R^2 = 0.9\). The average runtime for these 100 instances is 78.06 s, with a minimum of 62.34 s and a maximum of 93.47 s, which shows that our approach can also handle hard knapsack problems efficiently.
5.2.3 Impact of backroom space on profits and solution structures
To investigate the impact of backroom availability on profits and solutions structures, we first present a 2-item example below and then extend the analysis to a more comprehensive set of randomly generated data.
2-item example We consider two items (1 and 2) with identical demand and cost parameters. Both items have a length of \(l_i = 1\) and a width of \(w_i = 2\). The stock per facing \(g_{ib_i}\) depends on the visible facing width and is 1 in case of a lengthwise orientation, and 2 in case of a crosswise orientation. The only difference between the two items is that item 1 has a high space elasticity and item 2 has none (\(\beta _1 = 30\%, \beta _2 = 0\%\)). Below, we analyze how facings, display orientations, order frequencies and backroom quantities change if showroom and backroom space increase.
Figure 5 shows that with a showroom space of \(S=6\) and no backroom space (\(B=0\)), the highly space-elastic item 1 receives \(k_1 = 5\) facings and is replenished \(f_1=2\) times a week. Item 2 receives only the minimum of \(k_2 = 1\) facing because its space elasticity is zero. Item 2 needs to be ordered more often (at \(f_2=6\)) to still satisfy the demand for it. Both items are displayed lengthwise, and therefore, have a stock per facing of only one unit. If backroom space now becomes available (while showroom space remains the same), it is beneficial to decrease order frequencies for item 2 from \(f_2=6\) (\(B\le 1\)) to \(f_2=2\) (\(B\ge 4\)) and instead replenish it indirectly from the backroom where inventory holding cost is lower (\(y_2=2\)). If showroom space S is doubled from six to twelve (and no backroom exists), item 1 now receives only \(k_1=3\) facings, which are displayed crosswise. Item 2 is also positioned crosswise and receives \(k_2=1\) facings. Both items receive a stock of two units per facing due to the crosswise orientations. Two interesting observations are to be made: First, a showroom shelf space of only eight out of a total of twelve is occupied. The reason why the shelf space is not fully occupied is the following: Further space could theoretically be assigned to the highly space-elastic item 1, but since this would induce additional space-elastic demand that cannot fully be supplied by the showroom inventory, backroom quantities would need to be kept for item 1 to satisfy the demand for it (compare scenario with \(S=12\) and \(B=4\), where \(y_1=2\)). Since no backroom exists, item 1 remains at three facings. Second, the crosswise display orientation of item 2 allows for a stock of 2 units to be placed on the shelf. This allows for a decrease in the order frequency from \(f_2=6\) (at \(S=6, B=0\)) to \(f_2=3\) (at \(S=12, B=0\)). Because \(\beta _2=0\%\) and due to showroom inventory holding cost, it is also not beneficial to use the remaining shelf space for further units of item 2.
Obviously, a backroom space of \(B=2\) (or 3) is not yet sufficient to further decrease \(f_2\), but it can be used to reduce the inventory held in the showroom. The display orientation of item 2 therefore changes back to lengthwise, which results in a stock of only one. Inventory moves to the backroom, where it is cheaper to keep stock (\(y_2=1\)). If backroom space increases to \(B=4\) (or 5), priority is immediately given to item 1, since now the additional space-elastic demand caused by an increased number of facings (\(k_1=5\)) can be served from the backroom, which is completely occupied with item 1 (\(y_1=2\)). This requires putting item 2 back in a crosswise orientation, since this allows a shelf quantity of two units that could not be kept in the backroom fully occupied by item 1 (\(y_2=0\)). At \(B=6\) (or 7), item 2’s display orientation can again be changed to lengthwise, which shifts inventory holding cost from the expensive showroom to the less expensive backroom (\(y_2=1\)). At \(B=8\) (or 9,10,11), the additional backroom space is used to lower \(f_2\) to \(f_2=2\) again, similarly to the three scenarios with \(S=6\). Finally, at \(B=12\), \(f_2\) can even decrease to \(f_2=1\). Obviously backroom space is not enough to keep the lengthwise orientation. Item 2 is placed crosswise, and a stock of \(g_2=2\) units must be kept on the showroom shelf.
The example shows that items with a high space elasticity should clearly be given priority in shelf-space assignment. Furthermore, the trade-offs between availability of showroom and backroom space, facings, order frequencies and display orientations are illustrated. Even with this stylized example, it generally becomes evident that the availability of backroom space impacts optimal facings, display orientations and order frequencies. We can conclude, if retailers have the opportunity to use backrooms for intermediate storage, they should leverage them, because backroom space allows for more flexibility in planning showroom shelf-space and in-store replenishment processes.
Extended analysis To underline the impact of backroom space B on profit and solution structures, and to generalize the findings above, we analyzed additional randomly generated data sets. Each set contains \(N=50\) items. To focus on the main effects, we ignore the display orientation and set \(l_i=w_i=1\). We set \(F=6\) and \(K=15\) and assume a showroom shelf space of \(S=200\) and in the basic scenario a backroom space of \(B=100\), which is varied below. For each analysis, we report the average of 100 randomly generated data sets.
Figure 6 shows the impact of changing backroom size on financial performance (i.e., total profits, total gross margins, total direct and backroom replenishment cost). As seen above in the 2-item example, an increase in backroom space results in increased total profits. This is due to an increase in demand as well as lower total direct replenishment costs, i.e., direct replenishment and showroom inventory holding cost. By providing more flexibility in the form of additional backroom space B, more space for beneficial items can be reserved on the showroom shelf space to generate more sales (resulting in higher total gross margins) and the backroom can be more extensively used to refill showroom shelves if this is cost-beneficial. On the other hand, this induces an increase in total backroom replenishment costs, i.e., backroom replenishment and backroom inventory holding cost, which is shown in the right-hand graph.
Figure 7 provides the changes in the solution structure: Up to 80% of the items are given a different number of facings k if backroom space B decreases. An increase in backroom space B analogously induces changes in shelf-space assignment, but the upper limit of \(K=15\) limits the magnitude of this effect: Up to 20% of the items are given a different number of facings k if backroom space B is doubled.
In terms of order frequencies f, similar observations apply. Up to 54% of the items have a change in order frequencies f if backroom space B changes. The right-hand graph shows that the average number of orders per week decreases, as more backroom space B becomes available. A larger backroom space B allows for decreased order frequencies f, because backroom space can be used to store items and then replenish shelves from there. Note that as soon as backroom space B becomes available, order frequencies f increase slightly at first before gradually decreasing. This is because less profitable and less space-elastic items can be moved to the backroom to free up additional space in the showroom. This space is used to allocate more facings to high-profit and high space-elasticity items, which generates additional demand. Because showroom shelf S is scarce, this demand increase enforces an increase in order frequencies. These effects decrease in magnitude the more backroom space B becomes available, because it can be used to fulfill the additional demand without further increases in order frequencies f.
5.2.4 Impact of replenishment and inventory costs on profit and solution structure
To analyze the impact of replenishment and inventory costs, we conducted an “a posteriori” analysis. We considered a retailer who neglects the relevant cost elements and just accounts for item demand and margins, i.e., \(\mathrm{VC}_i^\mathrm{{DIR}}=\mathrm{VC}_i^\mathrm{{BR}}=\mathrm{FC}_i^\mathrm{{DIR}}=\mathrm{FC}_i^\mathrm{{BR}}=h_i^\mathrm{{SR}} =h_i^\mathrm{{BR}} =0\). Based on these assumptions, we ran the CSRP*-model and “a posteriori” evaluated the solution structure (k, b and f) assuming the actual costs. We set \(S=800\) and vary the available backroom space from \(B \in [0-100]\). Item dimensions vary as follows: \(w_i \in [2,10]\) and \(l_i \in [5,15]\). For these different backroom sizes, Table 5 presents the advantage a retailer has when correctly accounting for relevant cost elements and considering facings, display orientation and order frequency optimization from an integrated perspective. Depending on the size of the available backroom, the profit is up to around 22% higher and solution structures change significantly: 70% of the items are given a different number of facings k, 77–87% a different order frequency f and 43–45% a different visible facing width b. Moreover, we see that backroom utilization is much higher if not all relevant costs are properly accounted for: Backroom utilization is 80–85% versus 45–63% if replenishment and inventory holding costs are properly incorporated.
5.2.5 Comparison to sales-proportional allocation rule
This section compares the results of the CSRPBS to those generated with a sales-proportional allocation rule (SPA). For the SPA, we again use an “a posteriori” evaluation. This benchmark is denoted as CSRP* like in Sect. 5.1. The SPA rule does not define the display orientation. To allow a good comparison we assume that \(l_i = w_i\) and no display orientation is required. We use the same \(N=50\) item data sets as before. In the SPA, the overall showroom space S is allocated to the items in proportion to their sales share, and order frequencies are fixed for all items. We analyze six scenarios, with \(f_i=1,\ldots ,6\). Table 6 shows the profit advantage of the optimization model (that optimizes for \(f_i\) and \(k_i\)); the magnitude increases as order frequencies rise. Furthermore, we see the significant differences in solution structures. Note that the profit potential here is lower than in the case study (Sect. 5.1) because the unit margins we assumed here are lower than the unit margins in the case.
5.2.6 Impact of assortment decisions
In this section, we show how assortment decisions can be incorporated into the CSRPBS. The resulting model is denoted as CASRPBS, whereas the additional “A” represents the assortment decision. So far, we have assumed that the assortment is determined in a previous planning step and that the retailer must assign all items of set \({\mathbb {N}}\) to the shelf, i.e., we did not allow zero facings \(k_i=0\). Including the assortment decision allows more flexibility for two reasons: (1) Solutions for situations with \(S<N\), can now be generated and items delisted. (2) Even if \(S\ge N\), it might be beneficial to delist specific items and use the shelf space for more beneficial items, e.g., items with a higher margin and/or space elasticity. The inclusion of assortment decisions requires an adaptation of the demand function (cf. Eq. 3) to account for additional demand arousing from out-of-assortment (OOA) situations (Smith and Agrawal 2000; Kök and Fisher 2007). OOA substitution expresses the customer’s willingness to buy an alternative item if the preferred item is not listed. By taking substitution into account, demand and the profit for an item i also depend on the availability of all other items \(j, j \ne i\). This extension increases the combinatorial complexity of our model, since the cross-product interdependencies result in a quadratic problem and the isolated precalculation of the item-specific profits as input to the MIP (see Sect. 4) does not capture these product interlinks anymore.
The model complexity Y of the CSRPBS with \(Y(N,S,F) = \left( {\begin{array}{c}S-1\\ N-1\end{array}}\right) \cdot F^N \cdot 2^N\) increases to \(Y(N,S,F) = \left( {\begin{array}{c}N+S-1\\ S\end{array}}\right) \cdot F^N \cdot 2^N\) for the CASRPBS when including the assortment decision. Due to the increased complexity and product interlinks, we need a heuristic to iteratively determine the total demand \(D_i\) for an item considering the availability of other items. We therefore first develop the extended solution approach for the CASRPBS and then complete numerical examples to show its efficiency and the impact of assortment decisions.
Extension of model and solution approach To incorporate assortment decisions, we differentiate the total set of items \({\mathbb {N}}\) into the set of listed items \({\mathbb {N}}^+\) and the set of delisted items \({\mathbb {N}}^-\), with \({\mathbb {N}}^+, {\mathbb {N}}^- \subseteq {\mathbb {N}}\), \({\mathbb {N}}^+ \cup {\mathbb {N}}^-={\mathbb {N}}\) and \({\mathbb {N}}^+ \cap {\mathbb {N}}^- = \oslash\). Equation (3) is extended in the following way to account for OOA substitution:
Total demand \(D_i\) for item i now not only consists of its own space-elastic demand (\(d_i \cdot (k_i\cdot b_i)^{\beta _i}\)) but also of the OOA demand caused by the delisting of other items (\(d_i^{OOA}(\bar{k})\)). We calculate this new demand component as follows:
Equation (13) shows that if an item j is delisted (\(j \in {\mathbb {N}}^-\) and therefore, \(k_j=0\)) a certain share (\(\gamma _{ji}\)) of its minimum demand (\(d_j\)) is substituted by item i. \(\gamma _{ji}\) is the substitution rate between items j and i. We allow one round of substitution as in Smith and Agrawal (2000), Kök and Fisher (2007) or Hübner et al. (2016), i.e., sales are lost if the substitute is not available either. In the following, we use the aggregated substitution rate \(\delta _i\) for an item, which corresponds to the likelihood that a delisted item gets substituted at all, and then assume that this aggregated rate is split equally among the remaining items, i.e., \(\gamma _{ji}=\frac{\delta _i}{{\mathbb {N}}^+-1}\), \(\forall j \ne i\) (cf. Kök et al. 2015). To account for assortment decisions and to thoroughly compute the associated demand function, we apply the following heuristic:
-
Step 1 Ignore OOA substitution by setting \(d_i^{OOA}(\bar{k})=0\) in Eq. (12) and solve the MIP as introduced in Eqs. (6) to (10), including \(k_i=0\) in \({\mathbb {K}}_i\), \(\forall i \in {\mathbb {N}}\)
-
Step 2 Update the demand for all items using Eqs. (12) and (13) with the values for \(k_i\) and \(b_i\) obtained in Step 1
-
Step 3 Solve the MIP with the updated demand from Step 2, again including \(k_i=0\); afterwards update demand using Eqs. (12) and (13)
-
Step 4 Repeat Step 3 until there is no more change in solutions
Heuristic performance We investigate the performance of the heuristic in terms of solution quality and runtime. To investigate the solution quality, we compare the profits generated by our heuristic to the profits generated by an optimal full enumeration (FE). The optimal results via FE can only be obtained for small problem instances due to the combinatorial complexity of the problem. Figure 8 shows that with an average solution quality of >99.5% the heuristic yields near-optimal profits for three different problem instances with \(N>S\) and data generated as described in Sect. 5.2.1.
Regarding runtime, Table 7 shows that the heuristic is efficient. While the FE is faster for small problem instances, it is not capable of generating results for instances with \(N>50\) within four hours, while the heuristic still solves instances with \(N=2000\) and \(S=1500\) in about two minutes. Note that in all numerical examples the number of delisted items always corresponds to the difference between N and S, which shows that it is always more profitable to list an item than delisting it and using the respective space for additional OOA demand of substitutes.
2-item example To show under which circumstances the delisting of items is beneficial and to investigate how the possibility of delisting items impacts facing and order decisions, we again use the 2-item example. Items 1 and 2 compete for a showroom space of \(S=2\), i.e., the retailer can split this space or allocate it exclusively to either one of the items. In the base scenario [1], both items are completely identical and we choose item parameters as in the 2-item example in Sect. 5.2.3.
To focus on the core effects, we again assume \(l_i=w_i=1\), \(i \in \{1,2\}\). From here, we investigate the extended problem if item 1 is highly space-elastic and item 2 is not (Scenario [2]), if item 1 has a high and item 2 a low margin ((\(r_i-c_i)/c_i\), Scenario [3]), and if replenishment cost factors \(\mathrm {Cost}_i\), i.e., \(VC_i^\mathrm{{DIR}}\), \(VC_i^\mathrm{{BR}}\), \(FC_i^\mathrm{{DIR}}\) and \(FC_i^\mathrm{{BR}}\) of item 2 are 2–100 times as high as for item 1 (Scenarios [4a–4d]).
Table 8 shows that the showroom space is allocated equally (\(k_1=k_2=1\)) if both items are identical (Sc. [1]). This only changes across the seven scenarios if either margins are extremely different ([3]), where then only the high-margin item is listed (\(k_1=2\) and \(k_2=0\)), or if replenishment costs are very (unrealistically) different (Sc. [4d]), where item 2 with the 100 times higher replenishment costs is again delisted. Significant differences in space elasticities do not result in the delisting of items (Sc. [2]). In summary, if space is sufficient to potentially list all items, assortment decisions are only likely to be impacted by the joint shelf-space and reorder planning if items significantly differ in their margin. The results from this 2-item example are intuitive, and the findings do apply to larger instances in the same way.
5.3 Summary of numerical results
The application of our model to real and randomly generated data sets reveal several important insights. First, we show in a case study that a retailer can increase profits by around 29% compared to the status quo if our model is applied in full. Simultaneously optimizing facings, display orientations and order frequencies is superior to the strictly shelf-space-based optimization of facings and display orientation, without optimizing order frequencies. This underlines the importance of an integrated perspective on shelf-space optimization and in-store replenishment processes. Second, our model can be efficiently solved by a MIP model. The results consistently are optimal and even generated within a minimum amount of time for large-scale instances. Third, if backroom space is available, retailers can make use of it by assigning more showroom space to highly profitable items and moving less profitable items to the backroom, from where they are replenished more frequently. In other words, the available backroom space gives more degrees of freedom to the retailer in terms of shelf-space optimization. Fourth, our model can be extended to account for assortment decisions, which is especially relevant for situations where the available shelf space is not sufficient to list all possible items of a category. Finally, the profit advantage a retailer has when taking an integrated approach to facing, display orientation and order frequency optimization can amount up to around 22% compared to a case where facings and display orientation are optimized without considering the related costs for in-store replenishment. This is because significantly different solution structures result in terms of facings, display orientation and order frequencies if replenishment processes are neglected.
6 Conclusion and outlook
In this paper, we presented a capacitated shelf-space optimization model that contributes to the existing literature by accounting for in-store replenishment and the availability of backroom space. The model maximizes retail profits while considering costs for direct and backroom replenishment, cost for inventory, limited showroom and backroom space as well as space-elastic demand. Retailers are provided with additional flexibility from the optimized display orientations of items. We have quantified the relevant in-store processes cost by means of a time and motion study for a German retailer. Our process descriptions serve to further define in greater detail the in-store processes and cost types identified in the existing literature. To solve the resulting non-linear problem, we developed a mixed-integer model. Even for large-scale problems, our model yields optimal results efficiently within a feasible amount of time. We applied our model to the retailer’s canned foods category and showed how profits can be increased significantly by applying our model. After the results were presented to the retailer, he decided to change his current approach to shelf-space and in-store replenishment planning by applying our model. Furthermore, we have shown that an integrated perspective on shelf-space and replenishment optimization is crucial for retailers, because backroom space and replenishment cost have a significant impact on retail profits and shelf-space planning. An integrated perspective for shelf planning is specifically important, since in practice shelf-space decisions are made by a central sales planning unit which oftentimes ignores the consequences of shelf planning on in-store operations. Our model will help retailers to develop this integrated perspective.
Limitations and future areas of research The limitations of our model point to a variety of future areas of research. We follow the general literature on shelf-space management and assume a deterministic and stationary demand for the tactical problem. Because of this, demand is always satisfied. Hence, one area is to further generalize the demand modeling. Some authors argue that demand volatility can be handled with exogenously determined safety stocks. The resulting shelf space for the safety stock needs to be deducted from the total shelf space and only the remaining space can be distributed. However, our modeling approach has the advantage of being flexible enough to determine safety stocks endogenously. As safety stocks protect against uncertainty in demand (demand volatility) and supply (lead time volatility), the impact of both decision variables (i.e., the impact of the number of facings on the demand and the impact of the order frequency on supply) need to be taken into account. Hence, for all precalculated combinations of the decisions variables, one can calculate the safety stocks accordingly within the model. Furthermore, our model and solution approach is a good starting point to account for further demand effects. Focusing on demand volatility would imply the development of a stochastic model for our decision problem with replenishment costs to account for demand variations (cf. e.g., Hübner and Schaal 2016a). In such cases, out-of-stock substitutions resulting from potentially insufficient shelf and backroom quantities for specific items would need to be taken into consideration as well (cf. e.g., Kök and Fisher 2007; Hübner et al. 2016). A stochastic model would need to balance the trade-offs between understock and overstock situations, which is specifically relevant in the case of perishable items. These additional costs can be included in the precalculations. Apart from stochastic demand, further demand effects, such as item positioning (cf. e.g., Lim et al. 2004; Bianchi-Aguiar et al. 2015b) or cross-space elasticities (cf. e.g., Corstjens and Doyle 1981), would be worth considering when the model is applied to certain categories with these demand effects.
Our model concentrates on the cost associated with direct and indirect replenishment of shelves. Future models could incorporate further decisions and associated cost, such as upstream supply chain decisions and the cost of deliveries from warehouses to stores (cf. Sternbeck and Kuhn 2014; Holzapfel et al. 2016). Moreover, retail managers typically try to keep shelves as filled as possible, since empty space is generally believed to have a negative impact on sales (cf. Baron et al. 2011). This may result in differentiated refill costs. We have shown that our solution approach is capable of solving a problem with up to 2000 items within less than a minute. Although shelf-space and reordering decisions are typically made for each category separately, our model could be extended for store-wide shelf-space optimization across all categories, where common order patterns for different categories would also be considered.
Finally, the investigation of multi-store environments can be considered. A corresponding model would support retailers in deciding whether planograms should be more standardized or adjusted to store-specific needs. Such a model would need to balance the trade-off between store-specific demand fulfillment and the efficiency of upstream logistics processes.
Our optimization model takes the perspective of a retailer who wants to optimize category profit. In contrast, a manufacturer follows the objective of brand profit optimization, which raises the topic of “category captainship” (cf e.g., Kurtulus and Toktay 2011; Martínez-de Albéniz and Roels 2011). A comprehensive study will need to address all the relevant subjects of negotiation between manufacturers and retailers, such as assortment, prices and shelf space.
The model and solution approach proposed within this paper will be a good starting point to address the open areas of research mentioned above.
References
Barnes, R.M. 1949. Motion and time study. New York: Wiley.
Baron, O., O. Berman, and D. Perry. 2011. Shelf space management when demand depends on the inventory level. Production and Operations Management 20 (5): 714–726.
Bianchi-Aguiar, T., M.A. Carravilla, and J.F. Oliveira. 2015a. Replicating shelf space allocation solutions across retail stores. Working paper University Porto.
Bianchi-Aguiar, T., A. Hübner, M.A. Carravilla, and J.F. Oliveira. 2016. Retail shelf space planning problems: A comprehensive review and classification framework. Working paper University Porto.
Bianchi-Aguiar, T., E. Silva, L. Guimarães, M.A. Carravilla, and J.F. Oliveira. 2015b. Allocating products on shelves under merchandising rules: Multi-level product families with display directions. Working paper University Porto.
Borin, N., P. Farris, and J. Freeland. 1994. A model for determining retail product category assortment and shelf space allocation. Decision Sciences 25 (3): 359–384.
Broekmeulen, R., K. van Donselaar, J. Fransoo, and T. van Woensel. 2006. The opportunity of excess shelf space in grocery retail store. Operations Research 49: 710–719.
Chandon, P., W.J. Hutchinson, E.T. Bradlow, and S.H. Young. 2009. Does in-store marketing work? Effects of the number and position of shelf facings on brand attention and evaluation at the point of purchase. Journal of Marketing 73 (November): 1–17.
Corstjens, M., and P. Doyle. 1981. A model for optimizing retail space allocations. Management Science 27 (7): 822–833.
Cox, K. 1964. The responsiveness of food sales to shelf space changes in supermarkets. Journal of Marketing Research 1 (2): 63–67.
Curşeu, A., T. van Woensel, J. Fransoo, K. van Donselaar, and R. Broekmeulen. 2009. Modelling handling operations in grocery retail stores: An empirical analysis. Journal of the Operational Research Society 60 (2): 200–214.
Curhan, R.C. 1972. The relationship between shelf space and unit sales in supermarkets. Journal of Marketing Research 9 (4): 406–412.
DeHoratius, N., and T. Zeynep. 2015. The role of execution in managing product availability. In Retail supply chain management. International series in operations research & management science, vol. 122, ed. N. Agrawal, and S.A. Smith, 53–77. New York: Springer.
Desmet, P., and V. Renaudin. 1998. Estimation of product category sales responsiveness to allocated shelf space. International Journal of Research in Marketing 15 (5): 443–457.
Donselaar, KHv, V. Gaur, Tv Woensel, R.A. Broekmeulen, and J.C. Fransoo. 2010. Ordering behavior in retail stores and implications for automated replenishment. Management Science 56 (5): 766–784.
Drèze, X., S.J. Hoch, and M.E. Purk. 1994. Shelf management and space elasticity. Journal of Retailing 70 (4): 301–326.
EHI Retail Institute. 2014. Retail data 2014: Structure, key figures and profiles of international retailing.
Eisend, M. 2014. Shelf space elasticity: A meta-analysis. Journal of Retailing 90: 168–181.
Eroglu, C., B.D. Williams, and M.A. Waller. 2013. The backroom effect in retail operations. Production and Operations Management 22 (4): 915–923.
Fisher, M. 2009. Or forum-rocket science retailing: The 2006 Philip Mccord Morse Lecture. Operations Research 57 (3): 527–540.
Frank, R.E., and W.F. Massy. 1970. Shelf position and space effects on sales. Journal of Marketing Research 7 (1): 59–66.
Geismar, H.N., M. Dawande, B.P. Murthi, and C. Sriskandarajah. 2015. Maximizing revenue through two-dimensional shelf-space allocation. Production and Operations Management 24: 1148–1163.
Gutgeld, Y., S. Sauer, and T. Wachinger. 2009. Growth-but how? Akzente 3 (3): 14–19.
Hansen, J.M., S. Raut, and S. Swami. 2010. Retail shelf allocation: A comparative analysis of heuristic and meta-heuristic approaches. Journal of Retailing 86 (1): 94–105.
Hansen, P., and H. Heinsbroek. 1979. Product selection and space allocation in supermarkets. European Journal of Operational Research 3 (6): 474–484.
Hariga, M.A., and A. Al-Ahmari. 2013. An integrated retail space allocation and lot sizing models under vendor managed inventory and consignment stock arrangements. Computers and Industrial Engineering 64 (1): 45–55.
Hariga, M.A., A. Al-Ahmari, and A.-R.A. Mohamed. 2007. A joint optimisation model for inventory replenishment, product assortment, shelf space and display area allocation decisions. European Journal of Operational Research 181 (1): 239–251.
Holzapfel, A., A. Hübner, H. Kuhn, and M.G. Sternbeck. 2016. Delivery pattern and transportation planning in grocery retailing. European Journal of Operational Research 252 (1): 54–68.
Hübner, A.H., and H. Kuhn. 2011. Shelf and inventory management with space-elastic demand. In Operations research proceedings 2010, ed. B. Hu, K. Morasch, M. Siegle, and S. Pickl, 405–410. Berlin: Springer.
Hübner, A.H., and H. Kuhn. 2012. Retail category management: A state-of-the-art review of quantitative research and software applications in assortment and shelf space management. Omega 40 (2): 199–209.
Hübner, A., and K. Schaal. 2016. When does cross-space elasticity matter in shelf-space planning? A decision analytics approach. Working Paper KU Eichstätt-Ingolstadt.
Hübner, A., and K. Schaal. 2017. A shelf-space optimization model when demand is stochastic and space-elastic. Omega 68: 139–154.
Hübner, A.H., H. Kuhn, and M.G. Sternbeck. 2013. Demand and supply chain planning in grocery retail: An operations planning framework. International Journal of Retail & Distribution Management 41 (7): 512–530.
Hübner, A., H. Kuhn, and S. Kühn. 2016. An efficient algorithm for capacitated assortment planning with stochastic demand and substitution. European Journal of Operational Research 250 (2): 505–520.
Hwang, H., B. Choi, and G. Lee. 2009. A genetic algorithm approach to an integrated problem of shelf space design and item allocation. Computers and Industrial Engineering 56 (3): 809–820.
Hwang, H., B. Choi, and M.-J. Lee. 2005. A model for shelf space allocation and inventory control considering location and inventory level effects on demand. International Journal of Production Economics 97 (2): 185–195.
Irion, J., J.-C. Lu, F. Al-Khayyal, and Y.-C. Tsao. 2012. A piecewise linearization framework for retail shelf space management models. European Journal of Operational Research 222 (1): 122–136.
Kellerer, H., U. Pferschy, and D. Pisinger. 2004. Knapsack problems. Berlin: Springer.
Kök, G., M.L. Fisher, and R. Vaidyanathan. 2015. Assortment planning: Review of literature and industry practice. In Retail supply chain management. International series in operations research & management science, vol. 223, ed. N. Agrawal, and S.A. Smith, 175–236. New York: Springer.
Kök, G.A., and M.L. Fisher. 2007. Demand estimation and assortment optimization under substitution: Methodology and application. Operations Research 55 (6): 1001–1021.
Kotzab, H., G. Reiner, and C. Teller. 2007. Beschreibung, Analyse und Bewertung von Instore-Logistikprozessen. Zeitschrift für Betriebswirtschaft 77 (11): 1135–1158.
Kotzab, H., S. Seuring, M. Müller, and G. Reiner (eds.). 2005. Research methodologies in supply chain management. Heidelberg: Springer.
Kotzab, H., and C. Teller. 2005. Development and empirical test of a grocery retail instore logistics model. British Food Journal 107 (8): 594–605.
Kuhn, H., and M.G. Sternbeck. 2013. Integrative retail logistics: An exploratory study. Operations Management Research 6 (1–2): 2–18.
Kurtulus, M., and B.L. Toktay. 2011. Category captainship vs. retailer category management and limited retail shelf space. Production and Operations Management 20 (1): 47–56.
Lim, A., B. Rodrigues, and X. Zhang. 2004. Metaheuristics with local search techniques for retail shelf-space optimization. Management Science 50 (1): 117–131.
Martínez-de Albéniz, V., and G. Roels. 2011. Competing for shelf space. Production and Operations Management 20 (1): 32–46.
Maynard, H.B., G.J. Stegemerten, and J.L. Schwab. 1948. Methods-time measurement. New York: McGraw-Hill.
Murray, C.C., D. Talukdar, and A. Gosavi. 2010. Joint optimization of product price, display orientation and shelf-space allocation in retail category management: Special issue: Modeling retail phenomena. Journal of Retailing 86 (2): 125–136.
Niebel, B.W. 1988. Motion and time study. Homewood: Richard D. Irwin.
Pires, M., J. Pratasy, J. Lizy, and P. Amorim. 2016. A framework for designing backroom areas in grocery stores. International Journal of Retailing and Distritubtion Management (forthcoming)
Pisinger, D. 2005. Where are the hard knapsack problems? Computers & Operations Research 32 (9): 2271–2284.
Ramaseshan, B., N.R. Achuthan, and R. Collinson. 2008. Decision support tool for retail shelf space optimization. International Journal of Information Technology & Decision Making 7 (3): 547–565.
Ramaseshan, B., N.R. Achuthan, and R. Collinson. 2009. A retail category management model integrating shelf space and inventory levels. Asia-Pacific Journal of Operational Research 26 (4): 457–478.
Reiner, G., C. Teller, and H. Kotzab. 2013. Analyzing the efficient execution on in-store logistics processes in grocery retailing—The case of dairy products. Production and Operations Management 22 (4): 924–939.
Russell, Ra, and T.L. Urban. 2010. The location and allocation of products and product families on retail shelves. Annals of Operations Research 179: 131–147.
Seuring, P.D.S., P.D.M. Müller, M. Westhaus, and R. Morana. 2005. Conducting a literature review—The example of sustainability in supply chains. Research methodologies in supply chain management. Physica-Verlag: HD, 91–106.
Smith, S.A., and N. Agrawal. 2000. Management of multi-item retail inventory systems with demand substitution. Operations Research 48 (1): 50–64.
Sternbeck, M.G., and H. Kuhn. 2014. An integrative approach to determine store delivery patterns in grocery retailing. Transportation Research Part E: Logistics and Transportation Review 70: 205–224.
Urban, T.L. 1998. An inventory-theoretic approach to product assortment and shelf-space allocation. Journal of Retailing 74 (1): 15–35.
Yang, M.-H., and W.-C. Chen. 1999. A study on shelf space allocation and management. International Journal of Production Economics 60–61 (4): 309–317.
Zelst, S, K. van Donselaar, T. van Woensel, R. Broekmeulen, and J. Fransoo. 2009. Logistics drivers for shelf stacking in grocery retail stores: Potential for efficiency improvement. International Journal of Production Economics 121 (2): 620–632.
Zufryden, F.S. 1986. A dynamic programming approach for product selection and supermarket shelf-space allocation. Journal of the Operational Research Society 37 (4): 413–422.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hübner, A., Schaal, K. Effect of replenishment and backroom on retail shelf-space planning. Bus Res 10, 123–156 (2017). https://doi.org/10.1007/s40685-016-0043-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40685-016-0043-6