Abstract
Business process management (BPM) is an acknowledged source of corporate performance. A well-established element of the BPM toolbox by which organizations intend to tune the performance of their processes is business process standardization (BPS). So far, research on BPS has predominantly taken a descriptive perspective, analyzing how BPS affects different dimensions of process performance (e.g., cost, quality, time, flexibility). Only very few studies capitalize on the mature body of descriptive BPS knowledge to assist in determining an appropriate BPS level for an organization’s processes. Moreover, these studies do not resolve the BPS trade-off, i.e., the partly conflicting effects of BPS on process performance. To address this research problem, we propose a decision model that provides guidance on how to determine an economically appropriate BPS level for a business process. We thereby adopt the design science research (DSR) paradigm and draw from the body of knowledge on BPS as well as value-based management. We evaluated the decision model by discussing its design specification against theory-backed design objectives. We also validated the model’s applicability and usefulness in a real-world case where we applied the decision model and a prototypical implementation to the coverage switching processes of an insurance broker pool company. Finally, we challenged the decision model against the accepted evaluation criteria from the DSR literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Business process standardization (BPS), a well-established element of the business process management (BPM) toolbox, is driven by the ongoing pressure to tune process performance (Münstermann et al. 2010; Ramakumar and Cooper 2004). In an example of the large potential of BPS, IBM is reported to have saved more than $9 billion and to have increased both the quality and on-time delivery rates of its processes by 75 % (Hammer and Stanton 1999). Such success stories are leading an increasing number of organizations to consider standardizing their processes, driving the need for well-founded guidance on BPS decisions (Ludwig et al. 2011; Manrodt and Vitasek 2004; Rosenkranz et al. 2010). This industry need is consistent with the scholarly perspective that considers BPS an important yet under-researched topic (Münstermann and Weitzel 2008; Ungan 2006; Venkatesh 2006; von Stetten et al. 2008).
Providing guidance on BPS decisions requires that the fundamental BPS trade-off be addressed (Manrodt and Vitasek 2004). The BPS trade-off results from the interplay of two conflicting effects. On the one hand, BPS positively influences different dimensions of process performance, such as time, cost, and quality (Münstermann et al. 2010). On the other, BPS causes investments and may reduce an organization’s ability to meet customer needs (De Vries et al. 2006; Hammer and Stanton 1999). While BPS has been intensely studied from an information systems (IS), operations management, organizational design, and BPM perspective, the BPS trade-off is yet to be fully analyzed (Münstermann and Weitzel 2008; Venkatesh and Bala 2012). There is a mature body of descriptive knowledge on how BPS affects different dimensions of process performance and on the partially conflicting nature of these BPS effects (Münstermann et al. 2010; Rosenkranz et al. 2010; Schäfermeyer et al. 2010). However, only very few studies leverage this body of descriptive knowledge to support organizations in determining an appropriate BPS level for their processes (Münstermann and Weitzel 2008; Romero et al. 2015).
From an operations management perspective, Lee and Tang (1997), for instance, proposed a decision model for evaluating BPS by standardizing production processes until an output-specific treatment is unavoidable. Thereby, BPS creates value as it decreases the inventory buffers between process steps and enables organizations to balance demand uncertainties. Building on Lee and Tang (1997), the operations literature further analyzes the benefits that result from this postponement strategy. Aviv and Federguen (2001) specify the effects introduced by Lee and Tang (1997) for unknown demand distributions and correlations. Ma et al. (2002) analyze the postponement strategy in the context of a multi-stage assembly system, highlighting the role of lead-time dynamics for the value of standardization benefits. Nevertheless, the postponement strategy neglects essential parts of the BPS trade-off, such as improvements in quality and the reduced ability to meet customer needs. As another example, Letmathe et al. (2013) exploit a similar idea more generally by analyzing the economic effects that result from demand-related, intra-process and inter-process correlations on combined sales and manufacturing systems. Transferred to the BPS context, one can argue that BPS increases inter-process correlations and reduces diversification effects from higher process variation. From an IS/BPM perspective, Hammer and Stanton (1999) provide a rule of thumb for determining the optimal level of BPS, advising organizations to standardize their processes as far as possible without interfering with their ability to meet customer needs. They thus recommend standardizing a process up to the point where the BPS trade-off begins. Zellner and Laumann (2013), in contrast, integrate several BPS effects into a multi-dimensional decision model. However, they treat all BPS effects as equally strong, neglect relevant process characteristics, and abstract from the partially conflicting nature of the BPS effects. Summing up, despite the mature body of descriptive knowledge on BPS, there is a lack of prescriptive knowledge on how organizations can determine to what level they should standardize their processes, considering the partially conflicting effects of BPS on process performance. Therefore, we investigate the following research question: How can organizations determine the appropriate BPS level for their business processes, considering the effects of BPS on process performance?
To address this research problem, we developed a decision model that helps organizations determine the economically appropriate BPS level of a distinct business process. Like in every decision model, we had to make assumptions to transfer the real-world problem of BPS into a solvable, artificial representation. As we require deep knowledge of the users’ process behavior for parameterization, our decision model best fits mature processes that operate in a stable environment. As thinking about BPS is more relevant for mature organizations that have globally distributed processes and engage in operational excellence, our decision model can serve the most relevant fields of applications. Basically, the decision model is applicable to agile business processes in unstable environments as well. However, the results should be interpreted more consciously, e.g., via additional robustness analyses.
When constructing the decision model, we adopted the design science research (DSR) paradigm and drew from the literature on BPS as well as on value-based management (VBM) as justificatory knowledge (Gregor and Hevner 2013). This study design is sensible for several reasons: first, decision models are valid DSR artifacts (March and Smith 1995); second, there exists a mature body of descriptive knowledge on how BPS affects process performance, which can be used for prescriptive decision-making purposes (Münstermann et al. 2010; Romero et al. 2015); third, value orientation is a predominant paradigm of corporate management and, during the last years, has gained importance in process decision-making (Buhl et al. 2011; vom Brocke and Sonnenberg 2015). In process decision-making, value orientation is primarily used to integrate the effects of process decisions on process performance and to resolve conflicts (trade-offs) among these effects if necessary (Bolsinger 2015; Linhart et al. 2015; vom Brocke et al. 2010). By integrating the effects of BPS on process performance in terms of a BPS endeavor’s value contribution, value orientation also allows for bridging the strategic and the operational BPS layer (Romero et al. 2015). Finally, due to its focus on maximizing an organization’s long-term firm value, value orientation helps address the recommendation to focus on business value-driven BPS decisions (Kauffman and Tsai 2010).
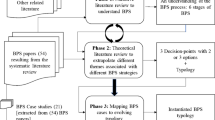
Following the DSR methodology as per Peffers et al. (2008), this study covers the identification of and motivation for the research problem, objectives of a solution, design and development, and evaluation. In Sect. 2, we outline justificatory knowledge related to BPS and VBM, and derive design objectives (objectives of a solution). In Sect. 3, we elaborate on the research method and evaluation strategy. In Sect. 4, we introduce the decision model’s design specification (design and development). Section 5 reports on our evaluation activities (evaluation). We conclude in Sect. 6 by pointing to limitations and future research possibilities.
2 Theoretical background and design objectives
2.1 Foundations of business process standardization
To define BPS, we first look at standardization in general. In this, we follow David (1987) who identifies compatibility and interface standardization, minimum quality standardization, and variety reduction standardization by categorizing standardization according to the economic problems it solves. Compatibility and interface standardization introduces technology standards to facilitate communication and ensure product compatibility. The economic phenomenon associated with this type of standardization is network externalities, the theory of which posits that the value of standardization depends on the number of adopters (Gowrisankaran and Stavins 2002). Interface standardization requires information technology (IT) and process standardization (Venkatesh and Bala 2012). Minimum quality standardization sets reference points for the quality of goods and services to reduce customers’ uncertainty. It prevents Akerlof’s (1970) markets for lemons where only poor-quality products are traded, which can occur if customers cannot properly evaluate the quality of goods and services. Variety reduction standardization reduces planned or unintentional variation to exploit economies of scale (Swann 2000).
In the literature, BPS is predominantly conceptualized as the unification or homogenization of process variants (Beimborn et al. 2009), acknowledging local variation in processes as inevitable and necessary (Tregear 2015). This conceptualization combines the idea of variety reduction standardization—sometimes interpreted strictly in an all-or-nothing sense—with the definition of processes. For our purposes, processes are structured sets of activities designed to create valuable output (Davenport 1993). They split into business, support, and management processes (Armistead et al. 1999). Business processes create value for external customers, support processes ensure that business processes continue to function, and management processes help plan, monitor, and control other processes (Dumas et al. 2013; Harmon 2010). Table 1 shows the selected BPS definitions together with the associated type of standardization.
From an operational perspective, BPS entails the alignment of process variants against a master process, which is also referred to as archetype, standard, or base process (Münstermann et al. 2010; Reichert et al. 2015; Tregear 2015). The master process can be set equal to an existing process variant, a newly designed target process that comprises selected tasks of existing processes, an external reference process, or an external best practice process (Beimborn et al. 2009). Further strategies for defining a master process are selecting the most frequently used variant, the process variant with the minimum average distance to other variants, and the superset or the intersection of all process variants (Reichert et al. 2015). In the three latter cases, the master process does not need to be a valid process variant that fits distinct process contexts, but may be an artificial process model that serves as foundation for deriving or configuring valid process variants. A process variant is an adjustment in the master process required by the peculiarities of a distinct process context, i.e., the environment or situation in which the variant is executed (Ghattas et al. 2014; Reichert et al. 2015). In practice, process variants are introduced deliberately or emerge from the dynamics of an organization’s technological and organizational environment (Beverungen 2014).
In the literature, there is no consensus whether the master process fits all or only a subset of the relevant process contexts. Some authors refer to the unification of process variants against the master process when defining BPS (Münstermann et al. 2010), an argumentation that implicitly makes the case for the master process being applicable to all contexts. Other authors highlight that the master process may not fit all process contexts due to local requirements such as legislative requirements, local market imperatives, or variations in the product/service offering (Reichert et al. 2015; Tregear 2015). This argumentation poses that the master process does not fit all, but at least several process contexts. In fact, aligning process variants against a master process would not make sense if the master process fitted very few process contexts only. We define the master process as a particular process variant that fits more than one and up to all process contexts. Context-specific process variants fit only one process context.
In case an organization adopts an all-or-nothing conceptualization of BPS for a distinct process, it makes the master process mandatory and eliminates context-specific process variants wherever possible, neglecting that process variants usually better fit the peculiarities of the contexts in which the process is executed (Hall and Johnson 2009; Hammer and Stanton 1999). In case an organization conceptualizes BPS from a more balanced variety reduction perspective, it deliberately decides about the appropriate process variant profile, reflecting which process contexts are served by the master process or by a context-specific variant. The more contexts served by the master process, the higher the level of BPS—and vice versa. Against this background, we formulate the following design objective:
-
(O. 1)
Business process standardization To determine the appropriate BPS level for a distinct process, it is necessary to account for process variants and process contexts. Moreover, process variants must be split into context-specific process variants and a standardized master process.
2.2 Effects of business process standardization on process performance
Process performance and the effects of redesign projects can be valued using the Devil’s Quadrangle, a multi-dimensional framework that encompasses time, cost, quality, and flexibility (Dumas et al. 2013). With BPS requiring processes to be redesigned when reducing the number of process variants or defining the master process, its effects can be assessed using the dimensions included in the Devil’s Quadrangle. The Devil’s Quadrangle earned its name from the fact that improving one dimension has a weakening effect on at least one other (Reijers and Liman Mansar 2005). It discloses the conflicts (trade-offs) among performance dimensions that need to be resolved during process redesign. Beyond affecting the performance dimensions included in the Devil’s Quadrangle, BPS mitigates outsourcing risk and enhances process governance (Wüllenweber et al. 2008). In line with our focus on the BPS trade-off, we focus on the dimensions of the Devil’s Quadrangle. Thus, we specify the following design objective:
-
(O. 2)
Process performance To determine the appropriate BPS level for a distinct process, process performance must be conceptualized as a multi-dimensional construct. It is also necessary to account for the partially conflicting effects of BPS on different dimensions of process performance.
Below, we compile those insights from the extant body of descriptive knowledge on BPS that indicate how BPS affects the dimensions of process performance included in the Devil’s Quadrangle. This compilation reveals that BPS features positive and negative effects, which together make up the BPS trade-off. BPS positively affects the performance dimensions quality, time, and costs, while negatively influencing flexibility. Table 2 provides an overview. Please note that “+” indicates improvements and not increased values. These effects are similar to that of the redesign pattern “triage”. Like BPS, this pattern addresses the balance of standardization and individualization, recommending the integration of two or more alternative tasks into one general task or the division of a general task into two or more alternative tasks, depending on the context (Reijers and Liman Mansar 2005).
2.2.1 Process flexibility
An often-discussed issue is the relationship between BPS and process flexibility. Process flexibility is the ability of a process to cope with contextual changes by adapting its structure and behavior in a goal-oriented manner (Wagner et al. 2011). From an operational perspective, process flexibility splits into functional and volume flexibility (Afflerbach et al. 2014). While volume flexibility enables increasing or decreasing the amount of the process output above or below the installed capacity (Goyal and Netessine 2011), functional flexibility enables delivering the output variety demanded by the organization’s customers (Anupindi et al. 2012). Volume flexibility relates to the establishment of scalable resources for process execution, whereas functional flexibility deals with variety at the process design level. In other words, functional flexibility relates to the creation of process designs and volume flexibility to the designs’ execution. Thus, functional flexibility is much closer to BPS as conceptualized from a variety reduction perspective, where process variants and the alignment of variants against a master process play a central role. This difference in closeness to BPS is corroborated by the fact that volume flexibility has been mainly researched from a capacity and a revenue management perspective, whereas functional flexibility has a rich tradition in BPM (Kumar and Narasipuram 2006; Reichert and Weber 2012). Moreover, one of the most popular means for implementing functional process flexibility is “flexibility by design”, a strategy that requires incorporating alternative process variants in a process design at build time and selecting the most appropriate variant at runtime (Schonenberg et al. 2008). This strategy shows the direct relationship between BPS and process flexibility, particularly functional process flexibility. This is why we henceforth focus on functional process flexibility.
Depending on the context, the relationship between BPS and process flexibility can be interpreted as conflicting or complementary (Afflerbach et al. 2014). On the one hand, BPS and flexibility appear to conflict, as BPS reduces the number of process variants and prohibits deviating from variants, whereas more process variants and degrees of freedom during execution help cope with a higher desired output variety (Pentland 2003). On the other hand, BPS and flexibility appear complementary when, for instance, processes are defined as modules with interfaces that enable assembling processes at runtime to meet the customers’ demands (Münstermann et al. 2009). In our case, where BPS is conceptualized from a variety reduction perspective, BPS and process flexibility conflict. If the reduction of process variants leads to a reduced output variety in the sense of output standardization, an organization loses the ability to assign that process variant to a context that fits it best (Ludwig et al. 2011). Instead, an organization must use the master process, which generally fits a distinct process context worse than the related context-specific process variant (Hall and Johnson 2009; Hammer and Stanton 1999). This negative effect on functional flexibility is supported by Davenport (2005) as well as by Hall and Johnson (2009), who identified output standardization as the main reason for BPS failure. They argue that individuality creates value for customers, which may not be available for highly standardized processes. Böhmann et al. (2005) share this line of argument. In the service domain, where customers are in many cases tightly integrated in an organization’s processes, the mere reduction of process variants may be enough to decrease the customers’ perceived individuality even if the output itself is not standardized.
2.2.2 Process costs
BPS reduces the costs of process execution. From a conceptual perspective, the positive effect of BPS on process costs is achieved through the elimination of errors (Wüllenweber et al. 2008), economies of scale (Sánchez-Rodríguez et al. 2006), and facilitated communication (Davenport 2005; Ramakumar and Cooper 2004). BPS fosters process experience and understanding, two effects that yield cost savings (Jayaram and Vickery 1998; Manrodt and Vitasek 2004). Moreover, standardized processes can be supported more easily by IT and, thus, allow for higher levels of automation and economies of scale (van Wessel et al. 2006). Another concept supporting the positive effect of BPS on process costs is the statistical theory of variation (Deming 1994). This theory suggests that process variation causes process outputs to deviate from their target specification and that the elimination of deviations leads to savings. As BPS reduces process variants, standardization implies less variation and lower costs. This relationship has also been validated empirically (Münstermann et al. 2010).
2.2.3 Process time
The consensus view is that BPS reduces process time, defined as the end-to-end time required to serve a customer or to create one unit of the process output (Münstermann et al. 2010). The positive effect of BPS on process time is supported both conceptually and empirically. First, standardized processes can be performed more easily than non-standardized processes and, thus, require less time (Lillrank and Liukko 2004). By reducing the number of process variants, BPS also enhances process knowledge and transparency, two effects that enable employees working faster (Wüllenweber et al. 2008). Second, BPS increases employees’ experience with executing the process tasks and handling material, making it easier to identify sources of delay and parallelization (Jayaram and Vickery 1998). Third, process documentations can significantly reduce process time (Siha and Saad 2008). Combined with the fact that the master process must be documented to be rolled out, BPS shortens the process time via the documentation of the master process (Ungan 2006). Beyond these conceptual underpinnings, two empirical studies corroborate the positive effect of BPS on process time. In a study of 57 top-tier suppliers to the North American automotive industry, Jayaram et al. (2000) found BPS to be the most influential enabler of time reductions. In addition, Münstermann et al. (2010) found in a cross-industry study that BPS had a significantly positive effect on the duration of human resource processes.
2.2.4 Process quality
BPS increases process quality, as it helps organizations establish best practice processes as standards that exhibit higher quality and smaller error probability than do context-specific process variants (Münstermann et al. 2010). As with process costs, variation is a main reason for bad quality (Lillrank 2003). The positive effect of BPS on process quality is also caused by the increased process experience that accompanies BPS (Jayaram and Vickery 1998; Lapré et al. 2000). This relationship has also been confirmed empirically, e.g., in the health-care industries (Fredendall et al. 2009; Münstermann et al. 2010).
2.3 Value-based management
The analysis of how BPS affects the performance dimensions of the Devil’s Quadrangle revealed that the BPS trade-off has positive effects on process quality, time, and costs as well as negative effects on process flexibility. With the Devil’s Quadrangle only proposing a heuristic means to deal with trade-offs (Reijers and Liman Mansar 2005), we adopt value-based BPM to resolve the BPS trade-off (Buhl et al. 2011). Thereby, value-based BPM applies the principles of VBM to process decision-making.
In economic research and practice, VBM has prevailed as the guiding paradigm of corporate management (Buhl et al. 2011). VBM aims at sustainably increasing an organization’s firm value from a long-term perspective (Ittner and Larcker 2001; Koller et al. 2010). It extends the shareholder value approach that goes back to Rappaport (1986) and was advanced by Copeland et al. (1994) as well as by Stewart and Stern (1991). Due to its long-term perspective, VBM also complies with the more general stakeholder value approach (Danielson et al. 2008). For VBM to be fully realized, all corporate activities on all hierarchy levels must be aligned with the objective of maximizing the firm value. To do so, organizations must not only be able to quantify the firm value on the aggregate level, but also the value contribution of individual assets and decisions considering their cash flow effects, the time value of money, and the decision-makers’ risk attitude (Buhl et al. 2011). In line with investment and decision theory, the valuation functions that are typically used for determining an organization’s firm value or the value contribution of individual assets or decisions depend on the decision situation and the decision-makers’ risk attitude (Buhl et al. 2011; Damodaran 2012). In case of certainty, decisions can be made based on the net present value (NPV) of future cash flows using a risk-free interest rate for discounting. Under risk and for risk-neutral decision-makers, decisions can be made based on the expected NPV again using the risk-free interest rate. In case of risk-averse decision-makers, alternatives can be valued via their risk-adjusted expected NPV, which may among others be calculated via the certainty equivalent method or a risk-adjusted interest rate (Copeland et al. 2005).
In the last years, VBM in general and the related valuation functions in particular have become increasingly central to process decision-making (vom Brocke and Sonnenberg 2015). Value-based BPM aims at increasing an organization’s long-term firm value by making process- and BPM-related decisions based on their value contribution (Buhl et al. 2011). As value-based BPM inherits VBM’s long-term orientation, it also accounts for non-monetary value dimensions such as ecological and social responsibilities, which are important to BPM, but hard to quantify (vom Brocke et al. 2011). Even more approaches adopt the principles of VBM to support process and BPM decisions in an economically well-founded manner (Bolsinger et al. 2015). Operating on the control flow level, some approaches help compare alternative process designs and/or propose recommendations for improvement (Bolsinger 2015; vom Brocke et al. 2010). Other approaches focus on process performance and process characteristics that capture how work is organized and structured (Afflerbach et al. 2014; Linhart et al. 2015). Still, very few approaches analyze BPM-related decisions such as the development of an organization’s BPM capability from a VBM perspective (Lehnert et al. 2014).
In the literature, numerous paradigms are related to value-based BPM. The most prominent examples are goal-oriented BPM (Neiger and Churilov 2004a), value-focused BPM (Neiger and Churilov 2004a; Rotaru et al. 2011), value-driven BPM (Franz et al. 2011), and value-oriented BPM (vom Brocke et al. 2010). For more details on these paradigms, please refer to Bolsinger (2015). Value-based BPM draws on the functions introduced above for comparing decision alternatives (Bolsinger 2015). In line with our intention to determine the economically appropriate BPS level for a distinct process, a problem that requires comparing many process variant profiles, we adopt value-based BPM. Thus, we define the following design objective:
-
(O. 3)
Value-based management To determine the appropriate BPS level for a distinct process, it is required to cater for cash flow effects and the time value of money. Moreover, the involved decision-makers’ risk attitude must be considered.
3 Research method and evaluation strategy
In the design and development phase of DSR, we combined normative analytical modeling and multi-criteria decision analysis as research methods to develop the decision model for determining the economically appropriate BPS level for a distinct business process. Normative analytical modeling captures the essentials of a decision problem in terms of closed-form mathematical representations to produce a prescriptive result (Meredith et al. 1989). Multi-criteria decision analysis assists with structuring decision problems, incorporating multiple criteria, resolving conflicts (trade-offs) among criteria, and appraising value judgments to support a deliberate choice among decision alternatives (Keeney and Raiffa 1993). Thereby, relevant decision criteria must be quantified, decision variables and constraints must be defined, and non-trivial assumptions must be made transparent (Cohon 2004). The result of applying normative analytical modeling and multi-criteria decision analysis is formulated in terms of a decision model including decision variables and alternatives, constraints as well as assumptions. Combining both research methods is reasonable, as determining the economically appropriate BPS level requires valuing and comparing multiple process variant profiles. Addressing the BPS trade-off also requires conceptualizing performance as a multi-dimensional construct and resolving conflicts among performance dimensions. Finally, determining an appropriate BPS level is so complex that decision alternatives, i.e., process variant profiles, can neither be valued nor compared manually. Thus, a mathematical design specification serves as direct input for implementing a software prototype.
When developing the decision model, we followed Cohon’s (2004) recommendations: We first introduce the decision model’s general setting and define the underlying demand model (Sects. 4.1 and 4.2). We then model the effects of BPS on each performance dimension separately, while highlighting relevant assumptions (Sects. 4.3 to 4.5). This complies with the literature that requires proposing mathematical functions for each decision criterion. Finally, we present the decision model’s objective function for determining the value contribution of process variant profiles (Sect. 4.6). This objective function operationalizes the valuation functions used in VBM and integrates the so far isolated effects of BPS on individual performance dimensions. Complying with the principles of VBM, the objective function accounts for the cash flow effects of a BPS endeavor, the time value of money, and the involved decision-makers’ risk attitude.
To demonstrate and evaluate the decision model, we followed Sonnenberg and vom Brocke’s (2012) framework of evaluation activities in DSR. This framework combines ex-ante/ex-post and artificial/naturalistic evaluation (Pries-Heje et al. 2008; Venable et al. 2012). Ex-ante evaluation is conducted before, ex-post evaluation after an artifact’s instantiation, e.g., a prototypical implementation. Naturalistic evaluation requires artifacts to be challenged in the real world by people, tasks, or systems. Making the case for a progressive design–evaluate–construct–evaluate pattern, Sonnenberg and vom Brocke’s (2012) framework comprises four evaluation activities (EVAL1 to EVAL4). EVAL1 aims at justifying the research topic as a meaningful DSR problem. It also requires deriving design objectives from justificatory knowledge to assess whether an artifact helps solve the research problem. We completed this activity in the introduction and the theoretical background section. Taking an ex-ante perspective, EVAL2 strives for validated design specifications. To validate the decision model’s design specification artificially, we discussed it against the design objectives at the end of Sect. 4, a method called feature comparison (Siau and Rossi 1998). From a naturalistic perspective, we validated the design specification by conducting expert interviews with senior executives (e.g., the Chief Executive Officer and Head of Marketing) from a German insurance broker pool company. This helped us check how organizational stakeholders assess the design specification’s understandability and real-world fidelity (Sonnenberg and vom Brocke 2012). EVAL3 is an artificial and ex-post evaluation, striving for validated artifact instantiations. We thus implemented the decision model in Microsoft Excel. We chose Excel as it is widely used for corporate decision-making and its functionality suffices to implement the decision model. Finally, EVAL4 requires validating the instantiation’s usefulness and applicability in naturalistic settings. We applied the Excel prototype to the coverage switching processes of the insurance broker pool company, whose executives we interviewed in the naturalistic part of EVAL2. Finally, based on the experience we gained throughout the real-world case, we discuss the decision model’s specification and prototypical implementation against accepted evaluation criteria (e.g., effectiveness and efficiency, impact on the artifact environment and user) that were proposed for EVAL4 purposes in the DSR literature (March and Smith 1995).
When presenting the demonstration and evaluation results, we focus on feature comparison to underpin the decision model’s contribution to answer the research question (EVAL2) and on the real-world case to assess the decision model’s usefulness and applicability (EVAL4). We briefly touch on the results of our naturalistic ex-ante evaluation (EVAL2) when discussing which of the decision model’s assumptions hold in the real-world case. When presenting the real-world case, we also focus on the challenges related to data collection. The results of EVAL2 are shown at the end of Sect. 4, whereas EVAL4 is shown in Sect. 5.
4 Design specification
4.1 General setting
The decision model’s unit of analysis is an individual, intra-organizational business process. The process is operated in multiple process contexts and aims at creating value for the organization’s customers. The organization already decided strategically to standardize the business process in focus. The organization is interested in which contexts should be served by the standardized master process and which by a context-specific process variant. Conceptualizing BPS from a variety reduction perspective, the decision model accounts for all possible process variant profiles, where the process variant profiles of complete standardization (i.e., all contexts are served by the master process) and complete individuality (i.e., all possible contexts are served by context-specific process variants) are two extremes out of many decision alternatives. To model the different process variant profiles as our decision alternatives, we use multiple variables \(x_{c} \in \left\{ {0;1} \right\}\), indicating whether a process context \(c\) is covered by the respective variant \(\left( {x_{c} = 1} \right)\) or the master process \(\left( {x_{c} = 0} \right)\). We further differentiate between process variant profiles prior to BPS (x c ) and after BPS \((x_{c}^{\text{std}} )\). With the decision model adopting the principles of VBM, we make the following assumption as a foundation for specifying the decision model’s objective function:
- (A1)
The organization adopts the principles of VBM. It judges process variant profiles according to their value contributions, measured in terms of the risk-adjusted expected NPV of the process cash flows.
Below, we first introduce the demand model underlying the decision model. After that, we model the effects of BPS on each dimension of the Devil’s Quadrangle separately and then integrate these effects into the decision model’s objective function, i.e., the risk-adjusted expected NPV of the process cash flows. An overview of all mathematical variables used in the decision model’s design specification can be found in ESM of Appendix F.
4.2 Demand model
As the process variant profile determines how the process demand is allocated to the master process and the context-specific process variants, we first model the periodic process demand. We assume:
- (A2)
The periodic process demand \(D_{t}\) follows a constant trend \(\mu_{D}\), where random deviations Z t from that trend occur in each period. The periodic deviations are normally distributed with an expected value of 0 and a standard deviation \(\sigma\). The periodic deviations are independent of each other.
Using a normally distributed demand with a constant trend is a widely adopted approach in economic (BPM) research (Buhl et al. 2011; Ryan 2004). The constant trend captures relative changes in the periodic process demand over time and allows for dealing with different planning horizons and economic situations. The normally distributed deviations represent the demand risk in terms of an unsystematic noise around the trend. The periodic process demand can be modeled based on the initial process demand \(D_{0}\), the constant trend, and the deviations as shown in Eq. (1):
4.3 Process flexibility
As argued in the literature, the main downside of BPS is that an accompanying output standardization may reduce the process’ functional flexibility. That is, the process may no longer be able to fully meet the output variety demanded by the organization’s customers (Hall and Johnson 2009). As process variants better fit the peculiarities of the process contexts than the master process does, BPS may reduce the demand for those process contexts served by the master process (Hammer and Stanton 1999). Thus, we make the following assumption:
- (A3)
The periodic process demand is allocated to process contexts according to constant demand weights \(w_{c} \in \left[ {0;1} \right]\), where \(\sum\nolimits_{c = 1}^{n} {w_{c} = 1}\) and n is the number of process contexts.
Prior to BPS, each process context has a specific periodic demand \(D_{c,t} = w_{c} D_{t}\). A distinct fraction of this demand \(f_{c} \in \left[ {0;1} \right]\) can only be tapped if the context is served by the related context-specific process variant. If, according to a distinct process variant profile, a process context is served by the respective process variant prior to BPS and the master process after BPS, its periodic demand relatively decreases by \(f_{c}\) to \(D_{t,c}^{\text{std}} = \left( {1 - f_{c} } \right)w_{c} D_{t}\). In the opposite situation, the periodic demand of the respective process context relatively increases by f c /(1 − f c ) to \(D_{t,c}^{\text{std}} = \left( {1 + f_{c} /\left( {1 - f_{c} } \right)} \right)w_{c} D_{t} = \left( {1 - f_{c} } \right)^{ - 1} w_{c} D_{t}\).
Based on the decision variables x c and \(x_{c}^{\text{std}}\), we can derive the periodic demand \(D_{t,v}^{\text{std}}\) for distinct process variants v and the periodic demand \(D_{t,0}^{\text{std}}\) that accumulates on the master process. We use the variant index v = 0 to refer to the master process and v > 0 to refer to context-specific process variants. The demand of a process context is allocated to the respective process variant if the process variant is offered after BPS (\(x_{c}^{\text{std}} = 1\)). The demand for all process contexts not served by the respective process variants after BPS is accumulated on the master process (\(x_{c}^{\text{std}} = 0\)). Equation (2) models the periodic demand and allocation effects of BPS via a power function that uses the difference between the decision variables before and after BPS as exponent:
The total periodic process demand after BPS \(D_{t}^{\text{std}}\) is determined by summing up the context-specific demands, as shown in Eq. (3). The demand factor \(\delta\) represents the total relative change in the process demand due to BPS. The BPS-adjusted demand weights \(w_{v}^{\text{std}} \in \left[ {0;1} \right]\) for a variant v are derived as the relation between the variant-specific periodic demand and the total periodic process demand, as shown in Eq. (4).
4.4 Process costs
We now integrate the positive effects of BPS on process costs (Münstermann et al. 2010). The experience curve, a widely accepted concept for modeling cost developments over time, assumes that the costs of creating an output unit decrease by a constant percentage each time the cumulated output doubles (Henderson 1979). The relationship between costs and cumulated output is often expressed by the power law function shown in Eq. (5):
Equation (5) calculates the costs of the next output unit if a distinct cumulated output or, in the absence of capacity restrictions, a cumulated demand \(D_{\text{cum}}\) has been reached. The process costs depend on the costs \(K\) for the first output unit, the cumulated demand as a measure for experience, and the elasticity of the process costs \(a \in {\mathbb{R}}^{ + }\) regarding the cumulated demand. As it is accepted that process cost elasticity is constant within industries, it can also be treated as constant across process variants (Henderson 1979). For repetitive processes in a steady state, the experience curve can be linearly approximated by its tangent at the flat end of the power function (ESM of Appendix A.1). Such a linear approximation implies almost no approximation errors. If the cumulated demand becomes large as it is the case for mature processes, the approximation error converges toward zero. For instance, if we assume a 90 % experience curve (a = 0.9), a cumulated demand up to the decision time of 1,000,000 U and a periodic demand of 1000 U, the relative approximation error is \(8.54 \times 10^{ - 7}\) for the first time period and \(8.46 \times 10^{ - 5}\) for the tenth period. Using such a linear approximation also fits our function for the periodic process demand from Eq. (1), as normal distributions are invariant against linear transformation. Using a linear approximation leads to the process costs function shown in Eq. (6).
In Eq. (6), the process costs C depend on the process costs at the decision point \(C_{0}\), on the cost reductions—which in turn depend on the elasticity of the process costs a adjusted by the cumulated demand \(D_{{0, {\text{cum}}}}\) up to the decision point—and on the cumulated demand \(D_{{t, {\text{cum}}}}^{\text{std}}\) that has been reached starting from the decision point. To justify the application of the linear approximation in our decision model, we assume:
- (A4)
The linear relationship between the cumulated demand and the process costs is constant across all process variants. The process costs remain constant within one period.
Based on the process costs, we can derive the periodic profit margin M t , as shown in Eq. (7) (ESM of Appendix A.2). We therefore determine the variant-specific periodic process costs by inserting the cumulated variant-specific demand into the linearly approximated experience curve from Eq. (6), including the master process as a particular variant. Subtracting this intermediate result from the sales price of the process output leads to the variant-specific periodic profit margins \(M_{v,t}\). Profit margins also depend on their value at the decision point \(M_{v,0}\) and increase linearly based on the adjusted elasticity of the process costs \(\widetilde{a}\). To calculate the total periodic profit margin, the variant-specific profit margins are aggregated based on the demand weights after BPS from Eq. (4). On this aggregated level, the total periodic profit margin can still be divided into profit margin M 0 at the decision point and the periodic increases resulting from experience curve effects,
As can be seen from Eq. (7), increases in the periodic profit margin depend not only on the cumulated demand that has been reached starting from the decision point and the elasticity of the process costs, but also on the cost-weighted Gini coefficient \(G_{\text{cost}}\) of the demand weights after BPS that result from a distinct process variant profile. In general, the Gini coefficient equals the sum of the squared frequencies or probabilities of a distribution and captures the concentration of a distribution (Gini 1921). In our case, the Gini coefficient G ∊ [0; 1] equals the sum of the squared variant-specific demand weights after BPS, as shown in Eq. (8). The cost-weighted Gini coefficient, as shown in Eq. (9), additionally considers variant-specific costs:
In our case, the Gini coefficient measures the concentration of the periodic process demand on process variants and the master process resulting from a process variant profile. The Gini coefficient therefore directly depends on the assignment of process contexts to the master process and context-specific process variants. The more process contexts are served by the master process, the more demand concentrates on it. For complete standardization, the process demand concentrates on the master process entirely, and the corresponding Gini coefficient is \(G = 1\) (if the master process fits all relevant process contexts). The more process demand concentrates on the master process, the stronger are the experience curve effects and, consequently, the more the process costs lower over time. Using the Gini coefficient is appealing because BPS can be easily measured as the concentration of the process demand on the master process. Moreover, each process variant profile leads to a distinct value of the (cost-weighted) Gini coefficient.
4.5 Process time and process quality
We integrate the positive effects of BPS on process time and quality in four steps. We first model the direct positive effects of BPS on time and quality. Second, we associate these quality and time effects with increased customer satisfaction (Anderson 1994). Third, we derive a positive effect of customer satisfaction on the retention rate, defined as the proportion of customers who buy the process output in the next period as well (Buchanan and Gillies 1990). Fourth, we integrate the retention rate into the constant trend of the process demand from Eq. (1). We provide more details on each step below.
In the first step, we model the direct effects of BPS on time and quality. We therefore determine the process variant profile—measured in terms of its Gini coefficient—as well as the corresponding time and quality values for two reference points to set up a linear extrapolation. Analogous to process costs, using the Gini coefficient is a reasonable way of modeling the BPS effects on time and quality, as BPS also reduces process time and improves quality due to the increased experience (Lapré et al. 2000; Jayaram and Vickery 1998). Building on previous empirical research that identified a linear relationship between BPS and the performance dimensions in focus, we assume (Münstermann et al. 2010):
- (A5)
The relationship between the time and quality effects of a process variant profile and the corresponding Gini coefficient is linear.
The first reference point to serve as input for the linear extrapolation can be determined using the Gini coefficient \(G\) prior to BPS as well as the corresponding quality \(Q\) and time \(T\) values. For the second reference point, we suggest using the process variant profile of complete standardization because the required values are comparatively easy to estimate. Therefore, we need the quality effect, defined as the relative increase in process quality \(s_{\text {Q}}\), and the time effect, defined as the relative reduction of process time \(s_{T}\), in case of complete standardization compared to the status prior to BPS. Both effects can be estimated by relying on the quality and time of an internal or external benchmark (e.g., a competitor, another business unit) that already uses standardized processes or by drawing from the results in Münstermann et al. (2010). In case of complete standardization, process quality and time equal \(Q \cdot \left( {1 + s_{\text{Q}} } \right)\) and \(T \cdot \left( {1 - s_{T} } \right)\), respectively, and the Gini coefficient equals \(G^{\text{std}} = 1\). On this foundation, we can capture the effect of various process variant profiles measured in terms of their Gini coefficient \(G^{\text{std}}\), as shown in Eqs. (10) and (11) (ESM of Appendix B.1):
In the second step, we derive the positive effects of process quality and time on customer satisfaction using Anderson’s (1994) model for customer satisfaction as a theoretical underpinning. The application of Anderson‘s (1994) work has two implications: first, process quality and time are integrated into our decision model based on empirically validated research; second, Anderson (1994) provides organizations with guidance on how to adjust his model to their needs. Both implications strengthen the applicability of our model, even if few case-specific data for customer satisfaction are available. Anderson (1994) determined and empirically validated multiple drivers of customer satisfaction \({\text{SAT}}\), each measured on a ten-point scale. One driver of customer satisfaction is the customers’ expectations \({\text{EXP}}\) of certain product characteristics (e.g., quality, time). Closely linked to the concept of expectations is the theory of confirmation/disconfirmation, according to which customers compare their experience of product characteristics with their expectations of the product (Yi 1990). In case of negative confirmation/disconfirmation \({\text{NCD}}\), the customers’ experiences fall short of their expectations and thus negatively affect satisfaction. The opposite holds true for positive confirmation/disconfirmation \({\text{PCD}}\). A third driver of customer satisfaction is quality \({Q}\). Equation (12) shows Anderson’s (1994) linear regression model for customer satisfaction:
Based on this analysis, we know that each process variant profile leads to relative changes in the process quality of \(s_{\text{Q}} \Delta G/\left( {1 - G} \right)\), a circumstance directly affecting customer satisfaction in Anderson’s (1994) model. We also know that the process time relatively decreases by \(s_{T} \Delta G/\left( {1 - G} \right)\). Assuming that the expectations for time and quality are uniformly distributed within the customer portfolio and considering that time and quality relatively improve by certain percentages, we can state that negative confirmation/disconfirmation relatively decreases and that positive confirmation/disconfirmation relatively increases by the sum of both percentages for a given process variant profile. The process quality affects customer satisfaction twofold—directly, via the respective variable in Anderson’s (1994) model, and indirectly, via positive and negative confirmation/disconfirmation. As the literature provides no guidance on whether or how BPS affects customers’ expectations, we assume that BPS does not influence customers’ expectation, meaning that this factor is constant across all process variant profiles. Therefore, we assume:
-
(A6)
The expectations for process time and quality are uniformly distributed within the organization’s customer portfolio. Moreover, BPS does not influence customers’ expectations, as modeled by Anderson (1994).
Given these intermediate results, we can determine how a process variant profile changes customer satisfaction relative to the status quo, as shown in Eq. (13) (ESM of Appendix B.2).
In the third step, we link the changes in customer satisfaction implied by the process variant profiles with the retention rate. To do so, we again refer to Anderson (1994), who also relates customer satisfaction to the retention rate using a linear regression model. The changes in the retention rate \(\Delta r\left( {G^{\text{std}} } \right)\) are shown in Eq. (14) (ESM of Appendix B.3):
In the fourth and last step, we integrate the retention rate into the constant trend of the periodic process demand. The retention rate can be interpreted as an integral part of the demand trend, as it influences how many customers buy the process output in subsequent periods. We therefore conclude that the demand trend \(\mu_{\text{D}}\) changes by \(\Delta r\left( {G^{\text{std}} } \right)/10\) for each process variant profile. The changes in the retention rate from Anderson’s (1994) model must be adjusted through a division by 10, as shown in Eq. (15):
4.6 Objective function
In line with the principles of VBM, the decision model uses the risk-adjusted expected NPV of the process cash flows caused by a process variant profile as objective function. We derive the objective function starting with the periodic process cash flows \({\text{CF}}_{t}\), which equal the product of the periodic process demand \(D_{t}\) and the periodic profit margin \(M_{t}\), as shown in Eq. (16):
The equations for the periodic process demand and the cumulated demand that has been reached starting from the decision point can be simplified using the law of geometric sequences (ESM of Appendix C.1). This simplification is justified because the constant trend of our demand model can be translated into a geometric progression—a sequence of numbers where each term after the first is derived by multiplying the previous term with a constant rate. As a result, the summation operator from the cumulated demand can be replaced by a constant growth factor. After the rewritten demand expression is inserted, the periodic process cash flows can be formulated as shown in Eq. (17). In the next step, we derive the expected value E(CF t ) of the periodic process cash flows, as shown in Eq. (18) (ESM of Appendix C.2). Admittedly, rewriting Eqs. (17) and (19) using the law of geometric sequences makes them look complex, but helps eliminate summation operations such that they can be implemented more easily in a software tool:
To obtain the risk-adjusted expected present value \({\text{PV}}\) as the central part of our objective function, the expected periodic process cash flows from Eq. (18) must be discounted using a risk-adjusted interest rate \(i\) and cumulated over the planning horizon \(\tau\). The same logic holds when the case of a risk-averse decision-maker is replaced by a risk-neutral decision-maker. In this case, the application of a risk-free interest rate becomes necessary. Again, the risk-adjusted PV can be rewritten using the law of geometric sequences (ESM of Appendix C.3). Finally, the risk-adjusted expected NPV of the process cash flows is determined by subtracting the investment outflows that go along with a distinct process variant profile from the risk-adjusted expected PV. Investment outflows occur whenever the process variant profile changes relative to the status quo. Technically, investment outflows have to be considered for a distinct process context if \(\left| {x_{c} - x_{c}^{\text{std}} } \right|\) equals 1, i.e., either the context-specific process variant is aligned against the master process or vice versa. The overall investment outflows \(I\) depend on the cash flows per process variant change \(I_{c}\) as shown in Eq. (19):
Based on the considerations so far, we can formulate the decision model’s objective function as shown in Eq. (20). According to the objective function, the decision model intends to identify the process variant profile that yields the highest risk-adjusted expected NPV of the process cash flows. The decision model allows for aligning context-specific process variants against the master process as well as for replacing the master process by context-specific variants, as expressed by the decision variables \(x_{c}^{\text{std}}\). The objective function caters to constraints via the constraint set \(R\), which captures restrictions regarding admissible values of \(x_{c}^{\text{std}}\). In line with our definition of the master process, we can thereby express that the master process is not applicable to distinct process contexts. The entire objective function together with all variables and constraints is shown in ESM of Appendix C.4:
To validate whether the decision model’s design specification suitably addresses the research question from an ex-ante artificial evaluation perspective, we discuss its characteristics against the design objectives derived from justificatory knowledge. Regarding design objective (O.1), the decision model allows for different process contexts and process variants. It also splits process variants into context-specific process variants and a standardized master process. Whereas context-specific process variants only fit a single context, the master process fits more than one and up to all process contexts. Conceptualizing BPS from a variety reduction perspective, the decision model considers all process variant profiles to determine the optimal BPS level, checking which contexts should be served by the respective variants or the standardized master process. As for design objective (O.2), the decision model treats process performance as a multi-dimensional construct. More precisely, it measures process performance in line with the performance dimensions included in the Devil’s Quadrangle. The partially conflicting effects of BPS on these dimensions make up the BPS trade-off. The decision model addresses the BPS trade-off by first modeling the effects of BPS on each performance dimensions separately and then integrating the partial models into an overarching objective function. On the one hand, the Gini coefficient as a measure for demand concentration and standardization incorporates learning effects in the dimensions time, quality, and costs. On the other, variant-specific cost and flexibility effects account for the peculiarities of process contexts. The objective function adopts the principles of VBM, reflecting the contribution of different process variant profiles to the organization’s long-term firm value. This makes the decision model comply with decision objective (O.3). To sum up, the decision model’s design specification addresses all design objectives. We therefore consider the design model as valid from an ex-ante artificial evaluation perspective. Accordingly, the decision model contributes to answering the research question. We revert to the mentioned limitations and ideas for future research in the conclusion.
5 Validating the decision model’s usefulness and applicability
To show that the decision model is useful and applicable, required data can be gathered and analyses can be conducted; we present a real-world case where we applied the decision model and its prototypical implementation to the coverage switching processes of a German insurance broker pool company. For reasons of confidentiality, we must not disclose the case company’s identity. We also had to anonymize and slightly modify all data. Below, we first introduce the case company (Sect. 5.1) as well as the case process together with process variants and the master process (Sect. 5.2). After that, we illustrate how we collected the required input data (Sect. 5.3). We then interpret the results of applying the decision model and conduct a robustness analysis where we check the results for sensitivity and challenge the master process pre-selected by the case company’s management (Sect. 5.4). In the end, we assess whether the decision model’s assumptions hold for the case at hand and challenge the decision model’s usefulness as well as applicability by discussing it against accepted evaluation criteria from the DSR literature (Sect. 5.5).
5.1 Case company
The broker pool supports insurance brokers’ daily business activities by taking over their back-office processes (e.g., the administration of insurance contracts). Pool members can then focus on their own business processes (e.g., selling insurance contracts, supporting their clients). In return, the pool claims a fraction of the brokers’ provisions.
Based on its business model, we can derive the objectives of the broker pool’s processes. First, the broker pool must consider insurance brokers as direct customers and the brokers’ customers as indirect customers. The broker pool’s processes must fit not only the brokers’ demands, but also those of the brokers’ customers. As a result, customer orientation and satisfaction are primary process objectives. Second, the broker pool’s success heavily depends on the cost of its processes, making cost efficiency another important objective. Third, the broker pool’s processes must be flexible to cope with different broker behaviors, making flexibility another objective. The broker pool thus faces the BPS trade-off.
Our contact points were the broker pool’s chief executive officer and the head of marketing, who is also in charge of the organization’s business processes. The case company’s management had already made the strategic decision to standardize the coverage switching process. It was interested to find out whether this decision should apply to all process contexts. From a strategic perspective, the management also decided not to close down their own call center. We considered this strategic decision in terms of an appropriate constraint set, i.e., at least one process context where the broker pool’s call center must be served by the respective process variant after BPS.
5.2 Case process
Before applying the decision model, the case company’s management presented the case process and the master process it had already pre-selected. This information enabled us to derive the process variants. The broker pool segments its activities according to insurance and provision types. It distinguishes life and property insurance as well as acquisition and follow-up provisions. The coverage switching process is located within the segment of follow-up provisions from property insurance contracts.
In general, insurance companies transfer provisions directly to the broker pool, which keeps the agreed fraction of the provisions and forwards the remainder to the brokers. To receive follow-up provisions, insurers must acknowledge the broker pool as the end customers’ advisor and transfer their insurance contracts. Otherwise, the customers’ contracts must be transferred to another insurance company through new contracts, after which, in contrast to the former insurer, the new insurer must grant follow-up provisions. For reasons of liability and customer satisfaction, new contracts must have the same risk coverage at a better premium than the former contract offered. Below, we analyze the coverage switching process that ensures follow-up provisions (Fig. 1).
Coverage switching processes adhere to the following blueprint. The process starts after an insurance broker, who is a member of the broker pool, acquires a new end customer. The process consists of three sub-processes: the registration process, the selection process, and the contract change process. In the registration process, the broker pool requests the end customer’s current insurer to transfer the customer’s contracts to the broker pool. If the current insurer accepts, the broker pool receives the follow-up provisions, and the end customer is successfully registered. If the insurer declines, the broker pool analyzes 5 months before the end customer’s current contract expires whether the customer can be served by a comparable or a standardized product. These activities are performed in the selection process. If a suitable substitute product can be identified, the broker pool buys this product in consultation with the end customer within the contract change process, and the broker pool receives the follow-up provisions. If no suitable substitute product can be identified or if the end customer rejects the new product, the broker pool does not receive follow-up provisions.
In the registration process, the broker submits relevant customer information (e.g., brokerage contract, current insurance policies, billings) in electronic or paper form. In case of electronic submission, the broker pool automatically adds the customer information to its customer relationship management (CRM) system. If customer information is submitted by paper, the broker pool manually adds the customer information to the CRM system. Next, the end customer’s current insurers are requested to transfer the current insurance contracts (Fig. 2).
In the selection process, the broker pool’s selection department analyzes whether the end customer’s current contracts can be transferred to another insurer by concluding new contracts. The selection process is executed separately for each contract, as each insurance type requires specific know-how and IT support. The broker pool has two options for a new insurance product. One option, the suitability of which is checked first, consists in choosing a standardized insurance product. The broker pool establishes strategic partnerships with insurers who agreed to cover the end customers’ risks with standardized insurance products at premiums that are 10 % smaller than those of the end customers’ current contracts. For the standardized product to be suitable, the current contracts must not contain any special conditions, such as the inclusion of e-bike insurance in a household policy. For end customers whose contracts cannot be transferred to the standardized product, the selection department analyzes the insurance market to identify comparable products with more favorable conditions (Fig. 3).
In the contract change process, the broker pool renews the end customer’s current insurance contract by buying a comparable or standardized product in consultation with the end customer. To do so, the broker pool informs the broker that the end customer’s contract can be switched to the new product identified in the selection process. The broker then has three options. The broker can signal a personal contract change, cancel the current contract, and buy the suggested product for the end customer. If the broker does not want to change the current contract personally, the broker must update the customer’s insurance-specific information (e.g., the customer’s residence) in the broker pool’s CRM system. If the broker does not react within 10 days, the broker pool’s call center directly contacts the end customer to update the information. If the required information is available, the new product is offered to the end customer. If the end customer declines the offer, no follow-up provisions are offered. If the end customer accepts, the broker pool receives the follow-up provisions (Fig. 4).
Based on the process models just introduced, we had to specify relevant process variants and the master process. To do so, we used the brokers’ preferences to define process contexts. In total, three execution options can be enabled or disabled, which leads to 23 = 8 process variants including the master process. First, brokers can submit end customer information in either electronic or paper form. Second and third, brokers can decide to update customer information and change the contract themselves or delegate these tasks to the broker pool’s call center. Table 4 (left-most column) provides an overview of the process variants including the master process. The status quo of the case company’s coverage switching process is the case of complete individuality, i.e., all execution options were available to the brokers. The master process has already been pre-selected by the case company’s management as one of the existing process variants. The management selected the process variant that allows for submitting customer information in electronic form only and where all tasks involving the brokers are assigned to the broker pool’s call center. The process model is shown in ESM of Appendix D. This is in line with the management’s strategic decision of not closing down the call center. We refer to the scenario where this process variant is used as master process as basic scenario. Although the selection of an appropriate master process is outside the decision model’s scope, we challenge this decision below, as the master process directly affects the optimal level of BPS in terms of the optimal process variant profile (Sect. 5.4.2).
5.3 Data collection
After the presentation of the case process, which was our first encounter with the case company’s management, we conducted a semi-structured interview with the chief executive officer and the head of marketing to collect the input data required for applying the decision model. Both senior executives were interviewed in a single interview by two researchers. One researcher went through the questionnaire and asked follow-up questions, while the other took notes. The interview took 2 h. To enable the interviewees to prepare for the interview, we shared the questionnaire in advance. In the same interview, we also collected the data required to challenge the basic scenario by trying two other process variants as master process (Sect. 5.4.2). The questionnaire and the collected data are summarized in the ESM of Appendix D. Below, we show the most important data and with their sources for the basic scenario.
5.3.1 Demand model
We first collected data regarding the process demand. According to our interviewees, the periodic process demand could be reasonably assumed to be normally distributed and independent of each other. The present demand was set at 9875 executions based on the broker pool’s sales information system. The demand trend was estimated at 10 % per year, whereas the standard deviation was set at 1200 executions per year based on historical data from the sales information system.
5.3.2 Execution options of the coverage switching process
The next important step was determining the demand weights and profit margins for each process variant. Our interviewees estimated that negative demand effects would occur if the execution options for personal contract changes and information updates by the brokers were eliminated. The reason was that the brokers highly appreciated these execution options, often using them to initiate further sales activities (e.g., cross- and up-selling). Eliminating the execution options for personal contract changes and information updates by the brokers would also have negative cost effects due to the higher workload for the broker pool. However, the interviewees also estimated that eliminating these options may increase end customer satisfaction and internal experience curve effects. The electronic form has positive cost effects on the submission of end customer information because it avoids the need to register end customers by hand. Nevertheless, the interviewees estimated that 5 % of the brokers would churn if paper submission were no longer possible. The interviewees’ estimation on what fraction of the brokers would churn if a distinct execution option were eliminated was based on a broker survey the company conducted when setting up its call center some years before. Information about the cost per execution and the fractions of covered demand were retrieved from the case company’s sales information as well as enterprise resource planning system. Table 3 summarizes the information about the execution option.
To derive the profit margins and demand weights of the process variants, we assumed, in accordance with the broker pool’s management, that the execution options of the coverage switching process are executed independently of each other. We then calculated the weights of the process variants by multiplying the weights of the respective enabled execution options. We obtained the profit margin of each process variant by subtracting the costs of the enabled execution options from the average revenue per process execution of 90 EUR. The average revenue was retrieved from the company’s sales information system. Table 4 shows the demand weights and the profit margins per process variant.
5.3.3 Experience curve effects
As the coverage switching process is highly repetitive with more than 9000 executions per year, we could legitimately assume the experience curve to be at its flat end. Based on the information from our questionnaire, the execution costs per process instance were reduced by 2.50 EUR to 48.25 EUR (a relative reduction of about 5 %) and the process demand realized on a level of 9875 executions in the last year. With this information, we could derive the slope of the experience curve through the relationship between the relative cost reduction and the realized process demand: \(\widetilde{a} = 0.05/9875 = 5.09 \times 10^{ - 6}\). Our interviewees retrieved this additional information from the company’s sales information as well as enterprise resource planning system.
5.3.4 Anderson’s model
To apply Anderson’s (1994) model, we gathered the quality in the status quo (Q = 8) as well as the time (s T = 0.633) and quality (s Q = 0.125) effects of complete standardization. Our interviewees could estimate these input parameters relatively easily as they planned to use an already running process variant as master process. If they had chosen a novel process variant as the master process, it would have been considerably harder to estimate the quality and time improvements. The derivation of the other parameters from Anderson’s model was based on the respective average values for these parameters and the adjustment procedures from Anderson (1994). ESM of Appendix D illustrates the adjustment factors, their derivation, and the values obtained from the questionnaire. Knowing the values for the company-specific factors, we calculated the values for positive and negative confirmation/disconfirmation using the following parameterized equations from Anderson (1994):
The beta-factors for customer satisfaction and the retention rate were derived analogously:
5.4 Application of the decision model
5.4.1 Optimization and interpretation
In combination with the general planning variables on the planning horizon \(\tau\) = 7 years and the yearly risk-adjusted interest rate \(i = 0.04\), which the company typically uses for investment decisions according to our interviewees, we derived the values of the objective function for all process variant profiles. To be precise, we only considered process variant profiles that complied with the case company’s strategic decision of not closing down the call center. In addition, we omitted possible investment outflows for the elimination of execution options in accordance with the broker pool’s management, because the costs for employees and IT systems are already included in the process costs. Given the seven process variants and the master process, we had to consider 27 = 128 process variant profiles. We could neglect those process variant profiles where the case company’s call center would be shut down. Table 5 shows the values for the objective function and other relevant parameters for the best three process variant profiles as well as for complete standardization as a benchmark. For a more intuitive analysis, we also indicate the delta of the objective functions between a BPS alternative and the status quo. This delta can be viewed as profits or opportunity costs.
In our basic scenario, the decision model suggests aligning process variant 4 against the master process (Table 4). The submission of end customer information for those brokers who personally execute contract changes is then only possible in electronic form. The standardization of process variant 4 increases the risk-adjusted expected NPV of the process cash flows, because the positive effects on customer satisfaction and on the cost advantages of the electronic submission exceed the negative effects on the process demand. Relatively to the second best process variant profile of complete individuality, representing the broker pool’s status quo prior to BPS, the objective function increases by about 21,018 EUR. Serving the fourth process context by the master process instead of the respective process variant reduces the context-specific demand by 5 % (Table 3, line 2), whereas the demand trend increases only marginally. As a result, the cumulative demand is larger for the status quo than for the standardization of process variant 4. However, the standardization directly increases the average profit margin of this context by 25 % (Table 3, lines 1 and 5). The cost advantages even accelerate over time due to experience curve effects. The net effect of the reduced process demand and the increased profit margin is positive and justifies the elimination of paper-based submission for brokers who personally execute contract changes.
5.4.2 Robustness analysis
To analyze the robustness of the optimization results, we conducted a sensitivity analysis of the basic scenario. We also challenged the master process, which has been pre-selected by the case company’s management, by analyzing two additional scenarios. Each additional scenario uses another existing process variant as the master process.
First, to ensure that potential estimation errors do not bias the optimization results of the basic scenario, we determined the optimal process variant profiles for different parameter constellations. We separately varied the values for all parameters except for the profit margins and the discount rate in a range between −50 % and +50 % of the original estimation in 10 % steps, leading to 80 scenarios (ESM of Appendix E). Although the values of the objective function change across the scenarios, the expected effects of BPS remain positive. Moreover, the process variant profile, which was determined as optimal for the basic scenario, remained optimal for all other scenarios. We therefore conclude that, in the case at hand, potential estimation errors did not bias the results.
Second, we challenged the pre-selected master process. We can think about using other process variants as master processes, as there are no regulatory requirements regarding the coverage switching process. As in our decision model, the parameters demand, time, cost, and quality refer to a specific master process, and they must be assessed separately for each master process. In the case at hand, the demand effects could be derived without involving the case company’s management from the information about the execution options (Table 3). The cost effects could also be extracted based on the questions that relate to the basic master process, whereas we had to include additional questions to estimate the quality and time effects for the alternative master processes (ESM of Appendix D). After discussions with the interviewees, we decided to try processing variants 4 and 3 as alternative master processes (Table 4). We did not check for candidates outside the case company, as there are no accepted reference models for the coverage switching process. As in the basic scenario, the interviewees could estimate the additional input data easily, as both alternative master processes were already existing process variants.
As for process variant 4, the only difference compared to the original master process is that process variant 4 implies a paper-based submission of end customer information. Using process variant 4 as master process has similar time and quality effects as the original master process. These effects amount to 90 % compared to those of the original master process, because the electronic submission process is marginally faster and more reliable than the paper-based submission. In addition, using process variant 4 as master process has cost disadvantages at equal demand effects (Table 3). In this case, the optimal process variant profile is the status quo that reflects complete individuality. That is, any standardization against process variant 4 as master process is economically disadvantageous. The reason is that the paper-based submission of end customer information has disadvantages regarding cost, time, and quality compared to the electronic submission. Thus, using process variant 4 as the master process is not a good idea.
In contrast, process variant 3 differs from the original master process regarding the interaction with end customers. While the original master process assigns the entire customer contact to the broker pool’s call center, process variant 3 assigns all these activities to the brokers. An alignment against process variant 3 would thus require closing down the broker pool’s call center. We investigated this case despite the management’s strategic decision against closing down the call center, because the management was interested in the potential economic consequences (opportunity costs) of this strategic decision. The circumstance that process variant 3 substantially differs from the original master process becomes manifest in the time and quality effects. As a call center-based execution is considerably faster and less error prone than a broker-based execution, standardization against process variant 3 provides significantly smaller time effects (1.5 times smaller) and quality effects (about half as large) than the standardization against the original master process (ESM of Appendix D). However, the cost significantly drops such that the profit margin of the process doubles, if the customer contact were outsourced. Moreover, there would be almost no negative demand effects (Table 3). The optimal process variant profile using process variant 3 as the master process is complete standardization. The cost advantage is so dominating that it overcompensates for the negative demand, quality, and time effects. The decreases in the demand dynamics are economically less important than the efficiency increases due to the high repetitiveness of the case process. The standardization against process variant 3 also causes a higher risk-adjusted expected NPV than the basic scenario. Whereas the optimal process variant profile in the basic scenario increases the risk-adjusted expected NPV by 21,018 EUR compared to the status quo, complete standardization against process variant 3 leads to an increase of 1,016,108 EUR. From a purely economic perspective, the case company should prefer using process variant 3 as master process instead of the basic scenario. As the case company’s management, however, decided against closing down the call center, and this would require dismissing 70 employees, it is reasonable to rely on the original master process.
5.5 Discussion
5.5.1 Validity of the assumptions
To substantiate the validity of the optimization results, we discussed the decision model’s assumptions with the interviewees, particularly with respect to whether the assumptions hold in the case at hand. To do so, we explained the assumptions to the interviewees and asked for their judgement on how far they can be considered fair.
The assumption regarding the principles of VBM (A1) was completely in line with the case company’s strategic orientation. For the case company, retaining a strong cash flow position and achieving long-term growth are the two most important strategic objectives. The assumption about the process demand that follows a trend with random deviations (A2) was judged as uncritical. The interviewees confirmed a stably increasing development of the customer base over the past 5 years. However, they could not exclude disruptive events over the entire planning horizon. A demand model that allows for such exogenous demand shocks would constitute a good extension of the decision model. However, the probability for demand shocks was estimated to be so low that the implementation of shock events would not dramatically affect the case results. Further, the interviewees considered the assumption regarding constant demand weights (A3) as fair. When deciding about setting up the call center, the company conducted a survey to predict the brokers’ behavior. Since the establishment of the call center, the company monitors the call center’s utilization to assess its profitability. The results indicate stable usage behaviors as well as a steady distribution over interaction channels. With the coverage switching process counting among the case company’s core processes, the interviewees confirmed the assumption about high process maturity (A4). Almost all end costumers traverse this process. In contrast to the positive feedback regarding assumptions (A1) to (A4), the interviewees criticized the assumptions on the mechanics of quality and time effects (A5, A6). Both the uniformly distributed time and quality tolerances and the linear relationships were judged as being unsuitable. The sensitivity analysis, however, showed that a violation of these two assumptions does not impact the optimal process variant profile in the case at hand (Sect. 5.4.2).
5.5.2 Discussion against evaluation criteria
As a final evaluation step, we discuss the decision model‘s applicability and usefulness based on criteria that were compiled and assessed by Sonnenberg and vom Brocke (2012) as valid for evaluation activity EVAL4. In line with the nature of the decision model and its prototypical implementation, we focus on evaluation criteria that relate to the artifact types model and instantiation. The discussion builds on the experience we gained throughout the real-world case. We also collected evaluation-related data in an additional interview with the case company’s chief executive officer and head of marketing. Wherever reasonable, we generalize beyond the real-world case at hand.
Assessing the applicability of our decision model, our real-world case illustrated its performance in naturalistic settings. As the model‘s calculation logic is complex and the number of process variant profiles grows exponentially with the number of process contexts (see effectiveness and efficiency), the decision model cannot be applied without the prototype. Another issue that affects applicability is that the decision model requires collecting and estimating input data regarding process contexts, process variants, and the master process as well as regarding the effects of BPS on the performance dimensions time, cost, quality, and flexibility. According to our interviews, the case company disposed of most input data and could estimate the rest. Especially, the effects of BPS on time and quality were hard to estimate, as the case company’s management stated in a feedback interview about potential estimation problems. To cope with estimation inaccuracies, which are inevitable in naturalistic settings, the prototype implements robustness analysis functionality, as discussed in Sect. 5.4.2. Nevertheless, we recommend building up a knowledge base to institutionalize data collection routines and compile reference data. The interviewees assessed the decision model’s ease of use—in the sense of ease of data collection—as appropriate in relation to the decision problem’s complexity and relevance. When reasoning about the decision model’s applicability, one must also challenge the settings to which the decision model is applicable. We thus take the case-specific reasoning about the decision model’s assumptions from Sect. 5.5.1 to a more general level to highlight industries, process types, and contexts that do not match the decision model. Starting with process types, the decision model is geared to business processes that offer their output to customers, whose demand depends on process quality and time, and for which organizations can in general freely choose which variants they offer. The decision model cannot be applied to support processes where time and quality may not affect process demand, but costs instead. Further, the decision model does not cover immature processes and/or highly dynamic environments. This is for three reasons: the learning curve effects are underestimated, customer behavior is unpredictable, and the input parameters cannot be estimated reliably. With BPS exploiting the learning curve effects, the decision model suggests higher BPS levels for higher learning curve parameters. It understandardizes processes if the learning curve effect is underestimated. This is what happens for immature process if learning curve effects are linearly approximated. In dynamic settings, customer behavior is unpredictable, a circumstance that causes the process demand not to be identically distributed across process contexts over the planning horizon. As BPS benefits tend to scale with increasing demand weights, it is crucial that involved decision-makers can reliably estimate how the customer behavior changes in case of standardization. In the case of highly dynamic environments, this may be impossible. Beyond the estimation of demand effects, applying the decision model requires deep insights into the process to estimate all input parameters. Such knowledge is not available for newly created processes. Following the same logic, the decision model is less suitable for highly dynamic companies or industries, such as start-ups. Organizations operating in such environments, however, typically follow an explorative strategy and, thus, are not the main stakeholders of BPS. Thinking about BPS is more relevant for mature organizations with globally distributed processes that engage in operational excellence. As for contexts, the decision model does not fit contexts that are highly restricted by regulations or legislation. Aligning respective processes against the master process may imply that relevant restrictions are violated. Further, if many contexts are regulated, it may not be possible to identify a sufficiently applicable master process. As argued for highly dynamic environments, BPS is not the dominant strategy in highly regulated contexts. Consequentially, these contexts are beyond the scope of our decision model, as we aim at providing those organizations with guidance that explicitly assess the potential of BPS. Finally, we conclude that the decision model particularly fits those organizations and business processes that need guidance on BPS.
Concerning the impact on the artifact environment and users, the decision model affected how the case company’s management thinks about BPS in general and in particular about how to address the BPS trade-off. On the one hand, the decision model‘s formal design specification provides insights into the BPS trade-off and into the interplay of central BPS-related constructs such as process contexts, process variants, and the master process. On the other hand, the prototype’s robustness analysis functionality helped the case company’s management understand the situation and possibilities for action in their organization. Our interviewees also agreed that the decision model enhances their organization’s process decision-making capabilities.
In terms of the model’s fidelity with the real-world phenomenon, we can conclude that our decision model covers relevant constructs (e.g., process variants, process contexts, master process) as well as performance dimensions, and it can handle different constellations that occur in naturalistic settings. An assessment of the assumptions’ validity (Sect. 5.5.1) underpinned that most assumptions hold in the investigated real-world case. Based on the results of the robustness analysis (Sect. 5.4.2), we could further show that the violation of two assumptions did not affect the optimization results in the case at hand. So far, we do not have experience on the extent the decision model fits different organizational contexts. This should be a subject for future research.
Referring to consistency, the decision model is internally consistent, as it was designed deductively and its components were modular such that side effects could not occur. Further, the decision model‘s design specification is available in terms of mathematical formulae, a property that facilitates checking internal consistency. As for external consistency, the decision model does not contradict accepted knowledge from other disciplines such as BPM or VBM. Rather, the model builds on knowledge from these disciplines as justificatory knowledge. These disciplines also served as foundation for deriving our design objectives (Sect. 2).
To evaluate the effectiveness and efficiency of our artifact, we analyze the performance of our prototype in our real-world case. When calculating the results of the different scenarios and conducting the robustness analysis, the prototype shaped up as an effective tool. In its current stage of development, the prototype can be applied to academic evaluation settings, and not to industry settings. With the decision model checking for each process context whether it should be served by a specific process variant or the standardized master process, the problem complexity grows exponentially with the number of process contexts (2n). As for efficiency, the prototype uses exhaustive enumeration to determine the optimal process variant profile. Although exhaustive enumeration entails much calculation effort, it is suitable for the decision problem at hand because the number of process variants typically involved is manageable and BPS decisions need not be made in real time. We conducted performance tests on regular workstations such as those used in business environments. The prototype efficiently processes industry-scale problems, but can only inconveniently be configured for different settings.
6 Conclusion
6.1 Summary and contribution
In this study, we investigated how organizations can determine an appropriate BPS level for their business processes, considering the partially conflicting effects of BPS on process performance that together define the BPS trade-off. Adopting the DSR paradigm, we developed a decision model that combines descriptive knowledge on BPS with prescriptive knowledge on VBM. The decision model structures the BPS effects on process performance according to the dimensions of the Devil’s Quadrangle and resolves conflicts among these dimensions using the contribution of different BPS levels to the organization’s firm value as objective function. The decision model formalizes BPS levels via process variant profiles. Process variant profiles indicate whether the contexts in which a process is executed are served by context-specific process variants or the standardized master process. In general, the decision model entails an optimal BPS level where, throughout a multi-period planning horizon, the demand reduction that results from reduced process flexibility is overcompensated by the higher demand trend that flows from better quality and time. Moreover, for the optimal BPS level, BPS investments are overcompensated by higher profit margins from experience effects. Providing guidance on which process context to serve via a context-specific process variant or the master process, the decision model contributes to the prescriptive body of knowledge on BPS.
When setting up the decision model, the main challenge was to integrate the partially conflicting effects of BPS into a single objective function. The investment outflows associated with a process variant profile as well as the negative BPS effect on process flexibility, i.e., the demand reduction that may result if distinct process contexts are served by the master process, could be directly integrated into the objective function. The positive effects of BPS on process costs were approximated with reference to variant-specific profit margins and the experience curve concept. The positive effects of BPS on process quality and time were integrated into the demand trend by applying the Gini coefficient of the process demand, which measures the demand concentration on the master process, to Anderson’s (1994) model of customer satisfaction and retention.
We evaluated the decision model by discussing its design specification against theory-backed design objectives and by prototypically implementing the design specification. Furthermore, we validated the decision model’s applicability and usefulness via a real-world case at an insurance broker pool company as well as by discussing the decision model’s design specification and the prototype against established evaluation criteria from the DSR literature.
6.2 Limitations and future research
While validating the decision model’s design specification, applicability, and usefulness, we identified directions in which the decision model should be advanced. Below, we present these directions together with ideas for future research.
Regarding its design specification, the decision model includes simplifying assumptions. The strongest assumption is that about the linear effects of BPS on process quality and time. Although this assumption is backed by empirical findings, the reality might be more complex. Moreover, risk and the decision-makers’ risk attitude are captured rather implicitly via a risk-adjusted interest rate. They could be addressed more explicitly by modeling the expected value and risk of the decision model’s objective function separately, e.g., using the certainty equivalent method. Moreover, the decision model is geared to individual business processes that offer their output to external customers as well as whose demand depends on process quality and time. In its current form, the decision model does not fit support processes where time and quality may not affect process demand, but costs. To make the decision model fit support processes, low quality can be modeled as additional process execution, and a high time may directly affect costs. For future research, we recommend deliberating which of these limitations should be relaxed. When extending the decision model, one has to keep in mind that models are purposeful abstractions that need not necessarily capture all the complexity of the real world. It is imperative to assess carefully whether an increase in closeness to reality outvalues the related increases in complexity and data collection effort.
As for applicability and usefulness, we concede that we applied the decision model once in the context of an insurance broker pool company. While this real-world case corroborated that relevant input data can be gathered and that the decision model provided the involved decision-makers with useful guidance, we neither have substantial experience in data collection nor about reference data to calibrate the decision model for various application contexts. Future research should thus focus on conducting more real-world case studies in different organizational contexts and on setting up a respective knowledge base. Case studies will not only help gain experience regarding data collection, but also identify how the decision model’s design specification must be tailored to fit additional contexts. To facilitate additional case studies, we also recommend further developing the prototype such that it can be used more conveniently in naturalistic settings and provide more sophisticated analysis functionality. Finally, future research should develop methods that assist corporate decision-makers in estimating the required input parameters and in determining an appropriate master process. Both topics heavily influence the results of any BPS endeavor, but were beyond this study’s scope.
References
Afflerbach, P., G. Kastner, F. Krause, and M. Röglinger. 2014. The business value of process flexibility. Business & Information Systems Engineering 6(4): 203–214.
Akerlof, G.A. 1970. The market for “lemons”: Quality uncertainty and the market mechanism. The Quarterly Journal of Economics 84(3): 488–500.
Anderson, E.W. 1994. Cross-category variation in customer satisfaction and retention. Marketing Letters 5(1): 19–30.
Anupindi, R., S. Chopra, S.D. Deshmukh, J.A. Van Mieghem, and E. Zemel. 2012. Managing business process flows: Principles of operations management, 3rd ed. New York: Prentice Hall.
Armistead, C., J.P. Pritchard, and S. Machin. 1999. Strategic business process management for organisational effectiveness. Long Range Planning 32(1): 96–106.
Aviv, Y., and A. Federgruen. 2001. Design for postponement: A comprehensive characterization of its benefits under unknown demand distributions. Operations Research 49(4): 578–598.
Beimborn, D., Joachim, N., Münstermann, B. 2009. When standards is not enough to secure interoperability and competitiveness for European exporters. In ECIS 2009 Proceedings, Paper, 215.
Beverungen, D. 2014. On the design of IT artifacts and the emergence of business processes as organizational routines. Business & Information Systems Engineering 6(4): 191–202.
Böhmann, T., Gottwald, R., Krcmar, H. 2005. Towards mass customized IT services: Assessing a method for identifying reusable service modules and its implication for IT service management. In AMCIS 2005 Proceedings, Paper, 409.
Bolsinger, M. 2015. Bringing value-based business process management to the operational process level. Information Systems and e-Business Management 13(2): 355–398.
Bolsinger, M., A. Elsäßer, C. Helm, and M. Röglinger. 2015. Process improvement through economically driven routing of instances. Business Process Management Journal 21(2): 353–378.
Buchanan, R.W., and C.S. Gillies. 1990. Value managed relationships: The key to customer retention and profitability. European Management Journal 8(4): 523–526.
Buhl, H.U., M. Röglinger, S. Stöckl, and K.S. Braunwarth. 2011. Value orientation in process management. Business & Information Systems Engineering 3(3): 163–172.
Cohon, J.L. 2004. Multiobjective programming and planning, 2nd ed. New York: Dover Publishings.
Copeland, T.E., T. Koller, and J. Murrin. 1994. Valuation: Measuring and managing the value of companies. New York: Wiley.
Copeland, T.E., J.F. Weston, and K. Shastri. 2005. Financial theory and corporate policy. Boston: Pearson Education.
Damodaran, A. 2012. Investment valuation—Tools and techniques for determining the value of any asset, 3rd ed. New York: Wiley.
Danielson, M.G., J.L. Heck, and D. Shaffer. 2008. Shareholder theory—How opponents and proponents both get it wrong. Journal of Applied Finance 18(2): 62–66.
Davenport, T.H. 1993. Process innovation—Reengineering work through information technology. Boston: Harvard Business School Press.
Davenport, T.H. 2005. The coming commoditization of processes. Harvard Business Review 83(6): 100–108.
David, P.A. 1987. Some new standards for the economics of standardization in the information age. In Economic policy and technology performance, ed. P. Dasgupta, and P. Stoneman, 206–239. Cambridge: Cambridge University Press.
De Vries, H.J., F.J. Slob, and V.G. Zuid-Holland. 2006. Best practice in company standardization. International Journal of IT Standards and Standardization Research 4(1): 62–85.
Deming, W.E. 1994. Out of the crisis. Cambridge: Cambridge University Press.
Dumas, M., M. La Rosa, J. Mendling, and H.A. Reijers. 2013. Fundamentals of business process management. Berlin: Springer.
Franz. P., Kirchmer, M., Rosemann, M. 2011. Value-driven business process management—Impact and benefits. https://www.accenture.com/mx-es/~/media/Accenture/Conversion-Assets/DotCom/Documents/Local/es-la/PDF2/Accenture-Value-Driven-Business-Process-Management.pdf. Accessed 22 Dec 2015.
Fredendall, L.D., J.B. Craig, P.J. Fowler, and U. Damali. 2009. Barriers to swift, even flow in the internal supply chain of perioperative surgical services department: A case study. Decision Sciences 40(2): 327–349.
Ghattas, J., P. Soffer, and M. Peleg. 2014. Improving business process decision making based on past experience. Decision Support Systems 59: 93–107.
Gini, C. 1921. Measurement of inequality of incomes. The Economic Journal 31(1): 124–126.
Gowrisankaran, G., and J. Stavins. 2002. Network externalities and technology adoption: Lessons from electronic payments. The Rand Journal of Economics 35(2): 260–276.
Goyal, M., and S. Netessine. 2011. Volume flexibility, product flexibility, or both: The role of demand correlation and product substitution. Manufacturing and Service Operations Management 13(2): 180–193.
Gregor, S., and A.R. Hevner. 2013. Positioning and presenting design science research for maximum impact. MIS Quarterly 37(2): 337–356.
Hall, J.M., and M.E. Johnson. 2009. When should a process be art, not science? Harvard Business Review 87(3): 58–65.
Hammer, M., and S. Stanton. 1999. How process enterprises really work. Harvard Business Review 77(6): 108–120.
Harmon, P. 2010. Business process change. Burlington: Morgan Kaufmann.
Henderson, B.D. 1979. Henderson on corporate strategy. Cambridge: Abt. Books.
Imai, M. 1997. Gemba kaizen: A commonsense, low-cost approach to management. New York: McGraw Hill Professional.
Ittner, C.D., and D.F. Larcker. 2001. Assessing empirical research in managerial accounting: A value-based management perspective. Journal of Accounting and Economics 32(1): 349–410.
Jayaram, J., and S.K. Vickery. 1998. Supply-based strategies, human resource initiatives, procurement lead-time, and firm performance. Journal of Supply Chain Management 34(1): 12–24.
Jayaram, J., S.K. Vickery, and C. Droge. 2000. The effects of information system infrastructure and process improvements on supply-chain time performance. International Journal of Physical Distribution & Logistics Management 30(3): 314–330.
Kauffman, R.J., and J.Y. Tsai. 2010. With or without you: The countervailing forces and effects of process standardization. Electronic Commerce Research and Applications 9(4): 305–322.
Keeney, R.L., and H. Raiffa. 1993. Decisions with multiple objectives: Preferences and value trade-offs. Cambridge: Cambridge University Press.
Koller, T., M. Goedhart, and D. Wessels. 2010. Valuation: Measuring and managing the value of companies. New Jersey: Wiley.
Kumar, K., Narasipuram, M.M. 2006. Defining requirements for business process flexibility. In CAiSE06 proceedings of the workshop on business process modeling, design and support (BPMDS06), pp. 137–148.
Lapré, M.A., A.S. Mukherjee, and L.N. Van Wassenhove. 2000. Behind the learning curve: Linking learning activities to waste reduction. Management Science 46(5): 597–611.
Lee, H.L., and C.S. Tang. 1997. Modelling the costs and benefits of delayed product differentiation. Management Science 43(1): 40–53.
Letmathe, P., L. Petersen, and M. Schweitzer. 2013. Capacity management under uncertainty with inter-process, intra-process and demand interdependencies in high-flexibility environments. OR Spectrum 35(1): 191–219.
Lehnert, M., A. Linhart, and M. Röglinger. 2014. Chopping down trees vs. sharpening the axe—Balancing the development of BPM capabilities with process improvement. In BPM 2014 proceedings, ed. S. Sadiq, P. Soffer, and H. Völzer, 151–167. Berlin: Springer.
Lillrank, P. 2003. The quality of standard, routine and nonroutine processes. Organization Studies 24(2): 215–233.
Lillrank, P., and M. Liukko. 2004. Standard, routine and non-routine processes in health care. International Journal of Health Care and Quality Assurance 17(1): 39–46.
Linhart, A., Manderscheid, J., Röglinger, M., Schlott. H. 2015. Process improvement roadmapping—How to max out your process. In ICIS 2015 Proceedings.
Ludwig, H., Y. Rankin, R. Enyedi, and L.C. Anderson. 2011. Process variation analysis using empirical methods: A case study. In BPM 2011 proceedings, ed. S. Rinderle-Ma, F. Toumani, and F. Wolf, 62–65. Berlin: Springer.
Ma, S., W. Wang, and L. Liu. 2002. Commonality and postponement in multistage assembly systems. European Journal of Operational Research 142(3): 523–538.
Manrodt, K.B., and K. Vitasek. 2004. Global process standardization: A case study. Journal of Business Logistics 25(1): 1–23.
March, S.T., and G.F. Smith. 1995. Design and natural science research on information technology. Decision Support Systems 15(4): 251–266.
Meredith, J.R., A. Raturi, K. Amoako-Gyampah, and B. Kaplan. 1989. Alternative research paradigms in operations. Journal of Operations Management 8(4): 297–326.
Münstermann, B., Joachim, N., Beimborn, D. 2009. An empirical evaluation of the impact of process standardization on process performance and flexibility. In AMCIS 2009 proceedings, Paper 787.
Münstermann, B., A. Eckhardt, and T. Weitzel. 2010. The performance impact of business process standardization: An empirical evaluation of the recruitment process. Business Process Management Journal 16(1): 29–56.
Münstermann, B., Weitzel, T. 2008. What is process standardization? In Conf-IRM 2008 proceedings, Paper 64.
Neiger, D., Churilov, L. 2004a. Goal-oriented business process engineering revisited: A unifying perspective. In CSAC proceedings, pp. 149–163.
Neiger, D., and L. Churilov. 2004. Goal-oriented business process modeling with EPCs and value-focused thinking. In BPM 2004 proceedings, ed. J. Desel, B. Pernici, and M. Weske, 98–115. Berlin: Springer.
Peffers, K., T. Tuunanen, M.A. Rothenberger, and S. Chatterjee. 2008. A design science research methodology for information systems research. Journal of Management Information Systems 24(3): 45–77.
Pentland, B.T. 2003. Conceptualizing and measuring variety in the execution of organizational work processes. Management Science 49(7): 857–870.
Pries-Heje, J., Baskerville, R., Venable, J.R. 2008. Strategies for design science research evaluation. In ECIS 2008 proceedings, Paper 87.
Ramakumar, A., and B. Cooper. 2004. Process standardization proves profitable. Quality 43(2): 5–42.
Rappaport, A. 1986. Creating shareholder value: The new standard for business performance. New York: Free press.
Reichert, M., and B. Weber. 2012. Enabling flexibility in process-aware information systems: Changes, methods, technologies. Heidelberg: Springer.
Reichert, M., A. Hallerbach, and T. Bauer. 2015. Lifecycle management of business process variants. In Handbook on business process management 1: Introduction, methods, information systems, 2nd ed, ed. J. vom Brocke, and M. Rosemann, 251–278. Berlin: Springer.
Reijers, H.A., and S. Liman Mansar. 2005. Best practices in business process redesign: An overview and qualitative evaluation of successful redesign heuristics. Omega 33(4): 283–306.
Romero, H.L., R.M. Dijkman, P.W.P.J. Grefen, and A.J. van Weele. 2015. Factors that determine the extent of business process standardization and the subsequent effect of business performance. Business & Information Systems Engineering 57(4): 261–270.
Rosenkranz, C., S. Seidel, J. Mendling, M. Schaefermeyer, and J. Recker. 2010. Towards a framework for business process standardization. In BPM 2009 workshops, ed. S. Rinderle-Ma, S.W. Sadiq, and F. Leymann, 53–63. Berlin: Springer.
Rotaru, K., C. Wilkin, L. Churilov, D. Neiger, and A. Ceglowski. 2011. Formalizing process-based risk with value-focused process engineering. Information Systems and e-Business Management 9(4): 447–474.
Ryan, S.M. 2004. Capacity expansion for random exponential demand growth with lead times. Management Science 50(6): 740–748.
Sánchez-Rodríguez, C., D. Hemsworth, Á.R. Martínez-Lorente, and J.G. Clavel. 2006. An empirical study on the impact of standardization of materials and purchasing procedures on purchasing and business performance. Supply Chain Management: An International Journal 11(1): 56–64.
Schäfermeyer, M., Grgecic, D., Rosenkranz, C. 2010. Factors influencing business process standardization: A multiple case study. In HICSS 2010 proceedings. doi:10.1109/HICSS.2010.207.
Schonenberg, H., R.S. Mans, N.C. Russell, N.A. Mulyar, and W.M.P. van der Aalst. 2008. Process flexibility: A survey of contemporary approaches. In Advances in enterprise engineering I, ed. J. Dietz, and A. Albani, 16–30. Berlin: Springer.
Siau, K., Rossi, M. 1998. Evaluation of information modeling methods—A review. In HICSS 1998 proceedings. doi:10.1109/HICSS.1998.648327.
Siha, S.M., and G.H. Saad. 2008. Business process improvement: Empirical assessment and extensions. Business Process Management Journal 14(6): 778–802.
Sonnenberg, C., and J. vom Brocke. 2012. Evaluations in the science of the artificial–reconsidering the build-evaluate pattern in design science research. In Proceedings of the 7th international conference on design science research in information systems: Advances in theory and practice (DESRIST), ed. K. Peffers, M. Rothenberger, and B. Kuechler, 381–397. Berlin: Springer.
Stewart, G.B., and J.M. Stern. 1991. The quest for value: The EVA management guide. New York: Harper Business.
Swann, G.M.P. 2000. The economics of standardization. Final Report for Standards and Technical Regulations Directorate, Department of Trade and Industry. https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/16506/The_Economics_of_Standardization_-_in_English.pdf. Accessed 16 Oct 2014.
Tregear, R. 2015. Business process standardization. In Handbook on business process management 2: Strategic alignment, governance, people and culture, 2nd ed, ed. J. vom Brocke, and M. Rosemann, 421–441. Berlin: Springer.
Ungan, M.C. 2006. Standardization through process documentation. Business Process Management Journal 12(2): 135–148.
van Wessel, R., Ribbers, P., de Vries, H. 2006. Effects of IS standardization on business process performance: A case in HR IS company standardization. In HICSS 2006 proceedings. doi:10.1109/HICSS.2006.141.
Venable, J., J. Pries-Heje, and R. Baskerville. 2012. A comprehensive framework for evaluation in design science research. In Proceedings of the 7th international conference on design science research in information systems: Advances in theory and practice (DESRIST), ed. K. Peffers, M. Rothenberger, and B. Kuechler, 423–438. Berlin: Springer.
Venkatesh, V. 2006. Where to go from here? Thoughts on future directions for research on individual-level technology adoption with a focus on decision making. Decision Sciences 37(4): 497–518.
Venkatesh, V., and H. Bala. 2012. Adoption and impacts of interorganizational business process standards: Role of partnering synergy. Information Systems Research 23(4): 1131–1157.
vom Brocke, J., J. Becker, A.M. Braccini, R. Butleris, V. Hofreiter, K. Kapočius, M. De Marco, G. Schmidt, S. Seidel, A. Simons, T. Skopal, A. Stein, S. Stieglitz, R. Suomi, G. Vossen, R. Winter, and S. Wrycza. 2011. Current and future issues in BPM research: A European perspective from the ERCIS meeting 2010. Communication of the AIS 28(1): 393–414.
vom Brocke, J., J. Recker, and J. Mendling. 2010. Value-oriented process modeling: Integrating financial perspectives into business process re-design. Business Process Management Journal 16(2): 333–356.
vom Brocke, J., and C. Sonnenberg. 2015. Value-orientation in business process management. In Handbook on business process management 2: Strategic alignment, governance, people and culture, 2nd ed, ed. J. vom Brocke, and M. Rosemann, 101–132. Berlin: Springer.
von Stetten, A., Münstermann, B., Eckhardt, A., Laumer, S. 2008. Towards an understanding of the business value of business process standardization-a case study approach. In AMCIS 2008 proceedings, Paper 20.
Wagner, D., Suchan, C., Leunig, B., Frank, J. 2011. Towards the analysis of information systems flexibility: Proposition of a method. In Wirtschaftsinformatik 2011 proceedings, Paper 34.
Wüllenweber, K., D. Beimborn, T. Weitzel, and W. König. 2008. The impact of process standardization on business process outsourcing success. Information Systems Frontiers 10(2): 211–224.
Yi, Y. 1990. A critical review of consumer satisfaction. Review of Marketing 4(1): 68–123.
Zellner, P., Laumann, M. 2013. Evaluation of business processes for business process standardization. In PACIS 2013 proceedings, Paper 248.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Afflerbach, P., Bolsinger, M. & Röglinger, M. An economic decision model for determining the appropriate level of business process standardization. Bus Res 9, 335–375 (2016). https://doi.org/10.1007/s40685-016-0035-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40685-016-0035-6