1 Introduction

A cost cap tariff is a two-part tariff that is a hybrid between a pure pay-per-use tariff (where costs accrue with usage) and a flat rate (where costs are independent of usage). The cost cap tariff is a pure pay-per-use tariff until the costs reach an upper limit. At this cost level, the tariff effectively becomes a flat rate because any further consumption is not charged to the consumer. Thus, the consumer might pay less, but never more than this upper limit.

Cost cap tariffs were first introduced in addition to existing pay-per-use plans and flat rates in the German mobile communications market in 2009. Provider O2/Telefonica introduced this new tariff type for voice communication in 2009 with a price of 0.15 €/min and a monthly cost cap of 60 €. At the time, this pricing was such that the minute price of the cost cap tariff exceeded the common market price for pure pay-per-use tariffs (0.09 €/min) while the cost cap was set at the level of comparable flat rate plans. The introduction of the cost cap tariff led to a clear increase in customers for O2 (Briegleb 2009). As a consequence, several competitive virtual mobile network operators soon followed with similar offers. While these mobile network operators are still offering cost cap tariffs, the initial provider O2 decided to no longer advertise its cost cap tariff. Thus, the long run effects on consumer choice and providers’ profits are an open research question. Furthermore, the use of cost cap tariffs is not limited to the telecommunications market. Insurance services often include deductibles which behave in the same fashion as a cost ceiling of consumer payment. Also rental services, e.g., for car or bike sharing, often include a time-dependent rate which is covered by predefined day rates. Table 1 illustrates some selective examples for different industries. Thereby, note that cost cap tariffs are offered both by the same company in addition to its pay-per-use and flat rate tariffs as well as in response to flat rate and/or pay-per-use tariffs by competitors.

However, from a theoretical perspective, the relationship between the pricing and the demand of cost cap tariffs, particularly in the presence of other tariffs, has not yet been investigated.

Table 1 Exemplary tariff structures in different industries (September 2013)
Full size table

In this article, a simple model of consumer surplus is developed that seeks to explain consumers’ rationale in choosing a cost cap tariff over pay-per-use plans and flat rates. We focus on the realistic case where the marginal price of the cost cap tariff is not smaller than the marginal price of the pay-per-use tariff and where the cost cap level is at or above the price level of the flat rate. Otherwise, the cost cap tariff would clearly dominate both the pay-per-use plan and the flat rate. Moreover, to disentangle the pure pricing effect of tariffs from other effects that may influence a consumers tariff choice, such as tariff biases or brand effects, we assume that consumers base their consumption decision solely on prices and their (uncertain) preference for the service offered.

We find that cost cap tariffs should never be chosen over pay-per-use or flat rate plans if consumers are certain about their preferences and consequently in their demand. In this case, the cost cap tariff is always dominated by either the pay-per-use plan or the flat rate. However, if consumers have uncertainty in their preferences, the cost cap tariff may generate a higher (expected) consumer surplus than a pay-per-use plan or a flat rate. This holds true even though consumers are charged more at the margin than in a pay-per-use tariff and the maximum possible bill amount is higher under a cost cap compared to a flat rate tariff. This is because the cost cap tariff does not only provide cost insurance in case of high demand (like a flat rate), but also cost flexibility in case of low demand (like a pay-per-use tariff). The main research questions that are addressed are (1) under which conditions are cost cap tariffs potentially chosen (over pay-per-use plans and flat rates)? and (2) what is the impact of demand uncertainty on tariff choice?

Finally, our theoretical predictions are compared to empirical data that was collected in a survey among a representative sample of German mobile telephony customers. We find a good model fit, both with respect to the predictions for expected telephony usage and for expected consumer surplus under a given tariff. However, we also find a systematic tariff bias, which is in line with previous research.

The remainder of this article is structured as follows. Next, Sect. 2 discusses the related literature on tariff research. Thereafter, Sect. 3 presents the consumer surplus model and the results on customer choice in the case where the customer has certainty about his preferences. Section 4 considers the optimal consumption pattern under cost tariffs when consumers have uncertainty about their preferences. Subsequently, the conditions under which it is optimal to choose cost cap tariffs over pay-per-use and flat rate plans are developed in Sect. 5. Finally, in Sect. 6, the consumer surplus model is evaluated empirically.

2 Related literature

Research on nonlinear pricing is rooted in welfare economics (Leland and Meyer 1976; Murphy 1977) and has been mainly studied from an analytical perspective (Essegaier et al. 2002; Hayes 1987; Oi 1971; Sundararajan 2004). Yet, there has been an increase in empirical research (Danaher 2002; Schulze et al. 2005; Iyengar et al. 2008; Lambrecht et al. 2007; Schlereth and Skiera 2012) within the last decade. An important aspect of modeling of consumer behavior under different tariffs is the literature on discrete/continuous choice models (Dubin and McFadden 1984; Hanemann 1984). These models assume that a discrete choice is made simultaneously with a continuous choice. Applied to the case of tariffs, the discrete choice of a tariff depends on the choice of continuous consumption and vice versa. Hausmann (1985) and Moffitt (1986) lay the groundwork for the application of these models on multi-part tariffs. The consumer’s calculus in these situations consists of two steps. First, the consumer surplus optimizing consumption on each tariff segment (e.g., the pay-per-use or flat rate segment) is calculated, then the segment which maximizes the overall consumer surplus is chosen, subject to the associated optimal consumption decision and the corresponding bill amount. In this context, note that the composition of a tariff with several tariff components, such as minute prices, allowances or cost caps, induces a nonlinearity in the consumer’s cost function. However, the tariff can be subdivided into linear tariff segments. For example, a cost cap tariff consists of a linear pay-per-use segment (i.e., from zero consumption until the cost cap is reached) and a linear flat rate segment (i.e., any consumption beyond the cost cap). These models have been extended in several ways, e.g., by incorporating uncertainty in consumption (Lambrecht et al. 2007) or attrition probabilities (Danaher 2002) (Table 2).

Table 2 Related literature on tariff choice modeling
Full size table

Most of the earlier literature which applied analytical tariff modeling focused on the impact of transaction costs (Sundararajan 2004) or capacity constraints (Essegaier et al. 2002) on a provider’s profit. Thereby, consumers’ tariff choice and consumption decision were addressed with rather simple consumer surplus models. In contrast, empirical research applied more sophisticated models (e.g., Albers and Skiera 2006) to explain observed tariff choice including certain irrationalities, such as tariff biases (Schulze et al. 2005) or brand effects (Iyengar and Jedidi 2012).

The papers that are most related to ours, but do not address the cost cap tariff, are Lambrecht et al. (2007) and Iyengar et al. (2008). More specifically, Lambrecht et al. (2007) develop an empirical model for uncertainty under three-part tariffs (consisting of a fixed fee, a usage allowance, and pay-per-use price for the usage that exceeds the allowance) by incorporating future usage shocks occurring prior to the consumption decision in the tariff choice stage. Within their model, uncertainty is a key driver for three-part tariff choice. Iyengar et al. (2008) derive the optimal consumption level for three-part tariffs under certainty first, and then allow for small variations of this level ex post. Thereby, both papers propose a similar consumer surplus model with the intention in mind to explain observed tariff choice by estimating the models’ underlying parameters. Schlereth and Skiera (2012) demonstrated that such models can be also used to predict tariff choice of innovative tariffs. The predictions of these models are, therefore, the result of a choice model that has been calibrated by actual tariff decisions, including consumers’ biases and irrationalities.

In contrast to the stated literature, we derive a consumer surplus model with the intention to explain the theoretically optimal tariff choice. Within this model, tariff choice relies on the preferences of a representative consumer, and not on an exogenous demand or observed choice. This modeling approach has the distinct advantage that the demand for tariff usage is derived endogenously and depends also on the chosen tariff and the pricing structure. In other words, given the same preferences, a consumer will exert a different consumption pattern under a cost cap tariff than under a pay-per-use or flat rate plan, because prices are different. This endogenous change in demand should be taken into account when choosing a tariff.

Thereby, we assume that consumers have uncertainty about their preferences ex ante (Kridel et al. 1993). This assumption is driven by the belief that consumers are uncertain about the realization of their preferences during the runtime of their contract when choosing a tariff, e.g., due to unforseen changes in their habits. Thus, uncertainty in consumption is driven by the uncertainty in preferences and not by external shocks as similarly stated by Hayes (1987). Consequently, the optimal consumption is uncertain as well. Therefore, even small levels of uncertainty do not simply imply kinks in the demand function as in Iyengar, Jedidi, and Kohli; instead, they may cause actual discontinuities in the demand functions (cf. Moffitt 1986, p. 320), because demand is shifted to a different tariff segment. In contrast to external shocks, these discontinuities in the demand function are tariff dependent.

Moreover, for the most part the present paper abstracts from any bias or other irrationality in tariff choice. Instead, a fully rational consumer is assumed, who may, however, face uncertainty about his preferences (demand). Since we abstract from any bias (or irrationality), we can provide insights under which condition a cost cap tariff should be chosen, even though it offers a higher variable rate than the concurrently offered pay-per-use tariff and a higher cost ceiling than the concurrently offered flat rate tariff.

Finally, it is worth mentioning that, with the exception of Krämer and Wiewiorra (2012), cost cap tariffs have not received academic attention before. Krämer and Wiewiorra conduct an empirical investigation of the flexibility effect in tariff choice in which they also consider the cost cap tariff. They highlight that there might exist a “cost cap bias”, by which customers favor cost caps over pay-per-use tariffs and flat rates even if the tariffs yield the same economic costs. In our empirical analysis, we can confirm such a cost cap bias, which exists over and beyond the rational choice of cost cap tariffs.

3 Tariff choice and consumption under certainty

In the following, we focus on the choice between a pay-per-use (PU), flat rate (FR) and cost cap (CC) tariff from the point of view of a single, representative consumer. Any feasible tariff under one of these three tariff types can be described by the tuple

$$ t=(b,p,c), $$
(1)

where b denotes a fixed base fee which must be paid independent of the consumption, p is a constant price for each consumption unit and c stands for a cost cap, i.e., an upper threshold for the total billing amount. More specifically, for the PU tariff, it holds that

$$ t_{\rm PU}=(0,p_{\rm PU},\infty). $$
(2)

The FR tariff is characterized by

$$ t_{\rm FR} = (b_{\rm FR}, 0, \infty). $$
(3)

And for the CC tariff, it holds that

$$ t_{\rm CC} = (0, p_{\rm CC}, c_{\rm CC}). $$
(4)

Depending on the tariff and given the consumption level \(n\ge 0,\) a customer has total costs of

$$\begin{aligned} k_t (n) = {\left\{ \begin{array}{ll} b_t + n p_t &\quad \text{if } b_t + n p_t \le c_t \\ c_t &\quad \text{otherwise.} \end{array}\right. } \end{aligned}$$
(5)

Like Iyengar et al. (2008), Lambrecht et al. (2007) and Schlereth and Skiera (2012), we assume a quadratic functional form for the consumer’s surplus function as follows

$$ u_t(n) = \beta_1 n - \beta_2 n^2 - k_t(n), $$
(6)

where \(\beta_1, \beta_2>0\) are the individual preference parameters that express the consumer’s gross surplus of consumption relative to the monetary units \(k.\) Notice that the consumer surplus function is quasi-concave and thus it implies that optimal consumption is bound, even at zero marginal costs (Hausmann 1985). However, our results are not limited to this specification and should hold for any quasi-concave consumer surplus function. An alternative modeling approach includes for instance the modified exponential function, as discussed in Albers and Skiera (2006).

More explicitly, for the three tariffs considered here, a consumer’s surplus can be written as follows:

$$ u_{\rm PU}(n)= \beta_1 n - \beta_2 n^2 - n p_{\rm PU} $$
(7)
$$ u_{\rm FR}(n)= \beta_1 n - \beta_2 n^2 - b_{\rm FR} $$
(8)
$$\begin{aligned} u_{\rm CC}(n)= {\left\{ \begin{array}{ll} \beta_1 n - \beta_2 n^2 - n p_{\rm CC}&\quad \text{if }n p_{\rm CC} \le c_{\rm CC}\\ \beta_1 n - \beta_2 n^2 - c_{\rm CC}&\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$
(9)

As noted above, we restrict our analysis to the interesting case where all parameters are non-negative and \(c_{\rm CC} > b_{\rm FR}\) and \(p_{\rm CC} > p_{\rm PU}.\) Moreover, we assume that \(\beta_1 > p_{\rm CC},\) which ensures that the optimal consumption levels under all tariffs are positive.

In a deterministic setting, where the consumer has no uncertainty about his preferences \(\beta, \) it is straightforward to show (by maximizing (7) and (8) with respect to \(n,\) respectively; see also Iyengar et al. 2008) that the optimal consumption levels under a PU and an FR tariff are

$$ n^*_{\rm PU}= \frac{\beta_1 - p_{\rm PU}}{2 \beta_2} ,\quad n^*_{\rm FR}= \frac{\beta_1}{2 \beta_2}, $$
(10)

respectively. The solutions are unique because the consumer surplus function is quasi concave and the corresponding cost function (5) is linear (see Hausmann 1985, p. 1257). The consumer surplus that is derived from these optimal consumption plans is given by substituting (10) back into (7) and (8), respectively:

$$ u_{\rm PU}(n^*_{\rm PU})= \frac{\left( \beta_1 - p_{\rm PU}\right) ^2}{4 \beta_2},\quad u_{\rm FR}(n^*_{\rm FR})= \frac{\beta_1^2}{4 \beta_2} - b_{\rm FR}. $$
(11)

A consumer is thus indifferent between a PU and an FR tariff if and only if \(u_{\rm PU}(n^*_{\rm PU}) = u_{\rm FR}(n^*_{\rm FR}).\) Solving this equation for the preference parameter \(\beta_1\) yields: \(\beta_{1}^{*} = 2 \beta_2 \frac{b_{\rm FR}}{p_{\rm PU}} + \frac{p_{\rm PU}}{2}.\) Thus, for every \(\beta_1 < \beta_1^*,\) the consumer prefers the PU tariff over the FR tariff and vice versa.

The derivation of the optimal consumption under a CC tariff is more complex because the cost function is concave here. In general, there will thus exist an optimal consumption level for each tariff segment (i.e., before and after reaching the cost cap) of the CC tariff. Therefore, it is necessary to calculate the consumer surplus maximizing consumption on each tariff segment before one can then choose the segment that generates the higher overall consumer surplus (cf. Hausmann 1985, p. 1256). In other words, first we derive the optimal consumption under a CC tariff under the expectation that the cost cap is not met (i.e., for the PU segment), constrained on the condition that the optimal consumption does not exceed the segment boundary. Second and independently, we derive the optimal consumption under a CC tariff under the expectation that the cost cap is met (FR segment), again constrained on the condition that the optimal consumption does not exceed the segment boundary. Hence, analogous to (10), the candidates for the optimal consumption level under the CC tariff (i.e., the optimal consumption for each tariff segment) are given by

$$ n1_{\rm CC}= \min \left\{ \frac{\beta_1 - p_{\rm CC}}{2 \beta_2}, {\hat{n}}\right\},\quad n2_{\rm CC}= \max \left\{ \frac{\beta_1}{2 \beta_2}, {\hat{n}}\right\}, $$
(12)

where \({\hat{n}}\) denotes the consumption level that corresponds to the cost cap boundary, i.e.,

$$ {\hat{n}} = c_{\rm CC}/{p_{\rm CC}}. $$
(13)

Notice, that for any \(p>0,\) it follows that \(n^*_{\rm PU} < n^*_{\rm FR}.\) Thus, at most one of the consumption candidates can exceed bounds and admit the corner solution of \({\hat{n}}.\) Furthermore, it can be shown that whenever a consumption candidate admits a corner solution, then the other consumption candidate is optimal. The corresponding proof is available in Appendix 1. Therefore, without loss of generality, we can restrict our attention to the case where neither consumption candidate admits a corner solution. Of course, a rational consumer would choose the consumption candidate that yields the higher consumer surplus. The corresponding threshold \(\beta_1^{**}\) is derived as follows:

$$ u_{\rm CC}(n1_{\rm CC})= u_{\rm CC}(n2_{\rm CC}, c_{\rm CC}) \Leftrightarrow $$
(14)
$$ \beta_1^{**}= 2\beta_2\frac{c_{\rm CC}}{p_{\rm CC}}+\frac{p_{\rm CC}}{2} = 2\beta_2{\hat{n}}+\frac{p_{\rm CC}}{2} $$
(15)

If \(\beta_1 < \beta_1^{**},n1_{\rm CC}\) is realized, otherwise \(n2_{\rm CC}.\) Consequently, the consumer surplus under a CC tariff is given by:

$$\begin{aligned} u_{\rm CC} = {\left\{ \begin{array}{ll} \frac{\left( \beta_1 - p_{\rm CC}\right) ^2}{4 \beta_2} &\quad \text{if } \beta_1 \le \beta_1^{**} \\ \frac{\beta_1^2}{4 \beta_2} - c_{\rm CC} &\quad \text{otherwise.} \end{array}\right. } \end{aligned}$$
(16)

However, because \(p_{\rm CC} > p_{\rm PU}\) (i.e., the marginal price is higher under the CC tariff than under the alternative PU tariff), it follows that \(u_{\rm CC}(n1_{\rm CC}) < u_{\rm PU}(n^*_{\rm PU})\) (i.e., the consumer’s utility under the PU segment of the CC cap tariff is lower than under the alternative PU tariff):

$$\begin{aligned}&u_{\rm CC}(n2_{\rm CC})= u_{\rm CC} \left(\frac{\beta_1}{2 \beta_2}\right)= \frac{\left( \beta_1 - p_{\rm CC}\right) ^2}{4 \beta_2} \\ &\quad<u_{\rm PU}(n^*_{\rm PU})= \frac{\left( \beta_1 - p_{\rm PU}\right)^2}{4 \beta_2} \end{aligned}$$
(17)

Likewise, because \(c_{\rm CC} > f_{\rm FR}\) (i.e., the maximum billing amount under FR segment of the CC tariff is higher than under the alternative FR tariff), it follows that \(u_{\rm CC}(n2_{\rm CC}) < u_{\rm FR}(n^*_{\rm FR})\) (i.e., the consumer’s utility under the FR segment of the CC cap tariff is lower than under the alternative FR tariff):

$$\begin{aligned}&u_{\rm CC}(n1_{\rm CC})= u_{\rm CC} \left(\frac{\beta_1 - p_{\rm CC}}{2 \beta_2}\right)= \frac{\beta_1^2}{4 \beta_2} - c_{\rm CC}\\ &\quad< u_{\rm FR}(n^*_{\rm FR})= \frac{\beta_1^2}{4 \beta_2} - b_{\rm FR}. \end{aligned}$$
(18)

Thus, irrespective of which consumption candidate is optimal under a CC tariff, both are consumer surplus dominated by the optimal consumption plans under either the FR tariff or the PU tariff.

Proposition 1

(CC choice under certainty) A rational consumer would never choose a cost cap tariff over a flat rate or pay-per-use tariff if he has certainty about his preferences.

4 Tariff consumption under uncertainty

In the following, we relax the assumption that the preferences are known with certainty and assume that \(\beta_1\) is a realization of the random variable \(B_1\) that is distributed according to the probability density function \(f_{B1}(\beta_1)\) and the corresponding cumulative distribution function \(F_{B1}(\beta_1).\) As discussed above, we assume uncertainty in preferences ex-ante (see Hayes 1987; Kridel et al. 1993), which also has an effect on optimal tariff choice. The only assumptions that are made about \(F_{B1}\) are that (1) \(F_{B1} (p_{\rm CC})=0,\) which ensures a positive consumption level for all \(\beta_1\) under all tariffs and (2) that \(0<F_{B1} (\beta_1^{**})<1,\) which ensures that both consumption candidates of the CC tariff, \(n1_{\rm CC}\) and \(n2_{\rm CC},\) are chosen with positive probability. Otherwise, the same logic as under certainty would apply and the CC tariff would never be chosen by a rational consumer.

Under an FR and a PU tariff, it is easy to see that every realization \(\beta_1\) of the random variable \(B_1\) directly determines the optimal consumption level according to Eq.(10). Thus, under these two tariffs, the optimal consumption level is derived by a linear transformation of the random variable \(B_1.\) Consequently, the optimal consumption levels, denoted by \(N_{\rm PU}\) and \(N_{\rm FR},\) respectively, are distributed according to

$$\begin{aligned} F_{N_{\rm PU}} (n)&= \text{Prob}(N_{\rm PU} \le n) = \text{Prob}\left(\frac{B_1 - p_{\rm PU}}{2\beta_2} \le n\right) \\ &= F_{B1} (2 \beta_2 n + p_{\rm PU}),\end{aligned}$$
(19)
$$ F_{N_{\rm FR}} (n)= F_{B1} (2\beta_2 n). $$
(20)

However, under a CC tariff the distribution of \(B_1\) does not linearly transform into the distribution of the optimal consumption levels. To see this, recall from Eq.(15) that given the realization \(\beta_1\) of the random variable \(B_1,\) the consumer will consume \(n1_{\rm CC}\) if \(\beta_1 < \beta_1^{**}\) and \(n2_{\rm CC},\) otherwise. Thus, at \(\beta_1 = \beta_1^{**},\) the consumer is indifferent between (1) consuming \(n1_{\rm CC} = \frac{\beta_1^{**} - p_{\rm CC}}{2 \beta_2}\) under the PU segment of the CC tariff, and (2) consuming \(n2_{\rm CC} =\frac{\beta_1^{**}}{2 \beta_2}\) under the FR segment of the CC tariff. However, since \(n1_{\rm CC} < n2_{\rm CC}\) for any \(\beta_1,p>0\), it follows that there exists a discontinuity in optimal consumption. More precisely, the consumption interval

$$\begin{aligned} \Delta = \left( \frac{\beta_1^{**} - p_{\rm CC}}{2 \beta_2}, \frac{\beta_1^{**}}{2 \beta_2} \right) \end{aligned}$$
(21)

is never optimal. Notice that by substituting (14) into (21), we can derive

$$\begin{aligned} \Delta = \left( {\hat{n}}- \frac{p_{\rm CC}}{4 \beta_2}, {\hat{n}}+ \frac{p_{\rm CC}}{4 \beta_2} \right) , \end{aligned}$$
(22)

which shows that the non-consumption interval is evenly spaced around the cost cap \({\hat{n}}\) and has a width of

$$\begin{aligned} \delta =p_{\rm CC}/{2 \beta_2}. \end{aligned}$$
(23)

This is also demonstrated by Fig. 1. The kink in the cost curve induces the consumer to avoid any consumption around the cost cap level. Intuitively, just below the cost cap level, the consumer would rather use the CC tariff like a flat rate because the negative effect of slightly higher costs is over-compensated by the positive effect of a much higher consumption level.

Fig. 1
figure 1

Cost curve of a cost cap tariff (solid) and optimal indifference curve (dashed) corresponding to preference parameter \(\beta_1^{**}.\) The consumer is indifferent between consuming below or above the cost cap level, but will never consume in the interval \(\Delta \) around the cost cap level

Full size image

Consequently, the distribution of the optimal consumption levels under a cost cap tariff, denoted by \(F_{N_{\rm CC}},\) has zero mass in the interval \(\Delta \) and can be written as follows:

$$\begin{aligned} F_{N_{\rm CC}} (n) = {\left\{ \begin{array}{ll} F_{B1} (2 \beta_2 n + p_{\rm CC}), &\quad \text{if } n \le {\hat{n}} - \frac{p_{\rm CC}}{4 \beta_2} \\ F_{B1} (2 \beta_2 {\hat{n}} + \frac{p_{\rm CC}}{2}), &\quad \text{if } {\hat{n}} - \frac{p_{\rm CC}}{4 \beta_2}< n \le {\hat{n}} + \frac{p_{\rm CC}}{4 \beta_2} \\ F_{B1} (2 \beta_2 n), &\quad \text{if } n > {\hat{n}} + \frac{p_{\rm CC}}{4 \beta_2} \end{array}\right. } \end{aligned}$$
(24)

Proposition 2

(CC consumption) A rational consumer of a cost cap tariff will never (expect to) consume exactly at the level at which the cost cap becomes binding.

5 Tariff choice under uncertainty

5.1 General case

We now investigate the tariff choice of a rational consumer under uncertainty. The representative consumer is considered to be risk-neutral and, thus, he will choose the tariff that maximizes expected consumer surplus. Note that a risk averse consumer is more likely to choose a cost cap tariff. Hence, we study tariff choice under the more conservative restriction of a risk-neutral consumer. From Eq. (11), which describe the consumer surplus under a pay-per-use and flat rate tariff given \(\beta_1,\) and Eq. (16), which describes the consumer surplus under a cost cap tariff, it follows that the expected consumer surplus under each tariff type is

$$\begin{aligned} E[u_{\rm CC}]&= \int\limits_{0}^{\beta_1^{**}} \underbrace{\frac{\left( \beta_1 - p_{CC}\right) ^2}{4\beta_2}}_{=u_{\rm CC}(n1_{\rm CC})}f_{B1}(\beta_1)\,\text{d}\beta_1 + \int\limits_{\beta_1^{**}}^\infty \underbrace{\left( \frac{\beta_1^2}{4\beta_2} - c_{\rm CC}\right) }_{=u_{\rm CC}(n2_{\rm CC})}f_{B1}(\beta_1)\,\text{d}\beta_1 \end{aligned}$$
(25)
$$\begin{aligned} E[u_{\rm FR}]&= \int\limits_{0}^{\infty } \underbrace{\left( \frac{\beta_1^2}{4\beta_2} -b_{\rm FR}\right) }_{=u_{\rm FR}(n^*_{\rm FR})} f_{B1}(\beta_1)\,\text{d}\beta_1 \end{aligned}$$
(26)
$$\begin{aligned} E[u_{\rm PU}]&= \int\limits_{0}^{\infty } \underbrace{\frac{\left( \beta_1 - p_{\rm PU}\right) ^2}{4\beta_2}}_{=u_{\rm PU}(n^*_{\rm PU})} f_{B1}(\beta_1)\,\text{d}\beta_1. \end{aligned}$$
(27)

We can then write the difference in expected consumer surplus between a CC tariff and an FR tariff as follows (see Appendix 5 for details):

$$\begin{aligned} &E[u_{\rm CC}]- E[u_{\rm FR}] \\ &\quad=\frac{1}{4\beta_2} \int\limits_{0}^{\infty } \beta_1^2 f_{B1}(\beta_1)\,\text{d}\beta_1 - \frac{2 p_{\rm CC}}{4\beta_2} \underbrace{\int\limits_{0}^{\beta_1^{**}} \beta_1 f_{B1}(\beta_1)\,\text{d}\beta_1}_{= F_{B1}(\beta_1^{**}) E[B_1|B_1 \le \beta_1^{**}]} \\ &\qquad+ \frac{p_{\rm CC}^2}{4\beta_2} \underbrace{\int\limits_{0}^{\beta_1^{**}} f_{B1}(\beta_1)\,\text{d}\beta_1}_{=F_{B1}(\beta_1^{**})} - c_{\rm CC} \underbrace{\int\limits_{\beta_1^{**}}^\infty f_{B1}(\beta_1)\,\text{d}\beta_1}_{=1-F_{B1}(\beta_1^{**})} \\ &\qquad- \frac{1}{4\beta_2} \int\limits_{0}^{\infty } \beta_1^2 f_{B1}(\beta_1)\,\text{d}\beta_1 + b_{\rm FR} \underbrace{\int\limits_{0}^{\infty } f_{B1}(\beta_1)\,\text{d}\beta_1}_{=1}, \end{aligned}$$
(28)

where \(F_{B1}(\beta_1^{**})\) is the probability that \(B_1 \le \beta_1^{**}\) and \(E[B_1|B_1 \le \beta_1^{**}]\) is the expected value of \(B_1\) under the constraint that \(B_1 \le \beta_1^{**}.\) Using \(c_{\rm CC} = p_{\rm CC}/{4\beta_2} (2\beta_1^{**} - p_{\rm CC})\) from Eq. (14), we can derive (see Appendix 5):

$$\begin{aligned} &E[u_{\rm CC}]- E[u_{\rm FR}] \\ &\quad=\underbrace{b_{\rm FR} - c_{\rm CC}}_{< 0} +F_{B1}(\beta_1^{**}) \underbrace{\frac{p_{\rm CC}}{2\beta_2}}_{\delta }\; \underbrace{\left( \beta_1^{**} - E[B_1 | B_1 \le \beta_1^{**}] \right) }_{>0}. \end{aligned}$$
(29)

Equation (29) demonstrates that the CC tariff may yield a higher expected consumer surplus than the FR tariff (1) if the cost cap \(c_{\rm CC}\) is not much larger than the flat rate price \(b_{\rm FR}\) and (2) if low values of \(\beta_1,\) i.e., \(\beta_1 < \beta_1^{**},\) are realized with a sufficiently high probability. The first condition ensures that the first, negative summand of Eq. (29) is not too small, whereas the second condition ensures that the second, positive summand is rather large.

Likewise, the difference between the expected consumer surplus of a CC tariff and a PU tariff can be written as (see Appendix 5 for details):

$$\begin{aligned} &E[u_{\rm CC}]- E[u_{\rm PU}] \\ &\quad=\frac{1}{4\beta_2} \left(p_{\rm CC}^2 \underbrace{\int\limits_{0}^{\beta_1^{**}} f_{B1}(\beta_1)\,\text{d}\beta_1}_{=F_{B1}(\beta_1^{**})} -2 (p_{\rm CC} - p_{\rm PU}) \underbrace{\int\limits_{0}^{\beta_1^{**}} \beta_1 f_{B1}(\beta_1)\,\text{d}\beta_1}_{= F_{B1}(\beta_1^{**}) E[B_1|B_1 \le \beta_1^{**}]}\right. \\ &\qquad- 4\beta_2 c_{\rm CC} \underbrace{\int\limits_{\beta_1^{**}}^\infty f_{B1}(\beta_1)\,\text{d}\beta_1}_{=1-F_{B1}(\beta_1^{**})} + 2 p_{\rm PU} \underbrace{\int\limits_{\beta_1^{**}}^\infty \beta_1 f_{B1}(\beta_1)\,\text{d}\beta_1}_{= (1-F_{B1}(\beta_1^{**})) E[B_1|B_1 \ge \beta_1^{**}]} \\ &\qquad\left.- p_{\rm PU}^2 \underbrace{\int\limits_0^\infty f_{B1}(\beta_1)\,\text{d}\beta_1}_{=1}\right),\end{aligned}$$
(30)

where \(1-F_{B1}(\beta_1^{**})\) is the probability that \(B_1 \ge \beta_1^{**}\) and \(E[B_1|B_1 \ge \beta_1^{**}]\) is the expected value of \(B_1\) under the constraint that \(B_1 \ge \beta_1^{**}.\)

Again, replacing \(c_{\rm CC} = p_{\rm CC}/{4\beta_2} (2\beta_1^{**} - p_{\rm CC})\) yields (see Appendix 5):

$$\begin{aligned} &E[u_{\rm CC}]- E[u_{\rm PU}] = \frac{1}{4\beta_2} \left( \underbrace{p_{\rm CC}^2 - p_{\rm PU}^2}_{>0} \right.\\ &\qquad+ 2 p_{\rm PU} \underbrace{\left( F(\beta_1^{**})E[B_1 | B_1 \le \beta_1^{**}] + (1-F(\beta_1^{**}))E[B_1 | B_1 \ge \beta_1^{**}] \right) }_{E{[B_1]}} \\ &\qquad\left.- 2 p_{\rm CC} \underbrace{\left( F(\beta_1^{**})E[B_1 | B_1 \le \beta_1^{**}] + (1-F(\beta_1^{**}))\beta_1^{**} \right) }_{={\hat{E}} \le E{[B_1]}} \right) \end{aligned}$$
(31)
$$\begin{aligned} E[u_{\rm CC}]- E[u_{\rm PU}]&= \frac{1}{4\beta_2} \left( \underbrace{(p_{\rm CC} - p_{\rm PU}) (p_{\rm CC} + p_{\rm PU} - 2 (E[B_1] + {\hat{E}} ))}_{<0} \right.\\ &\quad\left.+ 2 \underbrace{\left( E[B_1]\;p_{\rm CC} - {\hat{E}}p_{\rm PU} \right) }_{>0} \right), \end{aligned}$$
(32)

where \(E[B_1]\) is the expected value of \(B_1\) and \({\hat{E}}\) is a degenerate case of the expected value of \(B_1,\) where \(E[B_1|B_1 \ge \beta_1^{**}] = \beta_1^{**}.\) Of course, generally, it holds that \(E[B_1|B_1 \ge \beta_1^{**}] \ge \beta_1^{**}.\) Thus, it can be concluded that \({\hat{E}} \le E{[B_1]}.\)

Equation (32) reveals that the expected consumer surplus of a CC tariff may exceed that of a PU tariff if (1) the marginal price of the CC tariff, \(p_{\rm CC},\) is not much larger than the marginal price of the PU tariff, \(p_{\rm PU}\) and (2) if high values of \(\beta_1,\) i.e., \(\beta_1 > \beta_1^{**}\) are sufficiently likely. Again, the first condition ensures that the first, negative summand of Eq. (32) is not too small, whereas the second condition ensures that the second, positive summand is rather large because \(E[B_1] \gg {\hat{E}}.\)

Notice that in order for the CC tariff to dominate both the FR and the PU tariff, the consumer must face a sufficiently high probability for low and high values of \(\beta_1.\) Evidently, the CC tariff must additionally be reasonably priced in comparison to the FR and PU tariff.

5.2 Example

To exemplify the impact of the probability distribution and the pricing of the CC tariff on the choice of CC tariffs, consider the following uniform probability density function of \(B1:\)

$$\begin{aligned} f_{B1}(\beta_1) = {\left\{ \begin{array}{ll} 1/{\text{range}}, &\quad \text{if } \text{offset} - \text{range}/{2} <\beta_1<\text{offset} + \text{range}/{2} \\ 0, &\quad \text{otherwise} \end{array}\right. } \end{aligned}$$
(33)

It is characterized by the two parameters offset and range which characterize the expected level of the preference parameter \(\beta_1,\) i.e., \(E[B_1],\) and the level of uncertainty about \(\beta_1,\) respectively.

Fig. 2
figure 2

Expected utility under optimal tariff choice for different preference levels (offset) and uncertainty levels (range). The figure is derived for the values \(p_{\rm PU}=0.10,\,p_{\rm CC}=0.12,c_{\rm CC}=45,b_{\rm FR}=40,\beta_2=0.001\)

Full size image

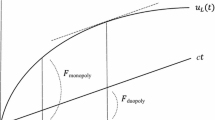
Figure 2 shows the optimal tariff choice of a risk-neutral consumer for different values of offset and range. In line with Proposition 1, the CC tariff is never optimal if the level of uncertainty is too low. In this case and depending on the offset of the preference parameter, i.e., whether the consumer is a ‘light’ or ‘heavy’ user, the FR or PU tariff is chosen, respectively. In reverse, the CC tariff is optimal in a region that is characterized by an intermediate offset level and a large range. Intuitively, this means that the CC tariff is optimal when a consumer has a high uncertainty about his demand, with both a high probability that the demand will be low and a high probability that the demand will be high. The corresponding profits of a provider who offers a choice of all three tariffs are illustrated in Fig. 3. Notably, offering a cost cap tariff over a pay-per-use tariff increases both consumer’s expected utility as well as provider’s profits when the level of uncertainty is rather large. To see this, notice in Fig. 3 that in this case the cost cap tariff is preferred by consumers and that expected profits jump to a higher level compared to the expected profit under a pay-per-use tariff. In Appendix 3, we also discuss the possibility of a provider to offer a single tariff on the market and thus optimize his profits by limiting consumer’s choice.

Fig. 3
figure 3

Corresponding provider’s expected profits depending on optimal tariff choice for different preference levels (offset) and uncertainty levels (range). The figure is derived for the values \(p_{\rm PU}=0.10,\,p_{\rm CC}=0.12,c_{\rm CC}=45,b_{\rm FR}=40,\beta_2=0.001\)

Full size image

Figure 4 additionally demonstrates the impact of the pricing of the CC tariff on tariff choice. More precisely, the figure shows the indifference hyperplanes between the different tariff options depending on the pricing ratios of the tariffs \((p_{\rm CC}/{p_{\rm PU}},c_{\rm CC}/{b_{\rm FR}})\) and the consumer’s preference level (offset). It can be seen that the PU and FR tariff are chosen over the CC tariff if the latter is priced too high, i.e., if \(p_{\rm CC}/{p_{\rm PU}}\) or \(c_{\rm CC}/{b_{\rm FR}}\) are sufficiently large, respectively. In this case, the choice between the FR and the PU tariff is independent of the pricing of the CC tariff, of course, and depends only on the expected level of demand (offset).

Fig. 4
figure 4

Optimal tariff choice for different preference levels (offset) and parameterizations of the cost cap tariff in relation to the pay-per-use and flat rate tariff \((p_{\rm CC}/{p_{\rm PU}}\) and \(c_{\rm CC}/{b_{\rm FR}}).\) The figure is derived for the values \(p_{\rm PU}=0.10,b_{\rm FR}=40,\beta_2=0.001\) and \(\text{range}=1\)

Full size image

To conclude, the example demonstrates that CC tariffs may indeed present an optimal tariff choice for a rational and risk-neutral consumer under certain parameter conditions. In particular, these depend on a consumer’s level of uncertainty about his preferences, which, by Eqs. (19) and (24), directly translates into demand uncertainty.

Proposition 3

(Choice of CC tariffs under uncertainty) A (reasonably priced) cost cap tariff may be chosen over a flat rate and a pay-per-use tariff by a risk-neutral consumer in the presence of a sufficiently high demand uncertainty.

6 Empirical evaluation

In the following, an empirical evaluation is presented to demonstrate the applicability of the previously developed consumer surplus model. To this end, the consumer surplus model is evaluated based on survey data. We contracted with a professional marketing research agency to conduct a survey online with a sample that is representative of the population of German mobile telephony users. A total of 122 respondents completed the survey, which consisted of two parts.

In the first part, respondents had to imagine that they use a PU tariff for mobile telephony and that this is the only tariff type available to them. In a repeated open-ended question design (Miller et al. 2011; Schulze et al. 2005), the respondents had to estimate their expected average monthly mobile telephony usage (in min) under a PU tariff, for each of the following minute prices (in €/min) \(p_{\rm PU}=\{0.40, 0.20, 0.10, 0.05\}.\) As will be described in detail below, the four consumption tuples \((E[N_{\rm PU}], p_{\rm PU})\) that are obtained in this part of the survey are used to estimate a respondent’s individual preference parameters \(E[B_1]\) and \(\beta_2,\) which are then employed to calibrate the individual consumer’s surplus function.

In the second part, respondents were presented six different mobile telephony tariffs. Each tariff type (PU, CC, FR) occurred twice with two different price levels (see Table 3). For each tariff, respondents had to estimate their minimum, average and maximum monthly usage (\(n_{\rm min},n_{\rm avg},n_{\rm max}\) in min). In addition, the attractiveness of each tariff had to be rated on a seven-point interval scale (1 = very unattractive, 7 = very attractive). As will be described below, the consumption data that are obtained in this part of the survey are used at first to estimate the individual level of uncertainty (from the difference of \(n_{\rm min}\) and \(n_{\rm max}\) under the PU tariff), which, together with the preference parameters obtained through the first part of the survey, completes the calibration of the individual consumer’s surplus function. The individually calibrated consumer’s surplus function can then be used to predict (1) the respondent’s stated average usage, \(n_{\rm avg},\) under a given tariff and (2) the respondent’s tariff rating.

Table 3 Tariffs to be evaluated by respondents
Full size table

6.1 Calibration of the individual consumer surplus function

At first, the respondent’s individual consumer’s surplus function is estimated using the data from the first part of the survey as well as the stated average maximum and minimum usage under the PU tariff from the second part of the survey as follows: In a similar fashion as Schulze et al. (2005), the data from the repeated open-ended question design in the first part of the survey are used to estimate the individual preference parameters \(E[B_1]\) and \(\beta_2.\) To this end, we utilize Eq. (10) which provides that \(n^*_{\rm PU} = \frac{\beta_1 - p_{\rm PU}}{2 \beta_2}.\) Consequently, a consumer should expect to consume \(E[N_{\rm PU}]\) minutes under the PU tariff according to:

$$\begin{aligned} E[N_{\rm PU}]=\frac{E[B_1]}{2 \beta_2}-\frac{1}{2 \beta_2}p_{\rm PU}. \end{aligned}$$
(34)

Then, using the four consumption price tuples \(\left( E[N_{\rm PU}],p_{\rm PU}\right) \) which the respondent stated in the first part of the survey (i.e., the stated average usage \(E[N_{\rm PU}]\) at minute prices (in €/min) of \(p_{\rm PU}=\{0.40, 0.20, 0.10, 0.05\})\), the following ordinary least squared regression can be conducted for each individual:

$$\begin{aligned} E[N_{\rm PU}]=\gamma_{0}+\gamma_{1}\; p_{{\rm PU}}+\epsilon, \end{aligned}$$
(35)

where \(\gamma_0\) and \(\gamma_1\) are the regression coefficients that are estimated and \(\epsilon \) is the error term.

With the help of Eq. (34), the coefficients \(\gamma_{0}\) and \(\gamma_{1}\) can then be transformed into the parameters \(E[B_1]\) and \(\beta_{2}\) of the consumer surplus function as follows:

$$\begin{aligned} &\gamma_{0}=\frac{E[B_1]}{2 \beta_{2}}\quad\Leftrightarrow\quad E[B_1]=2 \beta_{2} \gamma_{0}\end{aligned}$$
(36)
$$\begin{aligned} &\gamma_{1}=-\frac{1}{2 \beta_{2}}\quad\Leftrightarrow\quad \beta_{2}=-\frac{1}{2 \gamma_{1}}. \end{aligned}$$
(37)

Finally, to completely specify a respondent’s consumer surplus function, it is necessary to derive the individual distribution of \(B_1\) in addition to \(E[B_1].\) To this end, as in (33), a uniform distribution of \(f_{B1}(\beta_1)\) is assumed that is centered around \(E[B_1]\) (i.e., offset):

$$\begin{aligned} \beta_1 \sim {\mathcal U}(\beta_{1{\rm min}}=E[B_1]-\text{range}/{2},\beta_{1{\rm max}}=E[B_1]+\text{range}/{2}) \end{aligned}$$
(38)

Thereby, the range of the distribution [see (33)] is determined by the minimum \((\beta_{1{\rm min}})\) and maximum \((\beta_{1{\rm max}})\) value of \(\beta_1:\)

$$\begin{aligned} \text{range}\equiv \beta_{1{\rm max}}-\beta_{1{\rm min}}. \end{aligned}$$
(39)

Solving Eq. (10) for \(\beta_1\) yields \(\beta_{1}=2\beta_2n+p_{\rm PU}.\) Consequently, range can be computed from the stated minimum \((n_{\rm min})\) and maximum \((n_{\rm max})\) usage under the PU tariff in the second part of the survey as follows:

$$\begin{aligned} \text{range}\equiv \beta_{1{\rm max}}-\beta_{1{\rm min}}=2\beta_2(n_{\rm max}-n_{\rm min}). \end{aligned}$$
(40)

This completes the individual estimation of a consumer’s surplus function. An exemplary estimation of an individual consumer’s surplus function can be found in the Appendix 2.

We then evaluate our model in two different ways. First, given the expected usage under a given tariff (derived from the calibrated consumer’s surplus function) is compared to the reported average usage under each given tariff. Second, the expected consumer’s surplus (also derived from the calibrated consumer’s surplus function) is used as a predictor for the reported tariff rating.

6.2 Evaluation of the usage prediction

Given the individual preference parameters (\(E[B_1]\equiv \text{offset},\beta_2\) and range) a respondent’s expected usage is calculated according to Eqs. (10), (24) and (33) for each of the six tariffs. Note that each consumer’s preference parameters were derived independently of the reported average usage of the respective consumer, i.e., \(n_{\rm avg}.\) Thus, we use an OLS regression (Model 1a in Table 4) to study the correlation of predicted and reported average usage, while controlling for the different tariffs and price levels using dummy variables. To account for individual differences in rating behavior, a fixed-effect estimation is considered, which allows to have an individual intercept for each respondent, whereas the regression coefficients are constrained to be the same across all respondents:

$$\begin{aligned} n_{{\rm avg},i,t}=\gamma_{0}+\gamma_{1}E[N]_{i,t}+\gamma_{3}D_{t,{\rm CC}}+\gamma_{4}D_{t,{\rm FR}}+\gamma_{5}D_{t,{\rm HighPrice}}+\zeta_{i}+\epsilon_{i,t} \end{aligned}$$
(41)
\(D_{t,{\rm CC}}:\) :

Dummy variable identifying a cost cap tariff

\(D_{t,{\rm FR}}:\) :

Dummy variable identifying a flat rate tariff

\(D_{t,{\rm HighPrice}}:\) :

Dummy variable identifying the price level (1 = high or 0 = low) of each tariff

\(\zeta_{i}:\) :

Fixed-effect of subject \(i.\)

\(\epsilon_{i,t}:\) :

Error term

Furthermore, we use the median relative absolute error (MdRAE) (Armstrong and Collopy 1992) to evaluate the forecasting applicability of our model. The MdRAE is a measure based on relative errors. Thereby, the relative absolute error (RAE) states the relation of the prediction accuracy of our model compared to a simple mean forecasting model. It is calculated by the absolute difference between the forecast of our model and the actual stated usage for each respondent, divided by the absolute difference of a simple forecasting model, which predicts the stated usage by the mean of all stated usage:

$$\begin{aligned} \text{RAE}_i=\frac{|n_{{\rm avg},i,t}-E[N]_{i,t}|}{|n_{{\rm avg},i,t}-{\bar{n}}_{\rm avg}|} \end{aligned}$$
(42)

In contrast to measures based on percentage errors, such as the mean absolute percentage error (MAPE), relative errors do not suffer from skewed distributions when the data include small counts (Hyndman and Koehler 2006). Nevertheless, for completeness we state that our model exhibits an MAPE of 0.886, which outperforms a simple mean forecasting model with an MAPE of 3.974. However, as our data include small counts, we use the MdRAE as a relative error, which is less sensitive against outliers. Thereby, the MdRAE is the median of all respondents’ relative absolute errors in our data set:

$$\begin{aligned} \text{MdRAE}=\text{median}(\text{RAE}_i) \end{aligned}$$
(43)

Our data set exhibits an MdRAE of 0.303, which states that half of our model’s predictions have an error, which is a third or less compared to the error of the naive model. Thus, we can conclude that our model has an improved forecast applicability compared to a naive approach (Hyndman and Koehler 2006).

Furthermore, the coefficient in our regression in Table 4 is significant and with 0.901 close to one, indicating a good prediction quality (Iyengar et al. 2008, p.201). However, the theoretical model has a slight tendency to overestimate the reported usage. This is particularly true for the reported usage under the tariffs with a high price level. Moreover, we find that respondents tend to overestimate their usage under an FR tariff. This so-called overestimation effect is well known from previous research (see, e.g., Nunes 2000). Finally, the regression model explains 80.6 % of the total variance, indicating a good model fit.

6.3 Evaluation of consumer surplus prediction

Given the individual preference parameters, the consumer’s surplus for each tariff is predicted according to Eqs. (25), (26) and (27). Note that the expected consumer’s surplus takes into account tariff pricing, as well as the consumer’s preferences and uncertainty. A respondent’s expected consumer surplus under a given tariff is then regressed on his rating for this tariff, using the same type of regression model and controls as in (41):

$$\begin{aligned} \text{rating}_{i,t}=\gamma_{0}+\gamma_{2}E[u]_{i,t}+\gamma_{3}D_{t,{\rm CC}}+\gamma_{4}D_{t,{\rm FR}}+\gamma_{5}D_{t,{\rm HighPrice}}+\zeta_{i}+\epsilon_{i,t} \end{aligned}$$
(44)

Model 2a in Table 4 shows that there exists a significant and positive relationship between the expected consumer’s surplus derived from the theoretical model and a respondent’s tariff rating. Moreover, a significant portion of the total variance can be explained, which indicates a good model fit. Furthermore, we find a significant tariff bias. In comparison to the PU tariff, the CC tariff is assigned a 0.381 higher rating score, everything else equal. By far the largest bias is found for the FR tariff, however. This finding is in line with earlier research on tariff bias (see, e.g., Lambrecht and Skiera 2006).

6.4 Robustness of prediction

To additionally control for random coefficients with respect to expected usage, we report the results of a mixed-effects regression model (Models 1b and 2b), which also controls for potential dependence of observations nested within one subject:

$$\begin{aligned} n_{{\rm avg},i,t}=\gamma_{0}+(\gamma_{1}+\gamma_{1i})E[N]_{i,t}+\gamma_{3}D_{t,{\rm CC}}+\gamma_{4}D_{t,{\rm FR}}+\gamma_{5}D_{t,{\rm HighPrice}}+\zeta_{i}+\epsilon_{i,t}\end{aligned}$$
(45)
$$\begin{aligned} \text{rating}_{i,t}=\gamma_{0}+(\gamma_{2}+\gamma_{2i})E[u]_{i,t}+\gamma_{3}D_{t,{\rm CC}}+\gamma_{4}D_{t,{\rm FR}}+\gamma_{5}D_{t,{\rm HighPrice}}+\zeta_{i}+\epsilon_{i,t} \end{aligned}$$
(46)

\(\zeta_i, \gamma_{i1}\) and \(\gamma_{i2}\) are random effects that are common to observations from the same subject \(i.\) The random effects in these models are assumed to be independently normally distributed with mean zero and with a variance estimated through our regression. As can be seen from Table 4, the results are qualitatively the same as for the fixed effects model. However, note that the estimation of a random effects model may introduce a significant bias in the estimation (cf. Kennedy 2008, S.285), for which reason the fixed effects model is preferred.

Table 4 Fixed and mixed-effects OLS regressions of model predictions on reported values
Full size table

7 Conclusions

This paper has developed a consumer surplus model under cost cap tariffs by which the optimal consumption and choice under this new tariff type can be determined. Under a reasonable set of assumptions, we find that cost cap tariffs are only an optimal tariff choice for those consumers that face considerable uncertainty about their future demand, such that both relatively low and relatively high consumption levels are considered feasible. In this case, cost cap tariffs provide an insurance against extraordinary high costs (like a flat rate), but also cost flexibility in case of low demand (like a pay-per-use tariff). Therefore, consumers are willing to accept a higher marginal price compared to a pay-per-use tariff as well as a cost cap which is priced above the fixed fee of a flat rate. It was demonstrated that the model is useful for predicting the actual tariff usage and rating. The proposed model may, therefore, serve as a benchmark for future empirical research.

However, some limitations apply. The present model merely considers the rational choice of a risk-neutral consumer. However, our empirical results suggest that the rational tariff choice is systematically biased, e.g., due the above-mentioned insurance effect (Lambrecht and Skiera 2006), the flexibility effect (Krämer and Wiewiorra 2012), the overestimation effect (Nunes 2000), or brand effects (Schlereth and Skiera 2012). The detailed empirical investigation of the extent of a bias for cost cap tariffs, in particular, in relation to the well-known flat rate bias, therefore, seems to be a fruitful avenue for future research. Furthermore, for expositional clarity, our consumer surplus model assumes a quadratic functional form, as in Lambrecht et al. (2007) and Iyengar et al. (2008). However, alternative functions might be more appropriate to describe consumer surplus as discussed by Skiera (1999) and Albers and Skiera (2006). Thus, future work should address the implications and suitability of alternative modeling approaches.