1 Introduction

With the advancement of precision engineering technology and optical science [1], the demand for the development of large optical elements is increasing due to their applications in various fields of study, such as space/astronomical optics [2,3,4], accelerators [5,6,7], and high-power lasers [8, 9]. In particular, the development of high-quality large scale freeform optics with reduced weight is crucial for improving the performance of the optical systems regarding the compact configuration and beam transportation. Mechanical processing, such as a diamond turning machining (DTM), is widely known as one of the most suitable approaches for the precise manufacturing of large-scale freeform optics. Conventionally, surface finishing process [10,11,12] followed by machining process is considered as one of the standard procedures to improve the surface quality of optical elements. Further, the ultraprecision machining technology has been rapidly developed through numerous studies, such as parameter optimization [13,14,15,16,17] and random path generation [18, 19]. Although the surface finishing process has been developed as a way to indisputably improve the quality of optical surfaces, it is time-consuming and less economical owing to the additional efforts that are required after the machining process. In addition, as the size of the optical elements increase and their surface shapes become complicated, it is very challenging to reach high-quality surface figure and its roughness even if the surface finishing process is conducted. Thus, if we skip the final surface finishing process and secure a product with the desired optical performance only through the mechanical processing, such as DTM, it is expected to be able to maximize the efficiency of the whole optical manufacturing process.

During mechanical processing with a DTM, periodic structures, such as roughness (with a period of several μm) and waviness (with a period of several mm) are commonly formed mainly due to the radius/speed of the cutting tool and environmental factors (like temperature/humidity), respectively [20, 21]. It is important to minimize the roughness and waviness, because they will produce Bragg diffraction and Bragg scattering, respectively, [22, 23] in the laser beam profile propagating in the optical system. In particular, the waviness can affect the shape of the laser beam profile reflected from the optical surface over a long propagation distance (see Fig. 1a). As shown in Fig. 1b, considering the geometry of diffracted beam modes from the periodic structure, the decoupling distance (when the modes no longer overlap spatially) for the 0th and 1st order beam modes is given by

$$l = \frac{r}{{\sin \left( {\frac{{\Delta \theta_{0,1} }}{2}} \right)}} = \frac{r}{{\sin \left[ {\frac{1}{2}\left| {\theta_{i} + \sin^{ - 1} \left( {\frac{\lambda }{d} - \sin \theta_{i} } \right)} \right|} \right]}},$$
(1)

where l is decoupling distance, Δθ0,1 is the angle between the 0th and 1st order diffracted beam, θi is the angle of incidence, r is the beam radius, λ is the wavelength of the beam, and d is the period of the waviness on the optical surface. For optical elements on the scale of a few tens of millimeters or less, surface finishing processes such as polishing are typically applied to eliminate the waviness. In this case, even if some waviness remains, Bragg scattering produced by the periodic structure is not a dominant factor because the period is not so small compared to the size of optical elements. On the other hand, for optical elements larger than a few tens of millimeters, Bragg scattering can be more significant due to the high density of the periodic waviness structure relative to the size of the element. In particular, for large-scale freeform optics, removing the waviness is challenging even for advanced surface finishing processes as it requires nanometer-scale precision over the full freeform optical surface. In addition, since the usual surface finishing process works along a pre-calibrated path rather than correcting the position in real-time, it can be difficult to completely remove the waviness caused by various environmental factors during the production process. Above all, the interference caused by Bragg scattering does not simply degrade the optical performance, it renders the optical element useless as well.

Fig. 1
figure 1

a Schematic diagram of a large-scale freeform optics produced by a DTM. Due to the waviness with a period of several mm on the optical surface generated during the manufacturing, interference fringes are formed from diffracted beam modes (mainly − 1st, 0th, and 1st) caused by Bragg scattering. b Geometry of the diffracted beam modes (− 1st, 0th, and 1st) reflected from the optical surface with waviness, used to derive Eq. (1)

Full size image

Various studies on periodic micro/nano structure-based diffractive optical elements have been conducted. It is generally fabricated using the lithography technology as a part of the semiconductor process. It can also be manufactured by laser or mechanical processing. By applying the periodic structure, which differs depending on the wavelength of light, it is widely applied to polarizers, grating couplers, modulators, spectrometers, etc. [24, 25]. Recently, spectroscopic studies were actively conducted from the acoustic to x-ray region by maximizing the spectral resolution [26]. This micro/nano structure-based diffraction is a very useful technique for spectroscopic studies. On the other hand, for reflective (or transmissive) optical components (such as mirror and lens), which do not require spectral characteristics, Bragg scattering/diffraction can be a major reason for the deterioration of spatial quality (shape and intensity) of the beam.

Recent studies investigating the Bragg scattering produced by waviness on optical surfaces confirmed that it has a significant effect on the propagating beam profile due to the interference patterns caused by the Bragg scattering, even at extremely small aspect ratios (~ 10–5) [22, 23]. In [22], it was reported that the reflected light experiences Bragg scattering even on the optical surface, which has a periodic structure of the millimeter scale. Under this condition, the beam intensity changes periodically due to the interference between the 0th, 1st, and − 1st order diffracted beam modes, as the beam propagates after reflection from the optical surface. In [23], a generalized equation was presented for two diffracted beam modes represented by the arbitrary m-th and n-th order, which determines the period of constructive interference formed by Bragg scattering observed in [22]. In addition, two theoretical calculations—an analytical calculation based on the interference equation, and a numerical simulation based on Fourier optics—were conducted for all the diffracted beam modes to reflect the effects of higher-order diffraction. On the other hand, this study presents the first experimental result of maximizing the effectiveness of Bragg scattering caused by a periodic structure on the optical surface, confirmed through [22, 23] to improve the performance of the optical surface. In this study, we provide a new perspective on improving the laser beam profile by avoiding interference between the diffracted beam modes caused by Bragg scattering without attempting to eliminate the waviness through additional surface finishing processes. Since the scattering angle of higher modes is determined by the period of the waviness, engraving an artificial periodic structure with a period of a few hundred microns (compared to the original waviness period of a few millimeters) increases the scattering angle between the diffracted beam modes. Consequently, the beam quality could be improved at a propagation distance that spatially separates the diffracted beam modes only by DTM without the surface finishing process, such as polishing.

2 Experiment and Analysis

Two types of planar optical samples [aluminum (Al) plated with nickel phosphorus (NiP) with a diameter of 100 mm] were fabricated to measure and compare two laser beam profiles reflected from them. One is a typical planar sample (with a waviness period of several millimeters as mentioned above) produced naturally through DTM-based machining (Nanoform L1000) in a well-controlled environment (19.5 ± 0.02 °C temperature and 35 ± 5% humidity), while the other is a planar sample with an artificially produced periodic structure with a period of a few hundred microns. Specifically, the naturally produced sample had a period of 7 mm and an amplitude of ~ 50 nm, while the other sample had an artificially produced period of 0.5 mm and an amplitude of ~ 50 nm. The amplitudes of the two samples were kept at the same height to isolate the effect of the different periods for comparison.

The machining and tool specifications of DTM and machining path between workpiece and tool are given by Fig. 2. In this machining condition (see Fig. 2a), the naturally produced sample had a period of 7 mm and an amplitude of 50 nm, whereas the other sample had an artificially produced period of 0.5 mm and amplitude of 50 nm. The difference in the machining condition between the two optical samples is in the feed rate (μm/rev). The feed rate for the sample with 7 mm period and 50 nm amplitude is given by 1 μm/rev, whereas that for the sample with 0.5 mm period and 50 nm amplitude is given by 4 μm/rev. Considering the spindle speed of 1000 rev/min, these feed rates correspond to 1 mm/min (0.7 mm period waviness) and 4 mm/min (0.5 mm, artificial), respectively. In this condition, the machining path between the workpiece and tool for the two optical samples is described in Fig. 2b. For the naturally produced sample with a period of 7 mm and amplitude of 50 nm, the tool path is transferred from (x, z) = (50, 0) to (0, 0) with a function z(x) = 0·x (for 0 ≤ x < 50). Under the feed rate of 1 μm/rev, the optical surface leaves the periodic structure with 7 mm periodic waviness and the 50 nm amplitude due to the periodic variation of the environmental temperature. On the other hand, for an artificially produced period of 0.5 mm and amplitude of 50 nm, the tool path is transferred from (x, z) = (50, 0) to (0, 0) with a function z(x) = 0.00005·sin(4πx) (here, dimension is in mm) (for 0 ≤ x < 50). Under the feed rate of 4 μm/rev, the optical surface finally leaves the periodic structure with 0.5 mm artificial period and 50 nm amplitude.

Fig. 2
figure 2

a Machining and tool specifications for DTM. b Machining path between workpiece and tool

Full size image

This manufacturing process using only DTM without the final surface finishing step (such as the polishing process), supports green manufacturing. The polishing materials (e.g., polishing compounds such as cerium oxide and zirconium oxide, or polishing pads such as suede and polyurethane) used in the polishing process, which is a typical example of the final surface finishing process, can be harmful to our environment. Moreover, a considerable amount of waste is generated at the end of the polishing process, and the cleaning process generates contaminated alcohol, wastewater, and used cleaning tissues as wastes. The processes for their safe disposal are complicated. By omitting the final surface finishing step, such as the polishing process, we can avoid the generation of wastes that can pollute the environment.

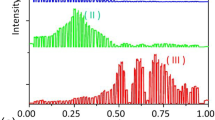
The two-dimensional (2D) surface topography and one-dimensional (1D) line profiles of the two samples were obtained with a Fizeau interferometer (S150, Apre Instruments) and a white light interferometer (CCI Optics, Taylor Hobson), respectively. Figure 3a and b show 2D images of the surface topography while Fig. 3c and d depict line profiles of the surface. Examining the surface topography, circular structures with a period of 7 mm (Fig. 3a) and 0.5 mm (Fig. 3b) were observed in the lateral directions over the entire optical surfaces. Since Fig. 3b contains a large number of periods in the displayed region, it is difficult to clearly distinguish the periodic structure compared to Fig. 3a. To complement this, the line profiles obtained are able to more clearly depict the amplitude and period of the relatively short-period structure formed on the optical surface. As can be seen in Fig. 3c, the sample with a period of 0.5 mm has an amplitude of ~ 50 nm (red solid line) over the measured distance of 0.85 mm. In the case of the sample with a period of 7 mm, the amplitude appears to be approximately zero over the same 0.85 mm distance (black solid line) since the measured region is small compared to the relatively long 7 mm waviness period. However, Fig. 3d shows that the amplitude of the waviness with a period of 7 mm obtained from the rectangular yellow dotted line in Fig. 3a also has an amplitude of ~ 50 nm when the line profile is measured over ~ 13 mm. Thus, the overall periods and amplitudes on both sample surfaces were appropriately fabricated through the mechanical DTM process. It was predicted that a planar sample with a waviness of 7 mm period and an amplitude of 50 nm (aspect ratio: 1.4 × 10–5) would form interference fringes in the propagating laser beam profile by Bragg scattering [22, 23]. The experimental configuration for measuring the laser beam profiles propagating after reflection from the two planar samples is described in detail in [22]. A laser beam with a wavelength of 808 nm was incident on the samples, and then the reflected beam profiles were measured with a beam profiler at two different propagation distances. In order to minimize any deterioration of the beam quality, which may be caused by transmissive optics, only reflective optics were utilized in this configuration. The 2D beam profiles reflected from the sample surface with the naturally formed waviness (period of 7 mm and amplitude of 50 nm) are shown in Fig. 4. Figure 4a shows the 2D beam profile measured at a propagation distance of 600 mm, while Fig. 4b shows the beam profile measured at a propagation distance of 1800 mm. Both profiles were measured after recollimation of the beam for detection. It is clear that interference fringes are formed by Bragg scattering at both distances. Thus, the waviness may be a critical factor degrading the quality of beam profile, since the interference fringes produce significant intensity variations despite the extremely small aspect ratio (1.4 × 10–5). Additionally, the center intensity of the interference fringes periodically changes as the laser beam propagates. This can be seen in the center intensity of Fig. 4a, which is weak compared to the strong center intensity of Fig. 4b. The variations are due to destructive (Fig. 4a) and constructive (Fig. 4b) interference between the 0th and 1st (− 1st) order diffracted beams. More importantly, the long waviness (7 mm) and small incident angle (3.15°) produce an extremely small diffraction angle (0.11 mrad) between the 1st (− 1st) order and the 0th order beam modes that gives rise to strong interference fringes with high visibility in the reflected beam profile. Thus, even over the long propagation distance of 1800 mm, the beam profiles of the 0th and 1st order modes still spatially overlap, producing interference fringes by Bragg scattering as shown in Fig. 4b. The interference fringes also become more pronounced as the size of the optical element grows, since the quantity of waviness on the optical surface increases.

Fig. 3
figure 3

2D surface topography (50 × 50 mm region) of optical element surface with a period of a 7 mm and b 0.5 mm. c 1D line profiles (0.85 mm length) of the optical element surface with a period of 7 mm (black solid line) and 0.5 mm (red solid line). d Line profile obtained from Fig. 2a over a longer distance to show amplitude and period

Full size image
Fig. 4
figure 4

2D beam profiles reflected from a flat optical element surface with a waviness period of 7 mm and amplitude of 50 nm, measured at propagation distances of a 600 mm and b 1800 mm after reflection

Full size image

Fundamentally, the interference in the beam profile could be removed within a relatively short propagating distance by increasing the diffracted angle between the beam modes formed from Bragg diffraction. The angle of the mth diffracted beam is given by

$$d\left( {\sin \theta_{i} \pm \sin \theta_{m} } \right) = m\lambda ,$$
(2)

where d is the period of waviness, θi is the angle of incidence, θm is the angle of reflection, m is order of diffracted beam mode, and λ is the light wavelength [25]. If a periodic structure with a period of a few hundred microns is artificially engraved during the initial mechanical processing, the diffracted angle between the beam modes can be increased compared to that produced by the waviness with a period of a few millimeters (Eq. 2). Thus, after a certain propagation distance, complete spatial separation between the beam modes (0th and 1st (− 1st) orders) can be achieved (Eq. 1).

Since the interference produced by Bragg scattering is influenced not only by the period on the optical surface, but also by its amplitude and the beam’s incident angle, the periodic amplitude (50 nm) and incident angle (3.15°) were kept constant to compare the optical surfaces with periods of 7 mm and 0.5 mm. The laser beam profiles observed at two propagation distances after reflection from the optical surface with a period of 0.5 mm are displayed in Fig. 5. The two beam profiles observed at propagation distances of 600 mm and 1800 mm are compared. At 600 mm (Fig. 5a), the interference fringes formed in the 2D beam profile are much denser than those seen in Fig. 4 due to the reduced period of 0.5 mm compared to 7 mm. However, at 1800 mm (Fig. 5b), the interference fringes are not seen in the 2D beam profile, because the two diffracted beam modes [0th and 1st (− 1st)] are completely spatially separated at this distance. In Fig. 5c, two line profiles obtained at each region shown by the rectangular red dotted lines in Fig. 5a and b are displayed. It is clear that there are no interference fringes at the distance of 1800 mm (blue solid line), whereas the interference fringes formed by the diffracted beam modes (0th, 1st and − 1st orders) are clearly observed at the distance of 600 mm (black solid line). From Eq. (1), if we consider the correction factor (in this experiment, Δθ0,1 increases by 7 times), which depends on the optical geometry for the detection of propagating beam profile, the decoupled distance between the 0th and 1st (− 1st) order beam modes becomes ~ 12,360 mm for the 7 mm period and ~ 880 mm for the 0.5 mm period respectively. Thus, the two beam profiles observed at propagation distances of 600 mm and 1800 mm from the optical surface with a 0.5 mm period could be clearly distinguished since these two distances fall on either side of the 880 mm decoupling distance.

Fig. 5
figure 5

2D beam profiles reflected from a flat optical element surface with a period of 0.5 mm and an amplitude of 50 nm measured at propagation distances of a 600 mm and b 1800 mm after reflection. c Line profiles obtained in the regions marked by rectangular red dotted lines on Fig. 4a and b. The black trace is obtained at a distance of 600 mm, and the blue trace is obtained at a distance of 1800 mm. d Line profiles calculated from Eq. (5). Three cases are shown in this figure. The black trace is obtained from the summation of the 0th, 1st, and − 1st-order beam modes; the blue trace is obtained from only the 0th-order beam mode; and the red trace is obtained from only the 1st-order beam mode

Full size image

The determination of an artificial period on the optical surface depends on the acceptable propagation distance (the distance between the optical surface with an artificial period and the next optical surface) of the beam in a specific optical system. As previously mentioned, when an artificial periodic structure with a period of 0.5 mm is engraved, a very clean beam profile can be obtained at the propagation distance of 880 mm, where the diffracted beam modes between the 0th and 1st (or − 1st) orders are spatially separated. If a periodic structure shorter than 0.5 mm is engraved, the scattering angle between the diffracted beam modes enlarges, and a very clean beam profile is obtained at a propagation distance shorter than 880 mm. Thus, 0.5 mm does not represent the optimized period for obtaining a clear (no interference fringes) beam profile by applying the effect of Bragg scattering.

In addition, the aspect ratio of the periodic structure affects the beam profile. A change in the aspect ratio can affect the intensity of the beam profile, whereas a change in the period affects the propagation distance where a clean beam profile is formed. Because the efficiency of the diffracted beam mode for each order is proportional to the square of the Bessel function (J2) [23] of the 1st kind as a function of the amplitude, the light efficiencies of the 0th-order and 1st-order diffracted beam modes for the amplitude of 50 nm (aspect ratio: 1.4 × 10–5) are 73% and 13%, respectively. If the amplitude is 25 nm (aspect ratio: 0.7 × 10–5), the light efficiencies of the 0th-order and 1st-order diffracted beam modes are 93% and 4%, respectively. Thus, the beam intensity for the 0th-order diffracted beam mode (corresponding to a clean beam profile) is as high as 20% when compared with that of the amplitude of 50 nm. On the other hand, at the amplitude of 100 nm (aspect ratio: 2.8 × 10–5), the light efficiencies of the 0th-order and 1st-order diffracted beam modes are 23% and 32%, respectively. Thus, the beam intensity for the 0th-order diffracted beam mode (corresponding to a clean beam profile) is 50% lower than that of the amplitude of 50 nm. In other words, as the amplitude (aspect ratio) increases, the intensity of the beam profile in the 0th-order diffracted beam mode (corresponding to a clean beam profile) weakens, because the efficiency of the higher-order diffracted mode increases.

3 Discussion

The wave function of the reflected beam can be expressed in the form of a Bessel function, which is a solution of the propagation equation for light that satisfies the boundary conditions of a periodic structure [27, 28]. To simplify the calculation, if we assume that the incident wave is a plane wave and the waviness is the shape of a sinusoidal line grating, the reflected wave ER is given by

$$E_{R} = E_{r} \sum\limits_{\alpha = - \infty }^{\infty } {J_{\alpha } \left( {2ka\cos \theta_{i} } \right)e^{ - iK \cdot r} } ,$$
(3)

where Er is the amplitude of a reflected wave accounting for the reflection coefficient, Jα is the αth-order Bessel function of the 1st kind, α is the order of a diffracted beam mode, k = 2π/λ, a is the modulation depth of the sinusoidal structure, θi is the angle of incidence, and K is the wave number determined by diffraction order and diffraction angle. From Eq. (3), the diffraction efficiency (η) of the αth-order beam is proportional to the square of αth-order Bessel function (η ∝ Jα2(2kacosθ)). The diffraction efficiencies of the 0th and 1st (− 1st) order beams for the 7 mm waviness period and 2kacosθ = 0.78 are proportional to 0.73Er2 and 0.13Er2, respectively, by Eq. (3). Here, higher-order beam modes above the 2nd (-2nd) order can be ignored because the intensities of the 0th and 1st (− 1st) order account for more than 99% of the total intensity.

From the above consideration regarding the efficiency of diffracted beam modes, we can quantitatively describe the interference caused by Bragg scattering at the position of the detector for the observation of propagating beam profiles. For N interfering beams, the general form of the intensity distribution (I (r)) is given by [29, 30]

$$I(r) = I_{0} \left[ {1 + \sum\limits_{j > i}^{\infty } {V_{ij} \cos \left( {\left( {k_{j} - k_{i} } \right) \cdot r} \right)} } \right],$$
(4)

where I0 is an intensity amplitude given by \(1/2 \cdot \sum\nolimits_{K = 1}^{N} {E_{k}^{2} }\), Vij is an interference coefficient given by Vij = EiEj(eiej)/Io, ei and ej are unit vectors in the i-th and j-th direction respectively, k is a wave number, and r is a position vector at the detector. For the three diffracted beam modes (0th, 1st, and − 1st), the intensity distributions of each mode correspond to the equations I0th = 1/2· E0th2 for the 0th order, I1st =  1/2·E1st 2 for the 1st order, and I− 1st =  1/2·E− 1st 2 for the − 11st order. If we consider all three beam modes, the intensity distribution (Ir) corresponds to the following equation:

$$I_{r} = I_{0} \left[ {1 + \frac{1}{{I_{0} }}\left( {E_{0th} E_{1st} \cos \left( {\frac{2\pi }{\lambda } \cdot x\sin \theta_{0,1} } \right) + E_{0th} E_{ - 1st} \cos \left( {\frac{2\pi }{\lambda } \cdot x\sin \theta_{0, - 1} } \right) + E_{1st} E_{ - 1st} \cos \left( {\frac{2\pi }{\lambda } \cdot 2x\sin \theta_{1, - 1} } \right)} \right)} \right],$$
(5)

where E0th = 0.86 E0, E1st = 0.36 E0, and E− 1st = 0.36 E0 for our experimental conditions; I0 = 1/2[(E0th)2 + (E1st)2 + (E− 1st)2] = 0.49E02; θ0,1, θ0,− 1, and θ1,− 1 are the angles between the 0th and 1st, 0th and − 1st, and 1st and − 1st order diffracted beam modes; and x is a position at the detector, respectively. Figure 5d shows line profiles of the intensity distributions obtained from these calculations (Ir, I0th, and I1st). Overall, both Fig. 5c and d display similar behavior in terms of the intensity ratios (between black and blue solid lines) and the period of the sinusoidal distribution (black solid line). The only difference is that the visibility of the observed sinusoidal intensity distribution (black solid line in Fig. 5c) is somewhat lower than that is predicted theoretically (black solid line in Fig. 5d). In fact, the Gaussian wave, which is typical in such experiments, differs from the plane wave assumption used in Eq. (5). It is thought that this leads to the differences in intensity amplitude and phase between the interfering beams at the detection and accordingly they may affect the visibility, which is related to the degree of coherence between the interfering beam waves [31]. More importantly, it can be seen that the level of the intensity distribution (blue solid line) obtained from only the 0th order beam mode in Fig. 5d remains constant at a low level of 30% with respect to the peak level of the sinusoidal intensity distribution. Additionally, the intensity distribution obtained from only the 1st order beam mode (red solid line) is just 5% of the peak value (black solid line). At first glance, it may appear that these results seem to violate the law of energy conservation due to the low intensity of the 0th and 1st order beam modes compared to the total. However, if we integrate the sinusoidal intensity distribution, the total energy (40% level considering the normalization) is almost the same as the summation of the 0th, 1st, and − 1st order beam modes. In light of these considerations, the intensity distributions observed at the two propagation distances of 600 mm and 1800 mm correspond well to the theoretical approach. Thus, it is expected that this approach could be one of the most efficient ways to acquire high quality laser beam profile from large-scale freeform optics, which is still a challenge in manufacturing by established final surface finishing processes, although its efficiency is a little low (75%) for 0th order diffracted beam mode.

4 Conclusion

In conclusion, we have improved the quality of a laser beam profile by manipulating the effect of Bragg scattering. Instead of the conventional engineering approach, such as surface finishing process, to remove the waviness with a period of a few millimeters, we maximized the effectiveness of the Bragg scattering caused by a periodic structure on the optical surface. To achieve this, we engraved an artificial periodic structure with a period of a few hundred microns using DTM on the optical surface to increase the scattering angle between the diffracted beam modes. As a result, by employing only DTM, the quality of the laser beam profile was greatly improved at propagation distances where the diffracted beam modes are spatially separated. Further, the characteristics of the optical surface became acceptable enough to apply as a suitable optical element owing to the elimination of interference patterns in the beam profile. It is expected that our results will be a crucial approach for the development of large-scale optical elements which is still very difficult to completely remove the periodic structure on the freeform optical surface even applying surface finishing process and which does not require high levels of light efficiency. Thus, the improvement of optical performance based on the effect of Bragg scattering without a final surface finishing step contributes toward green manufacturing in terms of energy saving and waste reduction in the manufacturing process.