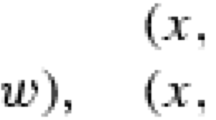Planar Sections of a Surface Close to an Umbilic

Abstract

We study the intersection between a smooth algebraic surface with an umbilic point and a plane parallel and close to the tangent plane at the umbilic. The problem has its origin in the study of isophote (equal illumination) curves in a 2-dimensional image. In particular, we study the circles which have exceptional tangency to this intersection curve: ordinary tangency at one point and osculating at another; ordinary tangency at three points; and 4-point tangency at a vertex. The centres of circles having ordinary tangency at two points trace out a curve whose closure is the symmetry set of the intersection curve, and the exceptional circles above give respectively cusps, triple crossings and endpoints of this set. We analyse the curves traced out by the contact points and centres of the exceptional circles as the plane approaches the tangent plane at the umbilic. We also briefly discuss the global structure of the symmetry set by means of a typical example.

1 Introduction: Origin of the Problem

The problem we consider originated in computer vision, in the study of isophotes in a 2-dimensional image, that is curves of equal brightness. These are level sets of a (smooth) ‘brightness function’ f(x, y) where x and y are Cartesian coordinates of a point in the plane of the image. They are therefore planar sections of the surface $M: z=f(x,y)$ by parallel planes $z=c$ where c is a constant, say close to $c=0$. Isophotes are used in medical applications of computer vision (see for example [15]), as features for object detection (see for example [9]) and in computer aided design for optical checking of the smoothness of surface intersections. Our interest is chiefly geometrical, since the symmetry set of a curve encodes so much geometrical information about the curve.

The particular object of interest is the symmetry set of the plane curve $f(x,y)=c$ and the manner in which it evolves as c passes through 0. This is the locus of centres of circles which are tangent to $f(x,y)=c$ at more than one point: ‘bitangent circles’ of the plane curve. When the plane $z=0$ is not tangent to the surface M then the level sets $f(x,y)=c$ evolve through a family of smooth curves for small c and the evolution of symmetry sets follows from [2]. But when $z=0$ is tangent to M the level set $f(x,y)=0$ is singular and the results of [2] do not apply.

The situation which we concentrate on here is that of an umbilic point on M, and parallel planes close to the tangent plane at this point. We are working in a situation of Euclidean invariance; thus M can be assumed to have Monge form $z=f(x,y)=x^2+y^2+$ higher order terms, scaling x, y, z by the same amount to make the coefficients in the quadratic terms equal to 1, and if necessary reversing the sign of z. The plane sections $z=c$, a constant, are therefore nonempty just for $c\ge 0$, and for $c=0$ the plane section is a single point at the origin. There has been previous work [4, 5] on the geometry of the level curves and in [6] a method is given for successive approximation of these curves, which is useful when studying examples. The existence of six vertices (extrema of curvature) on the curve $V_c: f(x,y)=c$ for small $c>0$ is ‘well-known’; see for example [12, sect. 15.3]. These are points where a circle has 4-point contact (‘$A_3$ contact’) with $V_c$ and the symmetry set has an endpoint at the centre of such a circle, pointing away from the vertex for a minimum of absolute curvature and towards the vertex for a maximum. The symmetry set has structure which is governed by other kinds of contact: a cusp at the centre of a circle tangent at one point of $V_c$ and osculating at another (‘$A_1A_2$ contact’), and a triple crossing of branches at the centre of a circle tangent in three places (‘$A_1^3$ contact’). See [3] or [2, Fig.7]. Figure 1 shows an example of the symmetry set of such a curve $V_c$. We discuss the global structure of this example in Sect. 5.

We extend and in some cases correct the calculations of [4, 5] in the umbilic case, which is in many ways the most interesting but also the most troublesome one.

Many examples of symmetry sets of planar sections of surfaces close to a singular section, including the umbilic case, were studied by the first author and Ricardo Uribe-Vargas during a visit to Liverpool in Spring 2008, using software written by Richard Morris [11]. The report on this visit, which was funded by the Research Centre in Mathematics and Modelling at Liverpool, was not published but is available at [7].

For applications of symmetry sets and their close relations medial axes to computer vision, see for example [8, 13, 14].

Fig. 1

Left: the symmetry set (locus of centres of bitangent circles) of the oval drawn,slightly enlarged compared with the oval itself. The oval is an example of a curve $V_c$ for c small, as in the text. There are six endpoints at the centres of circles having 4-point contact with $V_c$ and corresponding to the six vertices of $V_c$; six cusps at the centres of circles tangent at one point and osculating at another; and two triple crossings at the centres of triply tangent circles (one circle interior and one exterior to $V_c$). The endpoints of branches point away from minima of curvature and towards maxima. Right: the same but with the oval unchanged and the central part of the symmetry set enlarged more to make the structure more evident. See also Sect. 5 for further structure of this example

In this paper, we analyse the local structure of the symmetry set, proving that there are six cusps, two triple crossings and six endpoints, and determining the loci of these points and the corresponding contact points of circles, as the surface section shrinks to a point.

The structure of the paper is as follows: In Sect. 2, we consider in full detail the cusps on the symmetry set, resulting from circles having ‘$A_1A_2$’ contact with $V_c$, that is tangent ($A_1$ contact) and osculating ($A_2$ or 3-point contact) at distinct points. The results are collected in Propositions 2.7 and 2.8, the first in a plane where the origin has been blown up and the second in the initial plane of the surface section.

In Sect. 3, we turn to the case of tri-tangent circles, which produce a triple crossing on the symmetry set, showing there are two such circles, and calculating the trajectories and limiting directions of the contact points and centres. The results are collected in Propositions 3.1 and 3.2.

In Sect. 4, we cover the circles which are tangent at vertices of the plane section, corresponding to endpoints of the symmetry set: there are six such. The results are in Propositions 4.1 and 4.2.

It is striking that the limiting positions, as $c\rightarrow 0$, of all the three types of contact points of the above special circles are along the root directions of the ‘harmonic representative’ of the cubic form in the function f defining our surface, or else in the bisectors of these directions; see Remark 2.1 and Fig. 3.

There is more structure to be analysed, and we give some information on this in the final section Sect. 5.

2 Circles Tangent at One Point and Osculating at Another

For convenience and simplicity of exposition in this paper, we consider the algebraic case, when the defining function f(x, y) is a polynomial. We have no doubts that the results obtained in this polynomial setting are true for real analytic and smooth cases (see Remark 2.2 below), but leave the discussion of general setting to future work. Thus, consider a polynomial

$$\begin{aligned} \Phi (x,y)=x^2+y^2+\sum ^d_{i=3} q_i(x,y)\in {{\mathbb {R}}}[x,y] \end{aligned}$$

with real coefficients, where $q_i(x,y)$ are homogeneous of degree i and $d\geqslant 3$. The equation $\Phi (x,y)=0$ has the only solution (0, 0) near the origin — an isolated point of this “curve”. Now for a small $\varepsilon >0$ the curve

$$\begin{aligned} C_{\varepsilon }=\{\Phi (x,y)=\varepsilon \}\subset {{\mathbb {R}}}^2 \end{aligned}$$

is very close to the circle $x^2+y^2=\varepsilon$; in particular, it is convex, non-singular and the radius of curvature at every point is finite. Let us consider the set of pairs $\mathcal{T}(\varepsilon )$

$$\begin{aligned} (P_1,P_2)\in C_{\varepsilon }\times C_{\varepsilon }\setminus \{\text{ the } \text{ diagonal }\} \end{aligned}$$

such that the circle of curvature for $C_{\varepsilon }$ at $P_1$ is tangent to $C_{\varepsilon }$ at $P_2$ (in particular, it contains $P_2$). The set ${{\mathcal {T}}}(\varepsilon )$ is finite; it is defined by a number of algebraic equations so the union

$$\begin{aligned} \mathop {\bigcup }\limits _{0<\varepsilon <a} {{\mathcal {T}}}(\varepsilon ) \end{aligned}$$

must be a subset of an algebraic curve. Clearly, this curve contains the origin (0, 0), and the problem we are going to investigate is how does this curve look near the origin: is it non-singular or singular; in the latter case, how many branches does it have at (0, 0), are these branches non-singular or what is the type of singularity at each branch. We also want to develop technique to produce a parametric equation for each branch from the coefficients of the polynomial $\Phi (x,y)$.

The union of irreducible components of this curve containing the origin will be denoted by ${{\mathcal {T}}}$. The algebraic curve $\mathcal{T}$ is naturally embedded in ${{\mathbb {R}}}^2\times {\mathbb R}^2={{\mathbb {R}}}^4$. Since the definition of ${{\mathcal {T}}}$ involves the metric properties of the curves $C_{\varepsilon }$, we have very limited resource of transformations for the coordinates x, y that could be used to simplify the equation $\Phi$ without transforming ${{\mathcal {T}}}$ with the loss of its properties: we can only use the rotations around the origin and the uniform magnifications of the plane ${{\mathbb {R}}}^2$. It is easy to see that, applying a suitable rotation and a magnification, we can bring $q_3(x,y)$ to the form

$$\begin{aligned} x^3+\alpha x^2y+xy^2+\beta y^3, \ \ \alpha \ne \beta . \end{aligned}$$

(1)

(If $\alpha =\beta$ then the quadratic terms $x^2+y^2$ divide the cubic terms and this umbilic will occur generically only in a 1-parameter family of surfaces. Porteous in [12, p.207] calls it a pure lemon umbilic, following the ‘lemon’ nomenclature of Hannay [1].)

Remark 2.1

When the cubic terms C take this form, with $\alpha \ne \beta$, then the ‘harmonic representative’ of the cubic form has roots $y, y\pm x\sqrt{3}$, that is along three lines including the x-axis and making $60^{\circ }$ angles. See for example [10, p.119] or [12, p.132]. With quadratic part $Q=x^2+y^2$ we seek a linear form $ax+by$ for which $(\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2})(C+LQ)=0$, which works out as $L=-x-\frac{\alpha +3\beta }{4}$, and then the harmonic representative is $C+LQ$ which has the roots as above. In our case, these root directions turn out to be directly relevant to the limiting directions we seek, as indeed are the directions bisecting the root directions. See Fig. 3. (When $\alpha =\beta$ the harmonic representative is zero.)

Starting from this moment, we assume that the cubic form $q_3$is in the form (1).

Polynomials $\Phi (x,y)$ now have

$$\begin{aligned} 2+\sum ^d_{i=4} (i+1)=\frac{d^2+3d}{2}-7 \end{aligned}$$

unknown coefficients so are parametrized by point of the real affine space ${{\mathbb {A}}}^{\frac{1}{2} (d^2+3d)-7}$. We will consider the case of general position, that is, when the coefficients of $\Phi$ belong to a certain Zariski open subset of that affine space, which will later be defined by explicit conditions. Now we fix the notations:

$$\begin{aligned} q_i(x,y)=\sum ^i_{j=0} q_{ij} x^j y^{i-j} \end{aligned}$$

for $i\in \{4,\dots , d\}$, where $q_{ij}\in {\mathbb R}$.

2.1 Blowing Up the Origin

It is more convenient to work with a modified geometric object: let us consider the polynomial equation

$$\begin{aligned} z^2=\Phi (xz,yz)=z^2(x^2+y^2)+\sum ^d_{i=3} z^iq_i(x,y). \end{aligned}$$

Obviously, the curve

$$\begin{aligned} 1=x^2+y^2+\sum ^d_{i=3} (\sqrt{\varepsilon })^i z^iq_i(x,y) \end{aligned}$$

is $\frac{1}{\sqrt{\varepsilon }} C_{\varepsilon }$ (that is, obtained from $C_{\varepsilon }$ by magnification by $\frac{1}{\sqrt{\varepsilon }}$), and the curve

$$\begin{aligned} 1=x^2+y^2+\sum ^d_{i=3} (-\sqrt{\varepsilon })^i z^iq_i(x,y) \end{aligned}$$

is $\left( -\frac{1}{\sqrt{\varepsilon }}\right) C_{\varepsilon }$ (the curve above, reflected from the origin). Therefore, we set

$$\begin{aligned} f(x,y,z)=-1+x^2+y^2+\sum ^d_{i=3} z^{i-2} q_i(x,y) \end{aligned}$$

and consider the surface $S=\{f=0\}\subset {{\mathbb {R}}}^3$, which is non-singular for $z^2<a$ small enough. Note that we allow negative values of z as well. Fixing the value of z, we obtain a curve $S_z\subset {{\mathbb {R}}}^2_{x,y}$. Now we re-formulate the original problem as follows: let

$$\begin{aligned} \Gamma ^{\circ } \subset {{\mathbb {R}}}^2_{x_1,y_1}\times {\mathbb R}^2_{x_2,y_2} \times {{\mathbb {R}}}_z={{\mathbb {R}}}^5 \end{aligned}$$

be the set of triples

$$\begin{aligned} (S_z\ni P_1\ne P_2\in S_z, z\ne 0), \end{aligned}$$

such that the circle of curvature for $S_z$ at $P_1$ is tangent to $S_z$ at $P_2\ne P_1$. Denote by $\Gamma$ the closure of $\Gamma ^{\circ }$. Now $\Gamma$ is an algebraic curve in the space ${{\mathbb {R}}}^5$ with coordinates $(x_1,y_1,x_2,y_2,z)$, and we aim to study it near the hyperplane $\{z=0\}$,that is, for |z| small enough. In other words, we want to find the set

$$\begin{aligned} \{Q_1,\ldots , Q_k\}=\Gamma \cap \{z=0\} \end{aligned}$$

(the limiting points of $\Gamma ^{\circ }$ as $z\rightarrow 0$), parametrize the branches of $\Gamma$ at each of these points and determine the type of singularity for each of the branches. Note that if

$$\begin{aligned} (x_1(t),y_1(t),x_2(t),y_2(t),z(t)) \end{aligned}$$

is a local parametrization of one of these branches for |t| small enough and $z(0)=0$, then the pair of points

$$\begin{aligned} ((x_1(t)z(t),y_1(t)z(t)),\,\,(x_2(t)z(t),y_2(t)z(t))) \end{aligned}$$

belongs to ${{\mathcal {T}}}(z(t)^2)$, which gives us a parametrization of the corresponding branch of the curve ${{\mathcal {T}}}$ near the origin and the type of singularity of ${{\mathcal {T}}}$ at the origin for this branch, that is, a complete solution of the original problem.

2.2 Equations of the Curve $\Gamma$

Starting with the equation

$$\begin{aligned} 0=f(x,y,z)=-1+x^2+y^2+z(x^3+\alpha x^2y+xy^2+\beta y^3)+\sum ^d_{i=4} z^{i-2} q_i(x,y), \end{aligned}$$

let us write down the algebraic equations, defining the curve $\Gamma$. We assume that $z\ne 0$ (and then will take the closure).

Set $(a,b)=P_1\in S_z$.

The derivatives computed at the point (a, b, z) will be denoted as follows:

$$\begin{aligned} \left. \frac{\partial f}{\partial x}\right| _{(a,b,z)}=f_a, \quad \left. \frac{\partial f}{\partial y}\right| _{(a,b,z)}=f_b, \quad \left. \frac{\partial ^2 f}{\partial x^2}\right| _{(a,b,z)}=f_{aa}, \end{aligned}$$

etc. The first equation is obvious: $f(a,b,z)=0$. Now set, for a fixed $(a,b)\in S_z$,

$$\begin{aligned} X=x-a,\quad Y=y-b \end{aligned}$$

to be the coordinates shifted to the point (a, b) as the origin. The equation of $S_z$ in these coordinates is

$$\begin{aligned} 0=F_{a,b}(X,Y)=f_a X+f_b Y+\frac{1}{2} f_{aa} X^2+f_{ab} XY+\frac{1}{2} f_{bb} Y^2+\dots \end{aligned}$$

and the equation of the circle of curvature at the point $(a,b)\in S_z$ is

$$\begin{aligned} 0= & {} C_{a,b}(X,Y)=f_a X+f_b Y+ \lambda _{ab} X^2+\lambda _{ab} Y^2,\nonumber \\&\text{ where }&\nonumber \\ \lambda _{ab}= & {} \frac{\frac{1}{2} f_{aa} f_b^2-f_{ab} f_af_b+\frac{1}{2} f_{bb} f_a^2}{f_a^2+f_b^2}. \end{aligned}$$

(2)

Note that since $f_a=2a+z(\dots )$, $f_b=2b+z(\dots )$, where in the brackets, we have polynomials in a, b, z, we obtain

$$\begin{aligned} f_a^2+f_b^2=4+z(\dots ) \end{aligned}$$

and $\lambda _{ab}=1+z(\dots )$, so that $\lambda _{ab} \rightarrow 1$ as $z\rightarrow 0$. Now, subtracting the equation of the circle of curvature from that of $S_z$, we get

$$\begin{aligned} \left( \frac{1}{2} f_{aa}-\lambda _{ab}\right) X^2+f_{ab} XY+\left( \frac{1}{2} f_{bb}-\lambda _{ab}\right) Y^2+\dots , \end{aligned}$$

where the dots mean the terms of order $\geqslant 3$ in X, Y. The quadratic form above factors as

$$\begin{aligned} (f_a X+f_b Y)\left( \frac{\frac{1}{2} f_{aa}-\lambda _{ab}}{f_a} X+\frac{\frac{1}{2} f_{bb}-\lambda _{ab}}{f_b} Y\right) . \end{aligned}$$

Therefore, the restriction of this form onto the circle $C_{a,b}=0$ is equal to the restriction of the cubic form

$$\begin{aligned} -\lambda _{ab} (X^2+Y^2)\left( \frac{\frac{1}{2} f_{aa}-\lambda _{ab}}{f_a} X+\frac{\frac{1}{2} f_{bb}-\lambda _{ab}}{f_b} Y\right) . \end{aligned}$$

Now elementary computations yield:

$$\begin{aligned} \frac{\frac{1}{2} f_{aa}-\lambda _{ab}}{f_a}=\frac{\frac{1}{2} f_{aa}f_a+f_{ab}f_b-\frac{1}{2} f_{bb}f_a}{n_{ab}}, \\ \frac{\frac{1}{2} f_{bb}-\lambda _{ab}}{f_b}=\frac{-\frac{1}{2} f_{aa}f_b+f_{ab}f_a+\frac{1}{2} f_{bb}f_b}{n_{ab}}, \end{aligned}$$

where $n_{ab}=f_a^2+f_b^2$.

Lemma 2.2

$n_{ab}=4+8zq_3(a,b)+z^2(\dots )$.

Proof

We compute:

$$\begin{aligned} n_{ab}=4a^2+4b^2+4az(3a^2+2\alpha ab+b^2)+(4bz(\alpha a^2+2ab+3\beta b^2)+z^2(\dots ). \end{aligned}$$

Since $(a,b)\in S_z$, we have

$$\begin{aligned} 1=a^2+b^2+zq_3(a,b)+z^2(\dots ), \end{aligned}$$

and replacing $a^2+b^2$ in the first expression by $1-zq_3(a,b)$, we get the claim. $\Box$

It follows from the lemma that

$$\begin{aligned} \frac{1}{n_{ab}}=\frac{1}{4}-\frac{1}{2} zq_3(a,b)+z^2(\dots ). \end{aligned}$$

Let us set

$$\begin{aligned} r_a=\frac{1}{2} f_{aa}f_a+f_{ab}f_b-\frac{1}{2} f_{bb}f_a \end{aligned}$$

and

$$\begin{aligned} r_b=-\frac{1}{2} f_{aa}f_b+f_{ab}f_a+\frac{1}{2} f_{bb}f_b. \end{aligned}$$

Straightforward computations give:

$$\begin{aligned} \begin{array}{lcl} r_a &{} \equiv &{} z(4+6(\alpha -\beta )ab)\,\, \mathop {\textrm{mod}} z^2,\\ r_b &{} \equiv &{} z(4\alpha a^2+(6\beta - 2\alpha )b^2) \,\, \mathop {\textrm{ mod}} z^2,\\ \lambda _{ab} &{} \equiv &{} 1+z(a^3+(3\beta -2\alpha ) a^2b+ab^2+ \alpha b^3) \,\, \mathop {\textrm{ mod}} z^2,\\ f_{aaa} &{} \equiv &{} 6z \,\, \mathop {\textrm{ mod}} z^2,\\ f_{aab} &{} \equiv &{} 2\alpha z \,\, \mathop {\textrm{ mod}} z^2,\\ f_{abb} &{} \equiv &{} 2z \,\, \mathop {\textrm{ mod}} z^2, \\ f_{bbb} &{} \equiv &{} 6\beta z \,\, \mathop {\textrm{ mod}} z^2. \end{array} \end{aligned}$$

Since we have

$$\begin{aligned} f(x,y,z)\equiv -1+x^2+y^2+zq_3(x,y)\,\, \mathop {\textrm{ mod}} z^2, \end{aligned}$$

and taking into account the computations above, we get

$$\begin{aligned} F_{a,b}(X,Y)-C_{a,b}(X,Y) \equiv \left( \frac{1}{6} f_{aaa}-\frac{\lambda _{ab}}{n_{ab}} r_a\right) X^3+ \left( \frac{1}{2} f_{aab}-\frac{\lambda _{ab}}{n_{ab}} r_b\right) X^2Y \\ \qquad \quad +\left( \frac{1}{2} f_{abb}-\frac{\lambda _{ab}}{n_{ab}} r_a\right) XY^2 + \left( \frac{1}{6} f_{bbb}-\frac{\lambda _{ab}}{n_{ab}} r_b\right) Y^3\,\, \mathop {\textrm{ mod}} z^2 \\ \equiv -z\left( \frac{3}{2}(\alpha -\beta )abX^3-(\alpha (1-a^2)-\frac{1}{2} (3\beta -\alpha )b^2)X^2Y\right. \\ \qquad \quad \left. +\frac{3}{2}(\alpha -\beta )abXY^2-(\beta -\alpha a^2-\frac{1}{2} (3\beta -\alpha )b^2)Y^3\right) \,\, \mathop {\textrm{ mod}} z^2. \end{aligned}$$

Let $(P_{1,l}=(a_l,b_l),\, P_{2,l},\, z_l\ne 0)\in \Gamma ^{\circ }$ be a sequence of points such that $z_l\rightarrow 0$ and

$$\begin{aligned} (a_l,b_l)\rightarrow (a_{\infty }, b_{\infty })\in \{x^2+y^2=1\} \end{aligned}$$

as $l\rightarrow \infty$ (the curve $S_{z_l}$ converges to the unit circle). The polynomial

$$\begin{aligned} \frac{1}{z}\left[ F_{a_l,b_l}(X,Y)-C_{a_l.b_l}(X,Y)\right] , \end{aligned}$$

restricted onto the circle $\{C_{a_l,b_l}=0\}$, has a double zero for all l, so taking the limit as $l\rightarrow \infty$ (all coefficients of that polynomial are bounded uniformly and the circle $\{C_{a_l,b_l}=0\}$ converges to the unit circle), we conclude that the cubic form

$$\begin{aligned} \frac{3}{2}(\alpha -\beta )a_{\infty }b_{\infty }X^3- (\alpha (1-a_{\infty }^2)-\frac{1}{2}(3\beta -\alpha )b_{\infty }^2) X^2Y \\ +\frac{3}{2}(\alpha -\beta )a_{\infty }b_{\infty }XY^2- (\beta -\alpha a_{\infty }^2-\frac{1}{2}(3\beta -\alpha )b_{\infty }^2) Y^3, \end{aligned}$$

restricted to the unit circle, has a double zero. As $a_{\infty }^2+b_{\infty }^2=1$, after easy computations we get the following fact: the cubic form

$$\begin{aligned} 3a_{\infty }b_{\infty } X^3-3b_{\infty }^2X^2Y+3a_{\infty }b_{\infty } XY^2+(2-3b_{\infty }^2) Y^3 \end{aligned}$$

must be divided by the square of a linear factor. Its discriminant is equal to

$$\begin{aligned} -64\cdot 27\cdot b_{\infty }^2\cdot \left( b_{\infty }^2-\frac{3}{4}\right) ^2. \end{aligned}$$

The (double) roots of the discriminant are

$$\begin{aligned} b_{\infty } = 0,\,\, \frac{\sqrt{3}}{2},\,\, -\frac{\sqrt{3}}{2}. \end{aligned}$$

Therefore, we have 6 possible values for the limit point $(a_{\infty },b_{\infty })$:

$$\begin{aligned} (1,0),\quad (-1,0),\quad \left( \frac{1}{2},\frac{\sqrt{3}}{2}\right) ,\quad \left( -\frac{1}{2},\frac{\sqrt{3}}{2}\right) ,\quad \left( \frac{1}{2},-\frac{\sqrt{3}}{2}\right) ,\quad \left( -\frac{1}{2},-\frac{\sqrt{3}}{2}\right) . \end{aligned}$$

They are the points of intersection of the unit circle with the three lines

$$\begin{aligned} \{Y=0\},\quad \{Y=\sqrt{3}X\},\quad \{Y=-\sqrt{3}X\}, \end{aligned}$$

dividing the plane into 6 equal angles, $\frac{\pi }{3}$ each. Note that the rotation by $\frac{\pi }{3}$ transforms the homogeneous polynomial $q_3(x,y)$ into a form of the same type:

$$\begin{aligned} \left[ \frac{1}{2} -\frac{\sqrt{3}}{8}(\alpha +3\beta )\right] x^3+ \left[ \frac{\sqrt{3}}{2} +\frac{1}{8}(-5\alpha +9\beta )\right] x^2y \\ +\left[ \frac{1}{2} -\frac{\sqrt{3}}{8}(\alpha +3\beta )\right] xy^2+ \left[ \frac{\sqrt{3}}{2} +\frac{1}{8}(3\alpha +\beta )\right] y^3, \end{aligned}$$

which means that the behaviour of the curve $\Gamma$ at each of the limit points $(a_{\infty },b_{\infty })$ is the same. Therefore, from now on we will study the limit point (1, 0).

Note also that from the limiting arguments above it follows that if $P_{1,l}\rightarrow (1,0)$ as $l\rightarrow \infty$, then $P_{2,l}\rightarrow (-1,0)$ as the limit cubic form for $b_{\infty }=0$ takes the form $2Y^3$, so that $P_{2,\infty }=\lim \limits _{l\rightarrow \infty } P_{2,l}$ must lie on the line $\{Y=0\}$.

2.3 Local Analysis of the Curve $\Gamma$

Getting back to the curve $\Gamma$ embedded into the space

$$\begin{aligned} {{\mathbb {R}}}^5_{x_1,y_1,x_2,y_2,z}, \end{aligned}$$

let us describe it locally by explicit equations near the point

$$\begin{aligned} (1,0,-1,0,0). \end{aligned}$$

First, we shift the origin to this point:

$$\begin{aligned} x_1=1+u,\quad y_1=b,\quad x_2=-1+v,\quad y_2=w,\quad z=z \end{aligned}$$

and study $\Gamma$ in ${{\mathbb {R}}}^5_{u,b,v,w,z}$ near the origin. We get the following set of equations: the first one, (E1), is

$$\begin{aligned} g(u,b,z)=f(1+u,b,z)=0 \end{aligned}$$

(meaning that $(x_1,y_1)\in S_z$), which can be decomposed into homogeneous components

$$\begin{aligned} g=g_1+g_2+g_3+\dots , \end{aligned}$$

e.g. $g_1=2u+z$, $g_2=u^2+b^2+3uz+\alpha yz+q_{44}z^2$ etc., the segment $g_1+\dots +g_k$ will be denoted by $g_{\leqslant k}$.

The second equation (E2) is

$$\begin{aligned} h(v,w,z)=f(-1+v,w,z)=0 \end{aligned}$$

(meaning that $(x_2,y_2)\in S_z$), which we write as

$$\begin{aligned} h=h_1+h_2+h_3+\dots , \end{aligned}$$

$h_i$ is homogeneous of degree i, e.g.

$$\begin{aligned} h_1=-2v-z,\quad h_2=v^2+w^2+3vz+\alpha wz+q_{44} z^2 \end{aligned}$$

etc., again $h_{\leqslant k}=h_1+\dots +h_k$.

The third equation means that the point $(-1+v,w)$ lies on the circle of curvature for the curve $S_z$ at the point (a, b): $C_{a,b} (-2-u+v,w-b)=0$, where $a=1+u$, recall that $X=x-a$ and $Y=y-b$. Since the coefficients of the quadratic polynomial $C_{a,b} (X,Y)$ are rational functions, which is not very convenient for computations, we introduce a new equation, multiplying by $(f_a^2+f_b^2)$:

$$\begin{aligned}{} & {} R_{a,b}(X,Y)=(f_a^2+f_b^2) C_{a,b}(X,Y)=(f_a^2+f_b^2) f_a X \\{} & {} \quad +(f_a^2+f_b^2) f_b Y+ \left( \frac{1}{2} f_{aa} f_b^2-f_{ab} f_af_b+\frac{1}{2} f_{bb} f_a^2\right) (X^2+Y^2) \end{aligned}$$

and write the third equation $(E^*3)$ to be

$$\begin{aligned} R_{a,b}(-2-u+v,w-b)=0. \end{aligned}$$

We denote the equation by the symbol $(E^*3)$, not just (E3), because we will modify this equation later.

The fourth equation $(E^*4)$ means that the circle of curvature $\{R_{a,b}(X,Y)=0\}$ is tangent to the curve $S_z$ at the point $(-1+v,w)$ (in the x, y-coordinates: once again, recall that $X=x-a=x-(1+u)$ and $Y=y-b$, so that (X, Y)-coordinates of this point are $(-2-u+v,w-b)$ and $(E^*4)$ takes the form

$$\begin{aligned} \left| \begin{array}{ll} \frac{\partial f}{\partial x}(-1+v,w) &{} \frac{\partial f}{\partial y}(-1+v,w) \\ {} &{} \\ \frac{\partial R_{a,b}}{\partial X}(-2-u+v,w-b) &{} \frac{\partial R_{a,b}}{\partial Y}(-2-u+v,w-b) \end{array} \right| =0. \end{aligned}$$

Obviously, these four equations for $z\ne 0$ define the finite set of points of the branch of $\Gamma$ at the new origin lying in ${{\mathbb {R}}}^4_{u,b,v,w}$ with the fixed value of z. (We will see below that $\Gamma$ has only one branch at the new origin $(1,0,-1,0,0)$.) Unfortunately, the four equations (E1, 2) and $(E^*3,4)$ define in ${{\mathbb {R}}}^5$ a set which is larger than just $\Gamma$: when $z=0$, the curve $S_{\{z=0\}}$ is the unit circle, so coincides with its circle of curvature at every point and the equations $(E^*3,4)$ hold automatically. This means that, set-theoretically, the set of solutions of the four equations near the new origin is

$$\begin{aligned} \Gamma \cup \{\text{ the } \text{ unit } \text{ circle }\}^{\times 2}. \end{aligned}$$

We need to modify the equations $(E^*3,4)$, so that the new system of four equations would give precisely $\Gamma$ near the new origin.

2.4 Modified Equations

Let us consider first the two equations (E1, 2).

Proposition 2.3

The system of equations

$$\begin{aligned} g=0,\quad h=0 \end{aligned}$$

defines near the origin a non-singular three-dimensional submanifold (a real algebraic variety) $M\subset {{\mathbb {R}}}^5$ whose tangent space at $o=(0,\dots , 0)$ is

$$\begin{aligned} T_oM=\{2u+z=2v+z=0\}\subset {{\mathbb {R}}}^5. \end{aligned}$$

Proof

Obvious from the fact that $g_1$, $h_1$ are linearly independent linear forms.

$\square$

As the three linear forms

$$\begin{aligned} 2u+z,\quad 2v+z,\quad z \end{aligned}$$

are also linearly independent, we see that the intersection

$$\begin{aligned} Q=M\cap \{z=0\} \end{aligned}$$

is a non-singular surface near o (a 2-dimensional submanifold in M, containing the origin o) with the tangent space

$$\begin{aligned} T_oQ=\{u=v=z=0\}, \end{aligned}$$

so that (b, w) form a system of local coordinates on Q at o (whereas (b, w, z) form a system of local coordinates on M at o).

Proposition 2.4

The equation $(E^*4)$ is divisible by z.

Proof

Consider the ring homomorphism

$$\begin{aligned} {{\mathbb {R}}}[u,b,v,w,z]\rightarrow {{\mathbb {R}}}[u,b,v,w], \end{aligned}$$

setting $z=0$. It is easy to see that after this substitution $R_{a,b} (X,Y)$ turns into $(f_a^2+f_b^2) F_{a,b}(X,Y)|_{\{z=0\}}$ and $F_{a,b}(X,Y)|_{\{z=0\}}=2(1+u)X+2bY+X^2+Y^2$, which implies that $(E^*4)|_{\{z=0\}}=0$, as we claimed, so $z\mathbin {|} (E^*4)$.$\square$

Now explicit calculations via Maple give that the linear term of $(E^*4)$ is identically zero and the quadratic term is

$$\begin{aligned} 16z(\alpha u+\alpha v-(\alpha -q_{43})z). \end{aligned}$$

Set $(E4)=\frac{1}{z} (E^*4)$. Note that the forms

$$\begin{aligned} 2u+z,\quad 2v+z,\quad \alpha u+\alpha v-(\alpha -q_{43})z \end{aligned}$$

are linearly independent for $q_{43}\ne 2\alpha$ as

$$\begin{aligned} \left| \begin{array}{ccc} 2 &{} 0 &{} 1 \\ 0 &{} 2 &{} 1 \\ \alpha &{} \alpha &{} -\alpha +q_{43} \end{array} \right| =4(-2\alpha +q_{43}). \end{aligned}$$

Therefore, assuming that $q_{43}\ne 2\alpha$, we get that the equations (E1, 2, 4) define a non-singular surface $M_{124}\subset M$ near o with the tangent space at this point

$$\begin{aligned} T_oM_{124}=T_oQ=\{u=v=z=0\}. \end{aligned}$$

Finally, let us consider the equation $(E^*3)$. Writing a for $1+u$, we get the following fact.

Proposition 2.5

The following equality holds:

$$\begin{aligned} R_{a,b}(X,Y)|_{\{z=0\}}=4(a^2+b^2)(2aX+2bY+X^2+Y^2). \end{aligned}$$

Proof

This follows from the equalities

$$\begin{aligned}{} & {} f_a|_{\{z=0\}}=2a,\quad f_ab|_{\{z=0\}}=2b,\quad f_{aa}|_{\{z=0\}}=2, \\{} & {} \quad f_{ab}|_{\{z=0\}}=0,\quad f_{bb}|_{\{z=0\}}=2. \end{aligned}$$

$\square$

Therefore, we compute: $R_{a,b}(-2-u+v,w-b)|_{\{z=0\}}=$

$$\begin{aligned}{} & {} =4(1+2u+u^2+b^2)((-2u-u^2-b^2)+(-2v+v^2+w^2))= \\{} & {} \quad =4(1+2u+u^2+b^2)\left( -g|_{\{z=0\}}+h|_{\{z=0\}}\right) . \end{aligned}$$

So we modify $(E^*3)$, setting

$$\begin{aligned} (E3)=\frac{1}{z} ((E^*3)+4(1+2u+u^2+b^2)(g-h)). \end{aligned}$$

A computation via Maple gives that the linear term of (E3) is equal to

$$\begin{aligned} (-8)[5u+6(\alpha -\beta )b+5v+(2\alpha ^2-2q_{42}+4q_{44}+3)z], \end{aligned}$$

which does not contain w, whereas the matrix

$$\begin{aligned} \left( \begin{array}{cccc} 2 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 2 &{} 1 \\ 5 &{} 6(\alpha -\beta ) &{} 5 &{} 2\alpha ^2-2q_{42}+4q_{44}+3 \\ \alpha &{} 0 &{} \alpha &{} -\alpha +q_{43} \end{array} \right) \end{aligned}$$

has the determinant

$$\begin{aligned} -24(\alpha -\beta )(-2\alpha +q_{43})\ne 0 \end{aligned}$$

for $q_{43}\ne 2\alpha$. Therefore, the equations $(E1-4)$ define a non-singular branch parametrized by w.

Remark 2.6

One can see from the computations in the previous sections, which involve only partial derivatives of the function f(x, y) of order up to 4, that they can be performed without any changes in the smooth case: we present the curve $\Gamma$ in ${{\mathbb {R}}}^5$ as the set of common zeros of four functions with linearly independent linear terms at the origin, so the local existence and non-singularity of that curve follow from just Implicit Function Theorem. The computation of limiting points in Sect. 2.2 is also done in the way that applies in the smooth case. The same is true about our computation of limiting triples of points in Sect. 3 below. However, we restrict ourselves by the polynomial setting here and leave the discussion of the symmetry set in the general differentiable case to further work.

2.5 The Curves Traced Out by Contact Points and Centre of the Circle

Knowing that the other variables, b, u, v and z, can be expressed in terms of w we can now proceed to find the initial terms in expansions of these variables in terms of w and then, by blowing down to the initial x, y-plane, to find the loci of the contact points and of the centres of the $A_1A_2$ circles. These calculations are routine and we omit the details here, collecting the results in the following proposition.

Recall that we are considering the case where $(1+u,b)$ are the coordinates of the point of osculating $(A_2)$ contact and $(-1+v,w)$ the coordinates of the point of ordinary $(A_1)$ contact of the circle with the blown-up curve $f(x,y,z)=0$ for a fixed small z. There are five other symmetrically placed cases all of which will yield similar loci as $z\rightarrow 0$. Blowing-down amounts to multiplying the x and y coordinates by z; the resulting loci of contact points then work out as follows, where we assume $\alpha \ne \beta$ and $2\alpha \ne q_{43}=$ coefficient of $x^3y$ in f.

Proposition 2.7

The following are initial terms in the expansions of the remaining variables in terms of w:

$$\begin{aligned} z= & {} \frac{3(\alpha -\beta )}{2(2\alpha -q_{43})}w^2+ \frac{3(\alpha ^2-q_{42}+2q_{44}-1)(\alpha -\beta )}{2(2\alpha -q_{43})^2}w^3\\ b= & {} -\frac{\alpha ^2-q_{42}+2q_{44}-1}{2(2\alpha -q_{43})}w^2 \\{} & {} - \frac{3\alpha ^4-6\alpha ^2q_{42}+12\alpha ^2q_{44} -2\alpha ^2-4\alpha q_{43}+3q_{42}^2-12q_{42}q_{44} +q_{43}^2+12q_{44}^2+6q_{42}-12q_{44}+3}{6(2\alpha -q_{43})^2}w^3 \\ u= & {} -\frac{3(\alpha -\beta )}{4(2\alpha -q_{43})}w^2- \frac{3(\alpha ^2-q_{42}+2q_{44}-1)(\alpha -\beta )}{4(2\alpha -q_{43})^2}w^3\\ v= & {} \frac{\alpha +3\beta -2q_{43}}{4(2\alpha -q_{43})}w^2 +\frac{3(\alpha -\beta )(\alpha ^2-\alpha q_{43}+q_{42}-2q_{44}+1}{4(2\alpha -q_{43})^2}w^3 \end{aligned}$$

Note that the expansion of z up to this order is $-2$ times the expansion of u; however, this does not extend to the terms in $w^4$.

Blowing down to the initial plane, we have the following:

Proposition 2.8

Osculating $(A_2)$ contact: the locus is a rhamphoid cusp equivalent by changes of local coordinates in the plane to $(t^2, t^5)$.

Ordinary $(A_1)$ contact: the locus is an ordinary cusp equivalent to $(t^2, t^3)$.

In each case, ‘half’ the cusp is actually formed, since $z\rightarrow 0$ through positive values, equivalent to $t>0$ in the reduced forms above.

Proof

After blowing down, the osculating contact point is $((u+1)z, bz)$ whose initial terms are of the form $(x_1,y_1)=(Aw^2+Bw^3, Cw^4+Dw^5)$, where $A\ne 0$. Changing local coordinates by a local diffeomorphism in the plane $y_1-(C/A^2)x_1^2$ to remove the term $Cw^4$ results in

$$\begin{aligned} \left( \frac{3(\alpha - \beta )}{2(2\alpha - q_{43})}w^2, \ -\frac{\alpha - \beta }{4(2\alpha - q_{43})}w^5\right) ,\end{aligned}$$

which then by scaling reduces to $(w^2,w^5)$. This is known to be 5-determined under smooth changes of coordinates in source and target.

The locus of $A_1$ points $(x_2,y_2)=((v-1)z,wz)$ has initial nonzero terms which by scaling become $(w^2,w^3)$ and therefore has an ordinary cusp. $\Box$

Similarly, using the Eq. (2) of the circle of curvature at the $A_2$-point, that is the $A_1A_2$ circle under consideration, we can find the locus of centres of these circles as $z\rightarrow 0$. The result is the following—

Proposition 2.9

The locus of centres of curvature in the initial plane (after blowing down), that is the locus of cusp points on the symmetry set set as $z\rightarrow 0$, reduces under local diffeomorphism to the form $(t^4, t^6 + at^7)$. Using standard techniques for determinacy, this is a 7-determined germ under local diffeomorphic changes in source and target (‘${\mathcal {A}}$ equivalence’) provided $a\ne 0$. According to a Maple calculation, the additional condition for this is $31\alpha ^2 - 2\alpha q_{43} - 27q_{42} + 54q_{44} - 27\ne 0$. $\Box$

3 The Tritangent Circle Case

Assume that the curve $S_z$ given by

$$\begin{aligned} 0=-1+x^2+y^2+z(x^3+\alpha x^2y+xy^2+\beta y^3)+z^2(\dots ) \end{aligned}$$

meets the circle

$$\begin{aligned} 0=-1-C+x^2+y^2-Ax-By \end{aligned}$$

at three distinct points $P_1, P_2, P_3$ and the two curves are tangent at $P_1, P_2, P_3$. The triple $(P_1, P_2, P_3)$ depends on the four parameters

$$\begin{aligned} z,\quad A,\quad B,\quad C. \end{aligned}$$

As $z\rightarrow 0$, $z\ne 0$, it is obvious that A, B, C must also tend to zero as the tangent circle tends to the unit circle. Subtracting one equation from the other, we get the equation

$$\begin{aligned} 0=C+Ax+By+zq_3(x,y)+z^2(\dots ). \end{aligned}$$

If as $z\rightarrow 0$, the triple $(A,B,C)\rightarrow (0,0,0)$ as $z^{\lambda }$ with $\lambda <1$, then dividing the last equation by $z^{\lambda }$ and putting $z=0$, we get that a divisor of degree 6 on the unit circle is cut out on the circle by a line, which is impossible. Therefore, we can write

$$\begin{aligned} A=zA_1+\dots ,\quad B=zB_1+\dots ,\quad C=zC_1+\dots , \end{aligned}$$

where the dots denote functions divisible by $z^{\lambda }$ with $\lambda >1$. Now, dividing the equation by z and putting $z=0$, we get that the cubic polynomial

$$\begin{aligned} x^3+\alpha x^2y+xy^2+\beta y^3+A_1x+B_1y+C_1 \end{aligned}$$

cuts out the divisor

$$\begin{aligned} 2P^*_1+2P^*_2+2P^*_3=2(P^*_1+P^*_2+P^*_3) \end{aligned}$$

on the unit circle $x^2+y^2=1$. Note that the cubic polynomial above can be replaced by

$$\begin{aligned} (1+A_1)x+(\alpha +B_1)y+(\beta -\alpha )y^3+C_1. \end{aligned}$$

Using the parametrization of the unit circle, given by the stereographic projection from the “north pole” (0, 1),

$$\begin{aligned} x=\frac{2t}{t^2+1},\quad y=\frac{t^2-1}{t^2+1}, \end{aligned}$$

we obtain: the polynomial

$$\begin{aligned} (\beta +B_1+C_1)t^6+2(1+A_1)t^5+(4\alpha -3\beta +B_1+3C_1)t^4+ 4(1+A_1)t^3+ \\ +(-4\alpha +3\beta -B_1+3C_1)t^2+ 2(1+A_1)t+(-\beta -B_1+C_1) \end{aligned}$$

is, up to a constant, a full square of a polynomial of degree 3.

Assume first that $\beta +B_1+C_1\ne 0$ and divide through by $\beta +B_1+C_1$: we get a monic polynomial of degree 6, which is a square of a monic polynomial of degree 3. Setting

$$\begin{aligned}{} & {} a_1=a_5=\frac{2(1+A_1)}{\beta +B_1+C_1},\quad a_3=2a_1,\quad a_4=\frac{4\alpha -3\beta +B_1+3C_1}{\beta +B_1+C_1}, \\{} & {} \quad a_2=\frac{-4\alpha +3\beta -B_1+3C_1}{\beta +B_1+C_1},\quad a_0=\frac{-\beta -B_1+C_1}{\beta +B_1+C_1}, \end{aligned}$$

we get:

$$\begin{aligned} t^6+a_5t^5+\dots +a_0=(t^3+b_2t^2+b_1t+b_0)^2 \end{aligned}$$

for some real $b_0, b_1, b_2$. Using the fact that $a_1=\frac{1}{2} a_3=a_5$, we obtain the following relations:

$$\begin{aligned}{} & {} a_0=b_0^2,\quad a_1=2b_2=2b_1b_0,\quad a_2=b_1^2+2b_0b_2, \\{} & {} \quad a_1=b_0+b_1b_2,\quad a_4=b_2^2+2b_1. \end{aligned}$$

If $b_0\ne 0$, then $b_1=b_2/b_0$ and so, dividing through the equality $2b_2=b_0+b_1b_2$ by $b_0$, we get

$$\begin{aligned} 2b_1=1+b_1^2, \end{aligned}$$

which implies that $b_1=1$ and $b_2=b_0$. Setting $b_0=\lambda$, we see that

$$\begin{aligned}{} & {} a_1=a_5=2\lambda , \quad a_3=4\lambda ,\quad a_0=\lambda ^2, \\{} & {} \quad a_2=2\lambda ^2+1 \quad \text{ and }\quad a_4=\lambda ^2+2. \end{aligned}$$

In terms of our original parameters, we get the equalities

$$\begin{aligned} \frac{-\beta -B_1+C_1}{\beta +B_1+C_1}=\lambda ^2,\quad \frac{4\alpha -3\beta +B_1+3C_1}{\beta +B_1+C_1}=\lambda ^2+2 \end{aligned}$$

and

$$\begin{aligned} \frac{-4\alpha +3\beta -B_1+3C_1}{\beta +B_1+C_1}=2\lambda ^2+1, \end{aligned}$$

which simplify, respectively, to

$$\begin{aligned}{} & {} (\lambda ^2+1)B_1+(\lambda ^2-1)C_1=-(\lambda ^2+1)\beta , \\{} & {} \quad (\lambda ^2+1)B_1+(\lambda ^2-1)C_1=4\alpha -(\lambda ^2+5)\beta \end{aligned}$$

and

$$\begin{aligned} (\lambda ^2+1)B_1+(\lambda ^2-1)C_1=-2\alpha -(\lambda ^2-1)\beta . \end{aligned}$$

The right-hand sides of these linear equations (in $B_1$, $C_1$) must be equal, which gives $\alpha =\beta$. By our assumption, this is not the case. This contradiction implies that our original assumption that $b_0\ne 0$ can not be true. Therefore, $a_0=b_0=0$ and so $a_1=a_3=a_5=0$, which gives the equalities

$$\begin{aligned} A_1=-1\quad \text{ and }\quad C_1=\beta +B_1. \end{aligned}$$

So the polynomial

$$\begin{aligned} t^2\left( t^4+2\frac{\alpha +B_1}{\beta +B_1}t^2+ \frac{-2\alpha +3\beta +B_1}{\beta +B_1}\right) \end{aligned}$$

must be a full square. Therefore,

$$\begin{aligned} \left( \frac{\alpha +B_1}{\beta +B_1}\right) ^2= \frac{-2\alpha +3\beta +B_1}{\beta +B_1}, \end{aligned}$$

from which we get the equalities

$$\begin{aligned} B_1=-\frac{\alpha +3\beta }{4},\quad C_1=\frac{-\alpha +\beta }{4}, \end{aligned}$$

so that our polynomial turns out to be

$$\begin{aligned} t^2(t^2-3)^2 \end{aligned}$$

and the (double) roots are $t=0, \pm \sqrt{3}$. We deduce the following:

Proposition 3.1

The three limit points on the unit circle are:

$$\begin{aligned} P^*_1=\left( -\frac{\sqrt{3}}{2}, \frac{1}{2}\right) ,\quad P^*_2=(0,-1),\quad P^*_3=\left( \frac{\sqrt{3}}{2}, \frac{1}{2}\right) . \end{aligned}$$

This limit triple was obtained by the assumption that $\beta +B_1+C_1\ne 0$. If this is not the case, that is, $\beta +B_1+C_1= 0$, then we use the stereographic projection from the “south pole” $(0,-1)$ and get the other limit triple:

$$\begin{aligned} Q^*_1=\left( -\frac{\sqrt{3}}{2}, -\frac{1}{2}\right) ,\quad Q^*_2=(0,1),\quad Q^*_3=\left( \frac{\sqrt{3}}{2}, -\frac{1}{2}\right) . \end{aligned}$$

It is also possible to determine the loci of contact points of the tri-tangent circles as $z\rightarrow 0$, firstly in the blown-up situation and then after blowing-down, that is replacing (x, y) by (xz, yz). We find the following:

Proposition 3.2

(i) The locus of each of the six contact points of the two tri-tangent circles is smooth, with endpoint on the unit circle before blowing down and at the origin after, as $z\rightarrow 0$ through positive values. The limiting tangent for the contact points close to (0, 1) and (1, 0) has direction $(2\alpha +6\beta -2q_{41}-q_{43}, \ -3\beta (\alpha -\beta ))$ before blowing-down and (0, 1) after blowing-down.

(ii) The locus of centres of each of the tri-tangent circles forms a smooth curve with endpoint at the origin before blowing-down, with limiting tangent direction $(4, \alpha + 3\beta )$. After blowing down, it forms (half of) an ordinary cusp, with the same limiting direction for the tangent direction.

4 Circles with 4-Point Contact

Continuing with the same notation as Sect. 3 above, we consider here circles which are tangent to the curve $f(x,y,z)=0$ for small z at a vertex of this curve, that is at a point of stationary curvature. There are known to be six such vertices (see for example [12, Sect. 15.3] or [5, p.87]) and we are interested first in the limiting positions of those six vertices, as $z\rightarrow 0$, on the unit circle $f(x,y,0)=0$. The condition for a vertex on a curve $f(x,y)=0$ is given on [5, p.74]:

$$\begin{aligned} 0= & {} (f_x^2+f_y^2)(-f_y^3f_{xxx}+3f_xf_y^2f_{xxy} -3f_x^2f_yf_{xyy} +f_x^3f_{yyy}) \nonumber \\{} & {} +3f_xf_y(f_y^2f_{xx}^2+(f_x^2-f_y^2)f_{xx}f_{yy}-f_x^2f_{yy}^2) \nonumber \\{} & {} +6f_xf_yf_{xy}^2(f_x^2-f_y^2) \nonumber \\{} & {} +3f_{xy}(f_{xx}f_y^4-3f_x^2f_y^2(f_{xx}-f_{yy})-f_{yy}f_x^4) . \end{aligned}$$

(3)

Applying this to our function f(x, y, z) for a fixed small z, we suppose that the vertex lies at a point (x, y) where

$$\begin{aligned} x=\frac{2t}{t^2+1}+zX_{1}+z^2X_{2}+\ldots , \ \ y=\frac{t^2-1}{t^2+1}+zY_{1}+z^2Y_{2}+\ldots ,\end{aligned}$$

where the X and Y depend only on the coefficients in f.

With this notation the condition (3) has no constant term, since the circle $f(x,y,0)=0$ has a vertex at every point, and the coefficient of z is, apart from a multiplicative constant, $(3t^2 - 1)(t^2 - 3)(t^2 + 1)^4(\alpha - \beta )$. Provided $\alpha \ne \beta$ this gives the same six values for t as were found in Sect. 3. Hence:

Proposition 4.1

The six limiting positions on the unit circle of the vertices of the curves $f(x,y,z)=0$ as $z\rightarrow 0$ are, in terms of angles from the positive x-axis on the unit circle, $\{\pm \frac{1}{6}\pi , \pm \frac{1}{2}\pi , \pm \frac{5}{6}\pi \}$.

It is also possible to determine which vertices represent maxima and which minima of curvature—strictly of the square of curvature since maxima and minima are reversed when orientation of the curve is reversed. Of course, maxima and minima alternate round the curve. We find the following.

Proposition 4.2

For small $z>0$ the point of the curve $f(x,y,z)=0$ close to (0, 1) on the unit circle, that is with angle $\frac{1}{2}\pi$ in Proposition 4.1, is a maximum of the squared curvature if and only if $\alpha >\beta$. (Recall that we are assuming $\alpha \ne \beta$.) Thus, in this situation, the maxima occur at angles $\frac{1}{2}\pi , -\frac{1}{6}\pi , -\frac{5}{6}\pi$, i.e. points $(1,0), (\frac{\sqrt{3}}{2}, -\frac{1}{2}), (-\frac{\sqrt{3}}{2}, -\frac{1}{2})$. When $\alpha <\beta$ these are the minima of squared curvature.

Two examples are illustrated in Fig. 4.

Fig. 2

Left: $\alpha =4,\beta =2$ and no terms of degree $>3$ in f gives a maximum of squared curvature near the point (0, 1) and Right: $\alpha =2, \beta =4$ gives a minimum

The limiting positions of the contact points of the various circles ($A_1A_2, A_1^3$ and $A_3$) , in the blown-up form on the unit circle, are summarized in Fig. 3.

Fig. 3

The circle represents the blown-up origin, as in the text. The solid dots are contact points, in the limit, of $A_1 A_2$ circles, occurring in three diametrically opposite pairs. Each pair contributes two $A_1A_2$ circles, by reversing the roles of $A_1$ and $A_2$ points, so that there are six $A_1A_2$ circles. The open dots and open squares are limit points of contact of $A_3$ circles (vertices), three maxima and three minima of curvature given by the triples of the same symbol, and also, in the same triples, limit points of contact of the tri-tangent circles ($A_1^3$ circles). The coordinates of these points on the unit circle are also marked, as well as (round the outside of the circle) their t values, where $x=\frac{2t}{t^2+1}, y=\frac{t^2-1}{t^2+1}$, given by stereographic projection from (0, 1). Compare Remark 2.1: the solid dots are the roots of the harmonic representative of the cubic form $x^3+\alpha x^2y + xy^2 + \beta y^3$ (see (1) in Sect. 2) of our surface

5 Further Work

In this article, we have concentrated on the local structure of the symmetry set of a plane section of a surface with an isolated generic umbilic, establishing the number of cusps, triple crossings and endpoints, and finding expressions for the local structure of the curves traced out by the centres and the contact points of the corresponding circles as the pane section shrinks to a point. There remains the global structure of the symmetry set, and to explain this we give here what appears to be a typical example.

Fig. 4

The same oval and enlarged symmetry set (locus of centres of bitangent circles) as in Fig. 1. Here, we show the three branches of the symmetry set, labelled 1, 2, 3, which start at centres of curvature of vertices of the oval; these can be a maximum (max) or minimum (min) of curvature. The branches are shown extended to endpoints in the left-hand figure of Fig. 1. Here, $T_1, T_2$ indicate the two triple points, centres of tri-tangent circles. For further information, see the text

The figure shows the global symmetry set with the branches annotated. From experimental observations, it appears that the structure exhibited here holds in general. We can state this in the following empirical observation, where C stands for cusp, M (resp. m) for an endpoint corresponding to a maximum (resp. minimum) of curvature and $T_1,T_2$ for the triple crossing points.

The branches of the symmetry set follow the patterns (branches 1,2,3 in the figure)

$(1): MT_1CCT_1M; \ \ \ (2): mT_2CCT_2m; \ \$ and $(3): MT_1CCT_2m$.

That is, two branches pass twice through a single triple crossing, and these have the same kind of vertex, maximum or minimum, at each end. One branch passes through both triple crossings and has a maximum at one end and a minimum at the other. The triple crossing at the centre of a tri-tangent circle inside the oval is $T_1$ on branch 1. The exterior tri-tangent circle has its centre at $T_2$. There are other examples in [7].

We hope to explain this in a further article.