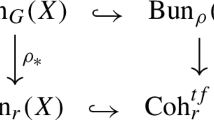Surfaces of Section for Seifert Fibrations

Abstract

We classify global surfaces of section for flows on 3-manifolds defining Seifert fibrations. We discuss branched coverings—one way or the other—between surfaces of section for the Hopf flow and those for any other Seifert fibration of the 3-sphere, and we relate these surfaces of section to algebraic curves in weighted complex projective planes.

1 Introduction

Global surfaces of section are an important tool for understanding the dynamics of non-singular vector fields on manifolds. For a given flow or class of flows, it is a basic question to understand the existence of such surfaces of section, and their topological properties.

Here are some recent results in this direction in the context of Reeb dynamics; for a more comprehensive overview of the literature, we refer to [1] and [18]. Hryniewicz–Salomão–Wysocki [9] establish sufficient (and $C^{\infty }$-generically necessary) conditions for a finite collection of periodic orbits of a Reeb flow on a closed 3-manifold to bound a positive global surface of section of genus zero. Building on the work of Hryniewicz [7], who found a characterisation of the periodic Reeb orbits of dynamically convex contact forms on the 3-sphere that bound disc-like global surfaces of section, existence results for higher genus surfaces of section have been established by Hryniewicz–Salomão–Siefring [8].

Even for one of the most simple flows in dimension three, the Hopf flow on the 3-sphere, global surfaces of section display rich features. The paper [1] determines the topology of such surfaces of section and describes various ways to construct them. Furthermore, it was shown there how to relate such surfaces of section to algebraic curves in the complex projective plane, and how to interpret them as a toy model for the elementary degenerations arising in symplectic field theory; this led to a new proof of the degree-genus formula for complex projective curves.

The aim of the present paper is to extend the results of [1] to all flows on 3-manifolds that define a Seifert fibration. We decide the existence question and give a topological classification of the global surfaces of section for such flows. For some classification statements, we restrict attention to positive surfaces of section, which means that the boundary components are supposed to be oriented positively by the flow (see Sect. 3 for details). This is motivated by the particular interest of these positive sections, for instance in Reeb dynamics.

We discuss branched coverings between surfaces of section for the Hopf flow and those of any other Seifert fibration of the 3-sphere $S^3$. Rather intriguingly, these branched coverings can go either way, and both approaches can be used to compute the genus of positive d-sections with a Riemann–Hurwitz argument.

We also relate the surfaces of section in $S^3$ to algebraic curves in weighted complex projective planes. On the one hand, the degree-genus formula for such algebraic curves can then be used to compute, once again, the genus of positive d-sections. Conversely, our direct geometric arguments for surfaces of section provide an alternative proof of this degree-genus formula. These considerations have contributed to filling a gap in the earlier versions of [6], and they give a more geometric alternative to the arguments in [16].

We hope that the explicit descriptions of global surfaces of section in the present paper will prove useful for the study of Besse manifolds (cf. Sect. 2.4) in Finsler geometry and Reeb dynamics.

2 Seifert Manifolds

Let M be a closed, oriented 3-manifold with a Seifert fibration $M\rightarrow B$ over a closed, oriented surface B. Many of the results in this paper also hold, mutatis mutandis, when M or B is not orientable. However, for the interpretation of the Seifert fibres as the orbits of a flow, and to be able to speak of positive surfaces of section, the fibres have to be oriented.

We refer the reader to [10] for the basic theory of Seifert fibred spaces.

2.1 Seifert Invariants

We recall the notation and conventions for the Seifert invariants from [3] that we shall use in the present paper. In the description of M as

$$\begin{aligned} M=M\bigl (g;(\alpha _1,\beta _1),\ldots , (\alpha _n,\beta _n)\bigr ), \end{aligned}$$

the non-negative integer g stands for the genus of B, the $\alpha _i$ are positive integers giving the multiplicities of the singular fibres, and each $\beta _i$ is an integer coprime with the respective $\alpha _i$, describing the local behaviour near the singular fibre. A pair $(\alpha _i,\beta _i)$ with $\alpha _i=1$ does not actually give rise to a singular fibre, but it corresponds to a modification of the fibration that contributes to the Euler number.

The non-singular fibres are called regular. Near any regular fibre, the Seifert fibration is a trivial $S^1$-bundle.

When we speak of a ‘Seifert manifold M’, we always mean that a Seifert fibration has been chosen on the 3-manifold M. Some 3-manifolds admit non-isomorphic Seifert fibrations [3, 4].

The topological interpretation of these invariants is as follows. Let $B_0$ be the surface with boundary obtained from B by removing the interior of n disjoint discs $D^2_1,\ldots ,D^2_n\subset B$. Denote by $M_0=B_0\times S^1\rightarrow B_0$ the trivial $S^1$-bundle over $B_0$. Write $S^1_1,\ldots , S^1_n$ for the boundary circles of $B_0$, with the opposite of the orientation induced as boundary of $B_0$. We write the (isotopy class of) the fibre in $M_0$ as $h=\{*\}\times S^1$. On the boundary of $M_0$ we consider the curves $q_i=S^1_i\times \{1\}$, with $1\in S^1\subset {\mathbb {C}}$. Let $V_i=D^2\times S^1$, $i=1,\ldots ,n$, be n copies of a solid torus with respective meridian and longitude

$$\begin{aligned} \mu _i=\partial D^2\times \{1\},\;\; \lambda _i=\{1\}\times S^1\subset \partial V_i. \end{aligned}$$

The Seifert invariants $(\alpha _i,\beta _i)$ then encode the identifications

$$\begin{aligned} \mu _i=\alpha _i q_i+\beta _i h,\;\;\; \lambda _i=\alpha _i'q_i+\beta _i'h, \end{aligned}$$

(1)

where integers $\alpha _i',\beta _i'$ are chosen such that

$$\begin{aligned} \begin{vmatrix} \alpha _i&\quad \alpha _i'\\ \beta _i&\quad \beta _i' \end{vmatrix}=1. \end{aligned}$$

The identifications (1) are equivalent to

$$\begin{aligned} h=-\alpha _i'\mu _i+\alpha _i\lambda _i,\;\;\; q_i=\beta _i'\mu _i-\beta _i\lambda _i. \end{aligned}$$

(2)

Writing $C_i$ for the spine $\{0\}\times S^1$ of the solid torus $V_i$, we deduce from (2) that the fibre h is homotopic to $\alpha _iC_i$ in $V_i$, and the boundary curve $q_i$, to $-\beta _iC_i$. For $\alpha _i>1$, the spine $C_i$ is the corresponding singular fibre.

The Euler number of the Seifert fibration is defined as

$$\begin{aligned} e=-\sum _{i=1}^n\frac{\beta _i}{\alpha _i}. \end{aligned}$$

2.2 Equivalences of Seifert Invariants

Up to isomorphism, a Seifert fibration is determined by the Seifert invariants. Different sets of Seifert invariants correspond to isomorphic Seifert fibrations if and only if they are related to each other by the following operations, see [10, Theorem 1.5]:

• (o) Permute the n pairs $(\alpha _i,\beta _i)$.

• (i) Add or delete any pair $(\alpha ,\beta )=(1,0)$.

• (ii) Replace each $(\alpha _i,\beta _i)$ by $(\alpha _i,\beta _i+k_i\alpha _i)$, where $\sum _{i=1}^n k_i=0$.

These operations allow one to write a Seifert manifold in terms of normalised Seifert invariants

$$\begin{aligned} M\bigl (g;(1,b),(\alpha _1,\beta _1),\ldots ,(\alpha _n,\beta _n)\bigr ), \end{aligned}$$

where $b\in {\mathbb {Z}}$ and $0<\beta _i<\alpha _i$. Notice that the Euler number is invariant under these operations. In general, we shall not be using normalised invariants. Occasionally it is convenient to collect all pairs $(\alpha _i,\beta _i)$ with $\alpha _i=1$ into a single pair (1, b), so that the remaining pairs actually correspond to singular fibres.

2.3 Surgery Description

For Seifert manifolds with $g=0$, one can easily translate the gluing prescriptions into a surgery diagram, and the equivalences of Seifert invariants then correspond to well-known transformations of surgery diagrams.

A surgery description of $S^2\times S^1$ is given by a 0-framed unknot $K_0$ in the 3-sphere $S^3$. Any meridian $m_i$ of $K_0$ corresponds to an $S^1$-fibre of $S^2\times S^1\rightarrow S^2$. The curves $q_i$ then correspond to a meridian of $m_i$, and the fibre h defines the Seifert framing of $m_i$ in the unsurgered $S^3$. So the gluing instruction $\mu _i=\alpha _iq_i+\beta _ih$ from (1) amounts to a surgery with coefficient $\alpha _i/\beta _i$ along $m_i$. It follows that the surgery diagram for $M(0;(\alpha _1,\beta _1),\ldots ,(\alpha _n,\beta _n))$ consists of a 0-framed unknot $K_0$ and n meridians with surgery framing $\alpha _i/\beta _i$, $i=1,\ldots ,n$.

Equivalence (i) in Sect. 2.2 corresponds to adding or removing an $\infty$-framed meridian of $K_0$, which defines a trivial surgery. Equivalence (ii) comes from performing Rolfsen twists (cf. [17, Section 9.H]) on the n meridians. Surgery along $m_i$ is defined by removing a tubular neighbourhood of $m_i$, and then regluing it according to the surgery instruction given by the surgery coefficient. A Rolfsen twist amounts to performing a $k_i$-fold Dehn twist, $k_i\in {\mathbb {Z}}$, along the ‘neck’ created by removing the tubular neighbourhood of $m_i$ before regluing a solid torus. This changes the surgery framing of $K_0$ by $k_i$, and the surgery coefficient of $m_i$ to $\alpha _i/(\beta _i+k_i\alpha _i)$, since the Dehn twist adds $k_i$ meridians to a parallel of $K_0$, and it sends $\alpha _iq_i+\beta _ih$ to $\alpha _iq_i+(\beta _i+k_i\alpha _i)h$. Observe that these Dehn twists preserve the $S^1$-fibration. The condition $\sum _i k_i=0$ comes from the requirement that the unknot $K_0$ should retain its 0-framing after the n Rolfsen twists, so that surgery along $K_0$ still realises $S^2\times S^1$.

For more on surgery descriptions of Seifert manifolds, see [19].

2.4 Besse Flows

Flows of non-singular vector fields where all orbits are closed are often referred to as Besse flows, in particular in Reeb dynamics; see [5, 11, 15]. In this context, it is worth mentioning that, by a classical result of Epstein [2], any Besse flow on a 3-manifold defines a Seifert fibration.

3 Global Surfaces of Section

The orientations of M and B in the Seifert fibration $M\rightarrow B$ induce an orientation on the fibres. Equivalently, we may think of the Seifert fibres as the orbits of an effective, fixed point free $S^1$-action. A singular fibre with Seifert invariants $(\alpha ,\beta )$, $\alpha >1$, consists of points with isotropy group ${\mathbb {Z}}_{\alpha }=\bigl \langle \mathrm {e}^{2\pi \mathrm {i}/\alpha }\bigr \rangle <S^1$.

A global surface of section is an embedded compact surface $\Sigma \subset M$ whose boundary is a collection of Seifert fibres, and whose interior intersects all other Seifert fibres transversely. The interior of $\Sigma$ will intersect every regular fibre (except those forming the boundary of $\Sigma$) in the same number d of points. A singular fibre of multiplicity $\alpha$ can also arise as a boundary component, or it will intersect the interior of $\Sigma$ in $d/\alpha$ points. For short, we speak of a d-section.

Note 3.1

Given a d-section $\Sigma$, the multiplicity $\alpha$ of a singular fibre not in the boundary of $\Sigma$ divides d.

We orient $\Sigma$ such that these intersection points are positive. The boundary orientation of a component of $\partial \Sigma$ may or may not coincide with the orientation as a Seifert fibre. If the orientations coincide for every component of $\partial \Sigma$, we call the d-section positive.

See [1] for a variety of explicit surfaces of section for the Hopf fibration $S^3\rightarrow S^2$.

4 1-Sections for Seifert Fibrations

We begin with a necessary criterion for the existence of a 1-section.

Lemma 4.1

If a Seifert manifold admits a 1-section, then every singular fibre is a boundary fibre, and the corresponding pair $(\alpha ,\beta )$ satisfies $\beta \equiv \pm 1$ $\mathrm {mod}~\alpha$, depending on whether the singular fibre is a positive or negative boundary component.

Proof

The first claim follows from Note 3.1. For the second statement, we consider a solid torus V around the singular fibre C as in Sect. 2. Let $\sigma$ be the curve $\partial V\cap \Sigma$, oriented as a boundary component of $\Sigma {\setminus }{{\,\mathrm{Int}\,}}(V)$. The curve $\sigma$ must be homotopic in V to $\pm C$, depending on the sign of the boundary fibre C.

The Seifert fibres lying in $\partial V$ represent the fibre class h. Since these fibres intersect $\Sigma$ positively in a single point, the intersection number $\sigma \bullet h$ on $\partial V$, computed with respect to the oriented basis $(\mu ,\lambda )$, equals $-1$ (sic!). Since $q\bullet h=1$, this means that $\sigma$ can be written as $\sigma =-q+ah$ for some $a\in {\mathbb {Z}}$, which in V is homotopic to $(\beta +a\alpha )C$. For this to equal $\pm C$, we must have $\beta \equiv \pm 1$ mod $\alpha$. $\square$

This lemma implies that a Seifert manifold admitting a 1-section is of the form $M\bigl (g;(1,b),(\alpha _1,\pm 1),\ldots ,(\alpha _n,\pm 1)\bigr )$, where we may assume that the $\alpha _i$ are greater than 1. The individual signs determine the topology of the Seifert manifold. For $\alpha _i=2$, both signs are possible.

We now show that manifolds of this form do admit a 1-section, and we can characterise those admitting a positive one.

Theorem 4.2

A Seifert manifold admits a 1-section with n singular boundary fibres and $b_{\pm }$ positive resp. negative regular boundary fibres if and only if it is isomorphic to $M\bigl (g;(1,b_+ - b_-),(\alpha _1,\pm 1),\ldots ,(\alpha _n,\pm 1)\bigr )$. The sign in $(\alpha _i,\pm 1$) determines the sign of the corresponding singular boundary fibre. Any two 1-sections on a given Seifert manifold are isotopic, provided they have the same number of positive resp. negative regular boundary fibres.

Example 4.3

In [1, Section 2.5], the reader finds an explicit example of a pair of pants 1-section for the Hopf fibration with two positive and one negative boundary fibres, corresponding to the description of the Hopf fibration as the Seifert manifold $M\bigl (0;(1,1),(1,1),(1,-1)\bigr )$.

Proof of Theorem 4.2

Given a Seifert manifold of the described form, we construct a 1-section as follows. Remove (open) solid tori around the n singular fibres, and a further $b_+ + b_-$ solid tori around regular fibres. The remaining part $M_0$ of M is of the form $B_0\times S^1\rightarrow B_0$, and we take the constant section $B_0\times \{1\}$ as the part of our desired 1-section over $B_0$.

For the gluing of a solid torus V corresponding to a singular fibre of type $(\alpha ,\pm 1)$, we may take $\alpha '=\mp 1$ and $\beta '=0$. This means we have the identifications

$$\begin{aligned} h=\pm \mu +\alpha \lambda ,\;\;\; q=\mp \lambda . \end{aligned}$$

Therefore, the oriented vertical annulus A in V with boundary $\partial A=\pm C\mp \lambda =\pm C+q$ will intersect each Seifert fibre in $V{\setminus }\{C\}$ transversely in a single positive point, and it glues with $B_0$ to extend the 1-section. (For the sign of the intersection point, notice that $-q=\pm \lambda$ takes the role of $\sigma$ in the preceding proof, and $\pm \lambda \bullet h=-1$.) Observe that this argument did not require $\alpha >1$. Thus, in the same way we may extend the 1-section over $b_{\pm }$ solid tori glued according to the prescription $(1,\pm 1)$.

Conversely, given a 1-section as described, we can use it to trivialise the Seifert fibration outside solid tori around the boundary fibres. Then $a=0$ in the notation of the proof of Lemma 4.1, and $\beta =\pm 1$.

The uniqueness statement is proved just like [1, Proposition 3.1]. The only difference is that we now have singular fibres, but if we fix the number of positive resp. negative regular boundary fibres, the signs in $(\alpha _i,\pm 1)$ must be the same for any two given sections, even when some of the $\alpha _i$ equal 2 (perhaps after reordering). This implies that the two sections can be assumed to coincide near the singular fibres after a preliminary isotopy. $\square$

5 d-Sections for Seifert Fibrations

Notice that in Theorem 4.2 it was not necessary to assume $\alpha _i>1$. We continue to work with unnormalised Seifert invariants, although occasionally it may be convenient to collect all pairs $(\alpha _i,\beta _i)$ with $\alpha _i=1$ into a single term.

5.1 A Necessary Criterion

Again we start with a necessary criterion for the existence of a section.

Lemma 5.1

Suppose $M\bigl (g;(\alpha _1,\beta _1),\ldots ,(\alpha _n,\beta _n)\bigr )$ admits a d-section. If the singular fibre $C=C_i$ with invariants $(\alpha ,\beta )=(\alpha _i,\beta _i)$, $\alpha _i>1$, is not a boundary fibre, then $\alpha |d$. If C is a boundary fibre, then $\alpha |(d\beta \mp 1)$, where the sign depends on C being a positive or negative boundary.

Remark 5.2

For $\alpha >1$, the two divisibility conditions are mutually exclusive (in the second case, $\alpha$ and d are coprime), so it is determined a priori—provided a d-section exists—which singular fibres will be boundary fibres. Also, the sign of the boundary fibres is predetermined, unless $\alpha =2$.

Proof of Lemma 5.1

For C not being a boundary fibre, use Note 3.1. If C is a boundary fibre, we argue as in the proof of Lemma 4.1, except that now we have $\sigma \bullet h=-d$. This implies that $\sigma =-dq+ah$ for some $a\in {\mathbb {Z}}$, which is homotopic in V to $(d\beta +a\alpha )C$, whence $d\beta +a\alpha =\pm 1$. $\square$

5.2 The ${\mathbb {Z}}_d$-Quotient

If we think of a Seifert fibration as a manifold M with an effective, fixed point free $S^1$-action, the subgroup ${\mathbb {Z}}_d=\bigl \langle \mathrm {e}^{2\pi \mathrm {i}/d}\bigr \rangle <S^1$ also acts on M, and the quotient $M/{\mathbb {Z}}_d$ is again Seifert fibred. The regular fibres of M have length $2\pi$, a singular fibre of multiplicity $\alpha$ has length $2\pi /\alpha$. In the quotient $M/{\mathbb {Z}}_d$, the regular fibres have length $2\pi /d$, and a singular fibre of multiplicity $\alpha$ in M descends to a singular fibre of length $2\pi \gcd (\alpha ,d)/\alpha d$, so its multiplicity is $\alpha /\gcd (\alpha ,d)$.

The Seifert invariants of $M/{\mathbb {Z}}_d$ can be computed from a section of $M\rightarrow B$ over $B_0\subset B$ (in the notation of Sect. 2), since this descends to just such a section of $M/{\mathbb {Z}}_d\rightarrow B$, see [10, Proposition 2.5].

Proposition 5.3

The ${\mathbb {Z}}_d$-quotient $\overline{M}=M/{\mathbb {Z}}_d$ of

$$\begin{aligned} M=M\bigl (g;(\alpha _1,\beta _1),\ldots ,(\alpha _n,\beta _n)\bigr ) \end{aligned}$$

is the Seifert manifold

$$\begin{aligned} \overline{M}=M\bigl (g;(\overline{\alpha }_1,\overline{\beta }_1),\ldots ,(\overline{\alpha }_n,\overline{\beta }_n) \bigr ), \end{aligned}$$

where $\overline{\alpha }_i=\alpha _i/\gcd (\alpha _i,d)$ and $\overline{\beta }_i=d\beta _i/\gcd (\alpha _i,d)$. In particular, the Euler numbers are related by $e(\overline{M}\rightarrow B)=d\cdot e(M\rightarrow B)$. $\square$

The quotient map $M\rightarrow \overline{M}$ is a branched covering, branched transversely to any singular fibre with $\gcd (\alpha _i,d)>1$, where the branching index is precisely this greatest common divisor.

5.3 d-Sections Descend to the ${\mathbb {Z}}_d$-Quotient

We now assume that M admits a d-section, so that the conclusion of Lemma 5.1 holds. We permute the Seifert invariants such that (for the appropriate $k\in \{0,\ldots ,n\}$)

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha _i|(d\beta _i\mp 1)\;\text {and}\;\alpha _i\not \mid d &{}\quad \hbox {for}\ i=1,\ldots ,k,\\ \alpha _i|d &{}\quad \text {for }i=k+1,\ldots ,n. \end{array}\right. } \end{aligned}$$

(3)

The assumption $\alpha _i\not \mid d$ in the first case of (3) is not, strictly speaking, necessary. It avoids the ambiguity where to place the $\alpha _i$ that equal 1, but the formulas we shall derive also hold when we count some of the $\alpha _i=1$ amongst the first alternative. For $i=1,\ldots , k$, we write $d\beta _i=a_i\alpha _i+\varepsilon _i$ with $a_i\in {\mathbb {Z}}$ and $\varepsilon _i\in \{\pm 1\}$. Then

$$\begin{aligned} \overline{M}=M\bigl (g;(1,\overline{b}),(\alpha _1,\varepsilon _1),\ldots , (\alpha _k,\varepsilon _k)\bigr ) \end{aligned}$$

with

$$\begin{aligned} \overline{b}=\sum _{i=1}^k a_i+\sum _{i=k+1}^n \frac{d\beta _i}{\alpha _i}. \end{aligned}$$

For $\alpha _i=2$ and d odd, or for $\alpha _i=1$ counted amongst the first alternative, there is an ambiguity in the choice of $\varepsilon _i$ (and the corresponding $a_i$), but this does not invalidate any of our statements.

With Theorem 4.2 we see that $\overline{M}$ always admits a 1-section, and a positive one precisely when $\overline{b}\ge 0$ and $\varepsilon _i=1$ for $i=1,\ldots ,k$. The Euler number $\overline{e}$ of $\overline{M}\rightarrow B$ equals

$$\begin{aligned} \overline{e}=-\overline{b}-\sum _{i=1}^k\varepsilon _i/\alpha _i, \end{aligned}$$

so the condition for $\overline{M}$ to admit a positive 1-section can be rephrased as: all $\varepsilon _i$ equal 1 and $\overline{e}\le -\sum _{i=1}^k1/\alpha _i$.

In fact, by the same topological arguments as in [1, Proposition 3.2] one can show that any d-section of M can be isotoped to one that is invariant under the ${\mathbb {Z}}_d$-action, and it then descends to a 1-section of $\overline{M}$. Conversely, any 1-section of $\overline{M}$ lifts to a ${\mathbb {Z}}_d$-invariant d-section of M. Also, a d-section of M, if it exists, is determined up to isotopy by its boundary orientations. For simplicity, we shall restrict the discussion of the topology of these d-sections to positive ones.

5.4 The Local Behaviour Near Singular Fibres

To gain a better understanding of d-sections, we briefly describe their behaviour near singular fibres. We write $(\alpha ,\beta )$ for the invariants of the fibre C in question.

If $\alpha |(d\beta \pm 1)$ and $\alpha \not \mid d$, then C is a boundary component of the d-section. Near C, the d-section looks like a helicoidal surface, where the number of turns around C is controlled by the condition that any neighbouring regular fibre cuts the surface in d (positive) points.

If $\alpha |d$, then the d-section near C consists of $d/\alpha$ transverse discs to C.

The quotient map $M\rightarrow \overline{M}$ restricts on any ${\mathbb {Z}}_d$-invariant d-section $\Sigma$ of M to a branched covering $\Sigma \rightarrow \overline{\Sigma }$, with $\overline{\Sigma }$ a 1-section of $\overline{M}$. Each singular fibre with $\alpha _i|d$ gives rise to $d/\alpha _i$ branch points of index $\alpha _i$ over a single point in the interior of $\overline{\Sigma }$. Along the boundary components, regular or singular, the covering $\Sigma \rightarrow \overline{\Sigma }$ is unbranched.

5.5 The Topology of Positive d-Sections

Here is our main theorem concerning positive d-sections.

Theorem 5.4

The Seifert manifold $M=M\bigl (g;(\alpha _1,\beta _1),\ldots , (\alpha _n,\beta _n)\bigr )$ admits a positive d-section if and only if, for some $k\in \{0,\ldots ,n\}$ (and after permuting the Seifert invariants), condition (3) is satisfied with the sign $\alpha _i|(d\beta _i-1)$ in the first alternative, and the Euler number e satisfies

$$\begin{aligned} de+\sum _{\alpha _i\not \mid d}\frac{1}{\alpha _i}\le 0. \end{aligned}$$

(4)

This positive d-section, if it exists, is unique up to isotopy. Unless $\alpha _i|d$ for all i and $e=0$, it is a connected, orientable surface of genus

$$\begin{aligned} \frac{1}{2}\left( 2- d\left( 2-2g+(d-1)e+\sum _{i=1}^n\frac{1}{\alpha _i}-n\right) -\sum _{\alpha _i\not \mid d}\left( 1-\frac{1}{\alpha _i}\right) \right) \end{aligned}$$

with

$$\begin{aligned} -de+\sum _{\alpha _i\not \mid d}\left( 1-\frac{1}{\alpha _i}\right) \end{aligned}$$

boundary components.

Proof

The left-hand side of inequality (4) equals the integer $-\overline{b}$, so the inequality is simply the reformulation of the condition $\overline{b}\ge 0$. The sign condition on the first alternative of (3) is equivalent to requiring $\varepsilon _1=\cdots =\varepsilon _k=1$.

The number of boundary components of the positive d-section $\Sigma$ equals that of the 1-section $\overline{\Sigma }$ of $\overline{M}$, which by Theorem 4.2 is

$$\begin{aligned} \overline{b}+k=-de+\sum _{\alpha _i\not \mid d}\left( 1-\frac{1}{\alpha _i}\right) . \end{aligned}$$

If $\Sigma$ has empty boundary, which happens when $e=0$ and $\alpha _i|d$ for all $i=1,\ldots ,n$, it may be disconnected, depending on the branching of the map $\Sigma \rightarrow \overline{\Sigma }$; an obvious case is a trivial $S^1$-bundle $M=B\times S^1\rightarrow B$. When the boundary is non-empty, $\Sigma$ is connected by the argument in the proof of [1, Theorem 4.1]. For the remainder of the proof, we assume this latter case.

Write ${\hat{\Sigma }}$ for the closed surface obtained by gluing $\overline{b}+k$ copies of $D^2$ to the d-section $\Sigma$ of M along its boundary components, and ${\hat{\overline{\Sigma }}}$ for the closed surface obtained in the same way from the 1-section $\overline{\Sigma }$ of $\overline{M}$. This gluing is done abstractly, that is, the surfaces ${\hat{\Sigma }}$ and ${\hat{\overline{\Sigma }}}$ are no longer embedded surfaces in M or $\overline{M}$, respectively. The Euler characteristic of ${\hat{\overline{\Sigma }}}$ equals $2-2g$, since the interior of the 1-section is a copy of the base B with $\overline{b}+k$ points removed.

The surface ${\hat{\Sigma }}$ is a branched cover of ${\hat{\overline{\Sigma }}}$ as follows. Each of the discs glued to one of the $\overline{b}+k$ boundary components gives rise to a single branch point in ${\hat{\Sigma }}$ of index d, since both a regular fibre in M as well as a singular fibre with $\alpha _i$ coprime to d is a d-fold cover of the corresponding fibre in $\overline{M}$.

Each singular fibre of M with $\alpha _i|d$ gives rise to a point in ${\hat{\overline{\Sigma }}}$ covered by $d/\alpha _i$ points of branching index $\alpha _i$. This statement about covering points and indices remains true for $\alpha _i=1$.

Thus, the Riemann–Hurwitz formula for the branched covering ${\hat{\Sigma }}\rightarrow {\hat{\overline{\Sigma }}}$ gives

$$\begin{aligned} \chi ({\hat{\Sigma }})=d\bigl (2-2g-(\overline{b}+k)-(n-k)\bigr )+(\overline{b}+k)+ \sum _{i=k+1}^n\frac{d}{\alpha _i}. \end{aligned}$$

The formula for the genus $(2-\chi ({\hat{\Sigma }}))/2$ of the d-section follows with some simple arithmetic. Notice that the formula is invariant under adding or removing pairs (1, 0) from the Seifert invariants. $\square$

5.6 Examples

Here are some elementary applications of Theorem 5.4.

5.6.1 The Hopf Flow on $S^3$

The Hopf fibration $S^3\rightarrow S^2$ has the description $M\bigl (0;(1,1)\bigr )$ as a Seifert manifold, with $e=-1$, see [1, Section 2.4]. The following is [1, Theorem 4.1].

Example 5.5

For any natural number d, the Hopf fibration admits a unique positive d-section, which has genus $(d-1)(d-2)/2$ and d boundary components.

5.6.2 Seifert Fibrations of $S^3$

According to [3, Proposition 5.2], a complete list of the Seifert fibrations of $S^3$ is provided by

$$\begin{aligned} M\bigl (0;(\alpha _1,\beta _1),(\alpha _2,\beta _2)\bigr ), \end{aligned}$$

where $\alpha _1\beta _2+\alpha _2\beta _1=1$ (in particular, $\alpha _1$ and $\alpha _2$ are coprime). To avoid duplications in this list, one may assume $\alpha _1\ge \alpha _2$ and $0\le \beta _1<\alpha _1$. For our purposes, this is not relevant, and so we shall not insist on this choice since we prefer to retain the symmetry in $\alpha _1$ and $\alpha _2$.

The corresponding $S^1$-action on $S^3\subset {\mathbb {C}}^2$ is given by

Notice the choice of indices. The fibre $C_1=\{z_2=0\}\cap S^3$ through the point (1, 0) has multiplicity $\alpha _2$, the fibre $C_2=\{z_1=0\}\cap S^3$ through (0, 1), multiplicity $\alpha _1$. The Euler number of this fibration is

$$\begin{aligned} e=-\frac{\beta _1}{\alpha _1}-\frac{\beta _2}{\alpha _2}= -\frac{1}{\alpha _1\alpha _2}. \end{aligned}$$

The Hopf fibration corresponds to the choice $\alpha _1=\alpha _2=1$.

We shall discuss these Seifert fibrations in more detail in Sect. 7. The following example answers a question posed to us by Christian Lange.

Example 5.6

The Seifert fibration $M\bigl (0;(\alpha _1,\beta _1),(\alpha _2,\beta _2)\bigr )$ of $S^3$ admits a positive $\alpha _1\alpha _2$-section, with boundary a single regular fibre, of genus $(\alpha _1-1)(\alpha _2-1)/2$.

Here is one way how to describe this $\alpha _1\alpha _2$-section explicitly. A more systematic treatment, using algebraic curves in weighted projective spaces, will be given in Sects. 7 and 8 . We replace the round 3-sphere $S^3\subset {\mathbb {C}}^2$ by its diffeomorphic copy

$$\begin{aligned} S^3_{\alpha _1,\alpha _2}:= \bigl \{(z_1,z_2)\in {\mathbb {C}}^2:\,|z_1|^{2\alpha _1}+|z_2|^{2\alpha _2}=1\bigr \}, \end{aligned}$$

The $S^1$-action is as in ($A_{2,1}$), and we write $C_1^{\alpha _1,\alpha _2}$, $C_2^{\alpha _1,\alpha _2}$ for the fibres through the points (1, 0) and (0, 1), respectively. Now consider the map

$$\begin{aligned} \begin{array}{rccc} \rho _{\alpha _1,\alpha _2}:\,&{} S^3_{\alpha _1,\alpha _2} &{} \longrightarrow &{} S^3\\ &{} (z_1,z_2) &{} \longmapsto &{} (z_1^{\alpha _1},z_2^{\alpha _2}). \end{array} \end{aligned}$$

(5)

We have

$$\begin{aligned} \rho _{\alpha _1,\alpha _2}\bigl (\mathrm {e}^{\mathrm {i}\alpha _2\theta }z_1, \mathrm {e}^{\mathrm {i}\alpha _1\theta }z_2\bigr )=\bigl (\mathrm {e}^{\mathrm {i}\alpha _1\alpha _2\theta } z_1^{\alpha _1},\mathrm {e}^{\mathrm {i}\alpha _1\alpha _2\theta }z_2^{\alpha _2}\bigr ), \end{aligned}$$

so each $S^1$-orbit on $S^3_{\alpha _1,\alpha _2}$ maps $\alpha _1\alpha _2:1$ to a Hopf orbit on $S^3$, except for the two exceptional orbits $C_i^{\alpha _1,\alpha _2}$, which are $\alpha _i$-fold coverings of the Hopf orbits $C_i$, $i=1,2$. So $\rho _{\alpha _1,\alpha _2}$ is a covering branched along (and transverse to) $C_1^{\alpha _1,\alpha _2}$, $C_2^{\alpha _1,\alpha _2}$ with branching index $\alpha _2,\alpha _1$, respectively.

Note 5.7

Points with the same image under $\rho _{\alpha _1,\alpha _2}$ do indeed come from the same $S^1$-orbit on $S^3_{\alpha _1,\alpha _2}$. For instance, the point $\bigl (\mathrm {e}^{2\pi \mathrm {i}/\alpha _1}z_1,z_2\bigr )$ lies on the same orbit as $(z_1,z_2)$, since there is a $k\in {\mathbb {Z}}$ with $k\alpha _2\equiv 1$ mod $\alpha _1$, and then with $\theta :=2\pi k/\alpha _1$ we have $\theta (z_1,z_2)= \bigl (\mathrm {e}^{2\pi \mathrm {i}/\alpha _1}z_1,z_2\bigr )$.

It follows that the quotient map $\pi _{2,1}:\,S^3_{\alpha _1,\alpha _2} \rightarrow S^3_{\alpha _1,\alpha _2}/S^1={\mathbb {C}}\mathrm {P}^1$ is given by

$$\begin{aligned} \pi _{2,1}(z_1,z_2)=[z_1^{\alpha _1}:z_2^{\alpha _2}]\in {\mathbb {C}}\mathrm {P}^1=S^2. \end{aligned}$$

Observe that the preimage of a point $[w_1:w_2]\in {\mathbb {C}}\mathrm {P}^1$, where we may assume that $|w_1|^2+|w_2|^2=1$, consists of the points $\bigl (\lambda _1(w_1)^{1/\alpha _1}, \lambda _2(w_2)^{1/\alpha _2}\bigr )\in S^3_{\alpha _1,\alpha _2}$ for some fixed choice of roots and $\lambda _1,\lambda _2\in S^1\subset {\mathbb {C}}$ with $\lambda _1^{\alpha _1}=\lambda _2^{\alpha _2}$, which means we can write $\lambda _1=\mathrm {e}^{\mathrm {i}\alpha _2\theta }$ and $\lambda _2= \mathrm {e}^{\mathrm {i}\alpha _1\theta }$ for a suitable $\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}$.

The element $\mathrm {e}^{2\pi \mathrm {i}/\alpha _1\alpha _2}\in S^1$ defines a ${\mathbb {Z}}_{\alpha _1\alpha _2}$-action on $S^3_{\alpha _1,\alpha _2}$. In other words, this is the action generated by

$$\begin{aligned} (z_1,z_2)\longmapsto \bigl (\mathrm {e}^{2\pi \mathrm {i}/\alpha _1}z_1, \mathrm {e}^{2\pi \mathrm {i}/\alpha _2}z_2\bigr ). \end{aligned}$$

By the Chinese remainder theorem, for $k\in \{0,1,\ldots , \alpha _1\alpha _2-1\}$, we obtain the $\alpha _1\alpha _2$ independent choices of roots of unity $\bigl (\mathrm {e}^{2\pi \mathrm {i}k/\alpha _1},\mathrm {e}^{2\pi \mathrm {i}k/\alpha _2}\bigr )$, so the map $\rho _{\alpha _1,\alpha _2}$ is in fact the quotient map under this ${\mathbb {Z}}_{\alpha _1\alpha _2}$-action.

Summing up, we have the following commutative diagram:

Remark 5.8

The quotient $S^3_{\alpha _1,\alpha _2}/{\mathbb {Z}}_{\alpha _1\alpha _2}$ can also be recognised as $S^3$ with the Hopf fibration by computing its Seifert invariants. By Proposition 5.3 we have

$$\begin{aligned} S^3_{\alpha _1,\alpha _2}/{\mathbb {Z}}_{\alpha _1\alpha _2}= & {} M\bigl (0;(1,\alpha _2\beta _1),(1,\alpha _1\beta _2)\bigr )\\= & {} M\bigl (0;(1,0),(1,\alpha _1\beta _2+\alpha _2\beta _1)\bigr )\\= & {} M\bigl (0;(1,0),(1,1)\bigr ), \end{aligned}$$

which describes the diagonal action of $S^1$ on $S^3\subset {\mathbb {C}}^2$.

For the Hopf fibration, it is easy to write down a disc-like 1-section, where the boundary fibre sits over the point $[1:1]\in {\mathbb {C}}\mathrm {P}^1$. Lifting this to $S^3_{\alpha _1,\alpha _2}$, one finds an $\alpha _1\alpha _2$-section as the image of the $\alpha _1\alpha _2$-valued map

$$\begin{aligned} {\mathbb {C}}\ni z\longmapsto \left( \left( \frac{z-1}{\sqrt{|z-1|^2+|z|^2}}\right) ^{1/\alpha _1}, \left( \frac{z}{\sqrt{|z-1|^2+|z|^2}}\right) ^{1/\alpha _2}\right) \in S^3_{\alpha _1,\alpha _2}. \end{aligned}$$

As $z\rightarrow \infty$, this becomes asymptotic to the (regular) fibre over $[1:1]\in {\mathbb {C}}\mathrm {P}^1$. For $z=0$ the map is $\alpha _1$-valued. This corresponds to the $\alpha _1$ points over [1 : 0] of branching index $\alpha _2$. Similarly, the point $z=1$ maps to the $\alpha _2$ branch points of index $\alpha _1$.

5.6.3 Existence of d-Sections

As a corollary of Theorem 5.4 and the discussion in Sect. 5.3, we mention the following existence statement, which is in response to a question by Umberto Hryniewicz.

Corollary 5.9

Every Seifert manifold admits a d-section for a suitable positive integer d. It admits a positive d-section if and only if its Euler number is non-positive.

Proof

For the Seifert manifold $M=M\bigl (g;(\alpha _1,\beta _1),\ldots , (\alpha _n,\beta _n)\bigr )$ we may choose d as a common multiple of the $\alpha _i$. Then the ${\mathbb {Z}}_d$-quotient is of the form $M\bigl (g;(1,\overline{b})\bigr )$. This admits a 1-section, which can be lifted to a d-section of M.

For this choice of d, condition (4) will be satisfied if and only if $e\le 0$. If e is positive, (4) will not be satisfied for any choice of d. $\square$

Remark 5.10

Changing the orientation of M amounts to changing the sign of the Euler number. So a Seifert manifold always admits a positive d-section for at least one of the two orientations. If $e\ne 0$, the Seifert fibration can be realised as a Besse Reeb flow [11].

6 Weighted Projective Planes

In this section, we recall the bare essentials of weighted projective planes that we shall need to give explicit realisations of surfaces of section for the Seifert fibrations of $S^3$. For more details, see [6].

6.1 The Definition of Weighted Projective Planes

Let $a_0,a_1,a_2\in {\mathbb {N}}$ be a triple of pairwise coprime positive integers. The quotient of ${\mathbb {C}}^3{\setminus }\{(0,0,0)\}$ under the ${\mathbb {C}}^*$-action given by

$$\begin{aligned} \lambda (z_0,z_1,z_2)=(\lambda ^{a_0}z_0,\lambda ^{a_1}z_1,\lambda ^{a_2}z_2) \end{aligned}$$

is called the (well-formed) weighted complex projective plane ${\mathbb {P}}(a_0,a_1,a_2)$ with weights $a_0,a_1,a_2$. The equivalence class of a point $(z_0,z_1,z_2)$ is written as $[z_0:z_1:z_2]_{{\mathbf {a}}}$, where ${\mathbf {a}}=(a_0,a_1,a_2)$.

The space ${\mathbb {P}}(a_0,a_1,a_2)$ is a complex manifold of complex dimension 2, except for three cyclic singularities at the points $[1:0:0]_{{\mathbf {a}}}$, $[0:1:0]_{{\mathbf {a}}}$ and $[0:0:1]_{{\mathbf {a}}}$. Indeed, the subset

$$\begin{aligned} U_0:=\bigl \{[z_0:z_1:z_2]_{{\mathbf {a}}}:\,z_0\ne 0\bigr \} \end{aligned}$$

can be identified with the quotient ${\mathbb {C}}^2/{\mathbb {Z}}_{a_0}$ under the action of the cyclic group ${\mathbb {Z}}_{a_0}< S^1\subset {\mathbb {C}}$ given by

$$\begin{aligned} \zeta (w_1,w_2)=(\zeta ^{a_1}w_1,\zeta ^{a_2}w_2),\;\;\;\zeta \in {\mathbb {Z}}_{a_0}. \end{aligned}$$

If we write $[w_1,w_2]_{a_0}$ for the equivalence class of $(w_1,w_2)$ in this cyclic quotient, the claimed identification is given by

$$\begin{aligned} \begin{array}{rcl} U_0 &{} \longrightarrow &{} {\mathbb {C}}^2/{\mathbb {Z}}_{a_0}\\ {[z_0:z_1:z_2]}_{{\mathbf {a}}} &{} \longmapsto &{} [z_0^{-a_1/a_0}z_1, z_0^{-a_2/a_0}z_2]_{a_0}. \end{array} \end{aligned}$$

The ambiguity in the choice of a root of order $a_0$ is accounted for by the equivalence relation on the right. This map is well defined, with inverse

$$\begin{aligned} {[}w_1,w_2]_{a_0}\longmapsto [1:w_1:w_2]_{{\mathbf {a}}}. \end{aligned}$$

There are analogous descriptions for the subsets $U_i=\{z_i\ne 0\} \subset {\mathbb {P}}(a_0,a_1,a_2)$ for $i=1,2$.

6.2 Algebraic Curves in Weighted Projective Planes

A complex polynomial F in the variables $z_0,z_1,z_2$ is called a degree-d weighted-homogeneous polynomial (with a choice of $a_0,a_1,a_2$ understood) if

$$\begin{aligned} F(\lambda ^{a_0}z_0,\lambda ^{a_1}z_1,\lambda ^{a_2}z_2)=\lambda ^d F(z_0,z_1,z_2) \end{aligned}$$

for some $d\in {\mathbb {N}}$ and all $(z_0,z_1,z_2)\in {\mathbb {C}}^3$ and $\lambda \in {\mathbb {C}}^*$. Then the zero set $\{F=0\}$ is a well-defined subset of ${\mathbb {P}}(a_0,a_1,a_2)$.

The polynomial F is called non-singular if there are no solutions to the system of equations

$$\begin{aligned} F=\frac{\partial F}{\partial z_0}=\frac{\partial F}{\partial z_1}= \frac{\partial F}{\partial z_2}=0 \end{aligned}$$

in ${\mathbb {C}}^3{\setminus }\{(0,0,0)\}$.

Proposition 6.1

If F is non-singular, then $\{F=0\}\subset {\mathbb {P}}(a_0,a_1,a_2)$ is a smooth Riemann surface.

Proof

The proof is completely analogous to the usual proof for algebraic curves in ${\mathbb {C}}\mathrm {P}^2={\mathbb {P}}(1,1,1)$, which can be found in [13], for instance. The only additional issue is to deal with curves that pass through one of the (at most) three singular points of ${\mathbb {P}}(a_0,a_1,a_2)$. However, this does not pose a problem, since these singularities are cyclic. A holomorphic chart around $0\in {\mathbb {C}}/{\mathbb {Z}}_{a_i}$ is given by $z\mapsto z^{a_i}$, so on the complex curve $\{F=0\}$ these points are non-singular. $\square$

7 Seifert Fibrations of the 3-Sphere

We now give a systematic and comprehensive description of the positive d-sections for all Seifert fibrations of $S^3$. Weighted projective lines appear naturally as the base of these fibrations. We first give a description of global surfaces of section using the topological arguments from Sect. 5. A description in terms of algebraic curves in weighted projective planes will follow in Sect. 8.

7.1 An Alternative Relation with the Hopf Fibration

As we shall see presently, it is convenient to replace the $S^1$-action ($A_{2,1}$) by

As before, $\alpha _1$, $\alpha _2$ may be any pair of coprime natural numbers, and the $S^1$-actions ($A_{1,2}$) constitute a complete list of the Seifert fibrations of the 3-sphere. In contrast with Sect. 5.6.2, we now regard these as actions on the round $S^3$.

Nonetheless, the spheres $S^3_{\alpha _1,\alpha _2}$ again have to play their part, and as before we consider the map $\rho _{\alpha _1,\alpha _2}$ defined in (5). We now compute

$$\begin{aligned} \rho _{\alpha _1,\alpha _2}\bigl (\mathrm {e}^{\mathrm {i}\theta }z_1, \mathrm {e}^{\mathrm {i}\theta }z_2\bigr )=\bigl (\mathrm {e}^{\mathrm {i}\alpha _1\theta }z_1^{\alpha _1}, \mathrm {e}^{\mathrm {i}\alpha _2\theta }z_2^{\alpha _2}\bigr ), \end{aligned}$$

which tells us that each Hopf $S^1$-orbit on $S^3_{\alpha _1,\alpha _2}$ is mapped 1 : 1 to an orbit of ($A_{1,2}$) on $S^3$, except for the Hopf orbits $C_i^{\alpha _1,\alpha _2}$, which are $\alpha _i$-fold coverings of the exceptional $A_{1,2}$-orbits $C_i$, $i=1,2$. Each regular $A_{1,2}$-orbit is covered by $\alpha _1\alpha _2$ Hopf orbits.

Remark 7.1

Beware that in the set-up of Sect. 5.6.2, the orbits $C_1^{\alpha _1,\alpha _2}, C_2^{\alpha _1,\alpha _2}$ were of multiplicity $\alpha _2,\alpha _1$, respectively, whereas here the orbits $C_1,C_2$ are of multiplicity $\alpha _1,\alpha _2$, respectively.

Observe that the quotient $S^3/S^1$ under the $A_{1,2}$-action can be naturally identified with the weighted projective line ${\mathbb {P}}(\alpha _1,\alpha _2)$, which is topologically a 2-sphere, and metrically an orbifold with an $\alpha _1$- and an $\alpha _2$-singularity. The quotient map $\pi _{1,2}:\,S^3\rightarrow S^3/S^1={\mathbb {P}}(\alpha _1,\alpha _2)$ is given by

$$\begin{aligned} \pi _{1,2}(z_1,z_2)=[z_1:z_2]_{(\alpha _1,\alpha _2)} \in {\mathbb {P}}(\alpha _1,\alpha _2).\end{aligned}$$

In conclusion, these maps fit together into the following commutative diagram, where $\overline{\rho }_{\alpha _1,\alpha _2}$ sends $[z_1:z_2]\in {\mathbb {C}}\mathrm {P}^1$ to $[z_1^{\alpha _1}:z_2^{\alpha _2}]_{(\alpha _1,\alpha _2)}\in {\mathbb {P}}(\alpha _1,\alpha _2)$:

Remark 7.2

Contrast this diagram with the one in Sect. 5.6.2. Whereas the earlier diagram was used to lift a 1-section of $\pi _{\mathrm {Hopf}}$ to an $\alpha _1\alpha _2$-section of $\pi _{2,1}$, the diagram here will allow us to lift d-sections of $\pi _{1,2}$, for all admissible d, to d-sections of $\pi _{\mathrm {Hopf}}$.

7.2 Positive d-Sections

Before we discuss the lifting of d-sections, we are going to derive the classification of the positive d-sections for the Seifert fibrations of $S^3$ as a corollary of Theorem 5.4.

Corollary 7.3

Table 1 constitutes a complete list of the positive d-sections $\Sigma$ of the Seifert fibrations of $S^3$ defined by $(A_{1,2})$.

Table 1 Positive d-sections $\Sigma$ for the Seifert fibrations of $S^3$

The expression #$(\partial \Sigma )$ in Table 1 stands for the number of boundary components of the d-section $\Sigma$. In the first line, in case $\alpha _i$ equals 1, the regular fibre $C_i$ may well be a component of $\partial \Sigma$.

Proof of Corollary 7.3

We need to check under which assumptions on d the necessary and sufficient conditions (3) and (4) are satisfied. Recall that we can write the Seifert fibrations of $S^3$ as $M\bigl (0;(\alpha _1,\beta _1),(\alpha _2,\beta _2)\bigr )$ with $\alpha _1\beta _2+\alpha _2\beta _1=1$, and the Euler number of this fibration is $e=-1/\alpha _1\alpha _2$.

If both $\alpha _1$ and $\alpha _2$ divide d, then $d=k\alpha _1\alpha _2$ for some $k\in {\mathbb {N}}$, and the left-hand side of (4) equals $-k$. Notice that one or both of the $\alpha _i$ may equal 1.

Next we consider the case that $\alpha _1|(d\beta _1-1)$ (and $\alpha _1\not \mid d$) and $\alpha _2|d$ (including the case $\alpha _2=1$). The divisibility condition $\alpha _1|(d\beta _1-1)$ is equivalent to $\alpha _1$ being a divisor of

$$\begin{aligned} d\beta _1-1+\alpha _1\beta _2=d\beta _1-\alpha _2\beta _1 =\beta _1(d-\alpha _2), \end{aligned}$$

and hence to $\alpha _1|(d-\alpha _2)$. This means that d has to be of the form $d=k\alpha _1\alpha _2+\alpha _2$ for some $k\in {\mathbb {N}}_0=\{0,1,2,\ldots \}$. The case with the roles of $\alpha _1$ and $\alpha _2$ exchanged is analogous.

If $\alpha _i|(d\beta _i-1)$, $i=1,2$, then the same argument as before shows that $\alpha _1|(d-\alpha _2)$ and $\alpha _2|(d-\alpha _1)$. For $\alpha _i\not \mid d$ (and in particular $\alpha _i>1$) these divisibility conditions are equivalent to $d=k\alpha _1\alpha _2+\alpha _1+\alpha _2$.

The remaining data in Table 1 on $\#(\partial \Sigma )$ and the genus of $\Sigma$ follow from Lemma 5.1 and Theorem 5.4. $\square$

Remark 7.4

Notice that every Seifert fibration of $S^3$ admits a disc-like d-section, that is, a section of genus zero with one boundary component. This underlines the subtlety of the construction in [14] of a Reeb flow on $S^3$ without any disc-like global surface of section; see also [12].

7.3 Lifting d-Sections

We now want to describe an alternative method for computing the genus of d-sections, based on lifting a d-section of $\pi _{1,2}$ to a d-section of $\pi _{\mathrm {Hopf}}$ in the diagram from Sect. 7.1, and then using previous results on surfaces of section for the Hopf flow [1].

Thus, let $\Sigma \subset S^3$ be a positive d-section for $\pi _{1,2}$. Write ${\widetilde{\Sigma }}\subset S^3_{\alpha _1,\alpha _2}$ for the lift of $\Sigma$ under the $\alpha _1\alpha _2$-fold covering $\rho _{\alpha _1,\alpha _2}:\,S^3_{\alpha _1,\alpha _2}\rightarrow S^3$. As in Table 1, we write $k\in {\mathbb {N}}_0$ for the number of regular boundary components of $\Sigma$. Additionally, one or both of $C_1,C_2$ may belong to the boundary. (If neither of them does, then $k\ge 1$.)

As observed in Sect. 7.1, each regular fibre of $\pi _{1,2}$ is covered 1 : 1 by $\alpha _1\alpha _2$ Hopf fibres. This contributes $k\alpha _1\alpha _2$ boundary components to ${\widetilde{\Sigma }}$. Away from the boundary, ${\widetilde{\Sigma }}$ is a d-section for $\pi _{\mathrm {Hopf}}$ for the same reason. In particular, if $C_1,C_2\not \subset \partial \Sigma$, then ${\widetilde{\Sigma }}$ is a positive d-section for the Hopf flow.

If $C_i\subset \partial \Sigma$ for at least one $i\in \{1,2\}$, the situation is more complicated. A point on $C_i$ has $\alpha _i$ preimages on $C_i^{\alpha _1,\alpha _2}$ under $\rho _{\alpha _1,\alpha _2}$, whereas each point on $\Sigma {\setminus }(C_1\cup C_2)$ has $\alpha _1\alpha _2$ preimages. It follows that along $C_i^{\alpha _1,\alpha _2}$ the lifted surface ${\widetilde{\Sigma }}$ is no longer embedded, but looks like a rather slim open book with spine $C_i^{\alpha _1,\alpha _2}$ and $\alpha _j$ pages, where (i, j) is a permutation of (1, 2). We shall describe how to modify the map $\rho _{\alpha _1,\alpha _2}$ to ensure that the lifted surface ${\widetilde{\Sigma }}$ is a d-section for the Hopf flow.

7.3.1 The Behaviour of ${\widetilde{\Sigma }}$ Near an Exceptional Boundary Fibre

Even though this is not relevant for the genus calculations, it is worth understanding the behaviour of ${\widetilde{\Sigma }}$ near a boundary fibre $C_1^{\alpha _1,\alpha _2}$, say. Let $\sigma$ be the curve $\partial V\cap \Sigma$ as in the proof of Lemma 4.1 or 5.1, with V a tubular neighbourhood of $C_1\subset S^3$. Write ${\tilde{\sigma }}$ for the lift of $\sigma$ to ${\widetilde{\Sigma }}$. This is a (possibly disconnected) curve on the boundary of a tubular neighbourhood ${\widetilde{V}}$ of $C_1^{\alpha _1,\alpha _2}\subset S^3_{\alpha _1,\alpha _2}$.

Write ${\tilde{\mu }}$ for the meridian on $\partial {\widetilde{V}}$, and ${\tilde{\lambda }}$ for the longitude determined by the class of a Hopf fibre. Since $C_1^{\alpha _1,\alpha _2}$ is an $\alpha _1$-fold cover of $C_1$, but ${{\,\mathrm{Int}\,}}({\widetilde{\Sigma }})$ is an $\alpha _1\alpha _2$-fold cover of ${{\,\mathrm{Int}\,}}(\Sigma )$ near the boundary, the curve ${\tilde{\sigma }}$ lies in the class $m{\tilde{\mu }}+\alpha _2{\tilde{\lambda }}$ for some $m\in {\mathbb {Z}}$. The fact that ${\widetilde{\Sigma }}$ is a d-section (away from the boundary) translates into $-d={\tilde{\sigma }}\bullet {\tilde{\lambda }}=m$, cf. the proof of Lemma 5.1. Thus, if $\alpha _2$ and d are coprime (which in the global picture is equivalent to $C_2$ being a boundary fibre, unless $\alpha _2=1$), the curve ${\tilde{\sigma }}$ is indivisible, and hence connected. Otherwise, by the alternative in (3), $\alpha _2$ is a divisor of d, and ${\tilde{\sigma }}$ is made up of $\alpha _2$ parallel curves on $\partial {\widetilde{V}}$.

When we remove thin collar neighbourhoods of $C_1^{\alpha _1,\alpha _2} \subset {\widetilde{\Sigma }}$ and $C_1\subset \Sigma$, then in the first case we obtain a covering ${\widetilde{\Sigma }}\rightarrow \Sigma$ with a single boundary component corresponding to $C_1^{\alpha _1,\alpha _2}$, which is an $\alpha _1\alpha _2$-fold covering of the corresponding boundary component of $\Sigma$. In the second case, $C_1^{\alpha _1,\alpha _2}$ gives rise to $\alpha _2$ boundary components in ${\widetilde{\Sigma }}$, each of which is an $\alpha _1$-fold cover of one and the same boundary component of $\Sigma$.

Beware, however, that this modification of ${\widetilde{\Sigma }}$ into a surface with embedded boundary need not give the correct topology of a positive d-section for the Hopf flow. Before we describe the proper desingularisation of ${\widetilde{\Sigma }}$, we analyse the case without exceptional fibres in the boundary.

7.3.2 The Case $C_i\not \subset \partial \Sigma$, $i=1,2$

When $C_1$ is not contained in the boundary of $\Sigma$, the d-section $\Sigma$ is near $C_1$ made up of $d/\alpha _1$ discs transverse to $C_1$. Every neighbouring regular fibre cuts these discs $\alpha _1$ times, and hence in a total of d points. Since $C_1^{\alpha _1,\alpha _2}\rightarrow C_1$ is an $\alpha _1$-fold covering, the lifted surface ${\widetilde{\Sigma }}$ cuts $C_1^{\alpha _1,\alpha _2}$ in d points, and the branching index of ${\widetilde{\Sigma }}\rightarrow \Sigma$ at these points equals $\alpha _2$.

Similarly, each of the $d/\alpha _2$ intersection points of $\Sigma$ with $C_2$ has $\alpha _2$ preimages in ${\widetilde{\Sigma }}$ of branching index $\alpha _1$.

Each of the k boundary components of $\Sigma$ is covered 1 : 1 by $\alpha _1\alpha _2$ boundary components of ${\widetilde{\Sigma }}$, so the branched covering ${\widetilde{\Sigma }}\rightarrow \Sigma$ extends to a covering of closed surfaces without additional branching points.

In [1, Theorem 4.1] it was shown that a positive d-section ${\widetilde{\Sigma }}$ for the Hopf flow is a connected, orientable surface of genus $(d-1)(d-2)/2$ and with d boundary components. Write g for the genus of $\Sigma$. Then the Riemann–Hurwitz formula gives

$$\begin{aligned} 2-(d-1)(d-2)=\alpha _1\alpha _2\left( 2-2g-\frac{d}{\alpha _1}- \frac{d}{\alpha _2}\right) +2d. \end{aligned}$$

With $d=k\alpha _1\alpha _2$ this yields the formula in the first line of Table 1.

7.3.3 The Case $C_i\subset \partial \Sigma$

We illustrate the situation when one or both of $C_1,C_2$ are boundary fibres by considering the case $C_1\subset \partial \Sigma$ and $C_2\not \subset \partial \Sigma$. The other cases can be treated in an analogous fashion.

To desingularise the lifted surface ${\widetilde{\Sigma }}$ near $C_1^{\alpha _1,\alpha _2}$, we modify the copy $S^3_{\alpha _1,\alpha _2}$ of the 3-sphere and the quotient map $\rho _{\alpha _1,\alpha _2}$. For some small $\varepsilon >0$, we define

$$\begin{aligned} S^3_{\alpha _1,\alpha _2,\varepsilon }:= \bigl \{(z_1,z_2)\in {\mathbb {C}}^2:\,|z_1|^{2\alpha _1}+|z_2^{\alpha _2}-\varepsilon z_1^{\alpha _2}|^2=1\bigr \}. \end{aligned}$$

This is still a (strictly) starshaped hypersurface with respect to the origin, and hence a diffeomorphic copy of the 3-sphere.

In the commutative diagram of Sect. 7.1, we replace $S^3_{\alpha _1,\alpha _2}$ by $S^3_{\alpha _1,\alpha _2,\varepsilon }$, and the map $\rho _{\alpha _1,\alpha _2}$ by

$$\begin{aligned} \rho ^{\varepsilon }_{\alpha _1,\alpha _2}(z_1,z_2):= \bigl (z_1^{\alpha _1},z_2^{\alpha _2}-\varepsilon z_1^{\alpha _2}\bigr ). \end{aligned}$$

The preimage of a point $(w_1,w_2)\in S^3$ under $\rho ^{\varepsilon }_{\alpha _1,\alpha _2}$ consists of the points

$$\begin{aligned} (z_1,z_2)=\bigl (w_1^{1/\alpha _1}, (w_2+\varepsilon w_1^{\alpha _2/\alpha _1})^{1/\alpha _2}\bigr ), \end{aligned}$$

where the choice of root $w_1^{1/\alpha _1}$ is the same in both components. If $w_1\ne 0$ and $w_2+\varepsilon w_1^{\alpha _2/\alpha _1}\ne 0$ for all choices of $w_1^{1/\alpha _1}$, this gives us $\alpha _1\alpha _2$ preimages. Hence, generically a fibre of $\pi _{1,2}$ is covered 1 : 1 by $\alpha _1\alpha _2$ Hopf fibres, as for $\rho _{\alpha _1,\alpha _2}$.

(i) The desingularised lift of $C_1$. While under $\rho _{\alpha _1,\alpha _2}$ the fibre $C_1$ of $\pi _{1,2}$ was covered $\alpha _1$ times by $C_1^{\alpha _1,\alpha _2}$, and in particular each point on $C_1$ had only $\alpha _1$ preimages, under $\rho ^{\varepsilon }_{\alpha _1,\alpha _2}$ the point $(w_1,0)\in C_1$ is covered by $\alpha _1\alpha _2$ points $\bigl (w_1^{1/\alpha _1},\varepsilon ^{1/\alpha _2}w_1^{1/\alpha _1}\bigr )$. Notice that the $\alpha _1$ different choices of $w_1^{1/\alpha _1}$ yield points on the same Hopf fibre, so the preimage of $C_1$ consists of $\alpha _2$ Hopf fibres in the boundary of ${\widetilde{\Sigma }}$, each of which is an $\alpha _1$-fold cover of $C_1$. This allows us to pass to closed surfaces ${\hat{{\widetilde{\Sigma }}}},{\hat{\Sigma }}$ as in the proof of Theorem 5.4, and the boundary component $C_1\subset \partial \Sigma$ contributes $\alpha _2$ points in ${\hat{{\widetilde{\Sigma }}}}$ of branching index $\alpha _1$ sitting over a single point in ${\hat{\Sigma }}$.

(ii) Branch points with $z_1=0$. One case when a point in $S^3$ has fewer than $\alpha _1\alpha _2$ preimages is when $w_1=0$, that is, points on $C_2$. The fibre $C_2$ of $\pi _{1,2}$ is covered $\alpha _2$ times by the Hopf fibre $C_2^{\alpha _1,\alpha _2}$. Since $C_2$ is a fibre of multiplicity $\alpha _2$, the d-section $\Sigma$ cuts it in $d/\alpha _2$ points. As in Sect. 7.3.2 this gives us d branch points upstairs on $C_2^{\alpha _1,\alpha _2}$ of branching index $\alpha _1$.

(iii) Branch points with $z_2=0$. The only other case when a point $(w_1,w_2)\in S^3$ has fewer than $\alpha _1\alpha _2$ preimages under $\rho ^{\varepsilon }_{\alpha _1,\alpha _2}$ is when $w_2+\varepsilon w_1^{\alpha _2/\alpha _1}=0$ for some choice of $w_1^{1/\alpha _1}$. These correspond to points upstairs with $z_2=0$, that is, points on $C_1^{\alpha _1,\alpha _2}$. The restriction of $\rho ^{\varepsilon }_{\alpha _1,\alpha _2}$ to $C_1^{\alpha _1,\alpha _2}$ is given by

$$\begin{aligned} \bigl (\mathrm {e}^{\mathrm {i}\theta },0\bigr )\longmapsto \bigl (\mathrm {e}^{\mathrm {i}\alpha _1\theta }, -\varepsilon \mathrm {e}^{\mathrm {i}\alpha _2\theta }\bigr ), \end{aligned}$$

so $C_1^{\alpha _1,\alpha _2}$ maps injectively to the $\pi _{1,2}$-fibre through the point $(1,-\varepsilon )$. We choose $\varepsilon >0$ small enough to ensure that this is not a boundary component of $\Sigma$.

For ease of notation we set $\lambda =\mathrm {e}^{\mathrm {i}\theta }$. We now ask: what are the preimages of $(w_1,w_2)=(\lambda ^{\alpha _1},-\varepsilon \lambda ^{\alpha _2})$, except for the point $(\lambda ,0)\in C_1^{\alpha _1,\alpha _2}$? The equations

$$\begin{aligned} \left\{ \begin{array}{l} z_1^{\alpha _1}=\lambda ^{\alpha _1},\\ z_2^{\alpha _2}-\varepsilon z_1^{\alpha _2}=-\varepsilon \lambda ^{\alpha _2} \end{array}\right. \end{aligned}$$

have the solutions

$$\begin{aligned} \left\{ \begin{array}{l} z_1=\lambda \mathrm {e}^{2\pi \mathrm {i}k/\alpha _1},\;\; k\in \{0,\ldots ,\alpha _1-1\}\\ z_2=\root \alpha _2 \of {\varepsilon }\lambda \bigl (\mathrm {e}^{2\pi \mathrm {i}k/\alpha _1}-1\bigr )^{1/\alpha _2}, \end{array}\right. \end{aligned}$$

where $\root \alpha _2 \of {\varepsilon }$ denotes the root in ${\mathbb {R}}^+$. For each $k\in \{1,\ldots ,\alpha _1-1\}$ (sic!) and given $\lambda$ we obtain $\alpha _2$ solutions on different Hopf fibres. For $k=0$ we obtain the unique solution $(\lambda ,0)$, where we have branching of index $\alpha _2$.

The d-section $\Sigma$ cuts the $\pi _{1,2}$-fibre through the point $(1,-\varepsilon )$ in d points. For each of these d points we obtain a single branch point upstairs of index $\alpha _2$.

Computing the genus of ${\widetilde{\Sigma }}$. We can now compute the genus of ${\widetilde{\Sigma }}$ by counting the branch points of ${\widetilde{\Sigma }}\rightarrow \Sigma$ upstairs. We have

• (i) $\alpha _2$ branch points of index $\alpha _1$,

• (ii) d branch points of index $\alpha _1$,

• (iii) d branch points of index $\alpha _2$.

The Riemann–Hurwitz formula then tells us that

$$\begin{aligned} 2-(d-1)(d-2)+\alpha _2(\alpha _1-1)+d(\alpha _1-1)+d(\alpha _2-1)= \alpha _1\alpha _2(2-2g). \end{aligned}$$

With $d=k\alpha _1\alpha _2+\alpha _2$ we obtain the formula in the second line of Table 1.

Remark 7.5

In the case when $C_1\not \subset \partial \Sigma$ and $C_2\subset \partial \Sigma$, one simply reverses the roles of $z_1$ and $z_2$ in the above argument. If both $C_1$ and $C_2$ are boundary fibres, one replaces $S^3_{\alpha _1,\alpha _2}$ by

$$\begin{aligned} S^3_{\alpha _1,\alpha _2,\varepsilon _1,\varepsilon _2}:= \bigl \{(z_1,z_2)\in {\mathbb {C}}^2:\,|z_1^{\alpha _1}-\varepsilon _1z_2^{\alpha _1}|^2 +|z_2^{\alpha _2}-\varepsilon _2 z_1^{\alpha _2}|^2=1\bigr \} \end{aligned}$$

for some small $\varepsilon _1,\varepsilon _2>0$, and $\rho _{\alpha _1,\alpha _2}$ by

$$\begin{aligned} \rho ^{\varepsilon _1,\varepsilon _2}_{\alpha _1,\alpha _2}(z_1,z_2):= \bigl (z_1^{\alpha _1}-\varepsilon _1z_2^{\alpha _1}, z_2^{\alpha _2}-\varepsilon _2 z_1^{\alpha _2}\bigr ). \end{aligned}$$

8 Surfaces of Section and Algebraic Curves

We now wish to relate surfaces of section for Seifert fibrations of $S^3$ to algebraic curves in weighted projective planes ${\mathbb {P}}(1,\alpha _1,\alpha _2)$. The degree-genus formula for such algebraic curves [16] then allows us to confirm Corollary 7.3. Conversely, our results on positive d-sections can be read as an alternative proof of the degree-genus formula. Moreover, the lifting of d-sections as described in Sect. 7.3 permits a natural interpretation as the lifting of algebraic curves from ${\mathbb {P}}(1,\alpha _1,\alpha _2)$ to ${\mathbb {C}}\mathrm {P}^2$.

In [1], it was explained how an algebraic curve $C\subset {\mathbb {C}}\mathrm {P}^2$ of degree d gives rise to a surface of section $\Sigma \subset S^3$ for the Hopf flow. Simply consider the affine part $C_{\mathrm {aff}}:=C\cap {\mathbb {C}}^2$ of C, and project $C_{\mathrm {aff}}{\setminus }\{(0,0)\}$ radially to the unit sphere $S^3\subset {\mathbb {C}}^2$. Under suitable assumptions on C, this will be a surface of section $\Sigma$ for the Hopf flow, with positive boundary components coming from points on C at infinity, and negative boundary components if $(0,0)\in C_{\mathrm {aff}}$. The multiplicity of the section is determined by the number of intersection points of $C_{\mathrm {aff}}{\setminus }\{(0,0)\}$ with a radial plane in ${\mathbb {C}}^2$.

Topologically, the algebraic curve is obtained from the corresponding surface of section by capping off the boundary components with discs. This means that the genus of the algebraic curve equals that of the surface of section.

For instance, if $C=\{F=0\}$ with F a homogeneous polynomial of degree d of the form

$$\begin{aligned} F(z_0,z_1,z_2)=f(z_1,z_2)-z_0^d, \end{aligned}$$

the intersection of $C_{\mathrm {aff}}$ with the punctured radial plane $P_{a,b}:=\{(az,bz):\,z\in {\mathbb {C}}^*\}$, where $(a,b)\in S^3\subset {\mathbb {C}}^2$, is given by the solutions z to the equation $f(a,b)z^d=1$. If $f(a,b)\ne 0$, this gives rise to d points $(az,bz)\in C_{\mathrm {aff}}\cap P_{a,b}$ whose projection to $S^3$ lie on the Hopf fibre through the point (a, b). If $f(a,b)=0$, there are no intersections of $C_{\mathrm {aff}}$ with the radial plane, but now the point [0 : a : b] at infinity lies on C and corresponds to a boundary fibre of $\Sigma$. The surface of section $\Sigma$ has no negative boundary components, since $F(1,0,0)\ne 0$.

It is this simple example that we want to generalise to positive d-sections of ($A_{1,2}$) and algebraic curves in weighted projective planes, as it illustrates some of the essential features of the correspondence between these two classes of objects. Moreover, we shall see (Remark 8.4) that every positive d-section can be realised by an algebraic curve of this form.

8.1 Weighted Homogeneous Polynomials

As explained in Sect. 6.2, an algebraic curve in ${\mathbb {P}}(1,\alpha _1,\alpha _2)$ is defined by a $(1,\alpha _1,\alpha _2)$-weighted homogeneous polynomial. We want to consider such polynomials of the form

$$\begin{aligned} F(z_0,z_1,z_2)=f(z_1,z_2)-z_0^d. \end{aligned}$$

(6)

The following lemma is the analogue of the factorisation of an unweighted homogeneous polynomial in two variables into linear factors [13, Lemma 2.8].

Lemma 8.1

If F is non-singular, then f is of the form

$$\begin{aligned} f(z_1,z_2)=(b_1^{\alpha _1}z_1^{\alpha _2}-a_1^{\alpha _2}z_2^{\alpha _1}) \cdot \ldots \cdot (b_k^{\alpha _1}z_1^{\alpha _2}-a_k^{\alpha _2}z_2^{\alpha _1}) \cdot z_1^{\varepsilon _1}\cdot z_2^{\varepsilon _2} \end{aligned}$$

with $\varepsilon _1,\varepsilon _2\in \{0,1\}$ and $[a_i:b_i]_{(\alpha _1,\alpha _2)}\in {\mathbb {P}}(\alpha _1,\alpha _2)$, $i=1,\ldots ,k$, pairwise distinct points different from $[1:0]_{(\alpha _1,\alpha _2)}$ and $[0:1]_{(\alpha _1,\alpha _2)}$. If at least one $\varepsilon _i$ equals 1, one may have $k=0$.

In particular, the degree d of F equals $d=k\alpha _1\alpha _2+\varepsilon _1\alpha _1+\varepsilon _2\alpha _2$.

Proof

We have $f(0,1)=0$ if and only if f is divisible by $z_1$. Similarly, $f(1,0)=0$ holds if and only if f is divisible by $z_2$. In either case, there can be at most one such factor each of $z_1$ or $z_2$, lest F be singular.

After dividing by these factors, in case they are present, we have a sum of complex monomials $c_{mn}z_1^mz_2^n$ with $\alpha _1m+\alpha _2n=\mathrm {const.}$ and at least one non-zero monomial each without a $z_1$- or $z_2$-factor, respectively. From the identity $\alpha _1m+\alpha _2n=\alpha _1m'+\alpha _2n'$ we deduce $\alpha _1|(n-n')$ and $\alpha _2|(m-m')$, which implies that f is of the form

$$\begin{aligned} f(z_1,z_2)=z_1^{\varepsilon _1}\cdot z_2^{\varepsilon _2}\cdot \sum _{i=0}^k c_iz_1^{i\alpha _2}z_2^{(k-i)\alpha _1} \end{aligned}$$

with $c_0,c_k\ne 0$.

The sum in this description is a homogeneous polynomial of degree k in $z_1^{\alpha _2}$ and $z_2^{\alpha _1}$, and hence, by [13, Lemma 2.8], has a factorisation into linear factors in $z_1^{\alpha _2}$ and $z_2^{\alpha _1}$. The condition on the $[a_i:b_i]_{(\alpha _1,\alpha _2)}$ is equivalent to f having no repeated factors. $\square$

8.2 Constructing d-Sections from Algebraic Curves

We now want to show how a complex algebraic curve $C=\{F=0\}$, with F as in (6), gives rise to a positive d-section of the $A_{1,2}$-flow. For this we need to work with a weighted ‘radial’ projection ${\mathbb {C}}^2{\setminus }\{(0,0)\} \rightarrow S^3$ given by sending $(z_1,z_2)$ to the unique point on $S^3$ of the form $(z_1/r^{\alpha _1},z_2/r^{\alpha _2})$, $r\in {\mathbb {R}}^+$. This projection map is smooth. We define weighted ‘punctured radial complex planes’ for $(a,b)\in S^3\subset {\mathbb {C}}^2$ as

$$\begin{aligned} P_{a,b}:=\bigl \{(az^{\alpha _1},bz^{\alpha _2}):\,z\in {\mathbb {C}}^*\bigr \}. \end{aligned}$$

Under the radial projection we have, for $z=r\mathrm {e}^{\mathrm {i}\theta }$,

$$\begin{aligned} \bigl (az^{\alpha _1},bz^{\alpha _2}\bigr )\longmapsto \bigl (\mathrm {e}^{\mathrm {i}\alpha _1\theta }a, \mathrm {e}^{\mathrm {i}\alpha _2\theta }b\bigr ), \end{aligned}$$

that is, $P_{a,b}$ projects to the $A_{1,2}$-orbit through (a, b) on $S^3$.

The following is the generalisation of [1, Proposition 5.1] from the Hopf flow to all Seifert fibrations of $S^3$.

Proposition 8.2

The complex algebraic curve $C=\{F=0\}$ in the weighted complex plane ${\mathbb {P}}(1,\alpha _1,\alpha _2)$, where F is a weighted homogeneous polynomial of the form (6), defines a positive d-section for the flow $(z_1,z_2)\mapsto \bigl (\mathrm {e}^{\mathrm {i}\alpha _1\theta }z_1,\mathrm {e}^{\mathrm {i}\alpha _2\theta }z_2\bigr )$ on $S^3$ if and only if F is non-singular.

The proof of this proposition is analogous to that of [1, Proposition 5.1], and we only sketch the necessary modifications.

The affine part $C_{\mathrm {aff}}= \bigl \{(z_1,z_2)\in {\mathbb {C}}^2:\,f(z_1,z_2)=1\bigr \}$ can be shown to intersect each $P_{a,b}$ in d points that do not lie on a real radial ray, and hence project to d distinct points on the corresponding $A_{1,2}$-orbit on $S^3$, except in the following cases.

• Solutions of the equation $f(z_1,0)=1$ or $f(0,z_2)=1$ correspond to $C_1$ or $C_2$ not being a boundary fibre, and they give rise to $d/\alpha _1$ or $d/\alpha _2$ intersection points, respectively.

• Solutions to the equation $f(z_1,z_2)=0$, that is, points at infinity on C, correspond to boundary fibres.

The correct asymptotic behaviour near the boundary fibres can be demonstrated with the explicit factorisation of f given by Lemma 8.1.

8.3 Branched Coverings of Algebraic Curves

The map $\rho _{\alpha _1,\alpha _2}:\,S^3_{\alpha _1,\alpha _2}\rightarrow S^3$ has a natural extension to

$$\begin{aligned} \begin{array}{rccc} \rho _{\alpha _1,\alpha _2}:\,&{} {\mathbb {C}}\mathrm {P}^2 &{} \longrightarrow &{} {\mathbb {P}}(1,\alpha _1,\alpha _2)\\ &{} [z_0:z_1:z_2] &{} \longmapsto &{} [z_0:z_1^{\alpha _1}: z_2^{\alpha _2}]_{(1,\alpha _1,\alpha _2)}. \end{array}\end{aligned}$$

A weighted algebraic curve $C=\{F=0\}\subset {\mathbb {P}}(1,\alpha _1,\alpha _2)$ lifts to the algebraic curve ${\widetilde{C}}=\{{\widetilde{F}}=0\}\subset {\mathbb {C}}\mathrm {P}^2$, where ${\widetilde{F}}$ is the homogeneous polynomial of degree d defined by ${\widetilde{F}}(z_0,z_1,z_2)=F(z_0,z_1^{\alpha _1},z_2^{\alpha _2})$. The lift ${\widetilde{C}}$ of a non-singular algebraic curve C may well be singular.

Under this extended map $\rho _{\alpha _1,\alpha _2}$, the standard punctured plane

$$\begin{aligned} \bigl \{(az,bz):\,z\in {\mathbb {C}}^*\bigr \}\subset {\mathbb {C}}^2, \end{aligned}$$

with $(a,b)\in S^3_{\alpha _1,\alpha _2}$, maps to $P_{a^{\alpha _1},b^{\alpha _2}}$.

The discussion in Sect. 7.3 carries over to algebraic curves $C=\{F=0\}$ with F as in (6), only changing notation to (weighted) homogeneous coordinates. This means that we can compute the genus of a weighted algebraic curve in ${\mathbb {P}}(1,\alpha _1,\alpha _2)$ by lifting it to an algebraic curve in ${\mathbb {C}}\mathrm {P}^2$, and then applying the Riemann–Hurwitz formula and the known results about algebraic curves in ${\mathbb {C}}\mathrm {P}^2$. In the covering ${\widetilde{C}}\rightarrow C$, we see the same branching behaviour as for the (extended) surfaces of section, and we can apply the same process of desingularisation in case C contains one or both of the points $[0:1:0]_{(1,\alpha _1,\alpha _2)}$ or $[0:0:1]_{(1,\alpha _1,\alpha _2)}$ at infinity.

8.4 Computing the Genus of Algebraic Curves via Surfaces of Section

Here is the general formula for computing the genus of a non-singular algebraic curve in a weighted projective plane, see [16, Corollary 3.5], [6, Theorem 5.3.7].

Theorem 8.3

The genus of a non-singular algebraic curve of degree d in the weighted projective plane ${\mathbb {P}}(a_0,a_1,a_2)$ is given by

$$\begin{aligned} g=\frac{1}{2}\left( \frac{d^2}{a_0a_1a_2}- d\sum _{i<j}\frac{\gcd (a_i,a_j)}{a_ia_j}+ \sum _i\frac{\gcd (a_i,d)}{a_i}-1\right) . \end{aligned}$$

$\square$

For $(a_0,a_1,a_2)=(1,\alpha _1,\alpha _2)$ this confirms the values in Table 1.

Remark 8.4

Consider the possible values of d for which there exists, according to Table 1, a positive d-section for the Seifert fibration of $S^3$ defined by ($A_{1,2}$). By Lemma 8.1, any such d can be realised as the degree of a weighted homogeneous polynomial F of the form (6). Hence, the algebraic curve $\{F=0\}$ in ${\mathbb {P}}(1,\alpha _1,\alpha _2)$ gives rise to a d-section with the chosen value of d. By the uniqueness statement in Theorem 5.4, this means that every surface of section for any Seifert fibration of $S^3$ comes from an algebraic curve $\{F=0\}\subset {\mathbb {P}}(1,\alpha _1,\alpha _2)$ with F as in (6).

Conversely, the arguments in Sect. 7.3—applied to coverings of algebraic surfaces as explained in Sect. 8.3—provide an alternative proof of Theorem 8.3 in the case $a_0=1$ and for such special algebraic curves; the latter restriction can be removed with genericity arguments as in [1, Section 6].

It seems plausible that the reasoning in Sect. 7.3 can be extended to a geometric proof of Theorem 8.3 in full generality.