Abstract
Finding underlying molecular mechanisms of diseases is one of the important issues in biomedical research. In which, prediction of novel disease-associated genes is mostly focused. Many methods have been proposed based on biological networks and shown effectively for the problem. These network-based methods are usually relied on a “disease module” principle that functionally similar genes are associated with similar phenotypes or diseases. Among them, methods solely based on gene/protein networks only exploit that principle by structural modules in the gene/protein networks. Meanwhile, others based on integration of these networks with a disease similarity network better exploit the principle and consequently result in higher prediction performance. In these studies, the disease similarity network is extracted from a disease similarity matrix which was calculated using text mining techniques on OMIM records. Considering that diseases have been recently well annotated by human phenotype ontology (i.e., a controlled vocabulary database) and semantic similarity measures can be used to calculate similarities among them. Therefore, it would be more accurate to construct disease similarity network based on semantic similarity measures on phenotype ontology database. In this study, we constructed such network and integrated them with several kinds of gene/protein networks. Experiment results show that the ontology-based disease similarity network much improves the prediction performance compared to the one based on OMIM records, irrespective of gene/protein networks. In addition, we show ability of our method in predicting novel Alzheimer’s disease-associated genes, in which 19 out of top 100 ranked candidate genes are supported with evidences from literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Disease gene prediction, the task of identifying the most plausible candidate disease genes, is an important issue in biomedical research and many studies have been done for this [1, 2]. Identification of disease-associated genes also leads to more effective researches about therapies for genetic diseases and gradually approaches a future of personalized medicine [3–5]. In past decades, linkage analysis was usually used to identify novel disease genes, in which susceptible loci including hundreds of genes are investigated, and thus it is much costly for doing many experiments in wet lab. Therefore, ranking/prioritization methods for such candidate genes are introduced (i.e., genes are ranked by their relevance to a disease of interest). Highly ranked genes are further investigated to find out associated biomedical evidences. And therefore, the goal of gene ranking/prioritization is to predict novel disease-associated genes.
The prediction of novel disease-associated genes are usually approached by three main directions: (1) functional annotation based; (2) machine learning based; and (3) network based. In which, functional annotation-based methods have prioritized candidate genes by measuring the degree of similarity of each candidate genes to a set of known disease genes based on profiles which were built from many functional annotation data sources [6–8]. Therefore, those methods mostly focused on the integration of various biological datasets to obtain more accurate similarity. However, those approaches are limited in that functional annotation data sources have not covered whole human genome yet. For the second approach, many learning techniques have been applied to predict disease-associated genes. In which, the problem is considered as a classification one, where a classifier is learned from training data; then the learned classifier is used to predict whether or not a test/candidate gene is a disease gene. Briefly, at the early, machine learning-based studies usually approached disease gene prediction as a binary classification problem [9], where the learning samples are comprised of positive training samples and negative training samples [9] such as decision trees (DT) [10, 11] k-nearest neighbor (kNN) [12], naive Bayesian classifier [13, 14], binary support vector machine classifier [15–17], artificial neural network (ANN) techniques [18] and random forest (RF) [9]. In these binary classifier-based methods, positive training samples are constructed from known disease genes, whereas negative training samples are the remaining which are not known to be associated with diseases. This is the limitation of binary classifier-based solutions for the disease gene prediction problem, since the negative training set should be actual non-disease genes. However, construction of this set is nearly impossible in biomedical researches. Therefore, more advanced machine learning techniques, which do not require to define a the negative training set, have been recently introduced for this problem [19]. However, the problem was still formulated as a classification, while it should be a ranking/prioritization one. Therefore, methods for prediction of disease-associated genes have extended to network-based ones [20, 21] and shown to outperform functional annotation- and machine learning-based ones [22, 23]. These network-based methods are mostly based on biological networks, which are constructed based on various kinds of biomedical data, and therefore they are not limited by the coverage of functional annotation data sources. In addition, these methods can be considered as positive and unlabeled learning techniques where the rankings of candidate genes are estimated based on their relative similarities to known disease ones and others. Moreover, the dominance of network-based methods is also because they are based on a principle of “disease module” (e.g., functionally similar genes are associated with similar phenotypes or diseases). Among methods solely based on gene/protein networks, a method using a random walk with restart (RWR) algorithm [22, 24, 25] is more dominant compared to other methods such as nearest neighbor, shortest path and clustering [26]. Because this algorithm calculates a global similarity among candidate and known disease genes on whole network and therefore not only genes directly connected to disease genes are considered, but also indirect ones. This algorithm has been successfully applied to other problems such as prediction of disease-associated miRNAs [27] and protein complexes [28]. However, this method can only exploit the “disease module” in the gene/protein network (i.e., genes/proteins associated with the same or similar diseases usually form functional/physical modules on gene/protein interaction networks [29–31]).
Recently, a variant of RWR algorithm, namely RWRH, was proposed for a heterogeneous network. This algorithm was then applied to predict disease-associated genes on a heterogeneous network of proteins and disease phenotypes [32]. This network was constructed by integrating a disease similarity network based on text mining algorithms on OMIM records [33] and a protein interaction network. As a result, it was reported that RWRH better exploit “disease module” principle than RWR [22] since then OMIM-based disease similarity network was additionally integrated [32]. More importantly, the RWRH algorithm can be extended to use any network of genes/proteins as well as disease similarity one. Indeed, a recent RWRH-based method has used a semantic similarity network of genes instead of the protein interaction network [34] and shown to outperform the original one [32]. We also note that a disease similarity network can be constructed based on shared disease gene [30], shared pathways [35], shared miRNA [36], shared protein complex [37], shared disease ontology [38] and disease comorbidity [39]. Similarly to RWR, RWRH algorithm has been successfully applied to other problems such as prediction of novel drug–target interactions [40] as well as novel disease-associated miRNAs [41] and long non-coding RNAs [42].
In this study, we extended the use of RWRH algorithm to the prediction of disease-associated gene by integrating semantic similarities among diseases and a gene/protein network. More specifically, considering that disease phenotypes have been recently annotated by human phenotype ontology (shortly called HPO) [43] (i.e., controlled vocabulary database) and a number of semantic similarity measures have been proposed to calculate the similarity between annotated biomedical objects [44], it would be more accurate to calculate the similarity among diseases based on such the measures. Therefore, we constructed a disease similarity network using a semantic similarity measure on HPO. Then, this network was integrated with a gene/protein network by known disease phenotype–gene associations. We compared our method with the one relied on the OMIM-based disease similarity network as in [32, 34]. In which, the gene/protein network can be the protein interaction network as in [32], the gene semantic similarity network as in [34] as well as one constructed based on expression profiles of genes. Experimental results show that the performance of our method is better than that based on the OMIM-based disease similarity network irrespective of the gene/protein networks. This indicates that HPO-based similarity calculation of diseases improves the performance of RWRH algorithm for the prediction of disease-associated genes. In addition, we used our method to find novel genes associated with Alzheimer’s disease. The evidence search from literature about the associations between 100 highly ranked candidate genes and Alzheimer’s disease confirmed 19 of them, which are not yet recorded in public disease–gene association database.
2 Methods
2.1 Construction of heterogeneous networks of diseases and genes
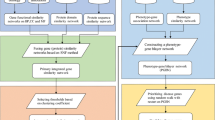
To build heterogeneous networks of diseases and genes, we constructed two kinds of networks: (1) gene/protein network, which connects genes/proteins by functional interactions; (2) disease similarity network, where a link between two diseases is specified by their similarity. Then, we connected these two networks by a bipartite network consisting of known disease–gene associations. Figure 1 shows construction of such heterogeneous networks of genes/proteins and diseases.
Gene/protein networks
Protein–protein interaction network
First, we collected a human protein interaction network (shortly called PPINet) containing 10,486 genes and 50,791 interactions from NCBI FTP repository.Footnote 1 Proteins in this network are connected by physical interactions. Therefore, we considered PPINet as an unweighted network.
Gene expression-based similarity network
Second, we constructed a weighted gene network based on gene expression data (shortly called GENet). More specifically, a gene co-expression database comprising 19,777 human genes was downloaded from COXPRESSdb [45]. To measure the similarity between a pair of genes, we employed the mutual rank method, which evaluates the strength of co-expression [46]. The mutual rank ranges from 0 to 19,776 and the normalized value \(w_{ij} =\frac{(19,776-MR(v_i ,v_j ))}{19,776}\), where MR(\(v_{i}, v_{j})\) denotes the mutual rank between gene \(v_{i}\) and \( v_{j}\). The GENet was constructed by replacing the original weight of each link in the PPINet network with the normalized mutual rank value of gene pairs that participate in the network.
Gene ontology-based similarity network
Third, we constructed another weighted gene network based on gene ontology data (shortly called GONet). To construct this network, we used the UniProtKB [47] corpus in the GO annotation database [48]. There were 18,245 Homo sapiens proteins in total. Among them, there were 15,576 proteins annotated with molecular function terms, 14,911 proteins annotated with biological process terms, and 16,983 proteins annotated with cellular component terms. Then, to construct the network, we first needed to introduce the information content (IC). The IC of a term e in the corpus is defined as follows:
where p(e) is the probability of e occurring in the corpus, i.e., \(p(e)=\frac{f(e)}{f(\mathrm{root})}\) such that \(f(e)=\mathrm{Annot}(e)\quad +\sum \nolimits _{c \in \mathrm{Children}(e)} {f(c)} \). In this formula, Annot(e) means the number of proteins annotated with e in the corpus, Children(e) represents the set of children terms of e in the GO graph and root is root term of the GO graph. Then, the semantic similarity between the two GO terms, \(e_{i}\) and \(e_{j}\), based on the most informative common ancestor approach [49], is calculated as follows:
where \(P(e_{i}, e_{j})\) is the set of shared ancestors of \(e_{i}\) and \(e_{j}\). The functional similarity between a pair of genes \(v_{i}\) and \( v_{j}\) is calculated as the maximum of simTerm values between all possible pairs of terms as follows:
where T(v) represents the set of terms annotating v. This value is normalized in range [0, 1] to account for an unequal number of GO terms for both genes as follows:
By employing the sub-ontology databases of biological process, cellular component and molecular function individually (i.e., root terms for these gene sub-ontology graphs are biological process, cellular component and molecular function, respectively), three GO-based weighted networks were constructed, in which the original weight of each link in the PPINet network was replaced by the normalized similarity value \(w_{ij}\) of two genes participating in each link. We referred to these as the BPNet, CCNet and MFNet networks, respectively. Finally, we integrated them using “per-edge average” method to construct GONet network as follows:
where M is number of networks containing interaction between gene \(v_{i}\) and \(v_{j}\). \((w_{ij} )_k\) is the weight of interaction between \(v_{i}\) and \(v_{j}\) in network k.
After selecting most connected component, we finally obtained PPINet, GENet and GONet networks with size as shown in Table 1.
2.2 Disease similarity networks
OMIM-based disease similarity network
First, following the same procedure as in [32, 34], we collected a phenotypic disease similarity matrix from [50], where an element of the matrix represents degree of similarity between two phenotypes. The similarities in this matrix were calculated based on various text mining algorithms on OMIM records, which describe diseases using natural language [33]. By selecting only five neighbors which have largest similarities for each node, we constructed a phenotypic disease similarity network (shortly called OMIMNet) consisting of 19,791 interactions among 5080 phenotypes.
HPO-based disease similarity network
Second, to construct another disease similarity network, we calculated similarity among disease phenotypes based on human phenotype ontology (HPO, a controlled vocabulary database) [43] (i.e., root term for this ontology graph is All). More specifically, we collected HPO terms and corresponding annotation data at Human Phenotype Ontology databaseFootnote 2 [43]. Then, we followed the same procedure as for gene ontology-based similarity networks to calculate similarity between every pair of disease phenotypes. Similarly, by selecting only five neighbors which have largest similarities for each node, we constructed a HPO-based disease similarity network (shortly called HPONet) consisting of 34,476 interactions among 6521 phenotypes.
2.3 A bipartite network
The bipartite network are known disease–gene associations collected from NCBI FTP repository.Footnote 3 This connects a total of 3284 diseases and 2761 genes.
2.4 RWRH-based method
Given a connected weighted graph G(V, E) with a set of nodes \(V=\{v_{1}, v_{2}, {\ldots }, v_{N}\}\) and a set of links \(E=\{(v_{i}, v_{j})\vert v_{i}, v_{j}\in V\}\), a set of source/seed nodes \(S\subseteq V\) and a \(N\times N \) adjacency matrix W of link weights. Here, we are going to introduce algorithms for measuring relative importance of node \(v_{i}\) to S. By modeling a heterogeneous network of genes and diseases as a graph, ranking/prioritization of candidate genes/diseases is to predict novel genes/diseases associated with a disease of interest (d). The rankings of candidate genes/diseases are based on their relative importance to a set of known d-associated genes and d. This value also measures how much a candidate gene/disease is associated with d.
2.5 Random walk with restart (RWR) algorithm
Random walk with restart (RWR) is a variant of the random walk and it mimics a walker that moves from a current node to a randomly selected adjacent node or goes back to source nodes with a back-probability \(\gamma \in \) (0, 1). RWR can be formally described as follows:
where \(P^t\) is a \(N \times 1\) probability vector of \(\vert V\vert \) nodes at a time step t of which the ith element represents the probability of the walker being at node \(v_{i}\in V\), and \(P^0\) is the \(N\times \)1 initial probability vector. \({W^{'}}\)is the transition matrix of the graph, the (i, j) element in \({W^{'}}\), denotes a probability with which a walker at \(v_{i}\) moves to \(v_{j}\) among \(V\backslash {\{}v_{i}{\}}\). All nodes in the network are eventually ranked according to the steady-state probability vector \(P^\infty \). The steady state of each node represents its relative importance to the set of source nodes S.
This algorithm was used for disease gene prediction based on a homogeneous network of genes/proteins [22, 24]. In which, the transition matrix \({W^{'}}\) is defined as follows:
where \(W_\mathrm{G}\) is adjacency matrix of the network of genes/proteins.
In addition, the set of source nodes (S) was specified by genes known to be associated with d. Therefore, the initial probability vector was defined as follows:
2.6 Random walk with restart on heterogeneous network (RWRH) algorithm
This algorithm can be considered a variant of the RWR algorithm, since it was defined in the same formula as for RWR. The difference is construction of transition matrix \({W^{'}}\). More specifically, \({W^{'}}\) was defined as follows:
where \(W_\mathrm{G}^{'}\) and \(W_\mathrm{D}^{'}\) are intra-subnetwork transition matrices of a network of genes/proteins and a disease similarity network, respectively. \(W_{\mathrm{GD}}^{'}\), \(W_{\mathrm{DG}}^{'}\) are inter-subnetwork transition matrices. Let \(\lambda \) be the jumping probability the random walker jumps from the network of genes/proteins to the disease similarity network or vice versa. Then, these matrices were defined as follows:
where \(W_\mathrm{D}\) and \(W_{\mathrm{GD}}\) are adjacency matrices of the disease similarity and the bipartite networks.
By letting \(\eta \) be the parameter to weight the importance of each network, the initial probability vector was defined as follows:
In case we are interested in a disease class/group, which contains set of diseases (D), \(P^0\) was defined as follows:
For these two algorithms, all remaining genes in the networks, which are not known to be associated with d or D, were selected as candidates for ranking.
3 Results and discussion
3.1 Performance comparison
Note that, our method was based on the construction of heterogeneous networks by integrating HPONet network with a gene/protein network. Therefore, three heterogeneous networks were constructed for our method, i.e., HPONet-PPINet, HPONet-GENet and HPONet-GONet. Meanwhile, heterogeneous networks in [32, 34] were OMIMNet-GONet and OMIMNet-PPINet, respectively. In addition to these five heterogeneous networks, we constructed OMIMNet-GENet for the comparison. To compare the performance of our method with that of others, we used leave-one-out cross-validation (LOOCV) method for each disease phenotype in a set of disease phenotypes which associates with at least one gene in the gene/protein networks. Due to the differences in size of gene/protein networks, the number of testing disease phenotypes was little different for different heterogeneous networks as shown in Table 1. Based on results of RWRH algorithm for prediction of disease-associated genes [32, 34] and prediction of disease-associated miRNAs [41], we set back-probability (i.e., \(\gamma )\), jumping probability (i.e., \(\lambda \)) and subnetwork importance weight (i.e., \(\eta \)) to 0.5, 0.6 and 0.7, respectively. For each disease phenotype (d), in each round of LOOCV, we held out one known d-associated gene. The rest of known d-associated genes and d were used as seed nodes. The held-out gene and remaining genes in the homogeneous network, which were not known to be associated with d, were ranked by the methods. Then, we plotted the receiver operating characteristic (ROC) curve and calculated the area under the curve (AUC) to compare the performance of the methods. This curve represents the relationship between sensitivity and (1\(-\)specificity), where sensitivity refers to the percentage of known d-associated genes that were ranked above a particular threshold and specificity refers to the percentage of genes which were not known to be associated top ranked below this threshold. Figure 2 shows that the performance of our method (i.e., HPONet-PPINet, HPONet-GENet and HPONet-GONet) was better than that of study [34] (i.e., OMIMNet-GONet), study [32] (i.e., OMIMNet-PPINet) and OMIMNet-GENet. In addition, the performance of heterogeneous networks, which were based on HPO, were comparable (i.e., AUC values for HPONet-PPINet, HPONet-GENet and HPONet-GONet were 0.927, 0.926 and 0.926, respectively). Similarly, the performance of heterogeneous networks, which were based on OMIM, were comparable (i.e., AUC values for OMIMNet-PPINet, OMIMNet-GENet and OMIMNet-GONet were 0.736, 0.73 and 0.71, respectively). These results indicate that HPO-based calculation of the disease similarity network (i.e., HPONet) better reflects functional relations among diseases than that based on text mining algorithms on OMIM records for the prediction of disease-associated genes.
3.2 Case study: Alzheimer’s disease
In this experiment, we tried to predict novel genes associated with Alzheimer’s disease (Shortly called AD) (MIM ID is 104300). AD is a multi-factorial and fatal neurodegenerative disorder for which the mechanisms leading to profound neuronal loss are incompletely recognized. There are 16 genes are known to be associated with AD [33]; however only eleven of them are available in the gene/protein networks. To predict novel genes associated with this disease, we selected the heterogeneous network comprising HPONet and GENet. Then we used these eleven genes and the MIM ID of AD as source nodes, and other genes in the homogeneous network as candidates. After all candidate genes were ranked, we selected 100 highly ranked candidates for evidence search about the association between them and AD from literature on PubMed using Entrez Programming Utilites [51]. Table 2 shows 19 evidenced candidate genes. For instance, study [52] (PubMed ID: 16378688) showed that SP1 deposition in hyper-phosphorylated tau deposits may have functional consequences in the pathology of AD. In addition, it was suggested that UBE2I polymorphisms might be associated with a risk of AD [53] (PubMed ID: 19765634). Also, low protein levels of UCHL1 are associated with high protein levels of BACE1 in sporadic AD brains [54] (PubMed ID: 22726800). Finally, enhancing CTSB activity could lower Abeta, especially Abeta42, in AD patients with or without familial mutations [55] (PubMed ID: 23024364). Other not yet evidenced genes in the top 100 genes can be good candidates for biologists for further investigation (see Online Resource 1).
4 Conclusions
It was reported in previous studies that disease similarity improves the performance of prediction of novel disease-associated genes, since it better exploits the “disease module” principle. Based on this, methods on a heterogeneous networks comprising a disease similarity network and a gene/protein network are superior to those which are solely based on the gene/protein network. However, construction of the disease similarity network in previous studies are limited since they mostly based on an out-of-date disease similarity matrix, which was constructed using text mining algorithms on OMIM records. Considering that human phenotype ontology is now available and it well annotates to disease phenotypes, disease similarity can be semantically calculated based on such the controlled vocabulary using semantic-based similarity measures. Therefore, in this study, instead of using the OMIM-based disease similarity network, we construct a HPO-based one using a semantic similarity measure. Using the random walk with restart algorithm on a heterogeneous network, we compared the performance of the heterogeneous network built based on our method with that based on the OMIM-based disease similarity network. Simulation results show that our method is better irrespective of gene/protein networks. This indicates that the HPO-based disease similarity network better exposed functional similarities among diseases than that of OMIM-based one. A case study on Alzheimer’s disease has been done to show the ability of our method in predicting novel disease-associated genes. We also note that, many other semantic similarity measures proposed to calculate similarity between annotated biomedical entities can be used to construct disease similarity networks. In addition, these networks can be constructed based on shared pathways [35], shared miRNA [36], shared protein complex [37], shared disease ontology [38] and disease comorbidity [39]. Therefore, it would be interesting for future studies to test which one is best for the prediction of novel disease-associated genes.
References
Kann, M.G.: Advances in translational bioinformatics: computational approaches for the hunting of disease genes. Brief. Bioinform. 11(1), 96–110 (2009). doi:10.1093/bib/bbp048
Tranchevent, L.-C., Capdevila, F.B., Nitsch, D., De Moor, B., De Causmaecker, P., Moreau, Y.: A guide to web tools to prioritize candidate genes. Brief. Bioinform. 12(1), 22–32 (2010). doi:10.1093/bib/bbq007
Fernald, G.H., Capriotti, E., Daneshjou, R., Karczewski, K.J., Altman, R.B.: Bioinformatics challenges for personalized medicine. Bioinformatics 27(13), 1741–1748 (2011). doi:10.1093/bioinformatics/btr295
Jones, D.: Steps on the road to personalized medicine. Nat. Rev. Drug Discov. 6(10), 770–771 (2007)
Reynolds, K.S.: Achieving the promise of personalized medicine. Clin. Pharmacol. Ther. 92(4), 401–405 (2012). doi:10.1038/clpt.2012.147
Adie, E.A., Adams, R.R., Evans, K.L., Porteous, D.J., Pickard, B.S.: SUSPECTS: enabling fast and effective prioritization of positional candidates. Bioinformatics 22(6), 773–774 (2006). doi:10.1093/bioinformatics/btk031
Aerts, S., Lambrechts, D., Maity, S., Van Loo, P., Coessens, B., De Smet, F., Tranchevent, L.-C., De Moor, B., Marynen, P., Hassan, B., Carmeliet, P., Moreau, Y.: Gene prioritization through genomic data fusion. Nat. Biotechnol. 24(5), 537–544 (2006)
Chen, J., Xu, H., Aronow, B., Jegga, A.: Improved human disease candidate gene prioritization using mouse phenotype. BMC Bioinform. 8(1), 392 (2007)
Le, D.-H., Xuan Hoai, N., Kwon, Y.-K.: A Comparative study of classification-based machine learning methods for novel disease gene prediction. In: Nguyen, V.-H., Le, A.-C., Huynh, V.-N. (eds.) Knowledge and Systems Engineering, vol. 326. Advances in Intelligent Systems and Computing, pp. 577–588. Springer International Publishing (2015)
Lospez-Bigas, N., Ouzounis, C.A.: Genome-wide identification of genes likely to be involved in human genetic disease. Nucleic Acids Res. 32(10), 3108–3114 (2004)
Adie, E., Adams, R., Evans, K., Porteous, D., Pickard, B.: Speeding disease gene discovery by sequence based candidate prioritization. BMC Bioinform. 6(1), 55 (2005)
Xu, J., Li, Y.: Discovering disease-genes by topological features in human protein-protein interaction network. Bioinformatics 22(22), 2800–2805 (2006). doi:10.1093/bioinformatics/btl467
Calvo, S., Jain, M., Xie, X., Sheth, S.A., Chang, B., Goldberger, O.A., Spinazzola, A., Zeviani, M., Carr, S.A., Mootha, V.K.: Systematic identification of human mitochondrial disease genes through integrative genomics. Nat. Genet. 38(5), 576–582 (2006)
Lage, K., Karlberg, E.O., Storling, Z.M., Olason, P.I., Pedersen, A.G., Rigina, O., Hinsby, A.M., Tumer, Z., Pociot, F., Tommerup, N., Moreau, Y., Brunak, S.: A human phenome-interactome network of protein complexes implicated in genetic disorders. Nat. Biotech. 25(3), 309–316 (2007)
Smalter, A., Lei, S.F., Chen, X.: Human disease-gene classification with integrative sequence-based and topological features of protein-protein interaction networks. In: IEEE International conference on bioinformatics and biomedicine (BIBM), pp. 209–216 (2007)
Radivojac, P., Peng, K., Clark, W.T., Peters, B.J., Mohan, A., Boyle, S.M., Mooney, S.D.: An integrated approach to inferring gene-disease associations in humans. Proteins Struct. Funct. Bioinform. 72(3), 1030–1037 (2008). doi:10.1002/prot.21989
Keerthikumar, S., Bhadra, S., Kandasamy, K., Raju, R., Ramachandra, Y.L., Bhattacharyya, C., Imai, K., Ohara, O., Mohan, S., Pandey, A.: Prediction of candidate primary immunodeficiency disease genes using a support vector machine learning approach. DNA Res. 16(6), 345–351 (2009)
Jiabao, S., Patra, J.C., Yongjin, L.: Functional link artificial neural network-based disease gene prediction. In: International joint conference on neural networks (IJCNN), 14–19 June 2009, pp. 3003–3010 (2009)
Le, D.-H., Nguyen, M.-H.: Towards more realistic machine learning techniques for prediction of disease-associated genes. In: Proceedings of the sixth international symposium on information and communication technology, Hue City, 2833269, ACM, pp. 116–120 (2015)
Wang, X., Gulbahce, N., Yu, H.: Network-based methods for human disease gene prediction. Brief. Funct. Genomics 10(5), 280–293 (2011). doi:10.1093/bfgp/elr024
Barabasi, A.-L., Gulbahce, N., Loscalzo, J.: Network medicine: a network-based approach to human disease. Nat. Rev. Genet. 12(1), 56–68 (2011)
Kohler, S., Bauer, S., Horn, D., Robinson, P.: Walking the Interactome for prioritization of candidate disease genes. Am. J. Hum. Genet. 82(4), 949–958 (2008)
Chen, J., Aronow, B., Jegga, A.: Disease candidate gene identification and prioritization using protein interaction networks. BMC Bioinform. 10(1), 73 (2009)
Le, D.-H., Kwon, Y.-K.: GPEC: a Cytoscape plug-in for random walk-based gene prioritization and biomedical evidence collection. Comput. Biol. Chem. 37, 17–23 (2012)
Le, D.-H., Kwon, Y.-K.: Neighbor-favoring weight reinforcement to improve random walk-based disease gene prioritization. Comput. Biol. Chem. 44, 1–8 (2013). doi:10.1016/j.compbiolchem.2013.01.001
Navlakha, S., Kingsford, C.: The power of protein interaction networks for associating genes with diseases. Bioinformatics 26(8), 1057–1063 (2010). doi:10.1093/bioinformatics/btq076
Le, D.-H.: Network-based ranking methods for prediction of novel disease associated microRNAs. Comput. Biol. Chem. 58, 139–148 (2015). doi:10.1016/j.compbiolchem.2015.07.003
Le, D.-H.: A novel method for identifying disease associated protein complexes based on functional similarity protein complex networks. Algo. Mol. Biol. 10(1), 14 (2015)
Feldman, I., Rzhetsky, A., Vitkup, D.: Network properties of genes harboring inherited disease mutations. Proc. Natl. Acad. Sci. 105(11), 4323–4328 (2008). doi:10.1073/pnas.0701722105
Goh, K.-I., Cusick, M.E., Valle, D., Childs, B., Vidal, M., Barabási, A.-L.: The human disease network. Proc. Natl. Acad. Sci. 104(21), 8685–8690 (2007). doi:10.1073/pnas.0701361104
Oti, M., Brunner, H.G.: The modular nature of genetic diseases. Clin. Genet. 71(1), 1–11 (2007). doi:10.1111/j.1399-0004.2006.00708.x
Li, Y., Patra, J.C.: Genome-wide inferring gene-phenotype relationship by walking on the heterogeneous network. Bioinformatics 26(9), 1219–1224 (2010). doi:10.1093/bioinformatics/btq108
Amberger, J., Bocchini, C.A., Scott, A.F., Hamosh, A.: McKusick’s online Mendelian inheritance in man (OMIM). Nucleic Acids Res. 37(suppl 1), D793–D796 (2009). doi:10.1093/nar/gkn665
Jiang, R., Gan, M., He, P.: Constructing a gene semantic similarity network for the inference of disease genes. BMC Syst. Biol. 5(Suppl 2), S2 (2011)
Li, Y., Agarwal, P.: A pathway-based view of human diseases and disease relationships. PLoS ONE 4(2), e4346 (2009)
Lu, M., Zhang, Q., Deng, M., Miao, J., Guo, Y., Gao, W., Cui, Q.: An analysis of human microRNA and disease associations. PLoS ONE 3(10), e3420 (2008)
Markou, M., Singh, S.: Novelty detection: a review—part 2: neural network based approaches. Signal Process. 83(12), 2499–2521 (2003)
Li, J., Gong, B., Chen, X., Liu, T., Wu, C., Zhang, F., Li, C., Li, X., Rao, S., Li, X.: DOSim: an R package for similarity between diseases based on disease ontology. BMC Bioinform. 12(1), 266 (2011)
Lee, D.S., Park, J., Kay, K.A., Christakis, N.A., Oltvai, Z.N., Barabasi, A.L.: The implications of human metabolic network topology for disease comorbidity. Proc. Natl. Acad. Sci. 105(29), 9880–9885 (2008). doi:10.1073/pnas.0802208105
Chen, X., Liu, M.-X., Yan, G.-Y.: Drug-target interaction prediction by random walk on the heterogeneous network. Mol. Biosyst. 8(7), 1970–1978 (2012). doi:10.1039/C2MB00002D
Le, D.-H.: Disease phenotype similarity improves the prediction of novel disease-associated microRNAs. In: 2015 2nd National Foundation for Science and Technology Development conference on information and computer science (NICS), 16–18 Sept 2015, pp. 76–81 (2015)
Zhou, M., Wang, X., Li, J., Hao, D., Wang, Z., Shi, H., Han, L., Zhou, H., Sun, J.: Prioritizing candidate disease-related long non-coding RNAs by walking on the heterogeneous lncRNA and disease network. Mol. Biosyst. 11(3), 760–769 (2015). doi:10.1039/C4MB00511B
Köhler, S., Doelken, S.C., Mungall, C.J., Bauer, S., Firth, H.V., Bailleul-Forestier, I., Black, G.C.M., Brown, D.L., Brudno, M., Campbell, J., FitzPatrick, D.R., Eppig, J.T., Jackson, A.P., Freson, K., Girdea, M., Helbig, I., Hurst, J.A., Jãhn, J., Jackson, L.G., Kelly, A.M., Ledbetter, D.H., Mansour, S., Martin, C.L., Moss, C., Mumford, A., Ouwehand, W.H., Park, S.M., Riggs, E.R., Scott, R.H., Sisodiya, S., Vooren, S.V., Wapner, R.J., Wilkie, A.O.M., Wright, C.F., Vulto-van Silfhout, A.T., Leeuw, N., de Vries, B.B.A., Washingthon, N.L., Smith, C.L., Westerfield, M., Schofield, P., Ruef, B.J., Gkoutos, G.V., Haendel, M., Smedley, D., Lewis, S.E., Robinson, P.N.: The Human Phenotype Ontology project: linking molecular biology and disease through phenotype data. Nucleic Acids Res. 42(D1), D966–D974 (2014). doi:10.1093/nar/gkt1026
Pesquita, C., Faria, D., Falcão, A.O., Lord, P., Couto, F.M.: Semantic similarity in biomedical ontologies. PLoS Comput. Biol. 5(7), e1000443 (2009)
Obayashi, T., Kinoshita, K.: COXPRESdb: a database to compare gene coexpression in seven model animals. Nucleic Acids Res. 39(suppl 1), D1016–D1022 (2011). doi:10.1093/nar/gkq1147
Obayashi, T., Kinoshita, K., Nakai, K., Shibaoka, M., Hayashi, S., Saeki, M., Shibata, D., Saito, K., Ohta, H.: ATTED-II: a database of co-expressed genes and cis elements for identifying co-regulated gene groups in Arabidopsis. Nucleic Acids Res. 35(suppl 1), D863–D869 (2006). doi:10.1093/nar/gkl783
UniProt Consortium: The Universal Protein Resource (UniProt) in 2010. Nucleic Acids Res. 38, D142–D148 (2010)
Barrell, D., Dimmer, E., Huntley, R.P., Binns, D., O’Donovan, C., Apweiler, R.: The GOA database in 2009—an integrated Gene Ontology Annotation resource. Nucleic Acids Res. 37(suppl 1), D396–D403 (2009). doi:10.1093/nar/gkn803
Resnik, P.: Using information content to evaluate semantic similarity in a taxonomy. Paper presented at the 14th international joint conference on artificial intelligence, vol. 1, Montreal
van Driel, M.A., Bruggeman, J., Vriend, G., Brunner, H.G., Leunissen, J.A.M.: A text-mining analysis of the human phenome. Eur. J. Hum. Genet. 14(5), 535–542 (2006)
Maglott, D., Ostell, J., Pruitt, K.D., Tatusova, T.: Entrez gene: gene-centered information at NCBI. Nucleic Acids Res. 39(suppl 1), D52–D57 (2011). doi:10.1093/nar/gkq1237
Santpere, G., Nieto, M., Puig, B., Ferrer, I.: Abnormal Sp1 transcription factor expression in Alzheimer disease and tauopathies. Neurosci. Lett. 397(1–2), 30–34 (2006). doi:10.1016/j.neulet.2005.11.062
Ahn, K., Song, J.H., Kim, D.K., Park, M.H., Jo, S.A., Koh, Y.H.: Ubc9 gene polymorphisms and late-onset Alzheimer’s disease in the Korean population: a genetic association study. Neurosci. Lett. 465(3), 272–275 (2009). doi:10.1016/j.neulet.2009.09.017
Guglielmotto, M., Monteleone, D., Boido, M., Piras, A., Giliberto, L., Borghi, R., Vercelli, A., Fornaro, M., Tabaton, M., Tamagno, E.: A\({\rm \beta } \)1-42-mediated down-regulation of Uch-L1 is dependent on NF-\(\kappa \)B activation and impaired BACE1 lysosomal degradation. Aging Cell 11(5), 834–844 (2012). doi:10.1111/j.1474-9726.2012.00854.x
Wang, C., Sun, B., Zhou, Y., Grubb, A., Gan, L.: Cathepsin B degrades amyloid-\(\beta \) in Mice expressing wild-type human amyloid precursor protein. J. Biol. Chem. 287(47), 39834–39841 (2012). doi:10.1074/jbc.M112.371641
Acknowledgments
This research is funded by Ministry of Education and Training (MOET) under Grant Number B2014-01-84.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Le, DH., Dang, VT. Ontology-based disease similarity network for disease gene prediction. Vietnam J Comput Sci 3, 197–205 (2016). https://doi.org/10.1007/s40595-016-0063-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40595-016-0063-3