Abstract
According to literature, there are two aspects of a successful approach for seasonal forecasting of tropical cyclones, including factors relating to the formation and operation of the storms and regression methods. Dealing with the factors, El Niño–Southern Oscillation, and other global factors such as Quasi-Biennial Oscillation, Pacific Decanal Oscillation, etc. and local factors such as sea surface temperature, sea level pressures, etc. were examined for tropical cyclone forecasting. For regression, the most previous works used the linear regression-based model for seasonal tropical forecasting. However, the seasonal tropical forecasting requires high-dimensional data, so the forecasting ability using linear regression will have drawback. In this work, we analyse literatures of forecasting factors and regression methods for tropical cyclone forecasting. A CF-ANFIS algorithm integrating a conjunct space cluster and Cascade-forward neural network are proposed to forecast the number of tropical cyclone making landfall. This algorithm resolves the drawback by considering all forecast factors with high-dimensional data. The experimental results indicated that the CF-ANFIS for seasonal forecast of tropical cyclones is a significantly effective approach with high accuracy in comparison with traditional ANFIS.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Literature review
1.1 Relationship between ENSO and cyclone activities
Many researches have initially focused on studying the relationship between the El Nino phenomenon and occurrences of cyclones [2–4, 7, 8, 14, 15, 22, 26]. Several differences have been found regarding the occurring locations and directions of the storm in different places during El Niño episodes (warm phase of ENSO). Afterwards, there were studies on the impact of La Nina (cold phase of ENSO) and the overall impact of three ENSO phases (warm, cold and neutral phase) on cyclone activities and tropical depression. Since the late 80s, scientists have shown that it is possible to predict seasonal cyclone activities through indicators of ENSO phenomenon [22, 23]. ENSO has a considerable impact on cyclonic activities on a global scale at different levels and on different aspects in terms of the characteristics of the storm.Footnote 1 Any changes in ENSO such as climate changes will affect the frequency and orbital motions of tropical storms. Research shows that in El Niño conditions, for example, the frequency of cyclones often decreases on an annual basis in Atlantic, western Pacific and Australian waters, but increases in the Central and Eastern Pacific Ocean. Therefore, it can be noted that the number of tropical storms in some areas reduced can be offset by the increase in cyclones elsewhere due to the global connections of atmospheric circulations in tropical regions.
It is known a tropical storm occurs only in areas where the sea surface temperature is below 27 \(^\circ \)C. There exists a relationship between the storm’s intensity and genesis location in the different phases of ENSO along with turbulent sea surface temperatures in the Northwest Pacific Ocean [2, 3]. Emily A. Fogarty’s researchFootnote 2 shows a certain relationship between the storm’s frequencies each year in China during different phases of ENSO. Chan’s research showed a clear effect of the ENSO phenomenon on intense cyclone activities in the North West Pacific Ocean. Several numerical approaches have been employed to analyse the influence of ENSO phenomenon on cyclone activities, but the results have been limited. The statistical analysis method has been used quite extensively in analysing the relationship between ENSO indices and cyclone activities in different regions around the globe.
In the work [19], the authors have conducted seasonal forecasting for the number of storms landing the East coast using regression statistical method based only on factors that predict the ENSO indices (ESOI and NINO3.4). They considered the values of the sea surface temperature disturbance in the Nino3.4 region and the Southern Oscillation Index hemisphere equator (ESOI) of the previous 15 months until the forecast date to analyse and pick out 5 months with the highest correlation of each aforementioned factor for inclusion in the forecast equation. Here the author has paid attention to the forecast during El Nino or La Nina episodes while we also have to predict for the neutral phase; therefore, many studies on forecasting cyclones season have further analysed the relationships between climate factors and other circulations not related to ENSO. For example, one of the important factors in predicting seasonal cyclones in Northwest Pacific region is a factor regarding the Western North Pacific Subtropical High often reflected in some layers of the atmosphere on regional circulation in the region 15–25\(^\circ \)N, 115–150\(^\circ \)E. Cyclones cannot occur in the subtropical high-pressure area of Northwest Pacific. Subtropical high pressure in the Pacific northwest region, when intensifying and encroaching the west land, will block the cyclone from sweeping north and west, so in these cases, cyclones tend to land more inclined on the west coast.
The study [13] describes an improved statistical scheme for seasonal forecasting of tropical cyclones landing annually ashore along the East coast using data from 1965 to 2005. Based on the factors affecting the impact range of the cyclones in the South China Sea, the factors that affect the cyclones making landfall in the mainland have been identified. This equation is then developed using these factors’ empirical orthogonal functions to predict the number of hurricanes in the first half of the hurricane season (from May to August) in April and in the second half of the hurricane season (from November to December), and the number of storms during the major months of the hurricane season from July to December. This new scheme is approximately 11 % more improved in accuracy when predicting how many storms that make landfall during the entire hurricane season compared to previous studies. Analysis of circulation models show that the conditions within South China Sea appears to be the main factor affecting the number of hurricanes landing here. In the years that the figure is at an above-normal level, the conditions within the East Sea is favourable for the development of storms, and vice versa. The value 500 hPa in the intensity of the subtropical high-pressure level is also seen as a factor in determining whether the cyclone from the Pacific Northwest can approach the South China Sea and whether it can hit the mainland or not.
In the study [30] conducted by Haikun and his colleagues, a statistical model was built to simulate the formation of tropical cyclones and another trajectory model used to simulate the tropical cyclones’ path, the effects of ENSO phenomenon on the trajectory of tropical cyclones during the major months of the hurricane season (from July to September) in the northwest Pacific region was assessed based on 14 El Niño and La Niña selected from the year 1950 to 2007. The analysis shows that during El Nino episodes, tropical cyclone activities grow significantly stronger in the south latitude 20\(^\circ \)N, particularly in the east longitude 130\(^\circ \)E. Tropical cyclones with prevailing northwest trajectory and impacting East Asia, including the island of Taiwan, mainland China, the Korean Peninsula and Japan, tend to move more to the west during El Nino years and tend to move more to the north during La Nina years. The numerical simulations also determined that changes related to ENSO in large-scale currents and cyclone forming positions can have a significant impact on the prevailing tropical cyclone trajectory.
In [18], Landsea indicates that one of the biggest impacts of ENSO phenomenon on the Earth’s climate system is the alteration of tropical cyclones’ characteristics on a global scale. This article by Landsea gives an overview of frequency, intensity and how genesis regions of tropical cyclones have alternated between one another in all storm occurring zones globally following the development phases of ENSO. Together with the impact of the ENSO phenomenon, global factors (such as Quasi-Biennial Oscillation, QBO) and the local factors (such as sea surface temperature, intensity and monsoon rain, sea-level field of pressure and vertical wind shear) can regulate the change of tropical cyclones. The relationship of these factors with the first tropical cyclones, especially a high correlation with the ENSO phenomenon, can be exploited to make seasonal forecasts of the tropical cyclone activities. The author has presented details of the methods developed for specific genesis regions of tropical cyclone activities in the North Atlantic, western North Pacific, South Pacific and Australia.
In the study [28], Wang and colleagues analysed a series of 35-year-long data (1965–1999) that shows the strong impact of the El Nino and La Nina phenomenon with high intensity on tropical cyclone activities in the northwest Pacific, although the total number of tropical cyclones formed over the entire North–West Pacific region did not change significantly from year to year. In the summer and autumn of the El Nino years the frequency of tropical cyclone formation increased considerably in the Southeast corner (0\(^{\circ }\)–17\(^{\circ }\)N, 140\(^{\circ }\)–180\(^{\circ }\)E) and decreased in the northwest corner (17\(^{\circ }\)–30\(^{\circ }\)N, 120\(^{\circ }\)–140\(^{\circ }\)E). The genesis location of cyclones in the period from July to September moves 6\(^\circ \) latitude lower from the average one in many years, while in the period from October to December this moves 18\(^\circ \) longitude eastward in dry years compared to the average locations in cold years. After El Nino (La Nina), tropical cyclone formation in the first half of the hurricane season (from January to July) decreases (increases). In dry (cold) years the tropical cyclone average lifespan is about 7 (4) days, and the average total number of tropical cyclone days is 159 (84) days. In autumn during the hot, strong El Nino years, the total number of tropical cyclones hovering north passing the latitude 35\(^{\circ }\)N is 2.5 times more than in the cold, strong La Nina years. This implies that El Niño substantially increases the movement toward the extremes of heat-moisture energy and impacts high latitudes via changing the formation of tropical cyclones and their trajectories. The emergence of tropical cyclones which were increased in the southeast corner of the Northwest Pacific region, is increasing the spin degree in lower levels generated by El Nino, inducing equatorial westerly wind. The reduction in the occurrence of tropical cyclones in the northwest corner is attributed to convergence on the top level caused by the deepening of the east Asia trench and the strengthening of the north-western Pacific subtropical high pressure. The both of these phenomena were caused by the impact of El Nino. Tropical cyclone activities in the month of the hurricane season from July to December are very likely to be forecast based on disturbance of the sea surface temperatures that occurred in the NINO3.4 region earlier from winter to spring, while we can predict tropical cyclones generated in the period from March to July through disturbances of the sea surface temperatures that occurred earlier in the NINO3.4 region from October to December.
In [29], Chang and colleagues pointed out that in September, October, and November, in the neutral year or in the second half of the hurricane season during the El Nino years the number of tropical cyclones making landfall in the Northwest Pacific coastal region, except for Japan and the Korean peninsula, decreased markedly. On the other hand, in the second half of the hurricane season in La Nina years, the number of tropical cyclones landing in China coast rose significantly in the La Nina years. The reduced number of tropical cyclones making landfall in the second half of the El Nino hurricane season seems related to the shift to the east of the average genesis location where cyclones occur and the disruption of the ridge on 500 mb level near the 130\(^{\circ }\)E longitude. In contrast, the number of tropical cyclones making landfall in the later half of the hurricane season in La Nina years seems to be related to the shift to the west of the average cyclone genesis location and the maintenance of the ridge on the 500-mb level.
In [17], Kim and colleagues suggest that the warming of the Pacific sea is divided into two distinct modes according the spatial distribution of the sea surface temperature turbulence: warming in the Eastern Pacific (EPW) and warming in the central Pacific (CPW). The 3rd mode is the cooling of the sea surface temperature in the Eastern Pacific region (EPC). These three modes cause different impacts on the operating mode of tropical cyclones over the North Pacific waters regulated by both the various local thermodynamic factors and large-scale circulations models. In years EPW (sea surface warming in the Eastern Pacific) the density and trajectory of tropical cyclone tend to increase in the southeast and decrease in the western Pacific with strong west wind shear. The expansion of the monsoon trough and the weak wind shear on the central Pacific region increased conditions for tropical cyclones in the east compared with the average position of tropical cyclones in many years. In the CPW years (sea water warming in the central Pacific), tropical cyclone activities often shift westward and expand in the area of the Western Pacific Northwest. The shift to the west of CPW entails turbulent heat movement of west wind heat and monsoon trough through the north-western region of the Western Pacific and creates more favourable conditions for the arrival of tropical cyclones. By contrast with the CPW years, there is a decline of tropical cyclone activities in the waters of the East Pacific. Over the EPC years (cooling of sea surface temperature in Eastern Pacific), all investigations on the parameters mostly draw a contrast reflection of the EPW years.
According to literature, forecasting methods can be categorized into qualitative and quantitative approaches. The former usually based on the opinions of people, which refers to a long or medium forecast by asking a group of knowledgeable experts for their opinions with regard to future values of the things being forecasted. The well-known method, called Delphi, involves a group of experts who eventually reach a consensus of a forecast. The later refers to quantitative, mathematical formulations or statistical forecasting, which includes time series models and casual models. The regression, a causal forecasting model that fits curves to the entire data set to minimize the forecasting errors, is often applied for the seasonal forecasting of tropical cyclones (TCs).
William Gray and his team pioneered the seasonal hurricane prediction enterprise using regression-based linear statistical models [15]. In a study, Chu [7], Fan and Wang [10] presented a multivariate linear regression model applied to predict the seasonal tropical cyclone count in the vicinity of Taiwan. The model is based on the least absolute deviation so that regression estimates are more resistant than those derived from the ordinary least square method. Kim et al. [16] used least absolute deviation (LAD) regression and the Poisson regression method. Poisson model is being slightly more skilful than the LAD model. Goh and Chan [11–13] presented an improved prediction scheme for the number of TCs making landfall on the coast of south China. The schemes for the early, late, and JD seasons all provide reasonable results. Chu and Zhao [5, 6] applied a hierarchical Bayesian change point analysis to detect abrupt shifts in the TC time series over the central North Pacific (CNP). Chu [4] extended the probabilistic Bayesian framework suggested in the prior works from the CNP [6], with a particular focus toward the vicinity of the Taiwan area. Different from prior studies, he adopts a feature classification approach based on the fuzzy clustering analysis of TC tracks.
2 Forecasting methods
According to the literatures review, the most previous works applied the linear regression-based models for seasonal tropical forecasting. However, the higher order polynomial models are used, the overall degree of error will be reduced. The seasonal tropical forecasting requires high-dimensional data, so the forecasting ability also is reduced for higher order polynomial models. According to Chu [4–7], Bayesian-based model for seasonal typhoon activity forecasting is more effective than linear regression-based models. In another aspect, Azizi [1] shows that ANFIS model provides better forecasting accuracy in comparison with Bayesian model. Hence, ANFIS model is recommended to be used for production estimation under random uncertainties. According our study, the ANFIS has been not yet applied for seasonal tropical forecasting up to our previous research [9]. Another reason to choose ANFIS model is that it can be used to combine all predictor factors for forecasting, while other approaches only use several factors by transforming high-dimensional data to low-dimensional data.
This work is an improvement of our previous research [9]. The aim of the previous work [9] was to offer usefully realistic supports for seasonal forecast of tropical cyclone activities along the Vietnam coast. The forecasting factors include ENSO, atmospheric and oceanographic data related to formation conditions and tropical cyclone activity in the study area in the 62-year period (1951–2012). The conjunct space cluster-based adaptive neuro-fuzzy inference system was applied for seasonal forecasting of tropical cyclones. This model integrated a conjunct space-based cluster method and a perceptron (called P-ANFIS). The perceptron is a linear regression model, so P-ANFIS still gets drawback with high-dimensional data. Here, an improved version of P-ANFIS is proposed by using cascade-forward neural network [1] instead of a perceptron, which is called CF-ANFIS.Footnote 3 The experimental results indicated that the CF-ANFIS for seasonal forecasting of tropical cyclones using ENSO is a significant effective approach with high accuracy in comparison with P-ANFIS.
3 Tropical cyclone forecasting using CF-ANFIS
An adaptive neuro-fuzzy inference system (ANFIS) is a machine learning technique capturing the advantage of both neural networks and fuzzy logic principles in a single framework. ANFIS has a learning capability to generate a set of fuzzy IF-THEN rules to be approximate nonlinear functions, which is used to make inference. Given data set \({T}_{\mathop \sum } \) as follows
where \(\bar{x}_i \) is the \(i{\mathrm{th}}\) input vector of the data set and \(y_i \). is the output; P is number of samples. A black-box type model expressing a mathematical relationship between input and output spaces of a system based on this given data set can be expressed by mapping as follows:
System modelling is defined by extrapolating the function f based on these known data. It is well known that there are some existing algorithms to solve this problem based on the fuzzy inference system, called T-S model, which was proposed by Takagi and Sugeno [27]. The \({k}{{\mathrm{th}}}\). rule of this fuzzy model is as following:
then
where \(\bar{x}=[x_{i1} ,x_{i2} ,\ldots , x_{in} ]^T\). is the \({i}{{\mathrm{th}}}\) input data vector of \(T_{\mathop \sum } \); \(B^{({{k}})}\). is input fuzzy set; \([a_0^{({{k}})} ,a_1^{({{k}})} ,\ldots , a_n^{({{k}})} ]^{\mathrm{T}}\). is the weight vector; \(y_{{{ki}}} \) is oput data; \({j}=1\ldots n\), n is dimension of input data set; \({k}=1\ldots m, m\) is the number of IF-THEN rules.
In this paper, the above mathematical model is expressed by the ANFIS. ANFIS is one of the most popular types of fuzzy neural network [20, 25–27]. The clustering techniques are commonly used to create fuzzy rules of ANFIS.
According to [27], each data cluster can be considered as a crisp frame on which different types of MFs (and firing strengths) can be adapted. Some serious drawbacks often affect the clustering algorithms adopted in this context, according to the particular data spaces where they are applied. To overcome such problems, Panella et al. [24] analysed various clustering methods adopting for ANFIS, including clustering in input space, clustering in output space and clustering in input–output space (conjunct space) [26]. The clustering based on the data set only in the input space, which assumed that points potentially belonging to the same cluster in the input space are mapped into points potentially belonging to the same cluster in the output space. Its disadvantage is that the output clusters could not reflect the real structure of the mapping in the output space. On the other the hand, the clustering method considers only output space, which can be ensure that the possibility to discover the real structure of the mapping in the output space. Unfortunately, there can be contradictory rules having similar input MFs but different output coefficients, which is unacceptable in ANFIS networks. To overcome these problems, M. Panella [24–26] and Dzung [20] presented a clustering method in conjunct space for ANFIS network construction. The clustering in input–output space mentioned in the previous works combines a linear cluster (e.g. hyperplane cluster) and Simpson’s min–max models for classification (min–max classification).
Relating to building the clustering data space, the algorithm for parting data system, named PDS [1], is used to build pure hyper-boxes in the input data space and hyperplanes in the output data space. The value corresponding to the kth data hyperplane is calculated as follows:
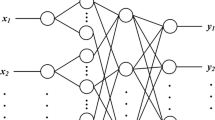
where \([a_0^{(q)} ,\ldots ,a_0^{(q)} ]^T\), is a vector of parameters. Relating to the NN, it can be sketched out as follows. It is a Cascade-forward neural network consisting of one input layer, one hidden layer and one output layer. In the input layer, number of input signals depends on optimal structure of the clustering data space built by the data separating process to establish data clusters. Number of neurons at the hidden layer is adaptively established in training process of the NN.
The hyperplane clustering algorithm is expressed as follows:
Initialization. The C-means algorithm is used to initialize hyperplanes by clustering the input space into M clusters \({\Gamma }^{({{k}})},k=1\ldots M\). The correspondence between such clusters and initialized hyperplanes is based on following criterion: If an input pattern \(\bar{x}_\mathrm{i} ,{i}=1..P\) belongs to the cluster \({\Gamma }^{({\mathrm{q}})},1 \le q\le M\), then the corresponding input–output pair (\(\bar{x}_i ,y_{\mathrm{i}} \)) is assigned to the hyperplane \(A_{\mathrm{q}} \). .
Step 1. The coefficients of each kth hyperplane, \(y_{\mathrm{t}} =\mathop \sum \nolimits _{j=1}^n a_j^{(k)} x_{tj} +a_0^{(k)} ,k=1\ldots M\), is updated using the pairs assigned to either in the initialization or in the successive step 2, where index t spans all the pairs assigned to the kth hyperplane using suited least-squares techniques.
Step 2. Each pair (\(\bar{x}_i ,y_i \)) is assigned to a hyperplane \({A}_{\mathrm{q}} \), which has the minimum orthogonal distance \({d}_{\mathrm{i}} \) from it. The stop condition is determined using a convergence quantity \(\sigma =(\vert D-D^{( {\mathrm{old}})}\vert /D^{( {\mathrm{old}})})\) where D is current approximation error defined by \(D=\frac{1}{P}\mathop \sum \nolimits _{i=1}^P d_i \) and \(D^{( {\mathrm{old}})}. \) is the previous approximation error. The algorithm will be stopped if it satisfies \({\sigma }\le \mathrm{a}\) predefined threshold \({\varepsilon }\); otherwise, it goes back to step 1.
The previous algorithm is a linear clustering that only yields the linear consequent of Sugeno rules. According to [25], several clusters of the input space could be associated with the same hyperplane. To solve this problem, the well-known Simpson’s min–max models for classification (min–max classification) were applied by Panella [24, 25] and Dung [20]. The combination of the hyperplane clustering and the max-min classification on the input space supports to effectively determine the ANFIS network for a given number of rules. The min–max classification technique uses hyperboxes (HBs) which have boundary hyperplanes parallel to the coordinate axes of the patterns of the training set.
We consider a set of the patterns \(T_t \) covered by the \(t{\mathrm{th}}\) min–max hyperbox \(\mathrm{HB}_t \). The \(\mathrm{HB}_t \) is determined using two vertexes, the max vertex \(\overline{{\omega _{t} }}=[\omega _{t1} \omega _{t2} \ldots \omega _{tn} ]\) and the min vertex \(\bar{v}_t =[v_{t1} v_{t2} \ldots v_{tn} ]\), where \(\omega _{tj} =\text{ max }(x_{ij} \vert \bar{x}_i \in T_t )\) and \(v_{tj} =\text{ min }(x_{ij} \vert \bar{x}_i \in T_t )\). If \(T_t \). consists of the patterns associated with the cluster labelling m only, then the \(\mathrm{HB}_t\) will be considered as a pure hyperbox labelling m and denoted \(\mathrm{pHB}_t^{(m)} \). An HB can be considered as a crisp frame on which different types of membership functions (MFs) can be adapted. Here, the original Simpson’s MF is adopted, in which the slope outside the HB is established by the value of the fuzziness parameter \(\gamma \),
where \(t=R_m \), and \(R_m\) is the number of pure hyperboxes labelling m. Several \(\mathrm{pHB}\) can be associated with the same cluster labelling m; thus the overall input MF, \(\mu _{\overline{B_i^{(m)} } } (x_i )\), is calculated as follows:
There are several approaches for min–max classification such as Simpson’s min–max models, ARC in [25] and CSHL in [20]. Here, the CSHL algorithm is applied for this work.
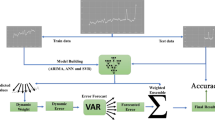
The combination of the hyperplane clustering followed by the min–max classification on the input space can be determined of the ANFIS network for a given number of rules. In this paper, the above mathematical model is expressed by a fuzzy-neuron structure (FNS). The proposed structure of the FNS depicted in Fig. 1 is a combination of a clustering data space and a Cascade-forward neural network, NN.
Structure of the NN is created as follows:
Input vector of the NN is \(M+n\) dimensions. The number of neuron N in the hidden layer is \(N=N_{0}\) at the beginning time of the training process and adaptively adjusted in the net training process. The number of neurons in the output layer is 1. The ’sum’ function is used for input of all of neurons. The ’purelin’ function, \(f(s)=s\), is used for output of the neuron at output layer. Transfer function is used for all of neurons at the hidden layer as follows:
The \(i{\mathrm{th}}\) input–output sample of the data set used for training the NN is established as follows:
This is combined by the \(i{\mathrm{th}}\) input–output sample of the data set (1) and values of corresponding hyperplanes \(y_k^{(i)} \) calculated by (2), \(y^{(i)} =[ {y_1^{{(i)}} \;y_2^{{(i)}} \ldots \;y_M^{{(i)}} } ]\).
Training process the NN to adjust net parameters is performed as follows:
Let W be the weight vector of the NN, \(W=[w_1 \;w_2 \ldots w_H ]^T\). The error equation of the NN can be written as follows:
where
Using the algorithm Levenberg–Marquardt, the weight vector W of the NN at the (\(k+1){\mathrm{th}}\) loop, signed \(W_{{k+1}}\), is calculated as follows:
where I is unit-square matrix, size H; \(\mu \) is an adaptive index; and J is the matrix Jacobian as follows:
Via the aspects aforementioned, the process of building the FNS can be briefly presented as follows.
Initializing:
-
The initial number of data clusters: \(M =M_{0}\).
-
The number of neurons in the hidden layer: \(N_{0}\).
Step 1. Cluster the data space: call the algorithm PDS of [20, 21].
The obtained result is a cluster data space having \(M_{\mathrm{op}} \) pure data clusters in which \(M_{\mathrm{op}} \) is the optimal number of data clusters.
Step 2. Building structure of the FNN as follows: input: \(( {{x}_i ,y_j^{i} })\), output: \({y^i_j}\), \(i=1\ldots P; j=1\ldots M\), with N neurons in the hidden to be N.
Step 3. Training the FNS.
During the training process, the FNS is evaluated and updated based on \(E_N\) as follows:
If \(E_N \le [E]\), the current structure of the FNS is the required one. The training process is stopped. Conversely, increasing the number of neurons in the hidden layer is performed and the training is resumed:
The flowchart of this work is depicted in Fig. 2.
4 Experimental results
4.1 Dataset
According to literature, the ENSO events affect the different characteristics in typhoon’s activity in Western North Pacific, South China Sea and in Vietnam. It causes the changes in the origin of typhoon formation, frequency, intensity, track and in other characteristics of acted typhoons in these regions. We collect factors relating to the formation and activity of the storms in the study area. In particular, the indices of El Niño–Southern Oscillation (ENSO) including warming phase (El Niño), cooling phase (La Niña) and neutral phase relate to the activity of the tropical storms and tropical depressions in the Vietnamese coast. In addition to ENSO, other global climate factors (such as the stratospheric Quasi-Biennial Oscillation, Pacific Decadal Oscillation (PDO), North Atlantic Oscillation, Arctic Oscillation, Antarctic Oscillation, the northern hemisphere oscillation, long-wave radiation equatorial Pacific, etc.) are selected as forecasting factorsaê. The local factors (such as sea surface temperature, monsoon intensity and rainfall, sea level pressures, tropospheric vertical shear, perceptible water, low-level relative vortices, and vertical wind shear) can also help modulate tropical cyclone variability.
The annual number of tropical depressions in the Vietnamese coast from 1952 to 2011 is shown as Table 1.
The data set with 30 of the original principal (initial factor) affects the number of storms in years (Table 2) are used to establish training set.
4.2 Result
We used the samples from 1951 to 2000 to train the CF-ANFIS network. The test samples are from 2001 to 2011.
The prediction error for the ith factor is calculated as follows (Fig. 3):
The dataset with 30 of the factors affecting the number of storms in years (see Table 2) are used to establish training set in two cases. Case 1: Survey 2 stages in each year, first 6 months and last 6 months. Case 2: each factor is used to determine initial 4-factor up to the value of the average quarterly (3 months in a row, 1–3, 4–6, 7–9, 9–12. Accordingly, set the training set with case 1 \(P = 61\) input–output data samples corresponding to the 61-year survey period, from 1951 to 2011; each sample \(n = 60\) data input (the factor) and 1 output (the number of storms in the corresponding year.) for case 2, we have \(P = 61\) but each sample \(n = 120\) data input, the factor number, 1 output is the number of storms in the respective years. In both of cases, the sample data input–output i is denoted as \({\bar{{X}}}_i {=[X}_{i1} \;{X}_{i2} \ldots {X}_{in} ],\) and \(y_i ,i=1\ldots P\) (see Fig. 3).
The mean square error of case 1 is LMS \(=\) \(8.89\times 10^{-4}\); case 2’s LMS \(=\) 2.9366 \(\times 10^{-6}\). This result shows that the factors is divided by quarter help the increasing number of data dimensions from 60 to 120, this leads to increase the accuracy of ANFIS in finding out the relationship between the elements affecting climate and storms occurring during the year. Qualitatively, the reason for the increased accuracy, because of the tropical climate, four seasons a year, quite clear, and therefore, the factor divided by quarter reflects better characteristics than divided by two seasons.
Figures 4 and 5 present the prediction error of 60 factors affecting to TC in the years, from 2001 to 2010.
Figure 6 shows the predicted number of TC versus reality in the years, from 2001 to 2011. The discrepancy between the number of predicted TC and reality in the years, from 2001 to 2011 is presented as Table 2 and Fig. 7.
The difference between the actual number of TCs and the number of TCs that was predicted in a given period (year) is measured as follows:
where, \(y_i^{\mathrm{data}} \) and \(y_i^{\mathrm{NF}} \) are the actual and predicted number of TCs in year i, respectively.
The mean absolute deviation: 0.075
The discrepancy between the actual number and the predicted number of TCs indicated that the forecast (in what?) is slightly lower than reality (see Fig. 7; Table 3). The mean error in the set of forecasts is only 0.099 and 0.075 for P-ANFIS and CF-ANFIS, respectively. From Fig. 6, we can say that the accuracy of prediction is significantly high for both P-ANFIS and CF-ANFIS.
5 Conclusions
This paper has presented a conjunct space cluster-based ANFIS for the seasonal forecasting of tropical cyclones making landfall along the Vietnam coast. The experimental result has indicated that the conjunct space clustering-based ANFIS is an effective approach with high accuracy for the seasonal forecasting of tropical cyclones. However, the perceptron-based ANFIS still has drawbacks in comparison with Cascade forward neural network-based ANFIS.
References
Azizi, A., Ali, Y.A., Ping, L.W.: Model development and comparative study of Bayesian and ANFIS inferences for uncertain variables of production line in tile industry. WSEAS Trans. Syst. 11(1), 22–37 (2012)
Chan, J.C.L.: Tropical cyclone activity in the Northwest Pacific in relation to the El Nino/Southern Oscillation phenomenon. Mon. Weather Rev. 113, 599–606 (1985)
Chan, J.C.L.: Interannual variability of tropical cyclones making landfall over China. In: ESCAP/WMO Typhoon Committee Annual Review Rev., pp. 85–94 (1993)
Chu, P.-S.: Bayesian forecasting of seasonal typhoon activity: a track-pattern-oriented categorization approach. J. Clim. 23, 6654–6668 (2010)
Chu, P.-S., Zhao, X.: Bayesian change-point analysis of tropical cyclone activity: the central North Pacific case. J. Clim. 17, 4893–4901 (2004)
Chu, P.-S., Zhao, X.: A Bayesian regression approach for predicting seasonal tropical cyclone activity over the central North Pacific. J. Clim. 15, 4002–4013 (2007)
Chu, P.S., et al.: Climate prediction of tropical cyclone activity in the vicinity of Taiwan using the multivariate least absolute deviation regression method. Terr. Atmos. Ocean. Sci. 18(4), 805–825 (2007)
Dong, K.: El Nino and tropical frequency in the Australian region and the northwest Pacific. Aust. Meteorol. Mag. 36, 219–225 (1988)
Duong, T.H., Nguyen, D.C., Nguyen, S.D., Hoang, M.H.: An adap-tive neuro-fuzzy inference system for seasonal forecasting of tropi-cal cyclones making landfall along the Vietnam coast. In: Advanced Computational Methods for Knowledge Engineering. Studies in Computational Intelligence, vol. 479, pp. 225–236. (2013)
Fan, K., Wang, H.: A new approach to forecasting typhoon frequency over the western North Pacific. weather Forecast. 24, 974–986 (2009). doi:10.1175/2009WAF2222194.1
Goh, A.Z.C., Chan, J.C.L.: Variations and prediction of the annual number of tropical cyclones affecting Korea and Japan. Int. J. Climatol 32(2), 178–189 (2012). doi:10.1002/joc.2258
Goh, A.Z.C., Chan, J.C.L.: Interannual and interdecadal variations of tropical cyclone activity in the South China Sea. Int. J. Climatol. 30, 827–843 (2010b)
Goh, A.Z.C., Chan, J.C.L.: An improved statistical scheme for the prediction of tropical cyclones making landfall in South China (2010c)
Gray, W.M., et al.: Atlantic seasonal hurricane frequency: part I: El Nino and 30 mb quasi-biennial oscillation influences. Mon. Weather Rev. 112, 1649–1668 (1984)
Gray, W.M., et al.: Predicting Atlantic seasonal hurricane activity 6–11 months in advance. Weather Forecast. 7, 440–455 (1992)
Kim, H.S., et al.: Seasonal prediction of summertime tropical cyclone activity over the East China Sea using the least absolute deviation regression and the Poisson regression. Int. J. Climatol. 30, 210–219 (2010)
Kim, H.M., Webster, P.J., Curry, J.A.: Modulation of North Pacific tropical cyclone activity by three phases of ENSO. J. Clim. 24, 1839–1849 (2011)
Landsea, C.W.: El Niño–Southern Oscillation and the seasonal predictability of tropical cyclones. In: Diaz, H.F., Markgraf V. (eds.) El Niño: Impacts of Multiscale Variability on Natural Ecosystems and Society (2000). (In press)
Liu, K.S., Chan, Johnny C.L.: Climatological characteristics and seasonal forecasting of tropical cyclones making landfall along the South China Coast. Mon. Weather Rev. 131, 1650–1662 (2003)
Nguyen, S.D., Ngo, K.N.: An adaptive input data space parting solution to the synthesis of neuro-fuzzy models. Int. J. Control Autom. Syst. 6, 928–938 (2008)
Nguyen, S.D., Choi, S.B.: A new neuro-fuzzy training algorithm for identifying dynamic characteristics of smart dampers. Smart Mat. Struct. 21(8), 1–14 (2012). (Article No. 085021)
Nicholls, N.: A possible method for predicting seasonal tropical cyclone activity in the Australian region. Mon. Weather Rev. 107, 1221–1224 (1979)
Nicholls, N.: Recent performance of a method for forecasting Australian seasonal tropical cyclone activity. Aust. Meteorol. Mag. 40, 105–110 (1992)
Panella, M., Rizzi, A., Frattale Mascioli, F.M., Martinelli, G.: ANFIS synthesis by hyperplane clustering. In: Proc. of IFSA/NAFIPS, vol. 1, pp. 340–345, Vancouver (2001)
Panella, M., Gallo, A. S.: An input–output clustering approach to the synthesis of ANFIS networks. IEEE Trans. Fuzzy Syst. 13(1), 69–81 (2012)
Shapiro, L.J.: The relationship of the quasi-biennial oscillation to Atlantic tropical storm activity. Mon. Weather Rev. 117, 1545–1552 (1989)
Takagi, T., Sugeno, M.: Fuzzy identification of systems and applications to modeling and control. IEEE Trans. Syst. Man Cybern. 15(1), 16–132 (1985)
Wang, B., Chan, J.C.L.: How strong ENSO events affect tropical storm activity over the western North Pacific*. J. Clim. 15, 1643–1658 (2002)
Wu, M.C., Chang, W.L., Leung, W.M.: Impacts of El Niño–Southern Oscillation events on tropical cyclone landfalling activity in the western North Pacific. J. Clim. 17, 1419–1428 (2004)
Zhao, H., Wu, L., Zhou, W.: Assessing the influence of the ENSO on tropical cyclone prevailing tracks in the western North Pacific. Adv. Atmos. Sci. 27(6), 1361–1371 (2010)
Acknowledgments
This research is funded by International University, VNU-HCM under Grant No. T2015-05-IT/HĐ-ĐHQT-QLKH.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Duong, T.H., Do, P.H., Nguyen, S.D. et al. ENSO-based tropical cyclone forecasting using CF-ANFIS. Vietnam J Comput Sci 3, 81–91 (2016). https://doi.org/10.1007/s40595-016-0061-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40595-016-0061-5