Introduction

Research on personalized education primarily centers on its potential and the techniques employed to achieve adaptive behavior (Kabudi et al., 2021; Maghsudi et al., 2021; Bhutoria, 2022). However, the current adoption of adaptive learning environments remains relatively limited. Although there are learning environments with a large user base, their scope of application is smaller than for other types of personalization (e.g., recommendation systems), and their adaptivity is often quite limited compared to the visions outlined in research papers. When addressing concerns regarding the use of artificial intelligence in education and the factors contributing to the slow adaption, issues like the role of teachers, usability, safety, and privacy often take the spotlight (Khosravi et al., 2020; Cukurova et al., 2023; Rizvi, 2023).

However, it is plausible that another, more fundamental obstacle hinders the widespread adoption of adaptive learning environments: the development of effective, large-scale adaptive systems is genuinely challenging. While research reports tend to emphasize their achievements and offer solutions to specific challenges, there are many obstacles and nuances that are not obvious from the current literature and complicate the development.

Fig. 1
figure 1

Simplified depiction of a learning environment and its context. The focus of this paper is on design issues, particularly on the modeling part of the learning environment

Full size image

The objective of this paper is to specifically highlight the challenging aspects of developing adaptive learning environments and to collect them in one place. The intention is not to convey pessimism but rather to serve as a cautionary note for designers of learning environments. The aim is to provide them with insights into the potential obstacles they may encounter and to help them set realistic expectations. The paper also aims to assist researchers by identifying aspects that warrant greater attention and more research efforts.

This paper draws extensively from my personal experiences in the field. I have been involved in the design and development of adaptive learning environments for over a decade, starting with small-scale academic projects, which progressed into a widely used platform (Umíme system used by over 15% of Czech schools). The list of issues presented here is not intended to be exhaustive; it is influenced by my own experiences. Due to personal experience, I know that these are not hypothetical academic issues; instead, they are all real challenges that we have encountered and had to address at various points in our work. I use the experience to illustrate the discussed issues on specific examples from several educational domains, particularly mathematics, programming, and language learning.

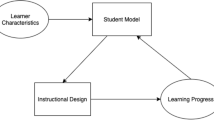
In order to maintain a clear focus, I focus on issues related to modeling. The development of adaptive learning environments is a comprehensive undertaking, encompassing various facets such as content authoring, model and algorithm design, user interface development, and teacher support. While challenges are present in many of these aspects, the modeling component is the most hidden and susceptible to unexpected difficulties. Figure 1 offers a simplified overview of the learning environment’s structure, highlighting the specific areas that are the central focus of this paper.

Setting the Scene

To make the following discussion of challenges and nuances more understandable, I will start with the description of a basic setting of an adaptive learning environment, examples of several typical tasks and modes of interaction, and a summary of the basic methods to achieve adaptivity. There are many different specific types of adaptive learning environments. My aim is to describe a relatively typical and basic setting; even this base case will be sufficient to illustrate numerous challenges. I also give an outline of the challenges and trade-offs that are then discussed in more detail in the following sections.

Expected Behavior

A typical adaptive learning environment may focus on a domain like mathematics or language learning. Minimal adaptive behavior involves adaptation with respect to cognitive skills, i.e., providing guidance and feedback appropriate to the student’s current knowledge.

The environment should also provide students with clear goals and visualization of progress towards these goals, e.g., in the form of a learning dashboard Bodily and Verbert (2017). The visualization of progress should be available not just for students but also for their teachers and parents. Additionally, the environment may also support personalization with respect to their interests, affect, or meta-cognition.

Fig. 2
figure 2

Illustration of various types of interactive tasks from several subjects

Full size image

Within an adaptive learning environment, interactive tasks play a key role. These tasks support student learning and simultaneously generate evidence about student knowledge. This evidence is then utilized to guide the adaptive behavior of the system. The tasks can have many different forms (Pelánek, 2020a); Fig. 2 provides several examples. The figure also illustrates various domains that I will reference during the discussion: language learning, mathematics, and programming.

Modeling Basics

To provide personalization, a learning environment needs three models (as illustrated in Fig. 1).

  • A student model provides an abstraction of a student that serves as a basis for adaptive decisions; typically, the model has the form of variables that describe a student’s state (e.g., cognitive skills, affective state, interests).

  • A domain model provides an abstraction of the domain to be learned, particularly an organization into learning units and a description of relations between these units.

  • A pedagogical model specifies the personalization strategy, i.e., how the information captured in the student model and the domain model should be translated into actions of the environment.

The terminology in education technology varies quite widely (Pelánek, 2022). Specifically, the pedagogical model is often described using different terms, e.g., “instructional strategy” or “recommendation algorithm.” Even though they may not be explicitly called “models,” any adaptive learning environment needs to have these three components in some form.

A concrete realization of the modeling for mathematics may look something like this:

  • We define individual knowledge components, e.g., greatest common divisor, addition of fractions, and linear equations. For each of these knowledge components, we create specific tasks (like the ones illustrated in Fig. 2).

  • To create a domain model, we specify the mapping of tasks to knowledge components and define prerequisite relations among knowledge components.

  • As a student model, we use one of the models of student knowledge (Pelánek, 2017), e.g., the standard Bayesian Knowledge Tracing model, which estimates the probability of a student’s mastery based on the sequence of answers.

  • Into the pedagogical model, we incorporate mastery learning driven by the estimates of the student model and personalized recommendations based on mastered skill and prerequisite relations.

These steps do not seem difficult to realize, and one may hope that they will quickly lead to an effective adaptive learning environment. In the rest of the paper, I will go through a variety of reasons why this impression is misleading.

Table 1 Outline of modeling challenges discussed in this paper
Full size table

Outline of Challenges

Table 1 provides an outline of challenges that are discussed in more detail in the following sections. The table gives a concise formulation of the core challenge; the discussion in the text then provides a more detailed description and specific examples.

These challenges are not insurmountable. In many cases, related research or partial guidance can be found to address these challenges. Nevertheless, I believe that the outlined challenges represent genuine obstacles to the practical development of efficient learning environments. Even when relevant research exists, it often takes various forms, such as the need to combine foundational insights from cognitive science about student learning with the appropriate application of statistical models and methodological approaches from machine learning. It is often hard to combine information from different sources and translate existing findings into practical design decisions. For instance, extensive research exists on the topics of forgetting and spaced repetition; however, much of this research primarily focuses on the outcomes of isolated and controlled experiments conducted in laboratory settings. In the context of adaptive learning environments, the challenge lies in adapting and implementing spaced repetition within a much more intricate and dynamic educational setting.

The primary difficulty in developing adaptive learning environments, however, does not stem from any isolated challenge but rather from their intricate interplay. It is not reasonable to select some of the challenges and to focus on their exhaustive treatment while disregarding others. If the development effort ignores some of the challenges or addresses them in some naive, baseline fashion, the efficiency of the learning environment can be significantly undermined.

Trade-offs

Before delving into individual challenges, I would like to discuss a recurring theme that complicates the design of adaptive learning environments: the need to make trade-offs without clear guidance on how to do so. Any practical application of adaptive learning is constrained by limited resources, e.g., time, money, and people. While these constraints may vary significantly among environments, they always exist. Consequently, it is important to consider the cost-effectiveness of different development steps and to choose suitable trade-offs.

This aspect is not, of course, specific to the design of adaptive learning environments. Trade-offs and limitations by constraints are present in any endeavor. What distinguishes dealing with trade-offs in the design of educational technology is the absence of guidance for making these trade-offs. While there is extensive research in learning science and many studies of previously developed educational technologies, the published research revolves around questions like “Does an approach X improve student learning?” While these inquiries are scientifically valuable, they do not provide sufficient guidance for the practical design process. The fact that an approach X can enhance student learning does not automatically mean that it should be implemented. Another approach Y may yield slightly smaller improvement while being much more easily realizable; in such a case, Y should often get a priority. Designers of learning environments face many such trade-offs and must make decisions for which there is currently limited guidance.

Student Model

The goal of a student model is to provide an abstract representation of a student’s state that is then used by a pedagogical model to guide the adaptive behavior of a system. The key type of modeling is concerned with cognitive skills. It may be useful to model many aspects of a student state, including affect, motivation, or meta-cognition, but it makes sense to focus on these only once we have a reasonable model of skills. Since even skill modeling is full of challenges, I focus primarily on this aspect.

Exact Meaning of Skill

Research papers on student modeling are often concerned primarily with the description of algorithms and their evaluation without specifying in detail what they mean by “skill”. In fact, it is surprisingly tricky to properly clarify the meaning of this notion, which is central to student and domain modeling.

One confusing aspect is terminology: different authors use different terms, sometimes as synonyms, sometimes with different shades of meaning. For the term skill, other closely related ones are “knowledge component” or “concept” (Pelánek, 2022; Koedinger et al., 2012).

The notion of skill links student models and domain models, e.g., greatest common divisor is some part of arithmetic and also some specific aspect of student knowledge. This linking is naturally (and often implicitly) used in many student models. But it also creates potential confusion. What exactly do we mean by “skill”? Skill may reference a learning unit (something independent of individual students) or student knowledge (something specific to individual students). Even within these two, there are several possible specific meanings.

When considering skill as referring to student knowledge, it can have at least two distinct interpretations. We may refer to skill as a latent construct: “what Jane knows about the addition of fractions.” This is the aspect that we genuinely care about, i.e., the actual student learning. However, this latent construct is not something we can directly work with. Alternatively, we can work with skill as a model estimate – a quantitative representation of a student’s proficiency. For example, when we state that “Jane’s skill is 0.8,” we are essentially saying that a model estimates an 80% likelihood that Jane is able to add two fractions.

When considering skill as a learning unit, it can also have several specific meanings. Skill can be interpreted as a set of rules, such as a procedural description of rules to add fractions, along with potential misconceptions related to the process. Alternatively, skill can simply denote a collection of specific tasks.

In the context of this paper, I employ the term knowledge component when discussing learning units or components within a domain model and the term skill when referencing student knowledge.

Exact Meaning of Skill Estimates

Even when considering skill estimates within student models, the exact meaning is nuanced (Pelánek, 2018a). The skill estimates typically take the form of a single number, e.g., for a Jane and addition of fractions, the skill estimate is 0.8. What is the exact meaning of this estimate? There are two principal interpretations:

  • The value expresses the uncertainty of a model estimate (while we assume a binary latent state of knowledge).

  • The number expresses the degree of knowledge (while we assume a continuous spectrum of knowledge).

The first approach is meaningful for skills that take the form of rules (like the addition of fractions), where the assumption of a binary latent state of knowledge is reasonable – it makes sense to talk about 80% chance that Jane knows how to add fractions. For factual knowledge (like vegetable vocabulary), however, it is more meaningful to use interpretation “Jane’s knowledge covers 80% of vegetable vocabulary.” Unless we use skills of very fine granularity, most skills are somewhere in between rules and factual knowledge, and thus, it would be useful to quantify both the uncertainty and degree of knowledge. This can be done using Bayesian modeling; see (Pelánek, 2018a) for a specific proposal. However, such a type of modeling increases the computational complexity of estimation and is not commonly used.

There are thus several approaches that a designer of a learning environment can use:

  • assume binary latent state even though it is, for some skills, a simplification, and use models that quantify the uncertainty of the estimate,

  • assume a more fine-grained spectrum of knowledge without quantifying uncertainty,

  • use a more complex model that addresses both uncertainty and degrees of knowledge but brings higher implementation and computational complexity.

This is a typical trade-off situation without a clear solution. Each of these approaches has its advantages and disadvantages. The proper choice depends on the circumstances, including the type of content, the available resources, and the required model precision for a personalization strategy that uses the model estimates.

Multiple Forms of Practice

Learning environments can offer students various modalities of practice to reinforce the same topic; Table 2 provides several specific examples. Incorporating diverse forms of practice has several advantages, e.g., it also enables better scaffolding of difficulty during learning and leads to more diverse and attractive practice.

Table 2 Examples of multiple forms of practice for the same topic
Full size table

Unfortunately, from the perspective of skill modeling, it leads to complications. Should different forms of practice on the same topic be considered the same skill or different skills? Simple, naive approaches are inadequate in addressing this matter. Treating various practice forms of practice as a single skill is clearly a significant oversimplification – abilities such as word recognition and spelling display are not completely aligned. For example, for Czech students, the term ‘broccoli’ is easy to recognize but challenging to spell correctly, whereas ‘tomato’ is relatively easy to spell yet often confused with ‘potato’ in multiple-choice questions. Modeling using entirely independent skills is an oversimplification as well.

It is possible to use modeling using correlated skills, e.g., using Bayesian networks (Käser et al., 2017) or an extension of the Elo rating system (Pelánek et al., 2017). However, it cannot be done easily with the most commonly used student modeling approaches.

Observational Data Used for Skill Modeling

Student modeling methods estimate skills based on the observed data about student performance while solving tasks. The most common student modeling approaches utilize only the binary information about the correctness of answers (Pelánek, 2017). This is a reasonable foundation: the correctness of answers is readily available in many settings, whereas other types of observations may differ based on context.

However, there are many other types of observational data that can be easily measured and carry potentially useful information about student knowledge:

  • response times,

  • specific values of incorrect answers,

  • information about the process of constructing the answer, e.g., sequences of moves or clicks in an interactive task,

  • timestamps or information processed based on timestamps (part of day, time intervals between answers),

  • use of instructional materials, e.g., video views,

  • contextual information, e.g., preceding activities.

Here, we face a typical design trade-off. We need to balance between the breadth of considered data sources, the depth of processing (complexity of used student models), and practical restrictions (computational requirements, implementation complexity). Fig. 3 illustrates the key choice: we need to balance the complexity of used models and observational data.

Fig. 3
figure 3

Simplified illustration of the trade-off between model complexity and observational data complexity

Full size image

Most research papers focus on model complexity while keeping the used observational data simple – this is a natural choice for research reports as it makes them more widely relevant; approaches that utilize specific observational data are necessarily tailored towards a specific application. For a practical application, however, it often makes sense to use a wide range of observational data while keeping the modeling simple, e.g., the use of statistics like exponential moving average. This approach is more easily applicable than complex models, and, thanks to richer input data, may produce better student models.

The practical feasibility of using both complex models and complex observational data is disputable. The use of complex, interpretable models tailored towards specific data is prohibitively expensive as it requires expert knowledge and is time-consuming. An alternative is to use black-box models based on deep learning (Piech et al., 2015; Minn et al., 2018); this avenue is currently explored in research papers, which, however, typically do not address issues necessary for the practical deployment of models in adaptive learning settings. I also consider the use of black-box models for student modeling highly risky due to the presence of biases in underlying data (Section 6). While the boundary of feasibility is disputable and will certainly extend in the future, the necessity of making trade-offs will probably remain for a long time.

Measuring Model Performance

The main point of student models is to try to estimate the latent student state. The quality of these models cannot be evaluated directly – the ground truth that we try to model is, by definition, latent and thus not directly observable. To evaluate models, we thus have to use proxy measures of model quality. Probably the most commonly used approach to the evaluation of student skill models is the evaluation of predictive accuracy for the next answer. Doing evaluation using just predictive accuracy is insufficient; see González-Brenes and Huang (2015) for more discussion and proposals for additional methods.

Even when we consider just the basic method for measuring model predictive accuracy, realizing it properly is more complex than it may seem. One issue that is not much discussed but rather important is the cross-validation approach. As is common in machine learning, student models are trained using one subset of data and evaluated on an independent subset of data; this train-test split can be done in several ways, e.g., in student-level, population-level, task-level, or with respect to time. The predictions can be computed statically based only on the train set or updated dynamically after each observation in the testing set. There is no universally correct approach to this choice (Pelánek, 2018b).

Another non-trivial issue is the choice of metrics. To quantify the model performance, we express the quality of predictions using a single number, e.g., Root Mean Square Error (RMSE) or Area Under the ROC Curve (AUC); there is no objectively correct metric to use and the choice of different metrics may lead to different results in model comparison (Pelánek, 2015). Moreover, the results of the model comparison can be influenced by such seemingly minuscule details as the approach used to averaging. Do we compute RMSE values for each student and then compute their average? Or do we compute RMSE directly over all predictions? Each of these approaches has its advantages and disadvantages, and each can produce different results (Pelánek, 2018b).

Moreover, the choice of prediction target is also unclear. Most commonly, the evaluation of student models focuses on predicting only the binary correctness of answers. However, richer data on answers are typically available, e.g., response times or specific answers. Incorporating these into prediction evaluation can lead to more valid predictions, e.g., if we care about the fluency of student knowledge, the response times are clearly important. However, the choice of suitable metric in this case becomes even more complex (Řihák, 2017).

The challenge of proper model evaluation interacts with other challenges. When we compare various approaches to student or domain modeling, the differences between models can often be relatively small or even dependent on the used measure. Are such differences practically important? This is hard to tell. Researchers have offered arguments against the exploration of models with minor differences in predictive accuracy (Beck and Xiong, 2013), as well as illustrations of situations where they may be important (Niznan et al., 2015). There is no easy, universal rule to decide when do differences in predictive accuracy matter.

Domain Model

The domain model provides a simplified representation of the domain that the environment tries to teach. The core of domain modeling lies in modeling knowledge components, which directly tie it with student modeling. Other aspects of domain models, like knowledge component relations, are used by the pedagogical model to implement adaptive behavior.

Knowledge Component Relations

Student skill with respect to individual knowledge components is not independent – student performance with respect to one knowledge component is related to performance on other knowledge components; the practice should thus be sequenced in a suitable order with respect to knowledge component dependencies. We thus need to model their relations.

The basic type of relation that we need to model is generalization-specialization. For example, knowledge components simplifying fractions, addition of fractions, and multiplication of fractions are all specializations of fractions. Beyond the use in student modeling and recommendation algorithms, this relation is also typically used for presentation purposes (listing of all topics in the system, navigation). The basic approach to modeling a generalization-specialization relation is using a tree, i.e., creating a taxonomy of a given learning domain (Pelánek, 2020b).

Modeling generalization-specialization using trees, however, leads to simplifications and omissions. Consider, for example, equations with fractions. This knowledge component naturally belongs both under equations and fractions; when using trees, we have to choose only one of these as a parent. A natural solution is to model generalization-specialization relations using a more general model: a directed acyclic graph or even a full-fledged ontology, which captures other types of relations as well. However, with these more complex models, all algorithms that use the relation become more complex. It is not clear whether such a complication is worthwhile; while knowledge components like equations with fractions clearly exists and deserve more parents, most skills can be naturally modeled using a single parent. This is a typical example of a trade-off that a designer of a learning environment faces.

Another typical type of relation are “sequential” relations (prerequisites, follow-ups). A typical example is the relation greatest common divisor \(\rightarrow \) simplifying fractions. Such a relation is universally useful across many learning domains and model applications. Unfortunately, the exact meaning of the relation cannot be stated in a simple, universal manner. The relation \(A \rightarrow B\) can have several distinct interpretations, and each of them is natural in some context:

  • Knowledge of A is absolutely necessary for understanding B, i.e., it is not possible to master B without mastering A. This is common in mathematics; typical example would be adding fractions \(\rightarrow \) equations of fractions.

  • Knowledge of A very useful for mastering B, i.e., it is possible to master B without A, but knowing A clearly helps. This naturally occurs in second language grammar, e.g., present simple tense \(\rightarrow \) past simple tense.

  • It is common to learn A before learning B but knowledge of A does not necessarily directly facilitate learning B. The primary reason for the sequence is not cognitive but rather motivation, practical usefulness, or habit. This is typically the case of vocabulary learning – although there are very few strict prerequisite relations, most learners learn vocabulary in similar order, e.g., colors \(\rightarrow \) clothes.

These three examples are not some clear-cut distinct categories but illustrations along a rather continuous spectrum. Even in mathematics, there are few completely necessary prerequisites; in many cases, the relations are somewhere between “absolutely necessary” and “useful.”

There are also other nuances. If we have a pair of relations \(A \rightarrow C, B \rightarrow C\), is their interpretation conjunctive or disjunctive? In order to learn C, does the student need to know both A and B, or is one of them sufficient? In a narrowly specialized learning environment, these issues may have a clear answer. But in any environment with a wider scope, design trade-offs are necessary.

Knowledge Component Combinations

A domain model needs to capture the mapping between the available tasks and knowledge components. A basic approach to do this is to map each task to a single knowledge component. Many modeling approaches, at least in their basic form, assume such simple mapping, e.g., the standard versions of Bayesian Knowledge Tracing or Elo rating system (Pelánek, 2017). In reality, however, many tasks require multiple skills. Evaluating an expression \((5-3)+6\times 2\) requires knowledge of addition, subtraction, multiplication, parenthesis, and operator priorities. Programming tasks typically involve the usage of multiple programming concepts.

One approach to address this is to keep the simple mapping and focus on a suitable choice of knowledge components. We can tag tasks according to their most complex element or introduce new “combined” knowledge components, e.g., combination of arithmetic operations, for loop with nested if.

Alternatively, we can use a modeling approach that directly supports multiple knowledge components per task. This mapping is often called Q-matrix (Barnes, 2005) and is used in approaches like the Additive Factors Model (Cen et al., 2006). This path, however, requires clarification of further issues, particularly the “credit assignment problem.” If a student answers incorrectly, which skill is to be “blamed” for this mistake? Is the skill combination compensatory (additive), conjunctive, or disjunctive? These issues have been addressed in multiple research studies, e.g., (Ayers and Junker, 2006; Koedinger et al., 2011; Gong et al., 2010; De La Torre, 2009), and there do not seem to be any universally applicable solutions. Moreover, the techniques used along these lines have been realized mostly in small-scale research studies and the methods used are often computationally intensive and non-trivial to scale.

Granularity of Knowledge Components

I have repeatedly used addition of fractions as an example of a knowledge component. This example is, however, disputable. Are the task \(\frac{2}{7} + \frac{4}{7}\) and \(\frac{5}{6} + \frac{8}{15}\) really covered by the same student skill? Maybe we should model separately addition of fractions with like denominators and addition of fractions unlike denominators. But what about \(\frac{1}{2} + \frac{1}{4}\)? This task has unlike denominators but is significantly simpler than \(\frac{5}{6} + \frac{8}{15}\). Should we introduce another knowledge component for tasks like these?

Tasks used to practice a given skill should be sufficiently similar, i.e., the performance on these tasks should be correlated, and there should be a transfer of learning between them. Research results mostly provide arguments for fine granularity of knowledge components as models with fine granularity provide a better explanation of data and can improve student learning; Koedinger et al. (2013b) provide a specific example. However, from a practical point of view, fine granularity brings costs and disadvantages. With the use of fine-grained models, it becomes harder to manage the task pool, construct mappings to knowledge components, and fit model parameters. When used in the user interface, fine-grained models may be confusing to students, who expect terms commonly used in textbooks. The data may support the desirability of a specific knowledge component “addition of fractions with unlike denominators, one denominator is multiple of another, only small numbers used”; it is, however, not something we want to display to students. These disadvantages may, in some cases, outweigh the benefits of a model with a better fit of data.

To better illustrate this point, I describe several other specific cases that I met during the development. In these cases, our analysis of data on student performance showed quite clearly that finer granularity is conceptually meaningful, but the practical merit of going for the finer granularity was unclearFootnote 1:

  • Modular division: The cases where the dividend is smaller than the divisor (e.g., \(5 \div 8\)) are more difficult than other modular division tasks.

  • English grammar, past tense, regular verbs: Forming a past tense for words ending with Y (e.g., try, carry, enjoy) is more difficult than for other regular verbs.

  • English grammar, present simple vs. continuous: The use of present continuous for describing irritating or annoying habits is more difficult than other uses of present continuous.

Differences in difficulty often serve as an indicator that a knowledge component could be split into two separate ones. This idea is the basis of techniques for domain model refinement (Koedinger et al., 2013b; Liu and Koedinger, 2017). However, there are multiple sources of differences in task difficulty, and it is not easy to disentangle them. Consider the case of basic linear equations and the following three tasks:

A.:

\(3x+2=11\)

B.:

\(4x+16=40\)

C.:

\(3x+20=11\)

The data on student performance clearly show that task A is simpler than the other two tasks, which have similar difficulty (the error rates are 14%, 26%, and 29%). Task C has a conceptual difference from task A; it involves the use of negative numbers, which may be meaningful to model as a separate knowledge component. However, the difference between A and B is mainly due to “larger numbers,” and there is a smooth transition in difficulty between A and B, which would not be meaningful to capture as a separate knowledge component.

Procedural and Declarative Knowledge

When dealing with procedural knowledge (e.g., addition of fractions), it is reasonable to represent a student’s knowledge with a single skill estimate. In essence, we assume that individual tasks are sufficiently homogeneous and that a singular skill estimate can effectively capture a student’s proficiency.

On the other hand, when we consider declarative knowledge (e.g., vegetable vocabulary, 3D shape names), the situation becomes more intricate. Using a single skill estimate is clearly a simplification – a student may know some terms while being unfamiliar with others. In such cases, a more precise modeling approach would involve assessing knowledge at the level of individual words. Nevertheless, even in the context of declarative knowledge, we still need to model the structure of knowledge – knowledge components like 3D shape names are useful, at least for organizing and presenting practice to students.

This leads to another trade-off between precision and practical usability: Should we opt for fine-grained granularity in modeling declarative knowledge at the level of individual facts, or should we prefer a less precise but simpler model that consolidates related facts into a single skill estimate?

Furthermore, the distinction between procedural and declarative knowledge is not always clear-cut. While there are clear examples like addition of fractions and vocabulary knowledge, many skills naturally combine both declarative and procedural aspects. Consider the following examples:

  • Mathematics, area of 2D shapes: a combination of the knowledge of key terms and equations and the ability to apply them.

  • English grammar, the choice between a/an determiners: procedural application of rules combined with the factual knowledge about the pronunciation of individual words; an example where you need both: “[a/an] honest boy.”

  • Programming, for loops in Python: procedural knowledge of program development combined with the declarative knowledge about the syntax and details of the language, e.g., the fact that for i in range(5) iterates through numbers 0 to 4, not 1 to 5.

Pedagogical Model

A pedagogical model captures pedagogical strategies that guide student learning. The modeled strategies utilize data from a student and domain model to decide how the environment should interact with the student.

Table 3 Examples of instructional strategies at various time frames with sample references
Full size table

The Choice of Strategies

A key problem with the pedagogical model is the choice of focus. There are many pedagogical strategies that are supported by research and that we may want to include in the system, see, for example, Dunlosky et al. (2013). Moreover, these strategies can often be combined in a wide range of ways (Koedinger et al., 2013a).

Instructional strategies that can be included in a pedagogical model target a wide range of scales, ranging from hints on the level of individual steps within a task to recommendations of long-term learning paths. Table 3 provides examples of strategies along this scale.

The table provides just sample references for illustration; there exists extensive research on individual strategies. This research is typically concerned with a single strategy in isolation; the research goal is typically to demonstrate that a given strategy works, i.e., that it improves learning outcomes with respect to a control group or another strategy of a similar type. However, when designing practical learning environments, we need to combine multiple strategies of different types and prioritize among them. This leads to questions that are hard to answer: For a given application domain, what are the most useful techniques? What is the relative contribution of individual strategies? How can we efficiently combine multiple strategies in the same environment? How do we resolve conflicts among strategies? An example of such conflict may be a situation, where a spaced repetition strategy recommends the repetition of insect vocabulary while personalization and novelty rules propose grammar practice on sentences from Harry Potter.

Balancing Multiple Aims

As previously discussed, during student and domain modeling, we encounter numerous design choices and trade-offs. The entire design process is further complicated by the fact that the appropriate choice of student and domain model often depends on the instructional strategies that we aim to implement within the pedagogical model. For instance, when considering adaptive hints or task difficulty adjustments, we may lean towards a model with a higher granularity of knowledge components. On the other hand, for long-term strategies and navigation within the learning environment, we may prefer a coarse-grained model and a different organizational structure for the model. In principle, we could employ distinct student models for various purposes, but managing parallel versions of several student models can quickly become a technical nightmare. Choosing a compromise model is also no simple task. How should we go about making this choice? What criteria should guide our decision-making process?

To make these dilemmas more concrete, let us consider specific examples. In second language learning, the basic dilemma is related to the procedural versus declarative knowledge issue discussed above. For vocabulary learning, it may be useful to have a model with granularity on the level of individual words and to model memory activation in detail, which can be used for difficulty adjustment and optimal spacing. For grammar practice, it may be more useful to focus the modeling on the level of knowledge components and their relations and their use for interleaved practice or follow-up recommendations. Do we use one compromise model or two separate models? When trying to use two separate models, we may find that the distinction between vocabulary and grammar is not completely clear-cut. For example, stative verbs, irregular verbs, and irregular plurals are closely connected to both vocabulary learning and grammar.

In mathematics, using modeling with multiple knowledge components per task specified by a Q-matrix is often natural and may be suitable for difficulty adjustment and mastery learning. However, this type of model is difficult to use for navigation and long-term recommendations.

In programming, we face design choices between focusing on conceptual aspects of tasks (programming constructs used) versus features of the used microworlds. From the perspective of the pedagogical strategies, the important facet is the conceptual aspects. However, from the perspective of feedback, navigation, and motivation, the salient features of tasks are also important – it is usually more understandable if the interface communicates in terms of these features: “you have mastered the robot clean-up mission, now is the right time to try to draw these interesting patterns with turtle graphics” rather than “you should strengthen your knowledge of for loops.”

Parameter Setting and Model Evaluation

Strategies captured in a pedagogical model require specific parameter values. The parameter values often need to strike a delicate balance. Mastery learning criteria employ mastery threshold parameters to navigate between over-practice and under-practice (Pelánek and Řihák, 2018). Spaced repetition strategies involve parameters that determine practice intervals, with optimal spacing contingent on the learning timeframe, for which there is no universal answer (Cepeda et al., 2008). Scaffolding strategies require specifying the speed of scaffolding removal. In the case of automatically displayed hints, a time threshold for hint display balances between being “too early” (inhibiting independent thought) and “too late” (causing frustration and disengagement). Moreover, when the pedagogical model includes multiple strategies, these strategies often end up in conflict as each recommends a different action to take. We thus have to specify a mechanism for resolving these conflicts, e.g., by using parameters specifying relative priorities of strategies.

Setting all these parameters can be challenging. While research literature offers valuable guidelines, the specific values almost always depend on the particular context. The parameter values also cannot be easily automatically optimized. The ultimate goal we aim to optimize is lifelong learning, a distant and indirectly measurable objective. We may utilize various proxies like engagement with the system or short-term learning gains. Yet, even these proxy measures prove quite challenging to quantify accurately, primarily due to data biases, as I will discuss in the next section.

More importantly, even when we succeed in quantifying them, it would be a mistake to straightforwardly optimize the system based on a chosen proxy measure. Specifically, it is easy to fall into the trap of optimizing for engagement, which is relatively easy to measure – we may inadvertently create a learning environment that appears fun and engaging but sacrifices actual learning outcomes in the process.

An alternative to relying on proxy measures involves the utilization of simulations. In this approach, we explore the impact of various parameter configurations on simulated students; for specific examples, see Fancsali et al. (2013); Pelánek (2018a); Käser and Alexandron (2023); Reddy et al. (2016). However, this method comes with its own drawbacks. Simulated students are, by necessity, simplifications of real students, and the accuracy of simulation results depends on the simplifying assumptions employed.

Data Biases

The process of modeling involves working with student data. These are used to obtain estimates of model parameters, to evaluate and compare models, or to get actionable insights into student behavior. Research papers often make a hidden, implicit assumption that the collected student data are of high quality, meaning that they have minimal noise and that all students engage with the system as expected (in a concentrated manner with the intention of learning). However, in reality, things are more complex. Some students may cheat or rapidly guess answers. The system itself may bias collected data, for instance, through attrition bias caused by the implementation of mastery learning. One may hope that these deviations simply add up as random noise, which could potentially be mitigated by gathering more data. Unfortunately, that is not the case.

Note that the term “bias” has many meanings; see, for example, Mitchell et al. (2021); Baker and Hawn (2021) for complex discussions. Here, I discuss primarily “statistical biases” that are connected with technical issues concerning data collection. Another type of bias is “societal bias,” which is concerned with fairness across various subpopulations, e.g., race, ethnicity, nationality, and gender. This type of bias is important, particularly in the use of machine learning methods on an institutional level. In the context of adaptive learning environments and skill modeling, however, the key biases are of a statistical nature.

Missing Data: Attrition Bias

Student and domain models are fitted using data collected during the student interactions with the learning environment. These data are not complete; we have observations only for some student-task pairs. The observed and missing data are not distributed randomly.

A key problem of this type is attrition bias. The number of answers per student (both globally and with respect to particular knowledge components) is not constant. Some students attempt to solve many more tasks than others. Some students quit the practice early, e.g., because they already mastered the topic. Some students may practice for a long time, e.g., because they have poor prior knowledge of the topic or because they are not sufficiently concentrated. These types of students typically systematically differ in their knowledge, which leads to systematic bias in the collected data.

Note that these effects may be actually a consequence of the adaptive behavior of the learning environment. A specific instance is the mastery attrition bias, which is caused by the implementation of mastery learning (Pelánek, 2018b). Researchers have illustrated how this bias confounds learning curves (Nixon et al., 2013) and proposed partial methods for alleviating it, e.g., by using disaggregation of learning curves (Murray et al., 2013) or mastery-aligned models (Käser et al., 2014). However, the specific impact of the bias is heavily dependent on a particular implementation of the adaptive behavior, and it cannot be addressed in any universal manner.

Missing Data: Unfinished Attempts

Other sources of potential biases due to missing data are connected to unfinished attempts. Consider a programming task. A student started solving the task, typed a few commands, but then abandoned it and went to practice something else. How should we store such interaction? How should we use it in the model fitting? The simplest solution is to just ignore unfinished attempts, but such an approach may create systematically biased data – the subpopulation that finishes a difficult programming task typically consists of more advanced students.

Another naive solution is to interpret all unfinished attempts as unsuccessful ones. Students may open a task without serious intent to solve it, e.g., because they are just interested in the problem statement or do not have time at the moment to solve it; it would be misleading to interpret such cases as indications of students’ inability to solve the task. There are, of course, various solutions between these two extremes, but it is hard to find a suitable balance that does not bring biases without requiring extensive tuning.

Ordering Bias

One of the principles used in learning environments is the sequencing of tasks from easier to more challenging ones. This pedagogical approach is beneficial for students, as it facilitates the gradual development of students’ skills. However, it comes with a drawback – the potential for biased data that complicates the process of parameter fitting. When students solve tasks in the same order, it is hard to disentangle student learning and increase in task difficulty.

As a specific illustration of this issue, consider two distinct scenarios:

  • A sequence of tasks of comparable difficulty, where minimal student learning occurs (students have already mastered the skill or the tasks themselves do not facilitate significant learning).

  • A sequence of tasks carefully designed to incrementally increase in difficulty, effectively guiding students along a learning curve that mirrors the task complexity.

From the perspective of the design of learning environments, the difference between these two scenarios is fundamental: the second one is the desirable case, while the first one is not. This key difference may be, however, very hard to capture in models fitted from student data. When all students follow an identical task sequence, the observed data from these two scenarios may be virtually indistinguishable. Čechák and Pelánek (2019) provide a specific illustration of this effect using simulation.

Aberrant Student Behavior: Cheating and Guessing

Much of the research on student modeling operates under the implicit assumption that students engage with our systems as intended, focusing on learning. Regrettably, this assumption does not always hold true. Students frequently exhibit aberrant behaviors, such as gaming the system by abusing hints (Baker et al., 2008), rapidly guessing answers (Wise, 2017), or even resorting to outright cheating (Ruiperez-Valiente et al., 2017).

Aberrant behavior has negative consequences, not just for students themselves. Aberrant behavior leads to biased data; it typically leads to lower response times and non-trivial changes in error rates of answers. When we fit student models to such data, these biases can have a non-trivial impact on parameter values and, consequently, also on any algorithms that use these models.

One may hope that the presence of aberrant behavior basically amounts to a random noise, which can be overcome by collecting more data. Unfortunately, that is not the case. The biases caused by aberrant behavior are often systematic (non-random) and not uniformly distributed.

For example, we have detected significant cheating in reading comprehension exercises; cheating occurs only in the more difficult exercises, which leads to misleading analytics results – objectively complex exercises seem to be easier than simple ones (Pelánek, 2021). For rapid guessing, we detected a significant portion of rapid guessing in multiple-choice questions on computational thinking (which were a bit laborious), whereas in many other domains (like English grammar), the presence of rapid guessing was much lower.

Feedback Loops

The issue of data biases is amplified due to the presence of feedback loops. The algorithms that guide adaptive environments decide what data get collected, and the collected data are used to fit models that are used by the algorithms. Adaptivity can lead to biases in data collection, and these biases can influence the behavior of adaptivity.

Consider a specific example that illustrates the potential for a negative impact of such feedback loops – an interaction between student rapid guessing and an algorithm for mastery criteria. Our system uses a mastery criteria algorithm that utilizes an estimate of the time intensity of individual tasks (Pelánek and Řihák, 2018). The presence of rapid guessing, concentrated in the practice of some knowledge components, led to smaller estimates of time intensity. This caused a slower progress towards mastery (since the algorithm assumed that the items in the topic were not very time intensive). This, in turn, led to student frustration and even more occurrences of rapid guessing. The consequence of this feedback loop was that for some knowledge components, the rapid guessing attempts comprised nearly half of all attempts, and it was not possible to reach mastery in a reasonable time. The problem was not very difficult to solve – we implemented a detector of rapid guessing and made the estimation of time intensity more stable. The main point is that such feedback loops are often hidden and can interact in unexpected ways.

Another impact of feedback loops concerns model evaluation. When a learning environment uses a model to guide adaptivity, the model determines which data are collected and later used to evaluate its impact. This can influence the results of model comparison (Pelánek et al., 2016).

Conclusions

Finally, I want to conclude with several high-level messages that are based on the previous discussion.

Be Aware of Challenges and Do Not Despair

Acknowledging the existence of challenges can be discouraging and demotivating. However, to get adaptive learning environments towards wider application, we need to address these hidden challenges, nuances, and trade-offs. Moreover, just the awareness of challenges can sometimes help us to move forward with practical development. In the design of learning environments, we often encounter challenging problems that seem difficult to resolve satisfactorily. At such times, being mindful of the fact that there are numerous other issues that the current design overlooks can aid in overcoming the specific problem at hand. For instance, it is not very meaningful to address every nuanced aspect of modeling prerequisites at the moment when the learning environment completely ignores the issue of student cheating.

Make the Trade-offs Explicit

Research studies often focus on optimizing specific aspects of a problem while neglecting others. A common example is the pursuit of predictive accuracy of student models while ignoring computational requirements. I do not want to disparage such kind of research; it is valuable in exploring the boundaries of what is achievable and discovering techniques that can later be optimized. However, it would be useful to have more research that explicitly takes various trade-offs into account. Such research can provide valuable tools and frameworks for making informed decisions in the design of learning environments.

In practical development, it is not possible to avoid the issue of trade-offs. It is beneficial to make these trade-offs explicit. For instance, when considering various instructional strategies that we may wish to implement, it is useful to explicitly outline their expected contributions to student learning and consider the associated costs, which encompass implementation, content authoring, data maintenance, and computational requirements.

Beware of Silver Bullets

The recent advancements in artificial intelligence have generated high expectations. However, even considering the rapid progress in AI, it’s improbable that we will witness swift, transformative changes in education. While deep machine learning has made significant strides, it may not necessarily translate into deep human learning.

Recent progress has been mainly due to black-box methods. These methods often concentrate on optimizing specific cost functions. In the context of learning environments, the real goal is fostering long-term student learning. This goal cannot be expressed using a readily measurable cost function. Relying on proxies that can be automatically optimized may lead to unintended consequences. For example, it is much simpler to measure student engagement than student learning. It may thus be tempting to use measures of student engagement as a cost function. With this approach, however, we might end up with engaging but ultimately ineffective educational solutions. Furthermore, there is the inclination of students to cheat or game the system and the presence of feedback loops. These aspects can easily wreak havoc with a black-box approach built to optimize a specific cost function.

Consider Avoiding Stupidity Perspective

The motivation behind personalized education is often described in terms of “optimizing the positive aspects” such as learning, motivation, engagement, and efficiency. However, to make practical progress, it may be more beneficial to emphasize “mitigating the negative aspects.” Many things that can go wrong in a learning environment, e.g., tasks may be ambiguously formulated, the learning curve may be too steep, teaching strategies may be implemented inefficiently, students may exploit the system through unanticipated uses of hints and feedback. The primary objective should be to prevent problems. Variations on this idea have emerged in recent literature. We have called it the “avoiding stupidity perspective” (Pelánek and Effenberger, 2022), while Mian et al. (2019) approach the discussion by asking “What’s most broken?” and Baker (2016) advocates for an approach termed “stupid tutoring system, intelligent humans”.

The practical implication of adopting this perspective is a shift in focus during the development of automated techniques. Rather than fixating solely on fully automated methods aimed at optimizing student learning, it encourages the use of human-in-the-loop approaches that leverage modeling and data analysis to identify and rectify problematic system behaviors.