Introduction

Advanced learning technologies support different forms of adaptivity that are harder for teachers to implement in their classroom (Koedinger et al., 2013a, b, c). These technologies can assess learners on multiple dimensions and can adjust their pedagogical decision making accordingly (Aleven & Koedinger, 2013; Conati & Kardan, 2013; Sottilare et al., 2013). A learning environment is defined to be adaptive if its design is based on data on common learning challenges in the targeted content area, if its pedagogical decision-making changes based on the learning measures of individual learners, and if it responds interactively to learner actions (cf. Aleven et al., 2015a, b; Aleven et al., 2013).

When adaptations are oriented toward improving student affect or motivation, they are often referred to as “personalization”. Such personalized adaptations typically make use of data about an individual students’ identity or interests. For example, Cordova and Lepper (1996) demonstrated motivation and learning benefits from a personalization intervention that used the student’s name and friends name as part of an educational game scenario. Walkington and Bernacki (2019) used student interest survey results to create math story problems that were personalized to individual student interests. Adaptations may also be oriented toward accelerating knowledge growth through data-driven selection of learning materials or activities that depend on a model that tracks student performance and knowledge growth. A general class of algorithms that engage in such tracking are referred to as “knowledge tracing”. Knowledge Tracing is a well-established research area of artificial intelligence in education, which aims to leverage students’ learning interactions to estimate their knowledge states (i.e., unlearned and learned) (Liu, 2022). One approach to knowledge tracing, called Bayesian Knowledge Tracing, uses closed-form equations derived from Bayes’ theorem applied to a simple two-state hidden Markov model (cf. Anderson et al., 1995). This model continually updates an assessment of learners’ knowledge growth and that assessment is used to select tasks that contain knowledge components that an individual student is not likely to have mastered. Bayesian Knowledge Tracing has been popular, for example, through its widely disseminated use within Cognitive Tutors (Ritter et al., 2016; Aleven et al., 2015a, b), perhaps because of its relative simplicity to implement. A more sophisticated approach to knowledge tracing uses more complex multi-state Bayesian Networks to model student knowledge and knowledge growth (cf. Conati et al., 2002). In our context, we chose the simpler BKT approach hypothesizing it would be adequate to make effective task selection decisions that would optimize student learning relative to the pre-existing non-adaptive system.

There are mixed results in prior research about the effectiveness of knowledge tracing. An early positive result comes from Atkinson (1972), who studied task selection techniques in the context of learning German vocabulary. He showed that automated item selection showed the greatest gain on a delayed posttest, in comparison with both learner control and random selection conditions. He also provided evidence that having parameters that estimate difficulty of different target components of knowledge enhances effectiveness. In another study, Corbett et al. found that knowledge tracing improved the effectiveness of student learning compared to giving all students the same problem set (Corbett et al., 2000). Corbett et al. also found that students in the baseline condition averaged 87% correct across six quizzes while students in the cognitive mastery condition averaged 95% correct, with a significant difference across conditions (Corbett et al., 2000). Zhao et al. (2013), on the other hand, found no difference between knowledge tracing and a fixed set of tasks in the context of second language English grammar instruction (Zhao et al., 2013). In Corbett (Corbett et al., 2000), students in the knowledge tracing condition spent more time than the baseline condition. Whereas in the Zhao study, the amount of time in instruction was the same. Thus, a potential alternative explanation can be that more time produces better learning.

In addition to the need for more investigation into whether and when knowledge tracing is effective, there is also a need to test the generality of the approach across different subject-matter domains and different technology approaches. Most knowledge tracing studies so far have focused on language and math learning. We explore knowledge tracing in the context of science learning and particularly in guided inquiry-based learning of early physics principles. Also, adaptivity has mostly been integrated in screen-based learning technologies.

In this paper, we integrated knowledge tracing adaptivity in a mixed-reality system - a new genre of Intelligent Science Stations we have developed, allowing children to do experiments in the 3D physical world with interactive feedback from a virtual helper that provides guidance based on proven learning mechanisms. We report on a randomized controlled experiment where we compare learning outcomes of children interacting with the Intelligent Science Station that has task-loop adaptivity incorporated, compared to another version that provides tasks randomly. This paper makes a unique contribution in that it investigates the impact of adaptivity on learning in a novel AI-based mixed-reality system where children are performing real-world experiments with personalized interactive feedback.

Intelligent Science Stations

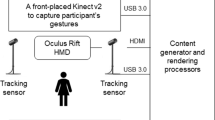
We have developed a new genre of Intelligent Science Stations (norillla.org) that use a specialized AI vision technology to track physical objects and children’s actions as they experiment and make discoveries in the real world (See Fig. 1). This AI-based technology encourages guided inquiry thinking processes through a predict, explain, observe, explain cycle. A gorilla character appears on a large display to guide students as they make predictions, observations and explain results in the physical environment (Yannier et al., 2016, 2021, 2022). Our design uses evidence-based principles from learning science (e.g., Clark & Mayer, 2016; Gibson & Gibson, 1955; Chi et al., 1989; White & Gunstone, 1992) and game design (e.g., Falloon, 2010) including contrasting cases, self-explanation, predict-observe-explain, and real-time interactive feedback. The principle of contrasting cases (Gibson & Gibson, 1955) suggests use of aligned cases with minimal differences to help students notice information that they might otherwise overlook. Building on this literature and more recent work (e.g., Schwartz et al., 2011; Rittle-Johnson & Star, 2009), we decided to include contrasting cases in our design.

Fig. 1
figure 1

Children interacting with the intelligent science station at the science center

Full size image

In our first Intelligent Science Station, EarthShake, students are shown two towers that differ on only one principle (symmetry, wide-base, height, or center of mass principles) and are asked to make a prediction about which one will fall first when the table shakes (see Fig. 2d). Another instructional feature is prompted self-explanation, which has been demonstrated to enhance learning and transfer (Aleven et al., 2002). In our system, we utilize a self-explanation menu to help children explain the reasoning for why a tower falls. The menu consists of explanation choices that target the underlying physical principles in child friendly language such as: “because it is taller”, “because it has more weight on top than bottom”, “because it is not symmetrical”, “because it has a thinner base”. We also utilize a predict-observe-explain (POE) cycle in our mixed-reality system, a teaching-learning strategy proposed by White and Gunstone (White & Gunstone, 1992), including three stages: Prediction, Observation and Explanation, to help activate discussions among students (Kearney, 2004). We utilize POE in our design to help children understand the physics principles of balance and stability and why structures fall.

Fig. 2
figure 2

Screenshots of the interface where children are making a prediction about which tower will fall first and explaining the results with interactive feedback from the system

Full size image

Our AI-based mixed-reality system also provides real-time interactive feedback, which is a critical component for effective learning. Immediate feedback has been shown to be more effective than feedback on demand in intelligent tutoring systems (Corbett & Anderson, 2001). Also, the phenomenon of “confirmation bias” (Nickerson, 1998) suggests that children can see their predictions as confirmed even when they are not, thus explicit feedback can reduce this tendency and enhance learning. (Hattie & Clarke, 2018). Research suggests that learning from obtained outcomes is biased: people preferentially take into account positive, as compared to negative prediction errors, and information that confirms their current choice (Palminteri et al., 2017). Furthermore, overconfidence produces under achievement, undermining student learning and retention (Dunlosky & Rawson, 2012). Explicit feedback can help lower confirmation-bias and overconfidence, by correcting errors, helping to unravel misconceptions and suggesting specific improvements (Hattie & Clarke, 2018). Explanatory feedback has also been shown to be effective for learning outcomes, enhancing sustainable learning outcomes (Clark & Mayer, 2016). Our system incorporates automated interactive and explanatory feedback in a real-world environment as the students are doing physical experiments to learn scientific concepts and critical thinking skills.

In addition to learning science principles, we have also utilized game design principles in our system including use of an animated character in a game-like scenario. Our system has a character and scenario that guides the students and gives immediate feedback. Characters and virtual environments have been shown to have potential to act as powerful communication mediums for students to facilitate understanding and foster engagement/motivation (Falloon, 2010; Cassell, 2000).

Our previous research has demonstrated that having a mixed-reality system combining hands-on experience with interactive AI guidance and feedback in our Intelligent Science Stations improves children’s learning significantly compared to a tightly matched screen-only version without the hands-on interaction (Yannier et al., 2015, 2016, 2021), as well as compared to hands-on exploration without the interactive AI layer (Yannier et al., 2020, 2022).

Scenario

In our scenario, users are first asked to place the towers shown on the screen on the physical earthquake table (See Fig. 1). These prebuilt towers are designed to be contrasting cases with only one difference between them so that the kids can focus on isolating the principles. A depth camera and our specialized computer vision detects if towers placed on the table match the ones on the screen and gives feedback accordingly. If they place the correct tower as displayed on the screen, a green check appears above the tower on the screen and the gorilla character says “Good job! Click to continue” (See Fig. 2b). Otherwise, if the tower they place does not match the tower on the screen, the computer vision system detects that it was not the correct tower, and a red cross appears on the tower on the screen, and they’re asked to place the correct tower (See Fig. 2c).

Our computer vision algorithm uses depth information from the depth-sensing camera, performing blob detection and physics-based moment of inertia calculations (Yannier et al., 2013, 2020) to recognize and differentiate objects of experimentation, i.e., the towers, and to recognize critical experimental outcomes, i.e., a falling tower. When students try to place a requested tower on the table, the vision algorithm computes a moment of inertia value that serves as a kind of signature of the identity of the tower, which is used to determine if the correct tower has been placed or not, to provide the pedagogical structure needed for guided inquiry. Once the user clicks continue, the gorilla character prompts him/her to make a prediction saying, “Which tower do you think will fall first when I shake the table?” (See Fig. 2d). They can choose either 1, 2 or the same by clicking on the buttons or one of the towers on the screen. Once they make a prediction, the gorilla character says: “You chose the left tower. Why do you think so? Discuss and then click SHAKE to see what happens”. Here they can discuss their prediction with their partners, why they think the tower they chose will fall first. After they discuss, they can then click the “Shake” button on the touch screen to shake the physical earthquake table (the touch screen triggers a relay that is connected to the motor of the earthquake table). After the physical table starts shaking and one of the towers falls, the depth camera and our specialized computer vision algorithm detects the fall and stops the earthquake table from shaking. Our specialized vision algorithm then detects whether the left or right tower fell and if it matches with the prediction of the user. If the student’s prediction was correct and the correct tower fell first, then the gorilla character says “Good job! Your hypothesis was correct! Why do you think this tower fell first?”, as he starts to jump and dance on the screen. If the user’s prediction was wrong and the tower that fell does not match the tower that was predicted by the user, then the gorilla character says “Uh oh! Your prediction was not quite right! Why do you think this tower fell first?”. Users are asked to explain why they think the tower that fell, fell first, using a scaffolding explanation menu with four different choices: “It is taller”, “It has a thinner base”, “It has more weight”, “It is not symmetrical”. These explanations are matched with the four different principles of stability and balance, that are primary science content learning objectives for EarthShake. When they choose one of the explanations in the menu, the gorilla character tells them if their explanation was correct or wrong, with a visualization laid over the images of the towers on the screen to explain why the tower fell (See Fig. 2f). For example, if the reason was because it was taller, and their explanation was not correct, he says: “Actually it fell first because it was taller than the other tower. Good try. Click CONTINUE to play again.” The visualization on the towers shows a ruler to highlight the height of each tower.

This scenario is repeated for different contrasting cases of towers (Fig. 3). 

Fig. 3
figure 3

Contrasting case tower pairs used in the system

Full size image

Bayesian Knowledge Tracing and Adaptivity in Intelligent Science Stations

Knowledge Tracing is a technique used in intelligent tutoring systems to model student growth of knowledge so as to determine when a target knowledge component (KC) has been mastered and if not, to give students more practice tasks to achieve mastery (Corbett & Anderson, 1994; Koedinger et al., 2013a, b, c). Bayesian Knowledge Tracing (BKT) is a widely used approach to knowledge tracing that models student knowledge growth as a latent variable using a two-state Hidden Markov Model. Domain knowledge is decomposed into KCs representing the skills and concepts that students need to correctly perform tasks (cf., Koedinger et al., 2012). For each KC, the student can either be in an “learned” or “unlearned” state, and Bayesian probability formulas are used to determine which of the two states a student is likely in based on their sequence of performance to achieve that KC. Each KC in BKT is modeled by four parameters: the initial probability of having already learned a KC, p (L0), the probability of a student transitioning from the unlearned to the learned state for a KC at a particular opportunity to practice the KC, p(T), the probability of a student answering incorrectly even though the KC is known (e.g., slipping up), p(S), and the probability of a student answering correctly even though the KC is not known (e.g., by guessing), p(G). Ln (the probability of being in the learned state, knowing the KC, after nth opportunity) is calculated from these four parameters using this formula:

$$\begin{array}{c}p\left(L_{t+1}\vert obs=correct\right)=\frac{p(L_t)\cdot(1-p(S))}{p(L_t)\cdot(1-p(S))+(1-p(L_t))\cdot p(G)}\\p\left(L_{t+1}\vert obs=wrong\right)=\frac{p(L_t)\cdot p(S)}{p(L_t)\cdot p(S)+(1-p(L_t))\cdot(1-p(G))}\\p(L_t+1)=p\left(L_{t+1}\vert obs\right)+(1-p(L_{t+1}\vert obs))\cdot p(T)\end{array}$$

We have implemented an adaptive, BKT-enhanced version of Intelligent Science Stations, where the tasks in the scenarios are determined based on the mastery levels of two types of knowledge components (i.e., prediction and explanation KC) for each task category (i.e., height, base-width, symmetry, center of mass). BKT does not determine how tasks are selected, but at what probability each KC in a task category is learned. If the probability of knowing a KC (Ln) is above a given threshold, typically 0.95, it is considered that this KC has been mastered. If both KCs in a task category is above 0.95, we determine that that task category has been mastered.

For task selection, different algorithms have been implemented (cf., Zhao et al., 2013; Koedinger et al., 2013a, b, c, 2010). Our task selection algorithm implements a “gentle slope” of improvement whereby among all the task categories involving unmastered KCs, we pick the one that is estimated to be closest to mastery (i.e., closest to 0.95 without being over). Each task category has a prediction (Ln_prediction) and explanation (Ln_explanation) score and the smaller of the two is used to determine closeness to mastery. The tasks are selected from a set of 10 tasks (targeting 4 different principles: height, base-width, symmetry, and center of mass) based on the proximity of the task category to the mastery level (95%). To insert some variety and interleaving, if the same task category is selected 3 times in a row, the next easiest unmastered task category is selected next. If prediction and explanation Ln scores are both above 95% for a certain task category (which means that task category has been mastered), then that task category is not considered. We selected initial values (L0) for each task category based on previous experiments (Yannier et al., 2015, 2016, 2020) where we found that height is easiest, and center of mass is hardest (height: 0.8; thinner base: 0.6; symmetry: 0.5; center of mass: 0.4). Correspondingly, we selected p(T) values in a similar fashion, height having the highest p(T) value since it is easier to learn compared to thinner base, symmetry and center of mass (height: 0.7; thinner base: 0.4; symmetry: 0.3; center of mass: 0.3). These values were estimated based on log data from previous experiments and experiences in pilot testing. We assumed that the chance of guessing p(G), and the chance of slipping p(S) are the same for each task category and set their values to be p(G) = 0.3, and p(S) = 0.1. Each time a student performs a task, the mastery level is updated by the BKT formulas shown above.

Table 1 illustrates knowledge tracing updates and associated task selection. Row 0 shows the initial L0 values for the four pairs of KCs (prediction and explanation for each of height, base width, symmetry and center of mass). Based on these values, the task selection picks a height task because the initial values (0.80 and 0.80) are closest to mastery threshold of 0.95. (When these values are different, the smaller one is used.) The first step of this task is to predict which tower will fall and in this case the student answers this prediction step correct. So, the Height Prediction Ln goes from 0.80 (L0 - init) to 0.98 (based on the formula given above) as shown in row 1a. In the second step, the student is asked to explain. The student selects the correct explanation, so the Ln value for the Height Explanation (H.Expl) KC goes from 0.8 to 0.98 also. Since both the Height Prediction and Explanation Ln’s are above 0.95 (see 1b), the next task will be determined by the highest Ln score not above 0.95 (The next highest category is Base (L0 = 0.60), so the next task given is a Base prediction task. For this task, the student predicts correctly (2a). Therefore, the Base Prediction Ln goes from 0.60 to 0.89. Then the student is given the Base explanation task and selects an incorrect explanation (2b). So, the Base Explanation Ln drops to 0.51. Since the Base Prediction Ln and Base Explanation Ln are not both above 0.95, the next task that will be given will be a Base task again.

Table 1 Example of how knowledge estimates update and drive task selection
Full size table

The experiment described below compares two different conditions, with BKT adaptivity or without (tasks randomly chosen), to evaluate whether or not BKT adaptivity improves children’s learning.

Methods

We conducted the experiment within a controlled setting in a science center. Participants were elementary aged students (first through fifth graders) attending the summer camp at the science center. We had an Institutional Review Board (IRB) approval for this research and every student had a consent form signed by the parent to participate in the study. The user group in this study is aligned with the design goals of the mixed-reality system and the early learning testing with K-5th grade children in our previous experiments. 36 children (18 pairs) interacted with the Intelligent Science Station at the exhibit floor, away from the rest of the summer camp activities. The ages of the children were balanced for both conditions (2.5 average grade level for both conditions). The pairs were randomly selected and assigned to different conditions of the experiment. An earlier study showed no significant difference in learning and enjoyment between students working in pairs versus solo (Yannier et al., 2015). However, since parents and teachers indicated a preference to have children interact collaboratively in pairs, we decided to conduct the study in pairs. Children interacted with the system in pairs in all conditions.

Measures

We used pre and post assessments that have been validated in previous experiments (29, 30) to measure scientific and engineering outcomes. To measure scientific outcomes, we used paper pre and posttests, where children were asked to explain their predictions of which of the given towers will fall first based on four principles of stability and balance (height, base-width, symmetry and more weight on top versus the bottom – center of mass) (Fig. 4). These explanation outcomes show a deep understanding of scientific concepts. The paper pre- and post-tests, that were validated in previous experiments, were based on the NRC Framework & Asset Science Curriculum (40).

Fig. 4
figure 4

Prediction (left) and explanation (right) items used in the paper pre/post-tests

Full size image

To measure engineering outcomes, we compared the quality of towers children built before and after interacting with the intervention, to see if they improved on any of the four scientific principles described above. We also evaluated students’ ability to predict which tower would fall first among the given pairs of towers. To measure pre- to post-test changes on the tower building task, we scored each student’s towers according to three principles: height, symmetry, and center of mass (we did not use the fourth principle, wide base, as all students were instructed to use the same base block). For each principle, students were given one point if their towers improved from pre- to post-test, -1 for the reverse, and 0 for no change. Comparing pre- and post- towers for the height principle, a shorter post-tower scores 1, a taller post-tower scores − 1, and towers of the same height score 0. Likewise, post-towers with more symmetry and a lower center of mass score one for each of those principles. Adding the scores for each principle yielded the student’s total score (Fig. 5).

Fig. 5
figure 5

Coding scheme for tower pre/posttests change

Full size image

Experimental Procedure

Children were randomly pulled out from their summer camps in pairs. They came to the museum floor where the equipment was set up (the exhibit was closed to the public during the times of the experiment). Before interacting with the system, students were first given a tower pre-test. First, the experimenter gave the students a bag of blocks and asked them to build a tower that they think will withstand an earthquake. Then they were asked to complete a paper pre-test, consisting of some prediction and some explanation items. Children then interacted with their assigned condition, either Randomized or Adaptive condition. We did piloting with both conditions to ensure balanced time for different conditions.

Children were randomly assigned to two different conditions: Randomized condition and Adaptive Condition. In the Randomized condition, the tasks that students were getting while interacting with the Intelligent Science Station were randomly selected from a set of 10 tasks that had a focus on (see Fig. 3). In the Adaptive condition we used Adaptive Task Selection (Aleven et al., 2016) based on Bayesian Knowledge Tracing (Yudelson et al., 2013) as described above. The tasks were selected based on the proximity of the knowledge component (KC) to the mastery level (95%). If both prediction and explanation mastery scores are above 95% for a certain KC, then the algorithm switches to the next KC. If the mastery score drops (the student keeps getting it wrong), the algorithm switches to the KC that is closest to mastery. We selected initial values for each KC based on previous experiments and the difficulty of each KC for students and the mastery level was updated after each task. Also, if they get more than 3 items per KC it switches to the next highest KC, with the goal of introducing some interleaving. We controlled the time for both conditions (~ 10 min). Based on the video and log data, average time on task for the intervention for Randomized Condition is approximately 9.61 min, and for Adaptive Condition is approximately 9.76 min with no significant difference between time on task in different conditions.

After interacting with the Intelligent Science Station, students were given a matched paper post-test, including prediction and explanation items. After the paper post-test, students were given the same tower building task as before the intervention, to see if their towers had improved after interacting with the game. Finally, children were asked to fill out a survey to see how much they enjoyed the game.

Results

We wanted to see the effects of adaptivity on learning in a mixed-reality setting. To accomplish this, we analyzed paper pre and post-tests, tower pre and post-tests, and the enjoyment surveys that were given after interacting with the system.

We analyzed the results for the pre and post-tests to identify any differences between conditions, adaptivity versus randomized. We confirmed that our pre and posttest results were sufficiently normal by visually inspecting the distribution and finding small Pearson median skewness values for the pre-test of 0.39 and post-test of -0.10 (between − 0.50 and 0.50 indicates symmetry associated with normality). An ANOVA with overall pre-test score as the outcome variable confirmed no differences between the conditions at pretest (p > 0.40). To test for learning benefits, we ran an ANCOVA with post-test score as the outcome variable and pre-test as the covariate. We found significant positive effects of the adaptivity condition. The overall results indicated that the average scores on the full post-tests (prediction and explanation items) was 69% for the adaptive condition and 54% for the randomized condition, F(1,34) = 4.02, p = 0.05, d = 0.66 (Cohen’s d). Our findings are summarized in Fig. 6. We did not find any significant interaction of test type on learning gains.

Fig. 6
figure 6

Overall post-scores were significantly higher for students in the adaptive group than those in the random group (p = 0.03) with non-significant trends in favor of the adaptive group for Tower Building scores

Full size image

An ANOVA testing the effect of the two conditions on transfer to engineering outcomes (tower building) showed a non-significant trend in favor of the adaptive condition (F(1, 34) = 1.75, p = 0.19, d = 0.48). The towers in the adaptive condition had a positive improvement (based on average score of improvement on height, symmetry and center of mass) while the randomized condition did not show any improvement.

We confirmed that the reduced variability in the adaptive condition (e.g., getting another base question once they get a base question wrong) did not reduce engagement. There was no significant difference in the enjoyment outcomes of the different conditions.

To understand the results better and investigate why the Adaptive condition might be learning better compared to the Randomized condition, we looked at our logs. We realized that in the Adaptive condition, students were getting more practice with the task categories they were having a hard time with (e.g., center of mass, see Fig. 7 − 3) and moving quickly through the concepts they already knew (e.g., height, see Fig. 7 − 1). Thus, they were able to master these concepts better. On the other hand, in the Randomized condition, they spent more time with height, and did not get enough opportunities with the more challenging concepts like center of mass, thus leading to less mastery of these concepts.

Fig. 7
figure 7

In the Adaptive condition (1), most students master the height principle in one opportunity, and thus are not given a second opportunity. On the other hand, in the Random condition (2), many students who get it right the first time nevertheless receive a second opportunity, taking away valuable time that could have otherwise been used to master other concepts that are not yet mastered. For the Weight (center of mass) concept, many students in the Adaptive condition (3) get multiple opportunities that lead to a high proportion of students mastering at the end. On the other hand, students in the Random condition (4) don’t get enough opportunities (too much time was spent on easy concepts) and do not reach mastery

Full size image

Our log data aims to provide a more in-depth understanding of the results of the pre and posttests which show that BKT adaptivity improves learning compared to random selection of items. As detailed below, our log analysis reveals that students in the Adaptive condition can spend more time on items that they are having difficulty mastering without losing time on items they already know (as a result of the adaptivity BKT algorithm provides).

Log Files Analysis

The log file analysis helps explain how knowledge tracing aids learning. Recall that we set the parameters in BKT based on prior data indicating that the height principle is easier to learn than the center of mass principle. Thus, the algorithm needs less observations of student success to determine mastery for height than center of mass. Figure 7 illustrates how students’ experience is thus better optimized in the adaptive condition, where tasks are selected based on BKT, than in the random condition. Comparing the first graph (see 1 in Fig. 7) to the second graph (in 2), we see that children in the Adaptive condition are assigned fewer height tasks (1–2 tasks) in comparison to children in the Random condition (2–3 tasks). Of the nine groups in the Adaptive condition, eight have the correct prediction (green boxes) on the first opportunity, which is enough for BKT to estimate them as having reached mastery (see “mastered” status indication to the right in 1). One other, group 2 (see the bottom of 1), gets the first opportunity wrong and so is given a second opportunity and they get it right, which is enough for BKT to estimate mastery. In contrast, in the Random condition, only two groups get the BKT-predicted ideal amount of practice (groups 8 and 10, see the “unmastered” status indication to the right in 2) whereas most get more practice than needed (those indicated as “over practiced”) and a couple do not reach mastery (groups 1 and 6). For the harder center of mass task (see 3 and 4 in Fig. 7) the situation is reversed: Because of the lower initial knowledge estimate for center of mass in BKT, children in the Adaptive condition are generally given more such tasks, especially if they make more errors, than children in the Random condition. In the Adaptive condition, most children reach mastery in predicting and explaining the center of mass tasks (6 of 9) and do so after 3 to 5 opportunities. (Note: If a group reached mastery in all four task categories before time ran out, they were given “extra practice” as happened for groups 3 and 7.) In the Random condition (on the right), none of the groups receive enough Center of Mass tasks to reach mastery.

Table 2 provides a summary across all groups on all four task types. In the Adaptive condition, over 80% of the 36 group-by-task sequences end in mastery. No Adaptive condition sequences involve over-practice (though some get some extra practice after mastering all four tasks). In contrast, in the Random condition, only 16.7% of the 36 group-by-task sequences end in mastery. 27.8% of the sequences involve over practice, taking away valuable learning time that could otherwise be used for the unmastered sequences. 55.5% of the sequences as a result are unmastered.

Table 2 A greater proportion of students master scientific principles in the adaptive condition
Full size table

Discussion and Conclusion

We found that adaptivity using Bayesian Knowledge Tracing in the context of a mixed-reality Intelligent Science Station led to better learning of scientific principles compared to random task selection, without sacrificing enjoyment. Our log analysis indicated that the students in the adaptive condition were getting more opportunities to work on concepts they were having a hard time learning, while the students in the adaptive condition overspent time on easy tasks and did not have enough opportunities to master the harder concepts. Thus, adaptivity helped focus the attention of students on concepts where they needed most help with, taking into account the variability among different students.

Prior results have shown the promise of improving learning through knowledge tracing (Atkinson, 1972), though in some cases with confounds in extra time (Corbett et al., 2000) and in other cases finding no benefit (Zhao et al., 2013). Our results provide positive evidence towards the effectiveness of knowledge tracing adaptivity without sacrificing time (time is controlled for both adaptive and random task selection conditions). Also, since most knowledge tracing studies so far have focused on language and math learning and in screen-based technologies, our results show the effectiveness of AI adaptivity in a new context: inquiry-based science learning in a mixed-reality system. Potential future work could explore alternative adaptation algorithms that, for example, incorporate student-specific adjustments to the core guess, slip, learn rate parameters (cf., Yudelson et al., 2013) or integrate information about student preferences. Nevertheless, our current positive results demonstrate that such approaches, while potentially desirable, are not necessary to improve student learning through adaptive task selection.

We have demonstrated that techniques for active learning with automated feedback can be effectively extended through automated mastery-based adaptation. Our log analysis shows how adaptive mastery can be applied at the level of scientific principles that students discover on their own with well-crafted feedback and as-needed guidance. We find some principles are more intuitive than others (e.g., height) and thus require less inquiry practice whereas other principles (e.g., center of mass) are more novel and take more inquiry practice for students to understand and transfer. Further, some students reach mastery sooner than others. Our mastery-based algorithm effectively adjusts the inquiry experience to adapt to these content and student differences producing better learning outcomes. It is worth noting that our previous experiment has shown that children interacting with the system in pairs versus alone did not have any significant difference in their learning outcomes (Yannier et al., 2016). This experiment was done in pairs, based on the preference of museum staff and teachers to have children work collaboratively. In future work, we plan to look into student conversations as well.

More generally, our results show the potential of adaptivity in a mixed-reality setting to improve science learning for children in informal or formal learning settings. This result is especially important given the limited number of controlled experiments on learning benefits of tangible interfaces and mixed-reality systems. Bringing computer-monitored mastery learning to the 3D world is a novel contribution of our work made possible by automated assessment of students’ experimentation afforded by the AI vision algorithm.