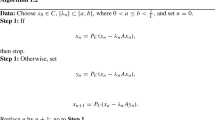1 Introduction

In the sequel, \(\mathbb {R}\) denotes the set of all real numbers and \(\mathbb {N}\) denotes the set of all positive numbers. Let H be a real Hilbert space with inner product \(\langle \cdot , \cdot \rangle \) and induced norm \(\Vert \cdot \Vert ,\) and let C be a nonempty, closed, and convex subset of H. Let \(A: H\rightarrow H\) and \(B: H\rightarrow 2^{H}\) be a single-valued and multivalued operator, respectively. The monotone variational inclusion problem (MVIP) is formulated as finding a point \(\bar{x} \in H\), such that

$$\begin{aligned} 0\in (A+B)\bar{x}. \end{aligned}$$
(1.1)

The set of solutions of MVIP (1.1) is denoted by \((A+B)^{-1}(0),\) which is referred to as the set of zero points of \(A+B.\) The problem in (1.1) has attracted great research attention and has application in several mathematical problems, which includes variational inequalities, convex programming, split feasibility, and minimization problems (see [1, 3, 15, 16, 37]). It is important to note that some concrete problems in machine learning, linear inverse, and image processing can be mathematically modelled as MVIP (1.1) (see [24, 30, 46]).

Several methods have been proposed by researchers for solving MVIP (1.1), but one of the most notable among them is the forward–backward splitting method proposed by the authors in [25, 35]. The forward–backward splitting method is presented as follows:

$$\begin{aligned} x_{n+1}=(I+ \lambda _{n}B)^{-1}(I-\lambda _{n}A)(x_{n}), \end{aligned}$$
(1.2)

where \(\lambda _{n}\) is a positive parameter, the operator \((I-\lambda _{n}A)\) is the so-called forward operator, and \((I+\lambda _{n}B)^{-1}\) is the resolvent operator introduced in [28] which is often called backward operator. The limitation of Algorithm (1.2) is that it gives a weak convergence result under the stringent condition that the single-valued operator A is co-coercive.

Takahashi et al. [49] in an attempt to obtain strong convergence result introduced the following algorithm but with a more stringent conditions on the control parameters:

Algorithm 1.1

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1, u \in H\\ x_{n+1}= \alpha _{n} u + (1-\alpha _{n})J_{\mu _{n}}^{B}(x_n-\mu _{n}Ax_{n}),\quad \forall n\ge 1, \end{array}\right. } \end{aligned}$$
(1.3)

where A is a k-inverse strongly monotone mapping. The authors obtained a strong convergence result for the proposed algorithm under the following stringent conditions on the control parameters: \( \{\alpha _n\}\subset (0,1),~~ \lim _{n\rightarrow \infty }\alpha _{n}=0,~~\sum _{n=1}^{\infty }\alpha _{n}=+\infty ,\sum _{n=1}^{\infty }|\alpha _{n+1}-\alpha _{n}|<+\infty ,\mu _n\subset [a,b]\subset (0, 2k),~~ \sum _{n=1}^{\infty }|\mu _{n+1}-\mu _{n}|<+\infty .\)

In 2000, Tseng [53] succeeded in relaxing the strong condition of co-coerciveness of the single-valued operator A by introducing the following splitting algorithm called the Tseng Splitting Method:

Algorithm 1.2

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1\in H\\ y_n=J_{\lambda _{n}}^{B}(x_{n}-\lambda _{n}Ax_{n})\\ x_{n+1}=y_{n}-\lambda _{n}(Ay_{n}-Ax_{n})\quad \forall n\ge 1, \end{array}\right. } \end{aligned}$$
(1.4)

where A is monotone and Lipschitz continuous. However, Algorithm 1.2 is limited by its weak convergence and the dependence of the step size on the Lipschitz constant of the operator A, which is often unknown or very difficult to compute.

To improve on the result of Tseng [53], Gibali and Thong [17] introduced the following Tseng-type algorithm for approximating the solution of the MVIP (1.1) in real Hilbert spaces:

Algorithm 1.3

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H\\ y_{n}=(1+\lambda _{n}B)^{-1}(I-\lambda _{n}A)x_{n}\\ z_{n}=y_{n}-\lambda _{n}(Ay_{n}-Ax_{n})\\ x_{n+1}=(1-\alpha _{n}-\beta _{n})x_{n}+\beta _{n}z_{n}\\ \lambda _{n+1}= \min \Big \{\frac{\phi \Vert x_{n}-y_{n}\Vert }{\Vert Ax_{n}-Ay_{n}\Vert }~,\lambda _{n}\Big \}, &{}\text {if}~ Ax_n -Ay_{n}\ne 0,\\ \lambda _{n},&{}\text {otherwise.} \end{array}\right. } \end{aligned}$$
(1.5)

The authors proved strong convergence result for Algorithm 1.3, when the single-valued operator A is monotone and Lipschitz continuous and B is maximal monotone. We need to point out that while the authors were able to relax the co-coercive assumption on the single-valued operator A and obtained strong convergence result, their result is not applicable when the operator A is nonLipschitz. This limits the scope of applications of their proposed method.

Another problem of interest in this study is fixed point problem (FPP). Let \(S: C\rightarrow C\) be a nonlinear mapping. A point \(x^*\in C\) is called a fixed point of S if \(Sx^*=x^*.\) The set of all fixed points of S is denoted as by F(S). That is

$$\begin{aligned} F(S)=\{x^*\in C:Sx^*=x^*\}. \end{aligned}$$

A mapping \(S:C\rightarrow C\) is called a nonexpansive mapping if

$$\begin{aligned} \Vert Sx-Sy\Vert \le \Vert x-y\Vert ,\quad \forall x, y \in C. \end{aligned}$$

The broad applications of the study of fixed point theory of nonlinear operators in economics, compressed sensing, and other applied sciences contributed immensely to its great success in recent years. It is worthy of note that variational inequality problems, convex feasibility problems, monotone inclusion problems, convex optimization problems, and image restoration problems can all be formulated as finding the fixed points of suitable nonlinear mappings; see [7, 11]. Several methods have been proposed for approximating fixed points of nonlinear mappings (see [20, 32, 38,39,40,41, 51]) and the reference therein.

Agarwal et al. [4], in 2007, introduced the following iterative scheme for approximating the fixed points of a nonlinear mapping S : 

Algorithm 1.4

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{1}\in C \\ y_{n}=(1-\beta _{n})x_{n}+ \beta _{n}Sx_{n}\\ x_{n+1}=(1-\alpha _{n})Sx_{n}+\alpha _{n}Sy_{n}\quad n\in \mathbb {N}, \end{array}\right. } \end{aligned}$$
(1.6)

where \(\{\alpha _{n}\}\) and \(\{\beta _{n}\}\) are sequences in (0, 1). It was shown by the authors that the proposed method in Algorithm 1.4 has a better convergence properties than Mann and Ishikawa iteration processes. The proposed method in Algorithm 1.4 and its modifications have been used by some authors to find common fixed points of two nonlinear mappings (see, for example, [9, 34]) and the references therein.

Polyak [36], through the heavy ball methods of a two-order time dynamical system, pioneered an inertial extrapolation method as an acceleration process to solve the smooth convex minimization problem. The inertial algorithm is a two-step iteration method in which the next iterate is defined by making use of the previous two iterates. This slight modification has been shown to have great effect on the convergence rate of iterative techniques. In this direction, many researchers have constructed some fast iterative algorithms using inertial extrapolation technique (e.g., see [10, 19, 27, 29, 33]).

Very recently, Thong and Vinh [52] proposed the following modified inertial forward–backward splitting method with viscosity technique for approximating the common solution of the MVIP and FPP of nonexpansive mapping T in the framework of Hilbert spaces:

Algorithm 1.5

Initialization: Select \(x_0, x_1\in H\) and set \(n:=1.\)

Step 1.:

Compute

$$\begin{aligned} w_n&= x_n + \vartheta _n(x_n - x_{n-1}),\\ z_n&= (I + \mu B)^{-1} (I - \mu A)w_n. \end{aligned}$$

If \(z_n=w_n\), then stop (\(z_n\) is a solution to MVIP (1.1)). Otherwise, go to Step 2.

Step 2.:

Compute

$$\begin{aligned} x_{n+1} = \alpha _nf(x_n) + (1-\alpha _n)Tz_n. \end{aligned}$$

Let \(n:= n+1\) and return to Step 1,

where \(T:H\rightarrow H\) is a nonexpansive mapping, \(f:H\rightarrow H\) is a contraction with constant \(\rho \in [0,1) A:H\rightarrow H\) is k-inverse strongly monotone (co-coercive), \(B:H\rightarrow 2^H\) is maximal monotone, and \(\mu \in (0,2k)\) is the step size of the algorithm. The authors obtained strong convergence result under the following conditions on the control parameters:

  1. 1.

    \(\{\alpha _n\}\subset (0,1), \lim _{n \rightarrow \infty }\alpha _n=0, \sum _{n=1}^{\infty }\alpha _n=\infty , \lim _{n \rightarrow \infty }\frac{\alpha _{n-1}}{\alpha _n}=1;\)

  2. 2.

    \(\{\vartheta _n\}\subset [0,\vartheta ), \vartheta >0, \lim _{n \rightarrow \infty }\frac{\vartheta _n}{\alpha _n}||x_n-x_{n-1}||=0.\)

We observe that the condition \(\lim _{n \rightarrow \infty }\frac{\alpha _{n-1}}{\alpha _n}=1\) in Algorithm 1.5 is too stringent. Moreover, the algorithm is only applicable when the single-valued operator A is co-coercive. These drawbacks can hinder the implementation of the method.

Motivated by the above results and the ongoing research in this direction, in this paper, we introduce a new inertial iterative scheme which combines the viscosity method with self-adaptive strategy for approximating a common element of the set of solutions of MVIP and CFPP of strict pseudocontractions in Hilbert spaces. The motivation for studying such a common solution problem is in its potential application to models whose constraints can be formulated as MVIP and CFPP. This is observed in practical problems, such as image recovery, signal processing, and network resource allocation. An instance of this is found in network bandwidth allocation problem for two services in a heterogeneous wireless access networks in which the bandwidths of the services are related mathematically (e.g., see [23, 26]).

On the other hand, the class of strict pseudocontractions is known to have many applications, due to their ties with inverse strongly monotone operators. It is well known that, if A is a strongly monotone operator, then \(T = I - A\) is a strict pseudocontraction. Thus, we can recast a problem of zeros for A as a fixed point problem for T,  and vice versa.

More precisely, our proposed method has the following features:

  • Our algorithm does not require the co-coercive (inverse strongly monotonicity) and Lipschitz continuity assumptions often employed by authors when solving MVIP.

  • The proposed method does not require any linesearch technique. Rather, it uses an efficient self-adaptive step size technique, which generates nonmonotonic sequence of step sizes. The step size is constructed, so that it reduces the dependence of the algorithm on the initial step size.

  • The adoption of the proposed method in Algorithm 1.4, which has been shown to have better convergence properties than many of the existing iterative methods in the literature.

  • We employ inertial technique together with viscosity method to accelerate the rate of convergence of our proposed algorithm.

  • The algorithm solves fixed point problem for a larger class of mappings than the class of nonexpansive mappings considered in [52].

  • Unlike the results in [17, 52] and several other existing results in the literature, the proof of our strong convergence result does not follow the conventional “two cases" approach. Moreover, our strong convergence result is established under more relaxed conditions on the control parameters.

Moreover, we apply our result to study other optimization problems. Finally, we present several numerical experiments and apply our result to solve image restoration problem to demonstrate the efficiency of the proposed method in comparison with the existing methods in the literature.

This paper is outlined as follows: In Sect. 2, some basic definitions and existing results needed for the convergence analysis of the proposed algorithm are recalled. In Sect. 3, the proposed algorithm is presented, while in Sect. 4, we analyze the convergence of the algorithm. In Sect. 5, we apply our result to study other optimization problems, and in Sect. 6, we present several numerical experiments and apply our result to image restoration problem. Finally, in Sect. 7, we give a concluding remark.

2 Preliminaries

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. The weak convergence and strong convergence of \(\{x_{n}\}\) to x are represented by \(x_{n}\rightharpoonup x\) and \(x_{n}\rightarrow x,\) respectively, and \(w_{\omega } (x_{n})\) denotes set of weak limits of \(\{x_{n}\},\) that is

$$\begin{aligned} w_{\omega } (x_{n})=\{x\in H: x_{n_j}\rightharpoonup x~~ \text {for some subsequence}~~\{x_{n_j}\}~~ \text {of}~~ \{x_{n}\} \}. \end{aligned}$$

Definition 2.1

Let H be a real Hilbert space H. The mapping \(T: H\rightarrow H\) is said to be:

  1. 1.

    Uniformly continuous, if, for every \(\epsilon >0,\) there exists \(\delta =\delta (\epsilon )>0,\) such that

    $$\begin{aligned} \Vert Tx-Ty\Vert<\epsilon \quad \text {whenever}\quad \Vert x-y\Vert <\delta ,\quad \forall x,y\in H. \end{aligned}$$
  2. 2.

    L-Lipschitz continuous, where \(L>0,\) if

    $$\begin{aligned} \Vert Tx-Ty\Vert \le L\Vert x-y\Vert , \quad \forall x,y \in H. \end{aligned}$$

    If \(L \in [0,1),\) then T is a contraction.

  3. 3.

    Nonexpansive, if T is 1-Lipschitz continuous.

  4. 4.

    Firmly nonexpansive, if

    $$\begin{aligned} \Vert Tx-Ty\Vert ^{2}\le \langle Tx-Ty, x-y \rangle , \quad \forall x, y \in H; \end{aligned}$$

    or equivalently

    $$\begin{aligned} \Vert Tx-Ty\Vert ^{2}\le \Vert x-y\Vert ^{2}-\Vert (I-T)x-(I-T)y\Vert ^{2},\quad \forall x,y \in H; \end{aligned}$$

    or equivalently, if and only if T is of the form \((I+S)/2\) where S is nonexpansive. See [21] and [42] for more details on firmly nonexpansive mappings.

  5. 5.

    k-Strictly pseudocontractive, if there exists a constant \(k \in [0,1)\), such that

    $$\begin{aligned} \Vert Tx-Ty\Vert ^{2}\le \Vert x-y\Vert ^{2}+k\Vert (I-T)x-(I-T)y\Vert ^{2},\quad \forall x,y \in H. \end{aligned}$$
  6. 6.

    \(\alpha \)-Strongly monotone, if there exists \(\alpha >0\), such that

    $$\begin{aligned} \langle x-y, Tx-Ty\rangle \ge \alpha \Vert x-y\Vert ^2,~~ \forall ~x,y \in H. \end{aligned}$$
  7. 7.

    \(\alpha \)-Inverse strongly monotone (\(\alpha \)-co-coercive), if there exists \(\alpha >0\), such that

    $$\begin{aligned} \langle x-y, Tx-Ty \rangle \ge \alpha ||Tx-Ty||^2,\quad \forall ~ x,y\in H. \end{aligned}$$
  8. 8.

    Monotone, if

    $$\begin{aligned} \langle Tx-Ty, x-y\rangle \ge 0, \quad \forall x,y \in H. \end{aligned}$$

It is important to note that when \(k=0\) in item (5), then T is nonexpansive, and T is pseudocontractive, if \(k=1.\) T is said to be strongly pseudocontractive, if there exists a positive constant \(\lambda \in [0,1)\), such that \(T-\lambda I\) is pseudocontractive. It is then clear that the class of k-strict pseudocontractions falls between the class of nonexpansive mappings and pseudocontractive mappings.

Moreover, it is known that if T is \(\alpha \)-strongly monotone and L-Lipschitz continuous, then T is \(\frac{\alpha }{L^2}\)-inverse strongly monotone. Furthermore, \(\alpha \)-inverse strongly monotone operators are \(\frac{1}{\alpha }\)-Lipschitz continuous and monotone, but the converse is not true. It is clear that uniform continuity is a weaker assumption than Lipschitz continuity.

It is well known that if D is a convex subset of H,  then \(T:D\rightarrow H\) is uniformly continuous if and only if, for every \(\epsilon >0,\) there exists a constant \(K<+\infty \), such that

$$\begin{aligned} \Vert Tx-Ty\Vert \le K\Vert x-y\Vert + \epsilon \quad \forall x,y\in D. \end{aligned}$$
(2.1)

We have the following result showing relationship between the class of nonexpansive mappings and the class of strict pseudocontractive mappings.

Lemma 2.2

[57] Let C be a nonempty closed convex subset of a real Hilbert space H and \(S:C\rightarrow C\) be a k-strict pseudocontractive mapping. Define a mapping \(S_\alpha :C\rightarrow C\) by \(S_\alpha x = \alpha x +(1-\alpha )Sx\) for all \(x\in C\) and \(\alpha \in [k,1).\) Then, \(S_\alpha \) is a nonexpansive mapping, such that \(F(S_\alpha )=F(S).\)

Lemma 2.3

[13, 54] For each \(x,y \in H\), and \(\delta \in \mathbb {R}\), we have the following results:

  1. (i)

    \(||x + y||^2 \le ||x||^2 + 2\langle y, x + y \rangle ;\)

  2. (ii)

    \(||x + y||^2 = ||x||^2 + 2\langle x, y \rangle + ||y||^2;\)

  3. (iii)

    \(||x + y||^2 = ||x||^2 - 2\langle x, y \rangle + ||y||^2;\)

  4. (iv)

    \(||\delta x + (1-\delta ) y||^2 = \delta ||x||^2 + (1-\delta )||y||^2 -\delta (1-\delta )||x-y||^2.\)

Definition 2.4

[21] Assume that \(T:H\rightarrow H\) is a nonlinear operator with \({Fix(T)}\ne \emptyset .\) Then, \(I-T\) is said to be demiclosed at zero if, for any \(\{x_{n}\}\) in H, the following implication holds: \(x_{n}\rightharpoonup x\) and \((I-T)x_{n}\rightarrow 0\implies x\in Fix(T).\)

Lemma 2.5

[57] If S is a k-strict pseudocontraction on a closed convex subset C of a real Hilbert space H, then \(I-S\) is demiclosed at any point \(y\in H.\)

Definition 2.6

A function \(c: H\rightarrow \mathbb {R}\) is called convex if for all \(t\in [0,1]\) and \(x,y\in H\)

$$\begin{aligned} c(tx+(1-t)y)\le tc(x)+(1-t)c(y). \end{aligned}$$

Definition 2.7

A convex function \(c: H\rightarrow \mathbb {R}\) is said to be subdifferentiable at a point \(x\in H\) if the set

$$\begin{aligned} \partial c(x)=\{u\in H |~c(y)\ge c(x)+\langle u,y-x\rangle ,~\forall y\in H\} \end{aligned}$$
(2.2)

is nonempty, where each element in \(\partial c(x)\) is called a subgradient of c at x, \(\partial c(x)\) is called the subdifferential of c at x, and the inequality in (2.2) is called the subdifferential inequality of c at x. We say that c is subdifferentiable on H if c is subdifferentiable at each \(x\in H\) [22].

Definition 2.8

Let \(B: H\rightarrow 2^{ H}\) be a multivalued operator on H. Then

  1. (i)

    The effective domain of B denoted by dom(B) is given by \(dom(B)=\{x\in H:Bx\ne \emptyset \}.\)

  2. (ii)

    The graph G(B) is defined by

    $$\begin{aligned} G(B):=\{(x,u)\in H\times H:u\in B(x)\}. \end{aligned}$$
  3. (iii)

    The operator B is said to be monotone if \(\langle x-y,u^*-v^*\rangle \ge 0\) for all \(x,y\in dom(B), u^*\in Bx\) and \(v^*\in By.\)

  4. (iv)

    A monotone operator B on H is said to be maximal if its graph is not properly contained in the graph of any other monotone operator on H.

  5. (v)

    The resolvent mapping \(J^{B}_{\lambda }: H\rightarrow H\) associated with B is defined as

    $$\begin{aligned} J^B_{\lambda }(x)=(I+\lambda B)^{-1}(x), \end{aligned}$$

    for some \(\lambda >0,\) where I is the identity operator on H. For a maximal monotone operator B,  the \(dom(J^B_{\lambda })= H.\)

Lemma 2.9

[47] Let \(B: H\rightarrow 2^{H}\) be a set-valued maximal monotone mapping and \(\lambda >0.\) Then, \(J_{\lambda }^{B}\) is a single-valued and firmly nonexpansive mapping.

Proposition 2.10

[21] In Hilbert space, a mapping T is firmly nonexpansive if and only if \(2T-I\) is nonexpansive.

Lemma 2.11

[6] Let \(B:H\rightarrow 2^{H}\) be a maximal monotone mapping and \(A:H\rightarrow H\) be a hemicontinuous, monotone, and bounded operator. Then, the mapping \(A+B\) is a maximal monotone mapping.

Lemma 2.12

[50] Suppose \(\{\lambda _n\}\) and \(\{\theta _n\}\) are two nonnegative real sequences, such that

$$\begin{aligned} \lambda _{n+1}\le \lambda _n + \phi _n,\quad \forall n\ge 1. \end{aligned}$$

If \(\sum _{n=1}^{\infty }\phi _n<\infty ,\) then \(\lim \nolimits _{n\rightarrow \infty }\lambda _n\) exists.

Lemma 2.13

[45] Let \(\{a_n\}\) be a sequence of nonnegative real numbers, \(\{\alpha _n\}\) be a sequence in (0, 1) with \(\sum _{n=1}^\infty \alpha _n = \infty \) and \(\{b_n\}\) be a sequence of real numbers. Assume that

$$\begin{aligned} a_{n+1}\le (1 - \alpha _n)a_n + \alpha _nb_n, ~~~ \text {for all}~~ n\ge 1, \end{aligned}$$

if \(\limsup _{k\rightarrow \infty }b_{n_k}\le 0\) for every subsequence \(\{a_{n_k}\}\) of \(\{a_n\}\) satisfying \(\liminf _{k\rightarrow \infty }(a_{n_{k+1}} - a_{n_k})\ge 0,\) then \(\lim _{n\rightarrow \infty }a_n =0.\)

3 Proposed algorithm

In this section, we present our proposed algorithm. The convergence of the algorithm is established under the following conditions:

Condition A:

  1. (A1)

    The mapping A is monotone and uniformly continuous and \(B:H\rightarrow 2^{H}\) is maximal monotone.

  2. (A2)

    The mappings \(S,(T):H\longrightarrow H\) are \(k_1,(k_{2})\)-strict pseudocontractions.

  3. (A3)

    The solution set \(\varGamma =F(S)\cap F(T)\cap (A+B)^{-1}(0)\) is nonempty.

  4. (A4)

    \(f:H\longrightarrow H\) is a contraction mapping with coefficient \(\rho \in [0,1).\)

Condition B:

  1. (B1)

    \(\{\alpha _n\}\subset (0,1),\lim \nolimits _{n\rightarrow \infty }\alpha _{n}=0,\sum _{n=1}^\infty \alpha _{n}=+\infty ,\) and \(\{\epsilon _{n}\}\) is a positive sequence satisfying \(\lim \nolimits _{n\rightarrow \infty }\frac{\epsilon _{n}}{\alpha _{n}}=0.\)

  2. (B2)

    Let \(\{\sigma _{n}\}, \{\delta _{n}\},\{\xi _{n}\} \subset [a,b]\subset (0,1)\), such that \(\alpha _{n}+\delta _{n}+\xi _{n}=1, \alpha \in [k_1, 1),\beta \in [k_2,1).\)

  3. (B3)

    Let \(\{\phi _n\}\) be a nonnegative sequence, such that \(\sum _{n=1}^\infty \phi _n<+\infty .\)

Now, the algorithm is presented as follows:

Algorithm 3.1

Initialization: Given \(\theta>0, \lambda _{1} >0, \phi \in (0,1).\) Let \(x_{0}, x_{1}\in H\) be two initial points and set \(n=1.\)

Iterative steps: Calculate the next iterate \(x_{n+1}\) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} w_{n}=x_{n}+\theta _{n} (x_{n}-x_{n-1})\\ u_{n}=(I+\lambda _{n}B)^{-1}(I-\lambda _{n}A)w_{n} \\ v_{n}=u_{n}-\lambda _{n}(A u_{n}- A w_{n})\\ z_{n}=(1-\sigma _{n})v_{n}+\sigma _{n}S_{\alpha }v_{n} \\ x_{n+1}=\alpha _{n} f (w_{n}) + \delta _{n}S_{\alpha }v_{n}+\xi _{n}T_{\beta }z_{n}, \end{array}\right. } \end{aligned}$$
(3.1)

where \(S_{\alpha }=\alpha I + (1-\alpha )S\) and \(T_{\beta }=\beta I + (1-\beta )T\)

$$\begin{aligned} {\theta }_n= & {} {\left\{ \begin{array}{ll} \min \Big \{\frac{\epsilon _n}{||x_n - x_{n-1}||}, ~ \theta \Big \}, &{}\quad \text {if}~ x_n \ne x_{n-1},\\ \theta , &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$
(3.2)
$$\begin{aligned} \lambda _{n+1}= & {} {\left\{ \begin{array}{ll} \min \Big \{\frac{\phi \Vert w_{n}-u_{n}\Vert }{\Vert A w_{n}-Au_{n}\Vert },~ \lambda _{n}+\phi _n\Big \}, &{}\quad \text {if}~ A w_{n}- A u_{n} \ne 0 \\ \lambda _{n}+\phi _n, &{}\quad \text{ otherwise. } \end{array}\right. } \end{aligned}$$
(3.3)

Remark 3.2

From (3.2) and condition (B1), we observe that

$$\begin{aligned} \lim _{n\rightarrow \infty } \theta _{n}\Vert x_{n}-x_{n-1}\Vert =0\quad \quad \text {and}\quad \quad \lim _{n\rightarrow \infty } \frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert =0. \end{aligned}$$

Remark 3.3

Observe that by Lemma 2.2, \(S_\alpha \) and \(T_\beta \) are nonexpansive. Moreover, \(F(S_\alpha )=F(S)\) and \(F(T_\beta )=F(T).\)

4 Convergence analysis

First, we establish some lemmas which are needed to prove our strong convergence theorem for the proposed algorithm.

Lemma 4.1

Let \(\{\lambda _n\}\) be a sequence generated by Algorithm 3.1, such that Conditions A and B hold. Then, \(\{\lambda _n\}\) is well defined and \(\lim \nolimits _{n\rightarrow \infty }\lambda _n=\lambda \in [\min \{\frac{\phi }{N},\lambda _1\}, \lambda _1+\varPhi ],\) for some \(N>0\) and \(\varPhi =\sum _{n=1}^{\infty }\phi _n.\)

Proof

Since A is uniformly continuous, then by (2.1) we have that for any given \(\epsilon >0,\) there exists \(K<+\infty \), such that \(\Vert Aw_n-Au_n\Vert \le K\Vert w_n-u_n\Vert +\epsilon .\) Therefore, for the case \(Aw_n-Au_n\ne 0\) for all \(n\ge 1\), we have

$$\begin{aligned} \frac{\phi \Vert w_n-u_n\Vert }{\Vert Aw_n-Au_n\Vert }\ge \frac{\phi \Vert w_n-u_n\Vert }{K\Vert w_n-u_n\Vert +\epsilon } = \frac{\phi \Vert w_n-u_n\Vert }{(K+\epsilon _1)\Vert w_n-u_n\Vert } =\frac{\phi }{N},\ \end{aligned}$$

where \(\epsilon =\epsilon _1\Vert w_n-u_n\Vert \) for some \(\epsilon _1\in (0,1)\) and \(N=K+\epsilon _1.\) Therefore, by the definition of \(\lambda _{n+1},\) the sequence \(\{\lambda _n\}\) has lower bound \(\min \{\frac{\phi }{N},\lambda _1\}\) and has upper bound \(\lambda _1 + \varPhi .\) By Lemma 2.12, the limit \(\lim \nolimits _{n\rightarrow \infty }\lambda _n\) exists and we denote by \(\lambda =\lim \nolimits _{n\rightarrow \infty }\lambda _n.\) Clearly, we have \(\lambda \in \big [\min \{\frac{\phi }{N},\lambda _1\},\lambda _1+\varPhi \big ]\). \(\square \)

Lemma 4.2

Suppose Conditions A and B hold. Let \(\{v_{n}\}\) be a sequence generated by Algorithm 3.1. Then, for all \(p\in \varGamma \), we have

$$\begin{aligned} \Vert v_{n}-p\Vert ^{2}\le \Vert w_{n}-p\Vert ^{2}-\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2, \end{aligned}$$
(4.1)

and

$$\begin{aligned} \Vert v_{n}-u_{n}\Vert \le \phi \frac{\lambda _{n}}{\lambda _{n+1}}\Vert w_{n}-u_{n}\Vert . \end{aligned}$$
(4.2)

Proof

By the definition of \(\{\lambda _{n}\}\), it is clear that

$$\begin{aligned} \Vert Aw_{n}-Au_{n}\Vert \le \frac{\phi }{\lambda _{n+1}}\Vert w_{n}-u_{n}\Vert ,\quad \forall n\in \mathbb {N}. \end{aligned}$$
(4.3)

The inequality (4.3) holds if \(Aw_{n}=Au_{n}\). If \(Aw_{n}\ne Au_{n},\) then

$$\begin{aligned} \lambda _{n+1}= \min \Big \{\frac{\phi \Vert w_{n}-u_{n}\Vert }{\Vert A w_{n}-Au_{n}\Vert },~ \lambda _{n}+\phi _n\Big \} \le \frac{\phi \Vert w_{n}-u_{n}\Vert }{\Vert A w_{n}-Au_{n}\Vert }, \end{aligned}$$

which implies that \(\Vert Aw_{n}-Au_{n}\Vert \le \frac{\phi }{\lambda _{n+1}}\Vert w_{n}-u_{n}\Vert .\) We therefore have that the inequality (4.3) holds when \(Aw_{n}=Au_{n}\) and \(Aw_{n}\ne Au_{n}.\)

Now, from the definition of \(\{v_n\}\) and by applying (4.3) and Lemma 2.3, we have

$$\begin{aligned} \Vert v_{n}-p\Vert ^{2}&=\Vert u_{n}-\lambda _{n}(Au_{n}-Aw_{n})-p\Vert ^{2}\nonumber \\&=\Vert u_{n}-p\Vert ^{2}+\lambda _{n}^{2}\Vert Au_{n}-Aw_{n}\Vert ^{2}-2\lambda _{n}\langle u_{n}-p, Au_{n}-Aw_{n}\rangle \nonumber \\&=\Vert w_{n}-p\Vert ^{2} +\Vert w_{n}-u_{n}\Vert ^{2} + 2 \langle u_{n}-w_{n}, w_{n}-p\rangle \nonumber \\&\quad + \lambda _{n}^{2}\Vert Au_{n}-Aw_{n}\Vert ^{2}-2\lambda _{n}\langle u_{n}-p, Au_{n}-Aw_{n}\rangle \nonumber \\&=\Vert w_{n}-p\Vert ^{2} +\Vert w_{n}-u_{n}\Vert ^{2} - 2 \langle u_{n}-w_{n}, u_{n}-w_{n}\rangle + 2\langle u_{n}-w_{n}, u_{n}-p \rangle \nonumber \\&\quad + \lambda _{n}^{2}\Vert Au_{n}-Aw_{n}\Vert ^{2}-2\lambda _{n}\langle u_{n}-p, Au_{n}-Aw_{n}\rangle \nonumber \\&=\Vert w_{n}-p\Vert ^{2} -\Vert w_{n}-u_{n}\Vert ^{2} + 2\langle u_{n}-w_{n}, u_{n}-p \rangle \nonumber \\&\quad + \lambda _{n}^{2}\Vert Au_{n}-Aw_{n}\Vert ^{2}-2\lambda _{n}\langle u_{n}-p, Au_{n}-Aw_{n}\rangle \nonumber \\&=\Vert w_{n}-p\Vert ^{2} -\Vert w_{n}-u_{n}\Vert ^{2} -2\langle w_{n}-u_{n}-\lambda _{n}(Aw_{n}-Au_{n}), u_{n}-p\rangle \nonumber \\&\quad +\lambda _{n}^{2}\Vert Au_{n}-Aw_{n}\Vert ^{2}\nonumber \\&\le \Vert w_{n}-p\Vert ^{2}-\left( 1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\right) \Vert w_{n}-u_{n}\Vert ^{2}\nonumber \\&\quad -2\langle w_{n}-u_{n}-\lambda _{n}(Aw_{n}-Au_{n}), u_{n}-p\rangle . \end{aligned}$$
(4.4)

Next, we show that

$$\begin{aligned} \langle w_{n}-u_{n}-\lambda _{n}(Aw_{n}-Au_{n}), u_{n}-p\rangle \ge 0. \end{aligned}$$
(4.5)

From \(u_{n}=(I+\lambda _{n}B)^{-1}(I-\lambda _{n}A)w_{n},\) we have \((I-\lambda _{n}A)w_{n} \in (I+\lambda _{n}B)u_{n}.\) Owing to the maximal monotonicity of B, we have that there exists \(t_{n}\in Bu_{n}\), such that

$$\begin{aligned} (I-\lambda _{n}A)w_{n}=u_{n}+\lambda _{n}t_{n}, \end{aligned}$$

which implies that

$$\begin{aligned} t_{n}=\frac{1}{\lambda _{n}}(w_{n}-u_{n}-\lambda _{n}Aw_{n}). \end{aligned}$$
(4.6)

Moreover, we have \(0\in (A+B)p\) and \(Au_{n}+t_{n}\in (A+B)u_{n}.\) Since \(A+B\) is maximal monotone, we have

$$\begin{aligned} \langle Au_{n}+t_{n}, u_{n}-p\rangle \ge 0. \end{aligned}$$
(4.7)

Applying (4.6) in (4.7), we obtain

$$\begin{aligned} \frac{1}{\lambda _{n}} \langle w_{n}-u_{n}-\lambda _{n}Aw_{n}+\lambda _{n}Au_{n}, u_{n}-p\rangle \ge 0, \end{aligned}$$

which gives

$$\begin{aligned} \langle w_{n}-u_{n}-\lambda _{n}(Aw_{n}-Au_{n}), u_{n}-p\rangle \ge 0. \end{aligned}$$

Consequently, by applying (4.5) in (4.4), we have

$$\begin{aligned} \Vert v_{n}-p\Vert ^{2}\le \Vert w_{n}-p\Vert ^{2}-\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2. \end{aligned}$$
(4.8)

Next, using the definition of \(v_{n}\) and inequality (4.3), we obtain

$$\begin{aligned} \Vert v_{n}-u_{n}\Vert \le \phi \frac{\lambda _{n}}{\lambda _{n+1}}\Vert w_{n}-u_{n}\Vert . \end{aligned}$$

This completes the proof of Lemma 4.2. \(\square \)

Lemma 4.3

Let \(\{x_{n}\}\) be the sequence generated by Algorithm 3.1. Then, \(\{x_{n}\}\) is bounded.

Proof

Let \(p\in \varGamma .\) Using the definition of \(w_{n}\) and the triangle inequality, we have

$$\begin{aligned} \Vert w_{n}-p\Vert&=\Vert x_{n}+\theta _{n}(x_{n}-x_{n-1})-p\Vert \nonumber \\&\le \Vert x_{n}-p\Vert +\theta _{n}\Vert x_{n}-x_{n-1}\Vert \nonumber \\&=\Vert x_{n}-p\Vert +\alpha _{n}\frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}.\Vert . \end{aligned}$$
(4.9)

From Remark 3.2, we have that \(lim_{n\rightarrow \infty }\frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert =0\). It follows that there exists a constant \(M>0\), such that

$$\begin{aligned} \frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert \le M \quad \forall n\ge 1. \end{aligned}$$

Thus, from (4.9), we get

$$\begin{aligned} \Vert w_{n}-p\Vert \le \Vert x_{n}-p\Vert +\alpha _{n}M. \end{aligned}$$
(4.10)

Since \(\lim \nolimits _{n\rightarrow \infty }\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )=1-\phi ^{2}>0,\) there exists \(n_{0}\in \mathbb {N}\), such that \(\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )>0\) for all \(n\ge n_{0}.\)

Thus, from (4.1), we get

$$\begin{aligned} \Vert v_{n}-p\Vert ^{2}\le \Vert w_{n}-p\Vert ^{2}\quad \forall n\ge n_{0}. \end{aligned}$$
(4.11)

Using the definition of \(z_{n}\) in the algorithm, (4.11) and Remark 3.3, we have

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2}&=\Vert (1-\sigma _{n})v_{n}+\sigma _{n}S_{\alpha }v_{n}-p\Vert ^{2}\nonumber \\&=\Vert (1-\sigma _{n})(v_{n}-p)+\sigma _{n}(S_{\alpha }v_{n}-p)\Vert ^{2}\nonumber \\&=(1-\sigma _{n})\Vert v_{n}-p\Vert ^{2}+\sigma _{n}\Vert S_{\alpha }v_{n}-p\Vert ^{2}-(1-\sigma _{n})\sigma _{n}\Vert S_{\alpha }v_{n}-v_{n}\Vert ^{2}\nonumber \\&\le (1-\sigma _{n})\Vert v_{n}-p\Vert ^{2}+\sigma _{n}\Vert v_{n}-p\Vert ^{2}-(1-\sigma _{n})\sigma _{n}\Vert S_{\alpha }v_{n}-v_{n}\Vert ^{2}\nonumber \\&\le \Vert w_{n}-p\Vert ^{2}-(1-\sigma _{n})\sigma _{n}\Vert S_{\alpha }v_{n}-v_{n}\Vert ^{2}\end{aligned}$$
(4.12)
$$\begin{aligned}&\le \Vert w_{n}-p\Vert ^{2}. \end{aligned}$$
(4.13)

Now, using (4.10), (4.11), and (4.13) together with Remark 3.3, we have for all \(n\ge n_{0}\)

$$\begin{aligned} \Vert x_{n+1}-p\Vert&=\Vert \alpha _{n}f(w_{n})+\delta _{n}S_{\alpha }v_{n}+\xi _{n}T_{\beta }z_{n}-p\Vert .\nonumber \\&=\Vert \alpha _{n}(f(w_{n})-f(p))+\alpha _{n}(f(p)-p)+\delta _{n}(S_{\alpha }v_{n}-p)+\xi _{n}(T_{\beta }z_{n}-p)\Vert .\nonumber \\&\le \alpha _n\rho ||w_n-p|| + \alpha _n||f(p)-p|| + \delta _n||v_n-p|| + \xi _n||z_n-p||\\&\le \alpha _n\rho (\Vert x_{n}-p\Vert +\alpha _{n}M) + \alpha _n||f(p)-p|| + \delta _n(||x_n - p|| + \alpha _nM) \\&\qquad + \xi _n(||x_n - p|| + \alpha _nM)\\&=(\alpha _n\rho +(1-\alpha _n))||x_n-p|| + \alpha _n||f(p)-p|| + (\alpha _n\rho +(1-\alpha _n))\alpha _nM\\&=(1-\alpha _n(1-\rho ))||x_n-p|| + \alpha _n(1-\rho )\Big \{\frac{||f(p)-p||}{1-\rho } + \frac{(1-\alpha _n(1-\rho ))M}{1-\rho } \Big \}\\&\le (1-\alpha _n(1-\rho ))||x_n-p|| + \alpha _n(1-\rho )\Big \{\frac{||f(p)-p||}{1-\rho } + \frac{M}{1-\rho } \Big \}\\&\le \max \Big \{||x_n-p||, \frac{||f(p)-p||+M}{1-\rho }\Big \}\\&\qquad \vdots \\&\le \max \Big \{||x_{n_0}-p||, \frac{||f(p)-p||+M}{1-\rho }\Big \}. \end{aligned}$$

This shows that the sequence \(\{x_{n}\}\) is bounded. Thus, sequences \(\{w_{n}\}, \{u_{n}\}, \{v_{n}\},\) and \(\{z_{n}\}\) are all bounded. \(\square \)

Lemma 4.4

The following inequality holds for all \(p\in \varGamma :\)

$$\begin{aligned} ||x_{n+1} - p||^2&\le \Big (1 - \frac{2\alpha _n(1 - \rho )}{(1-\alpha _n\rho )}\Big )||x_n - p||^2 + \frac{2\alpha _n(1 - \rho )}{(1-\alpha _n\rho )}\nonumber \\&\quad \Big \{\frac{\alpha _n}{2(1 - \rho )}M_{2} + \frac{3M_1((1-\alpha _n)^2+ \alpha _n\rho )}{2(1 - \rho )} \frac{\theta _n}{\alpha _n}||x_n - x_{n-1}||\nonumber \\&\quad + \frac{1}{(1 - \rho )}\langle f(p) - p, x_{n+1} -p\rangle \Big \}\nonumber \\&\quad - \frac{\delta _{n} (1-\alpha _n)}{(1-\alpha _n\rho )} \Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\nonumber \\&\quad -\frac{\xi _{n}(1-\alpha _{n})\sigma _{n}(1-\sigma _{n})}{(1-\alpha _n\rho )} \Vert S_\alpha v_{n}-v_{n}\Vert ^{2}. \end{aligned}$$

Proof

Using Cauchy–Schwarz inequality and Lemma 2.3, we have

$$\begin{aligned} \Vert w_n-p\Vert ^2&=\Vert x_n + \theta _n(x_n-x_{n-1})-p\Vert ^2\nonumber \\&=\Vert x_n-p\Vert ^2 + \theta _n^2\Vert x_n -x_{n-1}\Vert ^2 + 2 \theta _n \langle x_n - p, x_n - x_{n-1}\rangle \nonumber \\&\le \Vert x_n-p\Vert ^2 + \theta _n^2\Vert x_n - x_{n-1}\Vert ^2 + 2\theta _n \Vert x_n - x_{n-1}\Vert \Vert x_n-p\Vert \nonumber \\&=\Vert x_n-p\Vert ^2 + \theta _n \Vert x_n-x_{n-1}\Vert (\theta _n\Vert x_n-x_{n-1}\Vert +2\Vert x_n -p\Vert )\nonumber \\&\le \Vert x_n - p\Vert ^2 + 3 M_1 \theta _n \Vert x_n - x_{n-1}\Vert \nonumber \\&=\Vert x_n-p\Vert ^2 + 3M_1 \alpha _n \frac{\theta _n}{\alpha _n}\Vert x_n - x_{n-1}\Vert , \end{aligned}$$
(4.14)

where \(M_1:=\sup \{\Vert x_n-p\Vert , \theta _n\Vert x_n-x_{n-1}\Vert \}>0.\)

By applying Lemma 2.3, (4.1), (4.12), and (4.14), we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _n f(w_n)+ \delta _{n}S_{\alpha }v_{n} + \xi _{n}T_{\beta }z_{n}-p\Vert ^{2}\nonumber \\&\le \Vert \delta _{n}(S_{\alpha }v_{n}-p)+\xi _{n}(T_{\beta }z_{n}-p)\Vert ^{2}+2\alpha _{n}\langle f (w_{n})-p, x_{n+1}-p\rangle \\&\le \delta _{n}^{2}\Vert S_{\alpha }v_{n}-p\Vert ^{2}+\xi _{n}^{2}\Vert T_{\beta }z_{n}-p\Vert ^{2}+2\delta _{n}\xi _{n}\Vert S_{\alpha }v_{n}-p\Vert \Vert T_{\beta }z_{n}-p\Vert \nonumber \\&\quad +2\alpha _{n}\langle f(w_{n})-p, x_{n+1}-p\rangle \nonumber \\&\le \delta _{n}^{2}\Vert S_{\alpha }v_{n}-p\Vert ^{2}+\xi _{n}^{2}\Vert T_{\beta }z_{n}-p\Vert ^{2}+\delta _{n}\xi _{n}(\Vert S_{\alpha }v_{n}-p\Vert ^{2}\nonumber \\&\quad +\Vert T_{\beta }z_{n}-p\Vert ^{2})+2\alpha _{n}\langle f(w_{n})-p, x_{n+1}-p\rangle \nonumber \\&=\delta _{n}(\delta _{n}+\xi _{n})\Vert S_{\alpha }v_{n}-p\Vert ^{2}+\xi _{n}(\xi _{n}+\delta _{n})\Vert T_{\beta }z_{n}-p\Vert ^{2}\nonumber \\&\quad +2\alpha _{n}\langle f(w_{n})-p, x_{n+1}-p\rangle \nonumber \\&\le \delta _{n}(1-\alpha _{n})\Vert v_{n}-p\Vert ^{2}+\xi _{n}(1-\alpha _{n})\Vert z_{n}-p\Vert ^{2}\nonumber \\&\quad +2\alpha _{n}\langle f(w_{n})-f(p), x_{n+1}-p\rangle + 2 \alpha _{n}\langle f(p)-p, x_{n+1}-p\rangle \nonumber \\&\le \delta _{n} (1-\alpha _n)\Big (\Vert w_{n}-p\Vert ^{2}-\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\Big )\nonumber \\&\quad +\xi _{n}(1-\alpha _{n})\big (\Vert w_{n}-p\Vert ^{2} -\sigma _{n}(1-\sigma _{n})\Vert S_{\alpha }v_{n}-v_{n}\Vert ^{2}\big )\nonumber \\&\quad +2\alpha _{n}\langle f(w_{n})-f(p), x_{n+1}-p\rangle +2\alpha _{n} \langle f(p)-p, x_{n+1}-p\rangle \nonumber \\&\le \delta _{n} (1-\alpha _n)\Big (\Vert w_{n}-p\Vert ^{2}-\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\Big )\nonumber \\&\quad +\xi _{n}(1-\alpha _{n})\big (\Vert w_{n}-p\Vert ^{2}\nonumber \\&\quad -\sigma _{n}(1-\sigma _{n})\Vert S_{\alpha }v_{n}-v_{n}\Vert ^{2}\big )\nonumber \\&\quad +2\alpha _{n} \rho \Vert w_{n}-p\Vert \Vert x_{n+1}-p\Vert + 2\alpha _{n} \langle f(p)-p, x_{n+1}-p\rangle \nonumber \\&\le (1-\alpha _{n})^{2}(\Vert x_{n}-p\Vert ^{2}+3M_{1}\alpha _{n}\frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert )\nonumber \\&\quad -\delta _{n} (1-\alpha _n )\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\nonumber \\&\quad -\xi _{n}(1-\alpha _{n})\sigma _{n}(1-\sigma _{n})\Vert S_{\alpha }v_{n}-v_{n}\Vert ^{2}\nonumber \\&\quad +2\alpha _{n}\rho \Vert w_{n}-p\Vert \Vert x_{n+1}-p\Vert +2\alpha _{n}\langle f(p)-p, x_{n+1}-p\rangle \nonumber \\&\le (1-\alpha _{n})^{2}(\Vert x_{n}-p\Vert ^{2}+3M_{1}\alpha _{n}\frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert )\nonumber \\&\quad -\delta _{n} (1-\alpha _n )\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\nonumber \\&\quad -\xi _{n}(1-\alpha _{n})\sigma _{n}(1-\sigma _{n})\Vert S_{\alpha }v_{n}-v_{n}\Vert ^{2}+\alpha _{n}\rho (\Vert w_{n}-p\Vert ^{2}\nonumber \\&\quad +\Vert x_{n+1}-p\Vert ^{2})+2\alpha _{n}\langle f(p)-p, x_{n+1}-p\rangle \\&\le (1-\alpha _{n})^{2}(\Vert x_{n}-p\Vert ^{2}+3M_{1}\alpha _{n}\frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert )\nonumber \\&\quad -\delta _{n} (1-\alpha _n )\Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\nonumber \\&\quad -\xi _{n}(1-\alpha _{n})\sigma _{n}(1-\sigma _{n})\Vert S_\alpha v_{n}-v_{n}\Vert ^{2}+\alpha _{n}\rho (\Vert x_{n}-p\Vert ^{2}\nonumber \\&\quad +3M_{1}\alpha _{n}\frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert \nonumber \\&\quad +\Vert x_{n+1}-p\Vert ^{2})\\&\quad +2\alpha _{n}\langle f(p)-p, x_{n+1}-p\rangle . \end{aligned}$$

Consequently, this leads to

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&\le \frac{(1-2\alpha _n + (\alpha _n)^2+\alpha _n \rho )}{(1-\alpha _n \rho )}\Vert x_n - p\Vert ^2 \\&\quad + \frac{3M_1((1-\alpha _n)^2+\alpha _n\rho )}{(1-\alpha _n \rho )} \alpha _n \frac{\theta _n}{\alpha _n}\Vert x_n - x_{n-1}\Vert \\&\quad + \frac{2\alpha _n}{(1-\alpha _n\rho )} \langle f(p)-p, x_{n+1}-p \rangle \\&\quad - \frac{\delta _{n} (1-\alpha _n)}{(1-\alpha _n\rho )} \Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\nonumber \\&\quad -\frac{\xi _{n}(1-\alpha _{n})\sigma _{n}(1-\sigma _{n})}{(1-\alpha _n\rho )} \Vert S_\alpha v_{n}-v_{n}\Vert ^{2}\\&= \frac{(1-2\alpha _n +\alpha _n \rho )}{(1-\alpha _n\rho )}\Vert x_n - p\Vert ^2 + \frac{(\alpha _n)^2}{(1-\alpha _n\rho )}\Vert x_n -p\Vert ^2 \\&\quad +\frac{3M_1((1-\alpha _n)^{2}+\alpha _n \rho )}{(1-\alpha _n \rho )} \alpha _n \frac{\theta _n}{\alpha _n}\Vert x_n - x_{n-1}\Vert \nonumber \\&\quad + \frac{2\alpha _n}{(1-\alpha _n\rho )} \langle f(p)-p, x_{n+1}-p \rangle \\&\quad - \frac{\delta _{n} (1-\alpha _n)}{(1-\alpha _n\rho )} \Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\nonumber \\&\quad -\frac{\xi _{n}(1-\alpha _{n})\sigma _{n}(1-\sigma _{n})}{(1-\alpha _n\rho )} \Vert S_\alpha v_{n}-v_{n}\Vert ^{2}\\&\le \Big (1 - \frac{2\alpha _n(1 - \rho )}{(1-\alpha _n\rho )}\Big )||x_n - p||^2 + \frac{2\alpha _n(1 - \rho )}{(1-\alpha _n\rho )}\Big \{\frac{\alpha _n}{2(1 - \rho )}M_{2} \\&\quad + \frac{3M_1((1-\alpha _n)^2+ \alpha _n\rho )}{2(1 - \rho )} \frac{\theta _n}{\alpha _n}||x_n - x_{n-1}||\nonumber \\&\quad + \frac{1}{(1 - \rho )}\langle f(p) - p, x_{n+1} -p\rangle \Big \}\\&\quad - \frac{\delta _{n} (1-\alpha _n)}{(1-\alpha _n\rho )} \Big (1-\phi ^{2}\frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-u_{n}\Vert ^2\nonumber \\&\quad -\frac{\xi _{n}(1-\alpha _{n})\sigma _{n}(1-\sigma _{n})}{(1-\alpha _n\rho )} \Vert S_\alpha v_{n}-v_{n}\Vert ^{2}, \end{aligned}$$

where \(M_2:= \sup \{\Vert x_n -p\Vert ^2: n\in \mathbb {N}\}.\) We have, therefore, obtained the required inequality. \(\square \)

Lemma 4.5

Suppose \(\{w_n\}\) and \(\{u_n\}\) are two sequences generated by Algorithm 3.1 under Conditions A and B, such that \(\lim \nolimits _{j \rightarrow \infty }\Vert w_{n_j}-u_{n_j}\Vert =0\) for some subsequences \(\{w_{n_j}\}\) and \(\{u_{n_j}\}\) of \(\{w_n\}\) and \(\{u_n\},\) respectively. If \(\{w_{n_j}\}\) converges weakly to some \(x^*\in H\) as \(j\rightarrow \infty ,\) then \(x^*\in (A+B)^{-1}(0).\)

Proof

Let \((u,v)\in G(A+B),\) that is, \(v-Au\in Bu.\) Since

$$\begin{aligned} u_{n_j}=(I+\lambda _{n_j}B)^{-1}(I-\lambda _{n_j}A)w_{n_j}, \end{aligned}$$

we have

$$\begin{aligned} (I-\lambda _{n_j}A)w_{n_j}\in (I+\lambda _{n_j}B)u_{n_j}. \end{aligned}$$

From this, we obtain

$$\begin{aligned} \frac{1}{\lambda _{n_j}}\Big (w_{n_j}-u_{n_j}-\lambda _{n_j}Aw_{n_j}\Big )\in Bu_{n_j}. \end{aligned}$$

Since B is maximal monotone, we get

$$\begin{aligned} \left\langle u-u_{n_j},~~~ v-Au-\frac{1}{\lambda _{n_j}}\Big (w_{n_j}-u_{n_j}-\lambda _{n_j}Aw_{n_j}\Big )\right\rangle \ge 0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \left\langle u-u_{n_j},~~v\right\rangle -\left\langle u-u_{n_j},~~~ Au+\frac{1}{\lambda _{n_j}}\Big (w_{n_j}-u_{n_j}-\lambda _{n_j}Aw_{n_j}\Big )\right\rangle&\ge 0. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \left\langle u-u_{n_j},~~v\right\rangle&\ge \left\langle u-u_{n_j},~~~ Au+\frac{1}{\lambda _{n_j}}\Big (w_{n_j}-u_{n_j}-\lambda _{n_j}Aw_{n_j}\Big )\right\rangle \\&=\left\langle u-u_{n_j},~~Au-Aw_{n_j}\right\rangle +\left\langle u-u_{n_j},~~~\frac{1}{\lambda _{n_j}}(w_{n_j}-u_{n_j})\right\rangle \\&=\left\langle u-u_{n_j},~~Au-Au_{n_j}\right\rangle +\left\langle u-u_{n_j},~~Au_{n_j}-Aw_{n_j}\right\rangle \\&\quad +\left\langle u-u_{n_j},~~~\frac{1}{\lambda _{n_j}}(w_{n_j}-u_{n_j})\right\rangle \\&\ge \left\langle u-u_{n_j},~~Au_{n_j}-Aw_{n_j}\right\rangle +\left\langle u-u_{n_j},~~~\frac{1}{\lambda _{n_j}}(w_{n_j}-u_{n_j})\right\rangle . \end{aligned}$$

Since \(\lim \nolimits _{j \rightarrow \infty }\Vert w_{n_j}-u_{n_j}\Vert =0,\) by the continuity of A, we have \(\lim \nolimits _{j\rightarrow \infty }\Vert Aw_{n_j}-Au_{n_j}\Vert =0.\) Furthermore, since \(\lim \nolimits _{n \rightarrow \infty }\lambda _n=\lambda >0,\) we obtain

$$\begin{aligned} \left\langle u-x^*,~~v\right\rangle =\lim \limits _{j\rightarrow \infty }\left\langle u-u_{n_j},~~~v\right\rangle \ge 0. \end{aligned}$$

This together with the maximal monotonicity of \(A+B\) gives \(x^*\in (A+B)^{-1}(0)\) as required. \(\square \)

Theorem 4.6

Let \(\{x_{n}\}\) be the sequence generated by Algorithm 3.1, such that Conditions (A) and (B) are satisfied. Then, \(\{x_{n}\}\) converges strongly to a point \(\bar{x}\in \varGamma \), where \(\bar{x}=P_\varGamma \circ f(\bar{x}).\)

Proof

By definition of \(x_{n+1},\) and by applying Lemma 2.3 (iv), Remark 3.3, (4.11), (4.13), and (4.14), we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _{n} f (w_{n}) + \delta _{n}S_{\alpha }v_{n}+\xi _{n}T_{\beta }z_{n}-p\Vert ^2\nonumber \\&\le \alpha _{n}\Vert f (w_{n})-p\Vert ^2 + \delta _{n}\Vert S_{\alpha }v_{n}-p\Vert ^2 +\xi _{n}\Vert T_{\beta }z_{n}-p\Vert ^2\nonumber \\&\quad -\delta _{n}\xi _{n}\Vert S_{\alpha }v_{n}-T_{\beta }z_{n}\Vert ^2\nonumber \\&\le \alpha _{n}\Vert f (w_{n})-p\Vert ^2 + \delta _{n}\Vert v_{n}-p\Vert ^2 +\xi _{n}\Vert z_{n}-p\Vert ^2\nonumber \\&\quad -\delta _{n}\xi _{n}\Vert S_{\alpha }v_{n}-T_{\beta }z_{n}\Vert ^2\nonumber \\&\le \alpha _{n}\Vert f (w_{n})-p\Vert ^2 + \delta _{n}\Vert w_{n}-p\Vert ^2 +\xi _{n}\Vert w_{n}-p\Vert ^2\nonumber \\&\quad -\delta _{n}\xi _{n}\Vert S_{\alpha }v_{n}-T_{\beta }z_{n}\Vert ^2\nonumber \\&\le \alpha _{n}\Vert f (w_{n})-p\Vert ^2 + (1-\alpha _{n})\Big (\Vert x_n-p\Vert ^2 + 3M_1 \alpha _n \frac{\theta _n}{\alpha _n}\Vert x_n - x_{n-1}\Vert \Big ) \nonumber \\&\quad -\delta _{n}\xi _{n}\Vert S_{\alpha }v_{n}-T_{\beta }z_{n}\Vert ^2\nonumber \\&=(1-\alpha _{n})\Vert x_n-p\Vert ^2 +\alpha _{n}\nonumber \\&\quad \times \Big (\Vert f (w_{n})-p\Vert ^2 + 3M_1(1-\alpha _{n}) \frac{\theta _n}{\alpha _n}\Vert x_n - x_{n-1}\Vert \Big )\nonumber \\&\quad -\delta _{n}\xi _{n}\Vert S_{\alpha }v_{n}-T_{\beta }z_{n}\Vert ^2. \end{aligned}$$
(4.15)

Next, let \(\bar{x}=P_\varGamma \circ f(\bar{x}).\) From Lemma 4.4, we obtain

$$\begin{aligned} ||x_{n+1} -\bar{x}||^2&\le \Big (1 - \frac{2\alpha _n(1-\rho )}{(1-\alpha _n\rho )}\Big )||x_n - \bar{x}||^2 + \frac{2\alpha _n(1-\rho )}{(1-\alpha _n\rho )}\Big \{\frac{\alpha _n}{2(1-\rho )}M_{2}.\nonumber \\&~~ + \frac{3M_1((1-\alpha _n)^2+ \alpha _n\rho )}{2(1 - \rho )}\frac{\theta _n}{\alpha _n}||x_n - x_{n-1}|| + \frac{1}{(1 -\rho )}\langle f(\bar{x}) - \bar{x}, x_{n+1} -\bar{x}\rangle \Big \}. \end{aligned}$$
(4.16)

Now, we claim that the sequence \(\{\Vert x_n-\bar{x}\Vert \}\) converges to zero. By Lemma 2.13, it suffices to show that \(\limsup \limits _{k\rightarrow \infty }\langle f(\bar{x}) - \bar{x}, x_{n_k+1} -\bar{x} \rangle \le 0\) for every subsequence \(\{\Vert x_{n_k} - \bar{x}\Vert \}\) of \(\{\Vert x_n - \bar{x}\Vert \}\) satisfying

$$\begin{aligned} \liminf _{k\rightarrow \infty }(\Vert x_{n_k+1} - \bar{x}\Vert - \Vert x_{n_k} - \bar{x}\Vert ) \ge 0. \end{aligned}$$
(4.17)

Suppose \(\{\Vert x_{n_k} - \bar{x}\Vert \}\) is a subsequence of \(\{\Vert x_n - \bar{x}\Vert \}\), such that (4.17) holds. From Lemma 4.4, we have

$$\begin{aligned}&\frac{\delta _{n_k} (1-\alpha _{n_k})}{(1-\alpha _{n_k}\rho )} \Big (1-\phi ^{2}\frac{\lambda _{n_k}^{2}}{\lambda _{{n_k}+1}^{2}}\Big )\Vert w_{n_k}-u_{n_k}\Vert ^2+\frac{\xi _{n_k}(1-\alpha _{n_k})\sigma _{n_k}(1-\sigma _{n_k})}{(1-\alpha _{n_k}\rho )} \Vert S_\alpha v_{n_k}-v_{n_k}\Vert ^{2}\\&\quad \le \Big (1 - \frac{2\alpha _{n_k}(1 - \rho )}{(1-\alpha _{n_k}\rho )}\Big )||x_{n_k} - p||^2 - ||x_{{n_k}+1} - p||^2 + \frac{2\alpha _{n_k}(1 - \rho )}{(1-\alpha _{n_k}\rho )}\Big \{\frac{\alpha _{n_k}}{2(1 - \rho )}M_{2}\nonumber \\&\quad \quad + \frac{3M_1((1-\alpha _{n_k})^2+ \alpha _{n_k}\rho )}{2(1 - \rho )} \frac{\theta _{n_k}}{\alpha _{n_k}}||x_{n_k} - x_{{n_k}-1}|| + \frac{1}{(1 - \rho )}\langle f(p) - p, x_{{n_k}+1} -p\rangle \Big \}. \end{aligned}$$

Using (4.17) and the fact that \(\lim _{k\rightarrow \infty }\alpha _{n_k}=0,\) we have

$$\begin{aligned}{} & {} \frac{\delta _{n_k} (1-\alpha _{n_k})}{(1-\alpha _{n_k}\rho )} \Big (1-\phi ^{2}\frac{\lambda _{n_k}^{2}}{\lambda _{{n_k}+1}^{2}}\Big )\Vert w_{n_k}-u_{n_k}\Vert ^2\rightarrow 0;\quad \\{} & {} \frac{\xi _{n_k}(1-\alpha _{n_k})\sigma _{n_k}(1-\sigma _{n_k})}{(1-\alpha _{n_k}\rho )} \Vert S_\alpha v_{n_k}-v_{n_k}\Vert ^{2}\rightarrow 0. \end{aligned}$$

Consequently, by the conditions on the control parameters, we get

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert w_{n_k}-u_{n_k}\Vert \rightarrow 0,\quad k\rightarrow \infty ,\quad \Vert S_\alpha v_{n_k}-v_{n_k}\Vert \rightarrow 0,\quad k\rightarrow \infty . \end{aligned}$$
(4.18)

Similarly, from (4.15), we have

$$\begin{aligned}{} & {} \delta _{n_k}\xi _{n_k}\Vert S_{\alpha }v_{n_k}-T_{\beta }z_{n_k}\Vert ^2\le (1-\alpha _{n_k})\Vert x_{n_k}-p\Vert ^2 - \Vert x_{{n_k}+1}-p\Vert ^2 +\alpha _{n_k}\\{} & {} \quad \Big (\Vert f (w_{n_k})-p\Vert ^2 + 3M_1(1-\alpha _{n_k}) \frac{\theta _{n_k}}{\alpha _{n_k}}\Vert x_{n_k} - x_{n_k-1}\Vert \Big ). \end{aligned}$$

Again, applying (4.17) and the fact that \(\lim _{k\rightarrow \infty }\alpha _{n_k}=0,\) we have

$$\begin{aligned} \Vert S_{\alpha }v_{n_k}-T_{\beta }z_{n_k}\Vert \rightarrow 0\quad k\rightarrow \infty . \end{aligned}$$
(4.19)

By Remark 3.2, we obtain

$$\begin{aligned} \Vert w_{n_k}-x_{n_k}\Vert =\theta _{n_k}\Vert x_{n_k}-x_{n_k-1}\Vert \rightarrow 0,\quad k\rightarrow \infty . \end{aligned}$$
(4.20)

Applying (4.18) and (4.20) gives

$$\begin{aligned} \Vert x_{n_k}-u_{n_k}\Vert \rightarrow 0,~~k\rightarrow \infty ,~~ \Vert v_{n_k}-x_{n_k}\Vert \rightarrow 0,~~ k\rightarrow \infty . \end{aligned}$$
(4.21)

By inequality (4.2) and applying (4.18), we have

$$\begin{aligned} \Vert v_{n_k}-u_{n_k}\Vert \le \phi \frac{\lambda _{n_k}}{\lambda _{n_k}+1}\Vert w_{n_k} -u_{n_k}\Vert \rightarrow 0,~~k\rightarrow \infty . \end{aligned}$$
(4.22)

From the definition of \(z_n\) and by applying (4.18), we have

$$\begin{aligned} \Vert z_{n_k}-v_{n_k}\Vert&=\Vert (1-\sigma _{n_k})v_{n_k}+\sigma _{n_k}S_{\alpha }v_{n_k}-v_{n_k}\Vert \nonumber \\&\le (1-\sigma _{n_k})\Vert v_{n_k}-v_{n_k}\Vert +\sigma _{n_k}\Vert S_{\alpha }v_{n_k}-v_{n_k}\Vert \rightarrow 0,\quad k\rightarrow \infty . \end{aligned}$$
(4.23)

Using (4.18)–(4.23), we obtain

$$\begin{aligned}{} & {} \Vert T_\beta z_{n_k}-z_{n_k}\Vert \rightarrow 0;\quad \Vert x_{n_k}-z_{n_k}\Vert \rightarrow 0;\quad \Vert x_{n_k}-v_{n_k}\Vert \rightarrow 0;\quad \nonumber \\{} & {} \Vert S_{\alpha }v_{n_k}-x_{n_k}\Vert \rightarrow 0;\quad \Vert T_\beta z_{n_k}-x_{n_k}\Vert \rightarrow 0. \end{aligned}$$
(4.24)

Now, using (4.24) together with the fact that \(\lim \nolimits _{k\rightarrow \infty } \alpha _{n_k}=0,\) we have

$$\begin{aligned} \Vert x_{{n_k}+1}-x_{n_k}\Vert&=\Vert \alpha _{n_k} f (w_{n_k}) + \delta _{n_k}S_{\alpha }v_{n_k}+\xi _{n_k}T_{\beta }z_{n_k}-x_{n_k}\Vert \nonumber \\&\le \alpha _{n_k}\Vert f(w_{n_k}) -x_{n_k}\Vert + \delta _{n_k}\Vert S_{\alpha }v_{n_k}-x_{n_k}\Vert \nonumber \\&\quad +\xi _{n_k}\Vert T_{\beta }z_{n_k}-x_{n_k}\Vert \rightarrow 0,\quad k\rightarrow \infty . \end{aligned}$$
(4.25)

Since \(\{x_n\}\) is bounded, then \(w_\omega (x_n)\) is nonempty. Let \(x^*\in w_\omega (x_n)\) be an arbitrary element. Then, there exists a subsequence \(\{x_{n_k}\}\) of \(\{x_n\}\), such that \(x_{n_k}\rightharpoonup x^*\) as \(k\rightarrow \infty .\) By (4.20), we have \(w_{n_k}\rightharpoonup x^*\) as \(k\rightarrow \infty .\) Now, by invoking Lemma 4.5 and applying (4.18), we have \(x^*\in (A+B)^{-1}(0)\)

$$\begin{aligned} x^*\in (A+B)^{-1}(0). \end{aligned}$$
(4.26)

Moreover, by (4.24), we have \(v_{n_k}\rightharpoonup x^*\) as \(k\rightarrow \infty \) and we have \(z_{n_k}\rightharpoonup x^*\) as \(k\rightarrow \infty .\) Since \(I-S\alpha \) and \(I-T\beta \) are demiclosed at zero, then by Remark 3.3, (4.18) and (4.24), we have

$$\begin{aligned} x^*\in F(S_\alpha )=F(S)\quad \text {and}\quad x^*\in F(T_\beta )=F(T). \end{aligned}$$
(4.27)

Since \(x^*\in w_\omega (x_n)\) is arbitrary, it follows from (4.26) and (4.27) that:

$$\begin{aligned} w_\omega (x_n)\subset \varGamma . \end{aligned}$$

Moreover, by the boundedness of \(\{x_{n_k}\}\), there exists a subsequence \(\{x_{n_{k_j}}\}\) of \(\{x_{n_k}\}\), such that \(x_{n_{k_j}}\rightharpoonup x^\dagger \) and

$$\begin{aligned} \lim _{j\rightarrow \infty }\langle f(\bar{x}) - \bar{x}, x_{n_{k_j}} -\bar{x} \rangle = \limsup _{k\rightarrow \infty }\langle f(\bar{x}) - \bar{x}, x_{n_k} -\bar{x} \rangle . \end{aligned}$$

Since \(\bar{x}=P_\varGamma \circ f(\bar{x}),\) it follows that:

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle f(\bar{x}) - \bar{x}, x_{n_k} -\bar{x} \rangle = \lim _{j\rightarrow \infty }\langle f(\bar{x}) - \bar{x}, x_{n_{k_j}} -\bar{x} \rangle = \langle f(\bar{x}) - \bar{x}, x^\dagger -\bar{x} \rangle \le 0.\nonumber \\ \end{aligned}$$
(4.28)

From (4.25) and (4.28), we get

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle f(\bar{x}) - \bar{x}, x_{n_k+1} -\bar{x} \rangle = \limsup _{k\rightarrow \infty }\langle f(\bar{x}) - \bar{x}, x_{n_k} -\bar{x} \rangle = \langle f(\bar{x}) - \bar{x}, x^\dagger -\bar{x} \rangle \le 0.\nonumber \\ \end{aligned}$$
(4.29)

Applying Lemma 2.13 to (4.16), and using (4.29) together with the fact that \(\lim _{n\rightarrow \infty }\frac{\theta _n}{\alpha _n}||x_n - x_{n-1}|| =0\) and \(\lim _{n\rightarrow \infty }\alpha _n = 0,\) we obtain \(\lim _{n\rightarrow \infty }||x_n - \bar{x}||=0\) as required. \(\square \)

5 Application

In this section, we apply our result to study other optimization problems.

5.1 Variational inequality and common fixed point problems

Let \(A:C\rightarrow H\) be a nonlinear mapping where C is a nonempty closed convex subset of real Hilbert space H. The variational inequality problem (see [2, 18]) is to find \(\hat{x}\in C\), such that

$$\begin{aligned} \langle y-\hat{x}, A\hat{x}\rangle \ge 0,\quad \forall y\in C. \end{aligned}$$
(5.1)

Let the set of solutions of the problem (5.1) be denoted by VI(C, A). It is known that if A is continuous and monotone, then VI(C, A) is closed and convex (see [8, 31]). Recall that the indicator function of C is defined by

$$\begin{aligned} i_{C}(x)= {\left\{ \begin{array}{ll} 0, &{}\text {if} ~~x\in C,\\ \infty ,&{}\text {if}~~ x \notin C. \end{array}\right. } \end{aligned}$$

It is known that \(i_{C}\) is a proper lower semicontinuous and convex function with its subdifferential \(\partial {i_C}\) being maximal monotone (see [43]). Moreover, from [5], it is know that

$$\begin{aligned} \partial {i_C}(v)=N_{C}(v)=\{u \in H: \langle y-v, u \rangle \le 0\quad \forall y \in C \}, \end{aligned}$$

where \(N_{C}\) is the normal cone of C at a point v. Hence, the resolvent of \(\partial {i_C}\) can be defined for \(\lambda >0\) by

$$\begin{aligned} J_{\lambda }^{\partial {i_C}}(x) = (I+ \lambda \partial {i_C})^{-1}x,\quad \forall x\in H. \end{aligned}$$

It is shown in [48] that for any \(x\in H\) and \(z \in C,\quad z=J_{\lambda }^{\partial {i_C}}(x) \iff z=P_C(x)\), where \(P_C\) is the metric projection from H onto C.

Lemma 5.1

[44] Let C be a nonempty, closed, and convex subset of a Banach space E. Suppose \(A:C\rightarrow E^*\) is a monotone and hemicontinuous operator and \(T:E\rightarrow 2^{E^*}\) is an operator defined by

$$\begin{aligned} P(v) = {\left\{ \begin{array}{ll} Av + N_C(v),&{}\quad \text {if}~~ v\in C,\\ \emptyset ,&{}\quad \text {if}~~ v\notin C. \end{array}\right. } \end{aligned}$$

Then, P is maximal monotone and \(P^{-1}0 = VI(C,A).\)

Now, by setting \(B=\partial _{i_C}\) in Theorem 4.6, we obtain the following result for approximating the common solution of variational inequality problem and common fixed points of strict-pseudocontractions in Hilbert spaces.

Theorem 5.2

Let \(\{x_{n}\}\) be a sequence generated by the following algorithm, such that other conditions of Theorem 4.6 hold. Suppose that the solution set \(\varOmega =F(S)\cap F(T)\cap VI(C,A)\ne \emptyset .\) Then, \(\{x_{n}\}\) converges strongly to a point \(\bar{x}\in \varOmega \), where \(\bar{x}=P_\varOmega \circ f(\bar{x}).\)

Algorithm 5.3

Initialization: Given \(\theta>0, \lambda _{1} >0, \phi \in (0,1).\) Let \(x_{0}, x_{1}\in H\) be two initial points and set \(n=1.\)

Iterative steps: Calculate the next iterate \(x_{n+1}\) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} w_{n}=x_{n}+\theta _{n} (x_{n}-x_{n-1})\\ u_{n}=P_C(w_{n}-\lambda _{n}Aw_{n}) \\ v_{n}=u_{n}-\lambda _{n}(A u_{n}- A w_{n})\\ z_{n}=(1-\sigma _{n})v_{n}+\sigma _{n}S_{\alpha }v_{n} \\ x_{n+1}=\alpha _{n} f (w_{n}) + \delta _{n}S_{\alpha }v_{n}+\xi _{n}T_{\beta }z_{n}, \end{array}\right. } \end{aligned}$$

where \(S_{\alpha }=\alpha I + (1-\alpha )S\) and \(T_{\beta }=\beta I + (1-\beta )T\)

$$\begin{aligned} {\theta }_n= & {} {\left\{ \begin{array}{ll} \min \Big \{\frac{\epsilon _n}{||x_n - x_{n-1}||}, ~ \theta \Big \}, &{}\quad \text {if}~ x_n \ne x_{n-1},\\ \theta , &{}\quad \text {otherwise.} \end{array}\right. }\\ \lambda _{n+1}= & {} {\left\{ \begin{array}{ll} \min \Big \{\frac{\phi \Vert w_{n}-u_{n}\Vert }{\Vert A w_{n}-Au_{n}\Vert },~ \lambda _{n}+\phi _n\Big \}, &{}\quad \text {if}~ A w_{n}- A u_{n} \ne 0 \\ \lambda _{n}+\phi _n, &{}\quad \text{ otherwise. } \end{array}\right. } \end{aligned}$$

5.2 Monotone variational inclusion and equilibrium problems

Let C be a nonempty, closed, and convex subset of a real Hilbert space H,  and let \(F: C\times C\rightarrow \mathbb {R}\) be a bifunction. The equilibrium problem (EP) is defined as follows: Find a point \(\hat{x}\in C\), such that:

$$\begin{aligned} F(\hat{x}, y)\ge 0\;\;\;\text {for all}\,\,y\in C. \end{aligned}$$
(5.2)

The set of solutions of the EP (5.2) is denoted by EP(F, C).

Assumption 5.4

In solving the EP (5.2), the bifunction F is assumed to satisfy the following conditions:

(C1):

\(F(x,x) = 0\) for all \(x\in C;\)

(C2):

F is monotone, i.e., \(F(x,y) + F(y,x)\le 0\) for all \(x,y\in C;\)

(C3):

for each \(x,y,z\in C\), \(\lim _{t\rightarrow 0}F(tz+(1-t)x, y)\le F(x,y);\)

(C4):

for each \(x\in C\), \(y\rightarrow F(x,y)\) is convex and lower semicontinuous.

Lemma 5.5

[14] Let \(F:C\times C\rightarrow \mathbb {R}\) be a bifunction satisfying Asummption 5.4. For any \(r>0\) and \(x\in H,\) define a mapping \(T^F_r:H\rightarrow C\) as follows:

$$\begin{aligned} T^F_r(x)=\left\{ z\in C:F(z,y)+\frac{1}{r}\Big \langle y-z, z-x\Big \rangle \ge 0, \forall y\in C\right\} . \end{aligned}$$

Then, we have the following:

  1. 1.

    \(T^F_r\) is nonempty and single-valued;

  2. 2.

    \(T^F_r\) is firmly nonexpansive, that is

    $$\begin{aligned} \Big \langle T^F_rx-T^F_ry,x-y\Big \rangle \ge \Vert T^F_rx-T^F_ry\Vert ^2; \end{aligned}$$
  3. 3.

    \(F(T^F_r)=EP(F)\) is closed and convex.

Applying Theorem 4.6 and Lemma 5.5, we obtain the following result for approximating the common solution of monotone variational inclusion problem and equilibrium problems in the framework of real Hilbert spaces.

Theorem 5.6

Let H be a Hilbert space and let \(F_i:C\times C\rightarrow \mathbb {R},~~i=1,2\) be bifunctions satisfying conditions (C1)–(C4). Let \(\{x_n\}\) be a sequence generated by Algorithm 3.1, such that the conditions of Theorem 4.6 hold. Suppose that the solution set \(\varOmega =EP(F_1)\cap EP(F_2)\cap VI(C,A)\ne \emptyset .\) Then, \(\{x_{n}\}\) converges strongly to a point \(\bar{x}\in \varOmega \), where \(\bar{x}=P_\varOmega \circ f(\bar{x}).\)

Proof

It is known that every firmly nonexpansive mapping is nonexpansive, and hence strictly-pseudocontractive. Consequently, by setting \(S=T_r^{F_1}\) and \(T=T_r^{F_2}\) in Theorem 4.6, the desired result follows from Lemma 5.5. \(\square \)

6 Numerical experiments

In this section, we present some numerical experiments to illustrate the performance of our method, Algorithm 3.1 in comparison with Algorithms 1.1, 1.3, 1.5, Appendices 7.1 and 7.2. All numerical computations were carried out using Matlab version R2019(b).

In our computations, we choose \(\alpha _n = \frac{1}{2n+1},\epsilon _n = \frac{1}{(2n+1)^3},\delta _n=\xi _n=\frac{1}{2}(1-\alpha _n),\theta =0.85,\lambda _1=2.5,\phi =0.97,\alpha =0.125,\beta =0.134,Sx=\frac{2}{3}x, Tx=\frac{3}{5}x, f(x)=\frac{1}{2}x\) in our Algorithm 3.1, and we take \(\vartheta _n=\frac{1}{(2n+1)^2},\mu = 019, \mu _n=0.9.\)

Example 6.1

Let \( H_1= \mathbb {R},\) the set of all real numbers with the inner product defined by \(\langle x,y\rangle =xy, ~~~\forall ~~x,y\in \mathbb {R}\) and induced norm \(|\cdot |.\) We define \(A: H_1\rightarrow H_1\) by \( Ax= x + \sin x\) and \(B: H_1\rightarrow H_1\) by \(Bx=3x,\) for all \(x\in H.\) Clearly, A is \(\frac{1}{2}\)-inverse strongly monotone and B is maximal monotone.

We consider different initial starting points as follows with \(u=x_0:\)

  • Case I: Take \(x_0= \frac{53}{10} \) and \(x_1= 3 \).

  • Case II: Take \(x_0=\frac{9}{2}\) and \(x_1= 2 \).

  • Case III: Take \(x_0= \frac{37}{10} \) and \(x_1= \frac{19}{10} \).

  • Case IV: Take \(x_0= 5\) and \(x_1= \frac{9}{2}\).

We compare the performance of our Algorithm 3.1 with Algorithms 1.1, 1.3, 1.5, Appendices 7.1 and 7.2. We plot the graphs of errors against the number of iterations in each case using \(|x_{n+1}-x_{n}|< 10^{-4}\) as the stopping criterion. The numerical results are reported in Table 1 and Fig. 1.

Table 1 Numerical results for Example 6.1
Full size table
Fig. 1
figure 1

Top left: Case I; top right: Case II; bottom left: Case III; bottom right: Case IV

Full size image

Example 6.2

Let \( H_1= H_2=( l _2(\mathbb {R}), \Vert \cdot \Vert _2),\) where \( l _2(\mathbb {R}):=\{x=(x_1,x_2,\ldots ,x_n,\ldots ), x_j\in \mathbb {R}:\sum _{j=1}^{\infty }|x_j|^2<\infty \}, ||x||_2=(\sum _{j=1}^{\infty }|x_j|^2)^{\frac{1}{2}}\) and \(\langle x,y \rangle = \sum _{j=1}^\infty x_jy_j\) for all \(x\in \ell _2(\mathbb {R}).\) Let \(A: H\rightarrow H\) be defined by \( Ax=\frac{1}{2}x\) and \(B: H\rightarrow H\) be defined by \(Bx=5x,\) for all \(x\in H.\) Clearly, A is 2-inverse strongly monotone and B is maximal monotone.

We consider different initial starting points as follows with \(u=x_0:\)

  • Case I: \(x_0 = (4, 1, \frac{1}{4}, \ldots ),\) \(x_1 = (2, 1, \frac{1}{2}, \ldots );\)

  • Case II: \(x_0 = (-3, 1, -\frac{1}{3}, \ldots ),\) \(x_1 = (-2, 1, -\frac{1}{2}, \ldots );\)

  • Case III: \(x_0 = (4, 1, \frac{1}{4}, \ldots ),\) \(x_1 = (-2, 1, -\frac{1}{2}, \ldots );\)

  • Case IV: \(x_0 = (3, 1, \frac{1}{3}, \ldots ),\) \(x_1 = (2, 1, \frac{1}{2}, \ldots ).\)

We compare the performance of our Algorithm 3.1 with Algorithms 1.1, 1.3, 1.5, Appendices 7.1 and 7.2. We plot the graphs of errors against the number of iterations in each case using \(\Vert x_{n+1}-x_{n}\Vert < 10^{-4}\) as the stopping criterion. The numerical results are reported in Table 2 and Fig. 2.

Table 2 Numerical results for Example 6.2
Full size table
Fig. 2
figure 2

Top left: Case I; top right: Case II; bottom left: Case III; bottom right: Case IV

Full size image

7 Conclusion

In this paper, we studied the problem of finding the solution of monotone variational inclusion problem (MVIP) and common fixed points of strict pseudocontractions. We proposed a new inertial viscosity method which uses a self-adaptive step size for approximating the solution of the aforementioned problem. Unlike several of the existing results on MVIP in the literature, our method does not require the associated single-valued operator to be co-coercive nor Lipschitz continuous and the method does not involve any linesearch technique. Moreover, we proved a strong convergence result and applied our result to study other optimization problems. Finally, we presented several numerical experiments to demonstrate the efficiency of the proposed method in comparison with the existing methods in the literature.