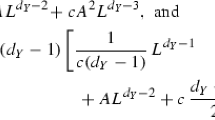Abstract
We prove that a vector bundle on a smooth projective variety is (semi)stable if the restriction on a fixed ample smooth subvariety is (semi)stable.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The purpose of this work is to show a property of slope-stability of vector bundles with respect to restriction to a given ample subvariety.
Given a slope-stable vector bundle E on a projective variety X, it is rather difficult to prove that the restriction of E to an ample subvariety is stable. This can be done for general subvarieties of sufficiently high degree (cf. [4, 6]).
On the converse, it is easy to show that, if the restriction of E on a general ample subvariety of high degree is slope-stable, then E is slope-stable as well.
The purpose of this work is to show that if the restriction of \(E_{|Y}\) to one given smooth ample hypersurface \(Y \subset X\) (of any degree) is (semi)stable, then the vector bundle E is (semi)stable on X. This result only appears in the literature as its generic version, which is almost elementary to prove, so we think it is useful to write it here, as we need it as a reference for future use, and for the interest of the result in itself.
Furthermore, we notice that, contrarily to its generic version, the result is not granted on slightly broader hypotheses, for example if we consider stability of a torsion free sheaf instead of a locally trivial one, or if we consider the restriction to a given singular hypersurface instead of a smooth one. See questions below.
1.1 Notation and main definitions
Throughout this work X is a smooth projective variety of dimension n over an algebraically closed field k.
Intersection products, pull-backs, push-forwards, and Chern classes will be considered in the Chow ring \(A^*(X)\) with integral coefficients, and we will identify divisors in \(A^1(X)\) with line bundles when useful. For a 0-cycle \(W = \sum \lambda _i p_i\), with \(p_i \in X\), \(\lambda _i \in {\mathbb {Z}}\) we will denote by
its degree. For any higher dimensional cycle Z, we will set \(\left<W\right>_X =0\). Therefore, the intersection number of two classes \(a,b \in A^*(X)\) with complementary dimensions will be denoted \(\left<a.b\right>_X\).
We will say that two cycles \(a,b \in A^*(X)\) are numerically equivalent when \(\left<a.c\right>_X=\left<b.c\right>_X\) for every cycle \(c \in A^*(X)\).
Definition 1.1
Let H be an ample divisor on X. Let F be a torsion free sheaf on X. Let n be the dimension of X.
- 1.:
-
We call slope of F (with respect to the polarization H) the rational number
$$\begin{aligned} \mu _H (F) := \frac{\left<c_1(F). H^{n -1}\right>_X}{\mathrm {rk}F} ~. \end{aligned}$$ - 2.:
-
We say that a vector bundle E on X is (semi)stable if for every torsion free subsheaf \(F \subset E\) with \(\mathrm {rk}F < \mathrm {rk}E\) the slopes satisfy
$$\begin{aligned} \mu _H(F) < \mu _H(E) ~~~(\mu _H(F) \leqslant \mu _H(E) \text { for semistability}). \end{aligned}$$
2 Lemmata
The following is the first useful observation:
Lemma 2.1
Let F be a torsion free sheaf on X. Suppose that F is locally free outside of a subset \(Z \subset X\) of codimension at least 3 in X. If \(Y \subset X\) is a hypersurface and H is its class in \(A^1(X)\), then
Proof
Let us first remark that, if \(i :Y \hookrightarrow X\) is the immersion of Y in X, then
In fact, this is obvious when F is a vector bundle. In general notice that \(c_1(F_{|Y})\) and \(i^* c_1(F)\) are two line bundles on Y, isomorphic on an open subset \(U = Y {\setminus } Z\) whose complementary \(Y \cap Z\) has codimension at least 2 in Y, therefore they are isomorphic. Hence \(c_1(F_{|Y}).(H_{|Y})^{n-2} = i^*(c_1(F).H^{n-2})\).
To complete the proof observe that \(\left<w\right>_Y = \left<i_* w\right>_X\) for any cycle \(w \in A^*(Y)\), and that by projection formula:
where [Y] is the identity class in \(A^*(Y)\), and clearly \(i_* [Y] = H\). \(\square\)
Lemma 2.2
Let E be a vector bundle on X.
-
(i)
Suppose that \(\mu _H(F) < \mu _H(E)\) for all subsheaf \(F \subset E\) such that the quotient E/F is torsion free, then E is stable.
-
(ii)
Suppose that \(\mu _H(F) < \mu _H(E)\) for all subsheaf \(F \subset E\) such that \(F \cong F^{**}\), where the dual sheaf of F is defined as the sheaf of homomorphisms \(F^* = {\mathcal {H}}om_{{\mathcal {O}}_X}(F, {\mathcal {O}}_X)\). Then E is stable.
Corresponding statements can be made on semistability.
Proof
To prove stability, we have to consider the slope of any subsheaf \(F \subset E\).
Suppose that condition (i) holds. Given any subsheaf \(F \subset E\) consider the exact sequence \(0 \rightarrow F \rightarrow E \rightarrow G \rightarrow 0\). If \(G = E/F\) is not torsion free consider its torsion \(T =T(G)\) and its torsion free quotient \(G \twoheadrightarrow G^{\prime } = G/T\). Then
Now, observe that \(c_1(T)\) is effective, in fact \(c_1(T) = c_1(F^{\prime }) \otimes c_1(F)^*\), and as \(F \subset F^{\prime }\) then the line bundle \(c_1(T)\) has a section. Therefore
Suppose now that condition (ii) holds. Given any subsheaf \(F \subset E\) consider the injection of F in its bidual: \(F \hookrightarrow F^{**}\). Now, \(F^{**}\) is a subsheaf of E as well. In fact, morphisms from F to E factor through \(F \hookrightarrow F^{**}\), as it can be seen from the computation of homomorphism from F to E, recalling that E is a vector bundle:
Therefore, \(F \subset F^{**} \subset E\) and we can proceed as above. \(\square\)
The following is a well known lemma (cf. [5], Lemma 1.5 and Theorem 1.9):
Lemma 2.3
Let F be a coherent sheaf on X, then
-
(i)
F is torsion-free if and only if it satisfies Serre’s condition S1: i.e. for all schematic points \(x \in X\)
$$\begin{aligned} \mathrm {depth} (F_x) \geqslant \min \{ 1 , \dim {\mathcal {O}}_{X,x} \} ~. \end{aligned}$$ -
(ii)
F is reflexive if and only if it satisfies Serre’s condition S2: i.e. for all schematic points \(x \in X\)
$$\begin{aligned} \mathrm {depth} (F_x) \geqslant \min \{ 2 , \dim {\mathcal {O}}_{X,x} \} ~. \end{aligned}$$
Corollary 2.4
Let F be a reflexive (respectively torsion-free) coherent sheaf on X. The singular locus of F,
has codimension at least 3 (respectively at least 2).
Proof
Suppose that F is a reflexive sheaf, let \(Z \subset X\) be an integral subscheme of codimension at most 2, and let \(z \in X\) be the generic point of Z. Then \({\mathcal {O}}_{X, z}\) has dimension at most 2. Therefore
However, as X is a smooth variety, then \({\mathcal {O}}_{X,x}\) is a regular ring for all \(x \in X\), so it satisfies the Auslander–Buchsbaum formula (cf. [1]): for any coherent sheaf F and any schematic point \(x \in X\)
where \(\mathrm {dh}(F_x)\) is the minimal length of projective resolutions of \(F_x\). In particular, for \(z \in X\) above, we have \(\mathrm {dh}(F_z) = 0\), therefore \(F_z\) is a free \({\mathcal {O}}_{X,z}\)-module. Therefore, \(\mathrm {sing}(F)\) cannot contain any 2-codimensional subscheme.
The same argument applies to the codimension of the singular locus of a torsion-free sheaf. \(\square\)
3 Main theorem
We give in this section the proof of the main theorem stated in the introduction.
Theorem 3.1
Let X be a smooth projective variety of dimension at least 2. Let H be an ample divisor on X. Let E be a vector bundle on X, and \(Y \subset X\) a fixed smooth hypersurface numerically equivalent to a multiple mH, with \(m \in {\mathbb {Q}}^{>0}\). Assume that \(E_{|Y}\) is (semi)stable with respect to the polarization \(H_{|Y}\). Then E is (semi)stable on X with respect to the polarization H.
Proof
Let us prove the statement concerning stability, the argument being essentially the same for semistability.
We want to prove that given a subsheaf \(F \hookrightarrow E\), we have \(\mu _H (F) < \mu _H(E)\), knowing that this property holds on Y.
According to Lemma 2.2 we can suppose that F is reflexive and that \(G:=E/F\) is torsion-free, so by Corollary 2.4 the singular locus of F
has codimension at least 3, and \(\mathrm {sing}(G)\) has codimension at least 2 in X.
Let us restrict the exact sequence \(0 \rightarrow F \rightarrow E \rightarrow G \rightarrow 0\) to the hypersurface Y:
and let us remark that, as \(\mathrm {codim}_X \mathrm {sing}(F) \geqslant 3\), then \(\mathrm {codim}_Y \mathrm {sing}(F_{|Y} ) \geqslant 2\).
As \(\mathrm {supp}({\mathcal {T}}or^1_{{\mathcal {O}}_X} (G, {\mathcal {O}}_Y) ) \subset \text {sing} (G) \cap Y\), and \(\mathrm {codim}_X \text {sing} (G) \geqslant 2\) in X, then \({\mathcal {T}}or^1_{{\mathcal {O}}_X} (G, {\mathcal {O}}_Y)\) is a torsion sheaf on Y, injecting in \(F_{|Y}\). Therefore, its support must be contained in \(\text {sing} (F_{|Y})\).
Hence, \(c_1 (F_{|Y}) = c_1 (F_{|Y}/ {\mathcal {T}}or^1_{{\mathcal {O}}_X} (G, {\mathcal {O}}_Y))\), because quotienting by subsheaves concentrated on high codimension subsets does not affect the first Chern class.
On Y, we have the following exact sequence
Hence by stability of \(E_{|Y}\) we have that
where \(\dim X =n\). As \(\mathrm {codim}_X \text {sing} (F) \geqslant 3\), and E is a vector bundle, then by Lemma 2.1 we have:
so
Therefore, we get stability on X. \(\square\)
4 Applications and questions
By recursive restriction to hypersurfaces it is immediate to prove the following consequence of the main theorem:
Corollary 4.1
Let X be a smooth projective variety of dimension n, and let E be a vector bundle on X. Let H be an ample divisor, let \(Y_i \equiv m_iH\) be hypersurfaces numerically equivalent to a rational multiple of H, for \(i = 1, \dots ,r\) with \(r < n\). Suppose that the complete intersections \(Z_s : =Y_1 \cap \dots \cap Y_s\) are irreducible and smooth for all \(s \leqslant r\). If \(E_{|Z_r}\) is (semi)stable on \(Z_r\), then E is (semi)stable on X (with respect to the polarizations induced by H).
Restriction to smooth curves obtained in such a way is used in various ways in the literature: in some works of the author (cf. [7, 8]), some complete intersection curves are constructed to prove the stability of vector bundles on higher dimensional varieties. Also, in [3], stability of Picard bundles is proven by restriction to curves which are intersection of theta divisors. Even though it is not needed to fix one subvariety in these cases, Corollary 4.1 could be used in these works.
Question 4.2
Since stability is obtained knowing stability on a fixed smooth subvariety, it is natural to ask about weakening the hypothesis to stability on a fixed singular hypersurface, possibly limiting the kind of singularities. We leave this question to further investigations.
Question 4.3
In addition, we can consider weaker hypothesis on E. We see from the proof that we can consider restrictions of a reflexive sheaf E to a fixed smooth ample hypersurface \(Y \subset X\). Then same result hold for stability of E, knowing stability of the restriction of E to Y. However the same cannot be said for torsion free sheaves, and therefore, we cannot apply this recursively to a fixed complete intersection of ample hypersurfaces with the same numerical class. A first obstruction in the proof lies in the fact that the restriction of a torsion free sheaf to a hypersurface is not necessarily torsion free. In addition, the dimensional properties used in the proof cannot be used for torsion free sheaves.
Remark 4.4
In the recent works (cf. [2, 9,10,11]), we consider asymptotic base loci of vector bundles, to get positivity properties, and construct Iitaka fibrations. It would be interesting to consider restrictions of stable vector bundles to (smooth subvarieties in) their asymptotic base loci as well. Any relationship between asymptotic base loci and stability would be surprising.
References
Auslander, M., Buchsbaum, D.A.: Homological dimension in local rings. Trans. Am. Math. Soc. 85, 390–405 (1957)
Bauer, T., Kovács, S.J., Küronya, A., Mistretta, E.C., Szemberg, T., Urbinati, S.: On positivity and base loci of vector bundles. Eur. J. Math. 1(2), 229–249 (2015)
Ein, L., Lazarsfeld, R.: Stability and restrictions of Picard bundles, with an application to the normal bundles of elliptic curves, Complex projective geometry (Trieste, 1989/Bergen, 1989), London Math. Soc. Lecture Note Ser., vol. 179, pp. 149–156. Cambridge University Press, Cambridge (1992)
Flenner, H.: Restrictions of semistable bundles on projective varieties. Comment. Math. Helv. 59(4), 635–650 (1984)
Hartshorne, R.: Generalized divisors on Gorenstein schemes. In: Proceedings of Conference on Algebraic Geometry and Ring Theory in honor of Michael Artin, Part III (Antwerp, 1992), K-Theory, vol. 8, no. 3, pp. 287–339 (1994)
Mehta, V.B., Ramanathan, A.: Semistable sheaves on projective varieties and their restriction to curves. Math. Ann. 258(3), 213–224 (1981/1982)
Mistretta, E.C.: Stable vector bundles as generators of the Chow ring. Geom. Dedic. 117, 203–213 (2006)
Mistretta, E.C.: On stability of tautological bundles and their total transforms. Milan J. Math. 87(2), 273–282 (2019)
Mistretta, E.C.: Holomorphic symmetric differentials and parallelizable compact complex manifolds. Riv. Mat. Univ. Parma (N.S.) 10(1), 187–197 (2019)
Mistretta, E.C.: Holomorphic symmetric differentials and a birational characterization of Abelian Varieties. Math. Nachr. 293(11), 2175–2186 (2020)
Mistretta, E.C., Urbinati, S.: Iitaka fibrations for vector bundles. Int. Math. Res. Not. IMRN (7), 2223–2240 (2019)
Acknowledgements
I am thankful to Alex Küronya for our recent discussions on this subject.
Funding
Open access funding provided by Università degli Studi di Padova within the CRUI-CARE Agreement. This research was partially funded by the PRIN research project “Geometria delle Varietà algebriche” code 2015EYPTSB-PE1, partially funded by the SID-Novelli research project “Positivity, Tropicalization, Mori Dream Spaces”, partly funded by GNSAGA group of INDAM - Istituto Nazionale di Alta Matematica, and partially funded by the research project PranzoDM-KT.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mistretta, E.C. A remark on stability and restrictions of vector bundles to hypersurfaces. Bol. Soc. Mat. Mex. 27, 36 (2021). https://doi.org/10.1007/s40590-021-00333-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40590-021-00333-3
Keywords
- Algebraic geometry
- Vector bundles in algebraic geometry
- Stability of vector bundles
- Moduli spaces of vector bundles