Abstract
The purpose of this note is to provide a purely algebraic interpretation for the cohomology class J. W. Milnor calls the diagonal cohomology class in [11] Chapter 11 and is used by him in his discussion of Poincaré duality and characteristic classes of manifolds. As defined there it is an element of the relative cohomology algebra \(H^n(M \times M ,M \times M \setminus \Delta (M))\) where \(\Delta : M \mathop {\hookrightarrow }\limits M \times M\) is the diagonal embedding and provides a replacement for the Thom class (see e.g., [3] and [10] page 56 et seq) of the tangent bundle of M. Here M should be a closed smooth oriented manifold of dimension n. We use one of Milnor’s Theorems to define an analogous element for any Poincaré duality algebra over a field and show that it is a Macaulay dual for the kernel of the multiplication map of that algebra. Using a formula of R. Thom then allows us to define Stiefel–Whitney classes if the Poincaré duality algebra has the structure of an unstable algebra over the Steenrod algebra. In such a case the algebra also has Wu classes and we show that the formulae of Thom and Wu relating these characteristic classes in the topological case hold in the more general algebraic context thereby recovering and extending an old result of J.F. Adams in a new way.

Similar content being viewed by others
Notes
As a reference for Poincaré duality algebras and Macaulay’s Duality Theorems we refer to [10].
We denote by \(\delta _{i ,j}\) the Kroneker delta function which is 1 if \(i=j\) and 0 otherwise.
The following proof avoids the messy matrix computation and left/right module problems. It is interesting to note that D. B. Zagier in his notes on equivariant Pontrjagin classes gives four proofs for a result similar to Lemma 1.1, see [19] pages 59–61 Propositions 1 and 2, as well as Eqs. (13), (14) so the author was not the only one to be surprised by this result. Using Poincaré duality one can turn a Poincaré duality algebra into a coalgebra and Milnor’s diagonal element then becomes the coproduct of the fundamental class. In the topological context of [11] D. B. Zagier essentially defines Milnor’s diagonal element to be \(\Delta !(1)\) where \(\Delta !\) is the Umkehrhomomorphism associated to the diagonal embedding \(\Delta : X \mathop {\longrightarrow }\limits X \times X\), and E.H. Spanier ([16] Lemma 6.10.1) provides the interpretation of Milnor’s diagonal element as \(\Delta ^*([X])\) where [X] is a fundamental class of X.
In the topological context where Milnor works the integer \(\dim _\mathbf{I\!F}(\mathrm{Tot}(A))\) would be replaced by the Euler characteristic \(\chi (A)\), so \(u^2 = \chi (A) \cdot ([A] \otimes [A]) \in A \otimes A\), where
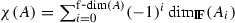 , cf. Corollary 11.12 in [11] since the form (1) is graded sign symmetric rather than symmetric.
, cf. Corollary 11.12 in [11] since the form (1) is graded sign symmetric rather than symmetric.Macaulay duals are in general not unique nor canonical, though they are well defined up to a nonzero scalar multiple, so the following result is special for the ideal \(J \subset A \otimes A\) in view of Lemma 1.1.
So we are regarding B as an A-module by change of rings along f as in [4].
Milnor has available a topological definition for the Stiefel–Whitney classes using the splitting principal for vector bundles and or employing the Thom isomorphism. His diagonal class in the topological context also has the interpretation as the Thom class in the sense of R. Thom of the tangent bundle.
For a definition and basic properties of a Thom module see, e.g., [3].
So in [1] the Wu classes are used to define Stiefel–Whitney classes by means of Wu’s Formula.
Likewise for the q-analogs (see e.g., [3]) to wit: if one defines \({\mathfrak {q}}_k \in A\) by the formula \({\mathfrak {q}}_k = \mathrm{\Phi }^{-1} \bigl ( \mathcal{P}^k(\mathrm{\Phi }(1)\bigr ) = \mathrm{\Phi }^{-1} (\mathcal{P}^k(u))\) is \({\mathfrak {q}}_k = \sum _{i + j = k} \mathcal{P}^i (\mathrm{Wu}_j)\)?
The maps \(\alpha \) and \(\beta \) are replacements for the slant product
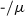 used by Milnor.
used by Milnor.As if the world needed yet another characterization of Artin–Gorenstein algebras.
Not to be confused with \(\mathrm{soc}(A)\), the socle of A, which is the annihilator ideal of \(\bar{A}\), the maximal ideal of A, and need not be concentrated in a single degree.
In particular Tony Iarrobino, Martina Kubitzke, Uwe Nagel, and Eran Nevo.
References
Adams, J.F.: On formulae of Thom and Wu. Proc. Lond. Math. Soc. 11(3), 741–752 (1961)
Bass, H.: On the ubiquity of Gorenstein rings. Math. Z. 82, 8–28 (1963)
Broto, C., Smith, L., Stong, R.E.: Thom modules and Pseudoreflection groups. J. Pure Appl. Algebra 60, 1–20 (1989)
Cartan, H., Eilenberg, S.: Homological Algebra. Princeton University Press, Princeton (1956)
Jacobson, N.: Lectures in abstract Algebra, vol. 2. D. van Nostrand Co., Princeton (1953)
Lambrecht, P., Stanley, D.: The rational homotopy type of configuration spaces of two points. Ann. Inst. Fourier 54, 1029–1052 (2004)
Macaulay, F.S.: The Algebraic theory of modular systems. Cambridge University Press, Cambridge (1916)
MacLane, S.: Homology. Springer, Heidelberg (1963)
McCrory, C.: A characterization of homology manifolds. J. Lond. Math. Soc. 16, 149–159 (1977)
Meyer, D.M., Smith, L.: Poincaré Duality Algebras. Macaulay’s dual systems, and steenrod operations, Cambridge University Press, Cambridge, UK, Tracts in Mathematics 167, (2005)
Milnor, J.W., Stasheff, J.D.: Characteristic classes, Annals of Math. Studies 76. Princeton University Press, Princeton (1974)
Serre, J.P.: Algèbre locale-multiplicités. Lecture notes in Math. Springer, Heidelberg (1965)
Smith, L.: Polynomial Invariants of finite groups. A.K. Peters Ltd, Wellesley (1995). (second printing 1997)
Smith L.: Group actions on Poincaré duality algebras and Lefschetz properties, J. Pure Appl. Algebra 219(8), 3535–3542 (2015)
Smith, L.: Notes on the Umkehrhomomorphism for maps of Poincaré duality Algebras. Preprint, AG-Invariantentheroie (2014) (available from the author)
Spanier, E.H.: Algebraic topology. McGraw Hill, New York (1966)
Steinberg, R.: Differential equations invariant under finite reflection groups. Trans. Amer. Math. Soc. 112, 392–400 (1964)
Stong, R.E.: Poincaré Algebras module an odd prime. Comment. Math. Helv. 49, 223–248 (1974)
Zagier, D.B.: Equivariant Pontrjagin classes and applications to orbit spaces. Lecture notes in Math. Springer, Berlin (1972)
Acknowledgments
This proof of Proposition 4.3 was communicated to the author by Mats Boij and Satoshi Murai and replaces a much more complicated proof of the author. In closing we note that the proofs of the results in this section do not make essential use of the grading and combined lead to a proof of the characterization of Artin–Gorenstein algebras in Proposition 4.4. Thanks are due to the referee for pointing out references [6] and [9] and for forcing the author to reread [16] Chapter 6 for the first time in 50 years.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to the memory of Sam Gitler.
Rights and permissions
About this article
Cite this article
Smith, L. J.W. Milnor’s diagonal element in Poincaré Duality Algebras, Macaulay Duality, the formulae of Thom and Wu, and a new characterization of Artin–Gorenstein Algebras. Bol. Soc. Mat. Mex. 23, 23–39 (2017). https://doi.org/10.1007/s40590-016-0095-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40590-016-0095-9



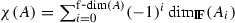 , cf. Corollary 11.12 in [
, cf. Corollary 11.12 in [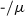 used by Milnor.
used by Milnor.