Skip to main content
SpringerLink
Log in

Strongly primitive species with potentials I: mutations

  • Original Article
  • Published:
Boletín de la Sociedad Matemática Mexicana Aims and scope Submit manuscript

Abstract

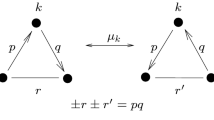
Motivated by the mutation theory of quivers with potentials developed by Derksen–Weyman–Zelevinsky, and the representation-theoretic approach to cluster algebras it provides, we propose a mutation theory of species with potentials for species that arise from skew-symmetrizable matrices that admit a skew-symmetrizer with pairwise coprime diagonal entries. The class of skew-symmetrizable matrices covered by the mutation theory proposed here contains a class of matrices that do not admit global unfoldings, that is, unfoldings compatible with all possible sequences of mutations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Which also go under the name of modulations of valued quivers.

  2. This material has been added following a suggestion of an anonymous referee.

References

  1. Berenstein, A., Fomin, S., Zelevinsky, A.: Cluster algebras III: upper bounds and double Bruhat cells. Duke Math. J. 126(1), 1–52 (2005). arXiv:math/0305434

    Article  MathSciNet  MATH  Google Scholar 

  2. Bernstein, J., Gelfand, I., Ponomarev, V.: Coxeter functors and Gabriel’s theorem. Uspehi Mat. Nauk 28(2) 19–33 (1973) [translated, Russian Math. Surveys 28, 17–32 (1973)]

  3. Bridgeland, T., Smith, I.: Quadratic differentials as stability conditions. Publications mathématiques de l’IHÉS (2014). doi:10.1007/s10240-014-0066-5, arXiv:1302.7030

  4. Irelli, Cerulli: G., Keller, B., Labardini-Fragoso, D., Plamondon, P.-G.: Linear independence of cluster monomials for skew-symmetric cluster algebras. Compos. Math. 149(10), 1753–1764 (2013). arXiv:1203.1307

    Article  MathSciNet  Google Scholar 

  5. Demonet, L.: Mutations of group species with potentials and their representations. Applications to cluster algebras. arXiv:1003.5078

  6. Derksen, H., Weyman, J., Zelevinsky, A.: Quivers with potentials and their representations I: mutations. Selecta Math. 14(1), 59–119 (2008). arXiv:0704.0649

    Article  MathSciNet  MATH  Google Scholar 

  7. Derksen, H., Weyman, J., Zelevinsky, A.: Quivers with potentials and their representations II: applications to cluster algebras. J. Am. Math. Soc. 23(3), 749–790 (2010). arXiv:0904.0676

    Article  MathSciNet  MATH  Google Scholar 

  8. Dlab, V., Ringel, C.M.: Indecomposable representations of graphs and algebras. Mem. AMS 6(173) (1976)

  9. Dupont, G.: An approach to non simply laced cluster algebras. J. Algebra 320(4), 1626–1661 (2008). arXiv:math/0512043

    Article  MathSciNet  MATH  Google Scholar 

  10. Felikson, A., Shapiro, M., Tumarkin, P.: Cluster algebras of finite mutation type via unfoldings. Int. Math. Res. Notices 8, 1768–1804 (2012). arXiv:1006.4276

  11. Fomin, S., Zelevinsky, A.: \(Y\)-systems and generalized associahedra. Ann. Math. 158(3), 977–1018 (2003). arXiv:hep-th/0111053

    Article  MathSciNet  MATH  Google Scholar 

  12. Fomin, S., Zelevinsky, A.: Cluster algebras I: foundations. J. Am. Math. Soc. 15(2), 497–529 (2002). arXiv:math/0104151

    Article  MathSciNet  MATH  Google Scholar 

  13. Fomin, S., Zelevinsky, A.: Cluster algebras II: finite type classification. Invent. Math. 154(1), 63–121 (2003). arXiv:math.RA/0208229

  14. Fomin, S., Zelevinsky, A.: Cluster algebras IV: coefficients. Compos. Math. 143, 112–164 (2007). arXiv:math/0602259

  15. Gabriel, P.: Indecomposable representations, II. Symp. Math. Inst. Nazionale Alta Mat. (Rome) 11, 81–104 (1973)

    MathSciNet  MATH  Google Scholar 

  16. Geuenich, J., Labardini-Fragoso, D.: Species with potential associated to triangulated surfaces with orbifold points of order 2 (in preparation)

  17. Keller, B.: The periodicity conjecture for pairs of Dynkin diagrams. Ann. Math. 177(1) (2013)

  18. Labardini-Fragoso, D.: Quivers with potentials associated to triangulated surfaces. Proc. Lond. Math. Soc. 98(3), 797–839 (2009). arXiv:0803.1328

    Article  MathSciNet  MATH  Google Scholar 

  19. Labardini-Fragoso, D.: Quivers with potentials associated to triangulated surfaces. Part IV: removing boundary assumptions. arXiv:1206.1798

  20. Marsh, R., Reineke, M., Zelevinsky, A.: Generalized associahedra via quiver representations. Trans. Am. Math. Soc. 355, 4171–4186 (2003). arXiv:math/0205152

    Article  MathSciNet  MATH  Google Scholar 

  21. Nagao, K.: Donaldson–Thomas theory and cluster algebras. Duke Math. J. 162(7), 1313–1367 (2013). arXiv:1002.4884

    Article  MathSciNet  MATH  Google Scholar 

  22. Nguefack, B.: Modulated quivers with potentials and their Jacobian algebras. arXiv:1004.2213

  23. Plamondon, P.-G.: Cluster algebras via cluster categories with infinite-dimensional morphism spaces. Compos. Math. 147, 1921–1954 (2011). arXiv:1004.0830

  24. Rupel, D.: On a quantum analogue of the Caldero–Chapoton formula. Int. Math. Res. Notices 14, 3207–3236 (2011). arXiv:1003.2652

  25. Rupel, D.: Quantum cluster characters. arXiv:1109.6694

  26. Speyer, D., Thomas, H.: Acyclic cluster algebras revisited. arXiv:1203.0277

  27. Speyer, D., Zelevinsky, A.: Unpublished example of a skew-symmetrizable matrix without global unfoldings

  28. Zelevinsky, A.: Unpublished definition of global unfoldings of skew-symmetrizable matrices

Download references

Acknowledgments

The collaborations [6, 7] of Harm Derksen and Jerzy Weyman with A. Zelevinsky have served as an inspiring and guiding source throughout the development of the present manuscript. We have made a conscious effort to follow [6] as much as possible, both in the structure of the paper, and in the form and proofs of the results. We thank Laurent Demonet, Claus Michael Ringel and Dylan Rupel for helpful discussions. We are particularly grateful to David Speyer for his collaboration [27] with A. Zelevinsky that showed the existence of skew-symmetrizable matrices without global unfoldings. D. Labardini-Fragoso thanks the Representation theory group of the National Autonomous University of Mexico, especially Michael Barot and Christof Geiss, for their hospitality and financial support during his several visits to UNAM’s Institute of Mathematics in Mexico City. Parts of the work presented here were completed in these visits. This project started several years ago, when D. Labardini-Fragoso was a Ph.D. student of A. Zelevinsky at Northeastern University’s Department of Mathematics (Boston, MA, USA). Unfortunately, Professor Andrei Zelevinsky passed away during the last stage of the preparation of this paper. D. Labardini-Fragoso is sincerely grateful to him for his enthusiasm and deep insights and contributions throughout the collaboration that led to the present paper. It is needless to say that any possible inaccuracies or mistakes should be attributed to D. Labardini-Fragoso alone. D. Labardini-Fragoso wishes to thank an anonymous referee for his/her thorough reading and a number of remarks and suggestions.

Author information

Author notes

  1. Daniel Labardini-Fragoso

    Present address: Instituto de Matemáticas, Universidad Nacional Autónoma de México, Mexico, Mexico

Authors and Affiliations

  1. Mathematisches Institut, Universität Bonn, 53115, Bonn, Germany

    Daniel Labardini-Fragoso

  2. Department of Mathematics, Northeastern University, Boston, MA, 02115, USA

    Andrei Zelevinsky

Authors
  1. Daniel Labardini-Fragoso
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrei Zelevinsky
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daniel Labardini-Fragoso.

Additional information

A. Zelevinsky passed away on April 10, 2013.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Labardini-Fragoso, D., Zelevinsky, A. Strongly primitive species with potentials I: mutations. Bol. Soc. Mat. Mex. 22, 47–115 (2016). https://doi.org/10.1007/s40590-015-0063-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40590-015-0063-9

Keywords

Mathematics Subject Classification

Search

Navigation