1 Introduction

Let \(C_j,~j=1,2, \ldots ,m\) be a family of nonempty, closed and convex subset of real Hilbert space \(\mathcal { H}\), the Convex Feasibility Problem (in short, CFP) is to find

$$\begin{aligned} x^* \in \mathcal { H}~\text {such that}~x^* \in \bigcap _{j=1}^{m}C_j, \end{aligned}$$
(1.1)

where \(m \ge 1\) is an integer. The CFP (1.1) has received a lot of attention due to its numerous applications in many applied disciplines such as image recovery and signal processing, approximation theory, control theory, biomedical engineering, geophysics and communication (see [4, 11, 22, 28] and the references therein). A special case of CFP (1.1) is the Split Feasibility Problem (in short, SFP), which is to find

$$\begin{aligned} x^* \in C~\text {such that}~Ax^* \in Q, \end{aligned}$$
(1.2)

where C and Q are two nonempty, closed and convex subsets of real Hilbert spaces \(\mathcal { H}_1\) and \(\mathcal { H}_2\), respectively, and A: \(\mathcal { H}_1 \rightarrow \mathcal { H}_2\) is a bounded linear operator. The SFP (1.2) was introduced in 1994 by Censor and Elfving [7] for modeling certain inverse problems. It plays a vital role in medical image reconstruction and in signal processing (see [5, 6, 20, 33] and the references therein). In 2002, Bryne [5] proposed a popular algorithm \(\{x^k\}\) that solves the SFP (1.2) as follows:

$$\begin{aligned} x^{k+1}=P_{C}(x^{k}-\gamma A^*(I-P_{Q})Ax^{k}), \end{aligned}$$

for each \(k \ge 0,\) where \(P_{C}\) and \(P_{Q}\) are metric projections onto C and Q, respectively, \(A^*\) denotes the adjoint of a mapping \(A: \mathcal { H}_1 \rightarrow \mathcal { H}_2,\) and \(\gamma \in (0, \frac{2}{\lambda })\) with \(\lambda \) being the spectral radius of \(A^*A.\) Since then, several iterative algorithms for solving SFP (1.2) have been proposed (see [1, 2, 5,6,7, 16, 19, 23]). The authors [24] studied the following SFP with multiple output sets in the setting of real Hilbert spaces: Let \(\mathcal { H}, \mathcal { H}_j, j=1,2, \ldots ,N\) be bounded linear operators. Let C and \(Q_j\) be nonempty, closed and convex subsets of \(\mathcal { H}\) and \(\mathcal { H}_j, j=1,2,\ldots ,N\) respectively. Suppose that \(\bigtriangleup :=C \cap (\bigcap \nolimits _{j=1}^{N}A_j^{-1}(Q_j)) \ne \emptyset ,\) then in other to solve for \(\bigtriangleup \). Reich et al. [24] proposed the following two iterative methods: For any \(x^{0}, y^{0} \in C,\) let \(\{x^{k}\}\) and \(\{y^{k}\}\) be two sequences generated by

$$\begin{aligned} x^{k+1}=P_{C}[x^{k}-\gamma ^{k}\sum \limits _{j=1}^{N}A_j^{*}(I-P_{Q})A_jx^{k}], \end{aligned}$$
(1.3)

and

$$\begin{aligned} y^{k+1}=\alpha ^{k} g(y^{k}) + (1-\alpha ^{k})P_{C}\Bigg [y^{k}-\gamma ^{k}\sum \limits _{j=1}^{N}A^{*}_j(I-P_Q)A_jy^{k}\Bigg ]. \end{aligned}$$
(1.4)

where \(g: C \rightarrow C\) is a strict contraction mapping with contraction coefficient \(a \in [0,1),~ {\gamma ^{k}} \in (0, \infty )\) and \(\{\alpha ^{k}\} \in (0,1).\) They established weak and strong convergence of the sequences generated by (1.3) and (1.4) using the following assumption on \(\{\gamma ^{k}\}\):

$$\begin{aligned} 0< a\le \gamma ^{k}\le b < \frac{2}{\max \limits _{j=1,2,\ldots ,N}\{\Vert A_j\Vert ^2\}}. \end{aligned}$$

Now, if \(C=F(T)\) and \(Q=F(S)\) in (1.2), then we obtain the following Split Common Fixed Point Problem (SCFPP) which is to find a point

$$\begin{aligned} x^* \in F(T)~\text {and}~Ax^* \in F(S), \end{aligned}$$
(1.5)

where \(F(T)=\{x \in C: x=Tx\},\) and F(S) denotes respectively, the set of all fixed points of T and S, respectively with \(A: \mathcal { H}_1 \rightarrow \mathcal { H}_2\) being the bounded linear operator. The SCFPP (1.5) was first studied by Censor and Segal [9]. Note that \(x^*\) is a solution of SCFPP (1.5) if the fixed point equation below stands:

$$\begin{aligned} x^*=U(x^*-\gamma (I-T)Ax^*), \gamma > 0. \end{aligned}$$

In order to solve SCFPP (1.5), Censor and Segal [9] introduced the following iterative method: For any arbitrary point \(x^{1} \in \mathcal { H}_{1}\), define the sequence \(\{x^{k}\}\) by

$$\begin{aligned} x^{k+1}=U(x^{k}-\gamma A^*(I-T)Ax^{k}), \end{aligned}$$
(1.6)

where U and T are directed operators, \(\gamma \in (0, \frac{2}{\Vert A\Vert ^2})\). They established that the sequence \(\{x^{k}\}\) generated by (1.6) converges weakly to a solution of (1.5). Subsequently, the result of [9] was extended to the classes of quasi-nonexpansive mappings [18] and demicontractive mappings [17], but still, the sequence \(\{x^{k}\}\) converges weakly to the solution of (1.5), see ([2, 3, 8, 27] and the references therein) for more results on SCFPP.

Remark 1.1

Though the difficulty occurs when one implements (1.6) because its step size does require the computation of the operator norm \(\Vert A\Vert \), alternative ways to solve this problem have been considered by several authors (see [21, 29, 31] and the references therein).

In this paper, we consider the following split common fixed point problem with multiple output sets in real Hilbert spaces: Let \(H,~ H_j, j=1,2, \ldots ,N\) be real Hilbert spaces and \(A_j: \mathcal { H} \rightarrow \mathcal { H}_j\) be bounded linear operators. Let \(T_j: \mathcal { H} \rightarrow \mathcal { H}\) and \(S_j:\mathcal { H}_j \rightarrow \mathcal { H}_j, j=1,2 \ldots , N\) be \(\lambda _j\) and \(k_j\)-demicontractive mappings respectively, then the SCFPP with multiple output sets is to find an element \(x^* \in \mathcal { H} \) such that

$$\begin{aligned} x^* \in \bigtriangleup :=\bigcap _{j=1}^{N}F(T_j) \bigcap \Bigg (\bigcap _{j=1}^{N}A_j^{-1}(F(S_j))\Bigg ) \ne \emptyset . \end{aligned}$$
(1.7)

Remark: If \(C_j=\bigcap \nolimits _{j=1}^{N}F(T_j)\) and \(Q_j=\bigcap \nolimits _{j=1}^{N}F(S_j),\) then problem (1.7) becomes the multiple set split feasibility problem considered in [24].

Remark 1.2

The class of demicontractive mappings is known to be of central importance in optimization theory since it contains many common types of operators that are useful in solving optimization problems, (see [24, 27] and other references therein).

Remark 1.3

We will like to emphasize that approximating a common solution of SCFPP for finite families of certain nonlinear mappings have some possible real life applications to mathematical models whose constraints can be expressed as fixed points of some nonlinear mappings. In fact, this happens in practical problems like signal processing, network resource allocation, image recovery, among others, (see [13]).

Inspired by the results of Reich et al. [24], Eslamian Padcharoen et al. [21], Reich et al. [25] and many other related results in the literature, we introduce a Halpern method for approximating the solution of split common fixed point problem for demicontractive mappings with multiple output sets in real Hilbert spaces. We prove a strong convergence result of the proposed method with the Armijo- linesearch. Finally, we provide some applications and numerical examples to illustrate the performance of our main result. Our results extends and complements many related results in the literature. We highlight our contributions as follows:

  1. (i)

    We establish a strong convergence result which is desirable to the weak convergence results obtained in [4, 9, 17, 18].

  2. (ii)

    We introduce a linesearch which prevents our iterative method from depending on operator norm (see [17, 24]).

  3. (iii)

    The problems considered in [9, 17, 25] are special cases of problem (1.7).

  4. (iv)

    Our method of proof is short and elegant.

2 Preliminaries

We state some known and useful results which will be needed in the proof of our main theorem. In the sequel, we denote strong and weak convergence by "\(\rightarrow \)" and "\(\rightharpoonup \)", respectively.

Let C be a nonempty, closed and convex subset of a real Hilbert space \(\mathcal {H}\). Let \(T: C \rightarrow C\) be a single-valued mapping, then a point \(x \in C\) is called a fixed point of T if \(Tx=x\). We denote by F(T), the set of all fixed points of T. The mapping \(T: \mathcal {H} \rightarrow \mathcal {H}\) is said to be

  1. (i)

    nonexpansive if

    $$\begin{aligned} \Vert Tx-Ty\Vert \le \Vert x-y\Vert ,\quad ~\forall ~x,y \in \mathcal { H}, \end{aligned}$$
  2. (ii)

    quasi-nonexpansive if

    $$\begin{aligned} \Vert Tx-Tp\Vert \le \Vert x-p\Vert ,\quad ~\forall ~x \in \mathcal { H}~\text {and}~p \in F(T), \end{aligned}$$
  3. (iii)

    directed (firmly quasi-nonexpansive) if

    $$\begin{aligned} \Vert Tx-p\Vert ^2&\le \Vert x-p\Vert ^2-\Vert x-Tx\Vert ^2,\quad ~\forall ~x\in \mathcal { H}~\text {and}~p \in F(T), \end{aligned}$$
  4. (iv)

    strictly pseudocontractive if there exists \(k \in [0,1)\) such that

    $$\begin{aligned} \Vert Tx-Ty\Vert ^2 \le \Vert x-y\Vert ^2 + k \Vert (x-y)-(Tx-Ty)\Vert ^2,\quad ~\forall ~x \in \mathcal { H}, \end{aligned}$$
  5. (v)

    pseudocontractive if

    $$\begin{aligned} \Vert Tx-Ty\Vert ^2&\le \Vert x-y\Vert ^2 + \Vert (x-y)-(Tx-Ty)\Vert ^2,\quad ~\forall ~x \in \mathcal { H}, \end{aligned}$$
  6. (vi)

    demicontractive (or k-demicontractive) if there exists \(k < 1\) such that

    $$\begin{aligned} \Vert Tx-Tp\Vert ^2&\le \Vert x-p\Vert ^2 + k\Vert x-Tx\Vert ^2,\quad ~\forall ~x \in \mathcal { H}~\text {and}~p \in F(T), \end{aligned}$$

    which is equivalent to

    $$\begin{aligned} \langle x-p, x-Tx\rangle \ge \frac{1-k}{2}\Vert x-Tx\Vert ^2,\quad ~\forall ~x \in \mathcal { H}~\text {and}~p \in F(T). \end{aligned}$$

Remark 2.1

It can be observed from the definitions above that if \(k=0\) in (iv), we get (i) and when k=0 in (vi), we get (ii). Also, it can be seen that the class of demicontractive mappings contains the the classes of quasi-nonexpansive and directed mappings. Every k-demicontractive mapping \((k \le 0)\) is characterized by quasi-nonexpansive. Also, every directed mapping is \((-1)\)-demicontractive.

Example 2.2

[30] Let \(\mathcal { H}=\ell _2\) and \(T: \ell _2 \rightarrow \ell _2, Tx=-kx, x \in \ell _2, k \ge 1.\) Then \(F(T)=\{0\}\) and T is an operator with endowed with the demicontractive property but not with the quasi-nonexpansive property.

Let C be a nonempty, closed and convex subset of a real Hilbert space H. For every point \(x \in H,\) there exists a unique nearest point in C,  denoted by \(P_C x\) such that

$$\begin{aligned} \Vert x - P_C x\Vert \le \Vert x - y\Vert ,~\quad ~\forall ~y\in C. \end{aligned}$$

\(P_C\) is called the metric projection of H onto C and it is well known that \(P_C\) is a nonexpansive mapping of H onto C that satisfies the inequality:

$$\begin{aligned} \Vert P_C x - P_C y\Vert \le \langle x - y, P_C x - P_C y \rangle . \end{aligned}$$

Moreover, \(P_C x\) is characterized by the following properties:

$$\begin{aligned} \langle x - P_C x, y - P_C x \rangle \le 0, \end{aligned}$$
(2.1)

and

$$\begin{aligned} \Vert x - y\Vert ^2 \ge \Vert x - P_C x\Vert ^2 + \Vert y - P_C x\Vert ^2,~\quad ~\forall ~x\in H,~y\in C. \end{aligned}$$

More information on metric projection can be found in [12, 15].

Lemma 2.3

[10] Let \(\mathcal {H}\) be a real Hilbert space, then for all \(x, y \in \mathcal {H}\) and \(\alpha \in (0,1)\), the following inequalities holds:

$$\begin{aligned} \Vert \alpha x+ (1-\alpha )y\Vert ^2&=\alpha \Vert x\Vert ^2+ (1-\alpha )\Vert y\Vert ^2-\alpha (1-\alpha )\Vert x-y\Vert ^2.\\ \Vert x+y\Vert ^2&=\Vert x\Vert ^2+ 2\langle x,y\rangle + \Vert y\Vert ^2.\\ \Vert x+y\Vert ^2&\le \Vert x\Vert ^2+ 2\langle y, x+y\rangle . \end{aligned}$$

Definition 2.4

Let \(T: \mathcal { H}\rightarrow \mathcal { H}\) be a mapping, then \(I-T\) is said to be demiclosed at zero if for any sequence \(\{x^{k}\}\) in \(\mathcal { H}\), the conditions \(x^{k}\rightharpoonup x\) and \(\lim \nolimits _{k \rightarrow \infty }\Vert x^{k}-Tx^{k}\Vert =0\) imply \(x=Tx.\)

Lemma 2.5

[32] Let C be a nonempty, closed and convex subset of a real Hilbert space \(\mathcal {H}\) and \( T: C \rightarrow C\) be a nonexpansive mapping. Then \(I-T\) is demiclosed at 0 (i.e., if \(\{x_n\}\) converges weakly to \(x\in C\) and \(\{x_n-Tx_n\}\) converges strongly to 0, then \(x=Tx\).

Lemma 2.6

[26] Let \(\{\alpha _n\}\) be sequence of nonnegative real numbers, \(\{a_n\}\) be sequence of real numbers in (0, 1) such that \(\sum \nolimits _{n=1}^{\infty }a_n=\infty \) and \(\{b_n\}\) be a sequence of real numbers. Assume that

$$\begin{aligned} a_{n+1} \le (1-\alpha _n)a_n + \alpha _n b_n,~\forall ~n \ge 1. \end{aligned}$$

If \(\limsup \nolimits _{k \in \infty }b_{n_k}\le 0\) for every subsequence \(\{a_{n_k}\}\) of \(\{a_n\}\) satisfying the condition

$$\begin{aligned} \liminf _{k \rightarrow \infty }(a_{n_{k+1}}-a_{n_k}) \ge 0, \end{aligned}$$

then \(\lim \nolimits _{k \rightarrow \infty }a_k=0\).

3 Main result

In this section, we present our algorithm and its convergence analysis.

Assumption 3.1

  1. (A1)

    Let \(\mathcal {H}\), \(\mathcal {H}_j, j=1,2,\ldots , N\) be real Hilbert spaces and let \(A_j: \mathcal {H} \rightarrow \mathcal {H}_j, j=1,2,\ldots ,N\) be bounded linear operators.

  2. (A2)

    Let \(S_j:\mathcal {H}_j \rightarrow \mathcal {H}_j, j=1,2,\ldots ,N\) be finite family of \(k_j\)-demicontractive mapping such that \(S_j-I\) are demiclosed at 0 and let C be nonempty, closed and convex subset of \(\mathcal { H}.\)

  3. (A3)

    For \(j=1,2,\ldots ,N,\) let \(T_j:\mathcal { H} \rightarrow \mathcal { H}\) be finite family of \(\lambda _j\)-demicontractive mappings such that \(T_j-I\) are demiclosed at 0.

  4. (A4)

    Assume that \(\bigtriangleup :=\bigcap \nolimits _{j=1}^{N}F(T_j) \bigcap (\bigcap \nolimits _{j=1}^{N} A_j^{-1}(F(S_j)))\) is nonempty.

Assumption 3.2

  1. (B1)

    \(\beta ^{k} \in (0,1)\) such that \(\lim \nolimits _{k \rightarrow \infty }\beta ^{k}=0\) and \(\sum \nolimits _{k=1}^{\infty }\beta ^{k}=\infty .\)

  2. (B2)

    \(\sum \nolimits _{j=1}^{N}\theta ^{k,j}=1\) and \(\liminf \nolimits _{k \rightarrow \infty } \theta ^{k,j}> 0.\)

figure a

Remark 3.4

We employed an Armijo linesearch in Step 1 of Algorithm 3.3 to prevent our sequence from depending on the operator norm. Our Armijo linesearch is easy to compute and gives more importance to our iterative method.

Lemma 3.5

Let \(\{x^{k}\},~ \{u^{k}\}\) and \(\{w^{k}\}\) be sequences generated by Algorithm 3.3, then the following inequality holds:

$$\begin{aligned} \Vert u^{k}-x^*\Vert ^2 \le \Vert x^{k}-x^*\Vert ^2-\left( \gamma ^{k}\sum _{j=1}^{N}(1-k_j)\Vert (S_j-I)A_jx^{k}\Vert ^2-\mu \Vert u^{k}-x^{k}\Vert ^2\right) . \end{aligned}$$
(3.4)

Proof

Let \(x^* \in \bigtriangleup ,\) then we obtain from Lemma 2.3, Algorithm 3.3 and the equality \(S_jA_jx^*=A_jx^*, j=1,2,\ldots ,N\) that

$$\begin{aligned} \Vert u^{k}-x^*\Vert ^2&=\Vert \left( x^{k}-\gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^{k}\right) -x^*\Vert ^2\nonumber \\&=\Vert \Bigg (x^{k}-\gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^{k}\Bigg )-\Bigg (x^*-\gamma ^{k}\sum _{j=1}^{N}A_j^*(S_j-I)A_jx^*\Bigg )\Vert ^2\nonumber \\&\le \Vert x^{k}-x^{*}-\gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^{k}\Vert ^2\nonumber \\&=\Vert x^{k}-x^*-\gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^{k}\Vert ^2-\Vert x^{k}-u^{k}\nonumber \\&\quad + \gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^{k}\Vert ^2\nonumber \\&=\Vert x^{k}-x^*\Vert ^2 + 2 \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, x^{k}-x^*\rangle \nonumber \\&\quad + \Vert \gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^{k}\Vert ^2\nonumber \\&\quad -\Vert u^{k}-x^{k}\Vert ^2 -2 \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, u^{k}-x^{k}\rangle \nonumber \\&\quad -\Vert \gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^{k}\Vert ^2\nonumber \\&=\Vert x^{k}-x^*\Vert ^2 + 2 \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, x^{k}-x^*\rangle \nonumber \\&\quad -\Vert u^{k}-x^{k}\Vert ^2- 2 \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, u^{k}-x^*\rangle \nonumber \\&=\Vert x^{k}-x^*\Vert ^2 + 2 \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, x^{k}-x^*\rangle -\langle u^{k}-x^{k}, u^{k}-x^{k}\rangle \nonumber \\&\quad - 2 \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, u^{k}-x^*\rangle \nonumber \\&\le \Vert x^{k}-x^*\Vert ^2 + 2 \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, x^{k}-x^*\rangle -\langle u^{k}-x^{k}, u^{k}-x^{k}\rangle \nonumber \\&\quad - \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, u^{k}-x^*\rangle \nonumber \\&=\Vert x^{k}-x^*\Vert ^2 + 2 \gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, x^{k}-x^*\rangle -\langle u^{k}-x^{k}\nonumber \\&\quad -\gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_jx^{k}, u^{k}-x^{k}\rangle . \end{aligned}$$
(3.5)

Using the fact that \(S_j, j=1,2, \ldots ,N\) are \(k_j\)-demicontractive and \(A_jx^* \in \bigcap \nolimits _{j=1}^{N}F(S_j),\) we obtain that

$$\begin{aligned} \langle x^{k}-x^*, A_j^{*}(S_j-I)A_jx^*\rangle&= \langle A_j(x^{k}-x^*), (S_j-I)A_jx^{k}\rangle \nonumber \\&=\langle A_j(x^{k}-x^*) + (S_j-I)A_jx^{k}\nonumber \\&\quad -(S_j-I)A_jx^{k}, (S_j-I)A_jx^{k}\rangle \nonumber \\&=\langle S_jA_jx^{k}-A_jx^*, (S_j-I)A_jx^{k}\rangle -\Vert (S_j-I)A_jx^{k}\Vert ^2\nonumber \\&=\frac{1}{2}\big (\Vert S_jA_jx^{k}-A_jx^*\Vert ^2 + \Vert (S_j-I)A_jx^{k}\Vert ^2\nonumber \\&\quad -\Vert (A_jx^{k}-A_jx^*)\Vert ^2-\Vert (S_j-I)A_jx^{k}\Vert ^2\nonumber \\&\le \frac{1}{2}\big (\Vert A_jx^{k}-A_jx^*\Vert ^2 + k_j\Vert (S_j-I)A_jx^{k}\Vert ^2\big ) \nonumber \\&\quad + \frac{1}{2}\big (\Vert (S_j-I)A_jx^{k}\Vert ^2-\Vert (A_jx^{k}-A_jx^*\Vert ^2)\nonumber \\&\quad -\Vert (S_j-I)A_jx^{k}\Vert ^2\nonumber \\&=\frac{k_j-1}{2}\Vert (S_j-I)A_jx^{k}\Vert ^2. \end{aligned}$$
(3.6)

Thus, we obtain from (3.6) that

$$\begin{aligned} \Bigg \langle x^{k}-x^*, \sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^*\Bigg \rangle =\sum _{j=1}^{N} \frac{k_j-1}{2}\Vert (S_j-I)A_jx^{k}\Vert ^2. \end{aligned}$$
(3.7)

From the last inequality in (3.5), it follows that

$$\begin{aligned}&-\Bigg \langle u^{k}-x^{k}-\gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_jx^{k}, u^{k}-x^{k}\Bigg \rangle \nonumber \\&\le \Bigg \langle x^{k}-u^{k}-\gamma ^{k}\sum _{j=1}^{N}A-j^{*}(S_j-I)A_jx^{k}, u^{k}-x^{k}\Bigg \rangle \nonumber \\ {}&\quad + \Bigg \langle u^{k}-x^{k}+ \gamma ^{k}\sum _{j=1}^{N}A_j^{*}(S_j-I)A_ju^{k}, u^{k}-x^{k}\Bigg \rangle \nonumber \\&=\gamma ^{k}\sum _{j=1}^{N}\langle A_j^{*}(S_j-I)A_ju^{k}-A_j^{*}(S_j-I)A_jx^{k}, u^{k}-x^{k}\rangle \nonumber \\&=\gamma ^{k}\sum _{j=1}^{N}\Vert A_j^{*}(S_j-I)A_ju^{k}-A_j^{*}(S_j-I)A_jx^{k}\Vert ~\Vert u^{k}-x^{k}\Vert \nonumber \\&\le \mu \Vert u^{k}-x^{k}\Vert . \end{aligned}$$
(3.8)

On substituting (3.7) and (3.8) into (3.5), it yields

$$\begin{aligned} \Vert u^{k}-x^*\Vert ^2&\le \Vert x^{k}-x^*\Vert ^2 + 2 \gamma ^{k}\sum _{j=1}^{N}\left( \frac{k_j-1}{2}\right) \Vert (S_j-I)A_jx^{k}\Vert ^2 + \mu \Vert u^{k}-x^{k}\Vert ^2\nonumber \\&\le \Vert x^{k}-x^*\Vert ^2-\left( \gamma ^{k}\sum _{j=1}^{N}(1-k_j)\Vert (S_j-I)A_jx^{k}\Vert ^2-\mu \Vert u^{k}-x^{k}\Vert ^2\right) . \end{aligned}$$
(3.9)

This completes the proof. \(\square \)

Lemma 3.6

Suppose \(\{x^{k}\}, ~\{u^{k}\}\) and \(\{w^{k}\}\) are sequences generated by Algorithm 3.3, and \(T_j: \mathcal { H} \rightarrow \mathcal { H}\) be a finite family of \(\lambda _j-\) demicontractive mapping. Then the following inequality holds:

$$\begin{aligned} \Vert w^{k}-x^*\Vert \le \Vert u^{k}-x^*\Vert ^2-\sum _{j=1}^{N}\theta ^{k,j}\frac{(1-\lambda _j)^2}{4}\Vert (T_j-I)u^{k}\Vert ^2. \end{aligned}$$

Proof

Let \(x^* \in \bigtriangleup ,\) then we obtain from Algorithm 3.3 and (3.6) that

$$\begin{aligned} \Vert w^{k}-x^*\Vert ^2&=\Vert u^{k}+ \sum _{j=1}^{N}\theta ^{k,j}\frac{1-\lambda _j}{2}(T_j-I)u^{k}-x^*\Vert ^2\nonumber \\&\le \sum _{j=1}^{N}\theta ^{k,j}\Vert u^{k}+ \frac{1-\lambda _j}{2}(T_j-I)u^{k}-x^*\Vert ^2\nonumber \\&=\sum _{j=1}^{N}\theta ^{k,j}\big (\Vert u^{k}-x^{k}\Vert ^2+ \left( \frac{1-\lambda _j}{2}\right) ^2\Vert (T_j-I)u^{k}\Vert ^2 \nonumber \\ {}&\quad +2\left( \frac{1-\lambda _j}{2}\right) \langle u^{k}-x^*, (T_j-I)u^{k}\rangle \big )\nonumber \\&=\sum _{j=1}^{N}\theta ^{k,j}\big (\Vert u^{k}-x^*\Vert ^2 + \left( \frac{1-\lambda _j}{2}\right) ^2\Vert (T_j-I)u^{k}\Vert ^2\nonumber \\ {}&\quad -2 \left( \frac{1-\lambda _j}{2}\right) \left( \frac{1-\lambda _j}{2}\right) \Vert (T_j-I)u^{k}\Vert ^2\nonumber \\&\le \Vert u^{k}-x^*\Vert ^2-\sum _{j=1}^{N}\theta ^{k,j}\frac{(1-\lambda _j)^{2}}{4}\Vert (T_j-I)u^{k}\Vert ^2. \end{aligned}$$
(3.10)

This completes the proof. \(\square \)

Lemma 3.7

Suppose \(\{x^{k}\},~ \{u^{k}\}\) and \(\{w^{k}\}\) are sequences generated by Algorithm 3.3. Then the aforementioned sequences are all bounded.

Proof

Let \(x^* \in \bigtriangleup ,\) then we obtain from Lemma 3.5 and Lemma 3.6 that

$$\begin{aligned} \Vert w^{k}-x^*\Vert ^2&\le \Vert u^{k}-x^*\Vert ^2-\sum _{j=1}^{N}\theta ^{k,j}\frac{(1-\lambda _j)^2}{4}\Vert (T_j-I)u^{k}\Vert ^2\nonumber \\&\le \Vert x^{k}-x^*\Vert ^2-\left( \gamma ^{k}\sum _{j=1}^{N}(1-k_j)\Vert (S_j-I)A_jx^{k}\Vert ^2-\mu \Vert u^{k}-x^{k}\Vert ^2\right) \nonumber \\ {}&\quad -\sum _{j=1}^{N}\theta ^{k,j}\frac{(1-\lambda _j)^2}{4}\Vert (T_j-I)u^{k}\Vert ^2 \end{aligned}$$
(3.11)
$$\begin{aligned}&\le \Vert x^{k}-x^*\Vert ^2. \end{aligned}$$
(3.12)

From Algorithm 3.3 and (3.12), we have

$$\begin{aligned} \Vert x^{k+1}-x^*\Vert&=\Vert \beta ^{k}u + (1-\beta ^{k})w^{k}-x^*\Vert \\&\le \beta ^{k}\Vert u-x^*\Vert + (1-\beta ^{k})\Vert w^{k}-x^*\Vert \\&\le \beta ^{k}\Vert u-x^*\Vert + (1-\beta ^{k})\Vert x^{k}-x^*\Vert \\&\vdots \\&\le \max \big \{\Vert x^{k}-x^*\Vert , \Vert u-x^*\Vert \}. \end{aligned}$$

Thus, by induction, we have

$$\begin{aligned} \Vert x^{k}-x^*\Vert \le \max \{\Vert x^{1}-x^{*}\Vert , \Vert u-x^*\Vert \}. \end{aligned}$$

Hence, \(\{x^{k}\}\) is bounded. Consequently, \(\{u^{k}\}\) and \(\{w^{k}\}\) are bounded. \(\square \)

Theorem 3.3

Assume that Assumptions (A1)–(A4) and (B1)–(B2) hold, then the sequence \(\{x^{k}\}\) generated iteratively by Algorithm 3.3 strongly converges to the solution of \(z \in \bigtriangleup ,\) where \(z=P_{\bigtriangleup }u\) and \(P_{\bigtriangleup }\) denotes the metric projection of H onto \(\bigtriangleup \).

Proof

Let \(x^* \in \bigtriangleup ,\) then from Lemma 2.3, Algorithm 3.3 and (3.11), we get

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&=\langle \beta ^{k}u + (1-\beta ^{k})w^{k}-z, x^{k+1}-z\rangle \nonumber \\&=(1-\beta ^{k})\langle w^{k}-z, x^{k+1}-z\rangle + \beta ^{k}\langle u-z, x^{k+1}-z\rangle \nonumber \\&\le \frac{(1-\beta ^{k})}{2}\big [\Vert w^{k}-z\Vert ^2 + \Vert x^{k+1}-z\Vert ^2\big ]+ \beta ^{k}\langle u-z, x^{k+1}-z\rangle . \end{aligned}$$
(3.13)

This implies that

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&\le (1-\beta ^{k})\Vert w^{k}-z\Vert ^2 + 2 \beta ^{k}\langle u-z, x^{k+1}-z\rangle \nonumber \\&\le (1-\beta ^{k})\Vert x^{k}-z\Vert ^2-(1-\beta ^{k})\Bigg (\gamma ^{k}\sum _{j=1}^{N}(1-k_j)\Vert (S_j-I)A_jx^{k}\Vert ^2\nonumber \\ {}&\quad -\mu \Vert u^{k}-x^{k}\Vert ^2\Bigg )\nonumber \\ {}&\quad -(1-\beta ^{k})\sum _{j=1}^{N}\theta ^{k,j}\frac{(1-\lambda _j)^2}{4}\Vert (T_j-I)u^{k}\Vert ^2+ 2 \beta ^{k}\langle u-z, x^{k+1}-z\rangle \end{aligned}$$
(3.14)
$$\begin{aligned}&\le (1-\beta ^{k})\Vert x^{k}-z\Vert ^2 + 2 \beta ^{k}\langle u-z, x^{k+1}-z\rangle . \end{aligned}$$
(3.15)

Put \(a^{k}=\Vert x^{k}-z\Vert ^2\) and \(d^{k}:=2 \langle u-z, x^{k+1}-z\rangle .\) Then the inequality (3.16) becomes

$$\begin{aligned} a^{k+1} \le (1-\beta ^{k})a^{k} + \beta ^{k}d^{k}. \end{aligned}$$

We now establish that \(a^{k} \rightarrow 0.\) In view of Lemma 2.6, we claim that \(\limsup \nolimits _{n \rightarrow \infty }d^{k_n} \le 0\) for a subsequence \(\{a^{k_n}\}\) of \(\{a^{k}\}\) satisfying

$$\begin{aligned} \liminf \nolimits _{n \rightarrow \infty }(a^{k_{n+1}}-a^{k_n}) \ge 0. \end{aligned}$$

Now, from (3.14), we obtain that

$$\begin{aligned}&\limsup _{n \rightarrow \infty }\big [(1-\beta ^{k_n})\gamma ^{k_n}\sum _{j=1}^{N}(1-k_j)\Vert (S_j-I)A_jx^{k_n}\Vert ^2-\mu \Vert u^{k_n}-x^{k_n}\Vert ^2\big ]\nonumber \\&\quad \le \limsup \nolimits _{n \rightarrow \infty }\big [(1-\beta ^{k_n})\Vert x^{k_n}-z\Vert ^2 -\Vert x^{k_{n+1}}-z\Vert ^2\big ] \nonumber \\&\qquad + \limsup _{n \rightarrow \infty }\big [2 \beta ^{k_n}\langle u-z, x^{k_{n+1}}-z\rangle \big ]\nonumber \\&\quad =-\liminf _{n \rightarrow \infty }\big [\Vert x^{k_{n+1}}-z\Vert ^2-\Vert x^{k_n}-z\Vert ^2\big ]\nonumber \\&\quad \le 0. \end{aligned}$$
(3.16)

By condition (B1), we obtain that

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert (S_j-I)A_jx^{k_n}\Vert =0=\lim _{n \rightarrow \infty }\Vert u^{k_n}-x^{k_n}\Vert =0. \end{aligned}$$
(3.17)

Also, using (3.14), we obtain that

$$\begin{aligned}&\limsup _{n \rightarrow \infty }\big [(1-\beta ^{k_n})\sum _{j=1}^{N}\theta ^{k_n,j}\frac{(1-\lambda _j)^2}{4}\Vert (T_j-I)u^{k_n}\Vert ^2\big ]\nonumber \\&\quad \le \limsup \limits _{n \rightarrow \infty }\big [(1-\beta ^{k_n})\Vert x^{k_n}-z\Vert ^2 -\Vert x^{k_{n+1}}-z\Vert ^2\big ] \nonumber \\&\qquad + \limsup _{n \rightarrow \infty }\big [2 \beta ^{k_n}\langle u-z, x^{k_{n+1}}-z\rangle \big ]\nonumber \\&\quad =-\liminf _{n \rightarrow \infty }\big [\Vert x^{k_{n+1}}-z\Vert ^2-\Vert x^{k_n}-z\Vert ^2\big ]\le 0. \end{aligned}$$
(3.18)

Thus, we obtain

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert (T_j-I)u^{k_n}\Vert =0. \end{aligned}$$
(3.19)

From step 3 of Algorithm 3.3 and (3.19), we obtain that

$$\begin{aligned} \Vert w^{k_n}-u^{k_n}\Vert \le \sum _{j=1}^{N}\theta ^{k_n,j}\frac{1-\lambda _j}{2}\Vert (T_j-I)u^{k_n}\Vert \rightarrow 0,~\text {as}~n \rightarrow \infty . \end{aligned}$$
(3.20)

Using step 4 of Algorithm 3.3, we get

$$\begin{aligned} \Vert x^{k_{n}+1}-w^{k_n}\Vert \le \beta ^{k_n}\Vert u-w^{k_n}\Vert \rightarrow 0~\text {as}~n \rightarrow \infty . \end{aligned}$$
(3.21)

From (3.17), (3.20) and (3.21), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \lim \limits _{n \rightarrow \infty }\Vert w^{k_n}-x^{k_n}\Vert =0,\\ \lim \limits _{n \rightarrow \infty }\Vert x^{k_{n+1}}-x^{k_n}\Vert =0. \end{array}\right. } \end{aligned}$$
(3.22)

Since \(\{x^{k_n}\}\) is bounded, there exists a subsequence \(\{x^{k_{n_j}}\}\) of \(\{x^{k_n}\}\) with \(x^{k_{n_j}} \rightharpoonup p \in H.\) Also, from (3.17) and (3.22), there exist subsequences \(\{u^{k_{n_j}}\}\) of \(\{u^{k_n}\}\) and \(\{w^{k_{n_j}}\}\) of \(\{w^{k_n}\}\) which converge weakly to p, respectively. By the demiclosedness principle of \(T_j-I, j=1,2, \ldots ,N\) at 0 and (3.19), we have that \(p \in F(T_j)=C, j=1,2,\ldots ,N\). Also, since \(A_j, j=1,2,\ldots ,N\) are bounded linear operators, we have the \(A_jx^{k_{n_j}}\rightharpoonup A_jp.\) Thus, by using the demiclosedness principle of \(S_j-I\) at 0 and (3.17), we obtain that \(A_jp \in F(S_j), j=1,2,\ldots N.\) Hence, we conclude that \(p \in \bigtriangleup .\)

Next, we show that \(\limsup \nolimits _{n \rightarrow \infty }d^{k_n}\le 0.\) Indeed, suppose that \(\{x^{k_{n_j}}\}\) is a subsequence of \(\{x^{k_n}\}\), then from the fact that \(z=P_{\bigtriangleup }u\) and applying (2.1), we deduce that

$$\begin{aligned} \limsup _{n \rightarrow \infty }\langle u-z, x^{k_{n+1}}-z\rangle&= \lim _{j \rightarrow \infty }\langle u-z, x^{k_{n_j}}-z\rangle \nonumber \\&=\langle u-z, p-z\rangle \nonumber \\&\le 0, \end{aligned}$$
(3.23)

that is \(\limsup \nolimits _{n \rightarrow \infty }d^{k_n} \le 0\). Hence all the assumptions of Lemma 2.6 are satisfied and hence \(a^{k} \rightarrow 0,\) that is \(x^{k} \rightarrow z=P_{\bigtriangleup }u\), as asserted. \(\square \)

Corollary 3.9

In this case \(T_j\) and \(S_j,\) \(j=1,2,\ldots ,N\) are finite families of quasi-nonexpansive mappings. Then, we have the following iterative algorithm.

figure b

4 Numerical example

In this section, we report some numerical example to illustrate the convergence of Algorithm 3.3.

Example 4.1

For all \(j=1,\ldots , N\) let \(\mathcal {H}=\mathcal {H}_j=\mathbb {R}\) and \(C=[0,+\infty )\) be a subset of \(\mathcal {H}.\) We define the mapping \(T_j: \mathcal {H}_j \rightarrow \mathcal {H}_j\) by

$$\begin{aligned}T_j(x)=\frac{x+2}{3(1+j)}\; \forall ~x \in \mathbb {R},~j=1,\ldots , N\end{aligned}$$

and \(S_j: \mathcal {H}_j\rightarrow \mathcal {H}_j\) be give by

$$\begin{aligned} S_j x= {\left\{ \begin{array}{ll} \frac{2x}{(x+j)}, \; ~~\qquad \forall x\in (1,+\infty )\\ 0, \hspace{1.5cm} \; \forall ~x \in [0,1]. \end{array}\right. } \end{aligned}$$

Then \(T_j\) and \(S_j\) are demicontractive mappings. Now let \(A_j: \mathcal {H} \rightarrow \mathcal {H}_j\) be defined by \(A_j=\frac{x}{j}\) for all \(x \in \mathcal {H}\) and \(j=1,\ldots , N.\) Let \(\beta ^k=\frac{1}{15k+1},\) \(l=0.0012,\) \(\rho =0.05,\) \(\mu =0.5\) and \(\theta ^{k,j}=\) \(\frac{3}{4j}+\frac{1}{N4^N}.\) We set \(u=0.1,\) \(j=1,2\) and choose \(E_n=\Vert x_{n+1}-x_n\Vert ^2=10^{-4}\) as the stopping criterion. The process is conducted for different initial values of \(x_1\) as follows:

  1. (Case 1)

    \(x_1=1.6;\)

  2. (Case 2)

    \(x_1=3.1.\)

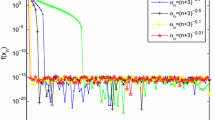
We present the report of this experiment in Fig. 1.

Fig. 1
figure 1

Numerical report for Example 4.1

Full size image

Example 4.2

Let \(\mathcal {H}=(\mathbb {R}^3,\Vert .\Vert _2)=\mathcal {H}\). Let \(S,T:\mathbb {R}^3\rightarrow \mathbb {R}^3\) be two mappings defined by

$$\begin{aligned} S \begin{pmatrix} a\\ b\\ c \end{pmatrix}=\frac{1}{2}\begin{pmatrix} a\\ b\\ c \end{pmatrix}, T\begin{pmatrix} a\\ b\\ c \end{pmatrix}=\begin{pmatrix} 0\\ a\\ b \end{pmatrix}. \end{aligned}$$
(4.1)

It is clear that both T and S are 0-demicontractive mappings. We assume that

$$\begin{aligned} A=\begin{pmatrix} 7 &{} -3 &{} -5\\ -2 &{} 4 &{} -2\\ -5 &{} -2 &{} 7 \end{pmatrix} \end{aligned}$$
(4.2)

We consider the following SCFP: Find a point \(x^*\in F(T)\) such that \(Ax^*\in F(S)\).

Let

$$\begin{aligned} x^*=\begin{pmatrix} a\\ b\\ c \end{pmatrix}\in \mathbb {R}^3, Ax^*\in \mathbb {R}^3 \end{aligned}$$
(4.3)

and \(Ax^*\in F(S)\), we have

$$\begin{aligned} Ax^*=S(Ax^*) \end{aligned}$$
(4.4)

From the definition of S, we obtain

$$\begin{aligned} Ax^*=\frac{1}{2}(Ax^*). \end{aligned}$$
(4.5)

That is,

$$\begin{aligned} Ax^*=0 \end{aligned}$$
(4.6)
$$\begin{aligned} \begin{pmatrix} 7 &{} -3 &{} -5\\ -2 &{} 4 &{} -2\\ -5 &{} -2 &{} 7 \end{pmatrix}\begin{pmatrix} a\\ b\\ c \end{pmatrix}=\begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \end{aligned}$$
(4.7)

Hence

$$\begin{aligned} x^*=\begin{pmatrix} a\\ b\\ c \end{pmatrix}=\begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}\in \mathbb {R}^3 \end{aligned}$$
(4.8)

Next, we show that \(x^*\in F(T)\). By definition of T, we obtain

$$\begin{aligned} Tx^*=T\begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}=\begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}. \end{aligned}$$
(4.9)

Therefore,

$$\begin{aligned} x^*=\begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}\in F(T). \end{aligned}$$
(4.10)

In this example, we choose \(N=u=1,\) \(\rho =2.5, \mu =0.5,, \theta ^{k,1}=\theta ^k=\frac{k}{2k+17}\) and \(\beta ^k=\frac{1}{k+2}.\) The stopping criterion for this experiment is \(\Vert x_{k+1}-x_k\Vert ^2=E_n=10^{-4}.\) The report is given in Fig. 2 for different initial values of \(x_1\) as follows:

  1. (Case a)

    \(x_1=[-2.3, -2.5,-2.1];\)

  2. (Case b)

    \(x_1=[3.1,2.7,3.5].\)

5 Conclusion

Fig. 2
figure 2

Numerical report for Example 4.2

Full size image

In this paper, we studied the Halpern method with Armijo-linesearch rule which is designed to solve finite family of split common fixed point problems for demicontractive mappings in the setting of real Hilbert spaces. Also, we established in an elegant and novel way how the sequence generated by our algorithm converges strongly to a solution of finite family of SCFPP. Finally, we present some numerical examples to illustrate the performance of our method.