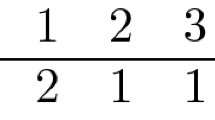1 Introduction

Over the last 60 years multilinear algebra made its way in the applied sciences. As a consequence, tensors acquired an increasingly central role in the applications and the problem of tensor rank decomposition has started to be studied by several non-mathematical communities (cf. e.g. [2,3,4, 6, 9, 11, 13, 40, 52]).

Fix \({\mathbb {C}}\)-vector spaces \(V_1,\dots ,V_k\) of dimensions \(n_1,\dots ,n_k\) respectively. A tensor \(T\in V_1\otimes \cdots \otimes V_k\) is called elementary if \(T=v_1\otimes \cdots \otimes v_k\) for some \(v_i\in V_i\) with \(i=1,\dots ,k\). Elementary tensors are the building blocks of the tensor rank decomposition and the rank r(T) of a tensor \(T\in V_1\otimes \cdots \otimes V_k\) is the minimum integer r such that we can write T as a combination of r elementary tensors:

$$\begin{aligned} T=\sum _{i=1}^{r} v_{1,i}\otimes \cdots \otimes v_{k,i}, \hbox { where all }v_{j,i}\in V_j \hbox { for }j=1,\dots ,k. \end{aligned}$$

A rank-r tensor T is identifiable if admits a unique rank decomposition up to reordering the elementary tensors and up to scalar multiplication. Remark that since the notion of rank does not depend on scalar multiplication, it is well defined for projective classes of tensors too.

The first modern contribution on identifiability of tensors has been given by Kruskal [41] and, starting from Kruskal’s result, over the years there have been many contributions on the identifiability problem (cf. e.g. [8, 12, 14, 18, 21,22,23,24,25, 31, 36, 44, 48]). In particular, working in the applied fields, one may also be interested in the identifiability of specific tensors. Indeed, when translating an applied problem into the language of tensors one may be forced to deal with a very specific tensor that has a precise structure by reasons related to the nature of the applied problem itself. Working with specific tensors, the literature review becomes more scattered and most of the results can be considered extensions or generalizations of Kruskal’s result (cf. [1, 16, 17, 25,26,27, 46, 54]).

The first complete classification on the identifiability problem appeared in [10] where, together with E. Ballico and A. Bernardi, we completely characterize all identifiable tensors of rank either 2 or 3. The classification is based on the classical Concision Lemma (cf. [42, Prop. 3.1.3.1] and also Sect. 2.1 below) and, in particular, for \(r=2\) it has been proved that the only non-identifiable rank-2 tensors are \(2\times 2\) matrices (cf. [10, Proposition 2.3]). A more interesting situation occurs for the rank-3 case, where there have been found 6 different families of non-identifiable concise rank-3 tensors (cf. [10, Theorem 7.1]).

In this manuscript we present an algorithm aimed to recognize if a given tensor falls into one of the 6 families above mentioned or not.

The paper is organized as follows. Section 2 is devoted to recollect basic notions needed to develop the algorithm. We start by recalling [10, Theorem 7.1] and explaining each case of the classification working in coordinates. In Sect. 2.1 we recall the coordinate description of the concision process for a tensor while Sect. 2.2 is devoted to review basic facts on matrix pencils. In Sect. 3 is presented the algorithm itself. In particular, Sect. 3.1 focuses on the 3-factors case, while Sect. 3.2 considers the general case of \(k\ge 4\) factors.

We end the manuscript with an appendix written together with E. Ballico and A. Bernardi in which we fix an imprecision in the statement of [10, Proposition 3.10] and consequently in an item in [10, Theorem 7.1]. In the following, if needed, we will refer to the correct statement of [10, Proposition 3.10 and Theorem 7.1] given in the forthcoming Proposition 4.5 and Theorem 4.1 respectively.

2 Preliminary notions

In the following we will work with tensors over \({\mathbb {C}}\).

Definition 2.1

Fix k vector spaces \(V_1,\dots ,V_k\) of dimension \(n_1+1,\dots ,n_k+1\) respectively and let \(N=\prod _{i=1}^k (n_i+1)-1\). By \(\nu \) we denote the Segre embedding

$$\begin{aligned} \nu : {\mathbb {P}}V_1\times \cdots \times {\mathbb {P}}V_k&\longrightarrow {\mathbb {P}}(V_1 \otimes \cdots \otimes V_k) ={\mathbb {P}}^N\\ ([v_1], \ldots , [v_k])&\mapsto [v_1 \otimes \cdots \otimes v_k] \end{aligned}$$

When dealing with complex projective spaces we will denote by \(X_{n_1,\dots ,n_k}=\nu (Y_{n_1,\dots ,n_k})\) the Segre variety of the multiprojective space \(Y_{n_1,\dots ,n_k}={\mathbb {P}}^{n_1}\times \cdots \times {\mathbb {P}}^{n_k}\).

We recall that the rth secant variety \(\sigma _k(X_{n_1,\dots ,n_k})\) of a Segre variety \(X_{n_1,\dots ,n_k}\subset {\mathbb {P}}^N\) is defined as

$$\begin{aligned} \sigma _r(X_{n_1,\dots ,n_k})=\overline{\{q\in {\mathbb {P}}^N :r(q)=r\}}. \end{aligned}$$

The variety \(X_{n_1, \dots ,n_k}\) is said to be r-defective if

$$\begin{aligned} \dim (\sigma _r(X_{n_1,\dots ,n_k}))< \min \{ r(\dim X_{n_1,\dots ,n_k}+1)-1,N \}. \end{aligned}$$

Since the algorithm we are going to present is based on the classification [10, Theorem 7.1], we briefly recall it here in the revised version of our Theorem 4.1.

The classification. [10, Theorem 7.1 revised]-Theorem 4.1in the present paper. A concise rank-3 tensor \(T\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k} \) is identifiable except if T is in one of the following families.

  1. a)

    [Matrix case] The first trivial example of non-identifiable rank-3 tensors are \(3 \times 3 \) matrices, which is a very classical case.

  2. b)

    [Tangential case] The tangential variety of a variety is the tangent developable of the variety itself. A point q essentially lying on the tangential variety of the Segre \(X_{1,1,1} \) is actually a point of the tangent space \(T_{[p]}X_{1,1,1}\) for some \(p=u\otimes v \otimes w\in ({\mathbb {C}}^2)^{\otimes 3}\). Therefore there exists some \(a,b,c\in {\mathbb {C}}^2 \) such that T can be written as

    $$\begin{aligned} T=a\otimes v\otimes w+u\otimes b \otimes w+u\otimes v \otimes c \end{aligned}$$

    and hence q is actually non-identifiable.

  3. c)

    [Defective case] We recall that the third secant variety of a Segre variety \(X_{n_1,\dots ,n_k}\) is defective if and only if \((n_1,\dots ,n_k)=(1,1,1,1),(1,1,a)\) with \(a\ge 3\) (cf. [5, Theorem 4.5]). We will see that the latter case will not play a role in the discussion and hence we can focus on the case \(k=4\). By defectivity, the dimension of \(\sigma _3(X_{1,1,1,1})\) is strictly smaller than the expected dimension and this proves that the generic element of \(\sigma _3(X_{1,1,1,1})\) has an infinite number of rank-3 decompositions and therefore all the rank-3 tensor of this variety have an infinite number of decompositions.

  4. d), e)

    [Conic cases] In this case one works with the Segre variety \(X_{2,1,1}\) given by the image of a projective plane and two projective lines.

    Let \(Y_{2,1,1}={\mathbb {P}}^2\times {\mathbb {P}}^1\times {\mathbb {P}}^1\). Consider the Segre variety \(X_{1,1} \subset {\mathbb {P}}^3\) given by the last two factors of \(Y_{2,1,1}\) and take a hyperplane section which intersects \(X_{1,1}\) in a conic \({\mathcal {C}}\). Let \(L_{{\mathcal {C}}}\) be the Segre given by the product of the first factor \({\mathbb {P}}^2\) of \(Y_{2,1,1}\) and the conic \({\mathcal {C}}\), therefore \(L_{{\mathcal {C}}}\subset X_{2,1,1}\). The family of non-identifiable rank-3 tensors are points lying in the span of \(L_{{\mathcal {C}}}\). In this case, the non-identifiability comes from the fact that the points on \(\langle {\mathcal {C}} \rangle \) are not identifiable and the distinction between the two cases reflects the fact that the conic \({\mathcal {C}}\) can be either irreducible or reducible. The distinction between the two cases can be expressed as follows working in coordinates:

    1. d)

      The non-identifiable tensor \(T\in {\mathbb {C}}^3\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\) and there exists a basis \(\{u_1,u_2,u_3\}\subset {\mathbb {C}}^3 \) and a basis \(\{ v_1,v_2 \} \subset {\mathbb {C}}^2 \) such that T can be written as

      $$\begin{aligned} T= u_1 \otimes v_1^{\otimes 2}+u_2\otimes v_2^{\otimes 2} + u_3 \otimes (\alpha v_1+\beta v_2)^{\otimes 2}, \end{aligned}$$

      for some \(\alpha ,\beta \ne 0 \);

    2. e)

      The non-identifiable tensor \(T\in {\mathbb {C}}^3\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\) and there exists a basis \(\{u_1,u_2,u_3\}\subset {\mathbb {C}}^3 \) and a basis \(\{ v_1,v_2 \} \subset {\mathbb {C}}^2 \) such that T can be written as

      $$\begin{aligned} T= u_1 \otimes v_1\otimes \tilde{p}+u_2\otimes v_2 \otimes \tilde{p}+ u_3\otimes \tilde{q} \otimes w, \end{aligned}$$

      for some \(\tilde{q}\in \langle v_1,v_2 \rangle \), where \(\tilde{p},w \in {\mathbb {C}}^2\) must be linearly independent;

  5. f)

    [General case] The last family of non-identifiable rank-3 tensors relates the Segre variety \(X_{n_1,n_2,1^{k-2}}\) that is the image of the multiprojective space \(Y_{n_1,n_2,1^{k-2}}={\mathbb {P}}^{n_1}\times {\mathbb {P}}^{n_2}\times ({\mathbb {P}}^1)^{(k-2)}\), where either \(k\ge 4\) and \(n_1,n_2\in \{1,2\}\) or \(k=3\) and \((n_1,n_2,n_3)\ne (2,1,1)\). The non-identifiable rank-3 tensors of this case are as follows. Let \( Y':={\mathbb {P}}^1\times {\mathbb {P}}^1\times \{ u_3\} \times \cdots \times \{ u_k\}\) be a proper subset of \(Y_{n_1,n_2,1^{k-2}} \), take \(q'\) in the span of the Segre image of \(Y'\) with the constraint that \(q'\) is not an elementary tensor. Therefore \(q'\) is a non-identifiable tensor of rank-2 since it can be seen as a \(2\times 2\) matrix of rank-2. Let \(p\in X_{n_1,n_2,1^{k-2}}\) be a rank-1 tensor taken outside the Segre image of \(Y'\). Now any point \(q \in \langle \{q',p \} \rangle {\setminus } \{q', p\} \) is a rank-3 tensor (cf. Proposition 4.5) and it is not identifiable since \(q'\) has an infinite number of decompositions and each of these decompositions can be taken by considering p together with a decomposition of \(q'\).

    For a coordinate description of this case, we take \(T\in \mathbb {C}^{m_1}\otimes \mathbb {C}^{m_2}\otimes (\mathbb {C}^2)^{\otimes (k-2)}\), where \(k\ge 3\), \(m_1,m_2\in \{2,3 \} \) such that \(m_1+m_2+ (k-2)\ge 4\). Moreover there exist distinct \(a_1,a_2\in {\mathbb {C}}^{m_1}\), distinct \(b_1,b_2\in {\mathbb {C}}^{m_2}\) and for all \(i\ge 3\) there exists a basis \( \{u_i,\tilde{u}_i\}\) of the ith factor such that T can be written as

    $$\begin{aligned} T= (a_1\otimes b_1+a_2\otimes b_2)\otimes u_3 \otimes \cdots \otimes u_k + a_3 \otimes b_3\otimes \tilde{u}_3 \otimes \cdots \otimes \tilde{u}_k, \end{aligned}$$

    where if \(m_1=2\) then \(a_3\in \langle a_1,a_2\rangle \) otherwise \(a_1,a_2,a_3\) are linearly independent. Similarly, if \( m_2=2\) then \(b_3 \in \langle b_1,b_2\rangle \), otherwise \( b_1,b_2,b_3\) form a basis of the second factor.

For a more detailed overview of the next couple of sections we refer to [53].

2.1 Concision

Fix a tensor \(T\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k}\), where \( k\ge 2\) and \(n_1,\dots ,n_k\ge 1 \). For all \( \ell =1,\dots , k\), denote by \({\mathcal {B}}_\ell =\{e^\ell _1,\dots ,e^\ell _{n_\ell }\} \) an ordered basis of \({\mathbb {C}}^{n_\ell } \) and by \({\mathcal {B}}^*_\ell =\{\eta ^\ell _1,\dots ,\eta ^\ell _{n_\ell } \} \) the corresponding dual basis. Let \(T= (t_{i_1,i_2,\cdots , i_k})\) be the coordinates of T with respect to those bases.

A useful operation that allows to store the elements of a tensor as a matrix is the flattening (cf. [42, Section 3.4]) and the oldest reference we found for a definition of this operation is [35, Section 7].

Definition 2.2

The \(\ell \)th flattening of a tensor \( T\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k}\) whose coordinates in the canonical basis \(\{e_{i_1}^1 \otimes \cdots \otimes e_{i_k}^k\}\) are \(t_{i_1,\dots ,i_k}\) is the linear map

$$\begin{aligned}&\varphi _\ell :({\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_{\ell -1}}\otimes {\mathbb {C}}^{n_{\ell +1}} \otimes \cdots \otimes {\mathbb {C}}^{n_k})^* \rightarrow {\mathbb {C}}^{n_\ell }\\&f\mapsto \sum _{i_1,\dots ,i_k} t_{i_1\dots i_k} f(e^1_{i_1} \otimes \cdots \otimes e^{\ell -1}_{i_{\ell -1 }} \otimes e^{\ell +1}_{i_{\ell +1}}\cdots \otimes e^{k}_{i_k}) e^\ell _{i_\ell } . \end{aligned}$$

We denote by \(T_\ell \) the \( n_\ell \times (\prod _{i\ne \ell } n_i)\) associated matrix with respect to bases \({\mathcal {B}}_\ell \) and \(\{\eta ^1_1\otimes \cdots \otimes \eta ^{\ell -1}_1\otimes \eta ^{\ell +1}_1 \otimes \cdots \otimes \eta ^k_1,\eta ^1_1\otimes \cdots \otimes \eta ^{\ell -1}_1\otimes \eta ^{\ell +1}_1 \otimes \cdots \otimes \eta ^k_2,\dots , \eta ^1_{n_1}\otimes \cdots \otimes \eta ^{\ell -1}_{n_{\ell -1}}\otimes \eta ^{\ell +1}_{n_{\ell +1}} \otimes \cdots \otimes \eta ^k_{n_k} \}\).

Definition 2.3

[35] Let \(T\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k}\). For all \(\ell =1,\dots ,k\) let \(T_\ell \) be the \(\ell \)th flattening of T as in Definition 2.2 and denote by \(r_\ell :=r(T_\ell ) \). The multilinear rank of T is the k-uple

$$\begin{aligned} mr(T):=(r_1,\dots ,r_k) \end{aligned}$$

containing the ranks of all the flattenings of T.

We remark that (cf. [20, Theorem 7]) for all \( \ell =1,\dots ,k\)

$$\begin{aligned} r_\ell \le r(T) \le \prod _{i\ne \ell }r_i \end{aligned}$$
(1)

and moreover it is classically known that

$$\begin{aligned} r(T)=1 \iff \textit{ the multilinear rank of } T \textit{ is } (1,\dots ,1). \end{aligned}$$

We are now ready to recall the concision process for a tensor. The following Lemma is the base step also for the algorithm we are going to construct in order to test the possible identifiability of a given tensor T.

Lemma 2.4

(Concision/Autarky, [42, Prop. 3.1.3.1], [7, Lemma 3.3]) For any \(T \in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k} \) one can uniquely determine minimal integers \(k'\le k\) and \(n'_1,\dots , n'_{k'}\) with \(n'_i\le n_i \) such that

  • \( T\in {\mathbb {C}}^{n'_1}\otimes \cdots \otimes {\mathbb {C}}^{n'_{k'}}\subseteq {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k} \);

  • the rank of T as an element of \({\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k} \) is the same as the rank of T as an element of \({\mathbb {C}}^{n'_1}\otimes \cdots \otimes {\mathbb {C}}^{n'_{k'}} \);

  • any rank decomposition of T can be found in \({\mathbb {C}}^{n'_1}\otimes \cdots \otimes {\mathbb {C}}^{n'_{k'}} \).

We denote by \({\mathcal {T}}_{n'_1,\dots ,n'_{k'}}:={\mathbb {C}}^{n'_1}\otimes \cdots \otimes {\mathbb {C}}^{n'_{k'}}\) and we will call it the concise tensor space of T.

The lemma states that for any tensor \(T\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k} \) there exists a unique minimal tensor space included in \({\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k} \) that contains both the tensor and all its possible rank decompositions. Let us review more in details a procedure that computes the concise tensor space \({\mathcal {T}}_{n'_1,\dots ,n'_{k'}}\) of a given tensor \( T\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k}\) working in coordinates.

After having fixed basis of \({\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k}\), let \(T=(t_{i_1,\dots , i_k})\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k} \) be its coordinate representation, where all \(n_i\ge 1 \) and \(k\ge 2 \). For all \(\ell =1,\dots ,k \) consider the \(\ell \)-th flattening \(T_\ell \) of T as in Definition 2.2. For the sake of simplicity take \(\ell =1 \). The first column of \( T_1\) is

$$\begin{aligned} (t_{1,1,\dots ,1},t_{2,1,\dots ,1},\dots ,t_{n_1,1,\dots ,1})^T =\sum _{i=1}^{n_1}t_{i,1,\dots ,1}u^1_i=\sum _{i,j=1}^{n_1} t_{i,1,\dots , 1}\alpha ^1_j (u^1_i), \end{aligned}$$

which is referred to \(u^2_1\otimes \cdots \otimes u^k_1 \). The same holds for the other columns of \(T_1 \). Once we have computed \(n'_1:=r(T_1)\) we can extract \(n'_1\) linearly independent columns from \( T_1\), say \(u^1_1,\dots , u^1_{n'_1} \). Since \(\hbox {Im}(\varphi _1)= \langle u^1_1,\dots ,u^1_{n'_1} \rangle \cong {\mathbb {C}}^{n'_1}\subseteq {\mathbb {C}}^{n_1} \), we rewrite the other columns as a linear combination of the independent ones. The resulting tensor \( T'\) will therefore live in a smaller space \({\mathbb {C}}^{n'_1}\otimes {\mathbb {C}}^{n_2} \otimes \cdots \otimes {\mathbb {C}}^{n_k} \). By continuing this process for each flattening we arrive to the concise tensor space

$$\begin{aligned} {\mathcal {T}}_{n'_1,\dots ,n'_{k'}}={\mathbb {C}}^{n'_1} \otimes \cdots \otimes {\mathbb {C}}^{n'_{k'}} \end{aligned}$$

where we may assume \(n'_i>1\) for all \(i=1,\dots ,k' \) and \( k'\le k\) since \({\mathbb {C}}^{n'_1}\otimes \cdots \otimes {\mathbb {C}}^{n'_{k'}}\otimes \{u_1\} \otimes \cdots \otimes \{u_{k-k'}\}\cong {\mathbb {C}}^{n'_1}\otimes \cdots \otimes {\mathbb {C}}^{n'_{k'}}\).

We remark that the above procedure to perform concision is essentially the way in which the sequentially truncated high order singular value decomposition (ST-HOSVD) works (cf. [58, Section 6]). The difference between this process and the ST-HOSVD is that in the ST-HOSVD is used a specific, numerically suitable basis of left singular vectors, rather than an arbitrary basis. We also remark that the standard way to compute concision would be using the ST-HOSVD (cf. [28]).

2.2 Matrix pencils

In this subsection we review some basic facts on matrix pencils that will be useful for the construction of the algorithm. We will briefly describe how to achieve the Kronecker normal form of any matrix pencil and we refer to [29, Vol. 1, Ch. XII] for a detailed exposition.

For the rest of this subsection, unless specified, we will work over an arbitrary field \({\mathbb {K}}\) of characteristic 0.

Fix integers \(m,n>0\). A polynomial matrix \(A(\lambda )\) is a matrix whose entries are polynomials in \(\lambda \), namely

$$\begin{aligned} A(\lambda )=(a_{i,j}(\lambda ))_{i=1,\dots , m, j=1,\dots , n}, \hbox { where } a_{i,j}(\lambda ):=a^{(0)}_{i,j}+a^{(1)}_{i,j} \lambda +\cdots + a^{(l)}_{i,j}\lambda ^l, \end{aligned}$$

for some \(l>0\). If we set \(A_k:=(a_{i,j}^{(k)})\), then we can write \(A(\lambda )\) as

$$\begin{aligned} A(\lambda )=A_0+\lambda A_1 +\cdots +\lambda ^l A_l. \end{aligned}$$

The rank \(r(A(\lambda ))\) of \(A(\lambda )\) is the positive integer r such that all \(r+1\) minors of \(A(\lambda )\) are identically zero as polynomials in \(\lambda \) and there exists at least one minor of size r which is not identically zero. A matrix pencil is a polynomial matrix of type \(A(\lambda )=A_0+\lambda A_1\). Given two matrix pencils \(A(\lambda )=A_0+\lambda A_1\) and \(B(\lambda )=B_0+\lambda B_1\), we say that \(A(\lambda )\) and \(B(\lambda )\) are strictly equivalent if there exist two invertible matrices P, Q such that

$$\begin{aligned} P(A_0+ \lambda A_1)Q=B_0+\lambda B_1. \end{aligned}$$

We shall see that the Kronecker normal form of a matrix pencil is determined by a complete system of invariants with respect to the strict equivalence relation defined above.

Any matrix pencil \(A_0+ \lambda A_1\) of size \(m\times n\) can be either regular or singular:

Definition 2.5

Let \(A_0,A_1\in M_{m,n}({\mathbb {K}})\). A pencil of matrices \(A_0+ \lambda A_1\) is called regular if

  1. (1)

    both \(A_0\) and \(A_1\) are square matrices of the same order m;

  2. (2)

    the determinant \(\det (A_0+ \lambda A_1)\) does not vanish identically in \(\lambda \).

Otherwise the matrix pencil is called singular.

We now recall how to find the normal form of a pencil \(A_0+ \lambda A_1\) depending on whether it is regular or not.

2.2.1 Normal form of regular pencils

In the case of regular pencils, normal forms can be found by looking at the elementary divisors of a given matrix pencil. In order to introduce them, it is convenient to consider the pencil \(A_0+ \lambda A_1\) with homogeneous parameters \(\lambda , \mu \), i.e. \(\mu A_0 +\lambda A_1\).

Let \(\mu A_0 + \lambda A_1\) be the rank r homogeneous matrix pencil associated to \(A_0+ \lambda A_1\). For all \(j=1,\dots ,r\), denote by \(D(\lambda ,\mu )_j\) the greatest common divisor of all the minors of order j in \(\mu A_0+ \lambda A_1\) and set \(D_0(\lambda ,\mu )=1\). Define the following polynomials

$$\begin{aligned} i_j(\lambda ,\mu ):=\frac{D_{r-j+1}(\lambda ,\mu )}{D_{r-j} (\lambda ,\mu )}, \hbox { for all } j=1,\dots ,r. \end{aligned}$$

Note that all \(i_j(\lambda ,\mu )\in {\mathbb {K}}[\lambda ,\mu ]\) can be split into products of powers of irreducible homogeneous polynomials that we call elementary divisors. Elementary divisors of the form \(\mu ^q\) for some \(q>0\) are called infinite elementary divisors.

One can prove that two regular pencils \(A_0+ \lambda A_1\) and \(B_0+\lambda B_1\) are strictly equivalent if and only if they have the same elementary divisors and infinite elementary divisors (cf. [29, Vol. 2, Ch. XII, Theorem 2]). Therefore elementary divisors and infinite elementary divisors are invariant with respect to the strict equivalence relation. Moreover they form a complete system of invariants for the strict equivalence relation since they are irreducible elements with respect to the fixed field \({\mathbb {K}}\). This is the reason why the polynomials \(i_j(\lambda ,\mu )\) defined above are actually called invariant polynomials for all \( j=1,\dots ,r\).

We recall that the companion matrix of a monic polynomial \(g(\lambda )=a_0+a_1\lambda +\cdots +a_{n-1}\lambda ^{n-1} +\lambda ^{n}\) is

$$\begin{aligned} L=\begin{bmatrix} 0&{} 1 &{} 0 &{}\ldots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{}\ddots &{} \vdots \\ 0 &{} \ldots &{}0 &{} 1&{}0\\ 0 &{}\ldots &{} \ldots &{}0 &{}1 \\ -a_0 &{} -a_1 &{}\ldots &{} \ldots &{} -a_{n-1} \end{bmatrix}. \end{aligned}$$

Theorem 2.6

[29, Vol. 2, Ch. XII, Theorem 3] Every regular pencil \(A_0+ \lambda A_1\) can be reduced to a (strictly equivalent) canonical block diagonal form of the following type

$$\begin{aligned} {[}N^{(u_1)};\dots ; N^{(u_s)};J_{v_1};\dots ; J_{v_t};L_{w_1};\dots ; L_{w_p}], \end{aligned}$$

where

  • The first s diagonal blocks are related to infinite elementary divisors \(\mu ^{u_1},\dots ,\mu ^{u_s}\) of the pencil \(A_0+ \lambda A_1\) and for all \(i=1,\dots , s\)

    $$\begin{aligned} N^{(u_i)}=\begin{bmatrix} 1 &{} \lambda &{} &{} \\ &{} \ddots &{}\ddots \\ &{} &{} 1&{} \lambda \\ &{} &{} &{} 1 \end{bmatrix} \in M_{u_i}({\mathbb {K}}). \end{aligned}$$

  • The blocks \(J_{v_i}\) are the Jordan blocks related to elementary divisors of type \((\lambda -\lambda _i)^{v_i}\).

  • The last p diagonal blocks \(L_{w_1},\dots ,L_{w_p}\) are the companion matrices associated to the remaining elementary divisors of \(A_0+ \lambda A_1\).

2.2.2 Normal form of singular pencils

In the previous case, a complete system of invariants was made by both elementary divisors and infinite ones. We shall see that, in case of singular pencils, this is not sufficient to determine a complete system of invariants with respect to the strict equivalence relation. Fix \(m\le n\) and let \(A_0+ \lambda A_1\) be a singular pencil of rank r, where \(A_0,A_1\in M_{m,n}({\mathbb {K}})\). Since the pencil is singular, the columns of \(A_0+ \lambda A_1\) are linearly dependent, therefore the system

$$\begin{aligned} (A_0+ \lambda A_1)x=0 \end{aligned}$$
(2)

has a non-zero solution with respect to x. Note that any solution \(\tilde{x}\) of the above system is a vector whose entries are polynomials in \(\lambda \), i.e. \(\tilde{x}=\tilde{x}(\lambda )\). It has been proven in [29, Vol. 2, Ch. XII, Theorem 4] that if equation (2) has a solution of minimal degree \(\varepsilon \ne 0\) with respect to \(\lambda \), the singular pencil \(A_0+ \lambda A_1\) is strictly equivalent to

$$\begin{aligned} \begin{bmatrix} L_{\varepsilon } &{} \\ &{} \hat{A_0}+\lambda \hat{A_1} \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} L_{\varepsilon }=\begin{bmatrix} \lambda &{} 1 &{}&{}\\ &{} \ddots &{} \ddots &{} \\ &{} &{}\lambda &{} 1 \end{bmatrix} \in M_{\varepsilon ,\varepsilon +1}({\mathbb {K}}), \end{aligned}$$

and \(\hat{A_0}+\lambda \hat{A_1}\) is a pencil of matrices for which the equation analogous to (2) has no solution of degree less than \(\varepsilon \).

By applying the previous result iteratively, a singular pencil \(A_0+ \lambda A_1\) is strictly equivalent to the block diagonal matrix

$$\begin{aligned} {[}L_{\varepsilon _1};\dots ;L_{\varepsilon _p};A_{0,p} +\lambda A_{1,p}], \end{aligned}$$

where \(0\ne \varepsilon _1\le \cdots \le \varepsilon _p\) and the last block is such that \((A_{0,p}+\lambda A_{1,p})x=0\) has no non zero solution, i.e. the columns of \(A_{0,p}+\lambda A_{1,p}\) are linearly independent. Then one looks at the rows of \(A_{0,p}+\lambda A_{1,p}\). If these are linearly dependent, one can apply the same procedure just described by considering the associated system of the transposed pencil.

Now let us treat the case in which there are some relations of degree zero (with respect to \(\lambda \)) between the rows and the columns of the given pencil \(A_0+ \lambda A_1\). Denote by g and h the maximal number of independent constant solutions of equations

$$\begin{aligned} (A_0+ \lambda A_1)x=0 \hbox { and } (A_0^T+\lambda A_1^T)x=0 \hbox { respectively}. \end{aligned}$$

Let \(e_1,\dots , e_g\in {\mathbb {K}}^n\) be linearly independent solutions of the system \((A_0+ \lambda A_1)x=0\), completing them to a basis of \({\mathbb {K}}^n\) and rewriting the pencil with respect to this basis, we get \(\tilde{A}_{0,1}+\lambda \tilde{A}_{1,1}=\begin{bmatrix} 0_{m\times g}&\tilde{A}_{0,1}+\lambda \tilde{A}_{1,1}\end{bmatrix}\). One can do the same by taking h linearly independent vectors that are solutions of the transpose pencil and hence the first h rows of \(\tilde{A}_{0,1}+\lambda \tilde{A}_{1,1}\) are zero with respect this new basis. Thus we obtain

$$\begin{aligned} \begin{bmatrix} 0_{h\times g} &{} \\ &{} \hat{A}_0+\lambda \hat{A}_1 \end{bmatrix}, \end{aligned}$$

where \( \hat{A}_0+\lambda \hat{A}_1 \) does not have any degree zero relation, and hence either \(\hat{A}_0+\lambda \hat{A}_1\) satisfies the assumptions of [29, Vol. 2, Ch. XII, Theorem 4] or it is a regular pencil.

There is a quicker way, due to Kronecker, to determine the canonical form of a given pencil, avoiding the iterative reduction just explained. It involves the notion of minimal indices. These last, together with elementary divisors (possibly infinite) will form a complete system of invariants for non singular pencils.

Let \(A_0+ \lambda A_1\) be a non singular pencil and let \(x_1(\lambda )\) be a non zero solution of least degree \(\varepsilon _1\) for \((A_0+ \lambda A_1)x=0\). Take \(x_2(\lambda )\) as a solution of least degree \(\varepsilon _2\) such that \(x_2(\lambda )\) is linearly independent from \(x_1(\lambda )\). Continuing this process, we get a so called fundamental series of solutions of the system

$$\begin{aligned} x_1(\lambda ),\dots , x_p(\lambda ), \hbox { of degrees } \varepsilon _1\le \cdots \le \varepsilon _p, \hbox { for some } p\le n. \end{aligned}$$

We remark that a fundamental series of solution is not uniquely determined, but one can show that the degrees \(\varepsilon _1,\dots , \varepsilon _p\) are the same for any fundamental series associated to a given system \((A_0+ \lambda A_1)x=0\). The minimal indices for the columns of \(A_0+ \lambda A_1\) are the integers \(\varepsilon _1,\dots ,\varepsilon _p\). Similarly, the minimal indices for the rows are the degrees \(\eta _1,\dots , \eta _q\) of a fundamental series of solutions of \((A_0^T+\lambda A_1^T)x=0\). Strictly equivalent pencils have the same minimal indices (cf. [29, Vol. 2, Ch. XII, Sec. 5, Par. 2]).

Now let \(A_0+ \lambda A_1\) be a singular pencil and consider its normal form

$$\begin{aligned} \begin{bmatrix} 0_{h\times g} &{} &{} &{} &{} &{} &{} &{}\\ &{}L_{\varepsilon _{g+1}} &{} &{} &{} &{} &{} &{}\\ &{} &{}\ddots &{} &{} &{} &{} &{}\\ &{} &{} &{} L_{\varepsilon _{p}} &{} &{} &{} &{}\\ &{} &{} &{} &{}L^T_{\eta _{h+1}} &{} &{} &{}\\ &{} &{} &{} &{} &{} \ddots &{} &{}\\ &{} &{} &{} &{} &{} &{} L^T_{\eta _{q}}&{}\\ &{} &{} &{} &{} &{} &{} &{} \hat{A}_0+\lambda \hat{A}_1\\ \end{bmatrix}. \end{aligned}$$
(3)

Remark 2.1

The system of indices for the columns (rows) of the above block diagonal matrix is obtained by taking the union of the corresponding system of minimal indices of the individual blocks.

We want to determine minimal indices for the above normal form (3). By the previous remark, it is sufficient to determine the minimal indices for each block. Clearly the regular block \(\hat{A}_0+\lambda \hat{A}_1\) has no minimal indices, the zero block \(0_{h\times g}\) has g minimal indices for columns and h minimal indices for rows all equal to zero respectively, namely \(\varepsilon _1=\cdots =\varepsilon _g=\eta _1=\cdots =\eta _h=0\). The block \(L_{\varepsilon _i}\in M_{\varepsilon _i,\varepsilon _i +1}({\mathbb {K}})\) has linearly independent rows, therefore it has just one minimal index for column \(\varepsilon _i\) for all \(i=1,\dots , p\). Similarly, for all \(j=1,\dots ,q \) the block \(L_{\eta _j}\) has just one minimal index for rows \(\eta _{j}\).

We conclude that the canonical form (3) is completely determined by both the minimal indices \(\varepsilon _1,\dots ,\varepsilon _p,\) \(\eta _1,\dots ,\eta _q\) and the elementary divisors.

Two arbitrary pencils \(A_0+ \lambda A_1\) and \(B_0+ \lambda B_1\) of rectangular matrices are strictly equivalent if and only if they have the same minimal indices and the same elementary divisors (possibly infinite); this result is classically attributed to Kronecker. We conclude this part by illustrating with an example how to construct the Kronecker normal form of a matrix pencil.

Example 2.1

Consider the pencil

$$\begin{aligned} A_0+ \lambda A_1= \begin{bmatrix} 1 &{} 0&{}\lambda &{} 3\lambda +1 &{} 1 &{} 2\\ 2\lambda &{} \lambda &{} \lambda &{} 3 &{} \lambda &{}0\\ 0 &{}0&{}0&{} 1&{}1&{}1\\ 2\lambda +1&{} \lambda &{} 2\lambda +1&{} 3\lambda +4 &{} \lambda +1 &{} 2 \end{bmatrix}. \end{aligned}$$

The kernel of the system \((A_0+ \lambda A_1)x=0\) is generated by

$$\begin{aligned} \textrm{Ker} (A_0\!+\! \lambda A_1)\!=\! \left\langle \begin{bmatrix} 1&1&-3&1&0&-1 \end{bmatrix}^T, \begin{bmatrix} 1&-3&0&0&1&-1 \end{bmatrix}^T, \begin{bmatrix} -\lambda ^2&2\lambda ^2-\lambda -1&\lambda&0&0&0 \end{bmatrix}^T \right\rangle . \end{aligned}$$

Since the minimum index of the non-constant solution is \(\varepsilon =2\), we know that the normal form of the pencil contains the following block

$$\begin{aligned} L_{2}=\begin{bmatrix} \lambda &{} 1 &{}0 \\ 0 &{} \lambda &{}1 \end{bmatrix}. \end{aligned}$$

Moreover, we see that there are \(g=2\) linearly independent constant solutions. Considering the transpose pencil, then

$$\begin{aligned} \textrm{Ker} ((A_0+ \lambda A_1)^T)=\left\langle \begin{bmatrix} -1&-1&0&1 \end{bmatrix}^T\right\rangle , \end{aligned}$$

so there is just one constant solution. Therefore, keeping the above notation, \(\eta =0\) and \(h=1\). Moreover the invariant polynomials of the pencil are \(i_4(\lambda ,\mu )=0\), \(i_3(\lambda ,\mu )=\mu \) and all the others are equal to 1. Therefore the Kronecker normal form of \(A_0+ \lambda A_1\) is

$$\begin{aligned} \left[ \begin{array}{c|c|c} \begin{matrix} 0&{}0 \end{matrix} &{} &{} \\ \hline &{} \begin{matrix} \lambda &{}1 &{} 0 \\ 0 &{} \lambda &{} 1 \end{matrix} &{}\\ \hline &{} &{} 1 \end{array}\right] . \end{aligned}$$

2.2.3 3-Factors tensor spaces and matrix pencils

From now on we work again over \({\mathbb {C}}\). Any tensor \(T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^m\otimes {\mathbb {C}}^n\) can be seen as a matrix pencil via the isomorphism

$$\begin{aligned} {\mathbb {C}}^2\otimes ({\mathbb {C}}^m)^* \otimes ({\mathbb {C}}^n)^*&\xrightarrow {\sim } \{{\mathbb {C}}^m\times {\mathbb {C}}^n\xrightarrow {\Phi } {\mathbb {C}}^2\} . \end{aligned}$$

We can easily pass from a tensor \(T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^m\otimes {\mathbb {C}}^n\) to its associated matrix pencil (and vice versa) by fixing a basis on each factor and looking at T in its coordinates with respect to the fixed bases. For example, let us fix the canonical basis on each factor and let \(T=(t_{ijk})\in {\mathbb {C}}^2\otimes {\mathbb {C}}^m\otimes {\mathbb {C}}^n\). We can associate to T the map

$$\begin{aligned} \Phi _{T}:{\mathbb {C}}^m\times {\mathbb {C}}^n&\longrightarrow {\mathbb {C}}^2\\ (v,w)&\mapsto (v^TA_0w,v^TA_1w) \end{aligned}$$

where

$$\begin{aligned} A_0=(t_{1ij})_{i=1,\dots ,m,j=1,\dots ,n} \hbox { and } A_1=(t_{2ij})_{i=1,\dots ,m,j=1,\dots ,n}. \end{aligned}$$

Fixing the integer m equal to either 2 or 3 in \({\mathbb {C}}^2\otimes {\mathbb {C}}^m\otimes {\mathbb {C}}^n\) leads us to consider very special tensor formats, namely \({\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^n \) and \({\mathbb {C}}^2\otimes {\mathbb {C}}^3\otimes {\mathbb {C}}^n\). In these cases there is a finite number of orbits with respect to the action of products of general linear groups (cf. [39]). Such cases have been widely studied in [50], where the author gave a complete orbit classification working in the affine setting.

Remark that for any tensor belonging to either \({\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^n\) or \({\mathbb {C}}^2\otimes {\mathbb {C}}^3\otimes {\mathbb {C}}^n\) one can consider the associated matrix pencil and, by computing its Kronecker normal form, it is possible to understand its rank. This last result comes from the following more general statement that is historically attributed to Grigoriev, JáJá and Teichert. We refer to [15, Remark 5.4] for a historical note on the theorem.

Theorem 2.7

[32, 37, 38, 57] Let \(T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^m\otimes {\mathbb {C}}^n\) and let A be the corresponding pencil with minimal indices \(\varepsilon _1,\dots ,\varepsilon _p,\eta _1,\dots ,\eta _q\) and regular part \(C=\hat{A}_0+\lambda \hat{A}_1\) of size N. Let \(\delta (C)\) be the number of non-squarefree invariant polynomials of C. Then T is a tensor of rank

$$\begin{aligned} \sum _{i=1}^p (\varepsilon _i +1) + \sum _{i=1}^q (\eta _j +1) + N + \delta (C). \end{aligned}$$
(4)

In [15] the authors reviewed the orbits classification made in [50] and gave a geometric interpretation of the projectivization of all the orbits closures appearing in both cases. In the following section we will refer to the classification of [15] when necessary.

3 Algorithm for the non-identifiability of rank-3 tensors

The purpose of this section is to write Algorithm 3 where we can determine if a rank-3 tensor is not identifiable.

All possible cases of non-identifiabile rank-3 tensors are collected in Theorem 4.1.

  • The input of the algorithm we propose is a tensor \( T=(t_{i_1,i_2,\cdots ,i_k})\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k} \) presented in its coordinate description with respect to canonical basis, where \(k\ge 3 \), all \( n_j\ge 1\) and all \( i_j=1,\dots , n_j\), \(j=1,\dots ,k\).

  • The output of the algorithm is a statement telling if the given tensor is a rank-3 tensor that falls into one of the cases mentioned above or not.

The first step of Algorithm 3 is to compute the concise tensor space \({\mathcal {T}}_{n'_1,\dots , n'_{k'}}={\mathbb {C}}^{n'_1}\otimes \cdots \otimes {\mathbb {C}}^{n'_{k'}}\) of T that we have already detailed in Sect. 2.1, hence from now on we will work with concise tensors. Based on the resulting concise tensor space \({\mathcal {T}}_{n'_1,\dots ,n'_{k'}}\), we split the algorithm into two different parts depending on whether \({\mathcal {T}}_{n'_1,\dots ,n'_{k'}}\) is made by three factors or not. Section 3.1 is devoted to the 3-factors case while we refer to Sect. 3.2 for the other case.

Remark 3.1

Fix a tensor \(T\in {\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k}\) and compute the multilinear rank of T. By using the left inequality in (1) on each flattening \(\varphi _\ell \), we are able to exclude some of the cases in which r(T) is higher than 3. In those cases the algorithm stops since we are interested in rank-3 tensors. Moreover, if the multilinear rank of T contains more than \(k-3\) positions equal to 1 then T is either a rank-1 tensor or a matrix and we can also exclude these cases. Lastly, we remark that since the concise Segre of a rank-3 tensor is \(\nu ({\mathbb {P}}^{m_1}\times \cdots \times {\mathbb {P}}^{m_{k}})\) where all \(m_i\in \{1,2\}\) for all \(i=1,\dots ,k\), if one of the values in \(mr(T)=(\dim ({\mathbb {C}}^{m_i+1}))_{i=1,\dots ,k} \) is different from either 2 or 3 then we can immediately stop the algorithm. Therefore, at the end of the concision process, we deal only with a tensor \(T'\in {\mathbb {C}}_1^{n'_1}\otimes \cdots \otimes {\mathbb {C}}_{k'}^{n'_{k'}} \) such that

  • \(r(T')\ge 2 \),

  • \( 3\le k'\le k\)

  • all \(n'_i\in \{ 2,3\} \).

Now, depending on whether \( k'=3\) or \(k'\ge 4\), we split the algorithm in two different parts.

3.1 Three factors case

This subsection is devoted to treat the case in which the concise tensor space of the tensor T given in input has three factors. By Remark 3.1, the concise space \({\mathcal {T}}_{n_1, \dots ,n_{k}}={\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_{k}}\) of a tensor T is such that all \(n_i\in \{2,3\}\). Moreover, if \(k=3 \) the only possibilities for \({\mathcal {T}}_{n_1,n_2,n_3}\), up to a reordering of the factors, are:

  • \({\mathcal {T}}_{2,2,2}={\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2 \);

  • \({\mathcal {T}}_{3,2,2}={\mathbb {C}}^3\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2 \);

  • \({\mathcal {T}}_{3,3,2}={\mathbb {C}}^3\otimes {\mathbb {C}}^3\otimes {\mathbb {C}}^2 \);

  • \({\mathcal {T}}_{3,3,3}={\mathbb {C}}^3\otimes {\mathbb {C}}^3\otimes {\mathbb {C}}^3 \).

Remark 3.2

The presence of a \({\mathbb {C}}^2\) in \({\mathcal {T}}_{2,2,2}, {\mathcal {T}}_{3,2,2},{\mathcal {T}}_{3,3,2}\) allows to see all their elements as a matrix pencil (cf. Sect. 2.2), in these cases we are also able to compute the rank of one of those tensors by classifying their at its associated matrix pencils (cf. Theorem 2.7).

All the considerations made in the following will be summed up in Algorithm 1 at the end of the subsection to which Algorithm 3 will refer for the case of 3-factors.

3.1.1 \({\mathcal {T}}_{2,2,2}={\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\)

The second secant variety of \(X_{1,1,1}=\nu ({\mathbb {P}}^1\times {\mathbb {P}}^1\times {\mathbb {P}}^1)\subset {\mathbb {P}}^7\) fills the ambient space, i.e. \(\dim \sigma _2(X_{1,1,1})=7 \). Consequently, any tensor \([T] \in {\mathbb {P}}^7{\setminus } X_{1,1,1} \) is either an element of the open part \(\sigma _2^0(X_{1,1,1}) \) or an element of the tangential variety \( \tau (X_{1,1,1})\) of \( X_{1,1,1}\). Therefore if the concise tensor space of T is \({\mathcal {T}}_{2,2,2}={\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\), rank-1 is excluded and T has rank either 2 or 3. To detect the rank of T one can use the Cayley’s hyperdeterminant which is the defining equation of \(\tau (X_{1,1,1})\) (cf. [30]). Hence, if T is a concise tensor in \({\mathcal {T}}_{2,2,2}\) and satisfies the hyperdeterminant equation, then T has rank 3 and it is not identifiable, otherwise it has rank 2.

3.1.2 \({\mathcal {T}}_{3,2,2}={\mathbb {C}}^3\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\)

The non-identifiable rank-3 tensors of \({\mathcal {T}}_{3,2,2}={\mathbb {C}}^3\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\) come from cases d) and e) of Theorem 4.1.

If \({\mathcal {T}}_{3,2,2}\) is the concise tensor space of T, then obviously \(r(T)\ge 3 \). Moreover, by [42, Theorem 3.1.1.1], one can show that actually \( r(T)=3\) (cf. also [15, Table 1]). Therefore every concise \( T\in {\mathcal {T}}_{3,2,2}\) is a rank-3 tensor. Moreover, since the dimension of the third secant variety of \(X_{2,1,1}=\nu ({\mathbb {P}}^2\times {\mathbb {P}}^1\times {\mathbb {P}}^1)\subset {\mathbb {P}}^{11} \) is \(\min \{ 14,11\} \), the generic fiber of the projection from the abstract secant variety \(\textrm{Ab}\sigma _3(X_{1,1,1}):=\overline{\{ ((p_1,p_2,p_3),q) \in X_{1,1,1}^3\times {\mathbb {P}}^7 :q\in \langle p_1,p_2,p_3 \rangle \}}\) to the secant variety has projective dimension 2, so the generic element of \( \sigma _3(X_{2,1,1})\) has an infinite number of decompositions. Therefore, by [34, Chapter II, Ex 3.22, part (b)], any rank-3 tensor in \(\sigma _3(X_{2,1,1})\) is not identifiable, from which follows that any tensor whose concise tensor space is \({\mathcal {T}}_{3,2,2}={\mathbb {C}}^3\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2 \) is a non-identifiable rank-3 tensor.

Remark 3.3

Rank-3 tensors can also live in \(\sigma _2(X_{2,1,1})\) but a concise rank-3 tensor \(T\in {\mathcal {T}}_{3,2,2}\) lies only on the third secant variety of \(X_{2,1,1}\).

Both cases d) and e) of Theorem 4.1 can be treated by looking at the matrix pencil associated to the corresponding tensor.

Remark 3.4

In order to be consistent with the matrix pencil notation used in Sect. 2.2 in which the first factor is used as a parameter space for the pencil, we swap the first and third factor of \( {\mathcal {T}}_{3,2,2}\), working now on \({\mathcal {T}}_{2,2,3}= {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\).

[15, Table 1] offers a complete description of all orbits in \({\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\), providing also the orbit closure in each case together with the Kronecker normal form of each orbit representative and its rank. Since we are working with concise rank-3 tensors of \({\mathcal {T}}_{2,2,3}\), we are interested in cases 7 and 8 of [15, Table 1], i.e.

Table 1 Concise rank-3 tensors in \({\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\)
Full size table

where we considered all \( a_i\), \(b_j\), \(c_k\) are linearly independent elements of the corresponding factors and \(\lambda , \mu \) represent homogeneous coordinates with respect to the first factor of \({\mathcal {T}}_{2,2,3}\). Let us see what is the relation between the above Kronecker normal forms and our examples of non-identifiable rank-3 tensors in \({\mathcal {T}}_{2,2,3}\).

Lemma 3.1

The matrix pencil associated to any tensor \(T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\) belonging to e) is of the following form:

$$\begin{aligned} \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} 0 &{} \lambda \end{bmatrix} \sim \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} 0 &{} \mu \end{bmatrix}. \end{aligned}$$

Proof

Let \( T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\) be as in case e), so

$$\begin{aligned} T=\tilde{p}\otimes v_1\otimes u_1 +\tilde{p} \otimes v_2 \otimes u_2 + w\otimes (\alpha v_1+\beta v_2 ) \otimes u_3. \end{aligned}$$

The matrix pencil associated to T with homogeneous parameters \(\lambda , \mu \) referred to the basis \(\{\tilde{p},w\} \subset {\mathbb {C}}^2\) is

$$\begin{aligned} A= \begin{bmatrix} \lambda &{} 0 &{} \alpha \mu \\ 0 &{} \lambda &{} \beta \mu \end{bmatrix}. \end{aligned}$$

Since A is a singular pencil (cf. Definition 2.5), in order to achieve the normal form of A, we have to look at the minimum degree \(\varepsilon \) of the elements in

$$\begin{aligned} \hbox {Ker}(A)=\left\langle \begin{bmatrix} -\alpha \mu&-\beta \mu&\lambda \end{bmatrix}^T \right\rangle \end{aligned}$$

with respect to \(\lambda ,\mu \) (cf. Sect. 2.2). Since \( \varepsilon =1\), the normal form of A should contain a block of size \(\varepsilon \times (\varepsilon +1) \) of this type

$$\begin{aligned} \begin{bmatrix} \lambda &{} \mu &{} &{} \\ &{} &{} \ddots &{} \ddots &{} \\ &{} &{} &{} \lambda &{}\mu \end{bmatrix}. \end{aligned}$$

Therefore we can conclude that

$$\begin{aligned} A=\begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} 0 &{} \lambda \end{bmatrix}. \square \end{aligned}$$

Corollary 3.2

Let \( T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\). The tensor T is a non-identifiable rank 3 tensor coming from case e) of Theorem 4.1 if and only if the pencil associated to T is of the form

$$\begin{aligned} \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} 0&{} \lambda \end{bmatrix} \sim \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} 0 &{} \mu \end{bmatrix}. \end{aligned}$$

Proof

By Lemma 3.1, the matrix pencil associated to any tensor that belongs to case e) is

$$\begin{aligned} \hbox { either } \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} 0 &{} \lambda \end{bmatrix} \hbox { or } \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} 0 &{} \mu \end{bmatrix}. \end{aligned}$$

The vice versa also holds since actually the left above pencil corresponds to the tensor

$$\begin{aligned} a_1\otimes b_1\otimes c_1 +a_1\otimes b_2 \otimes c_3 + a_2 \otimes b_1 \otimes c_2 \end{aligned}$$

(considering the first factor as a parameter space for the pencil) which is as in case e). \(\square \)

Lemma 3.3

The matrix pencil associated to a tensor \(T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\) that is as in case d) is

$$\begin{aligned} \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} \lambda &{} \mu \end{bmatrix}. \end{aligned}$$

Proof

Let \(T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\) be as in case d), i.e. there is a basis \(\{u_i\}_{i\le 3}\subset {\mathbb {C}}^3\) and a basis \(\{v_1,v_2\}\subset {\mathbb {C}}^2\) such that

$$\begin{aligned} T= v_1\otimes v_1\otimes u_1+ v_2\otimes v_2 \otimes u_2+ (\alpha v_1+\beta v_2) \otimes (\alpha v_1+\beta v_2)\otimes u_3, \end{aligned}$$

for some \((\alpha ,\beta )\in {\mathbb {C}}^2\setminus \{ 0\} \). The matrix pencil associated to T with homogeneous parameters \(\lambda , \mu \) referred to the basis \(\{v_1,v_2\}\subset {\mathbb {C}}^2\) is

$$\begin{aligned} A= \begin{bmatrix} \lambda &{} 0&{} \alpha ^2\lambda + \alpha \beta \mu \\ 0 &{} \mu &{} \alpha \beta \lambda + \beta ^2\mu \end{bmatrix}. \end{aligned}$$

The kernel of A is

$$\begin{aligned} \hbox {Ker}(A)=\left\langle \begin{bmatrix} \alpha ^2 \lambda \mu +\alpha \beta \mu ^2&\alpha \beta \lambda ^2+\beta ^2\lambda \mu&-\lambda \mu \end{bmatrix}^T \right\rangle , \end{aligned}$$

so the minimum degree \(\varepsilon \) of the elements in \(\hbox {Ker}(A)\) with respect to \(\lambda ,\mu \) is 2. Therefore, the normal form of A is

$$\begin{aligned} \begin{bmatrix} \lambda &{} \mu &{}0 \\ 0 &{} \lambda &{} \mu \end{bmatrix} \square \end{aligned}$$

Corollary 3.4

Let \( T\in {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^3\). The tensor T is a non-identifiable rank-3 tensor coming from case d) of Theorem 4.1 if and only if the pencil associated to T is of the form

$$\begin{aligned} \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} \lambda &{} \mu \end{bmatrix}. \end{aligned}$$

Proof

By Lemma 3.3, the matrix pencil associated to any tensor that belongs to case d) is

$$\begin{aligned} \begin{bmatrix} \lambda &{} \mu &{} 0\\ 0 &{} \lambda &{}\mu \end{bmatrix}. \end{aligned}$$

The converse also holds since actually the above pencil corresponds to the tensor

$$\begin{aligned} e_1\otimes e_1 \otimes e_1 + (e_1\otimes e_2+e_2\otimes e_1) \otimes e_2 + e_2\otimes e_2\otimes e_3 \end{aligned}$$

which is as in case d). \(\square \)

3.1.3 \({\mathcal {T}}_{3,3,2}={\mathbb {C}}^3\otimes {\mathbb {C}}^3\otimes {\mathbb {C}}^2 \)

Let \({\mathcal {T}}_{3,3,2}\) be the concise tensor space of the input tensor T. We recall that the only non-identifiable rank-3 tensors in this case are the ones of case f) of Theorem 4.1 (cf. also Proposition 4.5). More precisely, let \( Y'={\mathbb {P}}^1\times {\mathbb {P}}^1\times \{ w \}\subset Y_{2,2,1}={\mathbb {P}}^2\times {\mathbb {P}}^2\times {\mathbb {P}}^1\). Take \(q'\in \langle \nu (Y') \rangle {\setminus } \nu (Y_{2,2,1}) \) and \( p\in Y_{2,2,1}{\setminus } Y'\). Then \([T]\in \langle q', \nu (p)\rangle \) is a rank-3 tensor and it is not identifiable. If we take \(\{u_i\}_{i\le 3} \subset {\mathbb {C}}^3 \) as a basis of the first factor, \(\{v_i\}_{i\le 3}\subset {\mathbb {C}}^3 \) as a basis of the second factor and \(\{w,\tilde{w} \}\subset {\mathbb {C}}^2\) as a basis of the third factor, then T is of the form

$$\begin{aligned} T= u_1\otimes v_1\otimes w+u_2\otimes v_2 \otimes w+u_3 \otimes v_3\otimes \tilde{w}. \end{aligned}$$
(5)

Again we can look at this case by considering the associated matrix pencil of T. As before (cf. Remark 3.4), to be consistent with the matrix pencil notation we already introduced, we swap the first and third factor of \({\mathcal {T}}_{3,3,2}\), working now on \({\mathcal {T}}_{2,3,3}={\mathbb {C}}^2\otimes {\mathbb {C}}^3\otimes {\mathbb {C}}^3\).

In [15, Table 3] all Kronecker normal forms contained in \({\mathcal {T}}_{2,3,3}\) are collected. Since we are interested in rank-3 tensors having \( {\mathcal {T}}_{2,3,3}\) as concise tensor space, the only possibilities in terms of matrix pencils are

$$\begin{aligned} \begin{bmatrix} \lambda &{} 0 &{} 0\\ 0 &{} \lambda &{} 0 \\ 0 &{} 0&{} \mu \end{bmatrix} \hbox { and } \begin{bmatrix} \lambda &{} 0 &{} 0\\ 0 &{} \lambda +\mu &{} 0 \\ 0 &{} 0&{} \mu \end{bmatrix}. \end{aligned}$$
(6)

Remark 3.5

The matrix pencil associated to (5) is the first one in (6) and it is easy to check that the tensor corresponding to the first matrix pencil in (6) is actually T.

Therefore, if the concise tensor space of T is \({\mathcal {T}}_{2,3,3,}\), it is sufficient to consider the normal form of the concise tensor \(T'\) related to T and check if it corresponds to

$$\begin{aligned} \begin{bmatrix} \lambda &{} 0 &{} 0\\ 0 &{} \lambda &{} 0 \\ 0 &{} 0&{} \mu \end{bmatrix}. \end{aligned}$$

Moreover, as in the previous case, we are able to detect the rank of any tensor having \({\mathcal {T}}_{2,3,3}\) as a concise tensor space (cf. Remark 3.2).

3.1.4 \({\mathcal {T}}_{3,3,3}={\mathbb {C}}^3\otimes {\mathbb {C}}^3\otimes {\mathbb {C}}^3\)

By Theorem 4.1, all rank-3 tensors whose concise tensor space is \({\mathcal {T}}_{3,3,3}\) are identifiable. Therefore if the concise tensor space of T is \({\mathcal {T}}_{3,3,3}\) we can immediately say that T does not belong to one of the 6 families of non-identifiable rank-3 tensors.

We collect all the considerations made in this subsection in Algorithm 1.

figure a

Listing 1 contains an implementation Algorithm 1 with the algebra software Macaulay2 [33]. The input of the function is a concise 3-factors tensor \(T\in {\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\otimes {\mathbb {C}}^{n_3}\), with \(2\le n_1\le n_2\le n_3 \le 3\). In practice T must be given as a list of matrices \(\{ A_1,\dots , A_{n_1}\}\), where each \(A_i\in M_{n_2\times n_3}({\mathbb {C}})\) as displayed in the following image.

figure b

For the case \((n_1,n_2,n_3)=(2,2,2)\) the algorithm evaluates the Cayley’s hyperdeterminant in the entries of the tensor, while for the remaining cases it computes the Kronecker normal form of the matrix pencil associated to the given T.

figure c

3.2 More than three factors

We are now ready to develop the case in which a concise tensor space of a tensor has more than 3 factors, i.e.

$$\begin{aligned} {\mathcal {T}}_{n_1,\dots ,n_{k}}={\mathbb {C}}^{n_1} \otimes \cdots \otimes {\mathbb {C}}^{n_{k}} \end{aligned}$$

where \( k>3\) and all \( n_i \in \{2,3\}\). We will first treat the case in which \(k=4\) and \(n_1=n_2=n_3 =n_4=2\) and then we will treat all together the remaining cases.

3.2.1 Non-identifiable tensors with at least 4 factors

Consider for the moment the 4-factors case, i.e.

$$\begin{aligned} {\mathcal {T}}_{n_1,n_2,n_3,n_4}={\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\otimes {\mathbb {C}}^{n_3}\otimes {\mathbb {C}}^{n_4}, \end{aligned}$$

where all \(n_i\in \{ 2,3\}\). Following the classification of Theorem 4.1, working with 4 factors there are only two families of non-identifiable tensors, namely items c) and f). Case f) is referred to non-identifiable rank-3 tensors of [10, Proposition 3.10] adapted to the 4-factors case, while case c) contains any rank-3 tensor in \({\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\). Let us first treat the case of \({\mathcal {T}}_{2^4} ={\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\).

3.2.2 \({\mathcal {T}}_{2^4}={\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\)

As already recalled, the third secant variety of the Segre variety \(X_{1^4}\) is defective (cf. [5, Theorem 4.5]). Moreover, at the end of Section 6 and in Section 7 of [19] is explicitely stated that every element of \(\sigma _3(X_{1^4})\setminus \sigma _2(X_{1^4})\) is a rank-3 tensor. Therefore any tensor in \(\sigma _3(X_{1^4}){\setminus } \sigma _2(X_{1^4})\) is a non-identifiable rank-3 tensor.

Thus, working over \({\mathcal {T}}_{2^4}\), to detect whether a given tensor \(T\in {\mathcal {T}}_{2^4}\) is a non-identifiable rank-3 tensor it is sufficient to verify if \([T]\in \sigma _3(X_{1^{4}}) {\setminus } \sigma _2(X_{1^{4}})\), i.e. if T satisfies the equations of \(\sigma _3(X_{1^4})\) (cf. [51, Theorem 1.4]) and T does not satisfies the equations of \(\sigma _2(X_{1^4})\) for which we refer to [43].

3.2.3 \({\mathcal {T}}_{n_1,\dots ,n_{k}}\ne {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\), with \(k\ge 4\), \(n_i=2,3\) for all \(i=1,\dots ,k\)

Let now \(k\ge 4\) with \({\mathcal {T}}_{n_1,\dots ,n_{k}}\ne {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\). In this case, any non-identifiable rank-3 tensor comes from case f) of Theorem 4.1. More precisely, let

$$\begin{aligned} Y':={\mathbb {P}}^1\times {\mathbb {P}}^1\times \{u_3 \} \times \cdots \times \{ u_k\}\subset Y_{m_1,m_2,1^{k-2}}={\mathbb {P}}^{m_1}\times {\mathbb {P}}^{m_2}\times {\mathbb {P}}^1 \times \cdots \times {\mathbb {P}}^1, \end{aligned}$$

with \(m_1,m_2\in \{ 1,2\}\). Let \(q'\in \langle \nu (Y') \rangle {\setminus } \nu (Y_{m_1,m_2,1^{k-2}}) \) and \( p\in Y_{m_1,m_2,1^{k-2}}{\setminus } Y'\). We saw that any \([T]\in \langle q', \nu (p)\rangle \) is a non-identifiable rank-3 tensor. Let \(\{u_i,\tilde{u}_i\}\) be a basis of the \({\mathbb {C}}^{n_i}\) arising from the ith factor of \(Y_{m_1,m_2,1^{k-2}}\) for all \( i\ge 3\). Take distinct \(a_1,a_2\in {\mathbb {C}}^{m_1+1}\) and distinct \(b_1,b_2\in {\mathbb {C}}^{m_2+1}\) and if \(m_1=1\) then let \(a_3\in \langle a_1,a_2\rangle \) otherwise we let \( a_1,a_2,a_3\) form a basis of the first factor. Let \( b_3 \in \langle b_1,b_2\rangle \) if \(m_2=1\), otherwise \( b_1,b_2,b_3\) form a basis of the second factor. With respect to these bases T can be written as

$$\begin{aligned} T=&(a_1\otimes b_1+a_2\otimes b_2)\otimes u_3 \otimes \cdots \otimes u_k + a_3 \otimes b_3\otimes \tilde{u}_3 \otimes \cdots \otimes \tilde{u}_k. \end{aligned}$$
(7)

Since the only type of tensors that we have to detect corresponds to (7), we may restrict ourselves to consider the following tensor spaces:

  • \({\mathcal {T}}_{3,2^{k-1}}={\mathbb {C}}^3 \otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes \cdots \otimes {\mathbb {C}}^2\);

  • \({\mathcal {T}}_{3,3,2^{k-2}}={\mathbb {C}}^3 \otimes {\mathbb {C}}^3 \otimes {\mathbb {C}}^2\otimes \cdots \otimes {\mathbb {C}}^2\);

  • \({\mathcal {T}}_{2^{k}}={\mathbb {C}}^2 \otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes \cdots \otimes {\mathbb {C}}^2\) (with \(k\ge 5\)).

Definition 3.5

Let \({\mathcal {T}}_{n_1,\dots ,n_k}={\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_k}\), fix integer \(k'\le k\) and let \(I=\cup _{i=1}^{k'} I_i\) be a partition of \(\{1,\dots ,k\}\). A reshaping of \({\mathcal {T}}\) of type \(I_1,\dots ,I_{k'} \) is a bijection

$$\begin{aligned} \vartheta _{I_1,\dots ,I_{k'}} : {\mathcal {T}}_{n_1,\dots ,n_k} \longrightarrow {\mathbb {C}}^{N_1}\otimes \cdots \otimes {\mathbb {C}}^{N_{k'}}, \end{aligned}$$

where \({\mathbb {C}}^{N_i}\cong \bigotimes _{j\in I_i}{\mathbb {C}}^{n_j} \) for all \(i=1,\dots ,k'\), i.e. \(N_i=\prod _{j\in I_i}n_i\) and \({\mathbb {C}}^{N_i}\) is the vectorization of \(\bigotimes _{j\in I_i}{\mathbb {C}}^{n_j}\).

In other words a reshaping of a tensor space \({\mathcal {T}}_{n_1,\dots ,n_k}\) is a different way of grouping together some of the factors of \({\mathcal {T}}_{n_1,\dots ,n_k}\) and forgetting their tensor structure (eventually it is also necessary to reorder the factors of \({\mathcal {T}}_{n_1,\dots ,n_k}\)). In the following we will be interested in the reshaping grouping together two factors of a tensor space \({\mathcal {T}}_{n_1,\dots ,n_k}\). More precisely, we will consider the partition \(\{i,j\}\cup \left( \{1,\dots ,k\}{\setminus } \{ i,j\}\right) \) for some \(i,j=1,\dots ,k\) and to lighten the notation we will set \(\vartheta _{\{i,j\}, \{1,\dots ,k\}{\setminus } \{i,j\} }=\vartheta _{i,j}\), i.e

$$\begin{aligned} \vartheta _{i,j} :{\mathbb {C}}^{n_1}\otimes \cdots \otimes {\mathbb {C}}^{n_{k}}\xrightarrow {\sim } ({\mathbb {C}}^{n_i}\otimes {\mathbb {C}}^{n_j}) \otimes {\mathbb {C}}^{n_1}\otimes \cdots \otimes \widehat{{\mathbb {C}}^{n_i}} \otimes \cdots \otimes \widehat{{\mathbb {C}}^{n_j}}\otimes \cdots \otimes {\mathbb {C}}^{n_{k}}, \end{aligned}$$

where we put a widehat on the removed factors.

Example 3.1

Let \({\mathcal {T}}_{n_1,\dots ,n_k}={\mathbb {C}}^{n_1} \otimes \cdots \otimes {\mathbb {C}}^{n_k}\) and denote by \(\vartheta _{1,2}\) the reshaping grouping together the first two factors of \({\mathcal {T}}_{n_1,\dots ,n_k}\)

$$\begin{aligned} \vartheta _{1,2}: {\mathcal {T}}_{n_1,\dots ,n_k}&\longrightarrow \left( {\mathbb {C}}^{n_1} \otimes {\mathbb {C}}^{n_2}\right) \otimes {\mathbb {C}}^{n_3} \otimes \cdots \otimes {\mathbb {C}}^{n_k} \\ T=\sum _{i_1=1}^{n_1}\cdots \sum _{i_k=1}^{n_k} t_{i_1,\dots ,i_k} e_{i_1}\otimes \cdots \otimes e_{i_k}&\mapsto \sum _{i_1=1}^{n_1}\cdots \sum _{i_k=1}^{n_k} t_{i_1,\dots ,i_l}(e_{i_1}\otimes e_{i_2})\otimes e_{i_3} \otimes \cdots \otimes e_{i_k}. \end{aligned}$$

Since \({\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2} \cong {\mathbb {C}}^{n_1n_2}\), by sending the basis \(\{ e_{i_1}\otimes e_{i_2}\}_{i_1=1,\dots ,n_1,i_2=1,\dots ,n_2}\) of \({\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\) to the basis \(\{e_{i_1,i_2}\}\) of \({\mathbb {C}}^{n_1n_2}\), we write

$$\begin{aligned} \vartheta _{1,2}(T)= \sum _{ i_1,\dots ,i_k } t_{i_1,i_2,i_3,\dots ,i_k} e_{i_1,i_2}\otimes e_{i_3}\otimes \cdots \otimes e_{i_k}\in {\mathbb {C}}^{n_1n_2}\otimes {\mathbb {C}}^{n_3}\otimes \cdots \otimes {\mathbb {C}}^{n_k}. \end{aligned}$$

The following lemma tells us how to completely characterize non-identifiable rank-3 tensors lying on either \({\mathcal {T}}_{3,2^{k-1}}\) or \({\mathcal {T}}_{3,3,2^{k-2}}\) or \({\mathcal {T}}_{2^k}\).

Lemma 3.6

Let \(T\in {\mathcal {T}}_{n_1,n_2,2^{k-2}}={\mathbb {C}}^{n_1} \otimes {\mathbb {C}}^{n_2}\otimes {\mathbb {C}}^2\otimes \cdots \otimes {\mathbb {C}}^2\) be a concise tensor in \({\mathcal {T}}_{n_1, n_2,2^{k-2}} \), where \(n_1,n_2\in \{2,3\}\), \(k\ge 4\) and \({\mathcal {T}}_{n_1,n_2,2^{k-2}}\ne {\mathcal {T}}_{2^4}\). Then T is as in case f) of Theorem 4.1 if and only if the following conditions hold:

  1. (1)

    the reshaped tensor \(\vartheta _{1,2}(T)\in {\mathbb {C}}^{n_1n_2}\otimes ({\mathbb {C}}^{2})^{\otimes (k-2)}\) is an identifiable rank-2 tensor with respect to \( {\mathbb {C}}^{n_1n_2}\otimes ({\mathbb {C}}^{2})^{\otimes (k-2)}\)

    $$\begin{aligned} \vartheta _{1,2}(T)=T_1+T_2=x\otimes u_3\otimes \cdots \otimes u_k + y \otimes v_3\otimes \cdots \otimes v_k \in {\mathbb {C}}^{n_1n_2} \otimes ({\mathbb {C}}^{2})^{\otimes (k-2)} \end{aligned}$$

    for some independent \(x,y\in {\mathbb {C}}^{n_1n_2}\) and some \(u_i,v_i\in {\mathbb {C}}^2\) with \(\{u_i,v_i\}\) linearly independent for all \(i=3,\dots ,k\);

  2. (2)

    looking at \(x,y \in {\mathbb {C}}^{n_1n_2}\) as elements of \({\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\) then \(\{r(x),r(y)\}=\{1,2\}\).

Proof

Let \(T\in {\mathcal {T}}_{n_1,n_2,2^{k-2}}\) be as in case f) of Theorem 4.1, so T can be written as

$$\begin{aligned} T=a_1\otimes b_1\otimes u_3\otimes \cdots \otimes u_{k} + a_2 \otimes b_2\otimes u_3\otimes \cdots \otimes u_k + a_3 \otimes b_3 \otimes v_3\otimes \cdots \otimes v_k, \end{aligned}$$

where \(u_i\ne v_i \) for all \(i=3,\dots , k\), \(a_1,a_2,a_3\) are linearly independent if \(n_1=3\) and \(b_1,b_2,b_3\) are linearly independent if \(n_2=3\). Let \(\vartheta _{1,2}\) be the reshaping grouping together the first two factors of \({\mathcal {T}}_{n_1,\dots ,n_k}\). Let \(x:=a_1\otimes b_1, y:= a_2\otimes b_2\) and \(z:=a_3\otimes b_3\) and remark that \(r(x+y)=2\) and \(r(z)=1\). Therefore

$$\begin{aligned} \vartheta _{1,2}(T)&=x\otimes u_3\otimes \cdots \otimes u_k + y\otimes u_3\otimes \cdots \otimes u_k + z\otimes v_3 \otimes \cdots \otimes v_k\\&= (x+y)\otimes u_3\otimes \cdots \otimes u_k + z \otimes v_3\otimes \cdots \otimes v_k\\&= T_1 + T_2 \in {\mathbb {C}}^{n_1n_2} \otimes {\mathbb {C}}^2\otimes \cdots \otimes {\mathbb {C}}^2. \end{aligned}$$

Note that the rank of \((T_1+T_2)\in {\mathcal {T}}_{n_1n_2,2^{k-2}}\) is at most 2 and in fact \(r(T_1+T_2)=2\) since \(u_i,v_i\) are linearly independent for all \(i=3,\dots ,k\). Moreover, we recall that the only non-identifiable rank-2 tensors are matrices (cf. [10, Proposition 2.3]). Therefore, since the concise tensor space of \(T_1+T_2\) is made by at least 3 factors, then \(T_1+T_2\) is an identifiable rank-2 tensor.

Vice versa let \(T \in {\mathcal {T}}_{n_1,n_2,2^{k-2}}\) such that \(\vartheta _{1,2}(T)\in {\mathbb {C}}^{n_1n_2}\otimes ({\mathbb {C}}^2)^{\otimes (k-2)}\) is an identifiable rank-2 tensor

$$\begin{aligned} \vartheta _{1,2}(T)=T_1+T_2=a\otimes u_3\otimes \cdots \otimes u_k+b \otimes v_3\otimes \cdots \otimes v_k, \end{aligned}$$

for some unique \(a,b\in {\mathbb {C}}^{n_1n_2}\) with \(\langle a, b\rangle \cong {\mathbb {C}}^2\) and unique \(u_i,v_i\in {\mathbb {C}}^2\) with \(\langle u_i, v_i\rangle \cong {\mathbb {C}}^2\) for all \(i=3,\dots ,k\). By assumption \(\vartheta ^{-1}_{1,2} (a),\vartheta ^{-1}_{1,2}(b)\in {\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\) are such that \(\{r(\vartheta ^{-1}_{1,2} (a)),r(\vartheta ^{-1}_{1,2}(b))\} = \{ 1,2\}\) and by relabeling if necessary we may assume \(r(\vartheta ^{-1}_{1,2}(a))=2\) and \(r(\vartheta ^{-1}_{1,2}(b))=1\).

Let us see \(\vartheta _{1,2}(T)\) as an element of \({\mathcal {T}}_{n_1,n_2,2^{k-2}}={\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\otimes {\mathbb {C}}^2\otimes \cdots \otimes {\mathbb {C}}^2\). Since \(T_2\) is a rank-1 tensor, there exist \(v_1\in {\mathbb {C}}^{n_1}\), \(v_2\in {\mathbb {C}}^{n_2}\) such that \(\vartheta ^{-1}_{1,2}(b)=v_1\otimes v_2\), i.e.

$$\begin{aligned} \vartheta ^{-1}_{1,2}(T_2)=v_1\otimes v_2\otimes v_3 \otimes \cdots \ \otimes v_k. \end{aligned}$$

Moreover, since \(r(\vartheta ^{-1}_{1,2}(a))=2\) then there exist linearly independent \(a_1,a_2\in {\mathbb {C}}^{n_1}\) and linearly independent \(b_1,b_2\in {\mathbb {C}}^{n_2}\) such that \(\vartheta ^{-1}_{1,2}(a)=a_1\otimes b_1+a_2\otimes b_2\), i.e.

$$\begin{aligned} \vartheta ^{-1}_{1,2}(T_1)= a_1\otimes b_1\otimes u_3\otimes \cdots \otimes u_k + a_2\otimes b_2\otimes u_3\otimes \cdots \otimes u_k. \end{aligned}$$

We remark that the concise space of T is \({\mathcal {T}}_{n_1,n_2,2^{k-2}}\), therefore if \(n_1=3\) (or \(n_2=3\)) then \(a_1,a_2, v_1\) are linearly independent (\(b_1,b_2,v_2\) are linearly independent). Thus T is as in case f). \(\square \)

Remark 3.6

In Lemma 3.6 we assumed that dealing with a tensor as in (7) the non-identifiable part of the tensor was in the first two factors because it is always possible to permute the factors of the tensor space in this way. This assumption cannot be made in the algorithm and we have to be careful if either \((n_1,n_2)=(3,2)\) or \((n_1,n_2)=(2,2)\). Dealing with \((n_1,n_2)=(3,2)\), we have to check if there exists \(i=2,\dots ,k\) such that \(\vartheta _{1,i}(T)\) satisfies the conditions of Lemma 3.6.

Similarly, for the case of \((n_1,n_2)=(2,2)\) we have to check all reshaping of T if necessary, i.e. we have to check if there exist \(i,j\in \{1,\dots ,k\}\) with \(i\ne j\) such that \(\vartheta _{i,j}(T)\) satisfies the conditions of Lemma 3.6.

Recall that a concise tensor \(T\in {\mathbb {C}}^{n_1n_2}\otimes ({\mathbb {C}}^2)^{\otimes (k-2)}\) is an element of \(\sigma _2(X_{(n_1n_2-1),1^{k-2}}){\setminus } \tau (X_{(n_2n_2-1),1^{k-2}})\) if and only if there is a specific change of basis on each factors \(\tilde{g}=(g,g_3,\dots ,g_k)\in GL_{n_1n_2}\times GL_2\times \cdots \times GL_2\) such that

$$\begin{aligned} \tilde{g}\cdot T=x\otimes u_3\otimes \cdots \otimes u_k + y \otimes v_3\otimes \cdots \otimes v_k. \end{aligned}$$
(8)

By Lemma 3.6, given an identifiable rank-2 tensor \(T\in {\mathcal {T}}_{n_1n_2,2^{k-2}}\), in order to verify if T is as in case f), we do not need to find an explicit decomposition of T as in (8) but it is enough made the following steps:

  • distinguish \(x,y\in {\mathbb {C}}^{n_1n_2}\) and look at them as elements of \({\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\);

  • prove that either \(r(x)=2\) and \(r(y)=1\) or that \(r(x)=1\) and \(r(y)=2\).

Let us explain in detail how to do so.

3.2.4 Reshaping procedure for an identifiable rank-2 tensor of \({\mathcal {T}}_{n_1n_2,2^{k-2}}\) (how to find \(x,y\in {\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\))

Let T be an identifiable rank-2 tensor in \({\mathcal {T}}_{n_1n_2,2^{k-2}}={\mathbb {C}}^{n_1n_2}\otimes ({\mathbb {C}}^2)^{\otimes (k-2)}\). Remark that the rank of the first flattening \(\varphi _1:({\mathbb {C}}^2)^{\otimes (k-2)}\rightarrow ({\mathbb {C}}^{n_1n_2})\) of T is 2 and, to complete the concision process, there exist two independent elements \(\widehat{x},\widehat{y} \) of \(\hbox {Im}(\varphi _1)\) for which T can be written as

$$\begin{aligned} T=\widehat{x}\otimes u_3\otimes \cdots \otimes u_k + \widehat{y} \otimes v_3\otimes \cdots \otimes v_k\in {\mathbb {C}}^2\otimes ({\mathbb {C}}^2)^{\otimes k}. \end{aligned}$$

If we reshape our tensor space by grouping together all factors from the 4th one onwards, then T can be seen as

$$\begin{aligned}&\widehat{x} \otimes u_3\otimes \overbrace{(u_4\otimes \cdots \otimes u_k)}^{\widehat{u}}+\widehat{y}\otimes v_3 \otimes \overbrace{(v_4\otimes \cdots \otimes v_k)}^{\widehat{v}}\\&\quad =\widehat{x} \otimes u_3\otimes \widehat{u} + \widehat{y} \otimes v_3\otimes \widehat{v}\in {\mathbb {C}}^2 \otimes {\mathbb {C}}^2\otimes (({\mathbb {C}}^2)^{\otimes (k-3)}). \end{aligned}$$

We want to look at this 3-factors tensor as a pencil of matrices with respect to the second factor of \({\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes ({\mathbb {C}}^{2})^{\otimes (k-3)}\). Let \(u_3=(u_{3,1},u_{3,2})\), \(v_3=(v_{3,1},v_{3,2})\) and denote by

$$\begin{aligned} C_1:=\begin{bmatrix} u_{3,1} \widehat{x}\otimes \widehat{u} \\ v_{3,1} \widehat{y}\otimes \widehat{v} \end{bmatrix}, \; C_2:=\begin{bmatrix} u_{3,2} \widehat{x}\otimes \widehat{u} \\ v_{3,2} \widehat{y}\otimes \widehat{v} \end{bmatrix}\in {\mathbb {C}}^2\otimes ({\mathbb {C}}^{2})^{\otimes (k-3)}. \end{aligned}$$

We can write T as \(C_1\lambda +C_2\mu .\) Call \(X_3\) the matrix whose columns are given by \(\widehat{x}\) and \(\widehat{y}\) and denote by \(X_4\) the matrix whose rows are given by \(\widehat{u} \) and \(\widehat{v}\). Therefore

$$\begin{aligned} C_1 = \begin{bmatrix} \widehat{x}&\widehat{y} \end{bmatrix} \begin{bmatrix} u_{3,1} &{} 0 \\ 0 &{} v_{3,1} \end{bmatrix} \begin{bmatrix} \widehat{u} \\ \widehat{v} \end{bmatrix} = X_3 \begin{bmatrix} u_{3,1}&{}0\\ 0 &{} v_{3,1}\end{bmatrix}X_4, \\ C_2 = \begin{bmatrix} \widehat{x}&\widehat{y} \end{bmatrix} \begin{bmatrix} u_{3,2} &{} 0 \\ 0 &{} v_{3,2} \end{bmatrix} \begin{bmatrix} \widehat{u} \\ \widehat{v} \end{bmatrix} = X_3 \begin{bmatrix} u_{3,2}&{}0\\ 0 &{} v_{3,2}\end{bmatrix}X_4. \end{aligned}$$

Remark that \(C_2\) is right invertible and denote by \(C_2^{-1}\) its right inverse. Moreover \(r(X_3)=r(X_4)=2\), therefore \(X_3\) is invertible and there exists a right inverse of \(X_4\) that we denote by \(X_4^{-1}\). Thus

$$\begin{aligned} C_1C_2^{-1}&=\left( X_3 \begin{bmatrix} u_{3,1}&{}0\\ 0 &{} v_{3,1}\end{bmatrix}X_4\right) \left( X_3 \begin{bmatrix} u_{3,2}&{}0\\ 0 &{} v_{3,2}\end{bmatrix}X_4\right) ^{-1}\\&= X_3 \begin{bmatrix} \frac{u_{3,1}}{u_{3,2}}&{}0\\ 0 &{} \frac{v_{3,1}}{v_{3,2}}\end{bmatrix}X_3^{-1}. \end{aligned}$$

We have now an eigenvalue problem that we can easily solve to find \(\widehat{x},\widehat{y}\in {\mathbb {C}}^2\).

Remark 3.7

When computing the concision process of T with respect to the first factor of \({\mathcal {T}}_{n_1n_2,2^{k-2}}\), we concretely find a basis of \(\hbox {Im}(\varphi _1)\). Therefore, after we found \(\widehat{x},\widehat{y}\in {\mathbb {C}}^2\) with the above procedure, we can easily get back to \(x,y\in {\mathbb {C}}^{n_1n_2}\cong {\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\) and compute the rank of both x, y seen as elements of \({\mathbb {C}}^{n_1}\otimes {\mathbb {C}}^{n_2}\).

We remark that the above procedure describes a so-called pencil-based algorithm to compute the tensor rank decomposition and we refer to [45, 47, 55, 56].

We sum up how to find a non-identifiable rank-3 tensor of at least 4 factors in Algorithm 2.

A code implementation in Macaulay2 of the above algorithm is available at the repository website MathRepo of MPI MiS via the link https://mathrepo.mis.mpg.de/identifiabilityRank3tensors.

Example 3.2

Let \( {\mathcal {T}}_{3,2,2,2}={\mathbb {C}}^3\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\) and for all \(j,k,\ell = 1,2\) and for all \(i=1,2,3\) denote \(e_{i,j,k,\ell }=e_i\otimes e_j\otimes e_k \otimes e_\ell \). To lighten the notation we also set \(e_{i}e_{j}=e_i\otimes e_j\). Consider the tensor

$$\begin{aligned} T&=12 e_{1,1,1,1}+ 8e_{1,1,1,2}+ 6 e_{1,1,2,1}+4 e_{1,1,2,2} +30e_{1,2,1,1}+20e_{1,2,1,2}+15e_{1,2,2,1} \\&\quad +10e_{1,2,2,2}+8e_{2,1,1,1}+8e_{2,1,1,2}+5e_{2,1,2,1} +6e_{2,1,2,2}+35e_{2,2,1,1}+38e_{2,2,1,2}\\&\quad +23e_{2,2,2,1} + 30e_{2,2,2,2} + 16e_{3,1,1,1} + 16e_{3,1,1,2} +10e_{3,1,2,1} +12e_{3,1,2,2} \\&\quad +52e_{3,2,1,1} + 64e_{3,2,1,2} + 37e_{3,2,2,1} +54e_{3,2,2,2}. \end{aligned}$$

Let \(\vartheta _{1,2}:{\mathcal {T}}_{3,2,2,2}\rightarrow {\mathbb {C}}^6\otimes {\mathbb {C}}^2\otimes {\mathbb {C}}^2\) be the reshaping grouping together the first two factors of \({\mathcal {T}}_{3,2,2,2}\). Let

$$\begin{aligned}{} & {} \vartheta _{1,2}(e_1e_1)=e_{1,1}, \; \vartheta _{1,2}(e_1e_2)=e_{1,2}, \; \vartheta _{1,2}(e_2e_1)= e_{2,1},\\{} & {} \vartheta _{1,2}(e_2e_2) = e_{2,2}, \; \vartheta _{1,2}(e_3e_1) = e_{3,1}, \; \vartheta _{1,2}(e_3e_2)=e_{3,2} \end{aligned}$$

be a basis of \({\mathbb {C}}^6\) such that \(\vartheta _{1,2}(T)\) can be written as

$$\begin{aligned} \vartheta _{1,2}(T)&=12 e_{1,1}\otimes e_1e_1+ 8 e_{1,1} \otimes e_1e_2+ 6e_{1,1}\otimes e_2e_1+4 e_{1,1}\otimes e_2e_2\\&\quad +30e_{1,2}\otimes e_1 e_1+20e_{1,2}\otimes e_1 e_2+15 e_{1,2} \otimes e_2 e_1+ 10 e_{1,2} \otimes e_2 e_2\\&\quad +8 e_{2,1}\otimes e_1 e_1+8 e_{2,1} \otimes e_1 e_2+5 e_{2,1} \otimes e_2 e_1+6 e_{2,1} \otimes e_2e_2\\&\quad +35 e_{2,2}\otimes e_1 e_1+38 e_{2,2} \otimes e_1 e_2+23 e_{2,2} \otimes e_2 e_1 + 30 e_{2,2} \otimes e_2 e_2 \\&\quad +16 e_{3,1} \otimes e_1 e_1 + 16 e_{3,1} \otimes e_1e_2 +10 e_{3,1} \otimes e_2 e_1 +12 e_{3,1} \otimes e_2 e_2 \\&\quad +52 e_{3,2} \otimes e_1 e_1 + 64 e_{3,2} \otimes e_1 e_2 + 37 e_{3,2} \otimes e_2e_1 + 54 e_{3,2} \otimes e_{2}e_2. \end{aligned}$$

One can verify that \(\vartheta _{1,2}(T)\in \sigma _2(X_{5,1^{3}}) {\setminus } \tau (X_{5,1^{3}})\), therefore we can continue our procedure by considering the matrix associated to the first flattening \(\varphi _1:({\mathbb {C}}^2\otimes {\mathbb {C}}^2 )^*\rightarrow {\mathbb {C}}^6\) of T:

$$\begin{aligned} A= \begin{bmatrix} 12 &{} 8&{} 6 &{} 4 \\ 30 &{} 20&{} 15 &{} 10 \\ 8 &{} 8 &{} 5 &{} 6 \\ 35 &{} 38 &{} 23 &{} 30 \\ 16 &{} 16 &{} 10 &{} 12 \\ 52&{} 64 &{} 37 &{} 54 \end{bmatrix}. \end{aligned}$$

The rank of A is 2 and we take the first two columns \(\widehat{x},\widehat{y} \) of A as linearly independent vectors of \(Im(\varphi _1)\) and rewrite all the others as a linear combinations of \(\widehat{x},\widehat{y}\). Denote by \(T'\) the resulting tensor

$$\begin{aligned} T'= \widehat{x} \otimes e_1e_1 + \widehat{y} \otimes e_1e_2 +\left( \frac{1}{4}\widehat{x} +\frac{3}{8} \widehat{y} \right) \otimes e_2 e_1 + \left( -\frac{1}{2} \widehat{x} +\frac{5}{4}\widehat{y} \right) \otimes e_2 e_2. \end{aligned}$$

Let us consider now \(T'\in {\mathbb {C}}^2\otimes {\mathbb {C}}^2 \otimes {\mathbb {C}}^2\) as a matrix pencil with respect to the second factor

$$\begin{aligned} T'=\lambda \begin{bmatrix} 1 &{} 0\\ 0 &{} 1 \end{bmatrix} + \mu \begin{bmatrix} 1/4 &{} -1/2 \\ 3/8 &{} 5/4 \end{bmatrix} =\lambda C_1 + \mu C_2. \end{aligned}$$

It is easy to see that the eigenvectors of

$$\begin{aligned} C_1C_2^{-1}=\begin{bmatrix} 10/4 &{} 1\\ -3/4 &{}1/2 \end{bmatrix} \end{aligned}$$

are \( x=(-2,1) \) and \(y=(-2/3, 1)\), i.e.

$$\begin{aligned} x=-2\widehat{x}+\widehat{y} = -(16e_{1,1}+40e_{1,2} +8e_{2,1}+32e_{2,2}+16e_{3,1}+40e_{3,2}) =-\begin{bmatrix} 16 &{} 40 \\ 8 &{} 32 \\ 16 &{} 40 \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} y=-2/3\widehat{x} + \widehat{y} =8/3e_{2,1}+44/3e_{2,2}+16/3e_{3,1}+88/3e_{3,2} =\begin{bmatrix} 0&{}0 \\ 8/3 &{} 44 /3 \\ 16/3 &{} 88 /3 \end{bmatrix}. \end{aligned}$$

It is easy to see that \(r(x)=2\) and \(r(y)=1\), therefore T is a non-identifiable rank-3 tensor as in case f). Indeed by multiplying T with

$$\begin{aligned} g= \left( \begin{bmatrix} 1/2 &{} -1 &{} 1/2 \\ 0 &{} 2 &{} -1 \\ -1/2 &{} 0 &{} 1/2 \end{bmatrix}, \begin{bmatrix} 1 &{} 0 \\ -1/3 &{} 1/3 \end{bmatrix}, \begin{bmatrix} 1&{}-1\\ -1&{}2 \end{bmatrix}, \begin{bmatrix} 1/2&{} -1/4 \\ -1/2 &{} 3/4 \end{bmatrix}\right) \end{aligned}$$

we get

$$\begin{aligned} T=e_1\otimes e_1 \otimes e_1 \otimes e_1 +e_2 \otimes e_2 \otimes e_1 \otimes e_1 + e_3 \otimes (2e_1+3e_2) \otimes e_2 \otimes e_2. \end{aligned}$$
figure d

Remark 3.8

Since we already considered all concise spaces of tensors related to all non-identifiable rank-3 tensors of Theorem 4.1, any other concise tensor space will not be considered. Therefore, for any other concise space, the output of the algorithm will be T is not on the list of non-identifiable rank-3 tensors.

We conclude by collecting all together the steps made until now.

figure e