A novel particle–particle and particle–wall collision model for superellipsoidal particles

Abstract

In the framework of computational studies of particulate multiphase flow systems, either dilute or dense, particle–particle as well as particle–wall collisions need to be considered, which in the case of nonspherical particle shapes still presents a computational challenge. In this study, we present an efficient numerical implementation of a novel superellipsoidal particle collision model that can be used in general fluid flows. The superellipsoid shape formulation can be viewed as an extension of spherical or ellipsoidal shapes and can be used to represent spherical, ellipsoidal, cylindrical, diamond-like and cubic particles by varying solely five shape parameters. In this context, we present a fast, stable Newton–Raphson-based method for modeling frictional collisions of nonspherical superellipsoidal particles, and demonstrate the performance of our algorithms.

1 Introduction

1.1 Motivation

Particulate systems are widely used in various industries such as cement, petrochemical, wastewater treatment, and pharmaceutical, where different types of particles are transported, mixed, stored, or segregated [1, 2]. In addition, nonspherical particles are widely present in nature, from the composition of blood to dust particles in the air. To increase the efficiency of industrial processes or improve pharmaceutical applications such as targeted drug delivery, the physics of particulate systems must be well understood [3]. However, the understanding of the motion of arbitrarily shaped solids suspended in flows is still sparse [1]. To date, most researchers have focused on spherical particles due to their simple motion description, although, as mentioned above, real particles are in general irregularly shaped [3]. As argued by Lu et al. [3], the applicability of conclusions based on the assumption of spherical particles to real, arbitrarily shaped particle systems is usually questionable. In limited cases, such as aerosol transport, the assumption of a spherical shape is generally justified, see, e.g. [4,5,6,7]. Clearly, the behaviour of realistic arbitrary particles differs from the spherical assumption, since the orientation and rotation of the particle in the flow become important, leading to an altered translational and rotational motion. In addition, particle–particle or particle–wall collisions require a more complex description.

As Marchioli et al. [8] have shown prolate ellipsoidal particles in turbulent flows tend to cluster into groups creating fiber-free regions. This cluster formation increases the chance of particle–particle collisions in turbulent flows. Therefore, the development of efficient methods to model the motion of arbitrarily shaped particles and their collisions in flows is of utmost importance for understanding real particle systems [3].

1.2 Particle-shape description

In most applications, the shape of the particles has a non-negligible influence on the behaviour of the dispersed phase, so that modelling of non-spherical particles is required. Several methods are available for the simulation of particle-laden flows with respect to the handling of the dispersed phase, which we briefly introduce below. These options include the finite-size particle approach (geometric construct of the particle) and the point-particle approach [9], in which the particle shape is represented by a function of a local coordinate system [10].

1.3 Option 1: Geometrical construct of the particle shape

In the finite-size particle approach, the particle surface is resolved geometrically. In this field, the coupling of the Discrete Element Method (DEM) [11], and Computational Fluid Dynamics (CFD) is widely used [9]. This Computational Fluid Dynamics-Discrete Element Method (CFD-DEM) is increasingly employed to study particle-laden flows such as sediment transport, see [12, 13]. Particles are tracked individually in a Lagrangian framework, which provides more insight compared to describing the dispersed phase as a continuum [14].

In the literature, there are many different techniques to account for the nonsphericity of finite-size particles in DEM. According to Lu et al. [3], the most widely used approaches to model non-spherical particles in DEM are polygonal particles (polygon formulation) [15, 16], or composite particles [2, 17, 18]. Lu et al. [3], provides a thorough summary and review of the main theoretical developments in the field of nonspherical DEM.

A simple method for generating nonspherical particles is called the multi-sphere composite method, developed by Favier et al. [19] and Jensen et al. [20]. This modelling approach exploits a set of spherical particles (prime spheres) glued together to represent arbitrarily shaped particles [3]. As stated by Abbaspour-Fard [21], the main advantages of the composite method are its contact detection efficiency, since it uses a sphere-to-sphere contact detection for arbitrarily shaped particles, and its comparatively simple implementation. Third et al. [17, 18] performed simulations of nonspherical solids, approximating shapes by combining two spheres of different sizes. Kruggel-Emden et al. [22] performed a study on the validity of composite particle DEM and concluded that the number of prime spheres used to approximate arbitrary particles has a strong impact on the computation time as well as the accuracy of the shape description. It should be noted that the multi-sphere approach strongly depends on the number of prime spheres used and usually results in high computational costs to ensure a sufficiently smooth representation of the particle shape [3], otherwise the particles can result in a too knobbly representation of the real particle [10]. Another disadvantage of the composite method is the occurrence of multiple contact points [22], since approximating a convex shape (such as an ellipsoid) with more than one sphere always results in a non-convex shape [1]. The more composite spheres are used, the higher the number of contacts between particles [23]. Therefore, a major challenge in the composite method is the choice of an appropriate number of composite spheres [1].

Another way to represent non-spherical particles in DEM is to use polygon particles. As Houlsby [10] notes, contact detection simplifies to the main task of detecting edge or corner contacts when these polygon particles are restricted to convex shapes. Note that the computation time increases proportionally to the product of the number of vertices of the adjacent particles [10].

Hogue and Newland [15] simulated falling dominoes using the polygon formulation and achieved good agreement with experimental measurements. The authors divided the contact algorithm into a set of geometric problems by discretizing nonspherical particles in a two-dimensional polar coordinate system with vertices connected by segments [15]. Furthermore, Feng and Owen [16] present a 2D polygonal contact model for corner contacts, where the normal contact force is assumed to point in the direction of the fastest decrease in contact energy. A main drawback of the polygon-based method is its complexity and time-consuming nature, since it considers contacts involving faces, vertices, or edges separately [3]. Moreover, the extension to 3D is not straightforward, since collisions of 3D polyhedra collisions involve a range of contact options such as vertex-face as well as edge-edge contacts [10]. In this context, Latham and Munjiza [24, 25] investigated the use of simple polyhedral shapes, i.e. tetrahedral and cubic particles of different sizes and aspect ratios.

In addition to DEM, the immersed boundary method (IBM) is another option for modelling particles of finite size and coupling the dispersed phase with CFD. Note that IBM provides a full-way coupling between the dispersed and continuous phases, since the flow over the particles is solved [9]. There are a variety of models targeting spherical particle collisions in the framework of IBM [26, 27]. In addition, Ardekani et al. [28] studied sedimenting spheroidal particles using IBM and presented a collision algorithm for such particles based on the soft sphere model [28]. In this study, the authors approximated the spheroids as spheres with the same mass as the reference spheroid and a radius equal to the local curvature at the contact point. In addition, Hosaka et al. [29] studied the suspension of red blood cells in a channel flow, including collisions (platelets-platelets and platelets-wall) and adhesion effects using the IBM flow solver. Recently, Nagata et al. [9] proposed a collision algorithm for arbitrarily shaped particles for flow solvers using IBM based on the level set and ghost cell method [30]. In this study, the authors investigated collisions between spherical, cylindrical, and red-blood-cell shaped objects, as well as interactions between spheres and flat plates, and obtained good agreement with previous studies. As Hosaka et al. noted [29], the advantages of IBM are the lower computational cost of creating the particle-fitted mesh/surface and the re-creation of the mesh in the case of moving or deforming particles.

1.4 Option 2: Functional shape representation

An alternative way to describe particle shapes is to define the particle as a function of a local coordinate system [10]. There are two main options for functional shape representation, i.e. discrete function (DFR) [3, 31] or continuous function representation (CFR) [2, 3, 32]. In the CFR method, the particle is described by a surface equation, such as the commonly employed superellipsoid surface equation proposed by Barr [33]. Note that nonlinear constrained optimization approaches are required when using CFR contact detection methods [3]. As noted by Cleary et al. [34], the convergence difficulties of this optimization increase significantly as the squareness of particles increases. Mustoe and Miyata [35] studied cubic particles (using a superellipsoidal shape formulation) in a 2D horizontal rotating cylinder. The authors investigated the effect of squareness on the dynamic angle of response and found that this angle has an upper limit around $40\,^{\circ }$ [35].

In contrast to CFR, the discrete function representation (DFR) method proposed by Williams and O’Connor [31] describes the particle surface using a specified number of discrete points. It is discussed that the DFR method could be a justifiable alternative to the above methods due to its computational efficiency and applicability to a wide range of shapes [36]. The computational cost of DFR scales with the number of nodes N discretizing the particle surface with $\mathcal {O}(N)$ [3]. Although DFR is often described as computationally less expensive than the above methods, it requires some difficult decisions, such as how to conveniently discretize a given particle, i.e. the number of discretization points for sufficient resolution, the distribution of points over the surface, and a method to efficiently determine the contact point based on the chosen nodes [3].

1.5 Novelty and Advantages of the proposed approach

This paper presents a novel frictional collision model for nonspherical particles in particle–particle as well as particle–wall contacts based on the superellipsoid surface equation (CFR). By using CFR, we can avoid a number of difficulties, such as the discretization of a given particle shape, which is required in finite-size particle and DFR approaches. In addition, the model does not need to separately account for the contacts between faces, vertices, and edges, which is a main drawback of the polygon formulation.

Moreover, the model is applicable to any superellipsoidal particle collisions in flows. In this context, we present a novel approach to determine the collision points that ensures fast and robust identification while maintaining common normals. Moreover, the approach is capable of using tens of thousands of particles while performing simulations requiring thousands of time steps, since no discretization of particle surfaces is required, which is one of the main drawbacks of finite-size particle approaches such as DEM or IBM for non-spherical particles. In addition, unlike many other techniques, such as polygonal formulation, the novel approach is easily (and readily) extended to 3D. In combination with our previously presented superellipsoid force models (see [32, 37]), which allow accurate modelling of the motion of suspended nonspherical particles, i.e. trajectories and rotations, we take the simulation of nonspherical particles in flows one step further by including frictional particle–particle as well as particle–wall collisions.

1.6 Organisation of paper

This paper is organised as follows: The motion of superellipsoidal particles in multiphase flows is briefly discussed in Sect. 2. In addition, in Sect. 3, the contact detection methods available in the literature are first presented. Then, our novel efficient contact detection algorithm for superellipsoidal particles is proposed and validated. In Sect. 4, we present the collision model used for superellipsoid-superellipsoid as well as superellipsoid-wall collisions. Validation of simulations of superellipsoid-wall and superellipsoid-superellipsoid collisions based on the proposed method is presented along with demonstrative examples in Sect. 5, followed by the main conclusions of the study in Sect. 6.

2 Superellipsoidal particles

Notation: In this work, we express tensors of various orders using bold italic font. First-order tensors (vectors) are denoted by bold italic lowercase letters such as ${\varvec{a}}$, while second-order tensors are denoted by bold italic uppercase letters such as ${\varvec{A}}$. Using Einstein’s summation convention, we can write the coordinate representation in Cartesian coordinate systems with base vectors ${\varvec{e}}_i'$, ${\varvec{e}}_i$ ($i=1,2,3$) as follows:

$$\begin{aligned} {{\varvec{a}}} = a_i' {\varvec{e}}_i' = a_i {\varvec{e}}_i ~~~~\text {and}~~~~ {\varvec{A}} = A_{ij}' {\varvec{e}}_i' \otimes {\varvec{e}}_j'= A_{ij} {\varvec{e}}_i \otimes {\varvec{e}}_j\,, \end{aligned}$$

where $a_i'$, $a_i$ and $A_{ij}'$, $A_{ij}$ are the corresponding coefficients in the coordinate system ${\varvec{e}}_i'$, ${\varvec{e}}_i$, respectively. The tensor coefficients $a_i'$, $a_i$ and $A_{ij}'$, $A_{ij}$ can be arranged in coefficient matrices, which we denote by underlined italic letters:

$$\begin{aligned} \underline{a}'= & {} \left[ \begin{matrix} a_1' \\ a_2'\\ a_3' \\ \end{matrix}\right] , ~~ \underline{a} = \left[ \begin{matrix} a_1 \\ a_2 \\ a_3 \\ \end{matrix}\right] ~~~~\text {and}~~~~ \underline{A}' = \left[ \begin{matrix} A_{11}' &{} A_{12}' &{} A_{13}'\\ A_{21}' &{} A_{22}' &{} A_{23}'\\ A_{31}' &{} A_{32}' &{} A_{33}' \end{matrix}\right] , ~~\\ \underline{A}= & {} \left[ \begin{matrix} A_{11} &{} A_{12} &{} A_{13}\\ A_{21} &{} A_{22} &{} A_{23}\\ A_{31} &{} A_{32} &{} A_{33} \end{matrix}\right] . \end{aligned}$$

The rotation matrix $\underline{R}$ transforming coefficients with respect to the base vectors ${\varvec{e}}_i$ to coefficients with respect to the base vectors ${\varvec{e}}_i'$ follows as

$$\begin{aligned} \underline{R} = \left[ \begin{matrix} R_{11} &{} R_{12} &{} R_{13}\\ R_{21} &{} R_{22} &{} R_{23}\\ R_{31} &{} R_{32} &{} R_{33} \end{matrix}\right] \, ~~~~ \text {with} ~~~~ R_{ij} = {\varvec{e}}_i' \cdot {\varvec{e}}_j\,. \end{aligned}$$

(1)

Taken together, coefficient matrices of vectors and second order tensors transform as

$$\begin{aligned} \underline{a}' = \underline{R}\,\underline{a} ~~~~ \text {and} ~~~~ \underline{A}' = \underline{R} \,\underline{A}\, \underline{R}^T\,. \end{aligned}$$

(2)

2.1 Superellipsoidal surface equation

In this work we employ the superellipsoid surface equation as proposed by Barr [33]. This equation, formulated in the particle frame of reference (pFoR) [$x'$, $y'$, $z'$], gives [33]:

$$\begin{aligned} S(x',y',z')&= \left[ \left[ \frac{|x'|}{a}\right] ^{{2}/{\epsilon _2}} + \left[ \frac{|y'|}{b}\right] ^{{2}/{\epsilon _2}}\right] ^{{\epsilon _2}/{\epsilon _1}}\nonumber \\+&\left[ \frac{|z'|}{c}\right] ^{{2}/{\epsilon _1}}-1=0\,, \end{aligned}$$

(3)

where a, b and c denote the half-lengths of the considered particle in the direction of the principle axes. In the following, we employ that $c\le b \le a$ and $\lambda _1 = a/c \ge \lambda _2 = b/c$. Moreover, $\epsilon _1$ and $\epsilon _2$ control the squareness of the particle, determining the cross-sectional shape in the $y'-z'$ ($\epsilon _1$) and $x'-z'$ ($\epsilon _1$) as well as $x'-y'$ plane ($\epsilon _2$) [2, 3].

Fig. 1

Representative set of superellipsoidal shapes with $\lambda _1 >\lambda _2$ and varying shape factors $\epsilon _1 = [0.2-1.8], \epsilon _2 = [0.2-1.8]$

Figure 1 displays a set of representative superellipsoidal particles with $\lambda _1 >\lambda _2$ to illustrate the variety of shapes that can be generated with superellipsoids. Note that an ellipsoidal shape is obtained by setting the shape parameters to $\epsilon _1=\epsilon _2=1$ and a sphere when additionally $a=b=c$ ($\lambda _1 = \lambda _2 = 1$).

2.2 Motion of a superellipsoidal particle

The trajectory of an arbitrarily shaped particle is determined by its interaction with the surrounding fluid flow [38]. Each particle i obeys Newton’s second law and is tracked individually by solving its trajectory explicitly

$$\begin{aligned} m_i \frac{\textrm{d}{{\varvec{v}}_i}}{\textrm{d}t} = {\varvec{F}}_i\,, \end{aligned}$$

(4)

where $m_i$ and ${\varvec{v}}_i$ are the mass and velocity of particle i and d/dt denotes the total time derivative. Furthermore, ${{\varvec{F}}}_i$ denotes the total force acting on the particle i [1]. Note that sufficiently small particles (e.g. micro- and submicron particles) can be described as rigid. We describe particle transport in an Euler-Lagrangian framework using the Maxey–Riley–Gatignol equation of motion [38], for small rigid particles. In addition, we employ the drag expression for arbitrarily shaped particles as proposed by Brenner [39]. Thus, the drag force ${{\varvec{F}}}_D$ exerted on a superellipsoidal particle moving in a fluid is obtained by [32]:

$$\begin{aligned} {{\varvec{F}}}_D= \int _\Gamma {{{\varvec{\sigma }} \cdot {\varvec{n}}}} \textrm{d}\Gamma = \pi \rho _f \nu _f c {{\varvec{K}}} \cdot {\left[ {\varvec{u}}-{{\varvec{v}}}\right] }\,, \end{aligned}$$

(5)

where ${{\varvec{t}}={\varvec{\sigma }} \cdot {\varvec{n}}}$ labels the boundary traction exerted on the boundary $\Gamma$ of the particle, ${\varvec{\sigma }}$ the Cauchy stress tensor, ${\varvec{n}}$ the normal particle surface vector, ${{\varvec{K}}}$ the translational resistance tensor, c the semi-minor axis of the superellipsoidal particle, $\rho _f$ the fluid density, $\nu _f$ its kinematic viscosity, and ${{\varvec{u}}}$ the velocity of the fluid at the position of the particle center. The coefficient matrix of the resistance tensor in the particle reference frame (pFoR) ${\underline{K}}'$ is related to its counterpart ${\underline{K}}$ in the inertial frame of reference (iFoR) via the rotation matrix ${\underline{R}}$:

$$\begin{aligned} {\underline{K}}'={\underline{R}}\,{\underline{K}}\,{\underline{R}^T}\,. \end{aligned}$$

(6)

Followingly, we write:

$$\begin{aligned} m_p \frac{\textrm{d}{{\varvec{v}}}}{\textrm{d}t}&{=}&m_p \left[ \rho _p{-}\rho _f\right] {+}V_p\rho _f\,\frac{D{\varvec{u}}}{D t} {-} \frac{1}{2}V_p\rho _f \left[ \frac{\textrm{d}{\varvec{v}}}{\textrm{d}t}{-}\frac{\textrm{d}{\varvec{u}}}{\textrm{d}t}\right] \nonumber \\{} & {} {+} \pi \rho _f \nu _f c {\varvec{K}} \cdot {[{\varvec{u}}{-}{\varvec{v}}]}\, \end{aligned}$$

(7)

using the superellipsoidal surrogate approach as presented in Štrakl et al. [32]. In Eq. (7), we considers gravity, buoyancy, pressure gradient, added mass and drag force, whereas time history effects, aerodynamic lift as well as higher order terms are neglected [40]. Note that in Eq. (7), $D/Dt=\partial /\partial t + [{\varvec{u}} \cdot {\varvec{\nabla }}]$ represents the time derivative following the fluid element and $d/dt = \partial /\partial t + [{\varvec{v}} \cdot {\varvec{\nabla }}]$ describes the time derivative following the Lagrangian particle.

Using $L_0$ and $u_0$ to denote the characteristic scales of the problem and the fluid velocity, respectively (i.e. Reynolds number $\textrm{Re} = u_0 L_0 /\nu _f$) [40], we obtain the dimensionless parameters ${{\varvec{v}}}^* = {{\varvec{v}}}/u_0$, ${{\varvec{u}}}^* = {{\varvec{u}}}/u_0$, $t^* = t u_0/L_0$. It follows that we can write Eq. (4) as [38, 39]:

$$\begin{aligned} \frac{\textrm{d}{{\varvec{v}}^*}}{\textrm{d}t^*}= & {} \frac{A}{St} \left[ {{\varvec{v}}}_s^* + \frac{c}{3d_\textrm{eq}}{{\varvec{K}}} \cdot \left[ {{\varvec{u}}}^* - {{\varvec{v}}}^* \right] \right] + \frac{3}{2}R \frac{\partial {{\varvec{u}}}^*}{\partial t^*} \nonumber \\{} & {} + R \left[ \left[ {{\varvec{u}}}^* + \frac{1}{2}{{\varvec{v}}}^* \right] \cdot \mathbf{{\nabla }} \right] {{\varvec{u}}}^*, \end{aligned}$$

(8)

where ${{\varvec{v}}}_s^*$ denotes the dimensionless settling velocity, $d_\textrm{eq}$ the volume equivalent diameter of a sphere, and A and R dimensionless parameters depending on the fluid-particle density ratio [40]:

$$\begin{aligned} R = \frac{\rho _f}{\rho _p + 0.5 \rho _f}\,,~~~A = \frac{\rho _p}{\rho _p + 0.5 \rho _f}\,. \end{aligned}$$

(9)

Furthermore, St labels the Stokes number, which is the ratio of the characteristic particle response time $\tau _p$ to a characteristic time of the flow $\tau _f$. The Stokes number of a particle with volume equivalent sphere diameter $d_\textrm{eq}$ is obtained as follows:

$$\begin{aligned} St = \frac{\tau _p}{\tau _f}=\frac{\rho _p}{\rho _f}\,\frac{d_\textrm{eq}^2 u_0}{18 \nu _f L_0}\,. \end{aligned}$$

(10)

Using the dimensionless Eq. (8), we note that the factor A/St scales the importance of gravity and the drag force, while R scales the pressure gradient and the added mass term [40]. Thus, the latter forces can be considered negligible compared to the gravity and buoyancy force ${{\varvec{F}}}_{GB}$ and the drag force ${{\varvec{F}}}_{D}$ when $\rho _p \gg \rho _f$ as $R\ll 1$, see Eq. (9) [40]. Moreover, even if $\rho _p \approx \rho _f$, we can consider the effects of the additional forces to be minor compared to ${{\varvec{F}}}_{GB}$ and ${{\varvec{F}}}_{D}$ in the case of a sufficiently small Stokes number ($St \ll 1$), since consequently $A/St \gg 1$, see Eqs. (9–10).

To obtain the angular velocity of a particle, an accurate determination of the particle orientations is crucial [1]. Moreover, the point of contact between nonspherical particles (or a nonspherical particle and a wall) depends on the particle orientation. In general, the orientation of an arbitrarily shaped particle is described by quaternions ${\underline{e}}=[e_0,~e_1~,e_2~,e_3]^T$ (also referred to as Euler parameters) [41], which are singularity-free compared to the Euler angles [$\phi$, $\theta$, $\psi$] and describe a rotation of the iFoR $\underline{r}=\left[ x,~y,~z\right] ^T$ with respect to the pFoR $\underline{r}'=\left[ x',~y',~z'\right] ^T$ [1], i.e. $\underline{r}' = \underline{R}\, \underline{r}$. The Euler parameters are subject to the constraint $e_{0}^2+e_{1}^2+e_{2}^2+e_{3}^2=1$ [42]. The quaternions ${\underline{e}}$ can be constructed from the Euler angles as follows [41]:

$$\begin{aligned} {\underline{e}} = \begin{bmatrix} e_0 \\ e_1 \\ e_2 \\ e_3 \\ \end{bmatrix} = \begin{bmatrix} \cos \left[ 0.5\left[ \phi +\psi \right] \right] \cos \left[ \theta /2\right] \\ \cos \left[ 0.5\left[ \phi -\psi \right] \right] \sin \left[ \theta /2\right] \\ \sin \left[ 0.5\left[ \phi -\psi \right] \right] \sin \left[ \theta /2\right] \\ \sin \left[ 0.5\left[ \phi +\psi \right] \right] \cos \left[ \theta /2\right] \\ \end{bmatrix}\,. \end{aligned}$$

(11)

The rotation matrix ${\underline{R}}$ is constructed from the quaternion components using [1]:

$$\begin{aligned}{} & {} {\underline{R}}=\nonumber \\{} & {} \begin{bmatrix} e_{0}^2+e_{1}^2-e_{2}^2-e_{3}^2 &{}2[e_1e_2+e_0e_3]&{}2[e_1e_3-e_0e_2] \\ 2[e_1e_2-e_0e_3] &{}e_{0}^2-e_{1}^2+e_{2}^2-e_{3}^2&{}2[e_2e_3-e_0e_1] \\ 2[e_1e_3+e_0e_2] &{}2[e_2e_3-e_0e_1]&{}e_{0}^2-e_{1}^2-e_{2}^2+e_{3}^2 \\ \end{bmatrix} \,\nonumber \\= & {} \left[ \begin{array}{ccc} m_{11} &{} m_{12} &{} m_{13} \\ m_{21} &{} m_{22} &{} m_{23} \\ m_{31} &{} m_{32} &{} m_{33} \\ \end{array} \right] , \end{aligned}$$

(12)

where $m_{ij}$ represent elements of ${\underline{R}}$ expressed with Euler parameters. Note that the evolution of the quaternions is related to the angular particle velocity in the particle frame ${\underline{{\omega }}}'= \left[ \omega _{x'},~\omega _{y'},~\omega _{z'}\right] ^T$:

$$\begin{aligned} \begin{bmatrix} \textrm{d}e_0/\textrm{d}t \\ \textrm{d}e_1/\textrm{d}t \\ \textrm{d}e_2/\textrm{d}t \\ \textrm{d}e_3/\textrm{d}t \\ \end{bmatrix} = \frac{1}{2} \begin{bmatrix} -e_1 &{} -e_2 &{} -e_3 \\ e_0 &{} -e_3 &{} e_2 \\ e_3 &{} e_0 &{} -e_1 \\ -e_2 &{} e_1 &{} e_0 \\ \end{bmatrix} {\underline{{\omega }}}' \,. \end{aligned}$$

(13)

The rotational motion of an arbitrarily shaped particle moving in a fluid can be described in the pFoR as follows:

$$\begin{aligned} T_{x'}= & {} I_{x'}\,\frac{\textrm{d}\,\omega _{x'}}{\textrm{d}t}-\omega _{y'} \omega _{z'}\,\left[ I_{y'}-I_{z'}\right] , \end{aligned}$$

(14)

$$\begin{aligned} T_{y'}= & {} I_{y'}\,\frac{\textrm{d}\,\omega _{y'}}{\textrm{d}t}-\omega _{z'} \omega _{x'}\,\left[ I_{z'}-I_{x'}\right] , \end{aligned}$$

(15)

$$\begin{aligned} T_{z'}= & {} I_{z'}\,\frac{\textrm{d}\,\omega _{z'}}{\textrm{d}t}-\omega _{x'} \omega _{y'}\,\left[ I_{x'}-I_{y'}\right] , \end{aligned}$$

(16)

where $I_{x'}$, $I_{y'}$, $I_{z'}$ denote the principal values of the inertia tensor of the particle. In addition, $T_{x'}$, $T_{y'}$, $T_{z'}$ label the hydrodynamic torques on the particle with respect to the principal axes. The principal values of the inertia tensor for a superellipsoidal particle are [43]:

$$\begin{aligned} I_{x'}= & {} \frac{1}{2}\rho a b c \epsilon _1 \epsilon _2 \left[ b^2 B\left( 1.5 \epsilon _2,\frac{\epsilon _2}{2}\right) B\left( \frac{\epsilon _1}{2}, 2 \epsilon _1+1\right) \right. \nonumber \\{} & {} \left. + 4c^2B\left( \frac{\epsilon _2}{2},\frac{\epsilon _2}{2} +1\right) B\left( 1.5 \epsilon _1, \epsilon _1+1\right) \right] , \end{aligned}$$

(17)

$$\begin{aligned} I_{y'}= & {} \frac{1}{2} \rho a b c \epsilon _1 \epsilon _2 \left[ a^2 B\left( 1.5 \epsilon _2,\frac{\epsilon _2}{2} \right) B\left( \frac{\epsilon _1}{2}, 2 \epsilon _1+1\right) \right. \nonumber \\{} & {} \left. + 4 c^2 B\left( \frac{\epsilon _2}{2},\frac{\epsilon _2}{2}+1\right) B\left( 1.5 \epsilon _1, \epsilon _1+1\right) \right] , \end{aligned}$$

(18)

$$\begin{aligned} I_{z'}= & {} \frac{1}{2}\, \rho a\,b\,c\,\epsilon _1\,\epsilon _2\, \left[ a^2 + b^2 \right] \;\nonumber \\{} & {} \left[ B\left( 1.5\,\epsilon _2,\frac{\epsilon _2}{2}\right) \; B\left( \frac{\epsilon _1}{2}, 2\,\epsilon _1+1\right) \right] , \end{aligned}$$

(19)

where B is related to the Gamma function as

$$\begin{aligned} B(x,y)=\frac{\Gamma (x)\Gamma (y)}{\Gamma (x+y)}\,. \end{aligned}$$

(20)

Fig. 2

Sketch of common contact detection schemes: intersection (IS), geometric potential (GP) and common normal (CN)

Considering both rotational and shear flow contributions, the resultant torque ${{\varvec{T}}}$ is obtained using [32]:

$$\begin{aligned} {{\varvec{T}}}=\int _\Gamma {{\varvec{r}}}\times {{\varvec{t}}}\textrm{d}\Gamma ~\widehat{=}~ \pi \mu c^3\; \left[ \underline{\Pi }' \left[ \begin{matrix} f' \\ g' \\ h' \end{matrix} \right] +\underline{\Omega }' \left[ \begin{matrix} \xi ' - \omega _{x'} \\ \eta ' - \omega _{y'} \\ \chi ' - \omega _{z'} \end{matrix} \right] \right] \,, \end{aligned}$$

(21)

where $\underline{\Omega }'$ and $\underline{\Pi }'$ denote the rotation and deformation resistance coefficient matrix, respectively. Moreover, f, g, h are the off-diagonal elements of the deformation rate tensor and $\xi$, $\eta$ and $\chi$ label the spin tensor components, which are determined using:

$$\begin{aligned} f'=&\frac{1}{2}\left[ \frac{\partial u_{z'}}{\partial y}+\frac{\partial u_{y'}}{\partial z}\right] ,~~ g'=\frac{1}{2}\left[ \frac{\partial u_{x'}}{\partial z}+\frac{\partial u_{z'}}{\partial x}\right] ,~~\nonumber \\ h'=&\frac{1}{2}\left[ \frac{\partial u_{x'}}{\partial y}+\frac{\partial u_{y'}}{\partial x}\right] ,~~ \end{aligned}$$

(22)

$$\begin{aligned} \xi '=&\frac{1}{2}\left[ \frac{\partial u_{z'}}{\partial y}-\frac{\partial u_{y'}}{\partial z}\right] ,~~ \eta '=\frac{1}{2}\left[ \frac{\partial u_{x'}}{\partial z}-\frac{\partial u_{z'}}{\partial x}\right] ,~~\nonumber \\ \chi '=&\frac{1}{2}\left[ \frac{\partial u_{y'}}{\partial x}-\frac{\partial u_{x'}}{\partial y}\right] \,. \end{aligned}$$

(23)

3 Contact detection algorithms

3.1 Brief review of the state-of-the-art

A key step of the particle–wall as well as the particle–particle collision model is the determination of the contact point. The contact condition between two spherical particles is well defined, since the contact exists only when the distance between the particle centres is smaller than the sum of their radii [44]. However, the detection of the contact between nonspherical particles is usually not straightforward and its determination still poses a major difficulty [2]. As Lin and Ng [45], stated, there is no strictly defined ”correct” contact point for nonspherical particles, since different methods may lead to different contact points. The authors note that these determined contact points and particle overlaps should match with the analytical points in the case of two identical spheres when different contact schemes are used [45].

For ellipsoidal particle collisions, several analytical approaches have been proposed in the literature, including intersection (IS) [46,47,48], geometric potential (GP) [2, 44, 45], and common normal (CN) algorithms [34, 45, 49, 50]. Figure 2 illustrates these contact detection methods.

The IS algorithm for ellipses (2D) was proposed by Ting [46, 48], where the contact point $p_c$ is defined as the midpoint of the line connecting the two intersection points A,  B of the colliding ellipses. The intersection points A and B are found by solving a quartic equation obtained by combining the two ellipse equations [45, 46, 48]. Figure 2a is an illustration of this 2D contact detection concept. Rothenburg and Bathurst [47] proposed a similar approach, suggesting a slightly different formulation of the quartic equation. According to Lin and Ng [45], one of the major challenges of the IS method is that the generally small overlap of particles can lead to an ill- conditioned quartic equation, resulting in a significant loss of computational accuracy. In addition, the authors argue that the IS method cannot be easily extended to 3D [45].

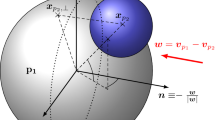
Ng [51] proposed a more stable contact detection algorithm than the IS method based on a geometric potential concept [45]. For the surface equation of an ellipsoid $E(x,~y,~z)=0$, a family of geometrically similar ellipsoids with identical origin represents a varying value of the potential $\Phi = E(x,~y,~z)$ [44, 45]. Figure 2b illustrates this concept of contact detection in a 2D example. As shown, there are two points $p_{c,1}$ and $p_{c,2}$ that generate the lowest potential to $E_2$ and $E_1$, respectively. A contact between the two collision partners is given if the potential values at the determined points are $\Gamma \le 0$ [44, 45]. The midpoint of the line connecting $p_{c,1}$ and $p_{c,2}$ is identified as the contact point [44, 45].

Lin and Ng [44, 45], showed that the GP-algorithm has the deficiency that the normal vectors of the colliding partners at $p_{c,1}$ and $p_{c,2}$ may not be parallel. Thus, the authors proposed a CN algorithm for colliding ellipsoidal particles [44, 45]. However, Kildashti et al. [50], demonstrated that the original formulation of Lin and Ng [44, 45], does not guarantee that the solution can satisfy the CN concept. Cleary et al. [34] proposed a CN scheme in which the problem is reduced from identifying two points (one on each collision partner) to one point by reversing the time evolutions until particle contact is established solely at a single point, while Wellmann et al. [49] proposed minimizing the distance between the two points.

In this study, we present a novel efficient Lagrange multiplier approach based on the CFR method [3], using a CN approach to solve for the contact point numerically, with the error tolerance set to $c \times 10^{-6}$, where c denotes the smallest particle half axis.

3.2 The wall equation

Let ${\varvec{a}}$, ${\varvec{b}}$, ${\varvec{c}}$ be three vectors defining three points on a plane representing a plane wall. The normal to the wall ${\varvec{n}}_w$ can be calculated using

$$\begin{aligned} {{\varvec{n}}}_w= \frac{[{{\varvec{c}}} - {{\varvec{a}} }]\times [{{\varvec{b}}} - {{\varvec{a}}}] }{||[{{\varvec{c}}}-{{\varvec{a}}}]\times [{{\varvec{b}}}-{{\varvec{a}}}]||_2}\,. \end{aligned}$$

(24)

The equation of the wall (vizualised in Fig. 3) is

$$\begin{aligned} W({{\varvec{r}}})={{\varvec{n}}}_w \cdot [{{\varvec{r}}} - {{\varvec{a}}}] = 0\,. \end{aligned}$$

(25)

The partial wall derivatives are

$$\begin{aligned} \frac{\partial W}{\partial x}=n_x, \qquad \frac{\partial W}{\partial y}=n_y, \qquad \frac{\partial W}{\partial z}=n_z. \end{aligned}$$

(26)

Fig. 3

Parametrisation of a plane (wall)

3.3 Superellipsoid equation

The surface equation for prolate ellipsoids is extended to superellipsoidal particles by using the inside-out function proposed by Barr [33]. In the following, $[x',y',z']$ denotes the pFoR, where $x'$ points in the direction of the semi-major axis a. The surface of the superellipsoid is defined in the local coordinate system as described in Eq. (3). In the global coordinate system, the centre of mass of the superellipsoid is at ${\underline{r}}_c$ and the orientation is described by the Euler parameters ${\underline{e}}=[e_0,~e_1,~e_2,~e_3]^T$. A point on the surface of a superellipsoid in the local coordinate system (pFoR) ${\underline{r}} '$ can be written in the global coordinate system as

$$\begin{aligned} {\underline{r}}={\underline{R}}^T{\underline{r}}'+ {\underline{r}}_{c}, \qquad {\underline{r}}'=[x',~y',~z']^T={\underline{R}}\,[ {\underline{r}}- {\underline{r}}_c], \end{aligned}$$

(27)

which reads in index notation

$$\begin{aligned} r'_i=m_{ij}[r_j-r_{c\,j}]\,. \end{aligned}$$

(28)

Note that ${\underline{R}}$ is the rotation matrix defined in Eq. (12) and ${\underline{R}}^T$ is its transpose.

We can express the superellipsoid surface equation with global coordinates as

$$\begin{aligned} S =&\left[ \left[ \frac{m_{11}[x-x_c]+m_{12}[y-y_c]+m_{13}[z-z_c]}{a}\right] ^{\frac{2}{\epsilon _2}} \right. \nonumber \\&+ \left. \left[ \frac{m_{21}[x-x_c]+m_{22}[y-y_c]+m_{23}[z-z_c]}{b}\right] ^{\frac{2}{\epsilon _2}}\right] ^{\frac{\epsilon _2}{\epsilon _1}} \nonumber \\&+ \left[ \frac{m_{31}[x-x_c]+m_{32}[y-y_c]+m_{33}[z-z_c]}{c}\right] ^{\frac{2}{\epsilon _1}} - 1 \nonumber \\&= 0\,. \end{aligned}$$

(29)

Furthermore the unit normal vector ${{\varvec{n}}}_s$ at a point on the superellipsoid can be determined using

$$\begin{aligned} {{\varvec{n}}}_s = \frac{{\varvec{\nabla }} S}{ ||{\varvec{\nabla }} S||_2}\,, \end{aligned}$$

(30)

which requires the determination of the surface gradient in the global frame

$$\begin{aligned} {\varvec{\nabla }} S = \left[ \frac{\partial S}{\partial x},~~\frac{\partial S}{\partial y},~~\frac{\partial S}{\partial z}\right] ^T\,, \end{aligned}$$

(31)

as well as its magnitude $||{\varvec{\nabla }}S||_2$. In the context of our novel collision detection, the partial derivatives of the superellipsoid surface normals in the global frame are needed, for which we introduce the derivatives of the surface gradient and the magnitude of the surface gradient separately. The first, second, and third order partial derivatives of the surface gradient in the global frame are given in Appendix A.

3.4 Superellipsoid wall collision

Let us consider a wall $W({{\varvec{r}}})$ and a superellipsoid $S( {{\varvec{ r}}})$, which is described by the shape parameters a, b, c, $\epsilon _1$, $\epsilon _2$ as well as the center point ${{\varvec{r}}}_{c}$ and the orientation ${\varvec{e}}$ of the particle.

3.4.1 Part 1: Collision point on a wall and inside the superellipsoid

Considering a point ${{\varvec{r}}}$, which is on the surface of the wall

$$\begin{aligned} W( {{\varvec{r}}})=0 \end{aligned}$$

(32)

and at the same time inside the superellipsoid

$$\begin{aligned} S({{\varvec{r}}})<0\,. \end{aligned}$$

(33)

Fig. 4

Detection of collision point $P_{c,1}$ on wall and inside superellipsoid

We want to find an ${{\varvec{r}}}$ that is deepest inside of S and at the same time located on the wall surface, see Fig. 4. The problem is then to find ${{\varvec{r}}}$ such that

$$\begin{aligned} {{\varvec{r}}}= {\textrm{arg}}\{\min \left( S({{\varvec{r}}}) \right) \}\,, \end{aligned}$$

(34)

with the constraint Eq. (32). In order to solve this optimization problem, we use the Lagrange multiplier approach, defining the Lagrangian as

$$\begin{aligned} L({{\varvec{r}}},\lambda )=S({{\varvec{r}}})+\lambda W( {{\varvec{r}}})\,. \end{aligned}$$

(35)

Using

$$\begin{aligned} \frac{\partial L}{\partial x}=0, \qquad \frac{\partial L}{\partial y}=0, \qquad \frac{\partial L}{\partial z}=0, \qquad \frac{\partial L}{\partial \lambda }=0, \qquad \end{aligned}$$

(36)

we obtain a nonlinear system of four equations for the unknown location [x, y, z] and $\lambda$. The general formula of partial derivatives of the Lagrangian with respect to x,  y,  z renders:

$$\begin{aligned} \frac{\partial L}{\partial x_i} =&\frac{\partial S}{\partial x_i}+\lambda \frac{\partial W}{\partial x_i}\,, \end{aligned}$$

(37)

The full derivation of Eq. (37) can be found in Appendix B. The derivative of the Lagrangian with respect to the Lagrange multiplier is

$$\begin{aligned} \frac{\partial L}{\partial \lambda }=W({{\varvec{r}}}). \end{aligned}$$

(38)

The system of equations for $[x,y,z,\lambda ]$ is thus

$$\begin{aligned} \begin{aligned} F_1=&\frac{\partial S}{\partial x}+\lambda \frac{\partial W}{\partial x} = 0,&F_2=&\frac{\partial S}{\partial y}+\lambda \frac{\partial W}{\partial y} = 0\, \\ F_3=&\frac{\partial S}{\partial z}+\lambda \frac{\partial W}{\partial z}=0,&F_4=&W, \end{aligned} \end{aligned}$$

(39)

where $F_4$ can be rewritten as:

$$\begin{aligned} F_4{=} W {=}n_x[x-a_x]{+}n_y[y-a_y]{+}n_z[z-a_z]=0. \end{aligned}$$

(40)

In order to use the Newton–Raphson method to find a solution of the system Eq. (58) we must provide the Jacobian

$$\begin{aligned} {\underline{J}}=\left[ \begin{array}{cccc} \frac{\partial F_1}{\partial x} &{} \frac{\partial F_1}{\partial y} &{} \frac{\partial F_1}{\partial z} &{} \frac{\partial F_1}{\partial \lambda } \\ \frac{\partial F_2}{\partial x} &{} \frac{\partial F_2}{\partial y} &{} \frac{\partial F_2}{\partial z} &{} \frac{\partial F_2}{\partial \lambda } \\ \frac{\partial F_3}{\partial x} &{} \frac{\partial F_3}{\partial y} &{} \frac{\partial F_3}{\partial z} &{} \frac{\partial F_3}{\partial \lambda } \\ \frac{\partial F_4}{\partial x} &{} \frac{\partial F_4}{\partial y} &{} \frac{\partial F_4}{\partial z} &{} \frac{\partial F_4}{\partial \lambda } \\ \end{array}\right] \end{aligned}$$

(41)

The elements of the Jacobian using a general expression for $F_i$, $i=1,2,3$ render

$$\begin{aligned} \frac{\partial F_i}{\partial x_j}{=}\frac{\partial S}{\partial x_j\partial x_i}{+}\lambda \frac{\partial W}{\partial x_j\partial x_i}\,,\frac{\partial F_i}{\partial \lambda }{=}n_i\,, \frac{\partial F_4}{\partial x_j}{=}n_j\,, \frac{\partial F_4}{\partial \lambda }{=}0\,. \end{aligned}$$

(42)

3.4.2 Part 2: Collision point on the superellipsoid with identical normal

To obtain the collision point that is on the surface of the superellipsoid and deepest inside the wall, the procedure could be repeated as in Part 1 (Sect. 3.4.1) by exchanging the constraint and the objective function: $L_{2*} = W({{\varvec{r}}}) + \lambda S({{\varvec{r}}})$. However, this would not guarantee that the identified points on the wall and superellipsoid have an identical (opposed) normal. Thus, the problem is to find a point ${{\varvec{r}}}$ that is located on the superellipsoid surface and has a superellipsoid surface normal ${{\varvec{n}}}_{s}=-{{\varvec{n}}}_{w}$, see Fig. 5, so the problem is to find ${{\varvec{r}}}$ such that

$$\begin{aligned} {{\varvec{r}}} = {\textrm{arg}} \{ \min ({{\varvec{n}}}_{w} \cdot {{\varvec{n}}}_{s}({{\varvec{r}}}))\}\,, \end{aligned}$$

(43)

with the constraint

$$\begin{aligned} S({{\varvec{r}}})=0\,. \end{aligned}$$

(44)

Fig. 5

Detection of collision point $P_{c,2}$ on superellipsoid and inside wall with common normal $n_s$ to $n_w$

Thus, the Lagrangian is set up as:

$$\begin{aligned} L_{2} ={{\varvec{n}}}_{w} \cdot \underbrace{\frac{\nabla S}{|| \nabla S||_2}}_{{{{\varvec{n}}}_{s}}} + \lambda S({{\varvec{r}}})\,. \end{aligned}$$

(45)

Using $\underline{n}_w = [n_x,~n_y,~n_z]^T$, Eq. (45) can likewise be written as:

$$\begin{aligned} L_{2}&= \underbrace{\left[ \left[ \frac{\partial S}{\partial x}\right] ^2 + \left[ \frac{\partial S}{\partial y}\right] ^2 + \left[ \frac{\partial S}{\partial z}\right] ^2\right] ^{-1/2}}_{||\nabla S||_2^{-1}}\nonumber \\&\quad \left[ n_{x}\frac{\partial S}{\partial x} + n_{y}\frac{\partial S}{\partial y} + n_{z}\frac{\partial S}{\partial z}\right] + \lambda S({\underline{r}})\,. \end{aligned}$$

(46)

The system of equations for $(x,y,z,\lambda )$ is given as

$$\begin{aligned} F_i= & {} \frac{\partial (|| \nabla S||_2^{-1})}{\partial x_i }[{{\varvec{n}}}_{w} \cdot \nabla S] \nonumber \\{} & {} + || \nabla S||_2^{-1}\frac{\partial ({{\varvec{n}}}_{w} \cdot \nabla S)}{\partial x_i}{+}\lambda \frac{\partial S}{\partial x_i} {=} 0,~~~~ i {=} 1,2,3, \end{aligned}$$

(47)

$$\begin{aligned} F_4= & {} S({{\varvec{r}}}) =0. \end{aligned}$$

(48)

The elements of the Jacobian using a general expression for $F_i$, $i=1,2,3$ render

$$\begin{aligned}{} & {} \frac{\partial F_i}{\partial x_j} = \frac{\partial (|| \nabla S||_2^{-1})}{\partial x_j \partial x_i }[{{\varvec{n}}}_{w} \cdot \nabla S] + \frac{\partial (|| \nabla S||_2^{-1})}{\partial x_i }\frac{\partial ({{\varvec{n}}}_{w} \cdot \nabla S)}{\partial x_j}\nonumber \\{} & {} \quad + \frac{\partial (|| \nabla S||_2^{-1})}{\partial x_j}\frac{\partial ({{\varvec{n}}}_{w} \cdot \nabla S)}{\partial x_j \partial x_i} \nonumber \\{} & {} \quad +\, || \nabla S||_2^{-1}\frac{\partial ({{\varvec{n}}}_{w} \cdot \nabla S)}{\partial x_j \partial x_i} + \lambda \frac{\partial S}{\partial x_j \partial x_i} = 0, \end{aligned}$$

(49)

$$\begin{aligned}{} & {} \frac{\partial F_i}{\partial \lambda }= \frac{\partial S}{\partial x_i} , \frac{\partial F_4}{\partial x_j}= \frac{\partial S}{\partial x_j} , \frac{\partial F_4}{\partial \lambda }=0. \end{aligned}$$

(50)

3.4.3 Algorithm

Combining Part 1 (Sect. 3.4.1) and Part 2 (Sect. 3.4.2), we obtain the following algorithm, presented in Fig. 6. The wall collision algorithm is designed to enable collision detection for particles moving in complex meshes. The meshes possess multiple plane boundary elements, further referred to as wall patches, defining its wall.

The first section of the algorithm is called the pre-evaluation. Here, we check whether there is a point on the particle that is inside one of the wall patches of a user-defined wall interaction range list. In this context, we use bounding sphere and oriented bounding box intersection tests [1, 52] to investigate whether contact is generally possible. As Ericson, [52], noted, testing bounding volume intersections prior to complex geometric evaluations allows for significant performance improvement by neglecting contact pairs without overlapping bounding volumes, thereby reducing the amount of work required to determine collisions and saving computation time. If a contact is possible, the optimization presented in Sect. 3.4.1 is solved numerically using the Newton–Raphson method. At the moment of initial contact, when the bounding box of the particle is in contact with the wall patch, all bounding box edge points are checked to determine the point of maximum overlap. The coordinates of this point are then used as the initial estimate for the Newton–Raphson procedure. In general, the pre-evaluation determines the wall patch that has the largest overlap with the current particle. This wall patch is then used as the collision partner of the particle in the full evaluation cycle. If no overlap is found, we proceed with the evaluation of the next particle.

Fig. 6

Particle–wall collision algorithm

3.5 Superellipsoid-Superellipsoid collision

Let us consider two superellipsoids: $S_1$ and $S_2$, which are described by $a_1$, $b_1$, $c_1$, $\epsilon _{1,1}$,$\epsilon _{2,1}$, ${{\varvec{r}}}_{c,1}$, ${{\varvec{e}}}_1$ and $a_2$, $b_2$, $c_2$, $\epsilon _{1,2}$,$\epsilon _{2,2}$, ${{\varvec{r}}}_{c,2}$, ${{\varvec{e}}}_2$, respectively.

3.5.1 Part 1: Collision point on particle 1 and inside particle 2

A contact between the two particles is only possible, if there exists an ${\varvec{r}}$, which is on the surface of $S_1$,

$$\begin{aligned} S_1({{\varvec{r}}})=0 \end{aligned}$$

(51)

and at the same time inside of $S_2$:

$$\begin{aligned} S_2( {{\varvec{r}}})<0\,. \end{aligned}$$

(52)

The tasks is to find ${\varvec{r}}$ such that

$$\begin{aligned} {\varvec{r}} = {\textrm{arg}}\{\min (S_2( {{\varvec{r}}}))\}\,, \end{aligned}$$

(53)

with the constraint of Eq. (51). In order to solve this optimization problem, we employ a Langrangian defined as:

$$\begin{aligned} L({\varvec{r}} ,\lambda )=S_2({{\varvec{r}}})+\lambda S_1({{\varvec{r}}})\,. \end{aligned}$$

(54)

The stationary conditions read

$$\begin{aligned} \frac{\partial L}{\partial x}=0\,, \qquad \frac{\partial L}{\partial y}=0\,, \qquad \frac{\partial L}{\partial z}=0\,, \qquad \frac{\partial L}{\partial \lambda }=0\,, \end{aligned}$$

(55)

thus we obtain a nonlinear system of four equations for the unknown location ${{\varvec{r}}}$ and $\lambda$:

$$\begin{aligned} \frac{\partial L}{\partial x_i}= & {} \frac{\partial S_2}{\partial x_i}+\lambda \frac{\partial S_1}{\partial x_i} = 0. \end{aligned}$$

(56)

The full derivation of Eq. (56) can be found in Appendix C. The derivative of the Lagrangian with respect to the Lagrange multiplier is

$$\begin{aligned}&\frac{\partial L}{\partial \lambda }=S_1({{\varvec{r}}}) = 0\,. \end{aligned}$$

(57)

The system of equations for $[x,y,z,\lambda ]$ is

$$\begin{aligned} F_1= \frac{\partial L}{\partial x}, F_2= \frac{\partial L}{\partial y}, F_3= \frac{\partial L}{\partial z}, F_4 = \frac{\partial L}{\partial \lambda }. \end{aligned}$$

(58)

Furthermore, the elements of the Jacobian are

$$\begin{aligned} \frac{\partial F_i}{\partial x_j}{=} \frac{\partial S_2}{\partial x_j \partial x_i}{+}\lambda \frac{\partial S_1}{\partial x_j \partial x_i}\,, \frac{\partial F_i}{\partial \lambda }{=} \frac{\partial S_1}{\partial x_i}\,, \frac{\partial F_4}{\partial x_j}{=} \frac{\partial S_1}{\partial x_j}\,, \frac{\partial F_4}{\partial \lambda }{=}0\,. \end{aligned}$$

(59)

3.5.2 Part 2: Collision point on particle 2 and inside particle 1

To obtain the contact point located on the surface of $S_2$, we define a virtual wall using the first identified collision point $p_{c,1}$ and the referring normalized surface gradient as the wall normal ${{\varvec{n}}}$, see Fig. 7. We can thus use a similar approach as in Sect. 3.4.2.

Fig. 7

Detection of collision point on superellipsoid 2 and inside superellipsoid 1 with common normal ${\varvec{n}}$

Fig. 8

Superellipsoid-superellipsoid collision algorithm

3.5.3 Algorithm

Combining Part 1 (Sect. 3.5.1) and Part 2 (Sect. 3.5.2), we obtain the following algorithm, shown in Fig. 8. The first section of the algorithm is called the pre-evaluation. Here, it is first evaluated whether a particle lies in the user-defined intersection range of the particle chosen as the sum of the semi-major particle axis. Furthermore, it is evaluated whether contact is generally possible by performing an oriented bounding box intersection test, [1, 52]. If contact is possible, optimization is performed, see Sect. 3.5.1, which is solved numerically using a Newton–Raphson approach. At the first moment of intersection, when the bounding boxes of the particles are in contact, all bounding box edge points are checked to determine the point of maximum overlap, which is then used as the initial guess for the Newton–Raphson procedure. Generally, the pre-evaluation determines the particle that has the largest overlap with the current particle. This particle is then used as the particle’s collision partner in the full evaluation cycle. If contact has occurred, we store the collision partners in a collision list and neglect them for further contact detection steps in the current time step. If no overlap is detected, we proceed to evaluate the next particle and its possible collision partners.

4 Collision model for superellipsoids

Having defined the collision point and the normal, we derive the collision model for superellipsoids. The problem to be studied is an eccentric rigid body collision in 3D space. The colliding particles are superellipsoids. The formulation itself is based on the assumption that the particles are rigid and in elastic contact (restitution coefficient $\epsilon _n \le 1$) and that there is possible friction between particle–particle and particle wall, which is accounted for by the tangential restitution coefficient $\epsilon _t$. We investigate two superellipsoidal particles with masses $m_1$ and $m_2$. Furthermore, we consider three coordinate systems, the global coordinate system [x,  y,  z], the particle coordinate system [$x',~y',~z'$] located at the center of mass of the particle and whose axis $x'$ points in the direction of the semi-major axis of the superellipsoid. Above we determined the point of contact P and the unit normal ${{\varvec{n}}}$ to the plane of contact, see Sect. 3. With ${\underline{n}}$ we define the collision coordinate system [$x'',~y'',~z''$], where $x''$ points in the direction of ${\underline{n}}$. Figure 9 illustrates the coordinate systems used.

4.1 The collision frame of reference

The choice of the frame of reference is to some extent arbitrary, but it is reasonable to choose such a frame that simplifies the description of the collision model as much as possible. The origin of the chosen reference frame, also called the collision reference frame, is at the contact point P and its unit basis vector ${{{\varvec{e}}_1''}}$ is oriented in the direction of the identified surface normal at that contact point. There are no preferred orientations of the orthogonal unit basis vectors ${{{\varvec{e}}_2''}}$ and ${{{\varvec{e}}_3''}}$. We consider two collision partners identified by their position ${{\varvec{r}}}_i$, $i=1,2$, their orientation expressed by the Euler parameters ${{\varvec{e}}}_i$ and the angular velocity ${\varvec{\omega }}_i$. For the evaluation of the collision, all physical quantities must be represented in a single reference frame, for which we choose the collision frame [$x'',~y'',~z''$]. Figure 9 illustrates the determination of the collision frame. First, we obtain the particle position vectors relative to the collision point ${{\varvec{r}}}_i^{\star }$, $i=1,2$ using the particle position vectors ${{\varvec{r}}}_i$, and the contact point position vector ${{\varvec{r}}}_P$:

$$\begin{aligned} {{\varvec{r}}}_i^{\star }={{\varvec{r}}}_i-{{\varvec{r}}}_P, \end{aligned}$$

(60)

In the next step, we perform a rotational transformation of $\underline{{r}}_i^{\star }$ to represent the vectors in the collision reference frame. Now we may transform coefficient vectors defined in the global frame [$\underline{r}_i^{ \star }$,$\underline{v}_i$] into the collision frame, by multiplication with the rotation matrix ${\underline{R}}_0$, that transforms from global to collision frame of reference

$$\begin{aligned} {\underline{r}}_i^{\prime \prime } = {\underline{R}}_0\, {\underline{r}}_i^*, \qquad {\underline{v}}_i'' = {\underline{R}}_0\, {\underline{v}}_i. \end{aligned}$$

(61)

Moreover, the angular velocity ${\underline{\omega }}_i'$ and the inertia matrix ${\underline{I}}'$, which are defined in the reference frame of the particle bodies, must be expressed in the collision frame. Thus, we start with the definition of the rotation matrix, denoted as ${{\underline{R}}_i}$, which represent the transformation from the fixed reference frame of the i-th particle body to the collision reference frame and ${\underline{R}_i}$ its coefficient matrix. These quantities of the body fixed frames are rotated using the following rules:

$$\begin{aligned} {\underline{\omega }}_i'' = {\underline{R}}_i\,{\underline{\omega }}_i', \qquad {\underline{I}}_i'' = {\underline{R}}_i \,{\underline{I}}_i'\,{\underline{R}_i}^T. \end{aligned}$$

(62)

Using the above transformations, particle position coefficients ${\underline{r}}_i''$, velocity coefficients ${\underline{v}}_i''$, angular velocity coefficients ${\underline{\omega }}_i''$ and inertia tensor coefficient matrix ${\underline{I}}_i''$ are now available in the collision reference frame.

Fig. 9

Two superellipsoidal particles undergoing collision

4.2 Conservation equations during collision

Let ${{\varvec{v}}}_i$ denote the particle velocity before and ${{\varvec{c}}}_i$ the particle velocity after collision. The corresponding angular velocities are ${{\varvec{\omega }}}_i$ and ${{\varvec{\psi }}}_i$. The conservation of linear momentum reads

$$\begin{aligned} m_1{{\varvec{v}}}_1+m_2{{\varvec{v}}}_2=m_1{{\varvec{c}}}_1+m_2{{\varvec{c}}}_2\,. \end{aligned}$$

(63)

The velocity of each particle at the contact point may be calculated from the centre of mass velocity and the angular velocity using

$$\begin{aligned} {{\varvec{v}}}_{iP}={{\varvec{v}}}_i-{{\varvec{\omega }}}_i\times {{\varvec{r}}}_i^*, \qquad {{\varvec{c}}}_{iP}={{\varvec{c}}}_i-{{\varvec{\psi }}}_i\times {{\varvec{r}}}_i^*, \end{aligned}$$

(64)

where ${{\varvec{r}}}_i^*$ points from the collision point to the respective particle center. The relative contact point velocity in the normal direction before and after collision is connected by:

$$\begin{aligned} {{\varvec{n}}} \cdot {{\varvec{c}}}_{2P}- {{\varvec{n}}} \cdot {{\varvec{c}}}_{1P} =-\epsilon _n \left[ {{\varvec{n}}} \cdot {{\varvec{v}}}_{2P}-{{\varvec{n}}} \cdot {{\varvec{v}}}_{1P}\right] \,, \end{aligned}$$

(65)

where $\epsilon _n = 1$ refers to conservation of normal velocity. Since we defined the collision reference frame by pointing ${{\varvec{e}}_1''}$ in the direction of the collision normal, the coefficient matrix of the normal in Eq. (65) is simply ${\underline{n}}''=[1,~0,~0]^T$. This yields

$$\begin{aligned} \begin{aligned}&c_{2x}''+r_{2y}''\psi _{2z}''-r_{2z}''\psi _{2y}'' -c_{1x}''-r_{1y}''\psi _{1z}''+r_{1z}''\psi _{1y}'' \\&\quad {=}{-}\epsilon _n \left[ v_{2x}''{-}r_{2z}''\omega _{2y}''{+}r_{2y}''\omega _{2z}''{-}v_{1x}''{+}r_{1z}''\omega _{1y}''{-}r_{1y}''\omega _{1z}'' \right] . \end{aligned} \end{aligned}$$

(66)

Since we consider friction with the tangential restitution coefficient $\epsilon _t = [-1,~1]$, where $\epsilon _t = 1$ refers to conservation of tangential velocity, the relative contact point velocity in the tangential directions before and after collision are connected by:

$$\begin{aligned} {{\varvec{t}}_i} \cdot {{\varvec{c}}}_{2P}- {{\varvec{t}}_i} \cdot {{\varvec{c}}}_{1P} =\epsilon _t \left[ {{\varvec{t}}_i} \cdot {{\varvec{v}}}_{2P}-{{\varvec{t}}_i} \cdot {{\varvec{v}}}_{1P}\right] , \end{aligned}$$

(67)

where $i=1,2$. Using ${\underline{t}}_1''=[0,~1,~0]^T$ and ${\underline{t}}_2''=[0,~0,~1]^T$ we obtain

$$\begin{aligned} \begin{aligned}&c_{2y}''-r_{2x}''\psi _{2z}''+r_{2z}''\psi _{2x}'' -c_{1y}''+r_{1x}''\psi _{1z}''-r_{1z}''\psi _{1x}'' \\&\quad =\epsilon _t \left[ v_{2y}''-r_{2x}''\omega _{2z}'' +r_{2z}''\omega _{2x}''- v_{1y}''+r_{1x}''\omega _{1z}''- r_{1z}''\omega _{1x}''\right] \end{aligned} \end{aligned}$$

(68)

and

$$\begin{aligned} \begin{aligned}&c_{2z}''-r_{2y}''\psi _{2x}''+r_{2x}''\psi _{2y}'' -c_{1z}''+r_{1y}''\psi _{1x}''-r_{1x}''\psi _{1y}'' \\&\quad =\epsilon _t \left[ v_{2z}''- r_{2y}''\omega _{2x}''+ r_{2x}''\omega _{2y}''-v_{1z}''+r_{1y}''\omega _{1x}'' -r_{1x}''\omega _{1y}'' \right] . \end{aligned} \end{aligned}$$

(69)

The conservation of angular momentum can be expressed for each particle separately as

$$\begin{aligned} {{\varvec{I}}}_{i}\cdot {{\varvec{\omega }}}_{i}+{{\varvec{r}}}_{i}\times m_i{{\varvec{v}}}_{i}= {{\varvec{I}}}_{i}\cdot {{\varvec{\psi }}}_{i}+{{\varvec{r}}}_{i}\times m_i{{\varvec{c}}}_{i}\,. \end{aligned}$$

(70)

This is true since here the reference point for the balance of angular momentum is the contact point, thus the contact force does not contribute to the momentum.

4.3 Particle–particle collision

In order to set up a linear system of equations in the form of ${\underline{A}}\,{\underline{x}} = {\underline{b}}\,$ we use the following algorithm:

Thus we obtain A and b as follows:

$$\begin{aligned} {\underline{A}} = \left[ \begin{array}{cccccccccccc } m_1&{} 0 &{} 0 &{} m_2&{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} m_1 &{} 0 &{} 0 &{} m_2&{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} m_1 &{} 0 &{} 0 &{} m_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} r_{1z}'' &{} -r_{1y}'' &{} 0 &{} -r_{2z}'' &{} r_{2y}'' \\ 0 &{}-1 &{} 0 &{} 0 &{} 1 &{} 0 &{} -r_{1z}'' &{} 0 &{} r_{1x}'' &{} r_{2z}'' &{} 0 &{} -r_{2x}'' \\ 0 &{} 0 &{} -1 &{} 0 &{} 0 &{} 1 &{} r_{1y}'' &{} -r_{1x}'' &{} 0 &{} -r_{2y}'' &{} r_{2x}'' &{} 0 \\ 0 &{} -m_1r_{1z}'' &{} m_1r_{1y}'' &{} 0 &{} 0 &{} 0 &{} I_{xx}'' &{} I_{xy}'' &{} I_{xz}'' &{} 0 &{} 0 &{} 0\\ m_1r_{1z}'' &{} 0 &{} -m_1r_{1x}''&{} 0 &{} 0 &{} 0 &{} I_{yx}'' &{} I_{yy}'' &{} I_{yz}'' &{} 0 &{} 0 &{} 0\\ -m_1r_{1y}''&{} m_1r_{1x}'' &{} 0 &{} 0 &{} 0 &{} 0 &{} I_{zx}'' &{} I_{zy}'' &{} I_{zz}''&{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -m_2r_{2z}'' &{} m_2r_{2y}'' &{} 0 &{} 0 &{} 0 &{} I_{xx}'' &{} I_{xy}'' &{} I_{xz}''\\ 0 &{} 0 &{} 0 &{} m_2r_{2z}''&{} 0 &{} -m_2r_{2x}''&{} 0 &{} 0 &{} 0 &{} I_{yx}'' &{} I_{yy}'' &{} I_{yz}''\\ 0 &{} 0 &{} 0 &{}-m_2r_{2y}''&{} m_2r_{2x}'' &{} 0 &{} 0 &{} 0 &{} 0 &{} I_{zx}'' &{} I_{zy}'' &{} I_{zz}''\\ \end{array}\right] \end{aligned}$$

(71)

$$\begin{aligned} {\underline{b}}=\left[ \begin{array}{c} m_1v_{1x}''+m_2v_{2x}''\\ m_1v_{1y}''+m_2v_{2y}''\\ m_1v_{1z}''+m_2v_{2z}''\\ -\epsilon _n \left[ v_{2x} - \omega _{2y}r_{2z} + \omega _{2z}r_{2y} - v_{1x} + \omega _{1y}r_{1z} -\omega _{1z}r_{1y} \right] \\ ~~~\epsilon _t \left[ v_{2y} - \omega _{2z}r_{2x} + \omega _{2x}r_{2z} - v_{1y} + \omega _{1z}r_{1x} -\omega _{1x}r_{1z} \right] \\ ~~~\epsilon _t \left[ v_{2z} - \omega _{2x}r_{2y} + \omega _{2y}r_{2x} - v_{1z} + \omega _{1x}r_{1y} -\omega _{1y}r_{1x} \right] \\ I_{1xx}''\omega _{1x}''+I_{1xy}''\omega _{1y}''+I_{1xz}''\omega _{1z}''+ m_1 r_{1y}''v_{1z}''- m_1 r_{1z}''v_{1y}'' \\ I_{1yx}''\omega _{1x}''+I_{1yy}''\omega _{1y}''+I_{1yz}''\omega _{1z}''+ m_1 r_{1z}''v_{1x}''- m_1 r_{1x}''v_{1z}'' \\ I_{1zx}''\omega _{1x}''+I_{1zy}''\omega _{1y}''+I_{1zz}''\omega _{1z}''+ m_1 r_{1x}''v_{1y}''- m_1 r_{1y}''v_{1x}'' \\ I_{2xx}''\omega _{2x}''+I_{2xy}''\omega _{2y}''+I_{2xz}''\omega _{2z}''+ m_2 r_{2y}''v_{2z}''- m_2 r_{2z}''v_{2y}'' \\ I_{2yx}''\omega _{2x}''+I_{2yy}''\omega _{2y}''+I_{2yz}''\omega _{2z}''+ m_2 r_{2z}''v_{2x}''- m_2 r_{2x}''v_{2z}'' \\ I_{2zx}''\omega _{2x}''+I_{2zy}''\omega _{2y}''+I_{2zz}''\omega _{2z}''+ m_2 r_{2x}''v_{2y}''- m_2 r_{2y}''v_{2x}'' \\ \end{array}\right] \,. \end{aligned}$$

(72)

4.4 Particle–particle collision (frictionless)

In the case of zero friction the impulse acts in the normal direction only, the tangential components of the particle velocity at the contact point are conserved, i.e. $v_{iy}''=c_{iy}''$, $v_{iz}''=c_{iz}''$ as well as the normal component of the angular velocity ${{\varvec{n}}}\cdot {\varvec{\omega }}_{i}={{\varvec{n}}}\cdot {\varvec{\psi }}_{i}$, i.e. $\omega _{ix}''=\psi _{ix}''$.

The following algorithm is used to solve for the unknown final particle velocity and angular velocity for a particle–particle collision without friction:

The system of equations simplifies to

$$\begin{aligned} \left[ \begin{array}{cccccc} m_1&{} m_2&{} 0&{} 0&{} 0&{} 0\\ -1&{} 1&{}r_{1z}'' &{}-r_{1y}'' &{}-r_{2z}'' &{}r_{2y}'' \\ m_1r_{1z}'' &{}0 &{}I_{1yy}'' &{}I_{1yz}'' &{}0 &{}0 \\ -m_1r_{1y}'' &{}0 &{}I_{1zy}'' &{}I_{1zz}'' &{}0 &{}0 \\ 0 &{} m_2r_{2z}'' &{}0 &{}0 &{}I_{2yy}'' &{}I_{2yz}'' \\ 0&{} -m_2r_{2y}'' &{}0 &{}0 &{}I_{2zy}'' &{}I_{2zz}'' \\ \end{array}\right] \left[ \begin{array}{c} c_{1x}'' \\ c_{2x}'' \\ \psi _{1y}'' \\ \psi _{1z}'' \\ \psi _{2y}'' \\ \psi _{2z}'' \\ \end{array}\right] = {\underline{b}} \,, \end{aligned}$$

(73)

where ${\underline{b}}$ is defined as:

$$\begin{aligned} {\underline{b}}=\left[ \begin{array}{c} m_1v_{1x}''+m_2v_{2x}''\\ \epsilon _n \left[ v_{1x}''+r_{1y}''\omega _{1z}''-r_{1z}''\omega _{1y}'' -v_{2x}''-r_{2y}''\omega _{2z}''+r_{2z}''\omega _{2y}''\right] \\ I_{1yy}''\omega _{1y}''+I_{1yz}''\omega _{1z}''+m_1r_{1z}''v_{1x}'' \\ I_{1zy}''\omega _{1y}''+I_{1zz}''\omega _{1z}''-m_1r_{1y}''v_{1x}'' \\ I_{2yy}''\omega _{2y}''+I_{2yz}''\omega _{2z}''+m_2r_{2z}''v_{2x}'' \\ I_{2zy}''\omega _{2y}''+I_{2zz}''\omega _{2z}''-m_2r_{2y}''v_{2x}''\\ \end{array}\right] . \end{aligned}$$

(74)

4.5 Particle - wall collision

Since we consider a collision with a wall of infinite mass, the relative contact point velocity in the normal direction before and after collision of Eq. (65) simplifies to:

$$\begin{aligned} {{\varvec{n}}} \cdot {{\varvec{c}}}_{P} =-\epsilon _n \left[ {{\varvec{n}}} \cdot {{\varvec{v}}}_{P} \right] \,. \end{aligned}$$

(75)

and the tangential components of the particle velocity are conserved. We defined the collision reference frame by pointing ${{\varvec{e}}_1''}$ in the direction of the collision normal. The coefficient matrix of the normal ${\varvec{n}}$ in Eq. (75) is given by ${\underline{n}''}=\left[ 1,~0,~0\right] ^T$. Thus, we can simplify Eq. (75) to

$$\begin{aligned} c_{x}'' -r_{z}''\psi _{y}'' +r_{y}''\psi _{z}'' =-\epsilon _n\left[ v_{x}''-r_{z}''\omega _{y}''+r_{y}''\omega _{z}'' \right] . \end{aligned}$$

(76)

Since we consider friction with the tangential restitution coefficient $\epsilon _t = [-1,~1]$, the relative contact point velocity in the tangential directions before and after collision are connected by:

$$\begin{aligned} {{\varvec{t}}_i} \cdot {{\varvec{c}}}_{P} = \epsilon _t \left[ {{\varvec{t}}_i} \cdot {{\varvec{v}}}_{P}\right] , \end{aligned}$$

(77)

where $i=1,2$ and $\underline{t}_1''=[0,~1,~0]^T$ and $\underline{t}_2''=[0,~0,~1]^T$. This yields

$$\begin{aligned} c_{y}'' - r_{x}''\psi _{z}'' + r_{z}''\psi _{x}'' =\epsilon _t \left[ v_{y}''-r_{x}''\omega _{z}'' + r_{z}''\omega _{x}''\right] \end{aligned}$$

(78)

and

$$\begin{aligned} c_{z}''-r_{y}''\psi _{x}'' +r_{x}''\psi _{y}'' = \epsilon _t \left[ v_{z}''-r_{y}''\omega _{x}'' + r_{ x}''\omega _{y}''\right] . \end{aligned}$$

(79)

The conservation of angular momentum can be expressed for the particle as

$$\begin{aligned} {{\varvec{I}}}\cdot {{\varvec{\omega }}}+{{\varvec{r}}}\times m{{\varvec{v}}}= {{\varvec{I}}}\cdot {{\varvec{\psi }}} +{{\varvec{r}}}\times m{{\varvec{c}}}\,. \end{aligned}$$

(80)

Thus we obtain:

$$\begin{aligned}{} & {} \left[ \begin{array}{cccccc} 1&{} 0 &{} 0 &{} 0 &{} -r_z'' &{} r_y'' \\ 0&{} 1 &{} 0 &{} r_z'' &{} 0 &{} -r_x'' \\ 0&{} 0 &{} 1 &{} -r_y'' &{} r_x'' &{} 0 \\ 0&{} -mr_z &{} mr_y &{}I_{xx}''&{}I_{xy}'' &{} I_{xz}'' \\ mr_z &{} 0 &{} -mr_x &{}I_{yx}''&{}I_{yy}'' &{} I_{yz}'' \\ -mr_y &{} mr_x &{} 0 &{}I_{zx}''&{}I_{zy}'' &{} I_{zz}'' \\ \end{array}\right] \left[ \begin{array}{c} c_{x}'' \\ c_{y}'' \\ c_{z}'' \\ \psi _{x}'' \\ \psi _{y}'' \\ \psi _{z}'' \\ \end{array}\right] \nonumber \\{} & {} \quad =\left[ \begin{array}{c} -\epsilon _n \left[ v_{x}'-r_{z}''\omega _{y}'''+r_{y}''\omega _{z}''\right] \\ ~~~\epsilon _t \left[ v_{y}'-r_{x}''\omega _{z}'''+r_{z}''\omega _{x}''\right] \\ ~~~\epsilon _t \left[ v_{z}'-r_{y}''\omega _{x}'''+r_{x}''\omega _{y}''\right] \\ I_{xx}''\omega _{x}''+I_{xy}''\omega _{y}''+I_{xz}''\omega _{z}''+ m r_{y}''v_{z}''- m r_{z}''v_{y}'' \\ I_{yx}''\omega _{x}''+I_{yy}''\omega _{y}''+I_{yz}''\omega _{z}''+ m r_{z}''v_{x}''- m r_{x}''v_{z}'' \\ I_{zx}''\omega _{x}''+I_{zy}''\omega _{y}''+I_{zz}''\omega _{z}''+ m r_{x}''v_{y}''- m r_{y}''v_{x}'' \\ \end{array}\right] .\nonumber \\ \end{aligned}$$

(81)

4.6 Particle - wall collision (frictionless)

If we assume frictionless collision, the impulse acts solely in the normal direction and the tangential components of the particle velocity are conserved,

$$\begin{aligned} v_{y}'' = c_{y}'', \qquad v_{z}''=c_{z}'' \end{aligned}$$

(82)

as well as the angular velocity ${{\varvec{n}}}\cdot {{\varvec{\omega }}}={{\varvec{n}}}\cdot {{\varvec{\psi }}}$:

$$\begin{aligned} \omega _{x}''=\psi _{x}''\,. \end{aligned}$$

(83)

Considering only y and z components of Eq. (80) and taking into account $v_{y}''= c_{y}''$, $v_{z}'' = c_{z}''$ and $\omega _{x}''=\psi _{x}''$ we obtain

$$\begin{aligned}{} & {} I_{yy}''\omega _{y}''+I_{yz}''\omega _{z}'' +mr_{z}''v_{x}''= I_{yy}''\psi _{y}'' +I_{yz}''\psi _{z}'' +mr_{z}''c_{x}'', \end{aligned}$$

(84)

$$\begin{aligned}{} & {} I_{zy}''\omega _{y}''+I_{zz}''\omega _{z}'' -mr_{y}''v_{x}''= I_{zy}''\psi _{y}'' +I_{zz}''\psi _{z}'' -mr_{y}''c_{x}''. \end{aligned}$$

(85)

The following algorithm summarizes how to solve for the unknown final particle velocity ${\varvec{c}}$ and angular velocity $\varvec{\psi }$ for frictionless particle–wall collision

We obtain the following system of equation:

$$\begin{aligned} \left[ \begin{array}{ccc} 1&{} -r_z'' &{} r_y'' \\ mr_{z}'' &{}I_{yy}'' &{} I_{yz}'' \\ -mr_{y}'' &{}I_{zy}'' &{} I_{zz}'' \\ \end{array}\right] \left[ \begin{array}{c} c_{x}'' \\ \psi _{y}'' \\ \psi _{z}'' \\ \end{array}\right] = \left[ \begin{array}{c} -\epsilon _n \left[ v_{x}''+r_{y}''\omega _{z}''-r_{z}''\omega _{y}''\right] \\ I_{yy}''\omega _{y}''+I_{yz}''\omega _{z}''+mr_{z}''v_{x}'' \\ I_{zy}''\omega _{y}''+I_{zz}''\omega _{z}''-mr_{y}''v_{x}'' \\ \end{array}\right] \,. \end{aligned}$$

(86)

5 Demonstration Examples

In the following, we validate the presented approach using various superellipsoidal shapes in demonstrative collision examples, i.e. head-on-collision, eccentric collisions for both particle–wall and particle–particle collisions. Moreover, we demonstrate the ability of the novel approach in the case of dense particle packing as in cylinder filling. In this context, we investigate the influence of the time step on the resulting particle trajectories. Note that our implementation in OpenFoam includes the possibility of subcycling, where a time step can be split into multiple collision substeps, which is important for particle collisions in flows where the particle Courant number has to be smaller than the fluid Courant number. This means that one time step of the fluid flow time step can be divided into several collision time steps.

5.1 Wall collision

First, we perform particle–wall collisions of four different superellipsoidal shapes, ranging from diamond-like particles to cuboids, see Table 1.

Table 1 Shape parameters of demonstrative particles, $d_\textrm{eq}=1\,\hbox {mm}$

We use two different initial orientations of the particles under consideration to simulate both centric particle–wall collisions (head-on collision) and eccentric particle–wall collisions. The initial orientations are $\varphi = 0\,^{\circ }$, $\theta = 0\,^{\circ }$, $\psi = 0\,^{\circ }$ for centric collisions and $\varphi = 45\,^{\circ }$, $\theta = 0\,^{\circ }$, $\psi = 0\,^{\circ }$ for eccentric collisions. The initial elevation of the particle is set to $p_{0,y}= 5\,d_\textrm{eq}$. The time it takes the particle to move $d_\textrm{eq}$ is denoted by $t_\textrm{Ref} = d_\textrm{eq}/|u_{0,y}|$, where $u_{0,y}$ denotes the initial velocities of the particles in the wall normal direction. Figure 10 illustrates the centric and eccentric wall collision using the example of a diamond-shaped particle.

Fig. 10

Sketch of centric and eccentric particle–wall collision

5.1.1 Centric collision

First, we evaluate the time evolution of the considered particles before and after the centric wall collision, while varying the time step of the simulation. As can be seen in Fig. 11a–d, convergence with decreasing time step is observed for all particle shapes studied. For all particles considered, no change in the trajectory is observed at a time resolution of $t/t_\textrm{Ref} \le 0.05$. However, even a time step that allows a motion of 10% $d_\textrm{eq}$ (i.e. $t/t_\textrm{Ref} = 0.1$) leads to small deviations of the translational motion. Moreover, the use of $t/t_\textrm{Ref} \le 1$ (100% $d_\textrm{eq}$ translation per time step) with 10 subcycles leads to similar accuracy as $t/t_\textrm{Ref} = 0.1$.

Fig. 11

Translation of a sphere, prolate, cube and diamond during a centric article-wall collision. $\Delta t/t_\textrm{Ref}$:    1,    0.5,      $1^*$,    0.1,      0.01,    0.001,    0.0001. ($^* =10$ subcycles)

Next, we evaluate the time evolution of the angular velocity of the particles before and after the centric particle–wall collision with respect to different time steps. Because of the centric collision, the angular velocities should remain zero after the collision. As can be seen in Fig. 12a–d, we observe convergence with decreasing time step for all particle shapes studied. For all particles considered, no change in angular velocity is observed at a time resolution of $t/t_\textrm{Ref} \le 0.1$. In general, we observe good agreement with the analytical result of zero angular velocity in centric particle–wall collision for all superellipsoids investigated.

Fig. 12

Angular velocity during a particle–wall centric collision of a sphere, prolate, cube and diamond. $\Delta t/t_\textrm{Ref}$:    1,    0.5,      $1^*$,    0.1,      0.01,    0.001,    0.0001. ($^* =10$ subcycles)

5.1.2 Eccentric collision

In a further step, we target eccentric particle–wall collisions. In this context, we investigate the effects of the time step on the translational and rotational motion of the four superellipsoidal shapes. Figure 13a–d shows the vertical position of the superellipsoids. Similar to the centric collision, we observe a convergence with decreasing time steps for all studied superellipsoids. A time resolution of $t/t_\textrm{Ref} \le 0.1$ leads to a sufficiently accurate motion for all particles considered. However, the use of $t/t_\textrm{Ref} \le 1$ (100% $d_\textrm{eq}$ translation per time step) leads to high deviations of the translational motion and is therefore not appropriate. Note that the use of $t/t_\textrm{Ref} \le 1$ with 10 subcycles results in similar accuracy as $t/t_\textrm{Ref} = 0.1$ and provides a sufficient description of the translational motion.

Fig. 13

Particle–wall eccentric collision of a sphere, prolate, cube and diamond. $\Delta t/t_\textrm{Ref}$:    1,    0.5,      $1^*$,    0.1,      0.01,    0.001,    0.0001. ($^* =10$ subcycles)

The time evolution of the angular velocity of the particles before and after the eccentric particle–wall collision is shown in Fig. 14. Due to the initial orientation $\varphi = 45\,^{\circ }$, $\theta = 0\,^{\circ }$, $\psi = 0\,^{\circ }$, only the component $\omega _z$ can be nonzero after the collision for all nonspherical particles. The components $\omega _x$ and $\omega _y$ are presented in Fig. 14b, d, f, h and remain zero after the collision for all superellipsoids investigated, which agrees with the analytical result. For large time steps such as $t/t_\textrm{Ref} \le 1$ (100% $d_\textrm{eq}$, however, we observe small deviations. We therefore recommend the use of $t/t_\textrm{Ref} \ll 1$. The $\omega _z$ components for the superellipsoids considered are shown in Fig. 14a, c, e, g. As shown in Fig. 14a, for the spherical particles also $\omega _z$ remains zero after the collision. For all considered nonspherical particles, such as the prolate (Fig. 14c), the cube-shaped (Fig. 14e), and the diamond-shaped particle (Fig. 14f), we obtain convergence of the angular velocity with decreasing time step. For both the prolate ellipsoid and the cuboid $t/t_\textrm{Ref} \le 0.1$ (10% $d_\textrm{eq}$) leads to accurate results, while for the diamond particle a smaller time step of $t/t_\textrm{Ref} \le 0.01$ (1% $d_\textrm{eq}$) is recommended.

Fig. 14

Particle–wall eccentric collision of a sphere, prolate, cube and diamond: Angular velocity components $w_z$ and ${\sqrt{\omega _x^2 + \omega _y^2 }}$. $\Delta t/t_\textrm{Ref}$:    1,    0.5,      $1^*$,    0.1,      0.01,    0.001,    0.0001. ($^* =10$ subcycles)

5.2 Particle–Particle Collision

Next, we perform the centric and eccentric collision of two particles (Fig. 15) of spherical, ellipsoidal, diamond, and cuboidal shapes, see Table 1. The initial orientation of the particles under consideration is set as follows: $\varphi = 0\,^{\circ }$, $\theta = 0\,^{\circ }$, $\psi = 0\,^{\circ }$ for particle A and $\varphi = -90\,^{\circ }$, $\theta = 0\,^{\circ }$, $\psi = 0\,^{\circ }$ for particle B in centric collision. For eccentric collision, the initial orientation of particle A is set to $\varphi = 45\,^{\circ }$, $\theta = 0\,^{\circ }$, $\psi = 0\,^{\circ }$. The initial positions are set to $p_{0,A}=[0.5,~1,~1]^T$ for particle A and $p_{0,B}=[0.503,~1,~1]^T$ for particle B. The initial velocities of the particles are $u_{0,A}=[1,~0,~0]\,m/s$ and $u_{0,B}=[0,~0,~0]\,m/s$. The time required for particle A to move $d_\textrm{eq}$ is denoted by $t_\textrm{Ref} = d_\textrm{eq}/|u_{0,A}|$.

Fig. 15

Sketch of centric and eccentric particle–particle collision. Note that $r_{eq}=0.5d_{eq}$

Fig. 16

Particle–particle head on collision.     Analytical collision time $t_{col}/t_\textrm{Ref}$. $\Delta t/t_\textrm{Ref}$:    1,    0.5,      $1^*$,    0.1,      0.01,    0.001,    0.0001. ($^* =10$ subcycles)

5.2.1 Centric Collision

First, we evaluate the time evolution of the four superellipsoid particles before and after the centric particle–particle collision, while varying the time step of the simulation. As displayed in Fig. 16a–h, convergence with decreasing time step is observed for all superellipsoids studied. Moreover, at a time resolution of $t/t_\textrm{Ref} \le 0.05$ no change in trajectory is observed and the analytical collision point can be accurately reproduced. However, even the time step size related to 10% $d_\textrm{eq}$ (i.e. $t/t_\textrm{Ref} = 0.1$) leads to negligible deviations in the trajectories. Moreover, the use of $t/t_\textrm{Ref} \le 1$ (100% $d_\textrm{eq}$ translation per time step) with 10 subcycles results in similar accuracy as $t/t_\textrm{Ref} = 0.1$. In all cases, a time step related to 100% $d_\textrm{eq}$ translation (i.e. $t/t_\textrm{Ref} = 1.0$) is insufficient to resolve the collision. In the case of a centric particle–particle collision, all angular velocities should remain zero as a consequence of the correct identification of the collision points. The angular velocity of the superellipsoid investigated before and after the collision is shown in Fig. 17a–h. For spheres and prolates, the angular velocities remain zero after the collision, as displayed in Fig. 17a–d. For cubes and diamond particles (Fig. 17e-h), we observe small nonzero angular velocities due to minor numerical shifts of the collision points from the actual collision plane. However, this deviation can still be considered negligible and can be further reduced by increasing the convergence criteria of the optimization problem.

Fig. 17

Particle–particle head on collision: Angular velocity $|{\varvec{\omega }}|$. $\Delta t/t_\textrm{Ref}$:    1,    0.5,      $1^*$,    0.1,      0.01,    0.001,    0.0001. ($^* =10$ subcycles)

5.2.2 Eccentric Collision

In the following, we investigate the effect of time step on the translational and rotational motion of superellipsoidal particles during an eccentric particle–particle collision Fig. 18a–h shows the trajectory of the four superellipsoids before and after the eccentric collision. Similar to the head-on particle–particle collision, we observe a convergence of the translational motion with decreasing time steps for all studied shapes. Again, a time resolution of $t/t_\textrm{Ref} \le 0.05$ leads to a sufficiently accurate motion for all particles considered. The use of $t/t_\textrm{Ref} \le 1$ (100% $d_\textrm{eq}$ translation per time step), however, leads to high deviations in the translational motion. Subcycling can improve these results, e.g. $t/t_\textrm{Ref} = 1$ with 10 subcycles, where we can obtain an accuracy similar to $t/t_\textrm{Ref} = 0.1$ and thus a sufficient description of the particle translation.

Fig. 18

Particle–particle eccentric collision of a sphere, prolate, cube and diamond. $\Delta t/t_\textrm{Ref}$:    1,    0.5,      $1^*$,    0.1,      0.01,    0.001,    0.0001. ($^* =10$ subcycles). Included position figures from time steps: $\Delta t/t_\textrm{Ref}=1,~2,~3,~4\,$

Next, we examine the angular velocity of the particles before and after the eccentric particle–particle collision, see Fig. 19. Due to the initial orientation $\varphi = 45\,^{\circ }$, $\theta = 0\,^{\circ }$, $\psi = 0\,^{\circ }$, only the component $\omega _z$ can result after the collision for all nonspherical particles. As shown in Fig. 19a, $\omega _z$ also remains zero after the collision for the spheres. For all nonspherical particles such as the prolate ellipsoid, see Fig. 19c, d, the cuboid, see Fig. 19e, f, and the diamond-shaped superellipsoid, see Fig. 19g, h, however, we obtain a nonzero $\omega _z$. For all particles, we observe a convergence of the angular velocity with decreasing time step, where a time resolution of $t/t_\textrm{Ref} = 0.1$ proved to be sufficient.

Fig. 19

Particle–particle eccentric collision of a sphere, prolate, cube and diamond. $\Delta t/t_\textrm{Ref}$:    1,    0.5,      $1^*$,    0.1,      0.01,    0.001,    0.0001. ($^* =10$ subcycles)

5.3 Cylinder Filling

To illustrate the ability of our model to also handle dense particle systems and thus multiple collisions, we perform simulations involving contacts between multiple particles, such as packing simulations (i.e. cylinder packing). The setup of the cylinder filling simulation is shown in Fig. 20. The length of the cylinder is set to $L=0.4\,\hbox {m}$ and the diameter to $D=0.057\,\hbox {m}$. Here we inject various superellipsoids to compare the final packing. The particles studied are described in Table 2. The superellipsoids have a volume equivalent diameter of $d_\textrm{eq}=0.01\,\hbox {m}$ and a density of $\rho _p= 1000\,\hbox {kg/m}^3$. The restitution coefficient for the particle–wall as well as the particle–particle interaction is set to $\epsilon _n = 0.2$ and we assume $\epsilon _t=1.0$. Note that the value of $\epsilon _n=0.2$ is chosen to allow collision of multiple particles while reducing the time required for the particles to come to rest. We inject 100 particles with initial zero angular velocity and random initial orientation into a cylindrical volume with height L and diameter D to ensure that the particles do not overlap at initialization. The particles settle in the cylinder due to gravity, as shown in Fig. 20. Figure 21 shows the resulting filling height, while Fig. 22 presents the particle distribution at the bottom wall of the cylinder. We employ a time step of $\Delta t = 1\mathrm {e-}{05}$, which has been shown to handle particle collisions with negligible overlap, as presented in Figs. 21 and 22. Thus, this study highlights the ability of the presented collision method to handle multiple collisions of particles-particle and particles with walls of various superellipsoidal shapes. Note that the identified overlap of particles is removed after each collision by a corresponding displacement of the particles according to the identified contact point and to surface normal.

Fig. 20

Sketch of cylinder domain with particles settling due to gravity

Table 2 Demonstrative particles for cylinder filling: $d_\textrm{eq}=0.01\,\hbox {m}$, $\rho _p= 1000\,\hbox {kg/m}^3$, $\epsilon _n = 0.2$ (particle–wall, particle–particle), $\epsilon _t = 1.0$ (frictionless particle–wall and particle–particle collision)

Fig. 21

Front view of cylinder filled with various superellipsoidal shapes using timestep $\Delta t = 1\mathrm {e-}{05}\,\hbox {s}$

Fig. 22

Bottom view of cylinder filled with various superellipsoidal shapes using timestep $\Delta t = 1\mathrm {e-}{05}\,\hbox {s}$

5.4 Emptying of a cylinder

In our final study we employ friction by using $\epsilon _t \ne 1$ to study the emptying of a cylindrical domain filled with 300 particles. Thus, we need to find a description for the relation between the tangential restitution coefficient $\epsilon _t$ and the friction coefficient $\mu$. In the case of spherical particles, Schwager et al. [53] used the following relation between $\epsilon _t$ and the friction coefficient $\mu$ for spheres in the limit of Coulomb friction:

$$\begin{aligned} \epsilon _t = \max \left( 0, 1- {\mu [1+\epsilon _n]} \alpha ^{-1}\frac{g_n}{g_t}\right) , \end{aligned}$$

(87)

using $g_n$ the relative normal velocity and $g_t$ the relative tangential velocity between the colliding partners in the contact point before collision as well as $\alpha$, which is obtained as follows:

$$\begin{aligned} \alpha = \left[ 1+ \frac{m_1 m_2}{m_1 + m_2}\left[ \frac{r_1^2}{I_1} + \frac{r_2^2}{I_2} \right] \right] ^{-1} \end{aligned}$$

(88)

and simplifies to $\alpha = 2/7$ for homogeneous spheres. For simplicity, we chose the relation presented in Eq. (87) to prove the concept of treating friction in our model. Note that the above description for $\epsilon _t$ using the presented $\alpha$ is valid only for spheres. The spherical particles studied have a (volume equivalent) diameter of $d_\textrm{eq}=0.011\,\hbox {m}$ and a density of $\rho _p= 1000\,\hbox {kg/m}^3$. The restitution coefficient for the particle–wall as well as the particle–particle interaction is set to $\epsilon _n = 0.2$. The friction coefficient for the particle–particle and particle–wall contact is set to $\mu = 0.25$. Particles are randomly injected into a cylindrical volume with height L and diameter D (see Sec 5.3) to ensure that particles do not overlap at initialization and are allowed to settle due to gravity, as shown in Fig. 23a. To mimic the removal of the cylinder walls, the particles are simply injected into a cubical domain with their final position after the preparatory filling process is completed. The cubical domain is assumed to be filled with water ($\rho _f=998.21\,\hbox {kg/m}^3$ and $\nu =1.0047\mathrm {e-}06\,\hbox {m}^2/s$).

Fig. 23

Front view of cylinder emptying simulation using timestep $\Delta t = 1\mathrm {e-}{05}\,\hbox {s}$

Figure 23 visualizes the horizontal and vertical spread of a collapsing particle stack for frictionless (a-e) and frictional (f-j) spheres. Figure 23 contains the current bounding box of the sphere stack for the frictionless case as a reference for all time steps presented. As shown in Fig. 23, we observe a clear difference between the frictionless and frictional case for all time steps shown. At $t=1.0\,\hbox {s}$ and $t=2.5\,\hbox {s}$, we observe different angles of the collapsing sphere stack with the plane surface, see Fig. 23b, g and c, h. Moreover, at $t=5.0\,\hbox {s}$ we identify a higher stacking of the frictional spheres, while the frictionless spheres spread further, see Fig. 23d, i. This trend continues up to $t=10.0\,\hbox {s}$, see Fig. 23e, j, where the difference in horizontal spread between frictionless and frictional spheres is even more pronounced.

6 Conclusions

In this article, we proposed a new method for efficient computation of three-dimensional frictional collisions between particles and between particles and walls using a superellipsoidal particle shape definition. In this context, we presented an efficient and robust Newton–Raphson-based Lagrangian multiplier optimization technique for accurate collision point detection, applicable to any particle using the superellipsoidal shape description. The advantage of superellipsoidal particles is that a wide range of complex, nonspherical particle shapes can be generated using only four shape parameters, saving significant computer memory compared to surface discretization techniques. The new superellipsoid-based approach to particle collisions mainly targets collisions that occur in dilute particle flows, such as particle clusters that form in turbulent flow structures. However, we have shown that the model can also capture multiple particle contacts, such as those that occur in dense particle systems, e.g. filling processes. In this work, we performed a time-step study as well as a validation of the collision model for superellipsoidal particles. In this context, for particle shapes ranging from cubes to diamonds, we identified a time resolution related to 10% $d_\textrm{eq}$ translation as sufficient to accurately resolve the collision and thus the resulting translational and rotational motion. Finally, a simplified relation between the tangential restitution $\epsilon _t$ and the friction coefficient $\mu$ for a spherical particle system was used to model frictional particle–particle and particle–wall collisions. In our future work, we aim to generalize the definition of $\epsilon _t$ and explore different friction models in the context of superellipsoidal particle collisions. The derived superellipsoidal particle contact models can be directly applied in CFD with Lagrangian particle tracking algorithms, but could also be implemented in the framework of DEM-based modeling approaches.

Appendices

Appendices

1.1 A Derivatives of the surface gradient

$$\begin{aligned}{} & {} \frac{\partial S}{\partial x_i} = \frac{2}{\epsilon _1} \left[ \left[ \frac{m_{1i}}{a}\left[ \frac{x'}{a}\right] ^{\frac{2}{\epsilon _2}-1} \frac{m_{2i}}{b}\left[ \frac{y'}{b}\right] ^{\frac{2}{\epsilon _2}-1} \right] \left[ w_3 \right] ^{\frac{\epsilon _2}{\epsilon _1}-1}\right. \nonumber \\{} & {} \quad \left. + \frac{m_{3i}}{c} \left[ \frac{z'}{c}\right] ^{\frac{2}{\epsilon _1}-1} \right] , \end{aligned}$$

(89)

$$\begin{aligned}{} & {} \frac{\partial ^2 S}{\partial x_j \partial x_i} = \frac{2}{\epsilon _1}\left[ \frac{2}{\epsilon _1}-1\right] \frac{m_{3j} m_{3i} }{c^2} \left[ \frac{z'}{c} \right] ^{\frac{2}{\epsilon _1}-2} \nonumber \\{} & {} \quad +\frac{2}{\epsilon _1}\left[ \frac{\epsilon _2}{\epsilon _1}-1\right] \frac{2}{\epsilon _2} \left[ \frac{m_{1i}}{a} \left[ \frac{x'}{a}\right] ^{\frac{2}{\epsilon _2}-1}\right. \nonumber \\{} & {} \quad \left. +\frac{m_{2i}}{b} \left[ \frac{y'}{b}\right] ^{\frac{2}{\epsilon _2}-1}\right] \nonumber \\{} & {} \quad \left[ \frac{m_{1j}}{a} \left[ \frac{x'}{a}\right] ^{\frac{2}{\epsilon _2}-1} + \frac{m_{2j}}{b} \left[ \frac{y'}{b}\right] ^{\frac{2}{\epsilon _2}-1}\right] \nonumber \\{} & {} \quad \left[ w_3 \right] ^{\frac{\epsilon _2}{\epsilon _1}-2} \nonumber \\{} & {} \quad + \frac{2}{\epsilon _1}\left[ \frac{2}{\epsilon _2} -1 \right] \left[ \frac{m_{1i}m_{1j}}{a^2} \left[ \frac{x'}{a}\right] ^{\frac{2}{\epsilon _2}-2} \right. \nonumber \\{} & {} \quad \left. +\frac{m_{2i}m_{2j}}{b^2} \left[ \frac{y'}{b}\right] ^{\frac{2}{\epsilon _2}-2}\right] \nonumber \\{} & {} \quad \left[ w_3 \right] ^{\frac{\epsilon _2}{\epsilon _1}-1}, \end{aligned}$$

(90)

$$\begin{aligned}{} & {} \frac{\partial ^3 S}{\partial x_k \partial x_j \partial x_i} = w_0 \frac{m_{3i}m_{3j}m_{3k}}{c^3} \left[ \frac{z'}{c}\right] ^{f_1-3} \nonumber \\{} & {} \quad + w_1 \left[ \frac{m_{1i}}{a} \left[ \frac{x'}{a}\right] ^{f_2-1}+ \frac{m_{2i}}{b} \left[ \frac{y'}{b}\right] ^{f_2-1}\right] \nonumber \\{} & {} \quad \left[ \frac{m_{1j}}{a} \left[ \frac{x'}{a}\right] ^{f_2-1}+ \frac{m_{2j}}{b} \left[ \frac{y'}{b}\right] ^{f_2-1}\right] \nonumber \\{} & {} \quad \left[ \frac{m_{1k}}{a} \left[ \frac{x'}{a}\right] ^{f_2-1}+ \frac{m_{2k}}{b} \left[ \frac{y'}{b}\right] ^{f_2-1}\right] {[}w_3]^{f_0 -3 } \nonumber \\{} & {} \quad + w_2 \left[ [f_2 -1]\left[ \frac{m_{1i}m_{1k}}{a^2} \left[ \frac{x'}{a}\right] ^{f_2 -2} \right. \right. \nonumber \\{} & {} \quad \left. \left. +\frac{m_{2i}m_{2k}}{b^2} \left[ \frac{y'}{b}\right] ^{f_2 -2}\right] \right. \nonumber \\{} & {} \quad \left. \left[ \frac{m_{1j}}{a} \left[ \frac{x'}{a}\right] ^{f_2 -1} + \frac{m_{1j}}{b} \left[ \frac{y'}{b}\right] ^{f_2 -1}\right] {[}w_3]^{f_0 - 2}\right. \nonumber \\{} & {} \quad \left. + [f_2 -1]\left[ \frac{m_{1j}m_{1k}}{a^2} \left[ \frac{x'}{a}\right] ^{f_2 -2} +\frac{m_{2j}m_{2k}}{b^2} \left[ \frac{y'}{b}\right] ^{f_2 -2}\right] \right. \nonumber \\{} & {} \quad \left. \left[ \frac{m_{1i}}{a} \left[ \frac{x'}{a}\right] ^{f_2 -1} + \frac{m_{1i}}{b} \left[ \frac{y'}{b}\right] ^{f_2 -1}\right] [w_3]^{f_0 - 2} \right. \nonumber \\{} & {} \quad \left. + [f_2 -1]\left[ \frac{m_{1i}m_{1j}}{a^2} \left[ \frac{x'}{a}\right] ^{f_2 -2} +\frac{m_{2i}m_{2j}}{b^2} \left[ \frac{y'}{b}\right] ^{f_2 -2}\right] \right. \nonumber \\{} & {} \quad \left. \left[ \frac{m_{1k}}{a} \left[ \frac{x'}{a}\right] ^{f_2 -1} + \frac{m_{1k}}{b} \left[ \frac{y'}{b}\right] ^{f_2 -1}\right] [w_3]^{f_0 - 2} \right. \nonumber \\{} & {} \quad \left. + [f_2 -2][f_2 -1] \left[ \frac{m_{1i}m_{1j}m_{1k}}{a^3} \left[ \frac{x'}{a}\right] ^{f_2 -3}\right. \right. \nonumber \\{} & {} \quad \left. \left. +\frac{m_{2i}m_{2j}m_{2k}}{b^3}\left[ \frac{y'}{b}\right] ^{f_2 -3}\right] [w_3]^{f_0 - 1} \right] , \end{aligned}$$

(91)

where the prefactors are defined as

$$\begin{aligned} w_0= & {} f_1 [f_1-2][f_1-1], w_1 = f_1 f_2 f_2 [f_0-2][f_0-1], \nonumber \\ w_2= & {} f_1 [f_1-f_2], w_3 = \left[ \frac{x'}{a}\right] ^{f_2}+ \left[ \frac{y'}{b}\right] ^{f_2} \end{aligned}$$

(92)

and $f_0$, $f_1$ and $f_2$ are given by

$$\begin{aligned} f_0 = \epsilon _2/\epsilon _1\,, \qquad f_1 = 2/\epsilon _1 \,, \qquad f_2 = 2/\epsilon _2 \,. \end{aligned}$$

(93)

The first and second order partial derivatives of $||{\varvec{\nabla }} S||^{-1}$ in the global frame are written as

$$\begin{aligned}{} & {} \frac{\partial \left( ||{\varvec{\nabla }} S||^{-1}\right) }{\partial x_i}= -\frac{1}{2} \left[ \left[ \frac{\partial S}{\partial x}\right] ^2 + \left[ \frac{\partial S}{\partial y}\right] ^2 + \left[ \frac{\partial S}{\partial z}\right] ^2 \right] ^{-\frac{3}{2}} \nonumber \\{} & {} \quad \left[ 2 \frac{\partial S}{\partial x} \frac{\partial S}{\partial x_i \partial x} + 2 \frac{\partial S}{\partial y} \frac{\partial S}{\partial x_i \partial y} + 2 \frac{\partial S}{\partial z} \frac{\partial S}{\partial x_i \partial z}\right] , \end{aligned}$$

(94)

$$\begin{aligned}{} & {} \frac{\partial \left( ||{\varvec{\nabla }} S||^{-1}\right) }{\partial x_j \partial x_i} = -\frac{3}{4} \left[ \left[ \frac{\partial S}{\partial x}\right] ^2 + \left[ \frac{\partial S}{\partial y}\right] ^2 + \left[ \frac{\partial S}{\partial z}\right] ^2 \right] ^{-\frac{5}{2}}\nonumber \\{} & {} \quad \left[ 2 \frac{\partial S}{\partial x} \frac{\partial S}{\partial x_j \partial x} + 2 \frac{\partial S}{\partial y} \frac{\partial S}{\partial x_j \partial y} + 2 \frac{\partial S}{\partial z} \frac{\partial S}{\partial x_j \partial z}\right] \nonumber \\{} & {} \quad \left[ 2 \frac{\partial S}{\partial x} \frac{\partial S}{\partial x_i \partial x} + 2 \frac{\partial S}{\partial y} \frac{\partial S}{\partial x_i \partial y} + 2 \frac{\partial S}{\partial z} \frac{\partial S}{\partial x_i \partial z}\right] . \end{aligned}$$

(95)

1.2 B Superellipsoid-Wall collision Part 1

The general formula of partial derivative of the Lagrangian with respect to x,  y,  z renders:

$$\begin{aligned} \frac{\partial L}{\partial x_i}&= \frac{\partial S}{\partial x_i}+\lambda \frac{\partial W}{\partial x_i}\nonumber \\&= \frac{2}{\epsilon _1} \left[ \left[ \frac{m_{1i}}{a}\left[ \frac{x'}{a}\right] ^{\frac{2}{\epsilon _2}-1} \frac{m_{2i}}{b}\left[ \frac{y'}{b}\right] ^{\frac{2}{\epsilon _2}-1} \right] \right. \nonumber \\&\quad \left. \left[ \left[ \frac{x'}{a}\right] ^{\frac{2}{\epsilon _2}} + \left[ \frac{y'}{b}\right] ^{\frac{2}{\epsilon _2}}\right] ^{\frac{\epsilon _2}{\epsilon _1}-1} + \frac{m_{3i}}{c} \left[ \frac{z'}{c}\right] ^{\frac{2}{\epsilon _1}-1} \right] \nonumber \\&\quad +\lambda n_i=0, \end{aligned}$$

(96)

where $m_{ij}$ are the components of the rotation matrix for the superellipsoid and $x',~y',~z'$ are obtained using Eq. (27). The derivative of the Lagrangian with respect to the Lagrange multiplier is

$$\begin{aligned} \frac{\partial L}{\partial \lambda }= & {} W({{\varvec{r}}}; {{\varvec{a}}}, {{\varvec{b}}},{{\varvec{c}}})= {{\varvec{n}}}\cdot \left[ {{\varvec{r}}} - {{\varvec{a}}}\right] \nonumber \\= & {} \frac{[{{\varvec{c}}}- {{\varvec{a}}}]\times \left[ {{\varvec{b}}}-{{\varvec{a}}}\right] }{|\left[ {{\varvec{c}}}-{{\varvec{a}}} \right] \times \left[ {{\varvec{b}}}-{{\varvec{a}}} \right] |} \cdot [{\varvec{r}} -{\varvec{a}}] = 0, \end{aligned}$$

(97)

1.3 C Superellipsoid-Superellipsoid collision Part 1

The nonlinear system of four equations for the unknown location ${{\varvec{r}}}_d = \left[ x,y,z\right] ^T$ and $\lambda$ reads

$$\begin{aligned}{} & {} \frac{\partial L}{\partial x_i}= \frac{\partial S_2}{\partial x_i}+\lambda \frac{\partial S_1}{\partial x_i} =\nonumber \\{} & {} \quad \frac{2}{\epsilon _1} \left[ \left[ \frac{m_{1i}^{(2)}}{a}\left[ \frac{x'}{a}\right] ^{\frac{2}{\epsilon _2}-1} \frac{m_{2i}^{(2)}}{b}\left[ \frac{y'}{b}\right] ^{\frac{2}{\epsilon _2}-1} \right] \left[ w_3 \right] ^{\frac{\epsilon _2}{\epsilon _1}-1}\right. \nonumber \\{} & {} \quad \left. + \frac{m_{3i}^{(2)}}{c} \left[ \frac{z'}{c}\right] ^{\frac{2}{\epsilon _1}-1} \right] \nonumber \\{} & {} \quad + \lambda \left[ \frac{2}{\epsilon _1} \left[ \left[ \frac{m_{1i}^{(1)}}{a}\left[ \frac{x'}{a}\right] ^{\frac{2}{\epsilon _2}-1} \frac{m_{2i}^{(1)}}{b}\left[ \frac{y'}{b}\right] ^{\frac{2}{\epsilon _2}-1} \right] \left[ w_3 \right] ^{\frac{\epsilon _2}{\epsilon _1}-1} \right. \right. \nonumber \\{} & {} \quad \left. \left. + \frac{m_{3i}^{(1)}}{c} \left[ \frac{z'}{c}\right] ^{\frac{2}{\epsilon _1}-1} \right] \right] = 0. \end{aligned}$$

(98)

where $m^{(1)}_{ij}$ and $m^{(2)}_{ij}$ are the components of the rotation matrix ${\underline{R}}$ of $S_1$ and $S_2$ respectively. The derivative of the Lagrangian with respect to the Lagrange multiplier is

$$\begin{aligned}&\frac{\partial L}{\partial \lambda }=S_1({{\varvec{r}}};{{\varvec{r}}}_{c,1},{{\varvec{e}}}_1) =\nonumber \\&\quad \left[ \left[ \frac{m_{11}[x-x_c]+m_{12}[y-y_c]+m_{13}[z-z_c]}{a}\right] ^{\frac{2}{\epsilon _2}} \right. \nonumber \\&\quad + \left. \left[ \frac{m_{21}[x-x_c]+m_{22}[y-y_c]+m_{23}[z-z_c]}{b}\right] ^{\frac{2}{\epsilon _2}}\right] ^{\frac{\epsilon _2}{\epsilon _1}}\nonumber \\&\quad {+} \left[ \frac{m_{31}[x{-}x_c]{+}m_{32}[y{-}y_c]{+}m_{33}[z{-}z_c]}{c}\right] ^{\frac{2}{\epsilon _1}} {-} 1 {=} 0\,. \end{aligned}$$

(99)