Material interface modeling by the enriched RKPM with stabilized nodal integration

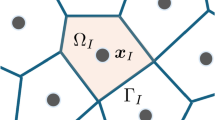
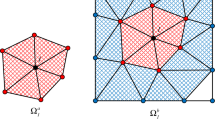
Abstract

In this paper, an enriched reproducing kernel particle method combined with stabilized conforming nodal integration (SCNI) is proposed to tackle material interface problems. Regarding the domain integration, the use of SCNI offers an effective NI technique and eliminates the zero-energy modes which occurs to direct NI. To model material interfaces, the method enriches the approximation by adding special functions constructed based on the level set function to represent weak discontinuities. Numerical examples with simple and complicated geometries of interface problems in two-dimensional linear elasticity are presented to test the performance of the proposed method, and results show that it considerably reduces strain oscillations and yields optimal convergence rates.

Appendix A: Derivation of the weak form

The basis for the assumed strain method [39, 40] is specified by the Hu-Washizu variational principle, which incorporates all field equations from Eqs. (14) and (16)–(18) into the functional and fulfills them in the weak sense. The admissible function spaces for the displacement $\varvec{u}$, stress $\varvec{\sigma }$, assumed strain $\tilde{\varvec{\varepsilon }}$ and Lagrange multiplier $\varvec{\lambda }$ are defined as

$$\begin{aligned} \mathbb {V}&= \{ \varvec{u}(\varvec{x}) \in [L^2(\varOmega )]^2: u_{i,j} \in L^2(\varOmega ), \; i,j = 1,2 \} , \end{aligned}$$

(49a)

$$\begin{aligned} \mathbb {S}&= \{\varvec{\sigma }(\varvec{x}) \in [L^2(\varOmega )]^{2\times 2}: \varvec{\sigma } = \varvec{\sigma }^T \} , \end{aligned}$$

(49b)

$$\begin{aligned} \mathbb {E}&= \{\varvec{\gamma }(\varvec{x}) \in [L^2(\varOmega )]^{2\times 2}: \varvec{\gamma } = \varvec{\gamma }^T \} , \end{aligned}$$

(49c)

$$\begin{aligned} \varLambda&= \{\varvec{\lambda }(\varvec{x}) \in [L^2(\varGamma _u)]^2\} , \end{aligned}$$

(49d)

respectively, and $L^2$ is the space of square integrable functions. Note that the satisfaction of the essential BCs is not required for elements of $\mathbb {V}$. Let $\varPi _{HW}:\mathbb {V} \times \mathbb {S} \times \mathbb {E} \times \varLambda \rightarrow \mathbb {R}$ be the Hu-Washizu functional which is defined as follows,

$$\begin{aligned}&\varPi _{HW}(\varvec{u},\varvec{\sigma }, \tilde{\varvec{\varepsilon }}, \varvec{\lambda }) \nonumber \\ {}&= \int _{\varOmega } { \Biggl \{ \frac{1}{2} \tilde{\varvec{\varepsilon }} : \mathbb {C}: \tilde{\varvec{\varepsilon }} - \varvec{b} \cdot \varvec{u} - \varvec{\sigma } : [\tilde{\varvec{\varepsilon }} - \frac{1}{2}(\nabla \varvec{u} + \nabla \varvec{u}^T)] \, \Biggr \} \textrm{d}V} \nonumber \\&\quad - \int _{\varGamma _t} {\varvec{\bar{t}} \cdot \varvec{u}} \, \textrm{d}S - \int _{\varGamma _u} {\varvec{\lambda } \cdot (\varvec{u} - \varvec{\bar{u}}) } \, \textrm{d}S. \end{aligned}$$

(50)

By taking the first variation of the functional $\varPi _{HW}$ in the standard manner, it yields

$$\begin{aligned}&\delta \varPi _{HW}(\varvec{u},\varvec{\sigma }, \tilde{\varvec{\varepsilon }}, \varvec{\lambda }) \nonumber \\&\quad = \int _{\varOmega } {\delta \tilde{\varvec{\varepsilon }} : (\mathbb {C}: \tilde{\varvec{\varepsilon }} - \varvec{\sigma })} \,\textrm{d}V - \int _{\varOmega } {\delta \varvec{\sigma } : (\varvec{\varepsilon } - \tilde{\varvec{\varepsilon }}) } \, \textrm{d}V \,&\nonumber \\&\qquad + \int _{\varOmega } {\delta \varvec{\varepsilon } : \varvec{\sigma } } \, \textrm{d}V - \int _{\varGamma _u} {\delta \varvec{\lambda } \cdot (\varvec{u} - \varvec{\bar{u}}) } \, \textrm{d}S \,&\nonumber \\&\qquad - \int _{\varGamma _u} {\delta \varvec{u} \cdot \varvec{\lambda } } \, \textrm{d}S - \int _{\varOmega } {\delta \varvec{u} \cdot \varvec{b} } \, \textrm{d}V - \int _{\varGamma _t} {\delta \varvec{u} \cdot \varvec{\bar{t}} } \, \textrm{d}S, \end{aligned}$$

(51)

where $\delta \varvec{u} \in \mathbb {V}$, $\delta \varvec{\sigma } \in \mathbb {S}$, $\delta \tilde{\varvec{\varepsilon }} \in \mathbb {E}$, and $\delta \varvec{\lambda } \in \varLambda$ are the admissible variations of the displacement $\varvec{u}$, stress $\varvec{\sigma }$, assumed strain $\tilde{\varvec{\varepsilon }}$ and Lagrange multiplier $\varvec{\lambda }$, respectively, and $\delta \varvec{\varepsilon } = (\nabla \delta \varvec{u} + \nabla \delta \varvec{u}^T) / 2$. Then, we pose the following variational problem: Find $(\varvec{u},\varvec{\sigma }, \tilde{\varvec{\varepsilon }}, \varvec{\lambda }) \in \mathbb {V} \times \mathbb {S} \times \mathbb {E} \times \varLambda$ such that,

$$\begin{aligned}&\int _{\varOmega } {\delta \tilde{\varvec{\varepsilon }} : (\mathbb {C}: \tilde{\varvec{\varepsilon }} - \varvec{\sigma })} \,\textrm{d}V = 0, \end{aligned}$$

(52a)

$$\begin{aligned}&\int _{\varOmega } {\delta \varvec{\sigma } : (\varvec{\varepsilon } - \tilde{\varvec{\varepsilon }}) } \, \textrm{d}V \, = 0, \end{aligned}$$

(52b)

$$\begin{aligned}&\int _{\varOmega } {\delta \varvec{\varepsilon } : \varvec{\sigma } } \, \textrm{d}V - \int _{\varOmega } {\delta \varvec{u} \cdot \varvec{b} } \, \textrm{d}V - \int _{\varGamma _t} {\delta \varvec{u} \cdot \varvec{\bar{t}} } \, \textrm{d}S \nonumber \\&\quad - \int _{\varGamma _u} {\delta \varvec{u} \cdot \varvec{\lambda } } \, \textrm{d}S = 0, \end{aligned}$$

(52c)

$$\begin{aligned}&\int _{\varGamma _u} {\delta \varvec{\lambda } \cdot (\varvec{u} - \varvec{\bar{u}}) } \, \textrm{d}S = 0, \end{aligned}$$

(52d)

for all $(\delta \varvec{u},\delta \varvec{\sigma }, \delta \tilde{\varvec{\varepsilon }}, \delta \varvec{\lambda }) \in \mathbb {V} \times \mathbb {S} \times \mathbb {E} \times \varLambda$. By the standard argument, it can be shown that Eqs. (52a)–(52d) are equivalent to Eqs. (14) and (16)–(18). Furthermore, carrying out integration by part on the first term of Eq. (52c) gives,

$$\begin{aligned}&\int _{\varOmega } {\delta \varvec{u} \cdot (\nabla \cdot \varvec{\sigma } - \varvec{b}) } \, \textrm{d}V - \int _{\varGamma _t} {\delta \varvec{u} \cdot (\varvec{\sigma } \varvec{n} - \varvec{\bar{t}})} \, \textrm{d}S \nonumber \\&\quad - \int _{\varGamma _u} {\delta \varvec{u} \cdot (\varvec{\sigma } \varvec{n} - \varvec{\lambda })} \, \textrm{d}S = 0. \end{aligned}$$

(53)

From Eq. (53), it illustrates that the physical significance of the Lagrangian term $\varvec{\lambda }$ is the traction on the essential boundary $\varGamma _u$. Hence, $\varvec{\lambda }$ can be replaced by $\varvec{\sigma } \cdot \varvec{n}$.

Let $\mathbb {V}^h$, $\mathbb {S}^h$, $\mathbb {E}^h$, and $\varLambda ^h$ be the finite-dimensional subspaces of $\mathbb {V}$, $\mathbb {S}$, $\mathbb {E}$, and $\varLambda$, respectively, i.e., $\mathbb {V}^h \subseteq \mathbb {V}$, $\mathbb {S}^h \subseteq \mathbb {S}$, $\mathbb {E}^h \subseteq \mathbb {E}$, and $\varLambda ^h \subseteq \varLambda$. Additionally, let $\varvec{\varepsilon }^h :=\varvec{\varepsilon }(\varvec{u}^h)$. We have the discrete version of the foregoing variational problem: Find $(\varvec{u}^h,\varvec{\sigma }^h, \tilde{\varvec{\varepsilon }}^h, \varvec{\lambda }^h) \in \mathbb {V}^h \times \mathbb {S}^h \times \mathbb {E}^h \times \varLambda ^h$ such that,

$$\begin{aligned}{} & {} \int _{\varOmega } {\delta \tilde{\varvec{\varepsilon }}^h : (\mathbb {C}: \tilde{\varvec{\varepsilon }}^h - \varvec{\sigma }^h)} \,\textrm{d}V = 0, \end{aligned}$$

(54a)

$$\begin{aligned}{} & {} \int _{\varOmega } {\delta \varvec{\sigma }^h : (\varvec{\varepsilon }^h - \tilde{\varvec{\varepsilon }}^h) } \, \textrm{d}V \, = 0, \end{aligned}$$

(54b)

$$\begin{aligned}{} & {} \int _{\varOmega } {\delta \varvec{\varepsilon }^h : \varvec{\sigma }^h } \, \textrm{d}V - \int _{\varOmega } {\delta \varvec{u}^h \cdot \varvec{b} } \, \textrm{d}V \nonumber \\{} & {} \quad - \int _{\varGamma _t} {\delta \varvec{u}^h \cdot \varvec{\bar{t}} } \, \textrm{d}S - \int _{\varGamma _u} {\delta \varvec{u}^h \cdot \varvec{\lambda }^h } \, \textrm{d}S = 0, \end{aligned}$$

(54c)

$$\begin{aligned}{} & {} \int _{\varGamma _u} {\delta \varvec{\lambda }^h \cdot (\varvec{u}^h - \varvec{\bar{u}}) } \, \textrm{d}S = 0, \end{aligned}$$

(54d)

for all $(\delta \varvec{u}^h,\delta \varvec{\sigma }^h, \delta \tilde{\varvec{\varepsilon }}^h, \delta \varvec{\lambda }^h) \in \mathbb {V}^h \times \mathbb {S}^h \times \mathbb {E}^h \times \varLambda ^h$.

The key step in deriving an assumed strain method is to construct an assumed strain field to satisfy the orthogonality condition [39, 40].

$$\begin{aligned} \int _{\varOmega } {\varvec{\tau } : \varvec{\gamma }} \; \textrm{d}V = 0, \; \text{ for } \text{ all } \; \varvec{\tau } \in \mathbb {S}^h \; \text{ and } \; \varvec{\gamma } \in \mathbb {E}^h_e, \end{aligned}$$

(55)

where $\mathbb {E}^h_e = \{\varvec{\gamma } \in [L^2(\varOmega )]^{2\times 2}: \varvec{\gamma } = \varvec{\varepsilon }^h - \tilde{\varvec{\varepsilon }}^h\}$. The orthogonality condition states that the space of admissible stress field is orthogonal to the space of the enhanced strain field, i.e., the difference between the compatible strain field and the assumed strain field. Furthermore, the fulfillment of the orthogonality condition allows expressing Eq. (54c) in terms of the assumed strains only by observing that

$$\begin{aligned}&\int _{\varOmega } {\delta \varvec{\varepsilon }^h : \varvec{\sigma }^h } \, \textrm{d}V \\&\quad = \int _{\varOmega } {(\delta \varvec{\varepsilon }^h - \delta \tilde{\varvec{\varepsilon }}^h) : \varvec{\sigma }^h } \, \textrm{d}V + \int _{\varOmega } {\delta \tilde{\varvec{\varepsilon }}^h : \varvec{\sigma }^h } \, \textrm{d}V \\&\quad = \int _{\varOmega } {\delta \tilde{\varvec{\varepsilon }}^h : \varvec{\sigma }^h } \, \textrm{d}V, \end{aligned}$$

and by (54a),

$$\begin{aligned} \int _{\varOmega } {\delta \varvec{\varepsilon }^h : \varvec{\sigma }^h } \, \textrm{d}V = \int _{\varOmega } \delta \tilde{\varvec{\varepsilon }}^h : \mathbb {C}: \tilde{\varvec{\varepsilon }}^h \, \textrm{d}V. \end{aligned}$$

(56)

Now, we consider whether or not the variational problem Eq. (54) with the assumed strain given a priori in Eq. (13) is variationally consistent. Firstly, assume that the discrete stresses $\varvec{\sigma }^h$ are computed by the relation

$$\begin{aligned} \varvec{\sigma }^h = \mathbb {C}: \tilde{\varvec{\varepsilon }}^h. \end{aligned}$$

(57)

Consequently, Eq. (54a) is fulfilled exactly. Next, we need to verify the orthogonality condition Eq. (55) satisfied by the given assumed strain.

Recall that the problem domain $\varOmega$ is decomposed into conforming and non-overlapping cells $\{\varOmega _L\}^{NP}_{L=1}$, and each cell $\varOmega _L$ is further subdivided into several conforming subcells $\{\varOmega _{L}^K\}^{NSC}_{{K}=1}$ where NSC is the number of subcells contained in $\varOmega _L$. The discrete counterpart of the assumed strain presented in Eq. (13) is given by

$$\begin{aligned} \tilde{\varvec{\varepsilon }}^h(\varvec{x}_{L}^{K}) = \frac{1}{A_{L}^{K}} \int _{\varOmega _{L}^K} {\varvec{\varepsilon }(\varvec{u}^h)} \, \textrm{d}V. \end{aligned}$$

(58)

Remark:

• If a cell $\varOmega _L$ is not subdivided, the discrete form of Eq. (15) is used instead.

• The assumed strain is defined to be constant over each subcell $\varOmega _{L}^K$ or a cell $\varOmega _L$ if it is not subdivided.

• The assumed strains $\tilde{\varvec{\varepsilon }}(\varvec{u}^h)$ only depend on the discrete displacement field $\varvec{u}^h$.

Now, we prove that the orthogonality condition Eq. (55) is satisfied for the given assumed strain. By assuming the material properties are constant in $\varOmega _{L}^K$ and using the fact that $\tilde{\varvec{\varepsilon }}^h(\varvec{x}_{L}^{K})$ is constant in $\varOmega _{L}^K$,

$$\begin{aligned}&\int _{\varOmega } {\varvec{\sigma }^h : \varvec{\varepsilon }^h } \, \textrm{d}V \\&\quad = \int _{\varOmega } {\tilde{\varvec{\varepsilon }}^h : \mathbb {C} : \varvec{\varepsilon }^h } \, \textrm{d}V \\&\quad = \sum _{L=1}^{NP} \int _{\varOmega _L} {\tilde{\varvec{\varepsilon }}^h : \mathbb {C} : \varvec{\varepsilon }^h } \, \textrm{d}V \\&\quad = \sum _{L=1}^{NP} \sum _{{K}=1}^{NSC} \int _{\varOmega _{L}^K} {\tilde{\varvec{\varepsilon }}^h (\varvec{x}_{L}^{K}): \mathbb {C} : {\varvec{\varepsilon }(\varvec{u}^h)} } \, \textrm{d}V \\&\quad = \sum _{L=1}^{NP} \sum _{{K}=1}^{NSC} \tilde{\varvec{\varepsilon }}^h (\varvec{x}_{L}^{K}): \mathbb {C} : \int _{\varOmega _{L}^K} {\varvec{\varepsilon }(\varvec{u}^h) } \, \textrm{d}V \\&\quad = \sum _{L=1}^{NP} \sum _{{K}=1}^{NSC} \tilde{\varvec{\varepsilon }}^h (\varvec{x}_{L}^{K}): \mathbb {C} : \tilde{\varvec{\varepsilon }}^h(\varvec{x}_{L}^{K}) \, A_{L}^K \\&\quad = \sum _{L=1}^{NP} \sum _{{K}=1}^{NSC} \int _{\varOmega _{L}^K} \tilde{\varvec{\varepsilon }}^h (\varvec{x}_{L}^{K}): \mathbb {C} : \tilde{\varvec{\varepsilon }}^h(\varvec{x}_{L}^{K}) \, \textrm{d}V \\&\quad = \int _{\varOmega } {\tilde{\varvec{\varepsilon }}^h : \mathbb {C} : \tilde{\varvec{\varepsilon }}^h } \, \textrm{d}V \\&\quad = \int _{\varOmega } {\varvec{\sigma }^h : \tilde{\varvec{\varepsilon }}^h } \, \textrm{d}V, \end{aligned}$$

where Eq. (58) is used in the fifth equality.

Therefore, the orthogonality condition is achieved with the use of the given assumed strain. Finally, using the fact that $\varvec{\lambda }^h = \varvec{\sigma }^h \varvec{n}$ on $\varGamma _u$ and Eq. (56) allows rewriting Eq. (54) into a single equation

$$\begin{aligned}&\int _{\varOmega } {\delta \tilde{\varvec{\varepsilon }}^h : \mathbb {C}: \tilde{\varvec{\varepsilon }}^h} \, \textrm{d}V - \int _{\varOmega } {\delta \varvec{u}^h \cdot \varvec{b} } \, \textrm{d}V - \int _{\varGamma _t} {\delta \varvec{u}^h \cdot \varvec{\bar{t}} } \, \textrm{d}S \nonumber \\&\quad - \int _{\varGamma _u} {\delta \varvec{u}^h \cdot \varvec{t}^h} \, \textrm{d}S - \int _{\varGamma _u} {\delta \varvec{t}^h \cdot (\varvec{u}^h - \varvec{\bar{u}}) } \, \textrm{d}S = 0, \end{aligned}$$

(59)

where $\varvec{t}^h = \varvec{\sigma }^h \varvec{n} = (\mathbb {C}: \tilde{\varvec{\varepsilon }}^h) \cdot \varvec{n}$. To improve the coercivity of the variational formulation in Eq. (59), adding a penalty-like term to it yields [47]

$$\begin{aligned}&\int _{\varOmega } {\delta \tilde{\varvec{\varepsilon }}^h : \mathbb {C}: \tilde{\varvec{\varepsilon }}^h} \, \textrm{d}V - \int _{\varGamma _u} {\delta \varvec{u}^h \cdot \varvec{t}^h} \, \textrm{d}S \nonumber \\&\quad - \int _{\varGamma _u} {\delta \varvec{t}^h \cdot (\varvec{u}^h - \varvec{\bar{u}}) } \, \textrm{d}S + \; \alpha \int _{\varGamma _u} {\delta \varvec{u}^h \cdot (\varvec{u}^h - \varvec{\bar{u}}) } \, \textrm{d}S \nonumber \\&\quad = \int _{\varOmega } {\delta \varvec{u}^h \cdot \varvec{b} } \, \textrm{d}V + \int _{\varGamma _t} {\delta \varvec{u}^h \cdot \varvec{\bar{t}} } \, \textrm{d}S. \end{aligned}$$

(60)