Skip to main content
SpringerLink
Log in

Initial particle arrangement for the arbitrarily complex geometry of mesh-free methods

  • Published:
Computational Particle Mechanics Aims and scope Submit manuscript

Abstract

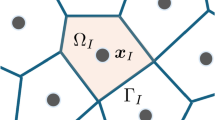
In the present study, a body-fitted and uniform initial particle arrangement method is proposed for mesh-free methods, such as SPH, MPS, and LSMPS. Single-layer boundary particles with/without normal direction vectors and multilayer boundary particles can be successfully generated. Typical tests show that the proposed method can successfully generate body-fitted and uniform initial particle distributions. Numerical simulation results using the generated initial particle distributions obtained satisfied results. It is then verified that the present method can be usefully and robustly for mesh-free particle simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig.1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics: theory and application to non-spherical stars. Mon Not R Astron Soc 181:375–389

    Article  MATH  Google Scholar 

  2. Lucy LB (1977) A numerical approach to testing the fission hypothesis. Astron J 82:1013–1024

    Article  Google Scholar 

  3. Koshizuka S, Oka Y (1996) Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl Sci Eng 123:421–434

    Article  Google Scholar 

  4. Morita K, Zhang S, Koshizuka S et al (2011) Detailed analysis of key phenomena in core disruptive accidents of sodium-cooled fast reactors by the COMPASS code. Nucl Eng Des 241:4672–4681

    Article  Google Scholar 

  5. Monaghan JJ (1994) Simulating free surface flows with SPH. J Comput Phys 110:399–406

    Article  MATH  Google Scholar 

  6. Benz W, Asphaug E (1995) Simulations of brittle solids using smooth particle hydrodynamics. Comput Phys Commun 87:253–265

    Article  MATH  Google Scholar 

  7. Zhang C, Rezavand M, Hu X (2021) A multi-resolution SPH method for fluid-structure interactions. J Comput Phys 429:110028

    Article  MathSciNet  MATH  Google Scholar 

  8. Siemann MH, Ritt SA (2019) Novel particle distributions for SPH bird-strike simulations. Comput Methods Appl Mech Eng 343:746–766

    Article  MathSciNet  MATH  Google Scholar 

  9. Alimirzazadeh S, Kumashiro T, Leguizamón S et al (2020) GPU-accelerated numerical analysis of jet interference in a six-jet Pelton turbine using finite volume particle method. Renew Energy 148:234–246

    Article  Google Scholar 

  10. Ji Z, Stanic M, Hartono EA et al (2018) Numerical simulations of oil flow inside a gearbox by smoothed particle hydrodynamics (SPH) method. Tribol Int 127:47–58

    Article  Google Scholar 

  11. Crespo AJC, Hall M, Domínguez JM, et al. (2018) Floating moored oscillating water column with meshless SPH method. In: ASME 2018 37th international conference on ocean, offshore and Arctic engineering, Madrid

  12. Zhang C, Wang J, Rezavand M et al (2021) An integrative smoothed particle hydrodynamics framework for modeling cardiac function. Comput Methods Appl Mech Eng 381:113847

    Article  MATH  Google Scholar 

  13. Domínguez JM, Crespo AJC, Barreiro A, et al. (2011) Development of a new pre-processing tool for SPH models with complex geometries. In: 6th international SPHERIC workshop, Hamburg

  14. https://dual.sphysics.org/

  15. Heimbs S (2011) Computational methods for bird strike simulations: a review. Comput Struct 89:2093–2112

    Article  Google Scholar 

  16. Diehl S, Rockefeller G, Fryer CL et al (2015) Generating optimal initial conditions for smoothed particle hydrodynamics simulations. Publ Astron Soc Austral 32:e048

    Article  Google Scholar 

  17. Vela LV, Sanchez R, Geiger J (2018) ALARIC: an algorithm for constructing arbitrarily complex initial density distributions with low particle noise for SPH/SPMHD applications. Comput Phys Commun 224:186–197

    Article  MathSciNet  Google Scholar 

  18. Fu L, Ji Z (2019) An optimal particle setup method with centroidal Voronoi particle dynamics. Comput Phys Commun 234:72–92

    Article  Google Scholar 

  19. Zhu Y, Zhang C, Yu Y, Hu X (2021) A CAD-compatible body-fitted particle generator for arbitrarily complex geometry and its application to wave-structure interaction. J Hydrodyn 33:195–206

    Article  Google Scholar 

  20. Osher S, Sethian JA (1988) Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J Comput Phys 79:12–49

    Article  MathSciNet  MATH  Google Scholar 

  21. Shu R, Liu A (1991) A fast ray casting algorithm using adaptive isotriangular subdivision. In: Proceedings of the 2nd conference on visualization, Washington

  22. Tamai T, Koshizuka S (2014) Least squares moving particle semi-implicit method. Comput Part Mech 1:277–305

    Article  Google Scholar 

  23. Lobovský L, BotiaVera E, Castellana F, MasSoler J, SoutoIglesias A (2014) Experimental investigation of dynamic pressure loads during dam break. J Fluids Struct 48:407–434

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Aeronautics and Astronautics, Zhejiang University, Hangzhou, 310027, China

    Shuai Zhang, Yun Kong, Qiaorui Cheng, Jifa Zhang & Yao Zheng

Authors
  1. Shuai Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yun Kong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qiaorui Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jifa Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yao Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jifa Zhang.

Ethics declarations

Conflicts of interest

The authors declare no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, S., Kong, Y., Cheng, Q. et al. Initial particle arrangement for the arbitrarily complex geometry of mesh-free methods. Comp. Part. Mech. 10, 663–675 (2023). https://doi.org/10.1007/s40571-022-00519-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40571-022-00519-0

Keywords

Search

Navigation