1 Introduction

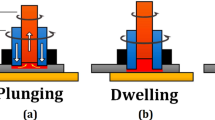
Friction stir welding (FSW) is a joining method, which in contrast to more common fusion welding processes produces a weld without melting of material. Instead of that, the material is stirred at elevated temperatures, resulting in some mixing and serious bonding of the matter without melting. Thus, the question arises what is causing the bonding of the material in the interface zone without mixing in liquid state. The process involves three phases which are introduced in Fig. 1. First, the rotating tool is plunged with high pressure into the weld line at the interface of two workpieces and dwells at this point to soften the material through heat generation resulting from friction. In the second phase, the tool starts the transversal movement along the weld line and with that creates the weld through ’bonding’ of the material. Finally, at the end of the weld, the tool is retracted from the workpiece.

The FSW process is characterized by various interdependent physical phenomena, including friction, visco-plasticity, inelastic heat generation, heat conduction, severe plastic strain, and others, resulting in a complex coupled thermomechanical problem [3, 4]. There are several research works, which developed improved smoothed particle hydrodynamics (SPH) models for simulation of FSW, e.g., [5, 6]. However, the common simplification is the consideration of two separate workpieces as just one continuum and no real bonding occurs. In this work, the aim is to introduce more physics and to include the bonding mechanism. This includes a simulation of two initially separate workpieces with contact between them, a bonding criterion definition, and a change from contact to continuum locally. This model extension will provide more insight into the quality of the resulting weld, as well as assist with process parameter choice.

As FSW involves topology changes and large deformations, it yields difficulties for the commonly used Finite Element Method (FEM), due to the unclear mesh connectivity. In contrast, SPH with its mesh-free nature provides a suitable framework for simulation of FSW, especially when an appropriate bonding mechanism is available. SPH is a Lagrangian discretization and computation method, where the spatial domain is described with moving approximation points, called SPH particles, which reduce the partial differential equations (PDEs) in time and space into ordinary differential equations (ODEs) in time only. Introduced in 1977 [7, 8], the SPH method was first applied to the simulation of solid material in the 1990s [9, 10]. The method proved its usefulness for simulation of various complex industrial applications, including orthogonal metal cutting [11], extrusion process [12], and impact problems [13].

Fig. 1
figure 1

Friction stir welding process [1, 2]

Full size image

This paper starts in Sect. 2 providing details and literature on the bonding mechanism. It follows a brief description of the used SPH framework in Sect. 3. The implementation of the bonding algorithm is presented in Sect. 4. Sect. 5 shows simulation results of two test cases, i.e., strong compression of two blocks and a complete FSW process, validating the implementation of bonding mechanism.

2 Bonding mechanism

FSW is a solid-state joining process where mechanically applied straining as well as heating are used to create the weld. The three bonding mechanisms for such forge welding processes are described in [14] as contaminant displacement/interatomic bonding, dissociation of retained oxides, and decomposition of the interfacial structure. When a local strain is applied at a contact surface, contaminants are displaced. This allows clean surfaces to be exposed to direct interatomic bonding. The higher temperature due to friction during the welding process supports this by increasing metal plasticity. The bonding can be further facilitated by a thermal dissolution of oxides or contaminants in the matrix, removing possible residues from the contacting surfaces. The first two mechanisms result in a highly dislocated structure at the bond interface which can negatively influence the weld quality. A decomposition of this structure, for example through recrystallization, can improve the weld quality. Diffusion is usually not considered to play an important role in the described quite fast forge welding processes. As stated in [15], diffusion may however become relevant when longer process times occur.

For the prediction of the joint integrity, knowledge about the bonding state of the two initially separated but contacting parts after welding, i.e., after the three bonding mechanisms have taken place, is desirable. An experimental investigation regarding the conditions when solid-state bonding occurs between aluminum alloys is presented in [16]. A thermomechanical testing system was used to push specimens under different strains, strain rates, and temperatures together. It was found that strain along with bonding time has the strongest influence on whether a good bond is created or not. The influence of temperature on bonding depended on the aluminum alloy composition.

A detailed atomistic modeling of the above described underlying physical phenomena is beyond the reach or intention of continuum mechanics simulations. Therefore, practical approaches were developed to predict if bonding takes place between two particles belonging to different parts. These criteria were originally not developed for friction stir welding, but for extrusion processes. Examples are the maximum pressure criterion [17], the pressure–time criterion [18], and the pressure–time–flow criterion [19]. The maximum pressure criterion only considers the maximum pressure occurring during the process. In the pressure–time criterion, the ratio between contact pressure and flow stress of the material, integrated over time, must exceed a certain threshold to yield bonding. In the pressure–time–flow criterion, an additional speed correction factor is introduced to account for the material velocity.

Although the criteria were developed for extrusion processes, the latter two are employed in [20] together with a numerical model to predict the joint integrity of friction stir welds. The results show a good correlation for the pressure–time–flow criterion between experimental findings and numerical calculations.

In this work, the pressure–time–flow criterion is also used to calculate if and where bonding occurs between the two welded parts. It is computed locally as

$$\begin{aligned} W' = \int _{0}^t \frac{p}{\sigma } v \text {d} t \end{aligned}$$
(1)

with the contact pressure p at the interface, the flow stress \( \sigma \) in the given welding conditions and the material velocity v. Threshold values for \( W' \), giving the information if two parts are welded locally or not, are taken from [20], resulting in a threshold value

$$\begin{aligned} W'_{thres}= A\,T^{B} \end{aligned}$$
(2)

with factors \( A = 1327661974.4\), \( B = -4.797\), and temperature T in degree Celsius. The resulting unit of measurement for \( W'_{thres}\) is meter.

3 SPH for solids

SPH is a Lagrangian meshless numerical method, where the continuum is discretized with so-called particles. These carry different material properties and physical values, and serve as the approximation points, at which the governing equations are evaluated. This is done by the weighted summation of each particle contribution within the influence domain smoothed with the help of a kernel function. In this work, the most common updated Lagrangian scheme is employed, detailed formulations can be found in, e.g., [2, 21]. For this framework the rate formulation is used, where the change of velocity \( {\varvec{v}} \) in time t described by linear momentum \( {\text {D}\varvec{v}}/{\text {D}t} = {1}/{\rho } \,\nabla \cdot \varvec{\sigma }+{\varvec{g}} \) with the Cauchy stress tensor \( \varvec{\sigma }\), density \( \rho \) and external forces \( {\varvec{g}} \). The approximation in SPH-compliant form is

$$\begin{aligned} \begin{aligned} \frac{\text {D}{\varvec{v}}_a}{\text {D}t}= \sum _b m_b \bigg (\frac{\varvec{\sigma }_a}{\rho _a^2}&+\frac{\varvec{\sigma }_b}{\rho _b^2} \bigg ) \cdot \nabla _a W_{ab}(r_{ab},h) + {\varvec{g}}_a, \end{aligned} \end{aligned}$$
(3)

where a indicates the current particle and b is a neighboring particle, m is a mass, \(\nabla _a W_{ab} \) is a gradient of kernel function evaluated for a specific pair of particles with distance \(r_{ab} \) between them and the kernel radius is h. In the current study the Wendland \( C^2 \) kernel is utilized [22]. To deal with spurious numerical particle oscillations [23], as well as to prevent unphysical fractures in tension [24], an hourglass control scheme is used to guarantee the stability while avoiding stiffness, when comparing with more traditional stabilization methods, such as artificial viscosity and artificial stress. The formulation can be found in [25, 26] and is simply an additional force that is added to the linear momentum Eq. (3).

The boundary forces, such as the interaction between solid triangles and SPH particles, are introduced in the term \( {\varvec{g}}_a \). After exhaustive investigation, the following strategy proved to be the most stable and accurate scheme to reproduce contact with friction for FSW simulation with particles. Normal forces are calculated using the following modified Lennard-Jones scheme [27]

$$\begin{aligned} g_{na}(r) := {\left\{ \begin{array}{ll} k \frac{(R-r)^4-(R-H)^2(R-r)^2 }{R^2H(2R-H)} &{} \text {if } r\le R,\\ [0.5em] 0 &{} \text {else,} \end{array}\right. } \end{aligned}$$
(4)

where r is the Euclidean distance between a particle’s center and triangle, R denotes the maximum influence distance, H is the distance where the force \( g_{na} \) changes the sign to opposite, and k stands for the stiffness scale factor. In the presented study \( H = R \), as only a repulsive force is needed for the presented models.

For the friction force, the Coulomb law is adopted by relating it to the normal force by the friction coefficient \( \mu \) using \( g_{ta} = \mu g_{na}\), similar to [28]. There is no explicit distinction between the slipping or sticking condition. However, as the force grows, the SPH surfaces particles are accelerated to the velocities close to the tool velocity, which results in near sticking condition.

Finally, the resulting force vector is assembled

$$\begin{aligned} {\varvec{g}}_a := g_{na} {\varvec{n}} + g_{ta} {\varvec{t}} \end{aligned}$$
(5)

with \({\varvec{n}} \) and \({\varvec{t}}\) representing normal and tangential vectors, respectively. The friction force is modeled to act in the direction opposite to the relative tangential velocity \({\varvec{v}}_r\) between the surfaces in contact, therefore the tangential vector is \( {\varvec{t}} =-{\varvec{v}}_r / \Vert {\varvec{v}}_r\Vert \). This is a modeling assumption which is reasonable here but maybe needs to be improved for special simulations or materials.

More details on the utilized SPH formulation and its implementation can be found in [2]. In this study, the broadly used Johnson–Cook (JC) flow stress model [29] is used, with its application to SPH described in [21].

4 Implementation

The bonding routine is implemented into the Pasimodo environment [30, 31], which is a particle-based simulation package with a modular way for bringing new concepts into implementation. The new features are added on top of existing functionality utilizing a sophisticated plugin mechanism.

Usually particles belonging to one part are sharing their contribution by the SPH summation yielding one continuum. Particles on different parts are exchanging interaction, e.g., by contact or friction forces, but are not contributing to the other parts SPH summation since they belong not to the same continuum. In the bonding procedure, a criterion between two particles on different parts is evaluated and if a criteria limit is reached, the bonding particles are defined to belong to both parts. At the same time particles, where the criterion is not reaching the limit, do still belong to just one, more precisely their original, part.

The general course of action for bonding is described in few steps. First the interaction between two separate parts is defined only as contact formulation, if they touch each other. Then, as soon as the bonding condition between two particles is satisfied, the interaction status is locally changed to the standard SPH formulation, meaning that these particles have merged to belong to both parts and are acting as a continuum. That yields five challenges for the implementation: distinction of part, contact formulation, bonding status definition, bonding criterion calculation, and change of bonding status.

To introduce the first function, namely to distinguish the separate parts, an additional part id M for each particle is added to its properties. Then, the type of interaction is picked based on the id type, i.e., two particles i and j that are located within the influence radius H are checked for their part ids. If they are the same (i.e., \(M_i=M_j\)), then the SPH interaction is used. If not, then the particles belong to separate parts and the contact formulation is applied.

The contact formulation has to be determined for the SPH–SPH interaction. The SPH particles are assumed to act like spheres with radius equal to particle spacing \( L_s \). For calculation of normal and friction forces, the approach used for the boundary forces is straightforwardly adopted (see Sect. 3). The modified Lennard-Jones potential is a penalty method, that provides a stable contact condition. This is provided by the fact that the force does not tend to infinity, as the distance between particle surfaces tends to zero, but it is equal to the stiffness scale. This modeling assumption is suitable, as the particle does not represent hard spheres, but rather smoothed boundary, which can be deformed under applied load. However, the stiffness calibration is required to ensure physical behavior, as it is not a physical parameter. The ’hard sphere approach’ from DEM guarantees that no overlap occurs but requires to solve the whole system simultaneously. Thus, here a penalty approach is selected which allows local treatment.

The two previous functionalities are aimed at distinction of two parts apart, while for obtaining the bonding status another identification is needed. For that purpose, a new flag C describing the bonding state is added. If the flag is set to true for that particle, that means that the particle has bonded and has SPH interaction with all the particles within the kernel support radius, even if the particles have a different part id. If it is false, the particle has SPH interaction only within own part, otherwise the contact formulation is enforced. At the beginning of the simulation, the bonding status flag \( C_i \) of all the particles i is set to false as an initial value. The flowchart explaining the logic behind the interaction decision is presented in Fig. 2.

Fig. 2
figure 2

Flowchart showing the selection of interaction type in the algorithm

Full size image

The pressure–time–flow criterion \( W' \) described in Eq. (1) has to be adopted for the current formulation. Similar to [20] the integrals are approximated by summation over time steps. The criterion is calculated for each particle using the additional iteration loop after time integration. The contact pressure p is computed by employing the normal force from the contact between the SPH particles using Eq. (4) and dividing it by contact area \(A_c\), producing the contact pressure \(p = g_{na}/A_c\). In this study \(A_c = L_\text {s}^2 \), with \(L_\text {s}\) representing the particle spacing. For the flow stress, von Mises equivalent stresses [32] \( \sigma ^{vM} \) is adopted, as it is already used for plasticity modeling in the presented framework. Finally, the material velocity v is the magnitude of velocity vector of SPH particle. The above concludes in the computation

$$\begin{aligned} W' = \sum _i \frac{p_i}{\sigma ^{vM}_i} v_i \varDelta t_i , \end{aligned}$$
(6)

which accumulates the history of pressure and flow along the simulation time for each particle. The value of \( W'_{thres} \) is also evaluated for each particle using the temperature at each time step, according to Eq. (2).

The last part that is missing for the full functionality is the change of bonding status. To achieve that, an additional loop at the end of each time step is needed, which iterates over all particles within the influence radius and belonging to different parts. For these the pressure–time–flow criterion \( W' \) is checked. If it reaches the critical value \( W_{thres}' \), then the bonding status flag is set to true for the particle pair as well as particles that are within kernel support radius H of each particle. This ensures the full particle support domain for the SPH integrals.

One relevant question is the consistency of the approach. It is important to guarantee that the contact force is replaced by continuum formulation smoothly, without additional impulse. Here it can be noted that the contact pressure is then not simply removed, but transferred into the internal pressure of the matter. This phenomena is illustrated in the following example. The impulse originated from the impact is physical and needs to be described and considered. However, it is important that no artificial impulse is introduced by the bonding process.

Fig. 3
figure 3

Initial setup of the compression test. (Color figure online)

Full size image

5 Results

5.1 Compression of two blocks

To test the concepts, an example with low physical and geometrical complexity is considered first. The idea for it is based on the hot pressure welding, where parts are joined together under elevated temperatures and high pressure which results in plastic deformation [33, 34] or the hot pressure test as shown in [16]. The idea is to press one block into another one until bonding is achieved. This example is tested for two scenarios: one just with simple contact and another one with added bonding functionality.

Two separate aluminum blocks with uneven circular surface are modeled using the parameters in Table 1. Each piece has width \(w = 0.2 \, \text {m}\), height \(h = 0.1 \, \text {m}\), thickness \(t = 0.025 \, \text {m}\) and fillet edges with radius \(r = 0.1 \, \text {m}\), the resulting geometries are presented in Fig. 3a. The initial contact area is measured to be \( 0.025 \cdot 0.085 \, \text {m}^2 = 2.125 \cdot 10^{-3} \, \text {m}^2\). Additional layers of 3 particles on the top and bottom, respectively, are added to both parts to impose the boundary conditions.

Both parts are discretized with a particle spacing \(L_\text {s} = 5.0 \cdot 10^{-3} \, \text {m}\), resulting in a total of \(10\,224\) SPH particles. The smoothing length of each particle is \(h = 1.7 L_\text {s} = 8.5\cdot 10^{-3} \, \text {m}\), support radius \(H = 2 h = 17\cdot 10^{-3} \, \text {m}\), an initial density of \(\rho _\text {s} = \rho _\text {0} = 2\,700 \, \text {kg} / \text {m}^3\), and a mass of \(m = L_\text {s}^3 \rho _\text {0} = 0.3375 \cdot 10^{-3} \, \text {kg}\). In order to reduce the calculation time, a mass scaling of factor 5.0 is employed.

The simulation scenario is as follows. The boundary conditions are applied as presented in Fig. 3b. The lower block is fixed from below, so the displacements of the 3 bottom layers of particles are set to zero. For the upper block, the upper boundary particles are set to move down with the velocity \(-0.01 \, \text {m/s}\) for the period of time \(t = 0.5 \, \text {s}\). After that instant the movement is reversed and the upper boundary particles are moved away with the velocity \(0.02 \, \text {m/s}\) until the end of simulation at \(t = 1.0 \, \text {s}\). Thus, this also corresponds to boundary condition where the displacement is prescribed. For all other boundary particles (shown in green and yellow color in Fig. 3b) the force is given (zero if no contact occurs, otherwise the computed contact force). With regard to initial condition, all particles of the upper part are set to have the initial velocity \(v_0 = -0.01 \, \text {m/s}\). Gravity is not considered in this scenario.

For the contact formulation between particles belonging to separate parts, SPH particles are assumed to have spherical surface (as explained in Sect. 3) with radius half of the particle spacing \(r = 0.5 \cdot L_\text {s} = 2.5 \cdot 10^{-3} \, \text {m}\). The simulation begins when the contact is just about to be introduced, i.e., with a distance \(d = 1.1 \cdot L_\text {s} = 5.5 \cdot 10^{-3} \, \text {m}\) between the two parts. Other parameters are as following: stiffness scale factor \(k = 2 \cdot 10^{4} \, \text {N}\), and friction scale factor \(\mu = 0.5\). Of course, an SPH particle is a part of a numerical discretization process and has no radius, shape, or surface. However, here additionally a geometry description is needed.

Hourglass control as introduced in Sect. 3 is used. As it is recommended in [26], the combination of both stiffness and viscosity-based formulation is utilized, as it proved to provide the best results for plasticity-dominated problems. The following parameters are used: stiffness-based scaling factor \( \xi = 0.01\), viscosity-based scaling factor \( \zeta = 4\), and combination weight factor \( \chi = 0.5\). For the time step control a Courant number, see [35], of \(\varUpsilon = 0.2\) is used in order to ensure the stability of the simulation while reducing computational time. The same stabilization parameters are later also applied to the following FSW simulation.

Fig. 4
figure 4

Simulation state at the end of simulation \(t = 1.0 \, \text {s}\), when the two parts have been pulled apart

Full size image
Fig. 5
figure 5

Reaction force acting on the boundary of lower part over the simulation duration

Full size image

In order to achieve bonding, the workpieces have to be heated up. For that reason the temperature of \(T = 573 \,\text {K} = 300 ^\circ \, \text {C}\) is assigned to all particles, according to [34] and [20]. Other effects, such as heat resulting from plastic deformation, are neglected in this verification simulation, as they have low impact, and the temperature is simply kept constant.

The effect of bonding is visualized by showing the state at the end of simulations at \(t = 1.0 \, \text {s}\) in Fig. 4. At this point in time, the parts already had contact and have been moved apart. In Fig. 4a, the scenario with simple contact without bonding is presented. It can be noted, that the parts after experiencing small plastic deformation have nearly retained their original shape as they are moved apart. In contrast to that, the simulation state with bonding is shown in Fig. 4b. There, the particles that had contact and reached the bonding criterion merged into a continuum which is stretched when pulled apart.

Fig. 6
figure 6

The pressure–time–flow criterion plotted over time for 2 different particles: 6365 is a particle on the contact surface of the upper part, 1427 is a particle on the contact surface of the bottom part

Full size image

The total reaction force acting on the boundary of lower part (Fig. 3b, in red) is tracked and plotted in Fig. 5. It is expected, that after the compressive motion is reserved, the case with no bonding will result in zero forces, while the bonding scenario will reverse the sign and have tensile forces. This fact can also be observed in the graph. First, both lines are overlapping until the bonding starts at \(t \approx 0.18 \, \text {s}\). There is a small bump there, as the interaction type is changing and some pressure between particles is released. However, there are no strong impulses observed, as it was discussed in Sect. 4. Then, the force is growing for both of the scenarios until the compression is released at \(t = 0.5 \, \text {s}\). The bonded part has then the resulting force with reversed sign. The tensile force is then slightly decreasing as the bonded area is shrinking and less particles are interacting. For the case without bonding, after the contact is separated, the reaction force is zero.

Fig. 7
figure 7

Simulation setup of FSW

Full size image
Fig. 8
figure 8

Progress of the FSW simulation. Material distribution and bond propagation (light blue: part 1, not bonded; light red: part 2, not bonded; dark blue: part 1, bonded; dark red: part 2, bonded). (Color figure online)

Full size image
Table 1 Material-related parameter values of the SPH models for the compression test and FSW
Full size table

Figure 6 provides more insight into the bonding procedure. Figure 6a shows the evolution of the pressure–time–flow criterion in time for two different particles in contact. The simulation is followed until \(t = 0.2 \, \text {s}\), as the bonding along the contact surface is achieved before that moment (Fig. 6d). The particle locations are presented in Fig. 6c. According to Eq. (2) the critical value in this example is \(W'_{thres}= 0.0017 \, \text {m}\). The blue particle, located on the verge of the contact surface of the upper part, is evaluated to reach this critical value at \(t \approx 0.178 \, \text {s}\), which corresponds with the value observed in Fig. 5. The higher value of the pressure–time–flow criterion is a consequence of higher contact pressure on the sides. This is conclusive with the stress flow in compression tests [36, 37], resulting from friction forces, which produces higher deformations on the sides and a ’dead zone’ in the middle of the contact surface. The red particle is located on the surface of the lower part and is the contact partner of the blue particle. This is the reason why these two particles are bonded at the same time. The lower pressure–time–flow criterion for the red particle can be explained by lower velocity: In the beginning of the contact the upper part moves with the initial velocity, while the lower part is at rest. Figure 6b shows how many particles are bonded due to criterion fulfillment (14) and how many are bonded due to the neighborhood location (816). The large share of bonded particles is neighborhood particles, which are needed to ensure full kernel support as explained in Sect. 4.

5.2 Friction stir welding

The new bonding feature is also applied to the simulation of FSW. However, several simplifications are still adopted similar to [21] as described in following. The simulation setup is presented in Fig. 7. Instead of an initial plunge phase simulation, the through hole is already created at the start of the weld and the tool is placed in it. Both the tool and the table are modeled using rigid triangles as can be seen in Fig. 7b. Instead of clamping, the workpiece is fixed trough the boundary condition. The five layers of the particles on each side are fixed by setting the deformation to zero as presented in Fig. 7a. The measurements and simulation parameters are summarized in Tables 1 and 2.

The simulation thus begins with a tool already in contact with the workpieces and inserted into the hole. The tool accelerates counterclockwise and dwells until \( t_a \), after which the transversal motion is started. The movement continues with constant rotational and transversal velocity until \(t = 22.95 \, \text {s}\).

Another simplification has to be assumed with regard to the thermal modeling. The fully coupled thermomechanical model was applied to this simulation, including heat generation from friction and plastic deformation, as well as heat transfer. However, the heat exchange with environment was neglected in this case. The straightforward approach of transferring the whole friction energy into heat results in over-predicted temperatures. According to [38, 39], it is still not completely understood what is the transition condition during FSW. It is widely varied from complete sticking, when only plastic deformation contributes to heat generation, to slipping with heat generated by friction. Additionally, the inclusion of heat conduction to the table, as well as heat radiation to environment might improve this issue. As this is not the central problem of this study, the temperature is simply constrained not to exceed \( 500 ^\circ \, \text {C}\), which is slightly above the maximum peak temperature of the weld, but remains below the melting point [40]. Additional research and extension of the model are required in order to further improve the results.

The simulation progress is represented in Fig. 8. There, both the material flow and the bond evolution are shown. It can be noticed that the material from the advancing side (blue), which would be in front of the tool pin, is moved around the tool and returned to the same side of the workpiece. These observations are consistent with other studies [41, 42]. As for the bond propagation, it can be seen how the continuum is formed throughout mixing of the material. However, the bonding effect happens ahead of the tool, which could be a result of a large bonding radius or over-predicted bonding pressure. Additional studies are required for more insight.

Table 2 Modeling parameters for simulation of FSW
Full size table

6 Conclusion

This paper introduces the simulation of a bonding mechanism, which is a vital feature for an accurate representation of FSW which is, however, typically not available in simulation codes. It is implemented as an extension of the existing SPH algorithm and tracks the continuum formation based on the process parameters. The compression of two blocks was used as a test example in order to validate the method. Finally, the scenario was applied to simulation of FSW.

The implemented extension proved to be useful in understanding the complete physics of FSW. In addition to multiple complex phenomena, the transition from contact to continuum was taken into account with the help of the bonding mechanism. This way the weld formation during the course of the simulation was observed based on the local process parameters. The resulting framework is of great value for prediction of weld quality in FSW.

Future steps include the development of a bonding criterion that is more focused on FSW and corresponds well to experimental observations. Ideally, the criterion not only predicts if bonding occurs in the weld, but also gives a prediction of the joint strength. Additional studies are needed to determine appropriate parameters and mechanisms for simulation of bonding for FSW.