A Voronoi strain-based method for granular materials and continua

Abstract

In a recent article (Frenning in Comp Part Mech 24:1–4, 2021), we demonstrated that a Delaunay-based strain estimate could be used as a starting point for the development of a particle-based method for continua. In this article, we argue that the Voronoi diagram, dual to the previously used Delaunay tetrahedralization, provides a more natural description of the underlying particulate system. For this reason, a Voronoi-based estimate of the deformation gradient is derived and used to the same effect. Although the gradient vectors cease to be antisymmetric, sums over nearest neighbors vanish, which results in a formulation that not only is linearly complete but also satisfies the patch test irrespective of initial particle placement. Pairwise forces, inferred from the local (nonaffine) deformation of each bond or contact, impart a physical stabilization. Forces are obtained from a discrete Lagrangian, thus ensuring that linear and angular momenta are conserved in the absence of external forces and torques. Methods to enforce different types of boundary conditions are described; these are exact for linear displacements, for constant stresses and for free surfaces. The performance of the method is assessed in a number of numerical tests.

1 Introduction

Particle scale simulations of the mechanics of granular materials at high relative density remain challenging [27, 51]. The main reason for this is that particle contacts cease to be independent of each other at a relative density of about 0.7–0.8 [37, 49], invalidating the commonly used discrete element method (DEM) [16] in its standard form.

The most common way to resolve this issue is to resort to the multi-particle finite element method (MPFEM; also referred to as the meshed DEM or the combined finite/discrete element method, FEM/DEM), whereby the discretization of each individual particle into finite elements enables an adequate representation of its mechanical behavior [28, 55]. Although the MPFEM has successfully been used to study compression of three-dimensional particle assemblies [23, 37], it is not practical for large systems due to its high computational cost [27].

As an alternative, there have been some efforts to develop what is commonly referred to as nonlocal contact models for the interaction between particles. The first such model, due to Harthong et al. [36], was based on curve fitting of MPFEM results for elastoplastic particles and utilized a stiffness that tends toward infinity when the local relative density approaches unity, as appropriate for incompressible particles. The local relative density was in turn determined from a Voronoi tessellation of space. Another nonlocal contact model for elastoplastic particles has been developed and calibrated in our laboratory [44]. This model utilizes particles of a (truncated) spherical shape and builds on the conceptions of Arzt [3], who likened the deformation of individual particles at high relative densities to that of an extrusion process. Particle deformation is compensated for by a corresponding increase in the particle radius, so that the particle volume is held constant. In effect, the model utilizes a contact pressure that is considered to be a function of the current particle volume, estimated from a Voronoi construction. Additional work in this field has been carried out by Gonzalez and Cuitiño [34] and Brodu et al. [10], who have devised nonlocal contact models for elastic particles. Related recent work has focused on nonlocal contact models for use in bonded particle packings (the so-called cohesive or bonded DEM) as a basis for fracture mechanics analysis [11, 12]. Finally, an interesting contact model has recently been devised by Giannis et al.  who included a nonlocal term based on the estimated average pressure in each particle, as obtained from the interparticle forces [31]. Despite their practical usefulness in simulations of powder compression [53], the existing nonlocal contact models are simplistic and typically do not properly account for tangential forces.

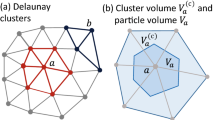
A natural way to formulate more satisfactory models would be to combine the DEM with an intrinsically nonlocal method such a particle-based method for continua (smoothed particle hydrodynamics, SPH, and related methods) [32, 46, 47]. In order to keep the representation of interacting particles intact, it appears desirable to include nearest-neighbor interactions only. If so-called virtual contacts [5] are included, the contact network is often considered to form a Delaunay tetrahedralization of space [17]. Hence, the Delaunay tetrahedralization and its dual, the Voronoi diagram, both constitute natural starting points for such an analysis. (For simplicity, we in this work confine ourselves to monodisperse granular materials; the appropriate generalizations for polydisperse materials are the regular tetrahedralization and the power diagram [4].)

To this end, we have recently shown how the most commonly used strain estimate for granular materials, due to Bagi [5], can be translated into a particle-based method for continua [24]. In effect, a compatible strain tensor [38] can be obtained for each particle as the volume average of the local deformation gradient over the corresponding Delaunay cluster (the union of all Delaunay tetrahedra that contain the particle in question; see also [58] where the term contiguous Voronoi cell is used). The Bagi strain thus is a Delaunay-based strain.

However, the Delaunay-based strain does, as any Delaunay-based quantity, suffer from a potentially serious shortcoming: It may change discontinuously when the reference state is updated (when a particle moves over the circumcircle of one of the tetrahedra) [39, 64]. For this reason, a Voronoi-based strain would be preferable, similar to the one proposed by Satake [57] (see [6]).

The specific objective of this work therefore is to devise a particle-based method for continua that is based on a Voronoi strain estimate. Such a method is expected to constitute an essential building block for future macroscopically consistent discrete methods for granular materials at high relative density. It is also hoped that the developed method shall be of interest in its own right.

Our method is related to the Voronoi component of the hybrid Lagrangian Voronoi–SPH scheme developed for fluids by Fernández-Gutiérrez et al. [19, 20]. Voronoi cells were recently used to estimate strain in DEM simulations via an SPH approach [52], but the underlying methodology is different from ours. In addition, Voronoi cells have been used in SPH to refine simulations via particle splitting [14], to calculate the volume attributed to each particle in order to improve the accuracy of the SPH method [29, 61] and as a means to obtain an optimal particle arrangement via centroidal Voronoi tesselation as obtained from Lloyd’s algorithm [29]. Additional related work includes the Voronoi finite element method due to Ghosh et al. [30] and the virtual element method on arbitrary polyhedral meshes [25]. Finally, the proposed method has some, but certainly not all, features in common with the recently proposed continuum-kinematics-inspired or kinematically exact peridynamics [41, 42].

2 Kinematics

2.1 Basic definitions

Fig. 1

Subdivision of the computational domain ${\mathcal {D}}$ into Voronoi cells (bounded by red lines) based on the referential placement of particles (filled circles) and ghosts (open circles). For clarity, the domain boundary $\partial {\mathcal {D}}$ is indicated by a thick red line and the boundary $\partial {\mathcal {V}}_a$ of Voronoi cell a by black lines. The thin gray lines drawn between the particle centers represent the underlying Delaunay tessellation. The black dots indicate the referential placement of boundary points (color online)

As illustrated in Fig. 1, we consider a set of particles that between them form a material domain ${\mathcal {D}}$. The material and spatial coordinates of (the center of) particle a are denoted $\varvec{X}_a$ and $\varvec{x}_a$, respectively. A standard Vornonoi tesselation is used to subdivide the material domain ${\mathcal {D}}$ into Voronoi cells ${\mathcal {V}}_a$, one for each particle, such that each material point $\varvec{X}$ is assigned to its closest particle center. The faces between particles thus are planar polygons, and two particles a and b are considered to be nearest neighbors if and only if they share a common face. To conveniently state and enforce boundary conditions, we introduce ghost particles as mirror images of particles located at the boundary $\partial {\mathcal {D}}$ of ${\mathcal {D}}$ [15, 19] and consider $\partial {\mathcal {D}}$ to be the union of a number of planar polygons. As a result, the boundary $\partial {\mathcal {V}}_a$ of ${\mathcal {V}}_a$ can be decomposed into a number of planar faces, such that each face $\partial {\mathcal {V}}_{ab}$ either separates two real particles a and b or a real particle a and a ghost particle b. This procedure is straightforward when the computational domain is bounded by flat surfaces, as in Fig. 1, since the Voronoi faces then reproduce the boundaries exactly, and can be extended to complex geometries [1]. Specifically, for each particle a located at a boundary, we determine a boundary point $\varvec{W}_{ab}$ by closest point projection of $\varvec{X}_a$ onto the boundary (indicated by black dots in Fig. 1) and determine the coordinates $\varvec{X}_b$ of the ghost particle from the equation $\varvec{W}_{ab} = (\varvec{X}_a + \varvec{X}_b)/2$. The volume $V_a$ of the Voronoi cell ${\mathcal {V}}_a$ is a function of the location of particle a and its nearest neighbors b. In the following, this set of particles (including particle a itself) will collectively be denoted by ${\mathcal {P}}_a$. Similarly, ${\mathcal {P}}'_a$ denotes the set of (proper) nearest neighbors to a, not including particle a itself. When stating boundary conditions (BCs), it will be convenient to subdivide the set ${\mathcal {P}}_a$ of nearest neighbors to a into the set ${\mathcal {E}}_a$ of external (ghost) particles and the set ${\mathcal {I}}_a$ of internal (real) particles. The reduced set ${\mathcal {P}}'_a$ is similarly divided into the sets ${\mathcal {E}}_a$ and ${\mathcal {I}}'_a$, where the prime again is used to indicate that particle a itself is not included. It proves convenient to subdivide the set ${\mathcal {E}}_a$ into the sets ${\mathcal {E}}_a'$ and ${\mathcal {E}}_a''$. Specifically, a ghost particle $b \in {\mathcal {E}}_a$ belongs to the set ${\mathcal {E}}'_a$ if and only if the current location of the boundary point $\varvec{w}_{ab}= (\varvec{x}_a + \varvec{x}_b)/2$ is fully prescribed. Consequently, the set ${\mathcal {E}}_a''$ contains those ghost particles for which $\varvec{w}_{ab}$ is not fully prescribed. Finally, we let ${\mathcal {E}}^T_a$ denote traction boundaries, i.e., a ghost particle $b \in {\mathcal {E}}_a$ belongs to the set ${\mathcal {E}}^T_a$ if and only if the traction is prescribed on the interface between particles a and b. Note that ${\mathcal {E}}^T_a$ is a subset of ${\mathcal {E}}_a''$, since the displacement is not fully prescribed on traction boundaries (most often not prescribed at all). The vectors $\varvec{X}_{ab} = \varvec{X}_b - \varvec{X}_a$ and $\varvec{x}_{ab} = \varvec{x}_b - \varvec{x}_a$ that point from the center of particle a to the center of a neighboring particle b in the reference and current configurations, respectively, are often referred to as branch vectors in the granular mechanics literature [5, 17].

2.2 Global particle deformation: the mean deformation gradient

For each particle a, we define a discrete mean deformation gradient $\varvec{F}_a$ as an average of the continuum deformation gradient, , over the corresponding Voronoi cell ${\mathcal {V}}_a$. Here, $\varvec{x}=\varvec{\varphi }(\varvec{X},t)$ is a motion that expresses the spatial coordinates $\varvec{x}$ as a function of the material coordinates $\varvec{X}$ and time t. From the definition of the deformation gradient and the divergence theorem, one obtains

$$\begin{aligned} \varvec{F}_a&= \frac{1}{V_a} \int _{{\mathcal {V}}_a} \varvec{F} \, \mathrm {d}{V} = \frac{1}{V_a} \int _{\partial {\mathcal {V}}_a} \varvec{\varphi } \otimes \hat{\varvec{N}} \, \mathrm {d}{A} \nonumber \\&= \frac{1}{V_a} \sum _{b \in {\mathcal {P}}'_a} \int _{\partial {\mathcal {V}}_{ab}} \varvec{\varphi } \otimes \hat{\varvec{N}}_{ab} \, \mathrm {d}{A}\;, \end{aligned}$$

(1)

where $\hat{\varvec{N}}$ is the material outward unit normal to the surface $\partial {\mathcal {V}}_a$ of ${\mathcal {V}}_a$. The final equality follows from a decomposition of the surface integral into integrals over the planar Voronoi faces $\partial {\mathcal {V}}_{ab}$ with material outward unit normals $\hat{\varvec{N}}_{ab}$. To proceed further, we assume that $\varvec{\varphi }(\varvec{X},t)$ varies linearly either on each face or in the whole Delaunay cluster [24] for particle a. The Delaunay cluster represents the union of all Delaunay tetrahedra that contain a certain particle. As such, it could be interpreted as the convex hull of the set of nearest neighbors of the particle. Assume first that $\varvec{\varphi }(\varvec{X},t)$ varies linearly on each face. Introducing the material centroid $\varvec{C}_{ab}$ of face $\partial {\mathcal {V}}_{ab}$ with area $A_{ab}$ as

$$\begin{aligned} \varvec{C}_{ab} = \frac{1}{A_{ab}}\int _{\partial {\mathcal {V}}_{ab}} \varvec{X} \, \mathrm {d}{A} \;, \end{aligned}$$

(2)

we can write $\varvec{\varphi } = \varvec{c}_{ab} + \varvec{G}_{ab} (\varvec{X}-\varvec{C}_{ab})$, where $\varvec{c}_{ab}=\varvec{\varphi }(\varvec{C}_{ab},t)$ and $\varvec{G}_{ab}$ is the constant gradient. For the assumed linear variation of $\varvec{\varphi }(\varvec{X},t)$ on each face, Eq. (1) takes the form

$$\begin{aligned} \varvec{F}_a = \frac{1}{V_a} \sum _{b \in {\mathcal {P}}'_a} \varvec{c}_{ab} \otimes \varvec{A}_{ab} \;, \end{aligned}$$

(3)

where $\varvec{A}_{ab} = A_{ab} \hat{\varvec{N}}_{ab}$ is the material area vector. However, this equation is not useful unless a practical way to determine $\varvec{c}_{ab}=\varvec{\varphi }(\varvec{C}_{ab},t)$ is found. For this reason, we instead follow Springel [64] and assume that $\varvec{\varphi }(\varvec{X},t)$ varies linearly in the whole Delaunay cluster, so that $\varvec{\varphi } = \varvec{x}_a + \varvec{G}_a (\varvec{X}-\varvec{X}_a)$, where $\varvec{x}_a=\varvec{\varphi }(\varvec{X}_a,t)$ and $\varvec{G}_a$ is the constant gradient. Hence, the integrand in Eq. (1) takes the form

$$\begin{aligned} \varvec{\varphi } \otimes \hat{\varvec{N}} = \varvec{x}_a \otimes \hat{\varvec{N}} + [\varvec{G}_a (\varvec{X}-\varvec{X}_a)] \otimes \hat{\varvec{N}} \;. \end{aligned}$$

(4)

It is realized that only the term $[\varvec{G}_a (\varvec{X}-\varvec{X}_a)] \otimes \hat{\varvec{N}}$ produces a nonzero result in Eq. (1), because a straightforward application of the divergence theorem demonstrates that the surface integral of the first term can be transformed to the volume integral of ${\text {Grad}}\varvec{x}_a=\varvec{0}$. To proceed further, we utilize to following tensorial analogue of the vectorial triple product expansion (‘BAC-CAB’ rule; see Appendix A):

$$\begin{aligned}{}[\varvec{G}_a (\varvec{X}-\varvec{X}_a)] \otimes \hat{\varvec{N}} =&(\varvec{G}_a\hat{\varvec{N}}) \otimes (\varvec{X}-\varvec{X}_a) \nonumber \\&+ \varvec{G}_a \times [ \hat{\varvec{N}} \times (\varvec{X}-\varvec{X}_a) ] \;. \end{aligned}$$

(5)

Only the term $( \varvec{G}_a \hat{\varvec{N}} ) \otimes (\varvec{X}-\varvec{X}_a)$ produces a nonzero result in Eq. (1), because another application of the divergence theorem shows that the surface integral of the second term corresponds to the cross product of $\varvec{G}_a$ and the volume integral of ${\text {Curl}}(\varvec{X}-\varvec{X}_a) = \varvec{0}$. It can be noted that $\varvec{G}_a \hat{\varvec{N}}_{ab}$ is the directional derivative of $\varvec{\varphi }$ in the direction $\hat{\varvec{N}}_{ab}$, which for a linearly varying function can be expressed as $\varvec{x}_{ab}/L_{ab}$, where $\varvec{x}_{ab} = \varvec{x}_b - \varvec{x}_a$ is the spatial branch vector and $L_{ab}=\left|\varvec{X}_{ab} \right|$. Since each directional derivative $\varvec{G}_a \hat{\varvec{N}}_{ab}$ is independent of $\varvec{X}$, Eq. (1) becomes

$$\begin{aligned} \varvec{F}_a = \frac{1}{V_a} \sum _{b \in {\mathcal {P}}'_a} \varvec{x}_{ab} \otimes \varvec{B}_{ab} \;, \end{aligned}$$

(6)

where we have introduced the material vector

$$\begin{aligned} \varvec{B}_{ab} = \frac{1}{L_{ab}}\int _{\partial {\mathcal {V}}_{ab}} (\varvec{X}-\varvec{X}_a) \, \mathrm {d}{A} = \frac{A_{ab}}{L_{ab}}( \varvec{C}_{ab} - \varvec{X}_a ) \;, \end{aligned}$$

(7)

henceforth referred to as the gradient vector.

Since the deformation gradient reduces to the identity tensor $\varvec{I}$ when the material coordinates are substituted for the spatial coordinates in Eq. (6), we obtain the following duality relation

$$\begin{aligned} \frac{1}{V_a}\sum _{b \in {\mathcal {P}}'_a} \varvec{X}_{ab} \otimes \varvec{B}_{ab} = \varvec{I} \end{aligned}$$

(8)

where $\varvec{X}_{ab} = \varvec{X}_b - \varvec{X}_a$ is the material branch vector. It proves convenient to introduce [60]

$$\begin{aligned} \varvec{B}_{aa} = -\sum _{b \in {\mathcal {P}}'_a} \varvec{B}_{ab} \end{aligned}$$

(9)

so that Eq. (6) can be restated as

$$\begin{aligned} \varvec{F}_a = \frac{1}{V_a} \sum _{b \in {\mathcal {P}}_a} \varvec{x}_b \otimes \varvec{B}_{ab} \;, \end{aligned}$$

(10)

where the sum now includes particle a itself.

2.3 The gradient vectors

Fig. 2

Illustration of gradient vectors $\varvec{B}_{ab}$. The scaled gradient vector $(L_{ab}/A_{ab})\varvec{B}_{ab}$ points from the center of particle a (large blue circle) to the centroid (small black circle) of the Voronoi face (red line) between particles a and b. Here, $L_{ab}$ is the interparticle distance and $A_{ab}$ is the Voronoi face area (color online)

As demonstrated by Flekkøy et al. [21] and Serrano and Español [60], the gradient vectors $\varvec{B}_{ab}$ exhibit interesting relationships with derivatives of the Voronoi cell volume $V_a$ with respect to its defining points $b \in {\mathcal {P}}_a$ (see Appendix B). It is also instructive to decompose the gradient vectors $\varvec{B}_{ab}$ into components that are normal and tangential to the face $\partial {\mathcal {V}}_{ab}$, denoted by $\varvec{B}_{ab}^{\mathrm {n}}$ and $\varvec{B}_{ab}^{\mathrm {t}}$, respectively. From definition (7) it is realized that the normal and tangential components behave differently upon interchange of the indices a and b: As illustrated in Fig. 2, the normal component is antisymmetric (i.e., $\varvec{B}_{ba}^{\mathrm {n}}=-\varvec{B}_{ab}^{\mathrm {n}}$) and the tangential component is symmetric (i.e., $\varvec{B}_{ba}^{\mathrm {t}}=\varvec{B}_{ab}^{\mathrm {t}}$). Moreover, it is realized that $-\varvec{B}_{ba}^{\mathrm {n}} = \varvec{B}_{ab}^{\mathrm {n}} = \varvec{A}_{ab}/2$, where $\varvec{A}_{ab} = A_{ab}\hat{\varvec{N}}_{ab}$ is the material area vector. This result has two important consequences. First, the material area vector can be expressed as a difference between oppositely directed gradient vectors:

$$\begin{aligned} \varvec{A}_{ab} = \varvec{B}_{ab} - \varvec{B}_{ba} \;. \end{aligned}$$

(11)

Second, summing Eq. (11) over $b \in {\mathcal {P}}'_a$, noting that the sum of outwards directed area vectors $\varvec{A}_{ab}$ over a closed surface vanishes as a consequence of the divergence theorem, it is seen that

$$\begin{aligned} \sum _{b \in {\mathcal {P}}'_a} \varvec{B}_{ab} = \sum _{b \in {\mathcal {P}}'_a} \varvec{B}_{ba} \;. \end{aligned}$$

(12)

Adding $\varvec{B}_{aa}$ to each member of Eq. (12), we obtain according to definition (9) a vanishing sum, i.e.,

$$\begin{aligned} \sum _{b \in {\mathcal {P}}_a} \varvec{B}_{ab} = \sum _{b \in {\mathcal {P}}_a} \varvec{B}_{ba} = \varvec{0} \;. \end{aligned}$$

(13)

This result carries significant practical implications. Since the deformation gradient shall be invariant under translations, the substitution of $\varvec{x}_b+\varvec{u}$ (where $\varvec{u}$ is a constant displacement) for $\varvec{x}_b$ in Eq. (10) shall have no effect. Clearly, this is true only if the sum of $\varvec{B}_{ab}$ over b vanishes. As demonstrated below, the patch test will not be fulfilled in general unless the sum of $\varvec{B}_{ba}$ over b vanishes.

2.4 Boundary treatment

The location of ghosts needs to be updated when the material deforms or undergoes rigid-body motion. This is straightforward when the location of boundary points is prescribed but less so on free boundaries. The location of free (coordinates of) boundary points, or equivalently of free (components of) branch vectors $\varvec{x}_{ab}$, can be determined from a least-squares minimization [15, 19]. Specifically, the location is here determined from minimization of the functional $\sum _{b \in {\mathcal {P}}'_a} \left|\varvec{x}_{ab} - \varvec{F}_a\varvec{X}_{ab} \right|^2$ over the space of branch vectors $\varvec{x}_{ab}$ subject to the constraints resulting from known locations of internal points or imposed displacement BCs. In order to enforce (total, symmetric and antisymmetric) displacement BCs, we introduce for each particle a located at the boundary of the domain ${\mathcal {D}}$ and each ghost particle $b \in {\mathcal {E}}_a$ a projection $\varvec{D}_{ab}$ onto the constrained degrees of freedom and for now assume that the remaining degrees of freedom are free. Specifically,

$$\begin{aligned} \varvec{D}_{ab} = {\left\{ \begin{array}{ll} \varvec{I} &{} \text {total,} \\ \hat{\varvec{N}}_{ab} \otimes \hat{\varvec{N}}_{ab} &{} \text {symmetric,} \\ \varvec{I} - \hat{\varvec{N}}_{ab} \otimes \hat{\varvec{N}}_{ab} &{} \text {antisymmetric,} \\ \end{array}\right. } \end{aligned}$$

(14)

where $\hat{\varvec{N}}_{ab}$ is a unit normal to the face (for simplicity assumed to be time independent, thus coinciding with the material normal). Likewise, we let $\varvec{D}_{ab} = \varvec{0}$ on free boundaries (since there are no constraints) and $\varvec{D}_{ab} = \varvec{I}$ for $b \in {\mathcal {I}}'_a$ (since the corresponding branch vector then is known). With the aid of the projection $\varvec{D}_{ab}$, we may specify constraints as $\varvec{D}_{ab} \varvec{x}_{ab} = \varvec{D}_{ab}\bar{\varvec{x}}_{ab}$, where the relevant components of $\bar{\varvec{x}}_{ab}$ are considered known. Specifically, for displacement BCs, $\bar{\varvec{x}}_{ab}=2(\varvec{W}_{ab} + \bar{\varvec{u}}_{ab}-\varvec{x}_a)$, where $\bar{\varvec{u}}_{ab}$ the prescribed displacement of the boundary point.

Introducing Lagrange multipliers $\varvec{\lambda }_{ac}$, the constrained minimization stated above is transformed into an unconstrained minimization of

$$\begin{aligned} {\mathcal {L}}_a = \sum _{c \in {\mathcal {P}}'_a} \left[ \left|\varvec{x}_{ac} - \varvec{F}_a\varvec{X}_{ac} \right|^2 -\varvec{\lambda }_{ac} \cdot \varvec{D}_{ac} (\varvec{x}_{ac} - \bar{\varvec{x}}_{ac}) \right] \;. \end{aligned}$$

(15)

Using Eq. (6), we may expand $\varvec{F}_a\varvec{X}_{ac}$ as

$$\begin{aligned} \varvec{F}_a\varvec{X}_{ac} = \sum _{d \in {\mathcal {P}}'_a} H_{acd} \varvec{x}_{ad} \end{aligned}$$

(16)

where $H_{acd} = \varvec{X}_{ac} \cdot \varvec{B}_{ad}/V_a$. The stationary values of $\varvec{x}_{ab}$ are obtained by letting . A straightforward but fairly lengthy calculation shows that

(17)

where

$$\begin{aligned} K_{abc} = \delta _{bc} - ( H_{abc} + H_{acb} ) + \sum _{d \in {\mathcal {P}}'_a} H_{adb} H_{adc} \;. \end{aligned}$$

(18)

Letting reproduces the constraint, i.e.,

(19)

Since $\varvec{D}_{ab}$ is a projection and hence symmetric and idempotent, we find by multiplication of Eq. (17) by $\varvec{D}_{ab}$ from the left that

$$\begin{aligned} 2 \varvec{D}_{ab} \sum _{c \in {\mathcal {P}}'_a} K_{abc} \varvec{x}_{ac} = \varvec{\lambda }_{ab} \cdot \varvec{D}_{ab} \end{aligned}$$

(20)

which when substituted back in Eq. (17) produces

$$\begin{aligned} (\varvec{I} - \varvec{D}_{ab}) \sum _{c \in {\mathcal {P}}'_a} K_{abc} \varvec{x}_{ac} = \varvec{0} \;. \end{aligned}$$

(21)

Clearly, Eq. (21) is trivially satisfied when the branch vector $\varvec{x}_{ab}$ is known, i.e., when $\varvec{D}_{ab} = \varvec{I}$, which is the case for interior particles ($b \in {\mathcal {I}}'_a$) or for total displacement boundaries ($b \in {\mathcal {E}}'_a$). Otherwise ($b \in {\mathcal {E}}''_a$), at least one component remains after projection, implying that the sum must vanish. We may form a coefficient matrix $\varvec{K}_a$ from the elements $K_{abc}$ with $b \in {\mathcal {E}}''_a$ and $c \in {\mathcal {P}}'_a$ and extract a symmetric matrix $\bar{\varvec{K}}_a$ from the elements $K_{abc}$ with $b,c \in {\mathcal {E}}''_a$. Provided that this matrix is nonsingular, we may for each $b \in {\mathcal {E}}''_a$ solve for $\varvec{x}_{ab}$. Letting $\varvec{x}_{ab}'$ denote the obtained solution, we may write

$$\begin{aligned} \varvec{x}_{ab}' = \sum _{c \in {\mathcal {I}}'_a \cup {\mathcal {E}}'_a} K_{abc}' \varvec{x}_{ac} \;, \end{aligned}$$

(22)

where the coefficients $K_{abc}'$ are obtained from the matrix $\varvec{K}_a' = -\bar{\varvec{K}}_a^{-1} \varvec{K}_a$. It is sometimes convenient to separate the sum in the above equation into sums over internal (real) and external (ghost) particles and to write

$$\begin{aligned} \varvec{x}_{ab}' = \sum _{c \in {\mathcal {I}}_a} K_{abc}' \varvec{x}_c + \sum _{c \in {\mathcal {E}}'_a} K_{abc}' \bar{\varvec{x}}_{ac} \end{aligned}$$

(23)

where we have let $K_{aba}' = -\sum _{c \in {\mathcal {I}}'_a} K_{abc}'$. Pre-multiplying $\varvec{x}_{ab}'$, as obtained from Eq. (22) or (23), with $\varvec{I}-\varvec{D}_{ab}$, we obtain the free components of $\varvec{x}_{ab}$. The constrained components are obtained from Eq. (19), and hence, we finally obtain

$$\begin{aligned} \varvec{x}_{ab} = \varvec{D}_{ab} \bar{\varvec{x}}_{ab} + (\varvec{I}-\varvec{D}_{ab}) \varvec{x}_{ab}' \end{aligned}$$

(24)

where the required components of $\bar{\varvec{x}}_{ab}$ are obtained from the displacement BCs.

2.5 A possible static condensation

We may separate the sum in Eq. (10) into sums over internal and external particles and use Eq. (24) in the latter. For convenience introducing

$$\begin{aligned} \bar{\varvec{B}}_{ab} = \varvec{B}_{ab} + \delta _{ab}\sum _{c \in {\mathcal {E}}_a} \varvec{B}_{ac} \end{aligned}$$

(25)

Eq. (10) can be restated as

$$\begin{aligned} \varvec{F}_a = \frac{1}{V_a} \left( \sum _{b \in {\mathcal {I}}_a} \varvec{x}_b \otimes \bar{\varvec{B}}_{ab} + \sum _{b \in {\mathcal {E}}_a} \varvec{x}_{ab} \otimes \varvec{B}_{ab} \right) \;. \end{aligned}$$

(26)

It can be noted that Eq. (26) reduces to Eq. (10) for internal particles (i.e., particles not located at the boundary). For boundary particles that are not subject to any displacement BCs, $\varvec{D}_{ab} = \varvec{0}$ in Eq. (24) and the second sum in Eq. (23) vanishes. Inserting the resulting expression in Eq. (26), we obtain

$$\begin{aligned} \varvec{F}_a = \frac{1}{V_a} \sum _{b \in {\mathcal {I}}_a} \varvec{x}_b \otimes \tilde{\varvec{B}}_{ab} \end{aligned}$$

(27)

where

$$\begin{aligned} \tilde{\varvec{B}}_{ab} = \bar{\varvec{B}}_{ab} + \sum _{c \in {\mathcal {E}}_a} K_{acb}' \varvec{B}_{ac} \;. \end{aligned}$$

(28)

Equation (27) represents a static condensation that can be used to evaluate the mean deformation gradient for boundary particles not subject to any essential boundary conditions.

2.6 Local particle deformation: local displacement

As in our previous work [24], we introduce a local displacement vector $\varvec{u}^{\mathrm {loc}}_{ab}$ as a measure of nonaffine deformation of the bond between particles a and b. For contact between two (real) particles (i.e., for $b \in {\mathcal {I}}_a'$), this vector is defined as

$$\begin{aligned} \varvec{u}^{\mathrm {loc}}_{ab} = \varvec{x}_{ab} - \varvec{y}_{ab} = \varvec{x}_{ab} - \varvec{F}_{ab} \varvec{X}_{ab} \;, \end{aligned}$$

(29)

where $\varvec{y}_{ab} = \varvec{F}_{ab} \varvec{X}_{ab}$ represents the image of the material branch vector $\varvec{X}_{ab}$ under the affine transformation represented by the mean deformation gradient $\varvec{F}_{ab} = ( \varvec{F}_a + \varvec{F}_b )/2$. In order to avoid complications resulting from a nonzero local displacement on free boundaries, we include the projection $\varvec{D}_{ab}$ in the definition for contact between a real particle a and a ghost b (i.e., for $b \in {\mathcal {E}}_a$), i.e.,

$$\begin{aligned} \varvec{u}^{\mathrm {loc}}_{ab} = \varvec{D}_{ab} ( \varvec{x}_{ab} - \varvec{y}_{ab} ) = \varvec{D}_{ab} ( \varvec{x}_{ab} - \varvec{F}_a \varvec{X}_{ab} ) \;, \end{aligned}$$

(30)

where $\varvec{y}_{ab} = \varvec{F}_a \varvec{X}_{ab}$. We can summarize Eqs. (29) and (30) by writing $\varvec{u}^{\mathrm {loc}}_{ab} = \tilde{\varvec{x}}_{ab} - \tilde{\varvec{y}}_{ab}$ where $\tilde{\varvec{x}}_{ab} = \varvec{x}_{ab}$ and $\tilde{\varvec{y}}_{ab} = \varvec{y}_{ab}$ if $b \in {\mathcal {I}}_a'$ and $\tilde{\varvec{x}}_{ab} = \varvec{D}_{ab}\varvec{x}_{ab}$ and $\tilde{\varvec{y}}_{ab} = \varvec{D}_{ab}\varvec{y}_{ab}$ if $b \in {\mathcal {E}}_a$.

3 Equations of motions, stresses and forces

3.1 Variational total Lagrangian formulation

As in our previous work [24], we derive the equations of motion in a total Lagrangian framework. The starting point is a discrete Lagrangian ${\mathcal {L}} = {\mathcal {T}} - {\mathcal {V}}$, where ${\mathcal {T}}$ is the total kinetic energy of the particle system and ${\mathcal {V}}$ is its potential energy (see, e.g., [33]). Specifically,

$$\begin{aligned} {\mathcal {T}} = \frac{1}{2} \sum _a m_a v_a^2 \;, \end{aligned}$$

(31)

where $m_a$ and $v_a = \left|\varvec{v}_a \right|$ are the mass and velocity of particle a, respectively. The potential energy ${\mathcal {V}}$ is expressed as

$$\begin{aligned} {\mathcal {V}} = {\mathcal {V}}^{\mathrm {int}} + {\mathcal {V}}^{\mathrm {cnt}} + {\mathcal {V}}^{\mathrm {ext}} \end{aligned}$$

(32)

where ${\mathcal {V}}^{\mathrm {int}}$ is the internal strain energy resulting from the global (affine) particle deformation, ${\mathcal {V}}^{\mathrm {cnt}}$ is the strain energy resulting from local (nonaffine) deformation at each contact and ${\mathcal {V}}^{\mathrm {ext}}$ is the energy imparted by agents external to the system, such as gravity. Specifically,

$$\begin{aligned} {\mathcal {V}}^{\mathrm {int}} = \sum _a V_a U_a(\varvec{F}_a) \end{aligned}$$

(33)

where $U_a$ is the internal energy per volume unit in the reference state, considered to be a function of the mean deformation gradient $\varvec{F}_a$. Similarly,

$$\begin{aligned} {\mathcal {V}}^{\mathrm {cnt}} = \sum _{a<b} U_{ab}(\tilde{\varvec{x}}_{ab},\tilde{\varvec{y}}_{ab}) \;. \end{aligned}$$

(34)

where $U_{ab}$ represents a pairwise interaction energy and the sum extends over all pairs of nearest neighbors a and b. For contact between internal (real) particles, $U_{ab}$ is considered to be a function of the current branch vector $\varvec{x}_{ab}$ ($=\tilde{\varvec{x}}_{ab})$ and the vector $\varvec{y}_{ab}$ ($= \tilde{\varvec{y}}_{ab}$), defined in Sect. 2.6, in order to facilitate a discrimination between the normal ($\hat{\varvec{x}}_{ab}$) and tangential directions. In order to obtain a unified treatment, $U_{ab}$ is expressed a function of $\tilde{\varvec{x}}_{ab} = \varvec{D}_{ab}\varvec{x}_{ab}$ and $\tilde{\varvec{y}}_{ab} = \varvec{D}_{ab}\varvec{y}_{ab}$ for contact between an internal (real) and an external (ghost) particle. This is possible because the normal and tangential directions are in this case defined by the normal to the boundary and not by the branch vector $\varvec{x}_{ab}$.

Considering a body force resulting from gravity (gravitational constant $\varvec{g}$) and nominal tractions $\bar{\varvec{T}}_{ab}$ acting on the boundary between the internal (real) particle a and the external (ghost) particle b, the energy due to external forces can be expressed as

$$\begin{aligned} {\mathcal {V}}^{\mathrm {ext}} = -\sum _a m_a \varvec{g} \cdot \varvec{x}_a -\sum _a \sum _{b \in {\mathcal {E}}^T_a} A_{ab} \bar{\varvec{T}}_{ab} \cdot \varvec{x}_a \;. \end{aligned}$$

(35)

The Euler–Lagrange equations (see, e.g., [33])

(36)

result in the equations of motion

(37)

where

(38a)

(38b)

(38c)

are referred to as the internal, contact and external forces, respectively. We remark that some care is needed to ensure a proper distinction between internal and external forces when ghost particles are used, as elaborated further upon below.

3.2 External force

Combining Eqs. (38c) and (35), the external force is immediately obtained as

(39)

Moreover, for displacement BCs, reaction forces yield an additional contribution to the external force, as elaborated further upon below.

3.3 Internal force

Using Eqs. (38a) and (33), together with the chain rule, the internal force is obtained as

(40)

where the colon indicates double contraction and is the first Piola–Kirchhoff stress tensor for particle b. If particle a is located in the interior of the domain (i.e., if none of the particles $b \in {\mathcal {I}}_a$ is located at the boundary), there is no need to explicitly take boundary effects into account. Hence, differentiation of expression (10) (most easily done in Cartesian components; see [24]) and substitution of the result in Eq. (40) produces the internal force in the form

$$\begin{aligned} \varvec{f}^{\mathrm {int}}_a = -\sum _{b \in {\mathcal {I}}_a} \varvec{P}_b \varvec{B}_{ba} \;. \end{aligned}$$

(41)

For interior particles, it follows from Eq. (41) that the force resulting from a constant stress field vanishes provided that the sum of $\varvec{B}_{ba}$ over b vanishes. This results is a special instance of the integration constraint derived by Chen et al. [13, 56]. That the integration constraint indeed is fulfilled follows from Eq. (13).

Using definition (9), noting that ${\mathcal {P}}_a = {\mathcal {I}}_a$ for particles in the internal of the domain, the internal force may alternatively be expressed as

$$\begin{aligned} \varvec{f}^{\mathrm {int}}_a = \sum _{b \in {\mathcal {I}}_a'} \left( \varvec{P}_a \varvec{B}_{ab} - \varvec{P}_b \varvec{B}_{ba} \right) = \sum _{b \in {\mathcal {I}}_a'} \varvec{f}^{\mathrm {int}}_{ab} \;, \end{aligned}$$

(42)

where $\varvec{f}^{\mathrm {int}}_{ab} = \varvec{P}_a \varvec{B}_{ab} - \varvec{P}_b \varvec{B}_{ba}$ represents the force on particle a caused by contact with particle b. When written in this form, the expression for the internal force embodied in Eq. (42) is valid also for particles located at boundaries. In the special case that $\varvec{P}_b = \varvec{P}_a$, it follows from Eq. (11) that the internal force can be expressed as $\varvec{f}^{\mathrm {int}}_{ab} = \varvec{P}_a \varvec{A}_{ab} = A_{ab} \varvec{T}_{ab}$, where $\varvec{T}_{ab} = \varvec{P}_a \hat{\varvec{N}}_{ab}$ represents the nominal traction on the interface between particles a and b. Likewise, for a total displacement BC, the reaction force on particle a caused by contact with ghost particle b is obtained as $\varvec{P}_a \varvec{A}_{ab}$. The reaction force represents a contribution that is to be added to expression (39). Hence, for a state of constant stress ($\varvec{P}_b = \varvec{P}_a$, without body forces), the total force $\varvec{f}^{\mathrm {int}}_a + \varvec{f}^{\mathrm {ext}}_a$ vanishes, as it should. When only some degrees of freedom are prescribed, the projection operator $\varvec{D}_{ab}$ shall be included to ensure that no spurious forces are picked up from free boundaries, i.e., the reaction force takes the form $\varvec{D}_{ab}\varvec{P}_a \varvec{A}_{ab}$.

The formulation described this far is fully satisfactory for static and quasi-static problems. In particular, it can be noted that identical expressions are obtained for forces due to applied tractions and for reaction forces (compare $\varvec{f}^{\mathrm {ext}}_{ab} = A_{ab} \bar{\varvec{T}}_{ab}$ with $\varvec{f}^{\mathrm {ext}}_{ab} = A_{ab} \varvec{T}_{ab}$ where $\varvec{T}_{ab} = \varvec{P}_a \hat{\varvec{N}}_{ab}$). However, an alternative expression for the internal force is preferable in highly dynamic situations. For particles located at free boundaries, the internal force provided by Eq. (41) is not in general derivable from a rotationally invariant potential energy, and as a consequence, the total angular momentum will not be conserved when this expression is used. To alleviate this issue, one can base the derivation on Eq. (26) rather than on Eq. (10). Moreover, (components of) branch vectors corresponding to prescribed displacements [i.e., $\varvec{D}_{ab}\bar{\varvec{x}}_{ab}$, c.f. Eq (24)] are treated as constants to ensure that no spurious external forces are obtained. Hence, differentiation of Eq. (26) and substitution of the derivative into Eq. (40) produces

$$\begin{aligned} \varvec{f}^{\mathrm {int}}_a = -\sum _{b \in {\mathcal {I}}_a}\!\left( \varvec{P}_b \bar{\varvec{B}}_{ba} +\!\sum _{c \in {\mathcal {E}}_b} \! K_{bca}' (\varvec{I}-\varvec{D}_{bc}) \varvec{P}_b\varvec{B}_{bc}\!\right) \;\!\!. \end{aligned}$$

(43)

Clearly, Eq. (43) reduces to Eq. (41) in the interior of the domain, as is should. It is also instructive to consider the special cases that all degrees of freedom are free or constrained. When $\varvec{D}_{bc} = \varvec{0}$ for all $c \in {\mathcal {E}}_b$,

$$\begin{aligned} \varvec{f}^{\mathrm {int}}_a&=-\sum _{b \in {\mathcal {I}}_a} \varvec{P}_b \left( \bar{\varvec{B}}_{ba} +\sum _{c \in {\mathcal {E}}_b} K_{bca}' \varvec{B}_{bc} \right) \nonumber \\&=-\sum _{b \in {\mathcal {I}}_a} \varvec{P}_b \tilde{\varvec{B}}_{ba} \;, \end{aligned}$$

(44)

which is identical in form to expression (41) valid for particles in the interior of the domain but with the effective gradient vectors $\tilde{\varvec{B}}_{ba}$ substituted for the total gradient vectors $\varvec{B}_{ba}$. This result is consistent with the one obtained from Eq. (27), as expected. On the other hand, when $\varvec{D}_{bc} = \varvec{I}$ for all $c \in {\mathcal {E}}_b$,

$$\begin{aligned} \varvec{f}^{\mathrm {int}}_a =-\sum _{b \in {\mathcal {I}}_a} \varvec{P}_b \bar{\varvec{B}}_{ba} \;, \end{aligned}$$

(45)

which again is identical in form to expression (41) valid for particles in the interior of the domain but with $\bar{\varvec{B}}_{ba}$ substituted for $\varvec{B}_{ba}$. Utilizing definition (25) of $\bar{\varvec{B}}_{ba}$ and definition (9) of $\varvec{B}_{aa}$, one finds that $\bar{\varvec{B}}_{aa}=-\sum _{b \in {\mathcal {I}}_a'} \varvec{B}_{ab}$. Hence, Eq. (45) reduces to Eq. (42) as it should.

3.4 Contact forces

The contact forces are obtained from Eqs. (38b) and (34) together with the chain rule. The derivation parallels the one outlined in [24] but is more technical and is therefore deferred to Appendix C. The final result can be expressed as

(46)

where $\varvec{M}_{bca}''$ is a symmetric second-order tensor defined in Appendix C and where we have let

$$\begin{aligned} \varvec{E}_{bc} = {\left\{ \begin{array}{ll} \varvec{I} &{} c \in {\mathcal {I}}_b' \\ 2\varvec{D}_{bc} &{} c \in {\mathcal {E}}_b \\ \end{array}\right. } \end{aligned}$$

(47)

in order to be able to combine the terms obtained for internal (real) and external (ghost) particles. Alternatively, one can let $\tilde{\varvec{M}}_{bca} = \varvec{M}_{bca}'' \varvec{E}_{bc}/2$ to simplify the appearance of the second sum somewhat. If b is located in the interior of the domain (i.e., not at the boundary), $\tilde{\varvec{M}}_{bca}$ reduces to ${\tilde{H}}_{bca}\varvec{I}$ with ${\tilde{H}}_{bca} \equiv H_{bca}/2$ so that the matrix–vector multiplication can be avoided.

4 Constitutive equations

We use the same constitutive equations as in our previous work [24], to which the reader is referred for further details. The mean (first Piola–Kirchhoff) stress was inferred from a neo-Hookean material model with strain energy of the form

$$\begin{aligned} U_a = \frac{\lambda }{2} \left( \ln J_a \right) ^2 - \mu \ln J_a + \frac{\mu }{2} \left( {{\,\mathrm{tr}\,}}\varvec{C}_a - 3 \right) \end{aligned}$$

(48)

where $\varvec{C}_a = \varvec{F}_a^{\mathrm {T}}\varvec{F}_a$ is the mean right Cauchy–Green deformation tensor for particle a, $J_a = \det \varvec{F_a}$ is the determinant of $\varvec{F_a}$ and ${{\,\mathrm{tr}\,}}\varvec{C}_a$ is the trace of $\varvec{C}_a$. The Lamé parameters $\lambda$ and $\mu$ were calculated from Young’s modulus E and Poisson’s ratio $\nu$ in a standard manner. The contact forces were derived from an elastic contact model with contact energy

$$\begin{aligned} U_{ab} = \frac{1}{2} K^{\mathrm {n}}_{ab} \left|\varvec{u}^{\mathrm {loc,n}}_{ab} \right|^2 + \frac{1}{2} K^{\mathrm {t}}_{ab} \left|\varvec{u}^{\mathrm {loc,t}}_{ab} \right|^2 \;. \end{aligned}$$

(49)

The normal ($K^{\mathrm {n}}_{ab}$) and tangential ($K^{\mathrm {t}}_{ab}$) contact stiffness were expressed as

$$\begin{aligned} K^{\mathrm {n}}_{ab} = \xi _{\mathrm {n}} \frac{E A_{ab}}{L_{ab}} \end{aligned}$$

(50a)

and

$$\begin{aligned} K^{\mathrm {t}}_{ab} = \xi _{\mathrm {t}} \frac{G A_{ab}}{L_{ab}} \end{aligned}$$

(50b)

where E is Young’s modulus, $G=\mu$ is the shear modulus, $A_{ab}$ is the initial area of the interface and $L_{ab} = \left|\varvec{X}_{ab} \right|$ is the initial distance between particle a and b. Finally, $\xi _{\mathrm {n}}$ and $\xi _{\mathrm {t}}$ are nondimensional parameters. Artificial viscosity was included in some simulations, in which case a viscous stress was incorporated as an addition to the elastic first Piola–Kirchhoff stress. This addition has the form $\varvec{P}^{\mathrm {visc}}_a = J_a \varvec{\sigma }^{\mathrm {visc}}_a \varvec{F}^{-\mathrm {T}}_a$ (see, e.g., [35]), where $\varvec{\sigma }^{\mathrm {visc}}_a$ is the viscous Cauchy stress for particle a. Assuming a homogenous material, the latter was calculated as [48]

$$\begin{aligned} \varvec{\sigma }^{\mathrm {visc}}_a = \rho \left( c_1 c_{\mathrm {p}} h + c_2 h^2 \left|{{\,\mathrm{tr}\,}}\varvec{d}_a \right| \right) \varvec{d}_a \;, \end{aligned}$$

(51)

where $\varvec{d}_a$ is the rate of deformation tensor for particle a, $\rho$ is the material density, $c_{\mathrm {p}} =\sqrt{(\lambda + 2\mu )/\rho }$ is the longitudinal wave speed and h is a characteristic size, here taken as the minimum length of the material branch vectors. Finally, $c_1$ and $c_2$ are two nondimensional constants.

5 Implementation details

Delaunay tetrahedralization and Voronoi tessellation were performed using TetGen (version 1.6) [62]. A standard leapfrog scheme was used to integrate the equations of motion in time, as is commonly done in SPH [50], and the velocity was calculated as described in [22] when damping was applied.

6 Numerical tests and examples

6.1 Patch test

Fig. 3

Geometry for the patch test. Particles are displayed as gray spheres and Voronoi cells are drawn in blue (faces) and black (edges) (color online)

Table 1 Results obtained from the patch test: Maximal errors (in the $L_2$ norm) in the force on or displacement of each particle

A patch test was used to assess the basic characteristics of the method. An irregular arrangement of $3 \times 3 \times 3$ particles was considered. The particles constituted a cube with side length $1\, \hbox {m}$, occupying the referential domain $0 \le X_1,X_2,X_3 \le 1\, \hbox {m}$. For illustrative purposes, the particles are displayed as gray spheres in Fig. 3 and the Voronoi cells formed from them and their ghost particles (not shown) are drawn in blue (faces) and black (edges). A linearly varying displacement was prescribed, of the form

$$\begin{aligned} \varvec{u} = \alpha \begin{bmatrix} 1X_1 + 2X_2 + 3X_3 \\ 4X_1 + 5X_2 + 6X_3 \\ 7X_1 + 8X_2 + 9X_3 \\ \end{bmatrix}\;, \end{aligned}$$

(52)

where $\alpha = {1\times 10^{-4}}$. The material parameters were $E ={1.0} \, \hbox {MPa}$, $\nu = 0.3$ and $\rho = {1.0\times 10^{3}}\,\hbox {kg/m}^{3}$ and the contact parameters were set to unity (i.e., $\xi _{\mathrm {n}}=\xi _{\mathrm {t}}=1$).

Following Taylor et al. [66], three different variants of the test were performed. First, the displacement was prescribed for all particles and force equilibrium was tested for each particle (test A). Second, the displacement was prescribed on all boundaries, and the displacement error was determined for each particle (test B). Third, the displacement was prescribed on the bottom face (i.e., for $X_3=0$) and the traction corresponding to the displacement field (52) was prescribed on all other boundaries (test C). When equilibrium solutions were sought (tests B and C), the displacements and/or tractions were gradually applied during $50\,\hbox {s}$ and damping was used. The obtained results are summarized in Table 1, in which the maximal errors (in the $L_2$ norm) in the force on or displacement of each particle are provided.

It is evident that all versions of the patch test are passed. (The error in test A is somewhat larger than those in tests B and C, since a minute error in displacement is translated into a larger error in force unless the material is very soft.) Satisfaction of test A demonstrates, firstly, that the expressions for the mean deformation gradient embodied in Eqs. (6) and (10) are exact for linear displacements and, secondly, that the Chen integration constraint [13] indeed is fulfilled. In essence, fulfillment of these requirements follows from the duality relation (8) and the fact that the sum of the gradient vectors over the first and second index vanishes, Eq. (13). Satisfaction of test B in addition shows that the stiffness is nonsingular, i.e., that no spurious zero-energy modes exist [65]. Finally, satisfaction of test C demonstrates that constant tractions can be prescribed exactly, as anticipated from the discussion following Eq. (42).

Fig. 4

Configurations used in the swinging cube test. The color of each particle represents the magnitude of its initial shear (von Mises) stress (color online)

Fig. 5

Convergence in the swinging cube test: Normalized displacement error (in the $L_2$ norm) vs. mean particle spacing

6.2 Swinging cube test

In this example, a cube with side length $L = 1\, \hbox {m}$ was considered, occupying the referential domain $0 \le X_1,X_2,X_3 \le 1\, \hbox {m}$. The normal motion was constrained on the boundaries at $X_1 = X_2 = X_3 =0$ (symmetric BCs), whereas the tangential motion was constrained for $X_1 = X_2 = X_3 =1 \, \hbox {m}$ (antisymmetric BCs). The initial displacement field $\varvec{u}_0$ was prescribed according to the following analytic solution [8, 59]

$$\begin{aligned} \varvec{u} = \cos ( \omega t ) \begin{bmatrix} U_1\sin ( k X_1 ) \cos ( k X_2 ) \cos ( k X_3 ) \\ U_2\cos ( k X_1 ) \sin ( k X_2 ) \cos ( k X_3 ) \\ U_3\cos ( k X_1 ) \cos ( k X_2 ) \sin ( k X_3 ) \end{bmatrix} \end{aligned}$$

(53)

which is valid in the linear regime for volume-preserving motions ($U_1 + U_2 + U_3=0$). Specifically, we let $U_1 = U_2 = {5.0\times 10^{-4}}\,\hbox {m}$ and $U_3 = -{1.0\times 10^{-3}}\,\hbox {m}$. Here, the angular velocity $\omega = \sqrt{3}\pi c_{\mathrm {s}}/(2L)$ with the transverse wave speed $c_{\mathrm {s}}= \sqrt{\mu /\rho }$ and the wave number $k = \pi /(2L)$. It can be noted that the investigated unit cube constitutes 1/8 of a bi-unit cube with all boundaries constrained in the normal direction only. The material parameters were $E = 17.0 \, \hbox {MPa}$, $\nu = 0.45$ and $\rho = {1.1\times 10^{3}}\,\hbox {kg/m}^{3}$ and the contact parameters were set to unity ($\xi _{\mathrm {n}}=\xi _{\mathrm {t}}=1$). No damping was used. This example is typically used to test the convergence of the solution [8, 59] and it was here also used to assess the boundary treatment (cf. Sect. 2.4). The four slightly irregular configurations displayed in Fig. 4 were considered, in which particles are colored according to the magnitude or their initial shear (von Mises) stress. The error of the numerical solution after ${5\times 10^{-3}}\,\hbox {s}$, which corresponds to about 1/6 of the period of oscillation, was benchmarked against the analytical result. The results are summarized in Fig. 5, which displays the normalized displacement error, measured in the $L_2$ norm, as a function of the mean particle spacing. It is evident that the displacement exhibits a quadratic convergence toward the correct solution, as expected for a second-order accurate method. This result is anticipated in the present context, since our Voronoi gradient estimate [Eqs. (6) or (10)] provides the material gradient. It deserves to be mentioned, however, that convergence issues have been identified for Voronoi gradient estimates on moving meshes [54] unless proper account is made for the change in geometry that occurs during each time step. In fact, the original spatial Voronoi gradient estimate derived by Springel [64], upon which our work is based, was abandoned in favor of a least-squares gradient estimate in the public release of the cosmological code AREPO [67].

Fig. 6

L-shaped block: Problem definition

Fig. 7

L-shaped block: Deformed shape at selected instants of time (color online)

6.3 L-shaped block

In this test, a free L-shaped block with dimensions provided in Fig. 6a was subjected to oppositely directed transient nominal tractions on two of its faces (shown in gray in the figure). Specifically, $\bar{\varvec{T}}_1 = -\bar{\varvec{T}}_2 = p(t) \times [150, 300, 900]^{\mathrm {T}} \,\hbox {N/m}^{2}$, where $p(t) = \max (2.5 - \left|kt-2.5 \right|,0)$ is a triangular impulse function (the rate constant $k = 1 \, \hbox {s}^{-1}$ has been included for dimensional consistency). The test was originally proposed by Simo [63] and has subsequently been used by many others ([2] and references therein). Its main purpose is to assess momentum preservation for $t>5\, \hbox {s}$ when no external forces are applied and, for this reason, the test was continued for an additional $50 \, \hbox {s}$. The material parameters were $E = 50.0 \, \hbox {kPa}$, $\nu = 0.3$ and $\rho = {1.0\times 10^{3}}\,\hbox {kg/m}^{3}$ and the contact parameters were set to unity ($\xi _{\mathrm {n}}=\xi _{\mathrm {t}}=1$). No damping was used. As shown in Fig. 7, the block starts to rotate and undergoes significant deformations as a result of the applied forces. The linear and angular momenta (about the origin) are provided in Fig. 8a. As expected, the components of linear momentum remain negligible throughout the test and the components of angular momentum increase in magnitude during the first $5\, \hbox {s}$ and thereafter stay constant. This claim is substantiated by the data presented in Fig. 8b, in which the change in linear momentum components from the start of the test and the change in angular momentum components from their value at the end of loading are displayed. Clearly, all momentum components can be considered to be conserved. This result is expected when the internal forces are calculated with Eq. (43) [but not with Eq. (41)], since the internal force is then derivable from a rotationally invariant potential energy.

6.4 Punch test

In this test, a rectangular specimen (width $1\, \hbox {m}$, height $0.5\, \hbox {m}$ and thickness $0.1\, \hbox {m}$) was considered. As illustrated in Fig. 9, a rigid punch indented the middle third of the top face (shaded in the figure). The velocity of the punch was $0.1\, \hbox {m/s}$ and it was assumed that friction was large enough to prevent any slip at the punch–specimen interface. The remainder of the top face was free. Symmetric BCs were enforced on all other boundaries (i.e., zero normal displacement). This test has previously been used to assess the performance of different formulations in the near incompressible limit (for $\nu \rightarrow 1/2$) [18, 45]. However, our objective here rather is to assess the performance of the proposed method in a compression-dominated problem, and therefore, a compressible material is considered. Specifically, the material parameters are $E = 1.0 \, \hbox {MPa}$, $\nu = 0.45$ and $\rho = {1.0\times 10^{3}}\,\hbox {kg/m}^{3}$ and the contact parameters are set to unity ($\xi _{\mathrm {n}}=\xi _{\mathrm {t}}=1$). Viscous damping was included in this example ($c_1=c_2=0.1$). Following [45], a discretization using $21 \times 11 \times 3$ particles was used. A regular particle arrangement was used in order to facilitate the identification of potential instabilities, which would be seen as irregular particle displacements and/or as hourglass patterns [26]. However, no sign of instability can be observed in Fig. 10, indicating that the contact forces, obtained from Eq. (46), imparted sufficient stabilization to the formulation. It is commonly observed that nodally integrated meshless methods exhibit severe pressure oscillations for highly constrained problems [18, 45]. However, no pressure oscillations are evident for this relatively compressible material, although a strong pressure gradient exists in the vicinity of the punch boundary. This is not surprising, since an analysis based on linear elasticity reveals that the pressure not only becomes infinite at this point but also exhibits an oscillatory behavior indicative of the breakdown of the linear theory [43, p. 49]. Note, however, that the described displacement-based method is not optimal in the near incompressible limit (when $\nu \rightarrow 1/2$).

Fig. 8

L-shaped block: (a) Components of linear and angular momentum (denoted by $p_1$, $p_2$, $p_3$ and $\ell _1$, $\ell _2$, $\ell _3$, respectively) and (b) magnitude of change in each momentum component from its value at the end of loading (color online)

Fig. 9

Punch test: Problem definition

Fig. 10

Punch test: Configurations for regular (a and b) and irregular (c and d) particle arrangements at 15 (a and c) and 30% (b and d) deformation (color online)

7 Conclusions

A Voronoi-based estimate of the mean deformation gradient has been derived and translated into a particle-based method for continua. The gradient estimate is expressed in terms of material gradient vectors, defined for each particle and its nearest neighbors, and has a structure that resembles strain estimates used in smoothed particle hydrodynamics and peridynamics. For each particle, the gradient vectors can be computed from the geometry of its material Voronoi cell (particle placement, face centroids and normals and cell volume). They can also be expressed in terms of the material gradient of the Voronoi cell volume. A decisive advantage of this Voronoi-based strain estimate over Delaunay-based estimates is that it is guaranteed to evolve smoothly when the reference state is updated. It is therefore expected to provide an important corner stone in future developments geared toward macroscopically consistent discrete method for granular materials. Moreover, the sum of the gradient vectors over either index vanishes, a fact that results in a formulation that not only is linearly complete but also satisfies the patch test when forces are derived from a discrete Lagrangian. Pairwise forces between particles, inferred from the local (nonaffine) deformation of each bond or contact, provide a physical stabilization. Procedures to enforce different types of boundary conditions in a consistent manner are provided. The presented numerical tests demonstrate that the formulation satisfies different versions of the patch test, exhibits a second-order convergence toward the correct solution and conserves linear and angular momenta in the absence of external forces and torques.

Appendices

Tensorial cross products

Although generalizations of the vectorial cross product to tensors have been discussed in textbooks [7, 40] and in recent scientific literature [8, 9], they may be less familiar to the reader. For our purposes, it is sufficient to note that the cross product between a second-order tensor $\varvec{T}$ and a vector $\varvec{v}$ produces a second-order tensor, denoted $\varvec{T} \times \varvec{v}$, defined so that the identity

$$\begin{aligned} ( \varvec{T} \times \varvec{v} ) \varvec{a} = \varvec{T}( \varvec{v} \times \varvec{a} ) \end{aligned}$$

(54)

holds for all vectors $\varvec{a}$. This definition is consistent with (and in fact follows from) the usual definition of the cross product between vectors, as can be seen by expanding $\varvec{T}$, $\varvec{v}$ and $\varvec{a}$ in an orthonormal Cartesian bases (i.e., $\varvec{T} = T_{ij} \hat{\varvec{e}}_i \otimes \hat{\varvec{e}}_j$, $\varvec{v} = v_{k} \hat{\varvec{e}}_k$ and $\varvec{a} = a_{\ell } \hat{\varvec{e}}_{\ell }$ where $\hat{\varvec{e}}_i$, etc., denote basis vectors). To prove Eq. (5) in the main text, we let the second-order tensor $\varvec{G}_a \times [ \hat{\varvec{N}} \times (\varvec{X}-\varvec{X}_a) ]$ operate on an arbitrary vector $\varvec{V}$, to obtain

$$\begin{aligned}&\{ \varvec{G}_a \times [ \hat{\varvec{N}} \times (\varvec{X}-\varvec{X}_a) ] \} \varvec{V}= \varvec{G}_a \{ [ \hat{\varvec{N}} \times (\varvec{X}-\varvec{X}_a) ] \times \varvec{V} \}= \nonumber \\&\varvec{G}_a \{ (\varvec{X}-\varvec{X}_a) (\hat{\varvec{N}} \cdot \varvec{V}) -\hat{\varvec{N}} [ (\varvec{X}-\varvec{X}_a) \cdot \varvec{V} ] \} = \nonumber \\&\{[\varvec{G}_a (\varvec{X}-\varvec{X}_a)] \otimes \hat{\varvec{N}} - (\varvec{G}_a\hat{\varvec{N}}) \otimes (\varvec{X}-\varvec{X}_a)\} \varvec{V} \end{aligned}$$

(55)

where the first equality follows from the definition (54), the second from the triple product expansion (‘BAC-CAB’ rule) for vectors and the third from the definition of the tensor product. Since the vector $\varvec{V}$ is arbitrary, Eq. (5) follows.

Gradient vectors as derivatives of Voronoi cell volumes

Fig. 11

Determination of directional derivatives of the Voronoi cell volume in directions (a) parallel and (b) perpendicular to the branch vector $\varvec{X}_{ab} = \varvec{X}_b - \varvec{X}_a$

Using a smoothed characteristic function of the Voronoi cells, Flekkøy et al. [21] and Serrano and Español [60] have provided elegant derivations of a number of Voronoi cell properties. Of particular relevance to this work are the derivatives of the Voronoi cell volume $V_a$ with respect to the coordinates of its defining points $\varvec{X}_b$, with $b \in {\mathcal {P}}_a$. These results can also be straightforwardly derived as follows. For $b\ne a$ (i.e., $b \in {\mathcal {P}}'_a$), it proves convenient to introduce a local coordinate system with origin at $(\varvec{X}_a + \varvec{X}_b)/2$, one axis ($\hat{\varvec{\zeta }}$) directed along the material branch vector $\varvec{X}_{ab} = \varvec{X}_b - \varvec{X}_a$ and the other two mutually perpendicular axes ($\hat{\varvec{\xi }}$ and $\hat{\varvec{\eta }}$) in the plane of the face $\partial {\mathcal {V}}_{ab}$, see Fig. 11. According to the definition of Voronoi faces, a change of $\varvec{X}_b$ in the normal direction $\hat{\varvec{\zeta }}$ by a small amount $\varDelta \zeta$ produces a translation of the face $\partial {\mathcal {V}}_{ab}$ in the same direction by an amount $\varDelta \zeta /2$ (Fig. 11a). Edge effects are of second order, and the change in volume of the Voronoi cell is obtained as $\varDelta V = A_{ab}\varDelta \zeta /2$. The directional derivative of $V_a$ with respect to $\varvec{X}_b$ in direction $\hat{\varvec{\zeta }}$, denoted by $D_{\hat{\varvec{\zeta }}} V_a(\varvec{X}_b)$, thus becomes

$$\begin{aligned} D_{\hat{\varvec{\zeta }}} V_a(\varvec{X}_b) = \frac{A_{ab}}{2} = \frac{A_{ab}}{L_{ab}} \times \frac{L_{ab}}{2} \;. \end{aligned}$$

(56)

A change of $\varvec{X}_b$ in the tangential direction $\hat{\varvec{\xi }}$ by a small amount $\varDelta \xi$ produces a rotation by an angle $\varDelta \xi /L_{ab}$ of the face $\partial {\mathcal {V}}_{ab}$ around an axis that is parallel to the $\hat{\varvec{\eta }}$ axis and passes through particle a (Fig. 11b). To the first order, the change in volume of the Voronoi cell can therefore be calculated as

$$\begin{aligned} \varDelta V = -\frac{\varDelta \xi }{L_{ab}} \int _{\partial {\mathcal {V}}_{ab}} \xi \, \mathrm {d}{A} = -\frac{\varDelta \xi }{L_{ab}} C_{\xi } A_{ab} \end{aligned}$$

(57)

where $C_{\xi }$ is the $\xi$ coordinate of the centroid of the face $\partial {\mathcal {V}}_{ab}$. Hence,

$$\begin{aligned} D_{\hat{\varvec{\xi }}} V_a(\varvec{X}_b) = -\frac{A_{ab}}{L_{ab}} \times C_{\xi } \;. \end{aligned}$$

(58)

An analogous calculation shows that

$$\begin{aligned} D_{\hat{\varvec{\eta }}} V_a(\varvec{X}_b) = -\frac{A_{ab}}{L_{ab}} \times C_{\eta } \;. \end{aligned}$$

(59)

Combination of Eqs. (56), (58) and (59) produces

(60)

Comparing this result with the definition (7) of the gradient vectors, one arrives at the interesting conclusion that

(61)

In addition

(62)

where the sum does not include particle a itself.

The contact force

The contact forces are obtained by differentiation of the pairwise interaction energy (34) according to Eq. (38b). It proves convenient to decompose this energy into contributions resulting from contact between internal (real) particles and between an internal and an external (ghost) particle. In this manner, one obtains

$$\begin{aligned} {\mathcal {V}}^{\mathrm {cnt}} = \frac{1}{2}\sum _{a,b} U_{ab} + \sum _{a} \sum _{b \in {\mathcal {E}}_a} U_{ab} \;, \end{aligned}$$

(63)

where the factor 1/2 is included because each pair is otherwise counted twice and where it is understood that $a \ne b$ in the first sum. A straightforward application of the chain rule shows that

(64)

The derivatives and are obtained from the material constitution; cf. Sect. 4. Moreover, the derivatives and equal $\varvec{I}$ if $b \in {\mathcal {I}}_a'$ and $\varvec{D}_{ab}$ if $b \in {\mathcal {E}}_a$; cf. Sect. 2.6. The task thus boils down to determining the derivatives and .

If $b \in {\mathcal {I}}_a'$, straightforward differentiation of the branch vector $\varvec{x}_{ab} = \varvec{x}_b - \varvec{x}_a$ produces

(65)

where $\delta _{ab}$ is the Kronecker delta. The result is less immediate if $b \in {\mathcal {E}}_a$, in which case we introduce the shorthand notation . When all displacement components are prescribed (i.e., for $b \in {\mathcal {E}}_a'$), $\varvec{D}_{ab}=\varvec{I}$ in Eq. (24). Hence, $\varvec{x}_{ab} =\bar{\varvec{x}}_{ab}$ and the derivative becomes

(66)

Otherwise (i.e., for $b \in {\mathcal {E}}_a''$), we find by differentiation of Eq. (24) that

(67)

where ${\bar{K}}_{abc}$ is defined as

$$\begin{aligned} {\bar{K}}_{abc} = K_{abc}' - 2\delta _{ac}\sum _{d \in {\mathcal {E}}_a'} K_{abd}' \;. \end{aligned}$$

(68)

In order to determine the derivative of $\varvec{y}_{ab}$, defined in Sect. 2.6, we introduce the vector $\varvec{z}_{ab} = \varvec{F}_a \cdot \varvec{X}_{ab}$. Since the material branch vector $\varvec{X}_{ab}$ is antisymmetric ($\varvec{X}_{ba}=-\varvec{X}_{ab}$), we find that $\varvec{y}_{ab}=\varvec{z}_{ab}-\varvec{z}_{ba}$ if $b \in {\mathcal {I}}_a'$ and that $\varvec{y}_{ab}=\varvec{z}_{ab}$ if $b \in {\mathcal {E}}_a$. Using Eq. (26), $\varvec{z}_{ab}$ can be expanded as

$$\begin{aligned} \varvec{z}_{ab} = \sum _{d \in {\mathcal {I}}_a} {\bar{H}}_{abd} \varvec{x}_d + \sum _{d \in {\mathcal {E}}_a} H_{abd} \varvec{x}_{ad} \end{aligned}$$

(69)

where ${\bar{H}}_{abd} = \varvec{X}_{ab} \cdot \bar{\varvec{B}}_{ad}/V_a$, $H_{abd}$ is defined in conjunction with Eq. (16) and where $\varvec{x}_{ad}$ is given by Eq. (24). Differentiation of the above equation with the help of Eqs. (66) and (67) produces

(70)

where the equivalence defines the second-order tensor $\varvec{M}_{abc}''$. Note that $\varvec{M}_{abc}''$ reduces to $H_{abc} \varvec{I}$ for internal particles [${\bar{H}}_{abc}=H_{abc}$ in this case; cf. Eq. (25)]. In summary, we can write

(71)

With these results in hand, the contact force is obtained from the chain rule, cf. Eq. (46) in the main text. The tensor $\varvec{M}_{abc}'$ does not appear in the final expression, since it enters in the form of the product $\varvec{D}_{ab}\varvec{M}_{abc}' = -2\delta _{ac} \varvec{D}_{ab}$ as a result of the orthogonality of $\varvec{D}_{ab}$ and $\varvec{I}-\varvec{D}_{ab}$.