Application and benchmark of SPH for modeling the impact in thermal spraying

Abstract

The properties of a thermally sprayed coating, such as its durability or thermal conductivity depend on its microstructure, which is in turn directly related to the particle impact process. To simulate this process, we present a 3D smoothed particle hydrodynamics (SPH) model, which represents the molten droplet as an incompressible fluid, while a semi-implicit Enthalpy-Porosity method is applied for modeling the phase change during solidification. In addition, we present an implicit correction for SPH simulations, based on well-known approaches, from which we can observe improved performance and simulation stability. We apply our SPH method to the impact and solidification of Al$_2$O$_3$ droplets onto a substrate and perform a comprehensive quantitative comparison of our method with the commercial software Ansys Fluent using the volume of fluid (VOF) approach, while taking identical physical effects into consideration. The results are evaluated in depth, and we discuss the applicability of either method for the simulation of thermal spray deposition. We also evaluate the droplet spread factor given varying initial droplet diameters and compare these results with an analytic expression from the previous literature. We show that SPH is an excellent method for solving this free surface problem accurately and efficiently.

1 Introduction

Thermal spraying is a coating technology where particles of a feedstock material are heated, fully or partially melted and accelerated to high speeds onto a substrate. Through the impact of many particles a coating is built up. As a coating technology, thermal spraying is divided into three major process variants: flame spraying, electric arc spraying and plasma spraying [1].

In our work, we look more closely at plasma spraying, which is characterized by particle velocities of up to v = $800\,\hbox {m s}^{-1}$ [2] and high plasma temperatures in the range of $T = 6000\,^{\circ }\hbox {C}$ to $T = 15{,}000\,^{\circ }\hbox {C}$, which are significantly above the melting temperature of any known material [1]. The injected particles are mostly in the size range of $d =20\,\upmu \hbox {m}$ to $90\,\upmu \hbox {m}$ [2]. As the particles spread upon impact, rapid solidification occurs with cooling rates in the range of ${\dot{q}}$ = $10^7\,\hbox {K s}^{-1}$ to $10^8\,\hbox {K s}^{-1}$ as a result of heat transfer from the liquid material to the underlying substrate and to the ambient atmosphere [3]. Thus, the particle deformation on the substrate, cooling, and solidification occur in rapid succession.

The properties of the coating, such as its durability or thermal conductivity, are directly related to its microstructure, which is in turn directly related to the particle impact process. Therefore, a detailed understanding of the dynamics of particle impact on the substrate is essential for better control of the coating build-up. The deposition of particles during plasma spraying can only be poorly observed experimentally, due to the fact that splat formation and solidification occur within a few microseconds [4]. Consequently, many studies have been devoted to numerical and analytical investigation of particle impact, splat formation, and solidification [5,6,7,8,9].

Apart from the simulation of the plasma jet and the heat transfer from the plasma to the particles, the impact of the melted particle onto the substrate and its subsequent deformation are of great interest.

Given this context, we present our contribution as the construction of a novel SPH model which heavily utilizes implicit solvers to great effect, and improves on both the simulation performance and stability. The novelty of our model comes from the unique combination of SPH models for the application to thermal spraying, as well as the implicit formulation of explicit models into a single unified implicit linear system. In this scope, we also propose implicit formulations for established SPH correction methods which aim to improve the physical accuracy. In order to better understand the capabilities of the SPH method for modeling droplet impacts, we quantitatively compare the performance of our own SPH implementation to the VOF method on Eulerian grids using Ansys Fluent for a highly simplified case. For this, we are able to show great agreement of the overall shape of the impacted droplet. Using our SPH method, we were also able to simulate the droplet in significantly higher resolution, while at the same time requiring a fraction of the computational cost.

Furthermore, we present and discuss SPH simulation results in terms of droplet spread factor with varying initial droplet diameters. For these simulations, we explicitly discretize the substrate and take into account the transient heat transfer between droplet and substrate as well as temperature-dependent material properties. Overall, we are able to show that SPH is a very suitable method for the simulation of droplet impacts in thermal spraying.

Finally, we plan to release the source code of this project as an addition to the already open-source SPlisHSPlasH [10] library. This may be very useful to engineers studying similar simulations, as the performance and stability improvements of using implicit solvers can result in faster iteration times.

2 Previous work

In the past, droplet impact simulations have often been performed with the Eulerian volume of fluid (VOF) method. The VOF method can be used for the simulation of the free surface interface between two or more immiscible fluids by tracking the volume fraction of each of the fluids in two- or three-dimensional meshes. However, in the process of particle impact a large deformation of the molten particle occurs, from spherical to a thin layer. Therefore, it requires a very fine, or spatially adaptive, mesh discretization over a large area of the simulation domain. While fine meshes require exponentially increasing computational resources, mesh adaptivity is very difficult to implement correctly and still incurs a noticeable performance penalty. Most of the computational cost of VOF algorithms is incurred by the cells that form the interfaces between different fluids [11].

Other than tracking the position of the free surface, the heat transfer and especially the effect of solidification strongly influences the dynamics of the particle impact process. A popular method to model the effect of solidification is the enthalpy-porosity method [12]. Here, the heat transfer is solved in the enthalpy formulation, with addition of a source term that is dependent on the solid fraction of the semi-solidified fluid in the so-called “mushy zone”, to account for the latent heat of melting and solidification. Furthermore, another related source term is added to the momentum equation to account for increased flow resistance of the fluid in the semi-solidified region, due to growth of dendritic structures. This momentum sink, also called Darcy-term, is dependent on the permeability, which in turn is also dependent on the solid fraction in the “mushy zone”.

Several works have applied the VOF method for modeling particle impact in the thermal spray process. Pasandideh-Fard et al. [13] developed a 3D model to simulate the impact and solidification of a molten droplet on a flat substrate by applying the fixed velocity approach for solidification, where the solid is defined as liquid with infinite density and zero velocity. Another example is Zheng et al. [14], who developed a 3D particle impact model during plasma spraying utilizing the momentum source method of Ansys Fluent for modeling the solidification.

While these studies helped to increase the understanding of the particle impact and solidification in thermal spraying, a lot of computational time was generally required. In previous works of the authors the particle impact and solidification was modeled using a modified momentum source approach [15] which was then applied to simulate multiple particle solidification [16]. The most recent work presents a calculation of the effective thermal conductivity using information of inter-splat gaps derived from a simulation of multiple splats of Al$_{2}$O$_{3}$ droplets [17]. However, while the experimental results showed the characteristic length of the gaps to be $<1\,\upmu \hbox {m}$, the simulation could only resolve gaps with a width of its cell size of $2.25\,\upmu \hbox {m}$. This was resolved by numerically smearing the particle boundaries in this model and then enabling an approximately correct calculation of the thermal conductivity. However, this was only an interim solution, not a physically correct representation of the problem.

Due to the high computational cost of VOF-based Eulerian approaches, there has been a range of works applying the smoothed particle hydrodynamics (SPH) method to the simulation of thermal spray deposition. Although the SPH method was originally introduced by Gingold and Monaghan [18] and Lucy [19] in the field of astrophysics, the method has already been used frequently for the simulation of the particle impact process. This is often due to the versatility regarding the simulation of changing domain topology, free surfaces as well as multiple phases.

Since the feedstock material in the thermal spray process consists of particles and at the same time the SPH method is based on discretization particles, first and foremost, the terms should be properly distinguished. For this reason, the term particle is from now on used for the SPH discretization particle of the numerical method, while the feedstock particle that is molten in the thermal spray process and projected towards the surface will be termed droplet.

Fang et al. [20] introduce many ideas for the SPH simulation of droplet spreading and solidification. They propose an improved pressure correction scheme and show simulations of droplets impacting on a solid substrate as well as similarities to some images obtained from experiments. In addition, for heat conduction, an artificial heat model based on internal energy is used. Particles are classified into liquid, melting and solid, and a source term in the momentum equation accounts for phase change. Results are then compared against an experiment.

A similar approach is pursued by Zhang et al. [21] without the pressure correction, but also considering melting of the substrate for high thermal conductivities, low thermal capacities and high droplet temperatures. However, a validation of the method was not performed.

Farrokhpanah et al. [22, 23] present a novel method for the simulation of latent heat in SPH with specific application to suspension plasma spraying, which is a variant of the thermal spray process. They use an explicit weakly compressible SPH approach with advected density, as well as an enthalpy-viscosity method to model the process of solidification.

Abubakar and Arif [24] introduce a hybrid approach for the simulation of spray deposition. The SPH method is used to model the dynamics of splat formation during the spray process, while the finite element method (FEM) is used in order to model the solidification and compute residual stresses. The results are validated qualitatively by comparison with experimental results in literature. While this approach is quite novel, it relies on a very complex system in which numerical errors can occur at many different places (especially during transfers between discretizations). A coupled Eulerian and Lagrangian approach is also pursued by Zhu et al. [25] where it is used in order to simulate spray deposition of semi-molten ceramic droplets.

Other relevant SPH works, especially regarding heat transfer, melting and solidification can be found in the simulation of arc welding processes [26,27,28]. Komen et al. [26] in particular also simulate the impact of molten droplets onto a substrate and investigate the effect on the weld pool, although the droplet impact velocities are significantly smaller and the droplet size is significantly larger than in thermal spraying.

3 Computational method

3.1 SPH discretization

In the following, we briefly outline our SPH discretization method of the Navier–Stokes equations for incompressible fluid flow. In general, SPH is a total Lagrangian discretization method which implies that fluid quantities are observed at positions which move along with the fluid. These discrete positions, or particles, are advected and tracked through time and carry associated field quantities with them. The SPH method uses a weighted interpolation, derived from the convolutional identity with the $\delta$-distribution, in order to compute unknown quantities and derivatives needed to solve partial differential equations (PDEs). An arbitrary scalar quantity $A_i = A(\varvec{x}_i)$ at particle position $\varvec{x}_i$ can be computed by weighted summation using

$$\begin{aligned} A_i = \sum _{j\in {\mathcal {N}}_i} V_j A_j W(\varvec{x}_i - \varvec{x}_j; h), \end{aligned}$$

(1)

where $W(\varvec{x}_i - \varvec{x}_j; h)$ is a compactly supported weighting function, the commonly used cubic-spline kernel function in our case, around particle i with smoothing length h and $\sum _{j\in {\mathcal {N}}_i}$ denotes a summation over the neighboring particles j of particle i, which lie within the compact support of W centered on particle i. Derivatives can easily be computed by differentiating Eq. (1) which shifts the derivative operator to the weighting function. When doing this, however, care has to be taken since the commonly used cubic-spline kernel does not have a smooth second derivative. For more information on derivatives, momentum conserving SPH sums, and SPH in general, the reader is referred to the works of Price [29] and Koschier et al. [30].

3.1.1 Incompressible fluid model

The equations typically used for the simulation of incompressible fluids are the continuity equation, Eq. (2), and the Navier–Stokes equation, Eq. (3):

$$\begin{aligned} \frac{D\rho }{Dt}&= 0 \quad \leftrightarrow \quad \frac{\partial \rho }{\partial t} = -\rho \nabla \cdot \varvec{v} \end{aligned}$$

(2)

$$\begin{aligned} \rho \frac{D\varvec{v}}{D t}&= -\nabla p + \mu \nabla ^2 \varvec{v} + \varvec{f}_{\hbox {ext}} + \varvec{f}_{\hbox {st}}. \end{aligned}$$

(3)

Here, $\rho$ denotes the fluid density (kg m$^{-3}$), $\varvec{v}$ the velocity (m s$^{-1}$), p the pressure (N m$^{-2}$), $\mu$ the dynamic viscosity (Pa s), $\varvec{f}_{\hbox {ext}}$ the external volumetric forces (N m$^{-3}$), e.g., gravity, and $\varvec{f}_{\hbox {st}}$ the force due to surface tension (N m$^{-3}$).

3.1.2 Pressure

The pressure force is computed using the divergence-free SPH (DFSPH) method as presented by Bender and Koschier [31], which is an implicit solver ensuring both constant density and a divergence-free velocity field, see Eq. (2). We have found that this method allows us to use larger time steps during simulation, in contrast to explicit pressure solvers which compute the pressure force using an equation of state (EOS), e.g., used by Farrokhpanah et al. [23] and described by Monaghan [32]. Also, recomputing the density (as is performed in DFSPH) in each time step avoids the possible loss of volume when advecting the local density using the continuity equation, Eq. (2). While implicit pressure solvers have been explored in related works, e.g., see Fang et al. [20], DFSPH also enforces a divergence-free velocity field which has been shown by Bender and Koschier [31] to improve the stability of the simulation.

3.1.3 Viscosity

The viscosity force is also computed implicitly using the model by Weiler et al. [33]. It is obtained by solving for accelerations $\varvec{a}_{\hbox {visc}}$ such that

$$\begin{aligned} \varvec{a}_{\hbox {visc}} = \frac{\varvec{v}_{\hbox {visc}}^{t+1} - \varvec{v}^t}{\varDelta t} = \nu \nabla ^2 \varvec{v}_{\hbox {visc}}^{t+1}. \end{aligned}$$

(4)

Discretizing this equation yields a system of linear equations for the velocity $\varvec{v}_{\hbox {visc}}^{t+1}$ which is then used to compute the resulting acceleration due to viscous forces $\varvec{a}_{\hbox {visc}}$ using the finite difference formula in Eq. (4). In general, the extensive use of implicit solvers enables the usage of larger simulation time steps without causing instabilities.

3.1.4 Surface tension

Surface tension computation in SPH is known to be a challenging problem, since it is very difficult to obtain a clear definition of the fluid surface. There exist formulations based on fluid surface curvature, often derived from the continuum surface force (CSF) model by Brackbill et al. [34], as well as formulations based on intermolecular forces. For our purposes, we have implemented the CSF model of Müller et al. [35] based on the model of Morris [36], where force $\varvec{f}_{i, \text {st}}$, curvature $\nabla ^2 c_i$ and surface normal $\varvec{n}_i$ are computed from a smoothed color field $c_i$:

$$\begin{aligned} c_i&= \sum _j \frac{m_j}{\rho _j} W_{ij}, \end{aligned}$$

(5)

$$\begin{aligned} \varvec{n}_i&= \sum _j \frac{m_j}{\rho _j} (c_j - c_i) \nabla W_{ij}, \end{aligned}$$

(6)

$$\begin{aligned} \nabla ^2 c_i&= -\sum _j \frac{m_j}{\rho _j} (c_i - c_j) \frac{2 ||\nabla W_{ij}||}{||\varvec{x}_i - \varvec{x}_j|| + \varepsilon }, \end{aligned}$$

(7)

$$\begin{aligned} \varvec{f}_{i, \text {st}}&= -\sigma \nabla ^2 c_i \frac{\varvec{n}_i}{||\varvec{n}_i||}. \end{aligned}$$

(8)

Here, $\sigma$ denotes the surface tension coefficient ($\hbox {N m}^{-1}$). The computation of the normals and especially the curvature is documented to be prone to errors due to particle disorder; however, we have not observed any significant instabilities in our simulations. This could be due to the extremely small time scale of our simulations as well as due to other forces being more dominant.

3.1.5 Solidification

Solidification is often considered to be one of the main determining factors of the dynamics of the thermal spray process. It depends on the splat thickness, the thermal conductivities of both the sprayed feedstock material as well as the underlying solid material, and the thermal contact resistance between the flattening droplet and the substrate. It directly affects the deformation behavior, the splat shape and the coating microstructure [2]. The fluid of the droplet is cooled upon contact with the wall and the subsequent solidification process is modeled by taking into account a Darcy term (momentum sink), after the well-known enthalpy-porosity method, for modeling the solidification of pure metals [37] and of binary alloys [38]. The latent heat of melting and solidification is neglected for the initial comparisons between our SPH model and Ansys to keep the comparison as simple as possible. However, as the heat transfer solver is formulated in terms of the enthalpy, it can be easily extended to include the latent heat, which is shown in the simulations presented in Sect. 4.2.

The considered Darcy term adds a deceleration to the Navier–Stokes equation which has a strong movement inhibiting effect on the fluid, once the temperature of the fluid becomes low enough. This so-called momentum sink accounts for the semi-liquid state in the so-called mushy zone, where already some nucleation and dendrite growth has occurred, thereby affecting the properties of the fluid. The effect is controlled by the liquid fraction $f_{\hbox {l}}(T)$, here modeled as a simple Heaviside function, Eq. (10), and by a morphological constant C:

$$\begin{aligned} \varvec{a}_{\hbox {porosity}}&= -\varvec{v} C f_{\hbox {l}}(T) \end{aligned}$$

(9)

$$\begin{aligned} f_{\hbox {l}}(T)&= {\left\{ \begin{array}{ll} 0 &{} T > T_{\hbox {l}}\\ 1 &{} T_{\hbox {l}}-\varDelta T_{\hbox {l}} \le T \le T_{\hbox {l}}\\ - &{} T \le T_{\hbox {l}}-\varDelta T_{\hbox {l}}. \end{array}\right. } \end{aligned}$$

(10)

In this equation, C has the unit (s$^{-1}$) which, intuitively, is related to the time span required during which the fluid will solidify completely, given that there are no other influences. In order to be able to capture the solidification process, regardless of simulation method, the maximum time step of the simulation should be selected to be smaller than $C^{-1}$. The liquidus temperature is denoted by $T_{\hbox {l}}$ and the temperature range of the mushy region by $\varDelta T_{\hbox {l}}$, such that the fluid is assumed to be completely solid as soon as $T \le T_{\hbox {l}}-\varDelta T_{\hbox {l}}$, see the last case of Eq. (10). The values for C are often very large, resulting in very large deceleration as soon as $T\le T_{\hbox {l}}$, so large in fact that simulations using explicit time stepping can become unstable. These instabilities are a result of the material solidifying in less than a single simulation step. This is remedied by constructing an algebraic equation which computes the acceleration using the projected velocity of the next time step as

$$\begin{aligned} \varvec{a}_{\hbox {porosity}}&= \frac{\varvec{v}^{t+1} - \varvec{v}^{t}}{\varDelta t} = -\varvec{v}^{t+1} C f_{\hbox {l}}(T)\end{aligned}$$

(11)

$$\begin{aligned} \varvec{v}^{t+1}&= \varvec{v}^t \frac{1}{1 + \varDelta t C f_{\hbox {l}}(T)}. \end{aligned}$$

(12)

The acceleration is then simply computed by inserting the expression for $\varvec{v}^{t+1}$

$$\begin{aligned} \varvec{a}_{\hbox {porosity}} = \frac{\varvec{v}^t}{\varDelta t}\left( \frac{1}{1 + \varDelta t C f_{\hbox {l}}(T)} - 1\right) . \end{aligned}$$

(13)

This semi-implicit formulation allows the usage of larger time steps in the simulation without causing instabilities, but comes at the cost of slightly dampening the effect. Additionally, if the time step is very large, the solidification may occur very quickly. Nevertheless, since the observed time intervals are often too large to observe the solidification process of single particles anyway, this is deemed to be an acceptable trade-off. The parameters used for the momentum sink are shown in Sect. 3.4.

3.1.6 Correction terms

In our implementation, we have found that it is also necessary to add correction terms, which improve the quality of SPH simulations. The first such term was documented by Monaghan [39] and reduces the interpenetration of particles by smoothing the velocity field while conserving linear and angular momentum, without adding dissipation. The acceleration of this correction, also sometimes called XSPH, is given by

$$\begin{aligned} \varvec{a}_{i,{\hbox {xsph}}} = - \frac{\alpha }{\varDelta t} \sum _{j\in {\mathcal {N}}_i} \frac{{\overline{m}}_{ij}}{{\overline{\rho }}_{ij}} (\varvec{v}_i - \varvec{v}_j) W_{ij}, \end{aligned}$$

(14)

where $\alpha$ denotes the (dimensionless) strength of this smoothing, $\overline{m_{ij}}$ the average mass between particle i and j and $\overline{\rho _{ij}}$ the averaged density. In the original work $\alpha = 1$ was proposed, yet we have found smaller values, in the range of 0.1 to 0.3, to also work very well.

The second correction addresses the issue of tensile instability at the surface of SPH fluids. When using a method which recomputes the density instead of advecting it, it occurs that the density estimate at free surfaces is erroneous due to missing particles and causes an uncontrollable artificial surface tension effect. This is solved in the DFSPH method by only considering “over”-pressures due to larger density values and clamping smaller densities to the rest density. This entirely removes the instability at the surface, but comes at the cost of reduced, non-surface tension, fluid cohesion. In order to restore fluid cohesion, a corrective force of the form

$$\begin{aligned} \varvec{a}_{i,{\hbox {cohesion}}} = -\gamma ^{\hbox {f}} \sum _{j\in {\mathcal {N}}_i^{\hbox {f}}} \frac{{\overline{m}}_{ij}}{{\overline{\rho }}_{ij}} (x_i - x_j) W_{ij}, \end{aligned}$$

(15)

is employed, where $\gamma ^{\hbox {f}}$ is a parameter controlling the strength of cohesion ($\hbox {N m}^{-1}$) and ${\mathcal {N}}_i^{\hbox {f}}$ denotes the neighborhood of fluid particle i within the same fluid phase.

Adhesion to other phases and boundaries is formulated analogously

$$\begin{aligned} \varvec{a}_{i,{\hbox {adhesion}}} = -\gamma ^{\hbox {b}} \sum _{j\in {\mathcal {N}}_i^{\hbox {b}}} \frac{{\overline{m}}_{ij}}{{\overline{\rho }}_{ij}} (x_i - x_j) W_{ij}, \end{aligned}$$

(16)

where $\gamma ^{\hbox {b}}$ is a parameter controlling the strength of adhesion ($\hbox {N\,m}^{-1}$) and ${\mathcal {N}}_i^{\hbox {b}}$ denotes the neighborhood of fluid particle i within the boundary phase. It should be noted that for the case that $\gamma ^{\hbox {b}} = \gamma ^{\hbox {f}}$ the net cohesive–adhesive force at the boundary is zero. Adhesion is therefore modeled by $\gamma ^{\hbox {b}} > \gamma ^{\hbox {f}}$ and repulsion by $\gamma ^{\hbox {b}} < \gamma ^{\hbox {f}}$. By design, this correction term only adds forces in regions with particle deficiency and is inspired by the work of Monaghan [40], yet instead of adding an additional repulsion term the attraction is first clamped by the implicit pressure solver and then reintroduced as cohesion and adhesion. A very similar cohesive force was also used by Becker and Teschner [41].

We note that due to the anti-symmetric nature of these formulations, they conserve angular and linear momentum. In order to further improve the stability and in order to be able to use larger time steps, we formulate these corrections implicitly in terms of velocity and incorporate them, together with the viscosity force, into a single linear system

$$\begin{aligned} \begin{aligned} \frac{\varvec{v}_i^{t+1} - \varvec{v}_i^t}{\varDelta t}&= \frac{\mu }{\rho _i} 2(d+2) \sum _{j\in {\mathcal {N}}_i} \frac{{\overline{m}}_{ij}}{\rho _j} \frac{\varvec{v}_{ij}^{t+1}\cdot \varvec{x}_{ij}}{||\varvec{x}_{ij}||^2 + 0.01 h^2} \nabla W_{ij} \\&\quad - \frac{\alpha }{\varDelta t} \sum _{j\in {\mathcal {N}}_i} \frac{{\overline{m}}_{ij}}{{\overline{\rho }}_{ij}} \varvec{v}_{ij}^{t+1} W_{ij} \\&\quad -\gamma ^{\hbox {f}} \sum _{j\in {\mathcal {N}}_i^{\hbox {f}}} \frac{{\overline{m}}_{ij}}{{\overline{\rho }}_{ij}} (x_i - x_j) W_{ij} \\&\quad -\gamma ^{\hbox {b}} \sum _{j\in {\mathcal {N}}_i^{\hbox {b}}} \frac{{\overline{m}}_{ij}}{{\overline{\rho }}_{ij}} (x_i - x_j) W_{ij}, \end{aligned} \end{aligned}$$

(17)

where $\varvec{v}_{ij} = \varvec{v}_i - \varvec{v}_j$, $\varvec{x}_{ij} = \varvec{x}_i - \varvec{x}_j$ and d is the number of spatial dimensions, i.e., $d=3$. This linear system is solved using the matrix-free conjugate gradient method.

We are not aware of any other works utilizing implicit solvers in SPH simulations to this degree. Doing this, we are able to observe a very significant performance improvement due to the ability of simulating with large time steps without causing instabilities.

Pseudocode of our full fluid solver is shown in Algorithm 1. It can be seen that the only explicitly computed component is the surface tension, while the pressure and remaining forces are independently implicitly integrated.

3.2 Heat transfer

Heat conduction is governed by the Fourier equation

$$\begin{aligned} \rho c_p\frac{D T}{D t} = \nabla \cdot \left( \lambda \nabla T \right) + {\dot{q}}''', \end{aligned}$$

(18)

where $\rho$ denotes the material density (kg m$^{-3}$), $c_p$ is the specific heat capacity (J kg$^{-1}$ K$^{-1}$), T is the temperature (K), $\lambda$ is the thermal conductivity (W K$^{-1}$ m$^{-1}$) and ${\dot{q}}'''$ is the contribution from volumetric heat sources (W m$^{-3}$). In all of our simulations, we set ${\dot{q}}''' = 0$, since we do not need any external heat sources. Instead of using the temperature as the main variable for heat transfer, we transform Eq. (18) using the relationship between specific enthalpy h (J kg$^{-1}$) and the temperature T

$$\begin{aligned} h(T) = \int _0^T c_p(T) dT, \end{aligned}$$

(19)

where $c_p$ may also be a function of temperature, taking into account, e.g., the latent heat of melting. Assuming that $c_p(T)$ is continuous results in a bijective function, such that h(T) as well as T(h) are well-defined. This results in the following equation which uses both the specific enthalpy h as well as the temperature:

$$\begin{aligned} \rho \frac{Dh}{D t} = \nabla \cdot \left( \lambda \nabla T \right) . \end{aligned}$$

(20)

The equation above is discretized using SPH and explicit Euler time integration, resulting in the following discrete equation for the fluid particle with index i

$$\begin{aligned} \rho _i \frac{h_i^{t+1} - h_i^t}{\varDelta t} = \nabla \cdot (\lambda \nabla T)_i^t. \end{aligned}$$

(21)

The discretization of the heat conduction term is given in the following equation:

$$\begin{aligned} \nabla \cdot (\lambda \nabla T)_i = \sum _{j\in {\mathcal {N}}_i}\frac{m_j}{ \rho _j}\frac{4\lambda _i\lambda _j}{\lambda _i + \lambda _j}(T_i - T_j)\frac{ \nabla _i W_{ij}\cdot \varvec{r}_{ij}}{||\varvec{r}_{ij}||^2}, \end{aligned}$$

(22)

as is also the case for other related work, e.g., Zhang et al. [21], and was initially proposed by Brookshaw [42]. It should be noted that $\lambda _i = \lambda (T_i)$ is generally a function of temperature and that $\varvec{r}_{ij} = \varvec{x}_i - \varvec{x}_j$ is the vector between the positions of particle i and particle j. Additionally, $\nabla _i W_{ij}$ denotes the gradient of $W_{ij} = W(\varvec{x}_i - \varvec{x}_j; h)$ with respect to the position of particle $\varvec{x}_i$.

Since heat can only be conducted within the material itself, the SPH formulation is adiabatic by construction. Finally, in order to reduce the computational requirements during simulation, the enthalpy is precomputed in terms of the temperature by integration of Eq. (19). Our heat solver algorithm is outlined in Algorithm 2, while the overall simulation pipeline is summarized in Algorithm 3.

3.3 Boundary conditions

Boundary contributions for all SPH terms are computed using the approach of Akinci et al. [43]. The only boundary present in our simulation is the substrate, which will be described further in Sect. 3.4. Using the approach of Akinci et al., the boundary is sampled using a single layer of particles on the surface of the boundary. The contribution of the boundary to the SPH summation of fluid particles can be generalized as

$$\begin{aligned} A_i = A_i^{\hbox {f}} + A_i^{\hbox {b}} = \sum _{j \in {\mathcal {N}}_i^{\hbox {f}}} V_j A_j W_{ij} + \sum _{j \in {\mathcal {N}}_i^{\hbox {b}}} V_j^{\hbox {b}} A_j^{\hbox {b}} W_{ij}. \end{aligned}$$

(23)

The superscript f indicates contribution from fluid particles, while b indicates contribution from boundary particles within the compact support of particle i. The volume of boundary particles is computed using

$$\begin{aligned} V_i^{\hbox {b}} = \frac{1}{\sum _{j\in {\mathcal {N}}_i^{\hbox {b}}} W_{ij}}, \end{aligned}$$

(24)

which is an SPH summation over the other boundary particles in the compact support of boundary particle i. The boundary volumes are incorporated into the summations of fluid particles by extending fluid quantities into the boundary region. This means for example using the rest density of the fluid to compute a mass from the boundary volume and utilizing this contribution for fluid density computations. Similar considerations can be made for all other cases, such as for the Fourier equation. The heat conduction term in Eq. (22) is extended by the following term for the boundary contribution

$$\begin{aligned} \nabla \cdot (\lambda \nabla T)_i^{\hbox {b}} = \sum _{j\in {\mathcal {N}}_i^{\hbox {b}}} V_j^{\hbox {b}} 2\lambda _i (T_i - T_j^{\hbox {b}})\frac{ \nabla _i W_{ij}\cdot \varvec{r}_{ij}}{\varvec{r}_{ij}^2}. \end{aligned}$$

(25)

This is equivalent to Eq. (22), when also using $\lambda _j^{\hbox {b}} = \lambda _i$ and prescribing the wall temperature $T_j^{\hbox {b}}$. This allows specifying a Dirichlet boundary condition on the substrate. According to Mostaghimi et al. [44] the estimated heat loss of the droplet to the surrounding gas is roughly three orders of magnitude lower than that of heat conduction into the substrate. Therefore, we assume the free surface of the droplet to be adiabatic, i.e., we neglect heat losses of the droplet into the surrounding gas for our current investigations.

3.4 Simulation domain

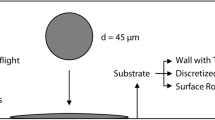
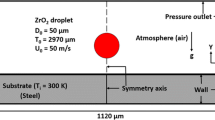
In the previous sections, we introduced our simulation model for droplet impact onto a substrate with solidification. Subsequently, we describe the simulation setup used to compare our SPH model with Ansys Fluent. Figure 1 shows the simulation domain for droplet impact. This includes the material properties, the initial droplet in-flight properties, the substrate wall properties and boundary conditions. The material properties of the ceramic droplet are listed in Table 1. Further, the simulation parameters in Ansys Fluent and for SPH are listed in Table 2.

Fig. 1

Schematic diagram of the simulation domain for the droplet impact

Table 1 Material properties of ceramic droplet and boundary conditions

Table 2 Simulation parameters

3.4.1 Ansys Fluent

A 3D thermal spray coating build-up model based on a previous publication of the authors [17] was created and implemented in Ansys Fluent. In this model, the impact of thermally sprayed ceramic droplets onto a flat substrate was simulated. A momentum source function was used to simplify the calculation of the solidification process, with parameters as shown in Table 2c. A laminar viscous model was used, and the energy solver was enabled. The dimensions of the spatial domain are $225\,\upmu \hbox {m} \times 225\,\upmu \hbox {m} \times 75\,\upmu \hbox {m}$, incorporating the droplet as well as a surrounding gaseous atmosphere which was assumed to be air. To shorten the computation time for the simulation of the impact of multiple droplets, a mesh edge length of $2.25\,\upmu \hbox {m}$ was chosen. The calculation mesh consists of 330,000 cells. The boundaries of the domain consist of an inlet for the droplet on top, with velocity $\varvec{v}_{p}= 200\,\hbox {m s}^{-1}$, the substrate as a free-slip wall at the bottom and outlets with pressure $p_{\hbox \mathrm{amb}}=101,325$ Pa and backflow total temperature $T_{\hbox {out}}=3000$ K. The interior domain is filled with air at $T_{\hbox {gas}}=2400$ K at the start of the simulation. The temperature of the substrate is set to $T_{\hbox {substrate}} = 300$ K. The free-slip boundary condition was applied for the contact between the droplet and the substrate, and a VOF approach was assumed for the calculation of the free surface of the ceramic droplet and the surrounding gas phase. Due to the rapid solidification resulting from the Dirichlet thermal boundary condition, the free-slip boundary condition appeared to be a reasonable assumption in our experiments. The numerical parameters of the simulation in Ansys Fluent are given in Table 2b. The simulations were performed using Ansys Fluent 2020 R2.

3.4.2 SPH

The same 3D thermal spray coating build-up model was created using our SPH method. The domain of the simulation model is shown in Fig. 2a. The numerical parameters for the simulation and for the momentum sink are each listed in Table 2a and c, respectively. The droplet has a diameter of $d = 62\,\upmu \hbox {m}$ and initial in-flight properties such as temperature of $T = 2500$ K and velocity of $v = 200\,\hbox {m s}^{-1}$. The droplet was discretized with particles with an individual radius of $r = 0.4\,\upmu \hbox {m}$ and consists of 238,310 particles. The substrate was modeled as a rigid body with a Dirichlet boundary condition for the temperature of $T_{\hbox {wall}} = 300$ K and a free-slip boundary condition for the momentum equation. The model was implemented in a custom branch of SPlisHSPlasH [10].

Fig. 2

Computational domain of droplet impact simulation

4 Results

In the following, we evaluate our SPH model in two different settings. First, we compare the results of our SPH model to the results obtained by a simulation using Ansys Fluent with the VOF method. For this, we consider simplified material parameters and boundary conditions in order to eliminate possible modes of deviation and inaccuracy in both methods. We first attempt to find sufficient discretization densities by conducting a mesh convergence analysis using the diameter of the splat as convergence indicator value. Additionally, we are able to show excellent agreement between the two methods, while our SPH method requires only a fraction of the computational cost for a higher density discretization.

Afterwards, we take into account temperature-dependent material properties, the latent heat of melting and the heat transfer into the substrate. With this, we evaluate the obtained splat shapes and spread factors of different diameter droplets and validate these results by comparison with an analytical expression.

Fig. 3

Convergence analysis of the simulation models in SPH and Ansys Fluent

4.1 Comparison to Ansys Fluent

Mesh convergence A sensitivity analysis of the mesh and particle resolution was conducted. The droplet impact simulation was run with different mesh sizes and particle resolutions. Both simulations were computed on 32 cores of a high-performance compute cluster. For the simulation in Ansys Fluent, the coarser, coarse, reference, and fine computational meshes consist of 83,349, 165,099, 330,000 and 540,000 cells, respectively. For the simulation using our SPH method, the coarser, coarse, reference, and fine particle resolution consist of 60,112, 119,129, 238,310 and 476,486 particles, respectively. The results in Fig. 3 show that as the resolution increases in SPH and Ansys Fluent, the diameters of the splats converge and remain nearly identical at resolutions above these values. In addition, the increasing resolution leads to a longer computation time. The computation time required to solve the simulation in Ansys Fluent from coarser to finer mesh resolution is about 5, 8, 20 and 30 min. On the other hand, SPH generally requires less computation time, which is about 1, 4, 5 and 20 min from coarser to finer particle resolution. Therefore, the reference mesh size of $2.25\,\upmu \hbox {m}$ and the reference particle radius of $0.4\,\upmu \hbox {m}$ are used in the further simulations for each method, respectively.

Fig. 4

Comparison of cross-sections of the droplet impact in SPH (left) and Ansys Fluent/VOF=0.5 (right), for several points in time

Results Figure 4 shows the droplet impact and the subsequent spreading of the droplet and solidification process modeled with SPH (left) and Ansys Fluent (right). The main dynamics of the process occurs at the shown three points in time. It can be seen that there is a relatively high agreement between both methods. However, it should be noted that the Ansys Fluent approach is performed with the VOF method for the modeling of the free surface of the liquid and therefore the presented shape represents the iso-surface of volume fraction 0.5 of the ceramic phase. While the overall resolution of the mesh is quite high, the mesh is relatively coarse in the region of interest, as shown in Fig. 5. As such, the dispersion of the fluid boundary surface can be considerable in the VOF method and the apparent area of the cross section appears somewhat smaller than the area of the cross section in the SPH method, although in both cases the total mass is conserved. Nevertheless, Fig. 6 shows the decrease in the ratio of mass enclosed by the VOF-0.5 contour with respect to the total fluid mass, as the mass disperses across a larger region. After impact at $t = 0.5\,\upmu \hbox {s}$, the mass share of the VOF-0.5 contour of the droplet decreases steadily and then levels out at $t = 1.4\,\upmu \hbox {s}$.

Fig. 5

Cross section of volume fraction of the ceramic phase in Ansys Fluent at $t = 1.0\,\upmu \hbox {s}$

Fig. 6

Mass share of the ceramic phase enclosed within the volume VOF$\ge 0.5$ of the total mass of the phase

Another peculiarity is the shape of the droplet in free flight. While in the SPH method, the shape is highly spherical, the VOF droplet appears to be elliptically compressed in the direction of flight in the VOF method. While the surrounding region of the droplet is filled with stagnant air, the droplet itself is immersed in an airstream of the impact velocity in order to avoid compression due to drag. As such, the slightly compressed shape can be explained by difficulties of achieving a perfect droplet shape using a transient inlet function.

Fig. 7

Top view of the simulated splats in SPH (bottom) and Ansys Fluent/VOF=0.5 (top) for several times. Times t = $1.5\,\upmu \hbox {s}$ and $t = 2.0\,\upmu \hbox {s}$ for Ansys Fluent are included for reference, although the resolution of the mesh is too low for the splat thickness to derive meaningful results

Figure 7 presents the top view for the droplet impact for several points in time. It can be seen that the shape of the splats in Fluent and SPH show an almost perfectly symmetric shape. Furthermore, it was observed that the splat seems to cool off faster in Fluent than in SPH. However, it should be noted here again, that the visible surface in Ansys Fluent corresponds to the volume fraction 0.5 of the ceramic phase. Additionally, for times $t \ge 1.0\,\upmu \hbox {s}$ the thickness of the splat became smaller than 5 to 6 mesh cells (see also Fig. 5), which is problematic in the VOF approach, as it disperses the boundary of the free surface and therefore requires several mesh cells for the transition from one fluid to the other. When the ratio of the number of cells in the transition region to the number of cells with volume fraction 1.0 becomes very large, it becomes more difficult to make accurate observations about the enclosed volume. This is due to the fact that observations about the enclosed volume become highly sensitive to the selection of the contoured volume fraction. It is therefore concluded that the results for $t \ge 1.0\,\upmu \hbox {s}$ should be considered with care, but they are included in this figure for reference.

The diameter and the height of the formed splat were compared for SPH and Ansys Fluent for several volume fractions of the ceramic phase (0.1, 0.5, 0.9) over time in Fig. 8. The droplet impacted the substrate at $0.5\,\upmu \hbox {s}$ and subsequently spread out, gaining in diameter and losing in height until it reached a steady state. When examining the diameter and height of the splat calculated with the VOF method in Ansys Fluent, it was found that the dimensions vary significantly depending on the volume fraction, which is in accordance with the observation shown in Fig. 5. Figure 8a shows that there is a good agreement in diameter for SPH compared with the VOF method. The diameter calculated with SPH lies between that of volume fraction 0.5 and 0.9. It should be noted that the parameter of the cohesion correction, see Sect. 3.1.6, was adjusted manually to reach this agreement. As discussed in the analysis of Fig. 7, the presented results of Ansys Fluent for $t \ge 1.0\,\upmu \hbox {s}$ do not have a sufficient mesh resolution, despite having a total of 330k cells, and are therefore not discussed further.

Fig. 8

Comparison of the diameter and height of the simulated splats over time for SPH and Ansys Fluent at several volume fractions (0.1, 0.5, 0.9) of the ceramic phase

The height, as shown in Fig. 8b, shows the same tendency for both approaches but a consistently smaller height was observed for all volume fractions of the ceramic phase in Ansys Fluent when compared to SPH. This is again consistent with the observed decrease in cross-section area in Fig. 5 and in mass share of the droplet in Fig. 6. However, since both the height as well as the diameter have a strong influence on the heat transfer from the splat to the substrate, this difference is of high significance. We attribute higher confidence to the SPH result regarding the height, because it does not suffer from the aforementioned volume dispersion.

Fig. 9

Comparison of the maximum, minimum and average radial and axial velocity of the droplet

Figure 9 shows a comparison of the simulated maximum, minimum and average velocity over time taken over a half space in radial (x) and height (y) direction of Ansys Fluent (at VOF$=0.5$) and SPH. As the droplet impacts the substrate at $t= 0.5\,\upmu \hbox {s}$, it can be seen in Fig. 9a that shortly after impact, a very strong increase in the maximum radial velocity from the initial maximum radial velocity of $0\,\hbox {m s}^{-1}$ occurs for both methods. This increase reaches roughly $350\,\hbox {m s}^{-1}$ for SPH, while the maximum radial velocity reaches nearly $600\,\hbox {m s}^{-1}$ in the case of Ansys Fluent. After this initial increase, the maximum radial velocity decreases towards zero for both cases for the time frame considered. Compared to this, the average velocity taken over a half space of both cases shows good agreement, with SPH exhibiting a consistently lower average radial velocity of the whole time frame considered. Furthermore, it can be observed that the minimum velocity in the Ansys Fluent case remains zero for the entire duration, while the minimum velocity in SPH becomes negative, with a small but distinct minimum of approximately $-40\,\hbox {m s}^{-1}$ at the moment of impact. During the time shortly after impact, the negative velocities in radial direction are somewhat contrary to the expected dynamic of the process, in which the fluid of the droplet would spread outward (positive velocity in radial direction) to form the splat. Upon further investigations, these particles are generally located near or on the cut plane where due to particle disorder some particles accelerating in negative $\times$ direction may appear.

In Fig. 9b, the maximum, minimum and average velocity in vertical direction are shown. Please note that the droplet moves towards the substrate, i.e., in negative y-direction. After impact at $t = 0.5\,\upmu \hbox {s}$, the maximum vertical velocity decays smoothly to zero in the case of Ansys Fluent. In contrast to this, the observed maximum vertical velocity shows a slightly different behavior in SPH. It has a peak of almost $-400\,\hbox {m s}^{-1}$ at the time of impact t = $0.5\,\upmu \hbox {s}$ before decreasing smoothly towards zero. The maximal vertical velocities of both cases for $t \ge$ $0.6\,\upmu \hbox {s}$ show an otherwise excellent agreement. Similarly, the minimum velocity drops rapidly after impact and remains at zero or close to zero in the case of Ansys Fluent, while the minimum velocity simulated in SPH shows a different post-impact behavior. At the time of the impact, the minimum velocity reaches an absolute minimum of roughly $50\,\hbox {m s}^{-1}$ before approaching zero.

It is noticeable that the peak of the maximum velocity precedes the negative peak of the minimum velocity. While this can be understood in terms of a rebound effect, the reason for the large spread between minimum and maximum velocity, as well as the deviation with Ansys Fluent of these observables will be discussed later in detail in the analysis of Fig. 10. Finally, the average velocities of both simulation methods have an excellent agreement over time, even better than was the case for the radial velocity in Fig. 9a. The droplet starts with a velocity of $-200\,\hbox {m s}^{-1}$ in both methods, then the average velocity in vertical direction decreases gradually after impact and reaches zero at $t = 1.0\,\upmu \hbox {s}$.

A more detailed analysis of the apparent disagreement noted in Fig. 9b can be seen in Fig. 10 for the moment of impact at t = $0.5\,\upmu \hbox {s}$. Figure 10 shows that a small fraction of particles at the side of the droplet have a very high vertical velocity of $-350\,\hbox {m s}^{-1}$ (color-coded in blue). Next to particles that are in contact with the wall, a small fraction of particles experience the rebound effect and their velocity reach nearly $50\,\hbox {m s}^{-1}$ (color-coded in red), before being counteracted by the bulk movement of the droplet. The main bulk of the particles has a velocity range from 0 to $-200\,\hbox {m s}^{-1}$, which corresponds to the in-flight velocity of the droplet and solidified particles. This observed peak of the velocity at the moment of impact is assumed to be the result of the sudden difference in velocity due to solidification of the fluid and the subsequent increase of local density and jump in pressure. However, this does not necessarily imply an un-physical result, but on the contrary it might actually capture the real conditions even more accurately than the Eulerian method in Ansys Fluent.

Note that the investigation of minimum and maximum velocities is difficult to compare quantitatively and are only discussed in order to give better insight into the dynamics of the process for each simulation method. While the actual values differ slightly, the overall trends visible in the minimum and maximum velocities are very similar for both methods.

Fig. 10

Axial velocity at the moment of impact; the in-flight velocity of the droplet is directed in negative y-direction. (Color figure online)

Table 3 Material properties of ceramic droplet and substrate. Note that the latent heat of melting and the specific heat capacity are included in the specific enthalpy

4.2 Simulation with substrate

We now investigate the spread factor of droplet impacts given different initial diameters. For this, we modify previous material properties to be temperature-dependent and to also take into account the latent heat of melting. In addition, we explicitly discretize the substrate and also introduce temperature-dependent material parameters. The modified material properties are summarized in Table 3, with the temperature dependent material properties being shown in Fig. 13. Note that only modified material properties are listed and that the cohesion $\gamma ^{\hbox {f}}$ and adhesion factors $\gamma ^{\hbox {b}}$ were adjusted to $\gamma ^{\hbox {f}} = 300\,\hbox {N m}^{-1}$ and $\gamma ^{\hbox {b}} = 300\,\hbox {N m}^{-1}$.

We simulate droplets of three different diameters: $30\,\upmu \hbox {m}$, $45\,\upmu \hbox {m}$ and $62\,\upmu \hbox {m}$. The droplets and substrate are discretized with a particle radius of $0.4\,\upmu \hbox {m}$. This resulted in a total of 1,908,591, 1,972,736, 2,119,910 particles for the three different droplet diameters, respectively. The computation time required to solve the simulation from the smallest to the largest droplet diameter was about 21, 51 and 53 min, respectively. The large number of particles in the simulation is mostly due to the discretization of the substrate, which may be further optimized in future work to reduce the computation time. The splat shapes of these droplets are shown in Fig. 11.

Fig. 11

Splat shapes of various initial droplet sizes after $2\,\upmu \hbox {s}$ of simulated time. From left to right: $62\,\upmu \hbox {m}$, $45\,\upmu \hbox {m}$, $30\,\upmu \hbox {m}$. The black circles denote the measured splat diameter. Best viewed zoomed in on the digital version

For all splats, movement has ceased after $2\,\upmu \hbox {s}$ of simulated time and a splat with splashes has formed, a process which is described in the literature for sufficiently large impact velocities [44]. The only remaining process is the solidification by heat conduction into the substrate. The speed of solidification is well-known to be governed by the thermal contact of droplet and substrate. This thermal contact is naturally modeled by our adhesion method which effectively governs the average distance of particles from the surface of the substrate and the particle density on the surface of the substrate. Higher adhesion values would result in a better thermal contact, while smaller values would inhibit thermal contact, which may be interpreted as describing the surface roughness of the sprayed surface on a macro-scale.

Fig. 12

Comparison of spread factors of various droplet sizes with maximum spread factors according to Passandideh-Fard et al. [45]

Fig. 13

Temperature-dependent material properties of ceramic droplet and substrate

Fig. 14

Ray-traced rendering of the droplet impact dynamic simulated with SPH

The maximum spread factor $\xi _{\hbox {max}} = \frac{D_{\hbox {max}}}{D_0}$ of the different initial droplet sizes $D_0$ equal to 30, 45 and $62\,\upmu \hbox {m}$ calculated by the SPH solver are shown in Fig. 12. These droplet diameters correspond to non-dimensional Reynolds numbers of 431, 646 and 891 for Re = $\frac{\rho V_0 D_0}{\mu }$, and Weber numbers 5,925, 8,888 and 12,245 for We = $\frac{\rho {V_0}^2 D_0}{\sigma }$. According to Passandideh-Fard et al. [45], since the Weber numbers are much larger than the Reynolds numbers, capillary effects can be neglected. Therefore, the maximum spread factor can be approximated as 0.5 Re$^{0.25}$. The maximal diameter of our simulations $D_{\hbox {max}}$ was evaluated by hand to $60\,\upmu \hbox {m}$, $100\,\upmu \hbox {m}$ and $142\,\upmu \hbox {m}$, respectively. The corresponding circles are shown in black in Fig. 11. The results obtained for the maximum spread factor with the SPH method show a good correlation ($R^2$ = 0.9565) with the analytical results approximated by Passandideh-Fard et al. [45] as well as with the results predicted by Farrokhpanah et al. [23] ($R^2$ = 0.9960). For a direct comparison of spread factors between our results and the analytical results see Fig. 12. We conclude that our model is able to reproduce the droplet spread factor increase that is known to occur with an increase in initial droplet diameter.

5 Discussion

In the previous section, we compared the results of our SPH simulation against a simulation using the commercial tool Ansys Fluent.

While in the real process, of course, the partial melting of the droplet and the heat transfer cannot be neglected, including the latent heat of melting and solidification, in this work, the main goal was to compare the performance of the fundamentally different numerical methods at the conditions present at the droplet impact in thermal spraying. It is therefore considered justified to initially keep the model as simple as possible, also neglecting most nonlinearities like temperature-dependent material parameters for the comparison.

We were able to use identical physical models and parameters for all phenomena, except for the corrective terms employed to improve the accuracy of the SPH simulation. The corrective factors were adjusted to be as small as possible in order to closely match the droplet dimensions computed by Ansys Fluent. From this, we were able to obtain excellent results and good agreement with the Ansys Fluent simulation.

In terms of computational efficiency, our proposed SPH method also compares very favorably to Ansys Fluent. In our SPH method, we used a total of 230k particles, while Ansys Fluent used a total number of 330k mesh cells. While it may seem at first that the discretization using SPH is coarser, the actual discretization density in the region of interest, i.e., in the droplet, was $\sim 2.8^3 \approx 22$ times higher than the discretization density used by Ansys Fluent, whose mesh edge-length was $2.25\,\upmu \hbox {m}$ which equated to 2.8 times the particle diameter of $0.8\,\upmu \hbox {m}$. At the same time, our SPH method was able to finish the simulation in roughly 5 min, while Ansys Fluent required roughly 20 min. This is a remarkable result, as it allows a significant refinement in the region of interest, while reducing the simulation time by a factor of 4. All the more interesting are the scaling implications for the simulation of multiple droplet impacts. The increased performance allows for faster iteration times when simulating multiple droplets as well as significantly more accurate resolution of gaps in the coating on the scale of $< 1\,\upmu \hbox {m}$, than was possible before by Bobzin et al. [17].

While a large part of the SPH code is already well-optimized, there are also some simple optimizations in reach that could further improve the SPH simulation performance.

We have also shown in our evaluations that the selection of the liquid fraction for contouring of the ceramic phase has a very significant impact on droplet diameter, but especially the droplet height. This has to do with the dispersion of the liquid surface that is ever-present for FVM-simulations using the VOF approach and adds an additional restriction on the mesh resolution. Using our SPH method, we were able to completely avoid the issue of dispersion and obtain a high-resolution simulation with a clearly defined surface. A ray-traced rendering of a surface reconstruction of the SPH particle data is shown in Fig. 14.

Finally, we extended our SPH simulations to explicitly discretize the substrate and to take temperature-dependent material parameters into account. Using this setup, we simulated three droplet impacts of different initial diameters and were able to show good agreement of the simulated spread factor when compared with the analytical expression proposed by Passandideh-Fard et al. [45].

6 Conclusion

In this article, we have shown that it is possible to simulate a molten droplet impact of the thermal spray process using nearly identical physical parameters in an SPH discretization as well as an FVM (finite volume method) discretization in Ansys Fluent. We were able to perform a quantitative analysis of the simulations by considering droplet height, diameter and velocity distribution over time. All of these showed good agreements, while the few dissimilarities were isolated and explained.

We introduced a novel SPH model which uses implicit integration for all forces except surface tension. Because of this, our simulations remain stable for a wide range of large time steps. We were also able to show that our SPH method is a very efficient and accurate alternative to the commercial FVM method of Ansys Fluent. Our SPH method is able to have a higher discretization density in the region of interest while only requiring a quarter of the simulation time.

As a next step, we can build upon this work by considering multiple droplets of varying size and velocity. When considering multiple droplets, the gaps in the coating may also be evaluated to a higher degree of accuracy than was previously possible. A further extension could enable the simulation of multiple, only partially melted droplets of both varying size as well as varying ratio of solid material at the core. Furthermore, the consideration of rough surfaces and resulting contact angles could also be interesting for future work.