Abstract
Friction stir extrusion (FSE) is a novel solid-phase processing technique that consolidates and extrudes metal powders, flakes, chips, or billets into high-performance parts by plastic deformation, which has the potential to save substantial processing time and energy. Currently, most studies on FSE are experimental and only a few numerical models have been developed to explain and predict the complex physics of the process. In this work, a meshfree simulation framework based on smoothed particle hydrodynamics (SPH) was developed for FSE. Unlike traditional grid-based methods, SPH is a Lagrangian particle-based method that can handle severe material deformations, capture moving interfaces and surfaces, and monitor the field variable histories explicitly without complicated tracking schemes. These aspects of SPH make it attractive for the FSE process, where in situ evolution of field variables is difficult to observe experimentally. To this end, a 3-D, fully thermomechanically coupled SPH model was developed to simulate the FSE of aluminum wires. The developed model was thoroughly validated by comparing the numerically predicted material flow, strain, temperature history, and extrusion force with experimental results for a certain set of process parameters. The validated SPH model can serve as an effective tool to predict and better understand the extreme thermomechanical conditions during the FSE process.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Friction stir extrusion (FSE) is a solid-phase processing technique that is used to consolidate and extrude high-performance wires, rods, and tubes from metal powder, chips, flakes, or a solid billet in a single step. The process was invented at The Welding Institute (Cambridge, UK) and patented by Thomas et al. [1] in the early 1990s. Subsequent development at Pacific Northwest National Laboratory (PNNL) has led to patents for using FSE to extrude tubes [2]. FSE process is nominally solid state, and the maximum temperature is self-limited by the loss of flow stress as the extruded material approaches its melting point. Generally, no auxiliary heating is required and only the material near the interface between the rotating die and the charge is heated due to material plastic deformation and friction, which reduces the energy and time required for extrusion. The enhanced microstructure and material mixing inherent to FSE yield products with much better ductility and energy absorption capacity than those made by conventional extrusion [3]. These advantages have spurred a rapid development in FSE in recent years, and FSE has shown tremendous potential in industries such as automotive, aerospace, advanced manufacturing, and metal waste recycling.
FSE is a thermomechanically coupled process involving severe shear plastic deformation, material mixing, and heat generation from plastic deformation and friction. Experimentally measuring the thermomechanical behaviors (e.g., material flow, strains, strain rates, and temperatures) of the processed material is challenging, expensive, or impossible. Thus, numerical simulation is necessary to obtain a better understanding of the complex physics and material behaviors during FSE. Due to the associated computational challenges and cost, few validated models for FSE are available in the literature. Behnagh et al. [4] proposed a multistep 2-D coupled Eulerian–Lagrangian (CEL) model in Abaqus to simulate the processing temperatures in FSE of magnesium chips and consequent distributions of grain size and microhardness in the material with different process parameters. Baffari et al. [5] developed a 3-D, Lagrangian, thermomechanical model in Design Environment for FORMing (DEFORM)® software to simulate FSE of AZ31 milling chips. They showed that the distributions of material strain, strain rate, microstructure, and temperature can be predicted well by the model. Zhang et al. [6] proposed a 3-D CFD model in the ANSYS Fluent for FSE of AA6061 wires with consideration of both heat transfer and material flow. Recently, Karwa [7] developed a finite element method (FEM) model in FORGE NxT® for FSE, and comprehensive studies were carried out on the simulation results to analyze all aspects of the FSE process.
As a solid-phase processing similar to FSE, friction stir welding (FSW) [8] has been intensively investigated in the past few decades, and the relevant simulation approaches for FSW may be applicable to FSE. The existing FSW models can be categorized into fluid-based and solid-based approaches, and their detailed numerical comparison was investigated by Bussetta et al. [9, 10]. In the fluid-based approach, the workpiece is considered as a non-Newtonian fluid due to the large material deformation that occurs in FSW, and the problem is solved using the principles of computational fluid dynamics (CFD). After Ulysse [11] first developed a CFD model for FSW using the fluid dynamics analysis program FIDAP, many studies were carried out based on fluid-based approach. Seidel and Reynolds [12] proposed a 2-D thermal model based on non-Newtonian flow around a circular cylinder. By assuming full sticking contact condition between the tool pin and welded zone, they observed significant vertical material mixing occurred during FSW. Colegrove and Shercliff [13] developed a 3-D thermal and material flow model for FSW of AA7449 thick plate in ANSYS Fluent, and the developed model was used to investigate different pin profiles and rotational speeds on the pin traversing force. Bastier et al. [14] conducted a two-step simulation of the steady state phase of FSW, in which the thermomechanical behavior of FSW was first studied using a CFD model, and the residual stresses induced by the process were studied in the second step. Albakri et al. [15] proposed a 3-D, thermomechanical CFD model for FSW of AZ31. The flow stress constitutive relation was experimentally corrected which yields more consistent temperature, material flow, and strain rate predictions. Despite its success in predicting experimentally validated quantities during FSW, one issue about the fluid-based approach is that it cannot include material hardening, because it assumes the workpiece as a non-Newtonian fluid with an effective viscosity. Moreover, the material elastic strains are assumed to be negligible and are ignored. This is valid for FSW but may lead to inaccurate elastic stage, extrusion force, and pressure predictions in FSE. On the other hand, the solid-based approach is based on the principles of computational solid mechanics (CSM), which allows the inclusion of material strength, elasticity, hardening, and strain rate dependence in the formulation. The solid-based approach also allows the modeling of complex contact conditions that exist at the interface of the workpiece and tool. The existing solid-based models for FSW include Lagrangian model and Eulerian model. Jain et al. [16] proposed an implicit Lagrangian model to simulate the plunging, dwelling, and welding stages of a FSW process. Zhang and Zhang [17] established a Eulerian model for FSW which addressed the large material deformation issue without remeshing. To balance the drawbacks of the Lagrangian and Eulerian finite element simulations, arbitrary Lagrangian Eulerian (ALE) model and CEL model have been applied to FSW problems to avoid the need for remeshing to handle large deformations in the stirred zone and describe the history of field variables more accurately. For example, Assidi et al. [18] implemented a thermomechanical ALE model for FSW process in the Forge3® finite element software. The Norton’s friction model was used for the contact between the tool and work piece, which provides good predictions of welding forces. Dialami and coworkers proposed an apropos kinematic simulation framework (ALE/Eulerian/Lagrangian) for FSW [19,20,21] as well as many enhancements to the proposed framework [22], such as a two-stage speed up strategy [23], subgrid scale stabilized mixed \({\mathbf {v}}/p\) formulations to avoid numerical locking and oscillations [24], and material flow tracing method [25]. Dialami et al. also presented a local-global strategy to predict residual stresses during FSW process [26]. Gupta et al. [27] developed a CEL model in Abaqus to predict weld interface and temperature in the friction stir scribe joining of dissimilar materials. More recently, Robe et al. [28] developed a R-ALE FEM approach to simulate heat transfer during FSW of AA2xxx and AA7xxx joint.
All the above-mentioned models for FSW and FSE were belonged to grid-based methods, where the local approximation of functions and their derivatives for solving the governing partial differential equations (PDEs) is based on a predefined grid, mesh, or stencil. Unlike the grid-based methods, SPH is an Lagrangian particle method first invented by Lucy [29] and Gingold and Monaghan [30] for astrophysics simulations. The general idea of SPH is to approximate a continuous field using a set of kernel functions centered at discrete particles, which carry the physical properties of the system [31]. Because no grid or mesh is needed to construct the set of algebraic equations with nodal unknowns for the field variables, SPH is capable of handling extremely large material deformations and mixing, which would cause severe mesh distortion issues in grid-based methods. The particle representation in SPH also enables a natural description of material interfaces, free surfaces, and moving boundaries during the simulation process, which is a challenging task for grid-based numerical methods. Furthermore, the Lagrangian nature of SPH allows for explicit tracking of material field variables. Over the past three decades, SPH has been mainly developed and applied to CFD simulations and thermal problems [32]. Libersky and Petschek [33] first used SPH to solve a solid mechanics problem based on the elastic–perfectly-plastic material constitutive model. Since then, interest has grown in applying SPH to a variety of solid mechanics problems. For instance, Gray et al. [34] addressed the tensile instability issue in SPH by introducing an artificial stress to the principal stresses. The improved SPH model was applied to elastic dynamics problems such as oscillating beams, colliding rings, and brittle solids. Gray and Monaghan [35] introduced a SPH formulation for elasticity problem to predict the stress fields and brittle fracture caused by stress concentration. It was found that SPH is a suitable tool for modeling damage and fracture due to its meshless nature. Cleary et al. [36] applied SPH to a 2-D metal forging problem with AA6061, and it was shown that the very large plastic material deformation during forging process can be well handled by SPH. Ba and Gakwaya [37] proposed a total Lagrangian SPH formulation for thermomechanical problems under large deformation. The effectiveness of the developed model was tested on a high velocity Taylor bar impact problem and hot forging problem.
As an ideal method to simulate solid-phase processing problems, SPH was first used to predict the material flow and temperature in FSW by Tartakovsky et al. [38] using the fluid-based approach. Later, Bhojwani [39] implemented solid-based SPH in the LS-DYNA program for FSW. In this work, only stress and strain fields were represented, using the Johnson–Cook constitutive law for the stress flow. The heat generation and material thermal softening were not considered. Pan et al. [40] predicted the temperature, grain size, microhardness, and texture evolution during FSW using a 3-D fluid-based SPH model. Fraser et al. [41] developed a robust and efficient SPH code, SPHriction-3D, for finding the optimal FSW process parameters. A coupled, thermomechanical, solid-based SPH model was implemented to predict the temperature, stress, strain, damage, and defect formation during the process. Ansari and Behnagh [42] developed a thermomechanical SPH model in Abaqus to simulate the plunging phase of FSW. More recently, Stubblefield et al. [43] created a fully thermomechanical coupled SPH approach for additive friction stir-deposition (AFS-D) process. As to work using SPH to simulate FSE, no studies have apparently been published yet.
In this study, a 3-D, thermomechanically coupled, solid-based SPH model is proposed to simulate FSE of aluminum wire from a billet. Johnson–Cook model is utilized to describe the thermo-viscoplastic behavior of the billet material during FSE, and Coulomb–Tresca friction law is used to describe the contact condition between the die tool and billet. Heat is generated from both the plastic deformation of the bulk material and the frictional sliding at the interface between the tool and billet. The evolutions of the material flow, strain, temperature, and extrusion force were predicted to gain a better understanding of the extreme thermomechanical conditions during the FSE process. The proposed model is thoroughly validated against the experimental observations for different sets of processing parameters. The remainder of this paper is outlined as follows: Sect. 2 describes the experimental procedure of FSE. The thermomechanical SPH model, together with the governing equations and constitutive model, is presented in Sect. 3. The model setup is detailed in Sect. 4. The numerical results are presented, experimentally validated, and discussed in Sect. 5. Finally, conclusions and remarks are drawn in Sect. 6.
2 Experimental procedure
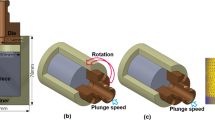
In this study, the FSE process was performed by a one-of-kind Shear Assisted Processing and Extrusion (ShAPE) machine designed by PNNL. Figure 1a shows the schematic representation of the FSE apparatus, which includes a cylindrical die tool with a flat face and a central orifice (Fig. 1b), a ring-shaped container for the billet, and a backing block at the billet end. The billet ring was placed in a larger water-cooled container. As the die tool rotates and advances, high shear and compressive forces are applied to the billet, plasticizing and generating heat from both friction and plastic deformation to soften the billet material, which is then extruded through the orifice of the die to form a wire, as shown in Fig. 1d.
A flat-face die fabricated from H13 tool steel with a 100:1 extrusion ratio (defined as the ratio of the cross-sectional area of the billet to that of the extruded wire) was used to extrude 2.54 mm diameter wire from a 25.4-mm-diameter cylindrical billet of AA1100-O. A marker insert technique was used to visualize the material flow in the wire. Specifically, 2.54 mm diameter AA2050-O wires were inserted into the center and at 1/3 of the radius (1/3r) from the center of the billet, as shown in Fig. 1c. The marker wires extended completely through the billet longitudinally. Constant die rotational and advance speeds were applied in this process, resulting in a constant extrusion speed with varied extrusion force. The die rotational and advance speeds used in the experiment are shown in Table 1, along with the final extruded wire lengths for each case. The extrusion force, die position, torque, and power were recorded by the ShAPE machine. A K-type thermocouple was placed 0.5 mm below the die face and 5 mm from the die central axis through a predrilled hole to measure the processing temperature of die face. After extrusion, the produced wires were sectioned transversely at different locations. The cross sections of the wire were ground, polished, etched, and imaged by optical microscopy to show the distribution of the marker wire at different locations along the wire. The strains at 1/3r of the wire cross section at the sectioned locations were estimated based on the spiral morphology of the 1/3r marker wires at those locations. The methodologies used for marker wire insertion and strain calculation can be found in greater detail in Li et al. [44].
3 Model description
3.1 Smoothed particle hydrodynamics (SPH) method
In SPH, a continuous function \(f(\varvec{x})\) and its spatial derivative \(\nabla \cdot f(\varvec{x})\) at point \(\varvec{x}\) in a continuous domain \({\Omega }\) can be approximated as \(\langle f(\varvec{x}) \rangle \) and \(\langle \nabla \cdot f(\varvec{x}) \rangle \), respectively, by a convolution integral based on the information of its neighboring particles as follows:
where \(W(\varvec{x}-\varvec{x}',h)\) is the kernel function in terms of the spatial distance between the function evaluation point \(\varvec{x}\) and the interpolation point \(\varvec{x}'\), and the smoothing length h defines the support domain of the kernel function. A h value between 1.05 and 1.3 is typically suggested, \(h=\) 1.2 is used in this study. The kernel function W should satisfy unity, support compactness, positivity, the Dirac delta function property, and smoothness conditions [32]. Among various kernel functions, the cubic B-spline kernel [45] is used in this study, which can be expressed as:
where R is the relative distance between two particles \(\varvec{x}\) and \(\varvec{x}'\), \(R=r/h=|\varvec{x}-\varvec{x}'|/h\), with r denoting the distance between the two points. The coefficient \(\alpha _{d}={3}/(2\pi h^3 )\) is defined in 3-D space. The definition of \(W=0\) when \(R\ge 2\) in Eq. (3) is to satisfy the support compactness condition. Therefore, the support domain with nonzero kernel function can be defined as \(\kappa h\), where \(\kappa \) is a constant related to the smoothing function for a particle at \(\varvec{x}\). The gradient of the cubic B-spline function can be expressed as:
In SPH, the continuous domain \({\Omega }\) of interest is discretized by a finite number of particles located at \(\varvec{x}_i(t), i\in {1,2,..,N}\). Each particle i carries unique physical properties such as density, velocity, stress, and temperature. These particles can be used not only to represent the field properties of the domain, but also for numerical integration, differencing, or interpolation. Now the continuous form of Eqs. (1) and (2) can be written in quadrature formulas as:
where \(N_i\) is the number of particles within the support domain of W at particle i and \(m_j\) and \(\rho _j\) are the mass and density of particle j. \({m_j}/{\rho _j}\) defines the “weight” of particle j in the quadrature. A schematic concept of a 2-D discrete particle approximation in SPH is shown in Fig. 2.
3.2 Governing equations
In this study, the billet is considered as a thermo-elastoplastic solid. Therefore, the billet material deformation is governed by the equations of mass, momentum, and energy conservation:
where \(\rho \) is the solid density, t denotes the time, \(\varvec{\sigma }\) is the Cauchy stress tensor, \(\varvec{v}\) and \(\varvec{b}\) are the velocity and external force vectors, respectively, \(C_p\) denotes the specific heat capacity, T is the temperature, \(\dot{q}\) is a heat source and sink term that describes the heat generation and loss in the system, \(\nabla \) is the spatial gradient operator, and \(\nabla \cdot \) denotes the spatial divergence operator. With the SPH kernel and particle approximation shown in Sect. 3.1, the three conservation equations can be written in discrete form and then solved for the unknowns at each discrete particle.
In the FSE process, heat is generated from two sources: (1) frictional sliding energy at the billet and the die tool interface and (2) mechanical work caused by the plastic deformation of the billet material. The primary heat sinks are the mass of the apparatus pieces and the active water-cooling system outside the billet container. The total heat source and sink term in Eq. (9) is then comprised of plastic work \(\dot{q}_\mathrm{p}\), frictional sliding energy \(\dot{q}_\mathrm{f}\), and surface convection \(\dot{q}_\mathrm{c}\) as follows:
Note that all the quantities, coordinates, and derivatives in Eqs. (7)–(10) are represented in the Lagrangian reference frame, making the SPH method a truly Lagrangian particle method.
3.3 Material constitutive model
The thermo-elastoplastic flow behavior of the AA1100-O billet is modeled using a Johnson–Cook (J–C) constitutive relation [46], which is expressed as follows:
where \(\sigma _\mathrm{f}\) is the flow stress, \(\varepsilon _{\mathrm {eff}}\) is the effective plastic strain, \({\dot{\varepsilon }}={\dot{\varepsilon }}_{\mathrm {eff}}/{\dot{\varepsilon }}_0\) is the normalized effective plastic strain rate, and \({\dot{\varepsilon }}_{\mathrm {eff}}\) and \({\dot{\varepsilon }}_0\) denote the effective plastic strain rate and reference total strain rate (typically 1.0 \(\mathrm{s}^{-1}\)), respectively. A, B, C, n, and m are material parameters: A is the initial yield stress, B and n are the strain hardening constants, while C denotes the material sensitivity to plastic strain rate. \(T^*=(T-T_\mathrm{r})/(T_\mathrm{m}-T_\mathrm{r})\) is the homologous temperature: \(T_\mathrm{r}\) is the reference temperature at which the material parameters are evaluated, \(T_\mathrm{m}\) is the material solidus temperature, and T is the instantaneous temperature. The terms in the first and second sets of parentheses in Eq. (11) represent the strain and strain rate hardening effects on the flow stress, whereas the term in the third set of parentheses describes the thermal softening effect.
Equation (11) describes the instantaneous stress required to sustain material plastic deformation or flow. Once the von Mises stress exceeds the flow stress, a radial return algorithm [47] is used to calculate the stress state resulting from the strain increment and the associated plastic strain. After that, the heat source term from plastic deformation \(\dot{q}_\mathrm{p}\) can be calculated as
where \(\eta \) is the coefficient characterizing the fraction of plastic work dissipated into thermal energy and \(\dot{\varvec{\varepsilon }}^p\) is the plastic strain rate tensor.
3.4 Contact condition and heat generation
The FSE process relies on the shear stress from the die tool face to generate heat to soften the billet material and deform it. Thus, a correct die–workpiece contact condition is of critical importance for more accurate material deformation and heat generation. Among the existing contact conditions for solid-phase processing such as FSW, the full sticking condition assumes no slippage between the materials on either side of the contact such that both sides have the same interfacial velocities [11]. However, the sticking condition can only account for the heat generation from material plastic deformation and it usually overestimates the maximum temperature [48]. It was indicated by Gerlich et al. [49] and Schmidt et al. [50] that the contact condition for in solid-phase processing is actually partial sliding/sticking, and frictional sliding energy and material plastic deformation are both responsible for temperature elevation. Using the frictional coefficient and slip rate parameter, many studies have numerically shown that the partial sliding/sticking can yield results that are closer to experimental observations [51,52,53,54].
In this study, a partial sliding/sticking contact condition is realized by Coulomb friction law with Tresca limit, as suggested by Schmidt and Hattel [55]. The Coulomb–Tresca friction law can be naturally implemented in the Lagrangian particle-based model, and it can consider heat generation from both plastic deformation and frictional sliding between workpiece and die. Adopting the Coulomb–Tresca friction law, the friction shear stress \(\varvec{\tau }_\mathrm{s}\) can be written as:
where \(\mu _\mathrm{f}\) is the friction coefficient, p is the contact pressure determined by the normal slave node force and the slave node area, \(\varDelta \varvec{v}_\mathrm{s}\) is the relative die–workpiece sliding velocity, \(\varvec{\tau }_{\max }=\frac{\sigma _y}{\sqrt{3}} \frac{\varDelta \varvec{v}_\mathrm{s}}{\Vert \varDelta \varvec{v}_\mathrm{s}\Vert }\) is the limiting shear force with \(\sigma _y\) being the equivalent material flow stress. This mechanical contact is modeled using the soft constraint penalty formulation that is suitable for treating contact between bodies with dissimilar material properties (e.g., steel-aluminum) [56]. In this method, each particle on the slave side is first checked for penetration through the master surface. Once penetration occurs, an artificial force proportional to the penetration distance and penalty stiffness is introduced to prevent penetration. The penalty stiffness is the minimum of the master segment and slave node stiffness. To avoid the excessive penetration on the contact side with weaker material, a stability contact stiffness is further added. The details of the soft constraint penalty formulation can be found in [56] and are omitted here.
The energy converted into heat resulting from frictional contact is expressed as
which is partitioned to each side of the contact. The frictional sliding energy partition fraction \(f_\mathrm{part}\) is dependent on the thermal diffusivity of the two materials in contact, which is discussed and determined in Sect. 4.2. The thermal contact between SPH particles and solid elements needs further elaboration and is discussed in Sect. 4.1
Note that although many studies showed satisfactory results with the Coulomb–Tresca friction law for both FSE and FSW [42, 54, 57, 58], the friction coefficient \(\mu _\mathrm{f}\) is purely empirical or hypothetical, and its value may affect the accuracy of the simulation result. The Coulomb–Tresca friction law is used in the current SPH model because it is a natural option when the Lagrangian framework is used. To obtain more accurate results, a more physics-based contact model should be developed and incorporated into the SPH model, which is out of the scope of this study.
3.5 Thermal boundary condition
To avoid overheating and preserve the die tool during the FSE process, pumped water provides active cooling to the billet container, as shown in Fig. 3. This thermal dissipation boundary condition is realized in the model by considering a heat flux (\(\dot{q}_\mathrm{conv}\)) on the container surface, which is expressed in a convection equation as:
where \(h_\mathrm{conv}\) is the convection coefficient, T denotes the container surface temperature, \(T_\mathrm{ref}\) is the reference temperature in the cooling system which is set as the room temperature in this study, and \(A_\mathrm{s}\) is the container surface area exposed to the cooling system. In accord with the experiment, the convection heat sink term in Eq. (15) is only applied on the free surface of the billet container in the model. The radiation source term is not considered in our model because it is negligible when the active cooling is present.
4 Model setup
The SPH model was implemented in the commercial software LS-DYNA [56]. Explicit dynamic analysis was used to solve this thermomechanically coupled problem with complex contact conditions.
4.1 Model geometry, assembly, and discretization
The model geometry is adapted from the experimental setup in Fig. 1a. The billet ring and backing plate are combined as a single billet container part with 1 mm container wall thickness and 2 mm backing plate thickness. The length of the die tool is 10 mm. The billet container and die tool were assumed to be rigid and discretized into solid elements for contact calculation. The AA1100-O billet part is deformable and will experience large deformation during the process, so it is discretized into SPH particles.
Accurate temperature field prediction is essential for FSE as it directly affects the temperature-dependent material and contact properties. Unlike solid elements that discretize the predefined boundaries and material interfaces of the solid parts, SPH uses particles to represent the changing free surfaces and moving material interfaces at different times. This introduces challenges to identify the SPH boundary at each time step to enable thermal contact between the SPH parts and solid parts. To this end, Fraser [41] recently developed detection methods for particles located at both free surfaces and particle–solid interfaces, which enabled the application of thermal boundary conditions to SPH parts and thermal contact between SPH parts and solid parts. Later, Xu and Wang [64] proposed a virtual SPH method to allow heat transfer between SPH particles and solid parts. In this method, the solid elements are adaptively transformed into virtual SPH particles, which move together with their associated solid elements. Since the virtual SPH particles share the same kernel function with the original SPH particles for the heat transfer equilibrium equation, an authentic thermal coupling between the original SPH parts and new virtual SPH parts can be achieved. The temperature fluctuations in the virtual SPH particles are then inherited by the associated solid elements, be transferred to other solid parts, and interact with the thermal boundary conditions defined on solid parts. In this study, the virtual SPH method proposed by Xu and Wang [64] was used to enable thermal contact between billet SPH particles and rigid parts solid elements.
To reduce the total number of SPH particles, the billet container was split into an inner one and an outer one, and the die was split into a top one and a bottom one. Only the solid elements in inner container and the top die were transformed into virtual SPH particles. As a result, there are five parts in the proposed model with detailed dimensions shown in Fig. 4a. Two longitudinal (z-direction) AA2050-O marker wires with a \(2\times 2\)-particle cross section are inserted: one at the billet center and the other at 1/3 r (radius) away from the billet center. The parts shown in Fig. 4a were assembled in the z-direction tightly with no gaps between them, as shown in Fig. 4b. Both dies rotate counterclockwise around the central axis (viewed in positive z-direction) at a constant rotational speed, and advance in negative z-direction at a constant speed.
For the discretization, an 8-node, 3-D, bilinear element was used for the rigid solid parts. To strike a good balance between the computational cost and numerical accuracy, the billet was discretized into 0.4 mm diameter particles, which leads to 96,768 particles. An element sized in 0.25 mm was used to mesh the solid parts, resulting in 486,984 solid elements, as shown in Fig. 5. Each solid element in the inner billet container and top die were transformed into one virtual SPH particle. The final model featured in this study consists of 198,704 SPH particles, as indicated in Fig. 5.
4.2 Material properties and model parameters
Because J–C model material parameters for AA1100-O were not available in the literature, the corresponding values for a similar alloy such as aluminum 2024-T351 are often used instead [65]. In our work, the strain rate hardening parameters C and \(\dot{\varepsilon _0}\) were obtained from [59] for AA1100-H12. The thermal softening exponent m was obtained from [60]. A major limitation of the J–C model is that the strain hardening is weakly correlated with the thermal softening. As a result, an unsaturated flow stress will be predicted even at high plastic strain and temperature [43]. To address this issue, the yield stress for AA1100-O in undeformed condition was assigned to initial yield stress A at room temperature, and the strain hardening parameters B and n were set at zero. J–C model parameters for AA2050-O were obtained from [61] also with B and n set to zero. The detailed Johnson–Cook material parameters used in this study are detailed in Table 2.
The rigid billet container and die tool were assigned the properties of H13 tool steel. The elastic and thermal properties of AA1100-O, AA2050-O, and H13 tool steel were obtained from a commonly available material database [62], which are tabulated in Table 3. Because the thermal properties of aluminum alloys are typically sensitive to temperature variation, same temperature-dependent thermal material properties taken from [63] were used for AA1100-O and AA2050-O. The thermal properties of H13 tool steel were kept constant throughout the simulation because they are insensitive to the temperature variation [63]. The density, Young’s modulus, and Poisson’s ratios are assumed to be temperature-independent since they were tested to have small impacts on the simulation results.
An effective friction coefficient \(\mu _\mathrm{f}\) in Eq. (13) was assumed for the contact between the billet and the container or die, the value for which was chosen as constant 0.57 between aluminum and AISI H13 tool steel [66]. All the frictional sliding energy is assumed to be converted into heat. The partition fraction \(f_\mathrm{part}\) of the sliding energy transferred to heat the billet can be calculated as [56]
Based on the material properties in Table 3, \(f_\mathrm{part}\) as a function of temperature is shown in Fig. 6. Since the steady-state temperature at the contact interface is about 400–600 \(^\circ \)C for FSE, \(f_\mathrm{part}\) is assumed a constant value of 0.7 in this study for simplicity. A dissipation coefficient of \(\eta =\) 0.9 was used for the plastic dissipation, implying that 90\(\%\) of the plastic work is converted into heat energy. Because no calibrated heat convection coefficient was available for the cooling system, the convection coefficient on the container surface was chosen as \(h_{\mathrm {conv}} = 1000\; \mathrm {W}/(\mathrm {m}^2\, ^\circ \mathrm {C})\), from the existing data for active liquid cooling on steel [67]. This value has been shown to yield reasonable heat dissipation and temperature profiles.
5 Numerical results and discussion
In this section, the numerical results obtained from the SPH model are presented and validated by the experimental data. Specifically, the material flow, strain, temperature, and extrusion force during the FSE process are investigated.
SPH is much more computationally intensive than conventional mesh-based methods because additional particle–neighborhood searching is needed to identify the kernel function and the bucket-sorting algorithm is required for the node-to-surface contact. To obtain a reasonable computational cost while maintaining accuracy of the results, we used a mass scaling technique to increase the time increment by artificially increasing the material density in the model. To this end, the target minimum step size chosen for the mechanical analysis was \(2\times 10^{-5}\)s, which requires a mass scaling factor of about \(3.91\times 10^5\). A fully implicit time integration was used for the transient thermal analysis, and an unconditionally stable thermal time step was set at \(2\times 10^{-3}\) s. Along with mass scaling, a time scaling technique was also used to further speed up the simulation by increasing the billet advancing and die rotational speeds by a factor of 15. With mass scaling and time scaling, the total simulation time can be reduced to about 52 hours running with 12 CPUs on a 12 core Intel Core i9-9920X with 64 GB memory.
It should be noted that to avoid significant deviation from the actual solution, the acceptable mass scaling factor should maintain the kinetic energy of the deforming SPH particles below 5–10\(\%\) of the internal energy caused by material deformation [68, 69]. Figure 7 shows the histories of the kinetic energy, internal energy, and their ratio for the billet material over the simulation time in the case of 300 rpm die rotational speed and 8 mm/min die advance speed. The figure shows that the kinetic energy is an order of magnitude smaller than the internal energy during the entire simulation. The maximum kinetic/internal energy ratio is about 4.2\(\%\) at the end of the simulation. This result indicates that the mass scaling factor used in this study is reasonable and has no significant effect on the predicted result.
Vertical point position tracking in the case of 300 rpm die rotational speed and 8 mm/min die advance speed (bottom view) at a \(t= 0\) s; b \(t= 7.5\) s; c \(t= 29.25\) s; d \(t= 36.75\) s; e cross section of extruded wire at 50 mm from wire start (black phase is 1/3r marker material); f cross section of extruded wire at 100 mm from wire start with 1/3r maker material (black phase is 1/3r marker material)
5.1 Material flow pattern
The billet material flow pattern during FSE is first investigated. Figure 8 presents snapshots of the billet deformation and effective plastic strain at different times predicted by the simulation with die rotational speed of 300 rpm and die advance speed of 8 mm/min. As shown in the figure, the rotating die gradually pushes against the billet with advance speed. The compressive extrusion forces and high shear forces from the die face help heat and deform the billet top in the high shear region. The plastic strain was first developed along the circumference of the top billet face where shear stress is large, as shown in Fig. 8a, b. With time increased, the billet temperature increased with reduction in material flow stress, and more billet materials in the high shear zone were plasticized, as shown in Fig. 8c, d. The softened and plasticized material was then extruded through the die orifice to form a wire. The total length of the simulated extruded wire is 795.5 mm for a 51-second processing time. Even though the billet material has undergone a large plastic deformation, no numerical problems were encountered because SPH is meshless. Moreover, since a penalty-based contact between particles and solid elements with restricted penetration check was employed, particle penetrations into the die were prevented. No particle splashing or obvious large gaps between particles were observed, indicating appropriate selection of time steps, material properties, and thermal boundary conditions for both mechanical and thermal analyses.
Figure 9 provides snapshots of the center and 1/3r marker material flows at different times in the case of 300 rpm die rotational speed and 8 mm/min die advance speed, from which distinct material flow pattern can be observed for different marker materials. The marker material at the billet center (yellow) was directly extruded from the die orifice without much lateral deformation. This is because they do not experience shear force applied by the rotating die. In contrast, the marker material at 1/3r from the billet center (green) was pushed against the die with pressure. With the die rotation, high shear force created by frictional contact between billet and die was applied to the 1/3r marker material, forcing it to rotate with the die. As the billet container advanced, the 1/3r marker materials close to the die orifice were extruded first, and the remaining marker materials continued to rotate until they were extruded.
Although the material flow pattern can be explicitly tracked by displaying the particle locations as shown in Fig. 9, only scattered data points are available, the number of which is restricted by the spatial density of the SPH particles. To obtain a smoother trajectory of the material flow, a cubic spline data interpolation is used to interpolate an additional 1000 query data points among the existing data points in the 3-D domain. The red dots in Fig. 10a to d represent the locations of the 1/3r vertical materials from the bottom view at \(t=\) 0, 7.5, 29.25, and 36.75 s, respectively. In the right-hand-side plot of each subfigure, both the original tracked points (red hollow circles) and the cubic spline fitted curve (black solid line) are given in the 2-D coordinate system. The coordinates of each point in these plots indicate the actual particle location in the billet and extruded wire. The same information in Fig. 10 is depicted in Fig. 11 but in a 3-D isometric view. From these figures, a clearly helical material flow pattern can be observed for the vertical 1/3r marker material. The prediction by the numerical model also indicates the helical material flow inferred by experimental observation of different cross sections of the extruded wire, as indicated by the black phases in Fig. 10e, f.
In addition to tracing the material vertically in the billet, the materials were also tracked horizontally and interpolated at different times. To this end, two lines of material, in the y direction and in the second SPH layer from the billet top surface, were selected, as shown in Figs. 12a and 13a. The material flow patterns at \(t = 7.5, 10.5\), and 18 s are plotted in Figs. 12b–d and 13b–d, respectively. Since there are two lines of horizontal materials in this case, the fitted spline curve is based on the average location of the two lines. The helical material flow pattern is observed again but is more obvious in these figures. One can also see that, although the particles close to the billet rim are highly deformed, they are unlikely to be extruded because they are far from the die orifice. The flow trajectories of these particles can help to explain the experimentally observed “dead zone” at the billet container corner where the material is difficult to be extruded.
5.2 Strain validation
A more quantitative comparison of the material deformation predicted by the simulation and experimentally observed was carried out by looking at the strain measurements. In the experiment, the strains at 1/3r of the wire cross section at 60, 100, 200, 300, 400, and 500 mm from the wire start were estimated based on the spiral shape of the 1/3r marker material at these locations [44]. The cylindrical coordinate system was used for the estimated experimental strains. To compare these to results from simulation obtain the same strain data must be converted into cylindrical coordinates. The strain tensors in the Cartesian coordinate system were extracted from the same locations in the wire, as indicated by the red dashed boxes in Fig. 14a. At each location, a 5-mm-long wire segment is selected and the strain tensors of all the particles at 1/3r of the wire segment are extracted, as indicated by the small white window in Fig. 14b. After the strain tensor and the displacement history are obtained for each particle within the small white window, a coordinate system transformation is performed to transfer the strain data from the Cartesian to cylindrical systems. After calculating all the strain tensors, the averaged values at each location are used to represent the simulated 1/3r strain in the cylindrical system.
Comparisons of longitudinal strain (\(\varepsilon _{zz}\)), tangential strain (\(\varepsilon _{\theta \theta }\)), radial strain (\(\varepsilon _{rr}\)), and the sum of strains (\(\varepsilon _{rr}+\varepsilon _{\theta \theta }+\varepsilon _{rr}\)) in the case of 300 rpm die rotational speed and 8 mm/min die advance speed obtained from simulation and experiment are shown in Fig. 15, where z, \(\theta \), and r denote the longitudinal, tangential, and radial directions, respectively. It is shown that the longitudinal strains at different locations match well, with magnitudes around 4. There are some mismatches in radial and tangential strains, especially at the locations closer to the wire start. This may be because at the start of the process, a steady state has not yet been reached and material has not been extruded from the entire plane of the billet. Nevertheless, the strain predictions are overall in good agreement with the experimental data, demonstrating the validity of the SPH model for predicting large strains during FSE.
5.3 Temperature validation and investigation
The proposed model was further validated by comparing the temperature data obtained from the simulation and experiment at three different processing parameters. The temperature variation in the experiment was recorded by a K-type thermocouple inserted 0.5 mm behind the die face and 5 mm from its central axis, as indicated in Fig. 1. Figure 16a shows the comparison results with 300 rpm die rotational speed, 8 mm/min (black) and 12 mm/min (red) die advance speeds, while Fig. 16b shows the ones with 8 mm/min die advance speed, 300 rpm (black) and 150 rpm (red) die rotational speeds. In both figures, the experimentally measured temperatures as a function of processing time are plotted as the dashed curves, and the simulated temperature variations at the same location relative to the die face are depicted as the solid curves.
As indicated in Fig. 16, the temperature variations on the die face predicted by the SPH model are generally in good agreement with the experimental measurement for all three sets of process parameters. The SPH model can capture the rapid temperature increase in the early extrusion stage (between 0 and 15 s) attributable to high material plastic deformation and frictional sliding energy. The temperatures increase slower in the middle and late stages (after 15 s), which is a result of material softening and more heat loss by active cooling at high temperature. When the die rotational speed is fixed at 300 rpm, a faster die advance speed leads to a faster temperature elevation on the die face as shown in Fig. 16a. This is because the billet material is plasticized more and extruded faster with a higher die advance speed, which leads to more heat generation during the same amount of time compared to the case with lower die advance speed. When the die advance speed is fixed at 8 mm/min, a faster die rotational speed results in a faster temperature development as shown in Fig. 16b. This is due the fact that the frictional shear stress applied on the billet is severer with a higher die rotational speed. This higher shear stress plasticizes the billet and generate heat faster compared to the case with slower die rotational speed.
Figure 16 shows that the simulation underestimates temperature in the late stage. This discrepancy may arise for two reasons: (1) the current model uses an approximated heat flux boundary condition on the container surface; (2) in the actual experiment, sometimes “flash” was extruded through the small gap between the outer surface of the die and the inner wall of the billet “ring.” The friction between this flash and the rotating die generated additional heat. A thermal boundary calibrated to the active cooling system could improve the accuracy of the predicted temperature variation, but that was not pursued here. This temperature validation indicates that the heat generation, conduction, and dissipation are reasonably captured and accounted for in the thermomechanically coupled SPH model. A high-fidelity temperature field again yielded more accurate material mechanical properties for use in simulating the FSE process.
5.4 Extrusion force validation
Figure 17 presents temperature distributions on the central cross section of the simulation domain at different times in the case of 300 rpm die rotational speed and 8 mm/min die advance speed, which are difficult to measure by experiment. The temperatures in the inner billet container and the top die are presented only on virtual SPH particles for better visualization. In the early stage (\(t = 4.5 \hbox {s}\)), most of the simulation domain remains at room temperature, while heat generation and conduction from the high-shear billet–die contact region begin. With increased processing time, heat is continuously generated by the frictional force and plastic deformation and is conducted to the rest of the domain, as shown in Fig. 17b–f. Our results show that a higher temperature always occurs at the billet–die contact. In the early stage, the highest temperature occurs close to the highly confined corner, as shown in Fig. 17b. As the temperature increases, the outer billet container dissipates more thermal energy, cooling down the billet particles that are close to the chamber. Temperatures gradually increase closer to the extrusion hole, as shown in Fig. 17c–f. Moreover, temperature transitions between the SPH billet and virtual SPH particles, and between virtual SPH particles and solid parts, are smooth, indicating that the virtual SPH particles effectively bridge the heat transfer between SPH parts and solid parts. The effectiveness of heat transfer by virtual SPH particles is observed in Fig. 18, which shows the simulated temperature profiles on the outer billet container and the bottom die at different times.
The temperature validated SPH model was then used to predict thermal histories at the point around the die hole and the central point on the billet bottom, whose locations are indicated by the white boxes in Fig. 17a. Figure 19 gives the predicted results with all three process parameters. It is shown that the cases with faster die rotational and advance speeds have faster temperature elevation and higher final temperature for points at both die hole and billet bottom. Temperatures at the die hole increase faster to higher values compared to the ones at the billet bottom. The final temperature at the die hole for the case of 300 rpm die rotational speed and 12 mm/min die advance speed reaches to 626.6 \(^\circ \)C, which is just below the solidus temperature of AA1100-O (643 \(^\circ \)C). These numbers for the cases of 300 rpm die rotational speed and 8 mm/min die advance speed, and 150 rpm die rotational speed and 8 mm/min die advance speed are 560.4 \(^\circ \)C and 498.6 \(^\circ \)C, respectively. The final temperatures at billet bottom for all three cases range from 479 to 525 \(^\circ \)C.
5.5 Extrusion force validation
Because constant die advance speeds were considered in FSE, the extrusion force varies. Therefore, extrusion force is also validated since it directly relates to the thermomechanical behavior of billet material. Figure 20a shows the comparison results with 300 rpm die rotational speed, 8 mm/min (black) and 12 mm/min (red) die advance speeds, while Fig. 20b shows the ones with 8 mm/min die advance speed, 300 rpm (black) and 150 rpm (red) die rotational speeds. Dashed curves indicate the experimental data and the solid curves denote the simulation results. As shown in Fig. 20, typical elastic stages are captured by the model, which agrees well with the experimental data. After 5 s, the extrusion force starts to decrease as the temperature increase to soften the billet material. This decrease in extrusion force obtained from simulation matches the experiment well, indicating the thermal field and material softening behavior were predicted accurately. A mismatch is observed in the peak load between 18 and 25 s for the case of 300 rpm die rotational speed and 8 mm/min die advance speed, where a large decrease in extrusion force occurs in the experimental data. A possible reason for the mismatch is that the contact between the sample and the backing block was imperfect in the experiment, while it is assumed to be perfect in the SPH model. Despite that, an overall good agreement between model predictions and experimental measurements was achieved.
6 Conclusions
In this work, a meshfree SPH model was developed for predicting the extreme thermomechanical conditions during the FSE process. In this model, the billet container and die tool were considered as rigid bodies, while the billet material was modeled as a thermo-elastoplastic solid described by Johnson–Cook material model. A virtual SPH approach was used to enable heat transfer between SPH parts and rigid solid parts. Contact between the billet and the solid parts was modeled by the Coulomb–Tresca friction law, and a heat dissipation thermal boundary condition was applied on the surface of the outer billet container. The developed SPH model was validated by comparing the numerically predicted material flow, strain, temperature, and extrusion force results with experimental observations at three different processing parameters. The comparisons indicated a good agreement between the numerical results and experimental data, demonstrating that the thermomechanical phenomena during FSE have been accurately simulated by the SPH model. Our numerical results reveal that the temperature elevates faster with faster die rotational speed and die advance speed due to more heat generation. The extrusion force is proportional to the die advance speed per rotational evolution.
The validated SPH model can be used to investigate the influences of various process parameters (e.g., billet material, die tool geometry, die rotational and advance speeds) on the field variables of the extrudate (e.g., material flow, temperature, strain, stress). Based on the field variables’ evolution histories, the material microstructure (e.g., grain size, microhardness, texture) evolution can be better understood through a weakly coupled post-processing metallurgical simulation. This model can also be used to optimize process parameters. A surrogate model could be constructed and calibrated to the input-response data generated by the SPH model. The trained surrogate model could be used to determine the optimum FSE process parameters to achieve certain desirable properties in the final extrudate.
In the current model, the Coulomb–Tresca friction law with a constant friction coefficient was used to describe the contact between the billet and rigid parts, and the phenomenological Johnson–Cook model was used for the thermomechanical response of the billet material. Future development of the SPH model should incorporate physics-based contact models by investigating the material attributes from lower length scales. Metallurgical aspects such as the effects of initial grain size, grain growth and recovery, and recrystallization can be included in the material constitutive model to fully describe the phenomena occurring during FSE. Moreover, detailed comparisons between SPH and grid-based FEM for FSE in terms of numerical accuracy and computational cost can be conducted in our future work.
References
Thomas WM, Nicholas ED, Needham JC, Murch MG, Templesmith P, Dawes CJ (1991) International Patent Application No. PCT/GB92/02203. GB Patent application no. 9125978.8
Lavender C, Joshi V, Grant G, Jana S, Whalen S, Darsell J, Overman N (2019) System and process for formation of extrusion process. U.S. Patent No. 10,189,063
Whalen S, Overman N, Joshi V, Varga T, Graff D, Lavender C (2019) Magnesium alloy ZK60 tubing made by Shear Assisted Processing and Extrusion (ShAPE). Mater Sci Eng, A 755:278. https://doi.org/10.1016/j.msea.2019.04.013
Behnagh RA, Shen N, Ansari MA, Narvan M, Kazem M, Givi B, Ding H (2016) Experimental analysis and microstructure modeling of friction stir extrusion of magnesium chips. J Manuf Sci Eng Trans ASME 138(4):1. https://doi.org/10.1115/1.4031281
Baffari D, Buffa G, Fratini L (2017) A numerical model for wire integrity prediction in friction stir extrusion of magnesium alloys. J Mater Process Technol 247:1. https://doi.org/10.1016/j.jmatprotec.2017.04.007
Zhang H, Li X, Deng X, Reynolds AP, Sutton MA (2018) Numerical simulation of friction extrusion process. J Mater Process Technol 253:17. https://doi.org/10.1016/j.jmatprotec.2017.10.053
Karwa C (2019) Finite element modelling and analysis of the friction stir extrusion process. Ph.D. thesis, Ohio State University
Mishra RS, Ma ZY (2005) Friction stir welding and processing. https://doi.org/10.1016/j.mser.2005.07.001
Bussetta P, Dialami N, Boman R, Chiumenti M, de Saracibar CA, Cervera M, Ponthot JP (2014) Comparison of a fluid and a solid approach for the numerical simulation of friction stir welding with a non-cylindrical pin. Steel Res Int 85(6):968. https://doi.org/10.1002/SRIN.201300182
Bussetta P, Dialami N, Chiumenti M, Agelet de Saracibar C, Cervera M, Boman R, Ponthot JP (2015) 3D numerical models of FSW processes with non-cylindrical pin. Adv Model Simul Eng Sci 2(1):1. https://doi.org/10.1186/S40323-015-0048-2
Ulysse P (2002) Three-dimensional modeling of the friction stir-welding process. Int J Mach Tools Manuf 42(14):1549. https://doi.org/10.1016/S0890-6955(02)00114-1
Seidel TU, Reynolds AP (2003) Two-dimensional friction stir welding process model based on fluid mechanics. Sci Technol Weld Join 8(3):175. https://doi.org/10.1179/136217103225010952
Colegrove PA, Shercliff HR (2006) CFD modelling of friction stir welding of thick plate 7449 aluminium alloy. Sci Technol Weld Join 11(4):429. https://doi.org/10.1179/174329306X107700
Bastier A, Maitournam MH, Dang Van K, Roger F (2006) Steady state thermomechanical modelling of friction stir welding. Sci Technol Weld Join 11(3):278. https://doi.org/10.1179/174329306X102093
Albakri AN, Mansoor B, Nassar H, Khraisheh MK (2013) Thermo-mechanical and metallurgical aspects in friction stir processing of AZ31 Mg alloy—a numerical and experimental investigation. J Mater Process Technol 213(2):279. https://doi.org/10.1016/j.jmatprotec.2012.09.015
Jain R, Pal SK, Singh SB (2016) A study on the variation of forces and temperature in a friction stir welding process: a finite element approach. J Manuf Process 23:278. https://doi.org/10.1016/j.jmapro.2016.04.008
Zhang Z, Zhang HW (2014) Solid mechanics-based Eulerian model of friction stir welding. Int J Adv Manuf Technol 72(9–12):1647. https://doi.org/10.1007/s00170-014-5789-4
Assidi M, Fourment L, Guerdoux S, Nelson T (2010) Friction model for friction stir welding process simulation: calibrations from welding experiments. Int J Mach Tools Manuf 50(2):143. https://doi.org/10.1016/j.ijmachtools.2009.11.008
Dialami N, Chiumenti M, Cervera M, Agelet De Saracibar C (2013) An apropos kinematic framework for the numerical modeling of friction stir welding. Comput Struct 117:48. https://doi.org/10.1016/J.COMPSTRUC.2012.12.006
Chiumenti M, Cervera M, Agelet de Saracibar C, Dialami N (2013) Numerical modeling of friction stir welding processes. Comput Methods Appl Mech Eng 254:353. https://doi.org/10.1016/j.cma.2012.09.013
Bussetta P, Dialami N, Chiumenti M, Agelet de Saracibar C, Cervera M, Ponthot JP (2015) 3D numerical models of FSW processes with non-cylindrical pin. Adv Mater Process Technol 1(3–4):275. https://doi.org/10.1080/2374068X.2015.1121035
Dialami N, Chiumenti M, Cervera M, Agelet de Saracibar C (2017) Challenges in thermo-mechanical analysis of friction stir welding processes. Arch Comput Methods Eng 24(1):189. https://doi.org/10.1007/s11831-015-9163-y
Dialami N, Cervera M, Chiumenti M, Agelet de Saracibar C (2017) A fast and accurate two-stage strategy to evaluate the effect of the pin tool profile on metal flow, torque and forces in friction stir welding. Int J Mech Sci 122:215. https://doi.org/10.1016/J.IJMECSCI.2016.12.016
de Saracibar CA, Chiumenti M, Cervera M, Dialami N, Seret A (2014) Computational modeling and sub-grid scale stabilization of incompressibility and convection in the numerical simulation of friction stir welding processes. Arch Comput Methods Eng 21(1):3. https://doi.org/10.1007/s11831-014-9094-z
Dialami N, Chiumenti M, Cervera M, Agelet de Saracibar C, Ponthot JP (2015) Material flow visualization in friction stir welding via particle tracing. Int J Mater Form 8(2):167. https://doi.org/10.1007/s12289-013-1157-4
Dialami N, Cervera M, Chiumenti M, de Saracibar CA (2017) Local-global strategy for the prediction of residual stresses in FSW processes. Int J Adv Manuf Technol 88(9–12):3099. https://doi.org/10.1007/s00170-016-9016-3
Gupta V, Upadhyay P, Fifield LS, Roosendaal T, Sun X, Nelaturu P, Carlson B (2018) Linking process and structure in the friction stir scribe joining of dissimilar materials: a computational approach with experimental support. J Manuf Process 32:615. https://doi.org/10.1016/j.jmapro.2018.03.030
Robe H, Claudin C, Bergheau JM, Feulvarch E (2019) R-ALE simulation of heat transfer during friction stir welding of an AA2xxx/AA7xxx joint on a large process window. Int J Mech Sci 155:31. https://doi.org/10.1016/J.IJMECSCI.2019.02.029
Lucy LB (1977) A numerical approach to the testing of the fission hypothesis. Astron J 82:1013. https://doi.org/10.1086/112164
Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics: theory and application to non-spherical stars. Mon Not R Astron Soc 181(3):375. https://doi.org/10.1093/mnras/181.3.375
Liu GR, Liu MB (2003) Smoothed particle hydrodynamics—a meshfree particle method. World Scientific Publishing Co. Pte. Ltd, Singapore. https://doi.org/10.1142/9789812564405
Liu MB, Liu GR (2010) Smoothed particle hydrodynamics (SPH): an overview and recent developments. Arch Comput Methods Eng 17(1):25. https://doi.org/10.1007/s11831-010-9040-7
Libersky LD, Petschek AG (1991) Smooth particle hydrodynamics with strength of materials. In: Advances in the free-lagrange method including contributions on adaptive gridding and the smooth particle hydrodynamics method. Springer, Berlin, Heidelberg, pp 248–257. https://doi.org/10.1007/3-540-54960-9_58
Gray JP, Monaghan JJ, Swift RP (2001) SPH elastic dynamics. Comput Methods Appl Mech Eng 190(49–50):6641. https://doi.org/10.1016/S0045-7825(01)00254-7
Gray JP, Monaghan JJ (2004) Numerical modelling of stress fields and fracture around magma chambers. J Volcanol Geotherm Res 135(3):259. https://doi.org/10.1016/j.jvolgeores.2004.03.005
Cleary PW, Prakash M, Das R, Ha J (2012) Modelling of metal forging using SPH. Appl Math Model 36(8):3836. https://doi.org/10.1016/j.apm.2011.11.019
Ba K, Gakwaya A (2018) Thermomechanical total Lagrangian SPH formulation for solid mechanics in large deformation problems. Comput Methods Appl Mech Eng 342:458. https://doi.org/10.1016/j.cma.2018.07.038
Tartakovsky A, Grant G, Sun X, Khaleel M (2006) Modeling of friction stir welding (FSW) process with smooth particle hydrodynamics (SPH). In: SAE technical papers (SAE International). https://doi.org/10.4271/2006-01-1394
Bhojwani S (2007) Smoothed particle hydrodynamics modeling of the friction stir welding process. Ph.D. thesis, The University of Texas at El Paso
Pan W, Li D, Tartakovsky AM, Ahzi S, Khraisheh M, Khaleel M (2013) A new smoothed particle hydrodynamics non-Newtonian model for friction stir welding: process modeling and simulation of microstructure evolution in a magnesium alloy. Int J Plast 48:189. https://doi.org/10.1016/j.ijplas.2013.02.013
Fraser K (2017) Robust and efficient meshfree solid thermo-mechanics simulation of friction stir welding. Ph.D. thesis
Ansari MA, Behnagh RA (2019) Numerical study of friction stir welding plunging phase using smoothed particle hydrodynamics. Model Simul Mater Sci Eng. https://doi.org/10.1088/1361-651X/ab1ca7
Stubblefield G, Fraser K, Phillips B, Jordon J, Allison P (2021) A meshfree computational framework for the numerical simulation of the solid-state additive manufacturing process, additive friction stir-deposition (AFS-D). Mater Des 202:109514. https://doi.org/10.1016/j.matdes.2021.109514
Li X, Tang W, Reynolds AP, Tayon WA, Brice CA (2016) Strain and texture in friction extrusion of aluminum wire. J Mater Process Technol 229:191. https://doi.org/10.1016/j.jmatprotec.2015.09.012
Monaghan JJ, Lattanzio J (1985) A refined particle method for astrophysical problems. Astron Astrophys (Berlin. Print) 149(1):135
Johnson GR, Cook WH (1983) A constitutive model and data from metals subjected to large strains, high strain rates and high temperatures. In: Proceedings of the 7th international symposium of ballistics, pp 541–547
Simo JC, Hughes TJ (2006) Computational inelasticity, vol 7. Springer, Berlin
Colegrove PA, Shercliff HR (2005) 3-Dimensional CFD modelling of flow round a threaded friction stir welding tool profile. J Mater Process Technol 169(2):320. https://doi.org/10.1016/j.jmatprotec.2005.03.015
Gerlich A, Yamamoto M, North TH (2007) Strain rates and grain growth in Al 5754 and Al 6061 friction stir spot welds. Metall Mater Trans A Phys Metall Mater Sci 38(6):1291. https://doi.org/10.1007/s11661-007-9155-0
Schmidt HN, Dickerson TL, Hattel JH (2006) Material flow in butt friction stir welds in AA2024-T3. Acta Mater 54(4):1199. https://doi.org/10.1016/j.actamat.2005.10.052
Wang H, Colegrove PA, Dos Santos JF (2013) Numerical investigation of the tool contact condition during friction stir welding of aerospace aluminium alloy. Comput Mater Sci 71:101. https://doi.org/10.1016/j.commatsci.2013.01.021
Su H, Wu CS, Pittner A, Rethmeier M (2014) Thermal energy generation and distribution in friction stir welding of aluminum alloys. Energy 77:720. https://doi.org/10.1016/j.energy.2014.09.045
Chen G, Ma Q, Zhang S, Wu J, Zhang G, Shi Q (2018) Computational fluid dynamics simulation of friction stir welding: a comparative study on different frictional boundary conditions. J Mater Sci Technol 34(1):128. https://doi.org/10.1016/j.jmst.2017.10.015
Wang X, Gao Y, Liu X, McDonnell M, Feng Z (2021) Tool-workpiece stick-slip conditions and their effects on torque and heat generation rate in the friction stir welding. Acta Mater 213:116969. https://doi.org/10.1016/j.actamat.2021.116969
Schmidt H, Hattel J (2005) A local model for the thermomechanical conditions in friction stir welding. Model Simul Mater Sci Eng 13(1):77. https://doi.org/10.1088/0965-0393/13/1/006
Hallquist J (2007) LS-DYNA keyword user’s manual. Livermore Softw Technol ANSYS 970:299–800
Fagan T, Lemiale V, Nairn J, Ahuja Y, Ibrahim R, Estrin Y (2016) Detailed thermal and material flow analyses of friction stir forming using a three-dimensional particle based model. J Mater Process Technol 231:422. https://doi.org/10.1016/j.jmatprotec.2016.01.009
Zhang Z, Chen JT, Zhang ZW, Zhang HW (2011) Coupled thermo-mechanical model based comparison of friction stir welding processes of AA2024-T3 in different thicknesses. J Mater Sci 46(17):5815. https://doi.org/10.1007/s10853-011-5537-1
Gupta NK, Iqbal MA, Sekhon GS (2006) Experimental and numerical studies on the behavior of thin aluminum plates subjected to impact by blunt- and hemispherical-nosed projectiles. Int J Impact Eng 32(12):1921. https://doi.org/10.1016/j.ijimpeng.2005.06.007
Pierazzo E, Artemieva N, Asphaug E, Baldwin EC, Cazamias J, Coker R, Collins GS, Crawford DA, Davison T, Elbeshausen D, Holsapple KA, Housen KR, Korycansky DG, Wünnemann K (2008) Validation of numerical codes for impact and explosion cratering: impacts on strengthless and metal targets. In: Meteoritics and planetary science, vol 43, pp 1917–1938. https://doi.org/10.1111/j.1945-5100.2008.tb00653.x
Hfaiedh N, Peyre P, Song H, Popa I, Ji V, Vignal V (2015) Finite element analysis of laser shock peening of 2050–T8 aluminum alloy. Int J Fatigue 70:480. https://doi.org/10.1016/j.ijfatigue.2014.05.015
ASM (1990) Metals handbook. Vol. 1. Properties and selection: irons, steels, and high-performance alloys. ASM International, Materials Park, Ohio 44073, USA
Valencia JJ, Quested PN (2013) Thermophysical Properties. ASM Handb 15:468
Xu J, Wang J (2017) Thermal coupling method between SPH particles and solid elements in LS-DYNA. In: 11th European LS-DYNA Conference, Salzburg, Austria. https://www.dynalook.com/conferences/11th-european-ls-dyna-conference/particles-metthods-sph-and-dem/thermal-coupling-method-between-sph-particles-and-solid-elements-in-ls-dyna
Corbett BM (2006) Numerical simulations of target hole diameters for hypervelocity impacts into elevated and room temperature bumpers. Int J Impact Eng 33(1–12):431. https://doi.org/10.1016/j.ijimpeng.2006.09.086
Pereira D, Gandra J, Pamies-Teixeira J, Miranda RM, Vilaça P (2014) Wear behaviour of steel coatings produced by friction surfacing. J Mater Process Technol 214(12):2858. https://doi.org/10.1016/j.jmatprotec.2014.06.003
Bergman T, Incropera F, Lavine A, DeWitt D (2011) Introduction to heat transfer. Wiley, Hoboken
Wang M, Yang H, Sun ZC, Guo LG, Ou XZ (2006) Dynamic explicit FE modeling of hot ring rolling process. Trans Nonferrous Met Soc China (Eng Ed) 16(6):1274. https://doi.org/10.1016/S1003-6326(07)60006-5
Wang L, Long H (2011) Investigation of material deformation in multi-pass conventional metal spinning. Mater Des 32(5):2891. https://doi.org/10.1016/j.matdes.2010.12.021
Acknowledgements
This work was financially supported by the Laboratory Directed Research and Development (LDRD) program at Pacific Northwest National Laboratory (PNNL) as part of the Solid Phase Processing Science initiative. PNNL is a multiprogram national laboratory operated by Battelle for the DOE under Contract No. DE-AC05-76RL01830.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open access funding is provided by Solid Phase Processing Science Initiative (SPPSi) at PNNL.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could appear to influence the work reported in this paper.
Availability of data and material
Available from the corresponding author upon request.
Code availability
Available from the correspond author upon request.
Additional information
Varun Gupta: Contributed to work while at PNNL.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, L., Gupta, V., Li, X. et al. Meshfree simulation and experimental validation of extreme thermomechanical conditions in friction stir extrusion. Comp. Part. Mech. 9, 789–809 (2022). https://doi.org/10.1007/s40571-021-00445-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40571-021-00445-7