Numerical simulation of particle impact drilling (PID) systems: a one-way coupled approach

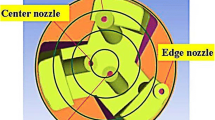
Abstract

A numerical technique based on a CFD-DEM method is presented for the analysis of particle impact drilling (PID) systems. The method is built from a preexisting finite element Navier–Stokes solver for the fluid phase and a discrete element method module for the steel particles which this drilling technology utilizes to enhance the penetration rate. We provide a detailed description of the most relevant implementation issues, including our choice of the hydrodynamic forces appropriate for power-law fluids. We also discuss several critical aspects related to the validity of the simplifying assumptions that will be helpful to simulation engineers. We apply our simple, one-way coupled approach on designs provided by an industrial partner to illustrate its potential as an analysis tool for this promising drilling technology. The goal of this work is, on the one hand, to provide evidence for the usefulness of the numerical approach as a design tool for PID systems, as well as a detailed discussion of the different aspects to be assessed for an effective simulation campaign. On the other hand, a series of modeling aspects that require further work are identified. The focus of the simulation campaign presented is on the particles and fluid flow characteristics within the drill bit.

Appendices

Appendix

A Details of the numerical method for the fluid equations

1.1 A.1 Finite element discretization

The FEM is based on the weak version of the problem formed by Eqs. (5) and (6), which is to find $(\varvec{u}; p) \in \varvec{\mathcal {X}} :=\varvec{\mathcal {V}}_D \times \mathcal {Q}$, where $\mathcal {V}_D$ and $\mathcal {Q}$ are appropriate function spaces for the velocity (vectors already fulfilling the Dirichlet boundary conditions) and the pressure fields.

$$\begin{aligned} \begin{aligned}&\rho _f( \frac{\partial \varvec{u}}{\partial t} ,\, \varvec{v} ) + \rho _f(\varvec{u} \cdot \nabla \varvec{u} ,\, \varvec{v}) \\&\quad + 2(\mu _{\text {eff}}(\varvec{u}) \nabla ^S \varvec{u} ,\, \nabla ^S \varvec{v}) - ( p, \nabla \cdot \varvec{v}) = \left\langle \varvec{f} ,\, \varvec{v} \right\rangle \\&\quad (q, \nabla \cdot \varvec{u}) = 0 \end{aligned} \end{aligned}$$

(30)

for all $(\varvec{v}; q)$ in $\varvec{\mathcal {Y}} :=\varvec{\mathcal {V}_0} \times \mathcal {Q}$, where $\varvec{\mathcal {V}_0}$ is the space of velocity-like fields that vanish on the Dirichlet boundary.

The basic strategy in the FEM is to replace the relevant (infinite-dimensional) spaces of functions above with finite dimensional counterparts in the variational version of the problem which leads to the algebraic system of equations that must be solved computationally.

Let us consider a conforming finite element partition $\mathcal {T}_h$ of the domain $\Omega$. For each element in the domain $\Omega _e \in \mathcal {T}_h$, we denote its diameter as $h_e$ and we define $h = \max {\left\{ h_e | \Omega _e \in \mathcal {T}_h \right\} }$. With these tools, it is possible to construct the finite element spaces in the usual way, as $\varvec{\mathcal {X}}_h = \varvec{\mathcal {V}}_{D,h} \times \mathcal {Q}_h$, with $\mathcal {V}_{D,h} \subset \mathcal {V}_{D}$, $\mathcal {Q}_h \subset \mathcal {Q}$. The finite element solution will be a function $\varvec{U}_h = [\varvec{u}_h, p_h] \in \varvec{\mathcal {X}}_h$, and since we will be using equal-order spaces for the velocity and the pressure, the solution can be expressed as (summation is assumed for repeated indices)

$$\begin{aligned} u_{h,j} = N^b U^b_{j}, \quad p_{h} = N^b P^b \end{aligned}$$

(31)

for $j = 1, ..., n_{\text {dim}}$ and $b = 1, ..., n_{\text {nodes}}$; where the $N^b$ are the shape functions, $n_{\text {dim}}$ is the number of space dimensions (2 or 3), and $n_{\text {nodes}}$ is the total number of mesh nodes.

Once the finite element discretization is defined, the problem presented in Eq. (30) can be expressed using a compact notation as find $\varvec{U}_h\in \varvec{\mathcal {X}}_h$ such that

$$\begin{aligned} (\mathbf {M} \frac{\partial }{\partial t} \varvec{U}_h ,\, \varvec{V}_h) + B(\varvec{U}_h,\varvec{V}_h) = L(\varvec{V}_h) \quad \forall \varvec{V}_h\in \varvec{\mathcal {X}}_{h,0} \end{aligned}$$

(32)

with

$$\begin{aligned}&B(\varvec{U}_h,\varvec{V}_h) {:=} (\varvec{u}_h \cdot \nabla \varvec{u}_h, \varvec{v}_h) {-} (p_h, \nabla \cdot \varvec{v}_h) + (\nabla \cdot \varvec{u}_h,\,q_h) \nonumber \\&\quad + 2\left( \frac{\mu _{\text {eff}}(\varvec{u})}{\rho _f}\nabla ^S (\varvec{u}_h), \nabla \varvec{v}_h\right) \end{aligned}$$

(33)

$$\begin{aligned}&L(\varvec{V}_h) :=(\varvec{f},\,\varvec{v}_h) + \int _{\Gamma _N} \varvec{t}_N \cdot \varvec{v}_h \, d\Gamma \end{aligned}$$

(34)

and

$$\begin{aligned} \mathbf {M} = \begin{bmatrix} 1 &{}0 &{}0 &{}0 \\ 0 &{}1 &{}0 &{}0 \\ 0 &{}0 &{}1 &{}0 \\ 0 &{}0 &{}0 &{}0 \\ \end{bmatrix} \end{aligned}$$

(35)

where we have divided through by the (constant) density of the fluid, $\rho _f$.

1.1.1 Stabilization

In the present work, we want to make use of the simplest linear simplex elements, for both the pressure and velocity approximations. However, for problems of the form of Eq. (32) (i.e., saddle-point problem, see [61]) not all velocity–pressure element pairs lead to viable numerical methods. A necessary condition to guarantee the stability of a particular combination is that the finite element spaces must fulfil the inf-sup or Ladyzhenskaya–Babusška–Brezzi (LBB) condition [61], and, in particular, the equal-order, piecewise linear spaces for the velocity and for the pressure ($\mathcal {P}_1/\mathcal {P}_1$ element) do not fulfil this condition [62]. Nonetheless, one can resort to stabilization methods to fix the numerical method resulting from the use of element pairs not fulfilling the LBB condition by modifying the weak form of the problem.

The variational multiscale method (VMS)  [63, 64] method provides a theoretical framework for the development of stabilized finite element formulations. These are based on the explicit consideration of the decomposition of the continuous solution into a part belonging to the finite element space $\varvec{\mathcal {X}}_h$ and its complement in the continuous solution space $\tilde{\varvec{\mathcal {X}}}$, or subscale.

In this work, we consider the algebraic sub-grid scales (ASGS) variant of VMS [65], which leads to rewriting the problem  Eq. (32) as find $\varvec{U}_h\in \varvec{\mathcal {X}}_h$ such that

$$\begin{aligned} \left( \mathbf {M} \frac{\partial }{\partial t} \varvec{U}_h ,\, \varvec{V}_h\right) + B_{ASGS}(\varvec{U}_h,\varvec{V}_h) = L_{ASGS}(\varvec{V}_h) \end{aligned}$$

(36)

where $B_{ASGS}(\varvec{U}_h,\varvec{V}_h)$ and $L_{ASGS}(\varvec{V}_h)$ are computed by adding a number of stabilization terms to the analogous terms in Eqs. (33) and (34), respectively. The resulting discrete problem does not suffer from the numerical instabilities that affect the Galerkin problem and allows us to work with the simplest finite element pair. A detailed derivation of the stabilized equations can be found in [37, 66].

1.2 Time integration and linearized system of equations

After assembling all the elemental contributions and imposing the boundary conditions, Eq. (36) leads to a system of equations of the form

$$\begin{aligned} \mathbb {M}\begin{bmatrix} \frac{\partial {\mathbb {U}}}{\partial t} \\ {0}\\ \end{bmatrix} + {\mathbb {C}}({\mathbb {U}},{\mathbb {P}}) \begin{bmatrix} {\mathbb {U}}\\ {\mathbb {P}}\\ \end{bmatrix} = {\mathbb {F}} \end{aligned}$$

(37)

where ${\mathbb {U}}$ and ${\mathbb {P}}$ stand for the nodal unknowns of the velocity and pressure, respectively. For the time discretization, we use a second-order Bossak time integration scheme [67], which defines the velocities as

(38)

The Bossak method introduces a relaxation factor in the acceleration of the system in Eq. (37)

$$\begin{aligned}&\left( 1-\alpha _B \right) \mathbb {M} \begin{bmatrix} \frac{\partial {\mathbb {U}}}{\partial t} \\ {0}\\ \end{bmatrix}^{n+1} + \alpha _B {\mathbb {M}} \begin{bmatrix} \frac{\partial {\mathbb {U}}}{\partial t} \\ {0}\\ \end{bmatrix}^{n} \nonumber \\&\quad + {\mathbb {C}}({\mathbb {U}}^{n+1},{\mathbb {P}}^{n+1}) \begin{bmatrix} {\mathbb {U}}\\ {\mathbb {P}}\\ \end{bmatrix}^{n+1} = {\mathbb {F}}^{n+1} \end{aligned}$$

(39)

where n is the time-step index. Combining Eqs. (38) and (39) and rearranging terms, one can rewrite Eq. (39) in residual form as

$$\begin{aligned} \begin{aligned}&{\mathbb {R}}({\mathbb {U}}^{n+1}, {\mathbb {P}}^{n+1}) = {\mathbb {F}} - \frac{1 - \alpha _B}{\gamma _N \Delta t}{\mathbb {M}} \begin{bmatrix} {\mathbb {U}} \\ {0} \\ \end{bmatrix}^{n} \\&\quad + \left( \left( 1 - \alpha _B \right) \left( \frac{1}{\gamma _N - 1} \right) + \alpha _B \right) {\mathbb {M}} \begin{bmatrix} \frac{\partial {\mathbb {U}}}{\partial t} \\ {0}\\ \end{bmatrix}^{n} \\&\quad + - \left( \frac{1 - \alpha _B}{\gamma _N \Delta t} {\mathbb {M}} + {\mathbb {C}} \right) \begin{bmatrix} {\mathbb {U}} \\ {\mathbb {P}}\\ \end{bmatrix}^{n + 1} \end{aligned} \end{aligned}$$

(40)

where we choose $\alpha = -0.3$ and $\gamma _N = 1/2 - \alpha _B$, as this combination of parameters provides maximal damping of the highest frequencies and a robust behavior overall [67]. The nonlinearities present in Eq. (5) are linearized using a first-order Taylor expansion. That is, at each nonlinear iteration i one solves

$$\begin{aligned} {\mathbb {R}}_{i+1}^{n+1} \approx {\mathbb {R}}_{i}^{n+1} + \left( \frac{\partial {\mathbb {R}}}{\partial {\mathbb {U}}\partial {\mathbb {P}}} \right) _{i+1}^{n+1} \begin{bmatrix} \delta {\mathbb {U}}\\ \delta {\mathbb {P}}\\ \end{bmatrix}^{n+1} = {0} \end{aligned}$$

(41)

Then, the solution and the residual are iteratively updated with Picard’s method as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} {\mathbb {U}} \\ {\mathbb {P}} \\ \end{bmatrix}_{i+1}^{n+1}&= \begin{bmatrix} {\mathbb {U}} \\ {\mathbb {P}} \\ \end{bmatrix}_{i}^{n+1} + \begin{bmatrix} \delta {\mathbb {U}}\\ \delta {\mathbb {P}}\\ \end{bmatrix}^{n+1}_{i+1} \\ {\mathbb {R}}_{0}^{n+1}&= {\mathbb {R}}({\mathbb {U}}^{n}, {\mathbb {P}}^{n})\\ {\mathbb {R}}_{i+1}^{n+1}&= {\mathbb {R}}({\mathbb {U}}_{i}^{n+1}, {\mathbb {P}}_{i}^{n+1}) \end{aligned} \end{aligned}$$

(42)

where, in evaluating the derivative of the residual, we use the following approximation

$$\begin{aligned} \frac{\partial {\mathbb {R}}}{\partial {\mathbb {U}}\partial {\mathbb {P}}} \approx \frac{1 - \alpha _B}{\gamma _N \Delta t} {\mathbb {M}} + {\mathbb {C}}_{i}^{n+1} \end{aligned}$$

(43)

where the indices are applied only to matrix ${\mathbb {C}}$, as ${\mathbb {M}}$ does not depend on the solution. Note that this approximation assumes that the variation of ${\mathbb {C}}$ is moderate compared to that of the solution vector itself; otherwise, convergence problems can appear. Consequently, the final system to be solved reads

$$\begin{aligned} -\left( \frac{1 - \alpha _B}{\gamma _N \Delta t} {\mathbb {M}} + {\mathbb {C}}_{i}^{n+1} \right) \begin{bmatrix} \delta {\mathbb {U}}\\ \delta {\mathbb {P}}\\ \end{bmatrix}^{n+1}_{i+1} = {\mathbb {R}}^{n+1}_i \end{aligned}$$

(44)