DPM model segregation validation and scaling effect in a rotary drum

Abstract

Discrete phase method (DPM) model was used to analyse rotary drum systems for segregation behavior. DPM simulations were performed for comparison with a dynamic segregation experimental measurement from the literature. This included dynamic segregation and time-averaged particle velocity field, which were validated with experimental data. In addition, a direct DPM and parcel scaled DPM simulation study was performed to analyse the effect of drum and particle parcel size scaling. The segregation dynamics was evaluated using the Lacey mixing index. This work shows segregation dynamics decreases with increasing drum size while keeping the same particle size. It further shows that for a given drum size the segregation dynamics deviate after a certain particle parcel scaling limit. The parcel scaling limit also increases with increasing drum size.

1 Introduction

Rotary drum industrial granulators and driers are widely utilized in chemical process industries to produce various types of granular products [1,2,3,4]. The chemical fertilizer industry produces a wide range of fertilizer types or grades using this method. Rotary drum operations are preferred while producing coarse-size particulate products. They are characterized by a long, low-angled cylinders rotating at low angular velocity, while internal flights are often added in order to improve materials mixing and increase their surface renewal [5].

In granulation drums, fine recycle particles are mixed with fresh melt inside a long rotary drum. Due to coating and agglomeration, the granules grow into a higher-size distribution. The granulation and drying operations are often separated between two successive drums. The dried and hardened particles move out through the drum outlet.

Industrial rotary drums operate in a loop system where screen filtration and crushers are utilized in recycle. These loop systems are known to experience periodic instability during operation where the particle size distribution flowing out of the granulator oscillates. This makes the loop to operate below their maximum design capacity and difficult to maintain the desired product quality [6,7,8]. Thus, understanding the granular flow patterns inside rotary drums is very relevant.

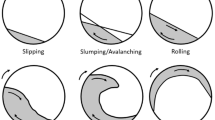
The operational regime of rotary drums is categorized depending on particle bed motion profile. The regimes in a typical rotary drum are slipping, rolling, cascading, centrifuging, etc. Drum regimes are fundamentally a function of the drum Froude number, fill fraction (i.e. the fraction of the total drum volume occupied by particles) and friction coefficients [9,10,11,12]. The Froude number is defined as:

$$\begin{aligned} Fr = \frac{\omega ^2 R}{g}, \end{aligned}$$

(1)

where $\omega$ is the rotational speed in rad/s, R is the drum radius and g is the gravitational acceleration constant.

Most granulation drum processes are operated in the rolling regimes, which is widely believed to be most optimum for steady particle processing. This regime produces a D-shaped particle bed that is internally circulating as shown in Fig. 1. This cyclic motion regime is preferred by chemical fertilizer industries due to higher particulate shear characteristics, minimum impact particle breakage and enhanced dispersion of melt. In this regime, the particles are carried up by the rotating boundary wall friction. They then come down due to gravity overflowing on the particulate mass [9]. Thus, the particle bed in a rolling regime consists of two layers, namely the active layer and the passive layer.

The active layer is a thin lens-like flowing zone, close to the free (planar) surface, where particles roll down the inclined bed in a way similar to an avalanche. In the active layer, high relative particle motion exists (between layers). However, the passive layer moves like a solid body, with little relative movement between the particles [13, 14]. A curved line can be drawn through the bed to define the interface between the active and passive layers. Along this line, the average horizontal velocity (defined parallel with respect to the bed surface) of particles is 0 which means they change flow directions here. In Fig. 1, this is shown with a dotted blue line and the horizontal here is defined along inclined bed surface plane in the described x-direction.

As a convention, the drum central axis is regarded as reference origin where the planar axial directions are aligned with respect to the angle of repose produced by particle bed as in Fig. 1.The x direction is along the angle of repose and y direction is perpendicular to it. Thus, in the active zone particles primarily flow in positive x-direction with negligible velocity (close to 0) in y-direction. Besides, the bed exists completely in the negative y-direction as the bed fill fraction is less than 50%. Percolative segregation primarily happens in the active layer, where particles can slide across each other [12].

Fig. 1

A cross-sectional view schematic diagram of a rotary drum in the rolling regime

If any flowing granular bed consists of particles with either different diameter or densities, the phenomenon of segregation will occur. Segregation is the de-mixing of a bi- or multi-disperse bed of particles, which occurs dynamically for a well-mixed granular system. Post-dynamic segregation a steady state is reached where no further segregation dynamics occurs. As an example, a radially segregated drum bed in the rolling regime at steady state consists of a core of mostly smaller/more dense particles surrounded by more larger/less dense particles. In the case that particles can be distinguished by their diameter, segregation is caused by percolation of small particles in between large particles [15,16,17]. With different densities, segregation is due to the difference in centrifugal force on denser particles relative to other. In fertilizer granulation production systems, the prior segregation type due to particle size distribution is relevant [4]. Thus, in this work, particle size based segregation is the focus.

Segregation phenomena is prevalent in both radial and lateral directions inside long rotary drums. A number of scientific works have studied and characterized both types of dispersions and segregations [18,19,20]. The scope of the current work is validating particulate DEM model with experimental measurements on segregative flow behavior in rotary drum and utilizing this model for drum scaling study to understand segregation mechanism.

Most experimental works on segregation are limited to small-laboratory-scale drum studies (less than 0.5 m drum diameter) where it is much easier to implement advanced measuring systems [10, 11]. However, industrial drums operating vary in size depending on application from small scale (about 0.5 m drum diameter) to very large scale (more than 5 m drum diameter). The interest of this work was to understand the how segregation phenomenon is influenced by drum size which has not been studied much in the past.

Some of the common measuring techniques known for granular flow research are electrical capacitance tomography, X-ray tomography, magnetic resonance particle tracking (MPT), positron emission particle tracking (PEPT), radioactive particle tracking (RPT), digital imaging analysis (DIA) and particle image velocimetry (PIV) [10, 21]. Among these discussed measuring techniques, RPT has been utilized to obtain highly resolved, detailed and accurate measurement of particle density and velocity distribution alongside dynamic segregation [13]. Thus, in the current work, this RPT-based measurement data from the literature has been used for model validation.

Most common modelling methods used to understand granular flow systems are discrete element method (DEM) and discrete particle method (DPM) [22, 23]. These methods involve individual particle tracking using Newton’s law of motion where discrete particle sphere experiences collision forces due to overlaps. These forces are modelled with parameters such as stiffness, restitution and friction [17]. Thus, depending on the collision properties of real particles model discrete phase collision parameters need to be tuned. Using such models that mimic real granular normal and shear properties, granular rotary drums are simulated.

RPT-based experimental data have been thoroughly used to validate DEM models by tuning the collision parameters [14, 24, 25]. The DEM collision model used in most previous works for experimental validation was Hertzian collision model [24, 26] and Cundall and Strack [27]. In the current computational study, the spring-dashpot collision model implemented in FLUENT 19.2 DPM solver has been used. This was the fundamental difference between this work and other previous works. Since Fluent DPM solver is a widely used commercial solver [28, 29], a comparison of this model with respect to scientific experimental measurement is of interest. This also provides the applicability of these solvers for granular flow research. The fundamental difference between the collision models discussed above is the relationship between collision force and particle overlap. However, this is known to have little difference in large granular simulation results.

One of the main limitations of using dense DPM models for industrial scale drum study has been the high computational cost [30]. Industrial-scale drums accommodate billions of particles, which is computationally expensive to track and needs several times MPI or GPU parallelization [31]. In recent times, efficient particle management has led to improved computational efficiency with DEM [32]. DPM particles can be scaled using parcel or coarse-graining-based approaches that can substantially reduce computational cost and so time to resolve the results. However, this is subject to effect on segregation behavior due to particle scaling in parcels. It should be noted that such particle scaling studies are often referred to as coarse-grain models [33], but in this work it has been referred as parcel scaling. In recent times, such scaling studies have been performed for different applications like conical spray driers [34], fluidized bed systems, etc. [35]. However, for segregation study in rotary drums this is a first such work involving parcel scaling.

In many previous works, DPM studies have been done on the effects of fill fraction, rotation speed, particle size ratio and density ratio on the segregation patterns using DPM [36, 37]. In the current work, DPM study was limited only to drum and parcel scaling effects on segregation mechanism for specific particle properties. Here, DPM has been used to study segregation characteristics for a laboratory-scale, medium-scale and industrial-scale rotary drum. This has of high relevance to industrial applications where drums are scaled for increasing productions. Here, DPM parcels are scaled from 2 times to 100 times to understand parcel scaling effects. Similar to some previous works, as a scaling criteria Froude number is kept constant (for varying drum sizes). This is achieved by adjusting the drum angular rotation speed with changing drum size.

Segregation has been quantified by several different types of indices, which are average height method [38], nearest-neighbour method, neighbour distance method [38], Lacey method [39], mixing entropy method [36], coordination number method [40], particle-scale index method [40] and Siiria method [41]. In the current work, Lacey mixing index is used as this method is known to be least effected by grid and scale. The particle domain was divided by Eulerian-type grids. The instantaneous particulate data on each grid were utilized to evaluate dispersed phase fractions, time-averaged velocities, etc. Such variables for different size classes were utilized for segregation study. This post-processing is discussed in detail further in later section.

The segregation study in this work provides interesting results to understand the segregation rate for industrial-scale granulation and drying drum modelling. Typically, such industrial drums of interest are 5 m, and larger, in diameter and several meters long. Simulating such drums with DPM models is computationally extremely expensive. Therefore, in this work, pseudo-2D-based drums are used to limit the DPM particle requirements to a few million (for large drum) in the simulations. Thus, only radial segregation profiles are quantified.

The DPM model implemented in ANSYS FLUENT 19.2 version was used [42]. The drum domain created was meshed, and the granular density data like phase fraction was evaluated at the cell centre position of the mesh grid points using user-defined functions (UDFs). Further details on the time-averaging various particle-related data on the Eulerian (mesh grid) have been discussed later in this work. The time-averaged data on the Eulerian grid were saved into CGNS file format, and the dynamic instantaneous particle data were saved in PARAVIEW VTU format. The visualization and post-processing work have been done in PARAVIEW [43, 44]. Other data processing with these data files was performed with MATLAB software [45].

Typically the Lagrangian DPM in ANSYS FLUENT is defined with respect to the Eulerian mesh grid in which it is instantaneously present and is coupled with an Euler-Lagrange coupling. This coupling is connected with exchange parameters such as drag and lift force. All these coupling parameters are set to 0 so that DPM particles follow independent collision motion as in a rotary drum system.

2 Modelling method

2.1 Discrete phase flow model

The discrete element method used in this work incorporates the standard granular flow methodologies where the motion of individual particles is tracked as Lagrangian points. The DPM modelling for pure drum particulate flow is relatively much simpler. Here the dynamic translational motion for any particle ‘a’ is a balance of gravity and contact forces (with ‘N’ neighbouring particles ‘b’) given by:

$$\begin{aligned} m_{a}\frac{\mathrm{d}^{2}\mathbf {r}_{a} }{\mathrm{d} t^{2}} = F_{g,a} + \sum _{b=1}^N F_{c,a}, \end{aligned}$$

(2)

and angular particle motion which is a function of torque acting is given by:

$$\begin{aligned} I_{a}\frac{\mathrm{d}^{2}\varvec{\theta }_{a} }{\mathrm{d} t^{2}} = \tau _\mathrm{p}, \end{aligned}$$

(3)

where $\mathbf {r}_\mathrm{p}$ and $\varvec{\theta }_\mathrm{p}$ represent the vector position and angular displacement of individual particles, respectively. Besides, $m_\mathrm{p}$ and $I_\mathrm{p}$ are the scalar particle mass and moment of inertia. Here, the gravity force acting on the particles is given by:

$$\begin{aligned} F_{g,a} = m_{a} \, \mathbf {g}, \end{aligned}$$

(4)

where $\mathbf {g}$ is the acceleration due to gravity. The Lagrangian particles interact with each other by collisions. The particle collision mechanics is modeled by the soft sphere model approach by Cundall and Strack [27]. In this work, only the normal and tangential interaction forces also known as spring-dashpot model are utilized. The tangential component is limited by the Coulomb’s friction law. The interaction force for two particles ‘a’ and ‘b’ in contact is given by:

$$\begin{aligned} F_{c,ab} = -k_n \delta _n \mathbf {n}_{ab}- \eta _n \mathbf {v}_{ab,n}, \end{aligned}$$

(5)

where $k_n$ is the normal spring stiffness, $\mathbf {n}_{ab}$ the normal unit vector between colliding particles ‘a’ and ‘b’ and $\mathbf {v}_{ab,n}$ is the normal relative velocity vector. $\eta _n$ is the normal damping coefficient that is a function of $k_n$ and the colliding particle masses [22, 46].

The overlap $\delta _n$ between the two Lagrangian particles is given by:

$$\begin{aligned} \delta _n = (R_a + R_b)-\left| \mathbf {r}_a - \mathbf {r}_b \right| \end{aligned}$$

(6)

where $R_a$ and $R_b$ denote the radii of the two particles while their position vectors are given by $\mathbf {r}_a$ and $\mathbf {r}_b$, respectively. Further details on the soft sphere collision modelling are available in the literature [22].

2.2 Experimental validation drum geometry and DPM setting

This experimental validation activity is based on an advanced RPT experimental technique developed by Alizadeh et al. [13]. In this experimental work, RPT technique was applied to study drum particle dynamics in a horizontal rotating drum made from plexiglass. The drum was 24 cm in inside diameter and was 36 cm long. The smooth glass beads of density 2500 kg/m$^3$ filled up to 35 vol% in the drum. The glass beads in this work were of 4 size classes, i.e. 3, 4, 5 and 6 mm size diameter. This work involved radioactive tracers of each particle class identical to their physical properties. The drum was surrounded with advanced detector system that allowed accurate tracking of the tracers in the drum.

Several different rotary drum experimental cases were done in the previous work [13]. The current work only considers the test run with polydisperse particles at 11.6 RPM drum speed. Here the four particles classes were used in the proportion of 15% (3 mm), 35% (4 mm), 35% (5 mm) and 15% (6 mm). This particular experimental run is specifically chosen in this work since it provides a detailed dynamic and steady-state data for a thorough advanced DPM validation.

The simple drum domain used in this work was developed in Ansys 19.2 version identical to the experimental drum. The drum domain was discretized or meshed with Eulerian grid so that particle distribution data could be post-processed or evaluated on the grid. The Eulerian grid was used to evaluate local dispersed phase fraction or particle fraction in the domain. This was further used to get time-averaged data. Figure 2 shows the geometry and mesh generated for this study. The mesh was generated using the standard hexa-dominant transition mesh with grid body sizing at 0.01 m. This size is 1.67 times the largest particle size (i.e. 6 mm) in the simulation.

The hexa block mesh system closer to the (radially) outer boundary wall provides uniform mesh size resolution. This supports a smoother time-averaged spatial data (for the different particle size) being studied. The meshing method has a transition to tetra mesh toward the drum center where the cells are much skewed. The dense particle bed is extremely sparse in this region due to the drum being just 35 % filled and in rolling regime. Therefore, the grid cell skewness close to the drum center does not affect the time-averaged (particle data) results much. The radial (curved) and side wall boundary condition for the drum was provided to be simple reflective wall boundary condition.

Fig. 2

Meshed domain identical to the experimental setup drum

The physical and mechanical properties of the glass beads used in the experimental work were measured and reported in previous work [13]. In most DPM simulation studies, same spring stiffness and friction parameters as that of real particles are not utilized. This is because real particles show very small collision times due to their high Young’s modulus and Poisson ratio. Simulating this requires extremely small DPM time step size (in the range $10^{-7}$–$10^{-8}$ s) depending on particle size. Therefore, particle spring stiffness and friction parameters are relaxed or modified such that the chosen DPM time step is practical as well as resolves particle collision processes well. This is a widely performed well-known exercise in DPM studies [30].

DPM settings for particle collision properties are adjusted to be able to replicate similar flow behavior characteristics as the RPT experiments [24]. Table 1 summarizes the DPM properties used to compare experimental measurements of Alizadeh et al. [13]. These parameters were tuned to be able to match the experimental distribution profiles produced by the smooth glass bead particles. Similar to the previous work, a high normal restitution coefficient (0.97) is used which is crucial to obtain a similar segregation rate. Besides, an identical wall boundary condition was used for both rotating and side walls of the drum, which was adjusted to get the right angle of repose (Table 1). This included a particle-wall normal and tangential coefficient of restitution and friction coefficient. Note that the side walls were also set to a rotating boundary condition.

Table 1 DPM simulation setting for model validation

Fig. 3

Friction coefficient as a function of particle relative velocity undergoing collision

The effective particle–particle friction coefficient is a function of relative velocity between colliding particles. This provides a dynamic frictional force during the collision process. The DPM implemented in FLUENT utilizes this dynamic treatment for collision in its model for spring-dashpot model. When the relative velocity is nearly 0, the friction coefficient is high at stick $\mu _\mathrm{st}$. It sharply reduces to a glide limit represented by $\mu _\mathrm{gl}$ at a relative velocity of $u_\mathrm{gl}$. Further, it slowly shifts to a limit friction $\mu _\mathrm{li}$. Reference [42] describes the theoretical background and equations in detail. Figure 3 shows the friction variation profile generated by the FLUENT DPM model. It has been shown in the past that rolling friction holds substantial influence on dense particle flow behavior, especially during experimental validation [47]. However, the FLUENT DPM model also provides rolling friction parameter that showed a concaving effect in the rotary drum particle bed simulations. Hence, rolling friction was excluded from this study.

The chosen collision parameters in this validation simulation (tabulated in Table 1) are discussed in detail in the next section. Alizadeh et al. [24] used the average distance of different particle size classes from bed center of mass as a measure for segregation.

$$\begin{aligned} S_{t}^{\mathrm{Alizadeh}} = \frac{1}{N_q} \sum _{i=1}^{N_q} \left| r_i^t - r_\mathrm{p} \right| , q = 1,2,\ldots . \end{aligned}$$

(7)

where q is the particle size class index, $r_i^t$ is the position of particle i at time t, $r_\mathrm{p}$ is the centre of mass position for particle size class p and $N_q$ is the number of particles in that class.

2.3 Scaling study drum geometry and DPM setting

The DPM method was used to evaluate segregation physics for fertilizer-type particle sizes. The scaling study in this work was performed for certain fertilizer grades, which have different physical and mechanical properties relative to glass beads. Most known fertilizer grades of interest have a much lower density compared to glass beads that are often used in the experimental research. They also have a lower particle restitution comparatively. These aspects were taken into account in this scaling study.

Most granulation drum operations produce a particle size distribution that is Poisson distribution in nature with expected rate parameter $\lambda$ around 2–5. The particle size range in fertilizer plants ranges from about 1–5 mm in size. A typical particle size distribution from such a drum at the outlet is provided in Fig. 4. This distribution represents for a drum of 5 m diameter size and 7 m long. This distribution is based on (time-averaged) plant data obtained from looped drum systems operating. In this work (to study segregation), a typical time-averaged distribution was utilized to divide the distribution mass into two equal half and the mean of each half was evaluated. This gave small particle size of 1.7 mm and large particle size of 3.0 mm. This simplification to a bi-disperse granular study is done so that segregation evaluation can be simplified.

Fig. 4

A representative particle size distribution exiting granulation drums

It is fundamentally known that the particle size distribution in any granular system may segregate much slower compared to a bi-disperse system. However, the study here is to understand the effect of drum scaling and particle scaling on segregation. In this study, 3 pseudo-2D drum size scale levels are included. These pseudo-2D drum were 0.25 m, 0.5 m and 5.0 m diameter, which as per scale are small (or lab scale) scale, medium (or pilot scale) scale and large (or industrial) scale, respectively. Figure 5 shows a schematic of the 3 drums (not to scale).

The drum scaling fundamentally required drum rotation speed adjustment so that same rolling regime condition could be maintained. This was achieved by maintaining a constant Froude Number discussed earlier in Eq. 1. Thus, using this equation the drum rotation speed was evaluated (for different drum diameters) by keeping the Froude number fixed at 0.1. This is tabulated hereby in Table 2.

Fig. 5

A schematic diagram (not to scale) of 3 pseudo-2D drum sizes used in this study

Table 2 Drums scaling criteria

Similarly, DPM particles were scaled as parcels, which are representative of multiple particles. Particle scaling as DPM particle parcels has long been used for granular flow simulations with the purpose of reducing computational costs. This scaling principle has specially been used for sparse particle systems such as spray drying and fast fluidization study [34, 48, 49]. In case of fluidization where gas-particle drag is involved, the drag forces are evaluated with particle diameter and most other forces use parcel diameter [34]. This principle has also in a limited manner been utilized for dense systems like pneumatic conveying, blending, chute flow or bubbling fluidization [50,51,52]. However, this is a first such work where DPM scaling is used for rotary drum segregation study. It is well known that dense systems are strongly influenced by collision forces and frequency, which varies with DPM size scaling. Thus, there is a need to carefully understand DPM parcel scaling effects on segregation.

In rotary drums (rolling regime), the primary effect is radial segregation that needs to be analysed for parcel scaling. In this work section, understanding DPM scaling effect on segregation is the primary aim. In principle, particle scaling is

$$\begin{aligned} V_\mathrm{parcel} = N_\mathrm{p} V_\mathrm{p} = N_\mathrm{p} \frac{\pi d_\mathrm{p}^3}{6} \end{aligned}$$

(8)

where $V_\mathrm{p}$ is particle volume, $N_\mathrm{p}$ is the number of representative particle per parcel and $d_\mathrm{p}$ is particle diameter. Thus, the parcel diameter is given by:

$$\begin{aligned} d_\mathrm{parcel} = \root 3 \of {\left( \frac{6 V_\mathrm{parcel}}{\pi }\right) } = \root 3 \of {(N_\mathrm{p})} d_\mathrm{p} \end{aligned}$$

(9)

This scaling principle has been widely used for treating scaled parcel-based simulations [34]. In this work, 1, 2, 5, 10, 25, 50 and 100 particle per parcel are analysed for rotary drums. This scaling criterion is simply shown in Fig. 6 (from 1 to 5 particle per parcel scaling), and the scaled parcel sizes are provided in Table 3.

The lower two drum scales of 0.25 m and 0.5 m drum diameter were simulated up to 5 times particle scaling (or 5 particle/parcel scale). Note the parcel size for 5 times scaling was 5.4 mm diameter. The thickness of the pseudo-2D drum for 0.25 m and 0.5 m drum diameter was 60 mm for all simulation cases (parcel sizes). Thus, the domain thickness was essentially about 11 times the largest parcel simulated for each drum size. This was done to minimize wall effects as much as possible. However, it is well known that with pseudo-2D drum cases wall effects persist and cannot be eliminated completely.

The Eulerian grid size was chosen such that there would be two grids in the z-direction (drum depth). This meant the grid size was 30 mm, which was greater than 3.5 times the largest parcel size. This was done so that grid size to largest particle size ratio was maintained high enough (above 3.5) to get a good particle samples per Eulerian grid for segregation calculations. This is generally essential to get a steady (low fluctuation) segregation index dynamics irrespective of the method used. Several previous works have maintained these criteria during segregation index studies as this provides a grid-size-insensitive results which is essential for quality data interpretation [30, 53].

Fig. 6

DPM parcel scaling used in this study to represent particles

Table 3 Standards for DPM scaling criteria

In case of drum size 5.0 m, due to large number of particle parcel requirement the drum depth in the z-direction was adjusted to 3.6 times the largest parcel size. This was to limit the number of particles or parcels needed to simulate the case. Simulations of smaller parcel scales had parcel numbers going into several millions. Table 4 shows this where with increasing large parcel size class the drum thickness was adjusted accordingly. Thus, in this case the drum depth direction had only 1 Eulerian grid.

Table 4 Drums of 5 m diameter size pseudo-2D thickness for varying DPM scale simulations

Table 5 Standards for DPM simulations

Fig. 7

Domain mesh grid partition used for simulating 5-m drum

The particle properties utilized for this drum scaling study are summarized in Table 5. The radially rotating curved walls were implemented with rotating or tangential velocity boundary condition that was as discussed earlier in Table 2 for different drum sizes. Besides, the side walls of the pseudo-2D drum were also given the same rotating boundary condition. Ideally, a periodic boundary condition for DPM particles would have been best suited. However, the DPM implemented in FLUENT has some particular stability issues due to which this was not possible.

Fig. 8

Long drum simulation showing the dynamic segregation from time $t = 2$ s to a steady-state image at time $t=100$ s

The particle containing Eulerian grid sizes varies substantially for different drum scales. As the drum size increases (for the same fill fraction) the particle containing Eulerian grids also increases. Thus, in this work, Lacey mixing index has been utilized which accounts for such factors influenced by drum scaling. Due to the large scale of 5.0 m drum simulation, up to 18-node parallelization was used. Figure 7 shows this partition in the drum cross-section. Here, the principal Y-axis inclined partition option in the FLUENT parallel optimization and load balancing tool was used. This partition rule created the angular 45-degree inclined partition that divided the granular rolling bed region uniformly between all the operating nodes and creating maximum parallelization efficiency. This partition rule was specifically used for 5-m drum with 2, 5 and 10 particle/parcel scaling simulation. It should be noted that massive parallelization does not necessarily lead to linear gain in speed. The 18-node parallelization provided the optimum speed and memory space needed for the particle simulation to be conducted in the needed time frame.

Lacey mixing index was developed using statistical analyzing and was used most extensively in many previous works [54]. The Lacey mixing index is based on the variance of a fully mixed and fully de-mixed system particle volume fraction. The particle volume fraction is evaluated based on an Eulerian grid (at least 3.5 times larger than largest particle) in the domain. The Lacey mixing index is given by:

$$\begin{aligned} S_{t}^\mathrm{Lacey} = \frac{\sigma _0^2 - \sigma ^2}{\sigma _0^2 - \sigma _r^2} \end{aligned}$$

(10)

where $\sigma$ represents the variance of a given particle size class fraction for a given grid cell. This is given by:

$$\begin{aligned} \sigma ^2 = \sum _{i=1}^{N_\mathrm{cell}} \frac{\alpha _i - \alpha _m}{N_\mathrm{cell}} \end{aligned}$$

(11)

where $\alpha _m$ is the mean particle volume fraction for a given size class and $\alpha _i$ is the particle volume fraction for the ith grid cell. $N_\mathrm{cell}$ was the number of grid cells in domain which is occupied by given size class of particles. $\sigma _0^2$ and $\sigma _r^2$ are the maximum and minimum variance as a function of the mean volume fraction $\alpha _m$ and number of particles per cell n. They are given by:

$$\begin{aligned} \sigma _0^2= & {} \alpha _m (1-\alpha _m) \end{aligned}$$

(12)

$$\begin{aligned} \sigma _r^2= & {} \alpha _m \frac{(1-\alpha _m)}{n} \end{aligned}$$

(13)

Lacey mixing index was an ideal choice for the segregation study done in this work as this study involved different scales of drum size and particle size. The primary purpose was to understand the dynamic variation of mixing index for the granular drums.

3 Results and discussion

3.1 Model validation simulations

Simulations were performed to validate the DPM model with experimental results from the literature [13]. This simulation was for a long horizontal drum operating at 11.6 RPM. This drum was initialized with particles of sizes 3, 4, 5 and 6 mm size uniformly distributed in a proportion described in the previous work [24]. The initial stage of simulation in the rolling regime at time $t = 2$ s is shown in Fig. 8 where the particles are well mixed. The well-mixed particles dynamically segregate and achieve a segregated steady state. This segregated state can also be seen clearly in Fig. 8 which was at time $t = 100$ s (or at 19.3 revolution).

The DPM model was further post-processed to validate dynamic and steady-state experimental measurement results. As discussed earlier, the dynamic segregation was measured with the average distance of different particle size class from the centre of mass of the bed. Figure 9 shows this dynamic radial segregation alongside experimental measurement. Similar to the previous work [24], the dynamic segregation in DEM was slower relative to experimental. However, the current spring-dashpot DPM model showed a relatively closer match with experiments relative to Hertzian DEM model of previous works where model segregation rate was slower.

The experimental measurements had a fluctuating behavior that can be observed in Fig. 9. But, interestingly the DPM model segregation parameters shows much less fluctuation here (Fig. 9). This, however, was not the case in previous works where much higher fluctuations were observed similar to experiments [24].

Post-segregation a steady state was achieved where no further segregative separation happens. For experimental measurement, this is achieved at about 4.5 revolutions and for simulations at about 5.5 revolutions. This steady-state datum was utilized to evaluate time-averaged velocity field. To perform this analysis, the reference frame co-ordinates were shifted (or rotated) by an angle equal to the dynamic repose angle. The co-ordinate axis is shown previously in Fig. 1. This is a common convention in analysis where the particle bed surface is observed horizontally with respect to the drum center [13]. Thus, the dynamic angle of repose generated by the rolling particle bed is a very important parameter for model validation of velocity field. The experimental drum showed an angle of repose of $27^{\circ }$ at the centre and $34^{\circ }$ near the side wall. In the current work, the dynamic angle of repose was $26^{\circ }$ and near the wall was $32^{\circ }$.

Fig. 9

Averaged radial distance dynamics from center of bed mass with respect to time for different particle size class

Table 6 Influence of friction coefficients on the dynamic angle of repose

As done in previous works, the right angle of repose (as in the experimental data) was obtained by adjusting the particle collision friction parameters [13]. Several of these parameters are known to influence; however, the most important factor was the friction coefficient glide $(\mu _\mathrm{gl})$ and limit $(\mu _\mathrm{li})$. Table 6 shows this sensitivity study performed in the range 0.05–0.3. As can be seen, the dynamic angle of repose of the bed reaches a maxima close to friction coefficient limit 0.1 and then it steady declines. Thus, the friction coefficient selection was made in the analysis.

Fig. 10

Time-averaged velocity field at the centre line co-ordinates

Fig. 11

Initialized pseudo-2D drum size 0.5 m for bi-disperse system of 1.7-mm and 3.0-mm particles

The axial velocity field at $x=0$ in the shifted reference frame was used to validate the velocity field with experimental data. This comparison is shown in Fig. 10. Since the shifted co-ordinates origin was at the drum center (Fig. 1), the x-direction velocity profile exists in the negative y-direction (active regime) where the particle bed surface was at about $y = -0.04$ m. The velocity field close to the free surface had a sharp negative velocity profile up to around $y = -0.06$ m where it crosses from active to passive regime. A relatively more flat velocity profile is formed in the positive direction from $y = -0.06$ m till $y = -0.12$ m at the drum boundary wall.

Fig. 12

Segregation phenomena occurring for drum size 0.25 m at different parcel scales

The tangential velocity at the drum wall boundary was 0.11 m/s. This shows the dense particle bed had a nearly no-slip velocity with respect to the wall boundary. The high particle–wall friction coefficient of 0.85 used (Table 5) achieves this low slip wall boundary velocity at $y = -0.12$. The flat velocity profile in the passive regime shows a high particle friction within the dense particle bed where particle relative velocities are low. Besides, the sharp linear velocity profile in the active regime shows a low collision particle friction at high relative particle velocity. This profile characteristics could be mimicked with the Fluent DPM model by using a high stick friction of 0.7 and low glide and limit friction of 0.11 and 0.1 (Table  5). The validation profile from simulations with such a setting is demonstrated in Fig. 10.

As can be seen in Fig. 10, the simulation velocity profile demonstrated by the spring-dashpot DPM model was not as sharp profile as the experimental velocity profile. However, in the previous works where Hertzian collision DEM model was used this profile matched relatively slightly better [24].

Fig. 13

Segregation phenomena occurring for drum size 0.5 m at different parcel scales

3.2 Drum and parcel scaling simulations

The experimental validation performed in the previous subsection demonstrated that the DPM model was suitable for rotary drum granular flow scaling study and analysis. Using particle properties similar to fertilizer-type particles (Table 5), DPM simulations were conducted in pseudo-2D rotary drum. As discussed earlier, these simulations were performed for 3 pseudo-2D drum scales (0.25 m, 0.5 m and 5.0 m) and 4 parcel scales (1, 2, 5 and 10 particles/parcel). The bi-disperse particles were initialized to create as much as possible a perfectly mixed granular system in the rotary drum. This typical particle or parcel initialization of drum is shown in Fig. 11 (at time $t = 0$ s). This particular initialization was for 0.5 m size drum.

The particle initialization was performed such that uniform distribution of particle size class could be achieved. This provided for a well-mixed system that had a high (Lacey) mixing index. Obviously the initialized particles settle onto the rotating drum bottom and enter into a rolling regime. The dynamic segregation of particles was monitored with time for all the drum simulations.

Figure 12 shows the drum simulations for 0.25-m and 0.5-m drum scales with 1 particle/parcel. These simulations are fundamentally the base case that helps understand the radial segregation effect with drum scaling. The well-mixed system segregated only for small scale drum (0.25 m). However, for the medium (0.5 m) scale drum the segregation dynamics was low. at time $t = 50$ s. Figure 12a shows the cross-sectional clipped view of the particle bed at time $t = 1.0$ s where the particles were well mixed. Note the clipped view was at midpoint of drum axis in the z-direction. Figure 12b shows the drum at time $t = 50$ s where the segregation is clearly visible for 0.25-m drum but not for 0.5-m drum.

Further, the particle size scaling studies were performed for each drum. In case of 0.25-m and 0.5-m drums, the simulation was performed for 3 parcel scales (1, 2 and 5). Figure 13a shows the medium-scale drum (0.5 m) in operation at time $t = 1.0$ s for different parcel scales, which were in a well-mixed condition. As can be seen in Fig. 13b, at time $t = 50$ s there was negligible segregation effect for 1 and 2 particle/parcel scaling. However, radial segregation was observed for the 5 particle/parcel scale simulations. A similar observation trend was made for the 0.25-m drum case where the 2 particle/parcel scaling simulations showed a limited segregation like that of 1 particle/parcel scaling simulations in Fig. 12. However, simulations with 5 showed a relatively higher segregation steady state.

The above simulation observations were well reflected in the Lacey mixing index plot with respect to time shown here in Fig. 14. The 1 particle/parcel mixing index initially begins at around 0.8 and reduces to 0.75 by 20 s for 0.25-m drum in Fig. 14a. The index remains steady at this level till the end at 120 s. This demonstrates the dynamic segregation leading to steady state. However, in case of medium-scale drum of 0.5 m the Lacey mixing index starts at 0.85 and remains nearly at the same value at end time of 120 s in Fig. 14b. Similarly, for large-scale drum the segregation rate is negligibly slow.

In terms of parcel scaling in 0.25 m drum, the Lacey mixing index for 2 (particle/parcel) showed a closer match with the base case, i.e. 1 particle/parcel. However, in case of 5 particle/parcel scale simulation the segregation rate was higher and the steady state was also relatively lower. This can be observed in the plot of Fig. 14a. In the 0.5-m drum simulations, the Lacey mixing index remains nearly constant at 0.85 for 1 and 2 particle/parcel scale. However, for the 5 particle/parcel scale the system segregated showing a breaks down relatively from the base mechanism. This was apparent from the plot in Fig. 14b.

The parcel scaling study for 0.25-m and 0.5-m drum shows that as the parcel sizes are scaled (increased) the particle segregation mechanism behavior deviates after a scaling point. This makes the parcel scaling valid only to a certain parcel scale limit. This limit for the 0.25-m and 0.5-m drum can be considered to be between 2 and 5 particle/parcel. It can also be anticipated that the parcel scaling limit for deviation is dependent on drum diameter size.

Fig. 14

Segregation phenomena occurring for drum size 0.25 m at different parcel scale

Fig. 15

Drum segregation Lacey mixing index for drum size 0.25 m with two different drum thicknesses

Fig. 16

Segregation Lacey mixing index for drum size 5.0 m at parcel scale 1–100 particle/parcel

An important aspect of pseudo-2D DPM simulation bed is the influence of side walls on the accuracy of simulations. As discussed earlier, the 0.25-m and 0.5-m size drums were simulated with 60 mm thickness and 5.0-m drum (industrial scale) was simulated at 3.6 times largest particle size. This was done due to the number limitation on large DPM simulation to save computation time. In order to check this, the simulation with 0.25-m drum was repeated with 3.6 times the large particle diameter thickness, i.e. 11 mm. Figure 15 shows this simulation for 0.06 and 0.011-mm drum thickness. Here it can be seen the Lacey mixing index was not much affected by reducing the drum thickness to 3.6 times the large particle diameter. Typically many previous works have used this lower limit for pseudo-2D DPM studies [30, 55, 56]. Below this thickness, it is believed that the side walls tend to influence the segregation. Thus, all simulations for the large-scale 5.0-m industrial drum were performed with drum thickness at 3.6 times the large particle diameter.

The simulations for this large-scale drum were conducted for 2, 5, 10, 25, 50 and 100 particle/parcel scaling. As expected, this was a computationally demanding exercise. Due to this, the 2 particle/parcel simulations were conducted till 25 s only. The 5 and 10 particle/parcel simulations were performed till 50 s. The 25 and 50 particle/parcel simulations were performed till 110 s. The 100 particle/parcel simulation was completed up to 120 s. The smaller parcel-scale simulations were relatively slow as the DPM tracking needed more time due to larger number. Thus, the simulations with smaller parcel size were conducted to a limited time. However, this already provided the necessary study results needed to make meaningful inferences.

The Lacey mixing index plot with respect to time for these simulation cases is shown in Fig. 16. These simulations showed negligible segregation dynamics for all the cases where the mixing index was close to 1.0. The simulation results showed minor shift in the Lacey mixing index value from 0.99 to 0.96 as parcel scaled from 2 to 100. The bi-disperse particles largely stay mixed for larger rotary drums with minimal segregation.

Fig. 17

Instantaneous DPM parcel (or particle) phase fraction on Eulerian grid cells within the cut-sectional view for 100 times parcel scaling at time $t=120$ s

Besides, the parcel scaling limit which was limited to between 2 and 5 particle/parcel scaling for smaller drums did not see any segregation dynamics deviation even at 100 particle/parcel scaling in large drum simulations. This is demonstrated in Fig. 17, which shows the simulation for the 5-m drum. Note that since the number of particles in these drum simulations was very high a good particle visualization for the drum cross-section was difficult. Therefore, the particle phase fraction on the Eulerian grid is used to represent in Fig. 17.

In this figure, the two cross-sectional drum particle phase fraction distributions are shown at time $t = 120$ s. The cross-sectional figure on left represents for only the smaller size parcels 8.3 mm (or equivalent to 1.7-mm-diameter particle). The cross-sectional figure on right represents the overall particle phase fraction. These figures clearly indicate particles are perfectly mixed with no segregation at 120-s simulations. This further demonstrates that for industrial-scale drums parcel scaling limit also increases.

It is well known that segregation in any rotary drum system occurs primarily on the active–passive boundary zone. Since the active–passive boundary zone in a rotating drum is an area, it does not scale directly with increasing drum size and bed mass. With respect to a cylindrical rotary drum, the drum size scales square of drum diameter and active passive boundary line might be scaling linearly with drum diameter. Thus, segregation rate should scale inversely with drum size. Thus, the segregation observations are natural where segregation rate decreases with increasing drum size.

The segregation time in the 0.25-m drum to reach steady state is about 15 s from Fig. 14a. If this is the case, then based on the above-discussed theory the segregation mechanism must achieve steady state at 30 s and 300 s for 0.5-m and 5-m drum cases. However, this does not seem to be the case at least for 0.5-m drum case in Fig. 14b where a steady state seems to be not achieved even at 120 s time. This shows that other granular collision properties or factors such as normal and tangential friction could be influencing the segregation while scaling.

4 Conclusion

This work performs DPM (spring dashpot) model simulations to match the long horizontal drum experimental results from the past works [13]. The current DPM model showed a reasonably good match of dynamic segregation with respect to time and time-averaged particle velocity field. The pseudo-2D drum segregation study with Lacey mixing index for (fertilizer-type particles) showed that only for (small scale) 0.25-m drum particles segregated. In case of 0.5 (medium scale) and 5.0 m (large scale), the segregation dynamics was extremely slow. Parcel scaling analysis was performed for each drum scales. This simulation results showed that at certain parcel scaling the segregation dynamics begins to deviate from base case (1 particle/parcel) simulations. In case of 0.25-m and 0.5-m drums, this deviation takes place between parcel scale 2 and 5 (particles/parcel). However, with large-scale drum of 5.0 m the parcel scaling up to 100 (particles/parcel) did not show any deviation. This shows with increasing drum size the parcel scaling limit (for reasonably matching segregation profile) also increases. Thus, allowing for more computationally cost-effective parcel scaled DPM simulations of industrial scale geometries. This study also showed that segregation time with respect to drum size scaling is not only dependent on active–passive boundary zone scaling. Particle collision properties seem to be influencing the segregation process.