Modified dynamic boundary conditions (mDBC) for general-purpose smoothed particle hydrodynamics (SPH): application to tank sloshing, dam break and fish pass problems

Abstract

Dynamic boundary conditions (DBC) for solid surfaces are standard in the weakly compressible smoothed particle hydrodynamics (SPH) code DualSPHysics. A stationary solid is simply represented by fixed particles with pressure from the equation of state. Boundaries are easy to set up and computations are relatively stable and efficient, providing robust numerical simulation for complex geometries. However, a small unphysical gap between the fluid and solid boundaries can form, decreasing the accuracy of pressures measured on the boundary. A method is presented where the density of solid particles is obtained from ghost positions within the fluid domain by linear extrapolation. With this approach, the gap between fluid and boundary is reduced and pressures in still water converge to hydrostatic, including the case of a bed with a sharp corner. The violent free-surface cases of a sloshing tank and dam break impact on an obstacle show pressures measured directly on solid surfaces in close agreement with experiments. The complex 3-D flow in a fish pass, with baffles to divert the flow, is simulated showing close agreement with measured water levels with weirs open and gates closed, but less close with gates open and weirs closed. This indicates the method is suitable for rapidly varying free-surface flows, but development for complex turbulent flows is necessary. The code with the modified dynamic boundary condition (mDBC) is available in DualSPHysics to run on CPUs or GPUs.

Introduction

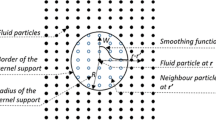
Smoothed particle hydrodynamics (SPH) is a meshless Lagrangian particle numerical method particularly adept at modelling complex, highly deforming interfacial and free-surface flows. In recent years, SPH numerical schemes have been successfully applied to a number of different phenomena, including sloshing tanks [1], sediment scour [2], debris flows [3], flow around bodies [4] and submarines [5], landslides and flooding [6, 7], fish pass flows [8], wave action on breakwaters [9] with encouraging results. The SPH method is based on an integral approximation incorporating a kernel function (typically of compact support and characterised by a smoothing length, h). The meshless nature of SPH and the issue of kernel truncation near boundaries can create difficulties in enforcing solid boundary conditions, and, accordingly, boundary conditions have been highlighted as one of the Grand Challenges of SPH [10]. A recent review addressing accuracy in SPH is provided by Lind et al. [11], and a review of applications in coastal and ocean engineering is available in Gotoh and Khayyar [12]

Many different approaches have been proposed in the literature to enforce solid boundary conditions, and they can be grouped into three main types: the first approach is the method of repulsive forces ([13, 14]), which enables the discretization of 2-D and 3-D irregular geometries. However, non-physical forces are added to prevent particle penetration and kernel truncation is not addressed and so the accuracy of SPH spatial interpolation near the walls is remarkably reduced. A second possible way to discretize the boundaries is the so-called semi-analytical formulation ([15,16,17]) where additional terms in the conservation equations are considered to compensate for the kernel truncation. At continuous level, there are no terms of SPH spatial interpolation, but when the particle discretization is introduced, surface integrals have to be approximated and this remains a challenge for complex 3-D geometries and/or multi-phase flows. The third class of boundary methods are based on fictitious particles to fill the space beyond the boundary interface to mimic the presence of a wall ([18,19,20,21]). A hybrid of the first and third classes has also been proposed [22]. The method herein proposed belongs to the third class and may be considered an extension of the dynamic boundary condition (DBC) currently used in the online version of DualSPHysics [23].

DualSPHysics [23] is an open source SPH code for simulating free-surface flows that is able to run on both CPUs and GPUs (graphics processing units) [24]. Using DBC, complex geometries can be created such as those in [3, 8] and [9]. This tackles one of the aspects of the Grand Challenge on boundary condition in SPH [10]. However, with DBC unphysical gaps form between the boundary and fluid particles. The work of [9] estimated the size of the gap to be of the order of the kernel smoothing length, but a realistic surface pressure may be obtained at this distance from the surface.

The main purpose of the present work is thus to avoid some of the limitations of DBC, while maintaining the capability for discretizing complex geometries, without affecting the efficiency of the GPU implementation. To reduce the gap and increase the accuracy of the pressure measured at the boundary particles, we follow the approach of [19] for updating physical quantities of the boundary particles by means of a first-order consistent SPH interpolation evaluated at ghost nodes, located inside the fluid domain. First-order consistency in the boundary is obtained by introducing the SPH corrected interpolation proposed in [25]. In this way, the flow properties may be extrapolated into the boundary and a fluid continuum is presented. Finally, the use of an adequate number of layers of boundary particles prevents inconsistencies due to kernel truncation effects for fluid particles located near the boundaries, as discussed in the early work of Vacondio et al. [26]. The corrected SPH interpolation herein adopted does not require an additional particle sweep, and thus the computational overheads of the proposed correction are low. The modified boundary conditions are named mDBC (modified DBC).

This paper is organised as follows: in Sect. 2 the SPH method used in this work is outlined; in Sect. 3 the DBC methodology is described and the advantages and issues with the method highlighted along with the new mDBC method. In Sect. 4 results for a number of 2D and 3D test cases are presented comparing between the existing DBC and the new mDBC, finally in Sect. 5 conclusions of the work are provided along with suggestions for future work.

SPH methodology

The open source SPH solver DualSPHysics is described as follows. The conservation of mass is defined in compressible form, including the density diffusion term

$$ \frac{{{\text{d}}\rho_{i} }}{{{\text{d}}t}} = \mathop \sum \limits_{j} m_{j} {\varvec{v}}_{ij} \cdot \nabla W_{ij} + \delta hc_{0} \mathop \sum \limits_{j} \frac{{m_{j} }}{{\rho_{j} }}\Psi_{ij} \cdot \nabla W_{ij} $$

(1)

where $\rho_{i}$ is particle density, $m_{i}$ its mass,$c_{0}$ is the speed of sound in the fluid, ${{\varvec{v}}}_{ij}= {{\varvec{v}}}_{i}-{{\varvec{v}}}_{j}$ is the velocity difference between particles $i$ and $j$, and ${\nabla W}_{ij}$ is the kernel gradient. $\delta$=0.1 is generally applied. The SPH kernel used in this work is the quintic Wendland kernel [27] given by

$$ W_{ij} = \alpha_{D} \left( {1 - \frac{{r_{ij} }}{2h}} \right)^{4} \left( {1 + \frac{{2r_{ij} }}{h}} \right) \quad for\; 0 \le {\varvec{r}}_{ij} \le 2h $$

(2)

where ${{\varvec{r}}}_{ij}$ is the distance between particles, $h=\kappa dp$ is the smoothing length ($\kappa =1.3$ or $2$ in this work) and the normalisation term ${\alpha }_{D}=7/4\pi {h}^{2}$ in $2\mathrm{D}$ and ${\alpha }_{D}=21/16\pi {h}^{3}$ in $3\mathrm{D}$. Two options for the density diffusion function ${\Psi }_{ij}$ are used, the first of Molteni and Colagrossi [28] is given by

$$ \Psi_{ij}^{{{\text{MOL}}}} = 2\left( {\rho_{j} - \rho_{i} } \right)\frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} }} $$

(3)

The second option is that of Fourtakas et al. [21] and is given by

$$ \Psi_{ij}^{{{\text{FOUR}}}} = 2\left( {\rho_{ji}^{T} - \rho_{ij}^{H} } \right)\frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} }} $$

(4)

where ${\rho }^{T}$ and ${\rho }^{H}$ are the total hydrostatic densities. The conservation of momentum is given by

$$ \frac{{{\text{d}}{\varvec{v}}_{i} }}{{{\text{d}}t}} = - \mathop \sum \limits_{j} m_{j} \left( {\frac{{P_{j} + P_{i} }}{{\rho_{i} \rho_{j} }} + \Pi_{ij} } \right)\nabla W_{ij} + {\varvec{g}} $$

(5)

where ${\varvec{g}}$ is the acceleration due to gravity, ${P}_{i}$ is the particle pressure and ${\Pi }_{ij}$ is the artificial viscosity given by

$$ \Pi_{ij} = \left\{ {\begin{array}{*{20}l} { - \alpha \frac{{c_{0} }}{{\rho_{i} + \rho_{j} }}\frac{{h{\varvec{v}}_{ij} \cdot {\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} + 0.01h^{2} }}} & {{\text{for}}\;{\varvec{v}}_{ij} \cdot {\varvec{r}}_{ij} < 0} \\ 0 & {{\text{for}}\;{\varvec{v}}_{ij} \cdot {\varvec{r}}_{ij} \ge 0} \\ \end{array} } \right. $$

(6)

A standard value of $\alpha = 0.01$ will be used unless otherwise stated.

Finally, the pressure is given by the Tait equation of state

$$ P = \frac{{c_{0}^{2} \rho_{0} }}{\gamma }\left[ {\left( {\frac{\rho }{{\rho_{0} }}} \right)^{\gamma } - 1} \right] $$

(7)

where ${\rho }_{0}=1000$ kg/m³ is the reference density of water and $\gamma =7$.

Time stepping is by the Symplectic predictor–corrector option with time step given a CFL (Courant–Friedrichs–Lewy) value of 0.2. The speed of sound is usually given a value of 10$\times$ times the wave speed, $\sqrt{gH}$, where g is the modulus of the gravitational acceleration and H is initial water depth.

Note that the SPH formulation adopted in the present work is variationally consistent and therefore conserves mass, linear and angular momentum. In particular, the conservative form of the momentum equation (Eq. (5)) is used here and it is used both for fluid–fluid and fluid-boundary interactions. Mass is also conserved, as in the proposed scheme each particle carries its own mass during the simulation. This allows the continuity equation to be written in non-conservative form (Eq. (1)) without breaking conservation of relevant physical quantities and allows density to be assigned to boundary particles through a consistency correction (Eq. (12)) which improves remarkably the accuracy of the pressure field.

mDBC formulation

Dynamic boundary conditions were first introduced in [29] and further studied in [18]. The boundaries consist of a set of particles that satisfy the same continuity equation as the fluid particles. To approximate the no-slip condition at solid boundaries, the velocities of the boundary particles are set to zero. The repulsion mechanism generated by the dynamic boundary particles works in the following way: the incoming fluid particle increases the density locally according to the continuity equation (Eq. 1), which results in an increase in pressure following equation of state (Eq. 7) and in an increase in the pressure term ($({P}_{j}+{P}_{i})/{\rho }_{i}{\rho }_{j}$). In consequence, this increase in the pressure term in momentum equation (Eq. 5) will lead to an increase in the acceleration magnitude ($\mathrm{d}{\varvec{v}}/\mathrm{d}t$) for the incoming fluid particle, which defines the repulsion force. The study of Domínguez et al. [30] showed how it is evident that as a repulsive force, this boundary keeps the particles at a certain distance from the boundary, and this “gap” was found to be of the order of the smoothing length (h). Therefore, this approach presents a drawback in that the evolution of density and pressure of the fixed boundary particles leads to unphysical values at the surface, with unphysically large boundary layers in the flow. The boundary pressure has to be output at a distance of a smoothing length from the actual surface to be representative and the dynamic boundary particles need to be initially created considering that “gap” in order to generate the repulsion force at the desired boundary limit. On the other hand, an advantage of these boundary particles is their computational simplicity, since density, and therefore pressure, can be calculated inside the same loops as fluid particles with a considerable saving of computational time. These conditions are able to represent complex shaped geometries. Validations with dam-break flows and wave flumes have been published and DBC has been successfully applied to coastal engineering problems, discretizing complex 3D geometries without the need for implementing complex mirroring techniques or semi-analytical wall boundary conditions. A good example is the work of Zhang et al. [9] where DualSPHysics was used to reproduce a laboratory test where a porous breakwater structure made of cubes was analysed. The SPH results were obtained for 52 numerical wave probes, and good agreement was obtained for this complex problem.

We propose here a new method to palliate the problems described for DBC that is named mDBC (modified dynamic boundary conditions). The boundary particles of mDBC are arranged in the same way as the boundary particles in the original DBC, with an additional boundary interface created between the fluid and the boundary particles. The boundary interface is located half a particle spacing ($dp/2$) from the layer of boundary particles closest to the fluid. For each boundary particle, a ghost node is projected into the fluid across the boundary interface in a procedure similar to Marrone et al. [19]. For a flat surface, the ghost node is mirrored across the boundary interface along the direction of the boundary normal pointing into the fluid (Fig. 1a) and fluid properties are found at this ghost node through a first-order consistent SPH spatial interpolation over the surrounding fluid particles only (Fig. 1b). For a boundary particle located in a corner, the boundary normal is ill defined with more than one option. However, the boundary interfaces of each solid boundary meet to form an interface corner, and the ghost node is mirrored through the point of this corner into the fluid region (Fig. 1c). Again, fluid properties are found at the ghost node through a first-order consistent SPH spatial interpolation of the surrounding fluid (Fig. 1d).

Fig. 1

Mirroring of ghost nodes (crosses) and the kernel radius around the ghost nodes for boundary particles in a flat surface (a) and a corner (c). Fluid particles (pink) included in the kernel sum around ghost nodes for boundary particles in a flat surface (b) and a corner (d)

The boundary particles receive fluid properties using the values calculated at the ghost node and an extrapolation method similar to the one used for open boundaries in [31]. For the density of the boundary particle ${\rho }_{b}$ the ghost density ${\rho }_{g}$ and its gradient $\left[{{\partial }_{x}\rho }_{g}; {{\partial }_{y}\rho }_{g}; {{\partial }_{z}\rho }_{g}\right]$ are computed at the ghost node using the first-order consistent SPH interpolation proposed by Liu and Liu [25], which requires solving the following linear system for each ghost node:

$$ {\mathbf{A}}_{g} \cdot \left[ {\begin{array}{*{20}c} {\rho_{g} } \\ {\partial_{x} \rho_{g} } \\ {\partial_{y} \rho_{g} } \\ {\partial_{z} \rho_{g} } \\ \end{array} } \right] = {\mathbf{b}}_{g} $$

(8)

where:

$$ {\mathbf{A}}_{g} = \left[ {\begin{array}{*{20}c} {\mathop \sum \limits_{j} W_{gj} V_{j} } & {\mathop \sum \limits_{j} \left( {x_{j} - x_{g} } \right)W_{ij} V_{j} } & {\mathop \sum \limits_{j} \left( {y_{j} - y_{g} } \right)W_{gj} V_{j} } & {\mathop \sum \limits_{j} \left( {z_{j} - z_{g} } \right)W_{gj} V_{j} } \\ {\mathop \sum \limits_{j} \partial_{x} W_{gj} V_{j} } & {\mathop \sum \limits_{j} \left( {x_{j} - x_{g} } \right)\partial_{x} W_{ij} V_{j} } & {\mathop \sum \limits_{j} \left( {y_{j} - y_{g} } \right)\partial_{x} W_{gj} V_{j} } & {\mathop \sum \limits_{j} \left( {z_{j} - z_{g} } \right)\partial_{x} W_{gj} V_{j} } \\ {\mathop \sum \limits_{j} \partial_{y} W_{gj} V_{j} } & {\mathop \sum \limits_{j} \left( {x_{j} - x_{g} } \right)\partial_{y} W_{ij} V_{j} } & {\mathop \sum \limits_{j} \left( {y_{j} - y_{g} } \right)\partial_{y} W_{gj} V_{j} } & {\mathop \sum \limits_{j} \left( {z_{j} - z_{g} } \right)\partial_{y} W_{gj} V_{j} } \\ {\mathop \sum \limits_{j} \partial_{z} W_{gj} V_{j} } & {\mathop \sum \limits_{j} \left( {x_{j} - x_{g} } \right)\partial_{z} W_{ij} V_{j} } & {\mathop \sum \limits_{j} \left( {y_{j} - y_{g} } \right)\partial_{z} W_{gj} V_{j} } & {\mathop \sum \limits_{j} \left( {z_{j} - z_{g} } \right)\partial_{z} W_{gj} V_{j} } \\ \end{array} } \right] $$

(9)

$$ {\mathbf{b}}_{g}^{T} = \left[ {\begin{array}{*{20}c} {\mathop \sum \limits_{j} W_{gj} m_{j} } & {\mathop \sum \limits_{j} \partial_{x} W_{gj} m_{j} } & {\mathop \sum \limits_{j} \partial_{y} W_{gj} m_{j} } & {\mathop \sum \limits_{j} \partial_{z} W_{gj} m_{j} } \\ \end{array} } \right] $$

(10)

where the volume $V$ _j is computed as ${V}_{j}={m}_{j}/{\rho }_{j}$.

To evaluate the matrix ${\mathbf{A}}_{g}$ and the vector ${\mathbf{b}}_{g}$ at each ghost node $g$, a new particle interaction loop needs to be set up. The new interaction requires the inversion of the matrix ${\mathbf{A}}_{g}$; however, this requires limited additional computational effort when compared to the original DBC formulation. Note also that the matrix ${\mathbf{A}}_{g}$ is diagonally dominant and in most cases remains well-conditioned (with condition numbers of O(10) even for disordered particle distributions) provided there is near complete support. Due to this property, the adopted formulation to compute ${\rho }_{g}$ and $\left[{{\partial }_{x}\rho }_{g}; {{\partial }_{y}\rho }_{g}; {{\partial }_{z}\rho }_{g}\right]$ is still suitable for real engineering applications with complex surfaces. If ghost node neighbours decrease to very low numbers (e.g. less than 3 or 4 fluid particles), the A_g matrix does become ill-conditioned and the matrix is not inverted. The density at the ghost node is then found through a Shepard filter evaluated at the ghost node according to:

$$ \rho_{g} = \frac{{\mathop \sum \nolimits_{j} \rho_{j} W_{gj} V_{j} }}{{\mathop \sum \nolimits_{j} W_{gj} V_{j} }} $$

(11)

Once the density and density gradient are computed at the ghost node, then the density of the boundary particle ${\rho }_{\mathrm{b}}$ is obtained by means of a linear extrapolation with the values found using the above relations through:

$$ \rho_{b} = \rho_{g} + \left( {{\mathbf{r}}_{{\text{b}}} - {\mathbf{r}}_{{\text{g}}} } \right) \cdot \left[ {\partial_{x} \rho_{g} ; \partial_{y} \rho_{g} ; \partial_{z} \rho_{g} } \right] $$

(12)

where ${{\varvec{r}}}_{\mathrm{b}}$ and ${{\varvec{r}}}_{\mathrm{g}}$ are the position of the boundary particle and associated ghost node, respectively. In this way, the boundary density is presented as part of a fluid continuum and pressure from the equation of state gives smoother and more physical pressure fields, avoiding the non-physical gap between the boundary and the fluid observed when using DBC. If the matrix is ill-conditioned, the boundary particle is given the Shephard filtered ghost node density found in Eq. (11). The boundary particles have zero velocity as before. As the boundary velocity is set to zero for all boundary particles; by definition, ${\varvec{u}}\bullet {\varvec{n}}=0$ (as ${\varvec{u}}=0$) is guaranteed on the boundary. It is noted, however, that this approach is at best first order for velocity and velocity gradients on and near the boundary are in general not as well approximated as they are in other velocity boundary condition approaches (see [19], for example). Neumann boundary conditions on the pressure, however, are approximated at higher order following from the formulation above, and this is sufficient to significantly improve results over the standard DBC.

Results

This section will show the capabilities of mDBC and the improvements comparing with original DBC. Initially 2D simulations are investigated including still water with a triangular corner (a wedge) and a sloshing tank, and the 3D cases of a dam break impacting a cuboid obstacle, and flow through a fish pass. In each test case the performance of the boundary conditions will be assessed.

Still water on bed with a wedge (sharp corner)

A 2D still water tank with dimensions of 2.4 m × 1.2 m encloses a trigonal wedge in the bottom centre of the tank with a height of $0.24$ m. The initial water height is $H=0.5$ m. Results are analysed during 4 s of physical time. The ratio of smoothing length $h$ to initial particle spacing $dp$, $h/dp=2$. Two simulations with different resolutions were executed (dp = 0.02 m and dp = 0.01 m).

The final instant (t = 4 s) is depicted in Fig. 2 for the two different resolutions and using DBC (left) and mDBC (right). The first row corresponds to dp = 0.02 m and the second row to dp = 0.01 m. Good results and improvements can be observed using mDBC with smoother and more physical pressure values now being obtained for the boundary particles, not only in the flat surface but also in the corners. Figure 3 shows more detail at the corners for the case with dp = 0.01 m, where this improvement becomes more apparent.

Fig. 2

Pressure in a 2D still water tank: last instant of the simulation for: a DBC dp = 0.02 m; b mDBC dp = 0.02 m; c DBC dp = 0.01 m, and d mDBC dp = 0.01 m

Fig. 3

Last instant of the still water simulation: a DBC dp = 0.01 m, and b mDBC dp = 0.01 m (close up of the pressure field in the corners)

The vertical distribution of pressure is plotted to show the accuracy of the hydrostatic pressure distribution. Values of depth ($z/H$) against pressure ($p/\rho gH)$ are plotted in Fig. 4 (at 4 s) for each fluid particle. For both resolutions, much improved hydrostatic pressure behaviour is obtained using mDBC, accurate down to the solid surface. In addition, the kinetic energy of the particles is measured. The time series for the summation of kinetic energy of all the fluid particles is shown in Fig. 5 (note a logarithmic scale is used). It is clear that mDBC generates much smaller particle movement than DBC. Runs up to 20 s showed negligible noise in the pressure, but a small amount of noise became apparent around 200 s.

Fig. 4

Particle pressure values versus depth at last instant of the still water simulation for: a DBC dp = 0.02 m; b mDBC dp = 0.02 m; c DBC dp = 0.01 m, and d mDBC dp = 0.01 m

Fig. 5

Time series of fluid particles kinetic energy during the still water simulation for initial partial spacings a dp = 0.02 m and b dp = 0.01 m

Sloshing tank (moving boundaries)

The second 2D test case reproduces an experiment with moving boundaries. This is the SPHERIC Benchmark Test Case 10 (https://spheric-sph.org/tests/test-10), consisting of a sloshing tank of 0.9 m × 0.508 m with an initial water level $H=0.093$ m (Fig. 6). The numerical pressures are obtained using DBC and mDBC and compared with the experimental values detected at Sensor 1 (Fig. 6). Two simulations with different resolutions are executed ($dp=0.004$ m and $dp=0.002$ m), again with $h/dp=2$.

Fig. 6

Initial setup of the sloshing tank including location of pressure sensor 1 and the centre of rotation denoted as COR

The instant of the simulation at time t = 2.47 s seconds is shown in Fig. 7, where the first impact of the fluid with left wall (Sensor 1) has just occurred. The colour of the particles corresponds to their pressure values.

Fig. 7

Sloshing tank simulation at time t = 2.47 s, with: a DBC dp = 0.004 m; b mDBC dp = 0.004 m; c DBC dp = 0.002 m, and d mDBC dp = 0.002 m

Figure 8 shows in more detail the pressure field of the particles with DBC (left) and mDBC (right) with $dp=0.002$ m. Two improvements can be observed using mDBC: (i) values of pressure for the boundary particles in the walls using mDBC are less noisy than the ones shown for DBC and (ii) the unphysical gap between the fluid and the boundary is negligible when mDBC is used. This is an important improvement since the computation of pressure values at Sensor 1 (Fig. 6) with DBC provides representative results only if the numerical pressure gauge is moved to take into account the size of the gap between the fluid and the boundary. The work of [32] estimated the size of the gap to be the smoothing length ($h$). There is a small high pressure region seen towards the top of the boundary of Fig. 8(b), which is a spurious but ineffectual pressure carried from a previous time step. This may occur when there are no nearby fluid particles: the correction matrix (Eq. (9)) does not meet the criteria to be solved due to its poor conditioning and the Shepard filter (Eq. 11) cannot be used as there are no fluid particles near a ghost node. This spurious pressure is not a concern in practice as it only results when there are no nearby fluid particles (within the support length of the ghost node) and so can have no effect on the fluid dynamics. As soon as there is fluid near the boundary, the correction matrix is able to solve and so provides correct densities (and pressures) in the boundary.

Fig. 8

Sloshing tank simulation at the time t = 2.47 s, close up of the pressure field in the corner and the lateral wall for DBC boundary (left) and mDBC boundaries (right)

The experimental pressure (black line) is compared with numerical results in Fig. 9. The blue line, in the first row, corresponds to numerical pressure computed using DBC with pressure gauge at the original location; however the results are erroneous due to the large gap (in the order of $h$) without fluid particles. The second row shows the numerical pressure (green line) using DBC with pressure gauge moved $+h$ into the fluid, much improving agreement with experimental data. However the use of mDBC, avoiding the gap and creating a realistic boundary layer, allows the computation of pressure at the exact location of the gauge obtaining very good results; the red line in the bottom panel of Fig. 9 shows again a good agreement with the experimental data. Note that negative pressures are observed in the experimental data and the mDBC numerical data around the time of the most violent impacts, coinciding with highly transient pressure shocks rebounding after high velocity water impact. The fact these transients are captured provides a further demonstration of the benefit of the mDBC approach over DBC. While persistent negative pressures can be an issue in SPH (leading potentially to the tensile instability), no evidence of this instability was observed here as the negative pressure event is so short-lived (existing for only O(1) time steps).

Fig. 9

Comparison of experimental and numerical ($dp=0.002$ m) pressures measured at probe location P1 with: (top) DBC and numerical probe in the correct location; (middle) DBC and numerical probe placed a distance of h from the wall, (bottom) mDBC with numerical probe in the correct location

3D Dam break over cuboid obstacle

This is the SPHERIC Benchmark Test Case 2 (https://spheric-sph.org/tests/test-2) shown in Fig. 10; surface elevation was measured at positions H1, H2, H3 and H4 and pressures on the centreline plane of the cuboid obstacle surface [33]. Particle spacings $dp =0.01$ m and 0.02 m were applied giving a particle number close to 1 million and 170,000, respectively. In this case $h/dp=1.3.$

Fig. 10

The geometric configuration of initial conditions for the dam break and obstacle (left) and pressure measurement points (right)

Results of surface elevation at H4, H3, H2 are shown in Fig. 11 to be in close agreement with experiment, closer than DBC which shows a spurious value for H2 for small time.

Fig. 11

3D Dam Break over cuboid obstacle: surface elevations at measured at points H4 (left), H3 (middle) and H2 (right)

Figure 12 shows the particle distribution at $t=0.8$ s with jet height close to maximum, and the spurious DBC value at H2 is due to jet formation too far upstream, in front of the obstacle.

Fig. 12

Dam break at t = 0.8 s from DBC and mDBC showing extent of jet formation

Pressures are shown at P2 (front face) and P5 (top corner of upper surface) in Fig. 13. For P2 agreement of mDBC with experiment is again close, generally closer than DBC. The peak pressures for P2 are in close agreement with experiment. Note again that DBC requires measurement at + h from the surface. For P5 mDBC with finer resolution is generally close to experiment as is DBC. Now the coarser mDBC shows some spurious fluctuations not present with the finer resolution.

Fig. 13

Time variation of pressure at probe P2 (left), probe P2 focussing on the first peak (middle) and probe P5 (right)

This test case demonstrates how SPH with mDBC predicts highly transient free surface flow and pressures quite accurately.

Fish pass

The complex 3D test case of a fish pass, as shown in Fig. 14, is now simulated. A fish pass is a structure that facilitates the natural migration of some species of fish on or around artificial and natural barriers (such as dams, locks and waterfalls). Technical fish passes include: pool and weir fish passes, which is the type treated in the present work; vertical slot fish passes, and Denil fish passes. The principle of a pool and weir fish pass is to divide a channel by installing cross-walls, in order to form a succession of stepped pools from the headwater to the tailwater. The discharge usually passes through openings in the cross-walls and fishes migrate from one pool to the next through the submerged orifices (or gates) or through the notches (or weirs). Previous examples of fish pass flows being simulated using DualSPHysics with DBC include the work of Novak et al. [8] for a vertical slot type fish pass.

Fig. 14

Fish pass: a scheme of the experimental setup, note reference z = 0 on wall 3; b detail of a vertical cross baffle; c 3-D view of the flow domain, showing pools, gates and weirs

The fish pass considered here comprises a long channel inclined at an angle of 4.5° to the horizontal with vertical cross baffles restricting the flow, dividing the pass into three pools. Each of the baffles has a gate in one of the bottom corners and a weir in the opposite top corner, the orientation of the gates and weirs alternates between pairs of baffles, as shown in Fig. 15. For this case $h/dp=1.3$, α in the range 0.01 (standard) to 0.001 was tested and particle shifting based of Fick’s equation [34] was applied to regularise the particle distributions. The particles are shifted a distance $\delta {{\varvec{r}}}_{s}$ according to the equation

$$ \delta {\varvec{r}}_{s} = \user2{ } - D\nabla C_{i} $$

(13)

where $C$ is the particle concentration and $D$ is the diffusion coefficient given by Skillen et al. [34] as

$$ D = A h {\varvec{u}}_{i} {\text{d}}t $$

(14)

where $A$ is a dimensionless constant which takes the value $A=2$ for this case.

Fig. 15

Water levels with gates open in pools 1 (top) and 2 (bottom) for flow rate Q2, results averaged using a moving mean over 0.3 s

Experiments conducted at the University of Parma are used for comparison. Five test cases were measured: two involving flow only through the gates; three involving flow over only the weirs. The flow rates and water depths are shown in Table 1.where all the water depths are measured with respect to the base of the weir in wall 3.

Table 1 Flow rates and water depths measured with respect to weir 3 for fish pass test cases

The numerical fish pass uses the inflow-outflow boundary conditions described in [31] to control the fluid particles entering and leaving the channel. The inlet is created in the centre of the upstream pool and the outlet in the centre of pool 3. To set up steady conditions, the experimental levels in each pool are first input and velocities are increased to provide the experimental flow rate. The correct flow rates are then maintained at inlet and outlet and water levels may be compared with experiment. H_in is the depth in the inlet zone above the base of the weir in Gate 3 ($z=0$ in Fig. 14). H1, H2, H3 are depths in the centre of pools 1, 2, 3.

Gate only cases

We consider Q2 with an initial particle spacing of $dp=0.01$ m (150,827 particles), $dp=0.005$ m (914,467 particles) and $dp=0.0025$ m (6,234,131 particles); results for Q1 were similar. Water level results are shown in Fig. 15. The water level in pool 1 with the smallest spacing is in close agreement with experiment although in pool 2 it is 0.0075 m, or three particle spacings, different.

Weir only cases

For the cases Q3–5 flow is only allowed to pass over the weirs, as the gates have been blocked off. Two particles spacings of $dp=0.01$ m (207,784 particles) and $dp=0.005$ m (1,372,059 particles) are used. We show results for Q5 as all cases are quite similar and the water levels are in close agreement with experiment, within one particle spacing, shown in Fig. 16.

Fig. 16

Water levels with weirs open in pools 1 (top) and 2 (bottom) for flow rate Q5, results averaged using a moving mean over 0.3 s

These results show that flow through a very complex geometry may be modelled with mDBC. The results with weir only show very close agreement with experiment while those with gate only were less close. This is probably because rapidly varying free surface flows are well suited to SPH, corresponding with accelerated flow over the weirs. With accelerated flow through the gates and relatively tranquil free surface flow, mixing due to turbulence will be significant and the SPH model does not have a turbulence model. With the flow over the gates mixing due to the jets over the gate is gravity dominated. Flow visualisation is shown in Fig. 17 for flow rate Q3 with particle spacing $dp=0.005$ m.

Fig. 17

Flow over weirs from SPH simulation with contours showing velocity magnitude, the set up shown if for flow rate Q3 with particle spacing $dp=0.005$ m (1,372,059 particles)

Computational performance

The computational performance of DualSPHysics on GPUs with mDBC and DBC is of practical importance as real problems generally require high resolution. This section compares the runtimes of DBC and mDBC for the same resolution, although mDBC achieves a given level of accuracy with lower resolution than mDBC. The performance of both boundary conditions is presented for two cases on a CPU for reference and on different generations of GPUs. The CPU device used here is an Intel Core i7-6700 K with a clock speed of 4.0 GHz and 8 execution threads (4 physical cores). The specifications of the GPU cards (commonly used for numerical computing) are shown in the Table 2.

Table 2 GPU specifications

Two SPHERIC benchmark cases are selected to analyse the performance with the different boundary conditions; a 2-D case with moving boundaries and a 3-D problem. The 2-D sloshing tank case shown in Sect. 4.2 was simulated for 7 physical seconds using dp = 0.002 m and 26,791 particles. This simulation was executed on the devices in Table 2, and the runtimes are shown in Table 3 with the ratio mDBC to DBC runtime. The 3-D dam break case was simulated for 6 physical seconds using dp = 0.02 m (172,422 particles) and dp = 0.01 m (1,015,809 particles). The execution times of the 3-D dam break case described in Sect. 4.3 are included in Table 4.

Table 3 Runtimes of the 2-D sloshing tank simulation using dp = 0.002 m with different hardware devices

Table 4 Runtimes of the 3-D dam break simulation with different hardware devices

The use of mDBC thus results in a 10–20% increase in execution time over DBC for 2-D and 3-D simulations for the same resolution. This increase depends on the number and distribution of boundary and fluid particles of the simulation case, since extra calculation time is required for the interpolation carried on the ghost nodes projected from the boundary particles into the fluid domain. In practice a given level of accuracy may be achieved with mDBC with a lower level of resolution than DBC, reducing execution time below that for DBC.

Conclusions

The dynamic boundary condition has been improved by providing solid boundary particles with density extrapolated from mirror positions within the fluid without sacrificing any of the robustness of the original formulation. Pressure on a solid surface is predicted accurately. This has been demonstrated for the still water case with a sharp corner by recovering hydrostatic pressure; for the dynamic 2D SPHERIC test case 10 of the sloshing tank; for the 3D SPHERIC test case 2 of the dam break impacting a cuboid obstacle; and for the new complex test case of fish pass flow with several gates and weirs. Agreement with experiment is good for the weirs only case where the flow is gravity dominated and less good for the gates only case with turbulent mixing and a tranquil free surface. The computational overhead on the original DBC is less than 25% and depends on application and the choice of GPU. However, this is more than compensated by mDBC enabling realistic simulation with lower resolution and a smaller number of particles. DualSPHysics is now available with this functionality. This capability should be particularly beneficial for complex problems requiring high resolution such as the rubble mound breakwater [32] and marine vehicles [5] studied previously with DBC.

Further work will allow fluid velocity at mirror points to be extrapolated to solid boundary particles. This will allow for the creation of more accurate no-slip boundaries as well as slip and partial slip boundaries for some non-Newtonian applications.