1 Introduction

Today, the transport of cargo by sea constitutes almost 90\(\%\) of world trade. According to a recent report [1], the amount of total cargo transported by ship has increased by almost 300\(\%\) over the last two decades. With the increase in ship traffic, the risk of ship collisions has increased as well. Several strategies regarding increased ship safety and improved risk analysis are presented in [2]. Furthermore, several design approaches to increase the crashworthiness of double hull ship are investigated in [3, 4]. Recently, Schöttelndreyer [5] proposed a design that helps to increase the potential crash energy absorption of a double hull ship by filling the compartment between the inner and the outer hull of the ship with lightweight granular materials. In [6, 7], the properties and bulk behavior of suitable granular materials, namely expanded glass granules, are investigated in detail. As mentioned in [8], the granular material should be able to increase the crashworthiness of ship, but should not increase its weight too much. Therefore, its usage is recommended in critical region only rather than whole ship. Based on the study carried out in the aforementioned work, a detailed analysis of a side structure of a particle-filled double hull vessel will be performed here. In [8], several experiments were carried out to investigate the suitability of granular materials as crash energy absorbing medium. In the current work, a detailed numerical analysis of the particle-filled double hull ship together with the comparison between the results and the experiments, as shown in [8, 9], is performed.

For the modeling of granular materials, the discrete element method (DEM) will be used. This method was introduced by Cundall and Strack (1979) for the modeling of many rigid bodies. Here, the bodies are assumed to be rigid, interacting through the contact forces. The contact forces are obtained from the overlap of the interacting particles. For a detailed study regarding the specific contact laws used for the expanded glass granules, the reader is referred to [6, 7]. For the modeling of the ship’s structure, the finite element method (FEM) will be used. For the collision problem, special attention will be paid to the material constitutive law, which undergoes degradation and damage.

A special highlight of the current work is the usage of a concurrent two-scale model. A model in which only the DEM is used for the modeling with the realistic size of the granules will involve millions of particles. In the experiments carried out in [8], it was observed that the granular materials directly in the vicinity of the colliding indenter undergo significant crushing or large displacement, see Sect. 7. In the region further away, however, significant deformation or crushing of particles is not observed. This allows for the usage of a concurrent two-scale model, which can help to circumvent the computationally expensive approach of modeling all particles with the DEM. Within this concept, the region exhibiting considerable granule deformation is modeled with the DEM while the region where deformation is not significant is modeled with the FEM. The coupling based on the Arlequin method covers the interaction between these two regions, as presented in [10,11,12]. In addition to the concurrent two-scale model, coarse graining of the particles is also used in the current work. This allows for a computationally efficient numerical model where the accuracy, by representation of particles with the DEM in the critical region, is not compromised. At the end, the numerical results are compared with the experiments given in [8]. This allows to validate the accuracy of the model and the assumptions made in the current work.

This paper is structured as follows: Sect. 2 gives a description of the homogenization approach, which is used for the material parameter estimation of the continuum model for the granular materials. Section 4 covers the FEM-based modeling of the ship’s structure. In Sect. 5, the Arlequin method and the concept of the concurrent two-scale model is explained. Section 6 offers a brief description of the experiments regarding the collision of the representative region of ship’s side structure. In Sect. 7, several numerical examples and their comparison with the experiments are performed. Finally, the results are summarized in Sect. 8.

2 Homogenization approach

In the context of the two-scale model, the region represented by a continuum material model is based on the averaged response of the granular materials, see [12] and Fig. 2. In this section, the concept of numerical homogenization will be explained, which is later used to estimate the material parameters for the Mohr–Coulomb model. In the context of numerical homogenization of non-cohesive granular materials, the literature offers several strategies. One approach is based on the definition of a representative volume element (RVE) as a periodic sample where periodic boundary conditions are enforced. This approach has been used considering a cubical- and cylindrical-shaped RVE as shown in [12,13,14]. Within this scheme, all particles are forced to remain in the initially defined domain. Consequently, particles leaving from one side of the RVE during its deformation will reenter from the opposite side. For the enforcement of periodic boundary conditions and a duplication of contact forces on the opposite sides of the RVE, ghost particles are introduced. A detailed description of this model can be found in [12]. Another approach is based on defining a RVE as a subdomain within a region of particles, see [15, 16]. Within this scheme, defining the boundary of the RVE in terms of particles can be challenging. In [15], the boundary particles of the RVE are used to construct the triangular mesh. The displacement of such a triangular mesh is used to calculate the strain, assuming a constant strain within the mesh. In case of significant movement of particles within the RVE, the boundary particles have to be updated and the assumption of constant strain for triangulated boundary particles may not be applicable.

In this work, the homogenization approach is based on a projection of the particle kinematics and stress applying meshless functions. This method was also used in [17] to calculate the strain of particle aggregates. The algorithm presented in [15, 18] used a fixed mesh that was based on coordinates of the particles. As mentioned earlier, such a geometric constraint can lead to erroneous results —especially in the case of extensive particle movement, which results in a large distortion of the mesh. In the case of meshless interpolation, there is no requirement of elements, and only particle nodal coordinates and associated fields are needed. The current strategy is based on projecting fields associated with the particle onto a background mesh which is later used for post-processing. This results in non-local projection of data, without being constrained by the mesh. It must be pointed out that in the current work, a meshless method is used for the projection purpose. No simulation based on this method is performed.

Fig. 1
figure 1

Graphical representation of meshless interpolation of particle data in the DEM

Full size image

The main idea of the method is sketched in Fig. 1. The figure shows a pictorial representation of the calculation of the continuum field based on discrete information of particles. A background mesh is introduced for the continuum-based representation of discrete fields associated with DEM. The displacement field at any nodal point within the mesh is based on the contribution from the displacement of particles that lie within its compact support. The region of compact support can be of arbitrary shape—but it is usually represented as a circular region in two-dimensional cases, or as a spherical region in three-dimensional cases. In the current work, both displacement and stress fields are interpolated by this scheme.

For the calculation of the displacement field at an arbitrary position within the particle-filled domain, the following interpolation function is used.

$$\begin{aligned} u({\varvec{x}})\approx \sum _{i=1}^{N_p} K_p({\varvec{x}}-{\varvec{x}}_i,{\varvec{x}}) {\varvec{u}}({\varvec{x}}_i)\Delta V_i \end{aligned}$$
(1)

The meshfree interpolant in Eq. (1) is given in terms of the displacement of particles and is based on the reproducing kernel particle method (RKPM), see [19]. Here, \(N_p\) represents the number of particles whose region of influence includes the point \({\varvec{x}}\). The first term on the right-hand side of Eq. (1) can be further expanded as

$$\begin{aligned} K_p({\varvec{x}}-{\varvec{x}}_i,{\varvec{x}})=C_\rho ({\varvec{x}}-{\varvec{x}}_i,{\varvec{x}})\Phi _{\rho }({\varvec{x}}-{\varvec{x}}_i,{\varvec{x}}). \end{aligned}$$
(2)

In Eq. (2), \(C_\rho \) represents the correction function while \(\Phi _{\rho }\) represents the kernel function defined as

$$\begin{aligned} \Phi _{\rho }=\frac{1}{\rho ^3} \Phi \left( \frac{{\varvec{x}}}{\rho }\right) . \end{aligned}$$
(3)

Here \(\rho \) represents the size of the kernel function. The kernel function is defined as a cubic spline function:

$$\begin{aligned} \Phi (x)=\left\{ \begin{array}{ll} \frac{1}{6} (x+2)^3 \quad \quad \quad -2 \le x \le -1 \\ \frac{2}{3}-x^2 (1+\frac{x}{2}) \, \quad -1 \le x \le 0 \\ \frac{2}{3}-x^2 (1-\frac{x}{2})\, \, \, \, \, \, \quad \, \, 0 \le x \le 1 \\ \frac{1}{6} (x-2)^3 \, \, \, \, \, \, \quad \quad \quad \, \, 1 \le x \le 2 \\ 0 \quad \quad \quad \quad \quad \quad \quad \quad \text {otherwise} \end{array} \right. \end{aligned}$$
(4)

In the three-dimensional case, \(\rho \) is defined in terms of the radius of the particle, \(\rho =2r\), and the kernel function is defined as

$$\begin{aligned} \Phi (x,y,z)=\Phi (x)\Phi (y)\Phi (z). \end{aligned}$$
(5)

In [19], the calculation of the correction function is based on solving a set of moment equations. However, solving these equations can be computationally expensive. Here, a simple condition as proposed in [17] is used. It is based on enforcing a simplified form of partition of unity at an arbitrary position \({\varvec{x}}\) inside the domain in order to determine \(C_\rho ({\varvec{x}}-{\varvec{x}}_i,{\varvec{x}})\).

$$\begin{aligned} \sum _{i=1}^{N_p} C_\rho ({\varvec{x}}-{\varvec{x}}_i,{\varvec{x}})\Phi _\rho ({\varvec{x}}) \Delta V_i=1 \end{aligned}$$
(6)

In Eq. (6), \(\Delta V_i\) represents the nodal weight, which is associated with the coordinates of the particle. For the calculation of the weight, a tetrahedral mesh based on particle coordinates is generated and calculated as

$$\begin{aligned} \Delta V_i=\frac{1}{N_v} \sum _{k=1}^{N_T} \Delta \Omega _k. \end{aligned}$$
(7)

Here, \(N_T\) represents all tetrahedral elements that share the particle center k as their vertex, and \(\Omega _k\) represents the volume of tetrahedron k. \(N_v\) represents the number of vertices of the polygon, which in the case of a tetrahedron is 4. The mesh generation is based on numerical library CGAL, [20].

2.1 Effective stress and strain

The calculation of effective stress is based on a two-step averaging procedure. Within the first step, the averaged stress for a single particle as shown in [21, 22] is calculated, see Eq. (10). Afterward, it is homogenized over the RVE of interest. This averaging procedure can be written as

$$\begin{aligned} \langle \varvec{\sigma } \rangle =\frac{1}{V_T}\sum _{i=1}^{N_E} V^i \bar{\varvec{\sigma }}^i_P. \end{aligned}$$
(8)

Here, \(\langle \varvec{\sigma } \rangle \) denotes the effective stress for the RVE, \(V_T\) the total volume for the RVE, \(N_E\) the total number of elements within the volume of averaging, \(V^i\) the volume of the element i within the RVE, and \(\bar{\varvec{\sigma }}^i_P\) the projected preaveraged stress within an element \(\textit{i}\)—while it is represented by \(\bar{\varvec{\sigma }}^i\) before projection. The starting point for calculating the stress tensor \(\bar{\varvec{\sigma }}^i\) is the following identity

$$\begin{aligned} \varvec{\sigma }^{T}=\text {div} ({\varvec{x}} \otimes \varvec{\sigma })-{\varvec{x}} \otimes \text {div} \varvec{\sigma } \end{aligned}$$
(9)

By using Eq. (9), the averaged stress \(\bar{\varvec{\sigma }}^{i}\) can be calculated as given

$$\begin{aligned} \bar{\varvec{\sigma }}^{i\,T}= & {} \frac{1}{V^{i,p}}\int _{V^i}\text {div}({\varvec{x}} \otimes \varvec{\sigma }^{'})\,\text {d}V\nonumber \\= & {} \frac{1}{V^{i,p}}\int _{\partial V^i}\text {div}({\varvec{x}} \otimes \varvec{\sigma }^{'})\cdot {\varvec{n}}\,\text {d}S\nonumber \\= & {} \frac{1}{V^{i,p}}\int _{\partial V^i}({\varvec{x}} \otimes {\varvec{t}}^{'})\,\text {d}S. \end{aligned}$$
(10)

Here, \(\varvec{\sigma }^{'}\) represents the stress at a particle coordinate \({\varvec{x}}\). \(\bar{\varvec{\sigma }}^{i\,T}\) is the transposed form of \(\bar{\varvec{\sigma }}^{i}\), and \(V^{i,p}\) represents the volume of particle i. In addition, the local form of equilibrium \(\text {div}\varvec{\sigma }^{'}={\varvec{0}}\) together with Gauss theorem is also applied. Furthermore, the third part of the equation results from the Cauchy theorem \({\varvec{t}}^{'}=\varvec{\sigma }^{'} {\varvec{n}}\), where \({\varvec{n}}\) represents the outward unit normal. The infinitesimal surface element dS can be written in terms of the contact area \(d s^c\) at the contact point c as follows

$$\begin{aligned} \text {d}S=\sum _{c=1}^{N_c}\delta (|{\varvec{x}}-{\varvec{x}}_c |)\text {d}s^c \end{aligned}$$
(11)

By integrating the delta function given in Eq. (11) together with the relation of the contact force \({\varvec{f}}_c\) with stress vector \({\varvec{t}}_c={\varvec{f}}_c/\mathrm {d} s^c\), Eq. (10) can be rewritten as

$$\begin{aligned} \bar{\varvec{\sigma }}^{i\,T}= & {} \frac{1}{V^{i,p}}\sum _{i=1}^{N_c} {\varvec{x}}_c \otimes {\varvec{f}}_c \quad \nonumber \\ \text {or} \quad \bar{\varvec{\sigma }}^{i}= & {} \frac{1}{V^{i,p}}\sum _{i=1}^{N_c} {\varvec{f}}_c \otimes {\varvec{x}}_c \end{aligned}$$
(12)

where \(N_c\) represents the total number of particles in contact with particle i. The projection of the stress is based on the formulation given in Eq. (1), where the stress field is used instead of the displacement field. Furthermore, the calculation of the current volume \(V^i\) is based on the following well-known identity

$$\begin{aligned} V^i=J\,V_0\quad \text {where} \, J=\text {det}({\varvec{F}}). \end{aligned}$$
(13)

For the calculation of the deformation gradient \({\varvec{F}}\), a hexahedral element-shaped background mesh is used. The first step for the calculation of \({\varvec{F}}\) involves a projection of the particle displacement onto the background mesh, as given by Eq. (1). Afterward, the projected displacement field, together with standard isoparametric shape functions, is used to calculate the deformation gradient. Once \({\varvec{F}}\) is known, it can be further utilized for the calculation of a strain, which in this case is the Green-Lagrange strain \({\varvec{E}}\)Footnote 1. Its calculation for each element inside the RVE is based on

$$\begin{aligned} {\varvec{E}}=\frac{1}{2} ({\varvec{F}}^T{\varvec{F}}-{\varvec{I}}). \end{aligned}$$
(14)

Finally, the calculation of the volume averaged strain is based on

$$\begin{aligned} \langle {\varvec{E}} \rangle =\frac{1}{V_T}\sum _{i= 1}^{N_E} V^i {\varvec{E}}^{i}_{P}. \end{aligned}$$
(15)

Here, \({\varvec{E}}^{i}_{P}\) denotes the Green–Lagrange strain, which is calculated from the projected particle displacement.

3 Coarse graining

In this section, the methodology for the coarse graining of particles will be explained. This procedure is quite extensively used in molecular dynamics (MD) simulations, where molecules are used for modeling instead of all-atom representations. In comparison with MD, research in the area of coarse graining in the scope of the DEM is limited. Among others, it includes propositions by [23, 24], where several particles are represented with a coarse representative particle. In order to ensure that the mechanical response is not affected by such coarsening, they used appropriate scaling laws. However, such a procedure will not be accurate if the system response depends on the size of the particles. In [25], adaptive coarse graining was used, with particles that were divided into actual and coarse scale. Actual-sized particles were used in the critical region, and coarse graining was applied to the other regions. This scheme was used for a dynamic problem, where the discharge of a silo was examined. Also, scaling laws were used to accurately represent the coarsely grained particles.

In the current work, coarse graining based on the work of [26] is applied. The basic idea proposed therein is to use particle scale-independent contact constitutive laws. For upscaling/coarse graining, it was proposed that the system must satisfy three similarity principles. These include mechanical, geometric, and dynamic similarity. For the imposition of mechanical similarity, particle strain \(\epsilon _p\) and stress \(\sigma _p\) are defined as

$$\begin{aligned} \epsilon _p\propto u_p/L_p; \quad \sigma _{p}\propto F_p/A_p, \end{aligned}$$
(16)

where

$$\begin{aligned} L_p = 2 R_p;\quad A_p = L_p^2; \quad V_p = L_p^3. \end{aligned}$$
(17)

Here, \(F_p\) is the resultant force acting on a particle due to interaction with neighbor particles and is a function of the overlapped distance \(u_p\). \(L_p\), \(A_p\), and \(V_p\) are the representative length, area, and volume, respectively. For a similar mechanical behavior, the following conditions are imposed

$$\begin{aligned} \epsilon _p=\epsilon _m; \quad \sigma _p=\sigma _m, \end{aligned}$$
(18)

where quantities with a subscript m represent its value in a coarse-grained system, while p represent its value in the physical/actual system. Equation (18) implies the following conditions:

$$\begin{aligned} \frac{u_m}{u_p}=\frac{L_m}{L_p}=\frac{R_m}{R_p}=h;\quad \frac{F_m}{F_p}=\frac{A_m}{A_p}=h^2 \end{aligned}$$
(19)

Here, h represents the ratio which can be defined in terms of the ratio of the radius of the coarse-grained particle to the actual sized particle. The first condition in Eq. (19) represents the scaling of the size of the particles with the ratio \(\textit{h}\), while the second condition—which is more important—implies the particle-size-independent contact law. Since the Hertz contact law is used in the current work, it will be elaborated on in more detail. The normal contact force can be written as

$$\begin{aligned} F=\frac{4 E^*}{3} (\mathrm{{Ru}}^3)^{1/2}. \end{aligned}$$
(20)

From this, the stress–strain relation can be obtained as

$$\begin{aligned} \sigma (R,\epsilon )=\frac{4E^*}{3 \sqrt{2}}\epsilon ^{3/2}. \end{aligned}$$
(21)

It can be seen that the Hertz contact law for normal interaction is scale-independent. A similar approach can be applied for tangential contact. The case of dynamic similarity becomes more relevant when the inertial forces have to be taken into account. Since the current problem is quasi-static, this condition can be relaxed. An important aspect of upscaling is geometric similarity. For an accurate reproduction of response with the coarse-grained particles, it must follow the scaling of particle’s size which is equivalent to h. This is accompanied with the scaling of the characteristic length of the domain. Scaling of the characteristic domain will result in the same number of coarse grained particles as in the actual model and will not result in any computational advantage. No scaling of the domain is performed in this work—and coarse graining is only applied in a region where the system response does not depend on the size of the particles. With this, the possible error due to relaxation of enforcement of exact scaling laws is minimized. An overview of discussions on exact scaling laws and relaxation in the context of coarse graining for the sake of computational efficiency is given in [27].

4 Finite element model

As mentioned earlier, the modeling of the ship’s structure is based on the FEM. This method requires that the constitutive material model along with the contact constraint during indentation is correctly implemented. In the literature, there are well-established theories regarding the phenomenological modeling of finite deformation of steel or metal in general, see [28, 29], which will be also used in the current work. During deformation, the structure undergoes an irreversible process which is referred to as plasticity. In order to model this behavior, the total deformation gradient is split into an elastic and a plastic part

$$\begin{aligned} {\varvec{F}}={\varvec{F}}^e {\varvec{F}}^p. \end{aligned}$$
(22)

For the integration of the evolution equations of the plasticity model, a classical return mapping algorithm is applied. For the current model, a von Mises yield criterion together with linear hardening,

$$\begin{aligned} \phi =\sqrt{{\varvec{s}} \cdot {\varvec{s}}}-\sqrt{\frac{2}{2}(Y_0+H \,\alpha )} \end{aligned}$$
(23)

is used. Here \({\varvec{s}}\) represents the deviatoric part of the Kirchhoff stress tensor, \(Y_0\) represents the initial yield stress, H is the hardening variable, and \(\alpha \) denotes the total accumulated plastic strain. Furthermore, the elastic strain energy function is based on a Neo-Hookean material model. For more details regarding this model, the reader is referred to [28]. During deformation beyond a certain limit, the steel structure is prone to degradation or rupture. This degradation is accounted for by considering a gradient-enhanced damage model. With the gradient enhancement, the problem of mesh-dependent solution is circumvented. The model in the current study is based on the work of [30]. The gradient enhancement is introduced with the inclusion of an additional field variable, \({\bar{z}}\). The damage driving force is represented by a local variable z. The variable \({\bar{z}}\) is related to the local part z with the Helmholtz type equation

$$\begin{aligned} {\bar{z}}-l^2 \nabla ^2 {\bar{z}}=z, \end{aligned}$$
(24)

where l represents the material-dependent length parameter and controls the localization region while \(\nabla ^2\) is the Laplace operator.

The evolution of z is based on

$$\begin{aligned} z_{n+1}=z_n+\Delta \alpha < 1+A \frac{\tau _h}{\tau _{\mathrm{{eq}}}} > \alpha ^B, \end{aligned}$$
(25)

where \(\tau _h\) represents the hydrostatic part of the Kirchhoff stress tensor, while \(\tau _{\mathrm{{eq}}}\) represents its deviatoric part. A and B are fitting parameters which control the evolution of damage. The damage variable given here contributes to the degradation of both the elastic strain energy and the yield criterion. This approach was also used in [31] for a phase-field model based crack propagation.

Due to the thin structure of the ship’s hull—and due to the fact that isochoric plastic deformation is considered—usage of a standard low-order hexahedral element formulation can result in volumetric and shear locking. In order to circumvent this problem, an enhanced assumed strain (EAS)-based formulation is used. The element formulation used in the current work is related to the work of Korelc et al. [32]. It is based on the introduction of incompatible parameters \(\varvec{\alpha }_e\), which are defined at the element level and are discontinuous across elements. This results in a modified displacement gradient

$$\begin{aligned} {\varvec{H}}= {\varvec{H}}_c+ {\varvec{H}}_u + {\varvec{F}}_0 \bar{{\varvec{H}}} \end{aligned}$$
(26)

and an additional set of incompatible shape functions. Here, \({\varvec{H}}_c\) represents the constant part of the compatible displacement gradient while \({\varvec{H}}_u\) represents its variable part. \(\bar{{\varvec{H}}}\) represents the variable part of the incompatible displacement gradient. Further details and a comparison with other element formulations can be found in [32].

The definition of the FEM model is completed by introducing the computational contact model. Within the weak form of the FEM problem definition, a contact constraint is introduced by adding

$$\begin{aligned} G^c= \int _{\partial _c {\mathcal {B}}} {\varvec{t}}_c\cdot (\varvec{\eta }_c^2-\varvec{\eta }_c^1) \,\mathrm {d}a, \end{aligned}$$
(27)

where \({\varvec{t}}_c\) represents the contact stress vector, while \(\varvec{\eta }_c^2\) and \(\varvec{\eta }_c^1\) represent the test functions corresponding to body 2 and body 1 in contact, respectively. The mortar method, as implemented in [33], serves to solve this contact problem. Due to the robustness of this method in the case of large deformation and sliding, it is to be favored over other techniques. In contrast to strong coupling of node pairs, the contact constraints are enforced in a weak sense. Here, the calculation of kinematic contact quantities of a slave node is based on averaging them over the adjacent slave elements.

5 Arlequin method

The prominent feature of our concurrent two-scale model is the Arlequin method based coupling of the FEM and the DEM domain. The domain \(\Omega _{\mathrm{{FE}}}\) and \(\Omega _{\mathrm{{DE}}}\) representing the continuum and the discrete element model can be discretized with well-established numerical methods. However, special care must be taken where the domains of these two methods overlap. For the overlapping domain \(\Omega _{A}\), weight functions \(w({\varvec{x}})\) as described in [12] are used. These functions must satisfy the following conditions:

Fig. 2
figure 2

Representation of the two-scale model

Full size image
$$\begin{aligned} w({\varvec{x}})= {\left\{ \begin{array}{ll} 0 \quad \forall \, {\varvec{x}}\in \Omega _{\mathrm{{FE}}} \setminus \Omega _{\mathrm{{DE}}}\\ 1 \quad \forall \, {\varvec{x}}\in \Omega _{\mathrm{{DE}}} \setminus \Omega _{\mathrm{{FE}}}\\ {}[0,1] \quad \forall \, {\varvec{x}}\in \Omega _{A} \end{array}\right. } \end{aligned}$$
(28)

Consequently, by using appropriate weights, an interpolation between the FEM and the DEM is used for the material in the overlapping domain \(\Omega _{A}\). By applying the weights given in Eq. (28), the weighted virtual work can be written as follows:

$$\begin{aligned}&\delta W=\delta W_{\mathrm{{FE}}}+\delta W_{\mathrm{{DE}}} \end{aligned}$$
(29)
$$\begin{aligned}&\delta W_{\mathrm{{FE}}}=\int _{\Omega _{\mathrm{{FE}}}} (1-w) [\varvec{\sigma }\cdot \delta \varvec{\epsilon }+\rho (\ddot{{\varvec{x}}}-{\varvec{b}})\cdot \delta {\varvec{u}}]\mathrm{{d}}v -\nonumber \\&\int _{\Gamma _{\mathrm{{FE}}}} (1-w)\hat{{\varvec{t}}}\cdot \delta {\varvec{u}}\mathrm{{d}}s \end{aligned}$$
(30)
$$\begin{aligned}&\delta W_{\mathrm{{DE}}}=\sum _{\alpha =1}^{n_P}\delta W_{\alpha }=\sum _{\alpha =1}^{n_P}\left[ \int _{\Omega _{A}} w \rho (\ddot{{\varvec{x}}}-{\varvec{b}})\cdot \delta {\varvec{u}}_{\alpha }\text {d}v \right] - \nonumber \\&\sum _{\alpha =1}^{n_P}\left[ \sum _{\beta =1}^{n_{\alpha }} w_{\alpha \beta } {\varvec{f}}_{\alpha \beta }\cdot \delta {\varvec{u}}_{\alpha } \right] \nonumber \\ \end{aligned}$$
(31)

Equation (30) represents the weighted virtual work of the finite element part, while Eq. (31) represents the weighted virtual work of the rigid body/DEM. Here, \(\delta {\varvec{u}} ({\varvec{x}})\) represents the virtual displacement of the deformable body, while \(\delta {\varvec{u}}_{\alpha } ({\varvec{x}})\) is the virtual displacement of the rigid body \(\alpha \), \(n_P\) denotes the total number of particles, and \(n_{\alpha }\) represents the total particles in contact with the particle \(P_{\alpha }\). In addition, \({\varvec{f}}_{\alpha \beta }\) denotes the contact force of particle \(P_{\beta }\) on particle \(P_{\alpha }\). The term \(w_{\alpha \beta }\) represents the weight factor at the point of contact of particle \(P_{\alpha }\) and \(P_{\beta }\). Equation (30) can be extended to include the weighted continuum-based contact force. For simplicity, it is assumed that the contact contribution in Eq. (27) is weighted by the value of w at the nodes of the contact element.

5.1 Kinematic constraint

Within the Arlequin framework, the interaction of non-cohesive granular materials and the continuum model is enforced by using kinematic constraints. As mentioned in [12], the constraints must be enforced in such a way that they do not completely constrain the particle’s displacement to the nodal displacement of the finite elements within the overlapping domain \(\Omega _A\). For the accuracy of the modeling of non-cohesive behavior of particles, it is necessary to allow relative motion of the particles. As described in [34], such a behavior can be incorporated by using a split of the total displacement of particles \({\varvec{u}}_{\mathrm{{DE}}}\) into a coarse \({\varvec{u}}^{c}_{\mathrm{{DE}}}\) and a fine-scale \({\varvec{u}}^{f}_{\mathrm{{DE}}}\) component

$$\begin{aligned} {\varvec{u}}_{\mathrm{{DE}}}={\varvec{u}}^{f}_{\mathrm{{DE}}}+{\varvec{u}}^{c}_{\mathrm{{DE}}}. \end{aligned}$$
(32)

The coarse-scale part in \(\Omega _A\) is represented by continuous interpolation functions, which are based on the finite-element-based ansatz functions. It can be written as

$$\begin{aligned} {\varvec{u}}^{c}_{\mathrm{{DE}}}({\varvec{x}})=\sum _{I\in {\mathcal {N}}^C} N_{I}({\varvec{x}}) {\varvec{u}}^c_{I,\mathrm{{DE}}} \end{aligned}$$
(33)

where \(N_{I}\) represents FE-based shape functions and \({\mathcal {N}}^C\) represents the set of nodes which belong to the elements within which particle center reside.

The calculation of \({\varvec{u}}^c_{I,\mathrm{{DE}}}\) is based on the requirement that it minimizes the volume-weighted squared difference between the total and coarse-scale displacement as given below:

$$\begin{aligned} \underset{{\varvec{u}}_{I,\mathrm{{DE}}}^{c}}{\text {min}} \sum _{\alpha \in P^{C}} V_{\alpha } \Vert {\varvec{u}}_{\alpha }-{\varvec{u}}_{\mathrm{{DE}}}^c({\varvec{c}}_{\alpha }) \Vert ^2 \quad \end{aligned}$$
(34)

Here \({\varvec{c}}_{\alpha }\) represents the central coordinates of the particles. By minimizing the equation above with regard to \({\varvec{u}}^c_{I,\mathrm{{DE}}}\), these unknown components can be obtained, see [12]. Once the nodal displacement components \({\varvec{u}}^{c}_{I,\mathrm{{DE}}}\) are known, interaction of particles with FE nodes within \(\Omega _A\) is enforced by a penalty-based constraint

$$\begin{aligned} C=\frac{\epsilon }{2} \int _{\Omega ^A}\Vert {\varvec{u}}_{\mathrm{{DE}}}^c-{\varvec{u}}_{\mathrm{{FE}}}\Vert ^2 \mathrm {d}v, \end{aligned}$$
(35)

where \(\epsilon \) is the penalty parameter. For the calculation of the nodal \({\varvec{f}}^C_{\alpha }\) and particle \({\varvec{f}}^C_{I}\) coupling forces, the variational form of the constraint term given in Eq. (35) is written as follows

$$\begin{aligned}&\delta C =-\sum _{\alpha \in P^C} \delta {\varvec{u}}_{\alpha }\cdot \underbrace{\left( -\sum _{I\in {\mathcal {N}}^C} \Pi _{I \alpha }{\varvec{f}}_I^C\right) }_{{\varvec{f}}_{\alpha }^C}\nonumber \\&\quad -\sum _{I\in {\mathcal {N}}^C} \delta {\varvec{u}}_I^{\mathrm{{FE}}} \cdot {\varvec{f}}_I^C \end{aligned}$$
(36)

where \(\Pi \) represents the projection matrix, which is obtained by solving Eq. (34). In the case of an implicit method, the variational form for coupling has to be linearized. The linearized term for Eq. (36) can be written as

$$\begin{aligned} \Delta \delta C = \sum _{I\in {\mathcal {N}}^C} \delta {\varvec{u}}_I^{\mathrm{{FE}}} \cdot \epsilon \sum _{J\in {\mathcal {N}}^c} \int _{\Omega ^A} N_I\, N_J \mathrm {d}v \Delta {\varvec{u}}_{\mathrm{{FE}}} \end{aligned}$$
(37)

6 Experiments

For the validation of the numerical framework discussed before, the results are compared with experiments. In this section, a description of the experiments will be given. The first experiment is a common test in geomechanics, namely a triaxial test. In this test, a cylindrical probe will be compressed under a fixed radial pressure. The second experiment shown here concerns a ship collision, regarding the question how suitable granules are as a crash-absorbing material. There, a bulbous bow is driven into a simplified double hull structure filled with granular material. The determination of the material properties of the granules is described in detail in [6].

6.1 Triaxial test

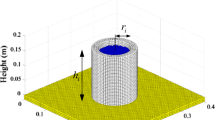
The triaxial compression test is based on DIN 18137-D. On the one hand, it can be used to determine the parameters for the Mohr–Coulomb material model by using the obtained Mohr circles from the test results. On the other hand, the test results can be used to validate the approach applied for the numerical homogenization, which will be shown in a later section. The setup of this test is shown in Fig. 3.

Fig. 3
figure 3

Test setup of a triaxial cell (from [8])

Full size image

A cylindrical probe with a diameter of \(50\;\text {mm}\) and a height of \(120\;\text {mm}\) is placed in a triaxial cell. The probe is contained by a membrane and surrounded with a cell fluid that can apply different levels of radial pressure. In addition, the pressure inside the specimen can be controlled. In the conducted experiments, the pore pressure valve is open—guaranteeing atmospheric pressure inside the specimen, which corresponds to the intended use case of the inside of a ship structure.

After applying the radial pressure, the specimen is given some time for consolidation before it is compressed in axial direction. For this, a constant strain rate is applied. Then, the values for the force and displacement as well as the changes in pressure and volume in the cell and specimen are measured. The latter values are used to cover effects such as dilatancy in the grain structure.

Due to the geomechanical properties of the granules, the compression can be performed with a relatively high velocity of \(1\;\text {mm/min}\), compared to the soil experiments [35]. However, the crushing of the particles limits the radial pressure to a level of \(400\;\text {kPa}\). In doing so, we still observe marginal crushing for higher loads. Thus, we consider lower radial pressures in this paper for comparison. Figure 4 shows a plot of principle stress ratio against axial strain for different confining pressures for expanded glass granules.

Fig. 4
figure 4

Principle stress ratio versus axial strain for different confining pressures

Full size image

6.2 Simplified side hull structure

To investigate the effects of the granules as crash-absorbing material, a simplified side hull structure is considered. A detailed description regarding this is given in [8]. The experimental setup shown here is adopted from the setup shown in [36]. Here, the structure is scaled down by a factor of 3. In order to keep the experiment as simple as possible, stiffening elements, such as stringers and stiffeners, are not taken into account to determine the influence of the granules.

The simplified side hull structure is shown in Fig. 5. The inner and outer hull of the ship is represented with steel plates with a thickness of \(3\;\text {mm}\). The distance between the hulls is \(280\;\text {mm}\). The edges of the steel plates are welded to a rigid frame, which can be reused and is placed on force sensors. To contain the granules, a rectangular box is welded between the two plates, with the dimensions shown in Fig. 5. The granules are poured into the structure via small openings at the corners, which are closed after filling the box. In order to obtain a compact packing, the box is intermittently moved during the pouring process. This packing procedure without usage of a compaction device ensures a similar filling process as would be applied in reality.

For the modeling of a bulbous bow of a colliding ship, a half sphere comprising of solid steel with a diameter of \(270\;\text {mm}\) is considered. This indenter is driven into the simplified double hull structure with a velocity of \(0.2\;\text {mm/s}\). The applied force and the displacement of the indenter are measured throughout the indentation process. Besides several other measured quantities, see [8], we will focus on the applied force and displacement of the box containing the granules. In [8], four experiments with two different boundary conditions were conducted in total—but we will focus on two of these experiments. For these experiments, movement of the rigid frame is blocked in the direction perpendicular to the axis of the indenter. The first experiment serves as a reference without granules inside the box. This allows us to examine the improvements due to the filling with granules in the second experiment.

6.2.1 Reference experiment

The first experiment is used as a reference experiment to determine the improvements in crash-worthiness when using granules. Figure 6 shows the force–displacement curve. The two plates can be clearly identified. The outer hull withstands a maximum force of \(400\;\text {kN}\) and ruptures at an indention depth of approximately \(150\;\text {mm}\). After this, the indenter comes into contact with the inner hull at a total displacement of \(280\;\text {mm}\). Then, the indenter pushes through the inner hull until it ruptures at \(415\;\text {mm}\) with a slightly lower force. The unloading/loading during this transition is due to the installation of an extension for the bulbous bow.

Fig. 5
figure 5

Dimensions of the simplified side hull structure. The granules are contained inside the black box

Full size image
Fig. 6
figure 6

Force–displacement curve for experiment 1

Full size image

6.2.2 Experiment with filled structure

The second experiment shown in this paper is conducted with granules inside the box. The resulting force–displacement curve is shown in Fig. 7.

Fig. 7
figure 7

Force–displacement curve for Experiment 2

Full size image

The curve related to the penetration of the outer hull is a bit steeper. The outer hull ruptures at an indentation of \(160\;\text {mm}\)—resulting in a force of \(520\;\text {kN}\). After rupture of the outer hull, the resulting metal flap is clamped between the indenter and the granules, as can be seen in Fig. 8. This, in addition to the extra resistance due to the granules, results in a plateau in the force–displacement curve. After an indentation of \(260\;\text {mm}\), we observe an increase in force. At this position, the granules are highly compacted and some of the force is transferred to the inner hull. At \(300\;\text {mm}\), the flap is ripped off from the outer hull, resulting in the drop in force level. Until the rupture of the inner hull, we can observe an increase in force.

Fig. 8
figure 8

Clamped outer hull between the indenter and the inner hull plus granules [from [8]]

Full size image

6.2.3 Comparison of the experiments

The improvement due to the granules can be measured in different ways. Here, we compare the dissipated energy until the inner hull ruptures. The resulting curves can be seen in Fig. 9. The later rupture of the filled hull and the increased resistance due to the granules result in a significant increase of \(146\text {\%}\). Compared to the experiments shown in [8], the increase in the resistance is probably overestimated in Fig. 9.

Fig. 9
figure 9

Dissipated energy during experiment 1 and experiment 2

Full size image

A realistic estimation—based on a similar rupture behavior for all considered steel sheets, as well on numerical simulations— indicates an increase around \(60\text {\%}\), see [8]. There, a second experiment was conducted with slightly different steel parameters, resulting in an increase of only \(22\text {\%}\), which was mainly caused by a late rupture of the inner hull in the reference experiment. Thus, more experiments could help to obtain a statistically more representative result, but the observed rupture behavior already shows that inserting a filling material is a promising means to increase the crash-worthiness of double hull ships.

7 Numerical results and comparison

7.1 Parameter identification for numerical homogenization

This section focuses on the estimation of the parameters for the Mohr–Coulomb material model. For this material model, five parameters will be calibrated and the procedure for their identification will be explained in the later part of this section. For the calculation of these parameters, an averaged response of the RVEs will be considered. The generation of an RVE is based on considering it as a subdomain within the finite domain, which consists of a particle-filled cylindrical region enclosed by a flexible membrane. This finite domain was also used for a triaxial test in [7]. For the homogenization, this test will be reconsidered and similar boundary conditions will be applied, see Fig. 10. However, instead of a cumulative response of all particles, only the response of particles within the RVE will be studied, see Fig. 10 (right). Here, the RVE is represented as a cylindrical-shaped region with a certain radius R and height H. In order to avoid any boundary effects, the radius R of the RVE is chosen to be smaller than the radius of the triaxial domain. The hexahedral elements within the background mesh are used to define the the domain of the RVE, and the averaged projected response of the particles on this domain is used for the parameter estimation.

Fig. 10
figure 10

Triaxial test for the particles with the introduction of the background mesh (left). Example of a RVE chosen within the assembly of particles (right)

Full size image

7.1.1 Validation

A comparison is carried out in order to validate whether the results from the homogenization are comparable to the results of the experiment. In Fig. 11, a comparison of the experimental results with the result from the volume averaged stress of RVE is performed. Here, the ratio of axial stress \(\sigma _{33}\) to the transverse stress \(\sigma _{11}\) along with the axial strain is plotted. For the comparison, a confining pressure of 75 kPa and 100 kPa is used. It can be seen from Fig. 11 that the initial response of the RVE is not as stiff as the bulk response from the experiment. However, after nearly 2\(\%\) axial strain, the response from the RVE becomes stiffer than the bulk response. Furthermore, the peak stress ratio is reached earlier for both RVEs in comparison with the experimental results. The ensemble of the particles within the RVE tends to shear earlier.

Fig. 11
figure 11

Comparison of experimental and simulation results for triaxial test

Full size image

It must be considered that the response of the RVE represents the localized behavior of the particles within its domain. It does not include the bulk response of the whole ensemble of particles. Therefore, this localized region can exhibit a behavior that cannot be compared exactly to the bulk response of all granular particles within the experimental setup. However, within 10\(\%\) strain, the response from the RVE is significantly close to the experimental results.

7.1.2 RVE size

For homogenization, the size of the RVE should be large enough to effectively represent the heterogeneities within the granular system. Also, it should be small enough to represent a volume element for its continuum representation. In this section, the effect of the size of the RVE on its resultant behavior is studied. For the cylindrical shape of the RVE, its radius R and height H are the two parameters that can be changed to enforce variations in its shape. When determining these parameters, it is important to make sure that the boundary effects do not influence the results. A variation in the range of 14–20 mm is considered for the radius, while a variation in the range of 22–30 mm is chosen for the height of the RVE. The total dimensions of the numerical experiment for the triaxial test are based on a value of radius of 25 mm and a height of 120 mm, see Fig. 10.

Fig. 12
figure 12

Resultant behavior of different RVEs with different radius R and height H

Full size image

It can be seen from Fig. 12 that within radius range of 17–20 mm, on average, the shearing of samples starts at a maximum stress ratio of approximately 4.4. This corresponds to the strain value of 5\(\%\). The effect of the variation of height (17–20 mm radius) on the resultant behavior of the samples is not significant. The overall standard deviation for this range is acceptable. However, for samples with a radius of 14 mm, the deviation in results is more significant. It has a maximum stress ratio of 4.4 corresponding to a height of 22 mm—and a minimum stress ratio of 4.1 corresponding to height of 30 mm. In addition, the shearing of samples for this size also occurs at different strain values, which ranges from nearly 4.5 to 5.2\(\%\). As can be seen from Fig. 12, the overall deviation for the aforementioned size of the RVEs is within an acceptable range.

7.1.3 Parameter identification

The non-associative Mohr–Coulomb material model, which will be used for a continuum representation of granular material in Sect. 7.3, requires five parameters. This includes Young’s modulus E, Poisson ratio \(\nu \), friction angle \(\phi \), dilatation angle \(\Psi \), and cohesion parameter c. The response from the RVEs will be used for the identification of these parameters. For the calculation of Young’s modulus and Poisson’s ratio, the initial response of the RVEs is used. It is assumed that the initial response of the granular material is elastic and that the onset of inelastic behavior starts in a later part of the deformation of the RVEs.

Fig. 13
figure 13

Estimation of Mohr–Coulomb parameters; a estimation of Young’s modulus from \(\sigma _3\) versus \(\epsilon _3\) curve, b estimation of average value of dilation angle, c estimation of Poisson’s ratio from initial response of RVE, d calculation of friction angle and cohesion parameter from Mohr circles

Full size image
Fig. 14
figure 14

Representation of geometry of the plate undergoing indentation

Full size image

For the calculation of the Young’s modulus, the stress strain curve \(\sigma _3\) versus \(\epsilon _3 \%\) is used. As can be seen in Fig. 13 and also observed in [12], the initial elastic response of RVEs is dependent on the lateral pressure used to confine the granular materials in the triaxial setup. The mean pressure serves to estimate an average value of Young’s modulus. From the initial response, a value of E = 15 MPa is estimated—and the initial response from the \(\epsilon _v\) versus \(\epsilon _3\) curve is used to calculate Poisson’s ratio. Its calculation is based on

$$\begin{aligned} \nu =\frac{1}{2}\left( 1-\frac{\Delta \varepsilon _V}{\Delta \varepsilon _1} \right) \end{aligned}$$
(38)

as given in [37]. For the calculation of the dilatation angle \(\Psi \), the following equation

$$\begin{aligned} \mathrm {sin}(\Psi )=\frac{\Delta \epsilon _v/ \Delta \varepsilon _a}{ \Delta \varepsilon _v / \Delta \epsilon _a-2} \end{aligned}$$
(39)

as given in [38] is used. Here, \(\epsilon _a\) represents the axial strain of the RVE, which in this case is \(\epsilon _3\). The shear G and bulk modulus K can also be calculated in terms of Young’s modulus and Poisson’s ratio :

$$\begin{aligned} G=\frac{E}{2(1+\nu )},\quad \quad K=\frac{E}{3(1-2\nu )} \end{aligned}$$
(40)

The calculation of \(\Psi \) is also based on the average response of the RVEs. Finally, in order to calculate the friction angle \(\phi \) and cohesion parameter c, the Mohr circles as shown in Fig. 13c are used. The friction angle \(\phi \) is calculated from the tangent to the Mohr circles and the cohesion parameter is calculated from the y-intercept of the tangent line.

7.2 Example of ductile damage model with EAS element

In this example, an indentation of a thin steel sheet is performed. The main purpose of this example is to show the effectiveness of the EAS element for predicting the damage behavior. As mentioned earlier, standard lower-order hexahedral element formulations for thin structures are prone to the problem of shear locking. In addition, the incompressibility constraint due to the plastic deformation can lead to volumetric locking. Considering these shortcomings, the finite element solution for thin structures undergoing damage can be erroneous. Since the example that will be considered in Sect. 7.3 is based on a thin steel structure, it is imperative to use a finite element formulation that is free of locking effects. Therefore, we apply the enhanced strain element formulation. The geometry of the problem that is considered here is shown in Fig. 14 and the material properties are given in Table 1.

Table 1 Material properties of a thin plate subjected to indentation
Full size table
Fig. 15
figure 15

Reaction force during indentation of thin sheet with ductile damage along with EAS element formulation

Full size image
Fig. 16
figure 16

Comparison of reaction force during indentation for standard hexahedral and EAS element

Full size image
Fig. 17
figure 17

Close view of state of granules after indentation

Full size image
Fig. 18
figure 18

Geometry of the model for two-scale problems (top-all dimensions in mm). Discretized box for FEM-based solution of indentation (bottom)

Full size image

The metal sheet has a thickness of 3 mm and the indenter has a diameter of 270 mm. The metal sheet is clamped at all edges and a punch is used for the indentation. The punch is driven by applying the displacement boundary conditions at its top surface. A mortar contact-based formulation is used for the interaction between the punch and the plate. The resultant behavior is shown in Fig. 15.

In addition, a comparison between a standard 8-noded lower-order hexahedral and an EAS element is carried out. From Fig. 16, it can clearly be seen that, in comparison to the EAS element, the response of the standard element is rather stiff and initiation of damage occurs quite earlier. In the case of the EAS, the softening of the material and the decrease in reaction force occurred at almost 145 mm displacement of the indenter–and at 80 mm for the standard hexahedral element. Furthermore, the peak value of reaction force in the case of the EAS is almost 400 kN. For the standard element, it is 12.6 MN. Therefore, a new element formulation is necessary to get an accurate response of the ship structure.

7.3 Two-scale model with punch test

As mentioned earlier, numerical modeling of the entire granular medium with the DEM, as shown in experiments in Sect. 6, can be computationally expensive. A model with a realistic granule size would require approximately 2.5 million particles for the simulation. Considering particle modeling with the DEM together with a highly nonlinear FEM model, this approach can have severe limitations in terms of computation time. For a computationally efficient numerical model, usage of a two- scale model as described in Sect. 5 is imperative. Considering the configuration of particles as shown in Fig. 17, it can clearly be seen that significant crushing of particles occurred in the vicinity of the punch rather than in the region further away. This provides an opportunity for the usage of the continuum model in the region further away.

Figure 18 shows a geometric representation of the numerical model used for the indentation of the box.

In this figure, the FEM-based region consists of two different materials. Region A belongs to the walls of the box, which consists of steel. For this region an elasto-plastic material model is used. For the current work, the material properties for the steel together with the damage parameters are shown in Table 2 while some of the material properties and parameters for the granular material are shown in Tables 3 and 4. From the experiments, a variation in the strength and Young’s modulus of the granules was observed, see Table 3 and [7]. Such a variation is also included in the current DEM model. In Table 4, \(\mu _{\mathrm{{par-par}}}\) represents the coefficient of friction between particles and \(\mu _{\mathrm{{par-rig}}}\) represents the coefficient of friction between particles and steel. Reader is referred to [7] for further details and parameters used for the current DEM model.

Table 2 Material properties of steel used for indentation problem
Full size table
Table 3 Experimental results for crushing force and Young’s modulus of expanded glass granules (2–4 mm) and its fractions as reported in [6]
Full size table
Table 4 Material properties of particles
Full size table
Fig. 19
figure 19

Representation of coarse- and actual-scale particles

Full size image

The initial yield strength and the Young’s modulus are derived from the experiments as shown in [8]. In order to determine the hardening modulus, the experimental results from an unfilled hollow box were used for the calibration. Here, a linear hardening-based plasticity model is assumed. Later, these parameters are also used for the particle-filled box. For the modeling of the ductile damage, the constants for the damage model, as shown in Sect. 4, are also calibrated using the experimental results from the indentation of the box. This includes the determination of the value of \(\kappa _i\), which represents the value at which initiation of damage occurs. The shape of the curve, which corresponds to the decrease in the reaction force, is determined by the parameter \(\beta \), as shown by the damage model in Sect. 4. The calibration of this parameter is based on the evolution of the crack from the experimental results. Considering the thickness of the steel wall and the incompressibility constraint due to the plasticity model, an enhanced strain-based element formulation as described in Korelc et al. [32] is used. Region A consists of 4212 elements. The region labeled as B is based on the Mohr–Coulomb material model and represents the effective behavior of the granules. The parameters for this material model are taken from the homogenization technique explained in Sect. 7.1.3. This region is based on the standard hexahedral 8-noded element formulation, where 960 elements are used. A mortar-contact-based model, as described in Weißenfels [33], captures the interaction of the elements in regions A and B and the indenter. The enforcement of the contact constraint is based on the penalty method. The coefficient of friction between the indenter and the surface of the hollow box is taken as \(\mu =\)0.45. This parameter is taken from the work presented in [39]. For the contact, multi-surface contact constraints are enforced. It consists of the contact surface between the indenter and the top surface of the box and additionally, contact due to the inner surface of the box and the outer surface of the region B, see Fig.  18.

Figure 19 shows an FEM-based region together with the configuration of particles. For the enforcement of the coupling between FEM and DEM, a projection matrix based on a lumping strategy is used, see [12]. The figure shows coarse-grained (in red) and realistically sized particles (in blue). A total number of 99,634 particles were used for the coarse-grained region. Since a significant crushing of particles will not occur in this region, the crushing model will not be used. However, the inelastic behavior of these particles is still taken into account. It is expected that during the application of external load, elastic behavior of the particles throughout the indentation will not be valid. The approximation of such behavior is accounted for by including inelastic behavior as described in Chaudry et al. (2018) [7]. A crushing model as presented in [40] is used for realistically sized particles that lie in the vicinity of the indenter. For the simulation, the behavior until the rupture of the outer hull is considered.

Fig. 20
figure 20

Representation of different stages of indentation of particle-filled box

Full size image

Figure 20 shows different instances of the particles and the mesh during the indentation process. Here, for the preparation of the particles packing, an algorithm as described in [12] is used. First, a geometric scheme is used to generate the particles. Afterward, these particles are allowed to settle under gravity so that a natural configuration of granular matter is achieved. In order to achieve a close packing as in the case of the experiment, they are slightly compressed and allowed to relax. After packing, the simulation phase of the particles starts. Figure 20a shows the configuration of the particles during the initial phase. Afterward, the indentation of the box initiates. Figure 20b–d shows different instances of the particles during indentation. Depending on the particle strength, gradual crushing of the particles during indentation occurred. In this model, particle crushing is only enforced up to a limit radius of the particles. As mentioned in Chaudry et al. [7], this strategy has often been used by researchers for the DEM-based simulations of crushing, see [41]. Figure 21 (left) shows the initial configuration of the particles before crushing, and Fig. 21 (right) shows the crushed particles at the end of the simulation. At the beginning of the simulation, there were 300,800 particles—compared to 523,601 particles at the end of the simulation, due to crushing. Here, an explicit time integration scheme is used for the DEM model, and an implicit time integration scheme is applied to the FEM problem. Since it is possible to use a larger critical time step for the implicit solver in the FEM problem, a subcycling scheme with a different time step for the DEM and FEM is also implemented for the current problem. The time step for the FEM model is almost 114 times the critical time step of the DEM model. This also increases the speed up of the computation.

Table 5 Simulation details for the indentation of the box
Full size table
Fig. 21
figure 21

Particles at the beginning (left) and at the end of simulation (right)

Full size image

In Fig. 22, a comparison of the results from the experiments and simulation is performed. In the case of the empty box, the initial response of the material is elastic. After a 20 mm displacement of the indenter, the initial yield strength limit is exceeded, and the plastic response for the metal sheet directly in contact with the indenter is initiated. Since the indenter is rigid and does not deform during the whole process, a linear elastic material with small deformation is assumed for it. From the experimental results, it can be observed that the fracture of the outer wall initiated at almost 145 mm displacement of the indenter. After that, there is a sudden decrease in the reaction force due to propagation of the fracture, see Fig.  22. For the particles, a significant crushing also occurred at around 145 mm. In the case of the filled box, however, the fracture initiated at a displacement of almost 160 mm.

Fig. 22
figure 22

Comparison of experiment and numerical results for the collision of the particle- filled box

Full size image
Fig. 23
figure 23

Result obtained from DIC for the strain on the surface of the box (left). Figure for computed accumulated plastic strain (right)

Full size image

The simulation for the filled box and for the empty box showed that propagation of the fracture occurred almost at the same displacement of the indenter. In the experimental results, there is a slight difference in the value of the displacement, where the decrease in load–displacement curve occurred. However, this difference is not significant. As can be seen in Fig.  22, the good agreement between the experimental and the simulation results shows that using the two-scale model does not compromise the accuracy of the numerical, but it still allows a computationally efficient simulation. In the context of an implicit FEM-based solution, as the value of damage D approaches a value of 1, it creates problems regarding convergence. Therefore, the results from the simulation are not compared with the experiments for the entire duration of indentation.

In [8], digital image correlation (DIC) was used for the punch test in order to monitor the value of the strain of the box. Figure 23 (left) shows the experimental value of the strain as calculated based on DIC. To allow for a qualitative comparison, the total accumulated plastic strain for the indentation is shown as well. The region with the maximum strain in DIC corresponds to the region where maximum equivalent plastic strain was observed during the simulation.

An important outcome of this experiment is the energy absorbed by the granular materials during the indentation process. The difference in area under both curves in Fig.  22 shows that the granular materials are able to absorb the energy. Therefore, it can be safely concluded that the particles, which act as sandwiched medium, are able to absorb impact energy and increase the crashworthiness of the ship.

8 Conclusion

The current work covers the numerical analysis of a novel idea for the increase in crashworthiness of double hull ship. Here, a detailed analysis of granular materials as crash absorbing material is carried out. For the modeling, granular materials were modeled with the DEM, while the structure of the ship was modeled with the FEM. For the structure, numerical experiment revealed that the response from the standard hexahedral element formulation is stiff and cannot be used for accurate modeling of damage. An enhanced assumed strain-based element formulation together with the gradient enhanced damage model was able to circumvent this problem. The experiments in [8] revealed that the displacement and crushing of particles in region further from the indenter is not significant. This allowed the usage of concurrent two-scale model for a computationally efficient numerical simulation. Here, the accuracy of modeling of the region with significant localization of granules was ensured by the DEM, while a continuum-based model was used for the other regions. The continuum- based region was treated with the Mohr–Coulomb material model, for which the material parameters were determined by numerical homogenization. For homogenization, meshless shape functions allowed continuum representation of discrete fields of particles. The comparison of the stress–strain curve from homogenization with the triaxial tests showed the suitability of the model. For final investigation, a representative region inside the structure of the ship was considered. Here, granular materials were able to dissipate energy by transfer of load from the outer to the inner hull together with the crushing in the vicinity of the indenter. The complete numerical model for the indentation of the particle filled box was compared with the experimental results given in [8], where a good agreement was achieved.

Although the model presented in current work is able to reproduce the effects observed in the experiments, there are certain aspects of this model that could be improved. For instance, for a realistic representation of the crushed particles, each spherical particle could be represented as a clump of bonded particles, see [42]. The limitation associated with the computation time of this approach can be overcome with the GPU- or MPI-based parallelization of the code. Furthermore, as mentioned in [12], rather than the Mohr–Coulomb material model, a model that includes the pressure-dependent behavior can further improve the accuracy. Finally, an adaptive scheme for the refinement of the DEM–FEM region can be used. With regard to the motion of the particles, the adaptive definition of both regions has advantages in terms of accuracy and overall speed-up of the model.