Abstract
This paper presents a brief review of grand challenges of Smoothed Particle Hydrodynamics (SPH) method. As a meshless method, SPH can simulate a large range of applications from astrophysics to free-surface flows, to complex mixing problems in industry and has had notable successes. As a young computational method, the SPH method still requires development to address important elements which prevent more widespread use. This effort has been led by members of the SPH rEsearch and engineeRing International Community (SPHERIC) who have identified SPH Grand Challenges. The SPHERIC SPH Grand Challenges (GCs) have been grouped into 5 categories: (GC1) convergence, consistency and stability, (GC2) boundary conditions, (GC3) adaptivity, (GC4) coupling to other models, and (GC5) applicability to industry. The SPH Grand Challenges have been formulated to focus the attention and activities of researchers, developers, and users around the world. The status of each SPH Grand Challenge is presented in this paper with a discussion on the areas for future development.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The smoothed-particle hydrodynamics (SPH) numerical method was originally introduced in 1977 for astrophysical simulations [41, 60]. Since then, SPH has progressed significantly and it is now a numerical technique adopted in numerous different fields from astrophysics, to engineering applications to biological flows. Its meshless Lagrangian nature, where the particles move according to the governing dynamics, has enabled it to be applied relatively easily to a large range of areas. Its particle–particle interactions with compact support mean that it is well suited to parallelisation for acceleration [17, 25, 75, 86, 88, 106]. This has led to the development and release of numerous SPH simulation codes that are now widely used. With its basis in Lagrangian and Hamiltonian mechanics, the meshless formulation has enabled progress in its fundamental mathematical analysis [99]. Despite this, SPH can be still considered a young numerical method and it presently suffers of some drawbacks in comparison with classical Eulerian mesh-based schemes such as Finite Difference Method (FDM), Finite Element Method (FEM) or Finite Volume Method (FVM). These drawbacks include complete proofs of convergence, standardisation of techniques, and use of parameters to run simulations. With SPH using smoothing kernels, and multiple formulations to represent media such as fluids and solids (for example, from weakly compressible to incompressible), the method has multiple features that require intensive investigation.
The SPH rEsearch and engineeRing International Community (SPHERIC), https://spheric-sph.org, was founded in 2005 with the aim of fostering collaboration and to push the development of the SPH method providing a network of researchers and industrial users around the world as a means to communicate and collaborate. Since then, it has continually strived to develop the fundamental basis of SPH, discuss current and new concepts, foster communication between research and users, provide access to existing software and methods, define benchmark test cases, and to identify the future needs of SPH. The annual international workshops, attended by over 130 delegates, have frequently been the events that have highlighted the gaps in our understanding and development needs. It is from these events that an awareness of key challenges in SPH has emerged. Conceived in 2012, the SPHERIC Steering Committee formulated five grand challenges (GCs) https://spheric-sph.org/grand-challenges to focus the attention of researchers, developers and users around the world.
The SPH Grand Challenges were initiated to bring the SPH community’s attention to areas of SPH that prevent its more widespread development and use. The GCs, and this paper specifically, do not aim to cover all fields where research in SPH is needed, for example fields such as turbulence modelling, multiphase flows (including the treatment of sharp interfaces) clearly need further investigation. Instead, the issues highlighted by the SPH Grand Challenges are general and must be addressed for SPH to compete with more established methods, such as FDM, FEM and FVM, whose theoretical foundations have been secured and whose state-of-the-art simulation packages are mature.
SPHERIC has defined the SPH Grand Challenges as:
-
GC1: Convergence, consistency and stability
-
GC2: Boundary Conditions
-
GC3: Adaptivity
-
GC4: Coupling to other methods
-
GC5: Applicability to industry.
It is essential that the SPH community around the world collaborates and addresses these SPH Grand Challenges. Without being able to demonstrate characteristics, behaviour and applicability that are fundamental to any numerical method, SPH will continue to be overlooked by some scientific and user communities. With the enormous range of applications, this is unacceptable. In the past decade, SPH has made massive progress, and this is evidenced by the increasing interest and uptake of the method, by developers and users in both industry and research and the exponentially increasing number of publications. In the years 2016–2019, there have been 5 review papers on SPH alone [44, 83, 102, 105, 110]. The SPH Grand Challenges have therefore been formulated to focus the worldwide developmental efforts in taking SPH to a point where the fundamental theory and practical use are mature so that SPH takes its rightful place in the range of methods at the disposal of scientists and engineers.
To incentivise this process, the SPHERIC Steering Committee inaugurated The Monaghan prize, https://spheric-sph.org/joe-monaghan-prize, named in honour of Prof. Joseph Monaghan, who has played such a key role throughout the entire life of SPH. The Monaghan Prize has been instigated to highlight and reward outstanding work that helps address and progress the SPH Grand Challenges. The first two Monaghan Prizes were awarded in 2015 to Colagrossi et al. [23] for their paper on free-surface boundary conditions and in 2018 to Marrone et al. [62] for their 2012 paper on developing the density diffusion technique now so widely used.
Despite progress, there is still much work to do. Hence, the SPHERIC Steering Committee considered it timely to ask the leaders and leading figures of each GC to summarise the current state of the art in their respective challenge. This paper presents a precis of each SPH Grand Challenge identifying progress, and most importantly the challenges that we face and must solve. Researchers and developers are strongly encouraged to focus attention on helping this collaborative effort.
2 Grand Challenge 1: Convergence, consistency and stability (Lind, Hu)
The notions of convergence, consistency and stability are fundamental and underpin all numerical methods, with these concepts easier to formalise in some methods than others. SPH is a method where there remains a significant lack of understanding and formalism concerning all three and, quite rightly, addressing this is a Grand Challenge. This viewpoint mentions some recent works in the literature that shine more light on these issues in SPH, as well as posing a few philosophical questions to stir debate. The above 3 properties are of course interlinked, after all the Lax Equivalence theorem proves that consistent finite difference schemes for well-posed linear problems are stable if and only if they are convergent: a method may be stable, but not converge; it may also be consistent to some level but not converge as expected.
Regarding stability, we have always been fortunate in SPH in comparison with other methods by being able to obtain physically meaningful results for time steps or resolutions where other methods often break down. Historically, the pairing and tensile instabilities have been a concern, but our understanding has much improved in recent years. For example, consider the pairing instability and the benefits of using the Wendland kernels [107] with nonnegative Fourier transforms [30]. Similarly, the use of a background pressure is beneficial in preventing the tensile instability, although excessive numerical dissipation can arise. Note the very fact that adding a constant background pressure affects SPH at all relates to issues around conservation and consistency, which we will mention shortly.
Clearly, particle distribution is key to maintaining stability and additional numerical treatments that improve distributions, such as particle number-density constraint [48], particle shifting [57, 69, 108] and transport formulation [2, 111], have increased in popularity in recent years given their efficacy and relative ease to implement. Practically speaking, in weakly compressible SPH (WCSPH) stability can also be maintained through diffusion (physical or numerical), and following the earliest uses of artificial viscosity, we now have some sophisticated approaches including, for example, delta-SPH [62] and its more recent variant deltaplus-SPH [90], which combines diffusive terms in the conservation of mass equation with shifting for improved particle distributions. Indeed, formulations incorporating artificial viscosity, delta-SPH [5, 62], and Riemann solvers [98] can all be seen as different stabilisation alternatives for the explicit spatially centred SPH scheme. An alternative SPH formulation is the so called Incompressible SPH (I-SPH), which is based on a divergence-free projection [27] of the velocity field, [48, 51, 57, 84]. I-SPH models generate smoother pressure fields, avoiding the introduction of additional explicit diffusive terms. We are still a long way from formalising much of this—important headway is being made regarding stability in time stepping in weakly compressible SPH [100] and in incompressible SPH [49, 101]—but a continued goal should be the determination of well-defined stability regions with bounds that have a known dependence on discretisation and kernel parameters, physical parameters, and numerical treatment parameters (e.g. shifting coefficients, delta parameters). The opportunity for further input from mathematicians/numerical analysts here is great.
Like stability, convergence depends critically on particle distributions. For example, Quinlan et al. [79] have provided important guidance on convergence, with dependence seen on smoothing length, particle spacing, kernel smoothness, and particle disorder. Two key contributions to the error include the error due to the smoothing operation and the numerical integration (or discretisation) error (due to the splitting of our domain into particles). The former is commonly second order in smoothing length, and the latter can be quantified if we split our integral into equi-spaced rectangular particles as per the rectangle or trapezoid rules. Consequently, as we refine and decrease smoothing length, the number of neighbours should also be increased appropriately. However, for practical reasons, this is often not done, resulting in the smoothing error eventually becoming saturated. If we take care in refinement over uniform (e.g. Cartesian) arrays of particles, SPH can be shown to converge in numerical experiments with rates of convergence matching theoretical error measures extremely well. Evers et al. [32] derived the rate of convergence of SPH numerical scheme using the least action principle. Franz & Wendland have recently provided a mathematical proof of convergence of SPH for a specific barotropic fluid and under certain properties of the underlying kernel [39]. However, as soon as some level of particle disorder is introduced, things become far more difficult. Errors and convergence rates are much more difficult to quantify, with convergence flat-lining, even diverging, once particles become sufficiently disordered—not ideal when your particles are Lagrangian.
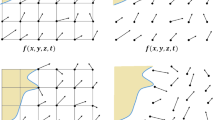
This close dependence of convergence on particle distribution seems to have motivated a growing number of researchers to explore Arbitrary Lagrangian Eulerian (ALE) formulations of SPH [74, 98]. The fully Eulerian SPH method can converge readily and to high orders of spatial accuracy [56] (see Fig. 1), while ALE-SPH (for example, [74]) permits study of a greater class of flows while also allowing control over particle distributions in order to improve accuracy and convergence. There is some really promising ongoing work here [7, 47, 71, 112], and this is an encouraging pathway, after all, even if one strongly values the Lagrangian nature, of classical SPH, a legitimate question is whether the determined particle velocity is indeed the Lagrangian velocity. Of course, mathematical formalism is lacking here also, and quantification of error and convergence rates for irregular distributions in particular should be a key goal.
High-order convergence of an SPH gradient for different kernels see [56] for more information
Consistency and convergence are closely linked, and while consistent formulations may be constructed for arbitrary particle distributions, this can be costly and convergence is not necessarily ideal. The SPH discretisation of derivatives has two typical formulations: the anti-symmetric and symmetric formulations. The numerical errors due to these two formulations are quite complex and are strongly dependent on particle distribution [79]. With the anti-symmetric formulation, the SPH discretisation for computing pressure forces on a particle implies that with momentum conservation of the particle system we cannot estimate correctly the vanishing gradient of a constant scalar field, in practice there is a non-vanishing total force acting on a particle in a field with constant pressure. On the other hand, with the symmetric formulation, the SPH discretisation for computing the density variation of a particle provides zero-order consistency, and a uniform velocity leads to a vanishing density variation. One may expect to cancel inconsistency error for the pressure field by applying the symmetric formulation to the discretised momentum equation. The dilemma is that the conservation of momentum, one of the most important properties of the original SPH method [66, 67], is not satisfied any more. Again, particle distributions remain key here, and recent investigations have focused on iterative redistribution procedures based on transport velocities ( [58]) or shifting [52, 93]. Such approaches have shown promise in recovering consistency without correction for SPH schemes which may also want to retain conservation. Importantly, with both consistency and conservation in place, there could be a route to formalising convergence in SPH via the Lax–Wendroff theorem, with convergent conservative schemes for hyperbolic equations providing at least weak solutions.
Thermodynamic consistency of SPH numerical schemes has been analysed by different authors, showing that Hamiltonian-consistent formulations ensure also total energy conservation [78]. For weakly compressible SPH, Antuono et al. [6] have shown how different energy terms evolve during the numerical simulation, and the same analysis has been extended to fluid–solid interaction in [18]. Khayyer et al. [53] have also investigated the energy conservation in incompressible SPH schemes showing that better energy conservation is achieved when corrected SPH interpolation is adopted.
In summary, a key goal of this grand challenge remains in improving the mathematical formalism around quantification of error, convergence, and stability. Hence, there are significant challenges going forward:
-
1.
The final objective of GC1 is to develop a rigorous framework where we understand the numerical mechanisms in SPH, the theoretical reasons explaining how SPH works, its limitations and the need for modifications to the methodology and accompanying analysis.
-
2.
This analysis is made extremely difficult by the flow being Lagrangian, as well as by the fact that particle volumes have no explicit spatial shape (no faces, cells) and do not form a partition of unity during the time evolution.
Nevertheless, further research on these topics will enable us to run informed simulations with confidence, and will inspire confidence in SPH in external fields and in industry. However, we should also not be afraid to pose questions and to highlight nuance. For example, what do we mean by convergence? If we are solving a partial differential equation, assuming there is a solution, then convergence becomes meaningful. If, however, we are working at the mesoscale, where many fashionable problems reside and where the continuum hypothesis starts to break down, the discrete particle system (that was always underlying) becomes apparent, and our usual notion of convergence loses meaning (i.e. we do not want \({\Delta }x\) to go to 0!). Of course, it is in such examples of the versatility and flexibility of SPH that we find the reasons for the method’s great appeal.
3 Grand Challenge 2: Boundary conditions (Souto-Iglesias)
In order to close the fluid dynamics equations, initial (ICs) and boundary conditions (BCs) are necessary. BC includes solid boundaries (free slip, no slip, pressure normal derivative), free surface, inlet/outlet (aka open BCs—OBCs), stress conditions in structural mechanics, those related to the coupling with other models, etc., and ICs are included in this challenge since they usually require special treatment in SPH, e.g. when a hydrostatic condition is needed. This need arises mostly due to unfeasibility to exactly link mass and volume in SPH. Due to the meshless nature of the method, imposing boundary conditions is far from trivial in SPH, leading to intense related research since the first applications of the method to bounded flows by Monaghan [64] in the nineties.
It is relevant to mention that in recent SPH review papers [42, 43, 65, 67, 102], there are specific review sections on BCs. The influential review by Price [78] does not, however, contain any reference to BCs as, in astrophysics, they are less of an issue than in typical engineering scales.
To include ICs and BCs in SPH, researchers use various techniques. There are a number of key issues that remain to be fully addressed, such as:
-
1.
How to include BCs without loosing intrinsic SPH conservation properties?
-
2.
How to include BCs consistently and without compromising stability? This is directly related with the role of boundary integrals.
-
3.
How to include solid wall BCs for actual geometries with complex shapes (2D, 3D)?
-
4.
How to provide an initial distribution of particles which avoids the onset of shocks once the time-integration starts?
-
5.
How to treat contact lines between free surfaces and solid boundaries?
-
6.
How to treat backflows (aka recirculation) when implementing OBCs?
-
7.
How to implement BCs in the interface between subdomains solved with different methods?
-
8.
How to accurately impose BCs in Incompressible SPH (ISPH) in complex flows?
-
9.
How to accurately impose BCs when particle shifting (within a consistent ALE framework or not) is used?
Some recent interesting references have looked into these questions: Ni et al. [70] implemented a wave flume with SPH using OBCs but did not look into recirculation issues. Along the same line, Bouscasse et al. [11] used OBCs for simulating the viscous flow around a submerged cylinder. In order to avoid backflow, they had to significantly extend the flow domain upstream and downstream, as well as limiting the simulation time (see Fig. 2). Back flow is held in FVM-VOF methods by indicating the physical properties of the incoming fluid, applying to it the local flow properties (velocity, temperature, etc.), but it is not clear how to implement it a Lagrangian approach. Tafuni et al. [91] have recently extended OBC algorithms to the popular GPU HPC implementation DualSphysics, and Wang et al. [104] have proposed a novel OBC implementation based on the method of characteristics using timeline interpolations.
Flow around a cylinder in the presence of a free surface at Reynolds number equal to 180 (see Bouscasse et al. [11] and Colagrossi et al. [24] for more details on this type of particular flows). The color code represents the streak-lines by identifying the vertical position in the unperturbed inlet. The horizontal and vertical coordinates are made non-dimensional with the cylinder diameter. (Color figure online)
Long-time-duration simulations of free-surface flows have been traditionally an issue in SPH due to the onset of stability problems. However, Green and Peiró [45] have recently been able to carry out long and accurate simulations of flows inside tanks by using fixed/prescribed motion dummy particles developed by Adami et al. [1], and by performing a good selection of simulation parameters. Extending flow fields outside of the boundaries to force BCs has been recently investigated by Fourtakas et al. [38]. They claim their locally uniform stencil-based formulation is able to model solid boundary conditions in complex 2-D and 3-D geometries, with improvements over existing techniques based on dummy particles (e.g. [1, 26]) partially achieved by using \(\delta -\)SPH [62] to reduce spurious pressure oscillations. However, validation with non-orthogonal geometries was not yet pursued. The flow field extension techniques have also been recently used in heat transfer applications by Wang et al. [103].
Regarding BCs affecting consistency of the operators, Fougeron and Aubry [36] have proposed a novel method based on non-boundary fitted clouds of points; they redefine the Lagrangian nature of the model by creating a set of nodes on the boundary, which then use to approximate the differential operators. They use this approach in elliptic equations, and though appealing ideas can be found, the application to typical SPH problems, such as wave-body interactions, is not evident to us.
Intrinsic good conservation properties are an asset of the SPH method. How these are affected by BCs has been investigated by Cercos-Pita et al. [18] in the presence of fluid–solid interactions, when these are modelled using ghost particles. They showed that due to the solid BCs, the energy equation of the particle system contains some extra terms that tend to vanish when the spatial resolution is increased (very slowly), and that affect the energy conservation of the system. Based on the test cases they run, they conjectured that the contribution is dissipative, but no rigorous proof was provided.
As for boundary integrals (see [35] for a fundamental reference on this kind of BC implementation, where formulae for first and second derivatives with a semi-analytic formulation with boundary integrals are proposed and validated), they provide consistent formulations and are a first choice in extremely fragmented flows, such as those found in hydroplaning simulations [19]. For this type of technique, Calderon et al. [13] have recently developed a formulation that improves the computation of the renormalisation factor in two and three dimensions. One main problem of boundary integrals is that the intrinsic good conservation properties of SPH are affected by the use of renormalised operators.
Looking into incompressible SPH and BCs, Takahashi et al. [92] provided an interesting discussion on the difficulties of imposing Dirichlet and Neumann BCs, including some improvements. Regarding ALE formulations, Oger et al. [74] reported the need to remove shifting when close to the free surface, defining in turn the ghost fluid properties without requiring any specific ALE-related correction and Khayyer et al. [52] applied the iterative shifting, originally proposed in [93] to multiphase and free-surface flows in the ISPH framework.
Looking ahead, there are some clear challenges going forward:
-
1.
Identifying and validating BCs that are robust for arbitrarily complex non-orthogonal geometries for the vast range of SPH applications.
-
2.
Extending the behaviour of SPH BCs to possess higher-order convergence properties.
-
3.
Maintaining the intrinsic conservation properties of SPH while retaining the consistency of operators.
-
4.
Supplementing the emerging proofs of convergence of GC1 with the added complication of BCs.
4 Grand Challenge 3: Adaptivity (Vacondio, Rogers)
Adaptivity is the capability of a numerical scheme to use a domain discretisation based on elements with different size. For Eulerian mesh-based methods such as finite volume, finite elements or finite differences those elements are the grid cells, whereas in Lagrangian meshless-based numerical methods they are the computational nodes that move with the fluid velocity. Adaptivity is a crucial feature for numerical schemes. It allows us to increase the number of computational nodes (cells or particles) only in the portions of the domain where the flow features require higher resolution. In this way, the total number of computational nodes (and so the computational cost for the simulation) used to discretise a domain can be dramatically decreased, for a given level of error. In mesh-based methods, variable resolution is a common feature and it has been introduced in several different ways. Often referred to as Adaptive Mesh Refinement (AMR), the most common approaches are unstructured grids or quadtree grids. Moreover, several different algorithms have been used successfully to dynamically adjust the mesh resolution, accordingly to some measures of the discretisation error or smoothness indicators for the numerical solutions (see, for example, [31, 50]). Despite the need to introduce variable resolution in SPH numerical schemes for fluids, almost all SPH codes are based on uniform resolution and this prevents the use of SPH models to simulate all engineering problems which are inherently multiscale.
For compressible fluids and astrophysical simulations, a consistent formulation which considers the space variability of the smoothing length has been derived many years ago [41, 46, 78], and in this approach, the conservation of fundamental properties is ensured and the resolution implicitly increases in high-density region (and decreases it in low-density one). Effectively, this creates particles with different volume but constant masses. Unfortunately, the same approach cannot be used for weakly compressible (or strictly incompressible) fluids where density remains (approximately) constant and so particles with different volumes have to have also different masses. Similar to astrophysical applications, in engineering the Lagrangian characteristics of SPH can lead to sparse or condensed distributions of particles, which can be addressed by merging/splitting particles to preserve a good interpolation accuracy. When the competing demands of adaptivity across phases with different distributions of particles are considered, one phase with a different distribution of particles might generate errors of a greater magnitude and therefore can have the opposite effect to the unified goal of targeting a local refinement and minimised error.
Initial efforts have been made for weakly compressible SPH models by introducing regions with different resolution at the beginning of the simulations [9, 10, 72, 76, 77]. Afterwards, with the aim of dynamically varying the particle resolution, some authors proposed some procedures to dynamically increase and reduce the particle resolution [8, 80, 94, 95]. Very recently, Sun et al. [89] simulated flow past different bodies in the presence of a free surface by using the Adaptive Particle Refinement (APR) methodology proposed in [21]. Spreng et al. [87] proposed a criterion to automatically adjust the particle resolution accordingly to some measure of the SPH spatial discretisation error. Despite the progresses in developing dynamic particle adaptivity, we think that some major challenges have still to be addressed in order to obtain a methodology that is sufficiently robust to be adopted by practitioners and industry. Looking far into the future, from the users’ perspective, dynamic adaptivity should be fully automated and activated only when needed. Full automation requires criteria to be developed that control the activation. A question then arises as to what these criteria should be and how they should operate? While this has been well investigated in adaptive mesh refinement (AMR), the same concepts do not necessarily apply in SPH since the nature of the discretisation is different. Most importantly, it is presently unclear what is the best general approach, and this requires (i) a focused research effort from the SPH community and (ii) an understanding from users that implementing and using adaptivity in SPH faces some key challenges and is far from straightforward. However, it is already clear that there are at least three key objectives:
-
1.
Error minimisation: it is impossible to avoid the introduction of error, but any form of SPH adaptivity should guarantee that the error has been minimised. To date, limited attention has been given to this [33, 94, 95]. Too often, schemes simply split particles into an arbitrary number (for example, 4) of so-called daughter particles (motivated by simplicity or ease-of-coding) with little consideration of the error and how it propagates throughout the solution. Similar to mature AMR schemes, error minimisation is a natural candidate as a criterion for APR.
-
2.
Uniform error distribution for a given resolution: the dynamic adaptation of particles should not generate additional error or inconsistencies due to the violation of conservation properties, in comparison with a uniform particle distribution configuration with the same resolution
-
3.
Robust schemes for all applications: due to its flexibility, the range of SPH applications is huge with highly complex processes. This naturally presents a challenging question—how to develop particle adaptivity that is widely applicable and robust? If certain types of adaptivity only work for a restricted number or type of applications, this calls into question the validity of the approach—in practice this means ensuring consistency and convergence.
In addition to the theoretical considerations and developments, there are multiple challenges going forward:
-
1.
Implementation with HPC and emerging technology: Even with APR, with its discretisation SPH will need some form of hardware acceleration for the foreseeable future. In the past decade, there has been a fundamental shift from faster clock speeds to different types of parallelism. For adaptivity, this poses the challenge of implementation. With different types of hardware continually appearing, developing implementations of adaptivity that are future-proofed will avoid costly recoding.
-
2.
Multi-phase implementations: Applications involving multiple phases can be extraordinarily complex, and to date, only simple cases or applications have been simulated in SPH. Developing robust adaptivity schemes for multi-phase flows whose properties can evolve represents a formidable challenge.
5 Grand Challenge 4: Coupling to other models (Marrone, Altomare, Le Touzé)
The SPH method is naturally able to resolve multi-mechanics problems and include different physical models in its meshless formalism. As with other Lagrangian meshless methods, SPH is very accurate and efficient when dealing with moving boundaries and complex interfaces, which are generally addressed with difficulties by conventional numerical methods (e.g. FVM, FEM). However, for problems where the latter methods are currently used and well established SPH is generally less effective and, for the same level of attained accuracy, results are more costly.
In several contexts, it can be much more effective to couple an SPH solver to another numerical solver, thus enhancing the capabilities of both methods within their specific application fields. In this way, a wider range of problems is efficiently addressed. The coupling algorithm and the related implementation complexity can largely vary depending on several aspects:
-
1.
One-way (offline) or two-way coupling;
-
2.
Heterogeneity of the modelled physics (e.g. potential flow/Navier-Stokes, fluid/solid, compressible/incompressible, etc.);
-
3.
Lagrangian or Eulerian approach adopted in the method coupled to SPH;
-
4.
Discrete coupling interfaces between solvers (mesh/meshless, sharp interface/blending region, etc.);
-
5.
Time stepping and stability of the coupled algorithm (e.g. explicit/implicit time integration, multiple time step);
-
6.
Preservation of conservative quantities by the coupling.
Besides, the complexities related to the coupling of very different solvers can be counterbalanced by impressive gains in terms of efficiency [20]. Most of the works regarding SPH coupling address fluid–structure interaction (FSI) problems for which the solid structure is generally solved by Finite Element Methods (FEM) and Discrete Element Methods (DEM). The Lagrangian character of those model has allowed a quite fast development of this kind of coupling and has been targeted in the first attempts of coupling the SPH method (see Attaway et al. 1994). In particular, SPH-FEM coupling is reaching maturity and has been used in several recent works addressing hydro-elasticity problems (see, e.g. [37, 55, 59, 109]) proving that this coupling paradigm can be highly competitive in FSI problems [85].
SPH-DEM coupling has been mostly used for problems in which several solid rigid bodies interact with a fluid flow [15, 81] including granular flows [16, 61]. Very recently coupling with open source multi-mechanics libraries has been implemented to simulate fluid-mechanism interactions by modelling frictional and multi-restriction-based behaviours [14].
Furthermore, SPH coupling has been largely developed for coastal engineering purposes. In this case, SPH is coupled with non-linear shallow water equation models [3, 4] or potential flow solvers in the form of spectral methods [73] or finite difference [96] for solving wave propagation in the far field and restraining SPH in the region where wavestructure interactions and wave-breaking are expected. In Fig. 3, one example of a coupling scheme between OceanWave3D and DualSPHysics [25] is shown. This includes the simulation of ship motions and the associated sloshing dynamics in the internal tanks as recently done in [82] and Bulian and [12]. Finally, a recent and growing branch is the coupling between Finite Volume Schemes (FVM) and SPH (see, for example, Fig. 4). In this case, the coupling strategy aims at flow simulations in which the accuracy and the ability of grid stretching of the FVM can be usefully coupled with the SPH properties in modelling complex interfaces [34, 54, 63, 68].
To summarise, coupling SPH models with other numerical solvers is a clear effective strategy to expand the intrinsic capabilities of SPH-based models to solve complex physics and hydrodynamics, while reducing the computational cost related to the meshfree nature of the method.
-
1.
Coupling algorithms are of complex implementation and generalisation due to the different nature of the coupled models: from one side a fully Lagrangian SPH method, from the other FEM, DEM, FVM, or finite difference schemes.
-
2.
In addition to the differences in formulations, there is the additional challenge of coupling methodologies that are suited, or have been highly optimised, to very different types of hardware acceleration and coding constructs. This is non-trivial.
Note, however, that the coupling task is eased by the meshless nature of the SPH method compared to couplings between heterogeneous mesh-based methods (e.g. FVM with FEM) where mesh interpenetration is a difficult issue. The achieved efficiency and first encouraging results justify the increasing use of coupling algorithms for practical applications and real engineering problems
Principle of 2D coupling between OceanWave3D and DualSPHysics around a structure under wave action from Verbrugghe et al. [96]. The top part shows the complete domain in OceanWave3D. The bottom part illustrates the DualSPHysics zone
Coupled SPH-FVM simulation of a sloshing flow in a tank with a corrugated bottom from Chiron et al. [20]. Top: SPH particles (blue) and FVM grid (black). Bottom: a time instant of the evolution showing vorticity contours and the free surface profile crossing the coupling interface. (Color figure online)
6 Grand Challenge 5: Applicability to industry (de Leffe, Marongiu)
Industry has been slow to accept the SPH method as a “serious” CFD method. Apart from some very specific applications, such as bird strike or high-pressure water jets impacting pelton turbine blades, it is only very recently that we can note a growing interest in the SPH method in the industrial world. The main reasons for this recent change are the research progress by the scientific community on Grand Challenges 1 and 2 has convinced engineers of the ability of the SPH method to solve applications with highly distorted complex interfaces with applications such as gearbox or tire aquaplaning becoming more frequent.
As the door of the industry begins to open, it is essential that the method continues to progress to maximise opportunities to demonstrate its suitability for future application. One of the first questions asked by an industrialist that is keen to use SPH for a specific application is related to the elapsed time of the simulation. The progress in High-Performance Computing (HPC) in accelerating SPH software on different architectures (CPU or GPUs), enables SPH to be competitive with conventional mesh-based methods. However, methods such as FVM and FEM have also progressed in capturing complex interfaces, so the challenge remains open and the fields where the SPH method is more efficient could be further reduced. Two fundamental characteristics make SPH inherently more expensive than classical mesh-based methods: (i) the much larger number of neighbours for a given computational point, and (ii) the smaller computational time step that has to be adopted due to the weakly compressible explicit formulation. For the first point, to date a mature technical solution has not yet emerged. However, work has been done to increase the order or convergence of SPH schemes for a given number of neighbours (see Grand Challenge 1). Nevertheless, this generates additional calculation, and the gain in terms of accuracy is not yet demonstrated for industrial applications. For the second point, an important work has been done to develop semi-implicit incompressible SPH (ISPH) schemes based on divergence-free projection [27]. The GPU implementation of ISPH, as reported in [22], will probably reinforce its efficacy.
The gain on the time step raises interesting questions if there is a loss of accuracy on the description of the free surface. A vital point to note here is that progress in HPC should not be pursued to the detriment of the accuracy of the numerical scheme. For example, when porting on GPU, the temptation of introducing simplifications in the adopted numerical scheme is to further increase its efficiency, losing the interest of hard-won gains in Grand Challenges 1 and 2. If the SPH method is not able to progress on the HPC objectives compared to other methods, SPH should be used in portions of the domain characterised by strong dynamics and complex interfaces. The complete simulation can be obtained by coupling SPH with other numerical methods (see Grand Challenge 4) [20].
The second question asked by an industrialist is the ability of the SPH method to simulate phenomena characterised by complex physics as turbulence, boundary layer, phase change, thermal diffusion and convection, surface tension, etc. Industrial SPH codes cannot simulate all the aforementioned phenomena (with the exception of thermal ones).
It is now crucial for the SPH method to include additional physical processes to simulate the full complexity of industrial cases. This is best illustrated with an example: the rocket or satellite tank in microgravity. The liquid phase is subjected to an important sloshing with a complex interface. The case therefore seems very promising for the SPH method. Except that there are competing dominating effects of surface tension with the contact angle and thermal physics due to the sun’s radiation. The fuel or oxidant is in equilibrium between its gaseous phase and liquid phase, causing significant phase changes. Another example is the water impact during slamming or ditching event. The case is dynamic with a complex free surface. The case therefore seems also very promising for the SPH method. Except that if the case has strong dynamics operating at different scales there is the dominating effect the gas phase, where the real compressibility of the gas must be considered. In some extreme cases, phenomena of cavitation may appear. The SPH method must progress to propose robust physical models to simulate these physical phenomena.
Many exciting challenges are waiting for the SPH method whether in HPC or in terms of modelling complex physics, if SPH wants to convince the industry on a long-term basis and not remain confined to a small application core. The progress made by the traditional volume-of-fluid (VOF) method or more recent method such as Lattice–Boltzmann Method (LBM), Material Point Method (MPM), Moving Particle Simulation (MPS), Particle Finite Element Method (PFEM) must serve as a motivation and a source of inspiration for the SPH community.
The recent contributions from the SPH research community have brought significant progress likely to foster the adoption of SPH among industry. The appearance of tools with Graphical User Interfaces (GUIs) for the pre- and post-processing of SPH simulations is noticeable (see, for example, Figure 5). DesignSPHysics [97] and VisualSPHysics [40] provide a complete simulation tool chain dedicated to SPH simulations. An alternative has been developed based on ParaView [29]. Advanced analysis of flow features still relies mainly on the projection of the particles data onto a grid. For the creation of the initial particle distribution in complex geometries, the particle packing algorithm has gained popularity as in [28]. The ease of use of the method will probably benefit from the recent improvements of the dynamic and adaptive particle refinement techniques. Significant contributions in this field have been given by [94] and [21]. A further development of these techniques will relieve simulation engineers from the burden of setting of the appropriate particle size for their application cases.
To summarise, the applicability to industry of the SPH method has been demonstrated on some applications with free surface, complex interface, and dynamic flow. To remain competitive with other methods and extend its field of application, especially in certain areas where at present no numerical method is relevant, the SPH method must continue to progress in order to:
-
1.
reduce the elapsed time,
-
2.
take into account complex physical phenomena (such as turbulence, surface tension, phase change)
-
3.
obtain effective coupling with other methods
The combined progress of all the GCs will enable SPH to rise these challenges.
7 Conclusion
A brief review of SPH grand Challenges of Smoothed-Particle Hydrodynamics (SPH) method has been presented in this paper. These SPH Grand Challenges have been identified to focus the development efforts of the SPH community and to advance the present state-of-the-art such that SPH competes with more established simulation techniques. SPH has made great progress over the past 15 years, and its attraction as a computational technique is clear from the increasingly large body of published work, SPH simulation packages and applications. The effort has been led by members of the SPH rEsearch and engineeRing International Community (SPHERIC). The SPH community, however, must focus on solving the SPH Grand Challenges to ensure that SPH becomes more accessible and is robust, reliable and adheres to the highest possible standards of academic rigour. The SPH Grand Challenges have been identified by SPHERIC as: (GC1) convergence, consistency and stability, (GC2) boundary conditions, (GC3) adaptivity, (GC4) coupling to other models, and (GC5) applicability to industry. In this paper, the state of each SPH Grand Challenge has been assessed. Examples of recent references have been discussed for each grand challenge, and future work threads proposed. From this paper, it is clear that the SPH Grand Challenges are not straightforward to solve and will require dedication and collaboration.
References
Adami S, Hu X, Adams N (2012) A generalized wall boundary condition for smoothed particle hydrodynamics. J Comput Phys 231(21):7057–7075. https://doi.org/10.1016/j.jcp.2012.05.005
Adami S, Hu X, Adams N (2013) A transport-velocity formulation for smoothed particle hydrodynamics. J Comput Phys 241:292–307. https://doi.org/10.1016/j.jcp.2013.01.043
Altomare C, Domínguez JM, Crespo AJC, Suzuki T, Caceres I, Gómez-Gesteira M (2016) Hybridization of the wave propagation model SWASH and the meshfree particle method SPH for real coastal applications. Coast Eng J. https://doi.org/10.1142/s0578563415500242
Altomare C, Tagliafierro B, Dominguez JM, Suzuki T, Viccione G (2018) Improved relaxation zone method in SPH-based model for coastal engineering applications. Appl Ocean Res. https://doi.org/10.1016/j.apor.2018.09.013
Antuono M, Colagrossi A, Marrone S, Molteni D (2010) Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput Phys Commun 181(3):532–549. https://doi.org/10.1016/j.cpc.2009.11.002
Antuono M, Marrone S, Colagrossi A, Bouscasse B (2015) Energy balance in the \(\delta \)-sph scheme. Comput Methods Appl Mech Eng 289:209–226. https://doi.org/10.1016/j.cma.2015.02.004
Avesani D, Dumbser M, Bellin A (2014) A new class of moving-least-squares WENO-SPH schemes. J Comput Phys 270:278–299. https://doi.org/10.1016/j.jcp.2014.03.041
Barcarolo D, Touzé DL, Oger G, de Vuyst F (2014) Adaptive particle refinement and derefinement applied to the smoothed particle hydrodynamics method. J Comput Phys 273:640–657. https://doi.org/10.1016/j.jcp.2014.05.040
Bonet J, Rodríguez-Paz MX (2005) Hamiltonian formulation of the variable-h SPH equations. J Comput Phys 209(2):541–558. https://doi.org/10.1016/j.jcp.2005.03.030
Børve S, Omang M, Trulsen J (2005) Regularized smoothed particle hydrodynamics with improved multi-resolution handling. J Comput Phys 208(1):345–367. https://doi.org/10.1016/j.jcp.2005.02.018
Bouscasse B, Colagrossi A, Marrone S, Souto-Iglesias A (2017) SPH modelling of viscous flow past a circular cylinder interacting with a free surface. Comput Fluids 146:190–212. https://doi.org/10.1016/j.compfluid.2017.01.011
Bulian G, Cercos-Pita JL (2018) Co-simulation of ship motions and sloshing in tanks. Ocean Eng. https://doi.org/10.1016/j.oceaneng.2018.01.028
Calderon-Sanchez J, Cercos-Pita J, Duque D (2019) A geometric formulation of the Shepard renormalization factor. Comput Fluids 183:16–27. https://doi.org/10.1016/j.compfluid.2019.02.020
Canelas RB, Brito M, Feal OG, Domínguez JM, Crespo AJ (2018) Extending DualSPHysics with a differential variational inequality: modeling fluid–mechanism interaction. Appl Ocean Res. https://doi.org/10.1016/j.apor.2018.04.015
Canelas RB, Crespo AJ, Domínguez JM, Ferreira RM, Gómez-Gesteira M (2016) SPH-DCDEM model for arbitrary geometries in free surface solid-fluid flows. Comput Phys Commun. https://doi.org/10.1016/j.cpc.2016.01.006
Canelas RB, Domínguez JM, Crespo AJC, Gómez-Gesteira M, Ferreira RML (2017) Resolved simulation of a granular-fluid flow with a coupled SPH-DCDEM model. J Hydraul Eng. https://doi.org/10.1061/(asce)hy.1943-7900.0001331
Cercos-Pita J (2015) Aquagpusph, a new free 3d SPH solver accelerated with opencl. Comput Phys Commun 192:295–312. https://doi.org/10.1016/j.cpc.2015.01.026
Cercos-Pita J, Antuono M, Colagrossi A, Souto-Iglesias A (2017) SPH energy conservation for fluid–solid interactions. Comput Methods Appl Mech Eng 317:771–791. https://doi.org/10.1016/j.cma.2016.12.037
Chiron L, de Leffe M, Oger G, Touzé DL (2019) Fast and accurate SPH modelling of 3D complex wall boundaries in viscous and non viscous flows. Comput Phys Commun 234:93–111. https://doi.org/10.1016/j.cpc.2018.08.001
Chiron L, Marrone S, Mascio AD, Touzé DL (2018) Coupled SPH-FV method with net vorticity and mass transfer. J Comput Phys 364:111–136. https://doi.org/10.1016/j.jcp.2018.02.052
Chiron L, Oger G, de Leffe M, Touzé DL (2018) Analysis and improvements of adaptive particle refinement (APR) through CPU time, accuracy and robustness considerations. J Comput Phys 354:552–575. https://doi.org/10.1016/j.jcp.2017.10.041
Chow AD, Rogers BD, Lind SJ, Stansby PK (2018) Incompressible SPH (ISPH) with fast Poisson solver on a GPU. Comput Phys Commun. https://doi.org/10.1016/j.cpc.2018.01.005
Colagrossi A, Antuono M, Le Touzé D (2009) Theoretical considerations on the free-surface role in the smoothed-particle-hydrodynamics model. Phys Rev E 79:056701. https://doi.org/10.1103/PhysRevE.79.056701
Colagrossi A, Nikolov G, Durante D, Marrone S, Souto-Iglesias A (2019) Viscous flow past a cylinder close to a free surface: benchmarks with steady, periodic and metastable responses, solved by meshfree and mesh-based schemes. Comput Fluids 181:345–363. https://doi.org/10.1016/j.compfluid.2019.01.007
Crespo A, Domínguez J, Rogers B, Gómez-Gesteira M, Longshaw S, Canelas R, Vacondio R, Barreiro A, García-Feal O (2015) DualSPHysics: open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput Phys Commun 187:204–216. https://doi.org/10.1016/j.cpc.2014.10.004
Crespo A, Gómez-Gesteira M, Dalrymple R (2007) Boundary conditions generated by dynamic particles in SPH methods. Comput Mater Continua 5:173–184
Cummins SJ, Rudman M (1999) An SPH projection method. J Comput Phys 152(2):584–607. https://doi.org/10.1006/jcph.1999.6246
Dauch TF, Okraschevski M, Keller MC, Braun S, Wieth L, Chaussonnet G, Koch R, Bauer HJ (2017) Preprocessing workflow for the initialization of SPH predictions based on arbitrary CAD models. Universidate de Vigo, Vigo, Spain
Dauch TF, Okraschevski M, Keller MC, Braun S, Wieth L, Chaussonnet G, Koch R, Bauer H-J (2017) SPHStudio: a ParaView based software to develop SPH simulation models. Universidate de Vigo, Vigo, Spain
Dehnen W, Aly H (2012) Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon Not R Astron Soc 425(2):1068–1082. https://doi.org/10.1111/j.1365-2966.2012.21439.x
Dumbser M, Zanotti O, Hidalgo A, Balsara DS (2013) Ader-weno finite volume schemes with space-time adaptive mesh refinement. J Comput Phys 248:257–286. https://doi.org/10.1016/j.jcp.2013.04.017
Evers JH, Zisis IA, van der Linden BJ, Duong MH (2018) From continuum mechanics to SPH particle systems and back: systematic derivation and convergence. J Appl Math Mech / Zeitschrift für Angewandte Mathematik und Mechanik (ZAMM) 98(1):106–133. https://doi.org/10.1002/zamm.201600077
Feldman J, Bonet J (2007) Dynamic refinement and boundary contact forces in SPH with applications in fluid flow problems. Int J Numer Methods Eng 72(3):295–324. https://doi.org/10.1002/nme.2010
Fernandez-Gutierrez D, Souto-Iglesias A, Zohdi TI (2018) A hybrid Lagrangian Voronoi-SPH scheme. Comput Particle Mech. https://doi.org/10.1007/s40571-017-0173-4
Ferrand M, Laurence DR, Rogers BD, Violeau D, Kassiotis C (2013) Unified semi-analytical wall boundary conditions for inviscid, laminar or turbulent flows in the meshless SPH method. Int J Numer Methods Fluids 71(4):446–472. https://doi.org/10.1002/fld.3666
Fougeron G, Aubry D (2019) Imposition of boundary conditions for elliptic equations in the context of non boundary fitted meshless methods. Comput Methods Appl Mech Eng 343:506–529. https://doi.org/10.1016/j.cma.2018.08.035
Fourey G, Hermange C, Touzé DL, Oger G (2017) An efficient FSI coupling strategy between smoothed particle hydrodynamics and finite element methods. Comput Phys Commun 217:66–81. https://doi.org/10.1016/j.cpc.2017.04.005
Fourtakas G, Dominguez JM, Vacondio R, Rogers BD (2019) Local uniform stencil (LUST) boundary condition for arbitrary 3-D boundaries in parallel Smoothed Particle Hydrodynamics (SPH) models. Comput Fluids 190:346–361. https://doi.org/10.1016/j.compfluid.2019.06.009
Franz T, Wendland H (2018) Convergence of the smoothed particle hydrodynamics method for a specific barotropic fluid flow: constructive kernel theory. SIAM J Math Anal 50(5):4752–4784. https://doi.org/10.1137/17M1157696
García-Feal O, Crespo AJ, Domínguez JM, Gómez-Gesteira M (2016) Advanced fluid visualization with DualSPHysics and Blender. Technische universität münchen, München, Germany
Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics: theory and application to non-spherical stars. Mon Not R Astron Soc 181(3):375–389. https://doi.org/10.1093/mnras/181.3.375
Gomez-Gesteira M, Rogers BD, Dalrymple RA, Crespo AJ (2010) State-of-the-art of classical SPH for free-surface flows. J Hydraul Res 48(sup1):6–27. https://doi.org/10.1080/00221686.2010.9641242
Gotoh H, Khayyer A (2016) Current achievements and future perspectives for projection-based particle methods with applications in ocean engineering. J Ocean Eng Mar Energy 2(3):251–278. https://doi.org/10.1007/s40722-016-0049-3
Gotoh H, Khayyer A (2018) On the state-of-the-art of particle methods for coastal and ocean engineering. Coast Eng J 60(1):79–103. https://doi.org/10.1080/21664250.2018.1436243
Green MD, Peiró J (2018) Long duration SPH simulations of sloshing in tanks with a low fill ratio and high stretching. Comput Fluids 174:179–199. https://doi.org/10.1016/j.compfluid.2018.07.006
Hernquist L, Katz N (1989) TREESPH—a unification of SPH with the hierarchical tree method. Astrophys J Suppl Ser 70:419–446. https://doi.org/10.1086/191344
Hu W, Trask N, Hu X, Pan W (2019) A spatially adaptive high-order meshless method for fluid–structure interactions. Comput Methods Appl Mech Eng 355:67–93. https://doi.org/10.1016/j.cma.2019.06.009
Hu X, Adams N (2007) An incompressible multi-phase SPH method. J Comput Phys 227(1):264–278. https://doi.org/10.1016/j.jcp.2007.07.013
Imoto Y (2019) Unique solvability and stability analysis for incompressible smoothed particle hydrodynamics method. Comput Particle Mech 6(2):297–309. https://doi.org/10.1007/s40571-018-0214-7
Johnson C, Hansbo P (1992) Adaptive finite element methods in computational mechanics. Comput Methods Appl Mech Eng 101(1):143–181. https://doi.org/10.1016/0045-7825(92)90020-K
Khayyer A, Gotoh H, Shimizu Y (2017) Comparative study on accuracy and conservation properties of two particle regularization schemes and proposal of an optimized particle shifting scheme in ISPH context. J Comput Phys 332:236–256. https://doi.org/10.1016/j.jcp.2016.12.005
Khayyer A, Gotoh H, Shimizu Y (2019) A projection-based particle method with optimized particle shifting for multiphase flows with large density ratios and discontinuous density fields. Comput Fluids 179:356–371. https://doi.org/10.1016/j.compfluid.2018.10.018
Khayyer A, Gotoh H, Shimizu Y, Gotoh K (2017) On enhancement of energy conservation properties of projection-based particle methods. Eur J Mech B/Fluids 66:20–37. https://doi.org/10.1016/j.euromechflu.2017.01.014
Kumar P, Yang Q, Jones V, McCue-Weil L (2015) Coupled SPH-FVM simulation within the OpenFOAM framework. In: Procedia IUTAM. https://doi.org/10.1016/j.piutam.2015.11.008
Li Z, Leduc J, Nunez-Ramirez J, Combescure A, Marongiu JC (2015) A non-intrusive partitioned approach to couple smoothed particle hydrodynamics and finite element methods for transient fluid-structure interaction problems with large interface motion. Comput Mech 55(4):697–718. https://doi.org/10.1007/s00466-015-1131-8
Lind S, Stansby P (2016) High-order Eulerian incompressible smoothed particle hydrodynamics with transition to Lagrangian free-surface motion. J Comput Phys 326:290–311. https://doi.org/10.1016/j.jcp.2016.08.047
Lind S, Xu R, Stansby P, Rogers B (2012) Incompressible smoothed particle hydrodynamics for free-surface flows: a generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves. J Comput Phys 231(4):1499–1523. https://doi.org/10.1016/j.jcp.2011.10.027
Litvinov S, Hu X, Adams N (2015) Towards consistence and convergence of conservative SPH approximations. J Comput Phys 301:394–401. https://doi.org/10.1016/j.jcp.2015.08.041
Long T, Hu D, Yang G, Wan D (2016) A particle-element contact algorithm incorporated into the coupling methods of FEM-ISPH and FEM-WCSPH for FSI problems. Ocean Eng 123:154–163. https://doi.org/10.1016/j.oceaneng.2016.06.040
Lucy LB (1977) A numerical approach to testing the fission hypothesis. Astron J 82(12):1013–1924
Markauskas D, Kruggel-Emden H, Sivanesapillai R, Steeb H (2017) Comparative study on mesh-based and mesh-less coupled CFD-DEM methods to model particle-laden flow. Powder Technol. https://doi.org/10.1016/j.powtec.2016.09.052
Marrone S, Antuono M, Colagrossi A, Colicchio G, Touzé DL, Graziani G (2011) \(\delta \)-sph model for simulating violent impact flows. Comput Methods Appl Mech Eng 200(13):1526–1542. https://doi.org/10.1016/j.cma.2010.12.016
Marrone S, Di Mascio A, Le Touzé D (2016) Coupling of smoothed particle hydrodynamics with finite volume method for free-surface flows. J Comput Phys. https://doi.org/10.1016/j.jcp.2015.11.059
Monaghan J (1994) Simulating free surface flows with SPH. J Comput Phys 110(2):399–406. https://doi.org/10.1006/jcph.1994.1034
Monaghan J (2012) Smoothed particle hydrodynamics and its diverse applications. Annu Rev Fluid Mech 44(1):323–346. https://doi.org/10.1146/annurev-fluid-120710-101220
Monaghan JJ (1992) Smoothed particle hydrodynamics. Ann Rev Astron Astrophys 30(1):543–574. https://doi.org/10.1146/annurev.aa.30.090192.002551
Monaghan JJ (2005) Smoothed particle hydrodynamics. Rep Prog Phys 68(8):1703–1759. https://doi.org/10.1088/0034-4885/68/8/r01
Napoli E, De Marchis M, Gianguzzi C, Milici B, Monteleone A (2016) A coupled finite volume-smoothed particle hydrodynamics method for incompressible flows. Comput Methods Appl Mech Eng. https://doi.org/10.1016/j.cma.2016.07.034
Nestor RM, Basa M, Lastiwka M, Quinlan NJ (2009) Extension of the finite volume particle method to viscous flow. J Comput Phys 228(5):1733–1749. https://doi.org/10.1016/j.jcp.2008.11.003
Ni X, Feng W, Huang S, Zhang Y, Feng X (2018) A SPH numerical wave flume with non-reflective open boundary conditions. Ocean Eng 163:483–501. https://doi.org/10.1016/j.oceaneng.2018.06.034
Nogueira X, Ramírez L, Clain S, Loubère R, Cueto-Felgueroso L, Colominas I (2016) High-accurate SPH method with multidimensional optimal order detection limiting. Comput Methods Appl Mech Eng 310:134–155. https://doi.org/10.1016/j.cma.2016.06.032
Oger G, Doring M, Alessandrini B, Ferrant P (2006) Two-dimensional SPH simulations of wedge water entries. J Comput Phys 213(2):803–822. https://doi.org/10.1016/j.jcp.2005.09.004
Oger G, Le Touzé D, Ducrozet G, Candelier J, Guilcher PM (2014) A coupled SPH-spectral method for the simulation of wave train impacts on a FPSO. https://doi.org/10.1115/omae2014-24679
Oger G, Marrone S, Touzé DL, de Leffe M (2016) SPH accuracy improvement through the combination of a quasi-Lagrangian shifting transport velocity and consistent ALE formalisms. J Comput Phys 313:76–98. https://doi.org/10.1016/j.jcp.2016.02.039
Oger G, Touzé DL, Guibert D, de Leffe M, Biddiscombe J, Soumagne J, Piccinali JG (2016) On distributed memory MPI-based parallelization of SPH codes in massive HPC context. Comput Phys Commun 200:1–14. https://doi.org/10.1016/j.cpc.2015.08.021
Omidvar P, Stansby PK, Rogers BD (2012) Wave body interaction in 2d using smoothed particle hydrodynamics (SPH) with variable particle mass. Int J Numer Methods Fluids 68(6):686–705. https://doi.org/10.1002/fld.2528
Omidvar P, Stansby PK, Rogers BD (2013) SPH for 3d floating bodies using variable mass particle distribution. Int J Numer Methods Fluids 72(4):427–452. https://doi.org/10.1002/fld.3749
Price DJ (2012) Smoothed particle hydrodynamics and magnetohydrodynamics. J Comput Phys 231(3):759–794. https://doi.org/10.1016/j.jcp.2010.12.011
Quinlan NJ, Basa M, Lastiwka M (2006) Truncation error in mesh-free particle methods. Int J Numer Methods Eng 66(13):2064–2085. https://doi.org/10.1002/nme.1617
Reyes López Y, Roose D, Recarey Morfa C (2013) Dynamic particle refinement in SPH: application to free surface flow and non-cohesive soil simulations. Comput Mech 51(5):731–741. https://doi.org/10.1007/s00466-012-0748-0
Robb DM, Gaskin SJ, Marongiu JC (2016) SPH-DEM model for free-surface flows containing solids applied to river ice jams. J Hydraul Res. https://doi.org/10.1080/00221686.2015.1131203
Serván-Camas B, Cercós-Pita JL, Colom-Cobb J, García-Espinosa J, Souto-Iglesias A (2016) Time domain simulation of coupled sloshing-seakeeping problems by SPH-FEM coupling. Ocean Eng. https://doi.org/10.1016/j.oceaneng.2016.07.003
Shadloo M, Oger G, Touzé DL (2016) Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: motivations, current state, and challenges. Comput Fluids 136:11–34. https://doi.org/10.1016/j.compfluid.2016.05.029
Shao S, Lo EY (2003) Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv Water Resour 26(7):787–800. https://doi.org/10.1016/S0309-1708(03)00030-7
Siemann M, Langrand B (2017) Coupled fluid-structure computational methods for aircraft ditching simulations: comparison of ALE-FE and SPH-FE approaches. Comput Struct 188:95–108. https://doi.org/10.1016/j.compstruc.2017.04.004
Spreng F, Schnabel D, Mueller A, Eberhard P (2014) A local adaptive discretization algorithm for smoothed particle hydrodynamics. Comput Particle Mech 1(2):131–145. https://doi.org/10.1007/s40571-014-0015-6
Spreng F, Vacondio R, Eberhard P, Williams J (2019) An advanced study on discretization-error-based adaptivity in smoothed particle hydrodynamics. Comput Fluids 198:104388
Springel V (2005) The cosmological simulation code gadget-2. Mon Not R Astron Soc 364(4):1105–1134. https://doi.org/10.1111/j.1365-2966.2005.09655.x
Sun P, Colagrossi A, Marrone S, Antuono M, Zhang A (2018) Multi-resolution delta-plus-SPH with tensile instability control: towards high Reynolds number flows. Comput Phys Commun 224:63–80. https://doi.org/10.1016/j.cpc.2017.11.016
Sun P, Colagrossi A, Marrone S, Zhang A (2017) The delta-plus-SPH model: simple procedures for a further improvement of the SPH scheme. Comput Methods Appl Mech Eng 315:25–49. https://doi.org/10.1016/j.cma.2016.10.028
Tafuni A, Domínguez J, Vacondio R, Crespo A (2018) A versatile algorithm for the treatment of open boundary conditions in smoothed particle hydrodynamics GPU models. Comput Methods Appl Mech Eng 342:604–624. https://doi.org/10.1016/j.cma.2018.08.004
Takahashi T, Dobashi Y, Nishita T, Lin MC (2018) An efficient hybrid incompressible SPH solver with interface handling for boundary conditions. Comput Graph Forum 37(1):313–324. https://doi.org/10.1111/cgf.13292
Vacondio R, Rogers BD (2017) Consistent iterative shifting for SPH methods. University of Vigo. Ourense, Spain
Vacondio R, Rogers B, Stansby P, Mignosa P (2016) Variable resolution for SPH in three dimensions: Towards optimal splitting and coalescing for dynamic adaptivity. Comput Methods Appl Mech Eng 300:442–460. https://doi.org/10.1016/j.cma.2015.11.021
Vacondio R, Rogers B, Stansby P, Mignosa P, Feldman J (2013) Variable resolution for SPH: a dynamic particle coalescing and splitting scheme. Comput Methods Appl Mech Eng 256:132–148. https://doi.org/10.1016/j.cma.2012.12.014
Verbrugghe T, Domínguez JM, Crespo AJ, Altomare C, Stratigaki V, Troch P, Kortenhaus A (2018) Coupling methodology for smoothed particle hydrodynamics modelling of non-linear wave-structure interactions. Coast Eng. https://doi.org/10.1016/j.coastaleng.2018.04.021
Vieira A, García-Feal O, Domínguez JM, Crespo AJC, Gómez-Gesteira M (2017) Graphical user interface for SPH codes: DesignSPHysics. Universidate de Vigo, Vigo, Spain
Vila JP (1999) On particle weighted methods and smooth particle hydrodynamics. Math Models Methods Appl Sci 9(2):161–209. https://doi.org/10.1142/S0218202599000117
Violeau D (2012) Fluid mechanics and the SPH method: theory and applications. Oxford University Press
Violeau D, Leroy A (2014) On the maximum time step in weakly compressible SPH. J Comput Phys 256:388–415. https://doi.org/10.1016/j.jcp.2013.09.001
Violeau D, Leroy A (2015) Optimal time step for incompressible SPH. J Comput Phys 288:119–130. https://doi.org/10.1016/j.jcp.2015.02.015
Violeau D, Rogers BD (2016) Smoothed Particle Hydrodynamics (SPH) for free-surface flows: past, present and future. J Hydraul Res 54(1):1–26. https://doi.org/10.1080/00221686.2015.1119209
Wang J, Hu W, Zhang X, Pan W (2019) Modeling heat transfer subject to inhomogeneous Neumann boundary conditions by smoothed particle hydrodynamics and peridynamics. Int J Heat Mass Transf 139:948–962. https://doi.org/10.1016/j.ijheatmasstransfer.2019.05.054
Wang P, Zhang AM, Ming F, Sun P, Cheng H (2019) A novel non-reflecting boundary condition for fluid dynamics solved by smoothed particle hydrodynamics. J Fluid Mech 860:81–114. https://doi.org/10.1017/jfm.2018.852
Wang ZB, Chen R, Wang H, Liao Q, Zhu X, Li SZ (2016) An overview of smoothed particle hydrodynamics for simulating multiphase flow. Appl Math Model 40(23):9625–9655. https://doi.org/10.1016/j.apm.2016.06.030
Wei Z, Edge BL, Dalrymple RA, Hérault A (2019) Modeling of wave energy converters by GPUSPH and Project Chrono. Ocean Eng 183:332–349. https://doi.org/10.1016/j.oceaneng.2019.04.029
Wendland H (1995) Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv Comput Math 4(1):389–396. https://doi.org/10.1137/17M1157696
Xu R, Stansby P, Laurence D (2009) Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J Comput Phys 228(18):6703–6725. https://doi.org/10.1016/j.jcp.2009.05.032
Yang X, Liu M, Peng S, Huang C (2016) Numerical modeling of dam-break flow impacting on flexible structures using an improved SPH-EBG method. Coast Eng 108:56–64. https://doi.org/10.1016/j.coastaleng.2015.11.007
Ye T, Pan D, Huang C, Liu M (2019) Smoothed particle hydrodynamics (SPH) for complex fluid flows: recent developments in methodology and applications. Phys Fluids 31(1):011301. https://doi.org/10.1063/1.5068697
Zhang C, Hu XY, Adams NA (2017) A generalized transport-velocity formulation for smoothed particle hydrodynamics. J Comput Phys 337:216–232. https://doi.org/10.1016/j.jcp.2017.02.016
Zhang C, Xiang G, Wang B, Hu X, Adams N (2019) A weakly compressible sph method with weno reconstruction. J Comput Phys 392:1–18
Acknowledgements
Dr. Corrado Altomare acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie Grant Agreement No. 792370. A. Souto-Iglesias acknowledges the funding by the Spanish Ministry for Science, Innovation and Universities (MCIU) under Grant RTI2018-096791-B-C21 “Hidrodinámica de elementos de amortiguamiento del movimiento de aerogeneradores flotantes”.
Funding
Open access funding provided by Università degli Studi di Parma within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vacondio, R., Altomare, C., De Leffe, M. et al. Grand challenges for Smoothed Particle Hydrodynamics numerical schemes. Comp. Part. Mech. 8, 575–588 (2021). https://doi.org/10.1007/s40571-020-00354-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40571-020-00354-1