1 Introduction

The material-point method (MPM) [48, 51] is a numerical technique suited to model large deformations in continuum mechanics. MPM has been successfully applied in the numerical simulation of complex engineering problems [3, 50, 59, 61]. It originates from the fluid-dynamics-oriented particle-in-cell (PIC) method [25] and is mainly based on a weak formulation of the momentum-balance equation. To avoid mesh distortion when the material undergoes large deformations, MPM combines a fixed Eulerian background grid and a set of Lagrangian point masses called material points. The MPM grid contains no permanent information about the continuum and is used only to assemble and solve the discretized governing equations. The material points travel freely through the background grid, while carrying the information about the continuum.

The optimal transportation meshfree (OTM) method [27] has been developed to simulate general solid and fluid flows and applied to a wide range of problems [19, 28, 29, 37]. The OTM method uses the concepts from optimal transportation theory (an overview is provided by Villani [54]) to translate the mass and momentum balance equations into a minimization problem for the total action of the solid over a time interval. The OTM method employs two sets of points: nodal points and material points. Nodal points carry information about the positions, while material points represent the continuum. This updated Lagrangian method is typically used with local maximum-entropy (maxent) basis functions [4, 46] that are fully defined by the nodal set and the domain of analysis.

Many similarities can be found between MPM and the OTM method. For instance, they both employ the idea of material points that represent the continuum, but are not used directly to compute the solution of the governing equations. Moreover, an alternative derivation of the OTM scheme has been provided by Weißenfels and Wriggers [56], where the method is obtained from the weak form of the equation of motion. Despite this, MPM method and the OTM method have been evolved and studied independently from each other. An in-depth analysis and direct comparison of the methods provide a better understanding of their relation, with potential improvements of MPM based on the present knowledge of the OTM method and vice versa.

This paper consists of two parts: The first part offers new insights into the relation between MPM and the OTM method by drawing a detailed comparison of their algorithms. Based on this comparison, it identifies the conditions, under which the two approaches can be related to each other, and highlights their fundamental differences. The second part of the study presents a novel unified approach that combines the design principles from B-spline MPM (BSMPM) [43] and the OTM method. The choice of BSMPM is motivated by previous studies. First of all, a number of studies have indicated that BSMPM is a viable alternative not only for MPM, but also for its more advanced versions such as dual domain material-point (DDMP) [60] and convected particle-domain interpolation (CPDI) [40] methods [20, 45, 53, 57]. Secondly, Cyron et al. [13] pointed out the strong similarities between B-spline and maxent basis functions. For example, both of them are non-negative, smooth and possess the partition of unity property. Although in the present paper, the unified approach is applied to relatively simple examples, all derivations are presented in their general form enabling its straightforward extension to more complex problems.

This paper is structured as follows: Section 2 presents the governing equations that serve as a basis for the development of both MPM and OTM. To be self-contained and allow for a direct comparison of the methods, Sects. 3 and 4 describe, respectively, the MPM and OTM schemes and provide their computational algorithms. Section 5 gives a step-by-step comparison of the algorithms and identifies the conditions, under which they can be related, as well as their main differences. Aside from the computational algorithms, the MPM and OTM methods can be classified by means of the basis functions typically used within them. For this reason, Sect. 6 describes the piecewise-linear Lagrange and maximum entropy basis functions. Since our unified approach and BSMPM adopt the B-spline basis functions, the section also presents the B-spline basis functions. After that, Sect. 7 introduces the unified approach that combines the advantages of BSMPM and the OTM method. Section 8 reports the results that show the difference between the MPM and OTM methods numerically. In addition, it demonstrates the results obtained with our unified approach and gives a comparison with BSMPM. Finally, Sect. 9 summarizes the main conclusions of this study.

2 Governing equations

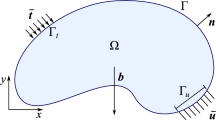
To describe the governing equations for the MPM and OTM schemes, we start by introducing some notation from continuum mechanics. It is assumed that the considered one-phase continuum occupies the domain \(\varOmega ^0 \subseteq \mathbb {R}^3\) at the initial time \(t^0\) and domain \(\varOmega ^t \subseteq \mathbb {R}^3\) at any later time \(t>t^0\). The initial position of the material is denoted by \(\mathbf {x}^0 = [x_{1}^0, \ x_{2}^0, \ x_{3}^0]^\mathsf {T}\), while the position at time t is \(\mathbf {x} = [x_{1}, \ x_{2}, \ x_{3}]^\mathsf {T}\). In abstract formulation, the deformation mapping is defined as \(\varphi :~\mathbb {R}^3\times [t^0, T]~\rightarrow \mathbb {R}^3\), where T is the final time. For a fixed time t, the mapping \(\varOmega ^0 \mapsto \varOmega ^t\) can be considered as the ‘push forward’ operator, which needs to be bijective, so that the current domain can also be ‘pulled back’ to the initial one via \(\varphi ^{-1}(\mathbf {x},t) : \varOmega ^t\rightarrow \varOmega ^0\). Likewise, it links the initial and current positions:

$$\begin{aligned} \mathbf {x} = \varphi (\mathbf {x}^0,t),\quad \mathbf {x}^0 = \varphi ^{-1}(\mathbf {x},t). \end{aligned}$$
(1)

The displacement, velocity, and acceleration vectors are denoted by

$$\begin{aligned} \mathbf {u}= & {} [u_{1}, \ u_{2}, \ u_{3}]^\mathsf {T},\quad \nonumber \\ \mathbf {v}= & {} [v_{1}, \ v_{2}, \ v_{3}]^\mathsf {T},\quad \nonumber \\ \mathbf {a}= & {} [a_{1}, \ a_{2}, \ a_{3}]^\mathsf {T}, \end{aligned}$$
(2)

respectively. The displacement at time t is defined as the difference between the current and initial positions:

$$\begin{aligned} \mathbf {u}(\mathbf {x} ,t) = \mathbf {x} - \mathbf {x}^0. \end{aligned}$$
(3)

The velocity and acceleration are defined by means of the material time derivative. Using \(\nabla = \Big [\frac{\partial }{\partial x_1}, \frac{\partial }{\partial x_2}, \frac{\partial }{\partial x_3}\Big ]^\mathsf {T}\), the material time derivative can be written as

$$\begin{aligned} \frac{{{\,\mathrm{d}\,}}}{{{{\,\mathrm{d}\,}}}t} = \frac{\partial }{\partial t} + \mathbf {v}\cdot \nabla . \end{aligned}$$
(4)

Since the convective effects can be neglected in Lagrangian computations (e.g., Donea et al. [16]), the velocity and acceleration are obtained from

$$\begin{aligned} \mathbf {v}(\mathbf {x} ,t)= & {} \frac{{{\,\mathrm{d}\,}}}{{{\,\mathrm{d}\,}}t}\mathbf {u}(\mathbf {x} ,t)= \frac{\partial }{\partial t}\mathbf {u}(\mathbf {x} ,t), \end{aligned}$$
(5)
$$\begin{aligned} \mathbf {a}(\mathbf {x} ,t)= & {} \frac{{{\,\mathrm{d}\,}}}{{{\,\mathrm{d}\,}}t}\mathbf {v}(\mathbf {x} ,t)= \frac{\partial }{\partial t}\mathbf {v}(\mathbf {x} ,t). \end{aligned}$$
(6)

Furthermore, the deformation gradient tensor \(\mathbf {F}\) is defined as

$$\begin{aligned} \mathbf {F} = \mathbf {I} + \frac{\partial \mathbf {u}}{\partial \mathbf {x}^0} = \mathbf {I} + \bigg \{\frac{\partial u_k}{\partial x^0_l} \bigg \}, \end{aligned}$$
(7)

where \(\mathbf {I}\) is the identity matrix.

For a continuum under purely mechanical loading, the motion is governed by the conservation laws given by the following system of coupled partial differential equations (PDEs):

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho \mathbf {v})= & {} 0, \end{aligned}$$
(8)
$$\begin{aligned} \frac{\partial (\rho \mathbf {v})}{\partial t} - \nabla \cdot \varvec{\sigma } - \rho \mathbf {b}= & {} 0, \end{aligned}$$
(9)

where \(\rho \) is the mass density, \(\varvec{\sigma }\) is the Cauchy stress tensor, and \(\mathbf {b}\) is a body force. Equations (8) and (9) describe the mass and momentum balance in the updated Lagrangian form, respectively. To specify the material, the above system needs to be supplemented with a suitable constitutive equation. In this paper, only linear elastic and neo-Hookean (hyperelastic) constitutive relations are considered. A multi-dimensional linear elastic model can be described as

$$\begin{aligned} \varvec{\sigma }= & {} \frac{\lambda }{J} {{\,\mathrm{tr}\,}}\left( \frac{1}{2}\left( \mathbf {F}+\mathbf {F}^\mathsf {T}\right) -\mathbf {I} \right) \mathbf {F} \nonumber \\&+ \frac{2 \mu }{J} \mathbf {F} \left( \frac{1}{2}\left( \mathbf {F}+\mathbf {F}^\mathsf {T}\right) -\mathbf {I} \right) , \end{aligned}$$
(10)

where \(\lambda \) and \(\mu \) are Lamé’s first parameter and the shear modulus, respectively. Denoting the determinant of \(\mathbf {F}\) by J, the neo-Hookean material model that can be used to describe a nonlinear stress–strain material behavior is given by

$$\begin{aligned} \varvec{\sigma } = \frac{\lambda \ln (J)}{J} \mathbf {I} + \frac{\mu }{J}\left( \mathbf {F}\mathbf {F}^\mathsf {T} - \mathbf {I}\right) . \end{aligned}$$
(11)

The details on the derivation of the conservation laws for a solid continuum and information on various constitutive models can be found in the works of Malvern [32] and Spencer [42]. It should be noted that while the choice of the constitutive model should not affect the approaches, it may lead to more complex algorithms for more elaborate nonlinear stress–strain relations.

3 Material-point method

MPM originates from the particle-in-cell (PIC) [25] and fluid-implicit particle (FLIP) [10] methods. After its introduction, several related methods have been proposed. For example, Bardenhagen and Kober [6] introduced a generalization of MPM, the generalized interpolation material-point (GIMP) method, where particles are represented by particle characteristic functions. In addition to the related methods, several versions of the MPM algorithm have been suggested. First, the original update stress last (USL) [48] version of MPM was transformed into the modified update stress last (MUSL) [51]. The main difference between the USL and MUSL algorithms is that USL computes the nodal velocities directly from the nodal accelerations, while MUSL obtains them from the material-point velocities, significantly improving the stability of the scheme. Next to USL and MUSL, the update stress first (USF) [5] and update stress averaged (USAVG) [36] MPM algorithms have been introduced. Both USF and USAVG attempt to improve the energy conservation within USL and MUSL. However, for the comparison of MPM and OTM algorithms, we focus on the most basic version of the MPM scheme, USL. Finally, a version of MPM, the so-called moving-mesh MPM, has been proposed where the background grid does not remain fixed as the simulation progresses in time. Moving-mesh MPM has been successfully applied to model complex problems such as the biological mechanics of cells [21] and the texture evolution in polycrystalline nickel [62].

MPM simplifies the momentum equation, Eq. (9), by assuming that the mass density is constant in time and solves the simplified equation on the fixed background grid adopting a variational formulation. The weak form of the momentum equation is given by

$$\begin{aligned} \int _{\varOmega ^t} w \rho \frac{\partial \mathbf {v}}{\partial t} \ \hbox {d}\varOmega ^t= & {} \int _{\partial \varOmega ^t} w \mathbf {n} \cdot \varvec{\sigma } \ \hbox {d}\varGamma ^t - \int _{\varOmega ^t}\nabla w\cdot \varvec{\sigma } \ \hbox {d}\varOmega ^t \nonumber \\&+\,\int _{\varOmega ^t} w \rho \mathbf {b} \ \hbox {d}\varOmega ^t, \end{aligned}$$
(12)

where \(\omega \) denotes an element of the test space that consists of all functions, which are sufficiently smooth and zero on the part of the boundary where essential boundary conditions are prescribed, \(\varGamma ^t = \partial \varOmega ^t\) is the boundary of the domain \(\varOmega ^t\), and \(\mathbf {n}\) is the outward unit normal vector. By adopting the standard approach in the finite element method (FEM) [11], Eq. (12) can be written in the following matrix-vector form for each direction \(x_k\):

$$\begin{aligned} \mathbf {M} \bar{\mathbf {a}}_k = \bar{\mathbf {f}}_k. \end{aligned}$$
(13)

where \(\bar{\mathbf {a}}_k = [a_{k,1}, a_{k,2},\ldots , a_{k,\mathcal {N}}]^\mathsf {T} \) is the unidirectional vector of the unknown acceleration coefficients,Footnote 1\(\mathbf {M} = \big [M_{ij}\big ] \in \mathbb {R}^{\mathcal {N}\times \mathcal {N}}\) is the consistent mass matrix, and \(\bar{\mathbf {f}}_k = [f_{k,1}, f_{k,2},\ldots , f_{k,\mathcal {N}}]^\mathsf {T}\) is the unidirectional force vector. Here, \(\mathcal {N}\) being the total number of nodes on the background grid. The entries of the mass matrix and force vector are given by

$$\begin{aligned} M_{ij}= & {} \int _{\varOmega ^t} \phi _i \rho \phi _j \ \hbox {d}\varOmega ^t, \end{aligned}$$
(14)
$$\begin{aligned} f_{k,i}= & {} \int _{\partial \varOmega ^t} \phi _i \tau _k \ \hbox {d}\varGamma ^t - \int _{\varOmega ^t} \sum _{l=1}^3 \frac{\partial \phi _i}{\partial x_l}\sigma _{lk} \ \hbox {d}\varOmega ^t \nonumber \\&+\, \int _{\varOmega ^t}\phi _i \rho b_k \ \hbox {d}\varOmega ^t, \end{aligned}$$
(15)

respectively. Here, \(\varvec{\tau }(\mathbf {x},t)\) is the prescribed traction at the boundary. In general, MPM can be implemented combining Eq. (13) for each k into one linear system. The implementation procedure of a multi-dimensional MPM can be found, for instance, in the thesis of Kafaji [2].

In MPM computations, the consistent mass matrix is typically replaced by the row-sum lumped mass matrix \(\mathbf {M}^L\), which can be obtained by summing the off-diagonal entries of \(\mathbf {M}\) in each row, adding them to the diagonal entry, and subsequently setting the off-diagonal entries to zero. If the basis functions maintain a partition of unity within the domain, that is

$$\begin{aligned} \sum _{j=1}^\mathcal {N} \phi _j(\mathbf {x}) = 1 \quad \forall \ \mathbf {x} \in \varOmega ^t, \end{aligned}$$
(16)

the diagonal entry of the lumped mass matrix can be expressed as follows:

$$\begin{aligned} M_{ii}^L&= \int _{\varOmega ^t} \phi _i \rho \ \hbox {d}\varOmega ^t. \end{aligned}$$
(17)

Furthermore, in MPM material points represent the material and carry all physical information about it (e.g., the mass, strain, and stress). While most material-point properties vary in time, the mass is time independent. This assures that the conservation of mass, Eq. (8), is satisfied. Furthermore, throughout a simulation, the integrals in Eqs. (14) and (15) are approximated by projecting the material-point information onto the background grid. Let the continuum be discretized by \(\mathcal {M}\) material points, then the integral of an arbitrary vector-valued function \(g(\mathbf {x})\) is approximated by

$$\begin{aligned} \int _{\varOmega } g(\mathbf {x}) \hbox {d}\varOmega = \sum _{p=1}^\mathcal {M} V_{p} g(\mathbf {x}_{p}), \end{aligned}$$
(18)

where \(V_{p}\) and \(\mathbf {x}_{p}\) represent the material-point volume and position, respectively. The information obtained by solving Eq. (13) is then mapped back to update the material points.

figure a
Fig. 1
figure 1

Schematic representation of the MPM solution strategy within each time step: a project material-point information onto the background grid; b solve the governing equations at the grid nodes; c update material-point information; d update material-point positions with respect to the grid

Full size image

In the considered version of MPM, the Euler–Cromer time-stepping scheme [12] is used for temporal discretization. The scheme applies the forward Euler method to advance the velocity and employs the backward Euler method for the displacement. The choice of the time integration technique is discussed in detail by Wallstedt and Guilkey [55]. A schematic representation of the MPM solution strategy that is followed within each of the N time steps is provided in Fig. 1. The complete form of the original MPM algorithm is presented in Algorithm 1, where it is assumed that only a constant body force is acting externally. In the algorithm, the notation used for the acceleration and force vectors, \(\bar{\mathbf {a}}_k\) and \(\bar{\mathbf {f}}_k\), is also adopted for global nodal vectors (e.g., the nodal velocity vector in the direction \(x_k\) is denoted by \(\bar{\mathbf {v}}_k=[v_{k,1}, v_{k,2} ,\ldots , v_{k,\mathcal {N}}]^\mathsf {T}\)).

4 Optimal transportation meshfree method

The OTM method is a meshless updated Lagrangian method that is based on the concepts from optimal transportation theory. In contrast to MPM, the OTM method explicitly includes the dependence of the mass density on time. For an arbitrary time interval \(\left[ t^0, T\right] \), it assumes that the density at time \(t^0\) and T is prescribed:

$$\begin{aligned} \rho \left( \mathbf {x}^0,t^0 \right)&= \rho ^{0}\left( \mathbf {x}^0\right) , \end{aligned}$$
(32)
$$\begin{aligned} \rho \left( \mathbf {x},T\right)&= \rho ^{T}\left( \mathbf {x}\right) , \end{aligned}$$
(33)

where \(\mathbf {x}^0\) and \(\mathbf {x}\) are given in Eq. (1). Benamou and Brenier [8] note that the mass and momentum balance equations together with Eqs. (32) and (33) can be translated into a minimization problem for the action of the solid over the time interval. The action over \(\left[ t^0, T\right] \) is given by

$$\begin{aligned} A\left( \rho ,\mathbf {v}\right) = \int _{t^0}^{T} K\left( \rho ,\mathbf {v}\right) \ \hbox {d}t, \end{aligned}$$
(34)

where \( K(\rho ,\mathbf {v})\) is the kinetic energy, which is equal to

$$\begin{aligned} K\left( \rho ,\mathbf {v}\right) = \int _{\varOmega ^T} \frac{\rho }{2} |\mathbf {v}|^2 \ \hbox {d}\varOmega ^T. \end{aligned}$$
(35)

Although Eqs. (34) and (35) are expressed in terms of mass density and velocity, in the OTM framework the flow is described by means of the deformation mapping \(\varphi \) that is defined in Eq. (1). The deformation mapping is related to velocity and density in the following way [27]:

$$\begin{aligned} \mathbf {v}(\mathbf {x},t)&= \frac{\partial \varphi }{\partial t} \left( \mathbf {x}^0,t \right) , \end{aligned}$$
(36)
$$\begin{aligned} \rho (\mathbf {x},t)&= \rho ^{0} \left( \mathbf {x}^0\right) /\det \left( \nabla \varphi \left( \mathbf {x}^0,t\right) \right) . \end{aligned}$$
(37)

Benamou and Brenier [8] also demonstrate that the deformation mapping that minimizes the action in Eq. (34) is given in terms of McCann’s displacement interpolation [33]:

$$\begin{aligned} \varphi \left( \mathbf {x}^0,t \right) =\frac{T-t}{T-t^0}\ \mathbf {x}^0+\frac{t-t^0}{T-t^0}\ \varphi \left( \mathbf {x}^0,T\right) . \end{aligned}$$
(38)

Here, \(\varphi \left( \mathbf {x}^0,T\right) \) is the optimal transportation map of \(\rho ^{0}\) into \(\rho ^{T}\) with respect to the cost function [27]:

$$\begin{aligned} C^{0 \rightarrow T}\left( \gamma \right) = \int _{\varOmega ^{0}} \left| \gamma \left( \mathbf {x}^0,T\right) -\mathbf {x}^0\right| ^2\rho ^{0} \left( \mathbf {x}^0\right) \ \hbox {d}\varOmega ^{0}, \end{aligned}$$
(39)

in which \(\gamma \left( \mathbf {x}^0, t\right) \) is a generic mapping of mass density.

To generate a numerical scheme, Eq. (34) is discretized in space and time. The time interval \(\left[ t^0,T\right] \) is divided into sub-intervals \(\left[ t^s,t^{s+1}\right] \) with \(s=0,1,\ldots ,N-1\), to which the above theory developed for \(\left[ t^0,T\right] \) is still applicable. The OTM method approximates a flow using the concept of the free energy of the solid U [29]:

$$\begin{aligned} U\left( \varphi \left( \mathbf {x}^s,t\right) \right) =\int _{\varOmega ^{s}} f\left( \nabla \varphi \left( \mathbf {x}^s,t \right) \right) \rho ^s \left( \mathbf {x}^s \right) \ \hbox {d}\varOmega ^{s}, \end{aligned}$$
(40)

where f is the local free-energy density per unit volume. Furthermore, the method employs the Wasserstein distance \(d_W\) between mass densities at two consecutive time instances [27, 28]:

$$\begin{aligned} d_W^2\left( \rho ^s, \rho ^{s+1}\right)&= \inf _{\begin{array}{c} \gamma :\ \varOmega ^s \rightarrow \varOmega ^{s+1} \\ \rho ^{s} = \rho ^{s+1} \det \left( \nabla \gamma \left( \mathbf {x}^s,t^{s+1}\right) \right) \end{array}}\, \nonumber \\&\quad \int _{\varOmega ^s}\left| \gamma \left( \mathbf {x}^s,t^{s+1}\right) -\mathbf {x}^s \right| ^2\rho ^{s}\left( \mathbf {x}^s\right) \ \hbox {d}\varOmega ^s \nonumber \\&= \inf _{\begin{array}{c} \gamma :\ \varOmega ^s \rightarrow \varOmega ^{s+1} \\ \rho ^{s} = \rho ^{s+1} \det \left( \nabla \gamma \left( \mathbf {x}^s,t^{s+1}\right) \right) \end{array}}\, C^{s \rightarrow s+1}\left( \gamma \right) . \end{aligned}$$
(41)
Fig. 2
figure 2

Schematic representation of the OTM method. Discretization of the domain by nodes (nodal points) and material points before and after deformation

Full size image

For elastic materials in unforced systems, the semi-discrete action sum is equal to [28]

$$\begin{aligned} A^{0 \rightarrow {N}} \left( \varphi ^{0},\dots ,\varphi ^{N}\right)&= \sum _{s=0}^{N-1} \left( \frac{1}{2}\frac{d_W^2\left( \rho ^s, \rho ^{s+1}\right) }{\left( t^{s+1}-t^s\right) ^2} \right. \nonumber \\&\quad \left. - \frac{1}{2} \left( U\left( \varphi ^{s}\right) +U\left( \varphi ^{s+1}\right) \right) \right) \nonumber \\&\quad \cdot \left( t^{s+1}-t^s\right) , \end{aligned}$$
(42)

where \(\varphi ^{s}\) is the deformation mapping at time \(t^s\). For the spatial discretization of Eq. (42), the OTM method employs two sets of points: nodal points and material points (see Fig. 2). Nodal points carry position information, while material points represent the continuum body and arise from the spatial approximation of the mass densities by point masses:

$$\begin{aligned} \rho ^s(\mathbf {x}) \approx \rho _{h}^s(\mathbf {x}) = \sum _{p=1}^{\mathcal {M}} m_{p}\delta \left( \mathbf {x}-\mathbf {x}_{p}^s\right) , \end{aligned}$$
(43)

where \(\delta \left( \mathbf {x}-\mathbf {x}_{p}^s\right) \) is the Dirac delta distribution centered at \(\mathbf {x}_{p}^s\). Material points are convected by the deformation:

$$\begin{aligned} \mathbf {x}_{p}^{s+1} = \varphi _{h}^{s\rightarrow s+1}\left( \mathbf {x}_{p}^s\right) , \end{aligned}$$
(44)

in which \(\varphi _h^{s\rightarrow s+1}(\mathbf {x})\) is the incremental deformation map. Fedeli et al. [19] explain that it can be described by general linear interpolation schemes of the form:

$$\begin{aligned} \varphi _{h}^{s\rightarrow s+1}(\mathbf {x}) = \sum _{i=1}^\mathcal {N} \phi _{i}^s(\mathbf {x}) \mathbf {x}_{i}^{s+1}, \end{aligned}$$
(45)

whereby the basis functions are assumed to be consistent. Consistent basis functions satisfy the following conditions [19]:

  • Partition of unity property

    $$\begin{aligned} \sum _{i=1}^\mathcal {N} \phi _{i}^s(\mathbf {x})= 1 \quad \forall \ \mathbf {x} \in \varOmega ^s. \end{aligned}$$
    (46)

  • Linear completeness

$$\begin{aligned} \sum _{i=1}^\mathcal {N} \mathbf {x}_{i}^s\phi _{i}^s(\mathbf {x}) = \mathbf {x} \quad \forall \ \mathbf {x} \in \varOmega ^s. \end{aligned}$$
(47)

Moreover, material points carry a fixed mass, serve as integration points, and store all local state data.

figure b

Using the definition of the Wasserstein distance and free energy, as well as Eq. (43), the fully discrete form of Eq. (42) is obtained (see Appendix A for more details):

$$\begin{aligned}&A_h^{0 \rightarrow N}\left( \varphi _h^{0},\dots ,\varphi _h^{N}\right) = \sum _{s=0}^{N-1} \sum _{p=1}^{\mathcal {M}} \Bigg (\frac{m_p}{2} \frac{\left| \mathbf {x}_{p}^{s+1}-\mathbf {x}_{p}^s\right| ^2}{\left( t^{s+1}-t^s\right) ^2}\nonumber \\&\quad \quad -\frac{m_p}{2} \left( f\Big (\nabla \varphi _{h}^{s}\left( \mathbf {x}_{p}^s\right) \right) \nonumber \\&\quad \quad +\, f\Big (\nabla \varphi _{h}^{s+1}\left( \mathbf {x}_{p}^{s+1}\right) \Big )\Big )\Bigg ) \left( t^{s+1}-t^s\right) . \end{aligned}$$
(56)

The OTM algorithm originates from applying discrete Hamilton’s principle [24] to the fully discrete action [22, 27]. A basic OTM algorithm for a solid material is summarized in Algorithm 2. For more details on the OTM method, we refer to the work of Li et al. [27] and Habbal [22].

5 Comparison of algorithms

While the derivations of MPM and the OTM method are fundamentally different, the resulting algorithms have many similarities. This section provides a side-by-side comparison of the computational steps from Algorithm 1 (USL-MPM) and 3 (OTM). Based on this comparison, it summarizes the conditions required to further relate the methods and highlights the principal differences between them.

  • In the beginning of the simulation, both algorithms initialize the nodal coordinates and material-point properties. While the MPM computation requires the material-point velocity for time step \(s=0\), the OTM method expects the material-point positions to be known at \(s=-1\). This difference arises from the explicit definition of the material-point velocity in MPM and its implicit use in the OTM method. This is further explained in the discussion of step 4 of both schemes.

  • After the initialization phase, the time step counter s is set to zero, which identifies the start of the solution phase. At the end of each time step, s is increased by one until the maximum number of time steps N is reached.

  • In step 3, the schemes compute the basis functions and their derivatives. However, in the OTM method, the basis functions are updated in each time step based on the nodal velocities, while in standard MPM, the basis functions remain fixed over time. This is an important difference between the methods. To distinguish between the basis functions, the OTM basis functions are denoted by \(\phi _{i}^s\) and the MPM basis functions by \(\phi _{i}^0\).

  • On the other hand, the schemes can be related in step 4. Assuming that the material-point velocity in MPM can be written as

    $$\begin{aligned} \mathbf {v}_{p}^s = \frac{1}{t^s-t^{s-1}}\left( \mathbf {x}_{p}^s-\mathbf {x}_{p}^{s-1}\right) . \end{aligned}$$
    (57)

    A direct substitution of Eq. (57) into the expression for the linear momentum in the MPM algorithm (Eq. 20) leads to the linear momentum formula used in the OTM method (Eq. 49).

  • Furthermore, steps 5 and 6 of the USL algorithm are implicitly included in step 5 of the OTM algorithm, where the nodal coordinates at time step \(s+1\) are computed. More precisely, from step 5 in the OTM algorithm, we obtain

    $$\begin{aligned} \varDelta \bar{\mathbf {x}}_{k}^{s+1}= & {} \bar{\mathbf {x}}_{k}^{s+1} - \bar{\mathbf {x}}_k^s = \left( t^{s+1}-t^s\right) \left( \mathbf {M}^s\right) ^{-1}\nonumber \\&\cdot \left( \bar{\mathbf {q}}_k^s + \frac{t^{s+1}-t^{s-1}}{2}\bar{\mathbf {f}}_k^s\right) . \end{aligned}$$
    (58)

    At the same time, the incremental nodal displacement in MPM can be written as

    $$\begin{aligned} \varDelta \bar{\mathbf {x}}_k^{s+1}&= \left( t^{s+1}-t^s\right) \left( \left( \mathbf {M}^s\right) ^{-1}\bar{\mathbf {q}}_k^s + \left( t^{s+1}-t^s\right) \bar{\mathbf {a}}_k^s\right) \nonumber \\&=\left( t^{s+1}-t^s\right) \left( \mathbf {M}^s\right) ^{-1}\left( \bar{\mathbf {q}}_k^s +\left( t^{s+1}-t^s\right) \bar{\mathbf {f}}_k^s\right) . \end{aligned}$$
    (59)

    It can be seen that Eq. (59) is equal to Eq. (58) for constant time-step sizes. From this, we conclude that the update of nodal positions is identical for both methods when the time-step size is fixed.

  • The definition of the incremental transport map (Eq. 45) implies that in step 6 of the OTM algorithm, material-point positions are obtained from

    $$\begin{aligned} \mathbf {x}_{p}^{s+1} = \sum _{i=1}^\mathcal {N} \phi _{i}^s\left( \mathbf {x}_{p}^s\right) \mathbf {x}_{i}^{s+1}, \end{aligned}$$
    (60)

    while step 7 in the MPM algorithm states that

    $$\begin{aligned} \mathbf {x}_{p}^{s+1} = \mathbf {x}_{p}^s+\sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \varDelta \mathbf {x}_{i}^{s+1}. \end{aligned}$$
    (61)

    The equality of the above expressions can be shown if linear completeness (see Eq. 47) of the MPM basis functions is imposed. That is, if the following condition is satisfied:

    $$\begin{aligned} \sum _{i=1}^\mathcal {N} \phi _{i}^0(\mathbf {x}) \mathbf {x}_{i}^s= \mathbf {x} \quad \forall \ \mathbf {x} \in \varOmega ^s, \end{aligned}$$
    (62)

    Equation (61) can be rewritten as

    $$\begin{aligned} \mathbf {x}_{p}^{s+1}= & {} \sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \mathbf {x}_{i}^s+\sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \varDelta \mathbf {x}_{i}^{s+1}\nonumber \\= & {} \sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \mathbf {x}_{i}^{s+1}. \end{aligned}$$
    (63)

  • Moreover, the OTM scheme avoids a direct update of the material-point velocity by adopting Eq. (57), whereas MPM performs the update in step 8. Nevertheless, assuming that

    $$\begin{aligned} \sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \mathbf {v}_{i}^s = \mathbf {v}_{p}^s, \end{aligned}$$
    (64)

    it is possible to relate the methods again. Substituting Eq. (64) in step 8 of MPM gives

    $$\begin{aligned} \mathbf {v}_{p}^{s+1}&= \sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \mathbf {v}_{i}^s + \left( t^{s+1}-t^s\right) \sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \mathbf {a}_{i}^s \end{aligned}$$
    (65)
    $$\begin{aligned}&= \sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \left( \mathbf {v}_{i}^s+\left( t^{s+1}-t^s\right) \mathbf {a}_{i}^s\right) . \end{aligned}$$
    (66)

    Substituting the updated nodal velocity from step 6 of the MPM algorithm yields

    $$\begin{aligned} \mathbf {v}_{p}^{s+1} = \sum _{i=1}^{\mathcal {N}} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \mathbf {v}_i^{s+1}. \end{aligned}$$
    (67)

    Therefore, the updated material-point velocity in MPM is equal to

    $$\begin{aligned} \mathbf {v}_{p}^{s+1}= & {} \frac{ 1}{t^{s+1}-t^s}\sum _{i=1}^\mathcal {N} \phi _{i}^0\left( \mathbf {x}_{p}^s\right) \varDelta \mathbf {x}_{i}^{s+1}\nonumber \\= & {} \frac{ 1}{t^{s+1}-t^s}\left( \mathbf {x}_{p}^{s+1}-\mathbf {x}_{p}^s\right) . \end{aligned}$$
    (68)

    The above equalities follow from the computation of the incremental nodal displacements in steps 6, and the update of material-point coordinates in step 7 of the MPM algorithm.

    The final expression in Eq. (68) is identical to the implicit material-point velocity update in the OTM algorithm. Although an extra assumption is required to establish a connection between the methods, it does not lead to an essential disparity between them.

  • Step 9 of both schemes can be shown to be identical as well. From step 6 in the OTM algorithm and the OTM definition of material-point velocity presented in Eq. (57), it follows that

    $$\begin{aligned} \nabla \varphi _{h}^{s\rightarrow s+1}\left( \mathbf {x}_{p}^s\right)&= \nabla \mathbf {x}_p^{s+1} = \nabla \left( \mathbf {x}_p^s + \left( t^{s+1}-t^s\right) \mathbf {v}_p^{s+1}\right) \nonumber \\&= \mathbf {I} + \left( t^{s+1}-t^s\right) \nabla \mathbf {v}_p^{s+1}. \end{aligned}$$
    (69)

    Therefore, step 9 is the same for the MPM and OTM algorithm.

  • Next, the update of the material-point volumes is investigated. MPM performs this update in step 10, while the OTM method computes the volume in step 7. To prove the equivalence of those steps, we need to show that

    $$\begin{aligned}&\det \left( \left( \mathbf {I} + \left( t^{s+1}-t^s\right) \nabla \mathbf {v}_p^{s+1} \right) \mathbf {F}_{p}^s\right) V_{p}^0\nonumber \\&\quad =\det \left( \nabla \varphi _{h}^{s\rightarrow s+1}\left( \mathbf {x}_{p}^s\right) \right) V_{p}^s. \end{aligned}$$
    (70)

    This identity can be proved in the following way:

    $$\begin{aligned}&\det \left( \left( \mathbf {I} + \left( t^{s+1}-t^s\right) \nabla \mathbf {v}_p^{s+1} \right) \mathbf {F}_{p}^s\right) V_{p}^0 \end{aligned}$$
    (71)
    $$\begin{aligned}&\quad =\det \left( \mathbf {I} + \left( t^{s+1}-t^s\right) \nabla \mathbf {v}_p^{s+1} \right) \det \left( \mathbf {F}_{p}^s\right) V_{p}^0 \end{aligned}$$
    (72)
    $$\begin{aligned}&\quad =\det \left( \nabla \varphi _{h}^{s\rightarrow s+1}\left( \mathbf {x}_{p}^s\right) \right) \det \left( \mathbf {F}_{p}^s\right) V_{p}^0 \end{aligned}$$
    (73)
    $$\begin{aligned}&\quad =\det \left( \nabla \varphi _{h}^{s\rightarrow s+1}\left( \mathbf {x}_{p}^s\right) \right) V_{p}^s. \end{aligned}$$
    (74)

    In the above, Eq. 70 and the definition of the deformation gradient tensor are used.

  • The remaining steps are identical for MPM and OTM.

In this section, we have shown that under certain conditions the MPM and OTM algorithms can be related to each other. Namely, assuming a constant time step and the validity of Eqs. (57), (62), and (64) for the MPM scheme, the only difference between the standard algorithms emerges from the update of the basis functions and their gradients.

However, this difference is fundamental. Since the nodes are fixed to their initial positions in the MPM basis-function update (step 3 of the USL algorithm), the method is considered to be a combination of Lagrangian and Eulerian approaches. At the same time, the OTM method is an updated Lagrangian particle method. For the implementation of the methods, this implies that the OTM method only discretizes the initial material domain, while MPM discretizes the complete domain, where the material is allowed to move, as well as the initial material domain. Consequently, the OTM method does not include inactive elements.

Fig. 3
figure 3

1D quadratic B-spline basis functions and their derivatives

Full size image

6 Basis functions

Section 5 identifies strong similarities between the OTM and MPM schemes without specifying the basis functions used within the methods. Since MPM typically uses piecewise-linear basis functions, while the OTM method exploits the local maximum-entropy (maxent) basis functions, both piecewise-linear and maxent basis functions are presented in this section. In addition, this section describes the B-spline basis functions frequently combined with the MPM algorithm and adopted in the unified approach provided in Sect. 7. For simplicity, the piecewise-linear and B-spline basis functions are presented in their one-dimensional form. The extension of these basis functions to quadrilateral elements is obtained by means of the tensor product.

6.1 Piecewise-linear basis functions

Given a set of nodes \(\{x_i\}_{i=1}^\mathcal {N}\), piecewise-linear basis functions are defined as

$$\begin{aligned} \phi _i =\left\{ \begin{array}{ll} 0 &{}\quad \text{ if } \; x< x_{i-1},\\ (x-x_{i-1})/(x_i-x_{i-1}) &{}\quad \text{ if } \; x_{i-1} \le x< x_i,\\ 1- (x-x_{i})/(x_{i+1}-x_{i}) &{}\quad \text{ if }\; x_{i} \le x < x_{i+1},\\ 0 &{}\quad \text{ if } \; x \ge x_{i+1}.\\ \end{array}\right. \end{aligned}$$
(75)

The corresponding derivatives are equal to

$$\begin{aligned} \frac{\hbox {d} \phi _i}{\hbox {d} x} = \left\{ \begin{array}{ll} 0 &{}\quad \text{ if } \, \, x< x_{i-1},\\ 1 &{}\quad \text{ if } \, \, x_{i-1} \le x< x_i,\\ -1 &{}\quad \text{ if } \, \, x_{i} \le x < x_{i+1},\\ 0 &{} \quad \text{ if } \, \, x \ge x_{i+1}.\\ \end{array}\right. \end{aligned}$$
(76)

These nonnegative basis functions possess the partition of unity property and have a compact support. In addition, they can be implemented in a straightforward manner. However, their gradients are discontinuous at the element boundaries. Within MPM, this can lead to unphysical results when material points cross element boundaries [6].

6.2 B-spline basis functions

Figure 3 provides an example of quadratic B-spline basis functions and their gradients. Generally, B-spline basis functions are defined in the parametric space, based on a knot vector. A knot vector in one dimension is a sequence of ordered non-decreasing coordinates. It is typically denoted as \(\varXi =\left\{ \xi _1, \xi _2, \dots , \xi _{n_{\bar{b}}+\bar{d}+1}\right\} \), where \(\xi _j \in \mathbb {R}\) is the jth knot, \(n_{\bar{b}}\) is the total number of basis functions, and \(\bar{d}\) is the polynomial order. The knot vector is uniform when its knots are distributed equidistantly. The knots are called repeated when more than one knot is positioned at the same coordinate in the parametric space. An open knot vector contains the first and last knots \(\bar{d}+1\) times ensuring that the resulting basis functions are interpolatory at the boundaries of the domain. A non-empty knot interval \(\left[ \xi _{j} \, \, \xi _{j+1} \right) \) is referred to as a knot span. For an open uniform knot vector, the number of spans is equal to \(n_{\bar{b}}-\bar{d}\).

The Cox-de Boor formula [14] defines B-spline basis functions recursively, starting with piecewise constants (no repeated knots, i.e., \(\bar{d}=0\)):

$$\begin{aligned} \phi _{j}^{0}(\xi ) = \left\{ \begin{array}{ll} 1 &{} \text{ if } \;\xi _{j} \le \xi < \xi _{j+1},\\ 0 &{}\text{ otherwise. } \\ \end{array}\right. \end{aligned}$$

For \(\bar{d}>0\), the basis functions are given by

$$\begin{aligned} \phi _{j}^{\bar{d}}(\xi ) = \frac{\xi - \xi _{j}}{\xi _{j+\bar{d}}-\xi _{j}} \phi _{j}^{\bar{d}-1}(\xi ) + \frac{\xi _{j+\bar{d}+1}-\xi }{\xi _{j+\bar{d}+1}-\xi _{j+1}}\phi _{j+1}^{\bar{d}-1}(\xi ) \quad \xi \in \hat{z}, \end{aligned}$$

where \(\hat{z}\) is the parametric domain. The derivatives of the B-spline basis functions can be computed from [14]:

$$\begin{aligned} \frac{\hbox {d} \phi _{j}^{\bar{d}}(\xi ) }{\hbox {d} \xi } = \frac{\bar{d}}{\xi _{j+\bar{d}} - \xi _{j}}\phi _{j}^{\bar{d}-1}(\xi )-\frac{\bar{d}}{\xi _{j+\bar{d}+1} - \xi _{j+1}}\phi _{j+1}^{\bar{d}-1}(\xi ). \end{aligned}$$

It should be noted that in the considered implementation of BSMPM, the parametric and physical domains are the same. Moreover, first-order B-splines basis functions are identical to piecewise-linear basis functions described previously.

B-spline basis functions were introduced within MPM by Steffen et al. [43, 44]. They form as a potential remedy to the grid-crossing and quadrature errors present in MPM. The concept of BSMPM was further investigated by combining B-spline basis functions with more advanced integration techniques [20, 53, 57] and adopting the method to unstructured grids [15].

6.3 Maximum-entropy basis functions

Maxent basis functions were introduced by Sukumar [46] for the construction of polygonal interpolants. Arroyo and Ortiz [4] presented local maxent basis functions and first used them within a meshfree method. After that, local maxent basis functions have been integrated within several meshfree schemes such as point collocation methods [18]. The schemes that combined meshfree methods with maxent basis function have been applied to a variety of problems including simulations of shear-deformable plates [23] and thin-shell analysis [34].

The construction of maxent basis functions combines elements from probability theory and optimization. In fact, within a convex hull of the nodal set \(\big \{\mathbf {x}_i\big \}\) (i.e., the smallest convex set that contains all nodes), the set of local maxent basis functions \(\big \{\phi _i(\mathbf {x})\ge 0\big \}_{i=1}^\mathcal {N}\) form the solution of the following constrained optimization problem [38]:

$$\begin{aligned} \max _{\phi \ \in \ \mathbb {R}_+^\mathcal {N}} \,- \sum _{i=1}^\mathcal {N}\phi _i(\mathbf {x})\ln \left( \frac{\phi _i(\mathbf {x})}{w_i(\mathbf {x})} \right) \end{aligned}$$
(77)

subject to

$$\begin{aligned}&\sum _{i=1}^\mathcal {N} \phi _i(\mathbf {x}) = 1, \end{aligned}$$
(78)
$$\begin{aligned}&\sum _{i=1}^\mathcal {N}\phi _i(\mathbf {x})(\mathbf {x}_i-\mathbf {x}) = 0, \end{aligned}$$
(79)

where \(w_i(\mathbf {x})\) is a nonnegative weight function or prior estimate of \(\phi _i\). The solution of this problem is typically found using the method of Lagrange multipliers [7] and can be written as

$$\begin{aligned} \phi _i(\mathbf {x}) = \frac{Z_i(\mathbf {x},\varvec{\lambda })}{Z(\mathbf {x},\varvec{\lambda })} \end{aligned}$$
(80)

with

$$\begin{aligned}&Z_i(\mathbf {x},\varvec{\lambda })=w_i(\mathbf {x})\exp (-\varvec{\lambda } \cdot (\mathbf {x}_i-\mathbf {x})), \end{aligned}$$
(81)
$$\begin{aligned}&Z(\mathbf {x},\varvec{\lambda })=\sum _i Z_i(\mathbf {x},\varvec{\lambda }), \end{aligned}$$
(82)

where \(\varvec{\lambda }\) represents the Lagrange multipliers.

In practice, the primal problem of maximization is transferred into the dual problem of minimization [46]. Considering the new formulation, \(\varvec{\lambda }\) is expressed as [1, 9]

$$\begin{aligned} \varvec{\lambda } = \arg \min \ln (Z). \end{aligned}$$
(83)

The Lagrange multipliers are typically found via Newton’s method. The solution procedure of this method (e.g., [39]) requires an initial guess for \(\varvec{\lambda }\) and both first- and second-order partial derivatives of \(\ln (Z)\) with respect to \(\varvec{\lambda }\).

The first derivatives of the local maxent basis functions are given by (e.g., [58])

$$\begin{aligned} \nabla \phi _i= & {} \phi _i \left( (\mathbf {x}-\mathbf {x}_i) \cdot \left( \mathbf {H}^{-1} - \mathbf {H}^{-1} \mathbf {A} \right) - \frac{\nabla w_i}{w_i} + \sum _{j=1}^{\mathcal {N}}\phi _j\frac{\nabla w_j}{w_j}\right) , \end{aligned}$$
(84)

in which the matrices \(\mathbf {H}\) and \(\mathbf {A}\) are computed in the following way:

$$\begin{aligned} \mathbf {H}&= \sum _{j=1}^{\mathcal {N}}\phi _j (\mathbf {x}-\mathbf {x}_j) \bigotimes (\mathbf {x}-\mathbf {x}_j) , \end{aligned}$$
(85)
$$\begin{aligned} \mathbf {A}&= \sum _{j=1}^{\mathcal {N}}\phi _j (\mathbf {x}-\mathbf {x}_j) \bigotimes \frac{\nabla w_j}{w_j}. \end{aligned}$$
(86)

Here, \(\bigotimes \) is the dyadic product (i.e., the dyadic product of any two vectors is equal to \(\mathbf {a} \bigotimes \mathbf {b} = \mathbf {a}\mathbf {b}^\mathsf {T}\)).

In the above description, the weight function remained unspecified due to a large number of viable options (e.g., Gaussian prior, cubic or quartic spline). In general, the prior functions are defined by means of the normalized radius of the support domain, \(r_i\), for node i:

$$\begin{aligned} r_i(\mathbf {x}) = \frac{||\mathbf {x}-\mathbf {x}_i||}{d_i}, \end{aligned}$$
(87)

where \(|| \cdot ||\) is the \(L^2\)-norm, and \(d_i\) is the size of the domain of support of node i, which is a user-defined parameter. In this paper, \(d_i\) is equal to

$$\begin{aligned} d_i = d_{\max }\zeta _i, \end{aligned}$$
(88)
Fig. 4
figure 4

1D cubic spline weight functions (a) and derivatives (b), as well as the corresponding local maxent basis functions (c), and their derivatives (d) for \(d_{\max }=2.0\)

Full size image

in which \(d_{\max }\) is a factor with a typical value between 2.0 and 4.0 (this value is selected by the user), and \(\zeta _i\) is the distance between node i and its nearest neighboring node. Alternative definitions of the normalized radius of the support domain can be found, for instance, in the work of Sukumar and Wright [47] and Yaw et al. [58].

Cubic spline weight functions, which are used in this paper, are given by

$$\begin{aligned} w_i(\mathbf {x}) = {\left\{ \begin{array}{ll} \frac{2}{3} - 4r_i^2(\mathbf {x})+4r_i^3(\mathbf {x}) , &{} \text {for }\; 0<r_i(\mathbf {x})\le \frac{1}{2},\\ \frac{4}{3} - 4r_i(\mathbf {x})+4r_i^2(\mathbf {x})-\frac{4}{3}r_i^3 (\mathbf {x}), &{} \text {for }\; \frac{1}{2}<r_i(\mathbf {x})\le 1,\\ 0 , &{} \text {for }\;r_i(\mathbf {x})>1. \end{array}\right. } \end{aligned}$$
(89)

Figure 4 shows the one-dimensional cubic spline basis functions and their derivatives, as well as the corresponding local maxent basis functions together with the derivatives.

Local maxent basis functions possess many desirable properties for meshfree algorithms. First of all, they are entirely defined by the nodal set and the domain of analysis. They are also non-negative, satisfy the partition of unity property, and provide an exact approximation for affine functions [4]. Furthermore, the local maxent basis functions have the so-called weak Kronecker delta property [4]. However, the local maxent basis functions are defined only within a convex hull of the nodal set. If non-convex domains are considered, the basis functions lose the weak Kronecker delta property at the non-convex parts of the domain [4]. In addition, the calculation of Lagrange multipliers is numerically challenging [22] and frequently requires significant computational costs.

7 Unified approach

The unified approach combines the OTM scheme and BSMPM. Similar to BSMPM, the proposed approach uses B-spline basis functions. However, it computes them based not only on the updated material-point positions, but also on the advected degrees-of-freedom set. B-spline basis functions of any order possess the partition of unity property, but only first-order B-spline basis functions satisfy the linear completeness property. Therefore, according to the definition in Sect. 4, higher-order basis functions are not consistent. Since Algorithm 2 is designed for consistent basis functions, the unified algorithm is mainly based on Algorithm 1 to ensure the compatibility of the unified algorithm with the higher-order B-spline basis functions. Furthermore, the proposed approach employs the consistent mass matrix. The unified algorithm is presented in Algorithm 3.

Both MPM and OTM provide motivation for the proposed unified method. On the one hand, the addition of the advected nodal points to update the basis functions is supposed to stabilize the computation when BSMPM is combined with a consistent mass matrix. Consistent mass matrices frequently cause stability issues in MPM [31], and BSMPM inherits these issues. For this reason, MPM and BSMPM are generally used with a lumped mass matrix. While mass lumping has little influence on the solution quality of lower order methods, its \(\mathcal {O}(h^2)\) approximation of the consistent mass matrix [44] can significantly influence the spatial convergence of higher-order methods such as BSMPM. Moreover, as was mentioned earlier, previous studies demonstrate that moving-mesh MPM can be used successfully for complex simulations.

On the other hand, within the OTM framework, the use of B-spline basis functions is expected to significantly reduce the computational costs. In contrast to maxent basis functions, B-spline basis functions do not require the adoption of iterative methods and have a purely analytical definition. It has been pointed out by Cyron et al. [13] that maxent and higher-order B-spline basis functions have many common properties. For example, they are both smooth, non-negative, have compact support, and satisfy the partition of unity property. Therefore, the use of B-spline basis functions provides a viable alternative to the massively parallel implementation of OTM (pOTM) [30]. In addition, B-spline basis functions do not require the use of search algorithms, frequently added to the standard OTM scheme for stabilization [22, 56]. Finally, the adoption of higher-order B-spline basis functions can lead to higher-order spatial convergence.

figure c
Fig. 5
figure 5

Comparison of the results obtained with MPM and the OTM method with piecewise-linear basis functions (left), and the unified approach (right) to the analytical solution. For MPM and the OTM method, the number of nodes is equal to 512, while for the unified approach, only 32 nodes were used

Full size image

We remark that in contrast to the OTM scheme, the proposed unified approach cannot be viewed as a meshless method. However, the study by De Koster et al. [15] shows the potential of BSMPM on arbitrary grids. The extension of the BSMPM to arbitrary grids in combination with an efficient remeshing technique (e.g., the remeshing strategy for large deformations proposed by Erhart et al. [17]) might bring the unified approach closer to the meshless algorithms. In this paper, the examples are restricted to relatively simple problems to study the basic properties of the considered methods. Thus, further research is required to evaluate the effect of mesh distortion on the proposed unified approach.

8 Numerical results

In this section, three benchmarks are considered to illustrate the performance of the discussed methods. The one-dimensional benchmarks describe the vibration of a bar, but have fundamentally different motion triggers and boundary conditions. In the first benchmark, where both ends of the bar are fixed, the domain contains only filled elements allowing for a straightforward implementation and analysis. The second benchmark, where a traction force is acting at one of the boundaries, contains multiple empty cells throughout the simulation, thereby serving as a representative example for the stability analysis. The last benchmark is two-dimensional; it further extends the numerical analysis of the considered algorithms.

The results are provided for the USL version of the MPM scheme (Algorithm 1) and OTM algorithms, as well as the proposed unified approach. For MPM, piecewise-linear, second-order B-spline and maxent basis functions are employed. The OTM algorithm is used only with consistent basis functions (i.e., piecewise-linear and maxent basis functions). For the one-dimensional benchmarks, the factor \(d_{\max }\) is set to 2.0 to compute the maxent basis functions, while for the two-dimensional problem, its value depends on the considered algorithm.

8.1 Bar with fixed ends

This example describes the vibration of a linear elastic bar of length l with fixed ends. The motion is generated by an initial velocity prescribed along the bar:

$$\begin{aligned} v(x^0,0) = v^0_{\max } \sin \left( \frac{\pi x^0}{l} \right) . \end{aligned}$$
(101)

Here, the length of the bar is set to 1 m, Young’s modulus is set to 4 kPa, while the initial density and amplitude of the velocity \(v_0\) are equal to 1 kg/m\(^3\) and 0.6 m/s, respectively. The total simulation time is set to 0.001 s, while the time-step size is equal to \(10^{-5}\) s. This relatively small time step is required to minimize the contribution of the temporal error to the total one. Moreover, the number of nodes varies between 8 and 512, while the number of material points per element remains equal to 12.

The analytical solution in terms of the displacement, velocity, and stress can be found in the work of Wobbes et al. [57]. For the convergence analysis, the root-mean-square (RMS) error in the displacement is computed. RMS error is defined as follows:

$$\begin{aligned} \sqrt{\frac{1}{\mathcal {M}}\sum _{p=1}^\mathcal {M}(u(x_p^0,T) - u_p)}, \end{aligned}$$
(102)

where \(u(x_p^0,T)\) and \(u_p\) are, respectively, the analytical and numerical solutions at position \(x_p^0\) at time T.

The left part of Fig. 5 depicts the final stress profiles obtained using MPM and the OTM method with piecewise-linear basis functions. Grid crossing causes severe oscillations in the MPM stress profile. The calculation of the basis functions with the advected nodal coordinates in the OTM method prevents these inaccuracies, significantly improving the results. Although the OTM-P1 method avoids grid-crossing errors, it provides only a piecewise-constant approximation of the stress profile due to the gradients of the P1 basis functions. The right part of Fig. 5 illustrates the performance of the unified approach. The use of second-order B-spline basis functions prevents the grid-crossing errors and improves the accuracy of the solution. The results obtained with maxent basis functions are similar to those computed with the unified approach. To avoid repetition, these results are not shown.

Table 1 provides the results in terms of computational time of all considered methods for 32 and 512 nodes. We remark that the maxent computations were performed without a search algorithm. For the coarse discretization, the MPM scheme-based approaches outperform the ones adopting the OTM algorithm. However, when 512 nodes are used, the efficiency of the computation depends on the choice of the basis functions instead of the algorithm. More precisely, replacing maxent by B-spline basis functions reduces the computational time by at least a factor of 2.

Table 1 Computational time required for the considered methods normalized with respect to the MPM-P1 computational time with the corresponding number of nodes
Full size table
Fig. 6
figure 6

Convergence behavior of the considered methods

Full size image

In addition, Fig. 6 illustrates the spatial convergence behavior of the considered methods at the end of the simulation. When piecewise-linear basis functions are used, both MPM and the OTM method demonstrate second-order convergence for relatively coarse grids. However, for fine meshes, the methods behave differently. In fact, MPM suffers from grid-crossing errors that result in a loss of the convergence. The OTM-P1 method preserves the second-order convergence until the final refinement, where only first-order convergence is achieved. A sudden decrease in the convergence rate is also observed in the computations when maxent and B-spline basis functions are employed within both MPM and OTM schemes. For this reason, it may be assumed that the loss of the convergence order is unrelated to the choice of the basis functions. Inaccurate numerical integration, time integration errors, round-off errors, or a combination of the above can contribute to the reduction in the convergence rate [44, 49, 55]. Furthermore, Fig. 6 shows that maxent basis functions lead to significantly lower errors than the piecewise-linear basis functions for both MPM and OTM schemes. With maxent basis functions, the convergence of MPM and the OTM method varies between linear and quadratic. It should be noted that the accuracy of MPM and the OTM method with maxent basis functions can be further improved by adapting more advanced implementations [4, 35, 52, 63]. The use of B-spline basis functions leads to similar results for BSMPM and the unified approach. These methods have third-order convergence until the limiting value is reached.

Fig. 7
figure 7

Comparison of the considered methods to the analytical solution. The material domain is discretized by 68 nodes

Full size image

8.2 Bar with dynamic traction boundary conditions

This benchmark describes the motion of a neo-Hookean bar with one free end. The bar is fixed at \(x^0=0\) and subjected to a traction force at the free end \(x^0=l\). The forcing function is equal to \( \tau \left( x^0,t\right) = \delta \left( x^0-l\right) \sigma \left( x^0,t\right) . \) Defining \(\omega = \pi /l\), the stress is given by

$$\begin{aligned}&\sigma \left( x^0,t\right) \nonumber \\&\quad = {\left\{ \begin{array}{ll} 0 &{} \text {for } t \in \left[ 0,l-x^0\right) , \\ \sin \left( \omega \left( t+x^0\right) \right) &{} \text {for } t \in \left[ l-x^0,l+x^0\right) , \\ \sin \left( \omega \left( t+x^0\right) \right) + \sin (\omega (t-x^0)) &{} \text {for } t \in \left[ l+x^0,3l-x^0\right) , \\ \sin \left( \omega \left( t-x^0\right) \right) &{} \text {for } t \in \left[ 3l-x^0,3l+x^0\right) , \\ 0 &{} \text {for } t \in \left[ 3l+x^0,4l\right] . \\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(103)

The initial length of the bar is set to 1 m, the density is equal to 100 kg/m\(^3\), and Young’s modulus is equal to 100 Pa. The length of the computational domain is set to 1.25 m. A more detailed description that includes an analytical solution for displacement is provided by Steffen et al. [43]. To illustrate the stress profile obtained with different methods, the material domain is discretized by 68 nodes, which results in 85 nodes for the complete domain. The material-domain discretization is sufficient for the unified and OTM methods due to their updated Lagrangian nature, whereas MPM requires the discretization of the complete domain. Each active element initially contains 4 particles. The computational time is set to 0.4 s, and the time-step size is equal to \(10^{-4}\) s.

Figure 7 depicts the obtained results. It shows that maxent and B-spline basis functions eliminate the grid-crossing error in MPM. However, MPM-maxent and BSMPM do not follow the analytical solution at the right edge of the bar. Within BSMPM, these inaccuracies can be significantly reduced by increasing the initial number of particles per elements. This suggests that the errors are caused by insufficient accuracy of the numerical integration in MPM. Thus, advanced numerical integration techniques (e.g., Taylor least squares [57]) may improve the BSMPM solution at the boundary. The inaccuracies within MPM-maxent have a different origin. They are most probably caused by the incomplete set of maxent basis functions, which arise from the presence of inactive elements throughout an MPM simulation. Figure 7 also shows that the OTM-P1, OTM-maxent, and unified methods provide significantly more accurate solutions than their MPM equivalents.

Similar to the benchmark discussed in Sect. 8.1, the use of B-spline basis functions instead of maxent basis functions considerably decreases the computational time for both MPM and OTM methods. In fact, the unified approach and BSMPM computations are approximately 10 times faster than the OTM and MPM computations with maxent basis functions (without a search algorithm) with the settings used for Fig. 7.

Fig. 8
figure 8

Convergence behavior of the considered methods. The number of nodes, in this case, refers to the number of nodes used to discretize the material domain

Full size image

Furthermore, the unified approach and BSMPM have the lowest RMS error and highest convergence rates compared to the other methods. This is illustrated in Fig. 8. To minimize quadrature and time integration errors, this figure is obtained placing 12 particles per cell at the beginning of the simulation and reducing the computational time to 0.1 s. In general, the obtained convergence orders of the considered algorithms are slightly lower than expected. This can be related to the discontinuities in the solution for the stress field.

The main advantage of the unified method over BSMPM arises from its stability properties. When a material point enters an empty element, BSMPM inherits stability issues from MPM. For instance, changing the total number of nodes to 81 results in a termination after 0.3 s. This issue in MPM is discussed in detail by, for example, Kafaji [2] and requires the use of the MUSL algorithm with a lumped mass matrix to circumvent the breakdown.

Fig. 9
figure 9

Comparison of the considered methods to the analytical solution. The material domain is discretized by 33 nodes in each direction

Full size image

8.3 Plate undergoing axis-aligned displacement

The final benchmark describes a two-dimensional neo-Hookean plate that is fixed at the entire boundary. The plate is assumed to be a unit square (\(l\times l\) with \(l= 1\) m), and its motion is triggered by a body force. The corresponding displacement is given by

$$\begin{aligned} u_{x_1}(x_1^0,t)= & {} A \ \text {sin}\left( \frac{2 \pi x_1^0}{l} \right) \text {sin}\left( \frac{c \pi t}{l} \right) , \end{aligned}$$
(104)
$$\begin{aligned} u_{x_2}(x_2^0,t)= & {} A \ \text {sin}\left( \frac{2 \pi x_2^0}{l} \right) \text {sin}\left( \frac{c \pi t}{l} + \pi \right) . \end{aligned}$$
(105)

Here, A denotes the maximum amplitude of the displacement, which is set to 0.005 m, whereas c is a constant defined as

$$\begin{aligned} c = \sqrt{\frac{E}{\rho ^0}}, \end{aligned}$$
(106)

with Young’s modulus E being equal to \(1\cdot 10^7\) Pa and initial mass density \(\rho ^0\) being set to \(1\cdot 10^7\) Pa. Furthermore, Poisson’s ratio is equal to 0.3. A detailed description of this benchmark is available [40] including an analytical solution obtained with the method of manufactured solutions [26, 55].

The domain is discretized by 33 nodes in each direction, and each element contains initially 16 particles. The computational time is set to \(3.5\cdot 10^{-3}\) s, and the time-step size equals \(10^{-4}\) s. The tensor product of the one-dimensional basis functions described in Sect. 6 is adopted for discretization. For the unified approach, the knot vector in each direction is updated based on the velocity field to approximate the moving nodes. For large deformations, however, the use of unstructured B-splines is preferred, such as PS-splines [41], as it gives the possibility to update the inner nodes independently of each other.

Figure 9 shows the normal stress in \(x_1\)-direction \(\sigma _{11}\) along the plate for material points with \(x_2^0\approx 0.07\) m. Employing piecewise-linear basis functions within both MPM and the OTM method leads only to a piecewise-constant approximation of the stress field. Due to grid-crossing errors, the stress profile obtained using MPM with piecewise-linear basis functions deviates significantly from the analytical solution. The simulations performed with the maxent basis functions show considerably more accurate stress approximations for both methods. To obtain these results with the MPM algorithm, the user-defined factor \(d_{\max }\) is set to 3.0, while for the OTM method, \(d_{\max }=2.0\) is taken. The unified approach and BSMPM lead to an even smoother stress profiles which are in close agreement with the analytical solution.

9 Conclusions

The first part of this paper provides a comparison between the MPM and OTM schemes. While the methods were derived in fundamentally different manners, the resulting algorithms are closely related. In fact, assuming a constant time step, the validity of the backward Euler scheme for material-point displacement in MPM, as well as the linear completeness of the MPM basis functions and their ability to translate nodal velocities into material-point velocities, the only difference between the algorithms emerges from the update of the basis functions. However, this difference is fundamental. Since MPM uses initial nodal positions in the basis-function update, it is viewed as a combination of Lagrangian and Eulerian approaches. At the same time, the OTM method is a fully updated Lagrangian method. Moreover, MPM is typically used with piecewise-linear basis functions, whereas the OTM method generally employs maximum-entropy basis functions.

In the second part of the paper, a unified approach is proposed. This approach combines BSMPM and the OTM method. Similar to BSMPM, the proposed approach uses B-spline basis functions. However, it computes the basis functions based not only on the updated material-point positions, but also on the advected degrees-of-freedom set. The obtained numerical results demonstrate that the proposed method preserves the convergence properties of BSMPM and remains stable when a consistent mass matrix is adopted. Furthermore, the unified approach does not contain user-defined parameters and is faster than computations with maxent basis functions for large size problems.