Abstract
Particle shape representation is a fundamental problem in the Discrete Element Method (DEM). Spherical particles with well known contact force models remain popular in DEM due to their relative simplicity in terms of ease of implementation and low computational cost. However, in real applications particles are mostly non-spherical, and more sophisticated particle shape models, like superquadric shape, must be introduced in DEM. The superquadric shape can be considered as an extension of spherical or ellipsoidal particles and can be used for modeling of spheres, ellipsoids, cylinder-like and box(dice)-like particles just varying five shape parameters. In this study we present an efficient C++ implementation of superquadric particles within the open-source and parallel DEM package LIGGGHTS. To reduce computational time several ideas are employed. In the particle–particle contact detection routine we use the minimum bounding spheres and the oriented bounding boxes to reduce the number of potential contact pairs. For the particle–wall contact an accurate analytical solution was found. We present all necessary mathematics for the contact detection and contact force calculation. The superquadric DEM code implementation was verified on test cases such as angle of repose and hopper/silo discharge. The simulation results are in good agreement with experimental data and are presented in this paper. We show adequacy of the superquadric shape model and robustness of the implemented superquadric DEM code.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In many engineering applications different types of particles have to be stored, transported, mixed, or segregated. Despite that, knowledge of the static and dynamic behavior of particulate solids is still not fully understood. Such knowledge is of major importance for a proper design of processing units of silos, rotating drums, and others [23]. The Discrete Element Method (DEM), developed by Cundall and Strack [14], has proven to be an efficient tool for modeling granular materials. In DEM granular material is treated as a system of distinct interacting particles. Each particle has own mass, velocity, position, and contact properties; it obeys Newton’s second law and is tracked individually. Together with the rapidly increasing computational power available, DEM becomes more and more popular among engineers and researchers. A comprehensive overview of major DEM applications can be found in [56].
Many DEM codes still employ disks (in 2D) and spheres (in 3D) to represent particle shapes due to their implementation simplicity and efficiency in speed of contact detection, which results in faster code development and lower computational time. The rolling friction correction can be theoretically linked to various physical effects to model particle non-sphericity using spherical particles, as emphasized by Ai et al. [2]. Moreover, the contact force models that include normal and tangential forces for a pair of interacting spheres are already established. An overview of the most popular contact forces is given in [55]. However, particles in granular and powder materials in nature and industry are mostly non-spherical. Moreover, spherical particles behave differently than complex-shaped particles, not only on the single grain level but also as an assembly. As summarized by Cleary [10], non-spherical particles differ from the spherical ones in the following ways: compacity of packed heap, resistance to shear and roll, and, as a result, ability to block the flow. Therefore, the physical validity of results obtained from simulations using spherical particles is usually questionable [31, 48].
Many approaches have been suggested in the literature to handle particle non-sphericity. Previously, Lu et al. [34] have summarized the main theoretical developments in non-spherical DEM and reviewed its applications. The most popular approach in the DEM community, according to Lu et al. [34], is the multisphere (MS) approach [1, 19, 30, 31, 37, 50]. In this method simple spheres are allowed to overlap and glued together to represent complex shapes. The method has the advantages that any shape can be represented by a set of glued (or prime) spheres and contact detection together with force calculation is based on that for spheres. One of the disadvantages is the fact that high accuracy of the shape approximation requires a significant number of prime spheres. Markauskas et al. [37] showed that approximation of ellipsoidal particles by 25 prime spheres increases CPU time by factor of 17. Marigo and Stitt [36] studied the influence of particle shape representation by the MS approach for a system of cylindrical pellets and found that about 160 primary spheres are required to be in agreement with experimental data. Another disadvantage of the MS method is the occurrence of multiple contact points [31] since an approximation of a convex particle (e.g., ellipsoid) by MS-particle is always non-convex if the number of primary spheres is more than one. The number of interparticle contacts increases with the increase of the number of the prime spheres [37]. Thus, a reasonable number of prime spheres should be chosen.
Polygonal (in 2D) and Polyhedral (in 3D) particles as introduced by Cundall [13] have been widely used in DEM to model granular materials. In this approach the particle surface is approximated by line segments (in 2D) or by triangles (in 3D), thereby providing a high level of versatility in particle shape representation. Different algorithms for collision detection were developed by Cundall [13], Chang and Chen [8], Boon et al. [5], and Nezami and Hashash [41]. The major drawback of this method is that the question of how contact forces between two colliding polyhedral bodies are calculated is still not completely answered.
The superquadric shape is an extension of spheres and ellipsoids. This shape was first introduced in mathematics by Barr [3], used in DEM by Williams and Pentland [52] in 2D DEM and by Cleary in 3D DEM simulations [9, 12] and later used by Lu et al. [35]. The superquadric equation given by Barr is as follows:
where a, b, c are the half-lengths of the particles along its principal axes, and \(n_1\) and \(n_2\) are blockiness parameters. Parameters \(n_1=n_2=2\) give an ellipsoid, and a cylinder is obtained if \(n_1=2\) and \(n_2\gg 2\) and a box-like particle if \(n_1\gg 2\) and \(n_2\gg 2\) (Fig. 1). Superquadrics give an excellent trade-off between model complexity and shape flexibility by simply changing 5 shape parameters (\(a,b,c,n_1,n_2\)) in formula (1). However, the use of superquadric particles is limited in that sense that only ellipsoidal, box-like and cylinder-like particles can be modeled. Another disadvantage of the superquadric approach is that the contact detection procedure can be implemented, possibly, only by using typically computationally expensive iterative methods (Newton’s method), convergence properties of which decrease with increase of blockiness parameters \(n_1\) and \(n_2\).
Four examples of superquadric particle shape composed by different shape parameters (\(a,b,c,n_1,n_2\)) as defined in Eq. (1)
Unfortunately, there is a lack of literature that could provide detailed descriptions of algorithms necessary for implementation of superquadric particles in DEM. In this study we will present the non-spherical DEM approach providing all necessary mathematical tools for an efficient implementation of superquadric particles in the DEM based on open-source DEM package LIGGGHTS [28], such that the reader can understand the underlying algorithms and analytical expressions for particle–wall contact and minimum bounding sphere. We show good versatility of the approach for the practical range of blockiness parameters. Validation work along with several application examples is presented.
2 Numerical model
2.1 Motion of an arbitrarily shaped particle
In DEM each particle i obeys Newton’s second law and is tracked individually by solving explicitly their trajectories:
where \(m_i\) and \(\varvec{X}_{Ci}\) are the mass and the position of a particle center, \(\mathbf {F}_{i}\) is the total force acting on a particle i that is the sum of normal particle–particle, tangential particle–particle and external non-particle forces like gravity.
The contact force and the contact point between two non-spherical particles depend on particles’ orientation, and hence accurate determination and integration of orientation becomes critical. Accurate determination of a particle’s orientation is also critical for the determination of the angular velocity of a particle. Orientation of a non-spherical particle is usually described as a rotation of the coordinate vectors \( \{ {\varvec{e}}_1, {\varvec{e}}_2, {\varvec{e}}_3\}\) that define the global observer-fixed reference frame to the coordinate vectors \( \{ \hat{\varvec{e}}_1, \hat{\varvec{e}}_2, \hat{\varvec{e}}_3\}\) that define the local body-fixed reference frame. This rotation can be tracked by rotation vectors [7] or by quaternions [22] that are singularity-free in contradistinction to the methods based on Euler angles. The quaternion of rotation \(\varvec{q}\) can easily be constructed from the unit axis of rotation \(\varvec{e} \) and the angle of rotation \(\alpha \) around this axis:
The rotation matrix \(\varvec{A}=\varvec{A(\varvec{q})}\) is constructed from the quaternion components:
By definition of the rotation matrix: \(\varvec{A}\cdot \varvec{e}_1= \hat{\varvec{e}}_1\), \(\varvec{A}\cdot \varvec{e}_2= \hat{\varvec{e}}_2\), \(\varvec{A}\cdot \varvec{e}_3=\hat{\varvec{e}}_3\), \(\varvec{A}^{-1}=\varvec{A}^T\). The orientation of a particle can be updated every time step using the following expression [32]:
where sign “\(\circ \)” denotes quaternion multiplication [22], \(\varvec{\omega }_i = (\omega _{ix},\omega _{iy},\omega _{iz})^T=\varvec{A}_{i}^{-1}{\varvec{\varOmega }}_i\) is the angular velocity in the particle-based (canonical) coordinate system, and \(\varvec{\varOmega }_i\) is the angular velocity in the observer-fixed coordinate system. Rotational motion of a particle is tracked by the following equation in the observer-fixed coordinate system:
where \(\varvec{L}_{i}=\varvec{I}_{i}\cdot {\varvec{\varOmega }_{i}}\) is the angular momentum of the particle i, \(\varvec{I}_i\) is the tensor of inertia, and \(\varvec{T}_{i}\) is the total torque acting on a particle i with respect to the particle center. Note that the normal force can also produce torque and must be taken into account while calculating \(\varvec{T}_{i}\). For a spherical particle Eq. (6) above can easily be resolved with regard to \(\varvec{\varOmega }\) since its tensor of inertia is always constant and only possesses non-zero elements in the diagonal: \(\varvec{I}_{sphere} = \frac{2}{5}mR^2\varvec{E}\), where \(\varvec{E}\) is the identity tensor. In general case the t \(\varvec{A}\cdot \hat{\varvec{I}}\cdot \varvec{A}^{-1}\), where \(\hat{\varvec{I}}\) is the principal tensor of inertia, i.e., the tensor of inertia in particle-based coordinate system which contains non-zero entries only in the diagonal: \(\hat{I}_{x}, \hat{I}_{y}\) and \(\hat{I}_{z}\). Moving to the body-fixed coordinate system yields the following general form of Eq. (6):
where \(\varvec{t}_i = (t_{ix},t_{iy},t_{iz})^T=\varvec{A}_{i}^{-1}{\varvec{T}}_i\) is the total torque acting on a particle in the particle-based coordinate system.
Equation (7) in conjunction with Eq. (5) can be solved by various methods, such as described by Miller et al. [38], Walton and Braun [51] and Omelyan [42–45]. Corresponding analytical expressions for volume and principal moments of inertia can be found in works by Jaklič et al. [25, 26].
2.2 Neighbor search
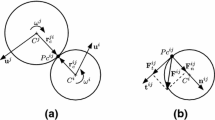
In this section we describe the broad phase of the contact detection algorithm. To perform simulations of large-scale systems, it is essential to optimize the computational strategy. The number of potential contact pairs can be minimized by employing a neighbor list to exclude particle pairs that are a priori too far from each other to be in contact [28]. Different techniques for constructing neighbor lists have been proposed in the literature. These include the Verlet-Neighbour List [49], Linked Cell method [46], NBS algorithm [39], and MR linear contact detection algorithm [40]. The number of potential contact pairs in a neighbor list can be reduced with the help of bounding volumes. A bounding volume is a simple volume that encapsulates a more complex body. According to Ericson [18] doing cheap bounding volume intersection tests before performing more complex geometric tests results in a significant performance gain since the amount of work needed to determine a collision is reduced and computational time is saved by rejecting contact pairs whose bounding volumes do not intersect. Such bounding volumes include bounding spheres and oriented bounding boxes (OBB) (Fig. 2).
The bounding sphere is the most memory-efficient bounding volume. The spheres’ intersection check consists in evaluating if the distance between the centers of the spheres is less or equal than the sum of their radii. If the answer is yes, than the narrow phase of the contact detection must be used. In this section we present an accurate analytical solution for the minimum bounding sphere, i.e., the bounding sphere of minimum volume, for a superquadric particle using its implicit shape equation. We seek the point (x, y, z) on the particle’s surface which has the largest distance to the particle center. This distance is the minimum bounding radius, which gives the minimum volume. This condition in terms of an optimization problem can be expressed as follows:
where f(x, y, z) is the superquadric equation in the body-based coordinate system (Eq. (1)). Without loss of generality we require \(x>0,y>0,z>0\). Using Lagrange multipliers this optimization problem can be rewritten as a system of non-linear equations:
Substituting \(x=a\tilde{x}, y=\alpha b\tilde{x}, z=\beta c\tilde{x}\) gives:
Doing one more substitution \(\gamma =(1+\alpha ^{n_2})^{n_1/n_2-1}\) yields:
The solution of this system provides the following:
The minimum bounding radius can now be easily obtained: \(r=\sqrt{x^2+y^2+z^2}\). For spherical and ellipsoidal particles (\(n_1=n_2=2\)), the system of equations degenerates, which has four solutions: \(x=0,y=0,z=0\) or \(x=a,y=0,z=0\) or \(x=0,y=b,z=0\) or \(x=0,y=0,z=c\). The minimum bounding radius becomes \(r=max(a,b,c)\). For the case of the cylinder (\(n_1>2, n_2=2\)), without loss of generality, let \(a>b\). This will give \(\alpha =0\). Other unknowns can be found using the equations above.
While the bounding sphere is an orientation invariant approximation of a particle, the oriented bounding box (OBB) can capture orientation and aspect ratio of the particle. The minimum oriented bounding box is a rectangular block with semi-axes a, b, c with the center located at the center of the particle in question and oriented as the particle. The intersection check methods between two OBBs are usually based on the concept of the separation axis and can be found in [17, 18, 47].
2.3 A contact detection algorithm
Equation (1) defines a superquadric surface in its local (canonical) coordinate system. We will refer to the function \(f(\varvec{x})\equiv \left( \left| \frac{x}{a} \right| ^{n_2}+\left| \frac{y}{b} \right| ^{n_2}\right) ^{n_1/n_2}+\left| \frac{z}{c} \right| ^{n_1}-1\) as the shape function. If for a certain point \((x,y,z)^T\) the value \(f<0\) then the point is located inside the particle, if \(f>0\), then \((x,y,z)^T\) is outside the particle. If \(f=0\), then \((x,y,z)^T\) lies on the particle surface.
For practical use it is necessary to be able to define a superquadric particle with respect to a global coordinate system which is usually observer-fixed. This is done by applying the usual translation and rotation operations. The shape function F of a superquadric particle with center \(\varvec{X}_C\) and quaternion \(\varvec{q}\) in a global frame is given by the following expression:
The points \(\varvec{X}\) and \(\varvec{X}_C\) are defined in the global frame. For a contact detection algorithm it is also necessary to be able to calculate 1st (gradient) and 2nd (Hessian matrix) derivatives of the shape function. The gradient of the shape function calculated at a point \(\varvec{x} = (x,y,z)^T\) in the local frame is the following:
The second derivatives are given by

where \(\nu =\left| \frac{x}{a} \right| ^{n_2}+\left| \frac{y}{b} \right| ^{n_2}\). The corresponding gradient vector and Hessian matrix read
The first and second derivatives of the shape function at a point \(\varvec{X}\) in the global coordinate system now can easily be established by calculating them in the local frame and applying the transition formulas:
Now we are ready to formulate the contact detection problem in terms of an optimization problem. Consider two superquadric particles with two times continuously differentiable (automatically fulfilled if \(n_1\ge 2\) and \(n_2\ge 2\)) shape functions \(F_1({\varvec{X}})\) and \(F_2({\varvec{X}})\) defined in global frame. Following Houlsby [24] and extending the algorithm for 3D case we seek a “midway” point P between the particles and “closest” to both. In other words, solve the following optimization problem:
Applying the Lagrange multipliers approach gives the Lagrange function in the following form:
The equation \(\nabla _{\varvec{X},\lambda }L(\varvec{X},\lambda )=0\) gives the condition for the stationary point:
Regrouping terms yields
Introducing \(\mu ^2=(1-\lambda )/(1+\lambda )\) brings us to the following system introduced by Cleary et al. [12]:
This system of 4 equations with 4 unknowns has to be solved at each DEM time step for each pair of particles. This system gives a mathematical condition for interparticle contact detection. If for point \(\varvec{X}_{0}\) conditions \(F_1(\varvec{X}_0)<0\) and \(F_2(\varvec{X_0})<0\) are fulfilled (Fig. 3), the contact between two particles takes place with the contact point \(\varvec{X}_0\) and the overlap direction \(\varvec{n}_{12}=\nabla F_{1}/||\nabla F_{1}||\) or \(\varvec{n}_{12}=-\nabla F_{2}/||\nabla F_{2}||\) calculated at the contact point.
Newton’s method for this system can be expressed as \(\varvec{J}\delta \varvec{Z} = -\varvec{\varPhi }, \varvec{Z} = (x,y,z,\mu )^T, \varvec{Z}^{n+1} = \varvec{Z}^{n} + \delta \varvec{Z}\), where \(\varvec{J}\) is the Jacobian matrix of the right-hand side term \(\varvec{\varPhi }\):
For stability reasons it is necessary to find a scalar parameter \(\alpha \in (0,1]\) such that \(\varvec{Z}^{n+1} = \varvec{Z}^{n} + \alpha \delta \varvec{Z}\), \(||\varvec{\varPhi }(\varvec{Z}^{n+1})||<||\varvec{\varPhi }(\varvec{Z}^{n})||\) at every iteration to ensure convergence of the algorithm. There are several methods to obtain such a scalar parameter. One of them is first to check if \(\alpha =1\) satisfies \(||\varvec{\varPhi }(\varvec{Z}^{n+1}||<||\varvec{\varPhi }(\varvec{Z}^{n})||\). If not, let \(\alpha :=\alpha /2\) and repeat or use the Golden section algorithm [27] with termination if any \(\alpha \) satisfying \(||\varvec{\varPhi }(\varvec{Z}^{n+1})||<||\varvec{\varPhi }(\varvec{Z}^{n})||\) is found. The solution from previous DEM time step can be used as a starting point (initial guess). Usually a few Newton iterations (\(1-3\)) are required to converge, depending on a user defined tolerance \(\varepsilon \ll 1\) for termination criterion \(||\varvec{\varPhi }(\varvec{Z}^{n+1})||<\varepsilon \).
If there is no information on the contact point from the previous step, let (\(a_0^1\), \(b_0^1\), \(c_0^1\), \(n_{10}^1\), \(n_{20}^1\)) and (\(a_0^2\), \(b_0^2\), \(c_0^2\), \(n_{10}^2\), \(n_{20}^2\)) be the shape and blockiness parameters of particle 1 and 2. The following approach is suggested:
-
(1)
Find the contact point for a pair of volume equivalent spheres with radii \(r_1\) and \(r_2\) and centers located at the same points as for given particles, \(\varvec{X}_C^1\) and \(\varvec{X}_C^2\). These spheres defined as superquadrics have the following shape and blockiness parameters: \(a^1=b^1=c^1=r^1\), \(a^2=b^2=c^2=r^2\), \(n_1^1=n_2^1=n_1^2=n_2^2=2\). The analytical solution for the sphere–sphere contact point is
$$\begin{aligned} \varvec{X}=(r_2 \varvec{X}_C^1+r_1 \varvec{X}_C^2)/(r_1+r_2). \end{aligned}$$(24)Use this point as a starting point.
-
(2)
Choose number of steps N and calculate
$$\begin{aligned} \begin{aligned}&\delta a^i = (a_0^i - r^i)/N \\&\delta b^i = (b_0^i - r^i)/N \\&\delta c^i = (c_0^i - r^i)/N \\&\delta n_1^i = (n_{10}^i - 2)/N \\&\delta n_2^i = (n_{20}^i - 2)/N \\&i=1,2 \\&k = 1. \end{aligned} \end{aligned}$$(25) -
3.
Modify shape and blockiness parameters.
$$\begin{aligned} \begin{aligned}&a^i:=r^i+k\cdot \delta a^i \\&b^i:=r^i+k\cdot \delta b^i \\&c^i:=r^i+k\cdot \delta c^i \\&n_1^i:=2+k\cdot \delta n_1^i \\&n_2^i:=2+k\cdot \delta n_2^i \\&i:=1,2 \\&k:=k+1. \end{aligned} \end{aligned}$$(26) -
(4)
Calculate the contact point for particles with shape parameters (\(a^1\), \(b^1\), \(c^1\), \(n_{1}^1\), \(n_{2}^1\)) and (\(a^2\), \(b^2\), \(c^2\), \(n_{1}^2\), \(n_{2}^2\)) using the iterative algorithm described above and the last computed starting point. Use the found contact point as a new starting point for the next step.
-
(5)
Repeat steps 3 and 4 for \(N-1\) times
Steps 1–5 of the iterative procedure listed above define the step-wise linear transition of the spherical shape parameters to the shape parameters of the given particles 1 and 2 where k is the iteration number. After \(k=N\) steps the shape and blockiness parameters will be the same as initial ones by construction of the procedure:
As a result, this procedure will give the contact point for the given pair of particles. This step-wise procedure ensures the convergence of the method and does not affect computational time significantly, since it must be called only once per pair of particles. We found that for the exponents \(n_1\),\(n_2\le 8\) convergence is guaranteed. In addition, Cleary and Sawley [11] studied influence of the blockiness parameters on the mass flow rate from a hopper and found that the values \(n_1, n_2>8\) fail to make any difference to the nature of the flow. Thus, we can safely recommend to use blockiness parameters in the range between 2 and 8.
2.4 Particle–wall contact
For industrial applications of DEM it is necessary to be able to resolve the contact between a particle and a flat surface. A flat surface (the wall) is usually defined by any point \(\varvec{x}_w\) on it and the unit normal vector \(\varvec{n}\) defined in the particle-based coordinate system. This yields the equation of the wall:
To establish the contact point we first seek a point \(\varvec{x}=(x,y,z)^T\) on the particle surface that has the minimum/maximum distance to the wall (Fig. 4). The mathematical condition in terms of an optimization problem is expressed by
The optimization problem has two solutions with different signs for \((x,y,z,\lambda )\). Without loss of generality the normal vector n is directed outwards with respect to the particle and its components \(n_x,n_y\), and \(n_z\) are positive. Hence, we seek a point x, y, z with positive signs. Applying the Lagrange multipliers approach we can rewrite the optimization problem as follows:
Performing the same variable change as in the previous section gives the following system:
The solution of this system provides the following expressions:
For the outer normal \(\varvec{n}=(n_x, n_y, n_z)^T\) with components of any signs the solution can be generalized:
The normal overlap vector \(\varvec{\delta }\) between the particle and the wall now can be easily established by calculating the projection \(\varvec{x}^{*}\) of the contact point onto the wall:
To calculate the overlap vector and the contact point in the global coordinate system, transition formulas (see Eq. (18)) can be applied. A corresponding algorithm for interaction between superquadric particles and walls of arbitrary shape has been developed in LIGGGHTS. This algorithm employs the solution for the contact between a particle and a flat wall presented above. However, the description of this algorithm is beyond the scope of this paper.
2.5 Contact force calculation
In the spherical Discrete Element Method the two following approaches are common: the hard-sphere and the soft-sphere approach. In the hard-sphere approach (event-driven), particles are assumed as rigid bodies, a sequence of collisions is processed, one collision at a time without the contact forces being explicitly considered. In the soft-sphere approach (time-driven) particles are allowed to deform slightly(overlap), and the contact forces are calculated as functions of the overlap [55]. This overlap is not real but intends to model the deformation of the interacting particles at a contact point in an indirect way.
Di Renzo and Di Maio [15] suggested using the linear spring Hertzian model without cohesion for the particle–particle and particle–wall contacts. This model employs the following formula for the interparticle contact force, acting from a spherical particle i with radius \(R_i\) and center at point \(\varvec{X}_{Ci}\) on a spherical particle j with radius \(R_j\) and center at point \(\varvec{X}_{Cj}\):
where
-
\(\varvec{F}_{n,ij}=k_{n,ij}\varvec{\delta }_{n,ij}+\gamma _{n,ij}\varvec{v}_{n,ij}\) is the normal force component,
-
\(\varvec{F}_{t,ij}=k_{t,ij}\varvec{\delta }_{t,ij}+\gamma _{t,ij}\varvec{v}_{t,ij}\) is the tangential force component,
-
\(\varvec{\delta }_{n,ij}=\delta _{n,ij}\varvec{n}_{ij}\) is the normal overlap vector,
-
\(\varvec{n}_{ij}=(\varvec{X}_{Cj}-\varvec{X}_{Ci})/||\varvec{X}_{Cj}-\varvec{X}_{Ci}||\) is the normal overlap direction,
-
\(\delta _{n,ij}=R_i + R_j - d_{ij}\) is the normal overlap distance,
-
\(d_{ij}=||\varvec{X}_{Cj}-\varvec{X}_{Ci}||\) is the distance between particles’ centers,
-
\(\varvec{v}_{n,ij}=((\varvec{v}_j-\varvec{v}_i)\cdot \varvec{n}_{ij})\varvec{n}_{ij}\) is the normal component of the relative velocity,
-
\(\varvec{v}_{t,ij} = \varvec{v}_j-\varvec{v}_i - \varvec{v}_{n,ij}\) is the tangential component of the relative velocity,
-
\(\varvec{\delta }_{t,ij}=\int _{T_{0}}^T \varvec{v}_{t,ij} d\tau \) is the tangential overlap [28].
Both normal and tangential forces contain a spring force and a damping force. The coefficients \(k_n, k_t, \gamma _n, \gamma _t\) are calculated from the material properties (density, coefficient of restitution, Poisson ratio, Young’s modulus, shear modulus), overlap, and radii of the particles. The corresponding expressions can be found in [4].
However, the models above are only applicable for spherical particles. Feng and Owen [20] proposed theoretical framework for developing energy-conserving normal contact models for arbitrarily shaped particles. It has been established that the normal force must be a potential field vector associated with a potential function \(\phi \) that is a function of the overlap volume [20]. However, the accurate calculation of the overlap volume may be computationally expensive and thus become not applicable for a case with millions of particles.
Previously, Zheng et al. [54] modified the Hertzian model taking into consideration two principal radii of curvature and applied it to ellipsoidal particles. They showed good agreement with the results calculated by means of the finite element method (FEM). However, the extension of the model to superquadric particles becomes quite complex. In this study we propose the following approach. The contact point \(\varvec{X}_0\) and the contact direction \(\varvec{n}_{ij}\) define the contact line. We seek points \(\varvec{X}_i\) and \(\varvec{X}_j\) as the nearest (with respect to \(\varvec{X}_0\)) intersection points between the contact line and the particles’ surfaces. In other words, we solve the following non-linear algebraic equations separately with respect to the scalars \(\alpha _i>0\) and \(\alpha _j<0\) at every DEM time step for each pair of overlapping particles:
Then the normal overlap vector is \(\varvec{\delta }_n\equiv \varvec{X}_i-\varvec{X}_j = (\alpha _i - \alpha _j)\varvec{n}_{ij}\).
These equations with respect to \(\alpha _i\) and \(\alpha _j\) are easier to solve if moved to their own local reference frames:
\(f_i(\varvec{x}_{i0}+\alpha _i \varvec{\hat{n}}^i_{ij})=0\),
\(f_j(\varvec{x}_{j0}+\alpha _j \varvec{\hat{n}}^j_{ij})=0\),
where \(\varvec{x}_{l0}=\varvec{A}^T_l\cdot (\varvec{X}_0-\varvec{X}_{Cl})\), \(\varvec{\hat{n}}^l_{ij}=\varvec{A}^T_l\cdot \varvec{n}_{ij}\), \(l=\{i,j\}\). Note that in both reference frames scalars \(\alpha _i\) and \(\alpha _j\) are the same for each particle. The equations can be easily solved by Newton’s iterations:
Calculation of the coefficients \(k_n, k_t, \gamma _n, \gamma _t\) in(35) requires knowledge of the equivalent radius \(R_{eq}\) [15]:
where \(R_i\) and \(R_j\) are the radii of particles i and j. We will use \(R=1/K\) as the particle radius, where \(K=K_{mean}=\frac{1}{2}(\kappa _1+\kappa _2)\) is the mean local curvature coefficient [21] calculated at \(\varvec{X}_i\) and \(\varvec{X}_j\) for each particle correspondingly, and \(\kappa _1\) and \(\kappa _2\) are the principal curvature coefficients:
Alternatively, one can use the Gaussian curvature coefficient \(K=K_{Gauss}=\sqrt{\kappa _1\kappa _2}\) [21]:
Obviously, \(K_{mean}=K_{Gauss}=1/R\) for a spherical particle of radius R.
One of the disadvantages of the proposed methodology (and hence of the possible extension of the method by Zheng et al. [54] to superquadrics) is that the curvature coefficients may become zero leading to infinite curvature radii if superquadric exponents \(n_1\) and \(n_2\) are more than 2, especially in face-to-face contact. The mean curvature radius becomes infinite if both principal curvature coefficients are zero. This occurs at 6 points on the particle surface: \(x=y=0,z=\pm c\), \(y=z=0,x=\pm a\) and \(x=z=0,y=\pm b\) (in the local reference frame). The Gaussian curvature radius becomes infinite if any of the principal curvature coefficients is zero. This occurs if \(x=0\), \(y=0\) or \(z=0\) (in the local reference frame). For this reason, we limit the curvature radius: \(R_{curvature}=\min (R_{curvature},qR_{vol})\), where \(R_{vol}\) is radius of the volume equivalent sphere, q is the limiting coefficient that must be chosen in advance. In the current implementation of LIGGGHTS \(q=10\) is used. The influence of the choice of the curvature radius and the limiting coefficient q on the simulation results is to be studied in the future publications.
3 Validation
3.1 Contact force between two ellipsoidal particles
Here we bring in contact two ellipsoidal particles (Table 1) oriented parallel to each other (Fig. 5). Particles are considered to be elastic and frictionless. The overlap distance was varied in the range between 0 and 5\(\mu \)m. Three radius models were tested: the mean curvature radius, the Gaussian curvature radius, and radius of the volume equivalent sphere. The normal contact force between overlapping ellipsoidal particles is plotted as a function of the overlap and presented in Fig. 6. Calculated results are compared with the FEM analysis carried out by Zheng et al. [54] and added to Fig. 6.
Normal force as a function of the overlap distance for different models of the equivalent radius. Results are compared with the FEM simulation results by Zheng et al. [54]
It can be observed that for elastic contacts the normal force can be well described by the Hertz theory using the Gaussian curvature radius for the particle radii \(R_i\) and \(R_j\) in Eq. (38) since it gives minimal discrepancy with respect to the FEM results. Despite this, only the mean curvature radius is used in the further test cases in this paper since it becomes infinite only at 6 points of the non-ellipsoidal (superquadric exponents \(n_1,n_2>2\)) particle surface rather than on the infinite number of points if the Gaussian curvature is used, as described in the previous section. A more comprehensive comparison of different curvature radii using different particle shapes at different orientations is to be discussed in a future paper.
3.2 Settling of particles under gravity and simulation speed
In the following test case we compare particles (Table 2) with different blockiness parameters in terms of computational time. The code was compiled with g\(++\) (5.2) compiler and run in serial mode on an Intel Core i7-4790 processor-based desktop computer. A total of 1000 particles were distributed randomly (Fig. 7, left) in the simulation box 0.1 \(\times \) 0.1 \(\times \) 0.25 m and allowed to settle under gravity along Z-direction and form a static packed bed (Fig. 7, right). Periodic boundary conditions are applied to the vertical faces \(x=0\), \(x=0.1\), \(y=0\) and \(y=0.1\). The horizontal walls \(z=0\) and \(z=0.25\) are considered as rigid walls of the same material as the particles. From Fig. 8 it is interesting to observe that the blockiness N does not affect the computational time significantly. A possible explanation is that after a certain moment of time (after about 23000th time step, inflection point of the curves) the contact point for each contact pair does not move significantly; Newton iterations are skipped since the contact point from previous time steps already satisfies the termination criterion for the Newton’s method on the next DEM time steps. As a result, computational speed is increased (angle of the tangent lines to the curves is decreased). It was obtained that for particles with high order of blockiness (\(N=10\)), the simulation time is about 1.6 \(\mathrm \mu s\) per contact pair in static regime and about 3 \(\mathrm \mu s\) in dynamic regime. These values are relative good in comparison with different studies [6, 16, 53]. However, in order to make an accurate comparison between different methods, the program codes must be run on the same hardware.
3.3 Particle–wall impact
In this test, as described by Kodam et al. [29], a cylindrical particle oriented at a specified angle, impacts a wall with a specified translational speed normal to the wall and zero angular velocity. The contact is assumed to be frictionless and without gravity. The post-impact angular and translational velocities, \(\omega ^{+}_{y}\) and \(V^+_{z}\) correspondingly, according to Kodam et al. [29], are given by
where m is the mass of the cylinder, \(\varepsilon \) is the coefficient of restitution at the point of contact, \(V^{-}_{z}\) is the pre-impact translational velocity of the cylinder, \(\alpha \) is the angle between the cylinder’s face and the line joining the contact point and the center of the particle, \(\theta \) is the angle between the cylinder’s face and the wall, and \(I_{yy}\) is the moment of inertia around the y-axis. The parameter r is the distance between the cylinder’s center and the corner point C (Fig. 9), which is assumed to be fixed. Particle parameters are listed in Table 3.
The post-impact angular and translational velocities were calculated for various orientation angles \(\theta \) for the DEM simulations and compared with analytical expressions in Fig. 10. The wall was removed immediately after collision to prevent the secondary contact that occurs in reality at low and high impact angles and is not taken into account in Eqs. (41) and (42).
For angles \(5^{\circ } \lesssim \theta \lesssim 86^{\circ }\) the superquadric DEM gives relative good agreement with analytics; however, for other angles there is small disagreement mainly due to the error in shape approximation, and, as a result, because of the corner point C, that is non-static with respect to the particle-based coordinate system. This corner point is always static at impact angles \(\theta \ne 0^{\circ }\) and \(\theta \ne 90^{\circ }\) for true cylinders. According to [29], multisphere simulations (with 54 prime spheres) show significant errors over most of the orientation range.
3.4 Piling of particles
For the second validation test case superquadric particles with the following shape parameters were used: \(a=2.0\) mm, \(b=2.0\) mm, \(c=1\) mm, \(n_1=n_2=4\). Particle parameters along with simulation setup data are listed in Table 4. They were compared with volume equivalent spherical particles of radius \(R=1.836\) mm. Domain boundaries are represented by rigid walls of the same material as the particles. In both cases the heap was formed by continuously dropping particles from a small area located above the center of the heap. As can be seen from Fig. 11 the heap shape for spherical particles (angle of repose \(31^{\circ }\)) differs from the heap shape for superquadric particles (angle of repose \(40^{\circ }\)). The heap becomes stable 1s after the dropping is stopped with almost zero maximum angular and translational velocity, which testifies the stability of the algorithms.
These simulations show importance of using non-spherical particle shapes in the Discrete Element Method. Having the same material properties the non-spherical particles can demonstrate different behavior in comparison to spherical ones just by changing the shape of the particles.
4 Numerical experiments
4.1 Angle of repose
In this test case the following particles were used: sugar cubes, “M&M’s” and chewing gum. The particles are randomly distributed in a cylindrical volume with random orientation. They are allowed to settle under gravity in the cylindrical volume. After the settling is completed, the vertical wall of the cylinder moves upwards such that some particles fall and leave the computational domain, while other particles remain on the plate and form a heap as a result. For this test case a set of experiments was conducted and compared with the simulations. The corresponding shape parameters for each sort of the particles were found and are listed in Table 5. Corresponding superquadric approximations of the particles in question are presented in Fig. 12. Material properties were chosen the same for each particle shape and are listed in Table 6.
From the pictures (Figs. 13, 14 and 15) it can be seen that there is only a qualitative agreement between the experiments and the simulations mainly due to relatively big size of the particles used in comparison to the cylinder diameter.
Packing of cylinders after dropping 250 particles, superquadric DEM (left), and experiment [29] (right)
Comparison of experimental (Liu et al. [33], top) and simulation (bottom) snapshots of the discharging candies from a hopper at different moments of time: t \(=\) 0 s, t \(=\) 0.9 s, t \(=\) 1.8 s, t \(=\) 2.7 s, t \(=\) 3.6 s, and t \(=\) 6.6 s (from left to right)
4.2 Static packing of cylinders
In this validation test we simulate a static packing of cylinders, defined as superquadric particles. The particles were dropped into a cylindrical container, and compared to the experimental data provided by Kodam et al. [29]. The DEM material properties along with particle properties are listed in Table 7. Particle size parameters, a, b, and c, were chosen such that particles in the simulation have the same diameter and length as in the experiment: \(a=b=D/2\), \(c=L/2\) (Table 7). Volume and principal moments of inertia of the cylinders defined as superquadrics have values smaller than those for true cylinders due to the rounded edges. The difference between a true cylinder and its superquadric approximation decreases with the increase of the blockiness/roundness superquadric shape parameter \(n_1\), however, leading to less stability of the method. Hence, a compromise value must be chosen. The superquadric cylinder in this simulation was set to have the same mass as the true cylinder by increasing density by 7 % and setting blockiness parameters to \(n_1=6.0, n_2=2.0\). DEM time step was set \(\Delta t=10^{-5}\) s.
The image of the final state from the simulation is shown in Fig. 16. The final experimental fill height according to Kodam et al. [29] is \(53.3\pm 2.0\) mm, while superquadric DEM simulation gives the fill height of roughly \(52.0\pm 3.0\) mm which is in good agreement with the experiment. Kodam et al. [29] simulated packing of the cylinders with the multisphere approach and found that 9-sphere particles underpredict the bed height by 21 %, while 54-sphere particles underpredict the fill height by 8 %.
4.3 Hopper discharge
We also use the method in simulating the discharge of Smarties®chocolate candies from a flat bottom hopper. These candies have ellipsoidal shape with the following shape parameters: \(2a=13.56\,\mathrm{mm}, 2b=2c=7.19\,\mathrm{mm}, n_1=n_2=2.0\), and density 1338 kg/m\(^3\). The hopper is 290 mm along the X-direction, 55mm in Y-direction, and has an orifice of 54 mm in X-direction and 55mm in Y-direction. Gravity is oriented along the Z-direction. The particle–particle and particle–wall coefficient of friction was set 0.4. Young’s modulus, Poisson’s ratio, and coefficient of restitution were chosen to be 10 GPa, 0.29, and 0.5 correspondingly. The hopper geometry and particle properties used in the DEM simulation are the same as those used by Liu et al. [33] and Dong et al. [16]. The DEM time step size was set \(\Delta t=2\times 10^{-5}s\). A total of 5500 particles are dropped in the hopper to form a bed of 0.4 m height and remain motionless until the orifice is opened. After the settling is completed, the orifice located at the center of the bottom is opened and particles discharge from the hopper by gravity exhibiting V-shaped flow pattern. The simulation results are shown in Fig. 17 at different time steps during the discharge along with the snapshots observed in the experiment by Liu et al. [33]. Good agreement between the simulation and the experiment can also be found in terms of discharge rate, i.e., ratio of the remaining particles in the hopper at different times (Fig. 18), which proves validity of the shape model. However, one can see that experimental results are consistently higher than the numerical results. The discrepancy between experimental and simulation values may be due to the coefficient of friction that must be calibrated to fit experimental data.
Ratio of the particles remaining in the hopper as a function of time. Experimental data (Liu et al. [33]) vs. simulation
4.4 Hopper discharge-influence of the aspect ratio
In the next validation test case we apply the superquadric DEM code to modeling of the discharge of cylindrical particle from a flat bottom hopper (Fig. 19). The simulated particles have density \(\rho =2500\) kg/m\(^3\), fixed bottom diameter \(D=1\) mmf, while the aspect ratio \(\alpha =h/D\), i.e., the ratio between the height and the bottom diameter, was varied. Young’s modulus, Poisson’s ratio, and coefficient of restitution are the same as in the previous section. The hopper is 11D along X-direction, 4D along Y-direction. Periodic boundary conditions are applied in the Y-direction. The orifice is 3.6D along X-direction and 4D along Y-direction. A total of 2100 particles were simulated with aspect ratio \(\alpha =0.33\), 1400 particles with \(\alpha =0.5\), 700 particles with \(\alpha =1\), and 467 particles with \(\alpha =1.5\) correspondingly. As a consequence, the total volume of particle before the discharge was 514 mm\(^3\) for all shapes. If the coefficient of friction is small (\(\mu =0.1\)), it can be seen (Fig. 20) that the volume of discharged particles as function of time is comparable for different shapes and is almost linear until the discharging is about to end [16], while the number of discharged particles, obviously, varies for different shapes. This phenomenon occurs in rheology of granular particles and can be a test case for validation of a non-spherical DEM code [32].
5 Conclusion
The superquadric shape model was implemented as a separate surface model in the open-source DEM package LIGGGHTS®[28] which is an extension of the open-source package LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) [46]. Both are massively parallel and written in C++. The program codes are available for public download.
The superquadric DEM has shown promising results along with qualitative and quantitative agreement with experimental data reported in the literature. This paper shows versatility and applicability of the superquadric DEM. The methods for contact detection, which can easily take up to 80 % of computational time [41], and contact force calculation between superquadric particles have been described in detail by using their implicit equations. The formulation employs the “contact point” which is midway and closest to both particles. The corresponding algorithms for particle–mesh interaction have also been developed but are not presented in this paper. The superquadric DEM code has been applied to various DEM problems which prove robustness and efficiency of the implemented algorithms. The methods have shown to be fast, and can be further optimized.
The superquadric particles are expected to give more accurate results than multisphere approximations for more reasonable computational time. Detailed comparison of superquadrics and multispheres in DEM is to be done in the future. The proposed methodology has the potential to be further extended for any other type of particles defined by a potential/shape function. The code is expected to be available for public download in 2017.
References
Abbaspour-Fard M (2000) Discrete element modelling of the dynamic behaviour of non-spherical particulate materials. Ph.D. thesis, The University of Newcastle upon Tyne http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.324869, https://theses.ncl.ac.uk/dspace/bitstream/10443/970/1/Abbaspour-Fard00.pdf
Ai J, Chen JF, Rotter JM, Ooi JY (2011) Assessment of rolling resistance models in discrete element simulations. Powder Technol 206(3):269–282. doi:10.1016/j.powtec.2010.09.030, http://linkinghub.elsevier.com/retrieve/pii/S0032591010005164
Barr AH (1981) Superquadrics and angle-preserving transformations. IEEE Comput Graph Appl 1(1):11–23. doi:10.1109/MCG.1981.1673799
Benvenuti L (2014) Establishing the predictive capabilities of DEM simulations: sliding and rolling friction coefficients of non-spherical particles. In: CFD 2014 Proceedings, pp 1–7
Boon CW, Houlsby GT, Utili S (2012) A new algorithm for contact detection between convex polygonal and polyhedral particles in the discrete element method. Comput Geotech 44:73–82. doi:10.1016/j.compgeo.2012.03.012, http://linkinghub.elsevier.com/retrieve/pii/S0266352X12000535
Boon CW, Houlsby GT, Utili S (2013) A new contact detection algorithm for three-dimensional non-spherical particles. Powder Technol. 248:94–102. doi:10.1016/j.powtec.2012.12.040, http://linkinghub.elsevier.com/retrieve/pii/S003259101200839X
Campello EMB (2015) A description of rotations for DEM models of particle systems. Comput Part Mech 2(2):109–125. doi:10.1007/s40571-015-0041-z, http://link.springer.com/10.1007/s40571-015-0041-z
Chang SW, Chen CS (2008) A non-iterative derivation of the common plane for contact detection of polyhedral blocks. IntJ Numer Methods Eng 74(5):734–753. doi:10.1002/nme.2174, http://doi.wiley.com/10.1002/nme.2174
Cleary PW (2004) Large scale industrial DEM modelling. Eng Comput 21(2/3/4), 169–204. doi:10.1108/02644400410519730, http://www.emeraldinsight.com/doi/abs/10.1108/02644400410519730
Cleary PW (2010) DEM prediction of industrial and geophysical particle flows. Particuology 8(2):106–118. doi:10.1016/j.partic.2009.05.006, http://linkinghub.elsevier.com/retrieve/pii/S1674200109001308
Cleary PW, Sawley ML (2002) DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge. Appl Math Model 26:89–111. doi:10.1016/S0307-904X(01)00050-6
Cleary, PW, Stokes, N, Hurley J (1997) Efficient collision detection for three dimensional super-ellipsoidal particles. Proceedings of 8th international conference on field programmable logic and applications, pp 1–7. http://citeseerx.ist.psu.edu/viewdoc/download?
Cundall P (1988) Formulation of a three-dimensional distinct element model-Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int J Rock Mech Min Sci Geomech Abst 25(3), 107–116. doi:10.1016/0148-9062(88)92293-0, http://linkinghub.elsevier.com/retrieve/pii/0148906288922930
Cundall PA, Strack ODL (1979) A discrete numerical model for granular assemblies. Géotechnique 29(1):47–65. doi:10.1680/geot.1979.29.1.47, http://www.icevirtuallibrary.com/doi/10.1680/geot.1979.29.1.47
Di Renzo A, Di Maio FP (2004) Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem Eng Sci 59:525–541. doi:10.1016/j.ces.2003.09.037
Dong K, Wang C, Yu A (2015) A novel method based on orientation discretization for discrete element modeling of non-spherical particles. Chem Eng Sci 126:500–516. doi:10.1016/j.ces.2014.12.059, http://www.sciencedirect.com/science/article/pii/S0009250914007866, http://linkinghub.elsevier.com/retrieve/pii/S0009250914007866
Eberly D (2014) Dynamic collision detection using oriented bounding boxes. http://www.geometrictools.com/Documentation/DynamicCollisionDetection.pdf
Ericson C (2005) Real-time collision detection. CRC Press, New York
Favier J, AbbaspourFard M, Kremmer M, Raji A, Abbaspour-Fard M, Kremmer M, Raji A (1999) Shape representation of axisymmetrical, nonspherical particles in discrete element simulation using multielement model particles. Eng Comput 16(4):467–480. doi:10.1108/02644409910271894, http://www.emeraldinsight.com
Feng YT, Han K, Owen DRJ (2012) Energy-conserving contact interaction models for arbitrarily shaped discrete elements. Comput Methods Appl Mech Eng 205–208(1):169–177. doi:10.1016/j.cma.2011.02.010, http://linkinghub.elsevier.com/retrieve/pii/S0045782511000454
Goldman R (2005) Curvature formulas for implicit curves and surfaces. Comput Aided Geomet Desig 33(7):632–658. doi:10.1016/j.cagd.2005.06.005
Hamilton WR (1847) LXIX. On quaternions; or on a new system of imaginaries in algebra. Philos Mag Ser 3 30(203), 458–461. doi:10.1080/14786444708645426, http://www.tandfonline.com
Höhner D, Wirtz S, Scherer V (2014) A study on the influence of particle shape and shape approximation on particle mechanics in a rotating drum using the discrete element method. Powder Technol 253:256–265. doi:10.1016/j.powtec.2013.11.023, http://linkinghub.elsevier.com/retrieve/pii/S0032591013007067
Houlsby G (2009) Potential particles: a method for modelling non-circular particles in DEM. Comput Geotech 36(6):953–959. doi:10.1016/j.compgeo.2009.03.001, http://linkinghub.elsevier.com/retrieve/pii/S0266352X09000469
Jaklič, A, Leonardis, A, Solina F (2000) Segmentation and recovery of superquadrics, computational imaging and vision, 20. Springer, Dordrecht. doi:10.1007/978-94-015-9456-1, http://link.springer.com
Jaklic, A, Solina F (2003) Moments of superellipsoids and their application to range image registration. IEEE Trans Syst Man Cybernet Part B Cybernetics 33(4), 648–57. doi:10.1109/TSMCB.2003.814299, http://www.ncbi.nlm.nih.gov/pubmed/18238214
Kiefer J (1953) Sequential minimax search for a maximum. Proc Am Math Soc 4(3):502–502. doi:10.1090/S0002-9939-1953-0055639-3, http://www.ams.org/jourcgi/jour-getitem?pii=S0002-9939-1953-0055639-3
Kloss C, Goniva C, Hager A, Amberger S, Pirker S (2012) Models, algorithms and validation for opensource DEM and CFD-DEM. Progress Comput Fluid Dyn Int J 12(2/3):140. doi:10.1504/PCFD.2012.047457, http://www.inderscience.com/link.php?id=47457
Kodam M, Bharadwaj R, Curtis J, Hancock B, Wassgren C (2010) Cylindrical object contact detection for use in discrete element method simulations. Part II-Experimental validation. Chem Eng Sci 65(22):5863–5871. doi:10.1016/j.ces.2010.08.007, http://linkinghub.elsevier.com/retrieve/pii/S0009250910004744
Kremmer M, Favier JF (2001) A method for representing boundaries in discrete element modelling-part I: Geometry and contact detection. Int J Numer Methods Eng 51(12):1407–1421. doi:10.1002/nme.184, http://doi.wiley.com/10.1002/nme.184
Kruggel-Emden H, Rickelt S, Wirtz S, Scherer V (2008) A study on the validity of the multi-sphere Discrete Element Method. Powder Technol 188(2):153–165. doi:10.1016/j.powtec.2008.04.037, http://linkinghub.elsevier.com/retrieve/pii/S0032591008002143
Langston PA, Al-Awamle MA, Fraige FY, Asmar BN (2004) Distinct element modelling of non-spherical frictionless particle flow. Chem Eng Sci 59(2):425–435. doi:10.1016/j.ces.2003.10.008
Liu SD, Zhou ZY, Zou PR, Pinson D, Yu AB (2014) Flow characteristics and discharge rate of ellipsoidal particles in a flat bottom hopper. Powder Technol 253:70–79. doi:10.1016/j.powtec.2013.11.001
Lu G, Third J, Müller C (2015) Discrete element models for non-spherical particle systems: From theoretical developments to applications. Chem Eng Sci 127:425–465. doi:10.1016/j.ces.2014.11.050, http://linkinghub.elsevier.com/retrieve/pii/S0009250914007040
Lu G, Third JR, Müller CR (2012) Critical assessment of two approaches for evaluating contacts between super-quadric shaped particles in DEM simulations. Chem Eng Sci 78:226–235. doi:10.1016/j.ces.2012.05.041, http://linkinghub.elsevier.com/retrieve/pii/S0009250912003223
Marigo M, Stitt EH (2015) Discrete Element Method (DEM) for Industrial applications: comments on calibration and validation for the modelling of cylindrical pellets. KONA Powder Part J 32:236–252. doi:10.14356/kona.2015016, https://www.jstage.jst.go.jp/article/kona/32/0/32_2015016/_article
Markauskas D, Kačianauskas R, Džiugys A, Navakas R (2009) Investigation of adequacy of multi-sphere approximation of elliptical particles for DEM simulations. Granular Matter 12(1):107–123. doi:10.1007/s10035-009-0158-y, http://link.springer.com
Miller TF, Eleftheriou M, Pattnaik P, Ndirango A, Newns D, Martyna GJ (2002) Symplectic quaternion scheme for biophysical molecular dynamics. J Chem Phys 116(20):8649. doi:10.1063/1.1473654, http://scitation.aip.org/content/aip/journal/jcp/116/20/10.1063/1.1473654
Munjiza, A, Andrews K (1998) NBS contact detection algorithm for bodies of similar size. Int J Numer 149(2), 131–149. doi:10.1002/(SICI)1097-0207(19980915)43:1<131::AID-NME447>3.0.CO;2-S. ftp://crack.seismo.unr.edu/downloads/russell/partitioning_space/munjiza_1998_nbs.pdf
Munjiza A, Rougier E, John NWM (2006) MR linear contact detection algorithm. Int J Numer Methods Eng 66(1):46–71. doi:10.1002/nme.1538
Nezami, E, Hashash Y (2004) A fast contact detection algorithm for 3-D discrete element method. Comput Geotech 31(7): 575–587. doi:10.1016/j.compgeo.2004.08.002, http://linkinghub.elsevier.com/retrieve/pii/S0266352X04001016, http://www.sciencedirect.com/science/article/pii/S0266352X04001016
Omelyan IP (1998) Algorithm for numerical integration of the rigid-body equations of motion. Phys Rev E 58(1):1169–1172. doi:10.1103/PhysRevE.58.1169, http://arxiv.org/abs/physics/9901027, http://link.aps.org
Omelyan IP (1998) Numerical integration of the equations of motion for rigid polyatomics: the matrix method. Comput Phys Commun 109(2–3):171–183. doi:10.1016/S0010-4655(98)00024-1, http://arxiv.org/abs/physics/9901026, http://linkinghub.elsevier.com/retrieve/pii/S0010465598000241
Omelyan IP (1998) On the numerical integration of motion for rigid polyatomics: the modified quaternion approach. Computn Phy 12(1):97–103. doi:10.1063/1.168642
Omelyan IP (1999) A new leapfrog integrator of rotational motion. The Revised angular-momentum approach. Mol Simul 22(3):213–236. doi:10.1080/08927029908022097, http://arxiv.org/abs/physics/9901025, http://www.tandfonline.com
Plimpton S (1995) Fast parallel algorithms for short-range molecular dynamics. J Comput Phy 117(1):1–19. doi:10.1006/jcph.1995.1039, http://linkinghub.elsevier.com/retrieve/pii/S002199918571039X
Portal R, Dias J, de Sousa L (2010) Contact detection between convex superquadric surfaces. Arch Mech Eng LVI I(2):165–186. doi:10.2478/v10180-010-0009-8, http://www.degruyter.com/view/j/meceng.2010.lvii.issue-2/v10180-010-0009-8/v10180-010-0009-8.xml
Rougier, E, Munjiza, A, Latham J (2004) Shape selection menu for grand scale discontinua systems. Eng Comput 21(2/3/4), 343–359. doi:10.1108/02644400410519820, http://www.emeraldinsight.com
Verlet L (1967) Computer “Experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys Rev 159(1):98–103. doi:10.1103/PhysRev.159.98
Vu-Quoc L, Zhang X, Walton OR (2000) A 3-D discrete-element method for dry granular flows of ellipsoidal particles. Comput Methods Appl Mech Eng 187(99):483–528. doi:10.1016/S0045-7825(99)00337-0
Walton, OR, Braun RL (1993) Simulation of rotary-drum and repose tests for frictional spheres and rigid sphere clusters. http://www.grainflow.com/index_files/Rotary_Drum_Simulation_DOE-NSF-1993.pdf
Williams JR, Pentland AP (1992) Superquadrics and modal dynamics for discrete elements in interactive design. Eng Comput 9(2):115–127. doi:10.1108/eb023852, http://www.emeraldinsight.com
Xu WX, Chen HS, Lv Z (2011) An overlapping detection algorithm for random sequential packing of elliptical particles. Phys A 390(13):2452–2467. doi:10.1016/j.physa.2011.02.048
Zheng QJ, Zhou ZY, Yu AB (2013) Contact forces between viscoelastic ellipsoidal particles. Powder Technol 248:25–33. doi:10.1016/j.powtec.2013.03.020
Zhu H, Zhou Z, Yang R, Yu AB (2007) Discrete particle simulation of particulate systems: theoretical developments. Chem Eng Sci 62(13):3378–3396. doi:10.1016/j.ces.2006.12.089, http://linkinghub.elsevier.com/retrieve/pii/S000925090700262X
Zhu H, Zhou Z, Yang R, Yu AB (2008) Discrete particle simulation of particulate systems: a review of major applications and findings. Chem Eng Sci 63(23):5728–5770. doi:10.1016/j.ces.2008.08.006, http://linkinghub.elsevier.com/retrieve/pii/S0009250908004168
Acknowledgments
Open access funding provided by University of Innsbruck and Medical University of Innsbruck. This work has been carried out as a part of the T-MAPPP project, an EU-funded Framework 7 Marie Curie Initial Training Network. The financial support provided by the European Commission is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Podlozhnyuk, A., Pirker, S. & Kloss, C. Efficient implementation of superquadric particles in Discrete Element Method within an open-source framework. Comp. Part. Mech. 4, 101–118 (2017). https://doi.org/10.1007/s40571-016-0131-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40571-016-0131-6