1 Introduction

Forces in granular materials are transmitted through inter-particle contacts. Physical experiments and numerical studies have revealed that the contact force network is highly heterogeneous [1–3]. Under non-isotropic stress conditions, the contact force network exhibits strong geometrical and mechanical anisotropy [4–6]. The heterogeneity of the contact force network underlies the complexity of the mechanical behavior of granular assemblies. Therefore, characterization of the contact force network is of crucial importance to understand the behavior of granular media. Radjai et al. [4] proposed that the contacts carrying above-average normal forces and the contacts bearing below-average normal forces have distinct roles in force transmission and work dissipation. Contacts bearing above-average normal forces form a ‘strong’ force network which transmits the majority of the applied loads. The remaining contacts form a ‘weak’ contact force network which stabilizes the ‘strong’ force network and accounts for most of the frictional energy dissipation in the system. These two sub-networks, which collectively comprise the entire contact force network, have different statistical distribution features [2]. This approach to partitioning the contact force network based on average normal force has been adopted in a number of subsequent research studies [5, 7–10]. Despite its widespread adoption, there is evidence to suggest that partitioning the contact force network in this manner may not be justified. Peters et al. [11] showed that only approximately half of the ‘strong’ contacts belong to the force transmission chains, and Huang et al. [12] found that the contribution of the ‘strong’ contacts to frictional dissipation is considerable when inter-particle friction is high. These findings indicate that the use of the above-average criterion to partition contact force networks requires further examination.

This study uses three-dimensional discrete element modeling [13] to study the force transmission mechanism within a granular medium. The contact force characteristics are investigated following the approach of Radjai et al. [4] considering the contribution to deviatoric stress and structural anisotropy. The applicability of the above-average criterion, which was initially proposed based on the results of 2D granular simulations, to more realistic 3D scenarios is explored.

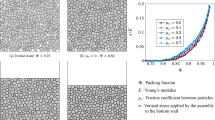
2 DEM simulations

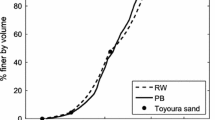
Most of the simulations were run using a modified version of the LAMMPS code [14]. These three-dimensional simulations contained 20,164 idealized spherical particles. As Fig. 1a shows, the particle size distribution (PSD) of Toyoura sand was approximated with the particle diameters lying between 0.115 mm and 0.408 mm [12]. Thus the size span \((d_{\max }-d_{\min })/(d_{\max }+d_{\min })\) is around 0.56, where \(d_{\max }\) and \(d_{\min }\) are the largest and smallest particle diameters, respectively. This is indicative of a moderate polydisperse system [3]. The samples were enclosed within a cuboidal periodic cell (Fig. 1b) and were initially isotropically compressed until the target stress state and solid fraction had been reached. They were then subjected to triaxial shearing. A simplified Hertz-Mindlin (SHM) contact model was used with a shear modulus of 29 GPa and a Poisson’s ratio of 0.12: parameters which approximate the properties of quartz sand [15]. Some periodic-cell simulations were performed using a linear elastic contact model with equal normal and tangential contact stiffnesses of \(10^{5}\hbox { N}/\hbox {m}\). An additional set of simulations used the same PSD and the SHM contact model, but 16,024 spheres enclosed within cylindrical rigid-wall boundaries and these simulations were run using PFC3D [16]. Gravitational body forces were neglected in all simulations. Loading was achieved by moving the upper boundary while the position of the lower boundary was fixed. A constant shear rate, \(v/L_{0}\), of \(1\hbox { s}^{-1}\) was used for all simulations where v is the velocity of moving boundary and \(L_{0}\) is the corresponding initial sample vertical dimension. The inertia number was below \(10^{-4}\) throughout all the simulations, indicative of quasi-static flow [17, 18]. Three loading scenarios were applied:

Fig. 1
figure 1

Simulation setup: a particle size distribution (PB shows the particle size distribution for periodic-boundary samples; RW represents the particle size distribution for rigid-wall samples; Toyoura sand grading is obtained from sieve analysis); b loading configuration

Full size image

  • type-a The sample was sheared while the lateral stresses were maintained constant;

  • type-b The sample was sheared with a constant-volume constraint imposed;

  • type-c The sample was sheared while the positions of lateral boundaries were adjusted accordingly to keep a constant mean stress \(p=(\sigma _{1}+\sigma _{2}+\sigma _{3})/3\) where \(\sigma _{1},\,\sigma _{2}\), and \(\sigma _{3}\) are the major, intermediate, and minor principal stresses, respectively.

In all the three loading regimes, the lateral stresses were kept approximately identical, i.e., \(\sigma _{2}=\sigma _{3}\). Therefore, the deviatoric stress can be simplified as \(q=\sigma _{1}-\sigma _{3}\) and the mean stress p equals to \(1/3(\sigma _{1 }+2\sigma _{3})\). Five different inter-particle friction coefficients (\(\mu \)) were used for the type-a loading scenario to investigate the influence of \(\mu \) on the stress transmission characteristics, while only \(\mu =0.25\) was applied to the type-b and type-c simulations. In all cases shearing continued to a sufficiently high strain level that critical state conditions were attained, i.e., the combination of stress level and packing density beyond which shearing continues at a constant deviator stress, constant mean stress, and constant packing density [19, 20].

Fig. 2
figure 2

Effect of \(\mu \) on the evolution of q (a) and solid fraction (b) during simulations using periodic boundaries and the type-a loading protocol

Full size image

3 Results and discussion

The stress and deformation responses of a representative subset of the simulations subject to the type-a loading condition using periodic boundaries and the SHM contact model are illustrated in Fig. 2. All these simulations considered the same initial isotropic conditions prior to shearing (initial solid fraction, s, of 0.652 and an initial isotropic mean stress, \(p_{0}\), of 100 kPa) and the confining pressure was maintained at 100 kPa during shearing. Referring to Fig. 2a, for all samples the deviatoric stress q initially increases rapidly to a peak value and subsequently decreases to become almost constant when the axial strain \(\varepsilon _{a}\) exceeds 20 %. The deviatoric stress initially increases with increasing \(\mu \) but becomes insensitive to \(\mu \) when \(\mu \) exceeds 0.5 due to the interplay between rotational behavior and sliding behavior at the contacts [12]. Figure 2b shows that all samples dilate from their initially high density and attain nearly constant solid fractions that decrease with increasing \(\mu \). The constant deviatoric stress and solid fraction at large \(\varepsilon _{a}\) levels represent the typical critical state (steady-state) response which is the ultimate state that a soil can approach [19, 20].

Fig. 3
figure 3

Accumulated q as a function of \(f_{n}/\langle f_{n} \rangle \) at 30 % axial strain (type-a loading , \(s=0.652,\,p_{0}=100\hbox { kPa}\))

Full size image
Fig. 4
figure 4

Projection of normal contact force on the \(\hbox {X}(\sigma _{3})-\hbox {Z}(\sigma _{1})\) plane at the critical state \((\varepsilon _{a}=30\,\%)\)

Full size image

The average stress within a granular assembly can be calculated directly from the contact forces [21]

$$\begin{aligned} \sigma _{ij} =\frac{1}{V}\sum \limits _1^{N_\mathrm{c}} f_i l_j \end{aligned}$$
(1)

in which V is the volume of the domain considered, \(f_{i}\) is the \(i\hbox {th}\) component of the contact force vector f, \(l_{j}\) is the \(j\hbox {th}\) component of the branch vector l that joins the centers of two touching particles and \(N_{c}\) is the number of contacts. The particle velocities and particle inertias are sufficiently small that the dynamic component of the stress tensor (as described in Claudin [22]) can be neglected. Following the approach of Radjai et al. [4], Fig. 3 presents the cumulative contribution of contact forces to the overall deviatoric stress as a function of \(f_{n}/\langle f_{n} \rangle \) for the type-a simulations considered in Fig. 2 at \(\varepsilon _{a}=30\,\%\) (at this axial strain level the critical state has been attained in all the simulations); \(\langle f_{n} \rangle \) is the mean normal contact force over the entire assembly and the corresponding q value for each \(f_{n}/\langle f_{n} \rangle \) considers the contribution of the subset of contacts with \(f_{n}/\langle f_{n} \rangle \) below the current value. To create Fig. 3, the contacts are firstly sorted in an ascending order according to the magnitude of \(f_{n}/\langle f_{n} \rangle \) (i.e., the \(\xi \) parameter in Radjai et al. [4]). The contribution of each contact to q is then calculated based on Eq. 1. Each data point in Fig. 3 represents the cumulative sum of the contributions to q considering contacts with \(f_{n}/\langle f_{n} \rangle \) below the current value. There is a range of \(f_{n}/\langle f_{n} \rangle \) values where the cumulative curves give \(q<0\). When the stress tensor is calculated considering only contacts with force values lying in this range, the resultant principal stress orientation will differ from the overall principal stress orientation by more than \(45^{\circ }\). An enlarged view of the range \(0< f_{n}/\langle f_{n} \rangle < 1\) is superimposed on the figure to enable a closer examination of the transition from negative to positive contributions to q. Contacts that make a positive contribution to q are on average considered part of the force transmission network following Radjai et al. [4]. The data show that at the strain level considered the characteristic normal contact force \(f^{*}\) which separates the positive and negative contributions to q is smaller than unity for all the \(\mu \) values considered.

Fig. 5
figure 5

Influence of \(\mu \) on the evolution of \(f^{*}\) considering the contribution to q (type-a loading, \(s=0.652\) and \(p_{0}=100\hbox { kPa}\))

Full size image
Fig. 6
figure 6

Evolution of \(f^{*}\) considering the contribution to q with axial strain: a for a representative simulation using the type-b loading protocol; b for a representative simulation using the type-c loading protocol; c for a representative simulation using the type-a loading protocol and the linear elastic contact model; d for a representative simulation using rigid-wall boundaries and the type-a loading protocol

Full size image

Figure 4 presents the projection of the normal contact force onto the \(\hbox {X}(\sigma _{3})-\hbox {Z}(\sigma _{1})\) plane at \(\varepsilon _{a} =30\,\%\). For clarity, only contacts within the middle part of the samples (10 % of the entire sample) are considered. The contacts are represented by lines connecting the centers of the particles in contact, and the thickness of each line is proportional to the magnitude of \(f_{n}/\langle f_{n} \rangle \). The overall contact force network is divided into two subsets according to the magnitude of \(f_{n}/\langle f_{n} \rangle \) with respect to \(f^{*}\), i.e., \(f_{n}/\langle f_{n} \rangle \ge f^{*}\) (on the left in black) and \(f_{n}/\langle f_{n} \rangle < f^{*}\) (on the right in gray). For the \(\mu \) values considered, the configurations of contact force networks are quite similar. The contacts within the \(f_{n}/\langle f_{n} \rangle \ge f^{*}\) subset are oriented along the major principal stress direction, while the orientations of the contacts belonging to the \(f_{n}/\langle f_{n} \rangle < f^{*}\) have a random orientation.This reflects the distinct roles of the two subsets: the \(f_{n}/\langle f_{n} \rangle \ge f^{*}\) subset acts as force-bearing backbones carrying the majority of deviatoric loading, while the \(f_{n}/\langle f_{n} \rangle < f^{*}\) subset is the supporting network which provides lateral support to the force-bearing network.

Figure 5 shows the evolution of \(f^{*}\) for q during shearing for the simulations presented in Fig. 2. For all the \(\mu \) values considered, \(f^{*}\) for q is relatively high at the isotropic state and varies during subsequent shearing, tending to nearly a constant value at the critical state \((\varepsilon _{a} \ge 30\,\%)\). Moreover, at all strain levels \(f^{*}\) increases with decreasing \(\mu \). The structural anisotropy also increases as \(\mu \) increases [12]. The non-uniqueness of \(f^{*}\) for q is also evident for the type-b (Fig. 6a) and the type-c (Fig. 6b) loading scenarios, for the type-a loading using the linear elastic model (Fig. 6c) and for the type-a loading using the rigid-wall boundaries (Fig. 6d). Figures 3, 4, 5, and 6 indicate that many of the contacts with \(0< f_{n}/\langle f_{n} \rangle <1\) which have been hitherto considered ‘weak’ are not only contributing to the secondary supporting force network but also to the deviatoric load and so their classification as “weak” may not be appropriate.

Fig. 7
figure 7

Accumulated \({\varPhi }_{d}\) as a function of \(f_{n}/\langle f_{n} \rangle \) at the critical state (type-a loading, \(s=0.652,\,p_{0}=100\hbox { kPa}\))

Full size image

The contact anisotropy is usually quantified using the fabric tensor [23]:

$$\begin{aligned} {\varPhi }_{ij} =\frac{1}{N_\mathrm{c}}\sum \limits _{k=1}^{N_\mathrm{c}} n_i^k n_j^k \end{aligned}$$
(2)

where \(n_i^k\) denotes the unit contact normal. The degree of contact anisotropy is evaluated using deviatoric fabric defined here as \({\varPhi }_d =\sqrt{\frac{1}{2}[\left( {{\varPhi }_1 -{\varPhi }_2 } \right) ^{2}+\left( {{\varPhi }_1 -{\varPhi }_3 } \right) ^{2}+\left( {{\varPhi }_2 -{\varPhi }_3 } \right) ^{2}]}\), where \({\varPhi }_{1}\), \({\varPhi }_{2}\), and \({\varPhi }_{3}\) are the major, intermediate, and minor principal fabrics, respectively, and these are the eigenvalues for the fabric tensor. It was found that \({\varPhi }_{2}\) and \({\varPhi }_{3}\) are effectively identical in the simulations as a \(\sigma _{2} =\sigma _{3}\) condition was imposed. Therefore, the deviatoric fabric can be simplified as \({\varPhi }_{d}= {\varPhi }_{1}-{\varPhi }_{3}\). Figure 7 shows \({\varPhi }_{d}\) as a function of \(f_{n}/\langle f_{n} \rangle \) at the critical state for each \(\mu \) value considered. To create Fig. 7, the contacts are firstly sorted in an ascending order according to the magnitude of \(f_{n}/\langle f_{n} \rangle \), as was required for Fig. 3. The contribution of each contact to \({\varPhi }_d\) is then calculated based on Eq. 2. Each data point in Fig. 7 represents the cumulative sum of the contribution to \({\varPhi }_d\) considering the contacts with \(f_{n}/\langle f_{n} \rangle \) below the current value. Analogous to the stress calculations described above, there is a range of \(f_{n}/\langle f_{n} \rangle \) values that give \({\varPhi }_d <0\) on the cumulative curves, and the fabric tensor calculated considering only contacts with force values lying in this range gives a principal fabric orientation that differs from the overall principal fabric orientation by more than \(45^{\circ }\). It can be seen from Fig. 7 that \({\varPhi }_{d}\) increases as \(\mu \) increases. This is because with increasing \(\mu \), the inherent stability of the force-bearing skeleton increases, the lateral supporting contacts orthogonal to the strong force chains are not activated, and hence the anisotropy increases.

Fig. 8
figure 8

Influence of \(\mu \) on the evolution of \(f^{*}\) considering the contribution to \({\varPhi }_{d}\) (type-a loading, \(s=0.652\) and \(p_{0}=100\hbox { kPa}\))

Full size image
Fig. 9
figure 9

Variation of \(f^{*}\) at the critical state with \(\mu \) for representative simulations using the type-a loading protocol

Full size image

The inset in Fig. 7 shows that for all \(\mu \) values considered, the \(f^{*}\) value which marks the transition from a negative contribution to a positive contribution to \({\varPhi }_{d}\) generally decreases with increasing \(\mu \) value. Figure 8 presents the variation of \(f^{*}\) considering the contribution to \({\varPhi }_{d}\) with axial strain \((\varepsilon _{a})\) during shearing for a representative set of the type-a simulations. It is clear that just as \(f^{*}\) for q varied, \(f^{*}\) for \({\varPhi }_{d}\) is also not a constant; it depends on \(\mu \) and the strain level. Similar to \(f^{*}\) for q, \(f^{*}\) for \({\varPhi }_{d}\) also remains approximately constant when the axial strain \(\varepsilon _{a}\) exceeds 30 % and critical state shearing conditions are attained. Figure 9 illustrates the variation of \(f^{*}\) at the critical state with \(\mu \) considering both contributions to q and \({\varPhi }_{d}\). \(f^{*}\) values defined for q differ from those defined for \({\varPhi }_{d}\); the former are smaller at small \(\mu \) values (\(<\) 0.75) but the two become almost identical at \(\mu \) values \(\ge \)0.75. Similar observations can also be made for other types of loading conditions for which data are not shown herein for conciseness. This is because apart from geometrical anisotropy \({\varPhi }_{d}\), q is also a function of mechanical anisotropies [4, 24]. Both \(f^{*}\) for q and \(f^{*}\) for \({\varPhi }_{d}\) decrease with increasing \(\mu \).

Fig. 10
figure 10

Correlations between the characteristic force \(f^{*}\) with mean stress p at the critical state: a critical state \(f^{*}\) for \({\varPhi }_{d}\) with p; b variation of power-law regression parameters with \(\mu \); c critical state \(f^{*}\) for q with p

Full size image

As shown in Figures 5, 6, and 8, just as is the case for the stress and volumetric responses at large strain levels, both \(f^{*}\) for q and \(f^{*}\) for \({\varPhi }_{d}\) become almost constant at the critical state. Figure 10a shows the relationship between the critical state \(f^{*}\) for \({\varPhi }_{d}\) and the mean stress p at the critical state. Due to the presence of oscillations, the critical state data presented in Fig. 10a are taken as the mean values of the corresponding quantities for the last 10 % of axial strain. \(f^{*}\) for \({\varPhi }_{d}\) at the critical state increases as p increases but decreases with increasing \(\mu \), in line with Figs. 7 and 8. This is the opposite of the correlations between \({\varPhi }_{d}\) at the critical state and \(p^{'}\) and between \({\varPhi }_{d}\) and \(\mu \) noted in [12]. The relationships between \(f^{*}\) for \({\varPhi }_{d}\) for different \(\mu \) values can be represented by a series of power-law functions, i.e., in a form of \(f^{*}=\eta p^{\xi }.\) The fitting parameters \(\eta \) and \(\xi \) for each \(\mu \) case are given in Table 1. \(\eta \) decreases with increasing \(\mu \) while the opposite trend is evident for \(\xi \). Figure 10b presents the variation of \(\eta \) and \(\xi \) with \(\mu \). Both of them follow a power-law relationship with \(\mu \). \(\eta \) decreases with increasing \(\mu \) and thus the fitting function has a negative power, while \(\xi \) increases with increasing \(\mu \) and the fitting function has a positive power. Figure 10c plots \(f^{*}\) for q at the critical state against p. In comparison to \(f^{*}\) for \({\varPhi }_{d}\), the relationship between the critical state \(f^{*}\) for q and p is more complicated; for all the \(\mu \) values considered, it initially decreases with increasing p, reaches a local minimum and then continues to increase as p is further increased.

Table 1 Regression parameters for the relationship between \(f^{*}\) for \({\varPhi }_{d}\) and p at the critical state
Full size table

4 Conclusions

This study presents a systematic investigation on the force transmission characteristics within granular media. The influences of multiple factors were considered including inter-particle friction coefficient, loading regime, packing density, contact model, and boundary conditions. The evidence presented in this study clearly suggests that some of the weak contacts carrying below-average normal contact forces also participate in stress transmission and contribute to structural anisotropy. It is shown that both the characteristic normal contact force which marks the transition from a negative to a positive contribution to the overall deviatoric stress and that marking the transition from a negative to a positive contribution to structural anisotropy vary until the critical state is reached and remain approximately constant thereafter. The characteristic normal contact force for the deviatoric stress and that for the structural anisotropy are not unique and differ from each other. Thus, using the average normal contact force \(\langle f_{n} \rangle \) as the transition point to separate a load-bearing network which is anisotropic and aligned along the external loading direction from a supporting network which is isotropic and orthogonal to the load-bearing network within a granular packing is not robust for three-dimensional systems.