Stable algorithm for event detection in event-driven particle dynamics

Abstract

Event-driven particle dynamics is a fast and precise method to simulate particulate systems of all scales. In this work it is demonstrated that, despite the high accuracy of the method, the finite machine precision leads to simulations entering invalid states where the dynamics are undefined. A general event-detection algorithm is proposed which handles these situations in a stable and efficient manner. This requires a definition of the dynamics of invalid states and leads to improved algorithms for event-detection in hard-sphere systems.

1 Introduction

Event-diven particle-dynamics (EDPD) is the oldest particle simulation technique [1] and has found application in a wide range of fields, from predicting vapor-liquid equilibria [7] to the design of granular vibration dampers [3]. Although typically used to simulate simple particle models such as the hard sphere, the EDPD technique remains a general approach to particle simulations as potentials can be discretized to accurately approximate more conventional model systems, such as Lennard-Jonesium [6], or directly fit to physical data [37]. Introducing the coefficient of restitution, EDPD algorithms can also be used to simulate systems of dissipatively interacting particles, such as granular flows.

Hard-sphere EDPD algorithms in particular are often much more efficient (sometimes by orders of magnitude) than “soft” models which must solve Newton’s equation of motion using time-stepping numerical integration techniques [16]. Disregarding machine precision, EDPD algorithms solve the dynamics of discontinuous-potential models (such as hard spheres) analytically and do not suffer from errors due to the finite time step always used in numerical quadrature [16].

Despite these advantages, there remain numerical difficulties in the implementation of the EDPD algorithm due to the finite precision of floating point calculations originating from the machine precision. Small numerical errors in the detection and processing of events can cause the simulation to enter states where the dynamics is undefined. Interestingly, this ambiguity in the dynamics of invalid states has also led to some difficulties in theoretical treatments in the past [11]. These difficulties are not discussed in the earliest EDPD implementations [1] as they are relatively rare and frequently resolve themselves; however, for large systems and/or large simulation times, one must provide rules to handle such situations. In addition, there are systems, such as dissipative (granular) gases, which are prone to clustering [22] such that even for small numbers of particles these finite-precision errors deteriorate until the simulation must be halted. Modified algorithms have been proposed to combat these difficulties but current solutions are complex and fail in certain cases [29, 32] or modify the system dynamics in an undesired way [8, 19].

In this work the difficulties of event-detection in EDPD simulations are outlined and a general algorithm for stable event-detection is proposed. In Sect. 2, the basic event-driven algorithm is outlined for the hard-sphere model. The origin of invalid states is then introduced in Sect. 3, before an improved version of the event-detection algorithm is presented in Sect. 4. Finally, in Sect. 5, a more complex example of a bouncing ball is used to illustrate that the dynamics of invalid states must be defined, and demonstrates the extension of the stable algorithm for hard spheres to fixed boundaries.

2 Basic event-driven algorithm for identical hard spheres

Considering only conservative pairwise interactions of pairs of particles $i$ and $j$, located at $\mathbf {r}_i$ and $\mathbf {r}_j$ respectively, summing up the total force, $\mathbf {F}_i$, acting on a particle $i$ yields

$$\begin{aligned} \mathbf {F}_i=\sum _{j\ne i}^N \mathbf {F}_{ij} = -\sum _{j\ne i}^N \nabla \phi (\mathbf {r}_{ij})\,; \quad \mathbf {r}_{ij}\equiv \mathbf {r}_{i}-\mathbf {r}_{j} \end{aligned}$$

(1)

where the sum is over all $N$ particles in the system, excluding self interactions and $\phi$ is the interaction energy. In traditional time-stepping simulations, the total force on each particle is inserted into Newton’s equation of motion and numerically integrated to determine all particle positions and velocities at later times.

In contrast, discrete potentials preclude the use of numerical quadrature to solve Newton’s equation of motion. For example, the fundamental property of hard-sphere particles is that they cannot deform one another, that is, their interaction energy reads

$$\begin{aligned} \phi ^\text {HS}\left( \mathbf {r}_{ij}\right) = {\left\{ \begin{array}{ll} \infty &{} \text {if~} \left| \mathbf {r}_{ij}\right| < \sigma \\ 0 &{} \text {if~} \left| \mathbf {r}_{ij}\right| \ge \sigma \end{array}\right. } \end{aligned}$$

(2)

where $\sigma$ is their collision diameter. Consequently, the particles move on ballistic trajectories except when two particles reach the distance $\sigma$. The divergence of $\phi ^\text {HS}(\sigma )$ implies that at this point, there is an infinite repelling force which in turn implies that the duration of the interaction approaches zero, that is, at this point the velocities alter instantaneously. Performing a momentum and energy balance over two colliding hard spheres [29] yields the collision rule for the evolution of the particle velocity, $\mathbf {v}_i$:

$$\begin{aligned}&\!\!\! \mathbf {v}_i^{\,\prime } = \mathbf {v}_i-\frac{2m_j}{m_i+m_j} \left( \hat{\mathbf {r}}_{ij}\cdot \mathbf {v}_{ij}\right) \hat{\mathbf {r}}_{ij}\,;\quad \nonumber \\&\!\!\! \mathbf {v}_{ij} \equiv \mathbf {v}_i-\mathbf {v}_j\,;\quad \hat{\mathbf {r}}_{ij}\equiv \frac{\mathbf {r}_{ij}}{\left| \mathbf {r}_{ij}\right| } \end{aligned}$$

(3)

where the primes denote post-collision values.

From here follows the main idea of EDPD: instead of numerically integrating Newton’s equation of motion, EDPD maps the dynamics of the many-particle system to a sequence of instantaneous pairwise interactions. The handling of these two-particle interactions relies on pre-computed collision operators, e.g. Eq. (3). Thus, the EDPD algorithm for hard spheres can be outlined as follows:

• 1. The simulation is started with certain initial conditions for the positions and velocities of the particles. Obviously, due to Eq. (2), any legal initial state requires that the particles must not overlap one another.

• 2. Each possible pairing of particles is tested to determine if and when a collision is encountered, and the results are used to construct a list of all possible future events. This list is then sorted to determine the earliest event, which is the only event in the list which is guaranteed to occur. If a particle has multiple events occuring at the same instant, an ambigutity in the event order is introduced; however, it is often implicitly assumed that the execution order in these cases is unimportant and these effects are not discussed here.

• 3. The particle positions are propagated along ballistic trajectories until the time of the earliest event.

• 4. The velocities of the two colliding particles are updated according to the collision rule, Eq. (3).

• 5. Any events in the future event list which involve either of the colliding particles are updated and the list is re-sorted to determine the next event to be processed.

• 6. Check for conditions to terminate the simulation, e.g. the total real time or number of events processed.

• 7. Continue with step 3.

In contrast to ordinary time-stepping MD algorithms, EDPD progresses irregularly in time. It jumps from one event to the next and, thus, is event-driven. The basic algorithm outlined above contains the basic ingredients of an EDPD algorithm, albeit it would be unstable due to precision errors and of time complexity $\mathcal{O}\left( N^2\right)$ per event processed. Indeed, there is a range of methods used to accelerate these calculations [18, 31], including the use of neighbor lists [1], the delayed states algorithm [17], calendar priority queues [28], and other optimizations [20, 34, 35] which reduce the calculation costs to constant time ($\mathcal{O}\left( 1\right)$) per event. Although the cost of simulating each event is now independent of system size it should be noted that, for equilibrium systems, the number of events to be processed per unit of simulation time still scales as $O(N)$. Nevertheless, common to all algorithms is that the primary cost of simulation arises from the detection of events.

While the algorithmic challenge of EDPD is the bookkeeping of the list of future events, the numerical challenge is the computation of the times of the events and it is the latter which is the subject of this paper. We will show that naïve algorithms will result in invalid states and eventually failure of the algorithm due to unavoidable numerical errors resulting from the finite machine precision.

These problems will be explored using the prototypical discrete potential, the hard sphere. We wish to point out that EDPD of hard spheres is not restricted to conservative interactions: Dissipative collisions may be characterized by the coefficient of normal restitution defined as the ratio of the post-collisional relative normal velocity of the particles and the corresponding pre-collisional value,

$$\begin{aligned} \varepsilon \equiv -\frac{\mathbf {v}_{ij}^{\,\prime } \cdot \mathbf {r}_{ij}}{\mathbf {v}_{ij}\cdot \mathbf {r}_{ij}}\,. \end{aligned}$$

(4)

In general, $\varepsilon$ is a function of the impact velocity and material properties. It may be analytically obtained by solving Newton’s equation of motion for an isolated pair of colliding particles with the assumption of a certain interaction force, e.g. [25, 33]. Alternatively, $\varepsilon$ may be obtained experimentally, e.g. [24]. The corresponding collision rule is obtained from the conservation of momentum and angular momentum and from the loss of kinetic energy quantified by the coefficient of restitution:

$$\begin{aligned} \mathbf {v}_i^{\,\prime } = \mathbf {v}_i-\frac{m_j}{m_i+m_j}(1 + \varepsilon ) \left( \hat{\mathbf {r}}_{ij}\cdot \mathbf {v}_{ij}\right) \hat{\mathbf {r}}_{ij}\,. \end{aligned}$$

(5)

From the point of view of physics, the main difference between integrating Newton’s equations of motion using a time-stepping algorithm for a standard model, such as the Hertz potential, and a EDPD simulation using hard spheres is the duration of collisions. This difference has some subtle consequences leading to limitations of the applicability of the hard-sphere models [26] which may be partially overcome [27].

3 Event calculation errors

During the population and updates of the future event list, pairs of particles must be tested to determine if and when they collide. For identical hard spheres, the equations of motion must be solved to find if the particle pair approaches to a distance equal to the interaction diameter, $\sigma$. Assuming that the particles are under identical acceleration by an external field such as gravity, this detection of events becomes a search for the time intervals $\varDelta t$ which satisfy

$$\begin{aligned} \left| \mathbf {r}_{ij}(t+\varDelta t)\right| = \left| \mathbf {r}_{ij}(t)+\varDelta t\,\mathbf {v}_{ij}(t)\right| = \sigma \,. \end{aligned}$$

(6)

Squaring of this expression simplifies it to a quadratic equation in $\varDelta t$

$$\begin{aligned} \varDelta t^2\,\mathbf {v}_{ij}^{\,2} + 2\,\varDelta t\,\mathbf {v}_{ij}\cdot \mathbf {r}_{ij} + \mathbf {r}_{ij}^{\,2} - \sigma ^2 = 0\,, \end{aligned}$$

(7)

where all variables are evaluated at the current time $t$. If this quadratic equation does not have a real root, the particles do not come into contact, otherwise there are two roots and the earliest time root corresponds to the collision. Figure 1 sketches the three classes of trajectories corresponding to zero, two, and one (degenerated) solution of Eq. (7).

Fig. 1

The three classes of trajectories for a pair of hard-sphere particles. a Colliding, b passing, and c glancing. The dotted line represents the trajectory of particle $i$ relative to the center of particle $j$. The dashed line indicates the border of the invalid state/infinite energy region, shaded in gray. Roots of Eq. (7), corresponding to inter-particle separations of $\sigma$, are marked with circles. A filled circle indicates the impacting root of the overlap function $f$ to be introduced in Eq. (8), and also marks the start of a section of the trajectory which satisfies the stable algorithms conditions for an interaction (solid line). Roots of the time derivative of the overlap function (Eq. (9)) are marked with triangles

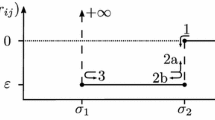
When computing the roots of Eq. (7), small numerical errors accumulate during the calculation due to the finite precision of floating point mathematics. Careful implementations can minimize these errors through algorithmic improvements or through arbitrary precision floating-point libraries [14] but complete elimination would require exact real arithmetic [23] which is relatively computationally expensive. These errors alter the prediction of the positions of the colliding particles at the time of impact, which causes the particles to either numerically overlap or stand a small distance apart at the time of impact (see Fig. 2).

Fig. 2

An exaggerated illustration of the effects of finite precision on the execution of events. Ideally, the particles are in contact at the time of the collision; however, due to the limited precision the particles are either separated by a small gap or end up in a slightly overlapped state

The overlapping case is problematic as the particles have numerically entered the infinite energy hard-core. To illustrate the magnitude of these errors, simulations of $N=13\,500$ hard spheres under periodic boundary conditions were performed and histograms of the measured impact distances, collected over $10^9$ collisions, are given in Fig. 3. The mean and mode separation on impact correspond to the interaction diameter, $\sigma$, but it is clear that particle separations on impact can fall on either side of this value. The overlapping states are relatively minor and typically resolve themselves in elastic systems as the particle pair is receding after the impact; however, Fig. 3 clearly demonstrates that the infinite energy core of the potential is numerically accessible and the magnitude of these errors are significantly increased in inelastic systems. The overlapped states may degenerate if one of the overlapping particles interacts before the overlap is cleared, effectively causing a three-body impact which is in direct conflict with the physical model of instantaneous collisions for hard spheres.

Fig. 3

Histograms of the impact separations for a simulation of $N=13,500$ hard spheres under periodic boundary conditions, collected over $10^9$ collisions. Each bar represents a single floating point number, marked at the top, and the range of continuous values that it represents due to the finite precision. Data for different elasticities, $\varepsilon$, and densities $\rho =N/V$, where $V$ is the primary image volume are presented as seperate histograms. There is a precision change at zero due to a change in the floating-point exponent when crossing $\left| \mathbf {r}_{ij}\right| =\sigma$

While errors resulting in $\left| \mathbf {r}_{ij}\right| \gtrsim \sigma$ are uncritical for the stability of the algorithm, the opposite case, $\left| \mathbf {r}_{ij}\right| \lesssim \sigma$ is fatal since the computation of the next event corresponds to a collision where $\mathbf {v}_{ij}\cdot \hat{\mathbf {r}}_{ij} > 0$. Execution of this collision approximates entangled circular rings and this entanglement will persist forever, unless it is resolved due to another numerical error in a future collision. As shown in Fig. 3, this situation is not a rare event but concerns approximately half of all collisions, therefore, any useful EDPD algorithm must provide measures to cope with this situation. There are two different approaches: a) avoid situations where $\left| \mathbf {r}_{ij}\right| < \sigma$, and b) admit such situations but provide methods to recover from them. One method exploiting solution a) to prevent overlaps from forming due to numerical errors is to retrospectively search along the pre-collision trajectory of colliding particle pairs for a collision state which is not overlapping [2]. Unfortunately, this iterative approach is expensive and will limit the computational speed of EDPD. A more efficient scheme to prevent overlaps by biasing the movement of particles by (temporarily) modifying the particle diameter so that detected interactions occur at a small distance from the invalid state is proposed by Pöschel and Schwager [29]. Unortunately, this approach does not exactly simulate the desired system but a slightly different system following a slightly different dynamics. It may also be shown that there are cases where these approaches fail to prevent overlaps forming [29].

Specific discussions on how to handle event detection for overlapping particle pairs corresponding to solution b) are common [2, 3, 9, 13, 15, 21, 32]; however, these approaches often either implicitly disable interactions between overlapped pairs, admit significant overlaps to form before attempting to correct them, or rewind simulation time in an uncontrolled manner, all of which fail to resolve three-body contacts/events. A one-dimensional illustration of a sequence of impacts which leads to a three-body contact is given in Fig. 4. Initially, two particles impact and overlap due to numerical errors in the event calculation. This situation typically resolves quickly as the particles are receding from each other, but in rare cases a third particle may impact the overlapping pair of particles before the overlap is resolved. This leads to a three-body contact where there are overlapping particles which are approaching each other. Figure 5 presents measurements on the frequency of these events in hard-sphere systems with different densities and elasticities. In dilute elastic systems ($\varepsilon =1$), these three-body events are extremely rare (${\approx }10^{-9}$ three-body events per event processed) which may explain why they are not discussed in the literature as published simulations are rarely this long. In inelastic systems, clustering effects [22] and partial collapse events increase the frequency of three-body events by three orders of magnitude, making it likely that several will occur during a single simulation run. If these three-body interactions cause overlapped particle pairs to approach, simple algorithmic implementations for hard-sphere event detection [1, 16] will return negative values of $\varDelta t$ for overlapped pairs. Execution of these events will cause the simulation to perform an unchecked rewind, leading to other particle pairs to overlap, particularly at high densities. It is clear that, even for simple discrete potentials like hard spheres, a stable simulation algorithm must account for these numerical errors and their consequences, particularly for inelastic systems and long simulation times.

Fig. 4

An illustration of two impacts leading to three overlapping particles. This situation is difficult to resolve using simple collision detection algorithms. All overlaps in this sketch are strongly exaggerated for improved visibility

Fig. 5

The frequency of three-body collisions resulting in a doubly overlapped particle in hard-sphere simulations as a function of the coefficient of restitution, $\varepsilon$, and reduced density

4 Stable EDPD for hard-sphere systems

4.1 General approach

A general approach for devising stable event-detection algorithms requires the introduction of an overlap function and the concept of stabilizing interactions. Overlap functions are common in studies on event-driven asymmetric-potential systems [2], where they have also been called the overlap potential [10] or the indicator function [38]. For a simple hard-sphere system with zero relative acceleration, a suitable overlap function, $f_\text {HS}$, is defined via Eq. (7):

$$\begin{aligned} f_\text {HS}(t + \varDelta t) = \varDelta t^2\,\mathbf {v}_{ij}^{\,2} + 2\,\varDelta t\,\mathbf {v}_{ij}\cdot \mathbf {r}_{ij} + \mathbf {r}_{ij}^{\,2} - \sigma ^2 \end{aligned}$$

(8)

where again all variables are evaluated at the current time $t$. The overlap function is a function of time which characterizes the relative position of particles moving along certain trajectories with respect to overlap. Typically it is proportional to the distance or squared distance between the closest points on the surfaces of the two tested objects. The overlap function is negative for particle pairs in an invalid state, and positive or zero in all valid states. In this sense, it is a penalty function for invalid states. By definition, the overlap function transforms the search for event times into a search for the roots of the overlap function, $f(t)$. In addition, the sign of the overlap function can be used as a test if the particle pair is in an invalid state. Crucially, these properties allow the derivative of the overlap function to be used as a test if an invalid state ($f(t)< 0$) is either improving or stable in time ($\dot{f}(t)\ge 0$) or not ($\dot{f}(t)<0$). For the hard-sphere case, the derivative is given by the following expression

$$\begin{aligned} \dot{f}_\text {HS}(t + \varDelta t) = 2\,\varDelta t\,\mathbf {v}_{ij}^{\,2} + 2\,\mathbf {v}_{ij}\cdot \mathbf {r}_{ij}\,. \end{aligned}$$

(9)

A stabilizing interaction is a collision that is performed by the algorithm immediately after a preceding collision to ensure that overlapping particles do not approach one another. It is generated in response to a negative and decreasing overlap function and prevents the overlap function decaying any further.

Using the overlap function and the concept of stabilizing interactions, a stable algorithm for hard-sphere systems can be defined as an algorithm which ensures the overlap function does not decrease for any particle pair in contact or in an overlapping state:

When testing for collisions between a pair of hard spheres at a time, $t$, consider the overlap function, $f_\text {HS}$. A collision occurs after the smallest non-negative time interval, $\varDelta t$, that satisfies the following condition:

$$\begin{aligned} \left( f_\text {HS}\left( t+\varDelta t\right) \le 0\right) \text {and } \left( \dot{f}_\text {HS}\left( t+\varDelta t\right) <0\right) \end{aligned}$$

(10)

For glancing interactions (see Fig. 1c), corresponding to degenerate roots of Eq. (8), no sign change in $\dot{f}_\text {HS}$ occurs. The definition of the stable algorithm will allow the particles to come into contact but, without a sign change in the derivative, no event will be scheduled and no impulse will be applied. This is acceptable for models without friction/rotation but it is a point of ambiguity in the implementation of models with tangential forces. Here we recommend that glancing interactions are also excluded from generating impulses in systems with friction as there are no forces in the normal direction of the contact.

4.2 Algorithmic implementation for hard-sphere systems

An implementation of a stable event detection algorithm for hard-sphere collisions, in accordance with the definition in the previous section, is presented in Algorithm 1. Unsurprisingly, this algorithm is similar to previously published algorithms [1, 16, 29] for detecting hard-sphere collisions; however, it differs by the addition of the second if-statement on Line 1. Only the earliest root of the overlap function generates interactions, as only the earliest root of the overlap function has a decreasing overlap function (marked with a filled circle in Fig. 1a). The calculation of this root suffers from catastrophic cancellation [30] and so the alternate form of the quadratic equation must be used, as suggested by Pöschel and Schwager [29]. Algorithm 1 shows no predefined precision threshold; hence it could be used directly with arbitrary [14] or exact [23] precision libraries to reduce the number of stabilizing collisions at the expense of more complicated dynamic data structures and significantly longer computation times.

Figure 6 sketches how this stable algorithm would resolve the interactions between the particles for the example system introduced in Sect. 3. The critical step is the stabilizing collision occurring between the lower two particles immediately after the execution of the first event at time $t_2$. It is this event which ensures the system moves towards a valid state, as shown in the last segment of Fig. 6. At no point are the overlaps, introduced by numerical error, allowed to increase in time during the free motion of the system. Thus, the stable algorithm proposed here handles three-body events by ensuring the overlap function never deteriorates.

Fig. 6

An illustration of two impacts leading to three overlapping particles. This situation is difficult to resolve; however, if a third “stabilizing” collision is executed between the two initially-overlapping particles, all particles will begin to move apart and the overlaps will clear after a short time. Note that although the directions of the velocities of the lower two particles are not changed by the stabilizing collision, the direction of the relative velocity is

Although the stable algorithm defines the dynamics for three-body interactions, it should not be used as a physical model for these effects. It only provides a stable definition of the dynamics for rare cases where multiple events occur at the same time (due to numerical errors). In systems where three-body collisions or persistent contacts are common, an appropriate model must be used. This model may also be event-driven (e.g., stepped potentials [36]) but this again requires the general approach outlined here to ensure that the simulation is stable with respect to numerical errors.

There are some cases where the execution of collisions will not cause the overlap function to increase. Fortunately, this behavior is often required to recover the correct dynamics, as illustrated in the following section.

5 Advanced example: bouncing ball

A simple system to extend and test the applicability of the stable algorithm introduced for hard spheres is the one-dimensional system of an inelastic hard sphere falling under the influence of gravity onto a hard plate, as described in Fig. 7. The exact solution to this system is that the sphere comes to rest after an infinite number of impacts in a finite time [12], known as an inelastic collapse [22].

Fig. 7

An illustration of the position $r$ of a ball of diameter $\sigma =1$ as it falls from a height $r(t=0)=r_{\mathrm {plate}}+1$ onto a plate located at $r_{\mathrm {plate}}$, coming to rest after a time $t_{\mathrm {final}}$

Attempting to numerically simulate the inelastic collapse highlights the dramatic effect that small precision errors can have. In the example explored here, the sphere is initialized with zero velocity, $v=0$, and positioned above the plate. The time until the next impact, $\varDelta t$, is calculated from the largest positive root of the following overlap function:

$$\begin{aligned} f_{\mathrm {ball}\rightarrow \mathrm {plate}}(t+\varDelta t)&= r+\varDelta t\,v+\frac{\varDelta t^2}{2}\,g - \hbox {r}_{\mathrm {plate}} - \frac{\sigma }{2} \end{aligned}$$

(11)

where $r$ and $v$ are the position and velocity of the particle of diameter $\sigma$ at time $t, r_{plate}$ is the position of the hard plate, and $g$ is the gravitational acceleration. Approaching this naively, the event time is given by the quadratic formula

$$\begin{aligned} \varDelta t&= -\frac{v+\sqrt{v^2 - 2\, g\,[r - r_{\mathrm {plate}} - \sigma /2]}}{g}\,. \end{aligned}$$

(12)

Although the current position of the sphere relative to the plane is different for the calculation of the first and all later impact times, there is no qualitative difference between these two cases. For the calculation of the first impact time the sphere is at a height of $r_{\mathrm {plate}}+1$, while for all later impacts the current height above the plate is $\sigma /2 + \delta$, where $\delta$ is a small deviation due to numerical precision. Once the next impact or “event” time is determined, the sphere is moved forward to the time of the impact, its velocity is inelastically reflected, $v'=-\varepsilon \,v$. This process is then repeated until a sufficient number of impacts has occurred or an error is encountered. To explore the algorithm’s stability, the origin of the plate, $r_{\mathrm {plate}}$, is uniformly sampled using $10^6$ points from the range $[0,1]$. All other parameters of this test are presented in Fig. 7 and a coefficient of restitution of $\varepsilon =0.5$ is used.

The simple coordinate transformation of varying $r_{\mathrm {plate}}$ should yield identical results; however, the finite precision of the floating point math causes some difficulties: for $\approx$50 % of the sampled values of $r_{\mathrm {plate}}$, the simulation must be halted after only ${\approx }30$ events on average as the argument of the square root in Eq. (12) becomes negative. This result arises due to the sphere overlapping the wall after a collision by a small amount ${\approx }10^{-16}\,\sigma$, exactly as in the hard-sphere system. The argument of the square root then turns negative once the velocity decays to the point where the peak of the trajectory no longer escapes the small overlap with the wall. A naive implementation may assume that if there are no real roots to Eq. (11) the ball misses the plate; however, this is clearly impossible in this system. This system demonstrates that for inelastic systems with external forces, it is easy to enter regions of undefined dynamics.

One possible treatment of this case is to halt the simulation immediately; however, this will leave the system with a non-zero velocity, a finite number of events in the trajectory, and an overlap. Applying the stable algorithm defined in Sect. 4.1 to the overlap function in Eq. (11) provides a more satisfactory resolution where the motion of the particle is continued until it reaches its peak, where the velocity reduces to zero. The algorithm also causes an infinite number of future events to take place at zero time to prevent the overlap from increasing again, which approximates the exact solution of inelastic collapse to the precision of the calculations. To complete the description of the stable algorithm in this case, an optimized stable event-detection rule for a ball falling onto a plane in three-dimensions is given in Algorithm 2.

6 Conclusions

A general and stable approach to event-detection in hard-sphere systems has been proposed and sample implementations given in Algorithms 1 and 2. It defines the dynamics of overlapping particles to minimize their effect on the trajectory of the system. The algorithm relies on treating interactions as stabilizing events for overlapping particle pairs which are not improving with time.

Although this work has focussed on the hard-sphere system, the general concept can be extended to the full range of particle systems studied using event-driven techniques. The extension to other assymmetric hard-core potentials is straightforward provided an overlap function, $f$, with the characteristics outlined in Sect. 4.1 and algorithms to determine its derivative and roots are available. These are available in certain cases [38] but are non-trivial and must be implemented numerically for some systems such as ellipsoidal particles [10].

Algorithm 2 demonstrates that the stable algorithm can be applied to boundary interactions. An extension of the algorithm to sphere-triangle interactions would allow the simulation of complex geometries in biological processes [5] and the rapid design and import of boundaries from CAD programs for the study of granular/solids processing systems [29]. The primary difficulty in this extension is the definition of a suitable overlap function for collision detection of composite objects.

To apply the technique to molecular systems, an extension to softer stepped [36] or terraced potentials is required. Such potentials, including the fundamental square-well potential, require additional care in the definition of the overlap function as the invalid states of the model depend on the interaction history of the particle pairs. The generalization to stepped potentials, composite objects, and complex shapes will be explored in future publications.

Reference implementations of all algorithms presented in this paper are available in the open-source DynamO [4] simulation package.