Abstract
To improve the controllability and utilization of distributed energy resources (DERs), distribution-level electricity markets based on consumers’ bids and offers have been proposed. However, the transaction costs will dramatically increase with the rapid development of DERs. Therefore, in this paper, we develop an energy sharing scheme that allows users to share DERs with neighbors, and design a novel incentive mechanism for benefit allocation without users’ bidding on electricity prices. In the energy sharing scheme, an aggregator organizes a number of electricity users, and trades with the connected power grid. The aggregator is aimed at minimizing the total costs by matching the surplus energy from DERs and electrical loads. A novel index, termed as sharing contribution rate (SCR), is presented to evaluate different users’ contributions to the energy sharing. Then, based on users’ SCRs, an efficient benefit allocation mechanism is implemented to determine the aggregator’s payments to users that incentivize their participation in energy sharing. To avoid users’ bidding, we propose a decentralized framework for the energy sharing and incentive mechanism. Case studies based on real-world datasets demonstrate that the aggregator and users can benefit from the energy sharing scheme, and the incentive mechanism allocates the benefits according to users’ contributions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Distributed energy resources (DERs) have been dramatically developing across the world in the past decades. However, the increasing penetration of DERs has imposed great challenges to the reliable and economic operation of power grids [1]. On the one hand, more traditional generation resources should be scheduled to smooth out the fluctuations of DERs. On the other hand, due to the limited controllability, the power grid cannot fully accommodate DERs, which greatly reduces the utilization of DERs. In China, for example, distributed solar capacity reached 6.06 GW in 2015, but the utilization rate was less than 60% [2].
To improve the controllability for DERs, a number of studies and pilot projects propose to establish a distribution-level electricity market. Reference [3] encourages the entries of DERs and microgrids by establishing a distribution system market, in which DERs submit bids/offers for energy and reserve capacity. A pilot project has been initiated by the US Department of Energy that allows end-use customers to bid on the electricity price. However, with the rapid development of DERs in distribution grids, it is challenging to collect the bids from ubiquitous DERs and clear the market in a centralized manner, which may result in considerable market transaction costs. Additionally, distinguished from the generators in a wholesale market, end-use customers pursue a convenient way to schedule their own DERs, and may thus be reluctant to frequently bid supply curves. A simple settlement mechanism is needed such that users just share the surplus of DERs and then get paid. To this end, the concept of energy sharing has been advocated as a promising solution to achieve peer-to-peer energy trading among the users in a community [4]. With the central theme of “access over ownership”, energy sharing enables electricity users to share the surplus energy from the rooftop solar and batteries with their neighbors, and then get paid for the shared energy.
As an emerging business model, sharing economy has gained substantial popularity among transportation and housing sectors. Firms like Uber and Airbnb give individuals economic incentives to provide ridesharing and rent out their houses, which realizes the optimization of resources through sharing excessive goods and services [5]. In recent years, a few studies have focused on the market implementation for sharing energy storage and rooftop photovoltaic (PV). In [6], a number of firms invest in storage and share the stored energy with each other to arbitrage against time-of-use prices. A Nash equilibrium is formed and the optimal strategies are explicitly expressed. In [7], renewable energy is shared among homes to balance local energy supply and demand. In [8], an optimal sharing algorithm is proposed to minimize the electricity charges of a collection of homes. The losses of shared energy are approximately considered. In [9], a hybrid energy trading market is designed, comprised of an external utility company and a local trading center. The local trading center allows users to exchange power. In [10], an optimal peer-to-peer scheme is proposed to minimize the total energy costs of users, incorporating the losses of distribution networks. In [11], a decentralized algorithm is presented to coordinate smart homes with renewable energy and energy storage systems (ESSs). These references focus on the optimal scheduling for DERs in the energy sharing framework. However, how to design an incentive mechanism to guarantee the effectiveness of energy sharing remains a critical task to be addressed.
Some of existing literature proposes market mechanisms to incentivize energy sharing. In [12], an incentive mechanism using Nash bargaining (NB) theory is designed for benefits allocation among microgrids. In [13], an incentive mechanism is proposed to encourage microgrids to provide ramping capacity. In [14], an incentive mechanism is presented to motivate DER owners to generate reactive power for local voltage control. Among these studies, the symmetric Nash bargaining theory is widely adopted to equally allocate the benefits among market participants. However, as electricity users make different contributions to energy sharing, a well-designed incentive mechanism should identify the values that different users create, and accordingly allocate the benefits. Therefore, in this paper, we strive to further address the following two issues: ① How to develop an energy sharing scheme without the need of users’ bidding on electricity prices? ② How to evaluate different users’ contributions to energy sharing and design an incentive mechanism for benefit allocation without users’ bids?
To fill the aforementioned gaps, an energy sharing scheme is developed, and a novel incentive mechanism is designed for benefit allocation without users’ bidding on electricity prices. In a distribution grid, an aggregator organizes a number of electricity users to cooperate as a single interest entity. Then the incentive mechanism is implemented to allocate the benefits to users that incentivizes users’ participation in energy sharing. The contributions of this paper are threefold:
- 1)
An energy sharing scheme is proposed and the benefits brought on by sharing DERs are evaluated. A novel index, termed as sharing contribution rate (SCR), is presented to measure each user’s contribution to energy sharing.
- 2)
An incentive mechanism is designed to determine the aggregator’s payments to users. Based on users’ SCRs, a closed-form expression of the aggregator’s optimal payments is obtained by solving an asymmetric Nash bargaining (ANB) model. The proposed mechanism is proved to satisfy individual rationality and other properties.
- 3)
To avoid users’ bidding, a decentralized framework is developed to coordinate the aggregator and users using alternating direction method of multipliers (ADMM).
2 Energy sharing scheme
In this paper, we consider that one aggregator organizes N energy users in a distribution grid in a day-ahead market. Each user has a PV system, an ESS and local load. The energy trading without and with energy sharing are compared.
2.1 Energy trading without energy sharing
In this case, energy users are assumed to be price-takers, who purchase electricity from the aggregator at a retail rate, and sell back the surplus power of DERs at a net metering rate (NMR). The following trading events happen in order.
- 1)
Each user schedules his/her local DERs and determines the net load to minimize individual costs under fixed rates.
- 2)
The aggregator collects the net load information of user, and trades with the connected power grid for energy balance.
- 3)
The aggregator charges each user for the net load at a retail rate, and pays each user for the net power at an NMR.
In practice, as the retail rate is generally higher than the NMR, the users cannot get sufficient and reasonable payments to justify the investments of DERs. For example, the NMR is about 3 cents/kWh in Pacific Gas and Electric Company (PG&E) in California in 2017. However, the retail rate during peak hours can reach 0.263 $/kWh [15].
2.2 Energy trading with energy sharing
As electricity is an undifferentiated good, a pool-based energy sharing platform [4] is considered, in which each energy user schedules the amount of shared energy and the aggregator determines the associated payment for each user. The following events happen in order.
- 1)
All users enroll sharing contracts with the aggregator, which sets up a rule that determines the sharing incentives to users for an amount of shared energy.
- 2)
Each energy user schedules his/her DERs and deviates from individual optimum to share DERs.
- 3)
The aggregator collects the net load and shared energy information of users, and trades with the connected power grid for energy balance.
- 4)
The aggregator charges each user for the net load at a retail rate, and pays each user for the net power at an NMR, and for the shared energy with the sharing incentives.
Instead of only trading with the aggregator, the users can share DERs with each other in the platform. The proposed energy sharing scheme enables the aggregator to organize users to cooperate as a single interest entity, and minimize the total costs. In contrast to the case without energy sharing, the proposed scheme achieves Pareto optimality of the aggregator and all users.
2.3 Decentralized implementation
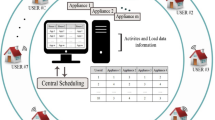
The proposed energy sharing scheme aims at maximizing the total benefits of the aggregator and users, which requires detailed information about users’ preferences and DERs. However, it is challenging to collect the private information of users and schedule energy sharing in a centralized manner. Thus, a decentralized framework is developed to preserve users’ privacy. The schematic is shown in Fig. 1.
Each user is equipped with an energy management controller (EMC), which controls the hourly load consumption and communicates this load information to the aggregator. The EMC also receives the price signals from the aggregator. Therefore, the bidirectional communication makes the interactions easy between the aggregator and users. Based on the price signal, the EMC of each user optimally schedules local load and DERs. Then the EMCs communicate the net power to the aggregator. After collecting the net power of all users, the aggregator updates the price signal and sends it back to the EMCs of users. The proposed energy sharing scheme can be applied in day-ahead and intra-day markets. In Section 5, the decentralized models and solution algorithm will be elaborated.
3 System model
Pursuing clarity and simplicity, the modeling assumptions are as follows: ① We consider one aggregator organizes N energy users in the distribution grid; ② The locational marginal prices (LMPs) in the connected power system are predefined and constant; ③ The distribution grid network and energy losses are not considered in this paper.
3.1 Net cost of aggregator
To depict the uncertainties in load and solar power, scenario-based stochastic programming is adopted. Thus the net cost of the aggregator \(O^{A}\) is calculated below:
where \(\gamma_{s}\) is the probability of scenario s; \(\lambda_{t,s}^{in}\) and \(\lambda_{t,s}^{out}\) are the prices for purchasing and selling electricity with the power grid, which are different in practice due to transmission service charges [16], tax [17], etc; \(\lambda_{t}^{S}\) and \(\lambda_{t}^{R}\) are the retail rate and net metering rate; \(P_{t,s}^{NL}\) and \(P_{t,s}^{NS}\) are the aggregated net load and surplus power of users; and \(P_{i,t,s}^{NL}\) and \(P_{i,t,s}^{NS}\) are the aggregated net load and surplus power of user i.
In (1), the first term represents the aggregator’s cost for purchasing electricity from the power grid, and the second term represents the revenue by selling electricity back. The third and fourth terms are the costs and revenues of the aggregator trading with users. Two ratios \(\omega^{in/out}\) are used to reflect the difference between \(\lambda_{t,s}^{in/out}\) and locational marginal prices (LMPs) \(\lambda_{t,s}^{LMP}\):
In (2) and (3), \(\left( \cdot \right)_{ + } = { \hbox{max} }\left\{ {0,\cdot} \right\}\). Equations (2) and (3) calculates the net load and power surplus of user. In practice, the net loads of distribution grids and the LMPs are influenced by each other. Analyzing the mutual influence needs solving the market equilibrium between the distribution grid and the connected power system, deserving an in-depth study in the future. To focus on energy sharing in a distribution grid, we do not consider the impacts of the net loads on LMPs, and model the LMPs as predefined constants.
3.2 A user model without energy sharing
In this paper, each user is modeled as an agent solving the following stochastic program:
s.t.
where \(U_{i} \left( \cdot \right)\) is the utility function of user i. Without loss of generality, we use a quadratic concave utility function [18]. \(c_{i}^{ESS}\) is the ESS operation cost of user i, which is caused by the degradation of the ESS’s charging and discharging [19, 20]. In practice, the cost of an ESS mainly comes from the capital cost, while the operation cost is measured as the replacement cost of the storage bank over the lifetime throughput [21], which is relatively a small fraction. The decision variables are denoted by \(\varvec{X}_{i}\), including user i’s net load \(P_{i,t,s}^{NL}\), surplus power \(P_{i,t,s}^{NS}\), hourly load \(P_{i,t,s}^{L}\), solar power \(P_{i,t,s}^{PV}\), the charging and discharging power \(P_{i,t,s,\alpha }^{ESS}\) and \(P_{i,t,s,\beta }^{ESS}\), and the stored energy in the ESS \(E_{i,t,s}^{ESS}\).
In (5), let \(O_{i}^{U}\) denote the objective function of user i, which is to minimize the difference between the total costs and his/her utility. In (6), the net power equals the difference between the load and the power of the PV and ESS. Note that the minimization of the objective function guarantees that at least one of \(P_{i,t,s}^{NL}\) and \(P_{i,t,s}^{NS}\) is 0. When the user’s net load is positive, \(P_{i,t,s}^{NL} > 0\) and \(P_{i,t,s}^{NS} = 0\). When the user’s net load is negative, \(P_{i,t,s}^{NL} = 0\) and \(P_{i,t,s}^{NS} > 0\). In (7), the feasible region \(\chi_{i}\) includes the constraints for user i’s PV, ESS and load, as described in Appendix A. In model (5)-(7), user i can only trade with the aggregator, without sharing DERs with others. Let \(O_{i}^{U,0}\) and \(O^{A,0}\) be user i’s objective value and the aggregator’s net cost without energy sharing, known as the disagreement point [12, 13].
3.3 Energy sharing model
In the proposed energy sharing scheme, the aggregator organizes all users to cooperate as a single interest entity, and the shared power from users can be optimized. Energy sharing requires users to deviate from individual optimal schedule to accommodate the surplus or demand from their neighbors. Thus, the aggregator should incentivize the users to share DERs by allocating the sharing benefits. The payment from the aggregator to user i is \(\pi_{i}^{ES}\). The net cost of user i is \(O_{i}^{U} - \pi_{i}^{ES}\), and the net cost of aggregator is\(O^{A} { + }\sum\limits_{i} {\pi_{i}^{ES} }\). The energy sharing model is to minimize the total costs of the aggregator and all users:
where \(P_{i,t,s}^{ES}\) is the variable for shared power, restricted by the capacity of a building’s fuse \(P_{{i,{ \hbox{max} }}}^{C}\). In contrast to (6), the decision variables for shared power are added to (9). Equation (10) is the constraint for balancing the shared power. Note that the loss of energy sharing and the distribution network are not considered in this paper [12]. The Lagrangian multiplier of constraint (10) is denoted by \(\lambda_{t,s}^{ES}\), interpreted as the clearing price for shared power. Let \(O_{i}^{U,1}\) and \(O^{A,1}\) be the objective value of user i and the net cost of aggregator by solving the energy sharing model.
Although the energy sharing model defines the amount of users’ shared power, it cannot reveal the payments to users that will incentivize the deviation from individual optimum. Thus, an incentive mechanism is proposed for benefit allocation according to users’ contributions.
4 Incentive mechanism
As energy sharing requires users to deviate from individual optimal schedule, thus increasing individual costs, an incentive mechanism is needed for benefit allocation so as to incentivize users to participate in energy sharing. In this paper, an incentive mechanism is required to satisfy the following properties [22]:
- 1)
Pareto optimality: there doesn’t exist another solution, in which the cost of every participant is no greater than that in the proposed energy sharing scheme, and the cost of some participants is strictly less than that in the proposed scheme.
- 2)
Individual rationality: the aggregator and all users should reduce their costs by energy sharing compared with their costs without energy sharing.
- 3)
No exploitation: the users without sharing DERs should not be given any benefits.
- 4)
Monotonicity: if a user makes more contributions to energy sharing, this user should gain more benefits.
- 5)
Budget balance: the total benefits are allocated among the aggregator and all users.
We firstly propose a novel index, termed as SCR, to evaluate users’ contributions to energy sharing. Then an ANB model considering SCRs is developed for benefit allocation.
4.1 Sharing contribution rate
In this paper, a user’s contribution to energy sharing is defined as the economic value of the shared DERs, \(C_{i,t,s}^{U}\):
where \(\left| {P_{i,t,s}^{ES*} } \right|\) is the amount of a user’s shared power; \(\lambda_{t,s}^{ES}\) is the clearing price for shared power; \(C_{i,t,s}^{U}\) can be interpreted as the economic value for sharing DERs, which is a straightforward choice to measure users’ contributions to energy sharing. Alternative definitions of users’ contributions deserve in-depth study in the future. Therefore, user i’s SCR, denoted by \(SCR_{i}\), is defined as his/her contributions over the total contributions of all energy users:
where \(\tau^{A} \in \left( {0,1} \right)\) is the rate of return of an aggregator, which is predefined and constant in this paper. In regulated environment, the permitted rate of return of an aggregator is regulated by the government. In deregulated markets, the selection of \(\tau^{A}\) involves the pricing strategy of an aggregator: a higher \(\tau^{A}\) can improve the rate of return of an aggregator, but lead to the loss of users. A lower \(\tau^{A}\) may attract more users, but the rate of return decreases. Note that for the users without participating in energy sharing, their shared power is always 0. According to (13), their SCRs equal 0.
4.2 Benefit allocation mechanism
The Nash bargaining problem studies how market participants share a surplus that they jointly generate by maximizing the product of market participants’ excess utilities [23]. In a few existing studies, symmetric Nash bargaining (SNB) models are adopted for cost allocation, in which market participants are assigned with identical contribution rates regardless of their distinct behaviors [12, 13]. However, users can make different contributions to the energy sharing. For example, a user shares 1 kWh electricity while another user shares 10 kWh electricity. These two users should be allocated with distinct benefits.
An asymmetric Nash bargaining model based on users’ SCRs is proposed for benefit allocation:
where the decision variables are \(\left\{ {\pi_{i}^{ES} ,P_{i,t,s}^{ES} ,\varvec{X}_{i} ,\forall i,t,s} \right\}\); \(\varPhi^{ES}\) represents the set of the users whose SCRs are positive. Constraints (15) and (16) are the individual rationality for the aggregator and users. By solving the ANB model, the aggregator’s payments to users can be obtained.
Theorem 1
The proposed incentive mechanism satisfies ① Pareto optimality, ② individual rationality ③ no exploitation, ④ monotonicity, and ⑤ budget balance. The solution to the ANB model defines the payments to users:
where \(\pi_{i}^{ES*}\) is the optimal payment to user i; and the total benefit \(\varDelta\) induced by energy sharing is:
Proof
See Appendix A.
According to Theorem1, the optimal payment to a user can be interpreted as two parts. The first is \(O_{i}^{U,1} - O_{i}^{U,0}\), representing the incremental cost after sharing DERs. The second is \(SCR_{i} \cdot \varDelta\),indicating a user’s share of the total benefits that all market participants jointly generate. The net benefits of the aggregator and users are derived below:
The benefit of each market participant is related to his/her SCR, reflecting the contributions he/she creates. Therefore, all participants can benefit from the energy sharing.
5 Decentralized implementation
The proposed energy sharing scheme and incentive mechanism requires detailed information about users’ utility levels and DER parameters. However, it is challenging for the aggregator to collect the private information of all users. Therefore, a decentralized framework is proposed in Fig. 1. In this section, the energy sharing and Nash bargaining models are decentralized, thereby avoiding users’ bidding.
5.1 Decentralized energy sharing
The energy sharing model is decentralized and solved by using ADMM [24]. The following auxiliary constraints are introduced to the energy sharing model:
where \(\hat{P}_{i,t,s}^{x}\) is an auxiliary variable, interpreted as the power recommended by the aggregator; NL, NS and ES represent net load, net surplus power and energy sharing. By relaxing these constraints, the energy sharing model can be decomposed into the local program of aggregator and the individual program of each user, shown as follows:
- 1)
Aggregator’s local program:
$$\hbox{min} \;\;O^{A} + \sum\limits_{i,t,s,x} {\gamma_{s} w_{i,t,s}^{x} \hat{P}_{i,t,s}^{x} } + \frac{\rho }{2}\sum\limits_{i,t,s,x} {\gamma_{s} \left( {\hat{P}_{i,t,s}^{x} - P_{i,t,s}^{x} } \right)^{2} }$$(22)s.t.
$$\sum\limits_{i} {\hat{P}_{i,t,s}^{ES} } = 0:\;\lambda_{t,s}^{ES} \quad \forall t,s$$(23)where the decision variables are \(\left\{ {\hat{P}_{i,t,s}^{x} ,,\forall i,t,s,x} \right\}\); \(w_{i,t,s}^{x}\) is the Lagrangian multiplier of (21); \(\rho\) is the step for updating the Lagrangian multiplier \(w_{i,t,s}^{x}\), i.e.,
$$w_{i,t,s}^{x} \left[ {k + 1} \right] = w_{i,t,s}^{x} \left[ k \right] + \rho \left( {\hat{P}_{i,t,s}^{x} - P_{i,t,s}^{x} } \right)$$(24)where \(w_{i,t,s}^{x} \left[ k \right]\) represents the Lagrangian multiplier in the kth iteration. In this paper, we set the step \(\rho = 1/\left( {k + 1} \right)\).
- 2)
User i’s individual program:
$$\hbox{min} \;\;O_{i}^{U} - \sum\limits_{t,s,x} {\gamma_{s} w_{i,t,s}^{x} P_{i,t,s}^{x} } + \frac{\rho }{2}\sum\limits_{t,s,x} {\gamma_{s} \left( {\hat{P}_{i,t,s}^{x} - P_{i,t,s}^{x} } \right)^{2} }$$(25)subject to (9) and (11), where the decision variables are \(\left\{ {{\mathbf{X}}_{i} ,P_{i,t,s}^{ES} ,,\forall t,s} \right\}\). Then the energy sharing model can be solved in a decentralized manner by iteratively coordinating the aggregator and users.
5.2 Decentralized settlement
After solving the energy sharing model, the optimal scheduling for DERs is obtained as well as the total benefits. Then the proposed ANB model is decentralized for benefit allocation to avoid users bidding. We firstly take the logarithm of the objective function of the ANB model:
Then the following auxiliary constraints are introduced:
where \(\hat{\pi }_{i}^{ES}\) is the auxiliary variable, interpreted as the aggregator’s recommended payment to user i. By relaxing these constraints, the local program of aggregator and the individual programs of users are shown as follows.
- 1)
Local program of aggregator:
$$\begin{aligned} & \hbox{min} \;\; - \tau^{A} \ln \left( {O^{A,0} - O^{A,1} - \sum\nolimits_{i} {\hat{\pi }_{i}^{ES} } } \right) \\ & \quad + \sum\limits_{i} {SCR_{i} \cdot w_{i}^{\pi } \hat{\pi }_{i}^{ES} } + \frac{\rho }{2}\sum\limits_{i} {\left( {\hat{\pi }_{i}^{ES} - \pi_{i}^{ES} } \right)^{2} } \\ \end{aligned}$$(28)where the decision variables are \(\left\{ {\hat{\pi }_{i}^{ES} ,\forall i} \right\}\); and \(w_{i}^{\pi }\) is the Lagrangian multiplier of (27).
- 2)
Individual program of user i:
$$\hbox{min} \;\; - \ln \left( {O_{i}^{U,0} - O_{i}^{U,1} + \pi_{i}^{ES} } \right) - w_{i}^{\pi } \pi_{i}^{ES} + \frac{\rho }{2}\left( {\hat{\pi }_{i}^{ES} - \pi_{i}^{ES} } \right)^{2}$$(29)where the decision variables is \(\pi_{i}^{ES}\).
The optimal solution to the models (28) and (29) can be directly obtained by solving the Karush-Kuhn-Tucker (KKT) conditions without the need of optimization. Due to the convexity of the energy sharing and ANB models, the convergence of ADMM can be guaranteed.
By decentralizing the energy sharing and Nash bargaining models, the scheduling for DERs and the associated settlement can be achieved without users bidding.
6 Case studies
Case studies are performed using MATLAB R2015b and CPLEX 12.4 [25] on a computer with 2.40 GHz CPU and 8 GB RAM. A distribution grid with 10 and 50 energy users is tested. Here, the users refer to large consumers in a distribution grid, e.g., industrial parks or commercial buildings.
The quadratic and linear coefficients of users’ utility functions are randomly generated from uniform distributions, i.e., \(a_{i} \in U\left[ { - 0.5, - 0.1} \right], b_{i} \in U\left[ {20,50} \right]\). The yearly load and solar power data of different users are collected from [26]. In the 10-user case, the load and solar data are described in Fig. 2.
The minimal and maximal loads of users are set to 0.8 and 1.2 times of the actual loads. Users’ daily minimum loads are set to his/her actual daily load demand. The ESS parameters of users are as follows: \(P_{i,t,s,\alpha /\beta }^{ESS}\) = 5 MW; \(\eta_{i}^{ESS}\) = 95%; \(E_{{i,{ \hbox{min} }}}^{ESS}\) = 5 MWh; \(E_{{i,{ \hbox{max} }}}^{ESS}\) = 30 MWh; \(c_{i}^{ESS}\) = 3.7 $/MWh [16]. The initial stored energy is randomly generated from U [5] MWh. The ESS operation cost is estimated as the replacement cost of storage bank over the lifetime throughput. According to the data from [27] and [28], the replacement cost per year is about 13400 $/MW, and the yearly charging/discharging hours are 1800 h. Therefore, the operation cost \(c_{i}^{ESS}\) is expressed as follows:
PG&E summer retail prices are 0.212 $/kWh from 1:00 to 8:00 and from 22:00 to 24:00, 0.239 $/kWh from 8:00 to 12:00 and from 18:00 to 22:00, and 0.263 $/kWh from 12:00 to 18:00. The net metering rate is 0.03 $/kWh [15]. The yearly LMP data at a bus in the PJM market are collected from [29]. The two ratios in (4) are \(\omega^{in} = 2.0\) and \(\omega^{out} = 1.5\). To verify the effectiveness of the proposed approach, three methods are compared, as shown in Table 1.
NS is the traditional energy trading scheme without sharing. ANB is the proposed sharing scheme settled by the ANB model considering SCRs. SNB is the proposed sharing scheme settled by the traditional symmetric Nash barging model, in which all energy users have identical weights without identifying different users’ contributions, i.e., \(SCR_{i} = \left( {1 - \tau^{A} } \right)/N\), where N is the number of users. In ANB and SNB, \(\tau^{A} = 0.2\). Note that since the proposed energy sharing scheme is adopted in both ANB and SNB, these two methods have identical dispatch results for energy sharing, but differ in the payments to the users.
6.1 Impacts of energy sharing
The average power curves of an energy user without and with energy sharing are compared in Fig. 3.
In the case without energy sharing, the user has no incentives to arbitrage with the ESS against retail rates. The ESS is only used to store the surplus of solar energy, and discharge to satisfy the night-time load. Due to the low NMR, the user will minimize his/her net load instead of selling back the surplus power.
However, in the case with energy sharing, the utilization of the ESS is greatly improved for shifting the day-time load to the night hours. As the net load shows, the user consumes electricity at night but supplies DERs at day time. In addition, by comparing the electrical load curves, one can observe that the load is also shifted from day time to night time after energy sharing. Figure 4 shows the average curves of the LMPs and aggregated loads. In the energy sharing scheme, the aggregator organizes users to respond to the LMPs. Compared with the case without sharing, energy sharing can provide additional 132.35 MWh power for the power grid during peak hours from 6:00 to 20:00, thereby contributing to power balance in the power grid.
Table 2 shows the daily total electrical loads, the energy charged/discharged by ESSs and the accommodated solar energy of 10 users.
As energy sharing provides users with a more profitable manner to consume electricity than the retail rates, some users will consume more electricity to increase the utility levels. Thus the users’ total loads increase by 2.27%. The utilization of ESSs dramatically increases by 173.06%. Due to zero operational costs of PV systems, the solar energy can be fully accommodated in both cases. The costs of the aggregator and users without and with energy sharing, i.e., by NS, ANB and SNB are listed in Table 3.
Note that “A” refers to the aggregator, and a negative cost represents a revenue. Compared with the case without energy sharing, energy sharing requires the users to deviate from individual optimal schedule, thus increasing users’ costs. However, by taking advantage of users’ shared DERs, the aggregator earns great benefits after energy sharing.
To guarantee that users have incentives to participate in energy sharing, the aggregator allocates some of the sharing benefits to users. As one can observe, both ANB and SNB can reduce users’ net costs. By ANB, the aggregator’s net revenues increase by 3.96%, and the users’ net costs decrease by 0.44–0.53 thousand dollars. Thus, the aggregator and users benefit from the energy sharing scheme.
6.2 Impacts of incentive mechanism
In SNB, the symmetric Nash bargaining model is used to allocate the sharing benefits. All users have identical weights, without distinguishing the users’ contributions to sharing. However, the proposed ANB identifies users’ contributions for benefit allocation. The cost savings of users by ANB and SNB are shown in Fig. 5.
As one can observe, the cost savings of all users are 0.49 thousand dollars in SNB. However, the cost savings range from 0.44 to 0.53 thousand dollars in ANB. As aforementioned, a user’s cost savings are related to his/her SCR, defined as the user’s proportion of the economic values of shared DERs. Figure 6 shows the relationship between users’ SCRs and shared DERs. Note that a user’s shared DERs refers to the total amount of the absolute value.
In ANB, users’ SCRs are positively related to the shared DERs, indicating that the more DERs a user shares, the higher level of contributions this user makes. However, all users’ SCRs equal 0.08 regardless of the distinct behaviors in SNB. Therefore, the proposed ANB can reveal the contributions of different users and then allocate the benefits.
6.3 Sensitivity analysis on storage capacity
In this subsection, we investigate the impacts of storage capacity on energy sharing. Based on the parameters of users’ ESSs mentioned above, a rate is introduced to expand or reduce the power capacity, energy capacity and initial stored energy of an ESS. The rate equal to x represents that the parameters of an ESS in the based case is multiplied by x. The total amounts of charged/discharged energy under different rates are shown in Fig. 7. Note that the rate 1.0 represents the base case.
With the increase in storage capacity, the total amounts of energy charged/discharged by ESSs increase in both cases without and with energy sharing. Without energy sharing, the utilization of ESSs only increases from 102.07 to 114.28 MWh when the rate varies from 0.5 to 2.0. However, in the energy sharing scheme, the utilization increases significantly from 200.13 to 376.28 MWh because the aggregator can make full use of users’ storage capacity to support the power grid. The users’ cost savings by ANB and SNB are shown in Fig. 8.
From the results, the increase in storage capacity can improve the benefits of energy sharing, while the marginal benefit decreases. With the rate varying from 0.5 to 2.0, the total benefits greatly increase by 60.05% from 4.43 to 7.09 thousand dollars.
6.4 Sensitivity analysis on aggregator’s rate of return
In this subsection, we conduct sensitivity analysis on the aggregator’s rate of return \(\tau^{A}\). The cost savings of the aggregator and users are shown in given different \(\tau^{A}\) (as shown in Fig. 9).
As one can observe, with the increase in the aggregator’s rate of return, the aggregator can get higher revenues, while the cost savings of the users decrease. The total cost savings of the aggregator and users remain a constant $ 6149.41, indicating that the proposed mechanism achieves Pareto optimality of the market participants in the distribution grid while influencing the profit sharing among them. The SCRs of different users can be directly calculated from the slopes of the cost saving curves, which can be explained in the theoretical analysis shown in (19).
6.5 Sensitivity analysis on net metering rates
In practice, the governments in many countries provide financial subsidies for the surplus energy from DERs to boost the development of demand side resources. In this subsection, we conduct sensitivity analysis on NMRs to analyze the impacts on energy sharing. Note that the NMR in this paper is the price at which the aggregator pays users for the surplus energy. The total amounts of charged/discharged energy under different NMRs are shown in Fig. 10. The NMR is 0.03 $/kWh in our base case.
As can be seen, with the increase in NMRs from 0.03 to 0.23 $/kWh, the utilization of ESSs without energy sharing decreases from 100.71 to 27.03 MWh because the rational users are willing to sell more surplus solar power instead of self-sustaining by storage. However, when the NMR reaches 0.33 $/kWh exceeding the retail rates, the utilization of ESSs significantly increases to 86.55 MWh because ESSs are used for arbitrage. In addition, the changes of NMRs will not influence the scheduling of energy sharing. The utilization of ESSs remain unchanged in the energy sharing scheme, equaling 302.31 MWh. This is because the proposed scheme minimizes the total costs of the aggregator and all users, in which the NMR is an internal transfer payment price. This result also implies that though energy sharing yields great benefits, the government should design an effective subsidy mechanism to encourage the development of DERs.
6.6 50-user case
To validate the effectiveness and robustness of the proposed scheme and mechanism, we collect the data of 50 users from [26]. The daily load and solar energy of 50 users are shown in Fig. 11. Figure 12 compares the storage energy of users without and with energy sharing.
As one can observe, most of the users improve the utilization of ESSs after participating in energy sharing. Over 50% of the users increase the daily storage energy by 27.80 MWh. Therefore, the total storage energy of all users can be dramatically increased from 311.85 to 1612.01 MWh.
The settlement results for 50 users are shown in Fig. 13. Figure 13a shows the cost savings of 50 users after energy sharing; Fig. 13b shows the relationship between users’ SCRs and shared DERs. From the results, all the users can earn profits after energy sharing, indicating that the proposed mechanism fulfills individual rationality. The cost savings lie within 0.23 and 0.30 thousand dollars, and over 50% of the users save 0.28 thousand dollars. In addition, the cost savings and the SCRs of the users are positively related to their shared DERs when settled by the propose mechanism. However, the traditional SNB mechanism ignores different users’ contributions, and equally assigns the users’ contribution rates as 0.016.
7 Conclusion
In this paper, an energy sharing scheme is proposed in which an aggregator organizes electricity users to cooperative as a single interest entity. Then we compare the cases and trading events without and with energy sharing. An incentive mechanism is designed for benefit allocation according to users’ SCRs. To avoid users bidding, a decentralized framework is proposed to schedule DERs in the energy sharing scheme and determine the aggregator’s payments to users. Case studies based on 10 and 50 energy users validate the effectiveness of the energy sharing scheme and incentive mechanism. Compared with the case without energy sharing, the utilization of DERs can be improved, and the total costs of the aggregator and all users can be significantly reduced by energy sharing. Additionally, in contrast to the traditional SNB model, the proposed ANB can identify different users’ contributions and accordingly allocate the benefits that incentivize users’ participation.
Two issues deserve in-depth studies in the future: ① the market equilibrium among distribution grids and the connected power grid in an energy sharing scheme; ② a systematic energy sharing model considering distribution networks and power losses.
References
Hu J, Yang G, Kok K et al (2017) Transactive control: a framework for operating power systems characterized by high penetration of distribution energy resources. J Mod Power Syst Clean Energy 5(3):451–464
Feng T, Yang Y, Yang Y et al (2017) Application status and problem investigation of distributed generation in China: the case of natural gas, solar and wind resources. Sustainability 9(6):1–19
Fu H, Zhang X (2017) Market equilibrium in active distribution system with μVPPs: a coevolutionary approach. IEEE Access 5:8194–8204
Wang JX, Zhong HW, Yu Y et al (2018) Incentive mechanism for cooperative energy sharing. In: Proceedings of 2018 IEEE power and energy society general meeting, Portland, USA, 5–10 August 2018, pp 1–5
Martin CJ (2016) The sharing economy: a pathway to sustainability or a nightmarish form of neoliberal capitalism. Ecol Econ 121:149–159
Kalathil D, Wu C, Poolla K et al (2019) The sharing economy for the electricity storage. IEEE Trans Smart Grid 10(1):556–567
Zhu T, Huang Z, Sharma A et al (2013) Sharing renewable energy in smart microgrids. In: Proceedings of the ACM/IEEE 4th international conference on cyber-physical systems, Philadelphia, USA, 8–11 April 2013, pp 219–228
Huang Z, Zhu T, Gu Y et al (2014) Minimizing electricity costs by sharing energy in sustainable microgrids. In: Proceedings of the 1st ACM international conference on embedded systems for energy-efficient buildings, Memphis, USA, 3–6 November 2014, pp 120–129
Wu Y, Tan X, Qian L et al (2015) Optimal pricing and energy scheduling for hybrid energy trading market in future smart grid. IEEE Trans Ind Inform 11(6):1585–1596
Liu T, Tan X, Sun B et al (2015) Energy management of cooperative microgrids with P2P energy sharing in distribution networks. In: Proceedings of 2015 IEEE international conference on smart grid communications, Miami, USA, 2––5 November 2015, pp 410–415
Celik B, Roche R, Bouquain D et al (2018) Decentralized neighborhood energy management with coordinated smart home energy sharing. IEEE Trans Smart Grid. https://doi.org/10.1109/tsg.2017.2710358
Wang H, Huang J (2018) Incentivizing energy trading for interconnected microgrids. IEEE Trans Smart Grid 9(4):2647–2657
Nguyen HK, Khodaei A, Han Z (2018) Incentive mechanism design for integrated microgrids in peak ramp minimization problem. IEEE Trans Smart Grid. https://doi.org/10.1109/tsg.2017.2696903
Nguyen HK, Mohsenian-Rad H, Khodaei A et al (2017) Decentralized reactive power compensation using nash bargaining solution. IEEE Trans Smart Grid 8(4):1679–1688
The Pacific Gas and Electric Company website (2017) https://www.pge.com/en_US/residential/solar-and-vehicles/. Accessed 8 November 2017
Wang J, Zhong H, Xia Q (2018) Optimal planning strategy for distributed energy resources considering structural transmission cost allocation. IEEE Trans Smart Grid 9(5):5236–5248
The PJM website: Market monitor report (2017) http://www.pjm.com/~/media/committees-groups/committees/mc/20150824-webinar/20150824-item-09-imm-report.ashx. Accessed 11 November 2017
Wang J, Zhong H, Lai X et al (2017) Distributed real-time demand response based on Lagrangian multiplier optimal selection approach. Appl Energy 190:949–959
Yan G, Liu D, Li J et al (2018) A cost accounting method of the Li-ion battery energy storage system for frequency regulation considering the effect of life degradation. Prot Control Mod Power Syst 3(4):1–9
Wang J, Qin J, Zhong H et al (2018) Reliability value of distributed solar+storage systems amidst rare weather events. IEEE Trans Smart Grid. https://doi.org/10.1109/tsg.2018.2861227
Zagoras N (2014) Battery energy storage system: A cost/benefit analysis for a PV power station. https://www.nrel.gov/grid/assets/pdfs/second_grid_sim_zagoras.pdf. Accessed 20 August 2018
Lin W, Bitar E (2014) Forward electricity markets with uncertain supply: cost sharing and efficiency loss. In: Proceedings of 2014 IEEE 53rd annual conference on decision and control, Los Angeles, USA, 15–17 December 2014, pp 1707–1713
Nash JF (1950) The bargaining problem. Econometrica 18(2):155–162
Boyd S, Parikh N, Chu E et al (2011) Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn 3(1):1–122
The IBM ILOG CPLEX website (2011) http://www-01.ibm.com/software/websphere/products/optimization/academic-initiative/index.html/. Accessed 11 November 2017
The Pecan Street website (2017) https://www.dataport.cloud/. Accessed 12 November 2017
The Tesla Powerwall website (2017) https://www.tesla.com/powerwall. Accessed 12 November 2017
World Energy Council (2016) E-storage:Shifting from cost to value wind and solar applications. https://www.worldenergy.org/wp-content/uploads/2016/01/Resources-E-storage-report-2016.01.14_final_version.pdf. Accessed 13 November 2017
PJM Data Directory: Day-ahead hourly LMPs (2017) http://dataminer2.pjm.com/feed/da_hrl_lmps/definition. Accessed 13 November 2017
Acknowledgements
This work was supported by National Natural Science Foundation of China (No. 51777102, No. 51537005), Chinese Association of Science and Technology Young Elite Scientists Sponsorship Program (No. YESS20170206) and the State Grid Corporation of China (No. 5210EF18000G).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 15 January 2019
Appendix A
Appendix A
1.1 Constraints of the energy sharing model
In Section 3, the feasible region \(\chi_{i}\) includes user i’s constraints, shown as follows:
where \(P_{i,t,s}^{APV}\) is the available solar power of user i; \(P_{{i,t,s,{ \hbox{min} }}}^{L} \quad {\hbox{and}}\quad P_{{i,t,s,{ \hbox{max} }}}^{L}\) represent the minimum and maximum hourly load of user i; \(Q_{i,s}^{L}\) is the daily load requirement of user i; \(P_{{i,\alpha /\beta ,{ \hbox{max} }}}^{ESS}\) are the maximal power of charging/discharging; \(\eta_{i}^{ESS}\) is the ESS efficiency of user i; \(E_{{i,{ \hbox{min} }}}^{ESS}\quad{ \hbox{and} }\quad E_{{i,{ \hbox{max} }}}^{ESS}\) are the minimum and maximum of the stored energy in the ESS; and \(N^{T}\) is the number of daily time slots.
Constraint (A1) shows the limit for the net power of user i. Constraint (A2) shows the solar power of user i is bounded by the forecast value. In (A3), the hourly load of user i is limited by the lower and upper bounds. Constraint (A4) shows the daily minimal load requirement of user i. Constraints (A5) and (A6) show the bounds of charging and discharging power of user i’s energy storage. Constraint (A7) shows the dynamics of the stored energy in user i’s energy storage, restricted by the lower and upper bounds in (A8). In (A9), the stored energy in the final time slot is equal to the initial value.
1.2 Proof of Theorem 1
According to the logarithm form of the proposed ANB model, the KKT conditions with respect to \(\pi_{i}^{ES}\) are:
By solving (A10), the optimal payment \(\pi_{i}^{ES*}\) is:
where
Note that \(\pi_{i}^{ES*}\) is the function of user i’s decision variables \(\varvec{X}_{i}\). Based on (A11), the objective function of the ANB model (14) can then be transformed as follows:
where the constant k is:
As \(O^{A,0}\) and \(O_{i}^{U,0}\) are constants determined by the models without energy sharing, the objective function (A13) is equivalent to the minimization of the total costs:
Therefore, the asymmetric Nash bargaining model is equivalent to the proposed energy sharing model that achieves Pareto optimality.
Note that individual rationality is naturally satisfied because of the constraints (15) and (16) of the ANB model.
In addition, for the users without energy sharing, their shared power \(\left| {P_{i,t,s}^{ES*} } \right|\) is always 0, so their SCRs are 0. The optimal payments and the net benefits are 0, which fulfills no exploitation.
It is obvious that if a user makes more economic values by sharing DERs, this user’s SCR will be larger, and he/she will earn more net benefits. Thus, monotonicity is satisfied.
The sum of the net benefits of the aggregator and all users are shown as follows:
Therefore, budget balance is fulfilled.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, J., Zhong, H., Qin, J. et al. Incentive mechanism for sharing distributed energy resources. J. Mod. Power Syst. Clean Energy 7, 837–850 (2019). https://doi.org/10.1007/s40565-019-0518-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-019-0518-5