1 Introduction

The offshore wind power has been widely developed in Europe, China, the United States and Australia [1]. Voltage source converter (VSC) based high voltage direct current (HVDC) transmission systems, including multi-terminal HVDC systems, are widely applied to transmit the power [2, 3], in which the modular multilevel converter (MMC) topology attracts the most attention of researchers [4]. The MMC topology is also used in DC distribution and power quality control, such as a unified power flow controller (UPFC) and static synchronous compensator (STATCOM) [5, 6]. Most research has focused on the operation and control strategy of MMCs [7,8,9,10,11], while their failure prediction has not received much discussion, although it is an important issue in power systems [12, 13]. Hence, there is a big motivation to find a solution for reliability evaluation and sub-module (SM) redundancy configuration of the MMC.

Some tentative work has been done in previous studies. For example, redundancy and reliability indexes of the MMC were defined in [14], but the general reliability function was not built. Also, using the k-out-of-n: G model and Gamma distribution, a reliability function of MMC was established [15], wherein the failure rates of SM components were based on the experience-hypothesis. Explicit models of components were not given. Some research has focused on the optimal number of SMs, without considering reliability evaluation [16, 17].

In this paper, the Markov model is proposed to analyze the failure rates of the MMC and its SMs, based on a graphical representation of system states. A general function for reliability evaluation of the MMC is given. The mean time to failure and reliability evaluation of the MMC with a redundant SM are both discussed.

The paper is organized as follows. In Section 2, the basic operation principles of the MMC are presented. In Section 3, the cause and impact of SM failure are discussed. Reliability analysis of MMC is given in Section 4, and with a redundant SM in Sections 5. Finally, an example analysis is provided in Section 6.

2 Basic operation principles of MMC

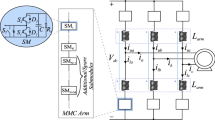
A three-phase MMC is shown in Fig. 1, which consists of six arms, with n SMs in each arm [18]. \(L_{0}\) is the arm inductor; \(U_{dc}\) is the DC bus voltage; \(u_{jm}\)(j=a, b, c) is the output voltage of phase j and \(u_{c}\) is the capacitor rated voltage.

Fig. 1
figure 1

Diagram of MMC

Full size image

Each SM has three states, as shown in Table 1. State A is called “ON” state, where switch \(S_{1}\) is ON and switch \(S_{2}\) is OFF. The output voltage is \(u_{c}\). State B is called the “OFF” state, where switch \(S_{1}\) is OFF switch \(S_{2}\) is ON. The output voltage is 0 V. State C is called the “BLOCK” state, where switch \(S_{1}\) and switch \(S_{2}\) are OFF. In the “BLOCK” state, when the current is flowing into the SM, \(i_{SM}\) is positive and the output voltage is \(u_{c}\). When the current is flowing out of SM,\(i_{SM}\) is negative and the output voltage is 0 V.

Table 1 Working mode of SM
Full size table

3 Cause and impact of SM fault

Each SM may be considered as a potential point of failure [19]. Hence, it is important to know the causes and impact of a SM fault.

3.1 Causes of SM fault

There are three main causes to trigger the failure of a SM.

  1. 1)

    Damage to a power electronic component

    The overload capability of power electronic components, such as insulated gate bipolar transistors (IGBTs) and diodes, is limited, so overvoltage and overcurrent might break them. Therefore, the damage to a power electronic component is one of the most common reasons to cause the SM fault.

  2. 2)

    Damage to a passive component

    The DC capacitor is a key passive component in a SM, and damage to it would also cause a SM fault. Fortunately, its failure rate is lower than that of power electronic devices.

  3. 3)

    A faulty trigger pulse

    If the trigger pulse signal experiences interference, it could not operate the SM correctly, and this might lead the SM to a fault in either short circuit or open circuit mode [20].

3.2 Impacts of SM fault

Once one SM is damaged, it would be bypassed and then replaced by the redundant SM, which can cause distortion of the output voltage and current and reduced performance of the converter. A fault of one SM can also cause the other components in the corresponding arm to fail and lead to total system collapse. When the quantity of broken SMs is more than the redundant ones, the MMC would work with asymmetrical operation. In the worst case, this might result in system failure.

4 Reliability analysis of MMC

To evaluate the MMC’s reliability, an analysis of the reliability of semiconductor devices (IGBTs and diodes) and capacitors is first required for use in the Markov model.

4.1 Component failure rate

Power electronic components play an important role in reliability of the whole system, so it is necessary to estimate their failure rates [21, 22]. An extensive database of various types of parts is provided in the RDF-2000 [23], which is widely accepted and frequently used to determine the reliability of electronic equipment. Using these data, mathematical models for power IGBT, aluminum electrolytic capacitor and power diode failure rates are expressed in (1), (2) and (3) respectively. The unit of failure rates is \(10^{ - 9}\)/h.

$$\begin{aligned} \lambda_{IGBT} & = \left( {\underbrace {{(\pi_{S} \lambda_{0} )\frac{{\sum\limits_{i = 1}^{y}{(\pi_{t})_i } { \tau_{i} } }}{{\tau_{on} + \tau_{off} }}}}_{{\lambda_{die} }} + \underbrace {{\pi_{I} \lambda_{EOS} }}_{{\lambda_{over} }}} \right. \\ &\quad \left. { + \underbrace {{\left( {2.75 \times 10^{ - 3} \sum\limits_{i = 1}^{z}{(\pi_{n})_i } { \left( {\Delta T_{i} } \right)^{0.68} } } \right)\lambda_{B} }}_{{\lambda_{pack} }}} \right) \\ \end{aligned}$$
(1)
$$\begin{aligned} \lambda_{diode} & = \left( {\underbrace {{(\pi_{U} \lambda_{0} )\frac{{\sum\limits_{i = 1}^{y}{(\pi_{t})_i} { \tau_{i} } }}{{\tau_{on} + \tau_{off} }}}}_{{\lambda_{die} }} + \underbrace {{\pi_{I} \lambda_{EOS} }}_{{\lambda_{over} }}} \right. \\ & \left. { + \underbrace {{\left( {2.75 \times 10^{ - 3} \sum\limits_{i = 1}^{z} {(\pi_{n})_i } { \left( {\Delta T_{i} } \right)^{0.68} } } \right)\lambda_{B} }}_{{\lambda_{pack} }}} \right) \\ \end{aligned}$$
(2)
$$\lambda_{cap} = 2.4 \times \left( {\frac{{\sum\limits_{i = 1}^{y}{(\pi_{t})_i } { \tau_{i} } }}{{\tau_{on} + \tau_{off} }}} { + 1.4 \times 10^{ - 3} \sum\limits_{i = 1}^{z}{(\pi_{n})_i } { \left( {\Delta T_{i} } \right)^{0.68} } } \right)$$
(3)

where \(\lambda_{IGBT}\) is the failure rate of the IGBT; \(\lambda_{diode}\) is the failure rate of the diode; \(\lambda_{cap}\) is the failure rate of the capacitor; \(\lambda_{0}\) is the base failure rate of the die; \(\pi_{S}\) is the charge factor; \({(\pi_{t})_i }\) is the \(i^{\text{th}}\) temperature factor related to the \(i^{\text{th}}\) junction temperature of the transistor mission profile; \(\tau_{i}\) is the \(i^{\text{th}}\) working time ratio for the \(i^{\text{th}}\) junction temperature of the mission profile; \(\tau_{on}\) is the total working time ratio; \(\tau_{off}\) is the time ratio in storage (or dormant) mode; \(\lambda_{die}\) is the failure rate of the die; \(\pi_{I}\) is the influence factor related to usage (protection interface or not); \(\lambda_{EOS}\) is the failure rate related to the electrical overstress in the application being considered; \(\lambda_{over}\) is the failure rate of the overstress; \({(\pi_{n})_i }\) is the \(i^{\text{th}}\) influence factor related to the annual cycles of thermal variation seen by the package, with the amplitude \(\Delta T_{i}\); \(\Delta T_{i}\) is the \(i^{\text{th}}\) thermal amplitude variation of the mission profile; \(\lambda_{B}\) is the base failure rate of the package; \(\lambda_{pack}\) is the failure rate of the package; \(\pi_{U}\) is the use factor.

According to the IGBT model and the rated working conditions of a practical system in Section 6, the average dissipated power of diode and IGBT is calculated as follows:

  1. 1)

    The average power dissipated by the diode is 53.47 W.

  2. 2)

    The average power dissipated by IGBT is 346 W.

  3. 3)

    The junction-ambient thermal resistance is 0.1618 °C/W.

Some corresponding fault parameter values of components are given in Table 2. Based on the failure rate models of components, the failure rates of IGBTs, diodes, and capacitors in the MMC have been calculated as shown.

Table 2 Parameters for failure rates of components
Full size table

4.2 Summary of Markov reliability model

The Markov model can be used to estimate a variety of reliability indexes, such as the failure rate, the mean time to failure (MTTF), the reliability and the availability [24, 25].

First of all, a random state function \(\left\{ {X(t),t > 0} \right\}\) is defined. At time t, the probability of the system in the \(i^{\text{th}}\) state can be expressed as:

$$P_{i} \left( t \right) = P\{ X(t) = i\}$$
(4)

With the transition to the \(j^{\text{th}}\) state after time \(\Delta t\), the probability \(P_{ij}\) can be expressed as:

$$P_{ij} \left( t \right) = P\{ X(t + \Delta t) = j|X\left( t \right) = i\}$$
(5)

The transition rate \(\lambda_{ij}\) that denotes the probability of the system transiting from the \(i^{\text{th}}\) state to the \(j^{\text{th}}\) state at time t is:

$$\lambda_{ij} = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{P_{ij} \left( t \right)}}{\Delta t}$$
(6)

The system transitions between different states due to faults and maintenance of the system components. The three-state transition diagram [26,27,28] is shown in Fig. 2. μ10 is the returning rate; State 0 stands for the system works well; State 1 stands for the system has a fault, but could still work; State 2 stands for the system could no longer work.

Fig. 2
figure 2

State transition diagram

Full size image

The state equation can be expressed as:

$$\frac{\text{d}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}c} {P_{0} } \\ {P_{1} } \\ {P_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \left( {\lambda_{01} + \lambda_{02} } \right)} & {\mu_{10} } & 0 \\ {\lambda_{01} } & { - \left( {\mu_{10} + \lambda_{12} } \right)} & 0 \\ {\lambda_{02} } & {\lambda_{12} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {P_{0} } \\ {P_{1} } \\ {P_{2} } \\ \end{array} } \right]$$
(7)

The probabilities of the system can be obtained by solving the state equation (7). \(P_{0}\), \(P_{1}\) and \(P_{2}\) are the probabilities of the system being in state 0, state 1 and state 2, respectively. \(P_{2}\) is also called the failure rate. The reliability function of the system is the sum of probability functions of all functional (non-failed) states, which is mathematically expressed as:

$$R(t) = P_{0} + P_{1}$$
(8)

Then, the MTTF can be derived as:

$$MTTF = \int_{0}^{\infty } {R(t){\text{d}}t}$$
(9)

4.3 Markov model of MMC reliability evaluation without redundant SMs

To reduce the order of the state equation and simplify the model, the same operating states and transition processes are assumed to apply to the SM. The reliability of the system could be considered as a summary of the reliability of multiple SMs. When the SM exits a fault state, it is considered as a permanent fault. Hence, the rate of return is equal to 0.

The Markov model of the MMC is shown in Fig. 3.

Fig. 3
figure 3

Markov model of MMC

Full size image

where State 0 is the normal working state, and State1 is the abnormal state, which means that there is one SM fault in any arm. The failure rate of SMs can be obtained by calculating the failure rates of the IGBTs, capacitors, and diodes in it.

Using the data in Table 2, the failure rate of a SM can be expressed in (10), because there are two IGBTs, two diodes, and one capacitor in each SM:

$$\lambda_{SM} = 2\lambda_{IGBT} { + }2\lambda_{diode} { + }\lambda_{cap} = 856 \times 10^{ - 9} / {\text{h}}$$
(10)

where \(\lambda_{SM}\) is the failure rate of the SM.

With 6n SMs in the MMC, \(\lambda_{01}\) can be obtained as:

$$\lambda_{01} = 6n\lambda_{SM} = 5. 1 4\times 10^{ - 6} n$$
(11)

Therefore equation (7) can be rewritten as:

$$\frac{\text{d}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}c} {P_{0} } \\ {P_{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - 5.136 \times 10^{ - 6} n} & 0 \\ {5.136 \times 10^{ - 6} n} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {P_{0} } \\ {P_{1} } \\ \end{array} } \right]$$
(12)

with initial conditions: \(P_{0} \left( 0 \right) = 1\); \(P_{1} \left( 0 \right) = 0\).

Solving (12) determines that:

$$\left\{ {\begin{array}{*{20}l} {P_{0} (t) = {\text{e}}^{{ - 5.136 \times 10^{ - 6} nt}} } \hfill \\ {P_{1} (t) = 1 - {\text{e}}^{{ - 5.136 \times 10^{ - 6} nt}} } \hfill \\ \end{array} } \right.$$
(13)

Therefore, the reliability function of the MMC is:

$$R(t) = {\text{e}}^{{ - 5.136 \times 10^{ - 6} nt}}$$
(14)

the failure rate function of the MMC is:

$$P(t) = 1 - {\text{e}}^{{ - 5.136 \times 10^{ - 6} nt}}$$
(15)

and the MTTF function is:

$$MTTF = \int_{0}^{ + \infty } {{\text{e}}^{{ - 5.136 \times 10^{ - 6} nt}} {\text{d}}t} = \frac{{1.947 \times 10^{5} }}{n}$$
(16)

where n is the number of SMs in any arm. Obviously, with an increasing number of SMs, the MTTF reduces proportionally.

The changing reliability and failure rate of the system with time and the number of SMs per arm (n) are shown respectively in Fig. 4 and Fig. 5.

Fig. 4
figure 4

Reliability function of MMC

Full size image
Fig. 5
figure 5

Failure rate function of MMC

Full size image

One can see that with fewer than 50 modules, the reliability does not drop rapidly with time, and before 1000 hours of operation, the reliability does not fall quickly with the number of SMs.

5 Reliability evaluation of MMC with a redundant SM by Markov model

As above, a general function for the reliability evaluation of the basic MMC is obtained.

Firstly, there are three main modes for the redundant operation of the SM [29, 30]:

  1. 1)

    The redundant SMs do not participate in normal operation of the MMC. When a SM fails, it is removed, and the redundant SM is put into operation.

  2. 2)

    The redundant SMs participate in normal operation. When a SM fails, it is removed, and the corresponding normal SM in the other phase is bypassed so that the system operates symmetrically.

  3. 3)

    The redundant SMs participate in normal operation. When a SM fails, only that SM is bypassed.

Mode 3 leads to asymmetric operation. Mode 2 is not economical because the corresponding SM in the other phase is removed and the redundant SMs are aged by operation. Therefore, mode 1 is chosen for discussion.

The Markov model for mode 1 is shown in Fig. 6, where the numbers of SMs and cold standby redundant SMs (\(n_{0}\)) in each arm are n and one, respectively.

Fig. 6
figure 6

Markov model of MMC with a redundant SM

Full size image

There are eight states in the model. State 0: All devices work well; State 1: One SM in any arm fails; State 2: Any two arms both have one SM failing; State 3, 4, 5: Respectively any three, four, five arms all have one SM failing; State 6: Six bridge arms all have one SM failing; State 7: The system can no longer work.

Take the transition from State 1 to State 2 as an example. Supposing that the MMC is in state 1, and an SM on the upper arm of phase A fails. Then, the faulty SM is removed and the redundant SM is put to use. The diagram of MMC in State 1 is shown in Fig. 7.

Fig. 7
figure 7

Diagram of MMC in state 1

Full size image

If another SM fails in one of the other five arms, the MMC can still run. The state transfers from state 1 to state 2. If another SM fails in the same arm, the MMC cannot run. The state transfers from state 1 to state 7.

Therefore, \(\lambda_{12}\) and \(\lambda_{17}\) are determined by:

$$\left\{ {\begin{array}{*{20}l} {\lambda_{12} = 5\lambda } \hfill \\ {\lambda_{17} = \lambda } \hfill \\ \end{array} } \right.$$
(17)

where \(\lambda\) is the failure rate of any arm and could be expressed as:

$$\lambda = 856n \times 10^{ - 9} / {\text{h}}$$
(18)

Other state transitions can be derived in a similar way, and the transition rates are:

$$\left\{ {\begin{array}{*{20}l} {\lambda_{01} = \lambda_{67} = 6\lambda } \hfill \\ {\lambda_{23} = \lambda_{47} = 4\lambda } \hfill \\ {\lambda_{57} = 5\lambda } \hfill \\ {\lambda_{34} = \lambda_{37} = 3\lambda } \hfill \\ {\lambda_{45} = \lambda_{27} = 2\lambda } \hfill \\ {\lambda_{56} = \lambda } \hfill \\ \end{array} } \right.$$
(19)

The equation of state can be expressed as:

$$\frac{\text{d}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}c} {P_{0} } \\ {P_{1} } \\ {P_{2} } \\ {P_{3} } \\ {P_{4} } \\ {P_{5} } \\ {P_{6} } \\ {P_{7} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - 6\lambda } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {6\lambda } & { - 6\lambda } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {5\lambda } & { - 6\lambda } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {4\lambda } & { - 6\lambda } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {3\lambda } & { - 6\lambda } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {2\lambda } & { - 6\lambda } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \lambda & { - 6\lambda } & 0 \\ 0 & \lambda & {2\lambda } & {3\lambda } & {4\lambda } & {5\lambda } & {6\lambda } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {P_{0} } \\ {P_{1} } \\ {P_{2} } \\ {P_{3} } \\ {P_{4} } \\ {P_{5} } \\ {P_{6} } \\ {P_{7} } \\ \end{array} } \right]$$
(20)

The sum of all states’ probabilities is:

$$\sum\limits_{i = 0}^{7} {P_{i} \left( t \right)} = 1$$
(21)

The initial conditions are \(P_{0} \left( 0 \right) = 1\); \(P_{i} \left( 0 \right) = 0\; (i = 1\,\sim\, 7 )\).

By solving (20) subject to (21) these probability functions are obtained:

$$\left\{ {\begin{array}{*{20}l} {P_{0} \left( t \right){={\text {e}}}^{ - 6\lambda t} } \hfill \\ {P_{1} \left( t \right)={ 6}\lambda t{\text{e}}^{ - 6\lambda t} } \hfill \\ {P_{2} \left( t \right)={ 15}\lambda^{2} t^{2} {\text{e}}^{ - 6\lambda t} } \hfill \\ {P_{3} \left( t \right)={ 20}\lambda^{3} t^{3} {\text{e}}^{ - 6\lambda t} } \hfill \\ {P_{4} \left( t \right)={ 15}\lambda^{4} t^{4} {\text{e}}^{ - 6\lambda t} } \hfill \\ {P_{5} \left( t \right)={ 6}\lambda^{5} t^{5} {\text{e}}^{ - 6\lambda t} } \hfill \\ {P_{6} \left( t \right) =\lambda^{6} t^{6} {\text{e}}^{ - 6\lambda t} } \hfill \\ {P_{7} \left( t \right)={ 1} - \lambda^{6} t^{6} {\text{e}}^{ - 6\lambda t} - 6\lambda^{5} t^{5} {\text{e}}^{ - 6\lambda t} - 1 5\lambda^{4} t^{4} {\text{e}}^{ - 6\lambda t} } \hfill \\ {\quad \quad \;\; - 2 0\lambda^{3} t^{3} {\text{e}}^{ - 6\lambda t} - 1 5\lambda^{2} t^{2} {\text{e}}^{ - 6\lambda t} - 6\lambda t{\text{e}}^{ - 6\lambda t} - {\text{e}}^{ - 6\lambda t} } \hfill \\ \end{array} } \right.$$
(22)

The reliability function is therefore:

$$\begin{aligned} R(t) & = \sum\limits_{i = 0}^{6} {P_{i} } \\ & = \lambda^{6} t^{6} {\text{e}}^{ - 6\lambda t} { + 6}\lambda^{5} t^{5} {\text{e}}^{ - 6\lambda t} { + 15}\lambda^{4} t^{4} {\text{e}}^{ - 6\lambda t} \\ & \;{ +\quad 20}\lambda^{3} t^{3} {\text{e}}^{ - 6\lambda t} { + 15}\lambda^{2} t^{2} {\text{e}}^{ - 6\lambda t} { + 6}\lambda t{\text{e}}^{ - 6\lambda t} {\text{ + e}}^{ - 6\lambda t} \\ \end{aligned}$$
(23)

and the MTTF function with a redundant SM is:

$$\begin{aligned} MTTF & = \int_{0}^{ + \infty } {\left( {\lambda^{6} t^{6} {\text{e}}^{ - 6\lambda t} { + 6}\lambda^{5} t^{5} {\text{e}}^{ - 6\lambda t} { + 15}\lambda^{4} t^{4} {\text{e}}^{ - 6\lambda t} } \right.} \\ & \left. {\; +\quad 20\lambda^{3} t^{3} {\text{e}}^{ - 6\lambda t} { + 15}\lambda^{2} t^{2} {\text{e}}^{ - 6\lambda t} { + 6}\lambda t{\text{e}}^{ - 6\lambda t} { + }{\text{e}}^{ - 6\lambda t} } \right){\text{d}}t \\ & = \frac{{7.349 \times 10^{5} }}{n} \\ \end{aligned}$$
(24)

The changing reliability of this MMC with time and the number of SMs per arm (n) is shown in Fig. 8.

Fig. 8
figure 8

Reliability function of the MMC with a redundant SM

Full size image

The work above could provide a theoretical basis for a practical application project. By using Markov model, a general function and a mathematical calculation is firstly presented for the reliability of MMC, although it is always difficult to give a precise reliability evaluation for MMC in a practical power system project, with a large amount of power electronic components.

6 A reliability evaluation for a practical distribution network project

In this section, a reliability evaluation of MMC is given for a practical DC distribution network project in Zhejiang Province, China. Some parameter values of MMC are shown in Table 3.

Table 3 Some parameter values of the MMC used in a practical project in Zhejiang
Full size table

The structure diagram of the DC distribution system in this project is shown in Fig. 9, where the rated DC voltage is 10 kV and the rated power is 10 MW. Each arm consists of 24 SMs.

Fig. 9
figure 9

Structure diagram of a practical DC distribution system project in Zhejiang

Full size image

By the project parameters above and the evaluation model, it could be found that the failure rate of any arm is \(2.054 \times 10^{ - 5}\)/h. Furthermore, according to (14) and (23) the reliability of the project converter with a redundant SM \(R_{1} (t)\) and without a redundant SM \(R_{2} (t)\) could be derived as follows

$$\left\{ \begin{aligned} R_{1} (t) & = {\text{e}}^{{ - 1.23 \times 10^{ - 4} t}} \\ R_{2} (t) & = \left[ {\left( {2.054 \times 10^{ - 5} } \right)^{6} t^{6} { + 6}\left( {2.054 \times 10^{ - 5} } \right)^{5} t^{5} } \right. \\ & \left. { + 15}\left( {2.054 \times 10^{ - 5} } \right)^{4} t^{4} { + 20}\left( {2.054 \times 10^{ - 5} } \right)^{3} t^{3} \right. \\ &\left. { { + 15}\left( {2.054 \times 10^{ - 5} } \right)^{2} t^{2} { + 6}\left( {2.054 \times 10^{ - 5} } \right)t{ + 1}} \right]{\text{e}}^{{ - 1.23 \times 10^{ - 4} t}} \\ \end{aligned} \right.$$
(25)

They are compared in Fig. 10.

Fig. 10
figure 10

Comparison of the reliability with and without a redundant SM

Full size image

Based on (16) and (24), the MTTF of the system with and without a redundant SM is more than 1200 days and less than 400 days respectively, as shown in Table 4.

Table 4 Comparison of two MTTFs
Full size table

The evaluation method proposed has a distinct effect to give a theoretical analysis and reliability evaluation for a practical project. For the DC distribution network project in Zhejiang, it could be found that the MTTF of the system with a redundant SM is more than 3 times that of the system without a redundant SM. Hence, it provides a theoretical proof that there should be at least one redundant SM in each arm to obtain a high reliability.

7 Conclusion

In a practical power system project, it is always difficult to provide a precise reliability evaluation for MMC because there is a large amount of power electronic components. In this paper, the Markov model is proposed to evaluate the reliability of the MMC. Based on the model, the mathematical calculation and a general function are firstly presented considering the failure of the electronic equipment in MMC. Based on that, the mean time to failure and the influence of redundant SMs are both discussed. Finally, they are applied to reliability evaluation for a practical DC distribution system. The system with a single redundant SM provides a factor of more than 3 improvement in reliability. The results give a further validation that the reliability evaluation based on Markov model could provide a useful reference for practical project design.