Abstract
The change of customer behaviors and the fluctuation of spot prices can affect the benefits of electricity retailers. To address this issue, an incentive-based demand response (DR) model involving the utility and elasticity of customers is proposed for maximizing the benefits of retailers. The benefits will increase by triggering an incentive price to influence customer behaviors to change their demand consumptions. The optimal reduction of customers is obtained by their own profit optimization model with a certain incentive price. Then, the sensitivity of incentive price on retailers’ benefits is analyzed and the optimal incentive price is obtained according to the DR model. The case study verifies the effectiveness of the proposed model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With the progression of the smart grid, demand response (DR) is an effective measure to influence the behaviors of demand side by price policies or incentive compensation when there is a price spike or abnormal incidents, which can ensure the stability and economy of grid operation [1]. For example, DR programs were introduced to induce demand reduction or control prices and incentives in order to improve the efficiency of distributed energy generation [2, 3]. A novel model was proposed to integrate the uncertainties of wind power into the supply side and roof-top solar photovoltaic (PV) on the demand side [4]. In addition, various electrical devices in a smart home, such as electric vehicles and energy storages, can be the flexible loads devoted to DR programs [5,6,7]. Particularly, when considering the process optimization of industrial manufacturing, DR programs are economical to apply [8]. Whereas the non-critical load at the residential and commercial levels allows for demand reduction was relatively easy, reducing the demand of industrial processes requires more sophisticated solutions [9].
In current studies, DR can be divided into two types: price-based DR (PBDR) and incentive-based DR (IBDR) [10]. PBDR programs influence customer behaviors through different price policies, where time-of-use (TOU) price is widely applied. Customer response strategies modelled by price elasticity and TOU price can alleviate the risks of supply side and reduce the market energy costs [11]. IBDR programs are popular as they can regulate load by providing incentives to customers [12]. IBDR schemes based on game theory and coupon rewards were proposed to provide a state-dependent compensation [13, 14] in order to ensure the profits of both suppliers and customers. However, new peak load might be created during other periods due to the transferred load with only PBDR programs, which may cause additional cost for retailers to meet the requirement of customers. Besides, the profits of customers from power consumption are not considered. Therefore, only PBDR programs could not guarantee the benefits of suppliers and customers [14].
Meanwhile, the profits of retailers, who gain the benefits from selling electricity and providing related services, should also be considered. Retail choice means that electrical customers can directly choose their suppliers of electricity services, which facilitates the competition to lower energy costs and produce prices that are closer to the “price of free competition” [15]. In [16], an efficient pricing method based on Vickrey–Clarke–Groves (VCG) mechanism, aiming to maximize the social welfare, was proposed to ensure the benefits of customers and retailers. A reward-based DR strategy for a cyber-physical distribution system was designed to maximize retailer benefits [17]. The benefits of both suppliers and customers are equally important in DR programs. Moreover, a genetic algorithm-based distributed pricing optimization algorithm for DR management with the aim to maximize the retailer’s profits was designed in [18]. However, most current studies on DR considering the benefits of customers and retailers mainly focused on the benefit change caused by the fluctuation of price, or made the dispatch plan of retailers from the view of power market dispatch institute in order to minimize the total cost of power system, which is not from the view of retailers and cannot effectively influence customer behaviors or adequately guarantee the profits. And the retailers in the market didn’t take fully advantage of the positivity and flexibility. The incurred consequence is that either retailers or customers might lose benefits in the programs.
In order to influence the behaviors of customers in DR more effectively and maximize the benefits of retailers, this paper innovatively proposes an IBDR model involving customers’ utility and elasticity to maximize retailer benefits. During peak periods, customers determine the optimal demand reduction by solving their own profit optimization model to maximize their benefits based on the utility with a certain incentive price. During valley periods, the optimal demand change is decided by the demand elasticity. Based on the optimization results of customer reduction at various incentive prices, the optimal incentive prices can be obtained by analyzing the sensitivity of incentive prices to retailer benefits according to the DR model that maximizes retailer benefits. Compared with ordinary PBDR model and the IBDR model with constant incentive price, the new DR model considers the benefits of customers without creating new peaks caused by existing DR programs because of the proactive adjustability of incentives, and increases the benefits of retailers.
2 DR model
Considering the benefits of retailers, a common DR model based on incentive price involving the load variation of customers is proposed, including the profit optimization of customers and IBDR model.
2.1 Customer profit optimization model
In normal conditions, customers buy electricity from the electrical retailers with the quantity Q at the retail price PR. It is assumed that a calendar day has 24 settlement periods and k represents the type of customers. Then, the profits of customers can be described as:
where Fcus,k represents the profit of customer k; Qk,t, PR,k,t and Uk(Qk,t) are the demand, retail price and utility of customer k at time t.
The behaviors of customers can be effectively modelled by certain utility functions as shown in (2)–(4). From the view of customers, profits and electricity consumption have an increasing utility function within certain constraints. In this paper, the utility of customers is built as a quadratic and logarithmic model using fuzzy mathematical theory [19, 20]. At the beginning, customers buy a quantity and then they obtain certain utility. k = 1,2,3 represents residential, commercial and industrial customers, respectively.
where α, γ, β and µ are constants; ω represents the customer willingness to reduce their demand. All the parameters can be obtained based on the statistic assessment of local customer behaviors.
The elasticity and utility of customers are introduced to examine the impact of load variations in valley and peak periods in the letter respectively.
In peak periods, customers receive an incentive to reduce the quantities and their optimization profit model M1 can be modelled as follows.
where ΔQk,t is the load reduction of customer k at time t; PC,k is the incentive price customer k received.
When the load is in the valley, the electricity consumption and utility of customers is low, thus the elasticity of customers, \(\varepsilon_{k}\), is introduced to decide their consumption. Therefore, the load variation in the trough is:
By solving M1 and (7), the optimal customers’ reduction with a certain incentive price in peak periods can be calculated.
2.2 IBDR model
In normal conditions, retailers buy electricity from the spot market with the quantity Q at the spot price PS,t lower than the retail price PR,k,t, and then sell it to customers. In this case, retailer benefits are equivalent to their financial loss. Then, the loss of retailers can be described as negative profits Fret:
In particular, based on the fitting analysis of the operation data from the spot market, it can be obtained from [21] that the fluctuation of spot price is closely related to load. Spot price obeys logarithmic normal distribution with related to load when the demand is high. While spot price obeys normal distribution when the demand is low, whose mean \(\mu_{i,t}\) and standard deviation \(\sigma_{i,t}\) are described in (9). It is worth noting that the fluctuation of spot price is not severe, and thus the scenario analysis in stochastic problem is not considered.
where ai, bi, ci and di are the coefficients; i represents the type of distribution of spot price.
PS,i,t is the spot price followed distribution i at time t. When i = 1, the load is low. PS,i,t follows the distribution:
When i = 2, the load is high. PS,i,ft follows the distribution:
The actual value of spot electricity PS,i,t can be obtained by integrating the above two spot electricity price probability density as shown in (10) and (11).
However, if the market has a peak, the spot price will suddenly climb and exceed the retail price. Thus, retailers introduce an incentive scheme to influence customer behaviors. Responsively, customers reduce their demand to Qt − ΔQt and gain a compensation. In the same way, customers can receive an incentive to increase consumption during valley periods, where ΔQt is negative. For maximizing retailer benefits, the IBDR model M2 is formulated as:
According to (5)–(7), the optimal customer reduction in the peak period and variation in valley periods can be obtained with different incentive prices. Then according to the optimization model M2 and the optimal demand variation of customers obtained by M1 and (7), the optimal incentive that retailers pay can be gained by analyzing the sensitivity of incentive price to retailers’ benefits prices.
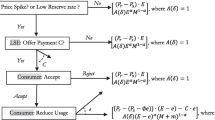
2.3 Flowchart of proposed IBDR model
The flowchart of the proposed IBDR model is shown in Fig. 1. In Fig. 1, steps 1–2 are designed to establish the customers’ profit optimization model M1, which is applied to obtain the optimal reduction with a certain incentive price in peak periods. While steps 3–8 are the modelling process of the IBDR model M2 aiming to maximize retailer benefits. Specifically, steps 3–7 put customer reduction that optimized by M1 into the retailer benefit function and calculate the maximum benefits of retailers in peak periods. Step 8 considers the elasticity of customers in valley periods in M2. Retailers gain more benefits due to the growth of customer consumption. The optimal incentive price can be decided by analyzing the sensitivity of inventive price and retailer benefits. The detailed modelling process is shown in Fig. 1.
3 Case study
The typical residential, commercial, industrial customers in a selected area are used to validate the proposed model. The demand and retail price dataset of the customers in 24 hours is acquired. The main inputs including price and demand can be found in [22]. The optimization model is programmed with MATLAB Yalmip toolbox. By solving M1, the optimal customer reduction points can be obtained at a certain PC. And then the optimal reduction at various incentive prices can be inputs of M2 to realize the maximization of retailer benefits.
3.1 Retailer benefits in peak periods based on DR model
As built in (2)–(4), the utility of commercial and industrial customers conforms to the logarithmic distribution, while the utility of residential customers is a piecewise function. With the parameter ω increasing, the value of customer utility becomes higher.
The profits of three types of customers are shown in Figs. 2, 3 and 4, respectively. Take industrial customer for an example in Fig. 2. When the incentive price is 100 $/MWh, as shown in the blue line, the biggest profit of industrial customers is $9294322. When the incentive price grows to 150 and 200 $/MWh, the profits also increase by much more incentive income, $9298344 and $9302563, respectively. Commercial and residential customers are in similar situations as shown in Figs. 3 and 4. Therefore, the profits of customers increase first and then decrease with the reduction grows, thus there exist the biggest profits at certain reduction points. Besides, as the incentive price increases, the value of the biggest customer profits are augmenting, so is the optimal customer reduction. Based on these results, the benefits of retailers can be calculated as follows.
Retailer benefits include two components: trading benefits and incentive payments. Due to the randomness of spot prices, the curve of benefits shows certain variations and the results of each program running have little variances. In Figs. 5, 6 and 7, retailer benefits gained by the trading with residential, commercial and industrial customers and the total retailer benefits with DR programs are shown as the blue lines. While retailer benefits and actual trading loss without DR programs are shown as red and purple dot lines respectively. Point P1 is the optimal point of retailer benefits while point P2 represents the biggest trading loss of retailers.
It is obvious that retailer financial loss, the sum of trading loss and incentive payment shown as the blue line, decreases first and then increases when retailers trading with all kinds of customers. Due to the various retail prices and utility of customers, the optimal incentive prices that customers obtained from 7 to 78 $/MWh, and the optimal retailer benefits gained by the trading with different customers are also various. As shown in Fig. 8, when the incentive price is 55 $/MWh, the biggest retailer benefit is $4715009. Compared with the benefits without DR, the benefits with DR achieve great improvement.
Besides, the retailer benefits applied the ordinary PBDR programs and IBDR with a constant incentive price are respectively $3698603 and $4127140, which is less than the benefits with the proposed model. Comparing with ordinary PBDR and IBDR model, the proposed DR model in this letter has better effect on controlling load peak and increasing retailer’s benefits.
3.2 Retailer benefits in peak and valley periods based on DR model
In Fig. 9, the values of elasticity of residential, commercial and industrial customers during valley periods are set as 0.05, 0.15, 0.10. With the incentive in peak periods, the retailer benefit with DR in the trough shown with the blue line has a lower loss, which is $6958030, while the incentive price is 66 $/MWh. Thus, introducing the incentive in both peak and valley periods can better benefit retailers.
Besides, elasticity plays an important role in retailer benefits. As shown in Fig. 10, the total retailer benefits with different customer elasticities are displayed. When residential, commercial and industrial customer elasticities are 0.05, 0.15 and 0.10, the retailer benefit is $6642635 and the incentive price is 66 $/MWh. However, when elasticities increase by three times, the optimal benefit is $15292347. Therefore, if customers have higher elasticity, retailers can make fewer incentive payments and receive more benefits.
4 Conclusion
In this paper, an incentive-based demand response model is proposed to maximize the benefits of electricity retailers. The innovation is that the models involve the utility and elasticity of various customers, considering their different behaviors during both peak and valley periods. By solving the customer profit optimization model in peak periods, the optimal reduction of customers with a certain incentive price can be obtained. During valley periods, the variation of customers can be calculated according to the elasticity with a certain incentive price. Then through analyzing the sensitivity of incentive prices to retailer benefits, the optimal incentive price can be found based on the proposed DR model. Results show that retailers can maximize the benefits with the proposed model.
References
Zheng W, Wu W, Zhang B et al (2018) Distributed optimal residential demand response considering operational constraints of unbalanced distribution networks. IET Gener Trans Distrib 12(9):1970–1979
Li C, Dong Z, Chen G et al (2015) Flexible transmission expansion planning associated with large-scale wind farms integration considering demand response. IET Gener Trans Distrib 9(15):2276–2283
Sakurama K, Miura M (2016) Communication-based decentralized demand response for smart microgrids. IEEE Trans Ind Electron 6496:5192–5202
Mahmoudi N, Shafie-Khah M, Saha TK et al (2017) Customer-driven demand response model for facilitating roof-top PV and wind power integration. IET Renew Power Gener 11(9):1200–1210
Shareef H, Ahmed MS, Mohamed A et al (2018) Review on home energy management system considering demand responses, smart technologies, and intelligent controllers. IEEE Access 6:24498–24509
Shao S, Pipattanasomporn M, Rahman S (2012) Grid integration of electric vehicles and demand response with customer choice. IEEE Trans Smart Grid 3(1):543–550
Bitaraf H, Rahman S (2017) Reducing curtailed wind energy through energy storage and demand response. IEEE Trans Sustain Energy 9(1):228–236
Wang Y, Li L (2013) Time-of-use based electricity demand response for sustainable manufacturing systems. Energy 63:233–244
Mohagheghi S, Raji N (2014) Dynamic demand response: a solution for improved energy efficiency for industrial customers. IEEE Ind Appl Mag 21(2):54–62
Asadinejad A, Tomsovic K (2017) Optimal use of incentive and price based demand response to reduce costs and price volatility. Electric Power Syst Res 144:215–223
Namerikawa T, Okubo N, Sato R et al (2015) Real-time pricing mechanism for electricity market with built-in incentive for participation. IEEE Trans Smart Grid 6(6):2714–2724
Wang Z, Gu C, Li F et al (2013) Active demand response using shared energy storage for household energy management. IEEE Trans Smart Grid 4(4):1888–1897
Zhong H, Xie L, Xia Q (2013) Coupon incentive-based demand response: theory and case study. IEEE Trans Power Syst 28(2):1266–1276
Soliman HM, Leon-Garcia A (2014) Game-theoretic demand-side management with storage devices for the future smart grid. IEEE Trans Smart Grid 5(3):1475–1485
Musco V (2017) The unsung benefits of wholesale, competition to electric utility customers who forgo retail, competition. Electr J 30(8):23–29
Samadi P, Mohsenian-Rad H, Schober R et al (2012) Advanced demand side management for the future smart grid using mechanism design. IEEE Trans Smart Grid 3(3):1170–1180
Reddy KS, Panwar L, Panigrahi BK et al (2017) Demand side management with consumer clusters in cyber-physical smart distribution system considering price-based and reward-based scheduling programs. IET Cyber Phys Syst Theory Appl 2(2):75–83
Meng FL, Zeng XJ (2017) A profit maximization approach to demand response management with customers behavior learning in smart grid. IEEE Trans Smart Grid 7(3):1516–1529
Samadi P, Mohsenian-Rad AH, Schober R et al (2010) Optimal real-time pricing algorithm based on utility maximization for smart grid. In: Proceedings of IEEE international conference on smart grid communications, Gaithersburg, USA, 4–6 October 2010, 6 pp
Hernandez-Hernandez D, Schied A (2007) Robust maximization of consumption with logarithmic utility. In: Proceedings of American control conference, New York, USA, 9–13 July 2007, 4 pp
Wang RQ, Yu-Zeng LI (2009) Load shedding strategies of power supplier considering impact of interruptible loads on spot price. Power Syst Technol 33:111–116
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (No. 51807127), in part by the Fundamental Research Funds for the Central Universities of China (No. YJ201654), in part by the National Key Research and Development Program of China (No. 2018YFB0905200).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 6 December 2018
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
CHAI, Y., XIANG, Y., LIU, J. et al. Incentive-based demand response model for maximizing benefits of electricity retailers. J. Mod. Power Syst. Clean Energy 7, 1644–1650 (2019). https://doi.org/10.1007/s40565-019-0504-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-019-0504-y