Regenerative energy management of electric drive based on Lyapunov stability theorem

Abstract

In recent years, urban rail systems have developed drastically. In these systems, when induction electrical machine suddenly brakes, a great package of energy is produced. This package of energy can be stored in energy storage devices such as battery, ultra-capacitor and flywheel. In this paper, an electrical topology is proposed to absorb regenerative braking energy and to store it in ultra-capacitor and battery. Ultra-capacitor can to deliver the stored energy to DC grid and to charge the battery for auxiliary applications such as lighting and cooling systems. The proposed system is modeled based on large signal averaged modeling, which leads to the simplicity of calculations. The control system is based on Lyapunov stability theorem which guarantees system stability. Also, an energy management algorithm is proposed to control energy under braking and steady-state conditions. Finally, the simulation results validate the effectiveness of the proposed control and energy management system.

1 Introduction

Capacity, reliability and safety of urban rail systems make these devices suitable for public transportation in developed countries [1, 2]. Considering energy price and climate change, energy saving has become an important subject for research studies. Consumed energy in urban rail systems is divided into two parts, traction usage and non-traction usage. In such systems, about 50% of total consumed energy is related to the traction requirements and the rest is related to non-traction usage or auxiliary systems, such as cooling systems and lighting systems [3, 4], and therefore designing a power electronic topology capable of providing energy for these usages, apart from many benefits, can be useful to the economy.

The topic of energy saving in urban rail systems has been investigated in different aspects. In [5], an energy management strategy for capacitor is proposed to adjust charging and discharging threshold voltage based on analysis of train operation states. The main parameter for energy calculations is state of charge (SOC) of energy storage device. In [6], capacitor is used for energy saving in train systems and a hierarchical control strategy is proposed based on energy management section and converter control section. The energy management system works based on an introduced machine and converter control mainly consist of a proportional-integral (PI) closed-loop strategy. Also an optimization algorithm is proposed to estimate the control parameter values at different operations. In [7], a train system considering renewable energy sources (photovoltage and wind power) and the capabilities of using regenerative braking energy is investigated. Apart from these aspects, uncertainties of renewable energies are considered through different scenarios and the whole problem is considered and solved as a large-scale nonlinear optimization problem. Energy and economic energy saving of the proposed system under different strategies is also studied.

In this paper, a topology for saving regenerative braking energy in storage devices is proposed and control system is designed. A bidirectional DC/DC converter and a unidirectional DC/DC converter are connected in series. Also, ultra-capacitor and battery are used as main energy storage devices. Regenerative energy generated by induction electrical machine (IEM) is a high power density package of energy which occurs during a very short period of time, so must be stored in a device with high power density such as ultra-capacitor [8,9,10]. To increase the reliability and system efficiency, ultra-capacitor is connected to DC link via a bidirectional DC/DC converter [11,12,13,14].

To control the proposed system, switching functions are extracted based on state-space equations [15]. Extraction of switching functions is a well-known method to control switching process of power electronic devices, in which, switching functions are obtained based on system’s requirements [16]. In this paper, switching functions are extracted using fundamentals of Lyapunov stability theorem. Fast and accurate tracking of reference values and maintaining system’s stability are main advantages of this method.

2 Modeling and control of proposed system

Schematic circuit diagram of the system is shown in Fig. 1a and power electronic model of the system is shown in Fig. 1b. As seen, the converter that is connected to the DC link and ultra-capacitor is bidirectional and the converter between ultra-capacitor and battery is unidirectional. I_m is the current from IEM to DC link capacitor. $I_{{L_{ 1} }}$ is the current of bidirectional converter and is positive if the converter works in buck mode, or negative if the converter works in boost mode. $I_{{L_{ 2} }}$ that is either positive or zero, is the current of buck converter. V_dc and C_dc are the voltage and capacitor of DC link, respectively. Also, C_uc, R_uc and V_uc are capacity, resistance and voltage of ultra-capacitor, respectively. V_b is voltage of the battery. d₁, d₂, d₃ are the duty cycles of switches S1, S2 and S3, respectively. L₁ and L₂ are the inductors of bidirectional and unidirectional converters, respectively. Moreover, there is a dynamic resistor R_dynamic that must dissipate surplus energy when DC link capacitor and ultra-capacitor are fully charged. Therefore, S_d and u_d are the switch and its duty cycle of the circuit that connect the dynamic resistor to the DC link.

Fig. 1

Complete proposed system for absorbing regenerative braking energy in battery and ultra-capacitor

A well-known method to model switching circuits is large signal averaged model, leading to simplicity of systems [17]. Averaged model of proposed system is shown in Fig. 2, where k is described as:

$$ k = \left\{ \begin{aligned} 1&\quad I_{{L_{ 1} }} { < 0\, {\text{(boost})}} \hfill \\ 0&\quad I_{{L_{ 1} }} {>0\, {\text{{(buck}})}} \hfill \\ \end{aligned} \right. $$

(1)

Fig. 2

Large signal averaged model of proposed system

Converters are controlled using switching functions, based on Lyapunov stability theorem. Switching functions are obtained separately for every state. In order to express the equations, first a new term named d₁₂ combined of d₁ and d₂ is generated as [18]:

$$ d_{12} = k(1 - d_{2} ) + (1 - k)d_{1} $$

(2)

where d₁₂ is the switching function of bidirectional converter.

2.1 Switching functions extraction using Lyapunov stability theorem

Equation (3) indicates the state-space matrix of the averaged model of Fig. 2.

$$ \left[ {\begin{array}{*{20}l} {\dot{I}_{{L_{1} }} } \hfill \\ {\dot{I}_{{L_{2} }} } \hfill \\ {\dot{V}_{dc} } \hfill \\ {\dot{V}_{uc} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\frac{{ - R_{uc} }}{{L_{1} }}} \hfill & {\frac{{d_{3} R_{uc} }}{{L_{1} }}} \hfill & {\frac{{d_{12} }}{{L_{1} }}} \hfill & {\frac{ - 1}{{L_{1} }}} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\frac{{d_{3} }}{{L_{2} }}} \hfill \\ {\frac{{ - d_{12} }}{{C_{dc} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {\frac{1}{{C_{uc} }}} \hfill & {\frac{{ - d_{3} }}{{C_{uc} }}} \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {I_{{L_{1} }} } \hfill \\ {I_{{L_{2} }} } \hfill \\ {V_{dc} } \hfill \\ {V_{uc} } \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} 0 \hfill \\ { - V_{b} } \hfill \\ {L_{2} } \hfill \\ {I_{m} } \hfill \\ {C_{dc} } \hfill \\ 0 \hfill \\ \end{array} } \right] $$

(3)

According to Lyapunov stability theorem, a non-linear autonomous system is globally stable if satisfies the following conditions [18]:

$$ \left\{ \begin{aligned} & V(0) = 0 \\ & \alpha \left( {||\varvec{x}||} \right) < V(\varvec{x}) < \beta \left( {||\varvec{x}||} \right) \\ & \dot{V}(\varvec{x}) < - \gamma \left( {||\varvec{x}||} \right) \\ & \lim \, V \to \infty \\ & ||\varvec{x}|| \to \infty \\ \end{aligned} \right. $$

(4)

where Lyapunov function V: ℝⁿ → ℝ ≥ 0 for $\dot{\varvec{x}} = \varvec{f}(\varvec{x})$ is a continuously differentiable function such that there exist $\alpha$, $\beta$ belong to class Κ_∞, a continuous positive definite function$\gamma$: ℝⁿ → ℝ ≥ 0 for x ∈ ℝⁿ [19]. State variables of the system must be defined as a form of their errors:

$$ \left[ {\begin{array}{*{20}l} {x_{1} } \hfill \\ {x_{2} } \hfill \\ {x_{3} } \hfill \\ {x_{4} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {I_{{L_{1} }} - I_{{L_{1} }}^{*} } \hfill \\ {I_{{L_{2} }} - I_{{L_{2} }}^{*} } \hfill \\ {V_{dc} - V_{dc}^{*} } \hfill \\ {V_{uc} - V_{uc}^{*} } \hfill \\ \end{array} } \right] $$

(5)

where x₁ to x₄ are the errors of state variables; superscript * represents the reference values of corresponding variables. Matrix $\dot{\varvec{X}}$ is introduced as:

$$ \dot{\varvec{X}} = \left[ {\begin{array}{*{20}l} {\dot{x}_{1} } \hfill \\ {\dot{x}_{2} } \hfill \\ {\dot{x}_{3} } \hfill \\ {\dot{x}_{4} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\frac{{ - R_{uc} }}{{L_{1} }}} \hfill & {\frac{{d_{3} R_{uc} }}{{L_{1} }}} \hfill & {\frac{{d_{12} }}{{L_{1} }}} \hfill & {\frac{ - 1}{{L_{1} }}} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\frac{{d_{3} }}{{L_{2} }}} \hfill \\ {\frac{{ - d_{12} }}{{C_{dc} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {\frac{1}{{C_{uc} }}} \hfill & {\frac{{ - d_{3} }}{{C_{uc} }}} \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {x_{1} } \hfill \\ {x_{2} } \hfill \\ {x_{3} } \hfill \\ {x_{4} } \hfill \\ \end{array} } \right] + \varvec{B} $$

(6)

where B is the input matrix and includes system inputs and constant values of state matrix, calculated as:

$$ \varvec{B} = \left[ {\begin{array}{*{20}l} { - \frac{{R_{uc} }}{{L_{1} }}} \hfill & {\frac{{d_{3} R_{uc} }}{{L_{1} }}} \hfill & {\frac{{d_{12} }}{{L_{1} }}} \hfill & { - \frac{1}{{L_{1} }}} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\frac{{d_{3} }}{{L_{2} }}} \hfill \\ { - \frac{{d_{12} }}{{C_{dc} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {\frac{1}{{C_{uc} }}} \hfill & { - \frac{{d_{3} }}{{C_{uc} }}} \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {I_{{L_{1} }}^{*} } \hfill \\ {I_{{L_{2} }}^{*} } \hfill \\ {V_{dc}^{*} } \hfill \\ {V_{uc}^{*} } \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} { - \frac{{\text{d}}I_{{L_{1} }}^{*} }{{\text{d}t}}} \hfill \\ { - \frac{{V_{b} }}{{L_{2} }} - \frac{{\text{d}}I_{{L_{2} }}^{*} }{{\text{d}t}}} \hfill \\ {\frac{{I_{m} }}{{C_{dc} }} - \frac{{\text{d}}V_{dc}^{*} }{{\text{d}t}}} \hfill \\ { - \frac{{\text{d}}V_{uc}^{*} }{{\text{d}t}}} \hfill \\ \end{array} } \right]$$

(7)

Lyapunov function can be introduced in any form, as a function of state variables and other parameters of the system. In this paper, in order to investigate the system stability, Lyapunov function is defined as:

$$ V = \frac{1}{2}L_{1} x_{1}^{2} + \frac{1}{2}L_{2} x_{2}^{2} + \frac{1}{2}C_{dc} x_{3}^{2} + \frac{1}{2}C_{uc} x_{4}^{2} $$

(8)

The matrix form of (8) can be written as:

$$ V = \varvec{X}^{\text{T}} \varvec{PX = X}^{\text{T}} \left[ {\begin{array}{*{20}l} {\frac{{L_{1} }}{2}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\frac{{L_{2} }}{2}} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\frac{{C_{dc} }}{2}} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\frac{{C_{uc} }}{2}} \hfill \\ \end{array} } \right]\varvec{X} $$

(9)

According to the second condition of (4), V must be between the smallest and the largest eigenvalues of P [20]. Therefore $\alpha$ and $\beta$ in (4) are equal to the smallest and the largest eigenvalues of P, respectively, namely λ_min and λ_max:

$$ \lambda_{\hbox{min} } (\varvec{P})||\varvec{x}|| \le V \le \lambda_{\hbox{max} } (\varvec{P})||\varvec{x}|| $$

(10)

The purpose is to find a relation for $\dot{V}$ condition in (4). Merging (9) and (11) results in:

$$ \varvec{X}^{\text{T}} \varvec{PX} \le \lambda_{\hbox{max} } (\varvec{P})||\varvec{x}|| $$

(11)

Multiplying both sides of (11) with −1/ λ_max:

$$ - ||\varvec{x}|| \le - \frac{1}{{\lambda_{\hbox{max} } }}\varvec{X}^{\text{T}} \varvec{PX} $$

(12)

According to $\dot{V} < - \gamma ||\varvec{x}||$ in (4) and (12):

$$ \dot{V} < - \gamma ||\varvec{x}|| < - \frac{\gamma }{{\lambda_{\hbox{max} } }}\varvec{X}^{\text{T}} \varvec{PX} $$

(13)

Therefore, it is certain that:

$$ \dot{V} < - \frac{\gamma }{{\lambda_{\hbox{max} } }}\varvec{X}^{\text{T}} \varvec{PX} $$

(14)

A new parameter called $\varvec{\delta}$ is defined as:

$$ \varvec{\delta}= \left[ {\begin{array}{*{20}l} \begin{aligned} \delta_{1} \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{aligned} \hfill & \begin{aligned} 0 \hfill \\ \delta_{2} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{aligned} \hfill & \begin{aligned} 0 \hfill \\ 0 \hfill \\ \delta_{3} \hfill \\ 0 \hfill \\ \end{aligned} \hfill & \begin{aligned} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \delta_{3} \hfill \\ \end{aligned} \hfill \\ \end{array} } \right] = \frac{1}{{2\lambda_{\hbox{max} } }}\left[ {\begin{array}{*{20}l} \begin{aligned} L_{1} \gamma_{1} \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{aligned} \hfill & \begin{aligned} 0 \hfill \\ L_{2} \gamma_{2} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{aligned} \hfill & \begin{aligned} 0 \hfill \\ 0 \hfill \\ C_{uc} \gamma_{3} \hfill \\ 0 \hfill \\ \end{aligned} \hfill & \begin{aligned} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ C_{dc} \gamma_{4} \hfill \\ \end{aligned} \hfill \\ \end{array} } \right] $$

(15)

Therefore:

$$ \dot{V} < \varvec{X}^{\text{T}} \varvec{\delta X} $$

(16)

Equation (8) satisfies the first, second and fourth conditions of (4). According to (16), the system is globally stable if the derivation of V satisfies the following inequality:

$$ \begin{aligned} & \dot{V} = L_{1} x_{1} \dot{x}_{1} + L_{2} x_{2} \dot{x}_{2} + C_{dc} x_{3} \dot{x}_{3} + C_{uc} x_{4} \dot{x}_{4} \\ & \quad \quad \le \delta_{1} x_{1}^{2} + \delta_{2} x_{2}^{2} + \delta_{3} x_{3}^{2} + \delta_{4} x_{4}^{2} \\ \end{aligned} $$

(17)

In this paper, references are time-invariant and constant. Therefore, the derivatives of reference values are zero and can be neglected in further calculations. Substituting (6) and (15) into (17), Lyapunov function’s derivative form is calculated as (18) in which some terms (such as $- R_{uc} x_{1}^{2}$) are always negative and neglected and some are simplified. Furthermore, d₃ and d₁₂ must be calculated in a way that (18) stays negative and system remains globally stable, therefore:

$$ \begin{aligned} & \dot{V} = L_{1} x_{1} \left( {\frac{{ - R_{uc} }}{{L_{1} }}x_{1} + \frac{{d_{3} R_{uc} }}{{L_{1} }}x_{2} + \frac{{d_{12} }}{{L_{1} }}x_{3} - \frac{1}{{L_{1} }}x_{4} } \right. \\ & \quad \quad \left. { - \,\frac{{R_{uc} }}{{L_{1} }}I_{{L_{1} }}^{*} + \frac{{d_{3} R_{uc} }}{{L_{1} }}I_{{L_{2} }}^{*} + \frac{{d_{12} }}{{L_{1} }}V_{dc}^{*} - \frac{1}{{L_{1} }}V_{uc}^{*} } \right) \\ & \quad \quad + \,L_{2} x_{2} \left( {\frac{{d_{3} }}{{L_{2} }}x_{4} + \frac{{d_{3} }}{{L_{2} }}V_{uc}^{*} - \frac{{V_{b} }}{{L_{2} }}} \right) \\ & \quad \quad + \,C_{dc} x_{3} \left( {\frac{{ - d_{12} }}{{C_{dc} }}x_{1} - \frac{{d_{12} }}{{C_{dc} }}I_{{L_{1} }}^{*} + \frac{{I_{m} }}{{C_{dc} }}} \right) \\ & \quad \quad + \,C_{uc} x_{4} \left( {\frac{1}{{C_{uc} }}x_{1} - \frac{{d_{3} }}{{C_{uc} }}x_{2} + \frac{1}{{C_{uc} }}I_{{L_{1} }}^{*} - \frac{{d_{3} }}{{C_{uc} }}I_{{L_{2} }}^{*} } \right) \\ & \quad \quad - \,\delta_{1} x_{1}^{2} - \delta_{2} x_{2}^{2} - \delta_{3} x_{3}^{2} - \delta_{4} x_{4}^{2} \le 0 \\ \end{aligned} $$

(18)

$$ d_{3} = \frac{{x_{1} V_{uc}^{*} + x_{2} V_{b} + \delta_{1} x_{2}^{2} + \delta_{2} x_{4}^{2} }}{{R_{uc} x_{1} x_{2} + R_{uc} x_{1} I_{{L_{2} }}^{*} + x_{2} V_{uc}^{*} - x_{4} I_{{L_{2} }}^{*} }} $$

(19)

$$ d_{12} = \frac{{R_{uc} x_{1} I_{{L_{1} }}^{*} - x_{4} I_{{L_{1} }}^{*} - x_{3} I_{m} + \delta_{4} x_{1}^{2} + \delta_{3} x_{3}^{2} }}{{x_{1} V_{dc}^{*} - x_{3} I_{{L_{1} }}^{*} }} $$

(20)

2.2 Energy management algorithm

As shown in Fig. 3, the switching between the modes is carried out according to SOC of battery, ultra-capacitor and DC link voltage, i.e., SOC_b, SOC_uc and V_dc. The maximum and minimum values of SOC_uc, SOC_b and V_dc are chosen according to the systems’ requirements. In this case, SOC_uc, SOC_b are chosen as a value between 0 and 100%, and V_dc,max and V_dc,min are voltage parameters based on operator’s choice. The system has three operational modes that are not enabled together, and priority of these modes is based on the followings: ① ultra-capacitor charging by DC link voltage when V_dc > V_dc,max, SOC_uc < SOC_uc,max; ② DC link capacitor charging by ultra-capacitor when V_dc < V_dc,min, SOC_uc > SOC_uc,min; ③ battery charging by ultra-capacitor when V_dc,min < V_dc < V_dc,max, SOC_uc > SOC_uc,min, SOC_b < SOC_b,max. And an auxiliary mode with following conditions: V_dc > V_dc,max, SOC_uc > SOC_uc,max.

Fig. 3

Flowchart of energy management algorithm of proposed system

Figure 4 shows the complete system diagram based on different sections, including controller, energy management system, IEM, inverter, and rectifier, where u₁, u₂ and u₃ are gating signal of S1, S2 and S3, respectively.

Fig. 4

Complete system circuit model

3 Simulation results

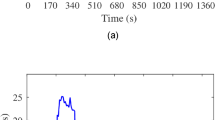
Parameters of the system are shown in Table 1. Figure 5a shows the speed characteristics of IEM during a 16 s cycle. It must be noted that the acceleration and the deceleration rates of IEM should be within a permissible range (less than 1 m/s²). As observed in the figure, the speed reaches 100 rad/s in 2 s and when braking, it decreases from 150 rad/s to 0 rad/s in 3 s.

Table 1 Parameters of electrical machine, grid and proposed drive

Fig. 5

IEM speed curve for 16-second period, IEM torque curve and DC link voltage due to IEM activity

Figure 5b shows torque curve during cycle. When the IEM accelerates, torque is positive and when the IEM brake, torque is negative. Figure 5c shows DC link voltage during this cycle. When the IEM accelerates at 5 s, V_dc drops and when IEM brakes at 11 s, V_dc increases.

The main idea of the proposed control system is to store regenerative energy in ultra-capacitor and battery. Besides that, whenever V_dc drops down, ultra-capacitor will supply DC link capacitor with its charged energy. The proposed system must work accurately based on flowchart shown in Fig. 3 and track the reference values of state variables, $I_{{L_{1} }}^{*} = 1{\text{ A}}$ (buck), $I_{{L_{1} }}^{*} = 20{\text{ A}}\,$(boost), $I_{{L_{2} }}^{*} = 2{\text{ A}}$, $V_{dc}^{*} = 500{\text{ V}}$ and $V_{uc}^{*} = 30{\text{ V}}$.

Figure 6 shows DC link voltages before and after applying the proposed system with control parameters δ₁ = −60, δ₂ = −0.2, δ₃ = −5, δ₄ = −0.1. After applying the proposed system, the extra energy resulted by braking process must be stored in ultra-capacitor. Also, DC link voltage drop resulted by acceleration process is compensated by energy stored in ultra-capacitor. As seen, at 11 s, V_dc rises during the braking of IEM. Before applying the proposed system, in this moment V_dc reaches 1800 V but after applying the proposed system, V_dc is limited near to 500 V. Energy management system decides whenever V_dc is higher than V_dc,max and SOC_uc is lower than SOC_uc,max, and then the bidirectional converter operated in buck mode. Other modes are basically applicable according to the requirements of the system and the energy management system designed in the previous section. As shown in Fig. 6, in the 5–7 s, DC link voltage drops, ultra-capacitor charges the DC link capacitor.

Fig. 6

Comparison of DC link voltage before and after applying proposed system

The energy management system works according to defined modes of Fig. 3. As seen in Fig. 7, there is not any interference between three modes, and it can be concluded that EMS works properly and in accordance with system’s needs. Reference values for modes 1, 2 and 3 are 1 A, 20 A and 2 A, respectively. As seen in the Fig. 7a ultra-capacitor charging and discharging currents are 20 A and 1 A, respectively, the same as reference values. Also, Fig. 7b shows battery charging current which is exactly 2 A, as seen the reference value is effectively followed.

Fig. 7

Currents of bidirectional converter and unidirectional converter

Figure 8 shows the SOC of ultra-capacitor and battery during the 16-second period. It can be observed that ultra-capacitor charges DC link capacitor or battery, or is charged by V_dc, and therefore the SOC of ultra-capacitor is always alternating (decreasing or increasing). However, since battery is operating only when unidirectional converter is activated, its SOC is sometime constant and the other times increasing.

Fig. 8

SOC of ultra-capacitor and SOC of battery

As seen in Fig. 1b, there is an auxiliary load that uses the energy stored in battery. Due to different reference currents of ultra-capacitors in modes 1 and 2, whenever the system operates in mode 2, SOC_uc rises sharply and whenever system works in mode 1, SOC_uc falls slowly. On the other hand, the incline of SOC_b is always constant because reference current of battery is always 2 A and doesn’t change. Because of very high amount of regenerative energy that is generated while braking, whenever the IEM enters braking mode, the SOC of ultra-capacitor sees the biggest changes. It is also observed that all of ultra-capacitor energy that is consumed by DC link capacitor and battery before 11 s, is compensated after 11 s due to braking process.

Figure 9 shows voltages during the 16-second period. It can be seen that whenever V_dc increases (and SOC_uc is lower than SOC_uc,max), bidirectional converter works in buck mode, ultra-capacitor gets charged and battery voltage remains constant. Whenever V_dc decreases, ultra-capacitor voltage decreases to charge the DC link capacitor and compensate voltage drop in DC link. In mode 3, whenever DC link voltage is in admissible range and SOC_uc is higher that SOC_uc,max, battery gets charged by the energy stored in ultra-capacitor. Whenever battery is being charged, a 0.9 V growth in battery voltage can be seen.

Fig. 9

Ultra-capacitor voltage and battery voltage

As seen in Fig. 10, the surplus energy must be consumed and dissipated in dynamic resistor to prevent any damage to DC link equipment. As seen in the figure, when the IEM starts to regenerate energy, ultra-capacitor gets charged and as soon as it reaches its maximum capacity, the surplus energy in DC link is consumed in dynamic resistor and dissipated as heat. When DC link enters its permissible range again, ultra-capacitor starts charging the battery with its stored energy. As mentioned before, only one mode can be enabled at any moment, therefore ultra-capacitor charging the battery and dynamic resistor modes can’t be enabled together.

Fig. 10

DC link voltage and SOC of ultra-capacitor

4 Conclusion

In this paper, a topology for saving regenerative braking energy in ultra-capacitor and battery was proposed. The proposed circuit is also able to compensate DC link voltage drop, while IEM needs to accelerate. The topology is based on cascade structure of DC/DC converters. The controller is designed based on Lyapunov stability theorem that guarantees system’s global stability. Simulation results validate that the proposed system works properly and all reference values are accurately tracked. It is also shown that energy management algorithm works in coordination with the controller. The proposed system can be implemented in all devices and facilities equipped with induction machines in order to store additional energy and consequently reducing the total costs.