1 Introduction

Due to technical and geographical limitations, it is difficult to extend the existing transmission and distribution lines to remote and regional areas. Hence, local power generation and distribution networks are usually built at such locations. As an example, except the towns at Australia’s east coast that are supplied through the National Electricity Market (NEM) and those few at its southwest that are supplied through the south-west interconnected system (SWIS), most towns in Australia’s regional and remote areas, in which almost 31% of the population lives, are supplied by local generators running on diesel or gas [1], which is expensive. The fuel transportation is occasionally difficult because of seasonal inaccessibility of the roads, and it pollutes the environment [2]. In addition to the lower reliability, the utilities also experience larger power losses due to long lines in those areas. This also results in high expenditures on supply, operation and maintenance. To reduce the overall cost of electricity generation, utilities prefer to use renewable energy-based distributed energy resources (DERs) within the electricity networks of remote areas [3, 4]. These systems, known as standalone microgrids (MGs), are usually designed to be self-sufficient and operate isolated [5]. As an example, the techno-economic analysis in [6] shows that the local utility supplying the rural town of Laverton in Western Australia can reduce its electricity supply cost by 70% when a group of renewable sources supplements diesel generators (DGs). Likewise, [7] shows that the levelized cost of electricity generation can be reduced by almost 50% when a set of renewable sources contributes to 75% of the total electricity demand of Rottnest Island (18 km west of Perth, Australia).

On the other hand, a large remote area can host multiple isolated MGs, each with a different operator (owner). This is highly probable because of the incentives that the governments are offering to attract private investors, for building and operating renewable sources [8]. In such a case, to improve the reliability, resiliency and self-healing of isolated MGs, it is suggested in [9,10,11] that they have some sort of physical connections amongst themselves to support each other during emergencies. The concept of coupled MGs (CMGs) has been proposed in [12] in which two or more neighboring MGs of a remote area can interconnect provisionally, to support each other during emergencies, such as power shortfalls, excessive generation and short-circuit faults [13].

This paper proposes a supervisory emergency controller (SEC) to coordinate various actions within MGs with an objective to remedy the emergencies, at least cost. The proposed SEC operates under a sequential-based multilayer scheme, and consists of soft, intermedial and hard actions. The soft actions, applied as the first resort, are adjusting the droop control parameters of the droop-regulated systems (DRSs) and charging/discharging control of battery energy storage systems (BESSs). Controlling the power exchange with neighboring MGs is the intermedial action. The hard actions, as a last resort, are curtailing some non-essential loads or no dispatchable DERS (NDDs) if the previous actions cannot remedy the emergencies. Note that the proposed SEC considers the impact of voltage and/or frequency deviations on the consumed power by the loads. A low-bandwidth communication is assumed available to transmit the required data from sensors to the secondary controllers of each MG and the central controller of remote areas. The decision outcomes from the SEC are also transmitted through this communication link to the relevant local controllers, via the secondary controllers of each MG. Noteworthy that the existing industrial processors by Intel® [14], National InstrumentsTM [15] and Analog DevicesTM [16] can be readily used to implement the proposed SEC, as they can satisfy the required processing speed and complexity.

In summary, the key advantages of the proposed SEC are:

  1. 1)

    alleviating the emergency of an MG;

  2. 2)

    realizing an acceptable voltage and frequency deviation in remote area MGs after emergencies, at least cost, while satisfying the technical constraints;

  3. 3)

    minimizing the rate of load-shedding and curtailment of NDDs in MGs.

Meanwhile, the main contributions of the paper can be summarized as:

  1. 1)

    developing an optimization-based SEC to remedy emergencies at remote-area MGs;

  2. 2)

    formulating an OF that considers controlling dispatchable DERs, curtailment of non-essential loads and NDDs, as well as the life loss value of BESSs, along with technical constraints, such as spinning reserve, the dependency of an MG to external MGs, the contribution of renewable sources and power loss in tie-lines;

  3. 3)

    validating the effective operation of the proposed technique using numerical analyses.

The remainder of the paper is organized as follows: Section 2 introduces the concept of the proposed SEC while the formulated objective function (OF) and the essential constraints are discussed in details in Section 3. The performance of the proposed technique is demonstrated through analyses in Section 4 while the main highlights and findings of the research are summarized in the last Section. Five Appendices are provided at the end of the paper that respectively discuss the operational principles of DRS, employed power flow analysis when evaluating the system and Genetic algorithm when solving the optimization problem, some possible interconnection topologies amongst neighboring MGs, and the probabilistic modeling of NDDs for the studies of this research.

2 A review of existing literature

Reference [17] provides a general overview of the control, integration and energy management within MGs while the recent advancements in control and dispatch of DERs, employed communication technologies, as well as load management and protection strategies are summarized in [18]. Considering the uncertainty of renewable sources, the reliability and load controllability of the system, various optimal planning techniques are proposed for MGs in [19,20,21]. Furthermore, [22,23,24,25,26] have discussed several methods for frequency control in MGs using DERs and BESSs.

Figure 1 shows two neighboring MGs of a remote area, connected through a tie-line and an interconnecting static switch (ISS). Under the CMG concept, an MG observing the emergency, referred to as the problem MG (PMG), can be provisionally supported by a neighboring healthy MG (HMG). Reference [27] has proposed a transformative architecture for coupling the nearby MGs to improve their resiliency during faults. References [28] and [29] identify the MG cluster with self-healing capabilities while the management of MG restoration after faults is explained in [30]. A decision-making-based approach is proposed in [31] to determine the most suitable HMGs to be coupled with a PMG, considering various criteria, such as the available surplus power, electricity cost, reliability and the distance between the neighboring MGs. Reference [32] discusses the conditions based on which the overloading of a PMG and the availability of excess power in the neighboring HMG can be detected. Reference [33] introduces interactive control of CMGs to guarantee adequate load sharing and system-wide stability. The dynamic operation of DERs within CMGs is investigated in [34] while [35] examines the dynamic security of the CMGs. The interaction among the DERs of the MGs in a CMG is studied in [36]. Reference [37] analyses the reliability aspects of a CMG while their voltage and current controllability, as well as small signal stability, are analyzed in [38,39,40]. References [41] and [42] present a technique to coordinate the CMG formation with the operation of BESSs within MGs. Coupling of MGs can be achieved by back-to-back isolating converters [43] or ISSes [29] (with a topology discussed in [44]), located between the adjacent MGs.

Fig. 1
figure 1

Two neighboring MGs forming a CMG through a tie-line and ISS and with the help of the developed SEC

Full size image

References [44] and [45] present an optimization technique to coordinate the MGs within a CMG while [46] and [47] discuss solving the least operation cost problem for CMGs, using various optimization techniques. It is shown in [48, 49] that CMGs can work in a cooperative mode, in networks with a high penetration of non-dispatchable distributed energy resources (NDDs), to observe a more robust performance. The concept of CMG is also expanded to DC MGs, and [50] presents a real-time power routing within such CMGs.

Some studies aim to coordinate the power exchange among MGs, load curtailment, and control of DGs. As an example, [51] has considered the fuel consumption and emission costs of DGs, along with power exchange with the utility grid, in the formulated OF. Reference [52] discusses the impact of load curtailment in MGs by considering the sensitivities in nodal power injection and the probabilistic uncertainties of loads and renewable sources. To this end, the cost of load-shedding, as well as the expense/revenue of exchanging power between the MG and a utility feeder, is focused. Above studies aim to maximize the footprint of renewable energies in supplying the demand and minimize the contribution of DGs. However, the curtailment of renewable energy resources was not considered, which is essential in case of an excessive generation in the MG. The voltage rise problem in MGs, because of renewable energy-based DERs, is solved in [53] by curtailing their output power using droop control. On the other hand, [54] employs an optimization technique to maximize the lifetime characteristics of BESSs within MGs when compensating the variabilities of loads and renewable sources. Alternatively, a bargaining technique is used in [55] to facilitate a proactive energy trading and fair benefit sharing among remote area interconnected MGs, in which the main considered criterion is the minimization of the total operational cost. In a similar way, [56] applies demand management in remote-area MGs, using a cooperative power dispatching algorithm, to minimize the MG’s operational cost while satisfying the load demand. References [12] and [57] have formulated economic dispatch problems, which aim at minimizing the power loss on top of the costs of fuel consumption, external power sharing and BESSs. Table 1 presents a comparison of the abovementioned studies while it also compares them with the characteristics of the proposed technique in this paper.

Table 1 Comparison of the main features of considered cost minimization techniques in literature and this paper
Full size table

3 Developed technique

Consider Fig. 1, which illustrates two neighboring MGs of a remote area, with a tie-line and ISS among each other to facilitate their temporary interconnection during an emergency. The proposed SEC is an agent located within the central controller of the remote area, as shown in Fig. 1. The SEC has the following responsibilities:

  1. 1)

    fetching data and information from secondary controllers of each MG;

  2. 2)

    identifying the PMG;

  3. 3)

    solving an optimization problem (discussed in the next Section) to select the suitable actions and their level of contribution to remedying the emergency;

  4. 4)

    transmitting these decision variables to the relevant local controllers, via the secondary controllers of each MG.

Thus, the required communication links are schematically shown in Fig. 1. To this end, a low-bandwidth point-to-multipoint wireless communication technique with a suitable latency is needed [58].

Now, let us define the HMG and PMG depending upon their mode of operations (i.e., corresponding to operational voltage and frequency limits) as shown in Figs. 2 to 5, where X represents the voltage and frequency. An HMG is the MG in which the frequency and all bus voltages lie within the safe mode of operation of Fig. 2. Figure 2a presents an HMG with voltage and frequency within the desired safe zone; Fig. 2b presents a PMG with unacceptable voltage and frequency deviation; and Fig. 2c presents the schematic illustra-tion of the impact of the proposed SEC controllers. However, the MG is considered as a PMG if the frequency or a bus voltage jumps into the alarm or unsafe modes of operation, as shown in Fig. 3. In this situation, the proposed SEC will immediately retain the voltage and frequency back to the safe mode, as shown in Fig. 4. Note that as MGs are at early stages of development, no well-developed international standards are available. However, some countries that host islanded networks (more or less similar to MGs) are developing some guidelines. As an example, the Australian Energy Market Commission has recently published a technical report [59] that discusses the settings of the frequency bands and time requirements for maintaining and restoring frequency in its islanded networks. According to this report, the normal frequency range is 49.5 to 50.5 Hz in islanded operation. The frequency is allowed to deviate down to 49 and up to 51 Hz, following a generation, load or network event, but it must be restored to the normal range within 5 minutes. As such, these limits can be respectively considered as the boundaries of safe and alarm regions for frequency in Fig. 2. This paper does not aim to define these boundaries, as they can be network and country-specific.

Fig. 2
figure 2

Operation mode of HHG and PMG

Full size image
Fig. 3
figure 3

Proposed multi-stage actions for the developed SEC

Full size image
Fig. 4
figure 4

Time-sequence of actions from an event causing emergency until PMG becomes an HMG

Full size image

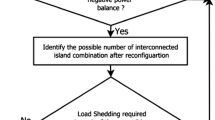
The proposed SEC is a multi-stage process in which successive layers of necessary actions are carried out to alleviate the emergencies in the PMG. These actions are schematically portrayed in Fig. 5:

Fig. 5
figure 5

Flowchart of the SEC

Full size image
  1. 1)

    soft actions: adjustment of droop parameters (i.e., droop coefficients, as well as voltage and frequency set-points) for DRSs, and power charged/discharged by BESSs;

  2. 2)

    intermedial action: determining the required power transaction with neighboring HMGs;

  3. 3)

    hard actions: defining the levels of NDDs curtailment and/or load-shedding.

The proposed SEC will firstly try to retain the voltage and frequency of the PMG within the safe mode by applying soft actions, i.e., finding the most suitable droop set-points for the DRSs, as shown in Appendix A, and required power exchange with existing BESSs. To this end, it will solve a non-linear optimization problem for the considered MG, which is described in the next Section. If successful, it will transmit the settings to the relevant local controllers of DRSs and BESSs. However, if it is not successful in resolving the emergencies in the PMG, the intermedial actions will be applied on top of the soft actions. Within the intermedial action, the SEC checks the availability of a neighboring HMG. If an HMG is found available to support the PMG, the SEC will solve an optimization problem to determine the suitable power transaction in the tie-lines within the desired CMG on top of the control variables of soft actions. If an HMG is not available or no feasible solution is found through solving the optimization problem, the SEC will apply all actions including curtailing either of the consumption of its non-essential loads or the generation output of its NDDs, as a last resort. This sequential process will guarantee that the SEC will alleviate the emergencies by the actions which are cheaper for the MG operator (such as adjustment of droop parameters and power exchange with BESSs or neighboring MGs) rather than the hard action of load-shedding or NDD curtailment, which are very expensive for them. Figure 4 schematically depicts the above-discussed operation sequence of the SEC following an event, which causes an HMG to become a PMG, until it recovers.

In summary, the transition of a PMG to an HMG includes several stages. These stages are respectively as:

  1. 1)

    the SEC defines the optimal decision variables and transmits this information to the relevant local controllers of BESSs, DGs, NDDs, loads and ISSes through a communication link;

  2. 2)

    the local controllers take action to adjust their power exchange by modifying their controllers’ set-points such that their power generation or consumption matches that defined by the SEC;

  3. 3)

    if the coupling of MGs is also required, the local controller of the ISS will use a suitable synchronization technique (such as the one proposed in [60]) to facilitate the correct sequence of the closing of ISSes, to provide a smooth power transfer from one MG to another.

At this stage, all required actions have taken place, and the frequency and voltage of PMG will be retained to the safe zone. Figure 5 illustrates the operational flowchart.

It is to be emphasized that, this paper has only focused on the SEC, which is an agent within the central controller of the remote area, as shown in Fig. 1. Hence, the central controller in the remote area is an entity that represents all MGs fairly and coordinates their operation during emergencies, such as power shortfalls, excessive generation and short-circuit faults, which have resulted in unacceptable voltage or frequency deviation. On top of the proposed SEC and independent from that, each MG has a secondary controller, which is owned by the respective operator of MG. And one of its functionalities is predicting the MG’s demand and the expected generation from NDDs in various horizons, e.g., year, season, month, day, 60-min, 30-min ahead, to be able to optimally operate the MG [61,62,63,64].

4 Problem formulation and technical constraints

An optimization problem is formed to determine the most economical solution to remedy the overloading or over-generation issue, which has subsequently caused under-voltage/frequency and over-voltage/frequency in the PMGs. This is formulated as an OF which is solved within the SEC to yield the most feasible solution while minimizing the overall operational cost and maximizing the footprint of renewables and spinning reserve and satisfying the considered technical constraints. It is formulated as a multi-objective problem with an OF in the following form:

$$ OF = w_{1} OF_{\text{tech}} + w_{2} OF_{\text{oper}} + w_{3} OF_{\text{cont}} $$
(1)

where \( OF_{\text{tech}} ,OF_{\text{oper}} \) and \( OF_{\text{cont}} \) are respectively the OFs denoting the technical, operational and desirable conditions in the CMG and the isolated PMG(s); and \( w_{1} \) to \( w_{3} \) are the weightings of the considered OFs. The calculated OF highly depends on the assumed weightings related to each OF; therefore, it is important to carefully select them. In power systems that have complex configurations, there is no systematic methods to define these weightings; however, an acceptable method is a census by the experts of the field to get their opinions on the importance of each OF [31]. The experts may express the importance in either form of a number (i.e., 0 to 100%) or linguistic (e.g. extremely/very/little big/small or neutral). Then these replies can be mapped into a digit in the range of {[0, 1]} and normalized. At the end, the weighting of each OF will be defined as the average of all normalized values as:

$$ w = \mathop \sum \limits_{k} w_{k} /N_{ \exp } $$
(2)

where \( N_{ \exp } \) is the number of experts participated in the census. For simplicity, it is assumed that \( w_{1} = w_{2} = w_{3} \) (i.e., equally important OFs).

In (1), \( OF_{\text{tech}} \) aims at selecting those sets of decision variables (actions) that yield the minimum voltage and frequency deviation in the CMG and the isolated PMGs. It is expressed as:

$$ OF_{\text{tech}} = \left| {\Delta f} \right| + \hbox{max} \left( {\left| {\Delta V_{i} } \right|} \right) + VI_{\text{vio}} \cdot PE_{\text{pe}}$$
(3)

where \( \left| {\Delta V_{i} } \right| \) and \( \left| {\Delta f} \right| \) represent respectively the level of voltage magnitude deviation in each buses of the MGs within the CMG and the isolated PMGs, and the corresponding frequency deviation (p.u.); and \( PE_{\text{pe}} \) is selected as a large value (e.g., 108) to eliminate the sets of decisions that violate any of the constraints or cause unacceptable voltage and frequency deviation or overloading the lines. Thus, the \( VI_{\text{vio}} \) is defined as:

$$ VI_{\text{vio}} = V_{\text{vio}} + I_{\text{vio}} + f_{\text{vio}} + CO_{{{\text{con}},{\text{vio}}}} $$
(4)

where

$$ V_{\text{vio}} = \left\{ {\begin{array}{*{20}l} 1 & {\exists \left| {V_{i} } \right| > \Delta V^{ \hbox{max} } \quad \forall i \in {BUS}} \\ 0 & {\text{otherwise}} \\ \end{array} } \right. $$
(5)
$$ I_{\text{vio}} = \left\{ {\begin{array}{*{20}l} 1 & { \exists \left| {I_{i} } \right| > I^{ \hbox{max} } \quad \forall i \in {LINE}} \\ 0 & {\text{otherwise}} \\ \end{array} } \right. $$
(6)
$$ f_{\text{vio}} = \left\{ {\begin{array}{*{20}l} 1 & { \left| {\Delta f} \right| > \Delta f^{ \hbox{max} } } \\ 0 & {\text{otherwise}} \\ \end{array} } \right. $$
(7)
$$ CO_{\text{cons,\,vio}} = \left\{ {\begin{array}{*{20}l} 1 & {{\text{if a constraint is not met}}} \\ 0 & {\text{otherwise}} \\ \end{array} } \right. $$
(8)

where \( \Delta V^{ \hbox{max} } \), \( \Delta f^{ \hbox{max} } \) and \( I^{ \hbox{max} } \) are respectively the permissible limits for voltage deviation, frequency deviation and the maximum line loading limit. Also, \( {BUS} \) and \( {LINE} \) are sets representing the buses and lines of the CMG and the isolated PMGs. These parameters are calculated from a power flow function as shown in Appendix B.

\( OF_{\text{oper}} \) in (1) aims at minimizing the overall operational cost of DGs, BESSs, power loss and power transaction within the CMG and the isolated PMGs. It also considers penalties because of curtailing NDDs or non-essential loads and emitting greenhouse gases. It is formulated as:

$$ OF_{\text{oper}} = \mathop \sum \limits_{k} (OF_{\text{DG}} + OF_{\text{BESS}} + OF_{\text{curt}} + OF_{\text{trans}} + OF_{\text{loss}} ) T \quad \quad \quad \quad \forall k \in {MG} $$
(9)

where \( OF_{\text{DG}} ,OF_{\text{BESS}} \) and \( OF_{\text{curt}} \) are respectively the OFs denoting the running cost of the DGs, life loss cost of BESSs, and the penalty cost of curtailing NDDs and non-essential loads of all MGs within the CMG and the isolated PMGs; \( OF_{\text{trans}} \) denotes the power transaction costs for selected HMGs within the CMG while \( OF_{\text{loss}} \) represents the corresponding cost of power loss in the tie-lines between the MGs of the CMG; The set \( {MG} \) includes the MGs within the CMG and the isolated PMGs while \( T \) is the total time required for the system to operate under the new condition, which is equal to \( \Delta T \) of Fig. 3c. The abovementioned OFs are derived respectively as:

$$ OF_{\text{DG}} = \mathop \sum \limits_{k} \left( {C^{\text{fuel}} + C^{\text{cfp}} \partial_{k} } \right)P_{k}^{\text{DG}} \quad \quad \quad \quad \forall k \in {DG} $$
(10)
$$ OF_{\text{BESS}} = \mathop \sum \limits_{k} C^{\text{BESS}} \left| {P_{k}^{\text{BESS}} } \right| \quad \quad \quad \quad \forall k \in {BESS} $$
(11)
$$ OF_{\text{curt}} = \mathop \sum \limits_{{k_{1} }} C_{\text{curt}}^{\text{NDDs}} P_{\text{curt}}^{\text{NDDs}} + \mathop \sum \limits_{{k_{2} }} C_{\text{curt}}^{\text{load}} P_{\text{curt}}^{\text{load}} \quad \quad \quad \quad \forall k_{1} \in {NDD} ,\quad k_{2} \in {LOAD} $$
(12)
$$ OF_{\text{trans}} = \mathop \sum \limits_{k} C^{\text{trans}} \left| {P_{k}^{\text{trans}} } \right|\quad \quad \quad \quad \forall k \in {MG} $$
(13)
$$ OF_{\text{loss}} = \mathop \sum \limits_{k} C^{\text{loss}} P_{k}^{\text{loss}} \quad \quad \quad \quad \forall k \in {LINE} $$
(14)

In (10), \( OF_{\text{DG}} \) aims to minimize the running cost of power generation by DGs (denoted by C in $/kWh) which includes the cost for fuel consumption and the corresponding Carbone footprints (respectively denoted by \( {\text{fuel }} \) and cfp) where\( \partial_{k} \) is the emission ratio (in kg/kWh). As the BESS does not have any ongoing operational costs, only the cost of its life loss is considered in \( OF_{\text{BESS}} \) in (11). Similarly, the corresponding cost of curtailing the generated power of NDDs by \( P_{\text{curt}}^{\text{NDDs}} \) and the consumed power of non-essential loads by \( P_{\text{curt}}^{\text{load}} \) (respectively denoted by \( C_{\text{curt}}^{\text{NDDs}} \) and \( C_{\text{curt}}^{\text{load}} \) in $/kWh) is used in (12) to determine \( OF_{\text{curt}} \). The corresponding cost of power transaction (\( \left| {P^{\text{trans}} } \right| \) in kW) over the tie-lines between the MGs of the CMG (denoted by \( C^{\text{trans}} \) in $/kWh) is used in (13) to define \( OF_{\text{trans}} \). Equation (14) aims at minimizing the power loss in the tie-lines between MGs of the CMG (\( P^{\text{loss}} \) in kW) when calculating \( OF_{\text{loss}} \) while \( C^{\text{loss}} \) is the associated power loss cost (in $/kWh). In (10)-(14), \( {DG}, {BESS}, {NDD} \) and \( {LOAD} \) are respectively sets representing the DGs, BESSs, NDDs, and loads in the MGs within the CMG and the isolated PMGs.

\( OF_{\text{cont}} \) in (1) aims at maximizing the contribution of NDDs in the overall demand supply, as well as maximizing the spinning reserve of the CMG and the isolated PMGs. It is formulated as:

$$ OF_{\text{cont}} = \left( {1 - RPL} \right) + \left( {1 - SRI} \right) $$
(15)

where \( RPL \) represents the renewable penetration level (RPL) of the CMG or isolated PMG, and is defined from

$$ RPL = \frac{{\mathop \sum \limits_{{k_{1} }} P^{\text{NDD}} }}{{\mathop \sum \limits_{{k_{2} }} P^{\text{load}} }}\quad \quad \quad \quad \forall k_{1} \in {NDD}, \forall k_{2} \in {LOAD} $$
(16)

to maximize the footprint of renewables at the system for any given demand while \( SRI \) is the spinning reserve index (SRI) of the MG, derived from

$$ SRI = 1 - \frac{{\mathop \sum \limits_{k} P_{k}^{\text{DG}} }}{{\mathop \sum \limits_{k} \left( {P_{k}^{\text{DG}} } \right)^{ \hbox{max} } }}\quad \quad \quad \quad \forall k \in {DG} $$
(17)

to have enough capacity in the system to respond appropriately and without being overloaded, following a sudden increase in demand or an unexpected drop in the output power of NDDs.

A genetic algorithm tool, as shown in Appendix C, is then employed to solve \( OF \) of (1) while considering the following constraint:

$$ \begin{aligned} & \mathop \sum \limits_{{k_{1} }} S^{\text{DG}} + \mathop \sum \limits_{{k_{2} }} S^{\text{NDD}} + \mathop \sum \limits_{{k_{3} }} \beta S^{\text{BESS}} + \mathop \sum \limits_{{k_{4} }} S^{\text{trans}} \\ & \quad = \mathop \sum \limits_{{k_{5} }} S^{\text{load}} \mathop \sum \limits_{{k_{6} }} S^{\text{line}} \quad \quad \quad \quad \forall k_{1} \in {DG}, \forall k_{2} \in {NDD}, \\ & \qquad \forall k_{3} \in {BESS}, \forall k_{4} \in {MG},\forall k_{5} \in {LOAD}, \forall k_{6} \in {LINE} \\ \end{aligned} $$
(18)
$$ \left\{ {\begin{array}{*{20}c} {P_{{k,{ \hbox{min} }}}^{\text{DG}} \le P_{k}^{\text{DG}} \le P_{{k,{ \hbox{max} }}}^{\text{DG}} } \\ {\left| {Q_{k}^{\text{DG}} } \right| \le \sqrt {\left( {S_{{k,{ \hbox{max} }}}^{\text{DG}} } \right)^{2} - \left( {P_{k}^{\text{DG}} } \right)^{2} } } \\ \end{array} } \right.\quad \quad \quad \quad \forall k \in {DG} $$
(19)
$$ \left\{ {\begin{array}{*{20}c} { - P_{{k,{ \hbox{max} }}}^{\text{BESS}} \le P_{k}^{\text{BESS}} \le P_{{k,{ \hbox{max} }}}^{\text{BESS}} } \\ {SoC^{ \hbox{min} } \le SoC^{k} \le SoC^{ \hbox{max} } } \\ \end{array} } \right.\quad \forall k \in {BESS} $$
(20)
$$ V^{ \hbox{min} } \le \left| {V_{k} } \right| \le V^{ \hbox{max} } \quad \quad \quad \quad \forall k \in {BUS} $$
(21)
$$ f^{ \hbox{min} } \le f \le f^{ \hbox{max} } $$
(22)
$$ I_{k} \le I_{k}^{ \hbox{max} } \quad \quad \quad \quad \forall k \in {LINE} $$
(23)

Constraint (18) shows the apparent power balance within the CMG and the isolated PMGs in which \( \beta \) is respectively +1 and −1 for the discharging and charging BESSs. Constraint (19) denotes the active and reactive power load of DGs. Likewise, the active power load and SoC limits of BESSs are given by (20). The variation limits of the voltage magnitude at all buses of the CMG or isolated PMGs and the frequency are given by (21)–(22) whereas (23) shows the current load of each line in those systems.

5 Performance evaluation

To evaluate the performance of the developed SEC in the successful alleviation of an emergency in a remote area MG, a Monte Carlo analysis is conducted in MATLAB®. An overloading or excessive NDD generation emergency is observed. The studies demonstrate that the developed SEC can effectively address the emergency of a PMG and can convert it to an HMG by finding optimal values for the assumed soft, intermedial and hard actions. A few of these study cases are described below.

First, let us consider a large remote area with six MGs (named MG-1 to MG-6) that are connected through a common central node, as illustrated schematically in Fig. 4. Other interconnection topologies are also possibleas, as shown in Appendix D; however, this paper does not aim to propose any specific topology for the interconnection of MGs.

For simplicity, all MGs of Fig. 6 are assumed to have the same topology as of Fig. 7. This is deemed acceptable as the performance (and not the outputs) of the proposed technique is independent of the assumed topologies of MG and ratings and internal characteristics of the components. Indeed, when the numerical input values, such as the Y-bus of the system and ratings of the building components, are different, the numerical outputs of the proposed SEC will be changed, as is expected from this technique. However, this will not influence the successfulness of the proposed technique in maintaining the voltage and frequency of the PMGs within the safe zone.

Fig. 6
figure 6

Possible physical communication links between MGs participating in CMG

Full size image
Fig. 7
figure 7

Topology of MGs for performance evaluation

Full size image

As seen from Fig. 7, each MG is presumed to have two photovoltaic and wind-based NDDs, one BESS and one DRS. The probabilistic modeling of the NDDs is discussed in Appendix E. It is assumed that all loads are connected to bus-4 of the MGs while the MGs can couple with a neighboring MG through an ISS and a tie-line at bus-6. The assumed nominal capacities of the loads, NDDs, DGs and BESSs of each MGs are provided in Table 2 while the impedance data for all buses of the MGs is taken from [31]. Table 3 lists the distance between the MGs while Table 4 summarizes the presumed different costs required in calculating the OF of (1).

Table 2 Considered nominal capacities for components of each MG of Fig. 4 in the numerical analysis
Full size table
Table 3 Assumed distance between each MG of Fig. 4 from central node
Full size table
Table 4 Considered costs in OF calculation of the numerical analysis
Full size table

Note that the common evaluation and validation mechanism, used by most researchers in this area, is numerical analysis. As such, researchers usually provide tables of input and output data for the assumed system, indicating the steady-state values for various parameters of the system, before and after applying their proposed technique. As such, the same approach has been used in this paper. Table 5 lists the values of the system’s critical parameters at the emergency condition and after applying the optimal decision variables, defined by the proposed SEC. Furthermore, Figs. 8 and 9 schematically illustrate the situations of the assumed MGs of Fig. 6 in these two periods. Dynamic (time-domain) results, illustrating the transition of the PMG to a HMG are beyond the scope of this work, and thus, they are not discussed here.

Table 5 Assumed steady-state inputs and results of applying the developed SEC on the important MGs in the considered study cases
Full size table
Fig. 8
figure 8

Schematic illustration of study case 1 to study case 4

Full size image
Fig. 9
figure 9

Schematic illustration of study case 5 to study case 8

Full size image

5.1 An overloaded PMG

Let us consider study case 1, as shown in Fig. 6a, in which MG-3 is defined as an overloaded PMG denoted by PMGOL because of operating within the unsafe mode with a frequency of 49.38 Hz and a minimum voltage of 0.912 p.u., both beyond the safe mode limits. As seen from Table 5, this MG has a load demand of 0.738 p.u., an SRI of below 1% and an RPL of 34%. The developed SEC proposes only soft action as the most optimal solution with an OF value of $5.26 to address the emergency of this MG and does not use any intermedial or hard actions. As a result, a support of 0.034 p.u. from the BESS is required which reduces the output power of the DRS from 0.498 to 0.446 p.u., and thus, the observed minimum voltage and frequency of the MG increase to 0.963 p.u. and 49.71 Hz, respectively.

Now, let us consider study case 2 in which MG-5 is defined as a PMGOL (i.e., a frequency drop to 49.29 Hz and a voltage drop to 0.923 p.u., both below the acceptable limits). At this condition, as seen from Table 5, the MG load demand is 0.782 p.u., its RPL is 30%, and its DRS supplies 0.548 p.u, which is nearly equal to its nominal capacity of 0.55 p.u., as seen from Table 2. Therefore, the SRI of the MG is almost zero. Without the developed SEC, the only possibility of recovering the MG into the safe mode is a load-shedding of 0.1 p.u.. Assume the implementation of the developed SEC, it takes action immediately when the voltage and frequency drop beyond the safe zone and solves this problem using a combination of soft and intermedial actions. As a result, MG-2 (an HMG with a load demand of 0.233 p.u., an RPL of 23%, a minimum voltage of 1.039 p.u., a frequency of 50.39 Hz and an SRI of 60%), along with MG-4 (an HMG with a load demand of 0.135 p.u., an RPL of 8.9%, operating at 50.41 Hz and observing a minimum voltage of 1.034 p.u. and an SRI of 58.6%), are coupled to MG-5. This is the most optimal solution with an OF value of $9. As a result, MG-5 imports a total of 0.096 p.u. (i.e., 0.067 p.u. from MG-2 and 0.039 p.u. from MG-4 after a 0.01 p.u. loss in the tie-lines) (see Fig. 8b). In addition, the DRS of MG-2 and MG-4 supply 0.224 and 0.163 p.u., respectively, which results in the DRS of MG-5 to reduce its output to 0.452 p.u.. Additionally, the BESS of MG-2 discharges 0.023 p.u.. As expected, CMG formation increases the bus voltages in MG-5, whereas they decrease in MG-2 and MG-4. Consequently, the CMG frequency settles at 50.21 Hz and a minimum voltage of 0.989 p.u. is observed throughout the CMG. As a result, CMG’s SRI becomes 35% while its RPL is 26%.

Now, let us consider study case 3 in which MG-3 is detected as PMGOL, as shown in Fig. 6c and Table 5 (with a frequency of 49.69 Hz which is within the permissible range but a minimum voltage of 0.937 p.u. which is below the minimum allowed limit). MG-3 has a load demand of 0.82 p.u., an RPL of 39% and an SRI of only 1%. The developed SEC proposes a combination of soft, intermedial and hard actions as none of the soft or intermedial actions alone can reach a feasible solution. The SEC proposes coupling of MG-1 (an HMG with a load demand of 0.206 p.u., an SRI of 52% and an RPL of 8%, and operating at a frequency of 50.32 Hz and a minimum voltage of 1.024 p.u.) to the PMG as the most economical solution which results in the optimal OF value of $8.7. Therefore, the output power of the DRS of MG-1 increases from 0.192 to 0.232 p.u., from which 0.056 p.u. is exported to the PMG while its BESS discharges by 0.016 p.u., along with a load-shedding of 0.008 p.u. in the PMG. Hence, MG-3 lowers the output of its DRS to 0.434 p.u.. Thus, the formed CMG will observe a minimum voltage of 0.987 p.u., and a frequency of 49.87 Hz along with an SRI of 74% and an RPL of 33.4%.

Now, let us consider study case 4, as shown in Fig. 8d, in which MG-2 is detected as a PMGOL with a frequency of 49.46 Hz and a minimum voltage of 0.91 p.u., both beyond the safe mode. As seen from Table 5, this MG has a load demand of 0.57 p.u., an SRI of below 1% and an RPL of 22%). The developed SEC proposes a combination of soft and hard actions as the most optimal solution with an OF value of $12.23 to address the emergency of this MG. The SEC does not use any intermedial actions for this study case. As a result, a load curtailment of 0.006 p.u., along with a 0.008 p.u. support from the BESS, reduces the output power of the DRS from 0.446 to 0.428 p.u. which will subsequently increase the observed minimum voltage and frequency to 0.955 p.u. and 49.61 Hz, respectively.

5.2 A PMG experiencing excessive generation

Consider study case 5, as shown in Fig. 9a, in which MG-5 is detected as a PMG observing excessive generation from its NDDs referred to as PMGOG and experiencing a maximum voltage and frequency of 1.056 p.u. and 50.6 Hz respectively, both beyond the safe mode limits). As seen from Table 5, MG-5 has a load demand of 0.251 p.u., an SRI of 67% and an RPL of 29%. Without the application of proposed SEC, a renewable curtailment of 0.03 p.u. is needed to retain this MG within the safe mode. The SEC finds a combination of soft and intermedial actions as the most optimal solution to address this emergency (with an OF value of $7.29). To this end, the SEC proposes the coupling of MG-5 to MG-6, which is an HMG with a load demand of 0.153 p.u., an SRI of 66.5% and an RPL of 12%, operating at a frequency of 49.7 Hz and a maximum voltage of 1.036 p.u.. As a result, MG-5 exports 0.032 p.u. out of which 0.026 p.u. is received by MG-6 considering the losses in the tie-line and all this power is charged into the BESS of MG-6. Thus, the CMG operates at a new frequency of 50.26 Hz and will observe a maximum voltage of 1.05 p.u., an SRI of 36% and an RPL of 23%.

Now, consider study case 6, as shown in Fig. 9b, in which MG-4 is detected as PMGOG (operating in the unsafe mode with a load demand of 0.20 p.u., an SRI of 44% and an RPL of 12%, with a frequency of 50.53 Hz and a maximum voltage of 1.061 p.u., both beyond the permissible limits). Without the proposed SEC, a renewable curtailment of 0.04 p.u. is required to alleviate the emergencies. The proposed SEC determines a combination of soft, intermedial and hard actions as the most suitable solution in addressing the emergency (with an OF value of $10). As a result, the SEC proposes to couple MG-1 (an HMG with a load demand of 0.32 p.u., an SRI of 26% and an RPL of 7%, operating at a frequency of 49.9 Hz and observing a maximum voltage of 1.018 p.u.) and MG-6 (an HMG with a load demand of 0.305 p.u., an SRI of 32% and an RPL of 12% operating at a frequency of 50.19 Hz and a maximum voltage of 1.036 p.u.) with MG-4. Therefore, MG-4 exports 0.045 p.u. (out of which 0.019 p.u. is imported by MG-1, whereas 0.023 p.u. is imported by MG-6 after, a total loss of 0.003 p.u.). In this period, the output power of the DRS of MG-4 increases from 0.168 to 0.205 p.u. while this value almost remains unchanged for MG-1 and MG-6. The imported power by these MGs is charged in their BESSs. Thus, the frequency in the formed CMG reaches to 49.88 Hz while a maximum voltage of 1.039 p.u. is observed. Also, the CMG observes an SRI of 29% and an RPL of 9%.

Consider study case 7, as shown in Fig. 9c in which MG-1 is detected as a PMGOG (observing a maximum voltage of 1.071 p.u. which is higher than acceptable permissible limit whereas its frequency is 50.48 Hz and within the safe mode range). This MG has a load demand of 0.346 p.u., an SRI of 74% and an RPL of 3%. The SEC defines a combination of soft and hard actions as the most suitable solution for this emergency with an OF value of $6.32. As seen from Table 5, the SEC proposes a renewable curtailment of 0.009 p.u. and a BESS charging by 0.013 p.u., which will reduce the output power of the DG from 35.6 to 0.334 p.u.. Thus, the MG will operate at a frequency of 50.21 Hz and will observe a maximum voltage of 1.032 p.u..

5.3 Multiple PMGs

Consider study case 8 (see Fig. 9d), in which MG-1 is defined as a PMGOG (observing a maximum voltage of 1.054 p.u. and a frequency of 50.61 Hz, both beyond the permissible limits of the safe mode, with a load demand of 0.132 p.u., an SRI of 67% and an RPL of 3%) while MG-4 is defined as a PMGOL (observing a minimum voltage of 0.937 p.u. and a frequency of 49.23 Hz, both beyond the permissible limits of the safe mode, with a load demand of 0.43 p.u., an SRI of almost zero and an RPL of 30%). The SEC finds a combination of soft, intermedial and hard actions in addressing this concurrent emergency in 2 of the considered MGs. To this end, the SEC proposes coupling of MG-3, which is an HMG with a load demand of 0.468 p.u., an SRI of 29% and an RPL of 24%, operating at a frequency of 51.28 Hz, and a minimum and maximum voltages of respectively 0.98 and 1.016 p.u., and MG-5, which is an HMG with a load demand of 0.296 p.u., an SRI of 46% and an RPL of 1%, observing a frequency of 49.59 Hz, and a minimum and maximum voltages of respectively 1.025 and 1.038 p.u., with both PMGs as the most optimal solution (with an OF value of $11.45). Therefore, MG-1 and MG-5 export respectively 0.074 and 0.065 p.u. while MG-3 and MG-4 import respectively 0.07 and 0.063 p.u.. The BESS of MG-1 and MG-3 charges by 0.031 and 0.037 p.u., respectively while the BESS of MG-5 discharges by 0.04 p.u.. Hence, the output power of the DRS of MG-1, MG-3 and MG-5 increases from 12.9, 35.4 and 29.2 to respectively 0.234, 0.387 and 0.32 p.u., whereas this figure decreases from 0.298 to 0.223 p.u. for MG-4. Thus, the frequency of the CMG reaches 49.77 Hz and observes minimum and maximum voltages of respectively 0.987 and 1.039 p.u.. It also has an SRI of 66% and an RPL of 16%.

5.4 Summary of study cases

The above eight study cases summarized in Table 6 are a few samples of a stochastic-based Monte Carlo analysis, conducted to investigate numerous emergencies and the corresponding taken actions by the proposed SEC. As seen from this table, depending on the assumed conditions for each study case, the proposed SEC has taken various actions. As an example, study cases 1 to 3 are illustrating an overloading emergency. In study case 1, the emergency is rectified by only soft actions while in study case 2, a combination of soft and intermedial actions was needed. Likewise, study case 3 shows an example in which all actions were vital to remedy the emergencies. On the other hand, study cases 5 to 7 are showing excessive generation-related emergencies. Meanwhile, study case 8 shows an example of observing two simultaneous emergencies in the remote area (i.e., an overloaded PMG and another PMG with excessive generation). Also, one group of study cases (i.e., study cases 2, 3, 5, 6 and 8) are examples in which a CMG is formed while another group (i.e., study case 1, 4 and 7) are examples of no CMG formation.

Table 6 Assumed study cases including considered emergency and taken actions by SEC to remedy emergencies
Full size table

6 Conclusion

This paper has presented a multi-stage SEC to remedy the overloading and excessive generation emergencies of MGs in remote areas. The controller is activated as soon as the voltage or frequency of an MG drops beyond the safe mode. It then determines a set of actions to alleviate the emergencies and recover the MG to the safe mode of operation. The alternatives are soft actions, such as adjustment of the droop parameters of the DRSs and charging/discharging control of BESSs, the intermedial action of power exchange with neighboring MGs, as well as the hard actions of load-shedding or renewable curtailment, which are considered on a sequential basis. The formulated OF aims to reduce the operational cost of conventional DGs while maximizing the RPL and SRI, along with minimizing the power loss in the tie-lines amongst MGs, as well as the frequency and voltage deviation. Through a Monte Carlo analysis in MATLAB®, the successful operation of the proposed technique is validated for a wide range of emergencies in an assumed large remote area, consisting of multiple MGs.

This paper only considers the direct connection of neighboring MGs to each other (i.e., via three-phase ac lines). However, they can also connect through a DC line with voltage source converters at two sides of the line. This will help the neighboring MGs to form a CMG and exchange power with each other, while each MG will operate at a separate frequency. Modifying and developing the proposed technique to cater such connection topologies can be an avenue of future research in this area.