Optimal configuration problem identification of electrical power cable in tidal turbine farm via traveling salesman problem modeling approach

Abstract

Electrical power cables in tidal turbine farms contribute a significant share to capital expenditure (CAPEX). As a result, the routing of electrical power cables connecting turbines to cable collector hubs must be designed so as to obtain the least cost configuration. This is referred to as a tidal cable routing problem. This problem possesses several variants depending on the number of cable collector hubs. In this paper, these variants are modeled by employing the approach of the single depot multiple traveling salesman problem (mTSP) and the multiple depot mTSP of operational research for the single and multiple cable collector variants, respectively. The developed optimization models are computationally implemented using MATLAB. In the triple cable collector cable hub variant, an optimal solution is obtained, while good-quality suboptimal solutions are obtained in the double and single cable collector hub variants. In practice, multiple cable collector hubs are expected to be employed as the multiple hub configurations tend to be more economic than the single hub configurations. This has been confirmed by this paper for an optimal tidal turbine layout obtained with OpenTidalFarm. Suggestions are presented for future research studies comprising a number of heuristics.

Introduction

Tidal current energy (TCE) is considered to be one of the few renewable energy technologies to reach the required stage for entry to market within the next few years. In accordance with the International Renewable Energy Agency, the technology readiness level (an internationally accepted metric for technology deployment, originally conceived by National Aeronautics and Space Administration) of TCE is in the scale range 7–8, which is the most advanced of all ocean renewable energy technologies [1].

The deployment of TCE on a large scale depends on two major inter-related factors: TCE turbine technology and geographical site TCE resource assessment. An up-to-date review of TCE turbine technology is provided in [2]. There exists an extensive reported study on the tidal resource assessment of specific geographical sites around the world [3,4,5,6]. The progress of the deployment of TCE is closely related to two inter-related cost elements: capital expenditure (CAPEX) and the levelized cost of energy (LCOE) [7, 8], where it is shown that the layout of a TCE turbine farm plays an important role in the determination of these cost elements. Tidal farm layout in turn depends on the placement of turbines within the fluid flow field in the geographical site under consideration [9,10,11,12].

As with other renewable ocean energy technology systems, the major components of CAPEX in TCE are the turbine arrays and the electrical systems (generators, power cables, submarine connectors, and onshore substations), whereby in general the electrical system cost is typically 25% of the total cost of the tidal farm [13]. In [14], it is pointed out that the substantial share of electrical systems, and particularly power cables, in total cost may, if not appropriately determined, play an adverse role in delaying the deployment of TCE. In [14], it is also shown that there are two major types of cable collector placements in a tidal farm: a single collector hub placement and a multiple hub placement.

Despite the important role that power cable cost plays in the total CAPEX of a tidal turbine farm, only one study has been reported on the quantitative assessment of its cost, in contradistinction to the corresponding problem in offshore wind turbine farms [15, 16]. In so far as electrical power cable routing and collector point placement are concerned, the two major questions that need to answered are as follows:

• 1) For the single hub collection case, which turbines are interconnected by power cables and in which sequence are these connected to the single hub?

• 2) For the multiple hub collection case, which sequence of turbines are connected to which hub?

These problems may be modeled within the framework of the classical traveling salesman problem (TSP) of operational research [17], which possesses extensive literature on its numerous variants [18] for a review of the TSP. In [16] the TSP modeling approach has been adopted and a genetic programming heuristic has been employed to solve the cable routing problem for the single hub collection case. In the study presented in this paper, not only the single hub problem but also the multiple hub problem have been formulated as variants of the TSP problem and solved employing the MATLAB/intlinprog branch-and-bound based module.

The paper is organized as follows. In Section 2, a general problem description is presented. In Section 3, a concise problem statement is furnished for both the single hub and the multiple hub electrical power cable routing problems. This is followed, in Section 4, by presenting the corresponding TSP models for each variant of the TSP problem and their computational implementation in MATLAB/intlinpog, and solutions employing the optimal tidal farm design in OpenTidalFarm. The paper is concluded in Section 5 by the assessment of the TSP modeling approach and the indication of possible future research directions on the tidal cable routing problem.

Problem characteristics

In the problem under consideration in this paper, starting with a given tidal turbine farm layout, electrical power that is generated by each turbine needs to be collected through electrical cables in one or more hubs for exportation to the electrical grid. The purpose of a hub is to collect three-phase electrical power cables and maintain a dry and secure environment for the enclosed electrical circuits during the deployment of a tidal turbine farm throughout its operational lifetime (typically twenty-five years). It is worth noting that the electrical power cables are expensive, e.g., $500 per meter. Furthermore, substantial lengths of cables are required in view of the offshore distances involved in connecting the turbines with each other and with the hub(s).

The connections of the cables from all tidal turbines to the hub(s) needs to be designed in the most economical way in view of the highly expensive electrical power cables, while also fulfilling its function. The required optimal design may be modeled via mathematical programming; however, being a combinatorial optimization model, it is best modeled employing the TSP framework. This is the modeling approach that is adopted in this paper, and this constitutes the major original contribution of this paper.

Problem statement

As stated in Sections 1 and 2, the tidal cable routing problem may be formulated via the TSP approach. The TSP approach is adopted in this paper and extended to the multiple hub problem. Prior to presenting the TSP formulations for the single and multiple hub problem variants employed in this paper, a concise problem statement is presented in the following subsection.

Single hub problem statement

Given the following pieces of information:

• 1) A set of identical tidal current turbines, with each of which a spatial location and a nominal power rating are associated.

• 2) A set of identical electrical power cables, with each of which a unit cost per length and a maximum electrical power capacity are associated.

• 3) A single collection point with each of which a spatial position and a distance from shore are associated.

• 4) Each turbine possesses at most one input cable segment and at most one output cable segment.

• 5) For each turbine pair and each inter-turbine cable segment, a cable segment length (distance between a turbine pair) and a cable power flow are associated.

It is necessary to find the least cost cable routing configuration, which will be the configuration using the shortest cable length.

In the single hub problem, the multiple traveling salesmen problem (mTSP) model is employed [18], which may be stated as follows.

$$\hbox{min} \, \sum\limits_{(i,j) \in T} {c_{ij} } x_{ij}$$

(1)

s.t.

$$\sum\limits_{j = 2}^{n} {x_{1j} } = \, C$$

(2)

$$\sum\limits_{j = 2}^{n} {x_{j1} } = \, C$$

(3)

$$\sum\limits_{i = 1}^{n} {x_{ij} } = \, 1 \qquad j = 2,3, \ldots ,n$$

(4)

$$\sum\limits_{j = 1}^{n} {x_{ij} } = \, 1 \qquad i = 2,3, \ldots ,n$$

(5)

$$u_{i} + \left( {L - 2} \right)x_{1i} - x_{i1} \le L \qquad i = 2,3, \ldots ,n$$

(6)

$$u_{i} + x_{i1} \ge 2\qquad i = 2,3, \ldots ,n$$

(7)

$$u_{i} - u_{j} + Lx_{ij} + \left( {L - 2} \right)x_{ji} \,\le\, L - 1 \qquad 2 \le i \ne j \le n$$

(8)

$$\sum\limits_{j = 2}^{n} { {c_{i1} } } = 0$$

(9)

$$x_{ij} \in \left\{ {0,1} \right\} \qquad\forall \left( {i,j} \right) \in V$$

(10)

where i, j denote index pair for cable segment connecting turbines i and j; C denotes set of cables; L denotes maximum allowed number of turbines connected to one cable (electrical power flow capacity); T denotes set of turbines; c_ij denotes cost of cable segment connecting turbines i and j; x_ij denotes binary variable, 1 if turbines i and j are connected, and 0 otherwise; u_i denotes number of connected turbines by cable C and passing through turbine i.

Objective function (1) depicts the total cost of electrical power cable segments employed. Constraints (2) and (3) ensure that exactly C cables leave from and return to the hub. Constraints (4) and (5) are the degree constraints. The inequality given in (6) serves as an upper bound for the number of turbines connected with one cable. Inequality (7) serves to initialize the value of u_i to 1 if and only if i is the first connected turbine for a given cable. The inequalities given in (8) ensure that u_j = u_i + 1 if and only if x_ij = 1. Thus, they prohibit the formation of any subtour between nodes in T; i.e., they are the subtour elimination constraints (SECs) of the mTSP model. Constraint (9) ensures that the cost of a cable segment returning to the hub is equal to 0. Constraint (10) defines the domain of the decision variables.

The hub is numbered as node 1 in this model. There is no lower limit to the number of turbines connected to one cable in this model, but this can also be implemented by adding a constraint to set a lower limit, say K. The number of separate cables C connecting hub and turbines must be predefined by the user as a parameter, which is varied as part of the solution strategy of the model.

Multiple hub problem statement

Given the following pieces of information:

• 1) A set of identical tidal current turbines, with each of which a spatial location and a nominal power rating are associated.

• 2) A set of identical electrical power cables, with each of which a unit cost per length and a maximum electrical power capacity are associated.

• 3) A set of cable collection points, with each of which a spatial position and a distance from shore are associated.

• 4) Each tidal turbine possesses at most one input electrical cable segment and at most one output electrical cable segment.

• 5) For each tidal turbine pair and each inter-turbine electrical cable segment, an electrical cable segment length and an electrical cable power flow are associated.

It is necessary to find the least cost electrical cable routing configuration, which will be the configuration using the shortest cable length.

The same notation is employed in the multiple hub optimization model as that in the single hub model, albeit with some modification. In the multiple hub problem, several hubs are connected to several cables. In order to include this possibility in the multiple hub optimization problem model, the set of nodes is divided into two subsets; i.e. the set of nodes V = D ∪ V’, where D represents the set of hub nodes, D = {1, 2, …, d} and V’ represents the set of turbine nodes, V’ = {d + 1, d + 2, …, d + n}. At each hub node, there are m_i cable segments as input and as output.

In the multiple hub problem, the mTSP model is employed [18], which may be stated as follows.

$$\hbox{min} \, \sum\limits_{(i,j) \in A} {c_{ij} x_{ij} }$$

(11)

s.t.

$$\sum\limits_{j \in V} {x_{ij} } = m_{i} \qquad i \in D$$

(12)

$$\sum\limits_{i \in V} {x_{ij} } = m_{j} \qquad j \in D$$

(13)

$$\sum\limits_{j \in V} {x_{ij} } = 1 \qquad i \in V$$

(14)

$$\sum\limits_{i \in V} {x_{ij} } = 1 \qquad j \in V$$

(15)

$$u_{i} + (L - 2)\sum\limits_{k \in D} {x_{ki} } - \sum\limits_{k \in D} {x_{ik} } \le L \qquad i \in V$$

(16)

$$- u_{i} - \sum\limits_{k \in \,D} {x_{ki} } \le 2 \qquad i \in V$$

(17)

$$u_{i} - u_{j} + Lx_{ij} + \left( {L - 2} \right)x_{ij} \le L - 1 \qquad i \ne j; \, i,j \in V$$

(18)

$$\sum\limits_{i \in V} {{c_{ik} } } = \, 0 \qquad k \in D$$

(19)

$$x_{ij} \in \left\{ {0,1} \right\} \qquad \forall \left( {i,j} \right) \in V$$

(20)

Objective function (11) depicts the total cost of the electrical power cable segments employed. For each i ∈ D, m_i outward and m_i inward arcs are guaranteed by constraints (12) and (13). Equations (14) and (15) are the degree constraints for the customer (turbine) nodes. Constraints (16) and (17) impose bounds on the number of nodes a salesman (cable) visits together when initializing the value of the u_i as 1 if i is the first node visited on the tour. Constraint (18) is a sub-elimination constraint (SEC) in that it breaks all subtours between the customer (turbine) nodes. Constraint (19) ensures that there is no cost related to the return from the last visited turbine to the hub. Constraint (20) defines the domain of the decision variables.

Computational implementation

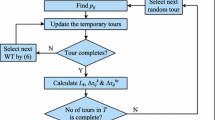
The solutions of the mTSP and the multiple depot mTSP models for the single hub and multiple hub optimal electrical cable layout problems, respectively, have been computationally implemented using the MATLAB/intlinprog module for mixed integer programming, which is based on the branch-and-bound heuristic algorithm [19]. It is worth noting that the MATLAB/intlinprog module has been used as it is implemented in MATLAB. The branch-and-bound algorithm, named after the work of [20], has become the most commonly used tool for solving NP-hard optimization problems. The branch-and-bound method consists of a systematic enumeration of candidate solutions by means of a state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set as the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm. The algorithm depends on the efficient estimation of the lower and upper bounds of a region/branch of the search space and approaches exhaustive enumeration as the size (n-dimensional volume) of the region moves to zero. To get an upper bound on the objective function, the branch-and-bound procedure must find feasible points. There are techniques for finding feasible points faster before or during the branch-and-bound procedure. Currently, the MATLAB/intlinprog module uses these techniques only at the root node, not during the branch-and-bound iterations. Figure 1 shows the flowchart.

Fig. 1

Flowchart of proposed procedure to solve tidal turbine farm electrical power cable optimal configuration problem via traveling salesman problem modeling approach

The problem for the MATLAM/intlinprog module is a general optimization problem, i.e.,

$$\min \;\varvec{f}^{\text{T}} \varvec{x}$$

(21)

where f is a column vector of constants and x is the column vector of unknowns. This module functions with both equality and inequality constraints, and is thus suitable for the cable layout problem under consideration.

The optimal tidal farm employed as an example is taken from the open-source model OpenTidalFarm, which consists of thirty-two turbines deployed in a rectangular channel of 640 m × 320 m. The array occupies an area of 320 m × 160 m located at the center of the channel. There are two standard layout configurations in tidal farms: in-line and staggered, which are shown in Fig. 2 and Fig. 3, where red diamond denotes tidal turbine. In general, under uniform flows, the staggered configuration yields larger power outputs than the inline configuration. Through layout optimiztion, the power output can be further increased, as is the case of the optimal array layout in Fig. 4 employed in this work as a basis for determining the optimal electrical cable routing configuration.

Fig. 2

In-line turbine layout

Fig. 3

Staggered turbine layout

Fig. 4

Optimal turbine layout

It should be noted that the turbines are placed in a flat bottom field.

Single hub problem

As stated above, the mTSP model formulation is used for the single hub problem. The objective function in the MATLAB/intlinprob module is a sum of terms, each of which contains each distance corresponding to each possible combination between the turbines. The last elements in this vector are set to zero, as there does not exist a cost/distance related to these elements.

In the implementation of the mTSP problem in the MATLAB/intlinprog module, iterations are made by changing the position of the single hub and the number of cables. As a preliminary step in the implementation, the number of cables has been set in the interval 6–9. The value of 6 cables has been selected, in view of the fact that the power capacity of each turbine has a minimum of 6 cables. The value of 9 cables has been chosen, as the computational cost significantly increases at higher values than that of 9; furthermore, preliminary computational experiments have demonstrated that the minimum cost/distance is reached with less than 9 cables.

Three scenarios have been implemented for the single hub problem, whereby the single hub has been placed in the middle of the field (y = 194 m), at an intermediate position between the top and the middle of the field (y = 223 m), and at an intermediate position between the middle and the bottom of the field (y = 154 m). The results of the optimization scenarios are shown in Table 1.

Table 1 Single hub optimization results for an array of 32 turbines with a cable capacity of 6 kV

In Table 1, the term “relative gap” refers to the difference between the current value and the lower bound of the objective function. From Table 1, it may be observed that the best optimal value is obtained at the seventh row, shown in bold letters and numbers, whereby the cable length equals 1478.9 m, which is 15.3% higher than the lower bound, employing 8 cables, and the single hub is placed at y = 194 m. Figure 5 illustrates the optimum cable layout solution for the single hub problem.

Fig. 5

Optimal cable layout for single hub problem

Multiple hub problem

As stated above, the multiple depot mTSP model formulation is employed for the multiple hub problem. Two cases are considered: two hubs and three hubs, as it is not necessary to employ more than 3 hubs in full scale tidal farms. Preliminary computational tests have been carried out for both two and three hubs, using different multiple hub locations, with a view to acquiring information with regard to the variation of cable cost/distance with hub locations. The major observation is that computational time taken by the MATLAB/intlinprob module increases substantially, as many more nodes are explored. The results of the double and triple hub cases are presented in Sections 4.2.1 and 4.2.2, respectively.

Double hub case

As the field extends from x = 160 m to x = 480 m, three different combinations are tested. In each combination, equal distances between the hubs are used. The optimization results are presented in Table 2.

Table 2 Optimization results of double hub case

As can be observed from Table 2, although an optimal has not been found, the suboptimal solution obtained is a feasible one with a fairly small relative gap, which is shown in the third row, and depicts a good quality optimal solution.

Triple hub case

Two different combinations have been tested. As in the double hub case, equal distances between the hubs have been used. The optimization results are presented in Table 3.

Table 3 Optimization results of triple hub case

As can be observed in Table 3, an optimal solution has been obtained for the first combination which is shown in the first row. A good quality suboptimal solution has been found for the second combination, which is shown in the second row.

Conclusion

The study reported on in this paper has shown that the single and multiple collector hub problems of electrical power cable routing in tidal turbine farms can be successfully modeled using the single depot mTSP approach and the multiple depot mTSP approach, respectively. This is the major original contribution of this paper. As to be expected, the three hub case results in the cheapest cable routing, in comparison with the double and single hub cases, notwithstanding that in using the MATLAB/intlinprog computing module, an optimal solution is obtained for the triple hub case, while good suboptimal solutions are obtained for the double and single hub cases.

The main limitation in using MATLAB is that it requires you to set the amount of cables, and/or hubs for the multiple hub version. Consequently, in order to find optimal solutions, computational runs are necessary for different settings of cables and hubs. Furthermore, for larger fields of turbines than that in the OpenTidalFarm, the TSP algorithm becomes very expensive in terms of computing time. The optimization approach used in MATLAB is based on the branch and bound algorithm, which may not be the best algorithm for this problem. Other heuristic algorithms, such as the Lagrangian relaxation and particle swarm optimization methods need to be explored and assessed in future research studies for addressing the optimal tidal cable routing configuration problem. Another approach that is worth exploring in future research studies is the shortest path problem approach, such as Dijkstra’s algorithm and extensions thereof, such as A*. By doing this, it may be possible to obtain optimal solutions for different amounts of cables/hubs by running the algorithm once and thus reducing the computational time for solving the problem for large scale tidal turbine farms.