1 Introduction

In recent years, renewable energy is widely used in the power system to solve the increasing energy crisis and environmental problems. In a modern power system, the penetration of renewable energy is much higher than ever before. The three-phase voltage source converter (VSC) is one of the key pieces of equipment to make full use of renewable energy because it can provide a sinusoidal current to the grid and flexible power control [1, 2]. However, the stability of the grid-connected VSC will affect the safety and stability of the power system in such a situation [3].

There are two main ways to perform the stability analysis of grid-connected converter systems [4]. One is the time domain method based on the state space model [5] and the other one is the frequency domain method which is based on the impedance model [6]. The time domain method is mainly suitable when the root locus analysis determines that the frequency is not changing, given a unified model of the grid-connected system [7, 8]. Thus, the stability analysis will be very complex when considering the influence of the phase-locked loop (PLL) and the grid impedance [9].

The frequency domain method is based on the impedance model which includes the impedance of the grid and the power converter and uses them to represent their external characteristics. Then, the stability of the system can be judged by stability criteria like the Nyquist criterion [10]. The impedance of the grid can be easily obtained by measuring through experiments or from a given X/R ratio [11]. However, the impedance of the converter is hard to obtain because of the various and complex control strategies and circuit parameters.

Much research effort has been devoted to impedance modeling of three-phase voltage source converters. In [12], several small-signal analysis methods used for modeling electric ship power systems are discussed. The conventional small-signal linearization techniques cannot be directly used because of the lack of a constant operating point during the periodic steady-state operation trajectory. Belkhayat linearized the system in the dq-coordinate reference frame by transforming the fundamental component into DC quantities in [13]. Then the nonlinearity can be eliminated to develop a small-signal model which can be used for control design and system stability analysis at a given operation point. But it is not suited for unbalanced conditions and provides no clear physical meaning for the d-axis and q-axis impedances. In [14], an impedance model of a three-phase VSC is proposed in the dq-frame considering the effect of PLL’s and the control strategy’s parameters. But the impedance in the dq-frame is hard to measure directly, and the stability criterion in the dq-frame is too complicated to be used in practice [4]. In [15], a small-signal model of a PV inverter containing the PLL and DC-side voltage and inner loops was proposed. It illustrates the PLL impacts on the output q-channel impedance of the inverter which can lead to instability. However, the coupling between the d-q channels has not been considered. In [16], a d-q impedance matrix of the inverter was proposed to analyze the stability of the system. In [17], the same model was used for analyzing stability of three-phase paralleled converters. The q-q channel impedance interaction leads to instability of the system. However, it is hard to obtain such impedances without some special equipment and instruments. The research above mainly focusses on situations of balanced grid voltage. However, there is still a gap because there is no mature method for impedance modeling of the VSC under practical three-phase unbalanced condition.

Harmonic linearization [18] is a method to transform a nonlinear periodically time varying system into a small-signal linear model, and has been successfully realized to get the impedance of uncontrolled diode rectifiers [6, 19] and single-phase PFC converters [20] as well as grid-connected inverters [21, 22]. Particularly, in [21, 22], the positive and negative sequence impedance model is proposed in a static frame and then can be applied in stability analysis. In [22], an impedance-based stability analysis method is studied initially for a grid-connected inverter working under unbalanced grid voltage. However, the method in this paper neglects the coupling effects between the positive and negative sequence impedances. Knowing the sequence admittance of a VSC under sustained grid faults is helpful for judging the stability of the grid-connected converter system [23, 24]. It is also helpful for the design of the control system and for admittance shaping to manage power quality of the converter [25,26,27]. Therefore, the harmonic linearization method should be improved for unbalanced situations.

In this paper, a simple and direct modeling method of a three-phase VSC under unbalanced grid voltage is proposed. Based on harmonic linearization, the coupling of the positive and negative sequence admittances is considered and the admittance matrix is given. This method can be used with some kinds of sustained grid faults such as unbalanced grid voltage. This would be caused by unbalanced sources or loads in the grid. These faults can be sustained, so the operation of the VSC will be highly affected by them. In our opinion, the impedance of the VSC would be changed by an unbalanced grid fault. However, some fault conditions may occur very quickly, in milliseconds, and the fault can be eliminated. These are transient faults. Actually, in responding to these transient faults, the VSC would be quite slow. For instance, the PLL is usually used with a bandwidth of 10–100 Hz, like a general used synchronous reference frame PLL (SRF-PLL). Therefore, during these kinds of transient fault, the output of PLL would be only slightly affected and in many cases the converter will keep operating. The rest of this paper is organized as follows: Section 2 proposes the improved sequence admittance of the three-phase VSC under unbalanced grid conditions by harmonic linearization. The unbalanced grid voltage can be introduced as a new variable of the original model. Section 3 shows the calculation method of the sequence admittance of the VSC based on this model. Section 4 verifies the admittance of the VSC by detailed circuit simulations and analyzes the influence of the admittance on the system stability. Section 5 concludes this paper.

2 Sequence admittance modeling

2.1 Topology and control strategy of VSC

Figure 1 illustrates the topology of a three-phase voltage source pulse-width modulation (PWM) converter. According to Kirchhoff’s law, the model of the converter working as an inverter referred to the three-phase stationary frame is:

$$L\frac{\text{d}}{{\text{d}t}}\left[ {\begin{array}{*{20}l} {i_{\text{a}} } \\ {i_{\text{b}} } \\ {i_{\text{c}} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}l} {V_{\text{a}} - V_{{\text{PCC,a}}} } \\ {V_{\text{b}} - V_{{\text{PCC,b}}} } \\ {V_{\text{c}} - V_{{\text{PCC,c}}} } \\ \end{array} } \right]$$
(1)

where ia, ib and ic are the output currents of the converter. The direction of the currents is towards the grid as shown in Fig. 1. VPCC,a, VPCC,b and VPCC,c are the voltages at the point of common coupling (PCC). Va, Vb and Vc are the output phase voltages of the converter. L is the output filter inductance. Vdc is the voltage of DC side.

Fig. 1
figure 1

Topology of three-phase voltage source PWM converter

Full size image

The control structure of the three-phase voltage source PWM converter is shown in Fig. 2a. The voltage at the PCC is sampled as the input of PLL. θPLL is the output angle of the PLL. I dr and I qr denote the reference current components on the d-axis and the q-axis. Vdc is assumed constant because of the large capacitance on the DC side and the low bandwidth of the voltage loop, and consequently I dr and I qr are also assumed constant. The current control signals ca, cb and cc are obtained by sampling the grid side currents ia, ib and ic as the input of the inner current controller. Then the switching function of the converter (Sa1, Sa2, Sb1,…,Sc2) can be obtained by inputting the current control signals into the PWM signal generator.

Fig. 2
figure 2

Control strategy of three-phase voltage source PWM converter

Full size image

Based on the average of the converter model and the topology and the control strategy, (1) can be rewritten as:

$$L\frac{\text{d}}{{\text{d}t}}\left[ {\begin{array}{*{20}l} {\overline{i}_{\text{a}} } \\ {\overline{i}_{\text{b}} } \\ {\overline{i}_{\text{c}} } \\ \end{array} } \right] = K_{m} V_{{\text{dc}}} \left[ {\begin{array}{*{20}l} {\overline{c}_{\text{a}} } \\ {\overline{c}_{\text{b}} } \\ {\overline{c}_{\text{c}} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} {V_{{\text{PCC,a}}} } \\ {V_{{\text{PCC,b}}} } \\ {V_{{\text{PCC,c}}} } \\ \end{array} } \right]$$
(2)

where \(K_{m}\) is the modulator gain.

The inner current controller is shown as Fig. 2b. The I d and I q are the current component on the d-axis and the q-axis obtained by transforming the grid side current using the Park Transformation. H i is the compensation factor for the inner current controller, which is usually a PI or a PR controller, and K d is its decoupling factor. c d and c q are the d-axis and q-axis current control signals after decoupling. The current control signals are obtained by the inverse Park Transformation.

As indicated in Fig. 2b, the d-axis and q-axis current control signals are obtained as follows:

$$\left\{ {\begin{array}{*{20}l} {c_{d} = H_{i} (I_{dr} - I_{d} ) - K_{d} I_{q} } \\ {c_{q} = H_{i} (I_{qr} - I_{q} ) + K_{d} I_{d} } \\ \end{array} } \right.$$
(3)

Thus, ca, the current control signal of phase A can be obtained as:

$$c_{\text{a}} = c_{d} \cos \;\theta_{{\text{PLL}}} - c_{q} \sin \;\theta_{{\text{PLL}}}$$
(4)

2.2 Sequence admittance modeling for balanced grid

This analysis generally follows [21]. Firstly, if the output of the PLL is not affected by the harmonic voltage of the PCC, θPLL increases linearly, and is an ideal sawtooth wave modulo 2π, given by θPLL=θ1=2πf1t. Then, assuming the voltage of phase A at the PCC has a small perturbation in the time domain, the voltage can be written as:

$$V_{{\text{PCC,a}}} = V_{1} \cos (2\uppi f_{1} t) + V_{p} \cos (2\uppi f_{p} t + \varphi_{p} ) + V_{n} \cos (2\uppi f_{n} t + \varphi_{n} )$$
(5)

where the V1, V p and V n are the magnitudes of the fundamental positive sequence voltage, positive sequence harmonic voltage and negative sequence harmonic voltage, respectively, and f1, f p and f n are the corresponding frequencies. φ p and φ n are the phases of the positive sequence and negative sequence harmonic voltage. Based on Euler’s law, the first term of (5) V1cos(2πf1t) can be changed to \((V_{1} /2)({\text{e}}^{{{{\text{j}}2\uppi} f_{1} t}} + {\text{e}}^{{ {- {\text{j}}2\uppi} f_{1} t}} )\). Thus, the equation for VPCC,a in the frequency domain is as follows:

$$V_{\text{a}} [f] = \left\{ {\begin{array}{*{20}l} {V_{1} \quad\quad f = \pm \, f_{1} } \\ {V_{p} \quad\quad f = \pm \, f_{p} \, } \\ {V_{n} \quad\quad f = \pm \, f_{n} } \\ \end{array} } \right.$$
(6)

where V1 corresponds to the fundamental positive sequence voltage of phase A in frequency domain, \(V_{p} = (V_{p} /2){\text{e}}^{{ \pm {\text{j}}\varphi_{p} }}\) to the positive sequence harmonic voltage, and \(V_{n} = (V_{n} /2){\text{e}}^{{ \pm {\text{j}}\varphi_{n} }}\) to the negative sequence harmonic voltage.

Assume that the current of phase A responds to the voltage in the time domain as:

$$i_{\text{a}} = I_{1} \cos (2\uppi f_{1} t + \varphi_{i1} ) + I_{p} \cos (2\uppi f_{p} t + \varphi_{ip} ) + I_{n} \cos (2\uppi f_{n} t + \varphi_{in} )$$
(7)

where I1, I p and I n are the magnitudes of the fundamental positive sequence current, positive sequence harmonic current and negative sequence harmonic current, respectively, and φi1, φ ip and φ in are their phases. Then, the equation of ia in the frequency domain is as follows:

$$I_{\text{a}} [f] = \left\{ {\begin{array}{*{20}l} I_{1} \quad\quad f = \pm \, f_{1} \\ I_{p} \quad\quad f = \pm \, f_{p} \\ I_{n} \quad\quad f = \pm \, f_{n} \\ \end{array} } \right.$$
(8)

where \(I_{1} = (I_{1} /2){\text{e}}^{{ \pm {\text{j}}\varphi_{i1} }}\) corresponds to the fundamental positive sequence current of phase A in frequency domain, \(I_{p} = (I_{p} /2){\text{e}}^{{ \pm {\text{j}}\varphi_{ip} }}\) corresponds to the positive sequence harmonic current, and \(I_{n} = (I_{n} /2){\text{e}}^{{ \pm {\text{j}}\varphi_{in} }}\) corresponds to the negative sequence harmonic current. The equation of \(I_{\text{a}} [f]\) after sampling is

$$I_{\text{a}} [f] = \left\{ {\begin{array}{*{20}l} {G_{i} ( \pm \, {\text{j}}2\uppi f_{1} )I_{1} \quad\quad f = \pm \, f_{1} } \hfill \\ {G_{i} ( \pm \, {\text{j}}2\uppi f_{p} )I_{p} \quad\quad f = \pm \, f_{p} \, } \hfill \\ {G_{i} ( \pm \, {\text{j}}2\uppi f_{n} )I_{n} \quad\quad f = \pm \, f_{n} } \hfill \\ \end{array} } \right.$$
(9)

Applying the Park Transformation to (8) gives:

$$\left\{ \begin{aligned} i_{d} (t) = I_{1} \cos \;\varphi_{i1} + I_{p} \cos (2\uppi (f_{p} - f_{1} )t + \varphi_{ip} ) \\ + I_{n} \cos (2{\uppi }(f_{n} - f_{1} )t + \varphi_{in} ) \\ i_{q} (t) = I_{1} \sin \;\varphi_{i1} + I_{p} \sin (2\uppi (f_{p} - f_{1} )t + \varphi_{ip} ) \\ + I_{n} \sin (2\uppi (f_{n} - f_{1} )t + \varphi_{in} ) \\ \end{aligned} \right.$$
(10)

According to [21], sampling at the fundamental frequency is neglected since \(G_{i} ( \pm \, \text{j}2\uppi f_{1} ) \approx 1\). Based on Euler’s law, sin(2πf1t) can be transformed to \(({\text{e}}^{{{{\text{j}}2\uppi} f_{1} t}} - {\text{e}}^{{ - {{\text{j}}2\uppi} f_{1} t}} )/(2{\text{j}})\), so the equations for I d and I q in the frequency domain are as follows:

$$I_{d} [f] = \left\{ {\begin{array}{*{20}l} {I_{1} \cos \;\varphi_{i1} \quad\quad\quad\quad \, \, \; \text{dc} } \hfill \\ {G_{i} (s \pm {\text{j}}2\uppi f_{1} )I_{p} \quad\quad\ f = \pm (f_{p} - f_{1} )} \hfill \\ {G_{i} (s \mp {\text{j}}2\uppi f_{1} )I_{n} \quad\quad\ f = \pm (f_{n} + f_{1} )} \hfill \\ \end{array} } \right.$$
(11)
$$I_{q} [f] = \left\{ {\begin{array}{*{20}l} {I_{1} \sin \;\varphi_{i1} \quad\quad\quad\quad\quad \, \, \; {\text{dc}} } \hfill \\ { \mp jG_{i} (s \pm {\text{j}}2\uppi f_{1} )I_{p} \quad\quad f = \pm (f_{p} - f_{1} )} \hfill \\ { \pm jG_{i} (s \mp {\text{j}}2\uppi f_{1} )I_{n} \quad\quad f = \pm (f_{n} + f_{1} )} \hfill \\ \end{array} } \right.$$
(12)

where \(I_{d} [f]\) denotes I d in the frequency domain and \(I_{q} [f]\) denotes I q in the frequency domain; dc represents that the frequency is 0 Hz. G i denotes the delay of the current sampling as follows:

$$G_{i} (s) = \text{e}^{{ - sT_{i} }} \frac{{1 - {\text{e}}^{{ - sT_{i} }} }}{{sT_{i} }}\frac{1}{{1 + s/\omega_{i} }}$$
(13)

where T i is the period of current sampling and ω i is the cut-off frequency of the analog-digital converter.

Figure 3 illustrates the assumption that the positive sequence harmonics of voltage only produce positive sequence harmonics of current at the same frequency. Similarly, the negative sequence harmonics of voltage only produce negative sequence harmonics of current at the same frequency. The positive and negative sequence components are decoupled from each other.

Fig. 3
figure 3

Signal flow diagram of positive sequence harmonic voltage

Full size image

Based on harmonic linearization, if

$$X(t) = Y(t)Z(t)$$
(14)

then a Fourier coefficient X[i] of the function X(t) can be calculated by the convolution of the Fourier coefficients of Y(t) and Z(t) as follows:

$$X\left[ i \right] = \sum\limits_{k = - \infty }^{\infty } {\left( {Y\left[ k \right]Z\left[ {i - k} \right]} \right)}$$
(15)

The equation of the inner current controller signal of phase A at the frequency f p can therefore be derived from (4) and (15) as follows:

$$C_{\text{a}} [ \pm f_{p} ] = C_{d} [ \pm (f_{p} - f_{1} )]\cos \;\theta_{{\text{PLL}}} [ \pm f_{1} ] - C_{q} [ \pm (f_{p} - f_{1} )]\sin \;\theta_{{\text{PLL}}} [ \pm f_{1} ]$$
(16)

where \(C_{\text{a}} [ \pm f_{p} ]\) corresponds to ca at ± f p in the frequency domain, \(C_{d} [ \pm (f_{p} - f_{1} )]\) corresponds to c d at ±(f p −f1) in the frequency domain, and \(C_{q} [ \pm (f_{p} - f_{1} )]\) corresponds to c q at ±(f p − f1) in the frequency domain. \(\theta_{{\text{PLL}}}\) corresponds to \(\theta_{{\text{PLL}}}\)in the frequency domain.

Thus, the positive sequence admittance of the converter, neglecting the effect of the PLL, can be obtained by (2)–(4), (6), (8)–(12) and (16) as follows:

$$Y_{p} (s) = \frac{{V_{\text{a}} [f_{p} ]}}{{ - I_{\text{a}} [f_{p} ]}} = \frac{1}{{K_{m} V_{\text{dc}} [H_{i} (s - \text{j}2\uppi f_{1} ) - \text{j}K_{d} ]G_{i} (s) + sL}}$$
(17)

Similarly, the negative sequence admittance is as follows:

$$Y_{n} (s) = \frac{1}{{K_{m} V_{\text{dc}} [H_{i} (s + \text{j}2\uppi f_{1} ) + \text{j}K_{d} ]G_{i} (s) + sL}}$$
(18)

However, a disturbance will be introduced at the output of the PLL due to the grid voltage, and this leads to nonlinearity in the Park Transform. So, the effect of PLL should be taken into consideration when modeling the admittance of the VSCs.

Figure 4(a) illustrates the principle of the PLL. HPLL is the forward loop gain. The harmonic voltage at the PCC will disturb the output of the PLL, and in order to get an accurate admittance of the converter, the disturbance must be modeled precisely. Assume that the disturbance of the output phase, Δθ, is a small disturbance around the rated operating point of the VSC system. The output phase of the PLL in the time domain is

Fig. 4
figure 4

PLL working principle and its equivalent diagram

Full size image
$$\theta_{{\text{PLL}}} (t) = \theta_{1} (t) + \Delta \theta (t)$$
(19)

Therefore, the output phase of the PLL in the frequency domain is:

$$\theta_{{\text{PLL}}} [f] = \left\{ {\begin{array}{*{20}l} {\theta_{1} \quad\quad\ f = \pm f_{1} } \hfill \\ {\Delta \theta\quad\quad{\text{At other frequency}}} \hfill \\ \end{array} } \right.$$
(20)

Define T(θ) to be the matrix of the Park Transformation using the angle θ. The relationship between T(θPLL) and T(θ1) is:

$$\varvec{T}(\theta_{\text{PLL}} ){ = }\left[ {\begin{array}{*{20}l} {\cos (\Delta \theta )} & {\sin (\Delta \theta )} & 0 \\ { - \sin (\Delta \theta )} & {\cos (\Delta \theta )} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\varvec{T}(\theta_{1} )$$
(21)

and the equivalent signal flow diagram of the PLL can be drawn as shown in Fig. 4b.

The V dv and V qv are the d-axis and q-axis components of the PCC voltage through the ideal Park Transformation. So the real q-axis component is:

$$V_{q} = V_{qv} \cos \;\Delta \theta - V_{dv} \sin \;\Delta \theta$$
(22)

Linearizing (22) gives

$$V_{q} \approx V_{qv} - V_{dv} \Delta \theta$$
(23)

The equations of V dv and V qv in the frequency domain are obtained by Park Transformation and (6) as follows:

$$V_{dv} [f] = \left\{ {\begin{array}{*{20}l} {V_{1} \quad\quad\quad\quad\quad\quad\quad \, \, \; \text{dc} } \hfill \\ {G_{v} (s \pm {\text{j}}2\uppi f_{1} )V_{p} \quad\quad f = \pm (f_{p} - f_{1} )} \hfill \\ {G_{v} (s \mp {\text{j}}2\uppi f_{1} )V_{n} \quad\quad f = \pm (f_{n} + f_{1} )} \hfill \\ \end{array} } \right.$$
(24)
$$V_{qv} [f] = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} { \mp {\text{j}}G_{v} (s \pm {\text{j}}2\uppi f_{1} )V_{p} \quad\quad f = \pm (f_{p} - f_{1} )} \hfill \\ \end{array} } \\ { \pm {\text{j}}G_{v} (s \mp {\text{j}}2\uppi f_{1} )V_{n} \quad\quad f = \pm (f_{n} + f_{1} )} \\ \end{array} } \right.$$
(25)

where G v is the delay of voltage sampling as follows:

$$G_{v} (s) = \text{e}^{{ - sT_{v} }} \frac{{1 - {\text{e}}^{{ - sT_{v} }} }}{{sT_{v} }}\frac{1}{{1 + s/\omega_{v} }}\frac{1}{{1 + s/\omega_{tv} }}$$
(26)

where T v is the period of voltage sampling; ω v is the cut-off frequency of the analog-digital converter; ω tv represents the delay of transducer.

Thus, the equation of Δθ in the frequency domain is

$$\Delta \theta [f] = \left\{ {\begin{array}{*{20}l} {G_{p} (s)G_{v} (s \pm {\text{j}}2\uppi f_{1} )V_{p} \quad\quad f = \pm (f_{p} - f_{1} )} \\ {G_{n} (s)G_{v} (s \mp {\text{j}}2\uppi f_{1} )V_{n} \quad\quad f = \pm (f_{n} + f_{1} )} \\ \end{array} } \right.$$
(27)

where G p (s) is the transfer function of the disturbance which is caused by the positive sequence harmonic voltage V p at the frequency ±(f p −f1), and G n (s) is the transfer function of the disturbance which is caused by the negative sequence harmonic voltage V n at the frequency ±(f n +f1). The equation for V q in the frequency domain is obtained from (23–27) is as follows:

$$V_{q} [f] = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} { \, [ \mp {\text{j}} - V_{1} G_{p} (s)]G_{v} (s \pm {\text{j}}2\uppi f_{1} )V_{p} \quad\quad f = \pm (f_{p} - f_{1} )} \hfill \\ \end{array} } \\ {[ \pm {\text{j}} - V_{1} G_{n} (s)]G_{v} (s \mp {\text{j}}2\uppi f_{1} )V_{n} \quad\quad f = \pm (f_{n} + f_{1} )} \\ \end{array} } \right.$$
(28)

Thus, in Fig.4b, the phase angle is

$$\theta_{{\text{PLL}}} (s) = H_{{\text{PLL}}} (s)V_{q}$$
(29)

and so

$$\Delta \theta = H_{{\text{PLL}}} \left( s \right)V_{q} \quad\quad f \ne \pm f_{1}$$
(30)

Thus, the equations of G p (s) and G n (s) are obtained from (27–30) as follows:

$$G_{p} (s) = \frac{{ \mp \text{j}H_{{\text{PLL}}} \left( s \right)}}{{1 + V_{1} H_{{\text{PLL}}} \left( s \right)}}$$
(31)
$$G_{n} (s) = \frac{{ \pm \text{j}H_{{\text{PLL}}} \left( s \right)}}{{1 + V_{1} H_{{\text{PLL}}} \left( s \right)}}$$
(32)

Because

$$\left\{ {\begin{array}{*{20}l} {\cos \theta_{{\text{PLL}}} = \cos \theta_{1} - \sin \theta_{1} \cdot \Delta \theta } \\ {\sin \theta_{{\text{PLL}}} = \sin \theta_{1} + \cos \theta_{1} \cdot \Delta \theta } \\ \end{array} } \right.$$
(33)

the equations of cos θPLL and sinθPLL in the frequency domain are as follows:

$$\cos \;\theta_{{\text{PLL}}} [f] = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\frac{{H_{{\text{PLL}}} \left( {s \mp {\text{j}}2\uppi f_{1} } \right)G_{v} (s)}}{{1 + V_{1} H_{{\text{PLL}}} \left( {s \mp {\text{j}}2\uppi f_{1} } \right)}}V_{p} \quad\quad f = \pm f_{p} } \\ {\frac{1}{2}\frac{{H_{{\text{PLL}}} \left( {s \pm {\text{j}}2\uppi f_{1} } \right)G_{v} (s)}}{{1 + V_{1} H_{{\text{PLL}}} \left( {s \pm {\text{j}}2\uppi f_{1} } \right)}}V_{n} \quad\quad f = \pm f_{n} } \\ \end{array} } \right.$$
(34)
$$\sin \;\theta_{{\text{PLL}}} [f] = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\frac{{ \mp {\text{j}}H_{{\text{PLL}}} \left( {s \mp {\text{j}}2\uppi f_{1} } \right)G_{v} (s)}}{{1 + V_{1} H_{{\text{PLL}}} \left( {s \mp {\text{j}}2\uppi f_{1} } \right)}}V_{p} \quad\quad f = \pm f_{p} } \\ {\frac{1}{2}\frac{{ \pm {\text{j}}H_{{\text{PLL}}} \left( {s \pm {\text{j}}2\uppi f_{1} } \right)G_{v} (s)}}{{1 + V_{1} H_{{\text{PLL}}} \left( {s \pm {\text{j}}2\uppi f_{1} } \right)}}V_{n} \quad\quad f = \pm f_{n} } \\ \end{array} } \right.$$
(35)

\(I_{dv}\) and \(I_{qv}\)are the d-axis and q-axis components of \(i_{\text{a}} (t)\) in the time domain after applying the ideal Park Transformation \(\varvec{T}(\theta_{1} )\). According to (21),

$$\left\{ \begin{aligned} I_{d} &= I_{dv} { + }\Delta \theta I_{qv} \hfill \\ I_{q} &= - \Delta \theta I_{dv} { + }I_{qv} \hfill \\ \end{aligned} \right.$$
(36)

Thus, the realistic d-axis and q-axis current components I d and I q at the frequency ±(f p −f1) and ±(f n +f1) may be obtained, and are given by (A1) in Appendix A.

The convolution of the frequency components of the inner current controller signals ca, cb and cc at the frequency ± f p is shown in Table 1. Given these, the equation of the inner current control signal of phase A at the frequency ± f p can be derived from (4) as follows:

Table 1 Relationship of frequency components
Full size table
$$\begin{aligned} C_{\text{a}} [ \pm f_{p} ] &= \sum {C_{dq} [f]\varvec{T}^{ - 1} (\theta_{{\text{PLL}}} )[ \pm f_{p} - f]} \hfill \\ &= C_{dq} \left[ {\text{dc}} \right]\varvec{T}^{ - 1} (\theta_{{\text{PLL}}} )[ \pm f_{p} ] + C_{dq} [ \pm (f_{p} - f_{1} )]\varvec{T}^{ - 1} (\theta_{{\text{PLL}}} )[ \pm f_{1} ] \hfill \\ &= C_{d} \left[ {\text{dc}} \right]\cos \theta_{{\text{PLL}}} [ \pm f_{p} ] - C_{q} \left[ {\text{dc}} \right]\sin \theta_{{\text{PLL}}} [ \pm f_{p} ] \hfill \\ &\quad + C_{d} [ \pm (f_{p} - f_{1} )]\cos \theta_{{\text{PLL}}} [ \pm f_{1} ] - C_{q} [ \pm (f_{p} - f_{1} )]\sin \theta_{{\text{PLL}}} [ \pm f_{1} ] \hfill \\ \end{aligned}$$
(37)

where T−1 denotes the inverse Park Transformation.

The positive sequence admittance of the converter can be obtained from (2–4), (31), (32), (34), (35), (A1) and (37) as follows:

$$\begin{aligned} Y_{p} (s) &= \left\{ {1 - K_{m} V_{{\text{dc}}} G_{v} (s)H_{{\text{PLL}}} (s - \text{j}2\uppi f_{1} )\left[ {1 + V_{1} H_{{\text{PLL}}} (s - \text{j}2\uppi f_{1} )} \right]^{ - 1} } \right. \hfill \\ &\quad \left. { \cdot \left[ {(C_{1} /2)\text{e}^{{\text{j}\varphi_{c1} }} + (I_{1} /2)\text{e}^{{\text{j}\varphi_{i1} }} \left( {H_{i} (s - \text{j}2\uppi f_{1} ) - jK_{d} } \right)} \right]} \right\} \hfill \\ &\quad \cdot \left[ {K_{m} V_{{\text{dc}}} \left[ {H_{i} (s - \text{j}2\uppi f_{1} ) - \text{j}K_{d} } \right]G_{i} (s) + sL} \right]^{ - 1} \hfill \\ \end{aligned}$$
(38)

Similarly, the negative sequence admittance is as follows:

$$\begin{aligned} Y_{n} (s) &= \left\{ {1 - K_{m} V_{{\text{dc}}} G_{v} (s)H_{{\text{PLL}}} (s + \text{j}2\uppi f_{1} )\left[ {1 + V_{1} H_{{\text{PLL}}} (s + \text{j}2\uppi f_{1} )} \right]^{ - 1} } \right. \hfill \\ &\quad \left. { \cdot \left[ {(C_{1} /2)\text{e}^{{ - \text{j}\varphi_{c1} }} + (I_{1} /2)\text{e}^{{ - \text{j}\varphi_{i1} }} \left( {H_{i} (s + \text{j}2\uppi f_{1} ) + \text{j}K_{d} } \right)} \right]} \right\} \hfill \\ &\quad \cdot \left\{ {K_{m} V_{{\text{dc}}} \left[ {H_{i} (s + \text{j}2\uppi f_{1} ) + \text{j}K_{d} } \right]G_{i} (s) + sL} \right\}^{ - 1} \hfill \\ \end{aligned}$$
(39)

where \((C_{1} /2){\text{e}}^{{ \pm {\text{j}}\varphi_{c1} }} = (C_{d} [{\text{dc}}] \pm {\text{j}}C_{q} [{\text{dc}}])/2 = C_{1}\) and \(C_{1} = (V_{1} + \text{j}2\uppi f_{1} I_{1} )/K_{m} V_{\text{dc}}\).

2.3 Proposed sequence admittance modeling for unbalanced grid conditions

Reference [21] proposes a modeling method for the sequence impedance of VSCs under balanced grid conditions using harmonic linearization. All variables of the system are transformed into the frequency domain firstly, such that V1 represents VPCC,a at ± f1 and V p represents VPCC,a at ± f p , and so on. Then, the output disturbance of the PLL due to the harmonic voltage can be modeled as shown in (27–35). This establishes the use of the Park Transformation considering the effect of Δθ, which is applied below under unbalanced grid conditions. Then, the realistic d-axis and q-axis current I d and I q are obtained in (A1). These allow the output signal of the inner current controller in dq-frame to be easily calculated using (3). Finally, the output signal of the inner current controller ca at the relevant harmonic frequency (± f p or ± f n ) can be calculated as shown in (37), which is derived using the convolution relationships in Table 1 and the inverse Park Transform. The sequence admittance can be obtained by putting the calculated Ca into the circuit equation of the system as shown in (2).

The modeling process for the sequence admittance of VSCs under unbalanced grid conditions is nearly the same as the process above. The unbalanced grid voltage can be introduced as a new variable in the original model. The unbalanced grid voltage V2 will lead to new frequency components of Δθ such as Δθ[±2f1]. It will also introduce a new frequency component in the Park Transformation at the fundamental negative frequency as shown in Fig. 5. The unbalanced grid voltage V 2 generates an unbalanced output current I2 from the VSC at the fundamental negative frequency. Then, I dq [±2f1] will be generated by the Park Transformation. Due to the existence of Δθ[±2f1], some new frequency components such as I dq [±(f p +f1)], I dq [±(f n −f1)], and so on, will be introduced when calculating I d and I q .

Fig. 5
figure 5

The proposed method to obtain the admittance model by harmonic linearization

Full size image

Then, the output signals of the inner current controller in the dq-frame can be easily obtained. In order to compare with the balanced condition, some new frequency components such as C dq [±(f p +f1)], C dq [±(f n −f1)] and C dq [±2f1] will be introduced. Ca can be calculated at the relevant frequencies such as ± f p and ± f n by considering all the possible convolution relationships of the frequency components.

Therefore, there are some new elements in Ca due to the unbalanced grid voltage V2. By putting the positive and negative components of Ca into each sequence circuit equations of the system, and solving them, the sequence admittance of VSCs can be obtained. The detailed step-by-step calculation is shown in Section 3.

3 Step-by-step admittance calculation of VSCs under unbalanced grid conditions

The converter is often running with unbalanced grid voltage on the grid side. There is not only the rated positive sequence voltage at the fundamental frequency, but also the negative sequence voltage at the fundamental frequency exists in the voltage at PCC. Assume that the equation of the voltage of phase A is:

$$\begin{aligned} V_{{\text{PCC,a}}} &= V_{1} \cos (2\uppi f_{1} t){ + }V_{2} \cos (2\uppi f_{1} t{ + }\varphi_{2} ) \hfill \\ &\quad + V_{p} \cos (2\uppi f_{p} t + \varphi_{p} ) + V_{n} \cos (2\uppi f_{n} t + \varphi_{n} ) \hfill \\ \end{aligned}$$
(40)

where the V2 and φ2 correspond to the magnitude and the initial phase of the negative sequence voltage at the fundamental frequency. Similarly, the equation of the current of phase A in the time domain is as follows:

$$\begin{aligned} i_{\text{a}} &= I_{1} \cos (2\uppi f_{1} t + \varphi_{i1} ){ + }I_{2} \cos (2\uppi f_{1} t + \varphi_{i2} ) \hfill \\ &\quad + I_{p} \cos (2\uppi f_{p} t + \varphi_{ip} ) + I_{n} \cos (2\uppi f_{n} t + \varphi_{in} ) \hfill \\ \end{aligned}$$
(41)

where I1 and φi2 correspond to the magnitude and initial phase of the negative sequence current at the fundamental frequency.

The detailed steps to obtain the admittance model by harmonic linearization considering the effect of the negative sequence voltage at the fundamental frequency are shown in Fig. 6.

Fig. 6
figure 6

Step-by-step detailed process to obtain impedance model with unbalanced grid voltage by harmonic linearization

Full size image

Thus, we can find Ca[f] which is the phase A output control signal of the inner current controller in the frequency domain.

The sequence components and their convolution relationships are shown in Table 2. Clearly, the positive sequence harmonic voltage at the frequency ± f p produces not only the positive sequence harmonic component, but also the negative sequence harmonic voltage at the same frequency. Similarly, the negative sequence harmonic voltage at the frequency ± f n produces not only the negative sequence harmonic component, but also the positive sequence harmonic voltage at the same frequency. The positive and negative sequence harmonic components couple with each other because of the negative sequence voltage at the fundamental frequency. The positive and negative sequence equation of the system is obtained from (2) as follows:

Table 2 Convolution relationship of frequency components
Full size table
$$sL\left[ {\begin{array}{*{20}l} {I_{p} } \\ {I_{n} } \\ \end{array} } \right] = K_{m} V_{{\text{dc}}} \left[ {\begin{array}{*{20}l} {C_{{\text{a},p}} } \\ {C_{{\text{a},n}} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} {V_{p} } \\ {V_{n} } \\ \end{array} } \right]$$
(42)

where Ca,p and Ca,n are the positive and negative sequence components of Ca respectively.

This can be expressed as follows:

$$\left[ {\begin{array}{*{20}l} {A_{pp} } & {A_{pn} } \\ {A_{np} } & {A_{nn} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {I_{p} } \\ {I_{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {B_{pp} } & {B_{pn} } \\ {B_{np} } & {B_{nn} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {V_{p} } \\ {V_{n} } \\ \end{array} } \right]$$
(43)

where the equations of A pp , A pn , A np , A nn , B pp , B pn , B np and B nn are obtained by solving (43).

Equation (43) can be written in matrix form as: A pn I pn  = B pn V pn . Thus,

$$\left\{ \begin{aligned} \varvec{I}_{pn} = - \varvec{Y}_{pn} \varvec{V}_{pn} = \varvec{A}_{pn}^{ - 1} \varvec{B}_{pn} \varvec{V}_{pn} \hfill \\ \varvec{V}_{pn} = - \varvec{Z}_{pn} \varvec{I}_{pn} = \varvec{B}_{pn}^{ - 1} \varvec{A}_{pn} \varvec{I}_{pn} \hfill \\ \end{aligned} \right.$$
(44)

where Z pn corresponds to the positive and negative output impedance matrix of the converter under the unbalanced condition, and Y pn is the admittance matrix corresponding to Z pn .

Assume that:

$$\varvec{Y}_{pn} = \left[ {\begin{array}{*{20}l} {Y_{pp} } & {Y_{pn} } \\ {Y_{np} } & {Y_{nn} } \\ \end{array} } \right]$$
(45)

and then according to (44) the admittance matrix Y pn can be obtained as follows:

$$\left( \begin{aligned} Y_{pp} &= - \frac{{A_{nn} B_{pp} - A_{pn} B_{np} }}{{A_{pp} A_{nn} - A_{pn} A_{np} }} = - \frac{{B_{pp} }}{{A_{pp} }} \hfill \\ Y_{pn} &= - \frac{{A_{nn} B_{pn} - A_{pn} B_{nn} }}{{A_{pp} A_{nn} - A_{pn} A_{np} }} = - \frac{{B_{pn} }}{{A_{pp} }} \hfill \\ Y_{np} &= - \frac{{ - A_{np} B_{pp} + A_{pp} B_{np} }}{{A_{pp} A_{nn} - A_{pn} A_{np} }} = - \frac{{B_{np} }}{{A_{nn} }} \hfill \\ Y_{nn} &= - \frac{{ - A_{np} B_{pn} + A_{pp} B_{nn} }}{{A_{pp} A_{nn} - A_{pn} A_{np} }} = - \frac{{B_{nn} }}{{A_{nn} }} \hfill \\ \end{aligned} \right.$$
(46)

4 Simulations and verifications

4.1 Detailed circuit simulations

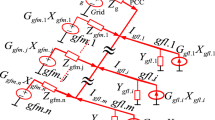
In order to prove the validity of the calculated admittance, cycle-by-cycle simulations have been carried out in Matlab Simulink. The circuit used in the simulations is shown in Fig. 7. The part shown as the “Converter” in Fig. 7 contains the whole control system.

Fig. 7
figure 7

Simulation circuit

Full size image

ΔV in Fig. 7 is a small perturbance of voltage on the grid side, and Δi is the variation of the current. The simulation parameters are shown in Table 3. The magnitude of the unbalanced voltage at the fundamental frequency is 0.1 p.u. The delay of the whole control loop can be considered as a sum of time delays. Then the time delay representing the whole control loop of the system can be set to model different practical applications.

Table 3 Parameters of system
Full size table

Figures 8, 9, 10 and 11 compare simulated with calculated result to verify the correctness of the equation of Y pn . The root-mean-square (RMS) difference in magnitude is 1.07 dB and the RMS phase difference is 2.56°, suggesting that we may have high confidence in the equation.

Fig. 8
figure 8

Simulation and calculation results of Y pp

Full size image
Fig. 9
figure 9

Simulation and calculation results of Y pn

Full size image
Fig. 10
figure 10

Simulation and calculation results of Y np

Full size image
Fig. 11
figure 11

Simulation and calculation results of Y nn

Full size image

4.2 Sensitivity analysis

Figures 12 and 13 compare the positive and negative admittances under normal conditions and with unbalanced grid voltage. It can be seen that the admittances in these two situations are nearly the same. The unbalanced voltage has little effect on the positive and negative admittances, but it will produce coupled admittances.

Fig. 12
figure 12

Comparison of Y pp under normal conditions and with unbalanced grid voltage

Full size image
Fig. 13
figure 13

Comparison of Y nn under normal conditions and with unbalanced grid voltage

Full size image

According to Fig. 5, the unbalanced grid voltage V2 will lead to a new frequency component of Δθ such as Δθ[±2f1]. Due to the existence of Δθ[±2f1], the coupled admittance will be introduced. The relationship between Δθ[±2f1] and V2 is:

$$\Delta \theta [ \pm 2f_{1} ] = \pm \text{j}\frac{{H_{{\text{PLL}}} \left( { \pm 2f_{1} } \right)}}{{1 + V_{1} H_{{\text{PLL}}} \left( { \pm 2f_{1} } \right)}}G_{v} ( \pm f_{1} )V_{2}$$
(47)

This indicates that the magnitude of V2 and the transfer function of the PLL will have big impacts on the coupled admittances. The transfer function of the PLL determines its bandwidth.

Figure 14 shows the variation of the magnitude of the coupled admittance Y np of the simulated VSC with different magnitudes of V2. All other parameters are as shown in Table 3. It can be seen that the increased magnitude of the negative sequence voltage at the fundamental frequency will lead to an increased coupled admittance of the VSC.

Fig. 14
figure 14

Coupled admittance Y np of VSC with different magnitude of V2

Full size image

Figure 15 illustrates the coupled admittance Y np of the VSC with a lower PLL bandwidth. All the parameters are as shown in Table 3 except for the smaller proportionality coefficient k p of the PLL. When it is set as 2, representing a lower bandwidth of PLL, Fig. 15 illustrates that the phase and magnitude of Y np decrease significantly. This suggests that a lower bandwidth of the PLL will lead to a decrease of the phase and magnitude of Y np .

Fig. 15
figure 15

Coupled admittance Y np of VSC with different bandwidth of PLL

Full size image

In [23], the sufficient criterion for stability of the converter according to its admittance is that the real part of the admittance of the VSC is above zero. Figure 16 shows that the output currents of the VSC with lower PLL bandwidth distort severely, which can be attributed to negative real parts of the coupled admittances for the central frequency. This means that a lower bandwidth of the PLL will decrease the phase and magnitude of Y np and lead to the distortion of the output currents.

Fig. 16
figure 16

Distorted output currents of VSC with a lower PLL bandwidth

Full size image

5 Conclusion

The sequence admittances of a three-phase VSC are independent of each other when it is operating under normal conditions. However, the positive and negative sequence harmonic components will be coupled with each other if three-phase grid-connected converter is running with unbalanced grid voltages. This is mainly caused by the negative sequence voltage at the fundamental frequency. This paper proposes a step-by-step modeling method to calculate the matrix of positive and negative sequence admittances of three-phase grid-connected converters under unbalanced grid voltage conditions, based on the method of harmonic linearization. The calculated admittances agree with simulated results within 1.07 dB of magnitude and 2.56° of phase, and can be easily applied in stability analysis.