Short-term local prediction of wind speed and wind power based on singular spectrum analysis and locality-sensitive hashing

Abstract

With the growing penetration of wind power in power systems, more accurate prediction of wind speed and wind power is required for real-time scheduling and operation. In this paper, a novel forecast model for short-term prediction of wind speed and wind power is proposed, which is based on singular spectrum analysis (SSA) and locality-sensitive hashing (LSH). To deal with the impact of high volatility of the original time series, SSA is applied to decompose it into two components: the mean trend, which represents the mean tendency of the original time series, and the fluctuation component, which reveals the stochastic characteristics. Both components are reconstructed in a phase space to obtain mean trend segments and fluctuation component segments. After that, LSH is utilized to select similar segments of the mean trend segments, which are then employed in local forecasting, so that the accuracy and efficiency of prediction can be enhanced. Finally, support vector regression is adopted for prediction, where the training input is the synthesis of the similar mean trend segments and the corresponding fluctuation component segments. Simulation studies are conducted on wind speed and wind power time series from four databases, and the final results demonstrate that the proposed model is more accurate and stable in comparison with other models.

1 Introduction

As fossil fuels are gradually being depleted, wind energy, as a non-polluting type of renewable energy, has been rapidly developed [1]. In recent years, the proportion of wind energy keeps increasing and this trend will continue for a long time [2]. In China, wind power has been vigorously developed. By the end of 2016, the installed capacity of wind power has increased to 149 GW, with an increment of 3% over 2015 [3]. With more and more wind power feeding into power systems, the randomness and intermittent nature of wind speed and wind power jeopardizes the stability and reliability of power system operation and raises the operating cost [4]. Therefore, in order to alleviate the adverse effects of wind power integration, more accurate and stable forecasting is critical and urgently needed [5].

Many researchers have devoted themselves to improving the accuracy of wind speed and wind power forecasting, and have put forward a number of forecast models. The mainstream models can be roughly classified into two categories: physical models and statistical models [6]. A physical model usually establishes a rigorous mathematical forecast model based on the principles of geophysical fluid dynamics and thermodynamics [7]. The numerical weather prediction (NWP) model, which is a typical physical model [8], simulates the physics of the atmosphere based on certain initial values and boundary conditions. However, the NWP model requires huge computational resources, and thus, it is operated on super computers, which limits its application in short-term forecasting [9]. Statistical models use historical data only, and outperform physical models in short-term forecasting [10]. Various models for wind speed and wind power forecasting are mushrooming in recent years, among which auto-regressive and moving average (ARMA) [11], artificial neural network (ANN) [12] and support vector regression (SVR) [13] are most widely used. The main advantages are that they compute the forecast results quickly, and can work on personal computers. In electricity markets, a great number of players need the real-time results of wind speed and wind power forecasting, such as system operators, wind power generators, and suppliers. In order to help them predict wind speed and wind power more accurately with less time, this paper proposes a short-term forecast model that is a statistical model.

In general, it is difficult to forecast from the original time series directly, as wind speed and wind power have the nature of rapid fluctuation and high randomness. Thus, it has been proposed to filter the original time series or to decompose it into multiple series by empirical mode decomposition (EMD) [14], wavelet transform (WT) [15], k-opening-closing and closing-opening (k-OCCO) filter [9], etc. EMD and WT decompose the original time series into several components and forecast each component respectively [14, 15]. However, such a strategy consumes more time, and the error arising in each component will be integrated, so that it leads to an unsatisfactory forecast result [16, 17]. The k-OCCO filter extracts the tendency of the original time series and treats the remainder as noise [18], which may induce a large fixed error.

Thus, in order to overcome the shortcomings mentioned above, this paper proposes a novel forecasting model which can avoid both error accumulation and fixed errors. The model is based on singular spectrum analysis (SSA) [19, 20] and locality-sensitive hashing (LSH) [21,22,23] for short-term forecasting. SSA is used for decomposing the original data into two components: the mean trend and the fluctuation component. According to previous research, local prediction performs better than global prediction [24]. Therefore, LSH is used to classify the sample segments based on hash functions and search for the similar segments of the forecast mean trend segment, which refers to the segment of the mean trend at the period of time when forecasting is to be done. To the best of our knowledge, it is the first time that LSH is used in wind speed/power forecasting to select similar segments, so that the size of the training data set can be reduced and the forecast result can be more accurate. Instead of forecasting the two components individually or the mean trend solely, this paper proposes to synthesize the similar mean trend segments and the corresponding fluctuation component segments into the training input of SVR for more accurate forecast results.

2 Methodologies

2.1 Singular spectrum analysis

SSA is a powerful method to study the meaningful features of nonlinear time series, which has gained more attention in recent years. It extracts and identifies the mean trend and the fluctuation component from an original time series, expecting to obtain a superior forecast result with a synthesis of these two components. Standard SSA is performed in the following steps.

Step 1: Embedding. For an original time series $\varvec{y}=[y_1\ y_2\ \cdots \ y_N]$ of length N, L is the selected embedding dimension or the window length in the SSA. The original time series $\varvec{y}$ is converted to L-lagged vectors $\varvec{x}_1, \varvec{x}_2,\cdots ,\varvec{x}_K$, $K=N-L+1$, and each L-lagged vector $\varvec{x}_i$ is defined as

$$\varvec{x}_i=\left[ y_i\ y_{i+1}\ \cdots \ y_{i+L-1}\right] ^{\mathrm{T}}\quad \ i=1,2,\cdots ,K$$

(1)

The trajectory matrix $\varvec{X}\in {\mathbb {R}}^{L\times K}$ is defined as

$$\varvec{X} = [x_{1}\;x_{2} \ldots x_{K} ]\left[ {\begin{array}{*{20}l} {y_{1} } \hfill & {y_{2} } \hfill & \ldots \hfill & {y_{k} } \hfill \\ {y_{2} } \hfill & {y_{3} } \hfill & \ldots \hfill & {y_{K + 1} } \hfill \\ \vdots \hfill & \vdots \hfill & \ldots \hfill & \vdots \hfill \\ {y_{L} } \hfill & {y_{L + 1} } \hfill & \ldots \hfill & {y_{N} } \hfill \\ \end{array} } \right]$$

(2)

Step 2: Singular value decomposition (SVD). The d eigenvalues of the covariance matrix $\varvec{S}=\varvec{X}\varvec{X}^{\text {T}}$ are calculated, which meet the requirement $\lambda _1\ge \lambda _2\ge \cdots \ge \lambda _d\ge 0$. Correspondingly, $\varvec{u}_1,\varvec{u}_2,\cdots ,\varvec{u}_d$ are the orthogonal eigenvectors. Then the trajectory matrix $\varvec{X}$ can be decomposed by SVD into

$$\varvec{X}= \varvec{e}_1+\varvec{e}_2+\cdots +\varvec{e}_d$$

(3)

$$\varvec{e}_i= \sqrt{\lambda _i}\varvec{u}_i \varvec{v}_i^{\text {T}}$$

(4)

$$\varvec{v}_i= \varvec{X}^{\text {T}}\varvec{u}_i\sqrt{\lambda _i}$$

(5)

$$d= {\text {min}}\{L,K\}\quad \ i=1,2,\cdots ,d$$

(6)

where the vectors $\varvec{v}_1,\varvec{v}_2,\cdots ,\varvec{v}_d$ are considered to be principle components of trajectory matrix $\varvec{X}$. Consequently, the collection $(\sqrt{\lambda _i},\varvec{u}_i,\varvec{v}_i)$ is defined as the ith triple feature vector of matrix $\varvec{X}$.

Step 3: Grouping. After decomposition, the indices $\{1,2,\cdots ,d\}$ are divided into m independent groups $I_1,I_2,\cdots ,I_m$ and $I_j=\{i_{j_1},\cdots , i_{j_p}\},\ j=1,2,\cdots ,m$ are denoted as a group of indices. The trajectory matrix $\varvec{X}$ is expressed as

$$\varvec{X}=\varvec{E}_{I_1}+\varvec{E}_{I_2}+\cdots +\varvec{E}_{I_m}$$

(7)

$$\varvec{E}_{I_j}= \varvec{e}_{i_{j_1}}+\varvec{e}_{i_{j_2}}+\cdots +\varvec{e}_{i_{j_p}}$$

(8)

where the contribution rate of $\varvec{E}_{I_j}$ is $\sum \limits _{i\in I_j}\lambda _i/\sum \limits _{i=1}^d \lambda _i$. In this paper, the original time series is decomposed into two components. Hence, we have $\varvec{X}=\varvec{E}_{I_1}+\varvec{E}_{I_2}$.

Step 4: Diagonal averaging. Each matrix $\varvec{E}_{I_j}\in {\mathbb {R}}^{L\times K}$ is converted to a time series by the following method. Let $z_{il}$, $i=1,2,\cdots ,L$, $l=1,2,\cdots ,K$ be the elements of the matrix with $\varvec{E}_{I_j}$. Set $L^*=\min \{L,K\}$, $K^*=\max \{L,K\}$, and $N=K+L-1$. $z^*_{il}=z_{il}$ when $L<K$; otherwise, $z^*_{il}=z_{li}$. Diagonal averaging converts matrix $\varvec{E}_{I_j}$ into a time series $\left[ y^{(j)}_1\ y^{(j)}_2\ \cdots \ y^{(j)}_N\right]$ via the following equation

$$y_{k}^{i} = \left\{ {\begin{array}{*{20}l} {\frac{1}{k}\sum\limits_{q = 1}^{k + 1} {z_{q,k - q + 2}^{*} } } \hfill & {1 \le k \le L^{*} } \hfill \\ {\frac{1}{{L^{*} }}\sum\limits_{q = 1}^{{L^{*} }} {z_{q,k - q + 2}^{*} } } \hfill & {L^{*} \le k \le K^{*} } \hfill \\ {\frac{1}{N - K + 2}\sum\limits_{{q = k - K^{*} + 2}}^{{N - K^{*} + 1}} {z_{q,k - q + 2}^{*} } } \hfill & {K^{*} \le k \le N^{*} } \hfill \\ \end{array} } \right.$$

(9)

In this paper, the diagonal averaging is applied to $\varvec{E}_{I_1}$ and $\varvec{E}_{I_2}$, respectively, and the two corresponding time series are $\varvec{y}^{(1)}=\left[ y^{(1)}_1\ y^{(1)}_2\ \cdots \ y^{(1)}_N\right]$ and $\varvec{y}^{(2)}=\left[ y^{(2)}_1\ y^{(2)}_2\right.$ $\left. \cdots \ y^{(2)}_N\right]$ according to (9). Thus, the initial time series $\varvec{y}$ is expressed by

$$\varvec{y}=\varvec{y}^{(1)}+\varvec{y}^{(2)}$$

(10)

where $\varvec{y}^{(1)}$ is the mean trend and $\varvec{y}^{(2)}$ is the fluctuation component.

An example is given in Fig. 1, where a time series collected from the wind power database of Elia, the Belgian transmission system operator (TSO), is decomposed into the mean trend and the fluctuation component.

Fig. 1

A time series of wind speed from the Elia database and the mean trend extracted by SSA

2.2 Locality sensitive hashing

Considering the continuity characteristics of meteorological data, wind speed and wind power at a certain time instant are strongly correlated with data collected in a short period of time before. Thus, instead of putting all the sample segments into training the model, it is more effective to use only the segments that follow the same tendency as the period of time when forecasting is to be done, called the forecast segment. In this paper, the LSH, which is a common and fast similarity search technique, is applied to select the similar segments. It proceeds in two steps: index building and similarity search.

Step 1: Index building. The mean trend $\varvec{y}^{(1)}$ is reconstructed into a higher-dimensional phase space with the embedding dimension s and time constant $\tau$. It can be reconstructed into $N-(s-1)\tau$ segments and each segment is expressed as

$$\varvec{y}_i^{(1)}=\left[ y^{(1)}_i\ y^{(1)}_{i+\tau }\ \cdots \ y^{(1)}_{i+(s-1)\tau }\right]$$

(11)

where $i=1,2,\cdots ,N-(s-1)\tau$.

Afterwards, segments $\varvec{y}_i^{(1)}$ are passed through the locality-sensitive hash function (LSHF) of $h(\varvec{y}_i^{(1)})$, and similar segments are hashed into a certain bucket with high probability, while dissimilar segments have low probability to be hashed into this bucket.

A family H is called locality sensitive, or more specifically $(r_1, r_2 , p_1, p_2)$-sensitive for D, if for any $\varvec{y}_i^{(1)}$ and $\varvec{y}_j^{(1)}$, it holds

$$ \left\{ \begin{aligned} &\mathrm{Pr}_H\left\{ h(\varvec{y}_i^{(1)})=h(\varvec{y}_j^{(1)})\right\} \ge p_1\quad \ D(\varvec{y}_i^{(1)},\varvec{y}_j^{(1)})\le r_1 \\ &\mathrm{Pr}_H\left\{ h(\varvec{y}_i^{(1)})=h(\varvec{y}_j^{(1)})\right\} \le p_2\quad \ D(\varvec{y}_i^{(1)},\varvec{y}_j^{(1)})\ge r_2 \end{aligned} \right. $$

where D is the distance measure; $\mathrm{Pr}_H$ is the probability with respect to a random choice of $h \in H$, and in order to ensure the family is practical, the conditions $p_1>p_2$ and $r_1<r_2$ should be guaranteed.

In this paper, the distance measure D based on normal Euclidean distance is selected. Correspondingly, the LSHF $h(\varvec{y}_i^{(1)})$ is given by

$$h_{\varvec{a},b}(\varvec{y}_i^{(1)})=\left\lfloor \frac{\varvec{a}^{\text {T}} \varvec{y}_i^{(1)}+b}{r}\right\rfloor$$

(12)

where $\varvec{a}$ is a d-dimensional vector which obeys the normal distribution; r is the width of the interval of a random bucket; b is a real number selected randomly from the range of [0, r].

Similarly, a hash table function $g(\varvec{y}_i^{(1)})$ is a concatenation of k LSHFs, $h_j(\varvec{y}_i^{(1)})\in {H}$, $j=1,2,\cdots ,k$ :

$$g(\varvec{y}_i^{(1)})= \left[ h_1(\varvec{y}_i^{(1)})\ h_2(\varvec{y}_i^{(1)})\ \cdots \ h_k(\varvec{y}_i^{(1)})\right] ^{\mathrm{T}}$$

(13)

$$g_{\varvec{A},\varvec{b}}(\varvec{y}_i^{(1)})= \left\lfloor \frac{\varvec{A}^{\text {T}}\varvec{y}_i^{(1)}+\varvec{b}}{r}\right\rfloor$$

(14)

where the projection matrix $\varvec{A}=[\varvec{a}_1\ \varvec{a}_2\ \cdots \ \varvec{a}_k]\in {\mathbb {R}}^{d\times k}$ and each column $\varvec{a}_i$ follows a normal distribution; $\varvec{b}$ is a k-dimensional vector with each element chosen uniformly from the range of [0, r]. $g_{\varvec{A},\varvec{b}}(\varvec{y}_i^{(1)})$ transforms the d-dimensional segment $\varvec{y}_i^{(1)}$ into buckets, such that segments in the same bucket are similar. A bucket is chosen at random and partitioned into uniform widths of r. To increase the accuracy of index building, l hash table functions $g_1(\varvec{x}), g_2(\varvec{x}), \cdots ,g_l(\varvec{x})$ are applied, thus forming l tables $\mathrm{H}_1\sim \mathrm{H}_l$.

Step 2: Similarity search. The forecast mean trend segment $\varvec{y}_{N-(s-1)\tau }^{(1)}$ is projected to l buckets by the l hash table functions. In each table, the segments hashed into the same bucket as the forecast segment are returned, and the $N_\mathrm{s}$ more similar ones, which have a smaller distance from the forecast segment, are selected to be used in local forecasting. Instead of computing the distance of all segments, LSH only calculates the distance of segments in the same bucket, which saves time remarkably.

3 Proposed forecast model

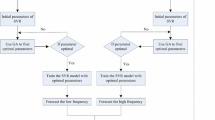
The framework of the proposed forecast model is shown in Fig. 2. In the first step, the decomposition of the original time series by SSA yields the mean trend and the fluctuation component, as shown in Fig. 1. The contribution rates of each eigenvector are illustrated in Table 1 and the first three eigenvectors are used for extracting the mean trend. Afterwards, as shown in Fig. 3, the mean trend will be reconstructed in the phase space and converted to the mean trend segments and fluctuation component segments, respectively. Due to the high randomness of the fluctuation component, similar segment searching is carried out on the mean trend segments, and a number of similar segments of the forecast mean trend segment are obtained by LSH. Figure 4 demonstrates an example of the result of similar segment searching. Finally, in order to avoid error accumulation and fixed errors, the training input is the synthesis of the similar mean trend segments and the corresponding fluctuation component segments. An example of the forecast result is given in Fig. 5, which intuitively is satisfactory.

For detailed instructions on how to implement the proposed model for forecasting, the pseudo code is listed in Algorithm 1.

Table 1 Contribution rates of eigenvectors

Fig. 2

Framework of proposed forecast model

Fig. 3

Reconstruction of the mean trend

Fig. 4

Searching for similar segments to forecast mean trend segment

Fig. 5

Results of 4-step ahead forecast of Elia data set

Algorithm 1 The proposed model
Initialization:
Build the proposed model according to Section 2.1 and Section 2.2. Set the values of L = 20, l = 10, k = 25, s = 7, τ = 1 and Ns = 500.
Body:
1: Load original time series ${\user2{y}}= [y_1\ y_2\ \cdots \ y_N]$, where N represents the number of samples for each season of each database. Determine the look-ahead steps p, embedding dimension s and time constant τ.
2: Apply SSA to decompose the original time series y into the mean trend ${\user2{y}}^{(1)}=\left[y^{(1)}_1\ y^{(1)}_2\ {\cdots} \ y^{(1)}_N\right]$ and the fluctuation component ${\user2{y}}^{(2)}=\left[y^{(2)}_1\ y^{(2)}_2\ {\cdots} \ y^{(2)}_N\right]$.
3: Reconstruct the mean trend ${\user2{y}}^{(1)}$ and the fluctuation component ${\user2{y}}^{(2)}$ into mean trend segments ${\user2{y}}_i^{(1)}$ and corresponding fluctuation segments ${\user2{y}}_i^{(2)},\ \ i=1,2,\cdots,N-(s-1)\tau$ in the phase space.
4: From the $(N-(s-1)\tau)$ mean trend segments, obtain Ns segments similar to the forecast mean trend segment ${\user2{y}}_{N-(s-1)\tau}^{(1)}$ by using LSH.
5: Synthesize the Ns mean trend segments ${\user2{y}}_i^{(1)}$ and fluctuation segments ${\user2{y}}_{i}^{(2)}$, to obtain the training input $\left[{\user2{y}}_{i}^{(1)}\ {\user2{y}}_{i}^{(2)}\right]$. Correspondingly, the training output is the actual value $y_{i+(s-1)\tau+p}$. Note that subscript i corresponds to Ns subscripts out of $1\sim N-(s-1)\tau-1$.
6: Build an SVR model of the training input and training output.
7: Perform the SVR model with the forecast segment $\left[{\user2{y}}_{N-(s-1)\tau}^{(1)}\ {\user2{y}}_{N-(s-1)\tau}^{(2)}\right]$ as the input and obtain the forecast value $\hat{y}_{N+p}$.
8: return Forecast value $\hat{y}_{N+p}$

4 Simulation studies

4.1 Data sources

To evaluate the performance of the proposed model, wind speed and wind power data from four databases are used for forecasting. The data are collected from different wind farms with abundant wind resource. The first database provides inshore wind power data collected from AESO, located in Alberta, Canada [9]. The second database includes the total wind power generation from Elia. The third database is the wind speed data collected from a surface radiation network (SURFRAD) station [25]. The fourth database is offshore wind speed data collected from a testing station in Darwin supported by the Australian Institute of Marine Science (AIMS). The data from the four databases in March are shown in Fig. 6, and their statistical measures (mean, standard deviation (Std), minimum and maximum) are given in Table 2. To test the performance of the forecast models in different seasons, the prediction is carried out in March, June, September and December and compared with the actual data.

Fig. 6

Data from four data sets in March

Table 2 Statistical properties of the data of each data set

4.2 Performance qualification

To evaluate the forecasting accuracy of the proposed model, two commonly used criteria are employed to measure the errors: the normalized mean absolute error (NMAE) and normalized root mean squared error (NRMSE) [26]. NMAE represents how close are the forecast results to the final outcomes and the NRMSE assesses the standard deviation between the forecast value and actual value, which reflects the stability of the forecast model. The smaller the NMAE or NRMSE value is, the more accurate and stable the forecast results are. They are defined by

$${NMAE}= \frac{1}{N}\sum \limits _{i=1}^N\frac{|y_i-{\hat{y}}_i|}{Y}\times 100\%$$

(15)

$${NRMSE}= \frac{1}{Y}\sqrt{\frac{1}{N-1}\sum \limits _{i=1}^N(y_i-{\hat{y}}_i)^2}\times 100\%$$

(16)

where N is the size of the validation data set; ${\hat{y}}_i$ is the forecast value; $y_i$ is the actual value. For wind power forecasting, Y is the installed capacity of the wind farm at the time of forecasting. For wind speed forecasting, Y is the maximum historical value of wind speed.

4.3 Models employed for performance comparison

To validate the accuracy of the proposed model, simulation studies are conducted with the persistence (Per.), SVR, SSA-SVR and SSA-LSH-SVR models. The Per. model indicates that future wind data are consistent with the last measured value. This model performs well in short-term forecasting of wind speed and wind power owing to the slow scale of meteorological changes. Therefore, the Per. model is always utilized as a benchmark for reference.

As a typical machine learning model, the SVR model generally performs well in a majority of forecasting applications, and is also regarded as a benchmark. The SSA-SVR model extracts the mean trend of the wind speed or wind power and treats the remainder as noise. Afterwards, the mean trend of the wind speed or wind power is input into the SVR model. It is expected that the application of SSA can reduce the effect of randomness. As for the SSA-LSH-SVR model, the function of SSA in this model is the same as in the SSA-SVR model, and LSH is employed to find similar segments to the forecast mean trend segment, which are then used to form the training input to build an SVR model. In this manner, a local forecast is achieved, and it is expected to show better performance than a global forecast. By comparing the SVR, SSA-SVR and SSA-LSH-SVR models with the Per. model, the contribution of the SVR, SSA and LSH algorithms can be highlighted.

Unlike the models mentioned above, the proposed model regards the remainder, which is produced by SSA, as the fluctuation component, and LSH is also used to find similar segments to the forecast mean trend segment. The training input for SSA-SVR and SSA-LSH-SVR models are the mean trend segments only, but for the proposed model, it is the synthesis of similar mean trend segments and the corresponding fluctuation component segments. In this way, the two components are treated independently in the SVR model, and the problems of error accumulation and fixed error can be solved.

Fig. 7

NMAEs of five models on Elia data set in June

Fig. 8

NRMSEs of five models on Elia data set in June

Fig. 9

NMAEs of proposed model on four data sets

Fig. 10

NRMSEs of proposed model on four data sets

4.4 Forecast results and discussion

Simulation studies were conducted by the Per., SVR, SSA-SVR, SSA-LSH-SVR models and the proposed model on the four data sets, respectively. Take the time series of Sect. 2, which is wind power data, as an example. The forecast results of 4 look-ahead steps in March based on the proposed model are shown in Fig. 5, which shows the forecast curve almost coincides with the actual one.

In order to assess the performance of the proposed model when forecasting for a range of look-ahead steps, simulation studies of $1\sim 20$ look-ahead steps are conducted and the forecasting performance is evaluated using NMAE and NRMSE. The results are shown in Figs. 7 and  8. As shown in the two figures, the NMAE and NRMSE of the proposed model are the smallest among the five models in all cases. Furthermore, NMAE and NRMSE are improved by 69.32$\%$ and 69.02$\%$ at 6 look-ahead steps, which is the biggest improvement, and by 14.62$\%$ and 17.06$\%$ at 20 look-ahead steps, which is the least, compared to the Per. model. As for the SSA-LSH-SVR model, it is more accurate than the SVR model and the SSA-SVR model, which demonstrates the advantage of the similar segment searching strategy of LSH. Last but not the least, the proposed model, which also adopts LSH for similar segment searching but is based on the synthesis of the similar mean trend segments and the corresponding fluctuation component segments, outperforms the other four models.

To examine the performance of the proposed model on various data sets, the NMAEs and NRMSEs of the proposed model on the four data sets for $1\sim 20$ look-ahead steps are plotted in Figs. 9 and 10. For the purpose of making a more comprehensive study, numerical results for 4, 12, and 20 look-ahead steps have been summarised in Tables 3, 4 5 and 6. As wind may have various natural characteristics in different seasons, the forecast is carried out in March, June, September and December. It can be seen that the proposed model gives the smallest NMAEs and NRMSEs for all of the four data sets, which indicates that the proposed model outperforms the other ones in both accuracy and stability.

Table 3 Performance evaluation of five forecast models on AESO data set

Table 4 Performance evaluation of the five forecast models on the Elia data set

Table 5 Performance evaluation of the five forecast models on the SURFRAD data set

Table 6 Performance evaluation of the five forecast models on the AIMS data set

Table 7 Performance evaluation of three forecast models on Elia data set

4.5 Comparison studies

In order to test the effect of LSH, simulation studies are conducted using the SSA-K-means-SVR, SSA-SOM-SVR and SSA-LSH-SVR models on the Elia data set, respectively, where the K-means and SOM (Self Organizing Maps) algorithms are employed to select the similar segments. The forecast results for 4, 12, and 20 look-ahead steps have been demonstrated in Table 7, and the SSA-LSH-SVR is superior to SSA-K-means-SVR in all cases.

Although when the look-ahead step becomes larger, LSH is not as accurate as SOM, it has great advantage in terms of computation load. All simulation studies are run on a Windows 7 PC with an Inter Core i7 CPU 3.40 GHz and 8GB memory, and the program is coded in MATLAB 2014a. Take the case of forecasting 4 look-ahead steps using the December data of the Elia data set for example. The computation time of SSA-K-means-SVR, SSA-SOM-SVR and SSA-LSH-SVR is 6.7798, 57.7116 and 1.0396 seconds, respectively. Therefore, LSH is a better choice as it sacrifices little accuracy (the largest difference is 0.46% for NMAE) with huge savings in time.

4.6 Discussion on parameters

The purpose of this paper is to make LSH effective and applicable in forecasting, and the proposed model further improves over the SSA-LSH-SVR model by replacing the training input by the synthesis of similar mean trend segments and the corresponding fluctuation component segments. However, it is necessary to analyze how to obtain the best parameters for the model.

A series of experiments are conducted on the Elia data set whose sample interval is 15 minutes, and the results show that as the number of look-ahead steps increases, a more accurate forecast could be obtained by increasing the embedding dimension L; yet, when L reaches a critical point, the accuracy begins to decrease. On the other hand, the number of hash tables, l, and the number of LSHFs, k, do not significantly affect the forecast results. For the number of segments, $N_{\mathrm{s}}$, the accuracy increases with the growth of $N_{\mathrm{s}}$ and finally converges to a certain value.

The best parameters for different kinds of data are different and should be obtained based on a large number of experiments. Some general advice may be given for carrying out the experiments more effectively. First, choose a suitable embedding dimension, L, for SSA ; considering the critical point described above, for each look-ahead step, there exists a value of L for which the NMAE is smallest. There is no strict restriction on the number of hash tables, l, and the number of LSHFs, k. Finally, to decide the best number of the similar segments, $N_{\mathrm{s}}$, simulation studies should be carried out starting with $N_{\mathrm{s}}=150$ and increasing in steps of 50.

5 Conclusion

In this paper, a forecast model based on SSA, LSH and SVR is proposed for short-term wind speed and wind power prediction. The SSA is used to decompose the original time series into two components: the mean trend and the fluctuation component, where the mean trend reveals the slowly changing tendency of the original time series, and the fluctuation component represents its stochastic characteristics. The training input for SVR is a synthesis of the mean trend and the fluctuation component, which helps to ensure that these two components are independent and do not interfere with each other, leading to more accurate forecast results.

Moreover, this paper succeeds in making LSH effective and applicable in forecasting. It is used to classify the mean trend segments and find those that are similar to the forecast mean trend segment. Involving only these similar segments in the SVR improves forecast results. This has been proved by the smaller NMAEs and NMRSEs obtained by the SSA-LSH-SVR model over the SSA-SVR model. Meanwhile, the application of LSH saves computation time remarkably than the SSA-K-means-SVR and SSA-SOM-SVR models.

The proposed model further improves over the SSA-LSH-SVR model by replacing the training input by the synthesis of the similar mean trend segments and the corresponding fluctuation component segments. Simulation studies have been conducted on two wind power data sets and two wind speed data sets, and the results have shown that the proposed model obtains remarkably smaller NMAEs and NRMSEs than the Per., SVR, SSA-SVR and SSA-LSH-SVR models, which indicates its advantage in both accuracy and stability.