Abstract
This study focuses on the potential role of plug-in electric vehicles (PEVs) as a distributed energy storage unit to provide peak demand minimization in power distribution systems. Vehicle-to-grid (V2G) power and currently available information transfer technology enables utility companies to use this stored energy. The V2G process is first formulated as an optimal control problem. Then, a two-stage V2G discharging control scheme is proposed. In the first stage, a desired level for peak shaving and duration for V2G service are determined off-line based on forecasted loading profile and PEV mobility model. In the second stage, the discharging rates of PEVs are dynamically adjusted in real time by considering the actual grid load and the characteristics of PEVs connected to the grid. The optimal and proposed V2G algorithms are tested using a real residential distribution transformer and PEV mobility data collected from field with different battery and charger ratings for heuristic user case scenarios. The peak shaving performance is assessed in terms of peak shaving index and peak load reduction. Proposed solution is shown to be competitive with the optimal solution while avoiding high computational loads. The impact of the V2G management strategy on the system loading at night is also analyzed by implementing an off-line charging scheduling algorithm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Plug-in electric vehicles (PEVs) have become a sustainable solution in response to the demand for more economic and environmentally-friendly vehicles in the transportation sector [1]. However, their impact heavily depends on the availability of resources and structure of the energy system [2]. These vehicles are capable of storing energy in their batteries and are only utilized in 4% of their lifetime for transportation [3]. That is, PEVs may be utilized for other services, particularly as distributed energy storage units, when they are parked and connected to the grid [4,5,6]. Vehicle-to-grid (V2G) technology provides the means for services such as peak shaving [5, 6], valley-filling [6], voltage and frequency regulation [7, 8], reactive power compensation [9, 10], and spinning reserve [11]. From the utility perspective, peak shaving service on the grid reduces distribution power losses, increases distribution level power quality, and extends the lifetime of transformers. Thus, the utility service provider can handle more electric loads without requiring further network reinforcements. From the upstream network perspective, minimizing peak loads can reduce power generation costs and carbon dioxide emissions [12]. The peak loads can be reduced either by unidirectional PEV charging management [12,13,14], or by discharging PEV batteries into the grid using V2G technology [5, 6]. The former approach, also called the load-shifting strategy, is based on the idea of shifting peak loads to off-peak hours. V2G service, on the other hand, suggests providing active power support back to the grid to flatten the base load profile making it more flexible and advantageous for the utility grid. However, heavier use of the vehicle batteries in V2G services contributes to the ageing of the batteries due to the increase in charge cycles which is a serious concern for PEV owners.
V2G can be implemented in two different control architectures, namely, centralized and decentralized controls [15], as shown in Fig. 1. In the centralized control, an aggregator (control center) is responsible to determine discharging set points for each PEV participating in V2G service in order to make a better use of network capacity [16, 17]. For this purpose, a bidirectional data flow takes place between the aggregator and electric vehicle supply equipments (EVSEs). The decentralized control architecture, on the other hand, allows each PEV to determine its own discharging profile [18,19,20]. It is more flexible in terms of PEV user convenience and easier to implement in the field. Various strategies for peak shaving have been presented in the literature [5, 6, 21,22,23]. Some of them determine the PEVs discharging rates in a decentralized fashion [5, 21]. However, the desired level of peak shaving cannot always be guaranteed in those approaches. Therefore, coordinated V2G strategies are needed. Most V2G schemes track a reference line to pull the demand load to a prefferred operating level by discharging PEVs into the grid [6, 22, 23]. The algorithms in these studies dictate a dynamic discharging pattern for PEVs in each time interval by considering only the grid load profile. Thus, a limited peak shaving is achieved in [22]. The algorithms in [6, 23] require very high PEV penetration levels for a satisfactory performance. Moreover, the V2G approaches proposed in [6] and [23] do not consider the stochastic nature of PEV mobility characteristics which makes it a further challenging task to accurately track the reference line. Furthermore, while user convenience is usually referred as the desired state of charge (SOC) at the departure time, the requirement of a minimum driving range for any emergency trips that might occur during the discharging process is often ignored in the literature [5, 6, 21, 23]. A more convenient PEV user experience with reduced range anxiety should definitely be considered for a realistic case study.
The performance of peak shaving algorithms depends on the number of PEVs connected to the grid and their mobility parameters. The total power required to support the grid should be fairly distributed among the PEVs connected to the grid. In addition, stochastic nature of the mobility parameters indicates that the discharging operation should be dynamic and coordinated for more efficient utilization of the stored energy. Both aspects have not been sufficiently explored within the same V2G algorithm in the literature. Moreover, the impact of V2G control algorithms has not been analyzed for a small-size distribution system with reduced PEV penetration rates indicating more realistic scenarios for near future implementations.
The goal of this paper is to coordinate PEV discharging considering PEV stochastic mobility data. The main idea is to use PEV battery capacities depending on the load profile characteristic to ensure an effective peak shaving throughout the peak times. This requires a coordinated V2G strategy by considering both the load profile and PEV characteristics connected to the grid. In this study, the optimal V2G solution is first found to provide a basis for assessing the performance of the developed algorithm. Then, a two-stage V2G control scheme is developed. The first stage includes an off-line operation to determine the desired level for peak shaving and the time period for V2G service based on a forecasted load profile. In the second stage, discharging rates for each PEV are simultaneously determined considering both the load profile level and the available capacities of PEVs participating in V2G service. From the distribution system operator (DSO) perspective, PEVs track the load profile in the distribution system so that the peak loads are shaved effectively. From a PEV user convenience point of view, a minimum SOC level is maintained for emergency departures at any time. This is also to avoid the deep discharging which causes premature aging of the batteries. To evaluate the impact of the extra charge energy need resulting from the V2G contribution, a simple charging scheduling strategy is employed at off-peak hours. The algorithms are tested on real residential distribution transformer loading data for heuristic user case scenarios with different PEV penetration rates and the performance of the algorithm is assessed by two metrics: peak shaving index (PSI) and peak load reduction (PLR) rate.
The paper is organized as follows. Section 2 describes the modeling of PEV mobility. The optimal and proposed V2G control algorithms, and the off-peak charging scheduling are developed in Sect. 3. Experimental data and case studies are presented in Sect. 4. Section 5 provides the main concluding remarks.
2 System modeling
2.1 Transportation mobility modeling
To better analyze the impact of the stochastic travel behaviors and charging demands of the PEV users on power grids, a realistic scenario should be designed. For this purpose, daily home arrival/departing time and daily travel distance data of 10 vehicles have been collected for a year using vehicle tracking devices [24]. The histograms obtained for the home arrival/departing times and the daily trip distances turn out to be quite similar to a Gaussian distribution. The mean and standard deviations of these Gaussian distributions are (7.55 PM, 1 hour 40 min),(7.47 AM, 0 hour 23 min) and (\(39.5\,\hbox {km}, 15.8\,\hbox {km}\)) for home arrival time and daily trip distance, respectively. PEVs are assumed to stay parked at home till the next morning departure time and occasional evening trips are ignored. However, this assumption does not change the performance of the proposed solution because as explained in the following section, the actual mobilities of PEVs are updated in real time.
2.2 Modeling of plug-in electric vehicle
This study considers five different PEV models which are currently available in the market. Table 1 shows the specifications of those PEV models (i.e., battery capacity, range, and charging/discharging power). The vehicles will be charged and discharged through their on-board chargers which are assumed to be capable of bidirectional power transfer. PEVs are connected to the grid using different EVSEs utilizing ac connections according to the IEC 61851 standard [25]. It is assumed that Mode-2 (1-phase, 32 A, for i3, Volt, Leaf, and Bolt) and Mode-3 (1-phase, 63A, for Model S) discharging ratings are employed for on-board discharging using required EVSE and cabling/conduit rating [25]. Since the charger limit imposed by EVSEs is much greater than the on-board charger power ratings, the maximum discharging power is determined by the each on-board charger power rating.
The initial SOC for the \(i^{\mathrm{th}}\) PEV at the time of home arrival can be calculated as follows:
where \(d_i\) is the daily distance travelled by the \(i^{\mathrm{th}}\) PEV and \(R_i\) is the nominal range of that PEV, which are listed in Table 1, under normal driving conditions. To prevent the battery from deep discharging, PEVs which participate in V2G service are warranted to maintain a minimum SOC at any time. That is, PEVs are allowed to discharge to the grid only down to a pre-defined SOC level. This level will be referred to as \(SOC_{\text {min}}\). \(SOC_{\text {min}}\) is defined such that it corresponds to an emergency range of \(50\,\hbox {km}\) which is an average distance to important destinations within the city of Ankara. It is determined for each PEV separately:
So, the maximum available energy which can be provided during the whole V2G process for the \(i^{\mathrm{th}}\) PEV is,
where \(C_{B,i}\) is the nominal battery capacity of that PEV; and \(\eta\) is the on-board charger efficiency. Finally, the energy required to fully charge the \(i^{\mathrm{th}}\) PEV is calculated as follows:
where \(SOC_{final,i}\) is the SOC of that PEV after the discharging process ends, which is equal to or greater than \(SOC_{\text {min},i}\). Using (4), the total charging time for the \(i^{\mathrm{th}}\) PEV to be fully charged at rated charging power can be calculated as:
where \(T_{ch,i}\) is the total charging time and \(P_i^{rated}\) is the rated charging power. Each on-board charger used in this study are assumed to have a constant 90% operating efficiency and 1.0 power factor at all operating points.
3 Development of two-stage V2G control algorithm
3.1 Problem formulation and optimal V2G solution
To define a peak loading period in the grid, we should first decide the preferred point-of-loading value which will be referred to as the reference line \(P_{ref}\). Once the peak period is identified, the objective of the V2G process becomes to level the grid load down to the \(P_{ref}\). Thus, the V2G procedure can be formulated as an optimal discharging control problem whose objective is to minimize the mean square error (MSE) between the load profile and the reference line making the objective function concave.
Let us consider a 24 hours time horizon divided into a T number of time slots of one minute each. Let \(P_{V2G,i}= \left\{ P_{V2G,i}(1), P_{V2G,i}(2),\cdots ,P_{V2G,i}(T)\right\}\) denote the discharging profile of the \(i^{\mathrm{th}}\) PEV, and n denote the number of PEVs participating in V2G service. Let \(P_{load}(t)\) and \(P_{V2G,i}(t)\) be the grid load and discharging rate of \(i^{\mathrm{th}}\) PEV at time t, respectively. \(t_{arr,i}\) is the arrival time of the \(i^{\mathrm{th}}\) PEV, respectively. \(t_{peak,s}\) and \(t_{peak,e}\) denote the start and end times of the peak period. Then, the objective function can be expressed as follows:
By minimizing the MSE, we aim to have an aggregated load profile that closely tracks \(P_{ref}\) and achieve an effective peak shaving. The first constraint in (6) is due to discharging limitations imposed by the on-board charger. The second constraint ensures that V2G operation can be performed between the arrival time of a PEV and the end of the peak period. The last constraint ensures that the provided energy should be equal to or less than the maximum available energy of the vehicle. As PEVs connect to the grid, the aggregator solves (6) iteratively, and broadcasts control signals to update the discharging profile of the PEVs in V2G service. As the number of PEVs in V2G service increases, the computational load of the optimal solution incrementally increases making it impractical for real-time implementations.
We propose another approach which significantly reduces the computational load of the V2G operation while providing a competitive peak shaving performance. The approach consists of two stages: off-line and on-line processing. The desired level of loading after peak shaving and the time period for V2G service are first determined. These parameters depend only on the load profile characteristic and can be forecasted off-line. Then, the discharging power rates for PEVs connected to the grid are simultaneously determined. As the load profile varies with time, discharging PEVs at variable rates by considering the peak load level and the available capacities of PEVs would be more effective. Therefore, the discharging power rates for each PEV in V2G service are updated adaptively whenever a new PEV is connected to the grid for V2G service.
3.2 Off-line operation
The desired value for the point-of-loading must be determined before the online stage. Forecasting the base demand profile is assumed to be undertaken by the DSO, and the forecasted demand is provided as an input to the algorithm developed here.
Suppose that the forecasted base load is as shown in Fig. 2. It is the daily average loading of a distribution transformer in the month of October 2014 which will be introduced in detail in Section IV. To find the location of the reference line, a local minima/maxima analysis is done on the load curve. The points indicated with a star (green) represent the local maxima, whereas the ones indicated with a hole (red) represent the local minima for the load curve in Fig. 2. The x-coordinate for the second local minimum in late afternoon corresponds to the time where the peak starts, \(t_{peak,s}\), and the corresponding y-coordinate is chosen to be the reference line value. The peak ends at the early hours after mid-night when the base curve and the reference line intersect second time, \(t_{peak,e}\). During the time between \(t_{peak,s}\), and \(t_{peak,e}\), which corresponds to the period between 16:10 and 00:50 for the base load in Fig. 2, V2G service takes place, and the base demand curve is shaved down to the reference line by the proposed algorithm.
3.3 On-line operation
Having determined the desired level for the demand curve and the time interval for the V2G service, the discharging power rates as a function of time should be sent to each PEV simultaneously. The discharging pattern of each PEV should be calculated such that when the total power support of PEVs that participate into V2G service is subtracted from the base load, the resulting load level is equal or within an acceptable distance to the reference line between \(t_{peak,s}\) and \(t_{peak,e}\). The reason why it may not exactly follow the reference line lies in the stochastic driving behaviors and number of PEVs connected to the grid. The peak power desired to be shaved at time t can be expressed as:
where \(p_{load}(t)\) is the actual base demand load at time t; and \(P_{ref}\) is the desired loading level at peak hours. The total energy to be shaved from time t to \(t_{peak,e}\) can be calculated by integrating the peak power over this period:
Then, the total available energy which can be utilized for peak shaving from time t till \(t_{peak,e}\) is found. It is equal to the sum of the available energy for each PEV participating in V2G process:
where n is the number of PEVs in V2G service at time t, and \(E_i^{av}(t)\) is the energy corresponding to a state of charge \((SOC_i(t)- SOC_{\mathrm{min},i}(t))\) for the \(i^{\mathrm{th}}\) PEV. Note that \(E_i^{av}(t_{arr,i})\) is equal to \(E_i^{av,{\mathrm{max}}}\). In order to shave the peak accurately and not to create a valley as more vehicles are included in V2G service, \(E_{total}^{av}(t)\) has to be updated each time in an adaptive manner. That is, if \(E_{total}^{av}(t)< E_{peak}(t)\), then the available energy should be fully utilized, and if otherwise, it should be adjusted in such a way that it is kept equal to \(E_{peak}(t)\). In addition, the share of the total support of a PEV at a time t is decided based on the ratio of its available energy to the total available energy of all vehicles. To sum up:
Finally, the discharging energy for each PEV at a time step \(\triangle t\) and the peak energy to be shaved at that time step are calculated as:
where
The discharging power of the \(i^{\mathrm{th}}\) PEV at time t is:
It is important to note that the remaining available energy of the \(i^{\mathrm{th}}\) PEV after a time step should be updated as:
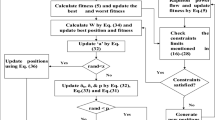
The overall structure of the proposed V2G controller is shown in Fig. 3. The flow chart summarizes (7)-(14). The controller updates the control signals at each time step by considering the load profile and the actual mobilities of PEVs connected to the grid. This requires a centralized control framework. A control center retrieves load profile data from the DSO, and charging/discharging requests and PEV characteristics from the electric vehicle supply equipment (EVSE) also known as charging stations. The controller calculates the discharging power references for each PEV for the remaining V2G period and each PEV discharges with respect to its own reference. Whenever a new PEV is connected to the grid, the controller adaptively readjusts the control signals for new discharging power references of PEVs.
3.4 Off-peak charging scheduling
For a complete scenario, PEV charging loads should also be considered and the impact of the extra charging energy need due to discharging PEVs at peak hours should be investigated. It is more convenient to charge the PEVs at off-peak hours, because the demand load and the electricity price are lower during these hours. Herein, we use the approach in [26] where charging is carried out with rated power in a scheduled manner. This approach has several advantages from the energy consumption and the charging time perspectives. Classical heuristic charging prioritizing policies can also be applied in charging scheduling. However, the off-peak charging scheduling can be better exploited to achieve a valley-filling behavior, i.e., a grid load profile with lower variance value [20]. This is important for DSOs, because minimizing variance is equivalent to maximizing the load factor and hence, minimizing the losses in the distribution network [27]. It was shown in [28] that the minimum variance can be achieved at best by scheduling PEVs starting from the time slots where the base load profile is at its lowest value. Thus, the off-peak charging, inferred from [28] is formulated as follows:
with
where \(P_{base}(t)\) is the grid base load; \(P_{ch,i}(t)\) and \(s_i(t)\;\in {\left\{ 0,1\right\} }\) denote the charging load and the binary charging decision of \(i^{\mathrm{th}}\) PEV at time t, respectively; \(t_{dept}\) is the departure time of the last PEV; and n is the number of PEVs to be charged at off-peak hours. The scheduling algorithm determines the appropriate time \(t_{i,start}\) to start charging . The objective function is subjected to the following constraint:
4 Experimental data and case studies
4.1 Distribution transformer loading data
Tests are carried out on a residential distribution transformer. The transformer rated at 1000 kVA, 34.5 kV/0.4 kV is located in the distribution network in the city of Ankara operated by Baskent DisCo. It is serving 1000 customers with 90% residential apartment dwellings and 10% small-scale commercial shops. The transformer loading data were recorded for 4 months using Schneider ION 7650 power quality meter that is installed at the low voltage side of the transformer. The measurements have been taken according to the IEC 61000-4-30, and the recorded data are transmitted to the Baskent DisCo servers via 3G communication. The power measurements are recorded at every ten minutes.
The daily average grid load profiles for four months are shown in Fig. 4. As observed in the figure, the active power demand varies between 150 kW and 410 kW in the Fall season. The maximum loading without PEV loads at this transformer is 40% of the rated power. The peak and lowest demands occur around 21:00 and 05:00, respectively. The time frame where peak loading occurs also coincides with the vehicle home arrival times. According to the triple tariff determined by the Energy Market Regulatory Authority (EPDK) of Turkey, the peak times correspond to the hours between 17:00 and 22:00. As shown in the figure, peak loading mostly occurs in these hours but also extends beyond 24:00. If the loads were shaved according to the peak hour definition by EPDK, the peak shaving operation would not be fulfilled effectively. Therefore, to determine the peak loading region depending on the load profile, a new reference line is used which was described in Section III-B.
4.2 Case studies
This section presents the results obtained with the proposed V2G algorithm in different discharging and charging scenarios with three PEV penetration rates. The same scenarios are also investigated with the optimal solution using the convex optimization toolbox CVX in MATLAB [29]. In these scenarios, PEV users select one of the two profiles at plug-in time: V2G service or standard (dumb) charging. PEVs which have an SOC level greater that \(SOC_{\mathrm{min}}\) at plug-in time are allowed to join the V2G service. This is to ensure a minimum driving range of \(50\,\hbox {km}\) for emergency trips. A first come-first serve basis is used for V2G service participation. Standard charging refers to full charging at on-board charger ratings. In this context, three different scenarios have been studied as reported in Table 2. The first scenario is selected to demonstrate the proposed algorithm performance on the base load profile. 40% of all PEVs join into the V2G service in this scenario. The remaining PEVs which do not join into V2G are assumed to wait until off-peak hours for charging. The second scenario is selected to quantify the algorithm performance on the aggregated load profile, including the base load and PEVs charging loads. In this scenario, 40% of all PEVs provide V2G service while the PEVs, which have an SOC level less than \(SOC_{\mathrm{min}}\), start charging at their on-board rated power until they reach \(SOC_{\mathrm{min}}\). Charging power required for emergency trips is determined as follows:
The other PEVs are again assumed to wait until off-peak hours for charging. The last scenario is to investigate the performance of the algorithm under heavy PEV charging loads. This scenario is the most realistic one because it also considers the PEV users who prefer to charge their vehicles immediately at the time of arrival. In this scenario, participation ratio is assumed to be 40% for V2G service and 20% for standard charging among all PEVs. At the same time, the PEVs with SOC levels less than \(SOC_{\mathrm{min}}\) start charging at their on-board rated power until they reach \(SOC_{\mathrm{min}}\). The remaining 20% PEVs wait until off-peak hours for charging. The standard charging power is determined as follows:
To implement these scenarios, a total of 1000 residential customers are considered and each one is assumed to possess only one vehicle. The PEV models listed in Table 1 are distributed homogeneously among all customers. The home arrival times and the daily trip distances for all PEVs are extracted from the models generated in Section II.A. The load profile in the month of October is used. For each scenario, three different PEV penetration rates are considered as 5% (short-term), 10% (middle-term), and 20% (long-term) to account for different market adoption levels.
The algorithms are implemented in MATLAB on a general-purpose computer with Intel Core i5-3337U CPU @1.80 GHz and 6 GB RAM. The simulation is run for 100 times to fairly assess the performance of the algorithm. The presented figures show the averaged results among 100 simulation runs.
Figure 5 depicts the load profiles for 10% PEV penetration rate under Scenario 1. The optimal V2G algorithm shaves all peak loads. As the number of PEVs in V2G service increases, the proposed solution converges to the optimal solution. Average total required time to compute the discharging profiles of PEVs for both algorithms under different PEV penetration rates is reported in Table 3. The computing time of the proposed algorithm is much lower than that of the optimal solution. The large number of iterations typically involved in optimal charging algorithm is a burden on computation time even for low penetration rates. Requiring high computation times makes optimal solution impractical at field implementation.
Figure 6 shows the actual and shaved load profiles with the proposed algorithm for 10% PEV penetration rate under all three scenarios. The corresponding discharging profiles for PEVs providing V2G service are illustrated in Fig. 7. As shown in Fig. 6, the PEVs in V2G service are able to shave the peak loads completely for all scenarios after the arrival of the required number of PEVs for V2G service. Since there are only a few PEVs arriving before 19:00, the peak can be shaved up to a certain extent. It can be observed from Fig. 7 that discharging power rates of PEVs are updated continuously at each time step considering the load profile and the available capacities of PEVs in V2G service. The proposed algorithm adjusts the discharging powers of PEVs in V2G service dynamically in such a way that they are discharged until the end of the peak period. Hence, the loads at early peak hours (before 19.00) are slightly shaved even if the total available PEV capacity in V2G service is sufficient to shave all the loads at that time. This is to guarantee that maximum peak shaving performance is attained throughout the whole peak period. Figure 8 illustrates the simulation results for 20% PEV penetration rate under heavy PEV charging loads (scenario 3). It is again observed that the proposed control system is able to shave the peak loads successfully even if the PEV charging loads are increased. This is mainly because of the increase in the amount of the available energy. Compared to the 10% PEV penetration in Fig. 6, the time when the load profile becomes flat is earlier for the 20% case due to the increased number of V2G-available PEVs. In conclusion, as the discharging patterns of each PEV are updated at each time step, the proposed algorithm achieves a good peak-shaving independent of the load profile characteristics.
The mean, standard deviation and median values of the number of charging cycles in 10% PEV penetration case, which corresponds to 40 PEVs, are given in Table 4. The average number of daily charging cycles increases from 0.17 to 0.44 when V2G service is provided. The PEV user should be compensated through a well-established market for the cost of the additional battery wear due to increased charging/discharging cycles.
The impact of V2G on the entire load profile are shown for 5% and 10% PEV penetration rates in Figs. 9 and 10, respectively. Note that the demand load in the figures does not include the energy demand to fully charge the PEVs but includes \(P_{emg}\) and \(P_{dumb}\), while the green line, which is the resulting load profile with the proposed algorithm, includes all PEVs’ charging loads at off-peak hours as well as the V2G support. It is observed that at 10% rate, a new peak occurs at off-peak hours. The main reason is that the transformer used in this study cannot accommodate such a penetration rate of beyond 30% [24]. However, the need of additional charging energy due to V2G process may also contribute to the peak at off-peak hours. Therefore, the desired level of peak shaving should be determined by considering the grid load and the number of PEVs with their mobility parameters.
The performance of the proposed V2G algorithm is evaluated in terms of two parameters: PSI and PLR rate. PSI represents the peak shaving performance, and it is calculated as the ratio of the total shaved energy to the total energy to be shaved,
Minimizing peak demand value enables the utility to supply more loads with the current generation capacity, and it is a concern for transmission system operators. Therefore, PLR rate can also be used to assess the performance of the proposed algorithm. It refers to what extent the peak value reduction is achieved and is calculated as follows:
where \((P_{load})_{\mathrm{max}}\) and \((P_{load,shaved})_{\mathrm{max}}\) are the peak value of the actual and shaved load profiles, respectively.
Table 5 summarizes PSI values and PLR rates of the proposed and optimal algorithms for three PEV penetration levels under aforementioned scenarios. As the penetration rate increases, PSI also increases due to the increased available capacities of PEVs in V2G service. For 20% PEV penetration rate, the peak loads are almost shaved under all scenarios. On the other hand, the PLR rate increases as the penetration level and transformer loading increases. The best PLR (40.73%) with the proposed strategy is obtained under the most realistic scenario (Scenario 3). The optimal solution gives the best performance for all cases. However, the proposed algorithm gives a near optimal solution. The proposed algorithm outperforms the approaches in [6] and [23] in terms of PLR. A PLR of 14% and 9% with 25% and 5% PEV penetration levels are reported in [6] and [23], respectively. The performance of the V2G algorithms is not reported in terms of PSI metric in the related literature. Also, it is not meaningful to make a comparison between the PSIs because the transformer loadings differ in each study. However, the proposed V2G algorithm can achieve a PSI of 98% at 20% PEV penetration.
5 Conclusion
In this study, we introduced an efficient coordinated V2G control scheme to reduce peak loads at distribution substation level. The proposed algorithm adjusts the discharging rates of PEVs in an adaptive manner by considering the grid load profile and PEV characteristics. Even at low PEV penetration rates, the algorithm achieves a good peak-shaving independent of the load profile characteristics. It is shown that 8% PEV V2G penetration achieves a peak shaving rate of approximately 99% on a 1MVA rated transformer. The results are also shown to be competitive with the optimal solution. Compared to the optimal solution, the computational cost is very low which makes the proposed algorithm more applicable at field implementation.
References
San Román TG, Momber I, Abbad MR et al (2011) Regulatory framework and business models for charging plug-in electric vehicles: infrastructure, agents, and commercial relationships. Energy Policy 39(10):6360–6375
Orsi F, Muratori M, Rocco M et al (2016) A multidimensional well-to-wheels analysis of passenger vehicles in different regions: primary energy consumption, \(\text{ CO }_2\) emissions, and economic cost. Appl Energy 169:197--209
Kempton W, Tomic J (2005) Vehicle-to-grid power fundamentals: calculating capacity and net revenue. J Power Sources 144(1):268–279
Garcıa-Villalobos J, Zamora I, San Martın J et al (2014) Plug-in electric vehicles in electric distribution networks: a review of smart charging approaches. Renew Sust Energy Rev 38:717–731
Alam MJE, Muttaqi KM, Sutanto D (2015) A controllable local peak-shaving strategy for effective utilization of pev battery capacity for distribution network support. IEEE Trans Ind Appl 51(3):2030–2037
Wang Z, Wang S (2013) Grid power peak shaving and valley filling using vehicle-to-grid systems. IEEE Trans Power Deliver 28(3):1822–1829
Clement-Nyns K, Haesen E, Driesen J (2011) The impact of vehicle-to-grid on the distribution grid. Electr Power Syst Res 81(1):185–192
Han S, Han S (2014) Development of short-term reliability criterion for frequency regulation under high penetration of wind power with vehicle-to-grid support. Electr Power Syst Res 107:258–267
Kisacikoglu MC, Ozpineci B, Tolbert LM (2010) Examination of a PHEV bidirectional charger system for V2G reactive power compensation. In: Proceedings of the twenty-fifth annual IEEE applications of power electronics conference and exposition (APEC), Palm Springs, USA, 21–25 Feb 2010, pp 458–465
Kisacikoglu MC, Kesler M, Tolbert LM (2015) Single-phase onboard bidirectional pev charger for V2G reactive power operation. IEEE Trans Smart Grid 6(2):767–775
Bessa R, Matos M (2014) Optimization models for an EV aggregator selling secondary reserve in the electricity market. Electr Power Syst Res 106:36–50
Ahn C, Li CT, Peng H (2011) Optimal decentralized charging control algorithm for electrified vehicles connected to smart grid. J Power Sources 196(23):10369–10379
Masoum AS, Deilami S, Moses P et al (2011) Smart load management of plug-in electric vehicles in distribution and residential networks with charging stations for peak shaving and loss minimisation considering voltage regulation. IET Gener Transm Distrib 5(8):877–888
Ramachandran B, Srivastava SK, Cartes DA (2013) Intelligent power management in micro grids with EV penetration. Expert Syst Appl 40(16):6631–6640
Mukherjee JC, Gupta A (2015) A review of charge scheduling of electric vehicles in smart grid. IEEE Syst J 9(4):1541–1553
Liu H, Hu Z, Song Y et al (2015) Vehicle-to-grid control for supplementary frequency regulation considering charging demands. IEEE Trans Power Syst 30(6):3110–3119
Xu N, Chung C (2016) Reliability evaluation of distribution systems including vehicle-to-home and vehicle-to-grid. IEEE Trans Power Syst 31(1):759–768
He Y, Venkatesh B, Guan L (2012) Optimal scheduling for charging and discharging of electric vehicles. IEEE Trans Smart Grid 3(3):1095–1105
Xing H, Fu M, Lin Z et al (2016) Decentralized optimal scheduling for charging and discharging of plug-in electric vehicles in smart grids. IEEE Trans Power Syst 31(5):4118–4127
Kisacikoglu MC, Erden F, Erdogan N (2018) Distributed control of PEV charging based on energy demand forecast. IEEE Trans Ind Inform 14(1):332–341
Rassaei F, Soh WS, Chua KC (2015) Demand response for residential electric vehicles with random usage patterns in smart grids. IEEE Trans Sustain Energy 6(4):1367–1376
Rahimi A, Zarghami M, Vaziri M et al (2013) A simple and effective approach for peak load shaving using battery storage systems. In: Proceedings of the 45th IEEE North American power symposium, Kansas State University, USA, 22–24 Sept 2013, 5 pp
Aswantara IKA, Ko KS, Sung DK (2013) A dynamic point of preferred operation (ppo) scheme for charging electric vehicles in a residential area. In: Proceedings of the IEEE international conference on connected vehicles and expo (ICCVE), Las Vegas, USA, Dec 2–6 2013, pp 201–206
Erden F, Kisacikoglu MC, Gurec OH (2015) Examination of EV-grid integration using real driving and transformer loading data. In: Proceedings of the IEEE 9th international conference on electrical and electronics engineering (ELECO), Bursa, Turkey, 26-28 Nov 2015, pp 364–368
Comission IE (2010) Electric vehicle conductive charging system- part-I: General requirements, Standard 61851–1
Binetti G, Davoudi A, Naso D et al (2015) Scalable real-time electric vehicles charging with discrete charging rates. IEEE Trans Smart Grid 6(5):2211–2220
Sortomme E, Hindi MM, MacPherson SJ et al (2011) Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses. IEEE Trans Smart Grid 2(1):198–205
Malhotra A, Erdogan N, Binetti G et al (2016) Impact of charging interruptions in coordinated electric vehicle charging. In: Proceedings of IEEE global conference on signal and information processing (GlobalSIP), Greater Washington, D.C., USA, Dec 2–5, 2016, pp 901–905
C. M. S. for Disciplined Convex Programming (2017) CVX: Matlab software for disciplined convex programming. http://cvxr.com/cvx/. Accessed Dec 2017
Acknowledgements
This work was supported in part by the Scientific and Technological Research Council of Turkey through the International PostDoctoral Fellowship Program under Grant 2219. The authors also would like to acknowledge the support of Baskent Electricity Distribution Company that provided the distribution transformer data within the scope of the project DAGSIS (Impact Analysis and Optimization of Distribution-Embedded Systems) funded by Turkish Energy Market Regulatory Authority (EPDK).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 23 November 2017
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
ERDOGAN, N., ERDEN, F. & KISACIKOGLU, M. A fast and efficient coordinated vehicle-to-grid discharging control scheme for peak shaving in power distribution system. J. Mod. Power Syst. Clean Energy 6, 555–566 (2018). https://doi.org/10.1007/s40565-017-0375-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0375-z