Damping control for a target oscillation mode using battery energy storage

Abstract

In this paper, a battery energy storage system (BESS) based control method is proposed to improve the damping ratio of a target oscillation mode to a desired level by charging or discharging the installed BESS using local measurements. The expected damping improvement by BESS is derived analytically for both a single-machine-infinite-bus system and a multi-machine system. This BESS-based approach is tested on a four-generator, two-area power system. Effects of the power converter limit, response time delay, power system stabilizers and battery state-of-charge on the control performance are also investigated. Simulation results validate the effectiveness of the proposed approach.

1 Introduction

Power system oscillation, whose frequency typically ranges from 0.2 to 2.5 Hz, often occurs in interconnected power grids, and is one of the major concerns in power system operations [1]. The phenomenon of power system oscillation can be caused by many factors such as insufficient system damping, forced oscillation [2], external periodic load perturbation [3], parametric resonance [4] and modal interaction [5], etc. Conventionally, this problem can be partially solved by fine-tuning the parameters of power system stabilizers (PSSs) of the involved generators. However, for an interconnected bulk power system, the offline tuning of PSS parameters of different generators by a coordinated scheme may involve the regulatory entities from different regions that require high-standard cooperation and information sharing. Furthermore, many researchers proposed to use a centralized control system for online tuning PSSs. However, this approach will also introduce the problems of the time delay and communication cost among different interconnected areas. An alternative option for oscillation damping is to use local flexible AC transmission system (FACTS) devices such as static var compensator (SVC), thyristor controlled series capacitor (TCSC), and static synchronous compensator (STATCOM) to provide extra damping support for the system [6,7,8]. Basically, those are passive elements/sources alleviating oscillations mainly by controlling reactive power or changing the line admittance.

With the fast development of energy storage and power electronics technologies, many utility-scale battery energy storage systems (BESSs) have been deployed in the power system industry and have participated in the power markets. As an active source, the BESS can be used for balancing the power systems to provide the ancillary services. In normal conditions of a power system, a BESS is operated in the normal state, i.e. either charging or discharging in a scheduled mode. However, due to their considerable initial investment, its function can be further exploited not only as a system balancing unit, but also to provide extra damping for system oscillations.

Some studies have been reported in recent literatures [9,10,11,12,13,14,15]. In [11], the analysis and design of a BESS controller for a two-machine system are discussed and tested, but the analysis for general multi-machine systems is not comprehensively covered. Designing the damping controller based on certain damping-torque relationships and indices is also a focused topic [12]. Those indices can be regarded as a generalization of the damping-torque coefficients in a single machine infinite bus (SMIB) system and can be combined with classic residual methods [13] in designing the PSS. Regarding robust control for damping oscillation by BESS, there are two mainstreams: linear and nonlinear robust control. In [14], the linear matrix inequality (LMI) method is used, which requires the solving of an optimization problem. In [15], the Port-Hamiltonian formulation and the related controller design method are applied on BESS to improve the transient stability.

This paper investigates this problem from an alternative view point, i.e. symbolically solving the equations regarding eigenvalues and then applying the analytical results on the design of the BESS based damping controller. Typically, the inter-area oscillation mode is the main concern for system operators and can be extremely harmful to power system reliability, which is required high priority to be damped. The method proposed here can damp a target mode to an expected damping ratio and, meanwhile, will not worsen other oscillation modes.

The remaining parts of this paper are organized as follows. In Sect. 2, based on the analysis of the power-electronics converter of a BESS, the model is simplified by a proper approximation. In Sect. 3, the linearized state-space model for a power system with a BESS is derived and the eigenvalues are solved. The solution is then used to design the controller to improve the damping ratio of a target mode to an expected value. Section 4 evaluates the effectiveness of the proposed method on both the SMIB system and the two-area system. Conclusions and discussions about the future work are given in Sect. 5.

2 BESS model for system oscillation study

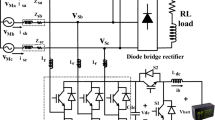
Typically, a BESS includes a storage part comprised of battery cells and a converter interface called a power conditioning system (PCS), as shown in Fig. 1. The PCS is essentially the set of power converters used to maintain the pre-specified voltage and power output. For the BESS, the PCS is typically composed of a DC/DC converter mainly used for battery charging/discharging control and a DC/AC converter (voltage source converter) mainly used for the AC-grid integration with desired voltage and power output.

Fig. 1

Topology of grid-connected BESS

Since most grid related control strategies are implemented in the DC/AC stage, in this paper, the PCS is modeled as voltage source converter focusing on the DC/AC part.

2.1 Storage part: battery cells

A battery can be modeled as an equivalent voltage source with the voltage dependent on the state of charge (SOC). Its equivalent circuit model considering SOC is shown in Fig. 2. Assumptions for this model are: ① the battery can never be discharged to a level under 20%. In this case the voltage is assumed to be linearly dependent on the SOC as shown in Fig. 3 [16]; ② the internal resistance is assumed to be a constant impedance Z, since it is typically very small when the battery is used in high power applications.

Fig. 2

Equivalent circuit model of battery considering SOC

Fig. 3

Typical discharge profile of lead-acid battery

With the above assumptions, the equation for the battery is given as:

$$V_{t} = E_{\hbox{max} } \cdot SOC + E_{\hbox{min} } (1 - SOC) - I \cdot Z$$

(1)

where E_min is the cell voltage when fully discharged; E_max is the cell voltage when fully charged; Z is the cell internal resistance; I is the cell discharge (> 0)/charge (< 0) current; V_t is the cell terminal voltage.

In power industry applications, the cell should be protected from deep charging/discharging for life-span consideration. An allowable depth of discharge (DOD) is typically 75% or 80% [17]. Thus, a preferable range of SOC is [20%, 80%] in this paper.

2.2 PCS: P-Q decoupled control

The classic P-Q decoupled control strategy has been widely applied [18, 19]. Figure 4 shows the basic control idea of the outer loop using the signal of frequency or voltage deviation to generate reference values for the inner loop. The inner-loop then generates the pulse width modulation (PWM) signal for the power converter, where P_ref and Q_ref are the reference values. In this paper, the proposed method focuses on devising the P_ref. The inner loop structure as shown in Fig. 5 is the same as the classic P-Q decoupled control scheme, which can be found in literature [18, 19]; thus, its details are not expanded here.

Fig. 4

P-Q decoupled control strategy: outer loop

Fig. 5

P-Q decoupled control strategy: inner loop

2.3 Power output model for BESS

The proposed damping controller adjusts the active power output meanwhile maintaining the BESS reactive output to zero, since the active power and system frequency are highly correlated [20]. Thus, the local generator speed (or approximately the terminal bus frequency) deviation can be used as the input signal for P_ref :

$$P_{ref} = - k_{es} \Delta \omega = - k_{es} (\omega - \omega_{0} ) \Leftrightarrow - k_{es} (\omega - 1)$$

(2)

In a typical P-Q decoupled control scheme, the active and reactive power can be regulated to their reference values. On the other hand, usually: (1) the response of the power-electronics device (i.e. switching on/off) is much faster than the dynamics of most electromechanical devices, such as synchronous generators; (2) the controller time constants, (e.g. the integral time constants of the PI controller) are typically much smaller than both the cycles of line frequency (e.g. 0.02 s) and the periods of the electromechanical oscillation modes (frequency in the range of 0.2–2.5 Hz). Thus the power output of the BESS can be modeled by a first order transfer function in the power system oscillation study [9, 18] as shown in Fig. 6, where T_es is the time constant of the BESS power response.

Fig. 6

Power output model of BESS used in oscillation study

2.4 Effect of T _es on proposed damping control

The effect of T_es is slightly reducing the desired damping ratio of the target mode, which will be verified in later sections. T_es usually ranges from 0.01 s to 0.05 s, depending on different specifications of the BESS. Thus, in the following section of small signal analysis, T_es will be set temporarily to zero during the mathematic derivation, while given as 0.05 s in simulations. Since T_es is much smaller than the inertia time constant of a generator [18, 21], in the following analysis, the actual power output of the BESS is approximated by the power output reference, i.e.:

$$\begin{aligned} P_{es} & = \frac{{P_{ref} }}{{1 + T_{es} s}} \\ & \quad \Rightarrow P_{ref} - P_{es} = T_{es} \frac{{{\text{d}}P_{es} }}{{{\text{d}}t}} \approx 0 \Rightarrow P_{es} \approx P_{ref} = - k_{es} (\omega - 1) \\ \end{aligned}$$

(3)

3 Proposed BESS based damping control

The basic idea of the proposed damping control is:

• 1) Deriving the analytic relationship between the gain k_es in BESS damping controller and the damping ratio ξ for a target oscillation mode.

• 2) Implementing that gain in the outer-loop controller of the BESS placed nearby the generator’s terminal bus.

In the following part, the SMIB system will be investigated first to derive the damping control algorithm. Then, the algorithm will be extended to multi-machine systems having a BESS placed near each generator.

3.1 BESS in SMIB system

3.1.1 Case 1: BESS at generator terminal bus

In Fig. 7, x₁ is the sum of the generator transient reactance x_d′ and the transformer reactance x_T, and x is the transmission line reactance.

Fig. 7

Case 1 of SMIB system

The system differential algebraic equations (DAEs) are:

$$\left\{ \begin{array}{l} \frac{{{\text{d}}\delta }}{{{\text{d}}t}} = \varOmega_{0} (\omega - 1) \hfill \\ \frac{{{\text{d}}\omega }}{{{\text{d}}t}} = \frac{1}{M}(P_{m} - P_{e} - D(\omega - 1)) \hfill \\ P_{es} = - k_{es} (\omega - 1) \hfill \\ P_{es} + P_{e} = P_{L} \approx \frac{{E^{\prime}_{q0} V}}{x}\sin \delta \hfill \\ \end{array} \right.$$

(4)

where Ω₀ = 377 rad/s for 60 Hz system; ω is the generator angular frequency and δ is the rotor angle; E′_q is the transient q-axis voltage of the generator. P_m and P_e are the mechanic power and electric power respectively. P_es is the active power output of energy storage. M (= 2H) is the generator inertia time constant. The last equation holds approximately in the SMIB system, in which the generator connected to the infinite bus by a long transmission line, i.e. x′_d + x_T << x.

Then, linearize (4) around the equilibrium (the quantities with subscript “0” represent the steady-state value, which can be solved from the power flow solution).

$$\left\{ \begin{array}{l} \frac{{{\text{d}}\Delta \delta }}{{{\text{d}}t}} = \varOmega_{0} \Delta \omega \hfill \\ \frac{{{\text{d}}\Delta \omega }}{{{\text{d}}t}} = \frac{1}{M}(\Delta P_{m} - \Delta P_{e} - D\Delta \omega ) \hfill \\ \Delta P_{es} = - k_{es} \Delta \omega \hfill \\ \Delta P_{es} + \Delta P_{e} = \Delta P_{L} \approx \frac{{E^{\prime}_{q0} V}}{x}\cos \delta_{0} \Delta \delta \hfill \\ \end{array} \right.$$

(5)

Linearize ΔP_e w.r.t. two state variables Δδ and Δω:

$$\Delta P_{e} = K_{1} \Delta \delta + K_{2} \Delta \omega$$

(6)

where K₁ and K₂ are constant coefficients to be determined. Substitute them into the swing equation (5):

$$\frac{{{\text{d}}\Delta \omega }}{{{\text{d}}t}} = \frac{1}{M}(\Delta P_{m} - K_{1} \Delta \delta - K_{2} \Delta \omega - D\Delta \omega )$$

(7)

Apply Laplace transformation to the swing equation and assume the mechanical power input of generator does not change, i.e. ΔP_m = 0 [21]:

$$\left\{ \begin{array}{l} s\Delta \delta (s) = \varOmega_{0} \Delta \omega (s) \hfill \\ s\Delta \omega (s) = \frac{1}{M}( - K_{1} \Delta \delta - K_{2} \Delta \omega - D\Delta \omega ) \hfill \\ \end{array} \right.$$

(8)

Then, the characteristic equation is:

$$s^{2} + \varOmega_{0} \frac{{(D + K_{2} )}}{M}s + \varOmega_{0} \frac{{K_{1} }}{M} = 0$$

(9)

Compare it with the standard characteristic equation of a second-order system,

$$s^{2} + 2\xi \omega_{n} s + \omega_{n}^{2} = 0$$

(10)

Equating (9) and (10) yields:

$$\left\{ \begin{array}{l} \omega_{n} = \sqrt {\frac{{\varOmega_{0} K_{1} }}{M}} \hfill \\ \xi = \frac{{D + K_{2} }}{{2M\omega_{n} }} \hfill \\ \end{array} \right.$$

(11)

Then, consider M = 2H in the above expression, we have:

$$\, \xi = \frac{{D + K_{2} }}{{4H\omega_{n} }}$$

(12)

In practice, D needs to be estimated from real system data [23]. For simulation studies, it can be treated as zero if generation and load are modeled in detail [20, 21]. Consider D = 0 here, then:

$$K_{2} = 4H\omega_{\text{n}} \xi = 8{\uppi }f_{\text{n}} H\xi$$

(13)

Therefore, the damping ratio ξ is related to K₂, i.e. the partial derivative of P_e to ω. From the last equation in (5), it then leads to:

$$\Delta P_{e} \approx \frac{{E^{\prime}_{q0} V}}{x}\cos \delta_{0} \Delta \delta - \Delta P_{es} \approx \frac{{E^{\prime}_{q0} V}}{x}\cos \delta_{0} \Delta \delta + k_{es} \Delta \omega$$

(14)

Thus, by (13) and (14) the relationship between ξ and k_es is:

$$k_{es} = K_{2} = 8{\uppi }f_{\text{n}} H\xi$$

(15)

3.1.2 Case 2: BESS at general locations

Now consider a more general case. As shown in Fig. 8, x₁ = x′_d + x_T + x_line-1, x₂ = x_line-2, where x_line-1 + x_line-2 = x (i.e. the total reactance of the previous transmission line).

Fig. 8

SMIB system with BESS in Case 2

The following (16) and (17) can be derived based on the power balance equation.

$$P_{e} = \frac{{E^{\prime}_{q} V_{es} \sin (\delta - \theta )}}{{x_{1} }} = \frac{{V_{es} V}}{{x_{2} }}\sin \theta - P_{es}$$

(16)

$$(E^{\prime}_{q} V_{es} \cos (\delta - \theta ) - V_{es}^{2} )x_{2} = x_{1} (V_{es}^{2} - V_{es} V\cos \theta )$$

(17)

By linearizing (16) and (17), the following expression is finally obtained after some manipulation:

$$\begin{aligned} \Delta P_{e} & = K_{7} \Delta \delta + K_{8} \Delta P_{es} = K_{7} \Delta \delta - K_{8} k_{es} \Delta \omega \\ & \quad (\because \Delta P_{es} = - k_{es} \Delta \omega ) \\ \end{aligned}$$

(18)

$$K_{8} = \frac{{ - E^{\prime}_{q} x_{2} (E^{\prime}_{q} x_{2} + Vx_{1} \cos \delta_{0} - 2V_{es0} (x_{1} + x_{2} )\cos (\delta_{0} - \theta_{0} ))}}{{E_{q}^{\prime 2} x_{2}^{2} + V^{2} x_{1}^{2} - 2E^{\prime}_{q} V_{es0} x_{2}^{2} \cos (\delta_{0} - \theta_{0} ) + 2E^{\prime}_{q} Vx_{2} x_{1} \cos \delta_{0} - 2V_{es0} V(x_{1} + x_{2} )x_{1} \cos \theta_{0} }}$$

(19)

The coefficient K₈ can be named as the “location effect constant” and its expression is given in (19). Then, to check the correctness of this formula for Case 1, letting x₁ = 0 and K₈ becomes − 1 as shown in (20) and (21).

$$\begin{aligned} K_{8} & = \frac{{ - E^{\prime}_{q} (E^{\prime}_{q} x_{2}^{2} - 2V_{es0} x_{2}^{2} \cos (\delta_{0} - \theta_{0} ))}}{{E_{q}^{\prime 2} x_{2}^{2} - 2E^{\prime}_{q} V_{es0} x_{2}^{2} \cos (\delta_{0} - \theta_{0} )}} \\ & = - \frac{{E_{q}^{\prime 2} x_{2}^{2} - 2E^{\prime}_{q} V_{es0} x_{2}^{2} \cos (\delta_{0} - \theta_{0} )}}{{E_{q}^{\prime 2} x_{2}^{2} - 2E^{\prime}_{q} V_{es0} x_{2}^{2} \cos (\delta_{0} - \theta_{0} )}} \, = - 1 \\ \end{aligned}$$

(20)

$$\Delta P_{e} = K_{7} \Delta \delta - \Delta P_{es} = K_{7} \Delta \delta + k_{es} \Delta \omega$$

(21)

It can be noticed that in (21), the coefficient of Δω is exactly the same as that in Case 1 when neglecting x₁. Finally, k_es is given by:

$$\xi = \frac{{K_{2} }}{{4H\omega_{n} }} = \frac{{ - K_{8} k_{es} }}{{4H\omega_{n} }} \Rightarrow k_{es} = \frac{{8{\uppi }{\kern 1pt} f_{n} H\xi }}{{ - K_{8} }}$$

(22)

To investigate the impact of the BESS installing location, denote k = x₁/(x₁ + x₂). δ is the rotor angle of the generator, typically within [− π/2, π/2] [20, 21]; E′_q, is the generator transient q-axis voltage with a typical range [0.5, 2.5].

Figure 9 depicts how − K₈ changes w.r.t. k for different combinations of δ and E′_q. − K₈ achieves its maximum value 1.0 at x₁ = 0. When the specified damping ratio ξ is given, the larger − K₈ leads to smaller k_es. Since k_es represents the BESS energy injection/absorption per unit time, a smaller k_es means a smaller BESS discharge/charge depth. This will be more attractive for utility companies and system planners, i.e. the BESS can be used as an ancillary service for oscillation damping with potentially lower energy cost.

Fig. 9

Plot of − K₈ versus different δ and E′_q under different line ratio k

3.2 BESS in multi-machine system

3.2.1 Small signal state space model

In an n-generator system, similar to the SMIB case, the BESS device can be installed at the terminal buses or nearby buses of generators. As shown in Fig. 10. P_ei, P_esi, P_gi are the electromagnetic power, the BESS output power and active power output of the ith generator respectively.

Fig. 10

Multi-machine system with BESS integration

Apply the reduced network technique [20] by keeping only the generator buses, the system model is:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{{\text{d}}\varvec{\delta}}}{{{\text{d}}t}} =\varvec{\varOmega}(\varvec{\omega}- 1) \hfill \\ \frac{{{\text{d}}\varvec{\omega}}}{{{\text{d}}t}} = \varvec{M}^{ - 1} (\varvec{P}_{m} - \varvec{P}_{e} - \varvec{D}(\varvec{\omega}- 1)) \hfill \\ \end{array} \right. \, \hfill \\ \varvec{P}_{e} = \varvec{P}_{g} - \varvec{P}_{es} \hfill \\ \end{aligned}$$

(23)

where $\varvec{M}^{ - 1} = {\text{diag}}[M_{i}^{ - 1} ]_{n \times n}$; $\varvec{\varOmega}= {\text{diag}}[\varOmega_{0} ]_{n \times n}$; $\varvec{\delta}= [\delta_{i} ]_{n \times 1}$; $\varvec{\omega}= [\omega_{i} ]_{n \times 1}$; $\varvec{P}_{e} = [P_{ei} ]_{n \times 1}$; $\varvec{P}_{m} = [P_{mi} ]_{n \times 1}$; $\varvec{P}_{es} = [P_{esi} ]_{n \times 1}$; $\varvec{P}_{g} = [P_{gi} ]_{n \times 1}$; $\varvec{D}{ = }\text{diag} { (}D_{1} , D_{2} , \cdots ,D_{n} )$; D_i is the damping constant for the ith generator; P_gi can be approximately expressed by [20]:

$$P_{gi} = E_{i}^{2} G_{ii} + E_{i} \sum\limits_{j = 1, \ne i}^{n} {E_{j} } (G_{ij} \cos \delta_{ij} + B_{ij} \sin \delta_{ij} )$$

(24)

where G_ij and B_ij are the real and imaginary part of the Y_ij in the reduced nodal admittance matrix [21].

Power output of each BESS in a compact form are:

$$P_{esi} = - k_{esi} \Delta \omega_{i} \Rightarrow \varvec{P}_{es} = - \varvec{K}_{es}\Delta \omega$$

(25)

where $\varvec{K}_{es} = {\text{diag}}[k_{esi} ]_{n \times n} , \, k_{esi} \ge 0$.

Then, linearize the above equations around the equilibrium point:

(26)

Here, the Jacobian matrix J_p is:

$$\varvec{J}_{P} (\varvec{\delta}) = \left. {\frac{{\partial (P_{e1,} P_{e2} , \ldots ,P_{en} )}}{{\partial (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} )}}} \right|_{{\delta_{i} = \delta_{i0} }} = \left. {\left( {\begin{array}{*{20}c} {\frac{{\partial P_{e1} }}{{\partial \delta_{1} }}} & \cdots & {\frac{{\partial P_{e1} }}{{\partial \delta_{n} }}} \\ \vdots & \ddots & \vdots \\ {\frac{{\partial P_{en} }}{{\partial \delta_{1} }}} & \ldots & {\frac{{\partial P_{en} }}{{\partial \delta_{n} }}} \\ \end{array} } \right)} \right|_{{\delta_{i} = \delta_{i0} }}$$

(27)

3.2.2 Analytic eigenvalue solutions

Step 1: Determinant simplification

From above section, the 2n-by-2n system matrix A is:

(28)

The eigenvalues λ are the roots of the determinant equation:

(29)

where I is the identity matrix of n-by-n.

Then the following block matrix lemma is utilized to derive the analytic solution. Its proof can be found in [24].

For matrix $\varvec{M} = \left( {\begin{array}{*{20}c} \varvec{A} & \varvec{B} \\ \varvec{C} & \varvec{D} \\ \end{array} } \right)$, if $\varvec{CD} = \varvec{DC}$, then

$$\det \varvec{M} = \det (\varvec{AD} - \varvec{BC})$$

To apply this lemma to (29), it requires:

$$\begin{aligned} & \varvec{M}^{ - 1} \varvec{J}_{P} (\lambda \varvec{I} + \varvec{M}^{ - 1} (\varvec{D} + \varvec{K}_{es} )) = (\lambda \varvec{I} + \varvec{M}^{ - 1} ( + \varvec{K}_{es} ))\varvec{M}^{ - 1} \varvec{J}_{P} \\ & \quad \Rightarrow \varvec{M}^{ - 1} \varvec{J}_{P} \varvec{M}^{ - 1} (\varvec{D} + \varvec{K}_{es} )= \varvec{M}^{ - 1} (\varvec{D} + \varvec{K}_{es} )\varvec{M}^{ - 1} \varvec{J}_{P} \\ \end{aligned}$$

(30)

Denoting $\varvec{S} = \varvec{M}^{ - 1} (\varvec{D} + \varvec{K}_{es} )$, it is easy to see that S is a diagonal matrix. If S is equal-diagonal, i.e. S = diag[S]_n×n:

$$\frac{{(D_{1} + k_{es,1} )}}{{M_{1} }} = \frac{{(D_{2} + k_{es,2} )}}{{M_{2} }} = \cdots = \frac{{(D_{n} + k_{es,n} )}}{{M_{n} }} = S$$

(31)

Then, it is easy to verify that (30) can hold.

Thus, if the unknowns k_esi are selected based on (31), then (32) can be obtained:

$$\det (\lambda \varvec{I} - \varvec{A}) = \det ((\lambda^{2} + \lambda \varvec{S})\varvec{I} +\varvec{\varOmega}_{0} \varvec{M}^{ - 1} \varvec{J}_{P} )$$

(32)

For matrix product M⁻¹J_P, by eigenvalue decomposition [23], it can be transformed to:

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{M}^{ - 1} \varvec{J}_{P} = \varvec{T}^{ - 1} \varvec{\varLambda T} \hfill \\\varvec{\varLambda}= \left( {\begin{array}{*{20}c} {\mu_{1} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {\mu_{n} } \\ \end{array} } \right) \hfill \\ \end{array} \right. \hfill \\ \hfill \\ \end{aligned}$$

(33)

where μ_i is the eigenvalue of M⁻¹J_P. The real matrix J_P is semi-definite and nearly symmetric [13]. M⁻¹ is diagonal. By matrix theory, μ_i is real non-negative number and the above diagonalization process can be guaranteed [24].

Step 2: Analytic solution of each eigenvalue

Apply the Laplace theorem [24] for the determinant of product matrices on (32):

$$\begin{aligned} & \det (\lambda \varvec{I}{ - }\varvec{A} )= \det (T^{ - 1} )\det \left( {(\lambda^{2} + \lambda \varvec{S})\varvec{I} +\varvec{\varOmega}_{0}\varvec{\varLambda}} \right)\det (\varvec{T}) \\ & \quad = \det (\varvec{T}^{ - 1} )\det (\varvec{T})\det \left( {(\lambda^{2} + \lambda \varvec{S})\varvec{I} +\varvec{\varOmega}_{0}\varvec{\varLambda}} \right) \\ & \quad = \det \underbrace {{\left( {(\lambda^{2} + \lambda \varvec{S})\varvec{I} +\varvec{\varOmega}_{0}\varvec{\varLambda}} \right)}}_{\text{diagonal}} = \prod\limits_{i}^{n} {(\lambda^{2} + \lambda \varvec{S} +\varvec{\varOmega}_{0} \mu_{i} )} \\ \end{aligned}$$

(34)

Thus, eigenvalues of the original system are the roots for each of the above n quadratic equations, i.e.:

$$\lambda = \frac{{ - \varvec{S} \pm \sqrt {\varvec{S}^{2} - 4\varvec{\varOmega}_{0} \mu_{i} } }}{2}$$

(35)

Furthermore,

$$\begin{aligned} & {\text{If}}\; \, \varvec{S}^{ 2} - 4\varvec{\varOmega}_{0} \mu_{i} \ge 0\quad \lambda \in R \\ & {\text{If}}\; \, \varvec{S}^{ 2} - 4\varvec{\varOmega}_{0} \mu_{i} < 0 \Rightarrow \, {\text{complext roots}} \, {\kern 1pt} {\kern 1pt} (\mu_{i} > 0): \\ & \lambda_{i} = \frac{{ - \varvec{S} \pm {\text{j}}\sqrt {4\varvec{\varOmega}_{0} \mu_{i} - \varvec{S}^{ 2} } }}{2} \Leftrightarrow \sigma_{i} \pm {\text{j}}\omega_{di} = - \xi_{i} \omega_{ni} \pm {\text{j}}\sqrt {1 - \xi_{i}^{ 2} } \omega_{ni} \Rightarrow \\ & \left\{ \begin{array}{l}\varvec{\xi}_{i} = \frac{\varvec{S}}{{2\sqrt {\varvec{\varOmega}_{0} \mu_{i} } }} \hfill \\ \varvec{S} = 2\varvec{\xi}_{i} \sqrt {\varvec{\varOmega}_{0} \mu_{i} } = 2\xi_{i} \omega_{ni} \hfill \\\varvec{\omega}_{di} = \frac{{\sqrt {4\varvec{\varOmega}_{0} \mu_{i} - \varvec{S}^{2} } }}{2}\, \hfill \\ \end{array} \right. \\ \end{aligned}$$

(36)

Step 3: Calculate k_esi

To make (31) hold, suppose the kth mode is our target mode (this can be easily identified by its natural oscillation frequency ω_nk). Then substitute S = 2ξ_kω_nk into (31):

$$\frac{{D_{i} + k_{esi} }}{{M_{i} }} = 2\xi_{k} \omega_{nk} \Rightarrow k_{esi} = 4H_{i} \xi_{k} \omega_{nk} - D_{i} \quad i = 1,2, \ldots ,n$$

(37)

Especially when $\,D_{i} = 0\,\; \Rightarrow \, \,\,k_{esi} = 4H_{i} \xi_{k} \omega_{nk}$.

4 Simulation study

4.1 SMIB system

To test the proposed method for the general location case, the system parameter for the SMIB system are: x₁ = x′_d + x_T1 = 0.05 + 0.10 = 0.15, x₂ = 0.35, k = x₁/(x₁ + x₂) = 0.3, i.e. about 1/3 of the electric distance between generator and infinity bus. Note that here x₁ is not much smaller than x₂. Mechanical input power P_m = 1.0 p.u., D = 0 and the nominal frequency f₀ = 60 Hz. K₈ = 0.71898 by (19).

Two groups of tests on the SMIB system with BESS under different generator inertia parameters (H = 5 s and H = 10 s) are performed targeting at 5% damping ratio. A three-phase fault is applied at infinite bus from 1 s and cleared at 1.1 s. Prony analysis is used to estimate the actual damping ratio from generator angle and speed waveforms. The results can closely match the expected damping ratio as shown in Table 1. Figure 11 illustrates the 20% damping ratio case to compare with the original system without BESS. Note that a damping ratio of 5% is usually enough for power system operations; here the test damping ratio ranges from 5% to 40% in order to verify the accuracy of the derived formula by simulations.

Table 1 Control performance of BESS in SMIB Case 2

Fig. 11

Simulation plots for SMIB with 20% damping ratio control

If the impact of T_es, i.e. the converter time constant, is considered, generally it will slightly reduce the expected damping ratio. In real power converters, T_es can be up to 50 ms. Consider the worst case here i.e. T_es = 50 ms. The result is listed in Table 2 for the case with H = 5 s.

Table 2 Effect of converter time constants T_es

From Table 2, the maximum reduction of damping ratio is only 20.16% − 19.26% = 0.009 for 20% case, so the negative impact of T_es is not severe for the proposed control method. A comparison on the active power output of the BESS for ξ = 20% is shown in Fig. 12.

Fig. 12

Comparison of BESS active power response considering T_es

4.2 Two-area system

In this section, the Kundur’s two-area system model [21] is used to investigate the performance of the proposed method on a multi-machine power system. The single line diagram is shown in Fig. 13. The simulation model is built in DIgSILENT/PowerFactory. The battery storage device is modeled by the DIgSILENT simulation language (DSL) [22].

Fig. 13

Single line diagram of the Kundur two area system

By modal analysis, the system has three oscillation modes: (1) 0.548 Hz with a damping ratio of 4.38%, is an inter-area mode between Area-1 (G1, G2) and Area-2 (G3, G4); (2) 1.002 Hz with a damping ratio of 4.86%; (3) 1.036 Hz with a damping ratio of 4.92%. The last two are local modes. The 0.548 Hz mode has the weakest damping, so its damping ratio needs to be improved. In simulation, a temporary three-phase ground fault is added at bus-8 at 2 sec and cleared after 0.02 s. The objective damping ratio is set to 5%. By (37), the k_esi (i = 1~4) is:

$$\left\{ \begin{array}{l} k_{esi} = 4H_{i} \xi_{1} \sqrt {\varOmega_{0} \mu_{ 1} } - D_{i} \approx 4H_{i} \omega_{n1} \Delta \xi_{1} \hfill \\ \Delta \xi_{1} = (\xi_{1}^{*} - \xi_{1} ) \hfill \\ \end{array} \right.$$

(38)

where ξ₁* = 5% and ξ₁ is 4.38%, ω_n1 = 2πf_n1 is the natural oscillation frequency for mode-1, i.e. the target mode.

4.2.1 Case a: adding BESS in original system

Control effects on three modes are shown in Table 3. It can be observed that the damping ratios of all the three modes have been improved. The improvement for the target mode is the most significant and reaches the 5% goal.

Table 3 Control effect of BESS on each mode

In Table 4, the performance of the proposed method is tested for expected damping ratios changing from 5% to 10%. Each result is close to the expectation.

Table 4 Control performance test for target mode with BESS

4.2.2 Case b: impact of converter power limit

Either for the sake of protecting the power switch device due to their thermal limits or other technical reasons, a realistic power converter will have a power limit, which may have impact on the control effect of the proposed method. On the other hand, utility-scale power converter output levels have been improved in recent years allowing the maximum power limit to reach 5 MW for single utility scale power converter [17, 25]. If considering aggregating configuration of multi-converters like in a wind farm or battery park [25], this limit can be enhanced to 30 MW [25].

To investigate the power limit impact on the proposed control, similar tests are done with results listed in Table 5.

Table 5 Control performance test considering BESS power limit

To visually inspect the nonlinear effect of converter power limit, the following case study is presented with a 10% damping ratio requirement for the target mode. Typically, that means more and faster energy injection/absorption from the BESS than 5% damping ratio requirement.

The power limit is set to 3 MW for each BESS. The BESS power output result is shown in Fig. 14. From the plots, it shows that each BESS is in charging state nearly all the time during this disturbance.

Fig. 14

BESS active power responses for ξ^* = 10% in Kundur system

The relative generator rotor angles are shown in Fig. 15. Gen-1 and Gen-4 belong to different areas. Thus, δ₁₄ mainly reflects the target mode at 0.548 Hz; the other two modes (1.002 Hz and 1.036 Hz) are mainly caused by oscillations between local generators inside each area, as shown by δ₁₂ and δ₃₄ respectively. Damping improvement for δ₁₄ is the most significant. The damping ratios for other two relative angles are also improved. This phenomenon verifies the control effect and is in consistence with the previous modal analysis result.

Fig. 15

Relative generator rotor angles for ξ^* = 10% in Kundur system

4.2.3 Case c: impact of converter time constant T _es

Like the previous study in SMIB case, the T_es is set to 50 ms. To better demonstrate the impact of T_es, no converter power limit is assumed here. Results are shown in Table 6.

Table 6 Control performance test considering time constant T_es

In Table 6, as expected, the effect of T_es is to slightly lower down the damping ratio, and its largest error is only 9.79% − 9.688% ≈ 0.001. This magnitude of error is acceptable in practical power system operations. This result again validates the assumption that, in the proposed method, the converter time constant can be ignored during the analytic formula derivation with small errors introduced. In Table 7, effect on each mode is listed. The target mode can meet the 5% damping ratio goal with other two modes slightly improved as in Table 3.

Table 7 Effect of converter time constant T_es on each mode

The BESS power responses are shown in Fig. 16.

Fig. 16

Zoom-in plot of BESS active power responses when T_es = 50 ms

4.2.4 Error analysis

The absolute percentage error (APE) of the damping ratio (|Δe| = |ξ − ξ*|/|ξ*|) for the above three cases are compared in Fig. 17, from which there are following observations: ① the APE for each case is below 5% which can satisfy practical engineering needs; ② the power converter time constant T_es has slightly more influence on the accuracy of the proposed method than other factors, because in the second subplot of Fig. 18, the mean values of APE for the three cases are respectively 1.20%, 1.65% and 1.85%, where the mean APE of case-c considering T_es is the largest; ③ the APE will slightly increase with the increase of the desired damping ratio. This can be explained because the proposed BESS controller is essentially a linear type. For most systems, a 5% to 10% damping ratio will be sufficient and reasonable for small-signal stability.

Fig. 17

Performance comparison and error analysis

Fig. 18

Error analysis for BESS damping control considering PSS

4.2.5 Case study on power system with PSSs

In a real power system, there could be multiple existing PSSs for oscillation damping control. To investigate the damping improvement by the proposed BESS controller on such a system, each generator in the two-area system is equipped with a PSS. All PSSs are designed to make the damping ratio of the target mode reach 4.99% without BESS. Suppose that a higher damping ratio is expected by adding the proposed controller. Then, the new damping ratio goal is set from 6% to 10%, respectively, to design the controller based on (37). The test results are in Table 8. The APE of the damping ratio is depicted in Fig. 18, which are all less than 2%. Note that here ξ₁ in (37) becomes 4.99%, so the calculated value of k_es is smaller than its values in previous case studies without a PSS. Since the k_es can be interpreted as the power output coefficient of the BESS converter during the disturbance, a smaller k_es means a smaller converter capacity required for the BESS. Since the converter capacity takes a major portion of the overall cost of a BESS, the investment on the BESS for damping control in a power system that already has PSSs can be decreased.

Table 8 Test results on power system with PSS

4.2.6 Impact on battery SOC

Consider the worst case in subsection-b, i.e. with 3 MW converter power limit for each BESS and 10% damping ratio requirement for the target mode. In Fig. 15, it is observed that the battery is mainly charged during the disturbance. The energy charged is nothing but the area under the power (absorption) curve during disturbance as shown in Fig. 19 (red section) of the zoom-in plot for − P_es4.

Fig. 19

Zoom-in plot of BESS-4 active power response

For example, for BESS-4, the energy absorbed is:

$$E_{es4} = \int_{{t_{0} = 1.99}}^{t = 16.0} {P_{es4} (t){\text{d}}t} = 5. 6 4 8 3\;{\text{MJ}} \Leftrightarrow 0. 0 0 1 6\;{\text{MWh}}$$

To evaluate the impact on SOC, assume a small energy capacity for BESS-4 (SOCs of other three BESS units can be calculated similarly) as 0.5 MWh (in utility scale BESS, this value can be larger [17, 25]). Then:

Depth of charge = 0.0016/0.5 = 0.0032.

A typical SOC range is [0.2, 0.8]. Thus the theoretical maximum and minimum new SOC are respectively:

SOC_new,max = 0.8 + 0.0032 = 0.8032, and the relatively change is only: 0.0032/0.8 = 0.4%;

SOC_new,min = 0.2 + 0.0032 = 0.2032, and the relatively change is only: 0.0032/0.2 = 1.6%.

Thus, in both cases the impact on SOC is small, implying that using a BESS for oscillation damping may not weaken its available capacity for other functions like load following/balancing because the energy provided/absorbed by oscillation is much smaller than the total BESS capacity during disturbance. Moreover, a small portion of energy means potentially a low cost in using BESS for damping oscillation. Due to this fact, the BESS is very promising as a new kind of ancillary service in providing auxiliary damping when needed.

5 Conclusion

This paper proposed a novel damping control method based on the usage of BESS. Analytic eigenvalue solutions were derived on both the SMIB and multi-machine systems. Controller based on those solutions was verified successfully by simulation. The results demonstrated a promising performance in damping target oscillation mode with quantifiable improvement of damping ratio. Thus, to alleviate system oscillations by providing extra damping support based on the proposed method is validated.

Future work includes time delay compensation of the converter time constant for higher control accuracy and studying potential combination of other successful methods like robust control considering parameters uncertainty.