Abstract
In this paper, a multi-stage stochastic model is presented for a renewable distributed generation (RDG)-owning retailer to determine the trading strategies existing in a competitive electricity market. Uncertainties associated with wholesale electricity market price, clients’ consumption and power output of wind resources are considered through auto regressive integrated moving average (ARIMA) approach. In the proposed method, three trading floors are addressed for the retailer to hedge against the uncertainties. In the first stage, the retailer participates in day-ahead market to supply the clients and in the second stage, intraday market is addressed to allow the retailer to modify the schedule of its clients’ consumption/RDG production. Due to unfavorable uncertainties, especially in renewable power production, real-time market is considered in the third stage to diminish the uncertainty at power delivery time. Cost function of wind resources considering capital, operation and maintenance (O&M) cost is incorporated in the objective function to increase the applicability of the mechanism. The proposed approach is formulated for risk-averse and risk-taker retailer through conditional value at risk (CVaR) approach. In order to study the impact of retail strategies on consumption pattern and consumers’ electricity bills, time-of-use (TOU) demand response programs are discussed in this paper. Formulating the problem, the mixed integer non-linear programming (MILNP) problem is transformed into mixed integer linear programming (MILP) by jointly using decomposition and disjunctive constraints. Finally, a case study containing wind power resources, energy storage system and retailer is considered to analyze the proficiency of the proposed approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In competitive electricity markets, retailers are new marketers who purchase electricity from a wholesale market at a variable price and sell it to the consumers based on agreed tariff at the retail level [1, 2]. In the wholesale market, retailers can purchase electricity from different trading markets such as pool markets, bilateral contracts or self-production facilities. In this regard, electricity price uncertainty/volatility is the major challenge of the retailer.
Regarding variables with imperfect data, electricity price and load level are the main uncertain variables in a retail problem. For this reason, many studies consider electricity price and load level as the main uncertain variables in their scheduling [3,4,5,6,7,8,9,10,11,12]. In general terms, as more uncertain variables are considered, the optimization problem becomes more complex, which usually increases the time required to solve the problem.
Considering the retail problem with stochastic variables, the probability distribution of uncertain data can be approximated by a collection of plausible sets of input data with associated probabilities of occurrence. These sets are called scenarios. In order to hedge against uncertainty in variables, different scenario generation techniques are discussed in previous studies. Auto regressive integrated moving average (ARIMA) is the most common way to generate scenarios in retail problems [4, 6, 7, 11]. Moreover, auto regressive moving average (ARMA), Monte Carlo simulation approach [13, 14] and Roulette wheel technique [15] are widely used in retail problems to forecast the electricity price variations, hourly wind speed and behavior of other rival retailers, respectively.
Retailers in wholesale electricity market can procure electrical energy through two different resources including wholesale markets and wholesale contracts. Considering wholesale market, day-ahead market (DAM) [16,17,18], real time market (RTM) [19, 20], intraday market (IDM) [19] and reserve market (RM) [21] are the most common markets used by retailers to purchase their obligated energy. Moreover, based on wholesale contracts, future contracts [18], forward contracts [22, 23], call option [7] and swing contracts [17] are typically used in different studies of retail problems.
In retail electricity markets, consumers can adjust their consumption pattern according to retailers’ offers or incentives through demand response programs (DRPs). Demand response can be defined as the changes in electricity usage by end-use customers from their normal consumption patterns in response to changes in the price of electricity over time [23]. Considering DRPs, different retail pricing schemes are proposed in the technical literatures [24]. Price based DRPs are based on dynamic pricing rates in which electricity tariffs are not flat. These rates include the time of use (TOU) rate [25], critical peak pricing (CPP), extreme day pricing (EDP), extreme day CPP (ED-CPP), and real time pricing (RTP) [26, 27].
In order to overcome the uncertainties of electricity price and load level, some retailers prefer to procure some blocks of their obligated energy from self-production facilities [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. In papers [8, 28] a thermal distributed generation (DG) is considered as self-generation facility to supply some blocks of energy. While most of the existing technical literatures have focused on using conventional DGs, there have been relatively few models discussing the optimal strategies of renewable DG-owning retailers.
Decisions in retail market need to be made with lack of perfect information; as a result, it motivates policy makers of retail market to use stochastic programming approach in their decision making process [29]. In addition, some papers, especially in recent years, have been concentrated on information gap decision theory (IGDT) [30] and robust optimization program [8] to optimize the trading strategies of the retail problem.
Among recent studies, reference [31] proposes a virtual electricity retailer (VER) with different electricity pricing strategies. The results show that the approach helps consumers save electricity while maximizing VER profits. In [32], a retail electricity market with high penetration of distributed energy resources is presented. By using game theory, the results demonstrate that the market players can maximize their expected payoff/profit by undertaking strategies through the price bidding strategy. Reference [33] proposes a mathematical program with equilibrium constraints determining retail electricity price for plug-in electric vehicles (PEVs) coordinated by an aggregating agent. Simulated analysis indicates that adequate competition in the retail market is necessary to limit the aggregator’s monopolistic profitability. In [34], the behavior of consumers towards flexible retail price is investigated. The results indicate that the retailer should devise the flexible procurement strategies according to the types of the consumers in the price-based DR to reduce/increase the costs/profit. In [35], interactions between a retailer and its customers are modeled considering renewable energy resources. It is shown that whole benefits of renewable integration go to the retailer when the capacity of renewable resources is relatively small. As the capacity increases beyond a certain threshold, the benefit from renewable that goes to consumers increases. Reference [36] investigates the impact of annual short-term revenue of photovoltaic (PV) systems for those households installing them and for their electricity retailers. The results indicate that the retailers’ revenue varies significantly according to the actual performance of the PV system. Systems with poor orientation/irradiation drive considerably smaller financial flows than well installed and maintained systems.
The intermediary role of the energy retailers in electricity market is depicted in Fig. 1.
This paper presents a multi-stage stochastic programming approach to determine optimal participation of a renewable DG-owning retailer in a competitive structure of electricity market. In this approach, the retailer can participate in a wholesale market proposing its own hourly offering curves. The retailer procures the required energy of consumers from two different resources: ① wholesale market; ② renewable self-generation facilities. In wholesale market, the retailer participates sequentially in three trading floors including day-ahead market, intraday market and real time market. In this way, the retailer faces the uncertainty of wholesale market prices and load levels. In addition, due to renewable production facilities, the retailer faces the intermittent power outputs of wind resources. In contrast to the conventional DGs, renewable resources increase the uncertain characteristics of the problem. Therefore, the complexity of the problem is further increased when the overall objective is to determine the trading strategies for a renewable DG-owning retailer. To study the impact of different energy storage systems (ESS) on consumers’ electricity tariffs, different technologies of electrical energy storage systems are considered in this paper. The results show how the electricity tariffs will change in response to the different charging/discharging modes during optimal operation of ESSs. The uncertainties are simulated through ARIMA approach. Moreover, in order to reduce the computation time and increase tractability of the problem, the size of generated scenarios are modified by Kantorovich distance method. In order to study the changes in electricity usage/electricity bills of end-use consumers in response to the changes in electricity price, demand response program considering elasticity factor is discussed. Moreover, to strike a right balance between risk and profit, risk study is incorporated in the objective function of the problem through conditional value at risk (CVaR) approach.
2 Conceptual framework
This section introduces the proposed multi-stage stochastic model to specify the optimal trading strategies for a renewable DG-owning retailer in retail electricity markets. In this study, the retailer faces three kinds of uncertainties including: wholesale electricity price, clients’ consumption and intermittent power output of wind resources. In order to hedge against the uncertainties, the retailer participates in a pool-based electricity market which includes three successive short-term trading floors as: ① day-ahead market; ② intraday market; ③ real time market.
First of all, day-ahead market takes place a day prior to the energy delivery time. The retailer, equipped with intermittent generation units, prepares offering curves based on predicted uncertainties associated with electricity price, clients’ consumption and wind power generation. In fact, the retailer, in this paper, is both the purchaser of electricity for its consumers and the seller of surplus of energy due to its wind power generation. Therefore, it prepares optimal offering curves which could optimize its trading strategies during the next 24 hours. In this paper, the retailer has no market power capability in either of the aforementioned market floors to change the electricity market clearing price (MCP). In the other words, the retailer only makes decision about purchasing/selling deficit/surplus of energy depending on its predicted electricity price, clients’ demand and intermittent power output of wind resources. Moreover, to evaluate the impact of different ESSs on electricity tariff of consumers, some well-known technologies of electrical energy storage systems, including Advanced Lead-Acid, Pumped Hydro and Sodium Sulfur with different efficiency and operation and maintenance costs are considered. In this way, the impacts of charging/discharging modes on changing electricity tariff for the consumers during the next 24 hours are evaluated. The mentioned measures are incorporated into the first step of proposed stochastic programming approach in this study.
Secondly, due to integration of renewable energy to the electricity market, an intraday market is considered between the closure of the day-ahead market and the beginning of energy delivery time to make it possible to take corrective actions. The intraday market is a trading floor with a planning horizon similar to that of the day-ahead market, where the retailer participates in order to make final adjustments to the energy previously traded for each period of the next day. Intermittency of power output for wind resources is strongly dependent on the magnitude of the time interval up to its realization. The intraday market takes place 10–60 minutes prior to energy delivery horizon; therefore, this market allows intermittent DG-owning retailer to incorporate into their offers the certainty gained on generation availability during the time interval between day-ahead market and energy delivery time by updating its production/consumption forecasts and hence, reducing the associated uncertainties. In addition, the retailer can modify its production/consumption pattern in response to unforeseen events, e.g. unexpected DG failures or sudden changes in clients’ behavior. In this study, the corrective actions in the intraday market are interpreted as second stage of stochastic programming approach. Note that the retailer participates in the intraday market as a price-taker entity.
The real time market is the trading floor in power market to ensure the balance between energy supplied by producers and energy demanded by the clients on a real-time basis. Regarding retail market, any retail agent, especially intermittent DG-owning retailers, expecting a final power schedule below or above the last power schedule resulting from trading in day-ahead and intraday market is motivated to amend its energy deviations through real time market. In this paper, a two-price based real time market is considered for balancing power deviations. The proposed mechanism motivates the DG-owning retailers to schedule power production or consumption with precision to make more profit staying in business. Balancing measures in the real time market is interpreted as the third stage of proposed stochastic programming approach. Note that the retailer is considered as a price-taker participant in this trading floor.
In this paper, the retailer has no market power capability in either of the aforementioned market floors. The objective function of the problem is to maximize expected profit from participation in day-ahead market and intraday market and minimize the expected cost imposed by energy deviations in real time market. Moreover, the cost function of wind resources considering capital investment cost and operation and maintenance cost is incorporated in the objective function.
To study the impact of retail strategies on end-use consumption pattern and electricity bills, a price-based demand response as TOU program are addressed in this paper. In order to strike a right balance between risk and profit, the proposed framework is evaluated for risk-taker and risk-averse retailer through CVaR criteria.
With considering the above framework, the contributions of this paper are summarized as follows:
-
1)
Proposing a retailer cost function considering intermittent power output of self-renewable production facilities.
-
2)
Presenting a method to achieve an optimal electricity bidding/offering strategy for retailers considering a dual role (a purchaser of clients’ obligated demand and/or seller of surplus of renewable energy) rather than a single role (a purchaser in the conventional studies).
-
3)
Analyzing the impact of demand response programs on consumption pattern and consumers’ electricity bills.
-
4)
Studying the impact of different ESS technologies and charging/discharging modes on the consumers’ electricity tariffs.
To sum up, Fig. 2 depicts the DG-owning retailer’s problem.
3 Proposed multi-stage stochastic model
This section introduces the proposed multi-stage stochastic model to specify optimal strategies of the retailer emphasizing increased use of green energy portfolio. First, we describe the procedure of determining maximum expected profit. The profit function of retailer consists of the revenue from the sale of energy to the wholesale market floors and customers minus the electricity acquisition costs from different wholesale market floors and intermittent DGs. These components are calculated as below:
where t, ω, i and j are the indices of time, scenarios, renewable-self production units and energy storage systems, respectively. In this way, NT, Nω, NDG and NESS refer to the number of time hours, scenarios, wind resources and storage systems. Regarding the electricity price variables, \(\lambda_{t}^{DA}\), \(\lambda_{t}^{ID}\) and \(\lambda_{t}^{RT}\) present the electricity price of day-ahead, intraday and real-time markets, respectively. Moreover, \(\lambda_{t}^{D}\) indicates the consumption tariff. Considering the traded power variables, \(P_{t,S}^{DA} \left( {P_{t,P}^{DA} } \right)\), \(P_{t,S }^{ID} \left( {P_{t,P}^{ID} } \right)\), \(P_{t,S}^{RT} \left( {P_{t,P}^{RT} } \right)\) are sold (purchased) power in (from) day-ahead, intraday and real-time markets, respectively. Note that the subscripts S and P show the sold and purchased power in electricity market, respectively. In addition, \(P_{t}^{D}\) and \(P_{t,i}^{W}\)are the load level and wind power, respectively; \(P_{ESS}^{dis}\) and \(P_{ESS}^{ch}\) are discharging and charging power of storage units, respectively; \(C_{W}^{OM}\) and \(C_{ESS}^{OM}\) are operation-maintenance cost of wind power units and energy storage systems, respectively. Furthermore, \(C_{i}^{CI}\) is the capital investment cost of wind generation unit i. Regarding CVaR variables, α and β are confidence level and risk aversion factor, respectively. Moreover, ζ and μ(ω) are auxiliary variables of CVaR approach. Note that π(ω) shows the probability of the occurrence of scenario ω.
The first term in (1) denotes the income from selling energy to the clients. The next three terms represent net income from selling energy to day-ahead market, intraday market and real time market, respectively. The fifth term denotes maintenance-operation and capital investment cost of wind resources. The sixth and seventh terms describe the objective function of the scheduling problem associated with energy storage systems. Finally, the last term indicates the CVaR(1−α) risk measure approach for the random parameters which their probability distribution functions are approximated through scenarios.
As mentioned before, a two-price-based structure is considered for deviations of balancing power in real time market. In this regard, the deviations that are in the opposite direction to the overall power system imbalance, which help the power system restore the balance between production and consumption, are priced at the day-ahead market price. On the contrary, imbalances of the same sign as that of the system are settled at the clearing price of the balancing market. Finally, two basic laws are introduced for operation of real time market as follows [38]:
-
1)
If there is a deficit of generation in the power system or the power system imbalance is negative:
$$\left\{ \begin{aligned} \lambda_{t}^{RT( + )} = \lambda_{t}^{DA} \;\;\;\;\;\;\forall t \in N_{t} \hfill \\ \left| \begin{aligned} \lambda_{t}^{RT( - )} = \lambda_{t}^{CRT} \hfill \\ \lambda_{t}^{CRT} \ge \lambda_{t}^{DA} \hfill \\ \end{aligned} \right.\;\;\;\;\;\forall t \in N_{t} \hfill \\ \end{aligned} \right.$$(2) -
2)
If there is an excess of generation in the power system or the power system imbalance is positive:
$$\left\{ \begin{aligned} \left| \begin{aligned} \lambda_{t}^{RT( + )} = \lambda_{t}^{CRT} \hfill \\ \lambda_{t}^{CRT} \le \lambda_{t}^{DA} \hfill \\ \end{aligned} \right.\;\;\;\;\forall t \in N_{t} \hfill \\ \lambda_{t}^{RT( - )} = \lambda_{t}^{DA} \;\;\;\;\;\;\forall t \in N_{t} \hfill \\ \end{aligned} \right.$$(3)
Considering two mentioned laws for real rime market, financial transaction of the real time market (FTRT), the forth term of (1), can be restated as follows:
where λ RT(+) t and λ RT(−) t are electricity prices for positive and negative imbalances at real time market, respectively; λ CRT t and ΔPt are cleared electricity price and power deviation at real time market, respectively.
The objective function of (1) with considering (4) cannot be solved through optimization techniques, because the real time financial transaction, problem (4), is a piecewise function. To solve the problem, by defining a binary variable xt(ω), the problem (4) can be restated as:
where M is a large positive number. Considering problem (5)–(7), the objective function, problem (1), is transformed into a mixed integer non-linear programming (MILNP) problem which has been proved to be less tractable than expected. Therefore, the proposed problem is transformed into mixed integer linear programming (MILP) by jointly using a simple decomposition and the disjunctive constraints. Thanks to the mentioned transformation, the problem (5)–(6) can be reformulated as:
where ΔP (+) t and ΔP (−) t are positive and negative imbalances, respectively.
According to simple reasoning [37], M1 and M2 can be fixed to appropriate constant values. M1 can be fixed to the summation of total wind power generation of all intermittent DGs, clients’ demand and total ESSs’ nominal power. The reason is that maximum positive energy deviation in a real time market occurs in scenarios where no wind power is forecasted for sale in day-ahead and intraday markets and similarly, in scenarios where clients purchase energy from these two trading markets, but the intermittent DGs eventually produce wind power during that period and clients do not purchase any amount of energy at the same period. Moreover, considering ESS, the worst case occurs in scenarios where the full power capacity of ESSs is scheduled to be charged in day-ahead market, but no power is sold in the time between day-ahead market and real time market.
Regarding M2, maximum negative deviations occur in scenarios where the full power capacity of all intermittent DGs is sold in day-ahead and intraday markets and in the same way, in scenarios where no clients purchase energy from these two trading floors, but the intermittent DGs eventually do not produce any amount of wind energy during that period and clients purchase energy at the same period. Moreover, considering ESS operation, the worst case occurs in scenarios where the full power of ESS is charged in the day-ahead and intraday markets, but no amount of energy can be delivered to the consumers due to unexpected failures/events.
Therefore, M1 and M2 can be fixed to constant values as follows:
where \(P_{ESS}^{nom}\) is the nominal power of ESS; and P W,max i is the installed capacity of wind turbine i.
Finally, the MINLP problem can be stated as a MILP problem which is tractable ensuring existence of theoretical results. In the next sub-sections, the objective function and constraints are described.
3.1 Objective function
The objective function of the retailer is to maximize its profit from participating in three trading floors emphasizing increased use of distributed wind generation. The final MILP problem can be reformulated as follows:
where \(P_{t}^{DA}\), \(P_{t }^{ID}\)and \(P_{t}^{RT}\) are the net powers traded in day-ahead, intraday and real-time markets, respectively.
The objective function (11) comprises five terms: ① the expected profit from selling energy to the clients ② the expected profit from trading in three market floors ③ cost function of renewable DGs as operation, maintenance and capital investment costs ④ the objective function of energy storage systems, including purchasing (charging) power from day-ahead market, selling (discharging) power to the real time market/consumers and operation and maintenance costs function ⑤ the CVaR(1−α) risk measure approach multiplied by the weighting factor to evaluate risk bearing capability of risk-taker/risk-averse retailers.
3.2 Constraints
The operational constraints of the DG-owning retailer are modeled as follows:
3.2.1 Power traded in day-ahead and intraday markets
These constraints refer to the amount of power traded in day-ahead and intraday market as follows:
Constraints (12)–(13) describe the net amount of power traded in day-ahead market and intraday market, respectively. Constraint (14) limits the amount of power traded in day-ahead market to the summation of clients’ demand and total ESSs’ nominal power. Constraint (15) limits the amount of power traded in intraday market to the summation of the total installed capacity of wind resources and total ESSs’ nominal power. The main reason for limiting the power traded in day-ahead and intraday markets is to prevent from speculating in the retail market.
3.2.2 Energy deviations in real time market
Due to inherent limitations of real time generation, the amount of power traded at real time market must be within a reasonable bound to prevent large variations in electricity price in response to high demand requests:
Constraints (16)–(17) specify the positive and negative energy deviations, respectively in the real time market.
3.2.3 Capacity limit of wind DGs
The power generation of renewable resources, should be within the allowed capacity thresholds during all scenarios and periods, as follows:
3.2.4 Energy storage system
The scheduling problem of the energy storage system is presented as the forth term in the objective function (11). The energy storage operation is optimized under the constraints given as follows:
where E ESS j,t is total stored energy at storage system j and time t; E nom ESS is nominal capacity of energy storage system; η ch ESS is charging efficiency and η dis ESS is discharging efficiency of ESS.
Constraint (19) describes the energy stored at time t considering indirect costs of losses through the charging/discharging efficiency parameters. Constraints (20)–(21) confine the charging/discharging of active power to the nominal power. Restriction on total stored energy at each time is presented through constraint (22).
3.2.5 Energy balance
During market operation, for each period and scenario, total generation of renewable resources plus purchased power from wholesale market should be equal to the sold power to the wholesale market plus the clients’ demand. Therefore, the energy balance constraint can be stated as follows:
3.2.6 CVaR(1−α) risk measurement
The constraints to describe the risk metric CVaR(1−α) are formulated as (24)–(25):
Note that if all profit scenarios are equiprobable, CVaR(1−α) is computed as the expected profit of the (1 − α) × 100% worst scenarios. Moreover, the CVaR(1−α) multiplied by the weighting factor β enables us to study the risk bearing capability of the retailer considering stochastic wind production.
3.2.7 Demand response
Through demand response programs, some consumers shift their demands from peak demand durations (with high electricity price) to off-peak demand durations (with low electricity price) to reduce the cost of electricity bills. In this way, some consumers may be able to increase their total energy consumption without having to pay additional cost through shifting non-essential demands from peak periods to off-peak periods. On the other hand, some consumers can decrease the cost of monthly electricity bills by shifting their demands. In this paper, the consumers participate in TOU demand response program as described in Fig. 3 [8]. The white part of demands in this figure is delay intolerant (DI) demands which does not participate in demand response program and the other section demonstrates the delay tolerant (DT) demands which can be shifted from one period to the other periods in response to the electricity price differences. Mathematically, shifting pattern of demand response program can be stated as follows [8]:
where P DI t is the delay intolerant demand; P DT t is the delay tolerant demand; P D t−1 is the demand level before DRP implementation; and P D t is the demand level after DRP implementation.
In this way, DRt denotes the model of consumers’ response to the offered electricity price. In this paper, a combined demand function, including linear-potential-exponential-logarithmic response is applied to model integrated consumers with various load patterns [9]:
where DRmax is the maximum level of load participation in DR Program; εlin, εpot, εexp and εlog are elasticity factors for liner, potential, exponential and logarithmic load functions, respectively.
Constraint (30) limits the amount of DR in each period of scheduling to a predefined maximum level.
3.2.8 Non-increasing offering curve
The retailer, in this paper, participates in competitive day-ahead electricity market to purchase/sell clients’ consumption/wind power production. Regarding the non-increasing condition for offering curves prepared for participation in the day-ahead market, the following constraints must be satisfied during participation in a day-ahead market:
4 Uncertainties characterization
Probabilistic forecasts give substantial information about the characteristics of the stochastic process of interest, i.e., renewable power production, clients’ demand and electricity market price which are considered in this study as the main uncertain variables. To hedge against the uncertainties, different realizations of wind power, clients’ demand and electricity price are modeled using the scenario generation process. In this regard, scenarios issued at time t and for a set of K successive lead times, are samples of the predicted cdf of uncertain variables. They consist in a set of J time trajectories as follows [37, 38]:
where \(\hat{y}_{t}\)is the time trajectories of uncertain variables.
In order to overcome the uncertainties associated with wind power of intermittent DGs, ARIMA approach [39] is used as scenario generation approach. The distribution function of wind speed is regularly considered using a Weibull distribution function [40]. On this basis, in this paper, Weibull distribution function has been considered to model the wind speed. Moreover, to calculate the produced power, corresponding to a specific wind speed, mathematical expression in accordance with [40] for wind power curve considering cut in, cut out and rated wind speed limitations is used.
In this study, the retailer generates a price distribution, i.e. equilibrium prices are defined by a probability density function, indicating the range of prices that the retailer may pay in trading floors of electricity market. In this paper, uncertainties associated with electricity price and load levels are modeled through ARIMA-based time series forecasting model. Moreover, in order to reduce the computation time and increase tractability of the problem, the size of generated scenarios are modified by Kantorovich distance method [39]. To sum it up, the stochastic decision variables can be stated as following:
5 Numerical studies
5.1 Data
In this study, a single day (24 hours) is considered with its demands, electricity price and wind power uncertainties. To describe price behavior in the day-ahead market, intraday market, real time market and demand behavior of end-use consumers, seasonal ARIMA models are used. In addition, non-seasonal ARIMA approach is used to simulate the behavior of wind power generation. The historical data used for the fitting process of electricity price and demand level belong to the electricity market of the PJM [41]. The key feature of PJM market is that the extracted data is realistic information of an applicable market which can increase the applicability of the studies.
The data correspond to the days between July 2015 and December 2015. Moreover, the wind historical data is extracted from Ottawa, Canada climate data [42]. We consider a wind farm having 42 2-MW Gamesa G87/2000 commercial wind generators [43]. The total installed wind power capacity of the wind farm is therefore 84 MW. It is assumed that the maintenance and operation costs of the wind turbines are 4 $/MWh, and the wind turbine capital cost is equal to 658 $/hour [9].
It is supposed that the retailer of the problem can procure 10% of the total demand of the PJM electricity market. The ARIMA models (p, d, q) × (P, D, Q)S fitted for the day considered in this paper are provided in Table 1. The scenarios associated with the uncertain amount of day-ahead electricity price are depicted in Fig. 4. Figure 5 describes ratio of real time electricity price to day-ahead electricity price for PJM market between July 2015 and December 2015. Classifications of load levels are illustrated in Table 2.
The initial number of generated scenarios for demand, day-ahead market price, intraday market price and real time market price is 50 (1200), 50 (1200), 50 (1200) and 50 (1200) for one hour (one day), respectively. Moreover, the initial number of scenarios simulated to characterize the wind speed between the closures of day-ahead market and intraday market is 25 (600). In addition, 50 (1200) scenarios are generated for wind speed realization after intraday market. The large number of original total scenarios yields an optimization problem which is intractable. To achieve tractability, the size of scenarios is reduced through Kantorovich distance approach. Consequently, the number of scenarios is reduced to 5, 10, 10, 10 scenarios for demand, day-ahead market price, intraday market price and real time market price, respectively. In addition, the number of scenarios for wind speed is reduced to 3 and 5 for the first and second time durations, respectively. As a result, total number of reduced scenarios equals to 75000 scenarios which is tractable.
5.2 Results and discussions
The retail strategy problem is formulated as an MINLP problem which is transformed into MILP by jointly using a decomposition and the disjunctive constraints and solved using CPLEX 12.5.1 solver in GAMS 24.1.2 software [44] on Intel Pentium CPU at 2 GHz and 1 GB of RAM.
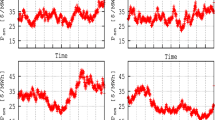
Considering the objective function (11) with the associated constraints (12)–(31), non-increasing offering curves of the retailer for participation in hourly day-ahead market are depicted in Fig. 6a–d for different time durations. In this way, for each hour of the 24-hour duration, an individual offering curve is proposed. It is worth mentioning that the retailer has no market power capability in either of the aforementioned market floors to change the MCP of the electricity market. In the other words, the retailer only makes decision about purchasing/selling deficit/surplus of energy depending on its predicted electricity price, clients’ demand and the power output of renewable resources to optimize its trading strategies. The hourly offering curves are depicted in four different subfigures to prevent from intersecting and lack of clarity.
As are shown in the offering curves, the retailer is able to offer a price curve in each hour of day-ahead market. It is evident that the offering curves vary noticeably from hour 1 to hour 24. These curves provide the fundamental information which is required by a retailer to participate in an hourly competitive day-ahead market.
Figure 7 describes the energy purchased from day-ahead market for different risk aversion factors (β) considering with and without DRP. Wind penetration factor (WPF) refers to the available capacity of wind energy resources. Reduction in WPF from 100% to 50% means that the available capacity of wind resources decreases from original capacity of 84 MW to 42 MW. According to the figure, as the wind penetration decreases, the retailer purchases more energy from day-ahead market. Moreover, the amount of energy purchased from day-ahead market increases with increasing β. The amount of energy difference between β = 0 and β = 3 decreases from 36 MWh to 19 MWh with decreasing WPF from 100% to 50%. In addition, the amount of energy purchased from day-ahead market with considering DR increases slightly.
Figure 8 illustrates the amount of energy sold to intraday market. In contrast to Fig. 7, the amount of energy sold to intraday market decreases significantly with increasing the risk aversion factor β. In addition, as the wind penetration decreases, the energy sold to the intraday market decreases considerably.
Figures 9 and 10 depict the amount of energy traded in real time market for positive and negative energy imbalances, respectively. As can be seen from Fig. 9, the amount of energy sold to real time market increases with increasing β. On the other hand, according to Fig. 10, as the risk aversion increases, the percent of procurement from real time market decreases. In fact, a risk averse retailer prefers to increase/decrease the amount of energy sold/purchased to/from the real time market. Also, Figs. 9 and 10 show that the amount of energy traded in negative deviations is more than positive deviations of the real time market.
Considering Figs. 7, 8, 9 and 10, as wind penetration decreases (which is interpreted as reduction in power resource uncertainty), the retailer prefers to procure less energy from market floors which are closer to the delivery time of energy. In contrast, the share of electricity procurement from day-ahead market (which has the lowest uncertainty in price variation) increases with decreasing the wind penetration.
Figure 11 shows the load profile for the study horizon considering with and without DR. The DR program is considered in this figure with elasticity factor -0.02. As can be seen from the graph, DRP implementation has flattened the load profile and decreased the maximum level of demand in different TOU periods. Applying DR program, some responsive consumers shifted their demands from peak duration to shoulder/valley periods.
Figure 12 describes the profit of retailer for different risk aversion and elasticity factors. As the graph reveals, the profit of retailer decreases with decreasing wind penetration. In contrast, DRP implementation has resulted in a significant rise in the profit of retailer. Similarly, as the elasticity factor increases, the profit of retailer increases moderately. It is evident that when more responsive consumers are considered in the program, the profit of retailer rises considerably. The reason is that the retailer reduces its energy procurement cost through purchasing less energy from peak durations (with high electricity price). In addition, it can be seen that a risk-taker retailer (with lower β) makes more profit in contrast to a risk averse retailer (with higher β).
Figure 13 depicts the cost paid by end-use consumers for electricity bills during a 24-hour period. Based on the graph, we can say that as the elasticity factor increases, the portion of consumers who shift their demands from peak period to shoulder/valley periods increases.
Table 3 describes the amounts of cost paid by the end-use consumers as a function of elasticity factor. The results clearly show that by increasing the elasticity factor, the cost of electricity bills paid by consumers reduces moderately.
Implementing DRP, DT consumers shift their demands from peak periods to off-peak periods to reduce the cost of electricity bills. In this way, these consumers maintain the same level of their total energy consumption with paying less cost through shifting non-essential demands from peak periods to off-peak periods. It is most evident that DRP implementation increases the profit of retailer and decreases the cost paid by the end-use consumers; consequently, it can be interpreted as a win-win game for both the retailer and consumers.
Table 4 illustrates the amount of CVaR for different risk aversion factors considering with and without DRP. For three case studies, the amount of CVaR increases with increasing the risk aversion factor. It means that when the retailer is more risk averse, the risk bearing capacity will decrease, and the trading strategy will be more conservative. In addition, implementation of DRP and reduction of wind penetration confine the variation of CVaR for a risk-taker retailer.
In order to study the behavior of ESSs towards retail strategies, the interaction of energy storage systems and electricity tariffs for the end-use consumers is evaluated through developing two different key concepts as follows:
-
1)
What are the impacts of different ESS technologies on the electricity tariffs?
-
2)
How do the electricity tariffs change when ESSs operate in charging/discharging modes?
Table 5 describes the characteristics of three ESSs with different technologies [45] considered in this paper.
To study the behavior of the ESSs, three storage technologies with nominal active power of 40 MW are considered in this paper. Figures 14 and 15 describe the variations of electricity tariffs in the presence of different ESS technologies for dynamic pricing and TOU pricing, respectively. As the graphs reveal, for all the ESS technologies, the electricity prices increase during off-peak periods, while they decrease during peak hours.
Generally, it is most evident that the presence of ESSs has flattened the profile of electricity price. Furthermore, it is shown that applying lead-acid storage system makes the most reduction in the electricity price during the peak periods. Considering the Pumped Hydro and Sodium-Sulfur in the second and third orders, respectively, we can say that the ESS with more charging/discharging efficiency and less operation cost has the most impact on reduction of electricity price.
Besides, Figure 16 depicts the charge/discharge scheduling of ESS during the study horizon. Based on the graph, we can say that the ESSs are in charging mode during the off-peak hours and are in discharging mode during the peak hours. As can be seen from Figures 14, 15 and 16, charging modes of ESSs increase the electricity tariff, while discharging modes decrease them gradually.
In order to study the risk sensitivity of the trading strategies with respect to different probability distribution functions (PDF) of the uncertain variables, Monte Carlo analysis is carried out. Monte Carlo analysis provides a useful means for quantifying the level of uncertainty present in an assumption through changing one uncertain variable while keeping the others constant. In this paper, three kinds of uncertainties are considered in the problem, including electricity price, clients’ consumption and wind speed. In the sensitivity analysis, different distribution functions were applied to each variable and 8000 trials were performed to study the impact of different PDFs on CVaR.
Figure 17 illustrates the statistical variations of risk criteria (CVaR) with respect to four electricity price PDFs, including Normal, Weibull, Log-normal and generalized extreme value (GEV) distributions [46, 47]. To provide a detailed analysis, the electricity price is divided into three levels: low, median and high price levels. The high price data are the prices higher than μ + σ, in which μ is the mean price and σ is the standard deviation of the price. The low price data are the prices lower than μ − σ. Other price data are considered as the median price data. The results show that Normal PDF imposes a low risk on the retailer in low price data, while it imposes a high risk in the high price data. In contrast, Log-normal PDF imposes a low risk in high price data. In fact, the electricity price does not follow the normal distribution in high price data, and it should be considered as logarithmic normal distribution if there were some price spikes, because the price spikes influence the statistical properties of electricity price. Furthermore, Weibull and GEV PDFs result in more risk in contrast to the Normal and Lognormal PDFs.
The risk sensitivity of the trading strategies with respect to demand PDF is depicted in Fig. 18. As the box-plot reveals, Normal PDF is an appropriate distribution for low load data whereas Lognormal PDF seems to impose a lower risk on the retailer in high load data in contrast to the other PDFs. The results clearly show that by decreasing (increasing) the clients’ consumption, the statistical and distributional characteristics of the electrical load incline toward the statistical properties of the Normal (Lognormal) distribution.
Figure 19 describes the risk sensitivity of the trading strategies with respect to the conventional wind speed PDFs. In this way, the wind regime is divided into two levels, including median speed and high speed. The median speed considers the wind speed between cut-in and rated speed. The high speed covers the speed values higher than the rated speed and lower than the cut-off speed. Regarding the graph, we can say that Weibull PDF imposes a lower risk on the retailer in contrast to Lognormal and GEV distributions. Moreover, the level of risk imposed on the retailer is lower in high speed than median speed for three PDFs. One reason is that in the high speed level, the control mechanisms of wind turbines try to maintain the blade’s speed around the rated speed; as a result, the power output of wind turbines maintains a rated level with minimum power fluctuations. Therefore, the trading strategies are less affected by high speed than the median speed. In addition, Weibull PDF imposes a lower risk on the retailer in contrast to GEV and Normal PDFs for the entire wind regime.
In this paper, one retailer is considered for the problem. The logical reason for this structure is to avoid increasing the complexity of the problem. In multi-retailer structures, each retailer is pressured to attract more clients in a retail electricity market. In this structure, if one retailer cannot propose a competitive price to the consumers, it may be omitted from the retail electricity market. The problem of multi-retailer structure can be a key issue for future studies.
6 Conclusion
In this paper, the market trading strategies for a renewable DG-owning retailer which participates in demand response programs have been proposed. The retailer is able to participate in an hourly day-ahead market according to its offering curves.
The retailer can procure the electrical energy from three market trading floors, including day-ahead market, intraday market, real time market and self-distributed wind generation facilities. It is shown that by participating in DR programs, the cost of consumers’ electricity bills decreases, because responsive consumers shift their loads from peak periods to off-peak periods. Besides, the profit of retailer increases and the load profile is flattened noticeably. In addition, maximum demand level of each period of the study horizon decreases.
The results show that the percentage of procurement from day-ahead market increases with decreasing wind penetration, while the procurement from intraday and real time market decreases with decreasing wind penetration. As a desired result, implementation of DR program increases the profit of retailer and reduces the amount of cost paid by the consumers.
In spite of the mentioned facts, some problems still remain for future research, such as considering Plug-in Hybrid Electric Vehicles (PHEVs) as a main source of demand response programs and studying the impacts of multi-retailer structures on retail strategies.
References
Shahidehpour M, Yamin H, Li Z (2002) Market operations in electric power systems. Wiley, New York
Kirschen DS, Strabac G (2004) Fundamentals of power system economics. Wiley, New York
García-Bertrand R (2013) Sale prices setting tool for retailers. IEEE Trans on Smart Grid 4(4):2028–2035
Hatami A, Seifi H, Sheikh-El-Eslami M (2011) A stochastic-based decision making framework for an electricity retailer: time-of-use pricing and electricity portfolio optimization. IEEE Trans on Power Systems 26(4):1808–1816
Kettunen J, Salo A, Bunn D (2010) Optimization of electricity retailer’s contract portfolio subject to risk preferences. IEEE Trans on Power Systems 25(1):117–128
Carrión M, Arroyo José M, Conejo A (2009) A Bilevel stochastic programming approach for retailer futures market trading. IEEE Trans on Power Systems 24(3):1446–1456
Hatami AR, Seifi H, Sheikh-El-Eslami M (2009) Optimal selling price and energy procurement strategies for a retailer in an electricity market. Electric Power Systems Research 79(1):246–254
Nojavan S, Mohammadi-Ivatloo B, Zare K (2015) Optimal bidding strategy of electricity retailers using robust optimization approach considering time-of-use rate demand response programs under market price uncertainties. IET Gen Trans & Dis 9(4):328–338
Shafie-khah M, Catalão J (2015) A Stochastic multi-layer agent-based model to study electricity market participants behavior. IEEE Trans on Power Sys 30(2):867–881
Wei W, Liu F, Mei S (2015) Energy pricing and dispatch for smart grid retailers under demand response and market price uncertainty. IEEE Trans on Smart Grid 6(3):1364–1374
Carrión M, Conejo A, Arroyo J (2007) Forward contracting and selling price determination for a retailer. IEEE Trans on Power Systems 22(4):2105–2114
Golmohamadi H, Keypour R, Hassanpour A et al (2015) Optimization of green energy portfolio in retail market using stochastic programming. In: Proceedings of North American power symposium, Charlotte, USA, 4–6 Oct 2015, 6 pp
Nguyen D, Bao L (2014) Optimal bidding strategy for microgrids considering renewable energy and building thermal dynamics. IEEE Trans on Smart Grid 5(4):1608–1620
Nazari M, Akbari Foroud A (2013) Optimal strategy planning for a retailer considering medium and short-term decisions. Electrical Power and Energy Systems 45(1):107–116
Ahmadi A, Charwand M, Aghaei J (2013) Risk-constrained optimal strategy for retailer forward contract portfolio. Electrical Power and Energy Systems 53(1):704–713
Hajati M, Seifi H, Sheikh-El-Eslami M (2011) Optimal retailer bidding in a DA market - a new method considering risk and demand elasticity. Energy 36(2):1332–1339
Yau S, Kwon R, Scott Rogers J et al (2011) Financial and operational decisions in the electricity sector: contract portfolio optimization with the conditional value-at-risk criterion. International Journal of Production Economics 134(1):67–77
Karandikar R, Khaparde S, Kulkarni S (2010) Strategic evaluation of bilateral contract for electricity retailer in restructured power market. Electrical Power and Energy Systems 32(5):457–463
Herranz R, San Roque A, Villar J et al (2012) Optimal demand-side bidding strategies in electricity spot markets. IEEE Trans on Power Systems 27(3):1204–1213
Mashhour E, Moghaddas-Tafreshi M (2011) Bidding strategy of virtual power plant for participating in energy and spinning reserve markets—part I. IEEE Trans on Power Systems 26(2):949–956
Shi L, Luo Y, Tu G (2014) Bidding strategy of microgrid with consideration of uncertainty for participating in power market. Electrical Power and Energy Systems 59(7):1–13
Charwand M, Moshavash Z (2014) Midterm decision-making framework for an electricity retailer based on Information Gap Decision Theory. Electrical Power and Energy Systems 63(12):185–195
Albadi M, El-Saadany E (2008) A summary of demand response in electricity markets. Electric Power System Research 78(11):1989–1996
Holmberg D, Hardin D, Bushby S (2014) Facility smart grid interface and a demand response conceptual model. National Institute of Standards, US Department of Commerce, Gaithersburg
Ferreira D, Barroso L, Rochinha Lino P et al (2013) Time-of-Use tariff design under uncertainty in price-elasticities of electricity demand: a stochastic optimization approach. IEEE Trans on Smart Grid 4(4):2285–2295
Zhang X (2014) Optimal scheduling of critical peak pricing considering wind commitment. IEEE Trans on Sustainable Energy 5(2):637–645
Namerikawa T, Okubo N, Sato R et al (2015) Real-Time pricing mechanism for electricity market with built-in incentive for participation. IEEE Trans on Smart Grid 6(6):2714–2724
Khojasteh M, Jadid S (2015) A two-stage robust model to determine the optimal selling price for a distributed generation-owning retailer. Int Trans on Elec Energy Sys 25:3753–3771
Nezhad A, Ahmadi A, Javadi M et al (2015) Multi-objective decision-making framework for an electricity retailer in energy markets using lexicographic optimization and augmented epsilon-constraint. Int Trans on Elec Energy Sys 25(12):3660–3680
Kharrati S, Kazemi M, Ehsan M (2015) Medium-term retailer’s planning and participation strategy considering electricity market uncertainties. Int Trans on Elec Energy Sys 26(5):920–933
Wang Z, Li Y, Shen Y et al (2017) Virtual electricity retailer for residents under single electricity pricing environment. Journal of Modern Power Systems and Clean Energy 5(2):248–261
Marzband M, Javadi M, Domínguez-García J et al (2016) Non-cooperative game theory based energy management systems for energy district in the retail market considering DER uncertainties. IET Gen Trans & Dis 10(12):2999–3009
Momber I, Wogrin S, Gómez San Román T (2016) Retail pricing: a bilevel program for pev aggregator decisions using indirect load control. IEEE Transactions on Power Systems 31(1):464–473
Sekizaki S, Nishizaki I, Hayashida T (2016) Electricity retail market model with flexible price settings and elastic price-based demand responses by consumers in distribution network. International Journal of Electrical Power & Energy Systems 81:371–386
Jia L, Tong L (2016) Dynamic pricing and distributed energy management for demand response. IEEE Trans on Smart Grid 7(2):1128–1136
Sebastian Oliva H, MacGill I, Passeyb R (2016) Assessing the short-term revenue impacts of residential PV systems on electricity customers, retailers and network service providers. Renewable and Sustainable Energy Reviews 54:1494–1505
Conejo A, Carrión M, Morales J (2010) Decision making under uncertainty in electricity market. Springer, Berlin
Morales J, Conejo A, Madsen H et al (2014) Integrating Renewables in electricity Markets. Springer, Berlin
Shumway H, Stoffer S (2011) Time Series Analysis and Its Applications. Springer, Berlin
Karki R, Hu P, Billinton R (2006) A simplified wind power generation model for reliability evaluation. IEEE Trans Energy Convers 21(2):533–540
The PJM energy market (2016) US. http://www.PJM.com. Accessed 13 May 2016
Weather data for Ottawa (2016) Canada. http://www.ottawa.weatherstats.ca. Accessed 3 May 2016
Wind power database (2016) France. http://www.thewindpower.net/turbine_en_46_gamesa_g87-2000.php. Accessed 9 May 2016
GAMS manual software (2016) US. http://www.gams.com/dd/docs/solvers/cplex.pdf. Accessed 29 May 2016
Rastler D (2010) Electricity energy storage technology options: a white paper primer on applications, costs, and benefits. Technical Report, Electric Power Research Institute, Palo Alto, CA
Xiaoxia Huang (2010) Portfolio Analysis. Springer, Berlin
Pierre-Yves Moix (2001) The measurement of market risk. Springer, Berlin
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 15 November 2017
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Golmohamadi, H., Keypour, R. Stochastic optimization for retailers with distributed wind generation considering demand response. J. Mod. Power Syst. Clean Energy 6, 733–748 (2018). https://doi.org/10.1007/s40565-017-0368-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0368-y