Abstract
In recent years, the increasing penetration level of renewable generation and combined heat and power (CHP) technology in power systems is leading to significant changes in energy production and consumption patterns. As a result, the integrated planning and optimal operation of a multi-carrier energy (MCE) system have aroused widespread concern for reasonable utilization of multiple energy resources and efficient accommodation of renewable energy sources. In this context, an integrated demand response (IDR) scheme is designed to coordinate the operation of power to gas (P2G) devices, heat pumps, diversified storage devices and flexible loads within an extended modeling framework of energy hubs. Subsequently, the optimal dispatch of interconnected electricity, natural gas and heat systems is implemented considering the interactions among multiple energy carriers by utilizing the bi-level optimization method. Finally, the proposed method is demonstrated with a 4-bus multi-energy system and a larger test case comprised of a revised IEEE 118-bus power system and a 20-bus Belgian natural gas system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, the organization patterns of the global energy systems have been greatly evolved with the rapid development and wide applications of renewable generation and energy storage technologies. In the meantime, electric power systems, natural gas systems, heat systems as well as others, have the tendency of being interconnected and coordinated by cutting-edge information technology to improve the overall economic efficiency of a multi-carrier energy (MCE) system and accommodate the ever-increasing capacity of renewable energy generation. Given this background, extensive research work has been focused on the integrated planning and optimal operation of multi-carrier energy systems in recent years [1,2,3,4].
To build a general modeling framework for MCE systems, the concept of the “energy hub” was proposed with a transition matrix to represent the process of distribution, conversion and storage of different energy carriers [5]. Planning and operation problems of multi-carrier systems have been studied in the presented framework. For example, a broad spectrum of modeling extensions and applications of energy hubs are discussed in [6,7,8]. The size and operation strategy of combined cooling, heat and power, as well as auxiliary boiler for users are optimized in [9]. Interconnected energy hubs are optimally designed and sized in [10]. The combined optimization problem of coupled multi-carrier power flows is addressed in [11] and [12].
Demand response (DR) programs are applied to reduce peak loads by changing energy usage patterns of end users based on energy prices or pre-designed incentives [13]. Furthermore, the notion of demand response can be expanded to the mutual alternatives and conversions of different energy carriers at the energy demand side. The integrated demand response (IDR) program [14] can not only adjust the quantity of the end demand, but also switch the form of the consumed energy with economic incentives. The optimal dispatch for a single energy hub with conversion, storage, and demand side management capabilities is studied in [15], but the coordinated operation of interconnected hubs is not addressed. Much research work has been done on optimal operation of energy hubs with demand side resources in the electricity market environment in [14, 16,17,18,19]. The interaction among smart energy hubs (SEHs), i.e. energy hubs equipped with smart grid technologies, is formulated as a non-cooperative game and solved by a distributed algorithm in [16,17,18], but the end demand shifts are not taken into account. Based on [16,17,18], further studies are made in [14] and [19] to take the end demand shifts into consideration. To the best of our knowledge, the coordinated scheduling of conventional thermal generation units, renewable energy sources and SEHs, as well as the integrated applications of power to gas (P2G) devices, heat pumps, multiple kinds of energy storages, flexible loads has not yet been systematically addressed in existing publications.
Diversified storage devices are playing more and more important roles in modern energy systems, and could be incorporated into the modeling framework of energy hubs. It is expected that energy carrier and storage methods will become diversified in MCE systems. For example, the power to gas (P2G) technology and hence natural gas storage provide a new way for energy storage [20]. The existing natural gas pipeline and storage equipment can be well utilized with no or marginal additional investment. The benefits of P2G are assessed in [21,22,23]. Driven by electricity, heat pumps draw the natural heat and provide to users with superior operational efficiency. The superfluous renewable energy can also be converted into and stored in the form of heat, and hence the adjustments of the electric power flow and heat flow can be achieved by scheduling the heat pumps [24].
In order to fully utilize potentials of the MCE system, the optimal operation strategy of interconnected electricity, natural gas and heat systems with diversified storage devices and IDRs is addressed in this work. The modeling framework of a SEH is extended with P2G devices, heat pumps, diversified storage devices equipped and IDR programs implemented. On this basis, a bi-level optimization model is established to build a coordinated strategy for optimal operation of MCE systems including conventional thermal units, renewable energy resources and SEHs. The overall energy efficiency and the capability of accommodating fluctuant generation outputs from renewable energy sources are evaluated within the proposed modeling framework.
The remainder of this paper is organized as follows. An extended modeling framework of energy hubs is presented in Sect. 2. The optimal operation scheme of SEHs with diversified storage devices incorporated and IDR program implemented is elaborated in Sect. 3. Based on the developed model, a coordinated bi-level optimization framework of MCE systems is presented in Sect. 4. In Sect. 5, case studies are carried out to demonstrate the basic characteristics and effectiveness of the proposed method. The paper is concluded in Sect. 6.
2 Modeling framework of an energy hub
2.1 Energy hub concept
As an interface between various energy producers, energy transmission facilities and end users, an energy hub takes responsibility for the inputs and outputs of multi-carrier energy flows, the conversions between energy forms, the storage of energies, and the others. The economic efficiency of an energy hub can be achieved by optimally dispatching different energy carriers.
-
1)
Energy conversion
An energy hub integrates a variety of energy converters such as transformers, gas turbines, gas furnaces and heat exchangers, where inputs/outputs of multiple energy carriers are usually available. The mathematical relationship between the inputs and outputs of an energy hub can be described by a coupling matrix C, which can be formulated as:
where P = [P1, P2, …, P ς ]T and L = [L1, L2, …, L ξ ]T respectively represent the inputs and outputs of different energy carriers in an energy hub, such as electricity, natural gas, heat, biomass energy and hydrogen energy; c ij denotes a designated element/an entry of C that stands for a specific correspondence between L i and P j , which will be further analyzed in the latter section.
-
2)
Energy storage
Energy storage technology has been widely utilized in electric power systems to smooth the fluctuations caused by renewable energy sources, and hence to improve the operation security and economics of the power system concerned [25,26,27]. However, the energy storage methods and characteristics will be more diverse and complicated when introducing other energy carriers, as stated in the previous section.
As energies can be stored in different carriers in a multiple-energy system, energy storage can also be described by a matrix in the energy hub modeling framework, and as shown as [15, 28]:
where E=[E1, E2, …, E ς ]T and E′=[E ′1 , E ′2 , …, E ′ ξ ]T respectively represent the original energy input vector through energy storages and the modified energy output vector of the energy hub; S denotes the energy storage coupling matrix; s ij , an element of S, describes the corresponding relationship between E ′ i and E j .
-
3)
DR
In a multiple-energy system, the DR schemes involve energy demand shifts and energy carrier conversions. As DR also changes the energy consumption patterns within various energy carriers, it can be regarded as an equivalent energy storage device.
Within the aforementioned energy hub framework, the DR output vector ΔL can be seen as a correction of the output vector L of the energy hub. The expression of DR can be described as follows [15, 28]:
where ΔL1, ΔL2, …, ΔL ξ and R1, R2, …, R ς respectively denote the elements of ΔL and R, which are the energy demand change vector and the equivalent energy input/output vector through the virtual energy storages; D denotes a response coupling matrix; d ij denotes the ij-th entry of D, which gives the mutually alternative and conversion relationship between ΔL i and R j .
As the correction of the energy outputs caused by energy storages and DRs should be integrated in the energy hub modeling framework, the mathematical expression can be unified as:
Assuming L′ = L + E′ + ΔL, C′ = [C S D], P′ = [P E R]T, then (4) can be rewritten as:
2.2 Modeling of an energy hub with P2G and heat pumps
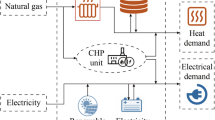
The imported energy of an energy hub will be assigned, stored and converted to meet the requirement of end users. For instance, a simple energy hub with a transformer, a CHP unit and a furnace is illustrated in Fig. 1a.
In Fig. 1, P e and P g represent the inputs of electric power and natural gas, respectively; L e and L h represent the outputs of electric power and heat, respectively; L g ′ and P g ′ represent the output of the P2G unit and the equivalent natural gas input of the energy hub, respectively.
The mapping between input ports and output ports is determined by the efficiencies of the converters and the dispatching factors of different input carriers among these converters. Taking the simple energy hub in Fig. 1a as an example, the energy flows between the input and output ports can be represented as:
where P e and P g represent the electricity and natural gas input flows, respectively; L e and L h represent the electricity and heat output flows, respectively; v (0 ≤ v ≤ 1) is a dispatching factor introduced to distribute the natural gas input between the CHP and the gas furnace; η T , ηFUR, ηCHPe and ηCHPh represent the transformer efficiency, gas furnace thermal efficiency, CHP unit electric efficiency and thermal efficiency, respectively.
The P2G technology is able to transform water into hydrogen or methane, which are the major components of synthetic natural gas (SNG). The efficiency of the P2G technology is around 60%–80% according to a recent study [22]. Generally, the P2G technology is recognized as a novel method to store, transport and reutilize the excessive electric power generation of renewable energy sources [29]. An energy hub incorporating the P2G technology as well as electricity, heat and natural gas storages is shown in Fig. 1b. With a P2G device in an energy hub, the following mathematical relationship can be attained:
where a dispatching factor u (0 ≤ u ≤ 1) is introduced to define the allocation of electric power between the transformer and the P2G unit; v (0 ≤ v ≤ 1) is introduced to define the allocation of natural gas between the CHP unit and the gas furnace; L g ′ represents the output gas flow of the P2G plant; η e2g is the efficiency of the P2G plant.
Based on the energy conservation law, the natural gas consumed by CHPs and gas furnaces equals to the total quantity of natural gas from the input of the energy hub, the output of gas storage devices and the output of P2G plants. Thus, the following constraints should be added to accommodate the impact of P2G plants:
where P g (t) and P g ′(t) represent the actual and equivalent natural gas inputs of the energy hub concerned at time t, respectively; L g ′(t) denotes the value of L g ′ at time t.
In this work, the interaction between electric power and heat is based on the operation of heat pumps in an energy hub. The performance of a heat pump is usually evaluated by the coefficient of performance (COP), which is defined by the ratio of power and heat quantity conducting from lower temperature objects to higher temperature objects. The COP of a heat pump generally ranges from 3 to 4 [24]. A heat pump is further incorporated in Fig. 1c. To integrate heat pumps, (6) can be further extended to the following formulation:
where h (0 ≤ h ≤ 1) is a dispatching factor to define the allocation proportion of electric power consumed by the heat pump; COP h denotes the value of COP of the considered heat pump.
3 IDR programs in SEHs
An energy hub is called a SEH if it is equipped with modern communication, computing and control technologies. The SEH receives or sends data such as energy prices, end demands and their operational schedules from or to the system operator by two-way communication facilities [19].
DR programs provide users more flexibility at the demand side, and have been widely studied and applied in some power companies [30]. In a MCE system, users also have the flexibilities to choose from various energy carriers in certain ranges. Thus, the economic incentive provided to one kind of energy carrier may lead to demand changes of others. As a result, the mechanisms of IDR in a MCE system will be more complicated. In general, the effects of IDR can be embodied in two aspects. On the one hand, it is “quantity adjustment”, which means that the end demand can be shifted throughout the timeline. For example, the load management of an individual energy carrier is a representative DR, i.e. shifting energy demand. On the other hand, it is “carrier conversion”, which means that one kind of energy demand can be supplied by other alternative energy resources at the demand side. For instance, the heat loads consumed by end users can be provided by the heat outputs of SEHs that are converted from either the imported natural gas or the imported electric power. In this section, the optimal operation strategy of the IDR programs in SEHs incorporating diversified storage devices and flexible loads is comprehensively studied.
3.1 Objective function
When the IDR program is implemented in a MCE system, SEHs adjust the energy consumption of end users and control the internal converters and energy storage devices according to the broadcast energy prices to minimize the operating cost and the dissatisfaction level of energy consumers.
The terminal loads at the output side of a SEH can be categorized into uninterrupted loads and several groups of flexible loads according to their flexible features and impacts on the satisfaction level of customers. For example, the comfort experience of customers will be impacted by load shifting of air conditioning to some extent, but will not be interfered by reasonable scheduling of charging electric vehicles. As the dissatisfaction of customers is related to the energy demand change, it is assumed that the dissatisfactory degrees of energy consumers rise with the square of quantities of energy demand change [31]. The dissatisfactory degree function of SEH i at time t can be expressed as:
where Δli,e,r(t) and Δli,h,r(t) denote the r-th electric and heat demand changes of SEH i at time t, respectively; βi,e,r and βi,h,r denote the dissatisfaction factor of users corresponding to Δli,e,r(t) and Δli,h,r(t), respectively; N R (e) and N R (h) denote the numbers of electric and heat flexible loads, respectively.
The objective of each SEH is to minimize the sum of energy purchasing costs and dissatisfaction costs of end users.
where P i,e (t) (P i,g (t)) and Pri,e(t) (Pri,g(t)) denote the consumed electricity(natural) gas and their prices in SEH i at time t, respectively; ω1 and ω2 respectively denote the weighting coefficients of energy purchasing costs and dissatisfaction costs of consumers, and both are set to 0.5 in this paper; N T denotes the number of considered time periods.
3.2 Constraints
The constraints concerning the operation of each energy hub must be respected. Generally, the operation constraints of each energy hub consist of energy balance equations and the operation limitations of the concerned components such as converters, energy storage devices and DRs.
-
1)
Energy balances and constraints of converters
where Pi,t′, Li,t′ and Ci,t′ denote the input vector, output vector and coupling matrix in (5) of SEH i at time t; Pi,α(t) denotes the α-th carrier’s input in Pi,t′; vi,α,k(t) denotes the dispatching proportion representing the percentage of Pi,α(t) that flows into the k-th converter; Pi,α/\(\overline{P}_{i,\alpha }\) and Pi,α,k/\(\overline{P}_{i,\alpha ,k}\) denote the lower/upper limits of Pi,α(t) and those of the k-th converter, respectively; S H , S E (i) and S C (i) denote the set of SEHs, input energy carriers and energy converters, respectively.
-
2)
Energy storage constraints
The capability of a battery in enhancing the accommodation of fluctuant renewable generation output is dependent on its capacity, rated charging/discharging power, charging/discharging efficiencies and energy loss rates over time. Similarly, the heat storages are restricted by the capacities of insulated containers, limitations of input and output heat flows, storage efficiencies and heat losses. It is assumed that the stored energy level at the end of the dispatching period concerned is equal to that at the beginning, so that the dispatching of energy storage can be repeated, and different dispatching schemes comparable. The constraints of multi-period electricity/heat storages can be expressed as follows:
where Si,e/h(t) represents the state of energy stored in electricity/heat storage devices of SEH i at time t; Si,e/h and \(\overline{S}_{i,e/h}\) respectively denote the lower and upper bounds of Si,e/h(t); E Ii,e/h (t) and E Oi,e/h (t) represent input and output electricity/heat flows of SEH i at time t, respectively; ξ Ie/h and ξ Oe/h stand for the input and output efficiency of the electricity/heat storage, respectively; γ e/h denotes the self-discharge rate/heat lose rate of the electricity/heat energy storages; t0 and t end denote the starting time and end time of the operation period, respectively.
Synthetic natural gas generated by P2G devices can be stored when the power generated from renewable energy sources is redundant. It is assumed that the loss of natural gas storage is negligible, and the initial stored natural gas level is equal to that at the end of a dispatching period as well, i.e., the net quantity of gas flow through gas storage equals to zero throughout the dispatching period. Multi-period boundary constraints of natural gas storages can be expressed as:
where Si,g(t) denotes the quantity of natural gas stored in the storage tank of SEH i at time t; Ei,g(t) denotes the natural gas input/output flow of SEH i at time t; Si,g and \(\overline{S}_{i,g}\) denote the lower and upper bounds of Si,g(t), respectively.
-
3)
DR constraints
Within the DR framework, some energy consumption can be transferred from peak periods to valley periods as well as from scarcest energy carriers to abundant energy carriers. However, arbitrary adjustments of load demands of customers may not always feasible and acceptable. As a result, the implementation of DR should always respect the customers’ choices. Moreover, the total quantity of energy consumption throughout the day should be maintained at an acceptable level to ensure that the DR schemes will not affect the operation of SEHs in the following time periods. Thus, it is assumed that the daily energy demand at the load side remain unchanged with the introduction of DRs.
The boundaries of DRs of different energy carriers are unified in a series of generalized expressions to simplify the problem formulation.
where ΔLi,e/h(t) denote the total electricity/heat load adjustment of SEH i at time t; Δli,e/h,r(t) and \(\overline{\Delta l}_{i,e/h,r} (t)\) denote the lower and upper bounds of Δli,e/h,r(t) within the customers’ discretion, respectively; Ri,e/h,r(t n ) and \(\overline{R}_{i,e/h,r} (t_{n} )\) denote the lower and upper limit of the r-th total electricity/heat load adjustment from t0 to t n , and t0 ≤t n ≤t end .
4 Optimal dispatch of a multi-carrier energy system
In a MCE system, a favorable dispatch strategy of energy flows, energy storages and IDR programs should contribute to the efficient utilization of various energy sources and the enhanced accommodation of renewable energy generation. In this section, a comprehensive optimization framework of a MCE system including interconnected SEHs, multi-carrier energy production and transmission systems is established to improve the overall operation efficiency.
With data received from SEHs including terminal demands of customers, flexible loads and internal configurations, a bi-level programming procedure is carried out by the system operator to attain an optimal operation strategy of the MCE system. The optimal power flow of the multi-carrier energy system is implemented in the upper-level to attain the day-ahead generating unit schedule and natural gas purchasing strategy, and the nodal prices of electricity and natural gas can be calculated to guide the employed strategies of SEHs. Subsequently, the decision-making process of each SEH is simulated in the lower level to minimize its operating costs and dissatisfactions costs of energy consumers based on nodal prices. The decision-making processes of SEHs are assumed to be completely rational. The optimized energy schedules of SEHs will be returned to the system operator for verification. Through iterations between these two levels, the optimal operation strategy of the MCE system can be achieved. The decision-making process of SEHs has already been described in Sect. 3, the optimization model of the multi-carrier energy system and the detailed solving approaches are presented in this section.
4.1 Objective function
Independent SEHs are interconnected through energy transmission systems which take responsibilities of the physical connections and energy transmissions among different SEHs. From the perspective of the system operator, the input energy of the SEH can be regarded as the load of the multi-carrier system. Specifically, the electricity transmission network and natural gas transmission network are discussed in this section. For example, the input side of SEH i may be connected to bus x in the electric power system and bus m in the natural gas network, so there exists a designated mapping relationship: i → (x, m).
From a systematic perspective, minimizing the total energy consumption cost of all energy carriers in a given time period is the objective. The cost of electric power and natural gas can be appropriately formulated as a quadratic function, and then the objective can be expressed as:
where P E (x,t) denotes the active power output from the generating unit at bus x at time t; P G (m,t) denotes the injection power of natural gas at bus m at time t; a xe /a mg , b xe /b mg and c xe /c mg are the cost coefficients of electricity /natural gas; N E , N G and N T denote the number of electric power system buses, the number of buses in the natural gas network and the number of considered time periods, respectively.
4.2 Constraints
4.2.1 Electricity transmission network
In an electricity transmission network, the optimal power flow is subject to both equality and inequality constraints. The equality constraints contain the AC power flow equations, as listed in (29)–(30). While the inequality constraints consist of active and reactive power output constraints of generators, limits of nodal voltage magnitudes and active power flows through power lines, which are described by (31)–(34), respectively.
where Q E (x,t) represents the reactive power output from the generating unit at bus x at time t; P e (x,t) and Q e (x,t) represent the active and reactive loads at bus x at time t, respectively; P Ex /Q Ex and \(\overline{{P_{Ex} }}\)/\(\overline{{Q_{Ex} }}\) denote the lower/upper limits of P e (x,t)/Q e (x,t); V x (t) and θ x (t) represent the voltage magnitude and phase angle of bus x at time t, respectively; V x and \(\overline{{V_{x} }}\) denote the lower and upper limit of V x (t); G xy and B xy represent the real and imaginary parts of the x-yth entry of the nodal admittance matrix, respectively.
4.2.2 Natural gas network
The steady state natural gas flow can be formulated similar to the electric power flow, where the compression stations and pipelines are treated as branches, while the junction nodes and load nodes can be regarded as buses [6]. The net injection of natural gas at each bus equals to the sum of natural gas flowing to its connected pipelines, and can be expressed as:
where P mn (t) denotes the power rate of the natural gas flowing through the pipeline from bus m to bus n at time t.
The steady state natural gas flow rate through a pipeline can be determined by its characteristics and the upstream and downstream pressures, and expressed as:
where p m (t) and p n (t) represent the gas pressures at buses m and n at time t, respectively; G HV denotes the gross heating value of natural gas; k mn is the transmission coefficient of the pipeline from bus m to bus n, and depends on the characteristics of this pipeline; s mn = 1 or − 1 represents that the natural gas flowing from bus m to bus n or vice versa.
During the natural gas transmission process, the gas pressure will decrease due to the frictional resistances in pipelines. In practice, a certain number of compression stations will be installed in the natural gas network to maintain the gas pressures at required levels. The operation of compression stations can result in loss of natural gas during the process, and be expressed as
where P com (t) denotes the power of natural gas consumed by the compression station at time t; k com is a coefficient related to the characteristics of the compression station; p k (t) denotes the natural gas pressure before compression at time t.
The natural gas transmission process is also subject to several constraints, such as the compression ratio limit of each compression station, nodal gas pressure constraints and gas injection constraints. These constraints are expressed as
where \(\overline{R}_{j}\) represents the max compression ratio of the j-th compression station; p m (t) and P sm (t) respectively represent the natural gas pressure and injected power rate at bus m at time t; p m /P sm and \(\overline{{p_{m} }}\)/\(\overline{{P_{sm} }}\) denote the lower/upper limits of p m (t)/P sm (t); S c and S n denote the sets of compression stations and buses in the natural gas system, respectively.
4.3 Solving approaches
IPOPT is employed to solve the upper-level nonlinear programming problem, while CPLEX is utilized to solve the lower-level quadratic programming problem. The calculation method of electric nodal prices can be found in [32], while the natural gas nodal prices are determined by the dual variables of the equality constraint (36) at the optimal solution point of the optimization model. The proposed bi-level optimization of the MCE system is solved through iterations between the two levels. The flowchart for solving this bi-level programming based multi-energy optimization model is shown in Fig. 2. In the first iteration, the multi-carrier optimal power flow is conducted based on the initialized energy demand at the electric and natural gas buses specified according to historical operation data. The iterative optimization process will terminate when the specified convergence criterion is reached; the convergence criterion is defined that the variation of the total energy cost between two successive iterations is less than a prespecified threshold ε in this work.
5 Case studies and discussions
A 4-bus multi-carrier system [6] and a larger test system comprised of the revised IEEE 118-bus electric system and 20-bus Belgian natural gas network are employed to illustrate the performances of the proposed method.
5.1 4-bus multi-energy test system
The 4-bus multi-carrier test system, shown in Fig. 3, is introduced with some revisions to demonstrate the characteristics of the proposed methodological framework. The four SEHs, denoted as H1-H4, are interconnected through electric power and natural gas systems in Fig. 3, while the configurations of SEHs and the energy transmission systems can be modified to match real world cases. This test system consists of two thermal power units G1 and G2, one wind turbine WT and one natural gas source N. The detailed test system configuration parameters and data are available at Tables A1–A3 in “Appendix A”.
Three scenarios are defined as follows.
-
1)
Scenario A: the configurations of H1–H4 are illustrated in Fig. 1a.
-
2)
Scenario B: the configurations of H1–H3 remain the same with Scenario A, while both a P2G device and energy storage devices are added to H4, as illustrated in Fig. 1b.
-
3)
Scenario C: the configurations of H1-H3 remain the same with Scenario A, while a P2G device, a heat pump device and an energy storage device are equipped and IDR programs implemented at H4, as illustrated in Fig. 1c.
The required iteration numbers of Scenario A, Scenario B and Scenario C are 4, 4 and 5, respectively; the consumed calculation time for Scenario A is 34.0s, for Scenario B is 42.1 s and for Scenario C is 79.6 s. Simulation results are analyzed and discussed as follows.
-
1)
Comparisons and analyses of day-ahead generating unit schedules
The day-ahead scheduling costs and wind power utilization rate in the above mentioned three scenarios are listed in Table 1. The total energy costs in Scenario B and C are lower by 2.13% and 3.35% respectively, than that in Scenario A. The wind power utilization rates in Scenario B and C are respectively 1.42% and 7.01% higher than that in Scenario A. It can be concluded that the fuel costs of thermal generating units can be considerably reduced, and the renewable energy utilized more sufficiently by comprehensively employing the energy storage devices and DR resources.
The schedules of thermal generating units, wind turbines and SEHs throughout the operating day are demonstrated in Fig. 4. During 2:00 am–6:00 am, actual wind power outputs increase in Scenarios B and C, and the power absorbed by SEHs increases simultaneously; during other periods such as 11:00 am–21:00 am, SEHs start to release the stored energy, and the outputs of thermal power units G1 and G2 decrease in Scenarios B and C. It can be seen that the thermal generating units, energy storages and DR resources can be coordinated so as to adjust their inputs/outputs to mitigate the fluctuations of wind power generation outputs and enhance the capability of accommodating wind power. Meanwhile, the inputs/outputs of SEHs can vary in a wide range so as to adapt to different operating conditions, and this means that they are not only able to produce energy but also absorb and store the surplus generation from renewable energy sources.
-
2)
Effects of diversified storage devices
The detailed operation schedule of energy storages in the MCE system in Scenario B is shown in Fig. 5. During 2:00 am–6:00 am, the estimated wind power generation is considerably abundant, and even exceeds the total electrical demand from these four SEHs. The energy storage devices are operated to consume the surplus wind power and release the stored energy during peak load periods. In this way, the curtailment of wind power generation output can be alleviated to some extent, and the energy utilization efficiency increased at the same time. The introduction of multi-carrier energy storages makes it possible to transform the redundant wind power generation into natural gas or heat and stored in different carriers, and in this way the total storage capacity is increased for accommodating renewable energy generation output.
As shown in Fig. 5, the batteries (electricity storages) are the most preferred energy storage method due to their minimum energy loss rates based on current technologies. However, the batteries suffer from expensive investment costs and fast degradation rates, and hence their utilizations are constrained. The P2G units will be dispatched if the limits of battery charging/discharging power or capacities are binding. The P2G units store energy in natural gas storage tanks and pipelines, and then achieve large storage capacities based on existing facilities. Similarly, the heat storages do not have the highest priorities in storing the excessive wind power generation, and their operation is deeply affected by the operation of CHP units for balancing the heat flows.
It can be observed that the surplus wind energy can be stored in various energy carriers based on the infrastructure of the MCE system and diversified storage devices, and then the generalized energy storage capacity is increased. Therefore, the advantages and characteristics of different kinds of energy storage can be comprehensively employed by complementing each other, and the operation efficiency of Scenario B is superior to that of Scenario A, as shown in Table 1 and Fig. 5.
-
3)
Effects of IDRs
The detailed operating schedule of both energy storage devices and IDRs in Scenario C is demonstrated in Fig. 6. Apparently, the introduction of IDR schemes is useful for enhancing the capability of accommodating the largest amount of wind power generation during 02:00 am–06:00 am in Fig. 6, and leads to the minimum daily energy cost. The simulation results demonstrate that the virtual storage functions of the IDR scheme provide extra energy storage capacities for SEHs for optimizing their daily operation schedules.
5.2 The revised IEEE 118-bus electric test system and 20-bus Belgian natural gas network
The proposed method is further tested on a larger system comprising of a revised IEEE 118-bus electric power system and a 20-bus Belgian natural gas system [33, 34]. There are 40 gas-electric coupled buses formulated as SEHs and 10 wind farms (WFs) assumed to be connected to the buses in the electric power system. The detailed test system configuration parameters and data are also available at Table A4 in “Appendix A”. The outputs of WFs are assumed to be the same as those in the 4-bus test system, while the electrical/heat loads are 20% of those in the 4-bus test system.
The simulation results of the following three scenarios are compared in this section.
-
1)
Scenario I: the configurations of all SEHs are illustrated in Fig. 1a.
-
2)
Scenario II: the SEHs that are directly connected to WFs are assumed to be equipped with the diversified storage devices and IDR programs, as illustrated in Fig. 1c.
-
3)
Scenario III: on the basis of Scenario II, the IDR programs are further integrated into all SEHs.
The iteration numbers of Scenario I, Scenario II and Scenario III are 4, 5 and 13, respectively; the consumed calculation time for Scenario I is 343.7s, for Scenario II is 525.4s, and for Scenario III is 1601.9s. As the proposed method is employed to attain the day-ahead schedule of a multi-carrier energy system, the calculation time consumption is acceptable.
Comparisons of operation costs and wind power utilization rates are listed in Table 2, while the compositions of electricity productions from various energy sources in three scenarios are shown in Table 3. The actual wind power outputs of WF1 in three scenarios throughout the day are compared in Fig. 7. It is shown that the curtailment of excessive wind power generation can be significantly relieved through the proposed schemes in a MCE system. Meanwhile, the cost of the natural gas system can be significantly reduced, as parts of terminal gas demands are supplied by the SNG produced by P2G devices. In Scenario III, as the IDR programs are extensively implemented, the economic efficiency of the MCE system and the accommodating capability for renewable energy generation are further enhanced.
The demand profiles of electric power and heat at SEH 5 in Scenarios I and III are compared in Fig. 8. Comparing Fig. 8 with Fig. 7, it can be inferred that, the electric power demand in Scenario III is higher than that in Scenario I as the result of the implementation of DRs during 2:00 am–6:00 am when wind power generation is abundant. Correspondingly, the CHP units will reduce their outputs to match this situation, and hence the heat demand is decreased. The electric power demands at 12:00 pm, 20:00 pm and 22:00 pm are high because the wind power outputs at these three time periods are relatively high. According to the energy conservation principle, the electric power demand is decreased and the heat demand is increased in other periods.
6 Conclusion
In this paper, a SEH modeling framework considering the inclusions of P2G devices, heat pumps, diversified storage devices and flexible loads is first proposed, and an optimized IDR scheme is designed on this basis to manage the demand side resources. Subsequently, a day-ahead optimal operation strategy of a MCE system including interconnected SEHs and multi-carrier energy production as well as the transmission system is presented to improve the economic efficiency of the whole system and to enhance the capability of accommodating renewable energy generation. Finally, two test systems are employed to demonstrate the feasibility and efficiency of the proposed method, as well as the potentials of the diversified storages and IDR scheme.
The emerging interconnected/integrated energy system makes energy storage methods more diversified and complicated, since the allocations of energy storage devices are impacted by various energy carriers. It is noteworthy that energy storage devices are easy to control but their performances are restricted by technical parameters such as capacities and charge/discharge rates. On the other hand, the DR resources at the side of users generally involve lower construction investment and operation costs, but their implementations are limited by the comfort requirements of customers. Further modeling of diversified storages and DRs will be focused on their complementation characteristics.
References
Gil M, Duenas P, Reneses J (2016) Electricity and natural gas interdependency: comparison of two methodologies for coupling large market models within the European regulatory framework. IEEE Trans Power Syst 31(1):361–369
Neyestani N, Yazdani-Damavandi M, Shafie-Khah M et al (2015) Stochastic modeling of multi-energy carriers dependencies in smart local networks with distributed energy resources. IEEE Trans Smart Grid 6(4):1748–1762
Zhang XP, Shahidehpour M, Alabdulwahab A et al (2015) Optimal expansion planning of energy hub with multiple energy infrastructures. IEEE Trans Smart Grid 6(5):2302–2311
Orehounig K, Evins R, Dorer V (2015) Integration of decentralized energy systems in neighborhoods using the energy hub approach. Appl Energy 154:277–289
Geidl M, Koeppel G, Favre-perrod P et al (2007) Energy hubs for the future. IEEE Power Energy Mag 5(1):24–30
Krause T, Andersson G, Frohlich K et al (2011) Multiple energy carriers: modeling of production, delivery, and consumption. Proc IEEE 99(1):15–27
Bozchalui MC, Hashmi SA, Hassen H et al (2012) Optimal operation of residential energy hubs in smart grids. IEEE Trans Smart Grid 3(4):1755–1766
Krause T, Kienzle F, Liu Y, et al (2011) Modeling interconnected national energy systems using an energy hub approach. In: Proceedings of the 2011 IEEE trondheim powertech conference, Trondheim, Norway, 19–23 Jun 2011, pp 1–7
Bahrami S, Safe F (2013) A financial approach to evaluate an optimized combined cooling, heat and power system. Energy Power Eng 5:352–362
Salimi M, Ghasemi H, Adelpour M et al (2015) Optimal planning of energy hubs in interconnected energy systems: a case study for natural gas and electricity. IET Gener Transm Dis 9(8):695–707
Geidl M, Andersson G (2007) Optimal power flow of multiple energy carriers. IEEE Trans Power Syst 22(1):145–155
Moeini-aghtaie M, Abbaspour A, Fotuhi-firuzabad M et al (2014) A decomposed solution to multiple energy carriers optimal power flow. IEEE Trans Power Syst 29(2):707–716
Mancarella P, Chicco G (2013) Real-time demand response from energy shifting in distributed multi-generation. IEEE Trans Smart Grid 4(4):1928–1938
Sheikhi A, Bahrami S, Ranjbar AM (2015) An autonomous demand response program for electricity and natural gas networks in smart energy hubs. Energy 89:490–499
Kienzle F, AhčIn P, Andersson G (2011) Valuing investments in multi-energy conversion, storage, and demand-side management systems under uncertainty. IEEE Trans Sustain Energy 2(2):194–202
Sheikhi A, Rayati M, Bahrami S et al (2015) Integrated demand side management game in smart energy hubs. IEEE Trans Smart Grid 6(2):675–683
Sheikhi A, Rayati M, Bahrami S et al (2015) A cloud computing framework on demand side management game in smart energy hubs. Int J Electr Power Energy Syst 64:1007–1016
Bahrami S, Sheikhi A (2016) From demand response in smart grid toward integrated demand response in smart energy hub. IEEE Trans Smart Grid 7(2):650–658
Kamyab F, Bahrami S (2016) Efficient operation of energy hubs in time-of-use and dynamic pricing electricity markets. Energy 106:343–355
Schiebahn S, Grube T, Robinius M et al (2015) Power to gas: technological overview, systems analysis and economic assessment for a case study in Germany. Int J Hydrog Energy 40(12):4285–4294
Clegg S, Mancarella P (2015) Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks. IEEE Trans Sustain Energy 6(4):1234–1244
Guandalini G, Campanari S, Romano MC (2015) Power-to-gas plants and gas turbines for improved wind energy dispatchability: energy and economic assessment. Appl Energy 147:117–130
Clegg S, Mancarella P (2016) Storing renewables in the gas network: modelling of power-to-gas seasonal storage flexibility in low-carbon power systems. IET Gener Transm Distrib 10(3):566–575
Huo D, Liu YH, Gu CH et al (2015) Optimal flow of energy-hub including heat pumps at residential level. In: Proceedings of the 2015 50th international universities power engineering conference, Stoke on Trent, UK, 1-4 Sept 2015, 1-5
Delille G, François B, Malarange G (2012) Dynamic frequency control support by energy storage to reduce the impact of wind and solar generation on isolated power system’s inertia. IEEE Trans Sustain Energy 3(4):931–939
Luo X, Wang JH, Dooner M et al (2014) Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl Energy 137:511–536
Shu Z, Jirutitijaroen P (2014) Optimal operation strategy of energy storage system for grid-connected wind power plants. IEEE Trans Sustain Energy 5(1):190–199
Ahcin P, šikić M (2010) Simulating demand response and energy storage in energy distribution systems. In: Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 Oct 2010, 1–7
Liu WJ, Wen FS, Xue YS (2017) Power-to-gas technology in energy systems: current status and prospects of potential operation strategies. J Mod Power Syst Clean Energy 5(3):439–450
Ni LN, Wen FS, Liu WJ et al (2017) Congestion management with demand response considering uncertainties of distributed generation outputs and market prices. J Mod Power Syst Clean Energy 5(1):66–78
Yao T (2014) Optimal scheduling based on real-time price in smart grid. Dissertation, Yanshan University, Yanshan, China
Chen LN, Suzuki H, Wachi T et al (2002) Components of nodal prices for electric power systems. IEEE Trans Power Syst 17(1):41–49
Wolf DD, Smeers Y (1999) The gas transmission problem solved by an extension of the simplex algorithm. Manag Sci 46(46):1454–1465
Munoz J, Jimenez-Redondo N, Perez-Ruiz J et al (2003) Natural gas network modeling for power systems reliability studies. In: Proceedings of the 2003 IEEE Bologna power tech conference, Bologna, Italy, 23–26 Jun 2003, 8 pp
Acknowledgments
This work is jointly supported by National Basic Research Program of China (973 Program) (No. 2013CB228202), National Natural Science Foundation of China (No. 51477151), and China Southern Power Gird (No. WYKJ00000027).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 7 September 2017
Appendix A
Appendix A
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
NI, L., LIU, W., WEN, F. et al. Optimal operation of electricity, natural gas and heat systems considering integrated demand responses and diversified storage devices. J. Mod. Power Syst. Clean Energy 6, 423–437 (2018). https://doi.org/10.1007/s40565-017-0360-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0360-6